Leveraging LD eigenvalue regression to improve the estimation of SNP heritability and confounding inflation

Summary

Heritability is a fundamental concept in genetic studies, measuring the genetic contribution to complex traits and bringing insights about disease mechanisms. The advance of high-throughput technologies has provided many resources for heritability estimation. Linkage disequilibrium (LD) score regression (LDSC) estimates both heritability and confounding biases, such as cryptic relatedness and population stratification, among single-nucleotide polymorphisms (SNPs) by using only summary statistics released from genome-wide association studies. However, only partial information in the LD matrix is utilized in LDSC, leading to loss in precision. In this study, we propose LD eigenvalue regression (LDER), an extension of LDSC, by making full use of the LD information. Compared to state-of-the-art heritability estimating methods, LDER provides more accurate estimates of SNP heritability and better distinguishes the inflation caused by polygenicity and confounding effects. We demonstrate the advantages of LDER both theoretically and with extensive simulations. We applied LDER to 814 complex traits from UK Biobank, and LDER identified 363 significantly heritable phenotypes, among which 97 were not identified by LDSC.

Introduction

In genetic studies, heritability is a fundamental quantity measuring the phenotypic variance explained by genetic components.^1,2 Heritability provides an upper bound of genetic risk-prediction performance³ and acts as a summarizing metric indicating the genetic architecture of complex traits.⁴ Accurate estimates of heritabilities help us better understand the degree to which the phenotype is influenced by measured genetic variants and thus provide insights about the genetic mechanisms of complex diseases.⁵ We can distinguish the heritability concept into the broad-sense heritability ($H^2$) and the narrow-sense heritability ($h^2$). The former accounts for the genetic variance explained by all genetic factors, including additive effects, dominance effects, and epistatic effects, whereas the latter chip-based heritability evaluates only the additive genetic effects and is our main focus in this study.

In the pre-genomic era, heritability estimation was mainly based on family/pedigree data with the linear mixed model (LMM).⁶ With the advance of high-throughput technologies, such as microarray/sequencing, we can accurately measure genotypes on millions of single-nucleotide polymorphisms (SNPs) for individuals with moderate cost. The advances have enabled thousands of genome-wide association studies (GWASs) exploring the genetic basis of various diseases, providing many resources for estimating heritability captured among SNPs. In recent years, a number of methods have been proposed to estimate heritability based on GWAS data, such as GCTA (genome-wide complex trait analysis),^7,8 BOLT-LMM (efficient large cohorts genome-wide Bayesian mixed-model association testing),⁹ FaST-LMM (factored spectrally transformed linear mixed models),¹⁰ and LDAK (LD-adjusted kinships).^11,12 These methods are based on individual-level genotype data and provide accurate estimates of heritability captured among SNPs, namely SNP heritability. However, the sample sizes of GWASs continue to grow, and individual-level-data-based methods are not as scalable to biobank projects that assay hundreds of thousands of individuals (e.g., UK Biobank, UKBB¹³) compared with summary-statistics-based methods.¹⁴ Due to computational and privacy issues, the summary-statistics-based methods become more attractive, as they require only publicly available GWAS summary statistics and the computational efficiency will not be influenced by the increasing sample sizes. The most widely used tool to estimate heritability based on summary statistics is linkage disequilibrium (LD) score regression (LDSC),¹⁵ which leverages LD between SNPs to estimate heritability.16, 17, 18 Extended from LDSC, SumHer relaxes the polygenic assumption and allows users to specify the heritability model.¹⁹ Despite the benefits of summary-statistics-based methods, such as decent data availability and increasing sample sizes, individual-level-data-based methods have more accurate estimates, as they are provided with more information from individual data. In this study, we focus on the summary-statistics-based methods and use the estimates of individual-level-data-based methods as the gold standard for the evaluation of different summary-statistics-based methods in real data analysis.

One challenge in analyzing GWAS summary statistics is to address the inflation attributed to confounding effects, such as cryptic relatedness and population stratification. The unadjusted confounding biases can generate spurious signals and lead to false positives in association mapping and upward bias of heritability.^20,21 In practice, genomic control is the most widely used method to address the inflation.22, 23, 24, 25 The intuition behind this method is that other than a small number of SNPs associated with the trait or disease, the test statistics for SNPs should follow the distribution under the null hypothesis. More specifically, the median χ² value over all SNPs should be around 0.455 under the null hypothesis. Inflation due to artificial confounding biases can be detected and corrected by comparing the median of test statistics with 0.455. Despite the simplicity of this approach, the rationale of genomic inflation factors relies on the assumption of sparsity, which is very likely violated due to the polygenic property of many diseases/traits.^26,27 In fact, polygenicity from underlying genetic architectures can also yield inflation in test statistics. Therefore, we need to distinguish the inflation attributed to polygenicity and confounding effects from the corrected inflation caused by the latter.

To date, LDSC is the most commonly used method to address the estimation of both heritability and confounding inflation. LDSC builds the model on the relationship between LD scores and the variance of the test statistics. The basic idea is that the SNPs in higher LD with other SNPs tend to have larger test statistics on average for a polygenic trait, because of more causal variants being tagged. Though LDSC is widely used, compared to individual-level-data-based methods, substantially larger standard errors (SEs), which influence accuracy and precision in the estimation of both heritability and confounding inflation factors, are observed.²⁸ One reason for the loss of precision is that LDSC utilizes the information of only a small part of the LD matrix.^28,29 To be more precise, only the diagonal elements of the squared LD matrix are utilized in LDSC. Some recent methods based on summary statistics utilize more complete LD information, such as HESS (heritability estimation from summary statistics), which estimates local SNP heritability,^14,26 and HDL (high-definition likelihood), which focuses on genetic correlation.²⁸

In this paper, we introduce LD eigenvalue regression (LDER), which extends the LDSC method and provides more accurate estimates of heritability and confounding inflation. The key difference between LDER and LDSC is that LDER makes full use of the information from the LD matrix. The regression equation of LDER is similar to LDSC, while LDER uses eigen-decomposition to diagonalize the LD matrix and aggregates the information onto the diagonal of the transformed LD matrix. Our method needs only GWAS summary statistics and consequently can be applied to large-scale datasets with high computational efficiency. Through simulations, we compared LDER with state-of-the-art estimation methods including LDSC, HESS, and HDL and found that LDER could provide more accurate estimates than all other methods, especially under small-sample-size scenarios. In addition, LDER achieves higher precision than LDSC. Real data applications on 10 common traits from UKBB also showed that the estimates of LDER are closer to the estimates of the individual-level-data-based method BOLT-LMM than other methods. We also applied LDER to 814 phenotypes from UKBB, including 221 continuous and 593 dichotomous traits,¹³ among which LDER identified 97 heritable phenotypes that were not significantly heritable in LDSC estimation.

Material and methods

LDER modeling

For a GWAS with n individuals and m SNPs, we first derive the marginal test statistics for each SNP based on linear regression for the quantitative traits and logistic regression for the dichotomous traits. We name the test statistic a Z score if its distribution is standard normal distribution under the null hypothesis. If the null distribution does not follow the standard normal distribution, the inverse cumulative distribution method (CDF) may be used for p values to obtain Z scores. We denote the underlying risk effects for all SNPs as $\mathit{\beta }$. The distribution of $\mathbf{z}$ conditioning on $\mathit{\beta }$ follows $N\left(\sqrt{n}\mathbf{R}\mathit{\beta },\lambda \mathbf{R}\right)$, where $\mathbf{R}$ is the LD matrix and λ is the inflation factor due to uncontrolled confounding effects.³⁰ Let $h_g^2$ denote the SNP heritability, under the polygenic model,⁷ $\mathit{\beta }\sim N\left(0,h_g^2/m\right)$. Then we have

$$\mathbb{E}\left(\mathbf{z}{\mathbf{z}}^T\right)=\mathbb{E}\left[\mathbb{E}\left(\mathbf{z}{\mathbf{z}}^T|\mathit{\beta }\right)\right]=\mathbb{E}\left[\text{Cov}\left(\mathbf{z}|\mathit{\beta }\right)+\mathbb{E}\left(\mathbf{z}|\mathit{\beta }\right)\mathbb{E}{\left(\mathbf{z}|\mathit{\beta }\right)}^T\right]=\mathbb{E}\left(\lambda \mathbf{R}+n\mathbf{R}\mathit{\beta }{\mathit{\beta }}^T\mathbf{R}\right)=\lambda \mathbf{R}+\frac{n{h}_g^2}{m}{\mathbf{R}}^2.$$ (Equation 1)

We denote the LD score for the i-th SNP as $l_i$, which is defined as $l_i={\sum }_{j=1}^m{R}_{ij}^2$. By considering the diagonal elements of Equation 1, we have $\mathbb{E}\left(z_i^2\right)=\lambda +n{h}_g^2{l}_i/m$, which is exactly the main equation used in the LDSC framework.¹⁵ However, this construction considers only the diagonal elements and leads to information loss. Therefore, we extend this model by leveraging the full information in Equation 1. We consider the eigen-decomposition $\mathbf{R}=\mathbf{U}\mathbf{D}{\mathbf{U}}^T$, where $\mathbf{U}$ and $\mathbf{D}$ are orthogonal and diagonal matrices, respectively. By defining $\tilde{\mathbf{z}}={\mathbf{D}}^{-0.5}{\mathbf{U}}^T\mathbf{z}$, we obtain:

$$\mathbb{E}\left(\tilde{\mathbf{z}}{\tilde{\mathbf{z}}}^T\right)=\mathbb{E}\left[\mathbb{E}\left(\tilde{\mathbf{z}}{\tilde{\mathbf{z}}}^T|\mathit{\beta }\right)\right]=\lambda \mathbf{I}+\frac{n{h}_g^2}{m}\mathbf{D}.$$ (Equation 2)

We note that the right-hand side of Equation 2 becomes a diagonal matrix, and thus for the i-th variant we have:

$$\mathbb{E}\left({\tilde{z}}_i^2\right)=\lambda +\frac{n{h}_g^2}{m}{D}_{ii}.$$ (Equation 3)

The formulation above has the same format to the regression equation of LDSC. Instead of regressing the square of Z scores on LD scores in LDSC, we regress the square of projected Z scores on LD eigenvalues. All information of the LD matrix inEquation 1 has been aggregated onto diagonal elements of Equation 2, and then used for the regression. We obtain the estimates of $h_g^2$ and λ by regressing ${\tilde{z}}_i^2$ on the eigenvalues $D_{ii}$. We further adopt a two-stage procedure in the estimation of heritability to reduce the variance (supplemental method 3.1). For both LDER and LDSC, we use a delete-block-jackknife procedure for estimating SEs.

For the dichotomous traits, we transform the observed-scale heritability to the liability-scale heritability, with $h_{liability}^2=h_{observed}^2\frac{K^2{\left(1-K\right)}^2}{\phi {\left({\text{Φ}}^{-1}\left(K\right)\right)}^{2}P\left(1-P\right)}$, where K is the frequency of the dichotomous trait in the population and P is the frequency of the dichotomous trait in the observed sample.³¹ The first denominator component $\phi {\left({\text{Φ}}^{-1}\left(K\right)\right)}^2$ is the squared probability density function evaluated at the K-percentile of the inverse CDF of the standard normal distribution.

Regression weights

Similar to LDSC, we account for heteroskedasticity in the regression weight. We weight by

$$1/{\left(1+n{h}_g^2{D}_{ii}/m\right)}^2,$$ (Equation 4)

the reciprocal of which is proportional to the variance of ${\tilde{z}}_i^2$ (supplemental method 3.2). To further ensure the robustness of the estimation, we impose a shrinkage weight, $\text{min}\left(D_{ii},1\right)$, to equations with small eigenvalues resulting from the rank-deficient LD matrix. Combining with Equation 4, the weights $w_i$ are constructed by:

$$w_i=\frac{\text{min}\left(D_{ii},1\right)}{{\left(1+n{h}_g^2{D}_{ii}/m\right)}^2}\propto \frac{\text{min}\left(D_{ii},1\right)}{\text{Var}\left({\tilde{z}}_i^2|\mathit{\beta }\right)}.$$ (Equation 5)

Simulation settings

We first conducted simulations based on generated GWAS summary statistics under varying genetic architectures. We fixed the number of genetic variants to $\mathrm{100,000}$. The simulated genetic architectures varied in three aspects: the sparsity of the causal SNPs, the heritability, and the confounding inflation. The effect sizes were simulated with a spike-and-slab distribution: ${\beta }_j\sim \left(1-\alpha \right){\delta }_0+\alpha N\left(0,\frac{h^2}{\alpha m}\right)$. The proportion of causal SNPs α varied between 0.005, 0.01, 0.05, and 0.1, and the heritability $h_g^2$ varied between 0.05, 0.1, 0.2, and 0.5. The inflation factor λ was set to 1 (with no confounding inflation) or 1.1 (with confounding inflation). Conditioning on the effect size $\mathit{\beta }$, the Z scores were simulated from $\mathbf{z}|\mathit{\beta }\sim N\left(\sqrt{n}\mathbf{R}\mathit{\beta },\lambda \mathbf{R}\right)$. We generated LD matrices $\mathbf{R}$ with block-wise autoregressive LD structures using the R package CorBin,³² where the correlation matrix ${\mathbf{R}}_l$ of the l-th LD block is

$${\mathbf{R}}_l=\left(\begin{array}{llll}1& {\rho }_l& \cdots & {\rho }_l^{m_l-1}\\ {\rho }_l& 1& \cdots & {\rho }_l^{m_l-2}\\ ⋮& ⋮& \ddots & ⋮\\ {\rho }_l^{m_l-1}& {\rho }_l^{m_l-2}& \cdots & 1\end{array}\right),$$ (Equation 6)

where m_l is the number of SNPs in the l-th LD block, and ${\rho }_l\sim$ Unif$[0.1,0.9]$. The correlations are higher for adjacent variants and decrease with the increase of the distance between the variants in each LD block, which mimic the real LD structures.³³ We equally divided simulated genomes into $\mathrm{1,000}$ LD blocks, which is in the same scale with the block number of the human genome partitioned by LDetect,³⁴ and the SNP number in each block was 100.

For the simulations based on real genotypes, we used genotypes from 276,050 independent UKBB European samples and extracted the HapMap 3 SNPs. We simulated effect sizes from the spike-and-slab distribution and fixed the heritability at 0.5. The sparsity of causal SNPs varied between 0.005 and 0.01. Then we generated continuous phenotypes with the additive model $\mathbf{y}=\mathbf{X}\mathit{\beta }+\mathrm{\epsilon }$, where $\mathbf{X}$ is the standardized genotype and the error term $\mathrm{\epsilon }$ satisfies the i.i.d. normal distribution, i.e., $\text{Var}\left(\mathrm{\epsilon }\right)=\left(1-h_g^2\right){\mathbf{I}}_n$. The summary statistics were computed using PLINK software.³⁵

Reference LD matrix construction

The in-sample LD matrix was estimated from 276,050 independent UKBB European samples. The external LD matrix was estimated from European samples of the 1000 Genomes Project (1000G) reference panel. There are 489 individuals and 9,997,231 SNPs in the 1000G after quality control. The SNPs from the 1000G dataset overlapped with the SNPs in the HapMap 3 dataset, and the GWAS summary data were included in the reference panel. In both cases, we employed a linear shrinkage method for the LD matrix estimation.^36,37 We partitioned the genome into $\mathrm{1,703}$ independent genomic blocks using LDetect,³⁴ based on the 1000G reference panel with European ancestry. The LD estimation, shrinkage, and eigen-decomposition were performed within each LD block.

UKBB GWAS summary statistics

The UKBB GWAS summary statistics were from the second round of results released in August 2018 by Neale’s group. They performed association studies on 361,194 individuals of White British ancestry and included with covariates including 20 principal components, and age, the square of age (age²), sex, the product of age and sex (age^∗sex), and age^2∗sex.

Quality control of the UKBB genotype data

We used phase 3 genotype data released by UKBB wherein the participants underwent genotyping with one of two closely related Affymetrix microarrays (UK BiLEVE Axiom Array or UKBB Axiom Array) for 820,000 variants. Additional genotypes were imputed centrally using the 1000G and Haplotype Reference Consortium (HRC) reference panels, yielding 93 million variants for each individual. We restricted the analysis to 404,892 autosomal variants also presented in the HapMap 3 dataset with a genotype-missing rate per marker $<0.01$, imputation quality score $>0.3$, Hardy-Weinberg p value $>1e-05$, and minor allele frequency $>0.05$.

Compared methods

We compared LDER with three state-of-the-art, summary-statistics-based heritability estimation methods, including LDSC,³⁸ HESS,²⁶ and HDL.²⁸ For LDER, LDSC, and HESS, we computed LD information from both UKBB genotypes and the 1000G reference panel. For HDL, we directly downloaded the pre-computed UKBB LD information of 336,000 British individuals in their website. By default, we let HDL automatically select the number of eigenvalues and eigenvectors used in the estimation.

Computational time

We compared the CPU time of LDER, LDSC, HESS, and HDL on the analysis of UKBB dataset. The LD preparation time was based on a subset of $\mathrm{10,000}$ individuals and $\mathrm{404,892}$ autosomal variants. The computation was performed with an Intel Xeon processor with 2.50 GHz and 48 cores. Among the four methods, LDER and HESS were performed with all 48 cores run in parallel. LDSC and HDL did not provide parallel computing capacity; thus we split the data into 22 chromosomes and ran the software on each chromosome in parallel.

Results

Method overview

Suppose there are n individuals and m SNPs in the GWAS data. For each SNP, we derive the marginal test statistics with linear regression for the quantitative traits and logistic regression for the dichotomous traits. The test statistic is referred to as a Z score if its distribution is standard normal distribution under the null hypothesis. Otherwise, we use the inverse function of CDF of standard normal distribution to get Z scores from p values. We assume the underlying risk effect for the m SNPs is $\mathit{\beta }$. In GWAS, we have $\mathbf{z}|\mathit{\beta }\sim N\left(\sqrt{n}\mathbf{R}\mathit{\beta },\lambda \mathbf{R}\right)$, where $\mathbf{R}$ is the LD matrix and λ is the inflation factor due to uncontrolled confounding effects.³⁰ A larger λ indicates a greater inflation, whereas $\lambda =1$ indicates inflation free. We denote the SNP heritability as $h_g^2$. Based on the polygenic model,⁷ we have $\mathit{\beta }\sim N\left(0,h_g^2/m\right)$ and

$$\mathbb{E}\left(\mathbf{z}{\mathbf{z}}^T\right)=\mathbb{E}\left[\mathbb{E}\left(\mathbf{z}{\mathbf{z}}^T|\mathit{\beta }\right)\right]=\lambda \mathbf{R}+\frac{n{h}_g^2}{m}{\mathbf{R}}^2.$$ (Equation 7)

Equation 7 reduces to LDSC if we only consider the diagonal elements of the matrices on both sides of the equation. However, utilizing only diagonal elements leads to information loss. Therefore, we first performed eigen-decomposition on the LD matrix, i.e., $\mathbf{R}=\mathbf{U}\mathbf{D}{\mathbf{U}}^T$, where $\mathbf{U}$ is an orthogonal matrix of eigenvectors and $\mathbf{D}$ is the diagonal eigenvalue matrix. By rotating the GWAS Z scores with $\tilde{\mathbf{z}}={\mathbf{D}}^{-0.5}{\mathbf{U}}^T\mathbf{z}$, we obtain

$$\mathbb{E}\left(\tilde{\mathbf{z}}{\tilde{\mathbf{z}}}^T\right)=\mathbb{E}\left[\mathbb{E}\left(\tilde{\mathbf{z}}{\tilde{\mathbf{z}}}^T|\mathit{\beta }\right)\right]=\lambda \mathbf{I}+\frac{n{h}_g^2}{m}\mathbf{D}.$$ (Equation 8)

This transformation aggregates all the information related to $h_g^2$ to the diagonal elements of Equation 8. For the i-th element in vector $\tilde{\mathbf{z}}$, we have

$$\mathbb{E}\left({\tilde{z}}_i^2\right)=\lambda +\frac{n{h}_g^2}{m}{D}_{ii},$$ (Equation 9)

where $D_{ii}$ is the i-th diagonal element of $\mathbf{D}$. Despite the similar formulation with LDSC, this expression uses full information of $h_g^2$ from the LD matrix $\mathbf{R}$. Similar to LDSC, we use the iterative reweighted least square to increase estimation efficiency (material and methods), which increases precision when the sample sizes are large (Figure S1). As the dimension of genotype matrices is usually high, we partition the genome into independent genomic blocks with LDetect³⁴ and perform eigen-decomposition in each block. We also employ a linear shrinkage method to the estimation of the LD matrix $\mathbf{R}$ to ensure the robustness of our algorithm accommodating different reference panels (material and methods).

Simulation based on generated summary statistics

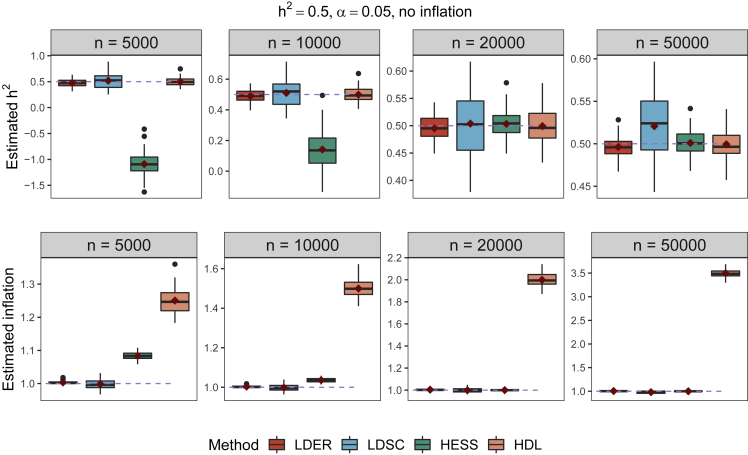
We first simulated GWAS summary statistics of 100,000 genetic variants to investigate the performance of LDER and other comparable methods including LDSC, HESS, and HDL under different genetic architectures. The simulated genetic architectures varied in three aspects: the sparsity of the causal SNPs, the heritability, and the confounding inflation factor (material and methods). We used true LD information as the input to all the methods. Simulation experiments were repeated 50 times. Figure 1 and Figure S2 show the heritability and inflation factor estimated by LDER and the three other methods. The accuracies of estimated heritabilities for all methods increased with increased sample sizes. LDER achieved higher accuracy with smaller standard deviations (SDs) in estimating heritability compared with LDSC and HESS. When the sample size was small (i.e., n = 5,000 and 10,000), the superiority of LDER was more significant, while the heritability estimator of HESS had downward bias. Despite the comparable estimates of heritability between LDER and HDL, HDL had severe upward bias in estimating inflation factors. Although the SDs of the inflation factor estimation increased with the sample sizes (see supplemental method 3.3), LDER retained high estimation accuracy. We note that the two-stage estimation procedure led to an underestimate of inflation factor by LDSC, as SNPs with test statistics larger than a certain threshold ($z_i^2>30$ in LDSC as default) were not included in the first step estimating the inflation factor.¹⁵ We further provide a comparison between LDER and LDSC without the two-stage procedure, and LDER still achieved more accurate and precise estimates than LDSC (Figure S3).

Figure 1.

Comparisons between LDER, LDSC, HESS, and HDL on the estimation of heritability and confounding inflation based on simulated GWAS summary statistics with varying sample sizes

The number of SNPs was fixed at 100,000. The proportion of causal SNPs was 5%. The effect sizes were sampled from a spike-and-slab distribution with heritability 0.5 and no confounding effects. The simulations were repeated 50 times. Dashed lines represent the true value. Diamonds indicate means in boxplots. The colors of the boxes differentiate the estimation methods.

Simulations based on real genotypes

We then analyzed simulated GWAS data with real genotypes from 276,050 independent UKBB European samples (material and methods). We simulated effect sizes from the spike-and-slab distribution mentioned above. The simulated phenotypes were generated by the sum of all genetic markers weighted by the simulated effect sizes and added by a normally distributed error term fixing the heritability at 0.5. The sparsity of causal SNPs varied from 0.005 to 0.01. We evaluated the estimation accuracy by the root-mean-square error (RMSE) and the precision, which was measured by the inverse of the SDs. Table 1 and Table S1 show that LDER still achieved higher accuracy with smaller RMSE and higher precision than LDSC under scenarios with different sample sizes. Among the four methods, HESS achieved the highest precision when the sample size was 5,000, but its RMSE was larger than LDER. We also notice that HDL severely underestimated the heritability. This may be because the UKBB LD reference panel provided by HDL (either 1,029,876 QCed UKBB imputed HapMap 3 SNPs or 307,519 QCed UKBB Axiom Array SNPs) contains SNPs that were not in the data we analyzed (∼50%), and significant deterioration of performance when there are different numbers of SNPs in GWAS and in the reference panel was reported.^28,39 Results in Table 1 and Table S1 demonstrate the robustness of LDER to the external LD by estimating the LD matrix with the 1000G reference panel. Despite that the accuracy and precision for all methods were influenced by external LD reference, LDER still showed the smallest or comparable RMSE among all methods. We also compared the one- and two-stage procedures for LDER and LDSC. The two-stage estimates yielded smaller RMSE and higher or comparable precision compared with the one-stage estimates for LDER and for LDSC with large sample sizes (Table S2).

Table 1.

Precision and accuracy of the heritability estimates with LDER, LDSC, HESS, and HDL

	Precision (1/SD)				RMSE
	LDER	LDSC	HESS	HDL	LDER	LDSC	HESS	HDL
n	Performance with in-sample LD estimated by UKBB European samples
5,000	17.82	12.51	20.72a	N/A	0.073a	0.095	0.082	0.461
10,000	23.53a	17.82	21.71	N/A	0.034a	0.053	0.076	0.500
20,000	40.18a	31.14	33.14	N/A	0.030a	0.041	0.035	0.499
50,000	73.79	53.77	54.87	154.68a	0.016a	0.022	0.169	0.461
n	Performance with external LD estimated by 1000 Genomes Project European samples
5,000	14.07	12.28	21.21a	–	0.077a	0.102	0.152	–
10,000	20.05	17.32	20.60a	–	0.047a	0.056	0.060	–
20,000	33.60a	30.84	27.99	–	0.032a	0.045	0.060	–
50,000	64.16a	53.84	56.47	–	0.017a	0.025	0.114	–

Simulations were based on UKBB genotypes and repeated 50 times. Heritability was fixed at 0.5, and the proportion of causal SNPs was 1%. N/A indicates the estimates are too close to zero, yielding infinite 1/SD.

^aHighest precision and smallest RMSEs

We also simulated a more realistic scenario with both polygenicity and confounding inflation. We used the UKBB genotype data and simulated polygenic phenotypes by drawing causal SNPs only from the chromosomes of odd numbers. All SNPs on chromosomes of even numbers were not causal. This strategy also avoids the influence of LD. We further included the environmental stratification component aligned with the first principal component of the genotype data. The mean χ² statistics in even chromosomes (with no causal SNPs) was regarded as the contribution of population stratification. In all simulation settings with sample sizes varying from 5,000 to 50,000, both LDER and LDSC accurately estimate the confounding inflation factors (Table S3).

Real data applications on UKBB phenotypes

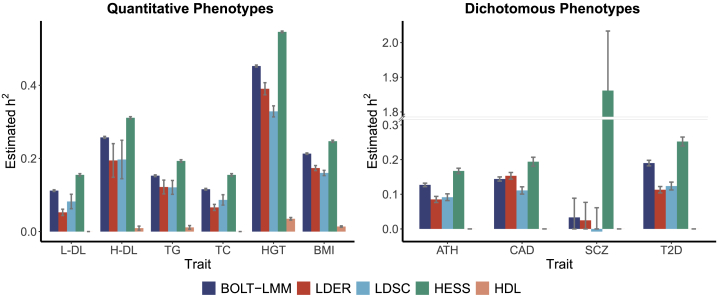
For better calibration and demonstration of the superiority of LDER, we performed analysis on 10 common UKBB traits with BOLT-LMM, which is an individual-level-data-based method known to provide more accurate estimates than LDSC³⁹ (Figure 2). Among the 10 common traits, low-density lipoprotein (L-DL), high-density lipoprotein (H-DL), triglyceride (TG), total cholesterol (TC), height (HGT), and body mass index (BMI) are quantitative phenotypes; asthma (ATH), coronary artery disease (CAD), schizophrenia (SCZ), and type 2 diabetes (T2D) are dichotomous phenotypes. We treated estimates from BOLT-LMM as the true values of the heritability and calculated the RMSE of LDER, LDSC, HESS, and HDL. The precision was measured by the reciprocal of the SEs reported by each method. In particular, the SE of LDER was estimated through block-jackknife (material and methods). In general, LDER and LDSC provided estimates lower than BOLT-LMM, while HESS derived estimates higher than BOLT-LMM. HDL had estimates of heritability close to zero, which was similar to the results in simulations with real genotypes. LDER still showed the most accurate estimation compared with the other methods, with the smallest RMSE (Figure 2 and Table S4). HESS provided estimates with the highest precision.

Figure 2.

Comparisons between the estimated heritability by BOLT-LMM and that by LDER, LDSC, HESS, and HDL on six quantitative phenotypes and four dichotomous phenotypes in the UKBB

Error bars indicate SEs of the estimates, which were derived from a delete-block-jackknife procedure for LDER.

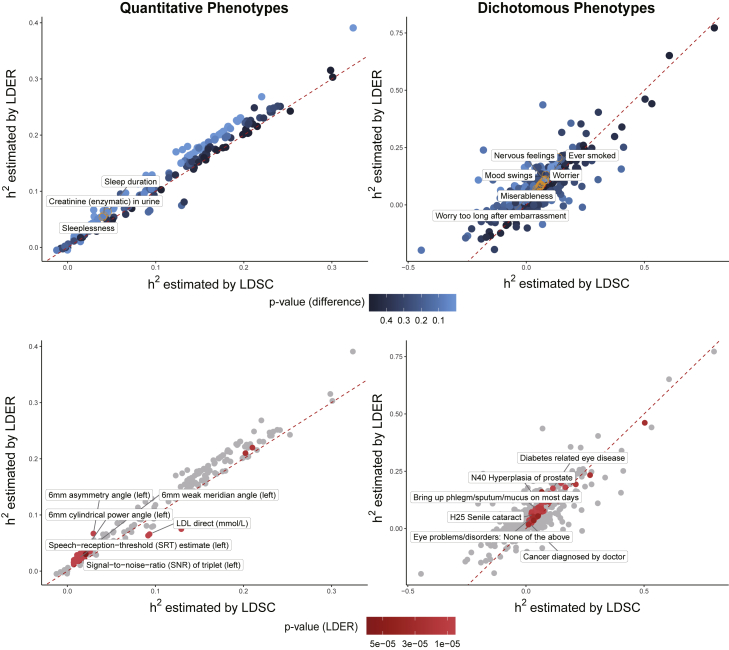
We applied LDER and LDSC to summary statistics of 814 complex traits, including 221 quantitative phenotypes and 593 dichotomous phenotypes (material and methods). On average, LDER yielded smaller SE than LDSC on both quantitative and dichotomous traits (Figure 3). After Bonferroni correction, LDER identified 363 significantly heritable phenotypes, among which 97 were not identified by LDSC (Table S5), such as ventral hernia (LDER p value = 6.1e−06) and non-insulin-dependent diabetes mellitus (LDER p value = 3.4e−05). We found the estimates of heritability by LDER and LDSC were significantly different for 20 phenotypes (p value < 0.05 after Bonferroni correction; see Table 2). A numerical comparison between the estimates of LDER and LDSC on the UKBB traits is provided in Tables S6 and S7.

Figure 3.

Heritability estimates with LDER and LDSC among 221 quantitative phenotypes and 593 dichotomous phenotypes in the UKBB

The color of the blue points indicates the significance level (p value) testing the difference of the estimates using two methods. The orange points highlight phenotypes with significantly different heritability estimates between LDER and LDSC (the upper panels). The red points highlight significantly heritable phenotypes (with Bonferroni correction) estimated by LDER but not identified by LDSC (the lower panels). For clearer visualization, the six smallest p values for heritability estimation are shown with labels for both quantitative and dichotomous phenotypes. The red dashed line indicates conditions where the heritability estimated by LDER and LDSC is equal. The estimated heritability for dichotomous phenotypes has been transformed to liability scale.

Table 2.

Estimates of SNP heritability on UKBB traits that are significantly different using LDER and LDSC

UKBB ID	Phenotype	Variable type	$h_{LDER}^2$	$h_{LDSC}^2$	p value (different)
1210	snoring	binary	0.086 (0.003)	0.058 (0.004)	2.8e−09
1920	mood swings	binary	0.097 (0.003)	0.067 (0.004)	1.6e−09
1930	miserableness	binary	0.087 (0.003)	0.062 (0.004)	3.1e−07
1950	sensitivity/hurt feelings	binary	0.083 (0.003)	0.057 (0.004)	5.7e−09
1970	nervous feelings	binary	0.108 (0.003)	0.077 (0.005)	6.2e−08
1980	worrier	binary	0.104 (0.003)	0.075 (0.004)	3.8e−08
2000	worry too long after embarrassment	binary	0.088 (0.003)	0.061 (0.004)	5.7e−10
2010	suffer from “nerves”	binary	0.071 (0.003)	0.052 (0.004)	3.2e−05
2020	loneliness, isolation	binary	0.070 (0.003)	0.044 (0.004)	2.9e−08
2030	guilty feelings	binary	0.076 (0.003)	0.054 (0.004)	6.8e−07
2040	risk taking	binary	0.085 (0.003)	0.064 (0.004)	6.6e−06
2188	long-standing illness, disability, or infirmity	binary	0.080 (0.003)	0.058 (0.004)	5.7e−07
2443	diabetes diagnosed by doctor	binary	0.207 (0.012)	0.136 (0.011)	8.4e−06
20160	ever smoked	binary	0.106 (0.003)	0.077 (0.004)	1.3e−08
6149$\_$100	mouth/teeth dental problems: none of the above	binary	0.053 (0.002)	0.038 (0.003)	1.0e−05
6149$\_$6	mouth/teeth dental problems: dentures	binary	0.110 (0.004)	0.080 (0.005)	7.3e−07
6150$\_$2	vascular/heart problems diagnosed by doctor: angina	binary	0.131 (0.008)	0.083 (0.010)	5.1e−05
30510$\_$irnt	creatinine (enzymatic) in urine	continuous$\_$irnt	0.057 (0.002)	0.041 (0.002)	3.2e−08
1160	sleep duration	ordinal	0.063 (0.002)	0.046 (0.002)	6.9e−09
1200	sleeplessness/insomnia	ordinal	0.054 (0.002)	0.040 (0.002)	3.3e−07

The estimates of heritability of binary traits have been transformed to liability scale.

Computational efficiency

Table S8 shows the computation time of LDER, LDSC, HESS, and HDL. We divided the total computational time into LD preparation and heritability estimation. HESS and LDER are more efficient in LD preparation compared with the other two methods. As for the estimation procedure, LDER and HDL take more time in estimating SEs using a jackknife procedure. We also note that although HESS is most efficient in the estimation step compared with other methods, it is necessary for HESS software to recalculate LD information when it is applied to a new trait. In contrast, LDER, LDSC, and HDL can be applied to the pre-computed LD information and can be efficient when estimation on multiple traits is required.

Discussion

In this article, we propose LDER, a summary-statistics-based method improving the accuracy and precision of estimation of SNP heritability and confounding inflation. As an extension of LDSC, LDER provides more accurate and precise estimates in both simulations and real data applications. The superiority of LDER can be attributed to the fact that it captures more information on the relationship between LD matrix and test statistics, whereas LDSC uses only partial information from the LD matrix. To be more precise, LDSC only utilizes the diagonal elements of the squared LD matrix.

To ensure the robustness of our algorithm accommodating reference panels from different sources, we employ a linear shrinkage method to the estimation of the LD matrices, which is computationally efficient and built in with our software. In addition, as the dimension of genotype matrices is usually high, estimating and shrinking the LD matrix and performing the eigen-decomposition can be time consuming. In practice, we partition the genome into independent genomic blocks with respect to ethnicity using LDetect³⁴ and perform eigen-decomposition for each LD block.

We provide the pre-computed eigen-decomposition information for 276,050 independent samples of European ancestry from UKBB and 489 samples of European ancestry from 1000G. Although the limited sample size and the potential mismatch between the target population and the LD reference panel may threaten the superiority of LDER, LDER remains robust with respect to the external LD reference and superior to LDSC.

For future directions, it would be advantageous to jointly model multiple complex traits to better estimate their genetic correlation, which quantifies the genetic similarity between complex traits. Summary-statistics-based methods for genetic correlation analysis enable study of a wide spectrum of complex human diseases, as the studied phenotypes do not need to be collected from the same individuals. It has also been revealed that SNPs in different functional categories (such as promoters, enhancers, etc.) provide disproportionate contributions to the disease heritability. Therefore, it is also of interest to derive the partitioned heritability within our framework to analyze multiple cell-type-specific functional categories.

Published: April 13, 2022

Data and code availability

LDER software (R package) and analysis scripts are available at https://github.com/shuangsong0110/LDER.

Web resources

1000 Genomes, http://www.1000genomes.org

HDL, https://github.com/zhenin/HDL

HESS, https://huwenboshi.github.io/hess-0.5/local_hsqg/

LDetect, https://bitbucket.org/nygcresearch/ldetect-data/src/master/

LDSC, https://github.com/bulik/ldsc/wiki

Neale Lab UK Biobank GWAS summary statistics, http://www.nealelab.is/uk-biobank/

PLINK software, https://zzz.bwh.harvard.edu/plink/profile.shtml

UK Biobank Resource, https://www.ukbiobank.ac.uk/

Supplemental information

Table S5. The 97 UKBB traits with significantly different heritability estimates (after Bonferroni correction) between LDER and LDSC

The SEs in brackets were estimated with block-jackknife. Heritability estimates of binary traits have been transformed to liability scale.

Table S6. A numerical comparison between the estimates of heritability and confounding inflation by LDER and LDSC on 221 UKBB quantitative traits

SEs in brackets were estimated with block-jackknife.

Table S7. A numerical comparison between the estimates of heritability and confounding inflation by LDER and LDSC on 593 UKBB dichotomous traits

The estimated heritability has been transformed to liability scale. SEs in brackets were estimated with block-jackknife.