Stabilizing deep tomographic reconstruction: Part A. Hybrid framework and experimental results

Summary

A recent PNAS paper reveals that several popular deep reconstruction networks are unstable. Specifically, three kinds of instabilities were reported: (1) strong image artefacts from tiny perturbations, (2) small features missed in a deeply reconstructed image, and (3) decreased imaging performance with increased input data. Here, we propose an analytic compressed iterative deep (ACID) framework to address this challenge. ACID synergizes a deep network trained on big data, kernel awareness from compressed sensing (CS)-inspired processing, and iterative refinement to minimize the data residual relative to real measurement. Our study demonstrates that the ACID reconstruction is accurate, is stable, and sheds light on the converging mechanism of the ACID iteration under a bounded relative error norm assumption. ACID not only stabilizes an unstable deep reconstruction network but also is resilient against adversarial attacks to the whole ACID workflow, being superior to classic sparsity-regularized reconstruction and eliminating the three kinds of instabilities.

Highlights

• •Deep reconstruction solution to the instabilities identified by a recent PNAS paper
• •Analytic compressed iterative deep (ACID) method is for hybrid reconstruction
• •ACID framework combines benefits from deep learning and compressed sensing
• •ACID is accurate and stable, superior to sparsity-regularized reconstruction alone

The bigger picture

Tomographic image reconstruction with deep learning has been a rapidly emerging field since 2016. Recently, a PNAS paper revealed that several well-known deep reconstruction networks are unstable for computed tomography (CT) and magnetic resonance imaging (MRI), and, in contrast, compressed sensing (CS)-inspired reconstruction methods are stable because of their theoretically proven property known as “kernel awareness.” Therefore, for deep reconstruction to realize its full potential and become a mainstream approach for tomographic imaging, it is critically important to stabilize deep reconstruction networks. Here, we propose an analytic compressed iterative deep (ACID) framework to synergize deep learning and compressed sensing through iterative refinement. We anticipate that this integrative model-based data-driven approach will promote the development and translation of deep tomographic image reconstruction networks.

We propose an analytic compressed iterative deep (ACID) framework for accurate yet stable deep reconstruction. ACID synergizes a deep reconstruction network trained on big data, kernel awareness from compressed sensing-inspired processing, and iterative refinement to minimize the data residual relative to real measurement. We anticipate that this integrative model-based data-driven approach will promote the development and translation of deep tomographic image reconstruction networks.

Introduction

Medical imaging plays an integral role in modern medicine and has grown rapidly over the past few decades. In the United States, there are more than 80 million computed tomography (CT) scans and 40 million magnetic resonance imaging (MRI) scans performed yearly.^1,2 In a survey on medical innovations, it was reported that “the most important innovation by a considerable margin is magnetic resonance imaging (MRI) and computed tomography (CT).”³ Over the past several years, deep learning has attracted major attention in medical imaging. Since 2016, deep learning has been gradually adopted for tomographic imaging, known as deep tomographic imaging.4, 5, 6, 7, 8, 9 Traditionally, tomographic reconstruction algorithms are either analytic (i.e., closed-form formulation) or iterative (i.e., based on statistical and/or sparsity models). Very recently with deep tomographic imaging, reconstruction algorithms have used deep neural networks (i.e., data driven).10, 11, 12 This new type of reconstruction algorithm has generated tremendous excitement and promising results in many studies. Some examples are included in the recent review articles by Wang et al. and Chen et al.^13,14

While many researchers are devoted to catching this new wave of tomographic imaging research, there are concerns about deep tomographic reconstruction, with the landmark paper¹⁵ by Antun et al. as the primary example. Specifically, Antun et al. performed a systematic study¹⁵ to reveal the instabilities of a number of representative deep tomographic reconstruction networks, including AUTOMAP.¹⁶ Their study demonstrates three kinds of network-based reconstruction vulnerabilities: (1) tiny perturbations on the input generating strong image artefacts (potentially, false positivity); (2) small structural features going undetected (false negativity); and (3) increased input data leading to decreased imaging performance. These critical findings are warnings and at the same time opportunities of deep tomographic imaging research. Importantly, the study by Antun et al.¹⁵ found that small structural changes (e.g., a small tumor) may not always be captured in the images reconstructed by the deep neural networks, but standard sparsity-regularized methods can capture these pathologies. It is worth noting that the issue of missing pathologies was one of the main concerns raised by radiologists in the fastMRI challenge in 2019.¹⁷

Historically, a debate, challenge, or crisis typically inspired theoretical and methodological development. In the context of tomographic imaging, there are several such examples. In the earliest days of CT reconstruction, analytic reconstruction received a critique that given a finite number of projections, tomographic reconstruction is not uniquely determined, meaning that ghost structures can be reconstructed, which do not exist in reality but are consistent with the measured data.¹⁸ Then, this problem was solved by regularization, such as enforcing the band limitedness of the underlying signals.¹⁹ Iterative reconstruction algorithms were initially criticized that image reconstruction was strongly influenced by penalty terms; in other words, what you reconstruct could be what you want to see. After selecting regularization terms and fine-tuning hyperparameters, these shortcomings were addressed. Hence, such algorithms have been made into clinical applications.^20,21 As far as compressed sensing (CS) is concerned, the validity of this theory is based on restricted isometry or robust null space properties.^22,23 The correct sparse solution will most likely be obtained under the assumed properties. However, these restricted isometry properties may not always be valid or verified in various applications such as few-view CT and fastMRI. In these cases, heuristically designed sampling patterns and empirically adjusted sampling parameters are often used to approximate an ideal random matrix-based data acquisition scheme so that a collected dataset is sufficiently informative.²⁴ In practice, encouraging results were widely reported in these relaxed applications of CS theory. Nevertheless, the sparsity constraint could be either too strong and smear features or too weak and result in artefacts. For example, a tumor-like structure could be introduced, and pathological vessels may be filtered out if the total variation is overly minimized, as demonstrated in purposely designed numerical examples.²⁵ Despite the limitations, multiple sparsity-promoting reconstruction algorithms are used on commercial scanners, with excellent overall performance.

The emerging deep tomographic imaging methods encounter challenges, as reported by Antun et al.¹⁵ In addition to extensive experimental data showing the instabilities of several deep reconstruction networks, Gottschling et al. pointed out that these instabilities are fundamentally associated with the lack of kernel awareness²⁶ and are “nontrivial to overcome.”¹⁵ However, their experiments show that CS-inspired reconstruction algorithms worked stably, while their selected deep reconstruction network failed under the same conditions,¹⁵ since CS-based algorithms use sparse regularization that has “at its heart a notion of kernel awareness.”²⁶

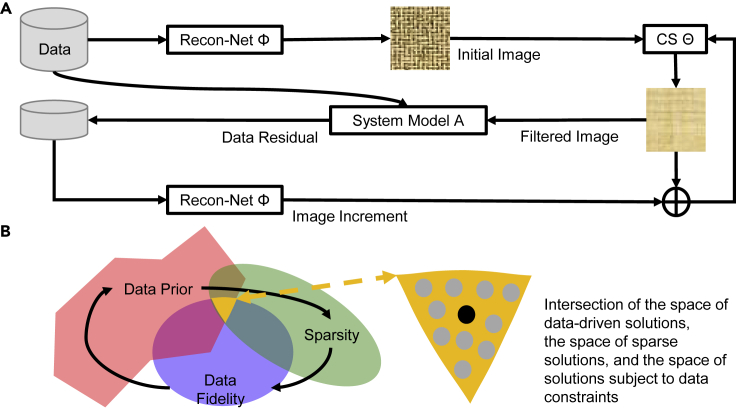
This article focuses on the feasibility and principles of accurate and stable deep tomographic reconstruction, demonstrating that deep reconstruction networks can be stabilized in a hybrid model with a CS module embedded and are superior to CS-based reconstruction alone. Specifically, to overcome the instabilities of the deep reconstruction networks, here, we propose an analytic compressed iterative deep (ACID) framework illustrated in Figure 1A. Given deep reconstruction network $\text{Φ}$ and measurement data ${\mathit{p}}^{\left(0\right)}$, an image can be, first, reconstructed, but it may miss fine details and introduce artefacts. Second, a CS-inspired module $\text{Θ}$ enforces sparsity in the image domain,²⁷ with a loss function covering both data fidelity and sparsity (e.g., total variation,²⁸ low-rank,²⁹ dictionary learning³⁰). Third, the forward imaging model projects the current image to synthesize tomographic data, which is generally different from the original data ${\mathit{p}}^{\left(0\right)}$. The discrepancy is called a data residual that cannot be explained by the current image. From this data residual, an incremental image is reconstructed with the deep reconstruction network $\text{Φ}$ and used to modify the current image aided by the sparsity-promoting CS module $\text{Θ}$. This process can be repeated to prevent losing or falsifying features. As a meta-iterative scheme, the ACID reconstruction process cycles through these modules repeatedly. As a result, ACID finds a desirable solution in the intersection of the space of data-driven solutions, the space of sparse solutions, and the space of solutions subject to data constraints, as shown in Figure 1B. Because this integrative reconstruction scheme is uniquely empowered with data-driven prior, ACID would give a better solution than the classic sparsity-regularized reconstruction alone; for details, see the method details section.

Figure 1.

ACID architecture for stabilizing deep tomographic image reconstruction

(A) Initially, the measurement data are reconstructed by the reconstruction network $\text{Φ.}$ The current image is sparsified by the CS-inspired sparsity-promoting module $\text{Θ}$ (briefly, the CS module). Tomographic data are then synthesized based on the sparsified image according to the system model $\mathit{A}$, and compared to the measurement data to find a data residual. The residual data are processed by the modules $\text{Φ}$ and $\text{Θ}$ to update the current image. This process is repeated until a satisfactory image is obtained.

(B) Illustration of the solution space.

An important question is whether the ACID iteration will converge to a desirable solution in the above-described intersection of the three spaces (Figure 1B). The answer to this question is far from trivial. A deep learning network represents a non-convex optimization problem, which remains a huge open problem (see more details in the review by Danilova et al.³¹). The non-convex optimization problem in a general setting is of non-deterministic polynomial-time hardness (NP hardness). To solve this problem with guaranteed convergence, practical assumptions must be made in almost all of the cases. These assumptions include changing a non-convex formulation into a convex formulation under certain conditions, leveraging a problem-specific structure, and seeking only a local optimal solution. Specifically, the Lipschitz continuity is a common condition used to facilitate performing non-convex optimization tasks.^32,33

Given the theoretically immature status of the non-convex optimization, to understand our heuristically designed ACID system in terms of its convergence, we assume that a well-designed and well-trained deep reconstruction network satisfies our proposed bounded relative error norm (BREN) property, which is a special case of the Lipschitz continuity as detailed in part B, the theoretical part³⁴ of our current papers. Based on the BREN property, the converging mechanism of the ACID iteration is revealed in our two independent analyses.³⁴

Here, we outline the key insight into the convergence of the ACID workflow. In reference to Figure 1, we assume the BREN property of a deep reconstruction network Φ, as characterized by the ratio being less than 1 between the norm of the reconstruction error and the norm of the corresponding ground truth (assuming a nonzero norm without the loss of generality); that is, the error component of the initial image reconstructed by the deep network Φ is less than the ground truth image in the L₂ norm. This error consists of both sparse and non-sparse components. The non-sparse component is effectively suppressed by the CS module Θ. The sparse errors are either observable or unobservable. The unobservable error is in the null space of the system matrix A and should be small relative to the ground truth image given the BREN property (the deep reconstruction network will effectively recover the null space component if it is properly designed and well trained). ACID can eliminate the observable error iteratively, owing to the BREN property. Specifically, the output of the module Θ is re-projected by the system matrix A, and then the synthesized data are compared with the measured data. The difference is called the data residual due to the observable error component. To suppress this error component, we use the network $\text{Φ}$ to reconstruct an incremental image and add it to the current image, and then refine the updated image with the CS module Θ. In this correction step, the desirable incremental image is the new ground truth image, and the BREN property remains valid as this step is a contraction mapping. In other words, the associated new observable error is less than the previous observable error, by the BREN property of the deep reconstruction network Φ. Repeating this process leads to the observable error diminishing exponentially fast (the BREN ratio less than 1). In doing so, the ACID solution will simultaneously incorporate data-driven knowledge, image sparsity preference, and measurement data consistency.

Note that, in a recent paper,³⁵ a two-step deep learning strategy was analyzed for tomographic imaging, in which a classical method was followed by a deep-network-based refinement to “close the gap between practice and theory” for that particular reconstruction workflow. The key idea is to use the null space network for data-driven regularization, achieving convergence based on the Lipschitz smoothness. We emphasize here that our analysis on the convergence of ACID is in a similar spirit.³⁴

Results

Given the importance of the recent study on the instabilities of some representative deep reconstruction networks,¹⁵ the main motivation of our work is to stabilize deep tomographic reconstruction. Hence, our experimental setup systematically mirrored what was described by Antun et al.,¹⁵ including datasets and their naming conventions, selected reconstruction networks, CS-based minimization benchmarks, and image quality metrics. As a result, the Ell-50 and DAGAN networks were chosen for CT and MRI reconstructions, respectively (details in the method details section and supplemental information). Both of those CT and MRI networks were subjected to the instabilities reported by Antun et al.¹⁵ In addition to the system-level comparison, we performed an ablation study on the ACID workflow and investigated its own stability against adversarial attacks. For details about adversarial attacks, see Antun et al.¹⁵ and our other paper.³⁴ The full descriptions of the original simulated cases of C1–C7, M1–M12 and A1–A4 are in the supplemental information, part I.

Stability with small structural changes

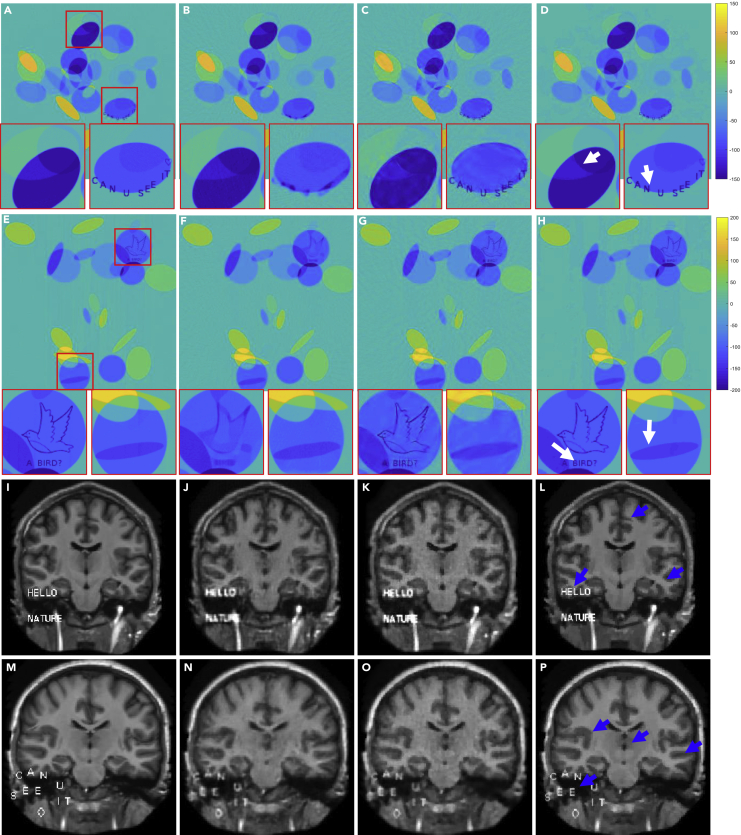
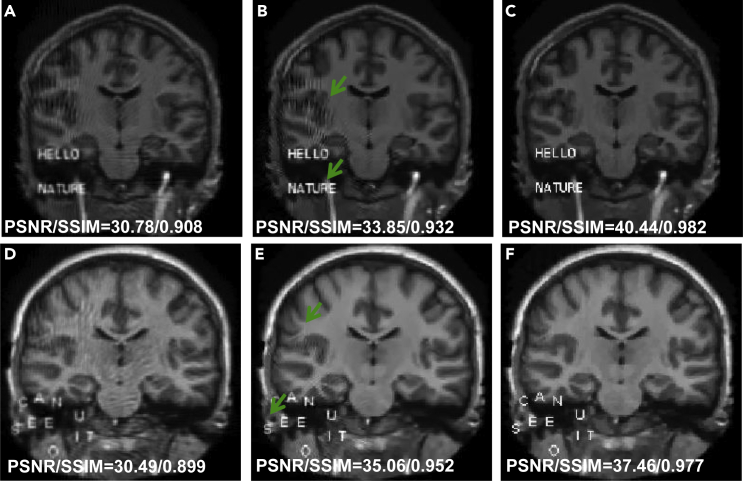
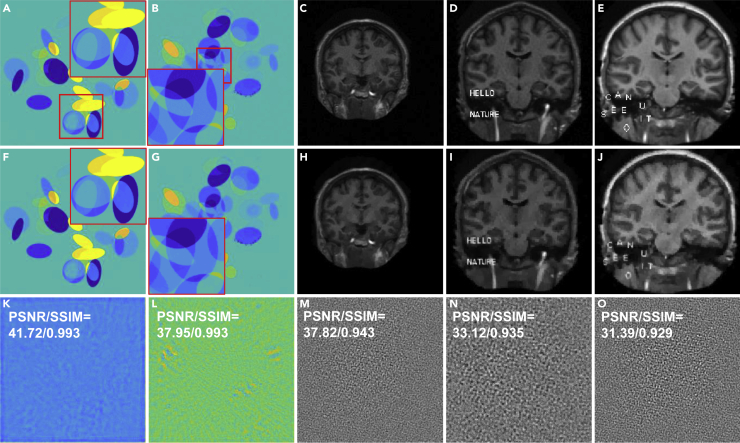
We demonstrated the performance of the ACID network with small structural changes. The Ell-50 network was used as a special FBPConvNet.³⁶ Figure 2 shows representative results in two simulated CT cases: C1 and C2 (the details can be found in the supplemental information, part I). To examine the degrees of small image structure recovery allowed by all of the reconstruction methods, some text, the contour of a bird, and their mixture were used to simulate structural changes in CT images. It is observed in Figures 2A–2H that the proposed ACID network provided a superior performance owing to the synergistic fusion of deep learning, CS-based sparsification, and iterative refinement. In this case, Ell-50 served as the deep network in the ACID workflow.

Figure 2.

Performance of ACID with small structural changes in the simulated CT and MRI cases, respectively

Four phantoms with structural changes are reconstructed by ACID and competing techniques.

(A) The original image of CT case C1 with 2 magnified regions-of-interest (ROIs).

(B–D) Ell-50, CS-inspired, and ACID results, respectively, from (A).

(E –H) Counterparts of C2. Each CT dataset contains 50 projections. The image structures marked by white arrows show the advantages of our ACID in terms of CT imaging.

(I) The original image of MRI case M1.

(J –L) The DAGAN, CS-inspired, and ACID results, respectively, from M1.

(M–P) Counterparts of M2. The subsampling rate of MRI is 10%. The display windows for C1, C2, M1, and M2 are [−150 150]HU, [−200 200]HU, [0 0.7], and [0 1], respectively. The blue arrows demonstrate that our ACID provides much clearer image edges as well as finer structures. The difference images are provided in supplemental information, part III.B.

It can be seen in Figures 2A–2H that CS-inspired reconstructions produced better results than the Ell-50 network. This is consistent with the results reported by Antun et al.¹⁵ The CS-based reconstruction approach retained the structural changes. The text and bird were still identifiable in the CS-inspired reconstruction but became unclear in the Ell-50 results. In contrast, the text “CAN U SEE IT” and bird were well recovered using our ACID network. While the contour of the bird was compromised in the CS reconstruction, ACID produced better image quality than the CS method.³⁷ In terms of edge preservation, the Ell-50 reconstruction gave better sharpness overall than the corresponding CS reconstruction. Furthermore, ACID corrected the structural distortions seen in the Ell-50 and CS results. A similar study was performed on MRI with small structural changes, as shown in Figures 2I–2P. Since DAGAN³⁸ was used as a representative network by Antun et al.,¹⁵ we implemented it for this experiment. The text was added to brain MRI slices (M1 and M2 cases; more details in supplemental information, part I). Figures 2I–2L show the M1 results reconstructed from data subsampled at a rate of 10%. It is difficult to recognize the phrase “HELLO NATURE” in the DAGAN reconstruction. The structures were effectively recovered by the CS method but with evident artefacts due to the low subsampling rate. In addition, the edges of “HELLO NATURE” were severely blurred, as was the text. However, our ACID network produced excellent results with the clearly visible words. To further show the power of ACID with small structural changes, another example (M2) in Antun et al.¹⁵ was reproduced as Figures 2M–2P. The text “CAN U SEE IT” was corrupted by both DAGAN and CS, rendering the insert hard to be read. Again, the text can be easily seen in the ACID reconstruction. Indeed, compared with the DAGAN and CS results, the ACID reconstruction kept sharp edges and subtle features. The reconstructed results of M2 (similar to the DAGAN results in Antun et al.,¹⁵ but with different subsampling rate and pattern) also support the superior performance of ACID.

In brief, ACID exhibited superior stability with structural changes over the competitors, as quantified by the peak signal-to-noise ratio (PSNR), structural similarity (SSIM), normalized root-mean-square error (NRMSE), and feature similarity (FSIM) in Table 1. In all of these cases, ACID consistently obtained the highest PSNR and SSIM scores indicated by boldface font.

Table 1.

Quantitative analysis results in the experiments

CT		Cases		C1		C2		C3		C4		C5
PSNR		Ell-50		31.80		31.49		34.02		29.57		25.57
		CS		32.62		31.81		33.52		30.44		22.49
		ACID		40.86		38.78		38.76		36.02		31.14
SSIM		Ell-50		0.922		0.953		0.924		0.882		0.651
		CS		0.951		0.954		0.933		0.944		0.769
		ACID		0.995		0.993		0.990		0.987		0.901
NRMSE		Ell-50		0.0120		0.0108		0.0124		0.0168		0.0236
		CS		0.0088		0.0084		0.0113		0.0112		0.0216
		ACID		0.0039		0.0046		0.0071		0.0079		0.0140
FSIM		Ell-50		0.960		0.981		0.955		0.938		0.868
		CS		0.964		0.971		0.949		0.955		0.877
		ACID		0.987		0.998		0.991		0.992		0.947
MRI		Cases		M1		M2		M3		M4		M5		M6
PSNR		DAGAN		29.59		29.16		28.22		27.55		29.33		29.06
		CS		30.91		30.23		29.83		29.33		29.58		29.35
		ACID		37.59		34.91		34.18		32.23		34.76		32.69
SSIM		DAGAN		0.923		0.896		0.877		0.851		0.907		0.906
		CS		0.951		0.941		0.936		0.926		0.933		0.929
		ACID		0.981		0.977		0.966		0.941		0.946		0.942
NRMSE		DAGAN		0.0338		0.0350		0.0402		0.0419		0.0353		0.0358
		CS		0.0285		0.0308		0.0322		0.0342		0.0332		0.0340
		ACID		0.0133		0.0188		0.0201		0.0260		0.0192		0.0249
FSIM		DAGAN		0.969		0.953		0.949		0.935		0.964		0.956
		CS		0.977		0.967		0.968		0.958		0.972		0.965
		ACID		0.990		0.985		0.977		0.969		0.976		0.970

Stability against adversarial attacks

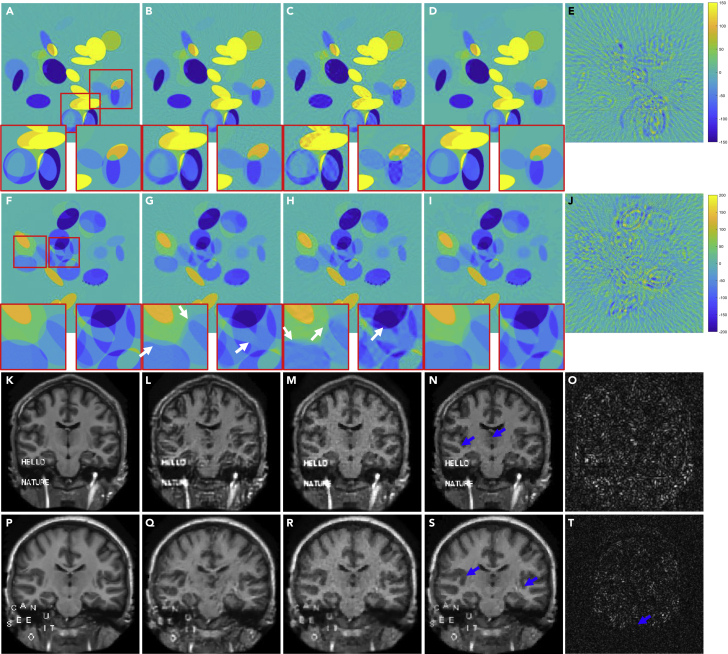
A tiny perturbation could fool a deep neural network to make a highly undesirable prediction,¹⁵ which is known as an adversarial attack.^39,40 To show the capability of the ACID approach against adversarial perturbations, the simulated CT (cases C3 and C4) and MRI (cases M3 and M4) reconstructions under such perturbations are given in Figure 3. Figures 3A–3D show that Ell-50 network led to distorted edges, as indicated by the arrows. Although the CS reconstruction had a stable performance against tiny perturbations, these distortions could not be fully corrected, with remaining subsampling artefacts. In contrast, this defect was well corrected by ACID. It is observed in Figures 3F–3I that the artefacts marked by the arrows induced by perturbation distorted the image edges in the Ell-50 reconstruction. This could result in a clinical misinterpretation. Although these artefacts were effectively eliminated in the CS reconstruction, CS-related new artifacts were introduced. Encouragingly, the corresponding edges and shapes were faithfully reproduced by ACID without any significant artefacts. In addition, the text “CAN YOU SEE IT” was completely lost in the Ell-50 reconstruction. In contrast, our ACID results preserved the edges and letters. The worst MRI reconstruction results from tiny perturbations were obtained by DAGAN, as shown in Figures 3L and 3Q. Compared with DAGAN, the CS-based reconstruction provided higher accuracy, but still failed to preserve critical details such as edges, as shown in Figures 3M and 3R. However, our ACID network overcame these weaknesses. Table 1 summarizes the quantitative evaluation results.

Figure 3.

Performance of ACID against adversarial attacks coupled with structural changes in the simulated CT and MRI cases

(A) The ground truth CT image in the C3 case with 2 magnified ROIs (window [−80 80]HU); (B)–(D) are Ell-50, CS, and ACID reconstructions; and (E) shows the adversarial sample (window [−5 5]HU). (F)–(J) are the counterparts in the C4 case (display window for (F)–(I) is [−150 150]HU and the display window for (J) is [−5 5]HU). The image structures indicated by white arrows show the advantages of our ACID in terms of CT imaging against adversarial attacks.

(K) The ground truth MRI image in the M3 case (normalized to [0, 0.7]).

(L–N) DAGAN, CS, and ACID reconstructions.

(O) The adversarial sample (window [−0.05 0.05]).

(P–T) The counterparts of MRI in the M4 case. The blue arrows demonstrate that our ACID provides much clearer image edges as well as finer structures against adversarial attacks. The difference images can be found in supplemental information, part III.B.

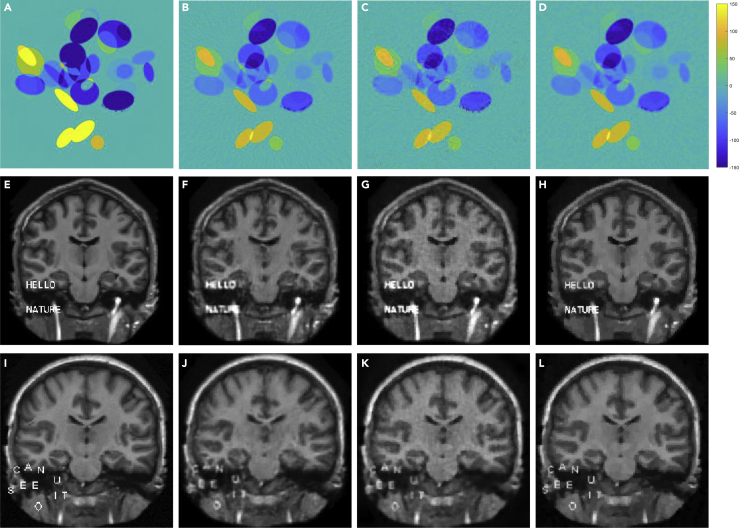
To demonstrate the ACID performance in a practical setting, more experiments were performed in these CT and simulated MRI cases with noisy data. The CT reconstruction results were obtained in the case C5, generated by adding Gaussian noise to the C1 data. Also, the reconstruction results were obtained in the experiments on M5 and M6, generated by adding Gaussian noise to the M1 and M2 datasets, respectively. With the original networks (including Ell-50 and DAGAN) and CS methods, the image edges and other features were notably blurred. However, all of the features including the embedded words were well recovered by ACID as shown in Figure 4. It is observed that ACID gave better quantitative results than the competitors. Specifically, ACID suppressed image noise more effectively than the CS-based reconstruction method, even though the network was not trained for denoising. The quantitative results are also given in Table 1.

Figure 4.

Reconstruction results in the simulated C5, M5, and M6 cases

(A–D) The ground truth, Ell-50, CS, and ACID results on C5.

(E–H and I–L) The ground truth, DAGAN, CS, and ACID results on M5 and M6, respectively.

Stability with more input data

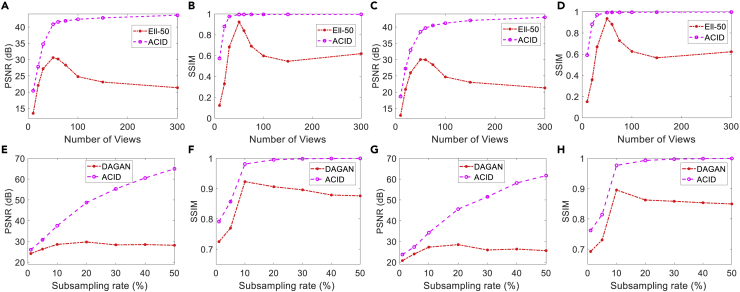
Intuitively, a well-designed reconstruction scheme is expected to increase its performance monotonically as more input data become available. It was pointed out by Antun et al.¹⁵ that the performance of some deep reconstruction networks, such as Ell-50 and DAGAN, degraded with more input data, which is certainly undesirable. To evaluate the performance of ACID with more input data, cases C1, C2, M1, and M2 were analyzed. The numbers of views in the CT cases were set to 10, 20, 30, 50, 60, 75, 100, 150, and 300, and in the simulated MRI cases, the subsampling rates were set to 1%, 5%, 10%, 20%, 30%, 40%, and 50%. Figure 5 shows that the performance of Ell-50 decreased with more projections than what were used for network training, being consistent with the observation by Antun et al.¹⁵ In contrast, ACID performed better with more views in terms of PSNR and SSIM. Similarly, the performance of DAGAN decreased when more data were collected at sampling rates higher than those used for DAGAN training, which agrees with the conclusion on DAGAN in the work of Antun et al.¹⁵ However, ACID produced better reconstruction quality in terms of PSNR and SSIM. The performance of ACID substantially improved with more input data, indicating that our ACID generalizes well to more input data, similar to the CS methods.

Figure 5.

Performance of ACID with more input data

(A and B) and (C and D) contain the PSNR and SSIM curves with respect to the number of views in cases C1 and C2, respectively.

(E and F) and (G and H) are the same type of curves with respect to different sub-sampling rates in cases M1 and M2, respectively.

Ablation study on ACID

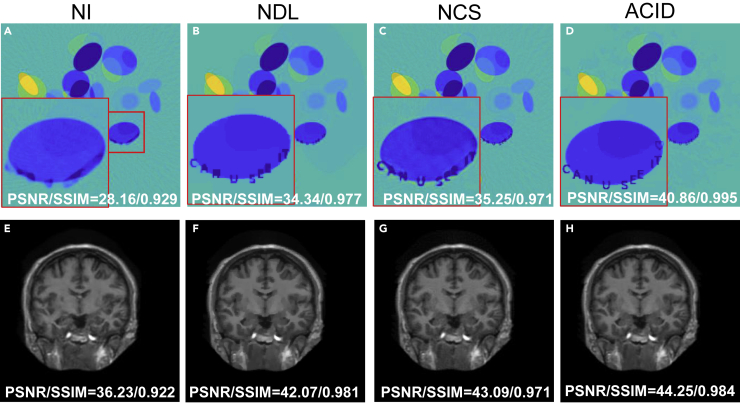
ACID involves deep reconstruction, CS-inspired sparsification, analytic mapping, and iterative refinement. To understand the roles of these algorithmic ingredients, we evaluated their relative contributions to the ACID reconstruction quality. Specifically, we reconstructed images using the three simplified versions of ACID by removing/replacing individual key components. The three versions include (1) improving the initial deep reconstruction with CS-inspired sparsification without iteration, (2) replacing deep reconstruction with a conventional reconstruction method, and (3) abandoning the compressed sensing constraint. Figure 6 shows that each simplified ACID variant compromised the ACID performance significantly.

Figure 6.

ACID ablation study in terms of visual inspection and quantitative metrics in the cases C1 and M7

NI denotes the reconstructed results by ACID without iterations (K = 1). NDL and NCS denote ACID without deeply learned prior and CS-based sparsification, respectively.

(A–D) These panels represent the reconstructed results by NI, NDL, NCS, and ACID in the C1 case.

(E–H) The reconstructed results by NI, NDL, NCS and ACID in the M7 case.

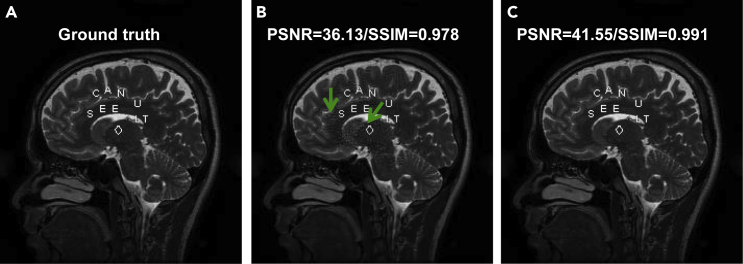
Comparison with classic iteration-based unrolled networks

Based on our experiences, we believe that the use of deep learning as a post-processor or an image-domain data-driven regularizer in a classic iterative reconstruction algorithm, as was suggested by Wang,⁴ is inferior to ACID that leverages the power of deep learning from the data space to the image space, since once an image is reconstructed using a classic method, some clues in the data space may be lost for deep learning-based reconstruction. It is mainly because the classic iterative reconstruction cannot take full advantage of data-driven prior, even if a deep learning image denoiser is used, such as in ADMM-net.⁴¹ Different from existing iteration-based unrolled reconstruction networks that only use deep learning to refine an intermediate image already reconstructed using a classic iterative algorithm, ACID reconstructs an intermediate image with a deep network trained on big data and through iterative refinement. To highlight the merits of ACID, the classic ADMM-net was chosen for comparison.⁴¹ The ADMM-net was trained on 20% subsampled data, with a radial sampling mask while the other settings are the same as that in Yang et al.⁴¹ Figures 7A–7C show that ACID achieved the best-reconstructed image quality, followed by ADMM-net and DAGAN sequentially. The phrase “HELLO NATURE” was blurred in the DAGAN reconstruction but became clearer in the ADMM-net reconstruction. However, the artefacts due to subsampling remain evident in the ADMM-net reconstruction. In Figures 7D–7F, there are strong artefacts in the reconstructed image by DAGAN. However, the image quality from ADMM-net is better than that of DAGAN, such as in terms of edge sharpness. The image edges and features in the ACID images are overall the best, as shown in Figure 7. To quantify the performance of these techniques, the PSNR and SSIM were computed, as shown in Figure 7.

Figure 7.

Comparison of reconstruction performance relative to the ADMM-net

(A–C) These panels represent the results reconstructed by DAGAN, ADMM-net, and ACID, respectively.

(D–F) Counterparts of another case.

The ACID flowchart can be unfolded into the feedforward architecture. However, such an unfolded reconstruction network (similar to MRI-VN⁴²) could still be subject to adversarial attacks, if kernel awareness is not somehow incorporated. Given the current graphics processing unit (GPU) memory limit, it is often impractical to unfold the whole ACID (up to 100 iterations or more) into a single network.

The unrolled reconstruction networks show great deep tomographic performance. For example, they can reconstruct high-quality images from sparse-view measurements. However, there are at least three differences between ACID and the unrolled reconstruction networks, such as MetaInv-Net.⁴³ First, large-scale trained networks, such as DAGAN³⁸ and Ell-50³⁶ could be incorporated into the ACID framework as demonstrated in this study. However, if the ACID scheme is unrolled into a feedforward network, only small subnetworks could be integrated—in other words, an unrolled ACID network could only use relatively light networks such as multiple layer convolutional neural networks (CNNs).^44,45 These sentences are not self-contradictory, because the ACID scheme is not an unrolled network. In fact, an unrolled network has a number of stages, each of which consumes a substantial amount of memory. Hence, the total size of the required memory is proportional to the number of stages. In contrast, ACID is computationally iterative, and thus the same memory space allocated for an iteration is re-used for the next iteration. Therefore, a large-scale network can work with ACID, but when the ACID scheme is unrolled, only a lightweight network can be used for ACID reconstruction. Second, the size of images reconstructed by an unrolled network is typically small. For example, the input image consists of small pixels for ADMM-net,⁴¹ MetaInv-Net,⁴³ LEARN,⁴⁴ and AirNet,⁴⁶ limited by the memory size of the GPU. The reconstructed low-resolution results could not satisfy the requirement of many clinical applications, especially for CT imaging tasks. Also, the unrolled networks were commonly designed for two-dimensional (2D) imaging, including the MetaInv-Net,⁴³ and they are difficult to use in 3D imaging geometry, since the memory increment is proportional to the number of stages. Third, it has not been intended by others to incorporate the theoretically grounded sparsity regularization module in such an unrolled architecture. This could be due to the fact that some needed operations (e.g., the image gradient L₀-norm⁴⁷) could not be effectively implemented with compact feedforward networks, which demanded big data and could not be easily trained. Nevertheless, ACID can stabilize these unrolled networks. For example, Figure 8 demonstrates the results using ACID with a built-in model-based unrolled deep network (MoDL).⁴⁵ MoDL performed well with structural changes but suffered from adversarial attacks.¹⁵ Synergistically, ACID with MoDL built in produced excellent image quality.

Figure 8.

Stabilization of MoDL using the ACID strategy

(A–C) These panels represent a representative reference, corresponding results reconstructed by MoDL and ACID (with MoDL built in), respectively, where adversarial attacks were applied to the MoDL network, which was then successfully defended using the ACID scheme with MoDL built in.

Adversarial attacks to the ACID system

As demonstrated above, ACID can successfully stabilize an unstable network. Then, a natural question is whether or not the whole ACID workflow itself is stable. To evaluate the stability of ACID in its entirety, we generated adversarial samples to attack the entire ACID system, with representative results in Figure 9. Because ACID involves both deep reconstruction and sparsity minimization in the iterative framework, the adversarial attack mechanism is more complicated for ACID than that for a feedforward neural network. (See part B³⁴ of this article for details on the adversarial attacking method that we used to attack ACID.) Using this adversarial method, C6, C7, and M10–M12 images were perturbed to various degrees, being even greater in terms of the L₂-norm than what were used to attack individual deep reconstruction networks. Our ACID reconstruction results show that the structural features and inserted words were still clearly reproduced even after these adversarial attacks. Consistently, the PSNR and SSIM results of ACID were not significantly compromised by the adversarial attacks.

Figure 9.

ACID being resilient against adversarial attacks

From left to right, the columns are ACID results in C6, C7, and M10–M12 cases, respectively. The first -third rows represent the ground truth plus tiny perturbation, reconstructed images, and corresponding perturbations.

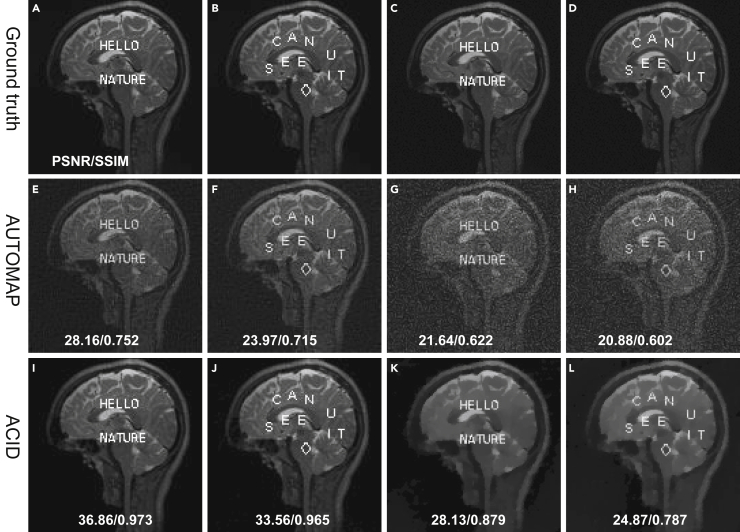
Stabilization of AUTOMAP

AUTOMAP, an important milestone in medical imaging, was used as another classic example by Antun et al.¹⁵ to demonstrate the instabilities of deep tomographic reconstruction. To further test the stability of ACID, cases A1 and A2 with structural changes and A3 and A4 cases with adversarial attacks were used, as shown in Figure 10 (details on cases A1–A4 are in supplemental information, part I). It is observed that AUTOMAP demonstrated good ability against structural changes but that it suffered from adversarial attacks.¹⁵ ACID produced significantly better image quality than AUTOMAP. Beyond the visual inspection, ACID achieved better PSNR and SSIM values than AUTOMAP. (See supplemental information, part I for more details.)

Figure 10.

Stabilization of AUTOMAP using ACID

The first and second columns represent the reconstruction results from structural changes, where the first, second, and third rows represent the reference, AUTOMAP, and ACID (with AUTOMAP built in) results, respectively. Third and fourth columns are the counterparts under adversarial attack, where the first, second, and third rows denote the reference plus perturbation, AUTOMAP, and ACID (with AUTOMAP built in) results, respectively.

Discussion

As clearly reviewed in the theoretical part of our article series,³⁴ the kernel awareness²⁶ is important to avoid the so-called cardinal sin. When input vectors are very close to the null space of the associated measurement matrix, if the input is slightly perturbed, then a large variation may be induced in the reconstructed image. If an algorithm lacks the kernel awareness, then it will be intrinsically vulnerable, suffering from false-positive and false-negative errors; for mathematical rigor, please see Theorem 3.1 in Gottschling et al.²⁶ For this reason, the deep tomographic networks were successfully attacked in Antun et al.¹⁵ However, sparsity-promoting algorithms were designed with the kernel awareness, leading to an accurate and stable recovery of underlying images, as also shown in Antun et al.¹⁵ As demonstrated by our results here, the kernel awareness has been embedded in the ACID scheme through both the CS-based sparsity constraint and the iterative refinement mechanism. Hence, ACID demonstrates a robust performance against noise, under adversarial attacks, and when the amount of input data is increased relative to what was used for network training. A different empirical method was also designed by peers,⁴⁸ which produced results complementary to ours.⁴⁹

It is important to understand how a CS-based image recovery algorithm implements the kernel awareness. The sparsity-constrained solution is iteratively obtained so that the search for the solution is within a low-dimensional manifold. That is, prior knowledge known as sparsity helps narrow down the solution space. Indeed, natural and medical images allow low-dimensional manifold representations.⁵⁰ It is critical to emphasize that a deep neural network is data driven, and the resultant data-driven prior is rather powerful to constrain the solution space greatly. While sparsity prior is just one or a few mathematical expressions, deep prior is in a deep network topology with a large amount of parameters extracted from big data. In this study, we incorporated the Ell-50 and DAGAN network into the ACID workflow. In fact, ACID as a general framework can integrate more advanced reconstruction neural networks,⁵¹ such as PIC-GAN⁵² and SARA-GAN.⁵³ These two kinds of priors (sparsity prior and deep priors) can be combined in our ACID workflow in various ways to gain the merits from both sides. Because the combination of deep prior and sparsity prior is more informative than sparsity prior alone, ACID or similar networks would outperform classic algorithms, including CS-inspired sparsity-promoting methods. Indeed, with a deep reconstruction capability, ACID outperforms the representative CS-based methods for image reconstruction, including dictionary learning reconstruction methods (see details in supplemental information, part II.B). Indeed, we only quantitatively evaluated the main reconstruction results in terms of PSNR, NRMSE, SSIM, and FSIM. Our current evaluative metrics directly correspond to what were used in the Proceedings of the National Academy of Sciences (PNAS) study.¹⁵ However, it will be valuable and interesting to assess the clinical influence of reconstructed results using other advanced assessment methods (local perturbation responses⁵⁴ and Frechet inception distance⁵⁵). In addition, the used deep tomographic networks are based on CNN architectures. Recently, the transformer as an advanced deep learning technique was used for image reconstruction. For example, Pan et al. developed a multi-domain integrative Swin transformer network (MIST-net) for sparse-view reconstruction.⁵⁶ Furthermore, the Swin transformer was used for MRI reconstruction.⁵⁷ How to stabilize transformer-based deep reconstruction networks is also important. We will pursue studies along this direction in the near future.⁵⁸

This study represents our specific response to the challenge presented in the PNAS paper by Antun et al.¹⁵ For that purpose and as the first step, the deep reconstruction networks and associated datasets we used are the same as what were used in the PNAS study, thereby making it clear and convincing for the readers to evaluate their relative performance. As a result, we also inserted the unrealistic features (e.g., bird, letters) used in the PNAS study. We emphasize that these experiments represent substantially easier inverse problems than real CT/MRI studies. How to evaluate and optimize the diagnostic performance of ACID-type algorithms in clinical tasks will be pursued in the future, which include real pathological features such as tumors.

In conclusion, our proposed ACID workflow has synergized deep network-based reconstruction, CS-inspired sparsity regularization, analytic forward mapping, and iterative data residual correction to systematically overcome the instabilities of the deep reconstruction networks selected in Antun et al.¹⁵ and achieved better results than the CS algorithms used by them. It is emphasized that the ACID scheme is only an exemplary embodiment, and other hybrid reconstruction schemes of this type can be also investigated in a similar spirit.^59,60 We anticipate that this integrative data-driven approach will help promote the development and translation of deep tomographic image reconstruction networks into clinical applications.

Experimental procedures

Resource availability

Lead contact

Hengyong Yu, PhD (e-mail: hengyong-yu@ieee.org).

Materials availability

The study did not generate new unique reagents.

Data and code availability

The codes, trained networks, test datasets, and reconstruction results are publicly available on Zenodo (https://zenodo.org/record/5497811).

Method details

Heuristic ACID scheme

In the imaging field, we often assume that the measurement ${\mathit{p}}^{\left(0\right)}=\mathit{A}{\mathit{f}}^{\ast }+\mathit{e}$, where $\mathit{A}\in {\mathbb{R}}^{m\times N}$ is a measurement matrix (e.g., $\mathit{A}$ is the Radon transform for CT⁶¹ and the Fourier transform for MRI⁶²), ${\mathit{p}}^{\left(0\right)}\in {\mathbb{R}}^m$ is an original dataset, ${\mathit{f}}^{\ast }\in {\mathbb{R}}^N$ is the ground truth image, $\mathit{e}\in {\mathbb{R}}^m$ is data noise, and most relevant, $m<N$, meaning that the inverse problem is underdetermined. In the under-deterministic case, additional prior knowledge must be introduced to recover the original image uniquely and stably. Typically, we assume that $\mathit{H}\in {\mathbb{R}}^{N\times N}$ is an invertible transform, $\mathit{A}$ satisfies the restricted isometry property (RIP) of order $s$⁶³ (note that ACID works even without RIP, but in that case the solution may or may not be unique; see the theoretical part of our articles, part B³⁴), and $\mathit{H}{\mathit{f}}^{\ast }$ is s-sparse. We further assume that the function $\text{Φ}(\cdot )$ models a properly designed and well-trained neural network with the BREN property that continuously maps measurement data to an image. To solve the problem of reconstructing $\mathit{f}$ from measurement ${\mathit{p}}^{\left(0\right)}$, the ACID scheme is heuristically derived from the following iterative solution (see part B of our article series³⁴):

$$\{\begin{array}{l}{\mathit{p}}^{(k+1)}=\frac{\lambda \left({\mathbf{p}}^{\left(0\right)}-\mathbf{A}{\mathit{f}}^{\left(\mathit{k}\right)}\right)}{1+\lambda }\hfill \\ {\mathit{f}}^{\left(\mathit{k}+1\right)}={\mathit{H}}^{-1}{S}_{\epsilon }\left(\mathit{H}\left({\mathit{f}}^{\left(\mathit{k}\right)}+\frac{1}{\lambda }\text{Φ}\left({\mathit{p}}^{(\mathit{k}+1)}\right)\right)\right)\hfill \end{array}$$ (Equation 1)

where $k$ is the index for iteration, $k=\mathrm{0,1,2},\dots$, $\lambda >0$ and $\epsilon >0$ are hyperparameters, ${\mathit{H}}^{-1}$ is the inverse transform of $\mathit{H}$, and $S_{\epsilon }(\cdot )$ is the soft-thresholding filtering kernel function defined as

$$S_{\epsilon }\left(x\right)=\{\begin{array}{ll}0,\hfill & \left|x\right|<\epsilon \hfill \\ x-sgn\left(x\right)\epsilon \hfill & \text{otherwise}\hfill \end{array}.$$ (Equation 2)

In our experiments, $\mathit{Hf}$ is specialized as a discrete gradient transform, and ${\mathit{H}}^{-1}$ is interpreted as a pseudo-inverse⁶⁴ (see part B of our article series³⁴). Under the same conditions described by Yu and Wang,⁶⁴ the ACID iteration would converge to a feasible solution subject to an uncertainty range proportional to the noise level (under the conditions and approximations discussed in part B of our article series³⁴).

Selected unstable networks stabilized in the ACID framework

The Ell-50 and DAGAN networks are two examples of unstable deep reconstruction networks chosen to validate the effectiveness of ACID, both of which were used in Antun et al.¹⁵ and suffered from the three kinds of instabilities. In addition, the results from stabilizing AUTOMAP, a milestone deep tomographic network, were also included.

The projection data for Ell-50-based CT reconstruction were generated using the radon function in MATLAB R2017b, where 50 indicates the number of projections. For fair comparison, we only used the trained networks by Jin et al.,³⁶ which were the same as those used in Antun et al.¹⁵ The test image for case C1 was provided by Antun et al.,¹⁵ which can be downloaded from the related website.¹⁵ Case C2 with the bird icon and text “A BIRD?” was provided by Gottschling et al.²⁶ and downloaded from the specified website.¹⁵ The test images are of 512 × 512 pixels containing structural features without any perturbation. To generate adversarial attacks, the proposed method in Antun et al.¹⁵ was used. Then, we obtained C3 and C4 images by adding perturbations to C1 and C2 images, respectively. Furthermore, Gaussian noise with zero mean and deviation 15 HU over the pixel value range was superimposed in case C1 to obtain case C5, and adversarial attacking was performed on the whole ACID workflow by perturbing C1 and C2 images to generate C6 and C7 images, respectively. More details on the datasets and implementation details are in the supplemental information.

To evaluate ACID in the MRI case, the DAGAN network was used,³⁸ which was proposed for single-coil MRI reconstruction. In this study, we set the subsampling rate to 10% and subsampled the resultant images with the 2D Gaussian sampling pattern. Also, the DAGAN network was re-trained, with the same hyperparameters and training datasets as those used by Yang et al.³⁸ The test images were a series of brain images, each of which consists of 256 × 256 pixels. Case M1 was randomly chosen from the test dataset,³⁸ then the phrase “HELLO NATURE” was placed in the image as structural changes. Case M2 was obtained in the same way as in Antun et al.,¹⁵ where the sentence “CAN U SEE IT” and “◊” were added to the original image. Also, we applied the same attacking technique used in Antun et al.¹⁵ to generate adversarial samples. These perturbations were added to M1 and M2 images to obtain M3 and M4 images, respectively.¹⁵ Furthermore, the Gaussian noise with zero mean and deviation of 15 over the pixel value range [0, 255] was superimposed to cases M1 and M2 to obtain M5 and M6 images. M7 was randomly chosen from the DAGAN test dataset, which can be freely downloaded.³⁸ In addition, cases M8 and M9 were generated by putting a radial mask of a 20% subsampling rate on the M1 and M2 images, which were used to compare ACID with ADMM-net.⁴¹ Cases M10 and M12 were generated by directly perturbing the entire ACID system. The comparative results are given in supplemental information, part I.B.

ACID was then compared with AUTOMAP for MRI reconstruction. The AUTOMAP network was tested on subsampled single-coil data. The trained AUTOMAP weights used in our experiments were provided by Zhu et al.¹⁶ The AUTOMAP network took a vectorized subsampled measurement data as its input. First, the complex k-space data were computed using the discrete Fourier transform of an MRI image. Second, subsampled k-space data were generated with a subsampling mask. Lastly, the measurement data were reshaped into a vector and fed into the AUTOMAP network. In this study, the images of 128 × 128 pixels at a subsampling rate of 60% were used for testing. The original image was provided in Antun et al.,¹⁵ “HELLO NATURE,” “CAN U SEE IT,” and “◊” were added to the test image to generate A1 and A2 with the structural changes. The perturbations were added to images A1 and A2 to obtain images A3 and A4.¹⁵ For representative results, please see supplemental information, part I.C.

Image quality assessment

To quantitatively compare the results obtained with different reconstruction methods, the PSNR was used to measure the difference between a reconstructed image and the corresponding ground truth image. Also, the SSIM was used to assess the similarity between images. In addition, the NRMSE and FSIM⁶⁵ are also used to assess the main results. For qualitative analysis, the reconstructed results were visually inspected for structural changes (i.e., the inserted text, bird, and patterns) and artefacts induced by perturbation. In this context, we focused mainly on details such as edges and integrity such as overall appearance.

To highlight the merits and stability of the ACID scheme, the representative CS-based methods served as the baseline. For CT, the sparsity-regularized method combining X-lets (shearlets) and total variation (TV) was used,⁶⁶ which is consistent with the selection in Antun et al.¹⁵ For MRI, the total generalized variation (TGV) method was chosen.⁶⁷ All of the parameters, including the number of iterations for these CS methods, were optimized for fair comparison, as further detailed in the supplemental information.

Numerical verification of convergence

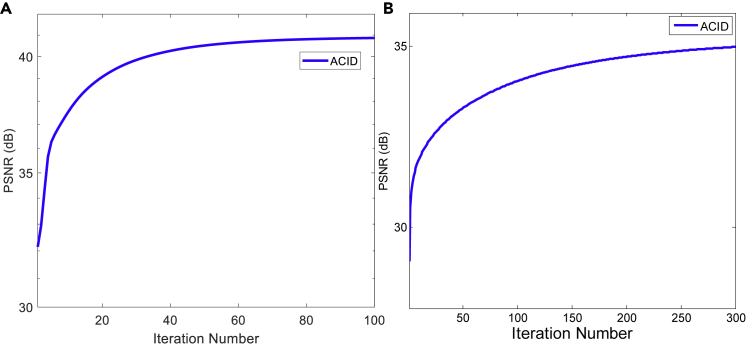
To verify the convergence of the ACID iteration, we numerically investigated the convergence rate and computational cost. We used PSNR as the metric to reflect the convergence of ACID (Figure 11). It can be seen that the ACID iteration converged after approximately 30 iterations for CT, and became stable after 250 iterations for MRI. In this study, we set the number of iterations to 100 and 300 for CT and MRI, respectively. In addition, we empirically showed the convergence of ACID in terms of the Lipschitz constant (see part B of our article series³⁴ for details).

Figure 11.

Convergence of the ACID iteration in terms of PSNR

(A and B) These panels show the convergence curves in the C1 and M2 cases, respectively.

ACID parameterization

The ACID method mainly involves two parameters, $\lambda$ and $\epsilon ,$ as defined in Equation 1. These parameters were optimized based on our quantitative and qualitative analyses, as summarized in Table 2.

Table 2.

Parameters optimized in the experiments

Variables	C1	C2	C3	C4	C5	C6	C7	M1
$\epsilon \left({10}^{-3}\right)$	0.700	0.700	0.500	1.100	0.35	0.100	0.700	0.333
$\text{λ}$	0.76	0.76	14	2.4	60	3.0	0.76	0.1
Variables	M2	M3	M4	M5	M6	M7	M8	M9
$\epsilon \left({10}^{-3}\right)$	0.333	0.500	0.500	0.667	0.667	0.333	0.500	0.500
$\text{λ}$	0.1	0.01	0.01	0.01	0.01	0.1	0.01	0.01
Variables	M10	M11	M12	A1	A2	A3	A4
$\epsilon \left({10}^{-3}\right)$	0.100	0.100	0.100	0.33	0.33	2.0	2.0
$\text{λ}$	0.01	0.01	0.01	3.10	3.10	6.10	6.10

Published: April 6, 2022