Automated detection of cerebral microbleeds via segmentation in susceptibility-weighted images of patients with traumatic brain injury

Highlights

• •Deep learning can be used in the diagnosis of Cerebral Microbleeds in moderate-to-severe TBI.
• •CNNs designed to segment Cerebral Microbleeds achieve human-level performance on small lesions.
• •Training with boundary loss helps CNNs in separating small lesions in microbleed clusters.

Abstract

Cerebral microbleeds (CMBs) are a recognised biomarker of traumatic axonal injury (TAI). Their number and location provide valuable information in the long-term prognosis of patients who sustained a traumatic brain injury (TBI).

Accurate detection of CMBs is necessary for both research and clinical applications. CMBs appear as small hypointense lesions on susceptibility-weighted magnetic resonance imaging (SWI). Their size and shape vary markedly in cases of TBI. Manual annotation of CMBs is a difficult, error-prone, and time-consuming task.

Several studies addressed the detection of CMBs in other neuropathologies with convolutional neural networks (CNNs). In this study, we developed and contrasted a classification (Patch-CNN) and two segmentation (Segmentation-CNN, U-Net) approaches for the detection of CMBs in TBI cases. The models were trained using 45 datasets, and the best models were chosen according to 16 validation sets. Finally, the models were evaluated on 10 TBI and healthy control cases, respectively.

Our three models outperform the current status quo in the detection of traumatic CMBs, achieving higher sensitivity at low false positive (FP) counts. Furthermore, using a segmentation approach allows for better precision. The best model, the U-Net, achieves a detection rate of $90\%$ at FP counts of $17.1$ in TBI patients and $3.4$ in healthy controls.

1. Introduction

Traumatic brain injury (TBI) is a major cause of death and disability among all age groups across the world (Maas et al., 2017). Injury severity ranges from mild TBI, sometimes referred to as concussions, to severe TBI, which includes comatose states. Severity is commonly determined using the Glasgow Coma Scale (GCS), a neurological assessment describing the level of consciousness (13–15: mild, 9–12: moderate, $⩽$8: severe) of a patient based on their eye-opening, verbal, and motor responses (Teasdale and Jennett, 1974). GCS assessment is used in the initial triage and diagnosis of TBI patients, but is also considered a predictor of a patient’s long-term outcome (King et al., 2005, McNett, 2007). However, due to its nature as an assessment of symptoms without inclusion of underlying neuropathological injury mechanisms like traumatic axonal injury (TAI), its prognostic value is limited.

TAI, also referred to as diffuse axonal injury when distributed diffusely over the brain, describes damage to the axons. It can occur as acute ruptures due to inertial forces, or as the result of axon degeneration after the initial shear injury (Hill et al., 2016). This damage is nearly impossible to visualize with current neuroimaging methods because axons are microscopic in size. However, axonal injury is often accompanied by damage to the surrounding vasculature which may result in cerebral microbleeds (CMBs) (Nandigam et al., 2009, Liu et al., 2014).

CMBs are small hemosiderin deposits found in the brain parenchyma. Greenberg et al. (2009) presents the seminal definition and description of CMBs. They can be visualized with magnetic resonance imaging (MRI), either on gradient-recalled echo (GRE) T2$*$-weighted or susceptibility-weighted images (SWI). CMBs appear as spherical hypo-intense lesions of $\le 10$mm in size. The magnetic properties of hemosiderin cause a signal void whose size depends on the MRI sequence and its parameters (Haacke et al., 2004). Thus, lesions will appear larger on MRI compared to their actual histopathological dimension. This is called the blooming effect. There are other tissues (e.g., veins, calcium and iron deposits) which may mimic the appearance of CMBs. It is important to note that while Greenberg et al. (2009) provides the most commonly cited definition in the research of traumatic CMBs, this seminal work draws a distinction between CMBs of vascular and traumatic origin, and recommends to treat a clinical history of TBI as an exclusion criterion for its guidelines on CMB interpretation.

While the majority of traumatic CMBs are consistent with Greenberg’s criteria, they may also appear curvi-linear in shape (Izzy et al., 2017). The size constraint of 10 mm diameter does not apply to curvi-linear CMBs. Furthermore, numerous traumatic CMBs may occur together in a cluster (Iwamura et al., 2012), closer in appearance to a macrobleed. There is no formal definition given in the literature that specifically addresses the variability and complexity of traumatic CMBs and their detection, although (Izzy et al., 2017) applies a more comprehensive definition.

Clinically, CMBs occur also in healthy individuals of advancing age (Vernooij et al., 2007), patients with stroke (Charidimou and Werring, 2012, Charidimou et al., 2013), Cerebral Amyloid Angiopathy (CAA) (Chao et al., 2006), patients who have undergone radiation therapy (Passos et al., 2017), and patients who have sustained a TBI (Scheid et al., 2003). In TBI, they are assumed to co-occur with axonal damage and are therefore considered a biomarker of TAI (Nandigam et al., 2009, Liu et al., 2014). In the absence of imaging methods that can capture the extent of TAI directly, CMBs may provide insight into severity, progression and outcome of TBI-patients.

In the last decade, various computer-aided detection (CAD) systems were proposed to aid researchers and physicians in the complex task of detecting CMBs, for a variety of neurological diseases (Barnes et al., 2011, Kuijf et al., 2012). Van den Heuvel et al. (2016) developed the first automated system for detecting CMBs in moderate to severe TBI, still using traditional feature-based machine learning methods. To date, this method represents the state-of-the-art in traumatic CMB detection. With the advent of deep learning, medical image analysis now usually employs convolutional neural networks (CNNs) (Krizhevsky et al., 2012, Litjens et al., 2017). The first deep learning based method for the detection of CMBs was presented by Dou et al. (2016). This study focused on stroke patients. Liu et al. (2019) trained and evaluated a system for a variety of CMB populations, including a cohort of mild TBI patients. Standvoss et al. (2018) investigated the use of CNNs in moderate to severe TBI cases in a smaller cohort.

The common aspect of all these CNN solutions is that they treat the detection of CMBs as a classification problem, i.e., they address the question whether a partial MR image volume contains a CMB. For neurological diseases that largely present with low numbers or sparse distribution of CMBs, this approach is without issue. In the case of TBI, however, such an approach would prove complicated. The number of CMBs can be very high depending on severity, e.g. $⩾100$ can be found in a single severe TBI patient. Additionally, CMB shapes are variable and they may occur in clusters. Thus, to accurately detect, count, and locate CMBs a segmentation approach might prove beneficial as it allows a more fine-grained segregation of individual CMBs. In this paper, we present a classification CNN (Patch-CNN) and two segmentation CNNs (Segmentation-CNN, U-Net) and compare their ability to detect and count CMBs both with each other, and with a previously published baseline in traumatic CMB detection (Van den Heuvel et al., 2016).

2. Material and methods

2.1. Materials

2.1.1. Patient data

The data for this study was collected at the Radboud University Medical Center, Nijmegen, The Netherlands. Its use was approved by the institutional ethics committee and informed consent was waived due to its retrospective nature.

The dataset consisted of brain MR imaging studies from 45 patients with moderate (GCS 9-$12$) to severe (GCS 3-$8$) TBI. For 20 of these patients, studies were available at two different timepoints. Furthermore, the studies of 18 healthy volunteers were included as controls resulting in a total of 81 MR studies (see Table 1). Studies included an SWI scan and T1 MP-RAGE scan, detailed in Table 21. All scans were collected on a 3T MRI Scanner (Siemens Magnetom Trio). 2

Table 1.

Characteristics of the 81 studies from 46 TBI and 18 control subjects.

Datasets	TBI	CMBs/scan2		Control
		FS	RS	(scans)
Training	$24$ / $41$	$30.0$$(18.0-67.0)$	–	4
Validation	$12$ / $12$	$15.5$ ($8.5-53.0$)	–	4
Testing	$10$ / $10$	$34.5$ ($26.3-41.8$)	$18.0$$(6.5-23.5)$	10

¹ Values indicate number of TBI Subjects/ Studies. Scans refers to the total number of MRI studies available in the listed dataset. For the training dataset, scans from multiple timepoints were included for a single patient.

² Values presented as median (interquartile range). TBI: Traumatic Brain Injury, CMB: Cerebral Microbleed, FS: Full Segmentation (CAD-assisted), RS: Reference Standard.

Table 2.

MRI sequence parameters. The same settings were used for all studies.

Sequence	TR	TE	Flip	BW	Voxel size
	(ms)	(ms)	angle	(Hz/pixel)	(mm × mm × mm)
T1	2300	2.98	9$°$	240	1.00 × 1.00 × 1.00
SWI	27	20	15$°$	120	0.98 × 0.98 × 1.00

TR: Repetition time, TE: Echo time, BW: Bandwidth.

2.1.2. Annotations

Training and evaluation of any CAD system requires expert-level annotations. Manual annotation of CMBs in TBI patients is a challenging and laborious task, especially when the observer is asked to manually segment the extent of the blooming effect which represents the CMB on the SWI image.

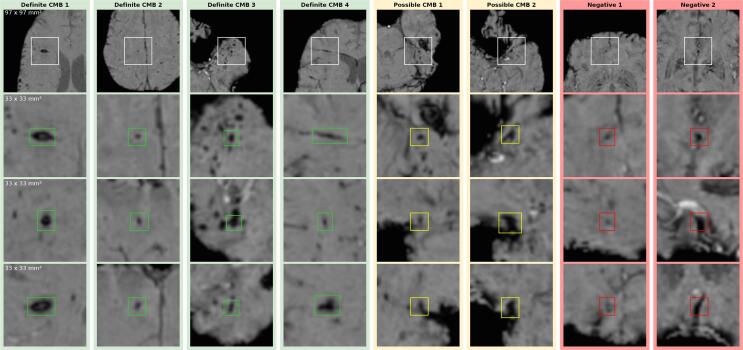
Fig. 1 illustrates the difficulty of detecting CMBs. It is challenging to precisely count the lesions in a cluster (Definite CMB 3)(Iwamura et al., 2012). Curvi-linear lesions (Definite CMB 4)(Iwamura et al., 2012, Izzy et al., 2017) and vessels (Negative CMB 2) can be hard to differentiate. Hypo-intense foci close to the brain boundary, vessels or artifacts can be problematic to discern. (The heterogeneous morphology of the CMBs is further illustrated in the Supplementary Material $6.2$. These difficulties apply both to human observers as well as CAD systems. Due to these challenges, Cordonnier et al. (2009) suggests to separate CMB classification into a “definite” and “possible” category.

Fig. 1.

Examples of definite CMBs (green), possible CMBs (yellow), and potential FPs/mimics (red). From top to bottom: contextual axial view (97 mm × 97 mm), close-up axial, close-up sagittal and close-up coronal view (33 mm × 33 mm). Definite CMB 1: comparatively large, clearly defined lesion – Definite CMB 2: typical small ovoid lesion – Definite CMB 3: lesion within CMB cluster – Definite CMB 4: curvi-linear lesion, – Possible CMB 1: hypo-intense spot, close to transverse fissure – Possible CMB 2: hypo-intense spot, close to nasal cavity noise artifacts – Negative 1: hypo-intense spot, part of a linear phase artifact – Negative 2: vessel mimicking an ovoid lesion in some orientations (here axial and sagittal).

Consequently, manual annotations, especially from multiple observers, are often difficult to obtain in sufficient volume. Therefore, this study employed different types of annotations for training and evaluation. Full segmentation of the blooming effect was used for training and validation. For evaluation, we used a majority vote constructed automatically from point annotations by six independent observers. see Fig. 2.

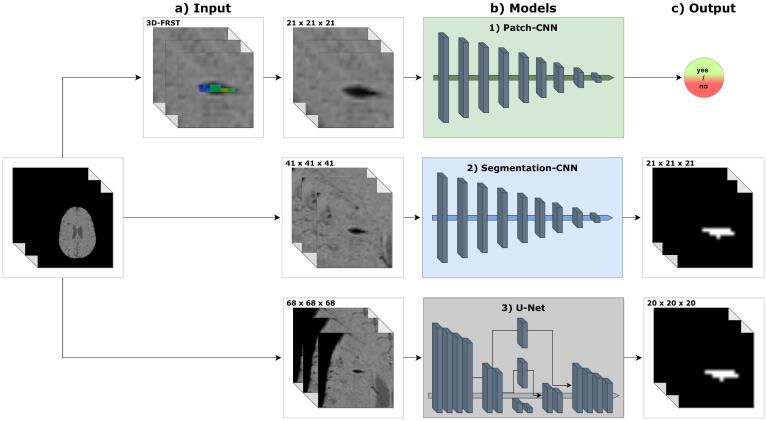
Fig. 2.

Overview of proposed models. a) Inputs are 3D patches of model-dependent size, e.g. in case of Patch-CNN the size is 21 mm³. b) Architecture schematics of proposed models. Patch-CNN: fully convolutional classification CNN. Segmentation-CNN: fully convolutional segmentation CNN. U-Net: segmentation CNN with down- and upsampling path, and skip connections. c) Outputs are a scalar for the Patch-CNN, and probability distributions for the Segmentation-CNN and U-Net.

Full Segmentations (CAD-assisted). CAD-assisted full segmentations were used for training and validation of the CNNs. They were generated with the CAD system developed in Van den Heuvel et al. (2016). Points predicted by the trained system were evaluated by an experienced neuroradiologist (AWvdE) into three categories: definite CMB, possible CMB, and false positive (FP). Furthermore, the neuroradiologist (AWvdE) added points she considered obviously missed CMBs. Finally, a medical student (MMP) manually segmented the full blooming effect of all these predictions under the supervision of the neuroradiologist (AWvdE).

CAD-assisted full segmentations are used for the development, training and validation of the models.

Reference Standard. Six medical observers of varying expertise in the detection of traumatic CMBs determined point annotations of CMBs for a subset of 10 studies. Each point could mark a definite or possible CMB. Using these points as seeds, region growing was employed to determine the extent of their blooming effect. The resulting maps were then algorithmically compared to determine definite and possible CMBs for evaluation.

The reference standard is used to evaluate the developed models. All results are generated on the reference standard.

In Van den Heuvel et al. (2016), the model was compared with each observer individually based on a majority vote of the five remaining observers. For this study, we opted for a single majority vote of all six observers as our reference standard to evaluate the models, while still evaluating individual observers against the majority vote of the other 5. Furthermore, we manually corrected the region-grown results when they encompassed multiple lesions. For detailed information on the majority vote calculation for both studies, i.e., how definite and possible lesions were determined, see the Supplementary Material Section $6.8$.

2.2. Methods

2.2.1. Preprocessing

Brain masking. By definition, CMBs only occur in the brain parenchyma (Greenberg et al., 2009, Gregoire et al., 2009, Cordonnier et al., 2009). Therefore, we calculated brain masks using the HD-BET software package (Isensee et al., 2019). This tool was not developed for SWI scans specifically, but visual inspection showed that for the described SWI sequence the tool achieved excellent brain masks.

Bias field correction. A potential confounder in various image analysis tasks is the presence of a low frequency intensity non-uniformity present in the image data also known as bias, inhomogeneity, illumination non-uniformity, or gain field. We used the N4-ITK bias field correction to correct these inhomogeneities as implemented in the SimpleITK framework (Tustison et al., 2010).

Normalization. The intensity with which tissue is recorded and presented is not normalized in MRI and can be subject to large variation. This variation occurs between patients, and even more so between different scanners. Therefore, the SWI scans were normalized by taking the peak value of the intensity histogram (brain masked to exclude the initial peak at 0) and defining this point as $-0.5$. The intensity histogram was then normalized to the range $[-1.0,)$ (see Supplementary Material $6.8$). The histogram peaks correspond the brain parenchyma in SWI scans.

2.3. Models

Many previously proposed methods for CMB detection employ a two-stage approach (Chen et al., 2015). First, candidate detection identifies hypo-intense foci as potential CMBs. Candidate detection must be highly sensitive, thus generates a large amount of FPs. In the case of CMBs, there have been initial candidate detections with simple thresholding (Barnes et al., 2011), radial symmetry transforms (Kuijf et al., 2012), or an initial machine learning algorithm trained on voxel-wise features (Van den Heuvel et al., 2016).

Second, a feature vector for each candidate is computed and true lesion likelihood determined by a machine learning classifier. A variety of classifiers have been used in the detection of CMBs, e.g., Random Forest Classifiers (Van den Heuvel et al., 2016), Support Vector Machines (Barnes et al., 2011), or CNNs (Chen et al., 2015).

Variants of this approach are used in most CMB detection systems Van den Heuvel et al., 2016, Dou et al., 2016, Liu et al., 2019. Segmentation models, detailed below, do not require a candidate detection step.

2.3.1. Baseline model

As a baseline for comparison of the deep learning models described in this study we used the predictions produced by Van den Heuvel et al. (2016). They presented a two-stage approach employing non-deep learning machine learning classifiers. In this study, results for the same test set are provided. We did not retrain the system, but re-evaluated the prediction maps obtained during the initial study with the refined majority vote.

2.3.2. Model 1: Patch-CNN – classification

For the initial detection of CMB candidates, we implemented the 3D fast radial symmetry transform (3D-FRST) (Loy and Zelinsky, 2003, Kuijf et al., 2012). The 3D-FRST is a technique that estimates local radial symmetry to highlight spherical points of interest in an image. This algorithm has been successfully applied in the detection of CMBs in other pathologies (Kuijf et al., 2012, Liu et al., 2019). As mentioned, traumatic CMBs can be more variable in shape and are not always spherical. This had to be considered in the selection of hyperparameters for the 3D-FRST.

The resulting candidates are used as center points for 3D-Patches of size $21\times 21\times 21$. A classification Patch-CNN was trained to determine true lesions from FPs. The Patch-CNN is a fully-convolutional CNN (architecture detailed in Supplementary Material Table 5).

2.3.3. Model 2: segmentation-CNN

The Segmentation-CNN model is equivalent to the Patch-CNN model in its architecture. Number of convolution layers, kernel size and feature volumes of its filters are identical (detailed in Supplementary Material Table 4 and 5). The only difference in architecture was the removal of the dropout layer because dropout is unnecessary to improve generalization in a segmentation task. Major distinction between the models is the size of the input and output layers (and subsequently, the effective size of intermediate layers), but in terms of parameters they are identical.

2.3.4. Model 3: U-Net

This model is based on the 3D-UNet proposed by (Çiçek et al., 2016). The original 3D-UNet was designed for the task of large scale volume segmentation, while our task is aimed at segmenting small structures, i.e., CMBs. Therefore, the input and output dimensions, as well as the network structure, were adjusted. The 3D-UNet receives an input subvolume of ${68}^3$ voxel size. The output layer is ${20}^3$ in size, which allows for a meaningful distinction of positive and negative samples in batch preparation. Compared to the original 3D-UNet, our model has two pooling and upsampling layers, respectively, instead of three. We also added an intermediate layer with a $1\times 1\times 1$ kernel into our skip connections. They aid in adjusting the activations between the encoder and decoder layers.

2.3.5. Post-processing during inference

As can be seen in Fig. 1 as ”Definite CMB 3”, traumatic CMBs often occur in clusters. A segmentation network will predict a confidence distribution akin to a heatmap. Although this distribution may contain multiple peaks, corresponding to individual lesions, a simple threshold and connected component analysis could result in a faulty single lesion prediction.

To accurately count individual lesions, we identify clustered components within the heatmap and subsequently assess whether a component is multi-modal, i.e., the heatmap contains 2 or more peaks in confidence which would suggest multiple underlying lesions. If the component is multi-modal, we separate it into its modes and derive multiple predicted components.

2.4. Training

The task of detecting or segmenting CMBs is complicated by severe class imbalance, with far more negative samples for both classification and segmentation approaches. There are several ways to address class imbalance. One is selective sampling, the other a proper choice in loss function.

2.4.1. Selective sampling

We set a desired ratio of positive and negative samples in batch preparation to ensure the model encounters a sufficient amount of positive samples during training.

Whether a sample is considered positive or negative depends on the presence or absence of definite CMB voxels within its center. The size of the center in consideration varies between the classification ($3\times 3\times 3$) and segmentation ($11\times 11\times 11$) pipelines. The partial volumes are sampled according to the 3D-FRST in the Patch-CNN pipeline, and at stride 8 in the segmentation pipelines.

Furthermore, we do not limit this sampling method to one negative sample class. Instead we employ hard mining after each epoch and separate the negative samples into “easy” and “hard” negative samples, i.e., samples that are correctly predicted and samples that contain FP voxels. The “hard” negative samples are more likely to be drawn from the dataset in the following epoch.

The ratios used were $1:7$ for positive and negative samples during the first epoch, and $1:1:6$ for positive, “hard” negative, and “easy” negative samples in all following epochs.

Loss functions. There are a variety of loss functions available for the training of deep learning models. In classification tasks, cross-entropy loss is usually employed. This was also used in previous works on CMB detection (Dou et al., 2016, Standvoss et al., 2018, Liu et al., 2019). Both cross-entropy (CE) and Dice loss are commonly used for training segmentation networks. However, these standard loss functions are not well-equipped to deal with large class imbalances as present in the voxel-wise segmentation of CMBs where healthy tissue is ${10}^6$ times more common than CMBs.

All three models (Patch-CNN, Segmentation-CNN, U-Net) were trained with CE-loss. In addition to our selective sampling approach, we assigned class weights to account for the imbalance. This approach is sufficient for the 3D-FRST-CNN because the CMB classification problem is less imbalanced. Additionally, training samples are limited to candidates detected with 3D-FRST.

For segmentation models, the imbalance is more egregious and the CE-loss is not sufficient for optimal training. Therefore we introduced a second loss function for training the Segmentation-CNN and 3D-UNet, namely boundary loss (BL) (Kervadec et al., 2018). BL was specifically developed for use cases with high class imbalance. While CE-loss is distribution based, and Dice loss is region-based, BL is designed to minimize the distance between the prediction and ground truth. This has two beneficial effects on the models: it reduces the number of total FPs and improves delineation of predictions in clusters of CMBs.

The combination of these losses is weighted at $0.95$ for CE-loss and $0.05$ for BE-loss, and they are respectively decreased and increased by $0.05$ with each epoch. The idea is to first opt for high sensitivity and then refine the model over epochs. Also, we limit the maximum distance for BL-loss computation to $10\mathit{mm}$. This improves the synergy of CE- and BL-loss for this task, otherwise the CE-loss tended to increase.

2.4.2. Data augmentation

Data augmentation is a valuable tool in increasing the variety of the dataset and achieve more robust results and better generalization. We employed several data augmentation techniques. Random flipping was performed exclusively in the axial plane. Given the larger context provided to the segmentation models, flipping of the other planes would generate samples incongruous with actual brain anatomy. Random affine transformations, including scaling, shearing and rotation were applied within a small range. To limit void information appearing at the boundaries of the sample, a larger subvolume was transformed and then cropped to input size. Furthermore, we randomly shifted and scaled image intensity by minor amounts to account for the variations in tissue intensity that are inherent to MR imaging.

2.5. Evaluation

Expert performance was evaluated for each observer on a majority vote of the other five observers, while the models were evaluated on a single majority vote of all observers. The results for the individual observers differ from the reported numbers in Van den Heuvel et al. (2016) because of our manual adjustments (described in Supplementary Material $6.3$).

On a detection task with multiple lesions per case, the established method to evaluate detection performance is the Free-response Receiver Operating Characteristic (FROC) (Miller, 1969). It compares a model’s detection sensitivity to the number of FP predictions at a continuous scale of operating points. We report results specifically at two operating points. The first is derived from a desired detection rate of $90\%$. This corresponds to the best sensitivity achieved by one of our observers. The other operating point is derived from an averaged FP count of 10 per TBI case. Most of the observers score below this FP count on the test set, and it represents a number of FPs that could reasonably be checked by a human observer and lead to a major reduction in reading effort.

Additionally, we report FPs over the number of CMBs. This is a better indicator of model performance when comparing models across different pathologies than the average number of FPs per case, as CMB counts vary significantly between pathologies. Also, we report the mean absolute error (MAE) and the normalized mean absolute error (nMAE) of CMB counts, comparing the reference with the prediction count. MAE is averaged over cases, nMAE is averaged over the amount of CMBs in the dataset.

$\mathit{MAE}=\frac{1}{n}\sum |({\mathit{FP}}_p+{\mathit{FN}}_p)-{\mathit{def}}_p|$

$\mathit{nMAE}=\frac{\sum |{\mathit{FP}}_p+{\mathit{FN}}_p)-{\mathit{def}}_p|}{\sum {\mathit{def}}_p}$

In an idealised version, the model would not require a second reader and could predict the CMB counts. MAE and nMAE give an indication of the workload for a second reader to correct initial model predictions, both FPs and missing CMB predictions.

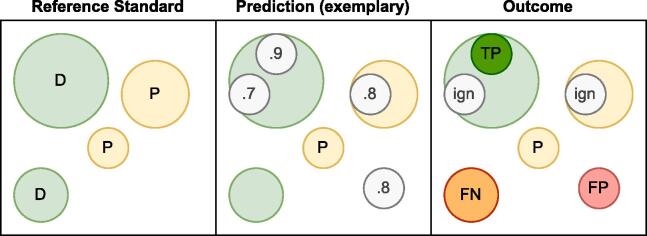
Fig. 3 illustrates how true positives (TPs) and FPs were counted for the FROC given the presence of possible CMBs in the reference standard, and in the case of multiple model predictions within a single reference lesion mask. Gregoire et al. (2009) found that the inter-rater reliability is significantly lower for possible CMBs than for definite CMBs. Therefore, we opted to exclude model predictions that occurred in the mask of possible CMBs, i.e., they neither counted as TPs nor as FPs for sensitivity and FPs metrics. (Other approaches to evaluating possible CMB are presented with their results in the Supplementary Material $6.8$) If multiple predictions were clustered within a single reference lesion, only the most confident prediction was considered the TP; lower confidence predictions were ignored.

Fig. 3.

Conceptual visualization illustrating how predictions are evaluated. The reference standard contains two definite and one possible CMB. The model predicts four lesion locations and confidences. The panel labeled ‘Outcome’ details how individual predictions are scored. Only the highest prediction within the mask of a definite CMB counts towards the TPs. Additional predictions as well as predictions that fall within the mask of possible CMBs are disregarded for evaluation purposes. D: definite CMB, P: Possible CMB, TP: true positive, FP: false positive, FN: false negative, ign: disregarded during evaluation.

We calculated the performance metrics in Table 3 on a single sample of the test set, while the FROC curves in Fig. 4 are bootstrapped over 1000 random 10-samples of the TBI test cases. We also report notable findings from visual inspection of the results.

Table 3.

Model performance.

Model	Sensitivity1	FPTBI2	FPhealthy2	FPall2/ CMBRS	MAETBI	nMAETBI	MAEall	nMAEall
Baseline	$80.3\%$$(13.7\%)$	$32.1$$(10.2)$	$29.3$$(17.1)$	$3.31$	$52.1$$(17.9)$	$2.89$	$40.7$$(20.5)$	$4.52$
Patch-CNN	$87.7\%$$(9.9\%)$	$20.6$$(9.8)$	$6.9$$(3.8)$	$1.51$	$61.2$$(30.8)$	$3.4$	$34.1$$(34.9)$	$3.78$
Segmentation-CNN	$91.0\%$$(8.1\%)$	$19.2$$(6.1)$	$5.5$$(3.1)$	$1.27$	$35.1$$(10.7)$	$1.95$	$20.3$$(16.8)$	$2.26$
U-Net	$92.2\%$$(8.3\%)$	$17.1$$(4.7)$	$3.4$$(2.1)$	$1.08$	$31.2$$(8.6)$	$1.73$	$17.3$$(15.2)$	$1.92$

All values are presented as mean (standard deviation) on the test set (not bootstrapped).

¹ Sensitivity is calculated an operating point of $10$ FPs averaged per TBI patient.

² FP count is calculated at an operating point of $90\%$ average sensitivity.

FP: False positive, TBI: Traumatic Brain Injury, CMB: Cerebral Microbleed, RS: Reference Standard (manually corrected majority vote), MAE: Mean Absolute Error, nMAE: normalized Mean Absolute Error.

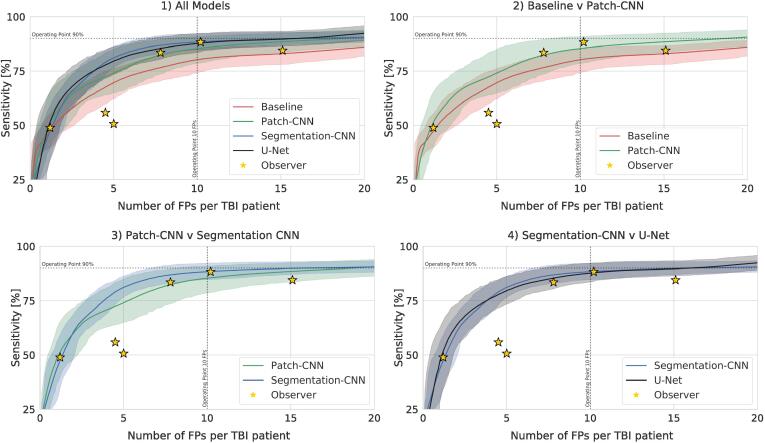
Fig. 4.

Performance (bootstrapped at 1000 random samples of the available test set) of individual models in comparison with observers using FROC curve of Sensitivity over average FPs per TBI case. 1) Comparison of all models. 2) Comparison of the classification models. 3) Comparison of classification and segmentation CNN with equivalent architecture. 4) Comparison of the segmentation models.

3. Results

Observer variability.Van den Heuvel et al. (2016) reported a Fleiss’ kappa of $0.24$ on the given test set. Since we adapted thew majority voting procedure and manually separated individual lesions in the reference standard, we calculated the inter-rater reliability anew, arriving at a Fleiss’ kappa value of $0.19$.

Model performance.Table 3 shows that at an operating point of 10 FPs averaged in TBI patients, the Baseline model detects $80.3\%$ of CMBs. If we choose $90\%$ sensitivity to determine the operating point, the system produces an average number of $32.1$ FPs in TBI patients and $29.3$ FPs in healthy controls. The FROC graphs in Fig. 4 show that the detection rate at low FP counts is consistently lower than the proposed CNN models. The count error for TBI cases reached an average of $52.1$, while for the entire test set it averages to $40.7$.

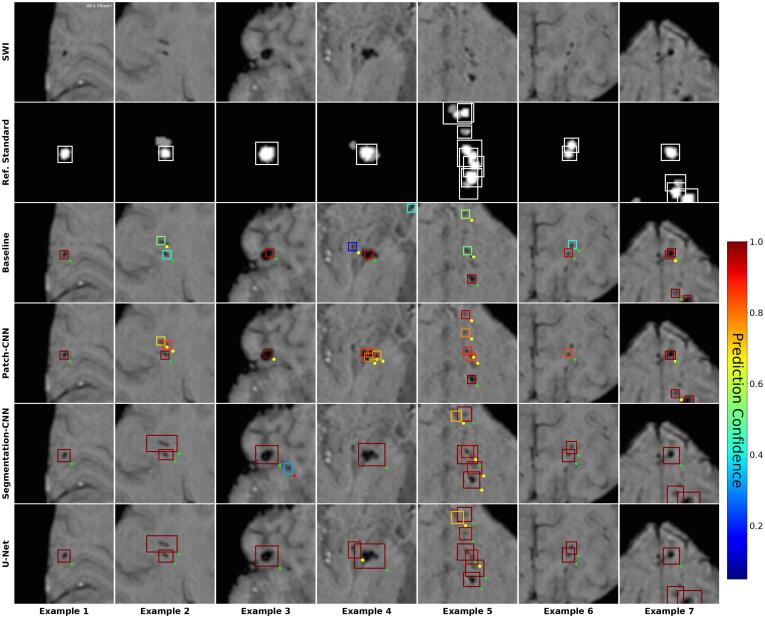
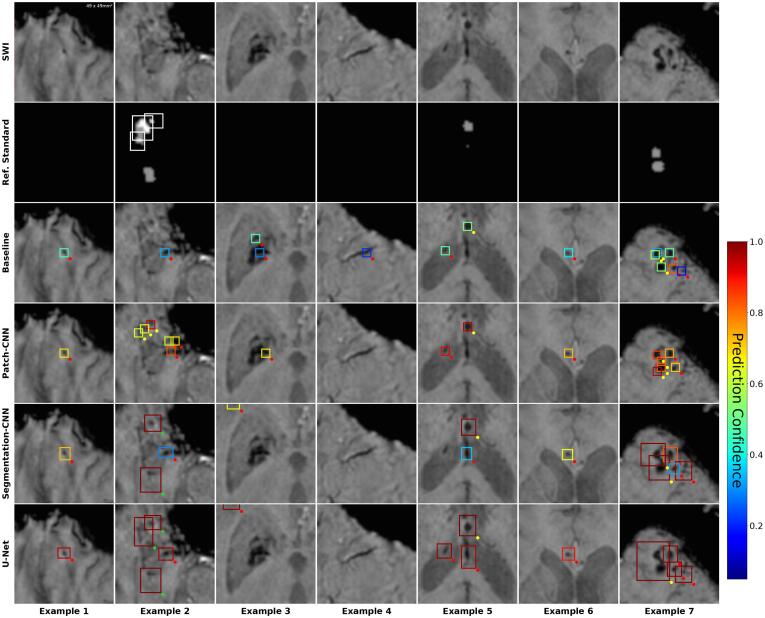
Visual inspection shows that the Baseline fails to identify all individual lesions within a cluster more often than the DL models (Fig. 5, Ex.5). It is also more prone to predict FPs in the case of calcifications (Fig. 6, Example 3) and vessels (Fig. 6, Example 4).

Fig. 5.

True positive predictions compared between individual models at operating point of $90\%$ sensitivity. SWI: Close-up axial patch of size 49x49mm². Ref. Standard: Majority vote. White bounding boxes show individual definite lesions. Grayed areas are possible lesions. Models: Baseline (Van den Heuvel et al., 2016), Patch-CNN, Segmentation-CNN, U-Net. Colored bounding boxes show predicted lesions (after post-processing). Color corresponds to prediction confidence. Dots at bottom-right of bounding boxes signify evaluation results, i.e. whether a predicted lesions is considered a TP (green), FP (red), or i.gnored (yellow).

Fig. 6.

False positive predictions compared between individual models at operating point of $90\%$ sensitivity. SWI: Close-up axial patch of size 49x49mm²Ref. Standard: Majority vote. White bounding boxes show individual definite lesions. Grayed areas are possible lesions. Models: Baseline: (Van den Heuvel et al., 2016), Patch-CNN, Segmentation-CNN, U-Net. Colored bounding boxes show predicted lesions (after post-processing). Color corresponds to prediction confidence. Dots at bottom-right of bounding boxes show evaluation results, i.e. whether a predicted lesions is a TP (green), FP (red), or i.gnored (yellow).

The Patch-CNN model predicts an average of $87.7\%$ of CMBs at an operating point of 10 FPs. At $90\%$ sensitivity, it produces $20.6$ FPs in TBI patients and $6.9$ FPs in healthy controls. The count error averages $61.2$ for TBI patients, and $34.1$ for all patients.

In conjunction with the FP-results from both the Baseline and Patch-CNN model, this points to a sub-optimal candidate detection which proposes multiple candidates within single definite lesions. This can be observed in several examples of Fig. 5, Examples 2 & 4, and Fig. 6, Examples 2 & 7. The Segmentation-CNN achieves an average of $91.0\%$ of CMBs at an operating point of 10 FPs. At $90\%$ sensitivity, it produces $19.2$ FPs in TBI patients and $5.5$ FPs in healthy controls. The count error averages to $35.1$ in TBI patients and $20.3$ in all patients.

The U-Net3 accurately predicts an average of $92.2\%$ of CMBs in TBI patients. At $90\%$ sensitivity, it produces $17.1$ FPs in TBI patients and $3.4$ FPs in healthy controls. The count error averages to $31.2$ in TBI patients and $17.3$ in all patients.

Both segmentation models show superior behavior in the prediction of CMB clusters to the classification models. They are less likely to miss CMBs (Fig. 5, Example 5) or predict single lesions doubly.

With regard to the FP counts of all models, it is important to note that a substantial amount of FPs corresponds to locations which are designated as CMBs in the full segmentation, i.e. the manually corrected results of the Baseline model. In Fig. 6, Examples 6 and 7 show predictions that were neither definite nor possible in the reference standard, but are considered definite CMBs in the full segmentation. Visual analysis of the results showed between 90–110 such FPs for each model.

The MAE results for all models may seem abnormally high given the other results, however it has to be considered that they do account for ignored predictions as described in Fig. 3.

Post-processing. The applied post-processing makes a major difference to the performance of the proposed segmentation models (Segmentation-CNN, U-Net). Without post-processing many individual lesions are missed or miscounted due to connected predictions of clusters and other neighbouring lesions. As a result, the segmentation models would perform on the same level as the Baseline model. This can be seen in the Supplementary Material $6.7$.Possible CMBs. Fig. 3 details how possible CMBs in the reference standard were counted towards the metrics. There are other approaches to their in- or exclusion from metrics which we detail in the Supplementary Material $6.8$. Option 1 is to treat possible CMBs as background; Option 2 is to consider them definite CMBs.

Given Option 1, sensitivity of all models decreases by 5–$8\%$ at the operating point of 10 FPs due to the increase in FPs re-aligning the prediction confidence threshold. The U-Net is less prone to identifying possible CMBs (with high confidence). Of note, there is no measurable difference for the segmentation models at 15 FPs between the regular evaluation method and Option 1. Metrics for the observers are changed as well: loss of sensitivity ranges from 1–$6\%$ with an increase of 3–$6$ FPs (except for one outlier).

Assuming Option 2, all models score 21–$23\%$ lower sensitivity. This shows that all models tend to predict possible CMBs with lower confidence. FP counts of observers are unaffected in this case, but their sensitivity is 5-$11\%$ lower compared to our regular method (with the previous outlier only losing $2.9\%$).

4. Discussion

In this work, we presented several deep learning based approaches for the detection of CMBs in TBI patients. We evaluated and compared the individual systems with each other and with the best system in the literature for this specific task (Van den Heuvel et al., 2016).

In the desired range of FP predictions, set at 10 FPs per scan, the segmentation models achieve the highest sensitivities. Considering all shown FP and MAE counts, the U-Net has a slight edge over the Segmentation-CNN and clearly outperforms the other two methods. It is important to note that the Baseline experiment could not be repeated, and was originally performed with a smaller dataset. Therefore, we can not definitively argue whether its potential performance would be closer to the presented deep learning models. Given the insights gained in the medical imaging and deep learning communities in the last decade (Litjens et al., 2017), it can be assumed that the results would still support our conclusions.

We demonstrated that CNNs which are designed to segment the full extent of the blooming effect of CMBs can achieve a higher sensitivity at a lower FP rate than direct classification approaches. Classification requires hyper sensitive candidate detection which results in large amount of FPs to exclude. While the Patch-CNN performs better at excluding FPs, both it and the Baseline fail to exclude multiple candidates in single lesions or clusters, which results in their large MAEs.

The segmentation approaches do not require candidate detection, instead rely on meaningful post-processing to separate the predicted probability distributions into single lesion predictions. A lesion’s probability distribution often has a high confidence center and lower confidence outline. This enables easy separation of lesions, and is largely independent of CMB shape. The results show that the segmentation approach is superior. Both the Segmentation-CNN and U-Net outperform the classification models in every metric.

The purpose of CAD systems is to aid researchers and clinicians in their daily duties, either by reducing their required efforts or by relieving them of a task completely. The latter is a high bar to achieve because the CAD system would have to be proven to reliably achieve human expert level or superior performance. The presented models are close in performance to the experts who contributed to the study, with similar performance to 3 and outperforming 3 considering the FROC curves in Fig. 4. However, we would not deem the models sufficiently accurate for stand-alone application given the MAE results and our evaluation criteria detailed in Fig. 3.

However, use of these models may significantly reduce the workload of any observer. Van den Heuvel et al. (2016) showed a significant decrease in annotation time given the Baseline results. The improved performance of our presented models in this study could further reduce the amount of decisions an observer would have to make. This could enable a routine and consistent investigation of CMBs in clinical use, which to date is not a common step taken in the diagnosis and prognosis of TBI.

Furthermore, CMB detection currently suffers from low inter-rater reliability. Van den Heuvel et al. (2016) reported a Fleiss’ kappa of $0.24$ on our test set, and with our manual separations of individual lesion the inter-rater reliability is even lower at $0.19$. This issue is exacerbated when considering possible CMBs (Gregoire et al., 2009). All the models show relative improvement compared to the observers (despite reduction in numerical performance), when possible CMBs are considered as background. This indicates that the models could aid in discriminating these difficult-to-judge lesions. If a single model would be employed by several research groups, this would help in improving the inter-rater reliability both within their own group and the larger research community.

There are a number of CMB detection systems proposed in the research literature for other pathologies than TBI, e.g., stroke (Dou et al., 2016). A comparison to these systems is difficult. Most other neuropathologies rarely present with the CMB counts occurring in moderate to severe trauma, although severe CAA can present with a large amount of CMBs as well (Chao et al., 2006). More importantly, the morphology of CMBs varies between traumatic and vascular causes, with traumatic CMBs presenting with a more varied morphology (Iwamura et al., 2012, Izzy et al., 2017). Therefore, consensus on a CMB detection is more difficult to reach. Reported statistics would not allow for a meaningful comparison and a system developed for non-traumatic CMB detection would unlikely be usable in the alternate use case, or vice versa.

This is also a concern for using our CAD system on mild TBI studies, because high counts of CMBs, curvi-linear, and clustered lesions are less likely to occur. An average FP count of 10 would present a significant aid if the actual count is high, but in cases with single lesions the work reduction might be negligible. Thus, the inclusion of only moderate to severe cases presents a limitation of this study. A complete CAD system for detecting traumatic CMBs has to be able of reliably deal with TBI cases of all severities.

Recently, at the MICCAI conference the VALDO challenge was hosted 4. One of the assigned tasks was CMB detection and segmentation. The challenge was won by an implementation of the nnUnet (Kuijf, 2021). The nnUnet is a self-organizing approach to deep learning often successfully removing the need for bespoke solutions in medical imaging (Isensee et al., 2018, Isensee et al., 2019). A direct comparison between our models and the nnUnet is not sensible because we matched the complexity of all proposed models for fair comparison and the nnUnet is larger by a factor of 10 for a single fold. Nonetheless, we performed initial tests with very promising results (Supplementary Material $6.9$). The nnUnet could the next step in CMB detection in moderate and severe TBI if combined with more engineered methods, e.g. boundary loss.

A universally usable CAD system for CMB detection will have to account for a large variety of MRI scanners and SWI and other high-sensitivity T2*-weighted sequences. As mentioned, magnetic field strength and certain sequence parameters influence the size of the blooming effect of CMBs, and thus their observability (Greenberg et al., 2009). In this work, development and evaluation was limited to a single scanner and SWI sequence type. However, the task of CMB detection across scanners and sequences is not trivial. Unlike long established sequences like T1 and T2, SWI is less harmonized across scanners and sites (Haacke et al., 2009). Subsequently, the visual appearance of CMBs, in addition to their natural heterogeneity, can vary due to the susceptibility of the blooming effect to parameters like magnetic field strength, image resolution, and echo time as well as repetition time (Nandigam et al., 2009, Haacke et al., 2009). We are planning to address both shortcomings in our next steps in this research.

Despite promising results, these systems have not reached a level of sensitivity and precision to allow for independent usage. In a clinical setting, we would suggest employing an operating point of approximately 10 FPs as an initial screening. A medical observer could then check all predictions to exclude the remaining FPs with reasonable effort.

We presented a deep learning approach to detecting traumatic CMBs by segmenting their blooming effect. Our best model achieves human-level performance and presents a fundamental step in the proliferation of CMB research, and potentially clinical employment.

CRediT authorship contribution statement

K. Koschmieder: Conceptualization, Methodology, Software, Validation, Writing - original draft, Writing - review & editing, Visualization. M.M. Paul: Data curation, Writing - review & editing. T.L.A. van den Heuvel: Data curation, Writing - review & editing. A.W. van der Eerden: Data curation, Writing - review & editing. B. van Ginneken: Supervision, Writing - review & editing. R. Manniesing: Conceptualization, Methodology, Supervision, Writing - review & editing.

Appendix A. Supplementary data

The following are the Supplementary data to this article: