Summary:
Electronic health records (EHRs) have become a platform for data-driven granular-level surveillance in recent years. In this paper, we make use of EHRs for early prevention of childhood obesity. The proposed method simultaneously provides smooth disease mapping and outlier information for obesity prevalence, which are useful for raising public awareness and facilitating targeted intervention. More precisely, we consider a penalized multilevel generalized linear model. We decompose regional contribution into smooth and sparse signals, which are automatically identified by a combination of fusion and sparse penalties imposed on the likelihood function. In addition, we weigh the proposed likelihood to account for the missingness and potential non-representativeness arising from the EHR data. We develop a novel alternating minimization algorithm, which is computationally efficient, easy to implement, and guarantees convergence. Simulation studies demonstrate superior performance of the proposed method. Finally, we apply our method to the University of Wisconsin Population Health Information Exchange database.
Keywords: Childhood obesity surveillance, disease mapping, electronic health records, fusion penalty, outlier detection, sparse penalty
1. Introduction
Childhood obesity prevention has become increasingly important to control the global obesity epidemic. Granular-level surveillance of childhood obesity that identifies and tracks obesity trends is needed to help design interventions and guide policy solutions when monetary resources are limited (Longjohn et al., 2010). Routinely collected massive health databases, such as Electronic Health Records (EHRs), are gaining attention as a platform for assessing trends and local childhood obesity risk (Friedman et al., 2013).
Statistical methods for geospatial surveillance may include two aspects: i) monitoring regional trends in prevalence (also known as “disease mapping”) and ii) identifying unexpected variation in the prevalence of different locations (also known as “hot spot detection”). Traditionally, these two tasks have been accomplished separately. For task i), obesity literature mainly used the standard generalized linear mixed effect model (GLMM) to account for individual factors and community environments. Those approaches assumed the regional random effects to be independent, although a spatial dependency exists even after adjusting for covariates (Panczak et al., 2016). To account for the spatial dependence, methods for smooth disease mapping have been proposed from both frequentist and Bayesian perspectives. Under Poisson log-linear models or multilevel logistic models, the region-specific effects were smoothed by kernels (Ghosh et al., 1999) or splines (Ugarte et al., 2010), or were modeled as a dependent random vector by conditional autoregressive (CAR) priors (Besag et al., 1991; Mercer et al., 2015). These strategies resulted in “clustered” risk maps, which enhanced interpretability, but did not explore identification of aberrant regions. For task ii), the most popular approach is the spatial scan statistic method (Kulldorff and Nagarwalla, 1995; Jung, 2009). The scan statistic methods search over a pre-specified set of geographical districts and conduct a generalized likelihood ratio test for testing whether the proportions of events are homogeneous across, inside, and outside the district. However, it may not be suitable for identifying multiple locations with heterogeneous sizes. Residuals generated from regression approaches can also be used to detect regional outbreaks, in a way that an observation with large residual is regarded as an outlier (Farrington et al., 1996; Zhao et al., 2011). However, residual cutoff-based outlier detection is known to fail when an outlier is a leverage point or there are multiple outliers (She and Owen, 2011).
Use of the fusion penalty for smoothing was first proposed in a least squares setup (Tibshirani et al., 2005), and then for public health research (Wang and Rodríguez, 2014). The resulting fit from the fusion penalty appears to be piecewise constant, yielding a natural clustering of fitted values. Smoothing by the fusion penalty enables an additional regularization using a different penalty, such as a sparse penalty, which may not be straightforward in other smooth disease mapping methods. Sparse penalty for outlier detection was used with the squared error loss (Kim et al., 2009; Tibshirani and Taylor, 2011; She and Owen, 2011). Kim et al. (2009) and Tibshirani and Taylor (2011) considered the ℓ1 penalty, and She and Owen (2011) reported that nonconvex penalties outperformed both ℓ1 penalty and cutoff-based approaches for detection in standard multiple linear regression.
We develop a new method that simultaneously produces an interpretable disease map and detects outlier regions. We formulate a multilevel logistic model to naturally incorporate risk factors. A novel hybrid regularization includes a smooth signal representing the region-specific effect and a sparse signal. The smooth signal is regularized by a fusion penalty so that adjacent locations tend to have similar fitted baseline obesity rates. A nonconvex sparse penalty is enforced for the sparse signals so that nonzero fitted coefficients signify potential outliers. It is worth mentioning that estimating population health metrics from EHRs can be challenging due to missingness and non-representativeness. Following Flood et al. (2015), we adopt a two-step weighting procedure to account for missing data and to adjust the covariate distribution for a nationally representative sample.
Our original contributions are twofold. First, while the hybrid regularization of the fusion and ℓ1 penalties has been considered in linear models (Kim et al., 2009; Tibshirani and Taylor, 2011), to the best of our knowledge we are the first to incorporate a fusion penalty and a nonconvex penalty to identify outliers. Second, we provide an efficient optimization algorithm that guarantees convergence for the hybrid regularization model and can leverage off-the-shelf software packages. Although our algorithm is described in a Bernoulli likelihood, it can be easily extended to handle other convex loss functions.
In Section 2, we describe the University of Wisconsin Electronic Health Record Public Health Information Exchange (PHINEX) database that motivated our study, and we introduce our method in Section 3. Simulation studies are presented in Section 4, which demonstrate the superior performance of our proposed method. We apply our method to PHINEX on childhood obesity surveillance in Section 5. We provide concluding remarks in Section 6.
2. Data
The University of Wisconsin Electronic Health Record Public Health Information Exchange (UW eHealth PHINEX) database contains EHR data from a south-central Wisconsin academic healthcare system. It consists of patient records with documented primary care encounters at family medicine, pediatric, and internal medicine clinics occurring from 2007 to 2012. All PHINEX data were derived from the Epic EHR Clarity Database (EpicCare Electronic Medical Record, Epic Systems Corp., Verona WI). Furthermore, the program geocodes to the census blockgroup and links EHRs with community-level social determinants of health. It was created to improve clinical practice and population health by understanding local variations in disease risk, patients, and communities (Guilbert et al., 2012).
In this paper, we focused on 93, 130 patients aged 2–19 years during 2011–2012. Body mass index (BMI) values (in kg/m2) were calculated from a subject’s height and weight, measured at the same visit. Any subject with a BMI at or above the 95th percentile was categorized as obese. Among all the patients, 34, 852 (37.4%) were missing a valid BMI. Individual-level covariates included sex, age, race/ethnicity, health service payor (i.e., insurance), and the 2010 census blockgroup information on subject residence. Region-specific covariates included economic hardship index (EHI) and urbanicity of the blockgroups, where EHI (Nathan and Adams, 1989) was used as a measure of blockgroup socioeconomic status and normalized for all Wisconsin census blockgroups. Urbanicity of a census blockgroup was based on its 11 Urbanization Summary Groups, according to ESRI (2012). These groups were derived from data on census blockgroup population density, city size, proximity to metropolitan areas, and economic/social centrality. Urbanicity integer values ranged from 1 (the most urban) to 11 (the most rural).
3. Method
3.1. Model setup
We use a double subscript, ij (j = 1, …, ni, i = 1, …, K) to indicate the j-th subject in the i-th region. Let Si be the position of the centroid of the i-th region. Let Xi denote the region-level covariates such as urbanicity and EHI. Let Yij be the obese indicator of the (ij)-th subject, with Yij = 1 indicating obese. Lastly, let Zij be a vector of the covariates of the (ij)-th subject such as gender, age, race/ethnicity, and insurance payor.
Let . We formalize our model for the pij as
| (1) |
| (2) |
| (3) |
where c1, c2 ⩾ 0, logit(t) = log{t/(1−t)}, and I(·) is the indicator function. The βis represent the regional contribution to obesity prevalence that is not explained by individual or other areal-level characteristics. Since the probability of a child being obese might be affected by the community environment, we expect the regional contribution to obesity prevalence to be similar for individuals in neighboring locations (Panczak et al., 2016), and thus a smoothness constraint (2) is imposed on βi. The fusion weight represents the strength of the “fusion” for each pair of i1 and i2. A higher value of will lead to a more similar pair of the fitted and . With an appropriate choice of tuning parameter, the values that βi could take are limited where similar locations are grouped together. We may interpret the distinct levels of βi as segmentation or clustering of the regions. γi is introduced to capture potential aberrant regions, where the i-th region is an outlier with unusual obesity prevalence if γi ≠ 0. Given the sparsity constraint (3), we expect γi will be zero (non-outlier) for most regions, but a few might be nonzero (outliers). Our formulation can be viewed as an extension of Wang and Rodríguez (2014), where we added a sparsity constraint on each region in addition to the fusion constraint. This addition enables capturing of aberrant outbreaks after adjusting for the dependency at the region level.
The model is identifiable if γi’s are sufficiently away from zero, but may not be otherwise. Although the idea of separating signals was considered in She and Owen (2011), Kim et al. (2009), Tibshirani (2014), and Chernozhukov et al. (2017), boundary values that determine the identifiability of the model have not been formally studied, and require further investigation. Note, however, that are identifiable.
3.2. Estimation with complete data
Denote , , β = (β1, …, βK)T and γ = (γ1, …, γK)T. If all patients had complete records, the parameters could be estimated by a penalized logistic likelihood, where , and the objective function ϕ is
| (4) |
The normalized negative log-likelihood function is
| (5) |
The second term is a fusion penalty that stems from the Lagrangian of (2), where . We use , where the denotes a distance between and . Here, geodistance is used to define d(·,·), but other measures of similarity can be employed. Without loss of generality, we assume , otherwise we can normalize it. Since the computational cost of the optimization involving fusion penalty increases quadratically in the number of nonzero , one may want to retain a few with large values and truncate the others at zero for ease of computation.
The third term, , is a sparse penalty that is a relaxation of the Lagrangian of (3), where qλ(·) is a univariate penalty function. In particular, we consider the hard penalty function as proposed in She and Owen (2011), qλ(t) = (λ|t| − t2/2)I(t < λ) + λ2/2I(t ⩾ λ). The hard penalty results in a nonconvex formulation on (4), which guarantees convergence to a local minima. We weigh the i-th penalty in by ni such that subjects across different regions are penalized equally.
3.3. Optimization algorithm
We developed an alternating minimization algorithm. It alternately updates α, β, and γ, each time minimizing one of them while keeping the others fixed. Denote the current iterates by α(t), β(t), and γ(t). In addition, we denote . Then .
Updating α. Fix β = β(t) and γ = γ(t). The objective function is equivalent to
with , which corresponds to a classical logistic regression on N individuals. One can run standard packages (such as glm in R) to obtain α(t+1).
Updating β. Fix α = α(t+1) and γ = γ(t), then
where for each i and j. For simplicity, define ψ(β) = ϕ(α(t+1), β, γ(t)), which is convex in β. To update β(t), we propose minimizing a surrogate objective function in which l(β) is replaced by its local quadratic approximation around β(t).
Write the second-order Taylor expansion of l(β) at β(t) as
where ∇β and are the first and the second derivative operators with respect to β. Define the surrogate objective function as . We calculate , where
with
For the calculation of , we applied the majorization-minimization algorithm proposed by Yu et al. (2015), which yields a stable solution and can be easily implemented.
To ensure , we adopt Lee et al. (2016)’s one-step modification of : if , let ; otherwise, , where . We will show in Proposition 1 that always exists and ψ(β(t)) ⩾ ψ(β(t+1)) holds over iterations.
Updating γ. Given that α = α(t+1) and β = β(t+1),
where . With a slight abuse of notation, we define a univariate objective function ϕi(γ) and a loss function li(γ) (i = 1, …, K) as
Clearly . Thus, it suffices to optimize K univariate functions ϕi(·), i = 1, …, K. Although each ϕi(γ) is nonconvex, we can find a global optimum of ϕi as follows. Let . Since is constant outside [−λ2, λ2], a minimizer of ϕi(·) either lies on [−λ2, λ2] or equals to . Hence, we propose a grid search approach. Let {t1, …, tT } ⊆ [−λ2, λ2], and .
The complete algorithm is provided in Web Appendix C. The following property is guaranteed by the proposed algorithm.
Proposition 1: Assume that for each i, there exist j1, j2 such that and . For any choice of α(t), β(t), and γ(t), the updated iterates α(t+1), β(t+1), and γ(t+1) by Algorithm 1 in Web Appendix C satisfy a monotone decreasing property: ϕ(α(t), β(t), γ(t)) ⩾ ϕ(α(t+1), β(t), γ(t)) ⩾ ϕ(α(t+1), β(t+1), γ(t)) ⩾ ϕ(α(t+1), β(t+1), γ(t+1)).
The proof is deferred to Web Appendix A. The assumption indicates that the naïve prevalence rate lies on (0, 1) for each i, which is crucial to guarantee the existence of the optima at each step. By Proposition 1, any limit point of {(α(t), β(t), γ(t))} is a stationary point if ϕ is continuous. Since the objective function ϕ is nonconvex, the proposed algorithm can only guarantee the convergence to a local optimum and requires a careful selection of the initial point. We could use the warm start strategy, where the solution under the previous tuning parameter is used as the initial point for the next choice of tuning parameter. This strategy performed well when implemented in our numerical studies. In addition, it is straightforward to extend the described algorithm to other (multilevel) generalized linear models. We can still solve α-step using an off-the-shelf package (e.g. glm in R), and β- and γ-steps using the same strategies.
3.4. Choice of tuning parameter
We implement a model selection procedure to tune the choice of λ1 and λ2. We used the modified Bayesian information criterion (BIC) proposed in She and Owen (2011), . Here, is defined in (5), and the degrees of freedom (DF) is calculated by combining the DF calculated in the lasso and fused lasso regressions (Tibshirani et al., 2005; Zou et al., 2007; Tibshirani and Taylor, 2011), where
| (6) |
We searched for the (λ1, λ2) among a candidate set that minimizes the BIC*(λ1, λ2).
3.5. Weighting to account for missingness and selection bias
As indicated in the previous sections, our dataset involves a large number of missing values for the obese indicators (Yij). Furthermore, the data may not be directly comparable to a national sample. We consider a two-step weighting procedure to adjust for both missing BMI values and selection bias.
The first step is to account for the missingness of BMI. We assume missing at random (MAR), where the probability of missing BMI is independent of its response conditional on the covariates (Little and Rubin, 2014). Let Rij = 1 if Yij is observed and Rij = 0 otherwise. The weight was defined as the inverse probability of observing BMI, , which can be estimated by a logistic regression. The second step is to adjust for the population distribution of age, sex, and race/ethnicity. We applied a post-stratification correction using 2012 national census data. The final weight for each subject was the product of the inverse probability weight and the post-stratification weight. The objective function and subsequent procedures are modified accordingly. Furthermore, we employed a bootstrap method with a first-order normal approximation (see e.g. Puth et al., 2015 and Efron and Tibshirani, 1994) to construct confidence intervals that account for the uncertainty of missingness and selection bias, where the weights and model estimates were recalculated for each resampled dataset. Details can be found in Web Appendix B.
4. Simulation studies
We compared the proposed method with a classic GLMM, the GLMM with a conditional autoregressive random effect (GLMM-CAR), and the covariate-adjusted spatial scan statistic proposed by Jung (2009) (Scan Statistic). The GLMM assumes where (r1, …, rK)T ~ MVN(0, IK) is the independent random effect, and δ is the global intercept. The model for GLMM-CAR is , where (b1, …, bK)T ~ MVN(0, Σ) represents the spatially smooth random effect, and Σ enjoys the form in the CAR model proposed by Besag et al. (1991). We used the function S.CARmultilevel() of R package CARBayes with the default option to implement GLMM-CAR. We use cutoff-based approaches to identify outlier regions once models are fitted via GLMM and GLMM-CAR. Let be the predicted random effect of the i-th region. The i-th region was declared as an outlier if , where is an estimated standard deviation of ri. The cutoff of is a popular choice in the literature (She and Owen, 2011). The covariate-adjusted scan statistic method (Jung, 2009) assumes . Here, S denotes a cluster of regions. For each , the method repeatedly fits the model and calculates the likelihood ratio test (LRT) statistic for testing H0 : θ = 0. Then the method selects as the hot spot if the corresponding LRT statistic is the largest. We also included three “oracle” versions of our method, where ϕ is minimized with respect to one of α, β, or γ while the other two are set to the true values: with respect to α (Oracle α); with respect to β (Oracle β); and with respect to γ (Oracle γ).
We considered K (K = 20, 40) regions where the number of subjects in each region was n (n = 50, 100). We generated Qij = (Zij, Xi)T, where Zij and Xi were drawn from Bernoulli distributions with a probability of 0.5. We set α = (α1, α2) = (−0.2, 0.2). For simplicity, we simulated K locations on a one-dimensional line with Si ~ Unif(5, 95), i = 1, …, K. βi was set to logit(0.4) if 5 ⩽ Si < 35, logit(0.5) if 35 ⩽ Si < 65, and logit(0.6) if 65 ⩽ Si ⩽ 95. We randomly chose KO regions, where γi = 2 for ⌊K0/2⌋ regions (⌊t⌋ is the maximum integer no larger than t) and γi = −2 for the remaining. Thus, those KO regions with γi ≠ 0 are the outliers. We varied the number of outliers so that KO/K = 0%, 5%, 10%, 15%. For each scenario, we repeatedly generated 1000 datasets. We applied different methods on each dataset and evaluated the performance metrics. The performance measures were averaged over 1000 replications. The tuning parameters were selected using the proposed modified BIC, among a pre-defined candidate set with λ1 ∈ [2−2, 212] and λ2 ∈ [2−5, 22].
To compare the performances in outlier detection, we used Matthews Correlation Coefficient (MCC), defined by
Here, TP stands for true positive, where the detected outlier region is indeed an outlier; TN stands for true negative, where the labeled normal region is normal; FP stands for false positive, where the detected outlier region is actually normal; and FN stands for false negative, where the labelled normal region is actually an outlier. A higher value of MCC is preferred, where MCC = 1 indicates a perfect classifier and MCC = 0 indicates a random guess. We evaluated the MCC on the proposed, GLMM, GLMM-CAR, Scan Statistic, and Oracle γ. The MCCs are presented in Figure 1. The MCC of the proposed method was comparable to its oracle counterpart, Oracle γ. It improved over increasing K and stabilized over increasing proportion of outliers. In contrast, the MCCs of the GLMM and GLMM-CAR decreased when either the proportion of outliers or the K increased. We further present the true positive rate (sensitivity) and the true negative rate (specificity) in the Appendix D.1 of the supplementary material. Figures S1 and S2 show that when the proportion of outliers increased, both GLMM and GLMM-CAR yield low sensitivities. This finding is consistent with existing literature, e.g, She and Owen (2011), suggesting that cutoff-based outlier detection may not operate well with multiple outliers, since the optimal choice of the cutoffs depends on the true residual distribution that is usually unknown. The MCC of the Scan Statistic was around zero, even when n and K were increased, indicating that the Scan Statistic failed to detect multiple outlier regions. In summary, our method showed promising performance in identifying outliers, especially when the proportion of outliers was increased.
Figure 1.
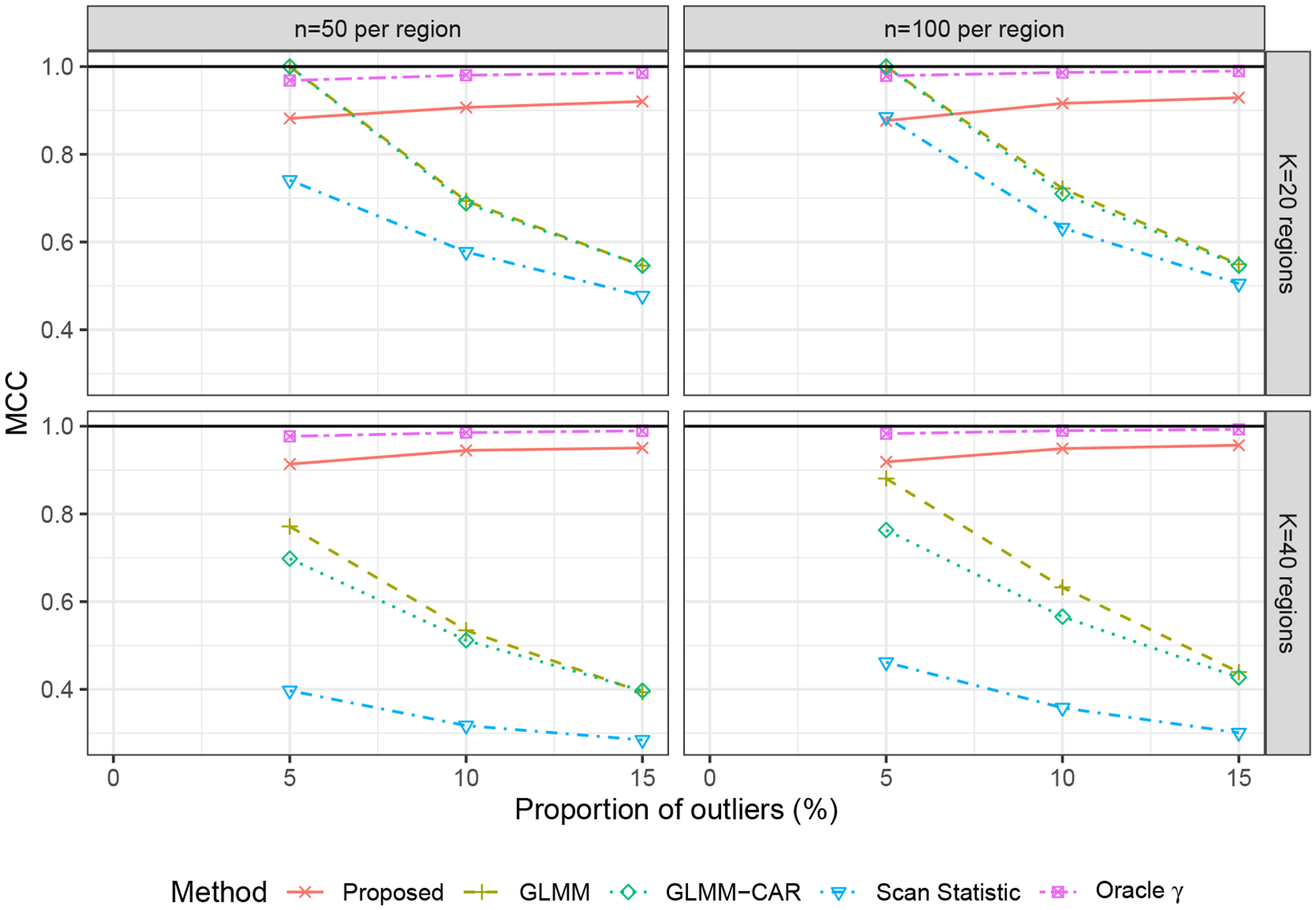
MCC, varying the number of outliers over 1000 replications.
We further compared the proposed method with GLMM, GLMM-CAR, and Oracle α in terms of the bias of the individual-level covariate effect and the community-level covariate effect ; the empirical coverage probabilities of and ; and the root mean squared error (RMSE) of the region-level prevalence rates . Here, and is the empirical average of the estimated individual-level prevalence estimates, , taken over j = 1, …, ni. The results are presented in Table 1. The scan statistic was excluded from the comparison because it did not provide estimators of α and pi. The biases of estimating α1, the individual-level covariate effect, were close to zero in the proposed method, especially when both n and K increased. The confidence intervals from different methods were comparable. The biases of , the region-level covariate effect, were reduced as K increased in the proposed method. The performances of the proposed method and Oracle α were similar in terms of the biases. The slightly lower coverage of α2 by the proposed method when K = 20 might be due to the relatively small K for estimating a large number of region-level parameters (β and γ). The method achieved nominal coverage when K increased to 40. The RMSEs of were smaller in the proposed method than in the two GLMMs, although, as anticipated, larger compared to Oracle α.
Table 1.
Biases (± standard errors) and empirical coverage probabilities of and , RMSE of , over 1000 replications, varying the proportion of true outlier regions (KO/K).
| KO/K | Method | n = 50 per region | n = 100 per region | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE of | RMSE of | ||||||||||
| Bias | CP | Bias | CP | Bias | CP | Bias | CP | ||||
| K = 20 regions | |||||||||||
| Proposed | −.004 ± .008 | .942 | .002 ± .011 | .909 | .053 | .003 ± .006 | .950 | −.011 ± .009 | .871 | .040 | |
| 0% | GLMM | −.004 ± .008 | .950 | −.008 ± .013 | .809 | .057 | .003 ± .006 | .951 | −.013 ± .011 | .684 | .044 |
| GLMM-CAR | −.004 ± .008 | .957 | −.013 ± .011 | .943 | .052 | .002 ± .006 | .956 | −.014 ± .009 | .956 | .038 | |
| Oracle α | −.002 ± .007 | .948 | .003 ± .006 | .958 | .016 | .003 ± .005 | .953 | −.003 ± .005 | .953 | .011 | |
| Proposed | −.006 ± .008 | .949 | −.004 ± .012 | .931 | .054 | .002 ± .006 | .957 | −.010 ± .010 | .898 | .041 | |
| 5% | GLMM | −.006 ± .008 | .951 | −.013 ± .016 | .663 | .062 | .001 ± .006 | .953 | −.026 ± .017 | .465 | .046 |
| GLMM-CAR | −.003 ± .008 | .955 | −.013 ± .016 | .912 | .062 | .001 ± .006 | .951 | −.017 ± .015 | .940 | .045 | |
| Oracle α | −.003 ± .007 | .944 | .006 ± .006 | .959 | .016 | .003 ± .005 | .953 | −.003 ± .005 | .945 | .011 | |
| Proposed | −.003 ± .008 | .936 | −.002 ± .013 | .943 | .055 | .004 ± .006 | .950 | −.011 ± .010 | .918 | .041 | |
| 10% | GLMM | −.003 ± .008 | .936 | −.012 ± .020 | .608 | .063 | .003 ± .006 | .951 | −.025 ± .020 | .466 | .046 |
| GLMM-CAR | −.005 ± .008 | .951 | .002 ± .019 | .920 | .063 | .002 ± .006 | .956 | −.006 ± .019 | .934 | .046 | |
| Oracle α | −.001 ± .007 | .943 | .005 ± .007 | .961 | .016 | .003 ± .005 | .953 | −.004 ± .005 | .951 | .011 | |
| Proposed | −.001 ± .009 | .937 | −.003 ± .014 | .947 | .056 | .003 ± .006 | .961 | −.010 ± .010 | .907 | .041 | |
| 15% | GLMM | −.002 ± .009 | .930 | −.012 ± .023 | .545 | .063 | .002 ± .006 | .956 | −.025 ± .023 | .400 | .046 |
| GLMM-CAR | −.005 ± .008 | .948 | .010 ± .023 | .911 | .063 | .002 ± .006 | .955 | .002 ± .023 | .924 | .046 | |
| Oracle α | .001 ± .007 | .950 | .005 ± .007 | .954 | .016 | .002 ± .005 | .956 | −.004 ± .005 | .940 | .011 | |
| K = 40 regions | |||||||||||
| Proposed | −.004 ± .006 | .948 | .010 ± .007 | .919 | .043 | −.000 ± .004 | .946 | −.002 ± .005 | .923 | .033 | |
| 0% | GLMM | −.004 ± .006 | .948 | .004 ± .009 | .804 | .055 | −.001 ± .004 | .950 | −.003 ± .008 | .683 | .043 |
| GLMM-CAR | −.003 ± .006 | .943 | .002 ± .007 | .961 | .047 | −.001 ± .004 | .949 | −.001 ± .005 | .983 | .035 | |
| Oracle α | −.005 ± .005 | .953 | .005 ± .005 | .950 | .012 | .000 ± .003 | .950 | −.001 ± .003 | .939 | .008 | |
| Proposed | −.003 ± .006 | .938 | .010 ± .008 | .948 | .045 | −.000 ± .004 | .950 | .000 ± .005 | .942 | .033 | |
| 5% | GLMM | −.004 ± .006 | .934 | .005 ± .011 | .639 | .061 | −.001 ± .004 | .950 | −.001 ± .011 | .507 | .046 |
| GLMM-CAR | −.004 ± .006 | .948 | .002 ± .010 | .947 | .059 | −.000 ± .004 | .945 | −.004 ± .010 | .944 | .044 | |
| Oracle α | −.004 ± .005 | .948 | .004 ± .005 | .938 | .012 | .000 ± .003 | .951 | −.000 ± .003 | .932 | .008 | |
| Proposed | −.006 ± .006 | .941 | .011 ± .008 | .963 | .046 | −.001 ± .004 | .943 | .003 ± .006 | .950 | .034 | |
| 10% | GLMM | −.006 ± .006 | .941 | .004 ± .014 | .589 | .062 | −.002 ± .004 | .943 | −.003 ± .014 | .423 | .046 |
| GLMM-CAR | −.004 ± .006 | .949 | −.002 ± .013 | .944 | .062 | −.002 ± .004 | .943 | −.007 ± .013 | .943 | .045 | |
| Oracle α | −.006 ± .005 | .951 | .006 ± .005 | .935 | .012 | −.001 ± .003 | .950 | .000 ± .003 | .946 | .008 | |
| Proposed | −.007 ± .006 | .945 | .010 ± .008 | .966 | .047 | .000 ± .004 | .947 | .001 ± .006 | .951 | .035 | |
| 15% | GLMM | −.006 ± .006 | .948 | .006 ± .016 | .512 | .063 | −.001 ± .004 | .949 | .005 ± .017 | .383 | .046 |
| GLMM-CAR | −.004 ± .006 | .950 | −.002 ± .016 | .950 | .063 | −.001 ± .004 | .945 | −.005 ± .016 | .945 | .045 | |
| Oracle α | −.006 ± .005 | .950 | .005 ± .005 | .948 | .012 | .000 ± .003 | .952 | −.000 ± .003 | .955 | .008 | |
We then compared the RMSE of β, , from the proposed method, GLMM-CAR, and Oracle β. The remaining methods were not included in the comparison because they did not provide an estimator of β. Figure 2 shows that the RMSE of decreased when n or K increased, and slightly increased with a larger proportion of outliers. The proposed method was comparable to Oracle β, and outperformed the GLMM-CAR. This indicates that the proposed method provides a good estimate of the baseline obesity rate.
Figure 2.
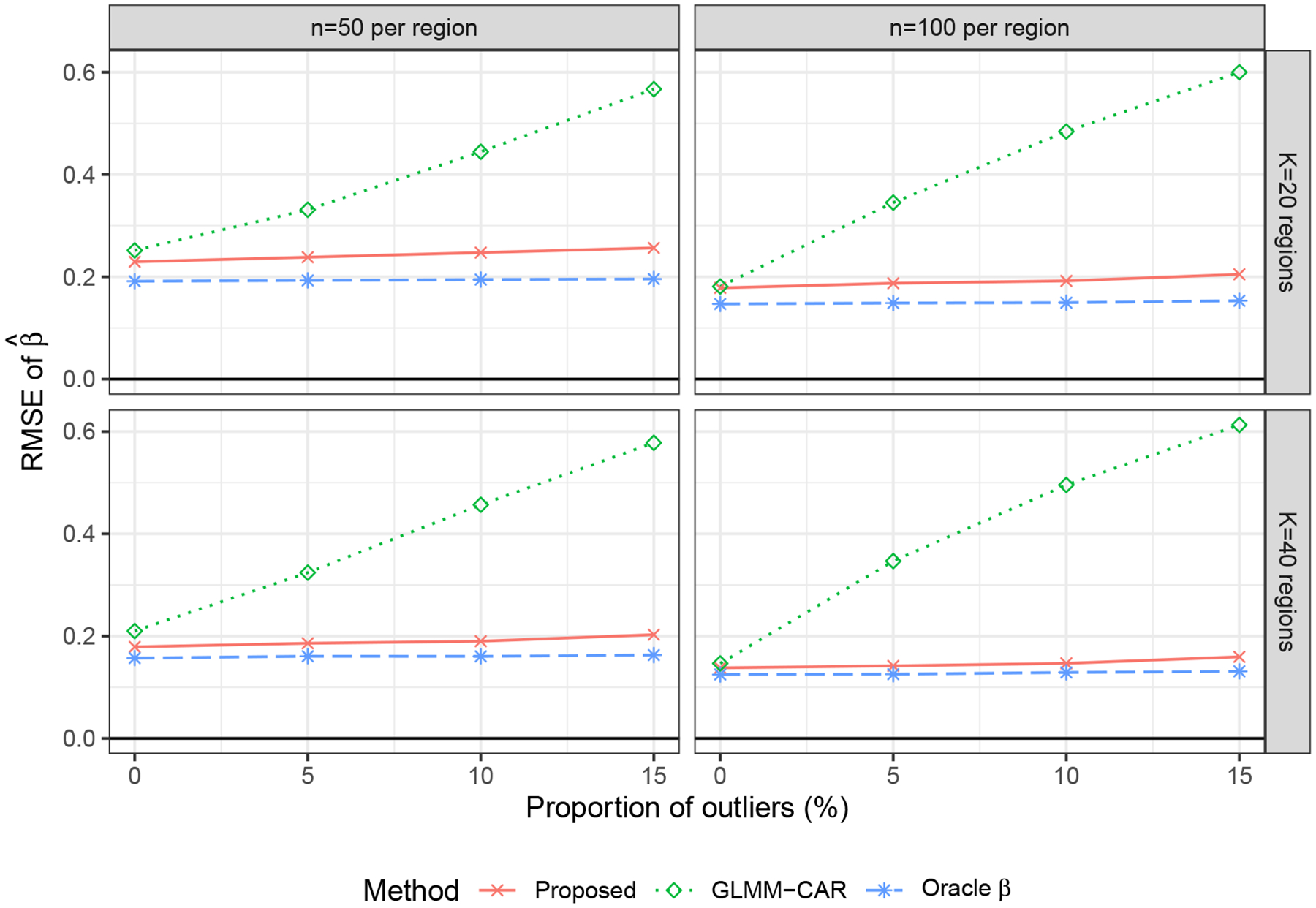
RMSE of , varying the number of outliers over 1000 replications.
In Web Appendix D.2 we report the performance of different methods when outcome Y could be missing. As anticipated, biases are larger in the estimated coefficients in the presence of missingness, but the proposed method outperformed the competitors overall.
5. Application to the PHINEX database
We considered census blockgroup as the geographic unit, and excluded certain blockgroups with small sample sizes, following the guidelines of Behavioral Risk Factor Surveillance System (CDC, 2016). The individual covariates Zij included sex, age as of 2012, race/ethnicity, insurance status, and the region-level covariates Xi included urbanicity and EHI. Age was categorized into 3 groups: 2–4 years, 5–9 years, and 10–14 years. Race and ethnicity were combined into a single covariate, and categorized into 4 groups: Hispanic, non-Hispanic white, non-Hispanic black, and non-Hispanic other. Patients with a commercial health service payor or Medicaid were included, and a few subjects with no insurance were excluded. Urbanicity, ranging from 1 to 11, was categorized into 3 groups: urban (1–4), suburban (5–8), or rural (9–11). We standardized EHI for numerical stability of the proposed algorithm. Raw-level frequencies of childhood obesity are presented in Web Appendix E.
The position Si was defined by a vector of the longitude and latitude of the centroid of the i-th block group. We constructed as the inverse of geodesic distances, , where denotes the greater circle distance between and . For the i1-th region, we retained the L largest and truncated the others at zero, where we treated L as a tuning parameter. A grid search on λ1 ∈ [2−1, 217], λ2 ∈ [2−5, 22] and L ∈ {3, 5, 7} was conducted to find the best combination of tuning parameters that maximizes BIC*. The confidence interval of each parameter was constructed using bootstrap over 1000 replications.
The estimated are summarized in Table 2. Overall, the proposed method had wider confidence intervals than GLMM and GLMM-CAR. This result was anticipated, given that our method had more parameters to estimate, which could lead to higher variabilities. The estimated coefficients from our model were comparable to those of GLMM and GLMM-CAR, except for the suburban effect. The obesity rate in females was lower compared to males, and younger children had lower obesity rates. Obesity rates in both non-Hispanic white and non-Hispanic other were lower than those in non-Hispanic black and Hispanic patients. The obesity prevalence was higher in subjects with Medicaid compared to those with commercial insurance. The EHI was positively associated with the estimated obesity rate.
Table 2.
Fitted coefficients and confidence intervals (in parentheses) for covariate effects.
| Model | |||
|---|---|---|---|
| Proposed | GLMM | GLMM-CAR | |
| Individual-level covariates | |||
| Sex (Base: Female) | |||
| ~ Male | .235 (.123, .347) | .226 (.147, .305) | .227 (.182, .274) |
| Age at 2012 (Base: Pre-school) | |||
| ~ School-aged | .568 (.449, .687) | .562 (.448, .675) | .558 (.489, .629) |
| ~ Adolescent | .875 (.773, .977) | .869 (.757, .981) | .864 (.798, .930) |
| Race/Ethnicity (Base: White, non-Hispanic) | |||
| ~ Black, non-Hispanic | .437 (.269, .605) | .434 (.315, .553) | .440 (.360, .519) |
| ~ Other, non-Hispanic | .035 (−.198, .269) | .042 (−.107, .191) | .054 (−.061, .166) |
| ~ Hispanic | .680 (.538, .822) | .667 (.556, .779) | .672 (.609, .734) |
| Insurance status (Base: Commercial) | |||
| ~ Medicaid | .522 (.417, .627) | .509 (.408, .611) | .509 (.452, .567) |
| Community-level covariates | |||
| Urbanicity (Base: Urban) | |||
| ~ Suburban | −.134 (−.217, −.051) | .037 (−.058, .132) | −.030 (−.071, .106) |
| ~ Rural | .125 (−.011, .262) | .237 (.095, .379) | .090 (−.084, .279) |
| Economic Hardship Index (standardized) | .120 (.083, .156) | .143 (.105, .181) | .096 (.044, .149) |
The fitted baseline obesity rates, , of the proposed method are displayed in the upper-left part of Figure 3, which appear to coincide with empirical knowledge of the greater Madison area. The lowest prevalence areas included the western portion of the Madison, Middleton, and Verona areas. It is known that these areas were recently developed and expanded, and include people who are generally younger and more socioeconomically advantaged compared to the surrounding areas. The intermediate prevalence areas, comprising the greater central and eastern Madison region, are more established, historic areas of the region, and are known to contain more stereotypical middle-class citizens. The highest prevalence areas are clearly the most geographically distant from the center of Madison, and are also all outside of Dane county, which contains Madison.
Figure 3.
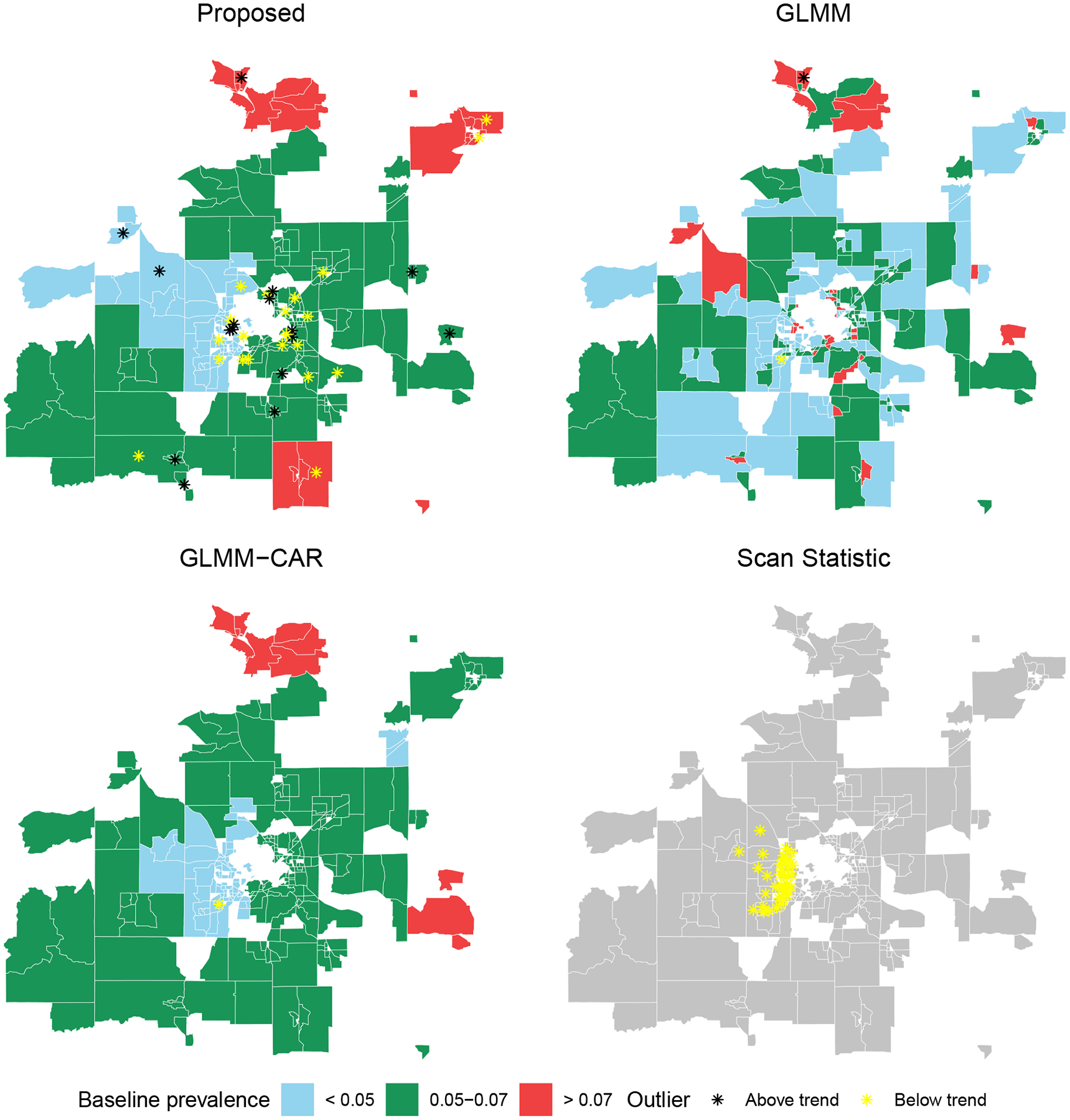
Estimated baseline prevalence rates and the identified outliers in childhood obesity surveillance. Each polygon represents a census blockgroup. Top-left: Result from the proposed method. Outliers are marked as black (yellow) as above the trend, (below the trend, ). Top-right: Result from the GLMM. Outliers are marked as black (yellow) as above the trend, (below the trend, ). Bottom-left: Result from the GLMM-CAR. Outliers are marked in the same manner with the GLMM. Bottom-right: Discovered cluster by the Scan Statistic with the highest likelihood ratio, which was below the trend.
The proposed method identified several outliers. Aberrant locations with obesity rates above the trend () and below the trend () are shown as black and yellow, respectively, in Figure 3. We identified 6% of blockgroups as outliers above the trend, and 8% as below the trend. Results are presented in Table 3, including:
crude obesity rates, ;
baseline obesity rates, ;
- obesity rates adjusted for covariates and outliers,
and frequencies of detections over B = 1000 bootstrap replications. We note that the outlier identification is relative to the fitted trend. For example, blockgroup 212 had an ordinary level of the estimated crude obesity rate (0.180). However, the crude rate was much higher than the fitted value of expected obesity prevalence (0.085). There existed unexplained information that could contribute to the elevated rate. Hence, it was declared as an outlier above the trend. The frequency of detection based on the bootstrap provides a glimpse of the uncertainty of aberrance. The outlier regions above the trend tended to have higher frequencies than those below the trend.
Table 3.
The anonymized IDs of the outlier blockgroups identified by the proposed method, their sample sizes, crude obesity rates, fitted baseline obesity rates, adjusted obesity rates, and frequencies of detections over B=1000 bootstrap replications.
| Blockgroup ID | Unweighted sample size (ni) | Crude obesity rate | Fitted baseline obesity rate | Fitted adjusted obesity rate | Frequency of detection |
|---|---|---|---|---|---|
| Above the trend | |||||
| 7 | 60 | .432 | .097 (.061, .150) | .264 (.153, .351) | .701 |
| 23 | 91 | .234 | .048 (.042, .057) | .129 (.110, .167) | .483 |
| 24 | 93 | .206 | .048 (.042, .057) | .113 (.095, .128) | .515 |
| 25 | 104 | .207 | .048 (.042, .057) | .115 (.094, .139) | .496 |
| 83 | 96 | .291 | .058 (.047, .064) | .174 (.133, .179) | .689 |
| 85 | 91 | .356 | .058 (.047, .064) | .187 (.139, .196) | .895 |
| 100 | 62 | .288 | .058 (.047, .064) | .149 (.117, .155) | .763 |
| 102 | 53 | .335 | .058 (.047, .064) | .217 (.147, .246) | .579 |
| 124 | 66 | .207 | .058 (.047, .064) | .117 (.090, .136) | .535 |
| 200 | 93 | .218 | .058 (.047, .064) | .133 (.102, .151) | .474 |
| 212 | 100 | .180 | .048 (.042, .057) | .085 (.076, .094) | .634 |
| 244 | 71 | .203 | .053 (.044, .064) | .121 (.096, .135) | .446 |
| 245 | 94 | .248 | .053 (.044, .064) | .148 (.105, .184) | .573 |
| 252 | 68 | .278 | .056 (.046, .073) | .148 (.108, .179) | .706 |
| 254 | 82 | .204 | .058 (.048, .071) | .103 (.080, .111) | .698 |
| 264 | 74 | .257 | .048 (.042, .057) | .130 (.092, .157) | .726 |
| Below the trend | |||||
| 22 | 110 | .063 | .048 (.042, .057) | .123 (.109, .151) | .363 |
| 32 | 221 | .045 | .048 (.042, .057) | .092 (.080, .101) | .079 |
| 35 | 146 | .067 | .048 (.042, .057) | .126 (.109, .151) | .300 |
| 70 | 67 | .168 | .058 (.047, .064) | .283 (.203, .292) | .269 |
| 73 | 109 | .175 | .058 (.047, .064) | .273 (.202, .279) | .136 |
| 82 | 259 | .173 | .058 (.047, .064) | .329 (.209, .342) | .106 |
| 94 | 134 | .105 | .058 (.047, .064) | .198 (.159, .210) | .383 |
| 115 | 68 | .061 | .058 (.047, .064) | .157 (.120, .161) | .468 |
| 118 | 192 | .141 | .058 (.047, .064) | .248 (.155, .253) | .062 |
| 125 | 81 | .047 | .058 (.047, .064) | .115 (.091, .115) | .277 |
| 127 | 295 | .051 | .058 (.047, .064) | .114 (.094, .121) | .195 |
| 128 | 125 | .054 | .058 (.047, .064) | .154 (.122, .175) | .698 |
| 136 | 466 | .038 | .048 (.042, .057) | .114 (.100, .132) | .684 |
| 153 | 469 | .045 | .048 (.042, .057) | .095 (.085, .103) | .047 |
| 159 | 202 | .081 | .058 (.047, .064) | .158 (.130, .176) | .345 |
| 168 | 139 | .117 | .056 (.046, .071) | .221 (.169, .247) | .418 |
| 186 | 66 | .097 | .058 (.047, .064) | .167 (.118, .184) | .204 |
| 229 | 133 | .139 | .077 (.048, .127) | .299 (.189, .395) | .599 |
| 235 | 61 | .139 | .077 (.048, .127) | .235 (.139, .312) | .365 |
| 246 | 210 | .060 | .053 (.044, .064) | .138 (.106, .158) | .283 |
| 262 | 90 | .076 | .081 (.050, .114) | .189 (.116, .237) | .459 |
The identified outliers by various methods do not fully overlap with each other, since the underlying mechanisms for detecting outlier regions are different. The crude method identifies the regions with the highest/lowest proportions without accounting for covariate effects. The GLMM method detects outliers based on the highest/lowest residual effects that do not rule out smooth regional effects. The proposed method and GLMM-CAR, on the other hand, declares a region as an outlier based on the residual regional effects after adjusting for the smooth regional effects. Unlike our method, both GLMM and GLMM-CAR identified very few outliers: two regions by GLMM and one by GLMM-CAR. As noted in Section 4, this conservative behavior is as expected. A different note is that the Scan Statistic only identified midwestern Madison area as abnormally low.
The localized outbreaks from our model may enable comparative investigations at granular levels. Obesity prevalence is determined by the interplay of patient demographic characteristics, behaviors, and community environmental factors. Our model has accounted for only a subset of them. Outliers could represent communities with meaningfully different environments than expected (e.g. much better or worse than average access to grocery stores, parks, etc), and/or it could represent community members with behaviors that are substantially different than expected (e.g. much greater or less physical activity, substantially better or worse dietary habits, etc.). Based on our results, healthcare professionals could look into risk factors within the outliers and compare these factors to adjacent blockgroups.
6. Concluding remarks
Motivated by childhood obesity surveillance using routinely collected EHR data, we developed a multilevel penalized logistic regression model, where the fusion and the nonconvex sparsity penalties are incorporated for simultaneous regional smoothing and outlier detection. While we only considered spatial surveillance, we are interested in generalizing the method to a longitudinal data setup for spatiotemporal surveillance.
In our paper, we assume that BMI is MAR, which is not testable in observational data. The feasibility of MAR for EHR data is an active area of research (Snyder et al., 2018). In the future, we can develop sensitivity analysis techniques that investigate sensitivity of the results to uncontrolled confounding (Greenland, 2004). Another future direction is to develop principled inferential procedures for the proposed work. We could potentially use ideas from inferential procedures for penalized generalized linear models (Taylor and Tibshirani, 2018).
Supplementary Material
Acknowledgement
We are grateful to the co-editor, associated editor, and all the reviewers for their helpful and insightful comments, which helped improve the manuscript. This work is supported by R21HD086754, P30CA015704, and S10OD020069 awarded by the National Institutes of Health, 2020R1G1A1A01006229 awarded by the National Research Foundation of Korea, and 1-1903-2017 awarded by Sookmyung Women’s University Research Grants. The authors thank Donghyeon Yu (Inha University, Incheon, South Korea) for sharing R source codes on the majorization-minimization algorithm and Albert Y. Kim (Amherst College, Amherst, MA) for sharing the source codes for the R package SpatialEpi.
Footnotes
Supporting information
Web Appendices, Tables, and Figures referenced in Sections 3, 4, and 5 are available with this paper at the Biometrics website on Wiley Online Library.
Data Availability Statement
The data that support the findings in this paper are not publicly available due to ethical restrictions. Interested readers could contact University of Wisconsin IRB committee (https://www.medicine.wisc.edu/research/uw-health-sciences-irbs) for details.
References
- Besag J, York J, and Molli A (1991). Bayesian image restoration, with two applications in spatial statistics. Annals of the Institute of Statistical Mathematics, 43(1):1–20. [Google Scholar]
- CDC (2016). Behavioral risk factor surveillance system, comparability of data BRFSS 2015 (Version #1—Revised: June 2016). Technical report. [Google Scholar]
- Chernozhukov V, Hansen C, and Liao Y (2017). A lava attack on the recovery of sums of dense and sparse signals. The Annals of Statistics, 45(1):39–76. [Google Scholar]
- Efron B and Tibshirani RJ (1994). An Introduction to the Bootstrap. Chapman and Hall/CRC. [Google Scholar]
- ESRI (2012). Environmental Systems Research Institute tapestry segmentation reference guide. CA: Redlands. [Google Scholar]
- Farrington CP, Andrews NJ, Beale AD, and Catchpole MA (1996). A statistical algorithm for the early detection of outbreaks of infectious disease. Journal of the Royal Statistical Society. Series A (Statistics in Society), 159(3):547–563. [Google Scholar]
- Flood TL, Zhao Y-Q, Tomayko EJ, Tandias A, Carrel AL, and Hanrahan LP (2015). Electronic health records and community health surveillance of childhood obesity. American Journal of Preventive Medicine, 48(2):234–240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman DJ, Parrish RG, and Ross DA (2013). Electronic health records and US public health: Current realities and future promise. American Journal of Public Health, 103(9):1560–1567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghosh M, Natarajan K, Waller LA, and Kim D (1999). Hierarchical Bayes {GLMs} for the analysis of spatial data: An application to disease mapping. Journal of Statistical Planning and Inference, 75(2):305–318. [Google Scholar]
- Greenland S (2004). The impact of prior distributions for uncontrolled confounding and response bias. Journal of the American Statistical Association, 98(461):47–54. [Google Scholar]
- Guilbert TW, Arndt B, Temte J, Adams A, Buckingham W, Tandias A, Tomasallo C, Anderson HA, and Hanrahan LP (2012). The theory and application of UW ehealth-PHINEX, a clinical electronic health record-public health information exchange. WMJ, 111(3):124–33. [PubMed] [Google Scholar]
- Jung I (2009). A generalized linear models approach to spatial scan statistics for covariate adjustment. Statistics in Medicine, 28(7):1131–1143. [DOI] [PubMed] [Google Scholar]
- Kim S-J, Koh K, Boyd S, and Gorinevsky D (2009). L1 trend filtering. SIAM Review, 51(2):339–360. [Google Scholar]
- Kulldorff M and Nagarwalla N (1995). Spatial disease clusters: Detection and inference. Statistics in Medicine, 14(8):799–810. [DOI] [PubMed] [Google Scholar]
- Lee S, Kwon S, and Kim Y (2016). A modified local quadratic approximation algorithm for penalized optimization problems. Computational Statistics and Data Analysis, 94:275–286. [Google Scholar]
- Little RJ and Rubin DB (2014). Statistical Analysis with Missing Data. John Wiley & Sons. [Google Scholar]
- Longjohn M, Sheon AR, Card-Higginson P, Nader PR, and Mason M (2010). Learning from State surveillance of childhood obesity. Health Affairs, 29(3):463–472. [DOI] [PubMed] [Google Scholar]
- Mercer LD, Wakefield J, Pantazis A, Lutambi AM, Masanja H, and Clark S (2015). Space–time smoothing of complex survey data: Small area estimation for child mortality. The Annals of Applied Statistics, 9(4):1889–1905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nathan RP and Adams CF (1989). Four perspectives on urban hardship. Political Science Quarterly, 104(3):483. [Google Scholar]
- Panczak R, Held L, Moser A, Jones PA, Rühli FJ, and Staub K (2016). Finding big shots: Small-area mapping and spatial modeling of obesity among Swiss male conscripts. BMC Obesity, 3(1):1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Puth MT, Neuhäuser M, and Ruxton GD (2015). On the variety of methods for calculating confidence intervals by bootstrapping. Journal of Animal Ecology, 84(4):892–897. [DOI] [PubMed] [Google Scholar]
- She Y and Owen AB (2011). Outlier detection using nonconvex penalized regression. Journal of the American Statistical Association, 106(494):626–639. [Google Scholar]
- Snyder JW, Bauer CR, Beaulieu-Jones BK, Pendergrass SA, Lavage DR, and Moore JH (2018). Characterizing and managing missing structured data in electronic health records: Data analysis. JMIR Medical Informatics, 6(1):e11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor J and Tibshirani R (2018). Post-selection inference for l1-penalized likelihood models. Canadian Journal of Statistics, 46(1):41–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R, Saunders M, Rosset S, Zhu J, and Knight K (2005). Sparsity and smoothness via the fused lasso. Journal of the Royal Statistical Society. Series B: Statistical Methodology, 67:91–108. [Google Scholar]
- Tibshirani RJ (2014). Adaptive piecewise polynomial estimation via trend filtering. The Annals of Statistics, 42(1):285–323. [Google Scholar]
- Tibshirani RJ and Taylor J (2011). The solution path of the generalized lasso. The Annals of Statistics, 39(3):1335–1371. [Google Scholar]
- Ugarte MD, Goicoa T, and Militino AF (2010). Spatio-temporal modeling of mortality risks using penalized splines. Environmetrics, 21(3–4):270–289. [Google Scholar]
- Wang H and Rodríguez A (2014). Identifying pediatric cancer clusters in Florida using log-linear models and generalized lasso penalties. Statistics and Public Policy, 1(1):86–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu D, Won J-H, Lee T, Lim J, and Yoon S (2015). High-dimensional fused lasso regression using majorization-minimization and parallel processing. Journal of Computational and Graphical Statistics, 24(1):121–153. [Google Scholar]
- Zhao Y, Zeng D, Herring AH, Ising A, Waller A, Richardson D, and Kosorok MR (2011). Detecting disease outbreaks using local spatiotemporal methods. Biometrics, 67(4):1508–1517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou H, Hastie T, and Tibshirani R (2007). On the “degrees of freedom” of the lasso. The Annals of Statistics, 35(5):2173–2192. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings in this paper are not publicly available due to ethical restrictions. Interested readers could contact University of Wisconsin IRB committee (https://www.medicine.wisc.edu/research/uw-health-sciences-irbs) for details.


