High-fidelity, accelerated whole-brain submillimeter in-vivo diffusion MRI using gSlider-Spherical Ridgelets (gSlider-SR)

Abstract

Purpose:

To develop an accelerated, robust, and accurate diffusion MRI acquisition and reconstruction technique for submillimeter whole human brain in-vivo scan on a clinical scanner.

Methods:

We extend the ultra-high resolution diffusion MRI acquisition technique, gSlider, by allowing under-sampling in q-space and Radio-Frequency (RF)-encoded data, thereby accelerating the total acquisition time of conventional gSlider. The novel method, termed gSlider-SR, compensates for the lack of acquired information by exploiting redundancy in the dMRI data using a basis of Spherical Ridgelets (SR), while simultaneously enhancing the signal-to-noise ratio. Using Monte-Carlo simulation with realistic noise levels and several acquisitions of in-vivo human brain dMRI data (acquired on a Siemens Prisma 3T scanner), we demonstrate the efficacy of our method using several quantitative metrics.

Results:

For high-resolution dMRI data with realistic noise levels (synthetically added), we show that gSlider-SR can reconstruct high-quality dMRI data at different acceleration factors preserving both signal and angular information. With in-vivo data, we demonstrate that gSlider-SR can accurately reconstruct 860 μm diffusion MRI data (64 diffusion directions at b = 2000 s/mm²), at comparable quality as that obtained with conventional gSlider with four averages, thereby providing an eight-fold reduction in scan time (from 1 h 20 min to 10 min).

Conclusion:

gSlider-SR enables whole-brain high angular resolution dMRI at a submillimeter spatial resolution with a dramatically reduced acquisition time, making it feasible to use the proposed scheme on existing clinical scanners.

1. Introduction

Diffusion MRI (dMRI) is a non-invasive imaging modality that permits the characterization of tissue microstructure as well as the structural connectivity of the human brain (1, 2). As it is sensitive to neural architecture, it is increasingly being used in the clinical investigation of several brain disorders (3, 4). dMRI holds the promise of being a key tool to explore and understand the human brain at an unprecedented level of detail. In the quest for a rich and detailed understanding of the human brain, it is the image resolution of dMRI that is the main limitation and is the focus of active research of the MRI community. Indeed, in clinical settings, diffusion-weighted images (DWI) are typically acquired at an isotropic resolution of 2 mm (5, 6). This causes undesirable partial volume effects, especially at the interface of different tissue types, such as the gray and white matter boundary. The limited resolution also has a significant impact on both white and gray matter studies. For example, in the superficial white matter regions, there is an abundance of short cortical association fibers (U-fibers) that connect cortical regions between adjacent gyri, which are difficult to trace at current resolutions. Increasing the current dMRI resolution will reduce the large partial volume effects, and facilitate the analysis of small structures that remain “hidden” at isotropic resolution of 2 mm (6).

Unfortunately, increasing the dMRI resolution, or equivalently, reducing the voxel size, is challenging since the Signal-to-Noise-Ratio (SNR) is proportional to the size of the voxel (7). A 1 mm isotropic dMRI acquisition will have eight times lower SNR compared to a 2 mm isotropic acquisition. While the SNR can be increased using multiple acquisitions and averaging, nevertheless, because the SNR is proportional to the square root of the number of averages, at least 64 repetitions would be needed to match the SNR of a 2 mm isotropic acquisition (6). Naturally, the total acquisition time of this averaging protocol is prohibitive, making this kind of approach impractical for human in-vivo settings.

The trade-off between image resolution, SNR, and acquisition time can be circumvented using super-resolution based methods. Super-resolution methods fall in the category of reconstruction frameworks where a high-resolution image is estimated from a set of low-resolution images, each one sampled with different geometric schemes. Formulated as the solution of an inverse problem, the restored image (or the super-resolution image), suffers less from SNR penalty than a direct isotropic acquisition since the SNR of the low-resolution images, normally, thick-slices images, is substantially higher. As the total acquisition time of the set of thick-slice images is comparable to that of the direct isotropic acquisition, super-resolution based methods effectively break the trade-off between image-resolution and SNR. Super-resolution was first applied in the context of MRI in (8), and ever since has been used in a multitude of cases, e.g, anatomical MRI (9, 10, 11, 12), quantitative relaxometry (13), and diffusion MRI (8, 14, 15, 16, 6). All of these super-resolution methods have been conceived and tested for resolutions > 1 mm. Recently, a multi-shot and multi-slab acquisition sequence was proposed in (17, 18) for submillimeter dMRI acquisition. This scheme has the advantage of good SNR, but at the cost of long acquisition times (about 30 min of scan time for only 12 gradient directions) along with complications from inter-slab registration due to head motion.

A turning-point in submillimeter diffusion MRI acquisition was the introduction of Slice Dithered Enhanced Resolution (Slider) (19) and recently the Generalized Slice Dithered Enhanced Resolution (gSlider) method (5). gSlider is an acquisition framework that utilizes a novel radio frequency (RF) encoding basis to excite multiple slabs of the whole human brain simultaneously, and then combine them to create a high-resolution thin-slice reconstructed volume. Specifically, several RF slab-encoded volumes are acquired in consecutive TRs, each volume encoded by a given “component” of what is called an RF-encoding basis, i.e., encoded by a particular RF excitation profile selected from a group of predefined RF waveforms (the basis). The elements of the RF-encoding basis are specifically designed to be highly independent between each other along with having a larger slice thickness to allow for increased SNR. When the simultaneously acquired slabs are unaliased with blipped-CAIPI, the set of RF-encoded thick-slice diffusion-weighted imaging (DWI) volumes are used to reconstruct a super-resolution thin-slice DWI volume using standard Tikhonov regularization (5). gSlider has been successfully applied to reconstruct diffusion MRI data with spatial isotropic resolution ranging from 660 μm to 860 μm with b-values between 1500 s/mm² and 1800 s/mm² (5, 20, 21).

To obtain high SNR and high angular resolution dMRI data, the current gSlider protocol requires long acquisition time. However, the redundancy within the RF-encoding as well as the different gradient directions (or q-space points) can be exploited to reduce the acquisition time dramatically to make it clinically feasible for whole-brain (submillimeter) in-vivo acquisition. In this work, we exploit this redundancy and propose an algorithm (termed gSlider-SR) to reconstruct high SNR gSlider data using a basis of spherical ridgelets (SR), which has been shown to be a highly sparse basis for dMRI data reconstruction, thereby allowing large undersampling factors (22, 23, 24, 25, 26, 27, 28). Specifically, for each diffusion direction, we propose to excite the slab-encoded volumes with just a subset of the RF-waveforms that constitute the RF-encoding basis of gSlider. Therefore, contrary to conventional gSlider, where each slab-encoded DWI volume that is probed at a given q-space point is encoded with all of the components of the RF-encoding basis, here we only employ a small subset of that basis. To provide complementary diffusion information, the subset of RF-encoding components is not static but varies along different q-space points. Note that within gSlider-SR, data from the RF-enconding space and the q-space is undersampled simultaneously, in a interleaved, synergistic fashion, offering more versatility than that achieved when undersampling is performed along a single dimension only, i.e., fully-sampled RF-encoding data with undersampled q-space data. Reconstructing thin-slice DWI volumes from such an undersampled set of measurements is an ill-posed, super-resolution reconstruction problem. However, we can cast this problem as that of reconstructing the entire dataset from a sparse set of measurements from the now unified RF-q space. Equipped with spherical ridgelets (SR), we recover the thin-slice DWI set by solving a constrained l₁ minimization problem whose theoretical background relies on the theory of Compressed-Sensing. We also accommodate for partial Fourier reconstruction and phase modeling in the gSlider-SR framework, which allows for estimating the thin-slice DWI set directly from complex thick-slice DWI sets, thereby avoiding noise bias that appears when working with magnitude data and high b value (29). We devised an optimization algorithm that solves for the l₁ minimization and the non-linear phase estimation problem simultaneously, allowing phase inconsistencies between different diffusion gradient directions. We validate gSlider-SR both qualitatively and quantitative with Monte-Carlo (MC) based simulations and in-vivo human brain data, where we showcase an accurate reconstruction of 64 DWI volumes (b = 2000 s/mm²) with 860 μm isotropic resolution in a scan time of approximately ten minutes.

An earlier version of the proposed gSlider-SR has been presented as an abstract at ISMRM 2016 (30). Spherical Ridgelets sparse basis were also used in the context of compressed-sensing to solve a super-resolution reconstruction problem with multiple overlapping sub-pixel shifted thick slices (6). In contrast to overlapping sub-pixel thick slices, we employ here gSlider slab encoded with different RF-pulses, which excite the sub-slices of the slab/thick-slice with different, spatially-variant patterns. We then constructed a substantially different forward-model than that of (6), which now accommodates for the particularities of the gSlider acquisition as well as phase modeling and partial Fourier reconstruction, which are inexistent in the work of (6). Note that unlike gSlider-SR, the work of (6) is designed for work with magnitude data only, which may incur in unacceptable noise bias for high b value acquisition (29). gSlider-SR then is statistically optimal since the data fidelity term of the cost function is adapted to Gaussian distributed data, and complex thick-slices DWI sets are coil-combined with the adaptive combine technique (31) which, being a linear operator, preserves Gaussian statistics (32). On top of that, gSlider-SR integrates an iterative affine registration step for in-vivo human brain data that accounts for eddy-current distortion as as well as rigid motion. Finally, the quantitative validation is substantially extended with a comprehensive Monte-Carlo based experiments, that includes High Angular Resolution Diffusion Imaging (HARDI)-based metrics.

2. Theory

2.1. Conventional gSlider reconstruction

In this section, the basic theory of conventional gSlider-based acquisition and reconstruction is covered. We also introduce the mathematical notation that will be used throughout the rest of the paper. In what follows, for simplicity, it is assumed that the simultaneously acquired gSlider slabs have been unaliased with parallel imaging and transformed into complex image space with a given coil combine technique. In a gSlider-based acquisition, each slab is encoded with K different Radio-Frequency pulses, whose corresponding slice-selective encoding profiles are shown in Fig.1.(a). The set of the K RF-profiles are called here a RF-encoding basis, and each of its RF-encoded profiles, the components of the basis. Those are designed to probe a thick slab (thickness: ∆_z mm) in K different ways, exciting the sub-slices that constitute the slab with a distinctive, spatially-variant pattern. From the K measurements, i.e., the thick-slices encoded values (Fig.1.(b)), one can resolve the K sub-slices that formed the slab by solving a linear equation system (Fig.1.(c)), thereby achieving thin-slices with a resolution of ∆_z/K mm. We direct the reader to (5) for more details about the RF-encoding basis.

Figure 1:

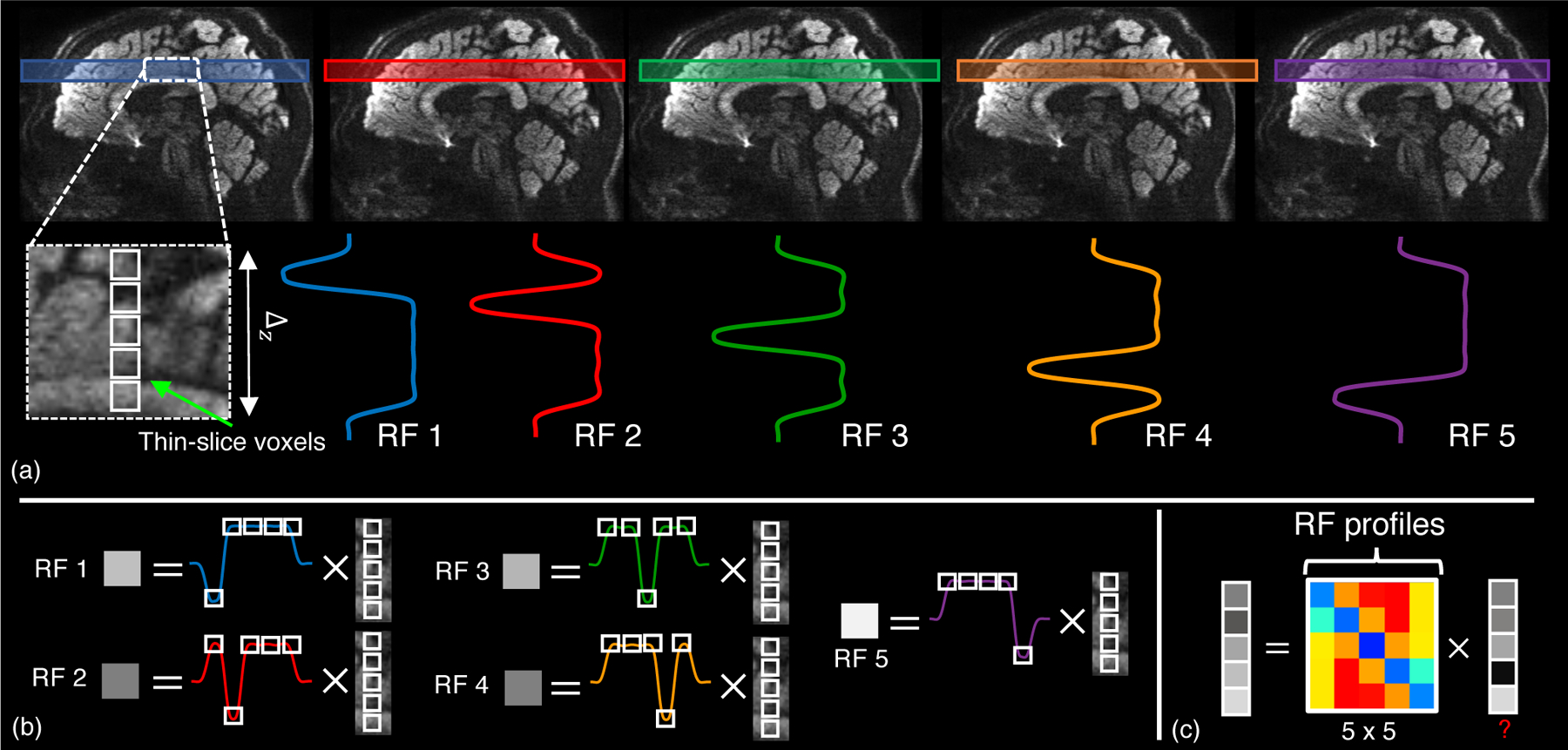
In gSlider, a slab of thickness ∆_z is encoded with K (five in this case) RF profiles, each one exciting the sub-slices of the slab with a distinctive spatially-variant pattern (a). This generates five different measurements, the voxels of the so-called thick-slices (b), that can be used to resolved the thin-slice voxels by solving a linear equation system (c).

By using vector notation, conventional gSlider reconstruction of a whole volume can be elegantly formulated in a concise way. Let us call the contiguous concatenation of the unaliased slabs along the slice-direction a thick-slice volume. The set of complex thick-slice volumes acquired at given q-space points q_j (j = 1, …, N_q) is named here as a thick-slice DWI set. The thick-slice DWI set that is encoded with the k-th component of the RF-encoding basis, i.e., each of the slabs which the volume comprises of is excited with the k-th RF-waveform, is denoted as ${\mathit{Y}}_k\in {ℂ}^{N_{LR}\times N_q}$. The number N_LR stands for the total number of voxels in each thick-slice DWI set and is given by N_LR = n_x × n_y × n_z-slices, where n_x × n_y is the size of the in-plane matrix, and n_z-slices is the number of thick slices that are acquired along the slice-encoding direction, z by convention. Such thick-slice DWI sets, Y_k, are related by means of the gSlider forward-model to an unobserved isotropic, high-resolution thin-slice (thickness of ∆_z/K mm ) real DWI set that we denote as $\mathit{S}\in {ℝ}^{N\times N_q}$, where the total number of voxels, N, is defined as N = n_x × n_y × n_z, with n_z = Kn_z-slices.

This forward-model, which connects S to Y_k, can be written as:

$${\mathit{Y}}_k=\mathit{M}\left(e^{i{\mathit{P}}_k}\odot {\mathit{D}}_k\mathit{S}\right)+{\mathit{\eta }}_k\hspace{1em}\text{with}\hspace{0.17em}k=1,\dots ,K,$$ [1]

where $\mathit{M}\in {ℂ}^{N_{LR}\times N_{LR}}$ is the in-plane point-spread-function of a (possible) partial Fourier acquisition, ${\mathit{P}}_k\in {ℝ}^{N_{LR}\times N_q}$ is the unknown phase information of each measured thick-slab acquisition with encoding profile k, ${\mathit{D}}_k\in {ℂ}^{N_{LR}\times N}$ is the gSlider downsampling operator that corresponds to the k-th RF-encoding basis and the term ${\mathit{\eta }}_k\in {ℂ}^{N_{LR}\times N_q}$ represents random noise of the acquisition. They symbol ☉ denotes Hadamard or point-wise product of matrices.

Reconstructing S from the low-resolution data Y_k is an inverse problem, in particular, a super-resolution reconstruction problem. In conventional gSlider, this process is accomplished in two-steps. First, Y_k are processed with background phase correction technique of (33). Next, the real-valued, phase-corrected thick slices, ${\mathit{Y}}_k^{†}$, are used to solve the following Tikhonov-regularized linear least squares (LLS) problem (5):

$$\underset{\mathit{S}}{\min }\frac{1}{2}\sum _{k=1}^K{\Vert {\mathit{Y}}_k^{†}-{\mathit{D}}_k\mathit{S}\Vert }_2^2+{\lambda }_{Tik}{\Vert \mathit{S}\Vert }_2^2.$$ [2]

2.2. Undersampling gSlider data in both the RF-encoding- and q-space

As mentioned in the introduction, while conventional gSlider is SNR-efficient compared to a full isotropic high-resolution acquisition, it, however, requires a relatively long-acquisition time. Indeed, let us say that N_q = 64 q-space points are needed for diffusion analysis. This implies that one have to acquired a total of KN_q = 320 thick-slice DWI sets in order to reconstruct N_q = 64 high resolution DWI sets (Fig.2.(a)). To shorten this long acquisition time, a straightforward action is either reducing the the number of RF-components, i.e., undersampling in the RF-space, or reducing the number of q-space points, in other words, undersampling in q-space. Reconstructing a thin-slice DWI volume with an incomplete RF-encoding basis is an ill-posed problem that cannot be solved if no information a priori is incorporated. On the other hand, it is possible to apply undersampling in q-space, and attempt to recover the diffusion signal at missing q-space points with a plethora of techniques (see (34) for a comprehensive review). In the context of gSlider, this modus operandi would constitute a three-step, sequential, process: 1) background-phase correction for Y_k, 2) Tikhonov-based gSlider reconstruction (Eq. 2), and 3) voxel-wise application of undersampled diffusion signal recovery methods. A downside of this approach is that, being a serial application, the last step will suffer from modeling-errors propagation (e.g., cost function of the dMRI signal recovery algorithm will not match the generation of input data) and modification of noise statistics will make the last step statistically suboptimal. Nevertheless, it has sense to combine the best of both worlds, and apply q-space and RF-encoding data under-sampling simultaneously and, importantly, in a complementary fashion. Further, to fully exploit the gSlider acquisition forward-model, the novel gSlider reconstruction scheme should be formulated as a unified, global, reconstruction approach.

Figure 2:

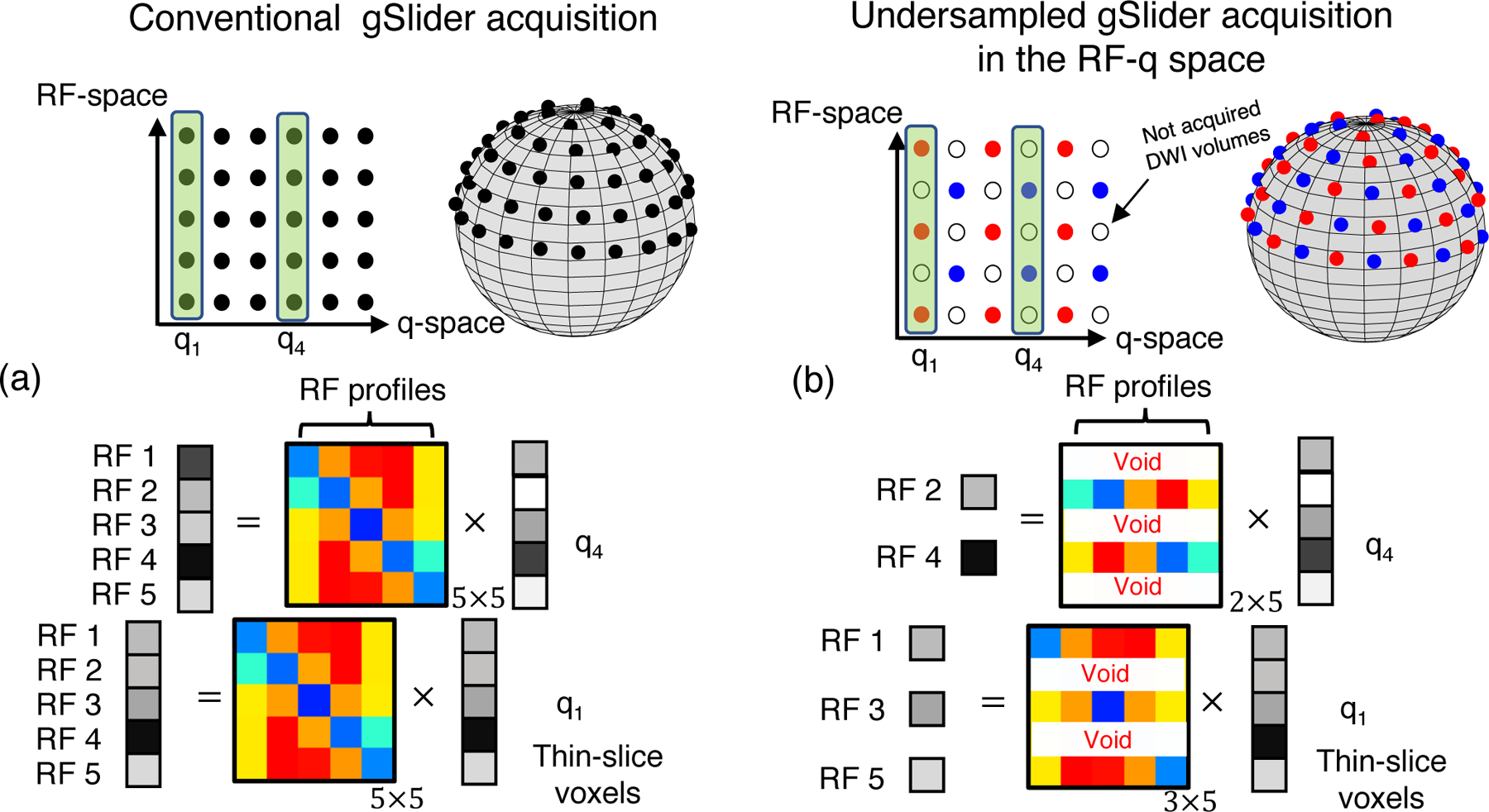
In a conventional dMRI gSlider acquisition (a) all the thick-slice DWI sets Y_k probed at the N_q = 64 q-space points (dark points) are encoded with the five RF-encoding profiles (vertical axis). However, in the undersampled gSlider acquisition in the RF and q-space (b), an incomplete RF-encoding basis is used to encode the thick-slices DWI volumes. In this example, DWI volumes that correspond to “red” q-space points, e.g., q₁, are encoded only with the first, third, and fifth RF-encoding profile, whereas DWI volumes probed with “blue” q-space points, e.g., q₄, are encoded with the second and fourth RF-encoding profile. This represents an undersampling scheme by a factor of 2. Therefore, the total acquisition time is reduced by half.

The basic idea is to exploit the expected diffusion MR signal redundancy to alleviate the ill-posed nature of the super-resolution thin slice problem for an incomplete RF-encoding basis. To gain insight into the problem, let us focus on the diagram shown in Fig.2.(b).

Let us suppose that an incomplete RF-encoding bases that comprises of three components (first, third, and fifth RF-waveform) is used for 32 of the 64 q-space points (red dots in the sphere of Fig.2.(b)), whereas the second and the fourth RF-wave form encode thick-slices of the remaining 32 q-space points (blue points). One one hand, for a fixed q-space point, this represents undersampling in the RF-space (acceleration of 5/3 or 5/2 X ). On the other hand, for a fixed RF-encoding component, k, this implies only $N_{q_k}=32$ DWI volumes are excited, e.g., a 2X undersampling factor in the q-space. Seen as a integrated, undersampling scheme in the joint RF and q-space, an acceleration factor of 2 X is achieved, as a total of only ${\sum }_{k=1}^K{N}_{q_k}=160$ DWI volumes are acquired, instead of 320 in conventional gSlider. Note that, in contrast to a 2 X acceleration factor application of q-space under-sampling after gSlider reconstruction, here all the diffusion directions are acquired at least once, gaining additional information.

The benefit of this interleaved, under-sampling in the joint RF-q space is that the missing RF-encoded information in the reconstruction problem of thin-slice DWI set, let us say probed at q-space point q₁, can be complemented with the acquired RF-encoded information corresponding to q-space point q₄, provided dMRI signal at points q₁ and q₄ shares “redundant” information. While an unformalized observation, it is, however, key to motivate the use of a dMRI signal representation that rigorously captures this redundancy and hence help solving the ill-posed super-resolution problem. Next subsection is devoted to this topic, but first, we present the complete, undersampled gSlider global forward model, which is written as,

$${\mathit{Y}}_k=\mathit{M}\left(e^{i{\mathit{P}}_k}\odot {\mathit{D}}_k\mathit{S}{\mathbf{\Omega }}_k\right)+{\mathit{\eta }}_k\hspace{1em}\text{with}\hspace{0.17em}k=1,\dots ,K,$$ [3]

where ${\mathbf{\Omega }}_k\left(N_q\times N_{q_k}\right)$ is a sampling mask $\left(N_{q_k}<N_q\right)$ which determines whether a given diffusion direction has been encoded by the k-th RF profile, and where now ${\mathit{P}}_k\in {ℝ}^{N_{LR}\times N_{q_k}}$ and ${\mathit{\eta }}_k\in {ℂ}^{N_{LR}\times N_{q_k}}$ and hence ${\mathit{Y}}_k\in {ℂ}^{N_{LR}\times N_{q_k}}$. As noted earlier, recovering $\mathit{S}\in {ℝ}^{N\times N_q}$ from Y_k, k = 1, …, K, in Eq. 3 is an ill-posed, super-resolution reconstruction problem, where many solutions exist. It, however, becomes tractable if prior knowledge about the structure of S is incorporated into the reconstruction framework. In this work, such a prior knowledge comes in form of spherical ridgelet (SR) basis (22), that we present briefly below.

2.3. Spherical ridgelets basis for diffusion signal recovery

Spherical ridgelets (SR) were proposed originally in (22), and have been successfully applied for diffusion signal recovery in many scenarios (22, 23, 24, 25, 26, 27, 28). In a nutshell, spherical ridgelets are functions defined on the unit sphere, $\mathrm{\Psi }\left(\mathit{q}\right)\left(\mathit{q}\in {\mathbb{S}}^2\right)$, that are designed to represent any dMRI signal. Given a collection of spherical ridgelets, ${\left\{{\mathrm{\Psi }}_m\right\}}_{m=1}^M$, any function s(q) with $\mathit{q}\in {\mathbb{S}}^2$ can be written as

$$s\left(\mathit{q}\right)=\sum _{m=1}^M{c}_m{\mathrm{\Psi }}_m\left(\mathit{q}\right),$$ [4]

where c_m, m = 1, …, M, are the SR coefficients. The number of SR functions, M, is defined as $M={\sum }_{j=-1}^J{\left(2^{j+1}{m}_0+1\right)}^2$, where J is the highest level of desired “resolution” and m₀ the minimum spherical order that fulfills a given error constraint (see construction of Spherical Ridgelets function in (24) for more details). We followed the recommendations of (24) and chose three resolution levels (J = 1) and m₀ = 4, giving a total of M = 395 SR functions. Let the column vector ${\mathit{s}}_n\in {ℝ}^{N_q}$ denote the diffusion signal observed at voxel n of the high-resolution DWI set S, i.e., S = [s₁, s₂, · · ·, s_N ]^T. It is then possible to write s_n = Ac_n, with

$$\mathit{A}=\left(\begin{array}{cccc}{\mathrm{\Psi }}_{11}& {\mathrm{\Psi }}_{12}& \cdots & {\mathrm{\Psi }}_{1M}\\ {\mathrm{\Psi }}_{21}& {\mathrm{\Psi }}_{22}& \cdots & {\mathrm{\Psi }}_{2M}\\ ⋮& ⋮& ⋮& ⋮\\ {\mathrm{\Psi }}_{N_{q}1}& {\mathrm{\Psi }}_{N_{q}2}& \cdots & {\mathrm{\Psi }}_{N_{q}M}\end{array}\right),$$ [5]

and where ${\mathrm{\Psi }}_{jm}$ is the m-th spherical-ridgelet function evaluated at q-space point q_j, and ${\mathit{c}}_n\in {ℝ}^M$ is the vector of SR coefficients at voxel n. It should be noted that the spherical ridgelets form an over-complete basis. As noted earlier, the dMRI signal can be represented in a sparse manner in the SR domain, thereby satisfying the theoretical guarantees for robust signal recovery from sparse measurements (35). Compressed-sensing theory asserts that, even with a very low number of measurements, accurate estimation of c_n, and hence S, is possible if c_n is sparse and if the spherical ridgelets representation matrix A is incoherent with respect to the diffusion sampling operator Ω_k. Robust signal recovery is obtained by solving an l₁ norm-based minimization approach to estimate c_n as described in the next section.

3. Methods

3.1. gSlider-SR: accelerated gSlider-Spherical Ridgelets reconstruction

3.1.1. gSlider-SR as a constrained, l₁-minimization problem

In this work, we propose to estimate the super-resolution DWI set S and the unknown thick-slice phase information P_k simultaneously, solving the following joint, phase-regularized, constrained l₁-minimization problem:

$$\begin{gathered} \underset{\mathit{S},{\mathit{P}}_k,{\left\{{\mathit{c}}_n\right\}}_{n=1}^N}{\min }\frac{1}{2}\sum _{k=1}^K{\Vert {\mathit{Y}}_k-\mathit{M}\left(e^{i{\mathit{P}}_k}\odot {\mathit{D}}_k\mathit{S}{\mathbf{\Omega }}_k\right)\Vert }_2^2+{\lambda }_{phase}\sum _{k=1}^K{\Vert \mathit{F}{e}^{i{\mathit{P}}_k}\Vert }_2^2+{\lambda }_{l_1}\sum _{n=1}^N{\Vert {\mathit{c}}_n\Vert }_1 \\ \text{subject}\hspace{0.17em}\text{to}\hspace{0.17em}\mathit{S}={\left[\mathit{A}{\mathit{c}}_1,\mathit{A}{\mathit{c}}_2,\cdots ,\mathit{A}{\mathit{c}}_N\right]}^T, \end{gathered}$$ [6]

where F is the matrix representation of a 2D finite difference operator (4 in-plane neighbors pixels are considered) that imposes smoothness on $e^{i{\mathit{P}}_k}$, and hence regularizes P_k, thereby avoiding problems with phase-wrapping that occur when smoothness is directly imposed over P_k (36). Note that discrepancy for phase between different diffusion direction is allowed since smoothness is only enforced within slab. The phase penalty parameter λ_phase controls the influence of the phase-regularization term over the data fidelity whereas the sparsity regularization term is weighted by ${\lambda }_{l_1}$.

The constrained problem of Eq. 6 can be efficiently solved using the Alternating Direction Method of Multipliers (ADMM) algorithm (37, 6). First, the so-called augmented Lagrangian function is constructed:

$$\frac{1}{2}\sum _{k=1}^K{\Vert {\mathit{Y}}_k-\mathit{M}\left(e^{i{\mathit{P}}_k}\odot {\mathit{D}}_k\mathit{S}{\mathbf{\Omega }}_k\right)\Vert }_2^2+{\lambda }_{phase}\sum _{k=1}^K{\Vert \mathit{F}{e}^{i{\mathit{P}}_k}\Vert }_2^2+{\lambda }_{l_1}\sum _{n=1}^N{\Vert {\mathit{c}}_n\Vert }_1+\frac{\rho }{2}\sum _{n=1}^N{\Vert {\mathit{s}}_n+{\mathbf{\Lambda }}_n-\mathit{A}{\mathit{c}}_n\Vert }_2^2,$$ [7]

where Λ_n is an auxiliary variable and ρ a regularization parameter intrinsic to the ADMM algorithm. Minimizing the Lagrangian (Eq. 7) for S, P_k and ${\left\{{\mathit{c}}_n\right\}}_{n=1}^N$ is equivalent to minimizing the following subproblems. Given an estimate of the SR coefficients ${\left\{{\mathit{c}}_n^{\left(t\right)}\right\}}_{n=1}^N$ at iteration (t), S^(t+1) and ${\mathit{P}}_k^{\left(t+1\right)}$ can be obtained as the solution of:

$$\underset{\mathit{S},{\mathit{P}}_k}{\min }\frac{1}{2}\sum _{k=1}^K{\Vert {\mathit{Y}}_k-\mathit{M}\left(e^{i{\mathit{P}}_k}\odot {\mathit{D}}_k\mathit{S}{\mathbf{\Omega }}_k\right)\Vert }_2^2+{\lambda }_{phase}\sum _{k=1}^K{\Vert \mathit{F}{e}^{i{\mathit{P}}_k}\Vert }_2^2+\frac{\rho }{2}\sum _{n=1}^N{\Vert {\mathit{s}}_n+{\mathbf{\Lambda }}_n^{\left(t\right)}-\mathit{A}{\mathit{c}}_n^{\left(t\right)}\Vert }_2^2.$$ [8]

We use a coordinate-descent algorithm to iterate between estimation of S and estimation of P_k. For fixed P_k, the minimum w.r.t. S is the LLS estimate of the cost function, which turns out to be linear. However, estimating P_k is a non-linear optimization problem. We employ the non-linear conjugate gradient (NLCG) algorithm to get a solution of this problem, with gradient in analytical form (formula is given in supplementary file) (36). Once we have estimates S^(t+1) and ${\mathit{P}}_k^{\left(t+1\right)}$, the estimation of the spherical ridgelets coefficients become decoupled,

$$\underset{{\left\{{\mathit{c}}_n\right\}}_{n=1}^N}{\min }\frac{\rho }{2}\sum _{n=1}^N{\Vert {\mathit{s}}_n^{\left(t+1\right)}+{\mathbf{\Lambda }}_n^{\left(t\right)}-\mathit{A}{\mathit{c}}_n\Vert }_2^2+\lambda \sum _{n=1}^N{\Vert {\mathit{c}}_n\Vert }_1.$$ [9]

Eq. 9 is the classical basis pursuit l₁ optimization problem that can be efficiently solved with the FISTA algorithm in a voxel-wise fashion. After solving Eq. 9, the auxiliary variable is updated as follows:

$${\mathbf{\Lambda }}_n^{\left(t+1\right)}={\mathbf{\Lambda }}_n^{\left(t\right)}+\left({\mathit{s}}_n^{\left(t+1\right)}-\mathit{A}{\mathit{c}}_n^{\left(t+1\right)}\right).$$ [10]

In summary, the final optimization algorithm consists of a inner loop that corresponds to the minimization of Eq. 8 and an outer loop (iteration variable t). In practice, we only iterate once in Eq. 8, whereas the outer loop is repeated until the relative l₂ norm between consecutive iterations is below a given tolerance, ϵ, or the number of iteration exceeds a given maximum number, N_iter.

It should be noted that the ADMM algorithm guarantees monotically decrease of the cost-function of Eq. 6 even if the cost-function to be minimized is nonconvex (38). Though we only iterate once in Eq. 8, that step guarantees a monotonically decrease of Eq. 8, which does not compromise the overall convergence of the ADMM algorithm to a local minimum (at least). In cases where there is lack of proof for convergence to a global minimum, a common guide of action is to provide a reasonably well-chosen initialization (6). We adopted that approach, initializing gSlider-SR with a a Tikhonov regularization-based solution, providing satisfactory results both in simulated and in-vivo data experiments.

Computational complexity

gSlider-SR was implemented in Matlab with some specific parts developed in C++, e.g.., the FISTA algorithm of Eq. 9. This l₁ optimization problem is separable for every voxel, and was implemented in parallel making use of multi-threading. For a super-resolution DWI set with N = 256 × 256 × 190 voxels and N_q = 64 q-space points, and a mask considering brain-tissue only, the computation time was about $T_{l_1}=15$ min in a computer with CPU: Intel Xeon Silver 4210 Processor with 20 cores at 2.2 GHz and 525 GB of RAM. Estimating S in Eq. 8 is a LLS problem that can be implemented very efficiently, about T_S = 10 min in Matlab code. The most computational demanding part was the non-linear estimation of thick-slice phase information P_k in Eq. 8. It took around $T_{{\mathit{P}}_k}=60$ min with a Matlab implementation of the NLCG method with Polak-Ribiere step. Solving the non-linear problem with quasi-Newton method would have perhaps converged faster, however, the memory requirements to estimate the Hessian would have rendered the problem unfeasible. Total time of the gSlider-SR algorithm is then the number of iterations multiplied by $T_{\mathit{S}}+T_{{\mathit{P}}_k}+T_{l_1}=85\min$. In the experiment section, we provide specific times for each experiment that is run with simulation and in-vivo data.

3.2. Experimental validation

The proposed super-resolution reconstruction framework was validated with simulated and in-vivo human brain data, both quantitatively and qualitatively.

3.2.1. Simulation experiments

Our goal with the simulation-based validation was to rigorously analyze, within a controlled scenario, the ability of gSlider-SR to reconstruct high resolution DWI for different grades of RF-encoded and q-space undersampled data. In order to isolate the effect of undersampled data from motion and phase estimation effects, which could lead to misleading interpretations, we assume that images were free from motion and that there was no need to estimate the thick-slice phase information, mimicking, for example, the case when thick-slices have already been corrected with background phase correction, thereby producing real-valued thick-slices. To do so, for a variety of undersampling scenarios, thick-slice DWI sets Y_k, k = 1, …, K = 5, were simulated following the forward-model of Eq. 3 selecting P_k = 0 and M = I where I is the identity matrix. The term η_k represents uncorrelated zero-mean Gaussian noise, a reasonably assumption when the acquired thick-slices coil images are combined with a linear operation, e.g., adaptive combined technique (31, 32), and the coil-combined complex thick-slice images are transformed into real-valued thick-slices with background phase correction (33).

The ground-truth (GT) high resolution DWI set S was created as described below.

Ground-Truth (GT) creation:

Whole human brain gSlider-SMS data was collected from a healthy male volunteer with a Siemens 3T Prisma scanner. Four scans of the full brain (FOV = 220 × 220 × 163 mm³) were obtained using the following parameters. With a single-shot EPI sequence, 38 thick axial slices (slice thickness ∆_z = 4.3 mm) were acquired with matrix size = 256 × 256 and 860 μm in-plane isotropic resolution, K = 5 RF-encodings, Multi Band (MB) = 2, phase-encoding with undersampling factor $R_{\text{in-plane}}=3$, partial Fourier = 6/8, TR / TE = 3500 / 81 ms, N_q = 64 diffusion directions (b = 2000 s/mm²) and 8 b0 images (non-diffusion weighted images). The N_q = 64 diffusion directions were approximately equally distributed over the hemisphere, $\left(x,y,z\right)\in {\mathbb{S}}^2$ with y > 0. The total acquisition time was about 1 h 20 min (20 min per scan). After k-space data reconstruction (slice and in-plane GRAPPA), all of the coil-combined (with adaptive combine technique (31)) complex thick-slice DWI images were transformed into real-valued images with background phase correction method of (33). Then, real-valued thick-slice DWI images were reconstructed using conventional gSlider approach (5), thereby creating high-resolution (860 μm) isotropic data. $B_1^{+}$ and T₁ corrections were applied with the method of (39). To account for eddy-current distortion and head motion, the high-resolution diffusion-weighted images (64 × 4 = 256 in total) were processed with the FSL tool EDDY_CORRECT. The reference b0-image used in EDDY_CORRECT was the last b0-image of the second scan.

Next, the processed four sets of high-resolution DWI were averaged to create a single, SNR-enhanced DWI dataset. Then, spherical harmonics were used to re-sample the DWI data so that the new q-space directions are equally spaced along a spherical spiral that covers the northern hemisphere of ${\mathbb{S}}^2$ (24). This was done to ensure efficient covering of the sphere for different undersampling factors.

Interleaved RF- and q-space undersampling schemes:

Four different interleaved RF-and q-space undersampling patterns with several acceleration factors (2 − 5X) were generated to assess the ability of the proposed algorithm for signal reconstruction. These schemes, which we called Scheme 2–5X respectively, are illustrated in Fig.3, and ultimately determine the diffusion sampling mask Ω_k that is used in Eq. 3 for k = 1, …, N_RF = 5 and for every acceleration factor.

Figure 3:

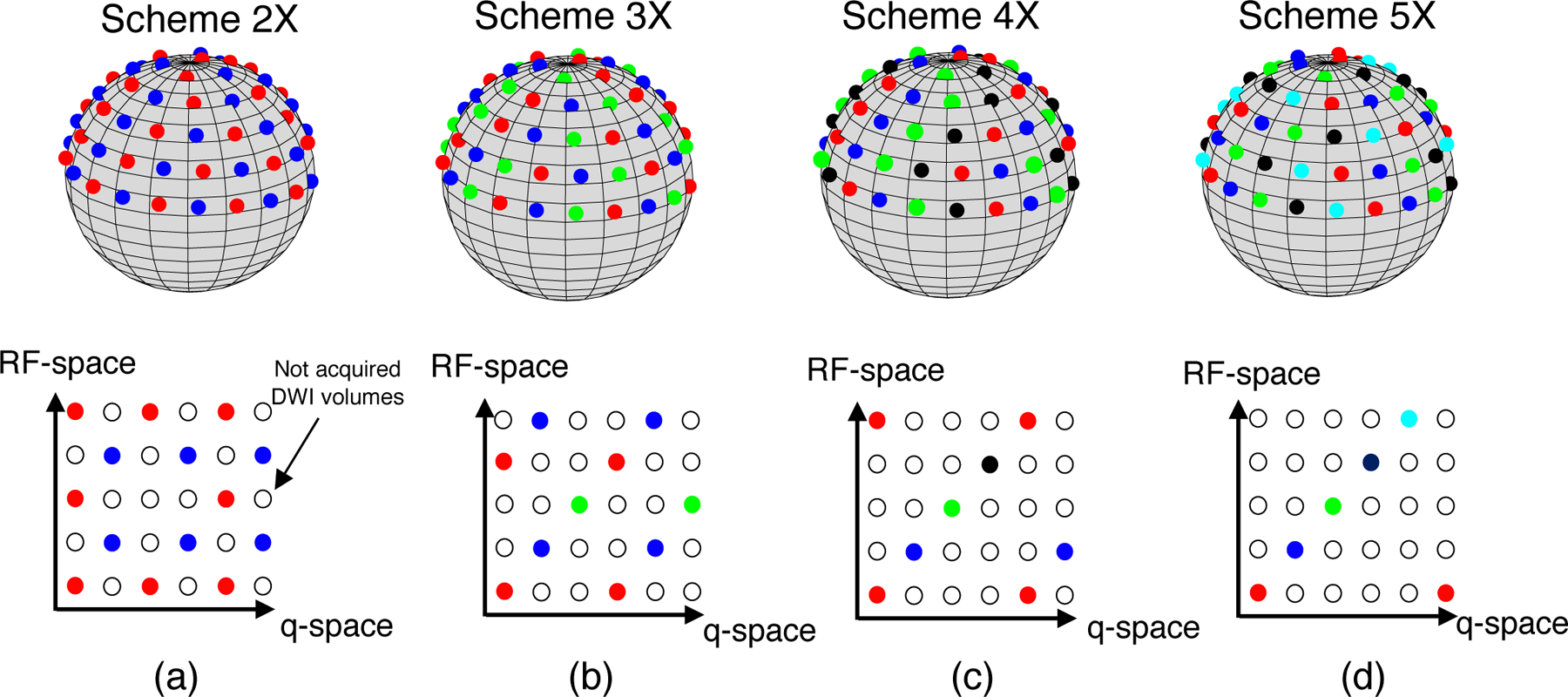
Undersampled RF and q-space schemes that are used in the MC-based simulation experiment. (a) 2 X: DWI volumes probed with red q-space points are encoded with the first, the third and the fifth RF-profile, whereas blue q-space points are encoded with the second and the fourth. (b) 3 X: red, blue and green q-space points are encoded with the first and the fourth, the second and the fifth, and the third RF-encoding profile, respectively. (c) 4 X: red, blue, green, and magenta q-points are encoded with the first and the fifth, the second, the third, and the fourth RF-encoding profile, respectively. (d) 5 X: red, blue, green, magenta and black q-space points are encoded with the first, the second, the third, the fourth, and the fifth RF-encoding profile, respectively.

The standard deviation of the noise term η_k was defined so as to produce a spatially-averaged SNR of 20 in the mean of the K b0 reference thick-slices images (34). For the proposed gSlider-SR algorithm, the following parameters were used: ${\lambda }_{l_1}=0.02$, $\rho =1$, $ϵ={10}^{-4}$, and N_iter = 16. These values were chosen heuristically (after exhaustive search) to provide best results. The reconstruction algorithm took about nine iterations to converge, with a total time of three hours.

For each under-sampling case (Scheme 2X to Scheme 5X ), a Monte-Carlo (MC) experiment was run. N_MC = 20 realizations of the forward-model of Eq. 3 were generated (e.g., N_MC = 20 different statistical noise realizations of η_k). For comparison purposes, we complement these results with a direct, high-resolution (HR) case with isotropic resolution of 860 μm, i.e., no gSlider downsampling operator. The SNR for the HR case in the b0 image was ∆_z = 4.3 times lower (SNR ≈ 4.5) than the SNR of the thick-slice DWI sets Y_k.

Metrics for quantitative validation:

Different performance measures were employed to assess the quality of the reconstructed high-resolution data $\widehat{\mathit{S}}$ in comparison to the ground-truth S. In particular, we were interested in evaluating the performance of gSlider-SR with respect to:

1. Quality of signal reconstruction. For each voxel n, we calculated the normalized mean-squared error (NMSE) between the estimate $\widehat{\mathit{S}}$ and ground truth S:

   $$\text{NMSE}=\frac{{\Vert {\widehat{s}}_n-{\mathit{s}}_n\Vert }_2^2}{{\Vert {\mathit{s}}_n\Vert }_2^2}.$$ [11]
2. Accuracy and precision for diffusion-tensor imaging (DTI). We fit a DTI model to the reconstructed high-resolution dMRI data $\widehat{\mathit{S}}$ with LLS fitting (FSL dtifit). Note that, while a high b-value (2000 s/mm²), the expected noise bias introduced in FA estimation (29) is avoided since noise follows a Gaussian distribution. For each voxel n, we assessed the accuracy and precision in estimating the fractional anisotropy (FA) with respect to the ground-truth FA (that derived from S). To assess accuracy, we use the relative sample bias, which is defined as

   $$\frac{\overline{\widehat{F}A}-F{A}_{GT}}{F{A}_{GT}},$$ [12]

   where $\overline{\widehat{F}A}$ is the sample mean (over MC = 20 realizations) of the estimated FA, $\widehat{F}A$, and FA_GT stands for the ground-truth FA. Precision is assessed by calculating the standard deviation of the MC = 20 estimates of the FA, $\left(\widehat{F}A\right)$.
   Furthermore, the angular error (in degrees), ∆_θ, between the principal diffusion directions was also computed:

   $${\Delta }_{\theta }=\frac{180}{\pi }\text{arccos}\left(\widehat{\mathit{u}}\cdot \mathit{u}\right),$$ [13]

   where $\widehat{\mathit{u}}$ is the main eigenvector of the tensor that is estimated from $\widehat{\mathit{S}}$ and u is that of the diffusion tensor estimated from S.

3. Quality of orientation distribution function (ODF) reconstruction. For each voxel n within the white-matter, the ODF $\widehat{\mathit{S}}$ was estimated using SR fitting, which was then compared to the ODF from the ground-truth data S. The principal diffusion directions and the number of fiber crossings (fiber peaks) were calculated. For a chosen peak in the ground-truth ODF, the angular error (in degrees) between the direction of that peak, u, and the corresponding direction from the reconstructed ODF $\widehat{\mathit{u}}$, was calculated as in Eq. 13. Next, a single average angular error per voxel ∆_θ was computed by averaging all errors from each of the ODF peaks in that voxel. We also calculated the percentage of false peaks P_false-peaks in the white matter region.

3.2.2. Experiments with in-vivo human brain data

The proposed gSlider-SR framework was also validated with in-vivo human brain data. In this experiment, we tried to assess how well gSlider-SR performs in a real scenario with undersampled gSlider data, in comparison to the fully-sampled case (N_q = 64 directions × 5 RF-encodings = 320 acquisitions). While not a ground-truth per se (due to the presence of spatially varying noise), the fully-sampled, averaged and hence SNR-enhanced DWI set was used as reference, and the high-resolution data reconstructed with gSlider-SR were compared to this set. For gSlider-SR, we used complex-valued thick slices Y_k, acquired as described in the GT creation section. No background phase correction was applied, but phase data P_k was jointly estimated as proposed in Eq. 6. Note that Gaussian noise assumption is still valid in the in-vivo experiment (32). To obtain the undersampled data, q-space points were removed from the original acquisition in such way as to obtain uniform coverage of the hemisphere. The following parameter settings were used ${\lambda }_{l_1}=0.06$, λ_phase = 10², ρ = 3, ϵ = 10⁻⁴, and N_iter = 16.

Accounting for subject motion and eddy-current distortions:

In-vivo real data typically suffer from subject motion and eddy current distortions, as mentioned in the simulation experiment section. In that setting, rigid motion and eddy distortions were corrected by registering S with affine transformations to a reference b0 image with the popular FSL tool EDDY_CORRECT. Therefore, the synthetically generated thick-slice DWI sets Y_k were free from motion and eddy distortions. In the real scenario, correcting for motion and eddy current distortion directly in the acquired Y_k is not advisable, since the RF-encoding information along slice direction can get mixed-up. An elegant (but computationally involved) solution to this problem was proposed in (20), which accounted for motion between RF-encodings, diffusion directions, and slab acquisitions.

In this work, we use a simpler iterative solution. We assume that there exist misalignment (affine deformations) between diffusion volumes only, and that relatively small or negligible motion exists between RF-encoding volumes of the same diffusion-weighted direction. Since the LLS problem for estimating S in Eq. 8 is separable along diffusion directions, the reconstruction of each high-resolution diffusion image is then free from motion artifacts. Nevertheless, the estimate DWI set S^(t+1) should be volume-wise registered before solving problem for Eq. 9, as spherical-ridgelets fitting requires the DWI data to be aligned. Coefficients ${\left\{{\mathit{c}}_n^{\left(t+1\right)}\right\}}_{n=1}^N$ are then estimated from a registered DWI dataset, $\mathcal{R}\left\{{\mathit{S}}^{\left(t+1\right)}\right\}$, where registration is performed with the FSL tool FLIRT (40). Next, the synthetically generated image defined by $\mathit{A}{\mathit{c}}_n^{\left(t+1\right)}$, n = 1,… N, (third summand in Eq. 8) is “unregistered” with the inverse transformation of $\mathcal{R}$, as the solution S in Eq. 8 is assumed to be affected by inter-volume motion, and voxel-wise correspondence is required. After iterating through this process, head motion and eddy-current distortion can be corrected using $\mathcal{R}\left\{{\mathit{S}}^{\left(t_{\text{end}}\right)}\right\}$ where t_end denotes the last iteration of the algorithm. The reference image for registration is the same b0 image that was used to account for eddy-current distortions and motion in the ground-truth dataset. With motion compensation incorporated (20 minutes per iteration approx.), gSlider-SR took about 14 h to converge in eight iterations with the desired tolerance ϵ.

4. Results

4.1. Simulation experiments

Fig. 4 shows an axial, coronal, and sagittal slice of a DWI volume from the fully-sampled ground-truth data S, as well as DWI volumes reconstructed with Tikhonov regularization and with gSlider-SR methods respectively (undersampling of 2 X). From Fig. 4, it is clear that Tikhonov regularization is not enough to reconstruct an accurate, high-resolution dMRI dataset with half of the q-space samples. Nevertheless, gSlider-SR is able to restore a highly detailed, artifact-free diffusion-weighted image, allowing the possibility of decreasing the acquisition time significantly without sacrificing image quality. This can be quantitatively confirmed from the NMSE maps of Fig. 5, where errors of about 2% are seen for whole brain (excluding CSF and ventricles) using gSlider-SR, but much higher errors are seen for a simple Tikhonov method.

Figure 4:

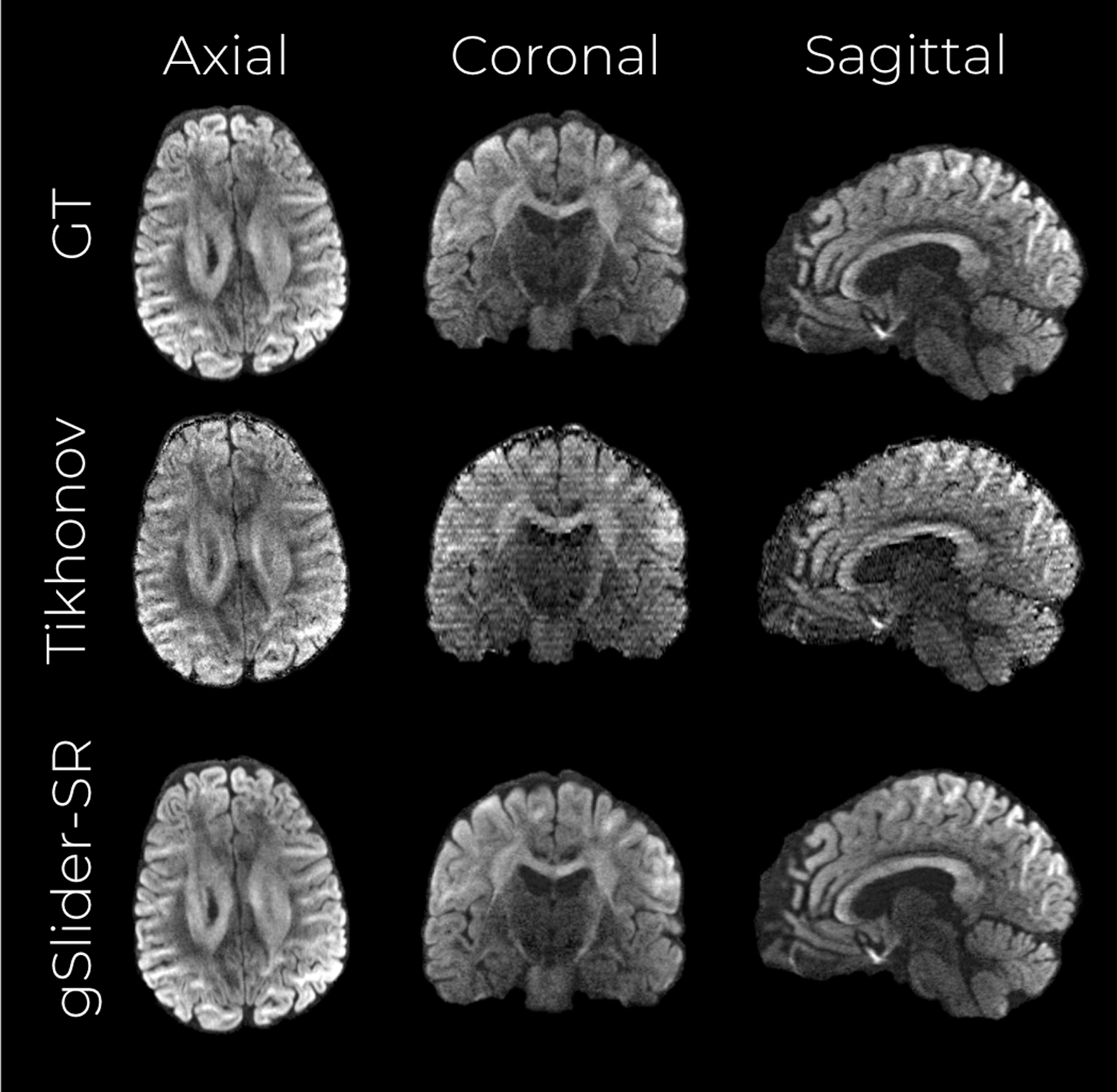
Simulation experiment with an acceleration factor of 2 X. A middle axial, coronal and sagittal slice of the NMSE maps from the reconstructed volumes are shown for the Tikhonov-based reconstruction (top row) and gSlider-SR -based reconstruction (bottom row).

Figure 5:

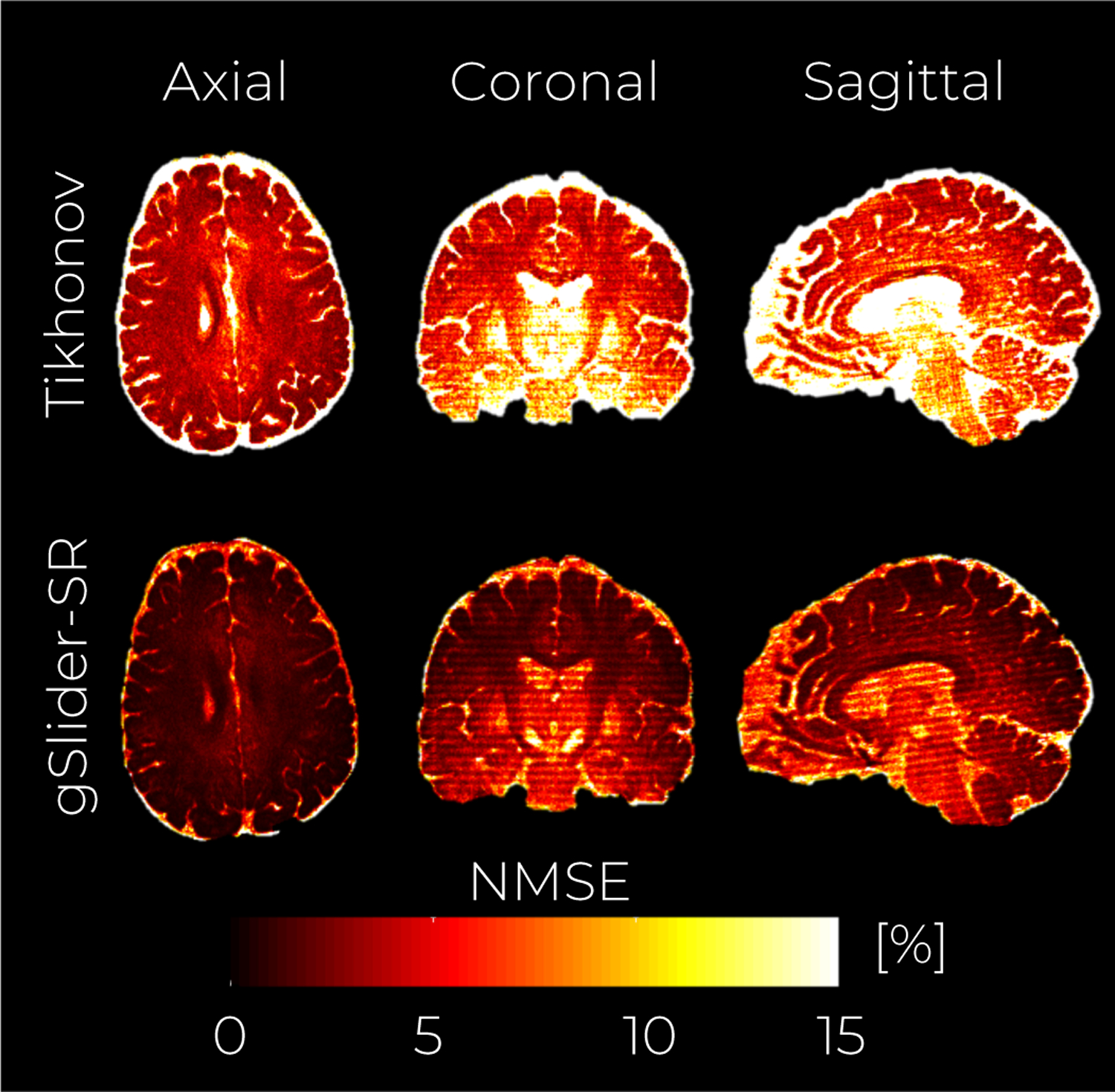
Simulation experiment with an acceleration factor of 2X. An axial, coronal and sagittal slice of the NMSE maps from the reconstructed volumes are shown for the Tikhonov-based reconstruction (top row) and gSlider-SR -based reconstruction (bottom row)

In Fig.6 we report quantitative metrics to evaluate the performance of gSlider-SR for various undersampling (and thereby acceleration) factors as well as the results with the fully sampled HR case. As expected, as the undersampling ratio increases, the performance of the gSlider-SR degrades. However, it is interesting to note that even for substantially high acceleration factors (4 X), more accurate and precise DTI parameters can be estimated from the high-resolution diffusion-weighted images reconstructed with the gSlider-SR method in comparison to those directly estimated from an isotropic, high-resolution (860 μm) acquisition, see results with label HR in Fig. 6.(b–c). Similar conclusions can be drawn for the angular error in estimating the principal diffusion direction from DTI as well as the directions of the peaks of the ODF, along with false/missing peaks results (Fig.6.(d–f)). Reconstructed high-resolution DWI sets as well as diffusion-metrics maps for all the acceleration factors are shown in Fig. 1–4 of the supplementary file.

Figure 6:

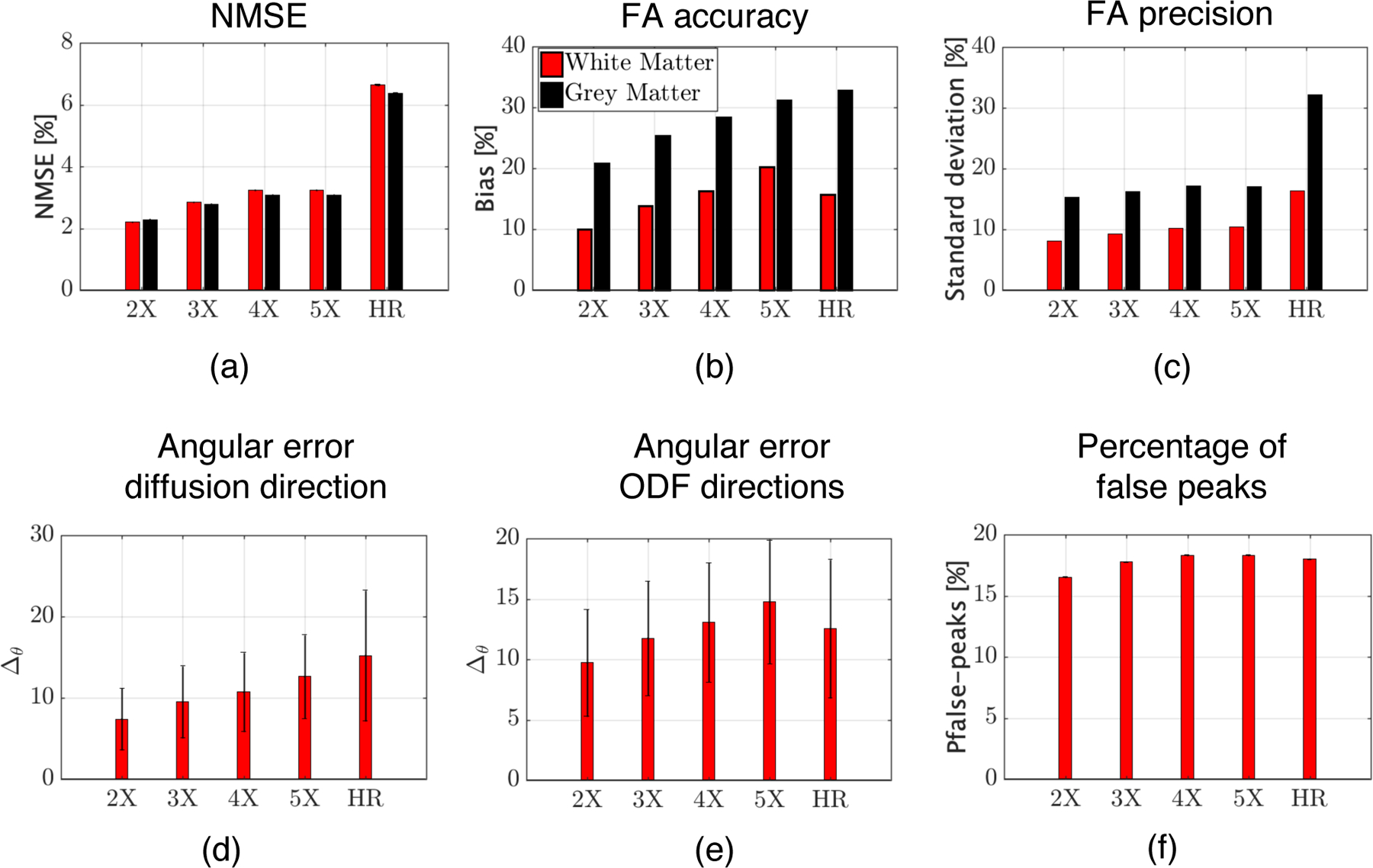
Quantitative validation of gSlider-SR reconstruction based on a MC-based simulation experiment for different undersampling schemes (2-5X). Results for the direct, 860 μm isotropic resolution acquisition (HR) are also shown

4.2. Experiments with in-vivo real data

An axial, coronal, and sagittal slice from a reconstructed high-resolution DWI volume is shown in Fig.7 for the reference set as well as different implementations of conventional gSlider and gSlider-SR. Moreover, the total time to acquire the thick-slice data to reconstruct such DWI sets is also reported. Estimated thick-slice phase images P_k are shown in Fig. 5 of the supplementary file. It can be seen that conventional gSlider reconstruction from one thick-slice DWI set (scan one in this case) suffers from severe noise. The SNR is enhanced if the alloted scan time is doubled to 40 min, and two DWI volumes reconstructed with gSlider are averaged (see gSlider two averages). The SNR-enhancing effect of the spherical ridgelets-based regularization seems evident in this experiment. In the unaccelerated case, gSlider-SR 1X, the reconstructed DWI volume is substantially less noisy than that obtained with conventional gSlider reconstruction, and even with the gSlider two averages case. Interestingly, the reconstructed volume with gSlider-SR 2X seems to present similar visual quality than the non-accelerated case, suggesting that 10 min may be enough to obtain, an artifact-free, SNR-enhanced, structure-preserving DWI volume that matches well with the reference data. Finally, as expected, averaging the four reconstructed scans with gSlider-SR 2X (40 min) produces the best results in terms of structural preservation and noise reduction (see zoomed-in area).

Figure 7:

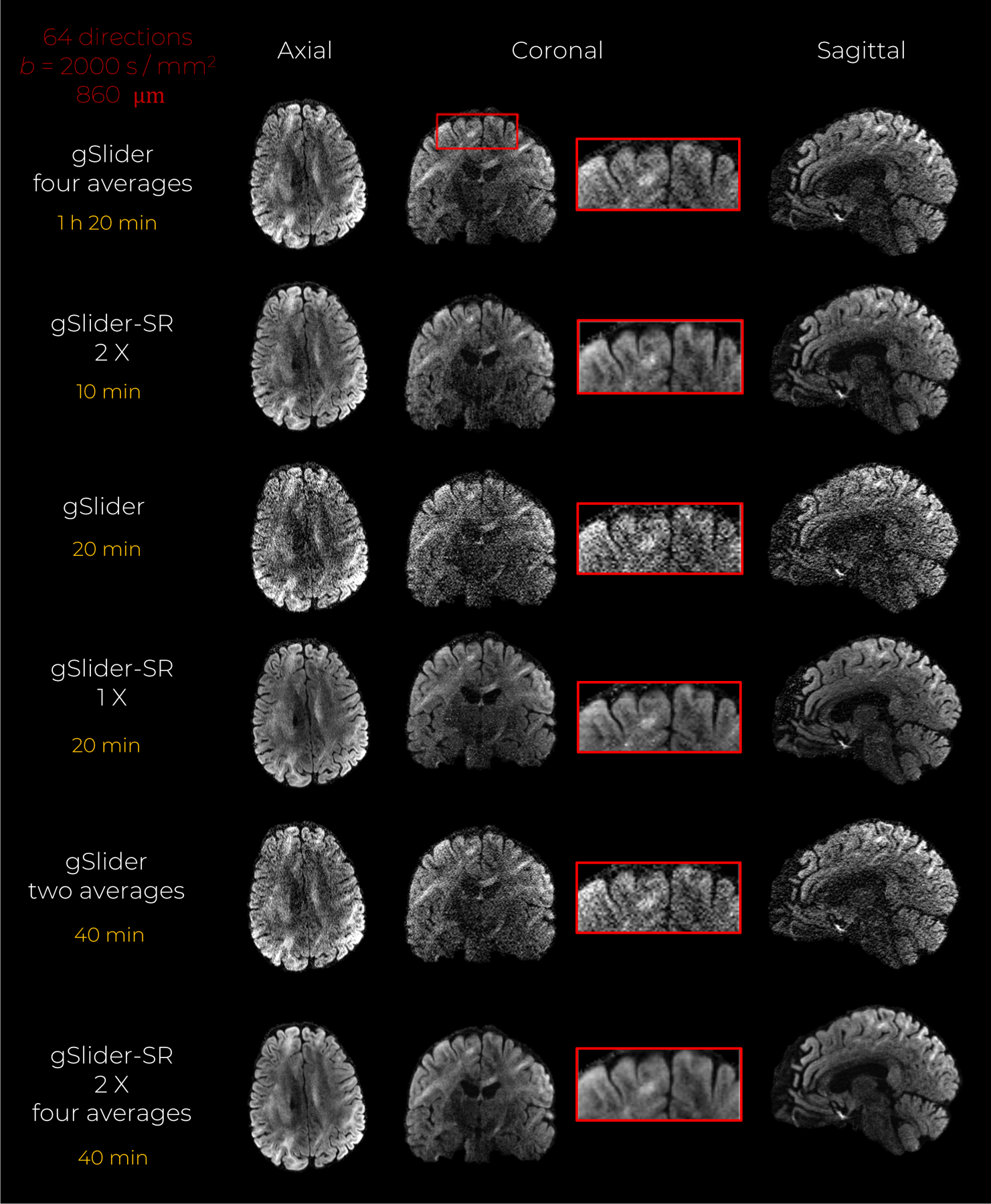
In vivo data experiment with an acceleration factor of 2X. An axial, coronal and sagittal slice of the same diffusion-weighted volume are shown for gSlider, and gSlider-SR based reconstruction, respectively

Quantitative NMSE maps presented in Fig.8 support the claims made above. Evidently, the reconstruction quality can be further improved if several thick-slice DWI sets are reconstructed with gSlider-SR, and averaged afterward. With a scan time-limit of 20 min, the gSlider-SR 1X method provides substantially better reconstruction than conventional gSlider (note the reduction of NMSE in white and grey matter). Reconstruction errors for different undersampling (and different scan times) are also shown in Fig.8. We note that, the data quality in the white matter from a 10-minute gSlider-SR method is quite comparable to that of the 80-minute gSlider four averages. Thus, if one were to account for the improved SNR, the proposed gSlider-SR 10-minute scan provides an 8-fold reduction in acquisition time, thereby making the method much more clinically practical. Color-encoded FA maps estimated with the DWI volumes obtained with gSlider-SR (2 X) also present similar visual quality as that obtained with the gSlider four-averages (Fig.9).

Figure 8:

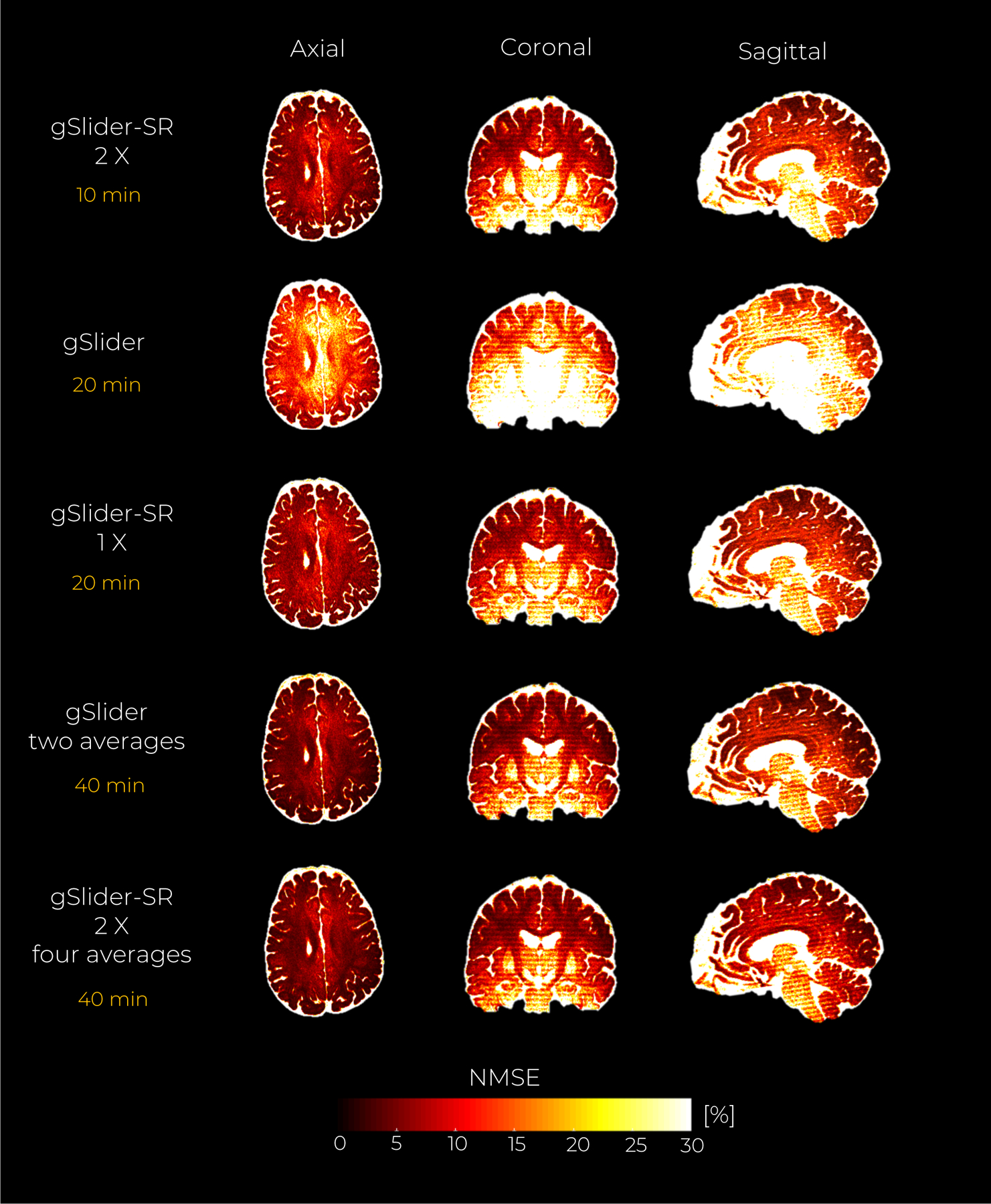
In vivo data experiment with an acceleration factor of 2X. An axial, coronal and sagittal slice of the NMSE maps from the reconstructed DWI volumes are shown for the gSlider, and gSlider-SR based reconstruction, respectively

Figure 9:

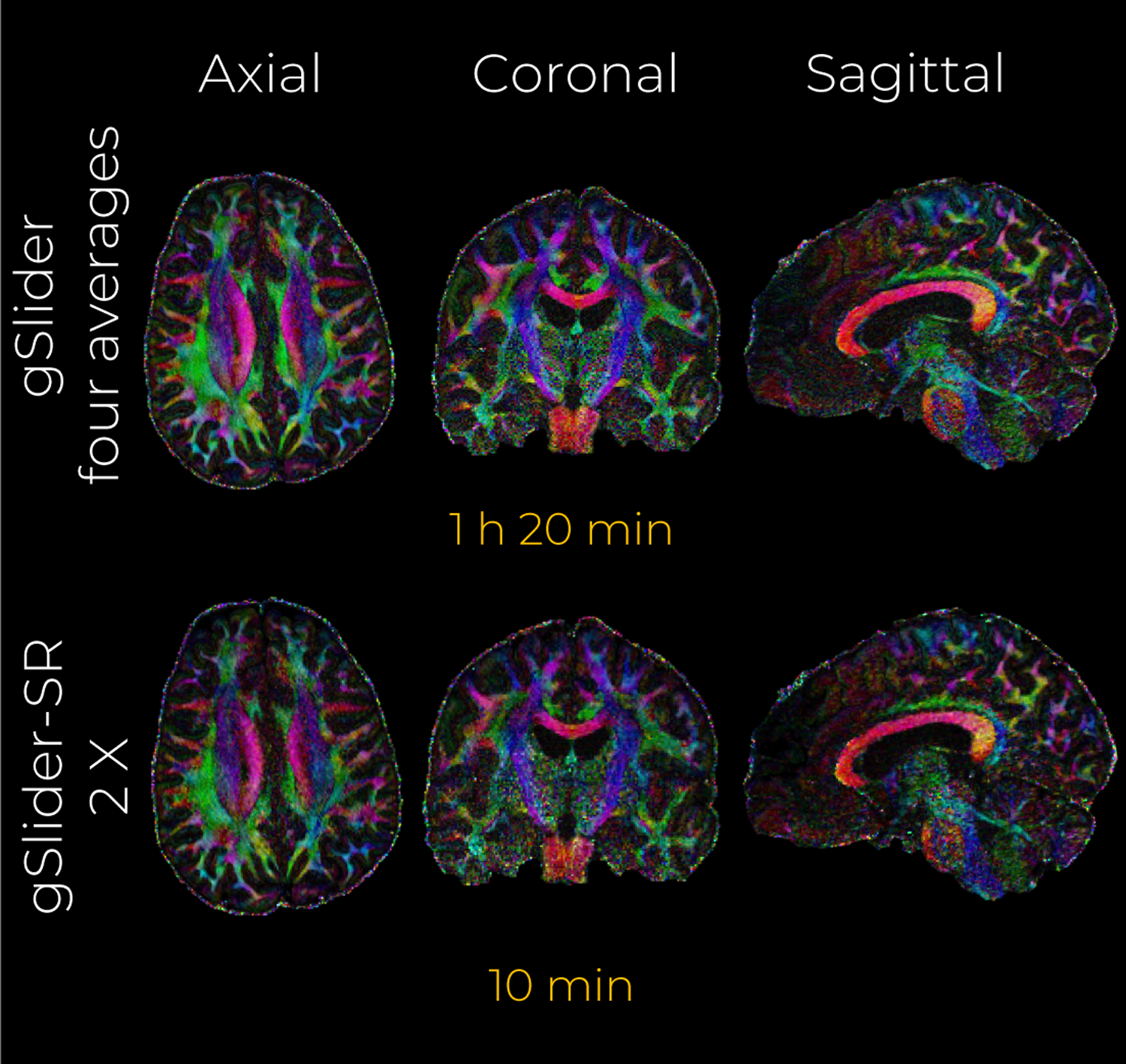
In-vivo data experiment with an acceleration factor of 2 X. A middle axial, coronal and sagittal slice of the color-encoded FA maps estimated from the reconstructed DWI volumes with gSlider (four averages) and gSlider-SR are shown.

Finally, we assess the ability of gSlider-SR to recover angular information from the four reconstructed in-vivo gSlider data scans. The angular error for DTI as well as the directions of the ODF peaks were computed, where the reference set was the gSlider four averages method. Results are shown in Tab. 1.

Table 1:

Quantitative validation of gSlider-SR reconstruction with in-vivo data (acceleration factor of 2 X). The gSlider four averages set was used as reference set.

Metric	Scan 1		Scan 2		Scan 3		Scan 4
	WM	GM	WM	GM	WM	GM	WM	GM
NMSE	10.6 %	11.4 %	11.1 %	12.0 %	10.4 %	11.2 %	10.4 %	11.3 %
	WM		WM		WM		WM
∆θ: tensor	17.8°		18.4°		17.0°		17.2°
∆θ: ODF peaks	17.8°		17.4°		16.7°		16.8°
Pf : ODF	32.4 %		33.9%		31.9%		31.9%

Although not a direct comparison on the same datasets, angular errors using gSlider-SR are consistently lower than those reported in (41), and comparable to those obtained with simulations (2 X).

5. Discussion

In this work, we proposed an accelerated gSlider reconstruction framework (gSlider-SR) which, by means of complementary sampling in the q- and RF-encoded space, robustly reconstructs whole human brain dMRI data at submillimeter isotropic resolution (860 μm) within a scan time frame that is substantially shorter than that required for conventional gSlider (4-averages). It is important to note that such high resolution data comes at an SNR that is comparable to four averages of standard gSlider data, i.e., the proposed method presents an 8-fold acceleration in acquisition time without compromising signal quality.

Using Monte-Carlo simulations, we demonstrated that gSlider-SR is able to accurately reconstruct, structure-preserving, artifact-free, high-resolution DWI datasets. While an acceleration of 2X gives the best performance in terms of normalized mean-square error, angular error as well as DTI-derived measure of FA, the performance is quite stable even for much higher acceleration factors. Comparison of gSlider-SR with conventional gSlider on realistic in-vivo human brain data demonstrated dramatically improved image quality, with significantly reduced scan time of two (gSlider-SR four averages) to eight (gSlider-SR) times shorter than the reference gSlider four averages dataset.

Below, we also discuss the limitations as well as future directions of this work. In-vivo real data that was used in the experiment section required a motion correction scheme, which we smoothly integrated in the gSlider-SR as an iterative registration step with the popular FLIRT algorithm (40). While this approach provided very good results, motion and eddy correction can be explicitly modeled within the forward-model of Eq. 3 as is done in (14, 42, 43, 20). This will ensure that the super-resolution DWI dataset and the motion parameters, which vary not only for each diffusion direction but also along with RF-encoding profiles, can be simultaneously estimated within an integrated framework, improving the performance of gSlider-SR (44, 42).

In this work, for simplicity, λ was kept constant all over the brain. A spatially varying λ could provide a more accurate reconstruction, especially one that can account for spatially varying noise in the image. Indeed, while spherical-ridgelets can model any dMRI signal, the level of sparsity in the gray matter is different than that in white matter. It makes sense then to have a different value of λ in gray matter tissue. Interestingly, gSlider-SR can easily include other constrained conditions on the diffusion signal as well as other regularizations terms in the cost function of Eq. 6. In particular, we envisage an improved image quality reconstruction due to further noise reduction when spherical ridgelets modeling is combined with low-rank matrix denoising approaches (45, 46, 47, 48) and more complex spatial smoothness functionals than simple TV regularization (49). This research line will be developed in our group in the near future. It should be noted as well that the proposed gSlider-SR reconstruction framework is not confined to single shell but can accommodate multi-shell schemes as well, as spherical-ridgelets have been properly modified for multi-shell diffusion MRI data recovery (25). Finally, the regularization parameters currently have to be chosen manually using a heuristic approach. Our future work entails developing algorithms that do not require manual parameter selection.

6. Conclusion

In this work, we have shown that in-vivo diffusion MRI (64 directions with b = 2000 s/mm²) of a whole-brain at isotropic resolution of 860 μm can be obtained in a clinically feasible scan time with our novel gSlider-SR method. gSlider-SR extends conventional gSlider by allowing both undersampled RF-encoding and q-space data, thereby substantially accelerating the acquisition time of the traditional gSlider protocol. The method allows submillimeter dMRI acquisitions within a clinically feasible scan time, allowing to probe anatomical details not possible with existing methods.