Deep learning geometrical potential for high-accuracy ab initio protein structure prediction

Summary

Ab initio protein structure prediction has been vastly boosted by the modeling of inter-residue contact/distance maps in recent years. We developed a new deep learning model, DeepPotential, which accurately predicts the distribution of a complementary set of geometric descriptors including a novel hydrogen-bonding potential defined by C-alpha atom coordinates. On 154 Free-Modeling/Hard targets from the CASP and CAMEO experiments, DeepPotential demonstrated significant advantage on both geometrical feature prediction and full-length structure construction, with Top-L/5 contact accuracy and TM-score of full-length models 4.1% and 6.7% higher than the best of other deep-learning restraint prediction approaches. Detail analyses showed that the major contributions to the TM-score/contact-map improvements come from the employment of multi-tasking network architecture and metagenome-based MSA collection assisted with confidence-based MSA selection, where hydrogen-bonding and inter-residue orientation predictions help improve hydrogen-bonding network and secondary structure packing. These results demonstrated new progress in the deep-learning restraint-guided ab initio protein structure prediction.

Graphical abstract

Highlights

• •Multi-tasking network architecture for multiple inter-residue geometries
• •Novel deep learning model for improved hydrogen-bonding modeling
• •Rapid and high-accuracy Ab initio protein structure prediction

Bioinformatics; Protein; Structural biology

Introduction

Despite significant efforts and progress, ab initio protein structure prediction, which aims to construct 3D models from the sequence alone, remains an important unsolved problem in computational biology (Zhang, 2008). A variety of methods have been proposed for ab initio structure prediction, based on fragment assembly simulations coupled with knowledge-based potentials (Simons et al., 1997; Xu and Zhang, 2012; Zhang and Skolnick, 2004a) or built on hybrid deep machine learning techniques (Senior et al., 2020; Yang et al., 2020; Zheng et al., 2021b).

The recent community-wide critical assessment of protein structure prediction (CASP) experiments demonstrated dominant advantages of deep-learning-based approaches in ab initio structure predictions (Abriata et al., 2019; Pereira et al., 2021). Because deep-learning-based approaches can predict abundant information on the probability distributions of geometrical characteristics of protein structures (Yang et al., 2020; Li et al., 2021a; Xu et al., 2021), using them as constraints can result in more accurate full-length structure models than that built from the classical knowledge-based potentials which are derived from simple statistics of the PDB. Inter-residue contacts were first utilized as a critical geometrical term to encode invariant interactions between protein atoms, where the contact models were initially predicted by the assumption of coevolution in multiple sequence alignment (MSA) (Korber et al., 1993; Morcos et al., 2011; Jones et al., 2012; Ekeberg et al., 2013). Later, the coevolution analysis data were further used as input features of machine learning models for improving the contact prediction accuracy (Wang et al., 2017; Li et al., 2019, 2021a). With the development of the deep learning algorithms, more detailed inter-residue geometrical terms, including distance (Senior et al., 2020; Xu, 2019) and torsion angle orientation (Yang et al., 2020), have been introduced and accurately predicted. These terms, when used as restraints for potential construction, have proven to be useful for further improving protein structure prediction (Ju et al., 2021; Xu et al., 2021; Yang et al., 2020; Zheng et al., 2021a; Mortuza et al., 2021).

Most recently, an end-to-end protein structure prediction protocol, AlphFold2 (Jumper et al., 2021a), was proposed and implemented through self-attention networks combined with 3D-equivariant structure transformation. AlphaFold2 participated in CASP14 and was able to construct correct fold for nearly all single domain protein targets. However, the training of such giant and complicated neural networks requires a high amount of computational resource which is unattainable for most academic groups. Alternatively, another end-to-end model, RoseTTAFold (Baek et al., 2021), was later proposed based on SE(3)-transformer. Based on the predicted geometry distributions, injected with the information from and end-to-end loss function, RoseTTAFold showed promising structure prediction results with less resource. Interestingly, models constructed from geometry restraints clearly outperformed those directly derived from the end-to-end training by RoseTTAFold (Baek et al., 2021), suggesting the advantage and usefulness of spatial restraints on high-accuracy protein structure prediction. Nevertheless, many of the critical procedures associated with the geometry-assisted 3D structure modeling, including network design, coevolutionary feature extraction, and geometrical term selection, remain to be optimized for maximizing the overall performance of ab initio structure predictions.

In this study, we developed a new deep learning architecture, DeepPotential, for protein structural geometry prediction, with the focus on systematically examining the impact of feature representation, neural network design, and effective geometrical term selection on spatial restraints and 3D model constructions. To enhance the modeling accuracy, multiple unary and pairwise features are trained through a hierarchical deep residual neural network (He et al., 2016) featured with parallel 1D and 2D network blocks followed by a set of sequential residual blocks, which can be practically trained with limited computation resources, i.e., single GPU with 10GB memory, to predict distance, torsion angles, and H-bond terms by a multi-tasking strategy, where the H-bond terms are the novel terms introduced for the first time to help recognize and refine the secondary structure patterns from C_α atoms. By integrating a newly constructed gradient-descent-based folding algorithm that can handle various kinds of restraint potentials powered by autograd mechanics in PyTorch, large-scale benchmark results demonstrated a significant advantage of DeepPotential over other state-of-the-art deep learning approaches on both geometrical feature prediction and full-length ab initio protein structure construction. The novel findings in this research could be easily extended, e.g., the H-bond terms could be considered as additional standard geometry terms for better H-bonding network modeling and the subsequent structural folding program could integrate arbitrary smooth potentials for protein structure prediction. The online server and standalone package of the DeepPotential program are freely accessible at https://zhanggroup.org/DeepPotential.

Results

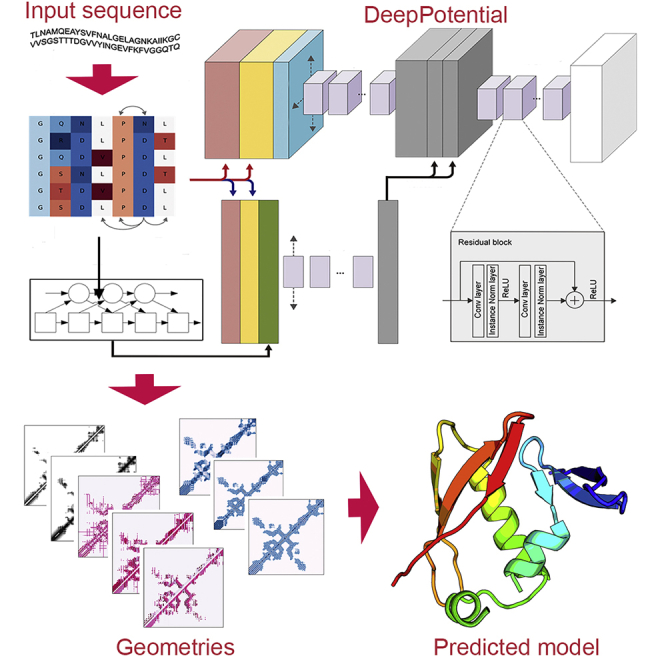
DeepPotential starts with the collection of MSAs by searching the query through multiple whole- and metagenome protein sequence databases (Zhang et al., 2020). Two complementary sets of coevolutionary features, pseudo-likelihood maximization (PLM) (Ekeberg et al., 2013; Balakrishnan et al., 2011) and mutual information (MI)(Korber et al., 1993), are then extracted from the MSAs and fed into a hierarchical neural network, which is composed of 1D and 2D residual blocks, to generate four sets of complementary local structural descriptor models, including distance maps, inter-residue angles, dihedral orientation angles, and backbone hydrogen-bonding networks. Full-length models are finally constructed from the structural descriptors using the limited-memory Broyden–Fletcher–Goldfarb–Shanno algorithm (L-BFGS) algorithm (Zhu et al., 1997) (see STAR Methods and Figure 1).

Figure 1.

The overview of the DeepPotential pipeline

The pipeline extracts evolutionary features from MSA using statistical models as the input. The outputs contain various geometric predictions which can be subsequently converted to potentials for ab initio protein structure prediction.

To test the performance of DeepPotential, three sets of proteins are collected. The first and second contain 27 and 22 Free-Modeling (FM) domains collected from CASP13 and CASP14 respectively, while the third set contains 127 Hard targets from continuous automated model evaluation (CAMEO) (Haas et al., 2013). For all datasets, targets with a sequence identity >30% to any of the DeepPotential training datasets have been excluded.

Contact and distance map predictions

Table 1 summarizes the results of DeepPotential for the long-range ($\left|i-j\right|>23$) contact prediction under different cutoffs (L/5, L/2, and L, with L being the sequence length) on the CASP13 and CAMEO datasets, in control with three state-of-the-art algorithms of trRosetta (Yang et al., 2020), CopulaNet (Ju et al., 2021), and RaptorX (Xu et al., 2021). Because DeepPotential does not generate contact model specifically, the predicted probability for a residue pair being in contact is calculated by summing the probabilities of all distance bins <8 Å for C_β atoms and sorted for top contact model output. Here, DeepPotential and the control methods used the same input MSAs created by deepMSA (Zhang et al., 2020). On both the CASP13 and CAMEO datasets, DeepPotential achieves the best accuracy under all cutoffs. Taking Top-L long-range contacts as an example, DeepPotential achieves precisions of 0.608 and 0.687 on two datasets, respectively, which are 5.2% and 7.0% higher than the second-best method by the most recent version of RaptorX (Xu et al., 2021). Despite the relatively small dataset, the corresponding p-values are 3.9 × 10⁻² and 3.4 × 10⁻¹⁶, respectively, showing a statistically significant superiority for contact map prediction by DeepPotential. AlphaFold1 (Senior et al., 2020) was not considered here because the program was not publicly available. Nevertheless, the Top-L precision of AlphaFold1 on CASP13 FM targets was reported as 45.5%, lower than the 60.8% obtained by DeepPotential. Because all methods in this comparison use the same MSAs collected by deepMSA, the data in Table 1 highlight the advantage of the multi-task neural network design and the specific two-level unary and pairwise feature extractions in DeepPotential.

Table 1.

Precision comparison of long-range Top-N contact prediction between DeepPotential and controlled methods on CASP13 and CAMEO datasets

Datasets	Methods	N = L/5	N = L/2	N = L
CASP13	trRosetta	0.794 (2.0 × 10−2)	0.688 (1.6 × 10−2)	0.546 (1.2 × 10−3)
	CopulaNet	0.810 (1.5 × 10−1)	0.682 (5.0 × 10−2)	0.531 (1.3 × 10−3)
	RaptorX	0.819 (1.1 × 10−1)	0.729 (1.8 × 10−1)	0.578 (3.9 × 10−2)
	DeepPotential	0.854	0.751	0.608
CAMEO	trRosetta	0.874 (3.0 × 10−4)	0.776 (1.3 × 10−12)	0.630 (1.9 × 10−26)
	CopulaNet	0.835 (5.9 × 10−10)	0.725 (1.6 × 10−16)	0.564 (7.6 × 10−24)
	RaptorX	0.867 (1.4 × 10−6)	0.780 (2.4 × 10−11)	0.642 (3.4 × 10−16)
	DeepPotential	0.902	0.822	0.687

The bold fonts highlight the highest precision values in each category

In Figures 2A and 2B, we listed a mean absolute error (MAE) of distance maps at different cutoffs (N), which is calculated by $\text{MAE}=1/N\sum _{i=1}^N|d_i-d_i^0|$, where $d_i$ is the estimated distance from the predicted distribution of ith residue pair as ranked by the total probability of the distance less than 20 Å, and $d_i^0$ is the distance of the corresponding residue pair on the target structure. While the MAE of Top-L/2 distance is comparable between DeepPotential and other programs, with the increase of evaluated residue pairs (from Top-L/2 to 10∗L), the MAE values for DeepPotential are increasingly more accurate than other competing methods. In fact, a high number of deep-learning distances are usually needed to fully define and smoothen the energy landscape so that the gradient-based model methods could be applied to identify energy minimum states. A recent study (Pearce et al., submitted) showed that a set of 93∗L distance restraints are required to achieve the best modeling results through L-BFGS optimization. Such results suggest that DeepPotential can produce higher-accuracy distance predictions on a large number of residue pairs for gradient-based structure constructions.

Figure 2.

Performance of contact and distance predictions by different methods

(A and B) Comparison of long-range Top-N distance prediction evaluated by MAE on CASP13 FM targets and CAMEO Hard targets, respectively.

(C) The Top-L/5 precision of the ten best servers in CASP14 on 22 FM targets, where DeepPotential is group 010. Data are mean and standard deviation of precision for each group.

(D) The Top-5∗L MAE of the ten best servers in CASP14 on 22 FM targets.

(E) The ablation analysis of DeepPotential on long-range Top-L precision by excluding specific components.

DeepPotential also participated in the most recent 14^th CASP experiment as an automatic server group (Group ID: 010) in the residue-residue contact category and ranked as one of the top groups among all servers. Figures 2C and 2D show a comparison of the average contact precision and distance MAE of DeepPotential with other top servers. On the 22 CASP14 FM targets, DeepPotential achieves an average Top-L/5 precision of 0.638, 3.6% higher than that of the second-best server, Group 183. For distance prediction, DeepPotential achieved the lowest Top-5∗L MAE of 3.098 Å. Table S1 summarizes the performance of contact and distance predictions of DeepPotential and the control methods (or their extensions) for the CASP14 FM targets on the blind test. The result is consistent with that of CASP13 and CAMEO dataset as listed in Table 1. For example, the Top-L contact precision of DeepPotential is 0.396 on the CASP4 FM targets, which is 18.6%, 33.8%, and 40.4% higher than that of trRosettaX (Group ID: Yang_FM), CopulaNet (Group ID: FALCON-DeepFolder), and RaptorX (Group ID: RaptorX), respectively. The leading performance in the blind CASP test shows the validity of the proposed pipeline for inter-residue contact and distance map predictions.

Orientation and H-bond predictions

In addition to the distance prediction, DeepPotential also provides probability distributions of dihedral angle orientations proposed by trRosetta (Yang et al., 2020), and three coarse-grained hydrogen-bond (H-bond) descriptors originally defined in I-TASSER (Yang et al., 2015) (Figure S4). Figure 3 shows the correlations between DeepPotential predictions versus the ground truth in the experimental structures. The predicted values are the means estimated from the predicted angle histogram. For the symmetric $\text{Ω}$ torsion angle and asymmetric $\text{Θ}$ or $\text{Φ}$ angle, long-range Top-5∗L and Top-10∗L predictions are evaluated, respectively, sorted by the total probability of C_β distance below 20 Å. On the combination set of 154 CASP13 FM and CAMEO Hard targets, DeepPotential achieves the circular correlation coefficient (CCC) of 0.729 and 0.861 for $\text{Ω}$ and $\text{Θ}$ torsion angles, and a Pearson correlation (PCC) of 0.880 for $\text{Φ}$ angle. These correlation coefficients are 15%, 4%, and 4% higher than those obtained by trRosetta (0.635, 0.827, and 0.848). Figures S2A–S2C further compares the MAE values of the orientation angles between DeepPotential and trRosetta. The average MAEs (degree) by DeepPotential are 35.94, 23.64, and 14.17 for $\text{Ω}$, $\text{Θ}$, and $\text{Φ}$ angles, respectively, which are significantly lower than the MAEs of 41.71, 27.39, and 15.91 for trRosetta (with p-values of 7.4 × 10⁻²², 7.0 × 10⁻¹⁴ and 8.5 × 10⁻²⁷, respectively). The major reasons for the better performance by DeepPotential are probably due to the more discriminative feature extraction and the multi-task training with H-bond terms which help calibrate the inter-chain torsion angle predictions in a corporative manner.

Figure 3.

Comparison of DeepPotential orientation and H-bond prediction with the experimental values

(A–C) Correlations on $\text{Ω}$, $\text{Θ}$, and $\text{Ψ}$ angles, respectively.

(D–F) Correlations on H-bond descriptors (aa, bb, and cc defined in Equation 3).

For the H-bond descriptors, Top-2∗L predictions are evaluated, as they are defined at a lower threshold of inter-C_α distance (10 Å). Figures 3D–3F show that DeepPotential generates H-bond descriptors with a PCC value of 0.867, 0.771, and 0.753 for aa, bb, and cc terms (Equation 3 in Materials and Methods), respectively, which are comparable with that of the torsional orientation terms. The Top-2∗L angle MAEs reach the lower scale of 17.70, 22.90, and 22.32, respectively, for the three H-bond terms. These angles and H-bond term predictions provide important restraints, complementary to distance/contact maps, for the DeepPotential-based ab initio protein structure prediction.

Comparative analyses show important advantages of MSA selection and network architecture design

We process to investigate the impact of different components of DeepPotential to the performance in Figure 2E. Compared to the previous DeepMSA approach (Zhang et al., 2020), one update in DeepPotential is that three additional metagenome databases have been used for MSA construction. As shown in Figure 2E (Panel 1 vs 6), the additional sequences bring a quite significant improvement, from 0.660 to 0.677 in contact-map precision, corresponding to a p-value of 1.3 × 10⁻⁷ in Student’s t test. One possible reason for the improvement should come from the greater MSA depths as the number of effective sequences (Neff) increases from 387.0 to 409.1 due to the utilization of the metagenome databases. Apparently, the increased number of homologous sequences facilitates the collection of more precise and robust coevolution information.

Nonetheless, the Neff value might not be an optimal indicator for the quality of MSA. In DeepPotential, we selected a favored MSA for each target from the candidate MSAs based on confidence score. For this, a quick distance prediction is performed on each candidate MSA, where the confidence score is computed as the average of the cumulative probability under a threshold $10$ Å of the top $4\ast L$ predicted C_β-C_β distance distributions for residue pairs whose sequential gap is over four residues. As shown in Figure 4A (Panel 2), the use of confidence score resulted in 3.4% higher contact precision (p-value = 1.1 × 10⁻⁴) than that using the Neff to select MSAs. Figure S3 presents the correlation between the contact precision and the confidence score and Neff of selected MSAs, where the PCC for the confidence score (0.827) is significantly higher than that for the Neff (0.503), suggesting that the confidence score is a more reliable indicator for MSA selections.

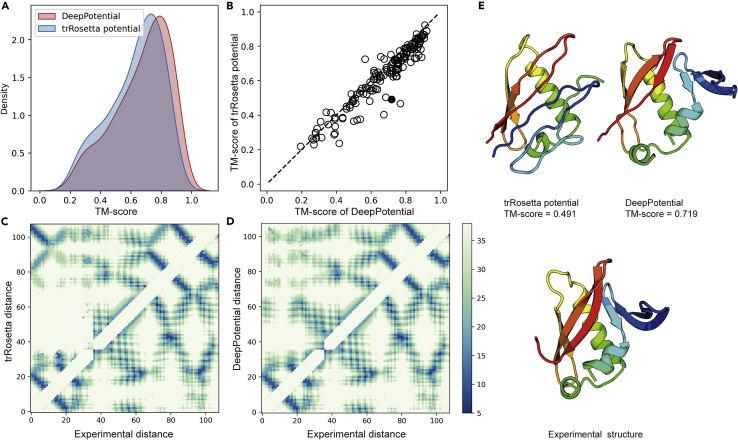
Figure 4.

3D structure prediction based on DeepPotential

(A) Comparison of TM-score distributions between DeepPotential and trRosetta potential.

(B) Head-to-head comparison of TM-score based on DeepPotential and trRosetta potential.

(C and D) Predicted distance histogram map versus distance histogram map from the experimental structure for trRosetta and DeepPotential, respectively.

(E) Predicted models of CASP13 FM target, T0957s1, based on trRosetta potential and DeepPotential, compared to the experimental structure.

We further check the MSA selection on two of the state-of-the-art protein structure prediction methods, AlphaFold2 and RoseTTAFold, on the CAMEO test dataset. For each target, two MSAs are selected using DeepPotential confidence score and Neff value, respectively. 79 out of 127 targets have different MSAs selected. The average TM-score (Zhang and Skolnick, 2004b) of AlphaFold2 based on confidence score-selected MSAs is 0.812, slightly higher than that based on Neff (0.806). Further improvements could be observed if we only consider those targets whose DeepPotential confidence score is x% higher than the confidence score of its MSA with the highest Neff value, where x% is the confidence threshold parameter. Table S2 shows the performance of MSA selection indexes with different confidence thresholds, where the TM-scores of AlphaFold2 based on confidence score-selected MSAs are 0.9%, 3.3%, 3.6%, and 6.2% higher than those based on Neff-selected MSAs, with the confidence thresholds from 1% to 4%, respectively. Similar results were observed for RoseTTAFold but the advantage is slightly less pronounced, possibly because that RoseTTAFold program only takes the first 1000 sequences from the input MSA (Table S2). These results suggest that the DeepPotential confidence score could be used as a general filter for MSA selections.

DeepPotential has integrated a set of eight structure descriptors on distance, inter-change angle and orientation, and hydrogen-bonds in the deep residual network training. The multi-tasking networks also contribute to the high performance of DeepPotential. As shown in Figure 2E (Panel 3), if we replace the deep learning model with the legacy architecture (Li et al., 2021a) with the same training set but only supervised by the distance bins, the contact precision would drop sharply to 0.598. In Panels 4 and 5 of Figure 2E, we also present the contact prediction results without orientation and H-bond tasks, respectively, where the two tasks added the improvement on contact accuracy predictions by 4.3% and 0.29%, respectively, which further confirms the advantage of multi-tasking networks.

In Figure S1, we also show the detailed head-to-head comparison of contact precision without corresponding components versus the full pipeline. The success rates for the components, i.e., the proportion of the cases for which the precision of the full pipeline is higher than or equal to that without the corresponding component, are 92.2%, 85.7%, 66.9%, 59.1%, and 54.5% for additional databases, MSA selection, DeepPotential architecture, orientation tasks, and H-bond tasks, respectively. These results are consistent with what were observed in Figure 2E.

DeepPotential-based 3D structure prediction

To examine the practical usefulness of DeepPotential on 3D protein structure prediction, we implemented a differentiable protein folding program that can construct twice-differentiable potentials and obtain the forces automatically using PyTorch (Paszke et al., 2017). The program thus enables the use of the gradient-descent-based optimization algorithm to identify the conformations with the lowest energy (Materials and Methods).

In Figure 4, we summarize the folding result of DeepPotential on the 154 hybrid test targets of CASP13 and CAMEO, in comparison with that of trRosetta which implements both distance and orientation predictions (Yang et al., 2020). Here, to have a clean and fair comparison of the two programs, we implemented the trRosetta potential in the same differentiable folding pipeline of DeepPotential, although we found that the default pyRosetta search engine (Chaudhury et al., 2010) generated a similar folding result to the DeepPotential folding pipeline for the two potentials. On the 154 hybrid targets, DeepPotential achieves an average TM-score of 0.672, which is 6.7% higher than that by the trRosetta potential (0.630), corresponding to a p-value of 2.6 × 10⁻¹⁶ and showing that the difference is statistically significant.

Figure 4A shows a clear TM-score shift of DeepPotential over trRosetta on the histogram distributions, where the 25%, 50%, and 75% percentile TM-scores are 0.558, 0.722, and 0.811 for DeepPotential, which are 6.7%, 8.6%, and 5.7% higher than those of trRosetta, respectively. Figure 4B presents a head-to-head comparison of TM-scores, where DeepPotential shows a better performance in 131 out of 154 targets (85%) and trRosetta does so only in 23 cases.

The major reason of better performance of DeepPotential is due to the higher accuracy of the spatial restraint accuracy. Here, we investigate an illustrative example from CASP13 T0957s1 which is a discontinuous domain (2–37,92-163 of original sequence) from the E. coli contact-dependent growth inhibition toxin, chain A of PDB: 6cp8, with 108 residues. As shown in Figures 4C and 4D, the top-L MAE of the distance map by DeepPotential (1.39 Å) is 1.11 Å lower than that of trRosetta (2.50 Å). Especially, the false-positive contact prediction at the upper-left region by trRosetta in Figure 4C resulted in the false anti-parallel beta-sheet structure prediction between N- and C-terminal. As a result, the structure built based on trRosetta potential has a TM-score of 0.491, which is 46% lower than that by DeepPotential (TM-score = 0.719) (Figure 4E). It is notable that the predictions of the two methods are based on the same MSA with a low Neff value of 3.41. The success of such an example highlights the effectiveness of the proposed DeepPotential that can help assist the protein structure prediction from a low number of homologous sequences.

Note that the advantage of DeepPotential might be overrated when compared to trRosetta which was trained on data from 2018, as DeepPotential should have access to more information when trained on data from 2019. In Table S3, we list the comparison results of DeepPotential with three other top methods, trRosetta2 (Anishchenko et al., 2020), AlphFold2 (Jumper et al., 2021a), and RoseTTAFold (Baek et al., 2021), which were all trained in and after CASP14. For a fair comparison, all the methods in the table used the same MSAs from DeepMSA, without using any template information. Unsurprisingly, AlphaFold2 outperforms all other methods with the average TM-score 20.1% and 26.6% higher than those of RoseTTAFold and DeepPotential, respectively. The superiority of AlphaFold2 may be contributed by its carefully designed recycling Evoformer neural networks that can iteratively optimize the models and the end-to-end protocol enabling equivariant protein structure learning. The two versions of RoseTTAFold have also slightly higher average TM-scores than DeepPotential (0.606 and 0.590 versus 0.575); this might also be brought due to the incorporated end-to-end information in the geometry distributions. Nevertheless, there are still some (2, 5, and 7) targets for which DeepPotential has a higher TM-score compared to AlphaFold2, RoseTTAFold, and RoseTTAFold_e2e, respectively, showing that DeepPotential could potentially provide information complementary to AlphaFold2 and RoseTTAFold. Compared with trRosetta2, an extension of trRosetta with additional features from pre-trained protein language models, DeepPotential has a better performance in terms of TM-score and RMSD. Based on insight obtained from Table S3, our future focus will be on the design of an effective recycling framework, the proper injection of end-to-end information during the training, and the collection of richer input features (e.g., protein/MSA language models), to further improve DeepPotential.

Hydrogen-bond prediction helps improve secondary structure packing

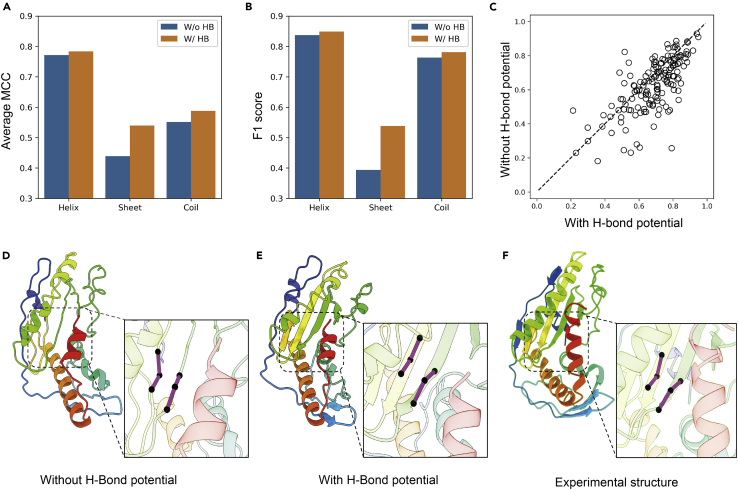
Compared to other deep learning models, one of the major new ingredients of DeepPotential is the H-bond network prediction. In our test on the 154 proteins, if the H-bond potential was excluded, the average TM-score of the DeepPotential models slightly drops from 0.672 to 0.663 with a p-value = 0.02, showing that the TM-score improvement brought by H-bond potential is modest but statistically significant.

The more significant impact of H-bond potential is on the secondary structure packing, which is expected because the form of local secondary structures in proteins is mainly driven by hydrogen-bonding interactions. In Figures 5A and 5B, we compare the Matthews correlation coefficient (MCC) and F1 score (harmonic mean of precision and recall) of the secondary structures in the DeepPotential model relative to the experimental structure, when using and without using the H-bond predictions in the DeepPotential-based folding. It is shown that the H-bond potential improves the accuracy for all three secondary structure classes (alpha-helix, beta-sheet, and coil). Especially for beta-sheets, the MCC/F1 score on the 154 test targets improves from 0.394/0.439 to 0.538/0.539. Figure 5C further displays a head-to-head target-wise F1 score comparison, which is computed by the average of F1 scores of the three classes for each target, where 111 out of 154 targets have an F1 score improved when folding with the H-bond potential.

Figure 5.

H-bond potential improves protein secondary structure packing

(A and B) Performance of classification comparison with and without H-bond potential.

(C) head-to-head comparison of F1 score for each target with and without H-bond potential.

(D and E) Predicted structures of a CAMEO target, 6ntvC, with and without H-bond potential, respectively.

(F) The experimental structure of 6ntvC. In D–F, the C_α atoms forming the local geometry systems for the residue pair (i = 126, j = 167) are zoomed in.

In Figures 5D–5F, we show an illustrative example from the CAMEO target chain C of PDB: 6ntv, which consists of 220 residues forming an α/β structure. Consistent with the average trend, the TM-score of the full-version DeepPotential model (0.748) is only slightly higher than that without using H-bond terms (0.734). However, the secondary structural F1-score (0.773) of the full-version model is significantly higher than the latter (0.472); this is mainly due to the H-bond potential, as the average errors (MAE) of aa, bb, and cc terms in the original model (17.54, 29.73, and 29.59) have been dramatically reduced to (13.16, 19.57, and 19.28) after introducing the H-bond restraints. In Figure 5D, we show an example of the residue pair (126, 167) whose (aa, bb, and cc) = (24.77, 155.82, and 148.47) in the original model without H-bond. Such geometry results in the loss of the hydrogen bond that is formed in the native structure with native (aa, bb, and cc) = (19.16, 168.15, and 162.41), as shown in Figure 5F. DeepPotential predicted a mean value of (aa, bb, and cc) = (22.24, 165.59, and 154.13) and the use of this restraint adjusts the relative C $\alpha$ orientation and regulates the (aa, bb, and cc) to (19.38, 165.65, and 156.63) in the 3D model, which results in the successful recovery of the hydrogen-bonding in this residue pair (Figure 5E). These results indicate that the H-bond potential of DeepPotential provides additional information of long-range inter-residue geometries, which help accurately model the H-bonding network of beta-sheets, in addition to their orientations.

Discussions and conclusions

We proposed a new deep neural network model, DeepPotential, to predict high-accuracy structural descriptors and full-length 3D models of proteins from the amino acid sequence and the co-evaluation information derived from multiple sequence alignments. The network architecture is featured with multiple inter-residue geometry term predictions powered with parallel 1D unitary and 2D pairwise blocks followed by a set of sequential residual blocks. Benchmark tests on two sets of CASP13 FM and CAMEO Hard targets showed that the DeepPotential could generate more accurate structural descriptors than the state-of-the-art deep learning models (trRosetta (Yang et al., 2020), CopulaNet (Ju et al., 2021), and RaptorX (Xu et al., 2021)), where the average TM-score of the DeepPotential models is 6.7% higher than the best of the control methods with a p-value of 2.6 × 10⁻¹⁶ in Student’s t test.

A former version of DeepPotential was tested (as Group 010) in the most recent CASP14 experiment and ranked as the best distance/contact server predictor (Li et al., 2021b). The DeepPotential models served as one of the important spatial restraint resources for I-TASSER and QUARK, which ranked at the top two positions in the automated 3D structure prediction in the CASP14 experiment (Zheng et al., 2021a). The detailed ablation analyses showed that several factors have made significant contributions to the superiority of the DeepPotential, which include: (i) multi-tasking architecture, (ii) confidence-based MSA selection and metagenome-based MSA collection, (iii) inter-residue orientation, and (iv) hydrogen-bonding prediction, following the magnitude of contact/distance map accuracy improvement. Despite the modest impact of H-bond terms on global structure topology, they demonstrated significant improvement on the hydrogen-bonding network and secondary structure packing of the DeepPotential models.

Limitations of the study

Nevertheless, DeepPotential still underperforms the most recently released AlphaFold2 and RoseTTAFold programs, although it provides complementary information for some of the targets. One of the major advantages of these programs is due to the utilization of the end-to-end training protocol which enables direct cycling and feedback from 3D structure coordinates, instead of the training on intermediate states such as contact and distance maps. Inspired by the new benchmark results and the encouraging achievement made in AlphaFold2 in the CASP14 (Jumper et al., 2021b), an extended DeepPotential model with new end-to-end network implements is under development, while the systematical examination of various critical network features performed by this study should provide a robust and useful base for the next step high-resolution ab initio protein structure prediction developments.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Uniclust30	Remmert et al., 2012	http://gwdu111.gwdg.de/∼compbiol/uniclust
Uniref90	UniProt Consortium, 2016	http://www.uniprot.org/uniref
Metaclust	Steinegger and Söding, 2018	https://metaclust.mmseqs.com
BFD	Steinegger et al., 2019b	https://bfd.mmseqs.com
Mgnify	Mitchell et al., 2020	https://www.ebi.ac.uk/metagenomics
IMG/M	Chen et al., 2021	https://img.jgi.doe.gov
Software and algorithms
HH-suite	Steinegger et al., 2019a	https://github.com/soedinglab/hh-suite
HMMER	Eddy, 1998	http://hmmer.org
TM-score	Zhang and Skolnick, 2004b	https://zhanggroup.org/TM-score
CCMPred	Seemayer et al., 2014	https://github.com/soedinglab/CCMpred
TripletRes	Li et al., 2021a	https://zhanggroup.org/TripletRes
CD-HIT	Fu et al., 2012	https://github.com/weizhongli/cdhit
CopulaNet	Ju et al., 2021	https://github.com/fusong-ju/ProFOLD
RaptorX	Xu et al., 2021	https://github.com/j3xugit/RaptorX-3DModeling
trRosetta	Yang et al., 2020	https://github.com/gjoni/trRosetta
AlphaFold2	Jumper et al., 2021a	https://github.com/deepmind/alphafold
RoseTTAFold	Baek et al., 2021	https://github.com/RosettaCommons/RoseTTAFold
PyTorch	Paszke et al., 2017	https://pytorch.org
Python	Python Software Foundation	https://www.python.org
DeepPotential	This paper	https://zhanggroup.org/DeepPotential

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Yang Zhang (zhng@umich.edu).

Materials availability

This study did not generate new unique reagents.

Method details

Benchmark dataset collection

DeepPotential was trained on a non-redundant set of experimental structures collected from the PDB, where a total number of 150,940 structures by Nov 2019 with a maximum length of 1000 residues were initially collected. CD-HIT (Fu et al., 2012) was then used to cluster the sequences at the sequence identity threshold of 35%, which resulted in 26,151 representative proteins that are used as the DeepPotential training set.

Prediction terms of protein structure

For a given residue pair ($i,j$), four classes of complementary inter-residue geometry descriptors are predicted by DeepPotential and used to assist 3D structure modeling.

Two-atom distance terms

The Euclidean distance of C_β(i)-C_β(j) (or $d_{i,j}^{C\beta }$) and C_α(i)-C_α(j) (or $d_{i,j}^{C\alpha }$) atoms are first predicted by DeepPotential (Figure S4A). The distance values are discretized into $n_{bin}(=36)$ bins in the range of [2, 20 Å], with an even bin width = 0.5 Å. Two additional bins in [0, 2 Å] and [20, $\infty$ Å] are counted for the distances beyond the normal range.

Three-atom angle terms

DeepPotential predicts the angles of C_α(i)-C_β(i)-C_β(j) (or ${\text{Φ}}_{i,j}$) and C_β(j)-C_β(i)-C_α(i) (or ${\text{Φ}}_{j,i}$), for which the angle values are discretized into 12 bins with the bin width = 15^o(=180^o/12) (Figure S4B). An additional bin is added to count for the angles when the distance $d_{i,j}^{C\beta }$ >20 Å, indicating that there are no significant interaction patterns predictable for the residue pair.

Four-atom dihedral terms

Two types of inter-residue dihedral angles are predicted (Figure S4B). While ${\text{Ω}}_{i,j}(={\text{Ω}}_{j,i})$ is the dihedral angle in C_α(i)-C_β(i)-C_β(j)-C_α(j), $\text{Θ}$ is defined by N(i)-C_α(i)-C_β(i)-C_β(j) (or ${\text{Θ}}_{i,j}$) and N(j)-C_α(j)-C_β(j)-C_β(i) (or ${\text{Θ}}_{j,i}$). Each dihedral angle is represented by a one-hot vector with a dimension size of 25. The 24 dimensions represent 24 bins with an interval of 15^o (=360/24), while the last dimension is assigned for all angles with $d_{i,j}^{C\beta }>d_{max}$.

Six-atom hydrogen-bond terms

To specify the coarse-grained H-Bonds, which only involve $C\alpha$ atoms, two types of auxiliary $C\alpha$ unit vectors are computed first by (Figure S4C):

$$\begin{array}{l}\{\begin{array}{l}{\overrightarrow{p}}_i=\left({\overrightarrow{ca}}_i-{\overrightarrow{ca}}_{i-1}\right)/|{\overrightarrow{ca}}_i-{\overrightarrow{ca}}_{i-1}|\hfill \\ {\overrightarrow{q}}_i=\left({\overrightarrow{ca}}_{i+1}-{\overrightarrow{ca}}_i\right)/|({\overrightarrow{ca}}_{i+1}-{\overrightarrow{ca}}_i|\hfill \end{array}\hfill \end{array}$$ (Equation 1)

where ${\overrightarrow{ca}}_i$ is the coordinate vector of C_α(i) atom. Three local geometry orthometric vectors are then defined by:

$$\begin{array}{l}\{\begin{array}{l}{\overrightarrow{a}}_i={\overrightarrow{p}}_i+{\overrightarrow{q}}_i\hfill \\ {\overrightarrow{c}}_i={\overrightarrow{p}}_i-{\overrightarrow{q}}_i\hfill \\ {\overrightarrow{b}}_i={\overrightarrow{a}}_i\times {\overrightarrow{c}}_i\hfill \end{array}\hfill \end{array}$$ (Equation 2)

The relative orientation of the vectors, which specify the backbone H-bond interactions, are predicted with

$$\begin{array}{l}\{\begin{array}{l}a{a}_{i,j}=\arccos \left(\frac{{\overrightarrow{a}}_i\cdot {\overrightarrow{a}}_j}{|{\overrightarrow{a}}_i||{\overrightarrow{a}}_j|}\right)\hfill \\ b{b}_{i,j}=\arccos \left(\frac{{\overrightarrow{b}}_i\cdot {\overrightarrow{b}}_j}{|{\overrightarrow{b}}_i||{\overrightarrow{b}}_j|}\right)\hfill \\ c{c}_{i,j}=\arccos \left(\frac{{\overrightarrow{c}}_i\cdot {\overrightarrow{c}}_j}{|{\overrightarrow{c}}_i||c_j|}\right)\hfill \end{array}\hfill \end{array}$$ (Equation 3)

where the angle values are discretized into 18 bins with 10^o interval if $d_{i,j}^{C\alpha }<10\text{ Å}$, meaning that the relative orientations are predictable. One additional bin is assigned for the probability that $d_{i,j}^{C\alpha }>10\text{ Å}$.

Deep neural network training of protein structure descriptors

Multiple candidate MSA construction

DeepPotential starts with the collections of multiple sequence alignments (MSAs) whose quality is critical to the final model training. As shown in Figure S5, DeepPotential constructs 6 sets of candidate MSAs from a query sequence through an iterative process. The first three MSAs were collected by searching the query through three genome sequence databases from Uniclust30, Uniref90, and Metaclust (Steinegger and Söding, 2018) sequence databases via HHblits (Remmert et al., 2012), Jackhmmer (Johnson et al., 2010; Eddy, 1998), and HMMsearch (Eddy, 1998), respectively, following the protocol of DeepMSA (Zhang et al., 2020). The second three MSAs are further searched through three metagenomic databases from BFD (Steinegger et al., 2019b), Mgnify (Mitchell et al., 2020), and IMG/M(Chen et al., 2021), respectively. The iterative searching process stops if the Neff value is above 128 with the last MSA returned. The homologous sequences generated by Jackhmmer or HMMsearch will be converted into a custom database in HHblits format using ‘hhblitdb.pl’ in HH-suite (Steinegger et al., 2019a), where such customization is particularly important to wipe out noisy sequences from the raw sequence hits (Zhang et al., 2020).

Feature extraction

Two types of pairwise and unary features are extracted from the returned MSA, which represent the inter-residue relationship and the individual residue profile, respectively.

First, the pairwise feature $\mathit{P}{\mathit{F}}_{i,j}$ ($\in R^{L\times L\times D_1}$) for residue pair ($i,j$) is defined as

$$\begin{array}{l}\mathit{P}{\mathit{F}}_{i,j}={\left(\mathit{PL}{\mathit{M}}_{i,j}^T;\mathit{M}{\mathit{I}}_{i,j}^T\right)}^T\hfill \end{array}$$ (Equation 4)

where L and $D_1$ are the length of the protein sequence and the dimension of the pairwise feature; $\mathit{PL}{\mathit{M}}_{i,j}$ and $\mathit{M}{\mathit{I}}_{i,j}$ are the feature vectors generated from coupling parameter P ($\in R^{L\times L\times Q\times Q}$) of PseudoLikelihood Maximized Potts model (Ekeberg et al., 2013) and Mutual Information matrices M ($\in R^{L\times L\times Q\times Q}$), respectively. Here, $Q=22$, representing 20 types of regular amino acids, plus the unknown residue type state and the gap state.

The coupling parameter P can be obtained by minimizing the loss function of

$${\mathcal{L}}_{PLM}=-\sum _{n=1}^N\sum _{l=1}^L\text{log}\frac{\exp \left({\mathit{e}}_i\left(X_{n,i}\right)+{\sum }_{j=1,j\ne i}^L{\mathit{P}}_{i,j}\left(X_{n,i},X_{n,j}\right)\right)}{{\sum }_{q=1}^Q\exp \left({\mathit{e}}_i\left(q\right)+{\sum }_{j=1,j\ne i}^L{\mathit{P}}_{i,j}\left(q,X_{n,j}\right)\right)}+{\lambda }_{single}\sum _{i=1}^L{\Vert {\mathit{e}}_i\Vert }_2^2+{\lambda }_{pair}\sum _{\begin{array}{l}i,j=1\hfill \\ i\ne j\hfill \end{array}}^L{\Vert {\mathit{P}}_{i,j}\Vert }_2^2$$ (Equation 5)

where e ($\in R^{L\times Q}$) represents the field parameters of the Potts model; X ($\in {[\mathrm{1,2},\dots ,Q]}^{N\times L}$) is the input MSA in the form of an integer matrix with each entry representing the residue type. ${\lambda }_{single}=1$ and ${\lambda }_{pair}=0.2\times (L-1)$ are the regularization coefficients for e and P respectively. The parameter ${\mathit{P}}_{i,j}(q_1,q_2)$ measures the linear coefficients of $q_1$ state of residue i and the $q_2$ state of residue j, conditioning on other residues and states. The conditional model can eliminate transitive interactions in the observed interactions.

After the optimization, the $\mathit{PL}{\mathit{M}}_{i,j}$ vector can be written as

$$\begin{array}{l}\mathit{PL}{\mathit{M}}_{i,j}={\left({\mathit{P}}_{i,j}\left(\mathrm{1,1}\right),\dots ,{\mathit{P}}_{i,j}\left(\mathrm{1,22}\right),\dots ,{\mathit{P}}_{i,j}\left(\mathrm{22,22}\right),S_{i,j}^1,S_{i,j}^2,S_{i,j}^3,{\mathit{P}}_{i,j}\left(X_{1,i},X_{1,j}\right)\right)}^T\hfill \end{array}$$ (Equation 6)

where the first $484(=22\times 22)$ terms, ${\mathit{P}}_{i,j}$, are the flattened vector of residue pair-specific potentials for residue pair (i, j). $S_{i,j}^1,S_{i,j}^2,\text{and}{S}_{i,j}^3$ are Frobenius norms of all edge potentials, edge potentials excluding gap state, and edge potentials excluding both gap and unknown states of residues i and j, respectively, with $S_{i,j}^k=\sqrt{\sum _{q_1,q_2}^{Q+1-k}{\mathit{P}}_{i,j}{\left(q_1,q_2\right)}^2}$ being the couplings at the residue-wise scale. The last term of Equation 6, ${\mathit{P}}_{i,j}(X_{1,i},X_{1,j})$, extracts the query-specific coupling potential, assuming that the first sequence in the MSA is the query sequence. Such a feature is an important part of the feature set since all other features are agnostic to the order of sequences within the MSA; for example, if a pair of aligned sequences in the MSA are swapped, those features will be unchanged. The optimization of the Potts model was implemented by a custom version of CCMpred program (Seemayer et al., 2014), which we modified to account for the unknown residue type state.

The PLM measures the dependency between residue positions conditional on other positions, which should be more relevant to the structural interaction terms between residue pairs. However, the optimization of PLM could be ill-posed when there are no sufficient aligned sequences in the MSA. A raw marginal correlation measurement, i.e., mutual information (MI) was utilized as another pairwise feature. Similar to Equation 6, the MI feature for residue i and j can be written as

$$\begin{array}{l}\mathit{M}{\mathit{I}}_{i,j}={\left({\mathit{M}}_{i,j}\left(\mathrm{1,1}\right),\dots ,{\mathit{M}}_{i,j}\left(\mathrm{1,22}\right),\dots ,{\mathit{M}}_{i,j}\left(\mathrm{22,22}\right),C_{i,j}^1,C_{i,j}^2,C_{i,j}^3,{\mathit{M}}_{i,j}\left(X_{1,i},X_{1,j}\right)\right)}^T\hfill \end{array}$$ (Equation 7)

Here, the raw MI matrices is defined as:

$$\begin{array}{l}{\mathit{M}}_{i,j}\left(q_1,q_2\right)=f_{i,j}\left(q_1,q_2\right)\ln \frac{f_{i,j}\left(q_1,q_2\right)}{f_i\left(q_1\right)f_j\left(q_2\right)}\hfill \end{array}$$ (Equation 8)

where $f_i\left(q_1\right)$ is the frequency of a residue type $q_1$ at position i of the MSA, $f_{i,j}\left(q_1,q_2\right)$ is the co-occurrence of two residue types $q_1$ and $q_2$ at positions i and j; $C_{i,j}^1,C_{i,j}^2,C_{i,j}^3$ are the MI at the residue-wise scale, and $C_{i,j}^k=\sqrt{\sum _{q_1,q_2}^{Q+1-k}{\mathit{M}}_{i,j}{\left(q_1,q_2\right)}^2}$. ${\mathit{M}}_{i,j}(X_{1,i},X_{1,j})$ extracts sequence-specific mutual information. Compared to the regular Pearson correlation, MI is capable to scale the non-linear relationships between variables.

Second, the unary features UF ($\in R^{L\times D_2}$) of DeepPotential are the combination of self-mutual information feature, field parameter of Potts model, one-hot sequence feature and HMM profiles. Here, $D_2$ is the size of the feature dimension for each site. For residue i, the self-mutual information feature $\mathit{U}{\mathit{M}}_i$ can be represented as:

$$\begin{array}{l}\mathit{U}{\mathit{M}}_i={\left(g_i\left(1\right),\dots ,g_i\left(22\right),g_i\left(X_{1,i}\right)\right)}^T\hfill \end{array}$$ (Equation 9)

where self-mutual information $g_i\left(q\right)=-f_i\left(q\right)\ln f_i\left(q\right)$ is Equation 8 when $i=j$ and $q_1=q_2=q$, which measures the entropy of residue type q at position i. And the field parameter feature $\mathit{U}{\mathit{P}}_i$ at residue i of the Potts model is defined as:

$$\begin{array}{l}\mathit{U}{\mathit{P}}_i={\left({\mathit{e}}_i\left(1\right),\dots ,{\mathit{e}}_i\left(22\right),{\mathit{e}}_i\left(X_{1,i}\right)\right)}^T\hfill \end{array}$$ (Equation 10)

Note that for both $\mathit{U}{\mathit{M}}_i$ and $\mathit{U}{\mathit{P}}_i$ the last dimensions are the sequential descriptors that introduce sequence-specific information in addition to the MSA-specific single-site features. The one-hot sequence feature for residue i is defined as $\mathit{U}{\mathit{V}}_i\in {\left\{\mathrm{0,1}\right\}}^Q$ and $\mathit{U}{\mathit{V}}_i\left(q\right)=1$ if the residue type at position i is in q state and $\mathit{U}{\mathit{V}}_i\left(q\right)=0$ elsewhere. HMM profile features $\mathit{UH}\in R^{L\times 30}$ (30 descriptors) are also considered by building a profile hidden Markov models from the input alignment using hhmake program in HHsuite package. Thus, the concatenated unary feature for residue i is calculated by

$$\begin{array}{l}\mathit{U}{\mathit{F}}_i={\left(\mathit{U}{{\mathit{M}}_i}^T;\mathit{U}{{\mathit{P}}_i}^T;\mathit{U}{{\mathit{V}}_i}^T;\mathit{U}{{\mathit{H}}_i}^T\right)}^T\hfill \end{array}$$ (Equation 11)

In total, the channel size of pairwise and unary input feature tensors are 976 (Equation 4) and 98 (Equation 11) respectively.

Neural network architecture

The 1D (unary) and 2D (pairwise) features extracted from MSA are fed into ten 1D residual blocks and ten 2D residual blocks, respectively, for structure descriptor prediction. A general structure of a residual block is shown in Figure 1 where a shortcut link is added from previous layers to the output, compared to the traditional neural networks. Here, the residual block is composed of two types of layers, i.e., the convolutional layer and the instance normalization layer (Ulyanov et al., 2016), which are collected sequentially. The transformed 1D features with 32 channels will be tiled vertically and horizontally and concatenated with transformed 2D features (64 channels). The composited 2D features (32∗2 + 64 = 128 channels) will further go through forty 2D residual blocks. The prediction layer for each potential term performs a simple pixel-wise linear transformation to the desired channel size, prior to a softmax layer.

Two types of neural networks with different output terms will be trained. The first one, orientation-related networks, output the C_β-C_β distance map and orientation matrices. The second type of networks, H-bond related networks, output C_β-C_β and C_α-C_α distance maps and the H-bond related pairwise geometry descriptors as defined in Equation 3. Dilation was applied for both 1D and 2D convolutional layers with the cycling of 1, 2, 4, 8, and 16. The padding size was then set accordingly to ensure the consistency of feature signal shapes. Dropout was used in all residual blocks and the dropout rate was set to 0.2 globally. The convolutional kernel size in 1D and 2D residual blocks are set to 3 and $3\times 3$, respectively.

Training DeepPotential models

The DeepPotential model was trained by minimizing the negative log-likelihood of $P\left(ter{m}_{i,j}^t\right|\mathit{PF},\mathit{UF})$ for each residue pair $(i,j)$ when predicting term t, marginally. More specifically, the loss function is defined as

$$\begin{array}{l}L\left(T\right)=-\sum _{i,j}\sum _{t\in T}{w}_t\log P\left(ter{m}_{i,j}^t|\mathit{PF},\mathit{UF}\right)\hfill \end{array}$$ (Equation 12)

where T is a set of predictive terms. i.e., distance, orientation, and H-bond terms. $w_t$ is the weight coefficient for the term t. During the training, $w_t=1$ for all terms, under the assumption that all terms contribute equally to the protein structure prediction. Adam optimizer (Kingma and Ba, 2014) was used to optimize DeepPotential models with an initial learning rate of 1E-3. Each model was trained for around 50 epochs with a batch size of three. The maximum sequence length was set to 256 which means that for any sequences with length >256 AA, a random continuous crop with the length of 256 (maximum sequence length) will be used during the training.

To improve the generalization of DeepPotential model, the MSAs of the training set are simply constructed by HHblits searching against Uniclust30 for 2 iterations. The training set was further augmented by sub-sampling each of the MSAs in the training set for 5 times, with proportions of 20%, 40%, 50%, 60% and 80% in all alignment sequences, respectively. The sub-sampled MSAs have the same weights at the early stage of the training but will be changed to 2.0, 1.5, 1.2, 1.0 and 0.6, respectively, at the later stage. Such training strategy puts extra emphasis on MSAs with fewer sequence homologs which should be beneficial to predicting Hard targets.

Protein structure prediction by automatic differentiation

For each pair of residues, the predicted probabilities of structural geometry terms will be converted into smooth potentials for the gradient-descent-based protein structure prediction. For each term, the negative log of the raw probability histogram will be interpolated by cubic spline as be used as potentials. Based on DeepPotential predictions, the folding potential can be written as

$$\begin{array}{l}{E}_{fold}=w_1{E}_{cb}+w_2{E}_{ca}+w_3{E}_{\text{Ω}}+w_4{E}_{\text{Θ}}+w_5{E}_{\text{Φ}}+w_6\left(E_{aa}+E_{bb}+E_{cc}\right)\hfill \end{array}$$ (Equation 13)

which are classified into distance potentials ($E_{cb}$ and $E_{ca}$), orientation potentials ($E_{\text{Ω}}$, $E_{\text{Θ}}$ and $E_{\text{Φ}}$), and H-bond potentials ($E_{aa}$, $E_{bb}$ and $E_{cc}$). The weights of corresponding terms are set empirically to ($w_1$, $w_2$, $w_3$, $w_4$, $w_5$, $w_6$) = (5.0, 0.1, 0.45, 0.45, 0.3, 0.5).

The backbone structure of proteins is specified by the $\phi /\psi$ backbone torsion angle of each residue along the query sequence, while the backbone torsion angle $\omega$ is set to 180°. Given a set of $\left({\phi }_i,{\psi }_i\right)$ parameters with $i=1,\cdots ,L$, the coordinates of backbone atoms (including C_β atoms) can be recovered (Derevyanko and Lamoureux, 2018), thus the energy of such decoy conformation, defined in Equation 13, can be computed according to the interpolated potential curves. With the help of the automatic differentiation in PyTorch (Paszke et al., 2019), the gradient with respect to the parameters could be readily obtained.

We implemented the L-BFGS algorithm (Zhu et al., 1997) to iteratively update the protein structure conformations. The whole backbone folding process will be performed 10 times with different initial structures built from random backbone torsion angle samplings. The final conformation with the lowest total energy will be returned. Once the optimal backbone conformation is obtained, the FASPR program (Huang et al., 2020) will be used to construct and repack the sidechain atoms.

Quantification and statistical analysis

Data were analyzed using Python. Details of specific statistical analyses are included in the main text. For differences between distributions, we used the single-tailed Student’s t test of the hypothesis that both individual distributions are drawn from the same underlying distribution, as indicated in the different parts of this study. Statistical significance was defined as p < 0.05.

Published: June 17, 2022

Data and code availability

The DeepPotential server is available at Zhang Lab (https://zhanggroup.org/DeepPotential). The standalone package of DeepPotential can be downloaded at https://zhanggroup.org/DeepPotential/files/DeepPotential.zip. The standalone package of protein folding can be downloaded at https://zhanggroup.org/DeepPotential/files/PotentialFold.zip. The training set of DeepPotential is available at https://zhanggroup.org/DeepPotential/files/new_pdb. Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.