Abstract
Microstructural changes in the pulmonary arteries associated with pulmonary arterial hypertension (PAH) is not well understood and characterized in humans. To address this issue, we developed and applied a patient-specific inverse finite element (FE) modeling framework to characterize mechanical and structural changes of the micro-constituents in the proximal pulmonary arteries using in-vivo pressure measurements and magnetic resonance images. The framework was applied using data acquired from a pediatric PAH patient and a heart transplant patient with normal pulmonary arterial pressure, which serves as control. Parameters of a constrained mixture model that are associated with the structure and mechanical properties of elastin, collagen fibers and smooth muscle cells were optimized to fit the patient-specific pressure-diameter responses of the main pulmonary artery. Based on the optimized parameters, individual stress and linearized stiffness resultants of the three tissue constituents, as well as their aggregated values, were estimated in the pulmonary artery. Aggregated stress resultant and stiffness are, respectively, 4.6 and 3.4 times higher in the PAH patient than the control subject. Stress and stiffness resultants of each tissue constituent are also higher in the PAH patient. Specifically, the mean stress resultant is highest in elastin (PAH: 69.96, control: 14.42 kPa-mm), followed by those in smooth muscle cell (PAH: 13.95, control: 4.016 kPa-mm) and collagen fibers (PAH: 13.19, control: 2.908 kPa-mm) in both the PAH patient and the control subject. This result implies that elastin may be the key load-bearing constituent in the pulmonary arteries of the PAH patient and the control subject.
1. Introduction
Pulmonary hypertension (PH) is a complex disorder that is characterized by high blood pressure in the pulmonary circulation. Based on the classification of PH by the World Health Organization [1], pulmonary arterial hypertension (PAH) (Group I of the classification) is associated with progressive vascular remodeling and structural changes that are believed to originate from the pulmonary microcirculation. The elevation of pulmonary arterial pressure over a prolonged period of time is associated with remodeling of the proximal arteries and right ventricular (RV) hypertrophy. [2–5].
Elevation in pulmonary vascular resistance (PVR) is a key feature and is used for diagnosis of PAH in the clinic [6]. Because PVR cannot take into account the pulsatile nature of blood flow [7, 8], it provides only limited insights of the disease. The pulsatility of blood flow is accounted by the pulmonary vascular stiffness (PVS), which is largely affected by changes in the stiffness of the proximal pulmonary arteries caused by vascular remodeling. Several clinical studies have shown that elevation of PVS is correlated with the mortality of adult PAH patients [9, 10], and is a better prognostic indicator of disease progression in pediatric PAH patients [11–14]. A number of indices are used in the clinic to quantify pulmonary vascular stiffness or compliance (inverse of stiffness) [15]. These indices include relative area change (RAC) of the pulmonary artery lumen [10, 16, 17], capacitance as defined by the ratio of stroke volume over pulse pressure [9], and distensibility as defined by the ratio of the RAC over the pulse pressure [11, 18]. A comprehensive list of commonly used metrics of arterial compliance and stiffness can be found in [19].
While these macroscopic or global indices are able to quantify (to some extent) the pulmonary vascular stiffness, it is difficult to connect these indices to changes in the tissue microstructure and constituents [20]. Moreover, vascular tissue samples from PAH patients, which can be directly used for investigating changes in the tissue microstructure, are scarce and the studies using these samples are mostly confined to biochemical immunochemistry and histological analyses [21]. Recently, animal studies have tried to address this issue by quantifying changes in the pulmonary arterial capacitance and associating it with microstructural changes in the vessels associated with PAH [22–24]. In those studies, extra-cellular matrix (ECM) remodeling (including collagen deposition) [25], changes in functional mechanical properties of elastin and an increase in elastolytic activity are found to be associated with the stiffer pulmonary arteries in PAH [26]. Animal models, however, may not fully reproduce the pathologies found in PAH patients. This is because there is currently no perfect animal model capable of reproducing all the clinical pathological features associated with any of the groups of PH in human [27, 28]. Computational modeling, on the other hand, can help provide physical insights on how changes in the pulmonary vascular stiffness are associated with changes in the tissue microstructure in PAH [29]. There are, however, limited patient-specific computer modeling studies of the pulmonary arteries compared to that of the systemic arteries [30, 31].
Motivated by the above-mentioned limitations, we seek here to develop an image-based inverse finite element modeling framework for investigating microstructural changes in PAH and their association with the vascular tissue mechanical behavior in the proximal PAs. Specifically, we develop a computational framework to estimate parameters of a constrained mixture model [32] from patient-specific measurements of PA pressure and diameter waveforms of a pediatric PAH patient and a heart transplant patient. The heart transplant patient has normal PA pressure and serves as the control subject of this study. The calibrated model parameters are then applied to characterize the stress and stiffness of the key load bearing constituents (elastin, collagen and smooth muscle cells), and their contribution to the aggregated tissue mechanical properties in PAH.
2. Methods
2.1. Clinical Study
Magnetic resonance (MR) imaging was performed on a pediatric PAH patient and a cardiac transplant (control) subject, labeled as PH and CT respectively. Invasive catheterization was also performed on both subjects under anesthesia to measure blood pressure in the pulmonary circulation (Figure 1(e)). The control subject had undergone an orthotopic heart transplant. Both the PAH patient and control subject are female, and are 16 and 21 years old, respectively.
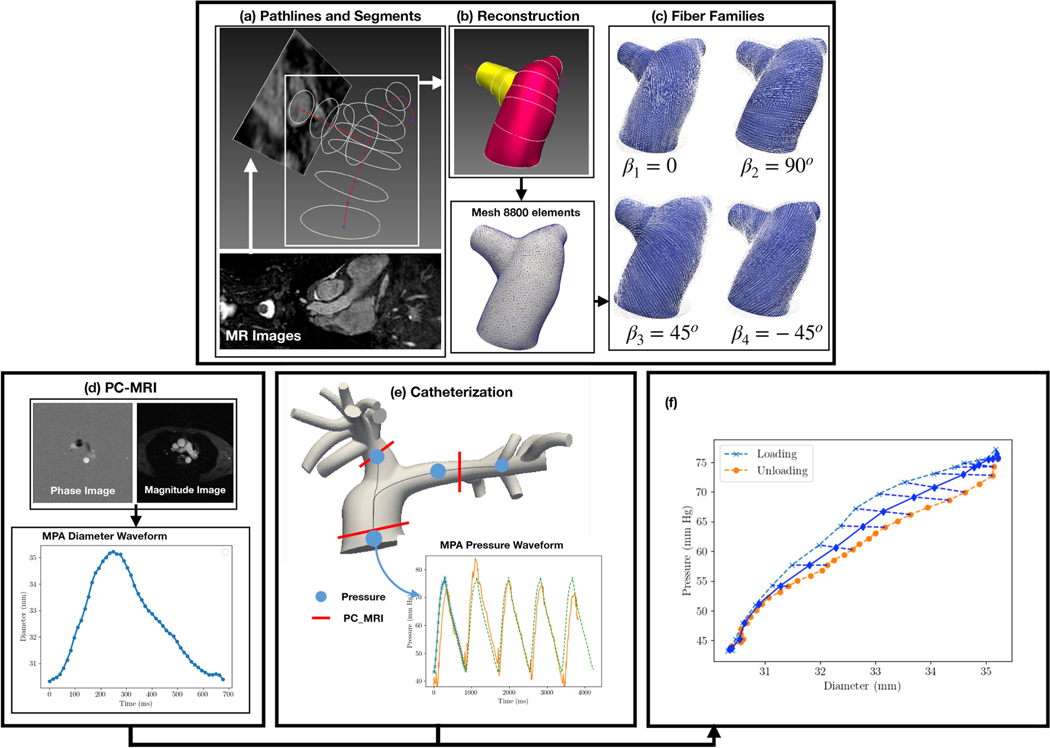
Figure 1:
Computational workflow to parameterize and analyze the PAs. (a) Longitudinal path-lines of the PAs are segmented from MR images. (b) Segmented lines are applied to reconstruct the geometry of the PAs, which is meshed using triangular elements in the 3D space. (c) Material axes are generated in the PAs. (d) Diameter waveform is obtained from PC-MRI of the MPA. (e) Pressure waveform at the MPA is acquired from catheterization. (f) Instantaneous P-D relation is reconstructed from the pressure and diameter waveforms. By the FE developments (a-c) and the clinical measurements (d-f) the characterization was carried out.
Geometries of the pulmonary arteries of each subject consisting of the main pulmonary artery (MPA), left pulmonary artery (LPA) and right pulmonary artery (RPA) were reconstructed from the MR images, which was acquired at the end of diastole, using the modeling software CRIMSON (www.crimson.software) (Figure 1(a-c)). Dynamic changes of the luminal area of the MPA over a cardiac cycle were obtained from the phase-contrast MR images (Figure 1(d)). The pressure and diameter waveforms of each subject were synchronized to obtain the characteristic pressure-diameter (P-D) relation. Hysteresis of the P-D relation is neglected by averaging the loading and unloading curves (Figure 1(f)).
The study was approved by the University of Michigan Board of Review (HUM00117706), and informed consent was obtained from the parents/guardians of the subjects.
2.2. Computational models of the pulmonary vasculature
Patient-specific finite element (FE) models of the pulmonary arteries were developed for the PAH patient and control subject by treating the arterial wall as a membrane structure. FE meshes, consisting of triangular elements in three-dimensional space, were generated from the reconstructed geometries (Figure 1(b)). The number of elements in the FE meshes are 5883 for the PAH patient and 8074 for the control subject.
Weak formulation
The Lagrangian formulation for the arterial wall subjected to a prescribed transmural pressure p is given as
| (1) |
where Π is the total potential energy of the pulmonary arterial wall, and are, respectively, the pulmonary arteries in the in-vivo reference and current configurations, u is the unknown displacement field, is the current position occupied by a material point in the surface, n is the unit normal vector in the deformed configuration, and w(u) is the strain energy per unit undeformed area.
The first variation of Π in the direction of a given arbitrary displacement δu under the same pressure is given as
| (2) |
where is the two-dimensional second Piola-Kirchhoff stress tensor (stress resultant over the thickness) [33], F is the deformation gradient tensor, (•)T denotes transpose, N is the unit normal vector on the undeformed surface. Weak formulation of the problem is obtained by setting the variation δΠ to zero, i.e.,
| (3) |
Dirichlet boundary conditions of zero-displacement are imposed at the inlet and outlets of the pulmonary arteries.
Constitutive model of the vasculature
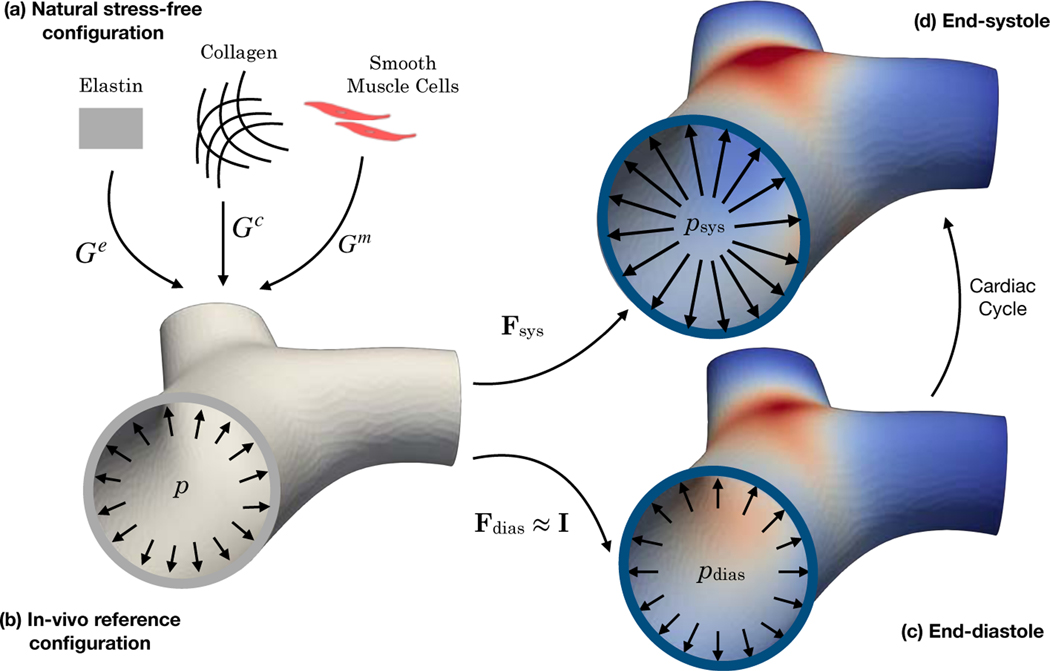
Mechanical behavior of the arterial tissue is prescribed using a constitutive model based on the theory of constrained mixture [32, 34]. In the constrained mixture formulation, we assume each tissue constituent α (with different structural and material properties) is endowed with a pre-stretch Gα taken with respect from its natural stress-free configuration (Figure 2(a)) to the in-vivo reference configuration [35, 36] (Figure 2(b)). The pre-stretch is balanced with the end-diastolic pressure. Thus, the deformation gradient tensor for constituent α from its natural configuration to any loaded configuration in the cardiac cycle is given as
| (4) |
Figure 2:
The major in-vivo configurations of the PA. (a) The natural stress-free configuration specific of each constituent. (b) The in-vivo reference configuration as each constituent is deposited from its natural configuration by the stretch Gα under the pressure near the end-diastolic pressure. (c) and (d) The in-vivo end-diastolic and end-systolic configurations.
We define four key vascular fiber directions (Mκ), namely, longitudinal (κ = 1), circumferential (κ = 2), 45° (κ = 3) and −45° (κ = 4) with respect to the longitudinal direction (Figure 1(c)) [34]. Fiber stretch in each direction κ for the constituent α is calculated as , where is the corresponding right Cauchy stretch. We consider the tissue strain energy function per unit reference area w(u) to be the sum of that of the elastin (α = e), collagen (α = c) and smooth muscle cells (SMC) (α = m) [37] that are described as follows.
Elastin
The strain energy function of the elastin amorphous matrix is given by
| (5) |
where c is a (structural and mechanical) property of elastin that accounts for its mass fraction and intrinsic stiffness. Pre-stretch of elastin is prescribed in the form of
| (6) |
Collagen Fiber Families
We consider four collagen fiber families that are each oriented along the different vascular fiber directions. As such, the strain energy function of collagen is defined as
| (7) |
where is the stretch of the κth collagen fiber, k1 is a parameter associated with the intrinsic stiffness and mass fraction of collagen, k2 is a material parameter and ϕk is the mass fraction of each collagen fiber family. Twenty percent of the total collagen is assumed to be equally distributed in the longitudinal and circumferential (κ = 1,2) fiber families (i.e., ), whereas the remaining 80% is distributed equally in the other two directions (κ = 3,4) (i.e., ). We also assume that the collagen fibers have the same properties and a pre-stretch Gc in all four directions. Correspondingly, we can define .
Smooth Muscle Cell
The SMC is assumed to be aligned circumferentially in the κ = 2 vascular fiber direction. The SMC strain energy density function is given as
| (8) |
where m1 and m2 are parameters (analogous to k1 and k2 in the collagen strain energy function). The rightmost term in Equation 8 describes the active tone of vascular SMC [38, 39], where S = 54 kPa is the stress at maximum contraction, ρ = 1040 kg/m3 is the density of mixture, and λM and λ0 are stretches at which the active force is, respectively, maximum and zero. We prescribe a pre-stretch Gm for the SMC i.e. .
2.3. Estimation of model parameters
The inverse problem was solved to estimate patient-specific model parameters in each subject from their corresponding in-vivo P-D relationship in the MPA. In this inverse problem, the cost functional describing the cumulative difference between the measured (Dc) and model predicted diameter (D) at discrete pressure pc in a cardiac cycle is minimized i.e.,
| (9) |
The set of parameters to be estimated is given as
| (10) |
These parameters are estimated by minimizing the cost functional in Equation 9 subjected to the constraints in Equation 3 (the forward problem) using the bound-constrained Broyden–Fletcher–Goldfarb–Shanno (L-BFGS-B) algorithm [40], which is a quasi-Newton technique. Because we have multiple parameters to optimize and only one constraint to satisfy, the gradient (of with respect to the parameters) is estimated more efficiently by solving the linear adjoint equation using dolfin-adjoint [41–43] than the tangent linear approaches [44, 45].
A common challenge of the gradient-based optimization techniques is the fact that the optimized parameters depend on the choice of the starting points. Different initial guesses may result in different optimized parameters (that may be located at a local minimum) and does not guarantee convergence to a global minimum [46]. To resolve this issue, we applied multiple sets of initial parameters and pick the “best” set that corresponds to the smallest value of the cost functional. Specifically, based on previous estimates of pre-stretch Gα = 1.0 ∼ 1.4 [34, 39, 47–49], we applied 3 different sets of parameters with pre-stretches (for all constituents) as initial guess. For each pre-stretch, we prescribed k2,0 = m2,01 = 1 as an initial guess for the exponent parameters of collagen and SMC. Initial guesses of the scaling parameters c0, k1,0, m1,0 were computed from the Laplace formula as described below.
To have a rough estimate of the circumferential stress, we inserted the clinically measured pressure pc and diameter Dc into the Laplace formula, . Then, knowing the constitutive relation of each constituent in Equations 5, 7 and 8 we can set the Cauchy stress as the summation of the constituents’ contribution using
| (11) |
where
| (12a) |
| (12b) |
| (12c) |
In Equation 11, and are the longitudinal and circumferential stretches computed using the pre-stretch selected from the corresponding set of initial guesses. The circumferential stretch is given by
| (13) |
where is the end-diastolic in-vivo diameter. The longitudinal stretch was assumed to be 1, and so for each constituent, . Therefore, all the parameters of Equation 11 are known according to the established initial guesses except c, k1 and m1. Their values were prescribed based on four different load combinations associated with each constituent. In the first, we distribute the rough estimate of Cauchy stress evenly between the three. And in other runs, we allocate 50% of it to one constituent and divide the other 50% between the other two. The optimized parameters were selected from the combination producing the lowest cost function. To prevent convergence issues in the forward problem and physically inadmissible numbers such as the negative stiffness, the parameters were constrained to lie within certain boundaries. The initial guesses of pre-stretch are bounded to be between 1.01 and 1.4, and the scaling parameters (c, k1 and k2) and the exponent parameters (k2 and m2) were bounded between 50% and 140% of their initial guesses.
2.4. Stress and stiffness analyses
To analyze the contribution of each tissue constituent to the mechanical response of the pulmonary vasculature, we computed the Cauchy stress resultant tensor for each constituent α as
| (14) |
and we define as the normal stress of constituent α in the κ direction, that is, . Note that the repeating index κ does not imply summation. Linearizing the Cauchy stress about the small strain tensor at the current configuration leads us to the stiffness tensor at the current configuration [36]. The fourth rank stiffness resultant tensor at the current configuration in index notation for constituent α is given as
| (15) |
where δij is the delta Kronecker tensor, for the constituent α, are the components of the deformation gradient tensor, are the components of the Cauchy stress tensor that are defined in Equation 14 at the current configuration. The rightmost derivative in Equation 15 is a fourth-ranked stiffness tensor, which can be derived directly from the strain energy functions. The normal stiffness, which is defined as the change in normal stress with respect to the change in normal strain in the same directions κ, is denoted as . This definition of stiffness is valid for any range of deformation and any material direction due to its tensorial nature. This definition reduces to the incremental elastic modulus Einc for a given diameter of a cylindrical vessel and the corresponding pressure in the circumferential direction as defined in the literature [50, 51].
The local stress and stiffness defined in Equation 14 and 15 are field variables in the PA material domain at each cardiac load-point. Global spatially averaged value of the stress and stiffness resultants of the pulmonary arteries are defined using the following operation
| (16) |
Squaring the integrand in Equation 16 prevents the tensile and compressive stresses from canceling each other. Mean value of the stress and stiffness resultants are defined as the temporal average of their global values over a cardiac cycle.
3. Results
3.1. Clinical Data
Clinical characteristics of the PAH patient and control subject are summarized in Table 1. Body surface areas (BSA) of the subjects were calculated by the DuBois formula. The BSA value of the control subject is higher (1.83 m2) compared to that of the PAH patient (1.44 m2). Mean pulmonary arterial pressure (mPAP) of the PAH patient (48 mmHg) was three times higher than that of the control subject (16 mmHg). Pulse pressure (PP) and PVR were also significantly higher in the PAH patient (PP: 37.0 mmHg, PVR: 9.9 WUm2) than that in the control subject (PP: 8.1 mmHg, PVR: 2.0 WUm2). Clinical indices commonly used for quantifying hypertension-induced stiffening/compliance were also obtained. The relative area change (RAC), defined as the relative increase in the artery lumen area over a cardiac cycle, was 18.9% for the control normotensive subject and 38.4% for the PAH patient. Distensibility, defined as the relative area increase over the PP, was lower in the PAH patient (56.3 %mmHg−1 vs. 174.2 %mmHg−1). The stiffness index [17, 52] was higher in the control subject than that of the PAH patient (3.1 vs. 1.7). Last the compliance values were 0.84 ml · mmHg−1 and 0.25 ml · mmHg−1 for the control subject and the PAH patient, retrospectively.
Table 1:
Subjects clinical characteristics
3.2. Optimized Parameters and P-D Response
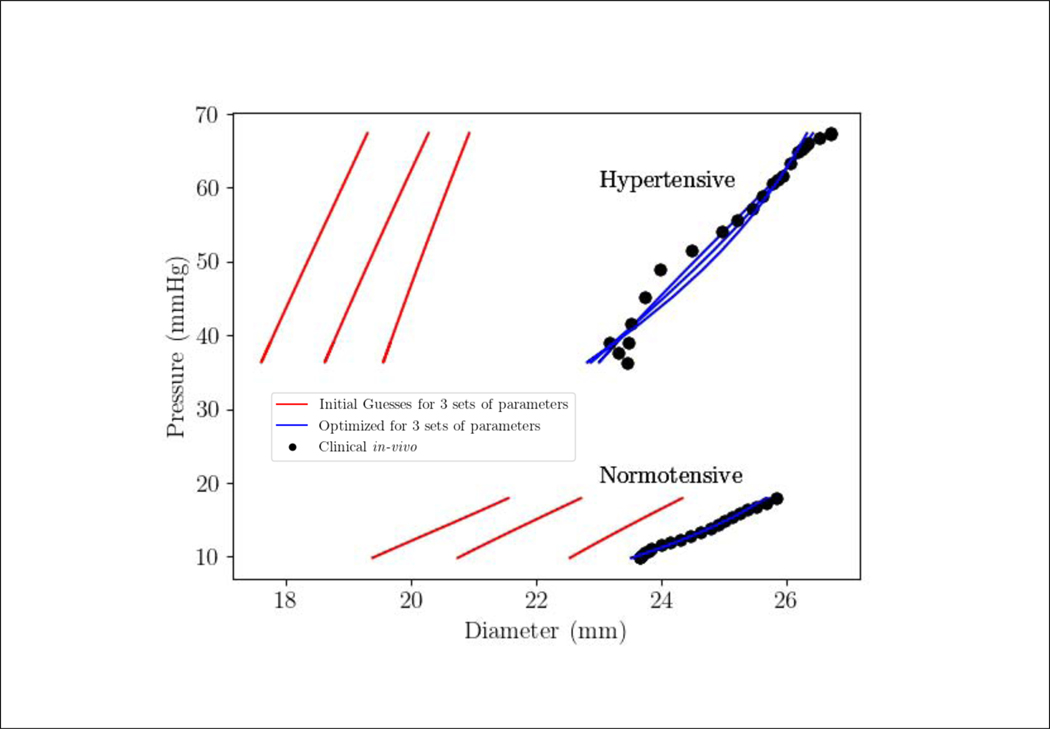
The model is able to fit the measured MPA P-D relation closely for the 2 cases with a correlation coefficient R2 > 0.94 using the 3 different sets of initial guess for the parameters (Figure 3). Optimized model parameters corresponding to the initial parameter sets are tabulated in Table 2. The optimized pre-stretch for elastin Ge has a smaller standard deviation 0.03168 compared to that for collagen (0.1208) and SMC (0.1053). Using higher values for the initial guess of the pre-stretches (Ge, Gm, Gc) results in higher optimized values for these parameters, and smaller optimized values for the parameters c, k1 and m1 in the 2 cases. The exponent parameters k2 and m2, however, did not deviate substantially from their initial guesses. Averaging the parameter values optimized with the different initial guesses for each case, we find that pre-stretch for all the constituents are slightly higher in the PAH patient (Ge = 1.160; Gc = 1.168; Gm = 1.151) compared to the control subject (Ge = 1.131; Gc = 1.133; Gm = 1.148). Scaling parameters (of the strain energy function) (c, k1, m1) are all higher in the PAH patient (60.49, 22.60, 13.57 kPa-mm) than those in the control subject (12.5, 13.5, 11.9 kPa-mm). We also find that the scaling parameters associated with elastin c is highest, followed by that of the collagen k1 and SMC m1 in the PAH patient. This trend is, however, not found in the control subject. The exponent parameters (k2, m2) are not different between the two cases.
Figure 3:
The best MPA P-D response by the inverse FE (blue line) converged from the three sets of initial guess (red line) against the in-vivo clinical measurements (solid black bullets) for the PAH patients (hypertensive) and control (normotensive).
Table 2:
Best optimized vascular parameters of mixture model.
| Elastin | Collagen | SMC | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||
| Set | c (kPa-mm) | Ge | (kPa-mm) | Gc | m1 (kPa-mm) | m 2 | Gm | R 2 | ||
| CT | (I) | 20.98 | 1.119 | 21.71 | 0.9436 | 1.028 | 21.10 | 0.9035 | 1.028 | 0.9949 |
| (II) | 9.892 | 1.127 | 11.61 | 1.212 | 1.103 | 10.19 | 1.214 | 1.176 | 0.9939 | |
| (HI) | 6.634 | 1.149 | 7.077 | 0.9807 | 1.268 | 4.282 | 0.9680 | 1.240 | 0.9900 | |
|
| ||||||||||
| PH | (I) | 83.34 | 1.116 | 35.74 | 1.005 | 1.054 | 23.92 | 1.005 | 1.057 | 0.9814 |
| (II) | 56.54 | 1.154 | 20.07 | 0.9631 | 1.158 | 11.30 | 0.9643 | 1.186 | 0.9651 | |
| (III) | 41.58 | 1.211 | 12.00 | 0.9246 | 1.291 | 5.485 | 1.1914 | 1.211 | 0.9437 | |
3.3. Tissue constituent stress and stiffness
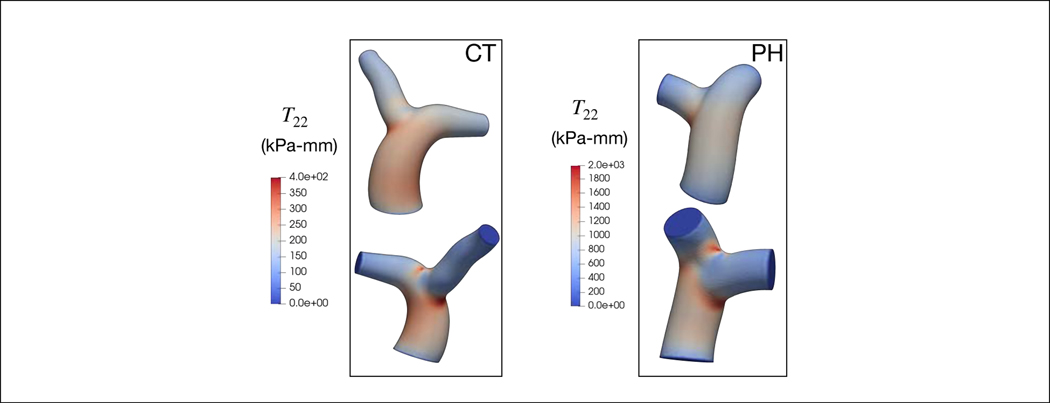
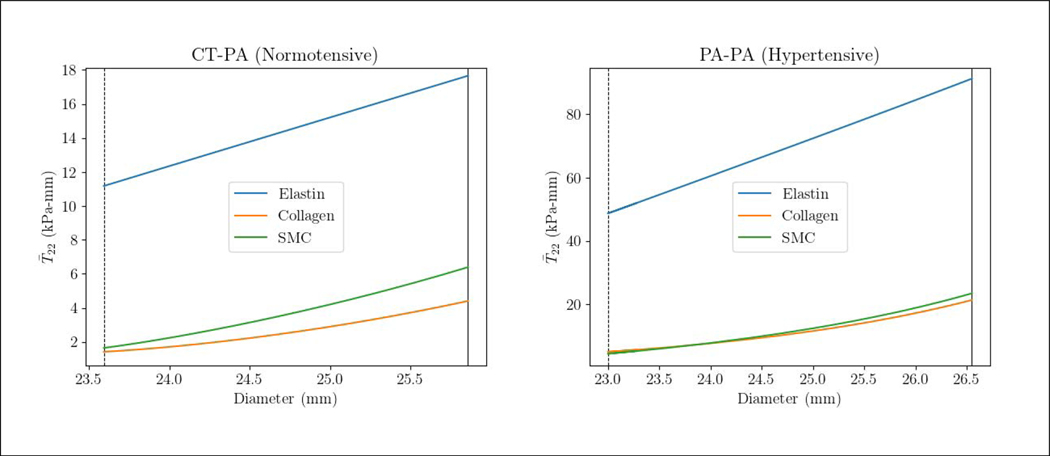
Maximum circumferential stress resultant T22 is located at the MPA-LPA and MPA-RPA bifurcation junctions in all subjects (Figure 4). The maximum stress resultant is substantially higher in the PAH patient than in the control subject (1984.0 vs. 197.7 kPa-mm). Resolving the stress resultant into its components, we find that the stress resultant of elastin is significantly higher than that of the collagen and SMC in both PAH patient and control subject for the range of MPA diameters over a cardiac cycle (Figure 5). Specifically, the mean stress resultant of elastin (averaged over a cardiac cycle) is 69.96 kPa-mm in the PAH patient and 14.42 kPa-mm in the control subject, which are both substantially larger than that of the collagen (PAH: 13.19, control: 2.908 kPa-mm) and SMC (PAH: 13.95, control: 4.016 kPa-mm). It is notable that the stress-diameter relationship of the three constituents are nearly linear, except for a slight exponential activation of the collagen and SMC near the end of systole (at high MPA diameter).
Figure 4:
The circumferential mixture stress distribution at the end-systole in PAs.
Figure 5:
The spatially averaged circumferential stress resultant over a cardiac cycle vs. the MPA diameter for the PAH and control subject and the three vascular constituents. The vertical line and dashed line are end-systole and end-diastole, respectively. Stress resultant in elastin and SMC in the circumferential direction is calculated directly from Equation 5 and Equation 8. For collagen, however, stress resultant was computed by summing the circumferential contribution of the four fiber families.
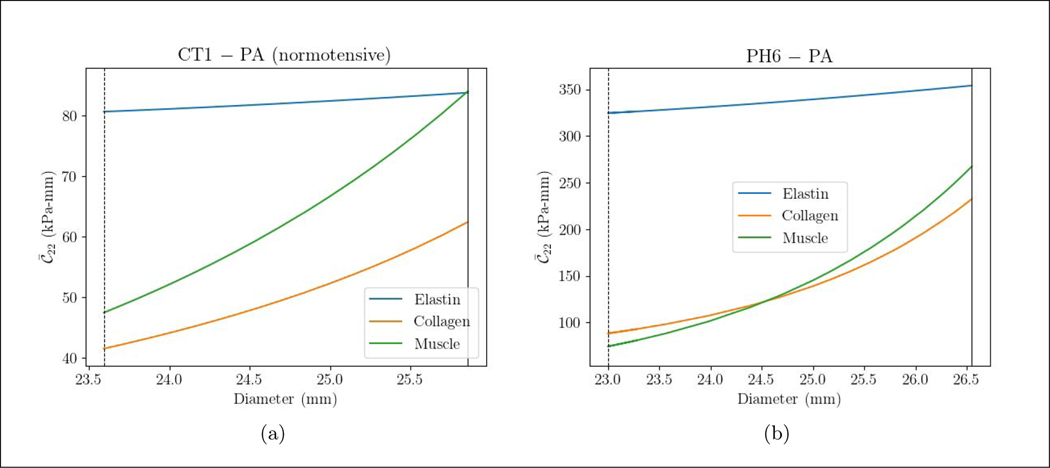
Circumferential stiffness resultant of the elastin is slightly increased while that of the collagen and SMC is increased more substantially with increasing MPA diameter (Figure 6). The mean stiffness resultant of elastin is higher ( = 339.3 kPa-mm) compared to that in the collagen ( = 160.3) and SMC ( = 170.8 kPa-mm) in the PAH patient. In the control subject, however, the mean stiffness resultant of the three constituents are comparable ( = 82.27, = 51.98, = 65.78 Pa-mm).
Figure 6:
The spatially averaged circumferential stiffness resultant over a cardiac cycle vs. the MPA diameter for different the PAH and control subject and the three vascular constituents. The vertical line and dashed line are end-systole and end-diastole, respectively. The same procedure for computing the circumferential stress is applied to obtain the circumferential stiffness.
3.4. Aggregated stress and stiffness of the tissue
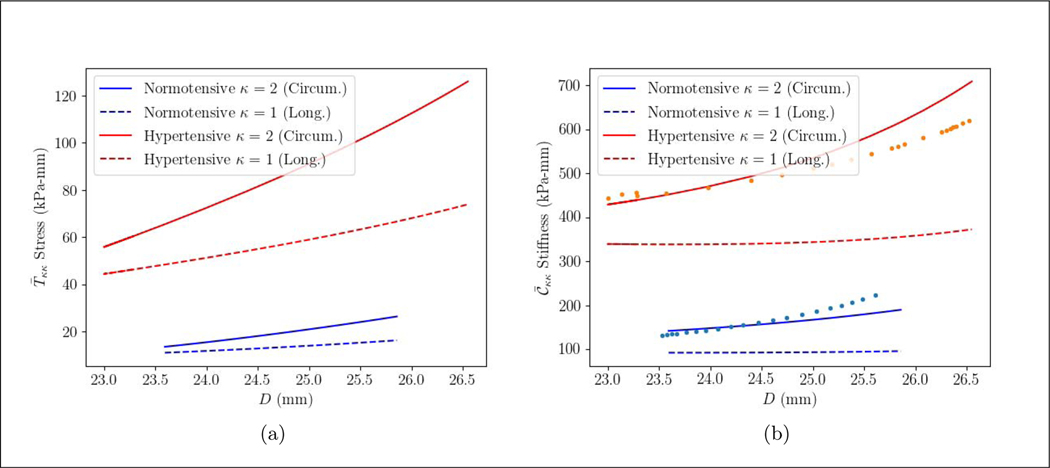
Aggregated tissue stress and stiffness resultant relationships with the diameter in the circumferential and longitudinal directions are higher in the PAH patient compared to the control subject (Figure 7). For all cases, the stress and stiffness resultants are higher in the circumferential direction than in the longitudinal direction. The mean aggregated tissue circumferential stress and stiffness resultants in the PAH patient are, respectively, 4.5 times (90.91 vs. 19.97 kPa-mm) and 3.4 times higher (568.7 vs. 166.1 kPa-mm) than the control subject. These ratios are fairly close to those obtained in the longitudinal direction, where the mean aggregated stress and stiffness resultants are 4.3 (59.15 vs 13.65 kPa-mm) and 3.8 (355.6 vs 94.45 kPa-mm) times higher in the PAH patient than in the control subject. As for the constituents, the mean stress resultant of elastin, collagen and SMC in the PAH patient are respectively 4.2, 4.5 and 3.4 times higher. Mean stiffness resultant of elastin, collagen, SMC are also, respectively, 4.1, 3.0 and 2.5 times higher in the PAH patient. The incremental elastic modulus of the tissue at the MPA wall in the circumferential direction is also calculated (Figure 7(b)). The incremental elastic modulus for both the control subject and the PAH patient is in agreement with the aggregated stiffness in circumferential direction. The mean value of the incremental elastic modulus of the PAH patient is 3.0 times higher (530.7 vs. 178.3 kPa).
Figure 7:
(a) overall stress resultant, (b) overall stiffness resultant in PA of the PAH and control subject over a cardiac cycle in the longitudinal (κ = 1) and circumferential direction (κ = 2). The incremental elastic modulus (Einc) (kPa) [50, 51] of the MPA is shown in solid dots (•).
We also note that both aggregated stress and stiffness resultants behave linearly with the diameter in the control subject. In the PAH patient, this linear trend could be observed for the stress over the cardiac cycle, but stiffness slightly increases exponentially towards the end of systole.
4. Discussion
We have developed a patient-specific inverse FE modeling framework and applied it to analyze the effects of PAH on the pulmonary arterial tissue and constituents’ mechanical behavior based on clinical data of a pediatric PAH patient and a control subject. Specifically, parameters of an arterial constitutive model based on the constrained mixture theory were estimated using patient-specific in-vivo P-D relationship measured at the MPA. The key findings of this study are: 1) Stress and stiffness resultants of the elastin are higher than those of the collagen and SMC fibers, 2) Total stress and stiffness resultants are higher in the PAH patient than in the control subject, 3) Elastin and collagen are responsible for the higher stress and stiffness resultants in the PAH patient.
4.1. Inverse FE and the PA micro-structural modeling
Investigations of the effects of PAH on in-vivo mechanical response of the pulmonary artery are largely confined to animal studies [53–55]. Existing studies characterizing the mechanical behavior of pulmonary arteries in PAH patients are, however, limited. Several indices are commonly used in the clinic to quantify changes in the pulmonary vascular stiffness/compliance, such as the relative area change (RAC), distensibility, stiffness index (β2) and capacitance. These indices, however, do not fully describe a change in the arterial stiffness. In general, the common clinical indices are lumped and provide only a rough estimate of the pulmonary vascular stiffness, which are confounded by anatomical changes of the vessels. Specifically, RAC is a purely kinematic index that does not take into account changes in pressure and internal forces [11]. In the work by Tian and Chesler [19], RAC or “area strain” is not a true measurement of stiffness. They argued that a very stiff artery could exhibit a small RAC and a very compliant artery could exhibit the same RAC in response to a smaller pressure change. In another work by Berger et al. [11], they found no difference in RAC (“vascular pulsatility” in that work) between patients with pulmonary vascular disease and the control subjects. They reasoned that RAC is the net result of a complex interaction between the intrinsic and extrinsic mechanical forces acting on the vessel wall. Nonetheless, there are also clinical studies using a lower RAC as an indicator for arterial stiffening in PAH [13, 17]. While a lower value of RAC has been often used for a suspected stiffer PA, this study found that RAC in the control subject is smaller compared to the PAH patient (Table 1), and thus may appear contradictory to the higher stiffness resultants found in the PAH patient (Figure 7). Reiterating the fact that RAC is a purely kinematic and geometry-dependent factor that may not capture the complex features of PAH, there are two possible reasons that may explain the apparently contradicting findings.
The size of the MPA at the end of diastole (Amin) in the control subject is slightly higher than that in PAH patient (440 mm2 for the control subject and 405 mm2 for the PAH patient). One would find this unexpected, given that chronic dilation is a general feature in PAH [56]. But the higher value of Amin in the control subject may be attributed to a larger BSA (1.83 m3 for the control vs. 1.44 m3 for the PAH patient). Therefore, if the values of Amin of the control subject and PAH patients are comparable, a significant increase of pulse pressure in PAH patient (37.0 mmHg vs. 8.1 mmHg) would result in a higher RAC.
The PAH patient of this study is younger. As a result, the patient may have higher elastin contentthat allows the artery to have a larger deformation in response to the higher pressure. Higher contents of elastin were found in the histopathology for young PAH patients in the study by Prapa et al. [57]. So age might be an important factor influencing RAC. For example, the young PAH patient in this study has larger RAC than the values obtained in adults in the study by Sanz et al. [17]. Specifically, the young PAH patient is 16 y/o whereas the adult patients from Sanz et al. had an average age of 53±17 y/o. The MPA size of the patient is also smaller (405 mm2 in this study vs. 850 (750–1005) mm2 in Sanz et al. [17]).
We reemphasize that distensibility, siffness index (β2) and capacitiance are all affected by geometry, and may not accurately reflect a change in the material stiffness [19]; They also presents the stiffness as an aggregate number over a cardiac cycle and do not account for the instantaneous stiffness at an specific cardiac point [20, 58]. The use of stiffness resultants computed in the inverse FE modeling framework not only enables to directly link to the changes in material stiffness associated with PAH, but also accounts for the changes in vascular stiffness over a cardiac cycle that may reflect the strain-induced stiffening [59]. Therefore, the stiffness resultants also account for any changes in directional stiffness as well as changes associated with the micro-constituents. This is in contrast to the incremental elastic modulus Einc, which is limited only to describing changes in the overall tissue stiffness in the circumferential direction.
The application of a constrained mixture constitutive model (in the inverse FE modeling), which can take into account the tissue microstructure, further enables one to characterize the load-carrying aspect of each tissue constituent (elastin, collagen and SMC) and their contributions to the aggregated mechanical behavior of the PA. Unlike fiber-based models [60–63], constrained mixture theory models take into account the collective contributions of the main arterial components (i.e., collagen, elastin and SMC) to the overall tissue mechanical behavior. This includes the constituent’s pre-stretch, which is postulated to be a major factor in fiber synthesis and development [35]. Pre-stretch is also postulated to play a significant role in differentiating whether the tissue mechanical behavior is controlled by the exponential behavior of collagen fibers or the rubber-like behavior of elastin [48]. For example, Seyedsalehi et al. [49] had used the constrained mixture theory model to estimate the pre-stretch of collagen from non-aneurysmal human abdominal arteries, and they found that collagen pre-stretch is strongly correlated to the subjects’ age. Constrained mixture theory models, however, have been applied only in the systemic arteries and not in the PAs in humans. The present study addresses the above-mentioned limitations that are associated with the characterization of microstructural remodeling in human pulmonary arteries caused by PAH.
4.2. Constituent mechanical behavior
The key finding here is that elastin is the primary load-bearing constituent in the PAs, and controls the approximately linear P-D relationship found in the PAH patient and control subject. This is reflected by the larger estimated scaling parameter in the strain energy function of elastin (c) (Table 2) and its stress resultant (Figure 5). This result is consistent with previous studies on children with PAH [31] and hypoxia-induced animals [53]. In the animal studies, elastin is found to be the key load-bearing tissue constituent in the large pulmonary arteries, especially at lower pressures near the end-diastole at which the artery is less stretched [24, 58, 64]. The dominance of elastin could be because the subjects in our studies are relatively young, which in principle, will have little degradation of elastin that is typically found in adults [49, 64].
4.3. Effect of PAH
Three major remodeling mechanisms causing the stiffening of pulmonary arteries in PAH have been put forward [20, 58, 65]. Based on our results, we discuss the possibility of these mechanisms in contributing to the pulmonary vascular stiffening in the PAH patient.
Vascular remodeling induced passive stiffening − This mechanism is associated with the change in the intrinsic material properties of the constituents. Our result suggests that this is the main mechanism causing stiffening of the large pulmonary arteries in the PAH patient. This is reflected by an increase in the constituents’ stiffness resultant, especially in elastin that plays a dominant role in the the mechanical response of the PA (Figure 6). In animal models, stiffness elevation is reported to be less than two times, 81% in calves [23] and approximately 60% in mice [66]. In this study, however, the four times increase in the PAH stiffness resultant accounts for both the increase in material stiffness and thickening. Among the structural changes associated with PAH, the thickening of arterial wall has been consistently encountered [65]. For example, Kobs and Chesler [66] observed 68% and 98% increase in elastin and collagen thickness, respectively, without appreciable thickening of the SMC in hypoxia animal models of PAH. In this study, PAH-induced thickening is not identifiable. However, based on previous findings that the stiffness in PAH patient is less than twice of that in healthy humans, the 4x higher stiffness resultant found here (see subsection 3.4) should, in principle, suggest that the pulmonary arterial wall thickness is more than 2x of that in healthy humans. This is consistent with human studies of PAH showing significant thickening of the pulmonary arterial wall [65]. Also, while collagen deposition could be a mechanism through which the artery is remodeled to prevent also damage (as found in a previous study [13]), elastin may be produced simultaneously in the thickening process as the subjects are young. The correlation between the larger elastin content in the young PAH patients is observed in the patients with PAH associated with congenital heart disease (CHD) [57]. In that study elastin/collagen ratio in histology images of the MPA was significantly higher in PAH/CHD compared to the control subjects. The lower values of this ratio was correlated with the patients with older ages due to abundance of collagen in advanced age. The larger content and stiffness of elastin was also reported in noenatal calves [23]. These two studies on young human and young animals with PAH are in consistence with the results of this study suggesting that elastin remains the critical load-carrying constituent in the PA.
Acute high-strain-induced passive stiffening − Ex-vivo tests performed on the PA obtained from an animal PAH model showed that collagen and SMC accounts for more stress on the artery wall and dominates the mechanical behavior in the PAs only at higher stretches [58]. Specifically, Kobs and Chesler [66] found a linear correlation between the elastic modulus of the PA and the elastin thickness at low-strain and the collagen thickness at high strain. It is therefore postulated that only at higher strain will the mixture be stretched sufficiently to recruit the collagen fibers and SMC. The transitioning in the tissue mechanical response from an elastin-dominated regime to a collagen-dominated regime is associated with this mechanism. The transitioning from elastin-dominated to collagen-dominated regime, however, may not be identifiable in-vivo, even under hypertensive condition. For example, Lammers et al. (2008) [23] used the curvature of the stress-strain curve to identify the transition point. They found that in normal calves, 62% of the in-vivo response remains in the elastin-dominant and 38% in the transition region, while the entire hypertensive response resides in the transition region. Similarly, the recruitment of collagen and SMC fibers that dominate the mechanical response is not likely to be present here, as reflected by the nearly linear P-D response and dominance of elastin.
Acute active stiffening due to SMC active response − In this study, we do not expect active stress elevation in the PAH. This is because the mean active stress resultant (PAH: 0.4723 kPa-mm; control: 0.3485 kPa-mm) is substantially lower than the mean passive stress resultant (PAH: 13.95 kPa-mm; control: 4.016 kPa-mm).
5. Limitations
There are some limitations associated with this study. First, the model parameters may not be identifiable in optimization process that is based only on the patient-specific P-D relationship. To ameliorate this limitation, we have applied different initial guesses in the optimization process and compared our findings with previous studies. Second, the model parameters and variables associated with the membrane formulation of the pulmonary arteries are integrated over the thickness. More detailed studies on thickness of the pulmonary arteries in PAH and healthy humans will shed significant light to have better assessments in the PAH remodeling progress. Increased pulmonary arterial thickness has been reported in animal models of PAH [24, 26, 53, 54, 67]. Nevertheless, the larger increase in thickness associated with collagen fibers (98% increase) compared with the increase in elastin (68% increase) in PAH mouse model [66] is not sufficient to account for the ~ 5 − fold increase in stress and stiffness resultants found in the PAH group compared to the control subject. Last, the interpretations are based on one PAH patient and one control subject. More specifically, the control subject is older and has a larger MPA (likely to somatic development). A stronger conclusion can be reached when dataset from larger groups of patients and control subjects within a narrower range of age are available.
Acknowledgment
This work was supported by American Health Association (AHA) (No. 17SDG33370110) and National Institutes of Health (NIH) (No. U01HL135842). CTB acknowledges financial support from the National Science Foundation Graduate Research Fellowship Program (DGE1256260) and the University of Michigan Rackham Merit Fellowship.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Simonneau G et al. Haemodynamic definitions and updated clinical classification of pulmonary hypertension. European Respiratory Journal 53, 1801913 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Durmowicz AG & Stenmark KR Mechanisms of structural remodeling in chronic pulmonary hypertension. Pediatr Rev 20, e91–e102 (1999). [PubMed] [Google Scholar]
- 3.Voelkel NF et al. Right ventricular function and failure: report of a National Heart, Lung, and Blood Institute working group on cellular and molecular mechanisms of right heart failure. Circulation 114, 1883–1891 (2006). [DOI] [PubMed] [Google Scholar]
- 4.Bogaard HJ, Abe K, Noordegraaf AV & Voelkel NF The right ventricle under pressure: cellular and molecular mechanisms of right-heart failure in pulmonary hypertension. Chest 135, 794–804 (2009). [DOI] [PubMed] [Google Scholar]
- 5.Greyson CR The right ventricle and pulmonary circulation: basic concepts. Revista Española de Cardiología (English Edition) 63, 81–95 (2010). [DOI] [PubMed] [Google Scholar]
- 6.Badesch DB et al. Diagnosis and assessment of pulmonary arterial hypertension. Journal of the American College of Cardiology 54, S55–S66 (2009). [DOI] [PubMed] [Google Scholar]
- 7.Weinberg CE. et al. Extraction of pulmonary vascular compliance, pulmonary vascular resistance, and right ventricular work from single-pressure and Doppler flow measurements in children with pulmonary hypertension: a new method for evaluating reactivity: in vitro and clinical studies. Circulation 110, 2609–2617 (2004). [DOI] [PubMed] [Google Scholar]
- 8.Hunter KS et al. Pulmonary vascular input impedance is a combined measure of pulmonary vascular resistance and stiffness and predicts clinical outcomes better than pulmonary vascular resistance alone in pediatric patients with pulmonary hypertension. American Heart Journal 155, 166–174 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mahapatra S, Nishimura RA, Sorajja P, Cha S & McGoon MD Relationship of pulmonary arterial capacitance and mortality in idiopathic pulmonary arterial hypertension. Journal of the American College of Cardiology 47, 799–803 (2006). [DOI] [PubMed] [Google Scholar]
- 10.Gan CT-J et al. Noninvasively assessed pulmonary artery stiffness predicts mortality in pulmonary arterial hypertension. Chest 132, 1906–1912 (2007). [DOI] [PubMed] [Google Scholar]
- 11.Berger RM, Cromme-Dijkhuis AH, Hop WC, Kruit MN & Hess J Pulmonary arterial wall distensibility assessed by intravascular ultrasound in children with congenital heart disease: an indicator for pulmonary vascular disease? Chest 122, 549–557 (2002). [DOI] [PubMed] [Google Scholar]
- 12.Ploegstra M-J et al. Pulmonary arterial stiffness indices assessed by intravascular ultrasound in children with early pulmonary vascular disease: prediction of advanced disease and mortality during 20-year follow-up. European Heart Journal-Cardiovascular Imaging 19, 216–224 (2018). [DOI] [PubMed] [Google Scholar]
- 13.Friesen RM et al. Proximal pulmonary vascular stiffness as a prognostic factor in children with pulmonary arterial hypertension. European Heart Journal-Cardiovascular Imaging 20, 209–217 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Schäfer M et al. Characterization of CMR-derived haemodynamic data in children with pulmonary arterial hypertension. European Heart Journal–Cardiovascular Imaging 18, 424–431 (2017). [DOI] [PubMed] [Google Scholar]
- 15.Thenappan T et al. The critical role of pulmonary arterial compliance in pulmonary hypertension. Annals of the American Thoracic Society 13, 276–284 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Rodes-Cabau J et al. Intravascular ultrasound of the elastic pulmonary arteries: a new approach for the evaluation of primary pulmonary hypertension. Heart 89, 311–315 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sanz J et al. Evaluation of pulmonary artery stiffness in pulmonary hypertension with cardiac magnetic resonance. JACC: Cardiovascular Imaging 2, 286–295 (2009). [DOI] [PubMed] [Google Scholar]
- 18.Santana DB, Barra JG, Grignola JC, Ginés FF & Armentano RL Pulmonary artery smooth muscle activation attenuates arterial dysfunction during acute pulmonary hypertension. Journal of Applied Physiology 98, 605–613 (2005). [DOI] [PubMed] [Google Scholar]
- 19.Tian L & Chester NC In vivo and in vitro measurements of pulmonary arterial stiffness: a brief review. Pulmonary Circulation 2, 505–517 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hunter KS, Lammers SR & Shandas R Pulmonary vascular stiffness: measurement, modeling, and implications in normal and hypertensive pulmonary circulations. Comprehensive Physiology 1, 1413–1435 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Tuder RM Pathology of pulmonary arterial hypertension in Seminars in Respiratory and Critical Care Medicine 30 (2009), 376–385. [DOI] [PubMed] [Google Scholar]
- 22.Stenmark KR, Gerasimovskaya E, Nemenoff RA & Das M Hypoxic activation of adventitial fibroblasts: role in vascular remodeling. Chest 122, 326S–334S (2002). [DOI] [PubMed] [Google Scholar]
- 23.Lammers SR et al. Changes in the structure-function relationship of elastin and its impact on the proximal pulmonary arterial mechanics of hypertensive calves. American Journal of Physiology-Heart and Circulatory Physiology 295, H1451–H1459 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kobs RW, Muvarak NE, Eickhoff JC & Chesler NC Linked mechanical and biological aspects of remodeling in mouse pulmonary arteries with hypoxia-induced hypertension. American Journal of Physiology-Heart and Circulatory Physiology 288, H1209–H1217 (2005). [DOI] [PubMed] [Google Scholar]
- 25.Wang Z, Lakes RS, Eickhoff JC & Chesler NC Effects of collagen deposition on passive and active mechanical properties of large pulmonary arteries in hypoxic pulmonary hypertension. Biomechanics and Modeling in Mechanobiology 12, 1115–1125 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Maruyama K et al. Chronic hypoxic pulmonary hypertension in rats and increased elastolytic activity. American Journal of Physiology-Heart and Circulatory Physiology 261, H1716–H1726 (1991). [DOI] [PubMed] [Google Scholar]
- 27.Stenmark KR, Meyrick B, Galie N, Mooi WJ & McMurtry IF Animal models of pulmonary arterial hypertension: the hope for etiological discovery and pharmacological cure. American Journal of Physiology-Lung Cellular and Molecular Physiology 297, L1013–L1032 (2009). [DOI] [PubMed] [Google Scholar]
- 28.Shimoda LA & Laurie SS Vascular remodeling in pulmonary hypertension. Journal of Molecular Medicine 91, 297–309 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tang BT et al. Wall shear stress is decreased in the pulmonary arteries of patients with pulmonary arterial hypertension: an image-based, computational fluid dynamics study. Pulmonary Circulation 2, 470–476 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Shavik SM, Tossas-Betancourt C, Figueroa CA, Baek S & Lee LC Multiscale Modeling Framework of Ventricular-Arterial Bi-directional Interactions in the Cardiopulmonary Circulation. Frontiers in physiology 11, 2 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zhang Y. et al. Application of a microstructural constitutive model of the pulmonary artery to patient-specific studies: validation and effect of orthotropy. Journal of Biomechanical Engineering 129, 193–201 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Baek S, Rajagopal K & Humphrey J A theoretical model of enlarging intracranial fusiform aneurysms. Journal of Biomechanical Engineering 128, 142–149 (2006). [DOI] [PubMed] [Google Scholar]
- 33.Kyriacou S, Humphrey J & Schwab C Finite element analysis of nonlinear orthotropic hyperelastic membranes. Computational Mechanics 18, 269–278 (1996). [Google Scholar]
- 34.Zeinali-Davarani S, Sheidaei A & Baek S A finite element model of stress-mediated vascular adaptation: application to abdominal aortic aneurysms. Computer Methods in Biomechanics and Biomedical Engineering 14, 803–817 (2011). [DOI] [PubMed] [Google Scholar]
- 35.Humphrey J & Rajagopal K A constrained mixture model for growth and remodeling of soft tissues. Mathematical Models and Methods in Applied Sciences 12, 407–430 (2002). [Google Scholar]
- 36.Baek S, Gleason RL, Rajagopal K & Humphrey J Theory of small on large: potential utility in computations of fluid–solid interactions in arteries. Computer Methods in Applied Mechanics and Engineering 196, 3070–3078 (2007). [Google Scholar]
- 37.Holzapfel GA, Gasser TC & Ogden RW A new constitutive framework for arterial wall mechanics and a comparative study of material models. Journal of Elasticity and the Physical Science of Solids 61, 1–48 (2000). [Google Scholar]
- 38.Zulliger MA, Rachev A & Stergiopulos N A constitutive formulation of arterial mechanics including vascular smooth muscle tone. American Journal of Physiology-Heart and Circulatory Physiology 287, H1335–H1343 (2004). [DOI] [PubMed] [Google Scholar]
- 39.Baek S, Valentin A & Humphrey J Biochemomechanics of cerebral vasospasm and its resolution: II. Constitutive relations and model simulations. Annals of Biomedical Engineering 35, 1498–1509 (2007). [DOI] [PubMed] [Google Scholar]
- 40.Fletcher R Practical methods of optimization (John Wiley & Sons, 2013). [Google Scholar]
- 41.Farrell PE, Ham DA, Funke SW & Rognes ME Automated derivation of the adjoint of high-level transient finite element programs. SIAM Journal on Scientific Computing 35, C369–C393 (2013). [Google Scholar]
- 42.Mitusch S, Funke S & Dokken J dolfin-adjoint 2018.1: automated adjoints for FEniCS and Firedrake. Journal of Open Source Software 4, 1292 (2019). [Google Scholar]
- 43.Chavent G Identification of functional parameters in partial differential equations. Joint Automatic Control Conference, 155–156 (1974). [Google Scholar]
- 44.Plessix R-E A review of the adjoint-state method for computing the gradient of a functional with geophysical applications. Geophysical Journal International 167, 495–503 (2006). [Google Scholar]
- 45.Finsberg H. et al. Efficient estimation of personalized biventricular mechanical function employing gradient-based optimization. International Journal for Numerical Methods in Biomedical Engineering 34, e2982 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Balaban G, Alnæs MS, Sundnes J & Rognes ME Adjoint multi-start-based estimation of cardiac hyperelastic material parameters using shear data. Biomechanics and Modeling in Mechanobiology 15, 1509–1521 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Zeinali-Davarani S, Raguin L & Baek S An inverse optimization approach toward testing different hypotheses of vascular homeostasis using image-based models. The International Journal of Structural Changes in Solids 3, 33–45 (2011). [Google Scholar]
- 48.Roccabianca S, Figueroa C, Tellides G & Humphrey J Quantification of regional differences in aortic stiffness in the aging human. Journal of the Mechanical Behavior of Biomedical Materials 29, 618–634 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Seyedsalehi S, Zhang L, Choi J & Baek S Prior distributions of material parameters for Bayesian calibration of growth and remodeling computational model of abdominal aortic wall. Journal of Biomechanical Engineering 137, 101001–1 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Hudetz AG Incremental elastic modulus for orthotropic incompressible arteries. Journal of Biomechanics 12, 651–655 (1979). [DOI] [PubMed] [Google Scholar]
- 51.Chesler NC, Thompson-Figueroa and J & Millburne K Measurements of mouse pulmonary artery biomechanics. J. Biomech. Eng. 126, 309–313 (2004). [DOI] [PubMed] [Google Scholar]
- 52.Stevens GR et al. RV dysfunction in pulmonary hypertension is independently related to pulmonary artery stiffness. JACC: Cardiovascular Imaging 5, 378–387 (2012). [DOI] [PubMed] [Google Scholar]
- 53.Hunter KS et al. In vivo measurement of proximal pulmonary artery elastic modulus in the neonatal calf model of pulmonary hypertension: development and ex vivo validation. Journal of Applied Physiology 108, 968–975 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ooi CY, Wang Z, Tabima DM, Eickhoff JC & Chesler NC The role of collagen in extralobar pulmonary artery stiffening in response to hypoxia-induced pulmonary hypertension. American Journal of Physiology-Heart and Circulatory Physiology 299, H1823–H1831 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Wang Y et al. Potential Damage in Pulmonary Arterial Hypertension: an Experimental Study of Pressure-Induced Damage of Pulmonary Artery. Journal of Biomedical Materials Research Part A. [DOI] [PubMed] [Google Scholar]
- 56.Raymond TE, Khabbaza JE, Yadav R & Tonelli AR Significance of main pulmonary artery dilation on imaging studies. Annals of the American Thoracic Society 11, 1623–1632 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Prapa M et al. Histopathology of the great vessels in patients with pulmonary arterial hypertension in association with congenital heart disease: large pulmonary arteries matter too. International journal of cardiology 168, 2248–2254 (2013). [DOI] [PubMed] [Google Scholar]
- 58.Lammers S et al. Mechanics and function of the pulmonary vasculature: implications for pulmonary vascular disease and right ventricular function. Comprehensive Physiology 2, 295–319 (2011). [DOI] [PubMed] [Google Scholar]
- 59.Golob MJ et al. Pulmonary arterial strain-and remodeling-induced stiffening are differentiated in a chronic model of pulmonary hypertension. Journal of biomechanics 55, 92–98 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Gasser TC, Ogden RW & Holzapfel GA Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. Journal of the Royal Society Interface 3, 15–35 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Stålhand J, Klarbring A & Karlsson M Towards in vivo aorta material identification and stress estimation. Biomechanics and Modeling in Mechanobiology 2, 169–186 (2004). [DOI] [PubMed] [Google Scholar]
- 62.Masson I, Boutouyrie P, Laurent S, Humphrey JD & Zidi M Characterization of arterial wall mechanical behavior and stresses from human clinical data. Journal of Biomechanics 41, 2618–2627 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Schulze-Bauer CA & Holzapfel GA Determination of constitutive equations for human arteries from clinical data. Journal of biomechanics 36, 165–169 (2003). [DOI] [PubMed] [Google Scholar]
- 64.Wagenseil JE & Mecham RP Vascular extracellular matrix and arterial mechanics. Physiological Reviews 89, 957–989 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Chazova I et al. Pulmonary artery adventitial changes and venous involvement in primary pulmonary hypertension. The American journal of pathology 146, 389 (1995). [PMC free article] [PubMed] [Google Scholar]
- 66.Kobs RW & Chesler NC The mechanobiology of pulmonary vascular remodeling in the congenital absence of eNOS. Biomechanics and Modeling in Mechanobiology 5, 217–225 (2006). [DOI] [PubMed] [Google Scholar]
- 67.Tabima DM & Chesler NC The effects of vasoactivity and hypoxic pulmonary hypertension on extralobar pulmonary artery biomechanics. Journal of Biomechanics 43, 1864–1869 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]