Single-nucleosome imaging reveals steady-state motion of interphase chromatin in living human cells

Abstract

Dynamic chromatin behavior plays a critical role in various genome functions. However, it remains unclear how chromatin behavior changes during interphase, where the nucleus enlarges and genomic DNA doubles. While the previously reported chromatin movements varied during interphase when measured using a minute or longer time scale, we unveil that local chromatin motion captured by single-nucleosome imaging/tracking on a second time scale remained steady throughout G₁, S, and G₂ phases in live human cells. This motion mode appeared to change beyond this time scale. A defined genomic region also behaved similarly. Combined with Brownian dynamics modeling, our results suggest that this steady-state chromatin motion was mainly driven by thermal fluctuations. Steady-state motion temporarily increased following a DNA damage response. Our findings support the viscoelastic properties of chromatin. We propose that the observed steady-state chromatin motion allows cells to conduct housekeeping functions, such as transcription and DNA replication, under similar environments during interphase.

Local chromatin motion remains steady during interphase, allowing cells to conduct housekeeping tasks under similar environments.

INTRODUCTION

Genomic DNA in eukaryotic nucleosomes is wrapped around core histones (1, 2) and associates with numerous other proteins and RNAs to fit inside the nucleus as chromatin, where it is accessed for various genome functions (3, 4).

Emerging evidence has demonstrated that chromatin structure is locally irregular and variable in vitro (5, 6) and in vivo (7–14). The highly dynamic nature of chromatin has long been observed in live cells using lacO/LacI-GFP (green fluorescent protein), H2B-EGFP (histone 2B–enhanced green fluorescent protein), and other related systems (15–24) and, more recently, using single-nucleosome imaging (25–27) and CRISPR-dCas9–based strategies (28, 29). Recent computational modeling also supported these findings (30, 31).

Understanding chromatin behavior in living cells, especially in terms of its physical nature, is important because the dynamic behavior of chromatin is assumed to be involved in genome functioning [e.g., transcription (information output), DNA replication (information copy), and DNA repair (information maintenance)] (3, 4, 32, 33).

On the basis of a polymer physics viewpoint, recent work has suggested that chromatin may have viscoelastic properties (34, 35), which means that the physical properties of chromatin can change depending on the time and size scales used for measurements. Chromatin appeared solid-like on a minute or longer time scale (6), as shown by the relative stability of each chromosome occupied in the territory (36) and a lack of chromosomes mixing (6). However, chromatin was locally more flexible and liquid-like when measured using a second time scale (26, 37, 38).

Thus, pursuing how chromatin behavior changes based on different time scales and phases of the cell cycle is intriguing. For instance, how does chromatin behavior change during interphase, where genomic DNA doubles (39) and the nucleus becomes larger (40–42)? Studies found that chromatin was very dynamic in G₁ and much more constrained in S and G₂ phases when yeast and human cells were analyzed on a 1-min or longer time scale (29, 43, 44). Although these studies suggested that chromatin movements varied during interphase, chromatin behavior (i.e., local chromatin motion) on a shorter time scale (~1 s) might be different from what has been observed using longer time scales, according to the viscoelastic properties of chromatin.

To test this hypothesis, we focused on local chromatin motion during the interphase cell cycle using single-nucleosome imaging on a time scale of approximately 1 s and a size scale of ~200 nm, which corresponds to the size of chromatin domains (14, 26, 32, 33, 45). Single-nucleosome imaging allows us to perform more detailed analyses on local chromatin behavior than lacO/LacI-GFP, and other related systems, and is a powerful tool to sensitively detect chromatin motion changes in living cells induced by various factors. For instance, knockdown of RNA Pol II (46) or the cohesin complex (26) greatly increased local nucleosome motion, while 1,6-hexanediol treatment severely suppressed the motion (47). Using single-nucleosome imaging, we found that local chromatin motion, which is mainly driven by thermal fluctuations, remained steady throughout the interphase cell cycle and was independent of nuclear growth, genomic DNA doubling, and genome chromatin density. This was different from chromatin movements observed using a minute or longer time scale (29, 43, 44). Steady-state motion of local chromatin is consistent with the viscoelastic properties of chromatin (34, 35). Given that local chromatin motion can govern genomic DNA accessibility for target searching (25) or recruiting a piece of machinery (44), our findings provide insight into understanding physical chromatin behavior for conducting housekeeping functions in living cells, such as RNA transcription and DNA replication.

RESULTS

Single-nucleosome imaging and tracking to study local chromatin motion in living human cells

We performed single-nucleosome imaging in living human cells (Fig. 1, A and B) to determine how nuclear changes associated with cell cycle progression affect local chromatin behavior. We used a similar strategy to our previous study with human retinal pigment epithelial 1 (RPE-1) cells (46). We established HeLa cells that stably express a core histone H2B labeled with HaloTag (H2B-Halo), which can be visualized with a HaloTag ligand tetramethylrhodamine (TMR) dye (fig. S1, A and B). H2B-Halo had genome-wide nucleosome incorporation, including euchromatic and heterochromatic regions (fig. S1B), probably because the turnover of histone H2B occurs within a few hours (21). Stepwise salt washing of nuclei isolated from HeLa H2B-Halo cells (fig. S1C) confirmed that expressed H2B-Halo behaved similarly to endogenous H2B, suggesting that H2B-Halo was properly incorporated into the nucleosomes in these cells.

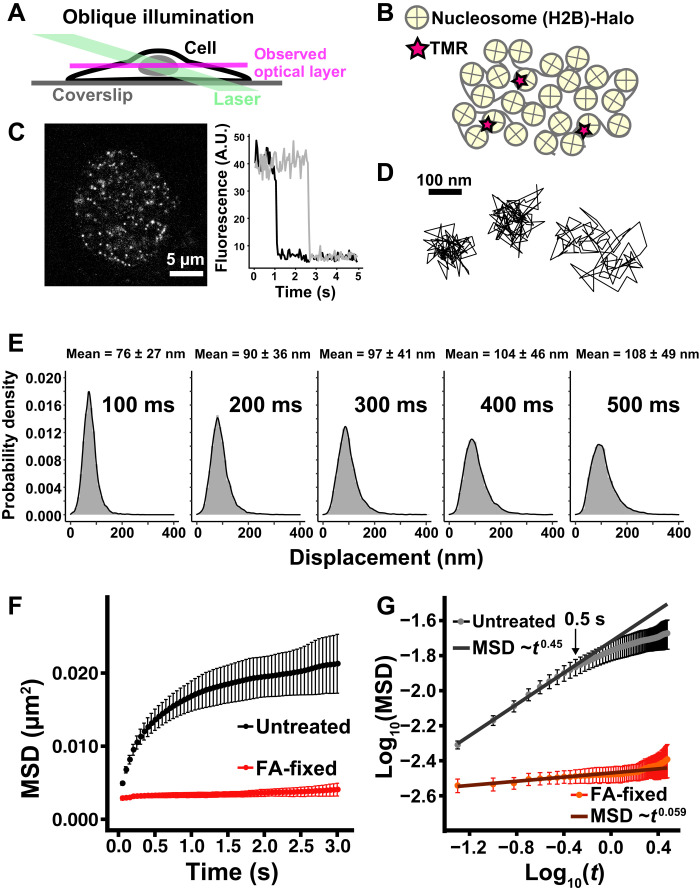
Fig. 1. Single-nucleosome imaging in living HeLa cells.

(A) Oblique illumination microscopy. The illumination laser (green) can excite fluorescent molecules within a limited thin optical layer (magenta) of the nucleus and reduce background noise. (B) A small fraction of H2B-Halo was fluorescently labeled with tetramethylrhodamine (TMR)-HaloTag ligand (red star) and was used to track nucleosome movements at super-resolution. (C) Left: Single-nucleosome (H2B-Halo-TMR) image of a living HeLa nucleus after background subtraction. Right: Single-step photobleaching of two representative nucleosome (H2B-Halo-TMR) dots. The vertical axis represents the fluorescence intensity of individual TMR dots. The horizontal axis is the tracking time series. A.U., arbitrary units. (D) Representative three trajectories of tracked single nucleosomes. (E) Displacement (movement) distributions (n = 15 cells) for 100, 200, 300, 400, and 500 ms. Means ± SD of displacement are indicated at the top. (F) Mean square displacement (MSD) plots (±SD among cells) of single nucleosomes in living untreated control (black) and formaldehyde (FA)–fixed (red) HeLa cells in a tracking time range from 0.05 to 3 s. For each sample, n = 10 to 15 cells. Rc (estimated radius of constraint of the nucleosome motion), 159 ± 15.2 nm (mean ± SD) in living cells; 69 ± 7.5 nm in FA-fixed cells. Their Rc values are significantly different: P = 1.2 × 10⁻⁵ by Kolmogorov-Smirnov test. (G) Log-log plot of the MSD data from (F). The indicated line on the untreated control was fitted using the data from 0.05 to 0.5 s. The plot cannot be fitted linearly beyond this time range, suggesting that the motion mode changes over 0.5 s.

We conducted single-nucleosome imaging and tracking (25–27, 46, 47) using oblique illumination microscopy to illuminate a thin area within a single nucleus with reduced background noise (Fig. 1A and fig. S1D) (48). Before the single-nucleosome imaging, we adjusted the angle of laser illumination to efficiently capture a nuclear interior using HeLa cells expressing Nup107-Venus, a nuclear envelope marker (fig. S1E) (42).

Very low concentrations of TMR were used to obtain sparse labeling of nucleosomes for single-nucleosome imaging (Fig. 1B). TMR-labeled nucleosomes were recorded at 50 ms/frame in the asynchronous HeLa cells (∼100 frames, 5 s total) (movie S1) and observed as clear dots (Fig. 1C, left). These dots showed a single-step photobleaching profile (Fig. 1C, right), which suggested that each dot represents a single H2B-Halo-TMR molecule in a single nucleosome. Notably, we tracked only the nucleosome-incorporated H2B-Halo-TMR at this frame rate since free H2B-Halo, which is not constrained in nucleosomes, diffused too fast to detect as dots and track. The individual dots were fitted with a two-dimensional (2D) Gaussian function to estimate the precise position of the nucleosome (49, 50). They were tracked using u-track software (51) [the position determination accuracy is 15.55 nm (46)]. From the obtained nucleosome trajectory data (e.g., Fig. 1D), we calculated displacement distributions (Fig. 1E) and mean square displacement (MSD) (Fig. 1F and also see fig. S2A), which shows how molecules spatially move in a certain time period.

MSD plots appeared subdiffusive (Fig. 1, F and G). Chemical fixation [formaldehyde (FA)] of the cells almost immobilized the TMR-labeled nucleosomes, indicating that most of the observed movement was derived from real nucleosome movements in living cells (Fig. 1F and fig. S2A). MSD neared a plateau at ~3 s (Fig. 1F), which is proportional to the square of the radius of constraint [Rc; P (plateau value) = 6/5 × Rc²; (52)]. The estimated radius of the nucleosome motion constraint was 159 ± 15.2 nm, which is similar to the chromatin domain size with a diameter of 100 to 300 nm (14, 26, 32, 45) and is also consistent with our previous analysis using RPE-1 cells (46).

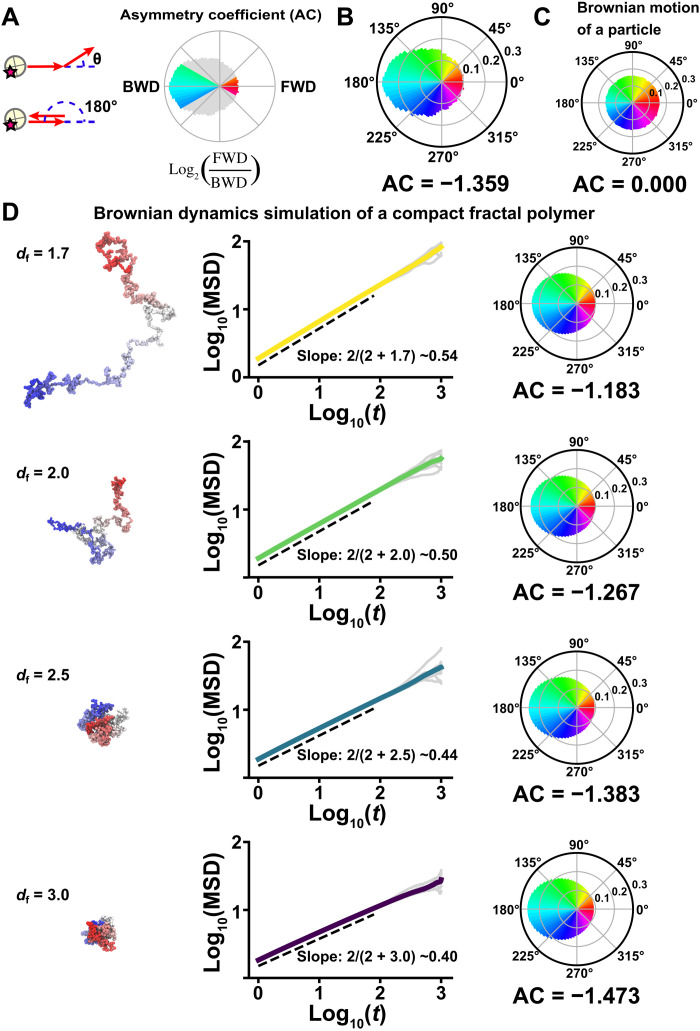
We further explored features of local chromatin motion in asynchronous HeLa cells. A log-log plot of the MSD data showed that the MSD of local nucleosome motion for the first 0.5 s was proportional to t^0.45 (Fig. 1G and fig. S2B). However, beyond 0.5 s, we could not fit the plot linearly in the double logarithmic graph (Fig. 1G), indicating that the motion mode differs past 0.5 s. Furthermore, the angle-distribution analysis of nucleosome motion (Fig. 2A, left) revealed that moving angles of individual nucleosomes are biased toward 180° (Fig. 2B) as compared to the Brownian motion of a control particle [Fig. 2C; also see Dendra2 data in (53)]. We obtained the asymmetry coefficient (AC) to quantitatively compare the motion angle distributions. The AC was calculated as the ratio between the frequency of forward angles (between −30° and 30°) and the backward angles (150° and 210°) (Fig. 2A, right), plotted on a logarithmic base 2 scale (53). The AC in nucleosome motions was negative (−1.359) as backward angles dominated, while the Brownian motion of a control particle was zero (Fig. 2C). These results suggest that nucleosomes are often pulled back to their original position in the constrained area, presumably the chromatin domain.

Fig. 2. Nucleosome motion angle distribution and Brownian dynamics simulation.

(A) Nucleosome motion angle-distribution analysis. Left: Schematic for angle-distribution analysis. Right: Schematic for asymmetry coefficient (AC). AC was calculated as the logarithm to the base of 2 of the ratio between the frequencies of forward (FWD) angles (−30° to +30°) and backward (BWD) angles (150° to 210°). AC shows deviation from a homogeneous distribution and is negative for angular distributions where the backward angles are dominant. (B) Measured angle distribution of nucleosomes (105,798 total number of angles). Moving angles of single nucleosomes are biased toward 180° and the AC is negative (for details, see Materials and Methods), indicating that they are pulled back to their original position. (C) Angle distribution of a simulated particle motion driven by thermal fluctuations (1,000,000 angles). The particle motion appears isotropic and the AC is 0.000. (D) Simulation of fractal polymer motion driven by thermal fluctuations (fractal dimension, d_f = 1.7, 2.0, 2.5, and 3.0). Left: Representative conformations of polymer models. Center: Log-log plots of averaged MSDs (colored) and 10 individual MSDs (gray). The slopes, obeying the theoretical relation 2/(2 + d_f) (54), are indicated: ~0.54 (d_f = 1.7), ~0.50 (d_f = 2.0), ~0.44 (d_f = 2.5), and ~0.40 (d_f = 3.0). Right: Corresponding motion angle distributions. The AC is indicated below each angle distribution. Note that a compact polymer (d_f = 2.5) motion profile closely recapitulated the profile of the measured angle distribution and the AC in (B) and the subdiffusion exponent in Fig. 1G and fig. S2B. Details of the fractal dimension defining the polymer compaction are described in Materials and Methods and (54).

To analyze the profile of observed local chromatin behavior, we performed polymer modeling based on our previous work (Fig. 2D) (movie S2) (54). The motion of a compact polymer (d_f = 2.5; exponent ~0.44; AC = −1.383) with thermal fluctuations well recapitulated the profile of the measured subdiffusion exponent of ~0.45 and the moving angle distribution (AC = −1.359) (Figs. 1G and 2B and fig. S2B) (for details, see, Materials and Methods). This suggested that the local chromatin motion we observed was mainly driven by thermal fluctuations. Since a simulated random motion of a particle driven by thermal fluctuations revealed isotropic angle distribution (Fig. 2C), the biased angular shape of the nucleosome motion should stem from both the polymeric nature of chromatin and thermal driving fluctuations. In the following section, we focused on this time range (<0.5 s) for single-nucleosome imaging.

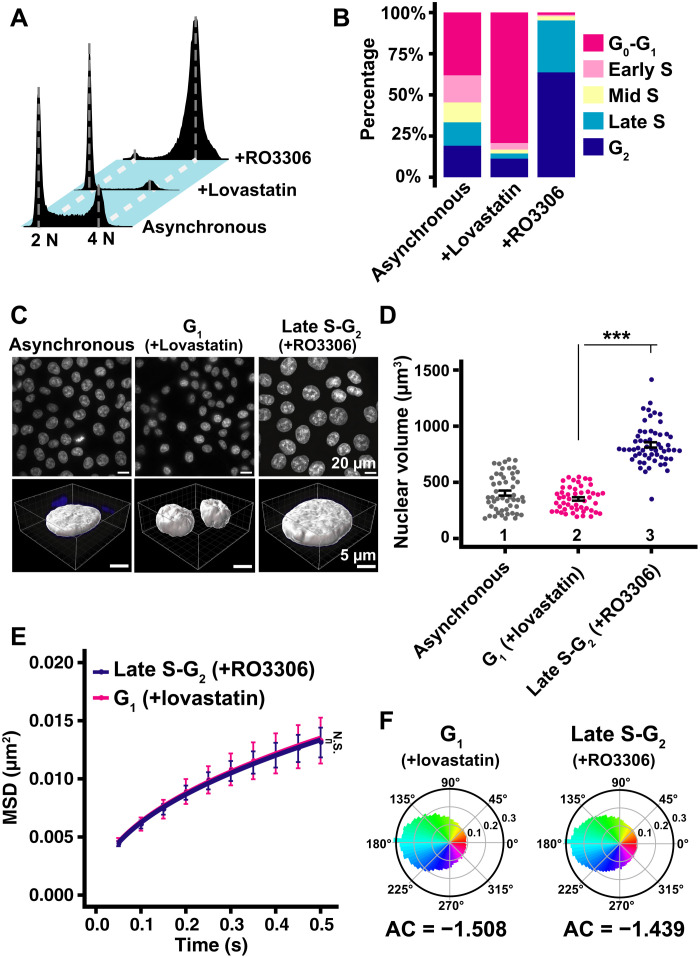
Nuclear volume expands 2.47 times with the cell cycle progression from G₁ to G₂ phase

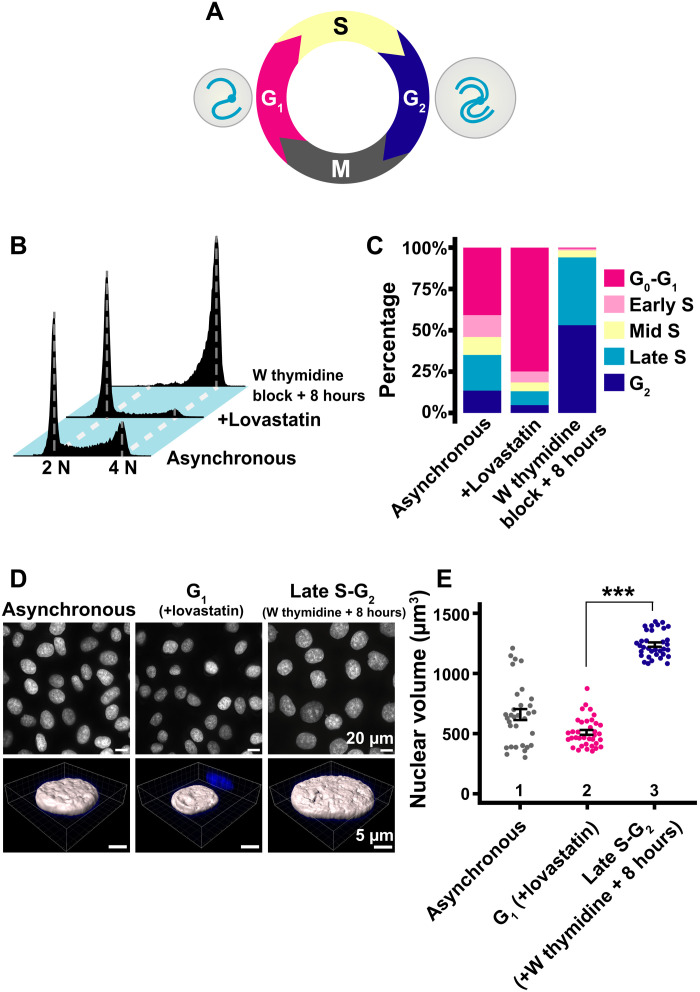
For single-nucleosome imaging, highly synchronized G₁ and late S-G₂ populations of HeLa cells were generated and the amount of their genomic DNA and nuclear volume were measured (Fig. 3A). G₁ phase cells were induced using lovastatin, a CDK2 inhibitor (see scheme in fig. S3), and late S-G₂ phase synchronization was achieved using a thymidine block and 8-hour release (fig. S3). Cell synchronization was verified by flow cytometry (Fig. 3, B and C). Seventy-five percent of cells were arrested in the G₁ phase by lovastatin treatment, while the double thymidine block and release arrested 94% of cells in late S and G₂ phases, which have twice as much DNA content as G₁ phase cells. Consistent with previous studies [see, e.g., (42)], nuclei in late S-G₂–synchronized cells appeared much larger than those in G₁ phase cells (Fig. 3D, top). Nuclear volumes of FA-fixed G₁ and late S-G₂ cells were imaged using confocal laser scanning microscopy (movie S3). Image stacks were analyzed by Imaris software (Fig. 3, D and E). The nuclear volume increased 2.47 times from G₁ (510 ± 121 μm³) to late S-G₂ phase (1263 ± 129 μm³), as genomic DNA doubled (Fig. 3E).

Fig. 3. Synchronization of HeLa cells in G₁ and late S-G₂ phases and nuclear volume measurements.

(A) Cell cycle progression. The nuclear volume (gray circle) increases as the cell cycle progresses from G₁ to G₂, with accompanying genomic DNA doubling. (B) Cellular DNA contents in indicated HeLa cell populations measured by flow cytometry. 2 N and 4 N show genomic DNA amount. “W thymidine block” means “double thymidine block.” Each histogram represents more than 16,000 cells. (C) Quantification from data in (B). (D) Top: Low-magnification images of 4′,6-diamidino-2-phenylindole (DAPI)–stained HeLa nuclei with the indicated conditions. Bottom: Reconstructed three-dimensional (3D) images of HeLa nuclei with the indicated conditions. (E) Quantitative data of nuclear volume (means ± SE) of the indicated HeLa cell populations. Mean volumes: lanes 1 (658 μm³, n = 32 cells), 2 (510 μm³, n = 36 cells), and 3 (1263 μm³, n = 37 cells). ***P < 0.0001 (P = 2.3 × 10⁻²¹) by Wilcoxon rank sum test.

Local chromatin motion is not affected by nuclear growth and genomic DNA doubling from G₁ to G₂ phase

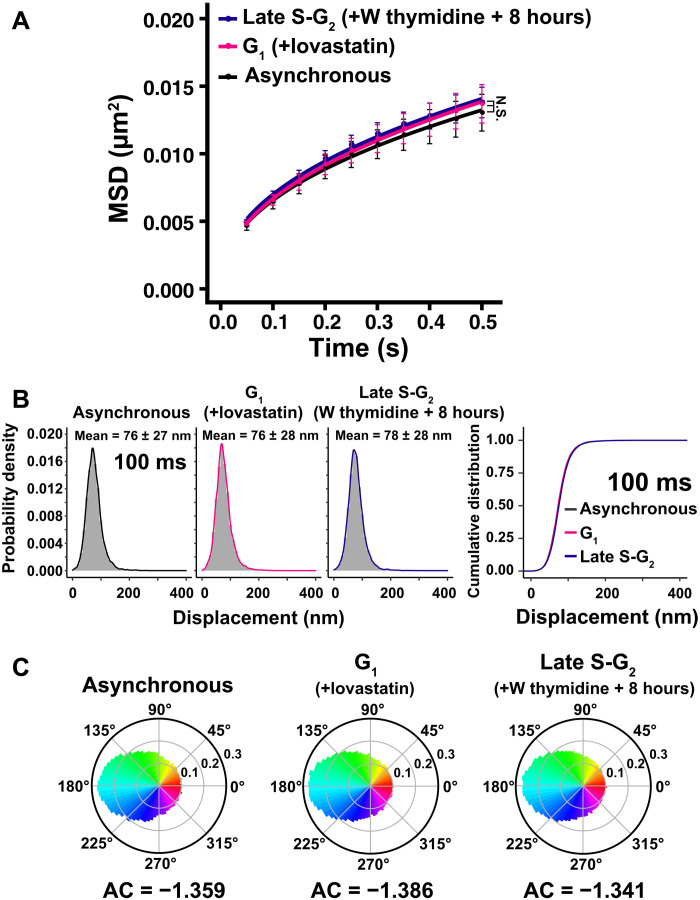
We performed single-nucleosome imaging in G₁- and late S-G₂–synchronized cells (Fig. 4A and movies S4 and S5). There were no significant differences in local chromatin motion among asynchronous, G₁-synchronized, and late S-G₂–synchronized cells (Fig. 4A and movies S4 and S5). Note that means and SDs of their displacement distributions (Fig. 4B and fig. S4) and their AC values (Fig. 4C) were also very similar. As shown in Fig. 3E, nuclear volume increased 2.47 times when genomic DNA was doubled from G₁ to G₂ phase. Together, local chromatin motion does not change, regardless of DNA amount and increasing nuclear volume during the interphase cell cycle. This result corroborates our previous nucleosome motion data of H2B-PAmCherry in HeLa cells at 8 hours (G₁), 13 hours (early S), 16 hours (mid S), 19 hours (late S), and 22 hours (G₂) released from mitotic cells (26). In this study, cells were more highly synchronized in G₁ or late S-G₂ phase.

Fig. 4. Local chromatin motion in G₁ and late S-G₂ phase HeLa cells.

(A) MSD plots (±SD among cells) of nucleosome motion in asynchronous (black), G₁ (magenta), and late S-G₂ phase (dark blue) HeLa cells from 0.05 to 0.5 s. Nucleosome trajectories used per cell: 617 to 863; n = 15 cells per sample. Not significant (N.S.) by Kolmogorov-Smirnov test for G₁ versus late S-G₂ (P = 0.93), asynchronous versus G₁ (P = 0.18), and asynchronous versus late S-G₂ (P = 0.38). “W thymidine block” means “double thymidine block”. (B) Left: Displacement distribution histograms of single nucleosomes (n = 15 cells) for 100 ms of asynchronous, G₁ phase (+lovastatin), and late S-G₂ phase (W thymidine block +8 hours) cells. Asynchronous data were reproduced from Fig. 1E. Means ± SD of displacement are indicated at the top. Note that the shape of the displacement distribution is similar among asynchronous, G₁, and late S-G₂ cells. Right: Cumulative distribution plots of the displacement. (C) Angle distribution of asynchronous (105,798 angles), G₁ phase (140,607 angles), and late S-G₂ phase cells (199,759 angles). The AC is indicated below each angle distribution. Asynchronous data were reproduced from Fig. 2B. Note that the angle-distribution profile and the AC are similar among asynchronous, G₁, and late S-G₂ cells.

Local chromatin motion is independent of genome chromatin density in the nucleus

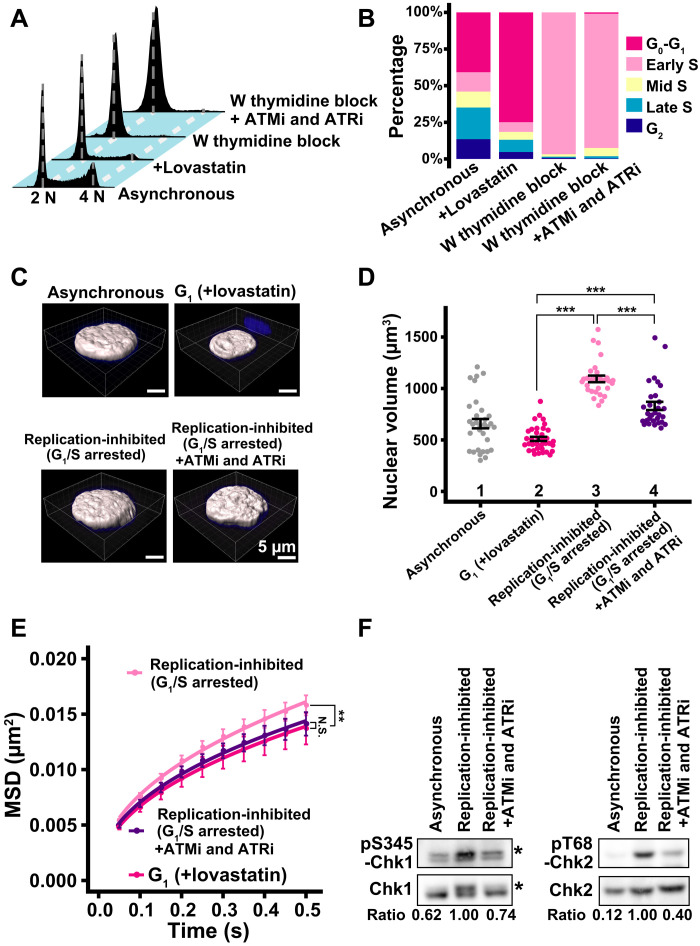
To further investigate the effects of nuclear volume and genomic DNA doubling on local chromatin behavior, we inhibited DNA replication of HeLa cells with a double thymidine block (scheme, fig. S5A). Ninety-seven percent of cells were arrested at the G₁/S phase boundary by the double thymidine block (replication-inhibited; Fig. 5, A and B). DNA replication and nuclear growth are independent events (40–42). Nuclei in replication-inhibited cells grew (1093 ± 173 μm³) 2.1-fold compared to G₁ cells (510 ± 121 μm³) (Fig. 5, C and D), suggesting that the chromatin density (i.e., total genome chromatin amount per nuclear volume) decreased in cells where replication was inhibited.

Fig. 5. Effect of chromatin density on local chromatin motion in HeLa cells.

(A) Cellular DNA contents in indicated HeLa cell populations measured by flow cytometry. Each histogram represents more than 16,000 cells. Asynchronous and +lovastatin data were reproduced from Fig. 3B. (B) Quantification from data in (A). (C) Reconstructed 3D images of HeLa nuclei with indicated conditions. Asynchronous and G₁ phase nuclei images were reproduced from Fig. 3D. (D) Quantitative data of nuclear volume (means ± SE) of indicated HeLa cell populations. Asynchronous and G₁ data were reproduced from Fig. 3E. Mean volumes: lanes 3 (1093 μm³, n = 29 cells) and 4 (831 μm³, n = 30 cells). ***P < 0.0001 by Wilcoxon rank sum test for lanes 2 versus 3 (P = 1.6 × 10⁻¹⁸), 2 versus 4 (P = 2.0 × 10⁻¹²), and 3 versus 4 (P = 3.7 × 10⁻⁷). (E) MSD plots (±SD among cells) of the nucleosome motion in HeLa G₁ (magenta), replication-inhibited (pale pink), and replication-inhibited + ATMi and ATRi (purple) cells. G₁ data were reproduced from Fig. 4A. Nucleosome trajectories used per cell: 617 to 875; n = 15 cells per sample. **P < 0.001 by Kolmogorov-Smirnov test for G₁ versus replication-inhibited (P = 3.5 × 10⁻⁴). N.S. for G₁ versus replication-inhibited + ATMi and ATRi (P = 0.68). (F) Inhibition of Chk1 and Chk2 activities by the inhibitor treatment. Western blotting of cell lysates using indicated antibodies. Asterisks denote positions of phosphorylated Chk1. The bottom values indicate the signal intensity ratio of phosphorylated Chk1 or Chk2 versus Chk1 or Chk2, respectively.

We noticed that MSD values in replication-inhibited (G₁/S arrested) cells were significantly higher than those in G₁-synchronized cells (Fig. 5E). The MSD exponent was 0.47 and slightly increased (fig. S5B). We hypothesized that this increase might be due to a DNA damage response (DDR) induced by replication inhibition, rather than decreased chromatin density, because we observed an increase in chromatin motion with ultraviolet exposure in our previous study (46). Inhibition of DNA replication can induce a DDR, which leads to chromatin decondensation (i.e., a decrease in local chromatin contacts) and an increase in chromatin motion (23, 44, 55). We observed prominent γH2AX signals, a DDR marker (56), in the replication-inhibited cells (G₁/S arrested cells; fig. S5C).

To confirm that DDR could increase local chromatin behavior, we repressed the DDR using an ATM inhibitor (KU-55933) and an ATR inhibitor (VE-821) (ATMi and ATRi, respectively). We validated if these inhibitors suppressed the phosphorylation levels of Chk1 and Chk2 (Fig. 5F), the downstream kinases of ATR and ATM, respectively (57). While the double-thymidine treatment substantially up-regulated phosphorylations of Chk1 and Chk2, the addition of ATMi and ATRi decreased them to their asynchronous control levels (Fig. 5F). These inhibitors also did not alter the overall cell cycle profile or the nuclear volume of treated cells (Fig. 5, B to D).

We then investigated the effects of ATMi and ATRi on local chromatin motion in replication-inhibited cells. We found that their local chromatin motion was similar to the G₁ cell level (Fig. 5E). On the other hand, the inhibitors did not significantly modify local chromatin motion in the thymidine-untreated control cells (fig. S5D). Our results indicated that increased local chromatin motion observed in the replication-inhibited cells was due to a DDR, but not due to decreased chromatin density. Local chromatin motion was not changed once DDR was inhibited, even in the replication-inhibited cells with enlarged nuclei. Local chromatin motion is thus independent of various nuclear changes during interphase, including genomic DNA amount, nuclear volume, and chromatin density.

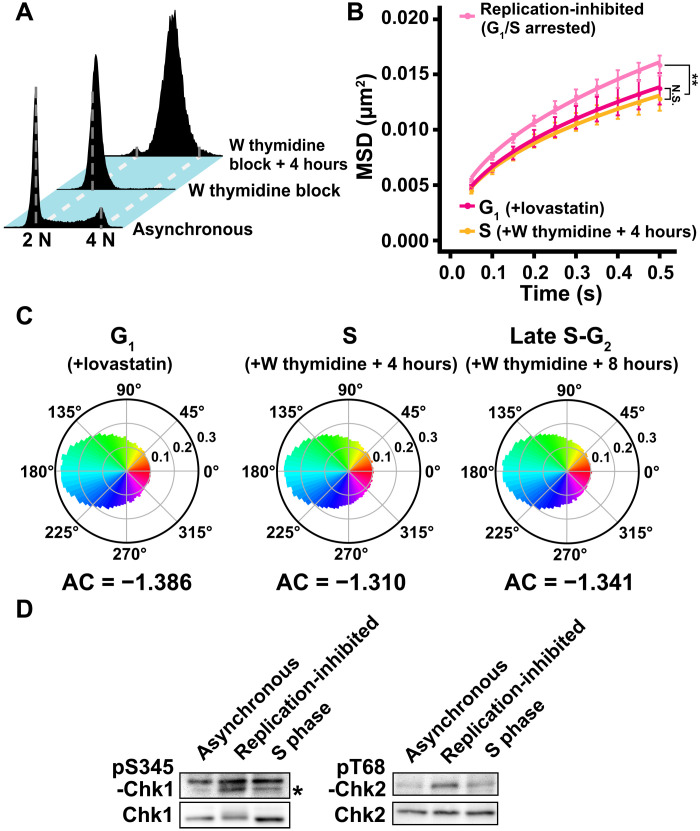
Notably, chromatin motions and their AC were comparable to those of asynchronous and G₁ cells when they were measured 4 and 8 hours after releasing the double thymidine block (S and late S-G₂ phases) (Fig. 6, A to C). DDR was no longer detected in the S phase cells released from the thymidine block (Fig. 6D). This indicated that the rise in chromatin motion, due to inhibition of DNA replication, was transient and returned to the original level sometime after the DDR diminished. Also, it should be emphasized that local chromatin motion appears steady with cell cycle progression through G₁, S, and G₂ phases.

Fig. 6. Local chromatin motion in the S phase.

(A) Cellular DNA contents in indicated HeLa cell populations measured by flow cytometry. Each histogram represents more than 27,000 cells. Asynchronous and W thymidine block data were reproduced from Figs. 3B and 5A. (B) MSD plots (±SD among cells) of the nucleosome motion in HeLa G₁ (magenta), replication-inhibited (G₁/S arrested) (pale pink), and S phase (W thymidine block + 4 hours) (orange) cells from 0.05 to 0.5 s. G₁ and replication-inhibited data were reproduced from Figs. 4A and 5E. Nucleosome trajectories used per cell: 628 to 925; n = 15 cells per sample. **P < 0.001 by Kolmogorov-Smirnov test for G₁ versus replication-inhibited (P = 3.5 × 10⁻⁴) and S versus replication-inhibited (P = 3.9 × 10⁻⁷). N.S. for G₁ versus S (P = 0.08). (C) Angle distribution of G₁ phase (140,607 angles), late S-G₂ phase (199,759 angles), and S phase cells (148,019 angles). The AC is indicated below each angle distribution. G₁ and late S-G₂ data were reproduced from Fig. 4C. Note that the angle-distribution profile and the AC are similar among G₁, S, and late S-G₂ cells. (D) DDR attenuation after release from W thymidine block. Left: Western blotting of cell lysates using anti-phospho–Chk1 (pS345-Chk1) (marked with asterisk, first row) and anti-Chk1 (second row) antibodies. Note that the upper bands are nonspecific. Right: Western blotting of cell lysates using anti-phospho–Chk2 (pT68-Chk2) (first row) and anti-Chk2 (second row) antibodies. The phosphorylated signals in S phase cells decreased to a similar level of asynchronous cells. Blots were cropped near the protein positions for clarity and space considerations.

Local chromatin motion is independent of chromatin amount, nuclear volume, and chromatin density in human HCT116 cells

We stably expressed H2B-Halo in human HCT116 cells to exclude the possibility that our findings were HeLa cell specific. HeLa cells used in this study have an abnormal karyotype (69 ± 4.2 chromosomes; n = 39 cells). HCT116 cells are human colon carcinoma cells with a near diploid of 45 chromosomes and have been widely used for recent genomics analyses.

We synchronized HCT116 cells in G₁ and late S-G₂ phases and measured their nuclear volumes. RO3306, a Cdk1-specific inhibitor, was used to enrich late S-G₂ phase cells (scheme, fig. S6), while the same procedure as HeLa cells was used for G₁ synchronization (fig. S3). Seventy-nine percent of cells were retained in G₁ using lovastatin while 95% of the RO3306-treated cells were in late S and G₂ (Fig. 7, A and B). We found a 2.37-times increase in nuclear volume from G₁ (352 ± 107 μm³) to late S-G₂ cells (833 ± 178 μm³) (Fig. 7, C and D). There was no significant difference in the MSD plots of nucleosome motion between G₁- and late S-G₂–synchronized HCT116 cells (Fig. 7E). Furthermore, AC values of their nucleosome motion angle distributions were also similar (Fig. 7F), again supporting the results that local chromatin motion was not influenced by nuclear growth and genomic DNA doubling in HeLa cells (Fig. 4A).

Fig. 7. Local chromatin motion in G₁ and late S-G₂ phase HCT116 cells.

(A) Cellular DNA contents in indicated HCT116 cell populations measured by flow cytometry. Each histogram represents more than 24,000 cells. (B) Quantification from (A) data. (C) Top: Low-magnification images of DAPI-stained HCT116 nuclei with indicated conditions. Bottom: Reconstructed 3D images of HCT116 nuclei with indicated conditions. (D) Quantitative data of nuclear volume (means ± SE) of indicated HCT116 cell populations. Mean volumes: lanes 1 (404 μm³, n = 52 cells), 2 (352 μm³, n = 49 cells), and 3 (833 μm³, n = 57 cells). ***P < 0.0001 (P = 3.7 × 10⁻¹⁸) by Wilcoxon rank sum test. Note that nuclear volumes in late S-G₂–synchronized cells appear much larger than those of G₁ cells in the asynchronous population, presumably because prolonged RO3306 treatment might enhance nuclear enlargement. (E) MSD plots (±SD among cells) of nucleosome motion in G₁ phase (magenta) and late S-G₂ phase (dark blue) HCT116 cells from 0.05 to 0.5 s. Nucleosome trajectories used per cell: 801 to 2110; n = 10 cells per sample. N.S. (P = 0.93) by Kolmogorov-Smirnov test. (F) Angle distribution of G₁ phase (81,610 angles) and late S-G₂ phase (289,328 angles). The AC is indicated below each angle distribution. Note that the angle-distribution profile and the AC is similar between G₁ and late S-G₂ cells.

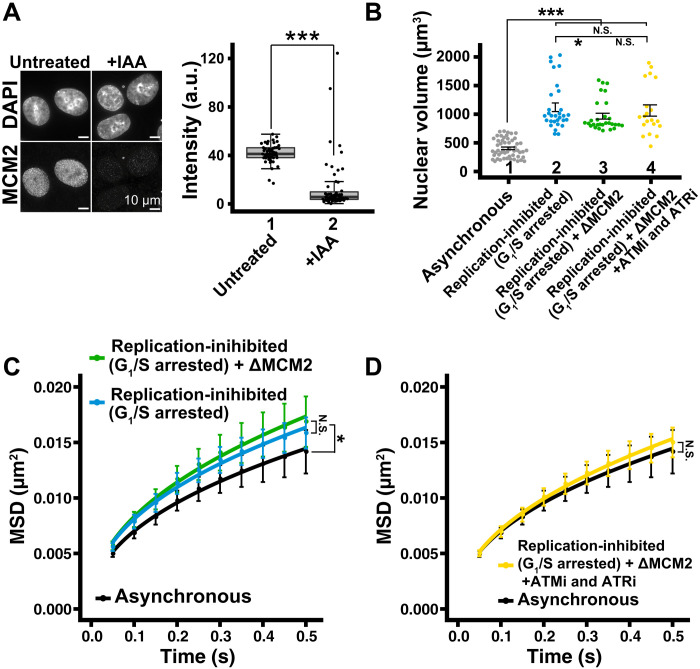
Effects on local chromatin motion in HCT116 cells, when chromatin density changed, were also examined. We combined a single thymidine block released from late S-G₂ phase cells (scheme, fig. S7A) and auxin-inducible degron (AID)–mediated rapid degradation of MCM2 (a component of the replicative MCM2–7 helicase) (schematic, fig. S7B) (58) to completely inhibit DNA replication in the cells. MCM2 was degraded efficiently following 4 hours of auxin [Indole-3-acetic acid (IAA)] treatment in HCT116 cells expressing both MCM2-mAID and H2B-Halo (Fig. 8A). Using this combined inhibition procedure, 79% of cells were arrested in early S phase (fig. S7, C and D) and had enlarged nuclei (965 ± 274 μm³) (Fig. 8B and fig. S7E). The local chromatin motion of these S phase cells also significantly increased (Fig. 8C). Treatment of cells with ATMi and ATRi again reduced the local chromatin motion to its asynchronous cell level (Fig. 8D), and these inhibitors did not alter the overall cell cycle profile (81% of cells in early S phase) (fig. S7, C and D) or the nuclear volume (1064 ± 440 μm³) (Fig. 8B and fig. S7E) of replication-inhibited cells. These results indicate that a change in chromatin density does not influence local chromatin motion in HCT116 cells, consistent with the findings from HeLa cells (Fig. 5E). Local chromatin motion was independent of chromatin amount, nuclear volume, and chromatin density in HCT116 cells, confirming that results obtained using HeLa cells were not cell line specific.

Fig. 8. Effect of chromatin density on local chromatin motion in HCT116 cells.

(A) Left: Immunostaining of MCM2 depletion. Right: Box plots of MCM2 signal intensity. Median values: lanes 1 (41.8, n = 49 cells) and 2 (13.9, n = 55 cells). ***P < 0.0001 (P = 2.7× 10⁻¹³) by Wilcoxon rank sum test. (B) Quantitative data of nuclear volume (means ± SE) of indicated HCT116 cell populations. Asynchronous data were reproduced from Fig. 7D. Mean volumes: lanes 2 (1121 μm³, n = 30 cells), 3 (965 μm³, n = 29 cells), and 4 (1064 μm³, n = 20 cells). ***P < 0.0001 by Wilcoxon rank sum test for lanes 1 versus 2 (P = 1.3 × 10⁻¹³), 1 versus 3 (P = 1.1 × 10⁻¹³), and 1 versus 4 (P = 1.9 × 10⁻⁹). *P < 0.05 for lanes 2 versus 3 (P = 0.032). N.S. for lanes 2 versus 4 (P = 0.38) and lanes 3 versus 4 (P = 0.33). (C) MSD plots (±SD among cells) of nucleosome motion in HCT116 asynchronous (black), replication-inhibited (light blue), and replication-inhibited + ΔMCM2 (green). Nucleosome trajectories used per cell: 1500 to 2590; n = 13 to 15 cells per sample. *P < 0.05 by Kolmogorov-Smirnov test for asynchronous versus replication-inhibited (P = 0.0037) and asynchronous versus replication-inhibited + ΔMCM2 (P = 0.013). N.S. for replication-inhibited versus replication-inhibited + ΔMCM2 (P = 0.16). (D) MSD plots (±SD among cells) of single nucleosomes in asynchronous (black) and replication-inhibited + ΔMCM2 + ATMi and ATRi (yellow). Asynchronous data were reproduced from (C). Nucleosome trajectories used per cell: 1500 to 2590; n = 13 to 15 cells per sample. N.S. by Kolmogorov-Smirnov test for asynchronous versus replication-inhibited + ΔMCM2 + ATMi and ATRi (P = 0.21).

Local movements of defined genomic loci are similar between G₁ and late S-G₂ phase cells

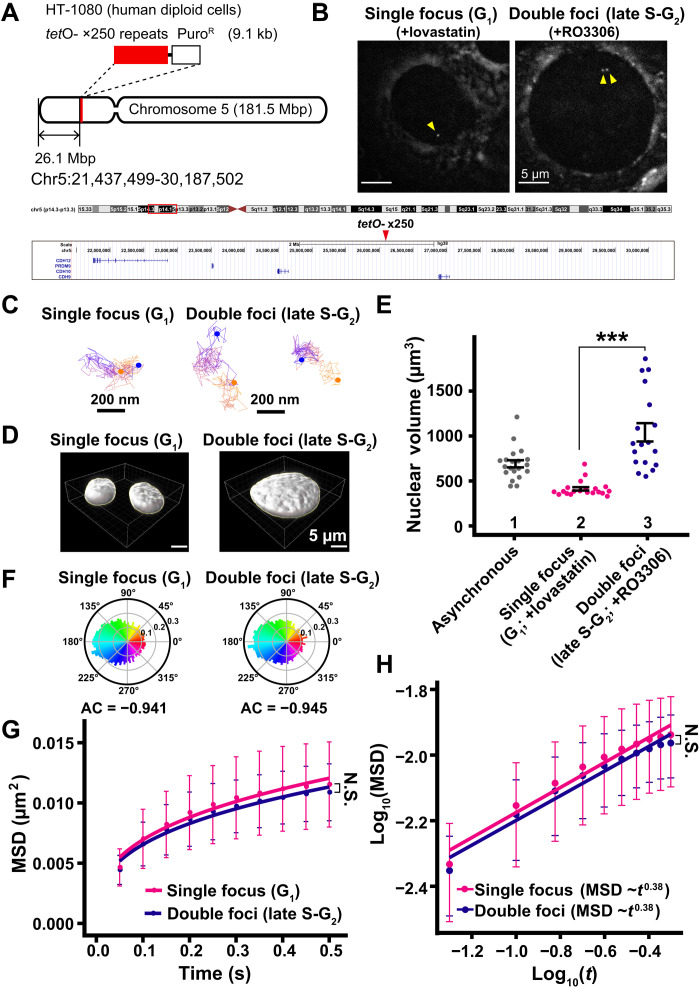
Last, to exclude the possibility that our “population analysis” of nucleosomes might overlook changes in local chromatin motion during the interphase cell cycle, we investigated movements of a well-defined specific genomic locus in living human cells. For this purpose, we used live HT-1080 diploid human cells, which have a tet operator (tetO) array integrated into a low gene density region of chromosome 5 (Fig. 9A) (59). The tetO repeats (×250) region, which roughly corresponds to ~35 nucleosomes, was bound by a Tet-repressor fused to four monomer-Cherry fluorescent proteins (TetR-4xmCh) to visualize as a red fluorescent focus (Fig. 9B) (59). Synchronized G₁ cells have a single TetR-4xmCh focus, and late S-G₂ cells have double foci (Fig. 9B). We observed movements of the TetR-4xmCh foci in live HT-1080 cells under a similar imaging condition used for our single-nucleosome imaging (Fig. 9C and movies S6 and S7). Note that a weaker laser power was used to image the TetR foci because its signal was much brighter than the signal obtained when labeling single nucleosomes with TMR.

Fig. 9. Motion of specific genomic loci in G₁ and late S-G₂ phase.

(A) Schematic depicting the location of tetO repeats (×250) in a gene-poor region of human chromosome 5. (B) TetR-4xmCh foci images of living HT-1080 cells after background subtraction. The cells were synchronized in G₁ (left, +lovastatin) and late S-G₂ (right, +RO3306) phases. Foci are indicated by yellow arrowheads. (C) Representative trajectories of tracked single focus and double foci. Starting points and end points are shown in orange or blue dots, respectively. (D) Reconstructed 3D images of HT-1080 nuclei with indicated conditions. (E) Quantitative data of nuclear volume (means ± SE) of indicated HT-1080 cell populations. Nuclear volume increased 2.53-fold from G₁ to late S-G₂ phase. Mean volumes: lanes 1 (691 μm³, n = 20 cells), 2 (412 μm³; n = 20 cells), and 3 (1041 μm³, n = 18 cells). ***P < 0.0001 (P = 1.1 × 10⁻⁹) by Wilcoxon rank sum test. (F) Angle distribution of single focus (G₁; +lovastatin; 12,315 angles) and double foci (late S-G₂; +RO3306; 14,685 angles). The AC is indicated below each angle distribution. Note that the angle-distribution profile and the AC are similar between G₁ and G₂ cells. (G) MSD plots (±SD among cells) of TetR-4xmCh foci motion in G₁ phase (magenta) and late S-G₂ phase (dark blue) HT-1080 cells from 0.05 to 0.5 s. For each sample, n = 21 cells. N.S. (P = 0.36) by Kolmogorov-Smirnov test. (H) Log-log plot of the MSD data from (G). The plots were fitted linearly: MSD = 0.016 t^0.38 in G₁ cells; MSD = 0.015 t^0.38 in late S-G₂ cells.

While nuclear volumes in late S-G₂–synchronized cells were 2.53-fold larger than those in G₁ cells (Fig. 9, D and E), we found that AC values and MSD plots of the TetR-4xmCh foci within 0.5 s were similar between G₁ and late S-G₂ cells (Fig. 9, F and G), consistent with our previous results (Figs. 4, A and C, and 7, E and F). These results exclude the possibility that motion changes during interphase might be embedded in our population analysis and strengthen our conclusion that local chromatin motion remains steady throughout the interphase cell cycle. Their MSD values and exponents (~ 0.38) are smaller (Fig. 9, G and H) and AC values are larger (Fig. 9F), as compared with those of nucleosomes (Figs. 1G and 2B), presumably because the movement of the TetR focus is assumed to be a centroid motion of ~35 nucleosomes in the corresponding region, or the region might be heterochromatic due to the ×250 tetO repeats.

DISCUSSION

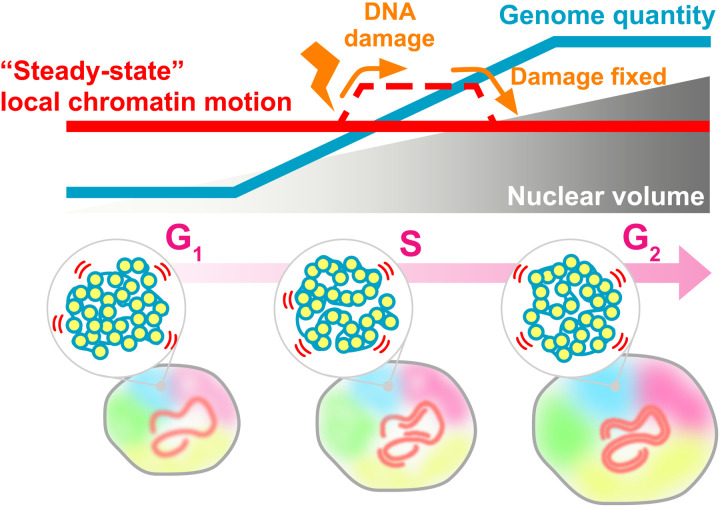
Using single-nucleosome imaging/tracking, we have demonstrated that the genome-wide local chromatin motion remains steady throughout interphase (namely, G₁, S, and G₂ phases), regardless of genomic DNA doubling by DNA replication and nuclear growth (Fig. 10). Our findings unveil the steady state of chromatin motion, mainly driven by thermal fluctuations (Figs. 10 and 2D). Here, we use “steady state” to express the unchanged nucleosome motion across interphase. Note that the rheological properties of chromatin allow this steady-state behavior of chromatin.

Fig. 10. A model scheme for steady state of chromatin motion.

Top: During cell cycle progression, genomic DNA quantity (blue line) doubles during replication accompanied by increasing nuclear volume (gray triangle). These nuclear changes do not affect local chromatin motion (steady-state chromatin motion, red line). On the other hand, chromatin motion transiently increases after perceived DNA damage, presumably for efficient repair process, and drops back to the original level when the damage is repaired or no longer detected (dashed line). Bottom: Local liquid-like chromatin motion (blue and yellow spheres in gray circles), which is mainly driven by thermal fluctuations, maintains a steady state during the cell cycle from G₁ to S and then to G₂. Five chromosomes are shown in different colors.

The MSD exponent of the steady-state motion was about 0.45 and a little smaller than that of a Rouse polymer (Fig. 1G and fig. S2B), which is an ideal chain consisting of beads connected by harmonic springs with an MSD exponent of 0.5 (18, 60). This finding implied that a chromatin polymer in the cell was more compact than this ideal chain, as shown in the compact polymer (d_f = 2.5) of Fig. 2D. Beyond the time scale of steady-state motion (> 0.5 s) (Fig. 1G), the motion mode seemed to change due to other hierarchy factors for chromatin organization (54), such as compartmentalization (3, 4). This notion is consistent with that of findings from Levi et al. (17), where a lacO/LacI system was used to suggest two kinds of chromatin motions in living mammalian cells exist: diffusive local motion (< 0.6 s) and long-range movement (> 0.6 s). Also, it should be emphasized that local motions of defined genomic loci are similar between G₁ and late S-G₂ phase cells (Fig. 9, F and G), excluding the possibility that motion changes during interphase might be embedded in our population analysis of nucleosome motions.

Steady-state motion allows cells to conduct their routine cellular housekeeping functions (e.g., RNA transcription and DNA replication) under similar nuclear environments. In other words, these motions could provide a similar reaction field for enzymes and accessibility to genomic DNA for target search processes throughout interphase. This concept reinforces the idea of a robust cell system because if nuclear size directly affects the chromatin state, then cellular housekeeping functions may be perturbed.

Local chromatin motion can govern genomic DNA accessibility for target searching (25) or recruiting a piece of machinery (44) and can be modulated from the steady state to cope with nuclear environmental changes. In other words, cells can transiently change the chromatin motion (~DNA accessibility) to perform their ad hoc jobs in response to signals from inside and outside the cell (44, 61). We observed this as chromatin motion increased after a DDR was induced and then returned to normal, after the DDR attenuated (Figs. 6D and 10). The steady state of local chromatin motion may enable cells to rapidly respond to signals modulating epigenome states, chromatin structure, and gene expression.

In this context, it is reasonable to surmise that the steady state of chromatin motion can vary depending on the cell type. While MSD profiles of HeLa and HCT116 cells appear to be similar in our study (Figs. 4A and 7E), mouse embryonic stem cells have higher chromatin motion (26, 62), suggesting that greater steady-state chromatin motion occurs in pluripotent cells. Chromatin motion becomes more and more constrained (e.g., more facultative heterochromatin forms) when these cells differentiate, supporting the concept of chromatin plasticity in pluripotent cells (22, 26, 62). Therefore, as plasticity is lost, we reason that differentiated cells should have a lower steady-state chromatin motion.

Our conclusion that local chromatin motion remains steady during the interphase cell cycle is consistent with previous results obtained by single-cell Hi-C (63) and mass spectrometry of histone modifications (64). Using single-cell Hi-C, Nagano et al. (63) revealed that convergent CTCF loops, which are presumably created by cohesin (65), are generally stable during interphase. Given that cohesin constrains local chromatin motion (26, 47), this single-cell Hi-C result reinforces our conclusion of steady-state chromatin motion. Our results also suggest that cohesin constrains local chromatin motion via chromatin loop formation, rather than sister chromatin cohesion [which is established during S phase (65, 66)]. Furthermore, mass spectrometry experiments demonstrated that histone modifications in G₁ and S phases are largely identical, again supporting our conclusion (64).

It is tempting to discuss the chromatin volume fraction in the nucleus because we found that genome-wide local chromatin motion was independent of chromatin density during interphase (Fig. 10). If we assume that the nucleosome is a sphere with a 10-nm diameter and a single G₁ phase HeLa cell has about 4.5 × 10⁷ nucleosomes [3 × 10⁹ base pairs (bp)/200 bp of nucleosome spacing × 2 sets of chromosomes × 1.5 aneuploidy factor of HeLa], the estimated total nucleosome volume is 23.6 μm³. Given that the measured nuclear volume in the G₁ phase HeLa cell is 510 μm³ (Fig. 3E), the obtained nucleosome volume fraction in the G₁ HeLa nucleus is 4.63%. In the case of G₁ phase HCT116 cells, the fraction value is 4.50%. Even considering additional factors (e.g., linker DNAs and associated proteins/RNAs), the fraction value was within the same order of magnitude, suggesting that the chromatin volume occupies less than 10% of the very crowded nuclear space. It is thus reasonable to infer that local chromatin motion, which is maintained by thermal fluctuations, is not affected by normal nuclear changes during interphase. Variability in this motion can be generated by constraints exerted on chromatin from several physical or geometrical factors such as nucleosome-nucleosome contacts, nucleoplasmic milieu (cations like Mg²⁺ and molecular crowding), chromatin proteins like cohesin (65, 66), and transcription machinery [discussed in (4)].

This argument may also be true during early development. Drastic reductions in cell and nuclear sizes are observed without changes in nuclear DNA content. Intuitively, chromatin motion would reduce if the nucleus became smaller and compacted the space chromatin was in. Such a relationship between the nuclear size and chromatin movement was observed in Caenorhabditis elegans early embryogenesis (20, 67). However, overall chromatin accessibility (opening) increased in Drosophila and human embryogenesis, possibly due to a combined action of pioneering transcription factors, chromatin remodelers, and other factors (68, 69). These factors can access target genome sequences and alter chromatin structure and dynamics even when the nuclear volume is reduced. This is consistent with our conclusion that constraints imposed by physical or geometrical factors can modulate the steady-state chromatin motion.

Local chromatin motion increased in replication-inhibited cells due to a DDR, but this increase was suppressed by using ATM and ATR inhibitors to inhibit the DDR (Figs. 5E and 8, C and D). This result is consistent with the recent reports by dos Santos et al. (55) where a DDR decondensed whole chromatin and promoted rapid diffusion of proteins in the DDR. Several studies have also reported localized chromatin decondensation around damaged areas and this decondensation is thought to lead to higher DNA repair efficiency (44, 70, 71). Our result of increased local chromatin motion with DDR likewise reflects chromatin decondensation. How such decondensation and increased chromatin motion are induced downstream of a DDR are intriguing questions to be further explored.

While our modeling suggested that the steady state of chromatin motion is mainly driven by thermal fluctuations (Figs. 10 and 2D), it is also important to discuss adenosine triphosphate (ATP) dependency of chromatin motion. Many studies concluded that chromatin motions across different time scales were ATP dependent based on ATP reduction experiments using cells that were treated with inhibitors of respiration (e.g., NaN₃) and/or glycolysis [e.g., 2-deoxyglucose (2-DG)] to reduce nuclear ATP levels (15, 17, 23, 44, 72). ATP reduction treatment led to a decrease in chromatin motion (fig. S8, A and B). However, as extensively discussed in (73), one must cautiously interpret their results because ATP reduction also results in chromatin condensation (fig. S8E) (26, 74–77), very likely owing to a rapid rise in Mg²⁺ upon ATP reduction (fig. S8, C and D) (76). The majority of the intracellular Mg²⁺ pool (10 to 20 mM) exists as a complex with ATP and other molecules such as proteins (78). ATP hydrolysis releases ATP-bound Mg²⁺(fig. S8, C and D), which contributes to chromatin condensation and a subsequent decrease in chromatin motion within the cell (fig. S8B) (26, 76). In addition, it was reported that the cytoplasmic polyamines were redistributed into the nucleus in response to ATP reduction, which can also contribute to chromatin condensation (77). Therefore, it cannot be definitively concluded that chromatin motion was ATP dependent and one must reconsider the ATP dependency of chromatin motion. On the other hand, longer chromatin movements that often correlate with RNA transcription or DNA double-strand break repair can still be ATP dependent [see reviews, e.g., (44, 72)] via an ATP-dependent remodeler or an ATP-driven motor. Because of our technical limitations, we also cannot exclude the possibility that their activities might affect local chromatin motion. Systematic and rapid knockdown analyses (79) of ATP-dependent motors and remodelers in the cell would provide insight into this issue.

The rapid degradation of MCM2 by the AID system (i.e., disassembly of the DNA replisome) (fig. S7B) (58) did not significantly affect local chromatin motion (Fig. 8D). This finding implies that a DNA replication complex, such as replisome, does not constrain chromatin genome-wide, which is distinct from what has been observed with transcription machinery. The depletion of RNA Pol I (80) and RNA Pol II (19, 46) increased local chromatin motion, indicating that transcriptional machinery constrains chromatin. This finding complements recent work that demonstrated RNA Pol II, Mediator, and other factors form condensates upon transcription, possibly by a phase separation process (81–83), and is also consistent with the classic transcription factory hypothesis (84) where clusters of RNA Pol II and other transcription factors immobilize genome chromatin to facilitate transcription. The DNA replication complex is a large complex (85) like transcription machinery, but it might not form a “factory” that constrains genome chromatin. It is also possible that the number of replisome complexes on genome chromatin is fewer than that of the active transcription machinery and therefore its degradation was not enough to observe effects on local chromatin motion.

This study has focused on the interphase cell cycle. We found that local chromatin motion, which is mainly driven by thermal fluctuations, exists in a steady state throughout interphase (Fig. 10). However, copied genomic DNA must be faithfully transmitted into two daughter cells as condensed chromosomes during mitosis (39). Chromatin in mitotic chromosomes seems much more constrained than chromatin in interphase (27, 86). Presumably, condensin (87), local nucleosome contacts (88), and other factors, such as Mg²⁺ (76), facilitate this tight compaction. During mitosis, the nuclear envelope is broken down (39) and the environment around chromatin appears to change drastically. How these changes affect the physical state of mitotic chromatin remains to be investigated.

MATERIALS AND METHODS

Cell lines and establishment of stable cell lines

HeLa S3 cells (89) and HT-1080 cells with tetO/TetR-mCherry (a clone of TT75, TT165, a gift from T. Tanaka at University of Dundee, UK) (59) were cultured at 37°C in 5% CO₂ in Dulbecco’s modified Eagle’s medium (DMEM) (D5796-500ML, Sigma-Aldrich) supplemented with 10% fetal bovine serum (FBS) (FB-1061/500, Biosera). HCT116 cells (CCL-247, American Type Culture Collection) were cultured at 37°C in 5% CO₂ in McCoy’s 5A medium (SH30200.01, HyClone) supplemented with 10% FBS.

For the establishment of HeLa cells that stably express H2B-HaloTag, the Flp-In system (V602020, Invitrogen) was used. pFRT-bla was first transfected into HeLa cells to integrate it into the genome using the Effectene Transfection Reagent kit (301425; QIAGEN). Cells that contained the flippase recognition target (FRT) site were selected using blasticidin S (5 μg/ml) (029-18701, Wako) and used for isolation of stable transformants. The isolation procedure using the Flp-In system was as previously described (42). pEF1-H2B-Halo-FRT was transfected into HeLa cells that harbored an FRT site and transformants were selected using hygromycin B (200 μg/ml) (10687-010, Invitrogen).

To obtain Nup107-Venus–expressed HeLa cells, EF-1α-Venus-Nup107-cHS4-FRT was transfected into HeLa S3 cells (42). After selection with hygromycin B (200 μg/ml) (10687010, Thermo Fisher Scientific), colonies were isolated for further analysis.

To stably express H2B-Halo in the HCT116 cell line, the transposon system was used. The constructed plasmid pPB-CAG-IB-H2B-HaloTag was cotransfected with pCMV-hyPBase (provided from Sanger Institute with a materials transfer agreement) to HCT116 cells with the Effectene Transfection Reagent kit. Transfected cells were then selected with blasticidin S (10 μg/ml). HCT116 cells expressing MCM2-mAID and AtAFB2 (58) or expressing RAD21-mAID-mClover and OsTIR1(F74G) (79) were used as a parental cell.

H2B-HaloTag expression and localization in HeLa cells

To check the expression level of H2B-HaloTag, transfected HeLa S3 cells were lysed in Laemmli sample buffer supplemented with 10% 2-mercaptoethanol (133-1457; Wako) and incubated at 95°C for 5 min to denature proteins. The cell lysates, equivalent to 1 × 10⁵ cells per well, were subjected to SDS–polyacrylamide gel electrophoresis (PAGE) (12.5%) and subsequent Western blotting. For Western blotting, the fractionated proteins in the gel were transferred to a polyvinylidene difluoride membrane (PVDF) (IPVH00010, Millipore) by a semidry blotter (BE-320, BIO CRAFT). After blocking with 5% skim milk (Morinaga), the membrane-bound proteins were probed by the anti-H2B rabbit (1:10,000 dilution; ab1790, Abcam) or anti-HaloTag mouse (1:1000; G9211, Promega) antibody, followed by the appropriate secondary antibody: anti-rabbit (1:5000 dilution; 170-6515, Bio-Rad) or anti-mouse (1:5000 dilution; 170-6516, Bio-Rad) horseradish peroxidase (HRP)–conjugated goat antibody. Chemiluminescence reactions were used (WBKLS0100, Millipore) and detected by EZ-Capture MG (AE-9300H-CSP, ATTO).

To examine H2B-HaloTag localization in HeLa S3 cells, cells grown on the poly-l-lysine–coated (P1524-500MG, Sigma-Aldrich) coverslips (C018001, Matsunami) were treated with 5 nM HaloTag TMR ligand (8251, Promega) overnight at 37°C in 5% CO₂. The cells were fixed with 1.85% FA (064-00406, Wako) on coverslips at room temperature for 15 min, permeabilized with 0.5% Triton X-100 (T-9284, Sigma-Aldrich) for 15 min, and stained with 4′,6-diamidino-2-phenylindole (DAPI) (0.5 μg/ml) (10236276001, Roche) for 5 min, followed by PPDI [20 mM Hepes (pH 7.4), 1 mM MgCl₂, 100 mM KCl, 78% glycerol, and paraphenylene diamine (1 mg/ml) (695106-1G, Sigma-Aldrich)] mounting. Optical sectioning images were recorded with a 0.2-μm step size using a DeltaVision microscope (Applied Precision) as described in the “Nuclear volume measurement” section.

Cell cycle synchronization

To obtain cells arrested in the G₁ phase, HeLa, HCT116, or HT-1080 cells were initially plated at 2.0 × 10⁵ cells/ml, left for 1 day, and then treated with 20 μM lovastatin (M1687, LKT Laboratories) for 24 hours (figs. S3 and S6).

For cell cycle synchronization of HeLa cells in the S or late S-G₂ phase, double thymidine block and release were performed as follows (fig. S3). Cells (1.0 × 10⁵ cells/ml) were plated with 3 mM thymidine (T9250-1G, Sigma-Aldrich) for 18 hours, released into a thymidine-free medium for 9 hours, and again treated with 3 mM thymidine for 17 hours for the G₁/S arrest. The arrested cells were then released into a thymidine-free medium for 4 hours (S phase) or 8 hours (late S-G₂ phase).

A double thymidine block was performed to inhibit DNA replication in HeLa cells and to collect cells at the G₁/S boundary (“replication-inhibited cells” or “G₁/S arrested”). Cells (1.0 × 10⁵ cells/ml) were plated with 3 mM thymidine for 18 hours, released into a thymidine-free medium for 9 hours, and again incubated with 3 mM thymidine for 17 hours for the G-S arrest. To inhibit the DDR, ATM inhibitor KU-55933 (SML1109-5MG, Sigma-Aldrich) (90) and ATR inhibitor VE-821 (SML1415-5MG, Sigma-Aldrich) (91) were added in the last 4 hours of the second thymidine treatment at the concentration of 40 and 10 μM, respectively (fig. S5A).

For cell cycle synchronization of HCT116 or HT-1080 cells in the late S-G₂ phase, cells were initially plated at a concentration of 1.0 × 10⁵ cells/ml, incubated for 1 day, followed by the treatment of 9 μM RO3306 (CS-3790, Funakoshi) for 18 hours (fig. S6).

Flow cytometry

Flow cytometry was performed to check the cell cycle profiles of drug-treated cells. Collected synchronized cells were fixed in 70% ethanol at −30°C for over 30 min. After fixation, cells were centrifuged at 603g for 1 min, and the cell pellets were washed with phosphate-buffered saline (PBS) containing 1% BSA (bovine serum albumin; A9647-100G, Sigma-Aldrich). After centrifugation, cell pellets were resuspended in 600 μl of PBS containing 1% BSA, ribonuclease A (50 μg/ml) (10109169001, Sigma-Aldrich), and propidium iodide (40 μg/ml) (P4170-10MG, Sigma-Aldrich) and then further incubated for 30 min at 37°C with light protection. Last, cells were analyzed by BD Accuri C6 Plus (BD FACS, San Jose, CA). At least 20,000 cells were used for each analysis, and the obtained results were displayed as histograms. The percentage of cell cycle stage distributions in the G₀/G₁, S, and G₂/M phase was analyzed by the ModFit LT software (Verity Software House, Topsham, ME).

Nuclear volume measurement

To measure nuclear volume, the cells were grown on poly-l-lysine–coated (P1524-500MG, Sigma-Aldrich) coverslips (C018001, Matsunami) and treated with drugs to synchronize the cell cycle stage (see the “Cell cycle synchronization” section). Subsequent processes were performed at room temperature. The cells were fixed with 1.85% FA for 15 min, permeabilized with 0.5% Triton X-100 for 15 min, and stained with DAPI (0.5 μg/ml) for 5 min, followed by PPDI mounting.

Z-stack images (every 0.4 μm in the z direction, 15 to 20 sections in total) of the cells were obtained using a FLUOVIEW FV1000 confocal laser scanning microscope (OLYMPUS) equipped with an Olympus UPLANSAPO 60×W objective [numerical aperture (NA), 1.20] at room temperature. Obtained Z-stack images were loaded to Imaris (Bitplane AG, Zurich, Switzerland) and converted to Imaris 3D image files (.ims). To calculate the nuclear volume, the tool “Surface” was used. A threshold value was manually determined to include all DAPI signals. Note that only well-isolated nuclei were recorded and analyzed.

To obtain wide-view images of the nuclei (e.g., Figs. 3D and 7C), Z-stack images (every 0.2 μm in the z direction, 20 to 25 sections in total) of the cells were obtained using DeltaVision Elite microscopy (Applied Precision) with an Olympus PlanApoN 60× objective (NA, 1.42) and a scientific complementary metal-oxide semiconductor (sCMOS) camera. InsightSSI light (∼50 mW) and the four-color standard filter set were also equipped. DeltaVision acquisition software, Softworx, was used to project deconvolved Z-stacks to cover the whole nucleus (seven optical sections).

Counting chromosome numbers

To count the chromosome numbers of HeLa cells, mitotic chromosome spreads were made. Cells were treated with colcemid (0.2 μg/ml) (045-16963, Wako) for 1 hour at 37°C. The following steps were performed at room temperature except the final fixation step. After washing with PBS, cells were trypsinized and resuspended in hypotonic buffer (75 mM KCl) for 10 min. Cells were then gently fixed by repeating the following treatment three times: fixation buffer (MeOH: acetic acid, 3:1) for 5 min, centrifuged at 850g for 4 min, and then resuspended in new fixation buffer. Last, the cells were completely fixed by treatment with 200 μl of fixation buffer at −30°C for at least 30 min. For imaging, 5 μl of this fixed cell suspension was dropped onto coverslips after mixing and completely dried by incubating at 60°C for 30 min. Dried cells were stained with DAPI (0.5 μg/ml) for 5 min, followed by PPDI mounting. Images of mitotic chromosome spreads were obtained using DeltaVision Elite microscopy with an Olympus PlanApoN 60× objective (NA 1.42) and an sCMOS camera. The number of chromosomes in one cell was counted manually.

Biochemical fractionation of nuclei from cells expressing H2B-HaloTag

Nuclei were isolated from HeLa S3 cells expressing H2B-HaloTag as described previously (26). Briefly, collected cells were suspended in nuclei isolation buffer [3.75 mM tris-HCl (pH 7.5), 20 mM KCl, 0.5 mM EDTA, 0.05 mM spermine, 0.125 mM spermidine, aprotinin (1 μg/ml) (T010A, TaKaRa), and 0.1 mM phenylmethylsulfonyl fluoride (PMSF) (P7626-1G, Sigma-Aldrich)] and centrifuged at 1936g for 7 min at room temperature. The cell pellets were resuspended in nuclei isolation buffer and again centrifuged at 1936g for 7 min at room temperature. Subsequent steps were performed at 4°C, unless otherwise noted. Cell pellets were resuspended in nuclei isolation buffer containing 0.025% Empigen (nuclei isolation buffer+; 45165-50ML, Sigma-Aldrich) and homogenized immediately with 10 downward strokes of a tight Dounce pestle (357546, Wheaton). The cell lysates were centrifuged at 4336g for 5 min. Nuclear pellets were washed in nuclei isolation buffer+. The nuclei were incubated on ice for 15 min in the following buffers containing various concentrations of salt: HE [10 mM Hepes-NaOH (pH 7.5), 1 mM EDTA, and 0.1 mM PMSF], HE + 100 mM NaCl, HE + 500 mM NaCl, HE + 1 M NaCl, and HE + 2 M NaCl. After each buffer incubation with increasing concentrations of salt, centrifugation was performed to separate the nuclear suspensions into supernatant and pellet fractions. The proteins in the supernatant fractions were precipitated by using 17% trichloroacetic acid (208-08081, Wako) and cold acetone. Both pellets were suspended in a Laemmli sample buffer and subjected to 12.5% SDS-PAGE, followed by Coomassie brilliant blue (031-17922, Wako) staining and Western blotting using rabbit anti-H2B (ab1790, Abcam) and rabbit anti-HaloTag (G9281, Promega) antibodies to confirm H2B-HaloTag expression.

Single-nucleosome imaging microscopy

Established cell lines were cultured on poly-l-lysine–coated glass-based dishes (3970-035, Iwaki). H2B-Halo incorporated in nucleosomes was fluorescently labeled with 80 pM HaloTag TMR ligand for 20 min at 37°C in 5% CO₂, washed with 1× Hanks’ balanced salt solution (HBSS) (H1387, Sigma-Aldrich) three times, and then incubated in the following media for more than 30 min before single-nucleosome imaging. HeLa S3 cells were observed in DMEM (21063-029, Thermo Fisher Scientific) and HCT116 cells were in McCoy’s 5A (1-18F23-1, BioConcept) media. These media were phenol red–free and supplemented with 10% FBS.

A live-cell chamber (INU-TIZ-F1, Tokai Hit) and digital gas mixer (GM-8000, Tokai Hit) were used to maintain cell culture conditions (37°C, 5% CO₂, and humidity) during microscopy. Single nucleosomes were observed using an inverted Nikon Eclipse Ti microscope with a 100-mW Sapphire 561-nm laser (Coherent) and sCMOS ORCA-Flash 4.0 camera or ORCA-Fusion BT (Hamamatsu Photonics). Live cells labeled with H2B-Halo-TMR were excited by the 561-nm laser through an objective lens (100× PlanApo TIRF, NA 1.49; Nikon) and detected at 575 to 710 nm. An oblique illumination system with the TIRF unit (Nikon) was used to excite fluorescent nucleosome molecules within a limited thin area in the cell nucleus and reduce background noise (fig. S1D). Sequential image frames were acquired using MetaMorph software (Molecular Devices) or NIS-Elements (Nikon) at a frame rate of 50 ms under continuous illumination.

Single-nucleosome tracking analysis

Image processing, single-nucleosome tracking, and single-nucleosome movement analysis were performed as previously described (46). Briefly, sequential images were converted to an 8-bit grayscale and the background noise signals were subtracted with the rolling ball background subtraction (radius, 50 pixels) of ImageJ. The nuclear regions in the images were manually extracted. Following this step, the centroid of each fluorescent dot in each image was determined and its trajectory was tracked with u-track [(51), MATLAB package]. We previously calculated the SD of the 2D movement of immobilized nucleosomes per 50 ms in FA-fixed RPE-1 cells (n = 10 nucleosomes) to determine the accuracy of the position of H2B-Halo nucleosomes. We found that 15.55 nm was the localization accuracy (46). For single-nucleosome movement analysis, the displacement distribution and the MSD of the fluorescent dots were calculated on the basis of their trajectory using a Python program. The originally calculated MSD was in 2D. To obtain the 3D value, the 2D value was multiplied by 1.5 (4 to 6 Dt). Graphs and statistical analyses of the obtained single-nucleosome MSD between various conditions were performed using R.

TetR-4xmCh foci imaging and tracking

TetR-4xmCh foci in live HT-1080 cells were observed under a similar imaging condition to our single-nucleosome imaging (see the “Single-nucleosome imaging microscopy” section), except that we used a weaker laser power setting because the TetR foci signals were much brighter than the signal obtained from single-nucleosome labeling with TMR. Cells were synchronized in G₁ or late S-G₂ phases (see the “Cell cycle synchronization” section), and we validated cells with a single focus as G₁ phase and those with double foci as late S-G₂ phase. The precise centers of these specific genomic loci were determined and tracked using the TrackMate plugin (92). MSDs of the foci were calculated on the basis of their trajectories using an R program. To focus on their local chromatin movements, displacements above 200 nm were not included in the MSD calculation because jumping (~150 nm) of the genomic loci was reported (17). Our observed genomic loci also showed similar trajectories to theirs, including jumps (Fig. 9C) (17).

Chemical treatment in single-nucleosome imaging

For chemical fixation, cells grown on poly-l-lysine–coated glass-based dishes were incubated in 2% FA in 1 × HBSS at 37°C for 15 min and washed with 1 × HBSS. To degrade MCM2-mAID rapidly, HCT116 cells expressing AtAFB2 were treated with 500 μM auxin (indole-3-acetic acid, IAA; 19119-61, Nacalai) for 4 hours (58). For ATP reduction, cells were incubated with 10 mM sodium azide (S2002, Sigma-Aldrich) and 50 mM 2-deoxyglucose (2-DG) (D3179, Sigma-Aldrich) in DMEM for 30 min at 37°C.

Confirmation of DNA damage response

To verify the level of DDR, cells were lysed in Laemmli sample buffer and blotted as described in the “H2B-HaloTag expression and localization in HeLa cells” section. The primary antibodies used were the following: rabbit anti–phospho-Chk1 (Ser³⁴⁵) (2341, Cell Signaling Technology) at 1:500; mouse anti-Chk1 (K0086-3, MBL Life Science) at 1:1000; rabbit anti-phospho–Chk2 (Thr⁶⁸) (2661, Cell Signaling Technology) at 1:500; and rabbit anti-Chk2 (2662, Cell Signaling Technology) at 1:500. The secondary antibodies used were HRP-linked goat anti–rabbit immunoglobulin G (IgG) whole antibody (170-6515, Bio-Rad) at 1:5000 for anti-phospho–Chk1 (Ser³⁴⁵), anti-Phospho–Chk2 (Thr⁶⁸), and anti-Chk2 or HRP-linked goat anti–mouse IgG whole antibody (170-6516, Bio-Rad) at 1:5000 for anti-Chk1.

Immunostaining was performed as follows. All processes were performed at room temperature. Cells grown on coverslips were fixed and permeabilized as described above. After washing twice with HMK [20 mM Hepes (pH 7.5) with 1 mM MgCl₂ and 100 mM KCl] for 5 min, the cells were incubated with 10% normal goat serum (NGS; 143-06561, Wako) in HMK for 30 min. The cells were incubated with diluted primary antibodies in 1% NGS in HMK for 1 hour: rabbit anti-gamma H2A.X (phospho S139) (1:500 dilution; ab2893, abcam) and rabbit anti-MCM2 (1:1000 dilution; 3619, Cell Signaling Technology). After being washed four times with HMK, the cells were incubated with diluted secondary antibodies in 1% NGS in HMK for 1 hour: goat anti–rabbit IgG Alexa Fluor 594 (1:500; A11037, Thermo Fisher Scientific) or goat anti–rabbit IgG Alexa Fluor 488 (1:500; A11034, Thermo Fisher Scientific), followed by washing four times with HMK. DNA staining and mounting were performed as described above. Optical sectioning images were recorded with a 0.2-μm step size using a DeltaVision microscope (Applied Precision) as described in the “Nuclear volume measurement” section. The mean intensities of the nuclear signals after background subtraction (the signals outside nuclei) were calculated and plotted.

Angle-distribution analysis

For the tracked consecutive points {(x₀, y₀), (x₁, y₁), ⋯, (x_n, y_n), ⋯} of a single nucleosome on the xy plane, we converted the data into a set of displacement vectors, ∆r_n = (x_{n + 1} − x_n, y_{n + 1} − y_n)^t. Then, we calculated the angle between two vectors ∆r_n and ∆r_{n + 1}. We carried out this procedure for all the points of each trajectory in our experiments and simulations. Last, we plotted the normalized polar histogram by our Python program. The angle distribution was normalized by 2π, and the values correspond to the probability density. Colors indicate the angles.

Exact fractal polymer model

Let (R₀, R₁, ⋯, R_{N − 1}) be the positions of N monomers of a polymer model. Then, we define the fractal polymer with the fractal dimension d_f by the following scaling relation for all pairs of monomers

$$\mathrm{\langle }{({\mathit{R}}_i-{\mathit{R}}_j)}^2\mathrm{\rangle }=b^2{\mid i-j\mid }^{\frac{2}{d_{\mathrm{f}}}}$$

where b represents the SD of the length fluctuation between adjacent monomers at thermal equilibrium. We have theoretically suggested and analyzed the fractal polymer model to explain single-nucleosome movements (54). However, since we used an asymptotic form in the analytical calculation, dynamics and structure in the simulation would not satisfy the exact scaling. Therefore, we developed the exact fractal polymer to achieve scaling without any approximation.

The mathematical framework is based on matrix transformations of the polymer network model, which was developed for deciphering Hi-C matrix data (93). To construct the exact fractal polymer model, eigenvalues and an orthogonal transformation based on the eigenvectors from the scaling definition needed to be identified. Fortunately, the inverse direction to discuss long-range interactions and scaling has been theoretically analyzed (94). Therefore, the orthogonal transformation Q_ip of the exact fractal polymer model is given by

$$Q_{i0}=\frac{1}{\sqrt{N}} (i=0,1,\cdots ,N-1),$$

$$Q_{\mathit{ip}}=\sqrt{\frac{2}{N}} \text{cos}\left(\frac{(2i+1)p\mathrm{\pi }}{2N}\right) (i=0,1,\cdots ,N-1 \text{and} p=1,2,\cdots ,N-1)$$

The scaling definition states that the variance matrix between two monomers for each freedom becomes ${\mathrm{\Sigma }}_{\mathit{ij}}^2=\frac{b^2}{3}{\mid i-j\mid }^{2/d_{\mathrm{f}}}$. The variance matrix relates to the covariance matrix M_ij as ${\mathrm{\Sigma }}_{\mathit{ij}}^2=k_{\mathrm{B}}T(M_{\mathit{ii}}+M_{\mathit{jj}}-2M_{\mathit{ij}})$, where k_B is the Boltzmann constant and T is the temperature of the environment. Since the matrix M_ij satisfies an additional condition Σ_jM_ij = 0, we can obtain all the elements of M_ij from ${\mathrm{\Sigma }}_{\mathit{ij}}^2$. Then, we can obtain the inverse of the eigenvalues by calculating ${\mathrm{\Lambda }}^{-1}=\text{diag}(0,{\mathrm{\lambda }}_1^{-1},{\mathrm{\lambda }}_2^{-1},\cdots ,{\mathrm{\lambda }}_{N-1}^{-1})=Q^t\mathrm{MQ}$.

For the α( = x, y, z) coordinate vector of the monomers R_α = (R_0,α, R_1,α, ⋯, R_{N − 1,α})^t, the dynamics for the transformed vector X_α = Q^tR_α = (X_0,α, X_1,α, ⋯, X_{N − 1,α})^t obeys

$$\mathrm{\gamma }\frac{d{\mathit{X}}_{\mathrm{\alpha }}(t)}{\mathit{dt}}=-\mathrm{\Lambda }{\mathit{X}}_{\mathrm{\alpha }}(t)+{\mathit{g}}_{\mathrm{\alpha }}(t)$$

with the fluctuation-dissipation relation for thermal random forces: 〈g_p,α(t)〉 = 0 and 〈g_p,α(t)g_q,β(s)〉 = 2γk_BTδ_αβδ_pqδ(t − s). Here, γ represents the friction coefficient of the monomers. In our Brownian dynamics simulations, we numerically solve this equation, and we convert X_α to R_α = QX_α to construct a polymer conformation. Also, the covariance for the vector X_α satisfies the following relation $\langle X_{p,\mathrm{\alpha }}{X}_{q,\mathrm{\beta }}\rangle =\frac{k_{\mathrm{B}}T}{{\mathrm{\lambda }}_p}{\mathrm{\delta }}_{\mathrm{pq}}{\mathrm{\delta }}_{\mathrm{\alpha }\mathrm{\beta }} (p,q=1,2,\cdots ,N-1)$

Brownian dynamics of the exact fractal polymer model

In our simulations, we normalized the spatial and temporal scales by b, k_BT, and γ: ${\overline{\mathit{R}}}_{\mathrm{\alpha }}={\mathit{R}}_{\mathrm{\alpha }}/b$, ${\overline{\mathit{X}}}_{\mathrm{\alpha }}={\mathit{X}}_{\mathrm{\alpha }}/b$, $\overline{\mathrm{\Lambda }}=\frac{b^2}{3k_{B}T}\mathrm{\Lambda }$, ${\overline{M}}_{\mathit{ij}}=\frac{3k_{B}T}{b^2}{M}_{\mathit{ij}}$, ${\overline{\mathrm{\Sigma }}}_{\mathit{ij}}^2={\mathrm{\Sigma }}_{\mathit{ij}}^2/b^2$, and the nondimensional step time $\mathrm{\epsilon }=\frac{k_{B}T\text{∆}t}{\mathrm{\gamma }{b}^2}$ for the real discrete time step ∆t. First, the parameters N, ε, and d_f are set. Here, we fixed N = 1000 and ε = 10⁻². Next, an initial state is given: X₀ = 0 so that the center of mass is the origin and X_p,α (p = 1,2, ⋯, N − 1) is a random variable obeying the normal distribution with mean 0 and variance $\frac{1}{3{\mathrm{\lambda }}_p}$. Then, we numerically integrated the discrete stochastic differential equation using Heun’s method: $\text{∆}{\overline{\mathit{X}}}_{\mathrm{\alpha }}=-3\epsilon \overline{\mathrm{\Lambda }}{\overline{\mathit{X}}}_{\mathrm{\alpha }}+\sqrt{2\mathrm{ϵ}}{\mathbf{\xi }}_{\mathrm{\alpha }}$, where ξ_p,α is a random variable obeying the normal distribution with mean 0 and variance 1.

For a given d_f, we carried out 10 Brownian dynamics simulations with 100,000 times iteration steps. Polymer conformation data were output every 100 iteration steps. Then, we analyzed the averaged MSD for all monomers and the angles for the 10,000,000 (= N × 100,000/100 × 10 ) trajectory points. We used VMD to visualize polymer dynamics (95).

ATP reduction, intracellular ATP, and Mg²⁺ measurements

For ATP reduction, cells were incubated with 10 mM sodium azide and 50 mM 2-deoxyglucose in DMEM for 40 min at 37°C. To measure ATP, aliquots of 0.5 × 10⁵ cells were seeded into a 12-well culture plate (IWAKI) and Cell ATP Assay Reagent (300-15363, Toyo B-Net Co. Ltd.) was used according to the manufacturer’s instructions. Bioluminescence was measured using a Lumat LB 9507 tube luminometer (EG&G Berthold). A standard plot of ATP concentration versus bioluminescence intensity verified that our measured ATP concentrations fell within a linear range. Both the reaction and measurement were performed at 23°C in the dark. The incubation time was 5 min from the addition of assay reagent to measurement.

Magnesium Green AM (K_d ∼ 1.0 mM; M3735, Thermo Fisher Scientific) was applied to the DMEM culture medium at 10 μg/ml with 0.02% Pluronic F-127 (P3000MP, Thermo Fisher Scientific), and the cells were incubated at 37°C for 1 hour. Magnesium Green fluorescence was measured by DeltaVision equipped with an Olympus PlanApoN 60× objective (NA 1.42) and an sCMOS camera with a FITC filter by using Softworx software. Cell culture conditions (37°C, 5% CO₂, and humidity) were maintained in a live-cell chamber under the microscope. The nucleoplasm intensity was measured using Softworx software and plotted after subtracting background signals outside the cells.

Supplementary Materials

This PDF file includes:

Figs. S1 to S8

Other Supplementary Material for this manuscript includes the following:

Movies S1 to S7

View/request a protocol for this paper from Bio-protocol.