Impact of Variability in Job Coding on Reliability in Exposure Estimates Obtained via a Job-Exposure Matrix

Abstract

Objectives

The use of a job-exposure matrix (JEM) to assess exposure to potential health hazards in occupational epidemiological studies requires coding each participant’s job history to a standard occupation and/or industry classification system recognized by the JEM. The objectives of this study were to assess the impact of inter-coder variability in job coding on reliability in exposure estimates derived from linking the job codes to the Canadian job-exposure matrix (CANJEM) and to identify influent parameters.

Method

Two trained coders independently coded 1000 jobs sampled from a population-based case–control study to the ISCO-1968 occupation classification at the five-digit resolution level, of which 859 could be linked to CANJEM using both assigned codes. Each of the two sets of codes was separately linked to CANJEM and thereby generated, for each of the 258 occupational agents available in CANJEM, two exposure estimates: exposure status (yes/no) and intensity of exposure (low, medium, and high) for exposed jobs only. Then, inter-rater reliability (IRR) was computed (i) after stratifying agents in 4 classes depending, for each, on the proportion of occupation codes in CANJEM defined as ‘exposed’ and (ii) for two additional scenarios restricted to jobs coded differently: the first one using experts’ codes, the other one using codes randomly selected. IRR was computed using Cohen’s kappa, PABAK and Gwet’s AC1 index for exposure status, and weighted kappa and Gwet’s AC2 for exposure intensity.

Results

Across all agents and based on all jobs, median (Q1, Q3; N_agents) values were 0.68 (0.59, 0.75; 220) for kappa, 0.99 (0.95, 1.00; 258) for PABAK, and 0.99 (0.97, 1.00; 258) for AC1. For the additional scenarios, median kappa was 0.28 (0.00, 0.45; 209) and −0.01 (−0.02, 00; 233) restricted to jobs coded differently using experts’ and random codes, respectively. A similar decreasing pattern was observed for PABAK and AC1 albeit with higher absolute values. Median kappa remained stable across exposure prevalence classes but was more variable for low prevalent agents. PABAK and AC1 decreased with increasing prevalence. Considering exposure intensity and all exposed jobs, median values were 0.79 (0.68, 0.91; 96) for weighted kappa, and 0.95 (0.89, 0.99; 102) for AC2. For the additional scenarios, median kappa was, respectively, 0.28 (−0.04, 0.42) and −0.05 (−0.18, 0.09) restricted to jobs coded differently using experts’ and random codes, with a similar though attenuated pattern for AC2.

Conclusion

Despite reassuring overall reliability results, our study clearly demonstrated the loss of information associated with jobs coded differently. Especially, in cases of low exposure prevalence, efforts should be made to reliably code potentially exposed jobs.

What’s Important About This Paper?

Little is known about the impact of variability in job coding on the exposure estimates obtained through a JEM. This explored its impact through two different exposure metrics (i.e. exposure status and intensity of exposure) often used for risk assessment purposes. Over the whole study population, inter-rater reliability was in the upper range of those observed in studies comparing exposure assessment methods. It was markedly lower for exposure metrics among jobs that had been coded differently, but all exposure information as lost when coding was discordant.

Introduction

Interest in using job-exposure matrices (JEMs) has greatly increased since the 1980s. The use of JEMs has become a common method to assign exposure estimates in population-based studies (Teschke et al., 2002; Koeman et al., 2013). As an alternative to measured exposure data—that are very seldom available—and to the expert assessment method, JEMs provide an easy and low-cost way to assess exposure based on descriptions of jobs and tasks (Mannetje and Kromhout, 2003; Friesen et al., 2015). Minimally a JEM has one axis for the occupation (or industry) codes and a second for the occupational agents. Each combination of a specific occupation and a specific agent constitutes a cell which may contain different metrics of exposure. Population-based JEMs can be agent specific (Koh et al., 2014; van Oyen et al., 2015) or specific to a particular family of agents (Brouwers et al., 2009; Martin-Bustamante et al., 2017), while others like FINJEM (Kauppinen et al., 1998), MATGÉNÉ (Fevotte et al., 2011), or more recently the Canadian job-exposure matrix (CANJEM) (Sauve et al., 2018; Siemiatycki and Lavoue, 2018) cover a greater diversity of agents. The latter three include, within the cells of the matrix, indicators of the presence, intensity, and/or probability of exposure to a specific agent in a specific job.

To use a JEM for individual exposure assessment, the job histories of each subject must be coded (manually or using automated methods) to a standard occupation and/or industry classification system recognized by the JEM. Assigning such codes usually comes with a certain amount of error. Published studies report agreement in coding ranging from 29.7 to 98% (Bushnell, 1997; Mannetje and Kromhout, 2003; Pilorget et al., 2003; Remen et al., 2018). Variability in coding means that exposure estimates will be extracted from different cells of the matrix, resulting in potential discrepancies in exposure assignment. Little information is available on the impact of variability in job coding on exposure estimates extracted from JEMs. Few studies have evaluated inter-rater reliability (IRR) in exposure estimates extracted from JEMs (Ge et al., 2018). In studies having used human coders, Pilorget et al. (2003) reported kappa for exposure status to asbestos ranging from 0.58 to 0.65 depending on the pair of coders considered, and Koeman et al. (2013) reported weighted kappa for IRR in exposure intensity (background, low or high exposure) ranging from 0.66 to 0.84 depending on the agents considered. Burstyn et al. (2014), in a study on development and validation of coding computer algorithms, reported kappa ranging from 0 to 0.8 for exposure status to different asthmagens.

The aim of this article is to assess the impact of variability in job coding between coders on exposure estimates for 258 occupational agents obtained after linking a population-based sample of jobs to CANJEM.

Methods

This project is built on two pre-existing resources: CANJEM and the Montreal case–control study of lung cancer. We briefly describe these.

CANJEM is a general population JEM (Sauve et al., 2018; Siemiatycki and Lavoue, 2018) that was created in Montreal based on data generated in the context of four case–control studies (Gerin et al., 1985; Labreche et al., 2003; Ramanakumar et al., 2006; Group, 2010). In each study, specially trained interviewers administered a semi-structured questionnaire to obtain details of each job in each subject’s occupational history. For each job ever held, the subject was asked about the company, its products, the nature of the work site, the subject’s main and subsidiary tasks. Experts in industrial hygiene assessed occupational exposures of over 8000 study subjects, using a checklist of nearly 300 occupational agents to consider. CANJEM was built on this database and includes 258 agents that were frequent enough to warrant inclusion. The agents in CANJEM include specific chemicals (e.g. benzene), chemical groups or functions (e.g. aromatic amines), mixtures of relatively fixed composition (e.g. gasoline) or variable composition (e.g. paints), complex materials (e.g. cement), as well as general categories (e.g. solvents). CANJEM is available in four occupation and three industry classifications and exposure metrics are provided for up to four different time periods. More information is available at www.canjem.ca.

One of the four studies conducted by our team and used in creating CANJEM was a population-based case–control study of lung cancer conducted in Montreal from 1996 to 2001 (Ramanakumar et al., 2006). We will simply refer to this as the Montreal Study. There was a total of 2740 subjects in the Montreal study, giving rise to a total of 13 992 different job descriptions elicited from all subjects’ job histories (hereafter referred to as ‘jobs’).

The current study was based on a random sample of 1000 jobs extracted from the Montreal study for the purpose of evaluating the CAPS-Canada coding assistant (Remen et al., 2018). This study involved three stages. First, two expert coders coded each job independently into several classification systems. Second, each set of codes was linked to CANJEM to obtain the corresponding exposure metrics for each agent. Third, we compared the two sets of exposure estimates. These three stages are summarized in a flow-chart available in Supplementary Material (see Supplementary Fig. S1, available at Annals of Occupational Hygiene online).

Job coding

Two coders (industrial hygienists with a year of experience in coding jobs for the creation of CANJEM at the time of this project) assigned codes for the 1000 randomly selected jobs using each of seven distinct classifications that are available as options in CANJEM. More details about the job coding stage are available elsewhere (Remen et al., 2018).

Linkage to CANJEM: derivation of exposure metrics

For the main analyses, we used CANJEM based on ISCO-1968 (five-digit resolution) and a single time period (1930–2005). We used the version of CANJEM that is restricted to occupation codes linked to at least 10 jobs in the CANJEM database, irrespective of how many subjects this entailed. This policy was recommended by CANJEM designers (Sauve et al., 2018; Siemiatycki and Lavoue, 2018).

The following two metrics, available for each cell of CANJEM, were used: (i) the probability of exposure, corresponding to the proportion of jobs in a cell (i.e. ISCO occupation code) exposed to a given agent and (ii) the distribution of intensity of exposure (low, medium, or high) among exposed jobs (Sauve et al., 2018). A job was considered exposed to a given agent if the agent was present in the workplace at levels above those in the general (non-occupational) environment. Low represented a concentration above the background environmental level, and high was generally used for occupations and processes associated with the highest levels encountered in the work environment.

In some JEMs, such as CANJEM and FINJEM, there is no explicit binary exposed/unexposed metric embedded in each cell of the matrix; rather, it is the probability of exposure, on a continuous scale, that is shown. Since many uses of exposure information involve a binary exposure variable, the most obvious tactic would be to use a cut-point on the probability scale to demarcate exposed from unexposed. For the current study, an occupation code was considered ‘exposed’ to a specific agent if the proportion of jobs with this code in CANJEM that were considered as exposed (by the experts) to this agent was greater than or equal to 25%, a threshold that has been used in several epidemiological studies using JEMs for exposure assessment (Lacourt et al., 2013; El-Zaemey et al., 2018; Hinchliffe et al., 2021).

For instance, the database used to create CANJEM included 30 jobs coded as ‘Mechanical Engineer (General)’ (ISCO-1968 code 0-24.10). Among these, six were considered ‘exposed’ to metallic dust. So, the probability of exposure to metallic dust for ‘Mechanical Engineer – General’ workers is 20% (=6/30). Based on our cut-point set at 25%, this occupation code was considered as ‘unexposed’ to this agent for the current study.

As indicated above, the information in a CANJEM cell was only used if there were at least 10 jobs for a particular occupation code. If there were fewer than 10 jobs in the denominator for probability of exposure, the exposure status was set as ‘undefined’.

The original expert coding on which CANJEM is based included an estimate of intensity of exposure to each agent thought to be present for a given job, using the three-point scale (low, medium, and high). This estimate for a given job held by an individual was based on the particulars of the detailed job description provided. For the current study, we converted the number of observations corresponding to each class of intensity into a unique ordinal index (low, medium, and high) of intensity of exposure for each occupation code. For this purpose, we first extracted for each code–agent combination the distribution of the exposed jobs across the intensity categories. Then, this distribution was transformed into a quantitative index by weighting the numbers of observations corresponding to each category by a 1–5–25 exponential scale (considered by the experts to reflect most closely the relationship of low to medium to high) (Sauve et al., 2018) and we calculated the mean value. In order to re-transform the continuous mean into a single ordinal value for the occupation code (low, medium, high), we used two cut-points corresponding to midpoints between the weights: √(1*5) = 1.93 between low (1) and medium (5), and √(5*25) = 11.18 between medium (5) and high (25). We selected this approach, rather than the simpler ‘most frequent category’, because its calculation is based on the intensity values of all exposed jobs. Moreover, the ‘most frequent’ approach is problematic in cases of ties as well as situations where, for example, there would be five jobs at high and four jobs at low, yielding, in our opinion, an unreasonable final rating of high.

For instance, among ‘Mechanical Engineers (General)’, 33.3% (10/30) of the jobs were considered as exposed to iron. The distribution of these 10 exposed jobs was 5, 5, and 0 for low, medium, and high exposure, respectively. Applying the 1–5–25 scale, the weighted mean calculated for this combination was 3 (=(5×1+5×5+0×25)/10), which falls within the interval (1.93–11.18), resulting in a final exposure category for the cell of ‘medium’ intensity.

IRR in exposure estimates

The computation of IRR in estimating exposure status between the two coders entailed several steps. First, we identified all jobs in our sample that could be linked to CANJEM for both occupation codes assigned by the coders. Jobs not meeting this criterion were excluded from analysis. Then IRR in exposure status between the 2 coders was then calculated for each of the 258 agents.

For computation of IRR in exposure status, we retained three distinct statistics each of which uses different approaches to estimate chance agreement probability: (i) the Cohen’s kappa coefficient (kappa), the prevalence and bias-adjusted kappa (PABAK) (Byrt et al., 1993), and the Gwet’s AC1 statistic (AC1) (Wongpakaran et al., 2013; Gwet, 2014).

IRR in exposure intensity also entailed several steps and its computation was restricted, for each agent, to jobs for which both experts’ occupation codes corresponded to an ‘exposed’ status. Considering these jobs (corresponding to cell ‘D’ in Table 1), only agents with at least 10 ‘exposed’ jobs (D ≥ 10) were kept for analyses, the other situation meaning that IRR computation is unfeasible (D = 0) or feasible but prone to large imprecision (0 < D < 10). IRR in exposure intensity was computed using both weighted kappa and Gwet’s AC2 (AC2), which is the weighted extension of AC1 to ordinal variables and ranges from −1 to 1 (Gwet, 2008, 2014). Their computation was based on linear weights.

Table 1:

Example of exposure status agreement crosstable

For each of 258 agents
Coder	2
1	Exposed	No	Yes
	No	A	B
	Yes	C	D

Additional scenarios

We computed the same IRR metrics as described above for two additional scenarios:

Restricted to jobs coded differently by the two experts (‘discordant codes’)

While the main analysis measures the overall agreement in a typical study population, discrepancy in exposure can actually only come from cases where the same jobs were coded differently. This sub-analysis focuses on these jobs. Significant agreement for jobs coded differently would support the following hypothesis: even if the coders attributed a different code, they were working with the same job descriptions. Therefore, even if the actual codes differ, they would reflect similar tasks/ environment and share similarities reflected in the corresponding exposure profiles.

Restricted to jobs coded differently based on codes randomly assigned (‘random codes’)

If the above hypothesis holds, IRR in metrics measured on jobs coded differently but based on evaluating the same job description should be higher than the IRR measured on occupation codes selected entirely at random. To verify this, we created the second additional scenario where, for each job coded differently by the two coders, and before assigning exposures, we replaced each expert assigned code by another code randomly selected from the list of occupations available in our version of CANJEM.

Finally, as we expected that prevalence of exposure would be associated with agreement results, we stratified the analysis according to the proportion of occupation codes considered as ‘exposed’ (i.e. with probability of exposure ≥ 25%) in CANJEM, the denominator being the number of occupation codes covered by the version of CANJEM used for the current study (N = 465 for ISCO-68 codes). Thus, depending on this proportion, each agent was classified in the corresponding classes defined arbitrarily: <5% (196 agents); [5–15%] (49 agents); [15–25%] (8 agents); and ≥25% (5 agents).

Sensitivity analysis

Considering that IRR in exposure estimates may also depend on the threshold used to define exposure status for the occupation codes, we repeated IRR computations by selecting two other thresholds of probability of exposure: 5 and 50%, limited to the agents for which the metrics were computable for the three thresholds.

Statistical analysis

Analyses were performed using SAS® v9.4. A SAS program was developed to automate IRR computations. Spot verifications were performed using the MAGREE macro.

Results

The two coders assigned the same ISCO code to 43.2% of the 1000 jobs in our sample.

Since we required at least 10 jobs for a CANJEM cell to be informative, those jobs that were coded by one or both of the coders with a code that did not satisfy this criterion were excluded from consideration. This led to the exclusion of 141 jobs, leaving in the analysis 859 jobs. Of these jobs, 406 (47.3%) were coded identically by the two coders.

IRR in exposure estimates obtained after linking to CANJEM

Exposure status

Kappa was computable for 220 of the 258 agents covered by CANJEM, the others having a probability of chance agreement equal to 1 leading to a null denominator. Across the 220 computed values, kappa varied between 0.00 and 1.00 with a median (Q1, Q3) of 0.68 (0.59, 0.75). PABAK, computed for each of the 258 agents, varied between 0.73 and 1.00, with a median of 0.99 (0.95, 1.00). AC1, computed for each of the 258 agents, varied between 0.75 and 1.00, with a median of 0.99 (0.97, 1.00). Detailed results by agent are presented in Supplementary Material (available at Annals of Occupational Hygiene online).

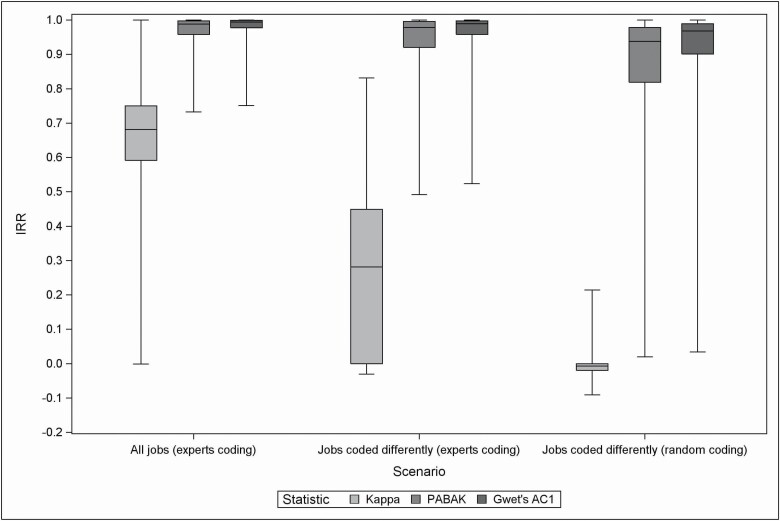
Figure 1 shows boxplots of the three indices across agents, stratified by the type of analysis: overall, discordant codes, and random codes. Figure 1 shows kappa was consistently lower than PABAK and AC1, which remained close to 1 across the three scenarios (although a decreasing visual trend is still discernible). In contrast, the median kappa went from 0.68 overall, to 0.28 for the ‘discordant codes’ scenario, and −0.01 for the ‘random codes’ scenario.

Figure 1.

Distribution of IRR statistic for exposure status to each of the 258 agents covered by CANJEM (using ISCO-1968 classification and based on 859 informative jobs). For each boxplot, the following information was provided: minimum, 25th–50th–75th percentiles and maximum. Exposure status was defined according to a 25% threshold of probability of exposure. Kappa statistic for exposure status was computable for 220, 209, and 233 agents when considering the scenarios based on all jobs (experts coding) and jobs coded differently (experts coding and random coding) respectively. For all scenarios, PABAK and AC1 statistics were computed based on 258 agents.

Results obtained with PABAK and AC1 statistics being very close as illustrated in Fig. 1, the next results are presented for Kappa and AC1 only. Results related to PABAK are available in Supplementary Material (available at Annals of Occupational Hygiene online).

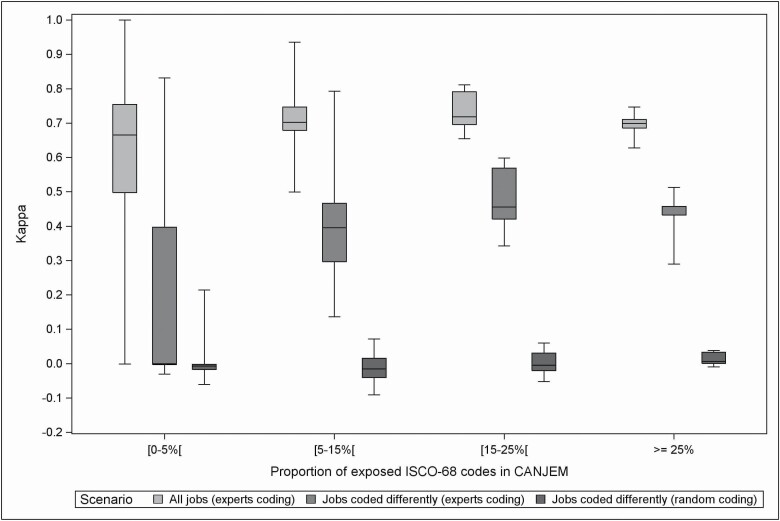
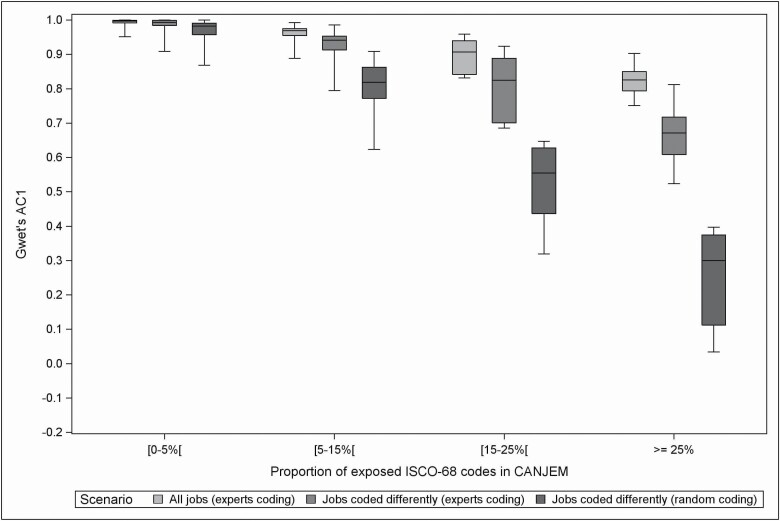
Figures 2 and 3 show the results of the stratification by exposure proportion (i.e. <5%; [5%–15%]; [15%–25%], and ≥25%).

Figure 2.

Distribution of Cohen’s kappa coefficient for exposure status to each of the 258 agents covered by CANJEM (using ISCO-1968 classification and based on 859 informative jobs) according to the proportion of exposed codes and for each scenario. For each boxplot, the following information was provided: minimum, 25th–50th–75th percentiles and maximum. Exposure status was defined according to a 25% threshold of probability of exposure. Numbers of agents retained for each proportion of exposed ISCO-68 codes in CANJEM ([0–5%[/[5–15%[/[15–25%[/≥25%):

Scenario based on all jobs: N = 158/N = 49/N = 8/N = 5.

Scenario based on jobs coded differently (experts coding): N = 147/N = 49/ N = 8/N = 5.

Scenario based on jobs coded differently (random coding): N = 171/N = 49/N = 8/N = 5.

Figure 3:

Distribution of Gwet’s AC1 statistics for exposure status to each of the 258 agents covered by CANJEM (using ISCO-1968 classification and based on 859 informative jobs) according to the proportion of exposed codes and for each scenario. For each boxplot, the following information was provided: minimum, 25th–50th–75th percentiles and maximum. Exposure status was defined according to a 25% threshold of probability of exposure. Numbers of agents retained for each proportion of exposed ISCO-68 codes in CANJEM ([0–5%[/[5–15%[/[15–25%[/≥25%):

All scenarios: N = 196/N = 49/N = 8/N = 5.

The trends illustrated in Fig. 1 (lower kappa compared to PABAK and AC1, decreasing agreement from ‘overall’ to ‘discordant codes’ to ‘random codes’) remain present across the strata of exposure proportion shown in Figs 2 and 3. In addition, Fig. 2 shows kappa, while more variable in the lower exposure proportion categories, is, in median, approximately stable across all categories. Figure 3, on the other hand, shows a strong trend of decreasing AC1 values when exposure proportion increases. These trends are further illustrated in Supplementary Figs S2–S4 (available at Annals of Occupational Hygiene online), which show scatterplots of agent-specific agreement values versus exposure proportion.

Intensity of exposure among exposed jobs

After restriction to jobs (among the 859) for which both assigned codes generated an ‘exposed’ status and to agents with at least 10 jobs defined as ‘exposed’ using both codes, 102 agents satisfied the condition. Considering these 102 agents, the number of jobs (among the 859) for which both codes generated an ‘exposed’ status ranged from 10 (5 agents) to 254 (PAHs from any source) with a median of 28 jobs.

Weighted kappa was computable for 96 of these 102 agents ranging from −0.36 to 1.00, with a median (Q1, Q3) value of 0.79 (0.68, 0.91) while median AC2 ranged from 0.53 to 1.00 with a median of 0.95 (0.89, 0.99) based on 102 agents. We investigated the influence of sample size on agreement (for a given agent, the number of jobs for which both occupation codes generated an ‘exposed’ status), and found no noticeable pattern. Supplementary Figs S5 and S6 (available at Annals of Occupational Hygiene online) show scatterplots of agent-specific agreement values versus sample size for weighted kappa and AC2, respectively. Detailed results by agent are presented in Supplementary Material (available at Annals of Occupational Hygiene online).

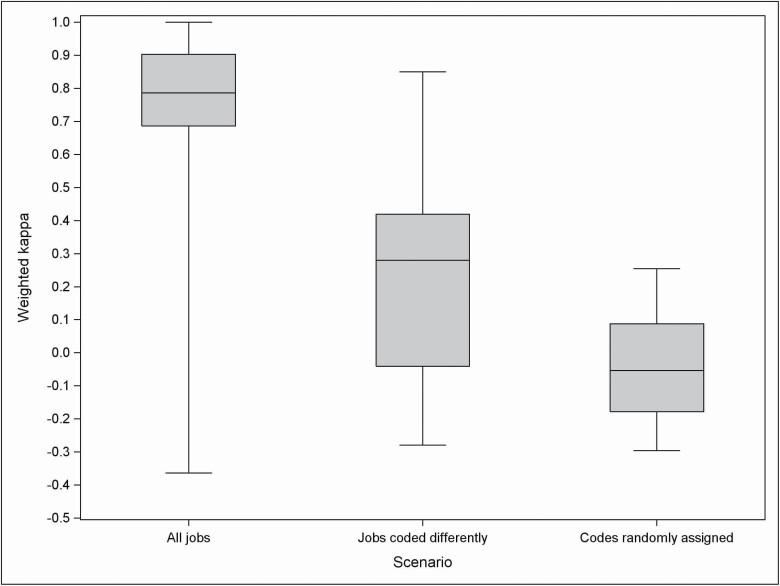
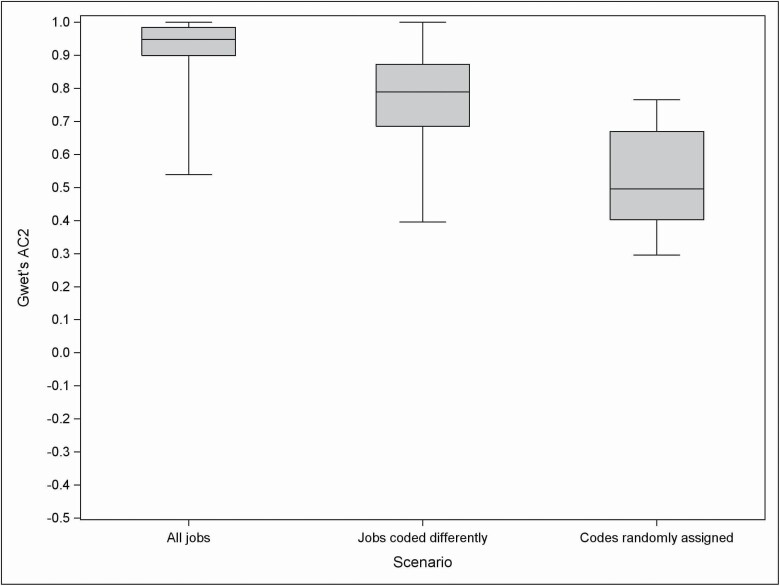
For the two additional scenarios, 40 (discordant codes) and 13 (random codes) agents satisfied the inclusion criteria, respectively. Distribution of IRR in exposure intensity among exposed agents for the three scenarios is presented in Fig. 4 based on weighted kappa and in Fig. 5 based on AC2. Figures 4 and 5 show a high contrast between the three scenarios when using weighted kappa, with almost null values when codes were randomly generated, and notable, albeit smaller, difference when using AC2.

Figure 4.

Distribution of weighted kappa coefficients for intensity of exposure among exposed subjects to each agent covered by CANJEM (using ISCO-1968 classification). For each boxplot, the following information was provided: minimum, 25th–50th–75th percentiles, and maximum. Number of agents retained for the analysis (using a threshold of exposure set at 25%): 96 with the scenario based on all jobs (expert coding), 39 with the scenario based on jobs coded differently (expert coding), and 13 with the scenario based on jobs coded differently (random coding).

Figure 5.

Distribution of Gwet’s AC2 statistics for intensity of exposure among exposed subjects to each agent covered by CANJEM (using ISCO-1968 classification). For each boxplot, the following information was provided: minimum, 25th–50th–75th percentiles, and maximum. Number of agents retained for the analysis (using a threshold of exposure set at 25%): 102 with the scenario based on all jobs (expert coding), 40 with the scenario based on jobs coded differently (expert coding), and 13 with the scenario based on jobs coded differently (random coding).

When focussing on a restricted list of 13 agents included in the ‘random codes’ analysis, so that comparison of the scenarios is made using the same agents, the median (Q1, Q3) weighted kappa for exposure intensity were 0.76 (0.72, 0.81), 0.33 (0.12, 0.36), and −0.05 (−0.18, 0.09) for the scenario based on all jobs, on jobs coded differently using experts’ codes and random codes, respectively. Similarly, median AC2 were 0.92 (0.90, 0.95), 0.83 (0.75, 0.88), and 0.50 (0.40, 0.67), respectively.

Sensitivity analysis

The selection of another threshold to define binary exposure status had different impact on levels of IRR in both exposure status and intensity depending on the metrics used (see Supplementary Table S1 and Supplementary Figs S8–S12, available at Annals of Occupational Hygiene online). For exposure status, no pattern emerged for Kappa, but agreement increased for PABAK and AC1 (~ median increase of 0.03–0.05 from 5 to 25%, the increase from 25 to 50% being negligible). For exposure intensity, a slightly stronger pattern was observed for both weighted kappa (+0.12/+0.03) and AC2 (+0.05/+0.02).

Discussion

Interest in using JEMs to estimate the occupational exposure of subjects in the workplace has led to their becoming increasingly common tools. But such an indirect method of exposure assessment requires the implementation of an occupation and/or industry coding stage which is prone to variability as reported in several studies (Mannetje and Kromhout, 2003; Pilorget et al., 2003) including the current one. Little was known about the impact of this variability on the exposure estimates obtained through a JEM; the current study provides some evidence for >250 chemical agents through two different exposure metrics (i.e. exposure status and intensity of exposure) often used for risk assessment purposes.

In terms of the job codes themselves, our experts agreed 47.3% of the time, a proportion higher than reported by Pilorget et al. (37.2%) in a study of 1344 jobs and Koeman et al. (36%), in a study of 210 jobs, but within the range provided in the review by Mannetje and Kromhout for various classification systems (Mannetje and Kromhout, 2003).

We observed several patterns in terms of the agreement in exposure estimates, the main contribution of this work because of the number of agents available in CANJEM and of the range of exposure prevalence covered. As measured by the traditional kappa, overall IRR in exposure status was, on average, quite high [median (Q1, Q3) of 0.69 (0.59, 0.75)], compatible with results reported by Pilorget et al. for asbestos (0.58–0.65), by Burstyn et al. for any asthmagen (0.4–0.8), and by Koeman et al. for 10 agents (0.66–0.84), although in the latter case they compared ordinal exposure categories (none, low, high). Our results are also in the same, even upper, range of inter-rater studies comparing exposure assessment by expert judgement and/or JEMs (Teschke et al., 2002; Ge et al., 2018). Agreement in exposure intensity, albeit measurable only on a subset of agents (102) with at least 10 jobs deemed exposed according to both coders, was similarly relatively high, with weighted kappa in median (Q1, Q3) of 0.79 (0.68,0.91), computable for 96 agents. These results would suggest, bearing in mind they varied across agents, that typical agreement in assigning occupation codes generally translates into acceptable reliability in exposure estimates, given the range of values reported for comparison of exposure estimates across different methods.

Differences between scenarios

The numbers above reflect reliability measured over the whole study population, and are the results of an average of perfect agreement for the jobs coded the same, and imperfect agreement for the jobs coded differently (in our case, approximately half the study population). IRR values for jobs coded differently directly reflect the loss of information caused by the disagreement. In our study, the loss was consistent across exposure status and intensity, with median values (kappa and weighted kappa) going down from ~0.7–0.8 to ~0.3–0.4. Koeman et al. hypothesized in their discussion that discordant codes could still reflect similar exposure. Together with results from the ‘random code’ scenario, showing median agreement close to zero both for intensity and exposure status (kappa and weighted kappa), our results provide, for the first time, quantitative empirical evidence of the exposure information retained despite disagreement in the assigned occupational codes.

Exposure prevalence/differences across metrics

Agreement in exposure status was computed using different metrics (kappa, PABAK, Gwet’s AC) because the cross tables corresponding to the agreement calculations were severely unbalanced due to the general low prevalence of occupational exposure. In this situation, the above metrics, based on different assumptions, tend to diverge. For example, in the case of very low prevalence kappa becomes very imprecise, whereas AC1 and PABAK (which evaluate chance agreement differently) may seem very high in part because of the high absolute proportion of agreement.

The stratification of the analysis for exposure status according to prevalence of exposure (in our case, proportion of occupation codes classified as exposed) led to a clear illustration of the differences between kappa, PABAK and AC1. Most agents (196 of 258) in our study are associated with low prevalence (<5% exposed occupation codes). For these, because of a very high chance agreement probability (most jobs are unexposed), the denominator for kappa will be close to zero, rendering its calculation very imprecise. Hence, our results show highly variable kappa values for these agents, variability decreasing with increasing exposure prevalence (Fig. 2 and Supplementary Fig. S2, available at Annals of Occupational Hygiene online). However, median kappa did not change across prevalence categories. This is in stark contrast with PABAK and AC1, both with very similar behaviour: overall values were very high, so as to almost render the three scenarios undistinguishable, and both decreased with exposure prevalence. The pattern was similar when comparing weighted kappa to Gwet’s AC2. The debate as to which metric best reflects agreement in our study is outside the scope of this work. In the end, we focussed on the more traditional kappa and weighted kappa because they showed better contrast across the scenarios studied and facilitated comparison to available literature. Moreover, the imprecise kappa values for individual agents (especially those with <5% exposed occupation codes) are less worrisome in our study, where we were interested in overall patterns, thanks to the large number of agents involved. Finally, the patterns observed with kappa and weighted kappa across scenarios were similar, the only differences being higher absolute values in AC1, AC2, and PABAK, and a decreasing agreement with higher prevalence. It is interesting (and expected) to note that for the higher prevalence category, kappa values yielded median values across scenarios quite close to PABAK and AC1 (~ 0.7–0.5–0 compared with ~0.8–0.7–0.3 for AC1 and 0.7–0.6–0.2 for PABAK).

Variation across agents

Apart from differences related to exposure prevalence, we expect variations in agreement metrics across agents to be mostly random depending on occupations where the difference occur and where the agents are present. Indeed, except for the lower strata of exposure prevalence (where kappa is known to be imprecise), kappa values were relatively narrowly distributed. AC1 and PABAK values were also relatively narrowly distributed, in their case within all strata of exposure prevalence.

Sensitivity analyses

Through our sensitivity analysis involving other thresholds used to define exposure status, median kappa remained stable across the three thresholds (after restriction to agents for which the metrics were computable for the three thresholds). For other metrics related to exposure status and intensity, we observed a slight decrease in levels of IRR when selecting the 5% threshold and an increase in IRR with the 50% threshold. For exposure status (AC1 and PABAK), such an observation is related to the higher probability of two different codes being considered as non-exposed as the threshold increases. For intensity of exposure, such an observation is related to the proportion of exposed jobs that falls in the medium category (the most frequent category for most agents) that generally increases with increasing threshold thereby reducing the unbalance compared to the low and high categories (see Supplementary Excel File, available at Annals of Occupational Hygiene online).

The pattern of results we found using ISCO-1968 was similar to those found when using the six other classifications covered by CANJEM (see Supplementary Tables S2–S3 and Supplementary Figs S13–S17, available at Annals of Occupational Hygiene online). For these classifications at least, it can be affirmed that the occupation and industry coding decisions made by different experienced coders combined with a JEM, leads to quite similar occupation agent estimates.

Impact on risk assessment

As mentioned above, our estimates of overall reliability are somewhat in the upper range of those observed in studies comparing exposure assessment methods (e.g. expert versus JEM) in population-based studies. This is reassuring given the elevated (though typical) proportion of different codes, and suggests that job coding errors would be a limited source of misclassification overall. However, the analyses based on jobs coded differently clearly showed a loss of information, albeit a partial loss. This loss will cause some impact of misclassification on risk estimation. It is hard to predict the direction of the effect, as it depends on a combination of sensitivity, specificity and prevalence, only indirectly associated with reliability. Interestingly, Burstyn et al. (2013) demonstrated a simulation-based method to obtain estimates of sensitivity and specificity from those of prevalence and reliability. In a later study, Burstyn et al. (2018) used the approach to correct for the impact of the associated misclassification on odds ratios in a case–control study of cancer (Pintos et al., 2012).

Conclusion

Especially when prevalence is low, when the 2*2 tables of exposure status will contain one cell (concordantly unexposed) with the overwhelming majority of data, it feels important to make efforts to reduce the errors associated with the small number of exposed. This would be achieved by concentrating coding resources on jobs deemed potentially exposed (from preliminary screening for example), and those ending up unexpectedly exposed, in an effort to preserve sensitivity and specificity.

Funding

Funding for the lung cancer study was provided by the National Cancer Institute of Canada, the ‘Fonds de recherche du Québec – Santé’ (FRQS), and the Canadian Institutes for Health Research. This study was funded by the Cancer Research Society, the FRQS, and the Quebec ‘Ministère de l’Enseignement supérieur, de la Recherche, de la Science et de la Technologie’. Dr Siemiatycki’s research team was supported in part by the Canada Research Chairs program and the Guzzo-SRC Chair in Environment and Cancer.

Conflict of interest

The authors declare no conflict of interest relating to the material presented in this article. Its contents, including any opinions and/or conclusions expressed, are solely those of the authors.

Data availability

The data underlying this article will be shared on reasonable request to the corresponding author.