Supercurrent diode effect and finite-momentum superconductors

Significance

Our work shows a fascinating application of finite-momentum superconductivity, the supercurrent diode effect, which is being reported in a growing number of experiments. We show that, under external magnetic field, Cooper pairs can acquire finite momentum so that critical currents in the direction parallel and antiparallel to the Cooper pair momentum become unequal.

Abstract

When both inversion and time-reversal symmetries are broken, the critical current of a superconductor can be nonreciprocal. In this work, we show that, in certain classes of two-dimensional superconductors with antisymmetric spin–orbit coupling, Cooper pairs acquire a finite momentum upon the application of an in-plane magnetic field, and, as a result, critical currents in the direction parallel and antiparallel to the Cooper pair momentum become unequal. This supercurrent diode effect is also manifested in the polarity dependence of in-plane critical fields induced by a supercurrent. These nonreciprocal effects may be found in polar SrTiO₃ film, few-layer MoTe₂ in the T_d phase, and twisted bilayer graphene in which the valley degree of freedom plays a role analogous to spin.

Shortly after the advent of the Bardeen–Cooper–Schrieffer (BCS) theory of superconductivity, it was predicted that a superconducting phase with a spatially varying order parameter exists in a narrow range of magnetic fields above the Pauli limit (1, 2). In this Fulde–Ferrell–Larkin–Ovchinnikov (FFLO) phase, pairing of opposite spin states on Zeeman-split Fermi surfaces gives rise to finite Cooper pair momentum. Extensive efforts have been devoted to the search for the FFLO phase in clean superconductors. Thermodynamic and NMR measurements have found evidence of a distinctive superconducting phase at high fields in several materials (3–12). However, the existence of finite Cooper pair momentum has not been demonstrated directly.

Recently, a new type of finite-momentum superconducting state has been predicted in two-dimensional (2D) systems with strong spin–orbit coupling (SOC) and broken inversion symmetry (13–27). Here SOC splits Fermi surfaces and creates (topologically) nontrivial spin textures in momentum space (27, 28). Upon the application of a parallel magnetic field, a BCS superconductor with spin-textured Fermi surfaces can smoothly evolve into a finite-momentum state with the phase of the superconducting order parameter being periodically modulated as $\mathrm{\Delta }(\mathit{r})=\mathrm{\Delta }{e}^{i\mathit{q}·\mathit{r}}$, where q is induced by and varies continuously with the magnetic field. This state is formed by pairing within each spin-nondegenerate Fermi surface. Such helical superconducting phase should be distinguished from the single-q FFLO (helical FF) state that is separated from the BCS state by a first-order transition. Possible realization of helical superconductivity has been proposed in several noncentrosymmetric materials (16, 24, 29). However, it has been unclear how to detect this state easily and unambiguously.

In this work, we show that helical superconductors exhibit an intrinsic supercurrent diode effect: The depairing critical currents in the direction along and against the underlying Cooper pair momentum ${\mathit{q}}_0$ are different, as shown in Fig. 1. This effect is also manifested in the polarity-dependent in-plane critical fields in the presence of a supercurrent. These nonreciprocal phenomena are a direct consequence of the Cooper pair momentum which breaks time-reversal and inversion symmetry in the equilibrium state.

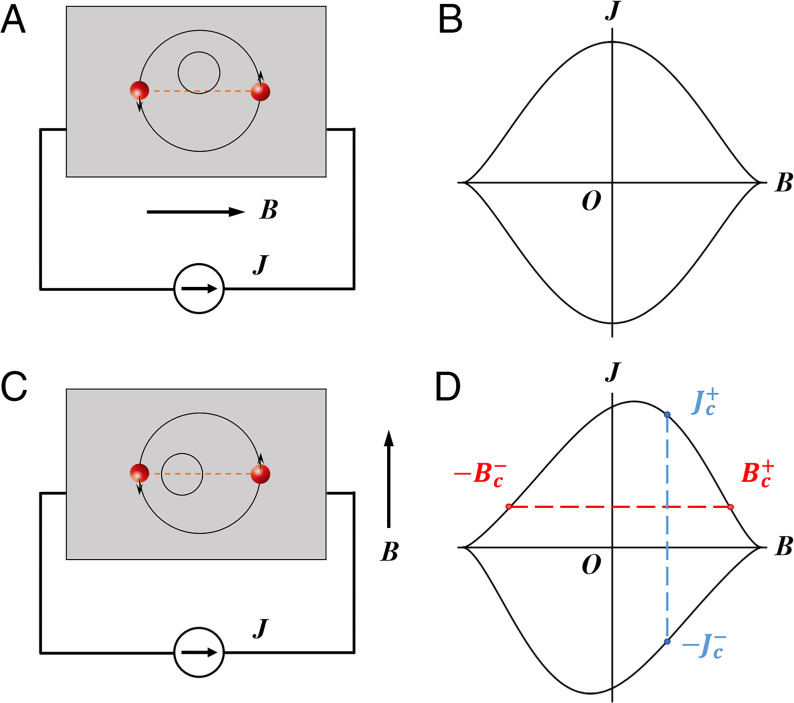
Fig. 1.

Supercurrent diode effect in a Rashba superconductor under in-plane magnetic field B and external current source J. (A and C) Device plots with circles denoting normal state Fermi surfaces, and (B and D) schematic phase diagrams in the B–J plane. When $\mathit{B}\parallel \mathit{J}$ in A, the phase diagram in B is symmetric with respect to both B and J axes. And, when $\mathit{B}\perp \mathit{J}$ in C, the phase diagram in D is skewed, indicating nonreciprocal critical current $J_c^{+}\ne J_c^{-}$ and polarity-dependent critical field $B_c^{+}\ne B_c^{-}$.

Our work is motivated by the recent observation of nonreciprocal critical current in an artificial metal film under a parallel magnetic field (30). Its origin is not yet fully understood and likely due to the orbital effect associated with the film thickness (31). We also note recent works showing that superconducting fluctuations enhance nonreciprocal resistance above T_c (32, 33) as well as works on nonreciprocal Josephson current across a weak link (34–42). Unlike these previous works, our focus is thin 2D superconductors where the orbital effect is suppressed, and our study provides a microscopic theory of intrinsic supercurrent diode effect in superconductors.

Helical Superconductivity

We consider a 2D electron system with SOC under in-plane magnetic field,

$$H_{\mathit{k}}={\xi }_{\mathit{k}}+{\mathit{g}}_{\mathit{k}}·\mathit{\sigma }+\mathit{B}·\mathit{\sigma },$$ [1]

where $\mathit{k}=(k_x,k_y)$ is the 2D momentum, ${\xi }_{\mathit{k}}=k^2/2m-\mu$ is the kinetic term, m is effective mass, μ is chemical potential, Pauli matrices $\mathit{\sigma }=({\sigma }_x,{\sigma }_y,{\sigma }_z)$ denote spin, ${\mathit{g}}_{\mathit{k}}$ is the SOC vector, and B is the Zeeman energy due to the in-plane magnetic field. Such 2D electron gas has two spin-split energy bands,

$${\xi }_{\mathit{k}}^{\pm }={\xi }_{\mathit{k}}\pm |{\mathit{g}}_{\mathit{k}}+\mathit{B}|,$$ [2]

and hence two spin-nondegenerate Fermi surfaces.

The location, shape, and spin configuration of both Fermi surfaces evolve with the in-plane magnetic field. We will take Rashba SOC ${\mathit{g}}_{\mathit{k}}={\alpha }_{\text{R}}\widehat{\mathit{z}}\times \mathit{k}$ as an example (27). At zero field, two concentric Fermi circles are centered at $\mathit{k}=0$, with helical spin textures. These two Fermi surfaces have different density of states (DOS) $N_{\pm }=1/2N_0(1\mp {\alpha }_{\text{R}}/\overline{v})$ ($\overline{v}=\sqrt{v_{\text{F}}^2+{\alpha }_{\text{R}}^2}$), where $N_0=4\pi m$ is the total DOS including spin degeneracy, and $v_{\text{F}}=\sqrt{2\mu /m}$ is the Fermi velocity. A small field $B\ll {\mathrm{\Delta }}_{so}\equiv m{\alpha }_{\text{R}}{v}_{\text{F}}$ displaces the centers of inner $(+)$ and outer $(-)$ Fermi pockets to opposite momenta, $\pm {\mathit{k}}_0=\pm \widehat{\mathit{z}}\times \mathit{B}/v_{\text{F}}$, respectively, as shown in Fig. 1 A and C. To the first order in B, the energy dispersion satisfies ${\xi }_{\mathit{k}+{\mathit{k}}_0}^{+}={\xi }_{-\mathit{k}+{\mathit{k}}_0}^{+},\hspace{0.17em}{\xi }_{\mathit{k}-{\mathit{k}}_0}^{-}={\xi }_{-\mathit{k}-{\mathit{k}}_0}^{-}.$ Therefore, each Fermi surface remains nearly symmetric with respect to its displaced center, and the spin configuration remains nearly helical.

At B = 0, short-range attractive interaction leads to a BCS superconductor with zero momentum pairing, where states at $\pm \mathit{k}$ of opposite spins within each Fermi pocket are paired. At small B, the approximate inversion symmetry of the outer (inner) Fermi pocket with respect to its displaced center $\mp {\mathit{k}}_0$ naturally favors BCS-type intrapocket pairing, which leads to a nonzero Cooper pair momentum $\mp 2{\mathit{k}}_0$. Since the outer pocket has larger DOS, the state with Cooper pair momentum ${\mathit{q}}_0\approx -2{\mathit{k}}_0$ is energetically favored. It has an isotropic gap on the outer Fermi pocket (see Eq. 5 below), whereas the gap on the inner pocket is anisotropic due to the combined pair-breaking effect of Zeeman field and Cooper pair momentum. As discussed in SI Appendix, the competition between $\mp 2{\mathit{k}}_0$ Cooper pairs can also lead to other phases, and, in the rest of this manuscript, we will focus on the single-q helical state unless specified otherwise.

Such a helical state induced by Zeeman and SOC effects at small B is smoothly connected to the $\mathit{q}=0$ BCS state in the limit B = 0. Provided that the SOC strength Δ_so is much larger than the BCS pairing gap ${\mathrm{\Delta }}_0$ at B = 0, the field-induced helical state persists in the strong disorder regime ${\mathrm{\Delta }}_0\ll {\tau }^{-1}\ll {\mathrm{\Delta }}_{so}$ (24). These properties of the helical superconductor clearly contrast with the helical FF state that is formed by pairing between inner and outer pockets, is separated from BCS state by a first-order transition at the Pauli limiting field, and is highly sensitive to disorder. The plethora of 2D superconductors recently found in spin–orbit-coupled systems (43) provides an unprecedented opportunity to find helical superconductivity. However, it is difficult to distinguish a helical superconductor having a spatially uniform full gap from the BCS state. A direct measurement of the Cooper pair momentum requires sophisticated interference experiments using a Josephson junction between a helical superconductor and a reference BCS superconductor (16).

Origin of Supercurrent Diode Effect

In this work, we predict that, as a direct consequence of nonzero Cooper pair momentum ${\mathit{q}}_0$ in equilibrium state, helical superconductors generally exhibit nonreciprocal critical current: The maximum current that can flow with zero resistance in the direction along ${\mathit{q}}_0$ differs from the one in the opposite direction. Here we consider the depairing critical current, which is associated with the reduction and eventual closing of the superconducting gap with increasing supercurrent.

The origin of nonreciprocal critical current in a helical superconductor can be understood heuristically from the gap structure. Assuming a local attractive interaction, the mean-field Hamiltonian of the helical superconductor reads

$$\begin{array}{l}{H}_{\text{MF}}={\displaystyle \sum _{\mathit{k}}{c}_{\mathit{k}}^{†}}{H}_{\mathit{k}}{c}_{\mathit{k}}+{\displaystyle \sum _{\mathit{r}}\mathrm{\Delta }}(\mathit{r})(c_{\mathit{r}\uparrow }^{†}{c}_{\mathit{r}\downarrow }+h.c.)\\ \phantom{H_{\text{MF}}}=\frac{1}{2}{\mathrm{\Psi }}_{\mathit{k}}^{†}{\mathcal{H}}_{\mathit{k}}{\mathrm{\Psi }}_{\mathit{k}},\end{array}$$ [3]

where $\mathrm{\Delta }(\mathit{r})=\mathrm{\Delta }{e}^{i\mathit{q}·\mathit{r}}$ is the superconducting order parameter, Δ is the pairing potential, q is Cooper pair momentum, ${\mathrm{\Psi }}_{\mathit{k}}={\left(c_{\mathit{k+}\frac{\mathit{1}}{\mathit{2}}\mathit{q}\uparrow },c_{\mathit{k+}\frac{\mathit{1}}{\mathit{2}}\mathit{q}\downarrow },c_{-\mathit{k+}\frac{\mathit{1}}{\mathit{2}}\mathit{q}\uparrow }^{†},c_{-\mathit{k+}\frac{\mathit{1}}{\mathit{2}}\mathit{q}\downarrow }^{†}\right)}^{\text{T}}$ is the Nambu basis, and the Bogouliubov–de Gennes (BdG) Hamiltonian ${\mathcal{H}}_{\mathit{k}}$ takes the form

$${\mathcal{H}}_{\mathit{k}}(\mathit{q},\mathrm{\Delta })=\left(\begin{array}{cc}{H}_{\mathit{k+}\frac{\mathit{1}}{\mathit{2}}\mathit{q}}& -i{\sigma }_y\mathrm{\Delta }\\ i{\sigma }_y\mathrm{\Delta }& -H_{-\mathit{k+}\frac{\mathit{1}}{\mathit{2}}\mathit{q}}^{*}\end{array}\right).$$ [4]

By construction, the BdG Hamiltonian satisfies the antiunitary particle–hole symmetry $\mathcal{P}{\mathcal{H}}_{\mathit{k}}^{*}{\mathcal{P}}^{-1}=-{\mathcal{H}}_{-\mathit{k}}$ where $\mathcal{P}={\tau }_x$ acts in Nambu space that double counts the degrees of freedom. The spectrum of ${\mathcal{H}}_{\mathit{k}}$ consists of pairs of opposite eigenvalues $E_{\lambda }(\mathit{k}),-E_{\lambda }(-\mathit{k})$ (Fig. 2), where $\lambda =\pm$ denotes quasiparticle states associated with the two spin-split energy bands of normal phase. At $B=q=0$, the presence of time-reversal symmetry leads to $\mathcal{T}{\mathcal{H}}_{\mathit{k}}^{*}{\mathcal{T}}^{-1}={\mathcal{H}}_{-\mathit{k}}$ where $\mathcal{T}=i{\sigma }_y$ acts on spin, and the spectrum of ${\mathcal{H}}_{-\mathit{k}}$ at every $\mathit{k}$ is symmetric with respect to E = 0 (Fig. 2A).

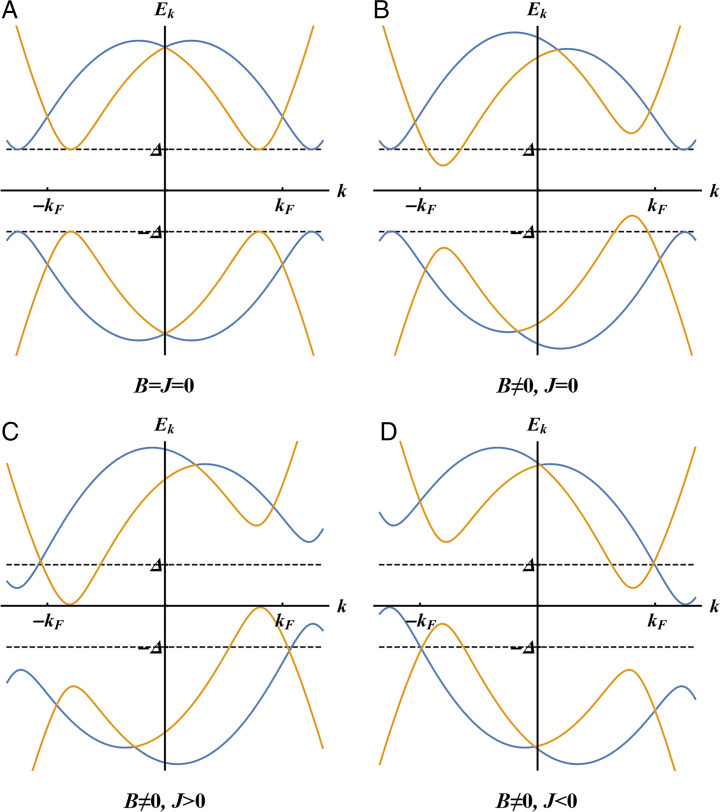
Fig. 2.

Energy spectra of superconductors with SOC: (A) conventional superconductor without external field and external current, (B) helical superconductor with external field without external current, and (C and D) helical superconductor with external field and external current along opposite directions. We use Eqs. 1 and 4 with $m=1,\mu =10,{\alpha }_{\text{R}}=1,\mathit{B}=B\widehat{\mathit{y}},\mathit{J}=J\widehat{\mathit{x}}$ and pairing potential Δ = 3. In B–D, $B=0.6\ll {\mathrm{\Delta }}_{so}=2\sqrt{5}$.

Due to the combined effect of field-induced Fermi surface displacement and Cooper pair momentum, the gap structure at $B\ne 0$ differs from the BCS state at B = 0. To the first order of q and B,

$$E_{\pm }(\mathit{k})=\sqrt{{({\xi }_{\mathit{k}}\pm |{\mathit{g}}_{\mathit{k}}|)}^2+{\mathrm{\Delta }}^2}+\frac{1}{2}{\mathit{v}}_{\mathit{k}}·\mathit{q}\pm {\widehat{\mathit{g}}}_{\mathit{k}}·\mathit{B},$$ [5]

where ${\mathit{v}}_{\mathit{k}}={\partial }_{\mathit{k}}{\xi }_{\mathit{k}}{|}_{\xi =0}=v_{\text{F}}\widehat{\mathit{k}}$ is the electron velocity, and ${\widehat{\mathit{g}}}_{\mathit{k}}={\mathit{g}}_{\mathit{k}}/\left|{\mathit{g}}_{\mathit{k}}\right|$.

Note that, in the Rashba case, we have ${\widehat{\mathit{g}}}_{\mathit{k}}·\mathit{B}=-{\mathit{v}}_{\mathit{k}}·{\mathit{k}}_0$ and ${\mathit{q}}_0=-2{\mathit{k}}_0$ so that $1/2{\mathit{v}}_{\mathit{k}}·{\mathit{q}}_0-{\widehat{\mathit{g}}}_{\mathit{k}}·\mathit{B}=0$. As shown in Fig. 2, at small B, the outer Fermi surface has a constant superconducting gap ${\mathrm{\Delta }}^{-}(\mathit{k})=\mathrm{\Delta }$ unaffected by the Zeeman field, while the inner Fermi surface is affected by the pair-breaking effect of the magnetic field and exhibits a strongly direction-dependent gap: ${\mathrm{\Delta }}^{+}(\mathit{k})=\mathrm{\Delta }+{\mathit{v}}_{\mathit{k}}·{\mathit{q}}_0.$ In the case of Rashba superconductors, ${\mathit{q}}_0\perp \mathit{B}$, and the superconducting gap is most strongly reduced in the direction perpendicular to the field.

At low temperatures, passing a supercurrent through the system creates an additional phase gradient in the superconducting order parameter, so that the current-carrying state has a Cooper pair momentum q different from the equilibrium one ${\mathit{q}}_0$. When the current is along the axis of ${\mathit{q}}_0$, the change of Cooper pair momentum $\delta \mathit{q}\equiv \mathit{q}-{\mathit{q}}_0$ is roughly proportional to the supercurrent density $\mathit{J}$ and further reduces the superconducting gap. As $\left|\mathit{J}\right|$ increases, the gap eventually closes. This gap-closing condition provides a rough estimate of the critical current. In the case of helical superconductors considered here, the gap closes on the inner pocket when the current is in the same direction as ${\mathit{q}}_0$ (Fig. 2C), and closes on the outer pocket when in the opposite direction (Fig. 2D). Since the two pockets have different gaps, the critical currents in opposite directions are different, resulting in supercurrent diode effect.

Our discussion, so far, of the supercurrent diode effect based on Bogouliubov band structures is heuristic. To rigorously demonstrate the supercurrent diode effect, one needs to work out the stable phase of superconductivity, which involves five energy scales: the bare pairing potential ${\mathrm{\Delta }}_0$ at zero temperature and zero field, the SOC energy ${\mathrm{\Delta }}_{so}={\alpha }_{\text{R}}{k}_{\text{F}}$, the Zeeman energy due to the magnetic field B, the temperature T, and Fermi energy μ. To determine the complete phase diagram in the 5D parameter space is enormously difficult. Nonetheless, near superconducting-normal phase transitions, Ginzburg–Landau theory applies, which may shed light on understanding the whole phase diagram.

In the following, we will present a theory of supercurrent diode effect. We first derive the explicit form of Ginzburg–Landau free energy from symmetry arguments, then calculate the nonreciprocal critical current from such free energy.

Theory of Supercurrent Diode Effect

We first review the supercurrent in a conventional BCS superconductor. Close to the superconducting phase transition, the free energy density $f\equiv \tilde{f}{N}_0$ as a functional of the superconducting order parameter $\mathrm{\Delta }(\mathit{r})$ reads

$$\tilde{f}=t|\mathrm{\Delta }(\mathit{r}){|}^2+a_0|(-i{\partial }_{\mathit{r}}-2e\mathit{A})\mathrm{\Delta }(\mathit{r}){|}^2+\frac{1}{2}\beta |\mathrm{\Delta }(\mathit{r}){|}^4,$$ [6]

and the supercurrent density is then

$$\mathit{J}=-\frac{\partial f}{\partial \mathit{A}}=4e{a}_0{N}_0\left\{\text{Im}[{\mathrm{\Delta }}^{*}(\mathit{r}){\partial }_{\mathit{r}}\mathrm{\Delta }(\mathit{r})]-2e|\mathrm{\Delta }(\mathit{r}){|}^2\mathit{A}\right\},$$ [7]

where $t\equiv (T-T_c)/T_c$ is reduced temperature, and $a_0,\beta >0$. When restricted to single-q order parameter $\mathrm{\Delta }(\mathit{r})=\mathrm{\Delta }{e}^{i\mathit{q}·\mathit{r}}$ and zero vector potential $\mathit{A}=\mathit{0}$, the corresponding free energy density and supercurrent density take the following forms:

$$\begin{array}{lll}\hfill \tilde{f}(\mathit{q},\mathrm{\Delta })& =& {\alpha }_{\mathit{q}}|\mathrm{\Delta }{|}^2+\frac{1}{2}\beta |\mathrm{\Delta }{|}^4,\\ \hfill \mathit{J}(\mathit{q})& =& 4e{N}_0{a}_0|\mathrm{\Delta }{|}^2\mathit{q},\end{array}$$ [8]

where ${\alpha }_{\mathit{q}}=t+a_0{q}^2$. Notice that $\mathit{J}=2e{\partial }_{\mathit{q}}f$ holds, and ${\partial }_{\mathit{q}}{\alpha }_{\mathit{q}}=2a_0\mathit{q}$ represents the superfluid velocity.

For 2D noncentrosymmetric superconductors under a parallel magnetic field, additional terms involving odd-power derivatives of $\mathrm{\Delta }(\mathit{r})$ are allowed in the free energy expression (27),

$$\tilde{f}={\mathrm{\Delta }}^{*}(\mathit{r})\widehat{\alpha }\mathrm{\Delta }(\mathit{r})+\frac{1}{2}\beta |\mathrm{\Delta }(\mathit{r}){|}^4,$$ [9]

where $\widehat{\alpha }$ is a differential operator involving the spatial derivative ${\partial }_{\mathit{r}}$. For example, $\widehat{\alpha }=t-a_0{\partial }_{\mathit{r}}^2$ in the conventional BCS case. Its Fourier transform ${\alpha }_{\mathit{q}}$ is obtained from pairing susceptibility of the normal state at wavevector q, as shown in SI Appendix. For spin–orbit-coupled superconductors considered in this work, $\beta >0$ generally holds. When ${\alpha }_{\mathit{q}}<0$, the above free energy is minimized by single-q order parameter: $\mathrm{\Delta }(\mathit{r})=\mathrm{\Delta }{e}^{i\mathit{q}·\mathit{r}}$. The corresponding free energy density takes the form

$$\tilde{f}(\mathit{q},\mathrm{\Delta })={\alpha }_{\mathit{q}}|\mathrm{\Delta }{|}^2+\frac{1}{2}\beta |\mathrm{\Delta }{|}^4.$$ [10]

The Cooper pair momentum ${\mathit{q}}_0$ in the equilibrium state is determined by minimizing ${\alpha }_{\mathit{q}}$ over q, that is,

$${\frac{\partial \alpha }{\partial \mathit{q}}\mid }_{{\mathit{q}}_{\mathit{0}}}=0,\hspace{0.17em}\text{and}\hspace{0.17em}{\det \frac{{\partial }^2\alpha }{\partial q_i\partial q_j}\mid }_{{\mathit{q}}_{\mathit{0}}}>0.$$ [11]

The in-plane critical field $B_c(T)$ is determined from the condition

$$\underset{{}_{\mathit{q}}}{\min }{\alpha }_{\mathit{q}}=0\hspace{0.17em}\text{at}\hspace{0.17em}B=B_c,$$ [12]

where ${\alpha }_{\mathit{q}}$ is temperature and field dependent. Equivalently, one also determines the critical temperature $T_c(B)$ at finite field B in the same way.

As shown above, the single-q order parameter is the stable phase near the superconducting phase transition. However, deep in the superconducting phase, either $B\ll B_c(T)$ or $T\ll T_c(B)$, the multiple-q order parameter (e.g., LO phase) will compete with the single-q one, and might be the stable phase in some cases (22, 44). Nevertheless, throughout this work, we focus on states close to the critical field line $B=B_c(T)$ whose stable phase is described by a single-q order parameter.

For the Rashba superconductor, the in-plane critical field $B_c(T)$ and the corresponding Cooper pair momentum ${\mathit{q}}_0$ at the superconducting transition is calculated numerically and shown in Fig. 3 A and B. Note that ${\mathit{q}}_0$ increases smoothly from zero with B, leading to a helical superconductor. The critical field is higher than the case of BCS phase (dashed line in Fig. 3A) in the absence of SOC.

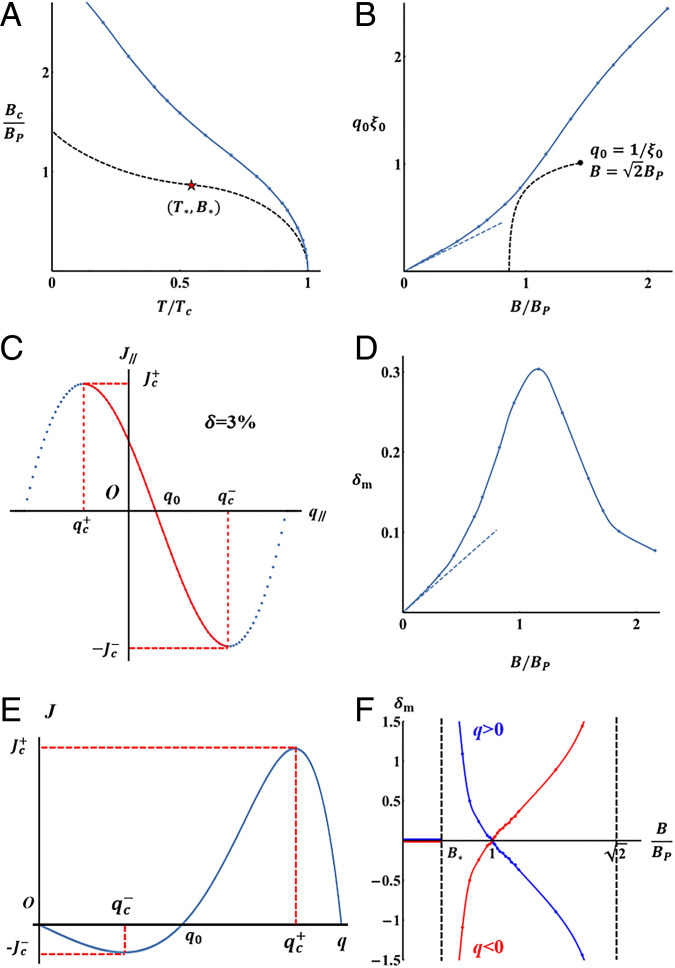
Fig. 3.

(A) In-plane critical field $B_c(T)$ as a function of temperature, for superconductors without SOC (dashed black line) and with Rashba SOC (blue line), where T_c is the zero-field critical temperature, and $B_P=1.25T_c$ is the Pauli limit. In the BCS case, the red star denotes the tricritical point of FFLO transition. In the Rashba superconductor, ${\alpha }_{\text{R}}=0.2v_{\text{F}},{\mathrm{\Delta }}_{so}=2{\mathrm{\Delta }}_0$, and ${\mathrm{\Delta }}_0=1.76T_c$ is the zero-temperature order parameter at zero field. (B) Along the curve $B_c(T)$ in A, field dependence of Cooper pair momentum magnitude q₀, where ${\xi }_0=v_{\text{F}}/{\mathrm{\Delta }}_0$ is the zero-temperature coherence length. Dashed blue line denotes Eq. 18 at weak fields. Dashed black line denotes the BCS case, whose maximum Cooper pair momentum is $q_0={\xi }_0^{-1}$ when $B=\sqrt{2}{B}_P$. (C) Supercurrent $\mathit{J}=J_{\parallel }{\widehat{\mathit{q}}}_0$ as a function of $\mathit{q}=q_{\parallel }{\widehat{\mathit{q}}}_0$ at $T=0.90T_c,B=0.31B_P$. Under external current, red solid line denotes stable states, and blue dots denote unstable states. (D) Along the curve $B_c(T)$ in A, field dependence of ${\delta }_{\text{m}}$ defined in Eq. 23. Dashed blue line denotes Eq. 19 at weak fields. (E) J versus q in a superconductor without SOC in the FF state (q > 0). (F) Along the dashed black curve $B_c(T)$ in A, ${\delta }_{\text{m}}$ as a function of B in a superconductor without SOC. When $B<B_{*}$, δ = 0, and, near B = B_P, there is a sign change of δ. Blue and red colors denote two types of FF states (q > 0 and q < 0).

By introducing vector potential $\mathit{A}$, the uniform supercurrent density $\mathit{J}$ can be calculated from the free energy density f as follows:

$$\mathit{J}=-{\frac{\partial f(\mathit{q-2eA},\mathrm{\Delta })}{\partial \mathit{A}}\mid }_{\mathit{A=0}}=2e{\partial }_{\mathit{q}}f,$$ [13]

with electron charge e < 0. The equilibrium state minimizes free energy density ${\partial }_{\mathit{q}}f=\mathit{0}$ and hence carries zero current. By connecting the system to an external source, one can pass a nonzero supercurrent $\mathit{J}$ through the system. Such a current-carrying state has a Cooper pair momentum $\mathit{q}\ne {\mathit{q}}_0$ that is determined by $\mathit{J}$ according to Eq. 13. Minimizing the free energy with respect to the gap magnitude Δ yields $|\mathrm{\Delta }{|}^2=-{\alpha }_{\mathit{q}}/\beta$ when ${\alpha }_{\mathit{q}}<0$. Then, Eq. 13 becomes

$$\mathit{J}=\frac{e{N}_0}{\beta }|{\alpha }_{\mathit{q}}|{\partial }_{\mathit{q}}{\alpha }_{\mathit{q}}.$$ [14]

Clearly, the supercurrent is the product of the superfluid stiffness $\left|{\alpha }_{\mathit{q}}\right|$ and the superfluid velocity ${\partial }_{\mathit{q}}{\alpha }_{\mathit{q}}$, both of which depend on the Cooper pair momentum q.

We first consider the BCS case without SOC and obtain the superconducting phase diagram in the B–J plane for temperatures close to the zero-field and zero-current critical temperature T_c. At B = 0, ${\alpha }_{\mathit{q}}=t+a_0{q}^2=t(1-{\xi }^2{q}^2)$ with coherence length $\xi \equiv \sqrt{a_0/\left|t\right|}\propto {(T_c-T)}^{-1/2}$, so that $\mathit{J}\propto (1-{\xi }^2{q}^2){\xi }^2\mathit{q}$. At q = 0, the superfluid stiffness is maximal, but the superfluid velocity vanishes. At $q={\xi }^{-1}$, the velocity is high, but the stiffness vanishes. The maximal supercurrent or the critical current J_c is achieved at an intermediate momentum $q_c={\xi }^{-1}/\sqrt{3}$ with $J_c\propto {(T_c-T)}^{3/2}$ (45). At $B\ne 0$ without external current, the Zeeman effect of in-plane magnetic field decreases the critical temperature of a BCS superconductor, leading to $T_c-T_c(B)\propto B^2$ or, equivalently, $B_c(T)\propto {(T_c-T)}^{1/2}$.

When both B and J are nonzero, the boundary between superconducting phase and normal phase in the B–J plane is defined by

$${\left(\frac{B}{B_c}\right)}^2+{\left(\frac{J}{J_c}\right)}^{2/3}=1,$$ [15]

where exponents 2 and 2/3 follow from the temperature scaling of the zero-current critical field B_c and the zero-field critical current J_c. The phase boundary is, in general, smooth except for the nonanalytical region near J = 0, due to the fractional exponent 2/3. This phase boundary is symmetric in J due to inversion symmetry of a conventional superconductor $\mathit{B}\to \mathit{B},\mathit{J}\to -\mathit{J}$, and is also symmetric with respect to the origin $J=B=0$, due to time-reversal symmetry $\mathit{B}\to -\mathit{B},\mathit{J}\to -\mathit{J}$.

In superconductors without inversion symmetry, the phase boundary in B–J phase space can become skewed, as sketched in Fig. 1D, in which case two closely related nonreciprocal effects appear. At a given magnetic field $B\ne 0$, the critical currents are nonreciprocal, and, in a given current-carrying state $J\ne 0$, the critical fields are polarity dependent. Both phenomena are manifestations of the supercurrent diode effect (30, 46).

As a concrete example, we consider Rashba superconductors in the following and derive, explicitly, the nonreciprocal critical current at weak field and temperatures near T_c. First, at small B, we can expand ${\alpha }_{\mathit{q}}$ as a power series in q and keep terms up to linear order in B (27),

$${\alpha }_{\mathit{q}}=t-(b_0-b_1{q}^2)\mathit{q}·(\mathit{B}\times \widehat{\mathit{z}})+a_0{q}^2,$$ [16]

with the parameters ${\alpha }_{\mathit{q}}=t-(b_0-b_1{q}^2)\mathit{q}·(\mathit{B}\times \widehat{\mathit{z}})+a_0{q}^2,$ derived from Fermi surface integrals as detailed in SI Appendix,

$$b_0=C_0\frac{{\alpha }_{\text{R}}}{{(\pi T_c)}^2},\hspace{0.17em}{b}_1=C_1\frac{v_{\text{F}}^2{\alpha }_{\text{R}}}{{(\pi T_c)}^4},\hspace{0.17em}{a}_0=\frac{1}{4}{C}_0\frac{v_{\text{F}}^2}{{(\pi T_c)}^2},$$

where $C_0=1.04$ and $C_1=0.38$ are numerical constants. In deriving the expressions of $a_0,b_0,b_1$, we have assumed SOC strength Δ_so is larger than the superconducting gap ${\mathrm{\Delta }}_0$. In Eq. 16, the B-linear terms arise from the field-induced shift (b₀) and deformation (b₁) of Fermi surfaces. By minimizing ${\alpha }_{\mathit{q}}$ over q, we find the Cooper pair momentum in the equilibrium state

$${\mathit{q}}_0=2{\alpha }_{\text{R}}(\mathit{B}\times \widehat{\mathit{z}})/v_{\text{F}}^2,$$ [17]

to the leading order in B.

Substituting Eqs. 16 and 17 into Eq. 14, we obtain the supercurrent along the axis parallel to the ${\mathit{q}}_0$ direction $J_{\parallel }$ as a function of $q_{\parallel }$, shown in Fig. 3C. Due to the third-order term, ${\alpha }_{\mathit{q}}$ is skewed with respect to its minimum at ${\mathit{q}}_0$. This skewness leads to different critical currents in the direction parallel and antiparallel to ${\mathit{q}}_0$. More specifically, upon the application of a weak in-plane magnetic field, critical current increases along one direction while it decreases along the opposite direction,

$$\frac{J_c^{\pm }}{J_c}=1\pm \gamma \frac{B}{B_c},$$ [18]

with

$$\gamma (T)=0.64\frac{{\alpha }_{\text{R}}}{v_{\text{F}}}\frac{B_c}{B_P}\sqrt{1-\frac{T}{T_c}},$$ [19]

where $B_P=1.25T_c$ is the Pauli limit. The dimensionless quantity γ measures the strength of the field-induced supercurrent diode effect at temperature T. $\gamma (T)$ is proportional to Rashba SOC and decreases to zero as $T_c-T$ near the critical temperature. Since $J_c\propto {(T_c-T)}^{3/2}$ and $B_c\propto {(T_c-T)}^{1/2}$, we have $J_c^{+}-J_c^{-}\propto {(T_c-T)}^2$.

More generally, at higher fields, the Cooper pair momentum q₀ is no longer small and reaches the order of ${\xi }_0^{-1}$ at $B\approx B_P$ (Fig. 3B), where ξ₀ is the zero-temperature, zero-field, and zero-current coherence length. Nonetheless, the critical current is always small near the superconducting transition temperature $T_c(B)$ at the corresponding field. Under this condition, we can expand ${\alpha }_{\mathit{q}}$ around its minimum ${\mathit{q}}_0$,

$${\alpha }_{\mathit{q}}=A[T-T_c(B)]+a\delta q_{\parallel }^2-b\delta q_{\parallel }^3,$$ [20]

where $A,a>0$, and $\delta q_{\parallel }=(\mathit{q}-{\mathit{q}}_0)·{\widehat{\mathit{q}}}_0$. From this expression, we find different critical currents $J_c^{\pm }$ in the direction along and against ${\mathit{q}}_0$. The nonreciprocity of critical current can be characterized by a “supercurrent diode coefficient” which we define as

$$\delta \equiv \frac{J_c^{+}-J_c^{-}}{J_c^{+}+J_c^{-}}.$$ [21]

At temperatures close to the superconducting phase transition, we find

$$\delta ={\delta }_{\text{m}}\sqrt{1-\frac{T}{T_c(B)}},\hspace{0.17em}\text{with}\hspace{0.17em}{\delta }_{\text{m}}=b\sqrt{\frac{A{T}_c(B)}{3a^3}}.$$ [22]

Our theory based on Eq. 20 applies to the regime $T\approx T_c$ at weak fields and also $T\approx 0$ at high fields, since $T_c(B)\to 0$ when B is large (Fig. 3A). The coefficients a, b can be computed by derivatives ${\partial }_q^2\alpha ,{\partial }_q^3\alpha$ at $\mathit{q}={\mathit{q}}_0$. One can numerically compute a and b from ${\alpha }_{\mathit{q}}$ as shown in SI Appendix, and δ can be obtained as shown in Fig. 3 C and D.

We numerically calculate and plot ${\delta }_{\text{m}}$ along the critical field line $B=B_c(T)$, as shown in Fig. 3D. Detailed derivation of Eqs. 18–20 and 22 can be found in SI Appendix.

It can be seen that ${\delta }_{\text{m}}$ is linear in B at weak fields as expected in Eq. 18 where $\delta =\gamma B/B_c$. As the field increases, ${\delta }_{\text{m}}$ reaches its maximum near $B=B_P$, and then decreases again. To understand the behavior of ${\delta }_{\text{m}}$ under a magnetic field, note that ${\alpha }_{\mathit{q}}=1/V-{\chi }_{\mathit{q}}$ (V is the attractive interaction) is determined by pairing susceptibility ${\chi }_{\mathit{q}}={\chi }_{\mathit{q}}^{+}+{\chi }_{\mathit{q}}^{-}$, where ${\chi }_{\mathit{q}}^{\pm }$ are the contributions from inner (+) and outer (–) Fermi surfaces, respectively. ${\chi }_{\mathit{q}}^{\pm }$ are nearly symmetric with respect to their respective maximum at $\mathit{q}\approx \pm 2{\mathit{k}}_0$, due to the Fermi surface shift, with k₀ on the order of $B/v_{\text{F}}$. The peak width is on the order of $T/v_{\text{F}}$. Due to the DOS asymmetry, the peak value of ${\chi }_{\mathit{q}}^{-}$ is higher than that of ${\chi }_{\mathit{q}}^{+}$. The differences in the peak position and height of ${\chi }^{+}$ and ${\chi }^{-}$ give rise to the skewness of ${\chi }_{\mathit{q}}$, the sum of the two. At high temperature, $T\lesssim T_c$, and low field, $B\ll B_P$, the peaks of ${\chi }_{\mathit{q}}^{\pm }$ are relatively broad and close to each other, so that the asymmetry in ${\alpha }_{\mathit{q}}$ is small. In the opposite limit of low temperature, $T\ll T_c$, and high field, $B\approx B_c(T)\gg B_P$, the two peaks are narrow and well separated and differ greatly in the height. ${\chi }_{\mathit{q}}$ is dominated by the main peak ${\chi }_{\mathit{q}}^{-}$ and therefore is nearly symmetric. Since the nonreciprocity in critical current becomes small at both low and high fields, the supercurrent diode coefficient ${\delta }_{\text{m}}$ —a measure of nonreciprocity near $T_c(B)$ —reaches its maximum around the Pauli limit $B=B_P$. We also discuss, in SI Appendix, the possibility of nonreciprocal critical current in the single-q FF (helical) phase without SOC.

Next, we derive the polarity-dependent critical field at small current for temperatures near T_c. This requires including the correction to ${\alpha }_{\mathit{q}}$ at second order in B as in the usual BCS superconductors without SOC. As shown in SI Appendix, we obtain the skewed phase boundary for Rashba superconductors in the B –J plane,

$${\left(\frac{B}{B_c}\right)}^2+{\mid \frac{\mathit{J}}{J_c}-\gamma \frac{\mathit{B}\times \widehat{\mathit{z}}}{B_c}{\left(1-\frac{B^2}{B_c^2}\right)}^2\mid }^{2/3}=1,$$ [23]

where γ is defined in Eq. 19. To the leading order in B, we recover Eq. 18 for nonreciprocal critical currents, and, to the leading order in J, we find the polarity-dependent critical field

$$\frac{B_c^{+}-B_c^{-}}{2B_c}=\frac{\gamma }{3}\frac{J}{J_c},$$ [24]

where the factor 1/3 is from exponents 2 and 2/3. Since $J_c\propto {(T_c-T)}^{3/2},\hspace{0.17em}{B}_c\propto {(T_c-T)}^{1/2}$, and $\gamma \propto (T_c-T)$, we find $B_c^{+}-B_c^{-}$ is temperature independent near T_c. Eq. 23 is our key finding about the supercurrent diode effect: It is exact (in the sense of temperature scaling) at temperatures near the zero-field, zero-current T_c.

At low temperatures, the entire phase boundary in the B–J plane can be determined numerically. From Eq. 23, we find the supercurrent diode effect in Rashba superconductors is maximized when $\mathit{B}\perp \mathit{J}$, and vanishes when $\mathit{B}\parallel \mathit{J}$, as shown in Fig. 1 B and D. The latter property is guaranteed when mirror symmetry $\mathit{B}\to \mathit{B},\mathit{J}\to -\mathit{J}$ is present.

Besides Rashba systems, the helical phase exists in noncentrosymmetric superconductors with the following point groups: ${\text{D}}_n,{\text{C}}_{n\text{v}},{\text{C}}_n,{\text{D}}_{2\text{d}},{\text{S}}_4,{\text{C}}_1(n=2,3,4,6)$. In these systems, crystal symmetry allows a linear coupling between the Cooper pair momentum q and Zeeman field B enabled by SOC. As a result, the field-induced Cooper pair momentum ${\mathit{q}}_0$ is linearly proportional to B at weak fields (27),

$${\mathit{q}}_0\propto {\nabla }_{\mathit{k}}({\widehat{\mathit{g}}}_{\mathit{k}}·\mathit{B}){|}_{\mathit{k=0}}.$$ [25]

The form of spin–orbit vector ${\mathit{g}}_{\mathit{k}}$ and therefore the direction of Cooper pair momentum depend on crystal symmetry. While ${\mathit{q}}_0\propto \widehat{\mathit{z}}\times \mathit{B}$ is perpendicular to the in-plane magnetic field in Rashba superconductors, ${\mathit{q}}_0\propto \mathit{B}$ is parallel to B in crystals with ${\text{D}}_{n\ge 3}$ point groups, and ${\mathit{q}}_0\propto (B_x,-B_y)$ forms a mirror pair with B in crystals with the ${\text{D}}_{\text{2d}}$ point group. While the direction of Cooper pair momentum relative to the magnetic field depends on crystal symmetry, the supercurrent diode effect is generally allowed when the current is passed along the axis of Cooper pair momentum.

For Ising superconductors with point group ${\text{D}}_{\text{3h}}$ such as transition metal dichalcogenides with an odd number of layers, the supercurrent diode effect is absent for in-plane field and in-plane current, where the combined symmetry of vertical mirror $I_z:z\to -z$ with respect to the basal plane and time-reversal $\mathcal{T}$ is preserved, $I_z\mathcal{T}:\mathit{J}\to -\mathit{J},\mathit{B}\to \mathit{B}$. However, one can realize nonreciprocal critical currents in an Ising superconductor by introducing an out-of-plane magnetization M_z (e.g., by ferromagnetic proximity effect), so that

$${\alpha }_{\mathit{q}}=t+a_0{q}^2+b(q_x^3-3q_x{q}_y^2)M_z,$$ [26]

and $a_0>0$, where a₀ and b are determined by Fermi surface properties of the Ising superconductor. Denoting θ as the angle between $\mathit{J}$ and x axis, the supercurrent diode coefficient is then

$$\delta =b\sqrt{\frac{\left|t\right|}{3a_0^3}}{M}_z\cos 3\theta .$$ [27]

We further consider the supercurrent diode effect in the limit of vanishing SOC. In this case, finite-momentum FFLO superconductivity occurs at high magnetic fields above the Pauli limit. In particular, the single-q FF state (which can be energetically favored over the LO state by weak SOC) breaks both inversion and time-reversal symmetry, thus giving rise to the diode effect as shown in Fig. 3E. In Fig. 3F, we also plot ${\delta }_{\text{m}}$ along the critical field line $B=B_c(T)$, where the normal phase, the BCS phase, and the FF phase meet at the tricritical point $(T_{*},B_{*})$ (Fig. 3A). As the magnetic field increases from $B_{*}$ to $B_c=\mathrm{\Delta }=\sqrt{2}{B}_P$, the Cooper pair momentum increases rapidly from zero to $1/{\xi }_0$, and the diode coefficient δ shows remarkable features.

The magnitude of the supercurrent diode effect $\left|\delta \right|$ becomes very large near both $B_{*}$ (the tricritical point) and B_c (the T = 0 end point of the FF phase). This can be understood from the behavior of Ginzburg–Landau coefficient ${\alpha }_{\mathit{q}}$. Near the tricritical point, we have

$${\alpha }_{\mathit{q}}=c_0+c_1{q}^2+c_2{q}^4,$$ [28]

with $c_0\propto T-T_{*},\hspace{0.17em}{c}_1\propto B_{*}-B$, and $c_2>0$. At B just above $B_{*}$, the Cooper pair momentum $q_0\propto \sqrt{B-B_{*}}$ is small. Nonetheless, α_q is highly skewed with respect to ${\mathit{q}}_0$: It increases very slowly as q decreases from q₀. As a result, $J_c^{+}\to 0$ while $J_c^{-}$ remains finite as $T\to T_{*},B\to B_{*}$. Thus the diode coefficient $\delta =(J_c^{+}-J_c^{-})/(J_c^{+}+J_c^{-})\approx 1$ reaches the maximum possible value near the tricritical point.

On the other hand, near the transition between the FF superconductor and normal phase at low temperature $T\to 0$, we have

$${\alpha }_{\mathit{q}}=\text{Re}\left[\log \left(\frac{B+\sqrt{B^2-v_{\text{F}}^2{q}^2}}{{\mathrm{\Delta }}_0}\right)\right].$$ [29]

Minimizing ${\alpha }_{\mathit{q}}$ over q yields a large Cooper pair momentum $q_0=B/v_{\text{F}}$ approaching $1/{\xi }_0$ as $B\to B_c$. In this case, due to the nonanalytic dependence of q, ${\alpha }_{\mathit{q}}$ is highly skewed with respect to ${\mathit{q}}_0$: It rises steeply as q decreases from q₀. This leads to the maximum possible diode effect with $\delta =(J_c^{+}-J_c^{-})/(J_c^{+}+J_c^{-})\approx -1$ near B_c, taking the opposite sign from the one near the tricritical point. Details of the supercurrent diode effect in the FF phase can be found in SI Appendix. Note that, at low temperature away from the critical line $B_c(T)$, the single-q FF state may yield to a multiple-q state. In the absence of SOC, the double-q LO state has a spatially modulated gap amplitude and constant phase, which does not show the diode effect.

Discussion

The supercurrent diode effect predicted in this work, including nonreciprocal critical current and polarity-dependent in-plane critical field, may be observed in polar SrTiO₃ films (47) and artificially engineered heavy fermion superlattices of YbCoIn₅ –YbRhIn₅ –CeCoIn₅ (29), where the layer stacking breaks inversion symmetry. In both cases, an upturn of the in-plane critical field has been observed and attributed to the Rashba spin splitting. Other candidates include transition metal dichalcogenide MoTe₂ in the low-symmetry T_d structure (48–50), and half-Heusler superconductors such as YPtBi with tetrahedral point group (51–54). These two classes of materials have strong spin–orbit interaction and small Fermi energy, which enhances the supercurrent diode effect.

Another interesting platform to search for supercurrent diode effect is magic-angle twisted bilayer graphene (55, 56), whose twisted bilayer structure breaks inversion symmetry. Although spin–orbit interaction is negligibly small, an in-plane magnetic field modifies the moiré band structure by giving electrons a momentum shift in the interlayer tunneling process. As we showed recently, a small field causes a shift of Fermi surface by $\delta \mathit{k}\propto \mathit{B}$ in the direction parallel to B (56). Therefore, field-induced finite-momentum superconductivity and the supercurrent diode effect may appear when the critical current is measured along the field axis.

Last but not the least, the supercurrent diode effect should also exist when the superconducting state spontaneously breaks time-reversal and inversion symmetry. Thus, nonreciprocal critical current at zero magnetic field and polarity-dependent critical field in the equilibrium state provide new probes of unconventional superconductivity with hidden orders.

Data Availability

All study data are included in the article and/or SI Appendix.

Note Added.

Recently, two related works (57, 58) on a similar topic have appeared.