An ensemble model based on early predictors to forecast COVID-19 health care demand in France

Significance

The COVID-19 pandemic is inducing significant stress on health care structures, which can be quickly saturated with negative consequences for patients. As hospitalization comes late in the infection history of a patient, early predictors—such as the number of cases, mobility, climate, and vaccine coverage—could improve forecasts of health care demand. Predictive models taken individually have their pros and cons, and it is advantageous to combine the predictions in an ensemble model. Here, we design an ensemble that combines several models to anticipate French COVID-19 health care needs up to 14 days ahead. We retrospectively test this model, identify the best predictors of the growth rate of hospital admissions, and propose a promising approach to facilitate the planning of hospital activity.

Abstract

Short-term forecasting of the COVID-19 pandemic is required to facilitate the planning of COVID-19 health care demand in hospitals. Here, we evaluate the performance of 12 individual models and 19 predictors to anticipate French COVID-19-related health care needs from September 7, 2020, to March 6, 2021. We then build an ensemble model by combining the individual forecasts and retrospectively test this model from March 7, 2021, to July 6, 2021. We find that the inclusion of early predictors (epidemiological, mobility, and meteorological predictors) can halve the rms error for 14-d–ahead forecasts, with epidemiological and mobility predictors contributing the most to the improvement. On average, the ensemble model is the best or second-best model, depending on the evaluation metric. Our approach facilitates the comparison and benchmarking of competing models through their integration in a coherent analytical framework, ensuring that avenues for future improvements can be identified.

Quick increases in hospital and intensive care unit (ICU) admissions have been common since the start of the COVID-19 pandemic. In many instances, this has put the health care system at risk for saturation, forced the closure of non-COVID-19 wards, the cancellation of nonessential surgeries, and the reallocation of staff to COVID-19 wards with negative consequences for non-COVID-19 patients. In this context, short-term forecasting of the pandemic and its impact on the health care system is required to facilitate the planning of COVID-19 health care demand and other activities in hospitals (1).

Hospital admission comes late in the history of infection of a patient, so forecasts that only rely on hospital data may miss earlier signs of a change in epidemic dynamics. There have been a lot of discussions about insights we might gain from other types of predictors (e.g., epidemiological predictors such as the number of cases, mobility predictors such as Google data, or meteorological predictors), but assessment of the contribution of these predictors has been marred by methodological difficulties. For example, while variations in case counts may constitute an earlier sign of change in epidemic dynamics, these data may be affected by varying testing efforts, making interpretation difficult. Associations between meteorological/mobility variables and SARS-CoV-2 transmission rates have been identified (2–5), but it is yet unknown whether the use of these data along with epidemiological predictors may improve forecasts.

Here, we develop a systematic approach to address these challenges. We retrospectively evaluate the performance of 12 individual models and 19 predictors to anticipate French COVID-19-related health care needs, from September 7, 2020, to March 6, 2021. We build an ensemble model by combining the individual forecasts and test this model from March 7, 2021, to July 6, 2021. Our analysis makes it possible to determine the most promising approaches and predictors to forecast COVID-19–related health care demand, indicating for example that the inclusion of early predictors (epidemiological, mobility, and meteorological) can halve the rms error (RMSE) for 14-d–ahead forecasts, with epidemiological and mobility predictors contributing the most to the improvement. Our approach facilitates the comparison and benchmarking of competing models through their integration in a coherent analytical framework, ensuring that avenues for future improvements can be identified.

Results

Overview of the Approach.

We first develop a set of individual models to forecast the number of hospital admissions at the national and regional level, up to 14 d ahead. These individual predictions are then combined into a single ensemble forecast (1, 6–10). Finally, we derive three other targets (number of ICU admissions, bed occupancy in general wards, and bed occupancy in ICU) from the number of hospital admissions predicted by the ensemble model (Materials and Methods and SI Appendix, Fig. S1).

We use a 2-stage procedure: 1) over the training period (September 7, 2020, to March 6, 2021), we select the predictors and evaluate the performance of the individual models to choose the best ones to include in the ensemble model, and 2) over the test period (March 7, 2021, to July 6, 2021), we assess the performance of the ensemble model on new observed data to mimic real-time analysis.

We use a cross-validation approach based on a rolling forecasting origin: For each day t, we make forecasts for the period t−1 up to day t + 14, using only past data up to day t−2, and computing evaluation metrics against the smoothed observed data. We start to make forecasts at t−1 because in real time, on day t, values at t and t−1 are not consolidated yet and the last reliable data point used for forecasts is the value at t−2.

Performance of Individual Models to Forecast Hospital Admissions over the Training Period.

Twelve individual models are considered to forecast the number of hospital admissions by region with a time horizon of up to 2 weeks. They use a variety of methods and rely on epidemiological, mobility, and meteorological predictors (Materials and Methods and SI Appendix, Supplementary Text and Figs. S2–S4). Over the training period, most of these models are able to broadly capture the dynamics of hospital admissions from September 2020 to March 2021 (SI Appendix, Fig. S5). They all overestimate the November peak since they were not designed to anticipate the impact of the lockdown before its implementation.

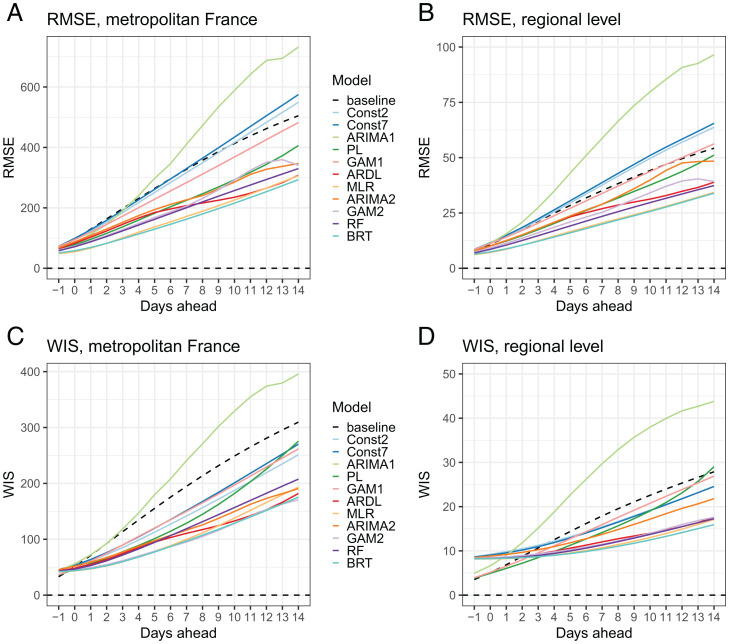
Models are compared using the RMSE for point forecast error and the weighted interval score (WIS) to assess probabilistic forecast accuracy (Materials and Methods). Overall, the performance of the models decreases with the prediction horizon (Fig. 1). Six models outperform the baseline model (characterized by no change in the number of hospital admissions) at all prediction horizons for both the RMSE and the WIS, at the national and regional levels: an autoregressive distributed lag model (ARDL), a multiple linear regression model (MLR), a generalized additive model (GAM2), an ARIMA model (ARIMA2), a boosted regression tree (BRT) model, and a random forest (RF) model. All these models describe the growth rate of hospital admissions rather than hospital admissions directly, and they include several predictors that are described in the section below. For each region, we rank the models according to the RMSE over all prediction horizons: Model ranking varies by region, but on average the BRT and the MLR models perform better (SI Appendix, Fig. S6).

Fig. 1.

Comparison of the performance of individual models over the training period at the national and regional levels, by prediction horizon, for hospital admissions. (A) RMSE in metropolitan France. (B) RMSE by region. (C) Mean WIS in metropolitan France. (D) WIS by region. Models: Const2, exponential growth model with constant growth rate (2 d window); Const7, exponential growth model with constant growth rate (7 d window); ARIMA1, autoregressive integrated moving average model; PL, exponential growth model with piecewise linear growth rate; GAM1, generalized additive model of hospital admissions; ARDL, autoregressive distributed lag model; MLR, multiple linear regression model; ARIMA2, multiple linear regression model with ARIMA error; GAM2, generalized additive model of the growth rate; RF, random forest model; BRT, boosted regression tree model.

Predictors.

The six best individual models include between 2 and 4 predictors (SI Appendix, Table S1). The best predictors are selected by cross-validation using a forward stepwise selection method (Materials and Methods and SI Appendix, Supplementary Text). One model has an autoregressive component—i.e., it includes lagged values of the growth rate of hospital admissions as covariates. All six models include at least one mobility predictor: Time spent in residential places is the one that is most often selected, followed by the volume of visits to transit stations (in percentage change from baseline). Four models use at least one predictor on confirmed cases: the growth rate of the proportion of positive tests (among all tests or among tests in symptomatic people) and/or the growth rate of the number of positive tests. Two models use one meteorological predictor: either absolute humidity or temperature.

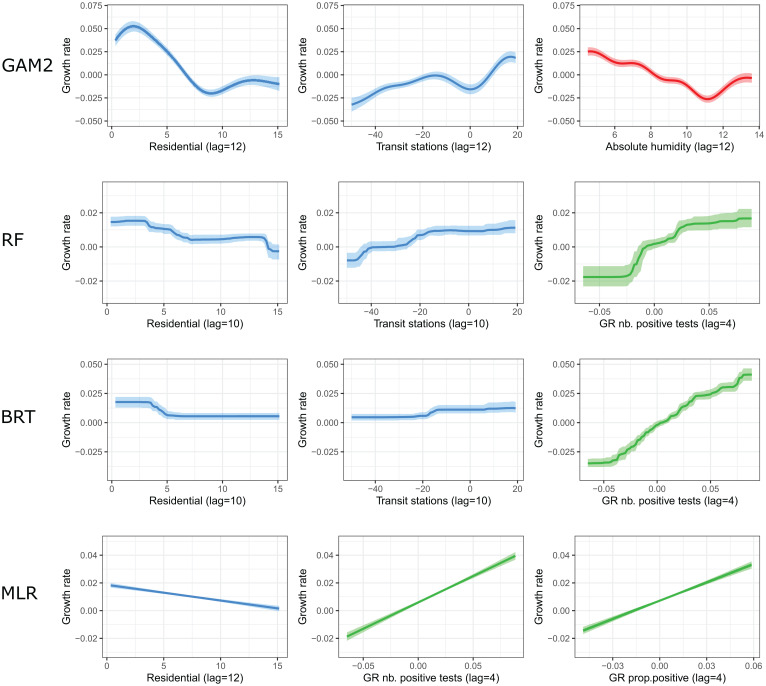
In order to determine the importance of the different predictors and explore their effect on the growth rate, we retrospectively fit four individual models (BRT, RF, MLR, and GAM2) from June 3, 2020 (once all predictors become available) to March 6, 2021, on all regions together, whenever possible. The parameters of the ARDL model vary with the prediction horizon, and those of the ARIMA2 model vary by region. Therefore, only four models (BRT, RF, MLR, and GAM2) are included in this subanalysis. Retrospectively, the models can reproduce the dynamics of the growth rate over time and by region reasonably well (SI Appendix, Fig. S7). Depending on the model, the most important predictors are mobility or epidemiological predictors (SI Appendix, Fig. S8). For instance, in the MLR model, the change in time spent in residential places and the growth rate of the positive tests both contribute to 47% of the explained variance. In the BRT model, the growth rate of the number of positive tests is the most important predictor (relative contribution of 89%) followed by the time spent in residential places (6%) and change in the volume of visits to transit stations (5%). Meteorological factors contribute to 37% in the GAM2 model but have no contribution in the three other models.

We find that an increase in the volume of visits to transit stations, a decrease in the time spent in residential places, or a decrease in absolute humidity is associated with an increase in the growth rate of hospital admissions 10 to 12 d later (Fig. 2). Regarding epidemiological predictors, the growth rate of hospital admissions is positively associated with the growth rate of the number of positive tests, with a lag of 4 d, and the growth rate of the proportion of positive tests, with a lag of 7 d.

Fig. 2.

Effects of mobility (blue), epidemiological (green), and meteorological (red) predictors on the growth rate of hospital admissions for the GAM2, RF, BRT, and MLR models. Abbreviation: GR, growth rate. Predictors are described in SI Appendix, Supplementary Text.

Performance of the Ensemble Model over the Test Period.

To build the ensemble model, we keep the six models that outperform the baseline model and take the unweighted mean of the individual forecasts. In addition to the previously selected predictors, we also include vaccine coverage and the proportion of variants of concern (VOC) (SI Appendix, Supplementary Text and Fig. S9) as these two predictors may significantly affect the dynamic of hospitalizations after March 2021. When retrospectively fitting the models from June 3, 2020, to July 6, 2021, the effects of the other predictors remain relatively stable, compared to the previous fit from June 3, 2020, to March 6, 2021 (SI Appendix, Fig. S10).

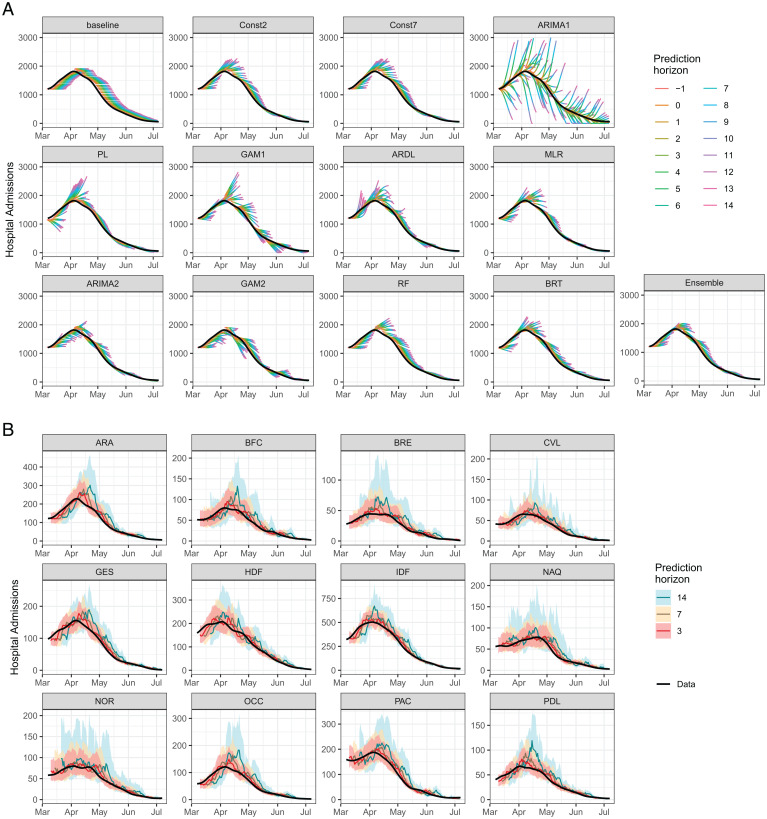
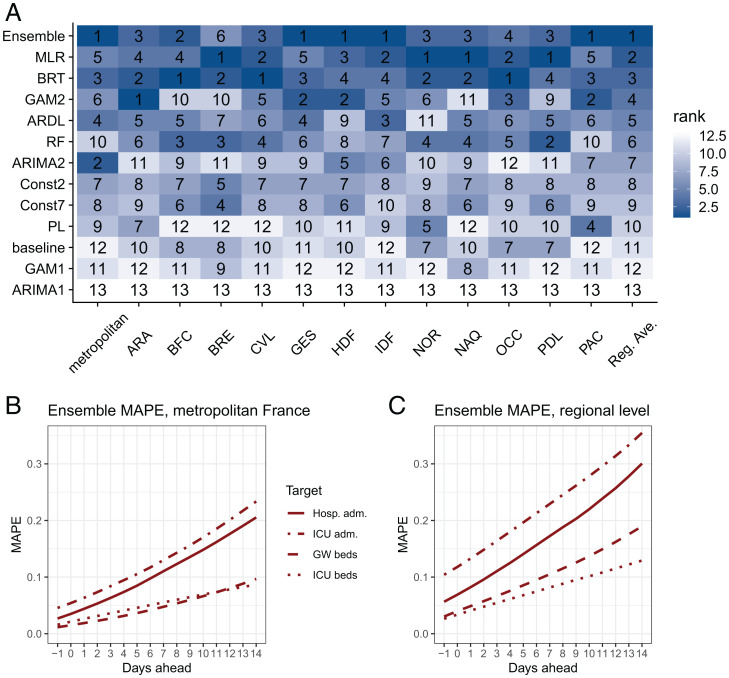
The ensemble model is evaluated over the test period (March 7, 2021, to July 6, 2021). It is able to capture the growth of hospital admissions in March and the decline in April to July, although it shows some delays in adjusting to the upward/downward trends (Fig. 3A). The ensemble model performs well in all regions (Fig. 3B). On average, the ensemble model is the best at the national level for both the RMSE and the WIS and at the regional level for the RMSE, and it is the second-best model at the regional level for the WIS (SI Appendix, Fig. S11). For each region or week, we rank the individual and ensemble models according to the RMSE over all prediction horizons. The best individual model is not the same in all regions (Fig. 4A) or in all weeks (SI Appendix, Fig. S12): Four models are ranked first in at least one region and eight models are ranked first in at least one week, but the ensemble model is ranked first on average across all regions/weeks.

Fig. 3.

Forecasts of hospital admissions over the test period (March 7, 2021, to July 6, 2021). (A) Trajectories predicted by the individual and ensemble models for all prediction horizons in metropolitan France. The black line is the eventually observed data (smoothed), and the colored lines are trajectories predicted on day t, for prediction horizons t−1 up to t + 14. (B) Forecasts of the ensemble model by region at 3, 7, and 14 d. The black line is the eventually observed data (smoothed). Shaded areas represent 95% prediction intervals. Regions: Auvergne-Rhône-Alpes (ARA), Bourgogne-Franche-Comté (BFC), Bretagne (BRE), Centre-Val de Loire (CVL), Grand Est (GES), Hauts-de-France (HDF), Île-de-France (IDF), Normandie (NOR), Nouvelle-Aquitaine (NAQ), Occitanie (OCC), Pays de la Loire (PDL), and Provence-Alpes-Côte d’Azur (PAC).

Fig. 4.

Model ranking by region and performance of the ensemble model for the four targets (hospital admissions, ICU admissions, general ward [GW] bed occupancy, and ICU bed occupancy) over the test period. (A) Ranks of the models. Models are ranked according to the RMSE over all prediction horizons. Reg. Ave. = regional average (RMSE computed over all regions except metropolitan France). (B) MAPE of the ensemble model by prediction horizon in metropolitan France. (C) MAPE of the ensemble model by prediction horizon at the regional level.

Finally, to assess the ensemble forecasts of hospital admissions, ICU admissions, and bed occupancy in the ICU and the general wards, we report the mean absolute percentage error (MAPE, mean of the ratio of the absolute error to the observed value) because its interpretation in terms of relative error is straightforward, as well as the 95% prediction interval coverage (proportion of 95% prediction intervals that contain the observed value) and the RMSE (SI Appendix, Fig. S13). For the four targets, the MAPEs at 7 d are 11%, 13%, 6%, and 5% at the national level (17%, 23%, 8%, and 11% at the regional level) for hospital admissions, ICU admissions, ICU beds, and general ward beds, respectively (Fig. 4B). At 14 d, these errors increase to 20%, 23%, 9%, and 10% at the national level (30%, 35%, 13%, and 19% at the regional level), respectively. The calibration is good for most of the targets, but the 95% prediction interval coverage is lower than 95% for hospital admissions and 14-d–ahead forecasts (SI Appendix, Table S2).

Discussion

In this study, we evaluated the performance of 19 predictors and 12 models to anticipate French COVID-19 health care needs and built an ensemble model to reduce the average forecast error. We can draw a number of important conclusions from this systematic evaluation. First, mathematical models are often calibrated on hospitalization and death data only, as these signals are expected to be more stable than testing data (1, 11, 12). However, we find that such an approach is outperformed by models that also integrate other types of predictors. These include predictors that can more quickly detect a change in the epidemic dynamics (e.g., growth rate in the proportion of positive tests in symptomatic people) or that may be correlated with the intensity of transmission (e.g., mobility data, meteorological data). The inclusion of such predictors can halve the RMSE for a time horizon of 14 d.

Second, of the three types of predictors used over the training period, epidemiological and mobility predictors are those that improve forecasts the most. In models where the lags are estimated, we find that epidemiological predictors precede the growth rate of hospital admissions by 4 to 7 d, while mobility predictors precede it by 12 d. This is consistent with our understanding of the delays from infection to testing and infection to hospitalization (11). Meteorological variables also improve forecasts, although the reduction in the relative error is more limited. Per se, this result should not be used to draw conclusions on the role of climate in SARS-CoV-2 transmission. Indeed, we are only assessing the predictive power of these variables, not their causal effect, in a situation where the hospitalization dynamics are already well captured by epidemiological predictors. In this context, the additional information brought by meteorological variables is limited and may already be accounted for by epidemiological predictors. Interestingly, despite the diversity of models and retained predictors, estimates of the effect of the different predictors on the growth rate are relatively consistent across models (Fig. 4). The effects of the predictors remain relatively stable between the two time periods, although the reduction of the effects of mobility predictors for the BRT model suggests a lower impact of mobility after March 2021 (SI Appendix, Fig. S10). Other potential predictors could have been considered, such as interregion mobility or spatial correlations. However, given the 10 d delay between infection and hospitalization, we expect that most patients who will be hospitalized in a given region in the next 2 weeks will have recently been infected in that region. The benefits of accounting for interregion mobility therefore appear limited for short-term predictions but may become more important when longer forecast horizons are being considered.

Third, rather than using the individual model that performs best, we find that it is better to rely on an ensemble model that averages across the best-performing models. This is consistent with the results of recent epidemic forecasting challenges (1, 6, 9, 13, 14). Relying on an ensemble model is appealing because it acknowledges that each model has limitations and imperfectly captures the complex reality of this pandemic. Although individual models may perform better in some situations, forecasts that build on an ensemble of models are less likely to be overly influenced by the assumptions of a specific model (15). The benefits are confirmed in practice, with the ensemble model performing best on average.

Fourth, the systematic evaluation also sheds light on important technical lessons for forecasting. We find that the best forecasts are obtained when using the exponential growth rate rather than the absolute value of epidemiological variables. This is true for the dependent variable we aim to forecast (hospital admissions) but also for predictor variables (e.g., the proportion of positive tests). This finding is not surprising since transmission dynamics are characterized by exponential growth and decline. Using the growth of epidemiological predictors such as the number of positive tests also helps controlling for changes in testing practice that may have occurred over longer time periods. We also find that the approach used to smooth the data is decisive in ensuring that forecast quality is not overly dependent on the day of the week (given the existence of important weekend effects) and to find the correct balance between early detection of a change of dynamics and the risk of repeated false alarms (Materials and Methods and SI Appendix, Figs. S14–S16).

The introduction of vaccines and the emergence of variants that are more transmissible than historical SARS-CoV-2 viruses (16) opened up new challenges for the forecasting of COVID-19 health care demand. Indeed, our models have been calibrated on past data to forecast the epidemic growth rate of the historical virus from a number of predictors, when vaccines were not widely used. These new factors (vaccination and variants) can modify the association between the different predictors and the epidemic growth rate: They may lead to an underestimation of the growth rate in a context where a more transmissible variant is also circulating or an overestimation of the growth in vaccinated populations. The flexibility of our approach allows us to adjust the models to this changing epidemiological situation: To account for these new factors, one can explicitly integrate the proportion of variants and the vaccine coverage as new predictors of the models over the test period. As expected, we find that vaccine coverage is negatively associated with the growth rate of hospital admissions. For the proportion of VOC, we find a positive association in some models but no association in others (SI Appendix, Fig. S10). This finding may be due to the correlation between the rise in vaccine coverage and in the proportion of VOC and/or to the fact that the effect of VOC is already accounted for by epidemiological predictors. In the meantime, since epidemiological predictors are intermediate factors between external predictors (mobility, climate, vaccine coverage, and VOC) and hospital admissions, we also run sensitivity analyses with models that use epidemiological predictors only, with no consideration of external predictors. We find that models with all types of predictors perform better than purely epidemiological models over the test period (SI Appendix, Fig. S17). Finally, as different predictors may be important at different stages of the epidemic, one could also update the variable selection at different time points to continuously revise the best predictors to include in the models.

The forecasts presented in this study were made retrospectively, not in real time. Such a retrospective approach makes it easier to perform a systematic evaluation of models and predictors and determine the key ingredients for a successful forecast within a single coherent analytical framework, but it may tend to overestimate the performance of the forecasting models, compared to what would be observed in real time. Indeed, we used consolidated data to conduct this retrospective study while in real time, delays in data availability or data revisions after their publication can increase the forecast error. We tried to overcome this limitation and to closely mimic real-time analysis by removing the last two data points that in real time are not yet consolidated, starting to make forecasts at t−1. In addition, the benefits of hindsight necessarily remain when working retrospectively. From early 2021, we produced real-time forecasts to support public health decision-making using an ensemble approach similar to the one presented here, although the models differed slightly (e.g., a different set of predictors). To illustrate the difference between prospective and retrospective evaluation of such models, we describe the performance of our real-time forecasts compared to the retrospective forecasts over the test period in the SI Appendix, Fig. S18. Real-time forecasts generally present higher errors than retrospective forecasts. For instance, the RMSE for hospital admissions is higher for the real-time forecasts than for the retrospective forecasts. For the three other targets, based on MAPE at the national level, the real-time forecasts are as good as, or even better than, the retrospective forecasts for ICU admissions and ICU beds, but the MAPE is 4% higher for hospital beds at 14 d.

Through a systematic evaluation, we determined the most promising approaches and predictors to forecast COVID-19–related health care demand. Our framework makes it straightforward to compare and benchmark competing models and identify current limitations and avenues for future improvements.

Materials and Methods

Hospitalization Data.

Hospital data are obtained from the SI-VIC database, the national inpatient surveillance system providing real-time data on COVID-19 patients hospitalized in French public and private hospitals (SI Appendix, Supplementary Text).

Smoothing.

Hospital data follow a weekly pattern, with fewer admissions during weekends compared to weekdays, and they can be noisy at the regional level. Therefore, in the absence of smoothing or with simple smoothing techniques, forecasts can be biased depending on the day of the week on which the analysis is performed. In order to remove this day-to-day variation and obtain a smooth signal at each date not depending on future data points, we smooth the data using a 2-step approach based on local polynomial regression and the least-revision principle (17) (SI Appendix, Supplementary Text and Figs. S14–S16).

Exponential Growth Rate.

We compute the exponential growth rate using a 2 d rolling window and smooth the resulting time series using local polynomial regression.

Overview of the Modeling Approach.

We build a framework to forecast four targets at the national (metropolitan France) and regional (n = 12) levels up to 14 d ahead: the daily numbers of hospital and ICU admissions, and the daily numbers of beds occupied in general wards and the ICU (SI Appendix, Fig. S1).

We first develop a set of individual models to forecast the number of hospital admissions, using a variety of methods. These individual predictions are then combined into a single ensemble forecast, called an ensemble model (1, 6–10). Finally, we derive the number of ICU admissions and bed occupancy in general wards and the ICU from the predicted number of hospital admissions.

We divide our study period into two periods (SI Appendix, Fig. S1): 1) over the training period, we select the predictors and evaluate the performance of the individual models in order to select the best ones to include in the ensemble model, and 2) over the test period, we evaluate the performance of the ensemble model on the new observed data.

Modeling Hospital Admissions.

In a first step, we evaluate 12 individual models, including exponential growth models with constant or linear growth rates, linear regression models, generalized additive models, a BRT model, a RF model, and autoregressive integrated moving average models (full description in SI Appendix, Supplementary Text). Some of the models directly predict the number of hospital admissions, while others predict the growth rate, from which hospital admissions are then derived using an exponential growth model. We also added a baseline model characterized by no change in the number of hospital admissions.

We evaluate and compare the performance of individual models over a period running from September 7, 2020, to March 6, 2021 (the training period). As the models are not designed to anticipate the impact of a lockdown before its implementation, we exclude from the training period the forecasts made between October 20, 2020, and November 4, 2020 (i.e., up to 6 d into the lockdown starting on October 30) for hospitalizations occurring after November 3. In other words, between October 20 and November 4, we consider that the models could not anticipate the impact of the lockdown.

We use a cross-validation approach based on a rolling forecasting origin: For each day t of the training period, we make forecasts for the period t−1 up to day t + 14, using only past data up to day t−2 as a training set and computing evaluation metrics against the smoothed observed data in t−1 to t + 14 (smoothed using the full data). We begin to make forecasts at t−1 because in real time, on day t, values at t and t−1 are not consolidated yet and the last reliable data point used for forecasts is the value at t−2.

Model performance is evaluated using two main metrics. Our primary metric for point forecast error, the RMSE, is used to evaluate predictive means (18), and our secondary metric, the WIS, is used to assess probabilistic forecast accuracy (1, 6, 19). The WIS is a proper score that combines a set of interval scores for probabilistic forecasts that provide quantiles of the predictive forecast distribution. It can be interpreted as a measure of how close the entire distribution is to the observation, in units on the scale of the observed data (6). The WIS is defined as a weighted average of the interval scores over K central 1-α predictions intervals bounded by quantile levels $(\frac{{\alpha }_k}{2},1-\frac{{\alpha }_k}{2})$:

$$WI{S}_{{\alpha }_{O:K}}(F,y)=\frac{1}{K+12}(\frac{1}{2}\mid y-m\mid +{\displaystyle \sum }_{k=1}^K(\frac{{\alpha }_k}{2}(u_k-l_k)+\left(l_k-y\right)1(y<l_k)+(y-u_k)1(y>u_k))),$$ [1]

where y is the observed outcome, F is the forecast distribution, m is the point forecast, 1(.) is the indicator function, and u_k and l_k are the predictive upper and lower quantiles corresponding to the central prediction interval level k, respectively. We use K = 11 interval scores, for α = 0.02, 0.05, 0.1, 0.2, …, 0.9.

We include in individual models a set of predictors, chosen for their availability in near–real time and their potential to help anticipate the trajectory of hospital admissions. Over the training period, three types of predictors are considered: nine epidemiological predictors describing the dynamics of the epidemics (e.g., growth rate of the number of hospital admissions, the number of positive tests, and the proportion of positive tests among symptomatic people), six mobility predictors (e.g., the change in volume of visits to workplaces, transit stations, residential places, or parks [Google data]), and four meteorological predictors [temperature, absolute and relative humidity, and the Index PREDICT de transmissivité climatique de la COVID-19 (IPTCC), an index characterizing climatic conditions favorable for the transmission of COVID-19 (20)]. All predictors and data sources are described in SI Appendix, Supplementary Text and Figs. S2–S4. For each individual model, covariates are selected using a forward stepwise selection approach over the training period (not using data from the test period) (SI Appendix, Supplementary Text).

In order to determine the importance of the different predictors and explore their effect on the growth rate, we retrospectively fit the best individual models from June 3, 2020, to March 6, 2021, on all regions together, whenever possible. We start the fit on June 3, 2020, when all the predictors are available. The parameters of the ARDL model vary with the prediction horizon, and those of the ARIMA2 model vary by region. Therefore, only four models (BRT, RF, MLR, and GAM2) are included in this subanalysis.

In a second step, to build the ensemble model, we keep the models that outperformed the baseline model at all prediction horizons for both the RMSE and the WIS, at the national and regional levels. Individual model forecasts are combined into an ensemble forecast by taking the unweighted mean of the point predictions and the unweighted mean of the 95% confidence intervals. We test the performance of the ensemble model on the period running from March 7, 2021, to July 6, 2021 (the test period).

To assess the performance of the ensemble model, in addition to the RMSE and the WIS used to compare the models, we also report the MAPE, the mean of the ratio of the absolute error to the observed value, because its interpretation in terms of relative error is straightforward, as well as the 95% prediction interval coverage (proportion of 95% prediction intervals that contain the observed value).

Over the test period, we use in individual models the previously selected predictors and include the vaccine coverage and the proportion of VOC (SI Appendix, Supplementary Text and Fig. S9). Indeed, these two predictors, which are negligible over the training period, can significantly affect the dynamic of hospitalizations observed from March 2021.

In order to determine whether the effects of the different predictors may have changed over time, we also retrospectively fit four of the individual models from June 3, 2020, to July 6, 2021, and compare the results with those obtained over the previous time period.

Modeling ICU Admissions and Bed Occupancy in ICU and General Wards.

Predictions for the number of ICU admissions and bed occupancy in the ICU and general wards are derived from predicted numbers of hospital admissions. The expected number $H_{\mathit{ICU}}(t)$ of ICU admissions at time t is given by the formula:

$$H_{\mathit{ICU}}\left(t\right)=p_{\mathit{ICU}}(t){\displaystyle \sum }_{u\le t}H(u)g_H(t-u),$$ [2]

where $H(u)$ is the number of hospital admissions at time u, $p_{\mathit{ICU}}(t)$ is the probability of being admitted to ICU once in the hospital, and $g_H(t - u)$ is the delay distribution from hospital to ICU admission—i.e., the probability for an individual who entered the hospital on day $u$ to have a delay of $d = t-u$ days before ICU admission. We compute $g_H(t-u)$ assuming that the delay from hospital to ICU admission is exponentially distributed with mean = 1.5 d (11). The probability of ICU admission in the time interval $T = [t_1, t_2]$ can be estimated as follows:

$$p_{\mathit{ICU}}\left(T\right)=\frac{{{\displaystyle \sum }}_{t\in T}{H}_{\mathit{ICU}}(t)}{{{\displaystyle \sum }}_{t\in T}{{\displaystyle \sum }}_{u\le t}H(u)g_H(t-u)}.$$ [3]

In practice, we estimate $p_{\mathit{ICU}}$ on a 10 d rolling window, which makes the estimates relatively stable.

The number of general ward ($B_H(t)$) and ICU ($B_{\mathit{ICU}}(t)$) beds occupied by COVID-19 patients at time t can be expressed as:

$$\begin{array}{c}{B}_H\left(t\right)=\left(1-p_{\mathit{ICU}}\left(t\right)\right){\displaystyle \sum }_{u}H\left(t-u\right)s_H\left(u\right)+p_{\mathit{ICU}}\left(t\right){\displaystyle \sum }_{u}H(t-u)s_{H-\mathit{ICU}}\left(u\right)\\ B_{\mathit{ICU}}\left(t\right)={\displaystyle \sum }_u{H}_{\mathit{ICU}}\left(t-u\right)s_{\mathit{ICU}}\left(u\right)\end{array},$$ [4]

where $s_H(u)$ is the probability of staying in the hospital for u days before discharge, $s_{H-\mathit{ICU}}(u)$ is the probability of spending u days in the hospital general ward and then moving to the ICU, and $s_{\mathit{ICU}}(u)$ is the probability of spending u days in the ICU. For $s_H$ and $s_{\mathit{ICU}}$ we use gamma survival functions with the mean to be estimated and the coefficient of variation (i.e., the SD over the mean) fixed at 0.9 for $s_H$ and 0.8 for $s_{\mathit{ICU}}$, while, analogous to $g_H$, we take $s_{H-\mathit{ICU}}(u)$ to be an exponential survival function with a mean of 1.5 d. We minimize the sum of squared errors over the last 5 data points to estimate the free parameters of $s_H$ and $s_{\mathit{ICU}}$. Once all the parameters are estimated and the forecast of $H$ is available, we use the equations above to forecast $H_{\mathit{ICU}}$, $B_H$, and $B_{\mathit{ICU}}$, assuming that all parameter estimates remain constant.

To account for uncertainty in parameter estimates, we use the bootstrapped smoothed trajectories of hospital admissions to generate 95% prediction intervals for the three other targets.

To assess the forecasts of ICU admissions and bed occupancy in the ICU and general wards, we report the MAPE because its interpretation in terms of relative error is straightforward, the 95% prediction interval coverage, and the RMSE.

Data Availability

Anonymized (aggregated COVID-19 hospitalization data for France) data and code have been deposited in Gitlab (https://gitlab.pasteur.fr/mmmi-pasteur/COVID19-Ensemble-model) (21).