Abstract
Abstract
The high spread rate of SARS-CoV-2 virus has put the researchers all over the world in a demanding situation. The need of the hour is to develop novel learning algorithms that can effectively learn a general pattern by training with fewer genome sequences of coronavirus. Learning from very few training samples is necessary and important during the beginning of a disease outbreak when sequencing data is limited. This is because a successful detection and isolation of patients can curb the spread of the virus. However, this poses a huge challenge for machine learning and deep learning algorithms as they require huge amounts of training data to learn the pattern and distinguish from other closely related viruses. In this paper, we propose a new paradigm – Neurochaos Learning (NL) for classification of coronavirus genome sequence that addresses this specific problem. NL is inspired from the empirical evidence of chaos and non-linearity at the level of neurons in biological neural networks. The average sensitivity, specificity and accuracy for NL are 0.998, 0.999 and 0.998 respectively for the multiclass classification problem (SARS-CoV-2, Coronaviridae, Metapneumovirus, Rhinovirus and Influenza) using leave one out crossvalidation. With just one training sample per class for 1000 independent random trials of training, we report an average macro F1-score for the classification of SARS-CoV-2 from SARS-CoV-1 genome sequences. We compare the performance of NL with K-nearest neighbours (KNN), logistic regression, random forest, SVM, and naïve Bayes classifiers. We foresee promising future applications in genome classification using NL with novel combinations of chaotic feature engineering and other machine learning algorithms.
Graphical abstract
Supplementary Information
The online version contains supplementary material available at 10.1007/s11517-022-02591-3.
Keywords: Neurochaos, Machine learning, SARS-CoV-2, Genome classification, Universal approximation theorem
Introduction
COVID-19 is an extremely contagious disease that was first reported in December 2019 at Wuhan city, Hubei province, China [1]. SARS-CoV-2 is the pathogen responsible for COVID-19 disease and initial genome sequence data confirmed that SARS-CoV-2 was a member of the Betacoronavirus genus and Sarbecovirus subgenus [2]. To date, seven coronaviruses have been identified which includes two Alphacoronavirus: Human coronavirus 229E (HCoV-229E), Human coronavirus NL63 (HCoV-NL63) and five Betacoronavirus: Human coronavirus OC43 (HCoV-OC43), Human coronavirus HKU1 (HCoV-HKU1), severe acute respiratory syndrome coronavirus (SARS-CoV-1), Middle East respiratory syndrome-related coronavirus (MERS-CoV) and severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). The SARS-CoV-2 virus has a very high spread rate [3] and affected all nations. On 11 March 2020, the World Health Organization (WHO) announced COVID-19 as a pandemic. Initial investigations have found that the genome sequence of SARS-CoV-2 shares 79% match with SARS-CoV-1 viral genome and 50% match with the MERS-CoV genome [4]. The epidemiological dynamics of SARS-CoV-2 is very different from SARS-CoV and MERS-CoV despite their close relatedness. This indicates that there is a striking biological difference between the highly infectious SARS-CoV-2 and other Betacoronavirus [1]. Some of the common symptoms found with people tested positive for SARS-CoV-2 are dry cough, shortness of breath and dyspnoea, myalgia, headache and diarrhoea [4]. An early identification of this deadly disease and isolation of patients from the rest of the population would have facilitated effective containment of disease spread. For this, we would need novel computational methods which can uniquely identify the signatures of SARS-CoV-2 virus from limited samples (available during the early stages of the outbreak). This turns out to be a classification problem, i.e. to classify whether a given nucleotide sequence belongs to SARS-CoV-2 or not. Such problems are ideal for machine learning (ML) and deep learning (DL) algorithms.
Recently, DL and ML are widely applied in genomic research [5]. This was enabled by the abundance of genome data after the success of the Human Genome Project and other projects like ENCODE [6], FANTOM [7] and Roadmap Epigenomics [8]. As a result, several ML/DL algorithms are applied in genomics research to obtain state-of-the-art performance. Recent research [9, 10] shows the effectiveness of convolutional neural networks (CNNs) to model the sequence specificity of protein binding. In [11], a three-layer CNN was used to predict the effects of non-coding variants from genome sequence. Similar to CNN, recurrent neural networks (RNNs) are another popular DL algorithm widely used in sequence modelling. The authors in [12] highlight the performance of hybrid architectures on a transcription factor binding site classification task. In [13], a deep learning architecture for the classification of SARS-CoV-2 viral genome sequence from other coronavirus has been proposed. Furthermore, the DL model is used for specific primer design. Authors in [14] use a DL model for the classification of SARS-COV-2 viral genome sequence from co-infecting RNA sequences (Coronaviridae, Metapneumovirus, Rhinovirus, Influenza). In [15, 16], classical machine learning techniques were used for the classification of SARS-CoV-2 genome sequence.
However in the case of COVID-19, especially during the early stages of the outbreak, ML/DL algorithms have only less data instances to learn and make decisions. The learning algorithms such as DL are ideally suited when the number of instances in the training data set is very high. In such a scenario, ML/DL algorithms would most likely fail to yield accurate classification of the virus sequence. It is in such situations, we demonstrate the usefulness of our proposed method, namely Neurochaos Learning (NL) for classification. As we shall demonstrate, NL yields high classification accuracies with very few samples of training. This could, in principle, be applied for future outbreaks of novel diseases.
Neurochaos Learning is motivated from the chaotic behaviour exhibited at the level of individual neurons in the brain [17, 18]. Neuronal cells exhibit a large range of firing patterns such as repetitive pulses (periodic), quasi-periodicity, and chaotic bursts of action potentials [17]. These firing patterns are driven by the external stimuli such as variations in the ionic environment driven by the effects of neuromodulators. This variability in the firing patterns indicates the presence of non-linearity and chaos at the level of neuron, axon etc. Such conclusions were inferred using classical intracellular electrophysiological recordings of action potentials in single neurons along with the help of macroscopic models [17]. A detailed study that supports the presence of chaos in the brain at various spatiotemporal scales and mathematical neuronal models exhibiting chaos is provided in [19] and [17]. Inspired by chaotic behaviours of neurons, we have recently proposed the ChaosNet architecture [20], where we used chaotic 1D generalized Lüroth series (GLS) neurons for extracting nonlinear features from the data for solving classification tasks. Furthermore, in [21], we augment the nonlinear features extracted from a single layer of GLS neurons with a support vector machine classifier (SVM) trained using a linear kernel (ChaosNet + SVM). The efficacy of ChaosNet + SVM in low training sample regime is highlighted in [21] for Iris dataset and synthetically generated data. In this work, we propose an overarching architecture titled ‘Neurochaos Learning’ (NL) that generalizes our previous research (ChaosNet+ [20], +ChaosNet++SVM [21]). We qualitatively contrast NL with ANN and further provide mathematical justification of the power of chaos that is employed in NL (at the level of individual neurons) in approximating a large class of discrete nonlinear functions (real-valued with finite support) — by proving a version of the universal approximation theorem. We also highlight the advantages of chaotic feature engineering which is implicit in NL architecture for the classification of coronavirus genome sequences in the high training sample as well as low training sample regimes.
The sections in this paper are arranged as follows: Section 2 explains the proposed NL architecture, Section 3 provides the information of dataset used in this research, and Section 4 highlights the experiments conducted on real world data. Section 5 deals with the limitations of the proposed method and Section 6 provides the scope for future work and the closing remarks.
Methodology
GLS neuron
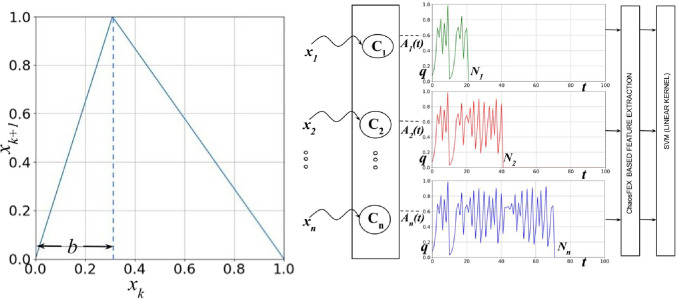
NL consists of an input layer of chaotic neurons. The chaotic neurons considered are the 1D skew tent map. The mathematical equation of skew tent map is provided in Eq. 1. A detailed study of the tent map and its various properties can be found in [22].
Tent map
is defined as:
| 1 |
where and b is the skew parameter (). Figure 1a depicts the first return map of 1D skew tent map. Skew tent map has the following properties:
Skew tent map has a positive Lyapunov exponent () suggesting its chaotic nature. A skew tent map with a skew parameter ‘b’ has a Lyapunov exponent [23].
Skew tent map has an invariant density function (the uniform distribution). This is exploited in chaotic cryptography [24].
Tent map has been widely applied in data compression, coding and cryptography [24, 25].
Fig. 1.
a First return map of the GLS neuron (skew tent map) used in this work [20]. b Neurochaos Learning (NL) architecture: ChaosFEX+SVM is an instance of NL architecture. ChaosFEX extracts features from the input layer of GLS neurons (). The stimulus or (normalized) input data to the architecture are represented as . The chaotic neuron, say , starts firing when it encounters the corresponding stimulus . The trajectory of k-th chaotic neuron is represented as . The trajectory continues until it reaches the neighbourhood of the stimulus. From the chaotic trajectory , we extract firing time, firing rate, energy of the chaotic trajectory, and entropy of the symbolic sequence of chaotic trajectory. These extracted features (ChaosFEX) are passed to SVM classifier with linear kernel
A neurochaos architecture for learning (NL)
Neurochaos Learning (or NL) architecture consists of a multi-layer neural network built of chaotic neurons. The proposed NL architecture is provided in Fig. 1b. The architecture consists of a single layer of GLS neurons (). All GLS neurons in the input layer have an initial neural activity of q units. The skewness of GLS maps is controlled by the discrimination threshold (b). By varying b, the chaotic neurons can exhibit weak and strong chaos (as determined by the value of the Lyapunov exponent). The stimulus or input data to the proposed architecture are represented as in Fig. 1b. The stimulus initiates the firing in chaotic neurons. The chaotic firing trajectory of the k-th GLS neuron, represented as , halts when the trajectory reaches the neighbourhood of the stimulus . The time taken () for to reach the neighbourhood of the stimulus () is defined as the Firing Time [26]. The chaotic firing is guaranteed to stop because of the topological transitivity [20, 27] property of chaos.
Thus, for a single stimulus say , the GLS neuron () outputs a chaotic trajectory. From this chaotic trajectory, we extract the following features, which we term as ‘ChaosFEX’:
Firing time: Time taken for the chaotic trajectory to recognize the stimulus [21].
Firing rate: Fraction of time the chaotic trajectory is above the discrimination threshold so as to recognize the stimulus [21].
Energy: For the chaotic trajectory x(t) with firing time n, energy is defined as .
- Entropy: For the chaotic trajectory x(t), we first compute the binary symbolic sequence S(t) as follows:
where to n (firing time). We then compute Shannon entropy of S(t) as follows bits, where and refer to the probabilities of the symbols 0 and 1 respectively.2
These extracted features are passed to SVM classifier with linear kernel. These extracted ChaosFEX features can be freely combined with any of the available classifiers or regression models from machine learning literature. Thus, the proposed Neurochaos Learning architecture allows for a great deal of flexibility to be combined with traditional ML algorithms. A comparison of the properties of NL with ANNs is provided in Table 1. The salient properties of NL are provided in Section S1 (Online Resource 1).
Table 1.
NL vs. ANN — a comparison of properties
| Properties | ANN | NL | Remarks |
|---|---|---|---|
| Neuron | Linear followed by a | Non-linear and chaotic | Chaos allows for a rich set |
| nonlinear activation | of properties to be exploited. | ||
| Output of a | Scalar | Variable length vector | Neurons in NL perform non-linear |
| neuron | computations as compared with simple | ||
| weighted linear addition in ANN. | |||
| Universal | Satisfies UAT | Satisfies UAT | NL satisfies UAT with an exact |
| approximation | specification on the number of neurons | ||
| theorem | needed for approximating a real-valued | ||
| (UAT) | discrete-time function with finite support. | ||
| Activation | Yes | No | The nonlinearity in ANN is provided by the |
| functions | activation function which is not needed for NL. | ||
| Backpropogation | Yes | No | Not currently used. NL could employ |
| backpropagation in the future if needed. |
Universal approximation theorem for NL
Let f(n) be a discrete time real valued function having a finite support L. The NL architecture consisting of a single layer with L chaotic neurons can approximate1f(n). Assuming that we use a chaotic 1D map for the i-th neuron in NL, and given any desired error , we have:
| 3 |
where q is the initial neural activity for all the neurons in NL, is the firing time of the i-th chaotic neuron and is the 1D chaotic map with the chaotic trajectory starting from q a dense orbit.
Proof
(by construction). Design an NL with one layer with exactly L chaotic neurons. Let each of the neurons be initialized with q and let the input to this NL be the L real-valued samples of the function f(n) which act as stimuli for the corresponding L chaotic neurons.
Now, for a given , we can always construct a neighbourhood of stimulus , such that for the k-th chaotic neuron of NL. This is always possible because of the topological transitivity property of chaos defined in Section 2 and since the chaotic trajectory starting from initial value q is dense. The topological transitivity property guarantees the chaotic firing to reach the neighbourhood () of stimulus in finite number of iterations () for the dense orbit starting from q. For any given , the following is true:
Note that since because is the firing time for and the orbit is dense. Hence, the set of chaotic neurons that constitute the input layer of NL can always approximate the function f(n) with an error bound. This theorem holds true for NL constructed with chaotic neurons that satisfies the topological transitivity property and has a dense orbit. Furthermore, having a single dense orbit implies countably infinite number of dense orbits.
Dataset details
This section provides a detailed description of real world datasets used to evaluate the efficacy of NL (ChaosFEXSVM). The real-world dataset consists of genome sequences of SARS-CoV-2 and other coronaviruses.
Multiclass classification
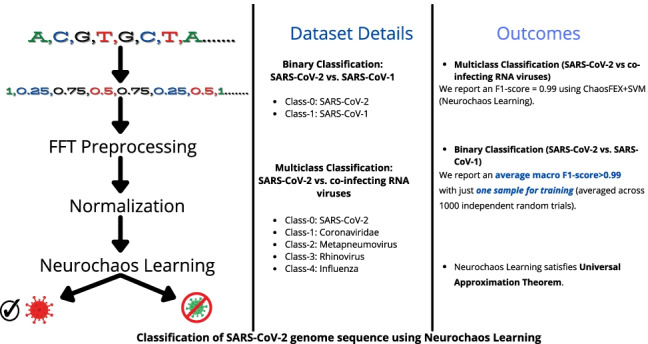
The classification of SARS-CoV-2 and other co-infecting RNA viruses is a challenging problem. We used the data provided by the authors of the paper titled ‘PACIFIC: a lightweight deep-learning classifier of SARS-CoV-2 and co-infecting RNA viruses’ [14]. The dataset consists of genome sequences corresponding to SARS-CoV-2 (class-0), Coronaviridae (class-1), Metapneumovirus (class-2), Rhinovirus (class-3) and Influenza (class-4). The dataset details are provided in Table 2. The authors [14] have made the data publicly available.2 A five class classification problem is formulated with this dataset. The data preprocessing is provided in Section S2 (Online Resource 1).
Table 2.
Multiclass classification: total number of data instances per class [14]
| Data | Genome | No. of genome assemblies |
|---|---|---|
| Class-0 | SARS-CoV-2 | 87 |
| Class-1 | Coronaviridae | 11 |
| Class-2 | Metapneumovirus | 5 |
| Class-3 | Rhinovirus | 130 |
| Class-4 | Influenza | 128 |
SARS-CoV-2 vs. SARS-CoV-1
For the binary classification of SARS-CoV-2 genomes from SARS-CoV-1 genomes, a total of 4498 and 101 genome sequences respectively were obtained from multiple data repositories until early April 2020. Three thousand nine hundred thirty SARS-CoV-2 sequences were obtained from GISAID, 407 from GenBank, and the remaining from Genome Warehouse, CNGBdb and NMDC databases through the China National Center for Bioinformation [28]. All SARS-CoV-1 sequences were obtained from GenBank. All sequences were chosen with the filters Nucleotide Completeness = ‘Complete’ AND host = ‘homo sapiens’. Accession IDs for all sequences as well as acknowledgement are provided in the GitHub repository.3 The data instance per class is provided in Table 3.
Table 3.
SARS-CoV-2 vs. SARS-CoV-1: total number of data instances per class
| Data | Genome | No. of sequences |
|---|---|---|
| Class-0 | SARS-CoV-2 | 4498 |
| Class-1 | SARS-CoV-1 | 101 |
Experiments and results
This section deals with the set of experiments evaluated on coronavirus genome sequences. We have used Python 3, LinearSVC [29], Numba [30], Numpy [31] and Scikit-learn [32] package for the implementation of ChaosFEX+SVM. We compare the performance of NL (ChaosFEX+SVM) with standalone SVM (RBF kernel), and standalone random forest. This learning paradigm with limited samples is referred as few shot learning. Few shot learning aims to develop ML models which generalizes from a small set of labeled training data. There has been previous research in few shot learning [33, 34].
Hyperparameter tuning
The hyperparameters used for ChaosFEX+SVM, standalone SVM (RBF kernel) and random forest for the multiclass classification and binary class classification are provided below:
ChaosFEX+SVM: For multiclass classification, the hyperparameters used are , , and . For binary classification, the hyperparameters used are , , and
SVM (RBF kernel): For multiclass classification, the hyperparameter used is . For binary classification, the hyperparameter used is
Random forest: For multiclass classification, the hyperparameters used are and . For binary classification, the hyperparameters used are and .
Performance metrics
From the multilabel and binary confusion matrix, the following metrics were derived for deeper understanding of the performance of the model. We follow the methodology for model evaluation as mentioned in [35].
Sensitivity (SE) =
Specificity (SP) =
Accuracy (ACC) =
Positive predictive value (PPV) =
Negative predictive value (NPV) =
False positive rate (FPR) =
False discovery rate (FDR) =
False negative rate (FNR) =
F1-score =
TP, TN, FP, FN refers to true positives, true negatives, false positives and false negatives respectively.
Multiclass classification
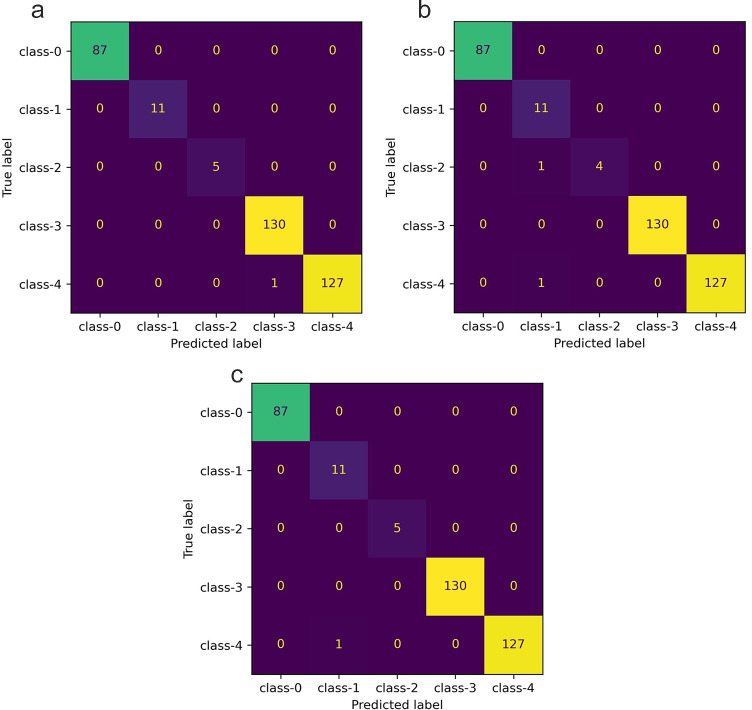
The dataset provided in Table 2 is highly imbalanced. So we carried out leave one out crossvalidation (LOOCV). From the multilabel confusion matrix, the following measures were used to evaluate the performance: SE, SP, ACC, PPV, NPV, FPR, FDR, FNR, and F1-score. The maximum and minimum sequence lengths we considered are 8000 and 6000 respectively. All sequences of length less than 6000 were not considered for the study (Table 2). Both ChaosFEX+SVM and standalone SVM (linear kernel) have only one misclassification for LOOCV. In the case of ChaosFEX+SVM, a single genome sequence belonging to Influenza was misclassified as Rhinovirus. Whereas in the case of standalone SVM (RBF kernel), a single genome sequence belonging to Influenza was misclassifed to Coronaviridae family. In the case of random forest, there are two misclassifications. This is depicted in the multilabel confusion matrix provided in Fig. 2a (ChaosFEX+SVM), c (standalone SVM (RBF kernel)), and b (random forest). The class-wise performance for ChaosFEX+SVM, random forest and standalone SVM are provided in Tables 4, 5 and 6 respectively. The average SE, SP and ACC for ChaosFEX+SVM are 0.998, 0.999, and 0.998 respectively. In the case of random forest, the average SE, SP and ACC are 0.958, 0.998 and 0.997 respectively. The average SE, SP and ACC using standalone SVM with RBF kernel are the same as ChaosFEX+SVM. The RBF kernel in standalone SVM maps the input data to a high dimensional space where the data is nearly linearly separable as indicated by the performance metrics. The similar performance of NL as compared to standalone SVM (RBF kernel) indicates the separability of input data in the nonlinear chaotic feature space. A perfect classification can be observed for SARS-CoV-2 (class-0), Coronaviridae (class-1) and Metapneumovirus (class-2) using NL (refer Table 4). In the case of standalone SVM (RBF kernel), a perfect classification can be seen for SARS-CoV-2 (class-0), Metapneumovirus (class-2) and Rhinovirus (class-3) (refer Table 6).
Fig. 2.
Multiclass classification — multilabel confusion matrix. a Confusion matrix corresponding to LOOCV using ChaosFEX+SVM (linear kernel). b Confusion matrix corresponding to LOOCV using standalone random forest (RF). c Confusion matrix corresponding to LOOCV using standalone SVM (RBF kernel)
Table 4.
Performance of ChaosFEX+SVM for the multiclass classification problem using LOOCV
| Classification | Class-0 | Class-1 | Class-2 | Class-3 | Class-4 |
|---|---|---|---|---|---|
| measures | |||||
| SE | 1.0 | 1.0 | 1.0 | 1.0 | 0.992 |
| SP | 1.0 | 1.0 | 1.0 | 0.996 | 1.0 |
| ACC | 1.0 | 1.0 | 1.0 | 0.997 | 0.997 |
| PPV | 1.0 | 1.0 | 1.0 | 0.992 | 1.0 |
| NPV | 1.0 | 1.0 | 1.0 | 1.0 | 0.996 |
| FPR | 0 | 0 | 0 | 0.004 | 0 |
| FDR | 0 | 0 | 0 | 0.008 | 0 |
| FNR | 0 | 0 | 0 | 0 | 0.008 |
| F1-score | 1.0 | 1.0 | 1.0 | 0.996 | 0.996 |
Table 5.
Performance of random forest for the multiclass classification problem using LOOCV
| Classification | Class-0 | Class-1 | Class-2 | Class-3 | Class-4 |
|---|---|---|---|---|---|
| measures | |||||
| SE | 1.0 | 1.0 | 0.8 | 1.0 | 0.992 |
| SP | 1.0 | 0.994 | 1.0 | 1.0 | 1.0 |
| ACC | 1.0 | 0.994 | 0.997 | 1.0 | 0.997 |
| PPV | 1.0 | 0.846 | 1.0 | 1.0 | 1.0 |
| NPV | 1.0 | 1.0 | 0.997 | 1.0 | 0.996 |
| FPR | 0 | 0.006 | 0 | 0 | 0 |
| FDR | 0 | 0.154 | 0 | 0 | 0 |
| FNR | 0 | 0 | 0.2 | 0 | 0.008 |
| F1-score | 1.0 | 0.917 | 0.889 | 1.0 | 0.996 |
Table 6.
Performance of SVM for the multiclass classification problem using LOOCV
| Classification | Class-0 | Class-1 | Class-2 | Class-3 | Class-4 |
|---|---|---|---|---|---|
| measures | |||||
| SE | 1.0 | 1.0 | 1.0 | 1.0 | 0.992 |
| SP | 1.0 | 0.997 | 1.0 | 1.0 | 1.0 |
| ACC | 1.0 | 0.997 | 1.0 | 1.0 | 0.997 |
| PPV | 1.0 | 0.917 | 1.0 | 1.0 | 1.0 |
| NPV | 1.0 | 1.0 | 1.0 | 1.0 | 0.996 |
| FPR | 0 | 0.003 | 0 | 0 | 0 |
| FDR | 0 | 0.083 | 0 | 0 | 0 |
| FNR | 0 | 0 | 0 | 0 | 0.008 |
| F1-score | 1.0 | 0.957 | 1.0 | 1.0 | 0.996 |
SARS-CoV-2 vs. SARS-CoV-1
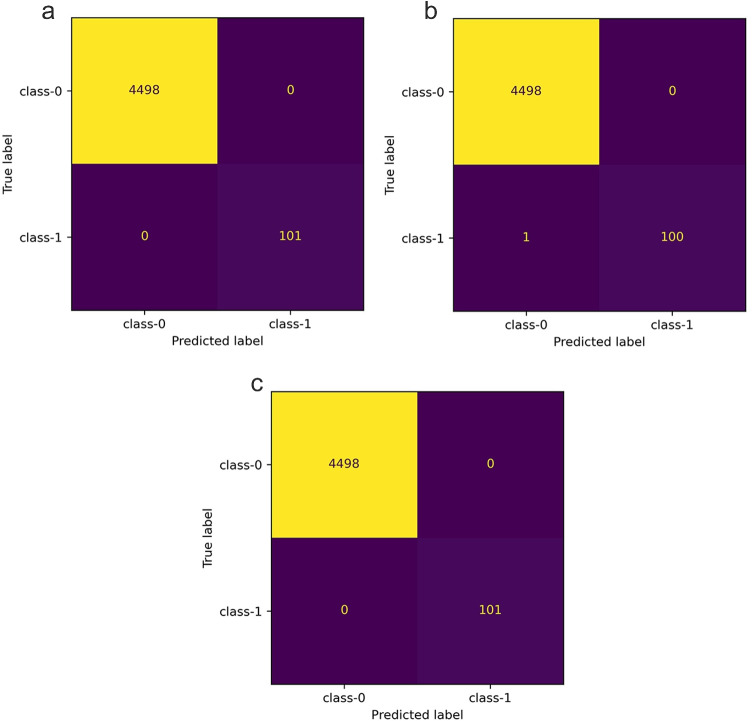
For the binary classification problem (Table 3), the number of genome sequences of SARS-CoV-2 is higher when compared to the genome sequence of SARS-CoV-1. The maximum and minimum sequence lengths we considered are 8000 and 6000 respectively. All sequences of length less than 6000 were not considered for the study. The class-wise performance of ChaosFEX+SVM, random forest and standalone SVM using LOOCV is provided in Table 7.
Table 7.
Performance of ChaosFEX+SVM for the binary class classification problem using LOOCV
| ChaosFEX+SVM | Random forest | SVM | ||||
|---|---|---|---|---|---|---|
| Classification | Class-0 | Class-1 | Class-0 | Class-1 | Class-0 | Class-1 |
| measures | ||||||
| SE | 1.0 | 1.0 | 1.0 | 0.990 | 1.0 | 1.0 |
| SP | 1.0 | 1.0 | 0.990 | 1.0 | 1.0 | 1.0 |
| ACC | 1.0 | 1.0 | 0.999 | 0.999 | 1.0 | 1.0 |
| PPV | 1.0 | 1.0 | 0.999 | 1.0 | 1.0 | 1.0 |
| NPV | 1.0 | 1.0 | 1.0 | 0.999 | 1.0 | 1.0 |
| FPR | 0 | 0 | 0.009 | 0 | 0 | 0 |
| FDR | 0 | 0 | 0.0002 | 0 | 0 | 0 |
| FNR | 0 | 0 | 0 | 0.009 | 0 | 0 |
| F1-score | 1.0 | 1.0 | 0.999 | 0.995 | 1.0 | 1.0 |
In the case of random forest, the first three significant values of the performance metric are used. This is done in order to avoid misinterpretation since several metric values close to 1.0 would be rounded to 1.0
The confusion matrices for ChaosFEX+SVM, standalone SVM (RBF kernel) and random forest are provided in Fig. 3a, b and c respectively. From these confusion matrices (Fig. 3a, c) and Table 7, the perfect classification obtained by both NL (ChaosFEX+SVM) and standalone SVM (RBF kernel) is evident. This shows the effectiveness of chaos-based nonlinear feature transformation in separating the data instances belonging to distinct classes.
Fig. 3.
Binary classification — confusion matrix. a Confusion matrix corresponding LOOCV using ChaosFEX+SVM (linear kernel). b Confusion matrix corresponding LOOCV using standalone random forest classifier. c Confusion matrix corresponding LOOCV using standalone SVM (RBF kernel)
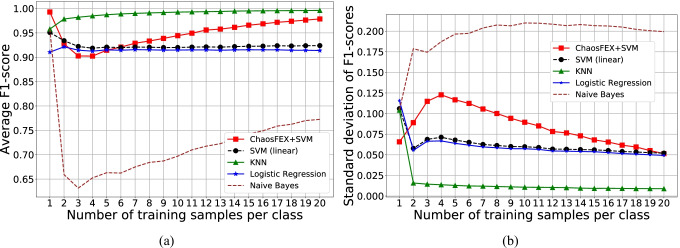
SARS-CoV-2 vs. SARS-CoV-1: low training sample regime
In the low training sample regime, we used samples per class and performed 1000 independent random trials of training in each case. The rest of the data was used for testing. We then computed the average macro F1-score of the test data. Figure 4a and b represents the average macro F1-score and the standard deviation of macro F1-scores of test data respectively.
Fig. 4.
SARS-CoV-2 vs. SARS-CoV-1 classification — low training sample regime ( samples per class). a Average macro F1-score of test data for 1000 random trials of training. b Standard deviation of macro F1-scores for 1000 random trials of training
In the case of low training sample regime for SARS-CoV-2 vs. SARS-CoV-1, NL yields a maximum average macro F1-score for training with one sample per class. As the number of training samples increases, the average F1-score shows a decreasingly increasing trend. The standard deviation of F1-scores as number of training samples increases shows an increasingly decreasing trend. NL slightly outperforms SVM with linear kernel and logistic regression in the low training sample regime except for training with 2, 3, 4 and 5 samples per class for SVM and 3, 4, 5 samples per class for logistic regression.
The low training sample regime highlights the requirement of only a single sample of SARS-CoV-2 and SARS-CoV-1 for classification using NL. From [36], SARS-CoV-2 and SARS-CoV-1 are genetically close to each other even though the SARS-CoV-2 is not a genetic descendent of SARS-CoV-1. However, our experiments seem to indicate that the difference between the ChaosFEX features of the genomic sequences of the 2 viruses is significant enough that from very few observed sequences (few shot learning) ChaosFEX is able to generalize for efficient classification of larger sets of sequences from the 2 viruses. Please note that hyperparameter tuning has not been performed for this dataset.
Limitations of NL
NL architecture works with the assumption of separability of data after a nonlinear chaotic feature transformation. In fact, it performs a nonlinear embedding in higher dimensions. However, this assumption may not be true in all scenarios. The present architecture of NL treats the input attributes as independent. But in real-world scenarios, this assumption may not be valid (especially in case of binary images). This limitation can be addressed by introducing coupled chaotic maps in the input layer of NL. Yet another limitation of NL is the absence of a principled way of hyperparameter tuning. The current implementation uses crossvalidation experiments to find the best q, b and .
Conclusions
Machine learning finds immense application in the classification of genome sequence. However, this problem becomes challenging when the number of training data instances are very less. Learning from very few training samples is a practical problem faced especially during the beginning of a disease outbreak. COVID-19 is the best example for this. A timely detection and isolation of patients in the early stage could have curbed the wide spread of the SARS-CoV-2 virus.
In this work, we proposed a Neurochaos Learning (NL) architecture, namely ChaosFEX+SVM for the classification of coronavirus. NL employs chaotic neurons (unlike traditional ANNs which has simple dumb neurons) and by combining chaos-based feature extraction with SVM-based classification, we demonstrate efficacy and robustness of such an approach. NL was shown to satisfy the universal approximation theorem (UAT). Our proof of UAT for NL is enabled by two properties of chaos — topological transitivity and existence of a dense orbit. An important benefit of our proof is the explicit construction of NL with the exact number of neurons needed to approximate a discrete time real valued function with finite support to any desired accuracy. Such an equivalent is not available for ANNs to the best of our knowledge. Thus, the benefit of using the rich features of chaos is evident in our work.
The proposed method finds application especially when the training data instances are less. In the experiments, we evaluated the performance of NL both in low and high training sample regime for classification of coronavirus genome sequence data. In the case of classification of SARS-CoV-2 vs. SARS-CoV-1, NL gave an average F1-score > 0.99 with just one training sample per class. This shows the robustness of the ChaosFEX features and its ability to generalize with very few training samples.
The ChaosFEX features that we have used in NL in this work can in fact be combined with any other machine learning algorithm (not limited to SVM). Combining ChaosFEX with deep learning and reinforcement learning algorithms are a future line of work.
Supplementary Information
Below is the link to the electronic supplementary material.
Biographies
NB Harikrishnan
is currently a Research Associate in Consciousness Studies program at National Institute of Advanced Studies, Indian Institute of Science Campus, Bengaluru. His research interest includes experimental and theoretical understanding of learning algorithms such as deep learning and machine learning. He also attempts to develop a theory for chaos based learning algorithms.
SY Pranay
received the M.B.B.S. degree from King Edward Memorial VII Hospital and Seth GS Medical College, Mumbai, India in 2015; the M.Phil. degree in Neurophysiology from the National Institute of Mental Health and Neurosciences, Bangalore, India in 2018. He is currently studying for a PhD at the Medical Research Council Cognition and Brain Sciences Unit, University of Cambridge, UK. His research interests include biomedical informatics, cognitive neurosciences and mental health.
Nithin Nagaraj
is currently Associate Professor at National institute of advanced studies. His areas of research interests are scientific theories of consciousness, causality and brain inspired artificial intelligence.
Funding
This study was financially supported by Tata Trusts.
Availability of data and material
Not applicable
Data availability
Accession IDs as well as acknowledgement of the genome sequence used in the classification of SARS-CoV-2 vs. SARS-CoV-1 are available in the GitHub repository: https://github.com/HarikrishnanNB/genome-classification-nl/tree/main/sequence_usage_acknowledgements.
Code availability
The codes used in this research are available in the following link: https://github.com/HarikrishnanNB/genome-classification-nl.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
For quantifying this approximation, we use the sum of absolute differences as the distance metric. In other words, for any two real-valued vectors , .
https://github.com/HarikrishnanNB/genome-classification-nl/tree/main/sequence_usage_acknowledgements
Harikrishnan N. B. thanks ‘The University of Trans-Disciplinary Health Sciences and Technology (TDU)’ for permitting this research as part of the PhD programme.
Contributor Information
N. B. Harikrishnan, Email: harikrishnannb@nias.res.in
S. Y. Pranay, Email: mail@pranaysy.com
Nithin Nagaraj, Email: nithin@nias.res.in.
References
- 1.Zhang Y-Z, Holmes EC. A genomic perspective on the origin and emergence of SARS-CoV-2. Cell. 2020;181(2):223–227. doi: 10.1016/j.cell.2020.03.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lu R, Zhao X, Li J, Niu P, Yang B, Wu H, Wang W, Song H, Huang B, Zhu N, et al. Genomic characterisation and epidemiology of 2019 novel coronavirus: implications for virus origins and receptor binding. The Lancet. 2020;395(10224):565–574. doi: 10.1016/S0140-6736(20)30251-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Salehi AW, Baglat P, Gupta G (2020) Review on machine and deep learning models for the detection and prediction of coronavirus. Mater Today Proc. 10.1016/j.matpr.2020.06.245 [DOI] [PMC free article] [PubMed]
- 4.Lai C-C, Shih T-P, Ko W-C, Tang H-J, Hsueh P-R (2020) Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) and coronavirus disease-2019 (COVID-19): the epidemic and the challenges. Int J Antimicrob Agents, pp 105924 [DOI] [PMC free article] [PubMed]
- 5.Ahmed I, Jeon G (2021) Enabling artificial intelligence for genome sequence analysis of COVID-19 and alike viruses. Interdiscip Sci Comput Life Sci, pp 1–16 [DOI] [PMC free article] [PubMed]
- 6.Dunham I, Birney E, Lajoie BR, Sanyal A, Dong X, Greven M, Lin X, Wang J, Whitfield TW, Zhuang J, et al. An integrated encyclopedia of DNA elements in the human genome. Nature. 2012;489(7414):57–74. doi: 10.1038/nature11247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kawai J, Shinagawa A, Shibata K, Yoshino M, Itoh M, Ishii Y, Arakawa T, Hara A, Fukunishi Y, Konno H, et al. Functional annotation of a full-length mouse cDNA collection. Nature. 2001;409(6821):685–689. doi: 10.1038/35055500. [DOI] [PubMed] [Google Scholar]
- 8.Kundaje A, Meuleman W, Ernst J, Bilenky M, Yen A, Heravi-Moussavi A, Kheradpour P, Zhang Z, Wang J, Ziller MJ, et al. Integrative analysis of 111 reference human epigenomes. Nature. 2015;518(7539):317–330. doi: 10.1038/nature14248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Alipanahi B, Delong A, Weirauch MT, Frey BJ. Predicting the sequence specificities of DNA-and RNA-binding proteins by deep learning. Nature Biotechnology. 2015;33(8):831–838. doi: 10.1038/nbt.3300. [DOI] [PubMed] [Google Scholar]
- 10.Zeng H, Edwards MD, Liu G, Gifford DK. Convolutional neural network architectures for predicting DNA-protein binding. Bioinformatics. 2016;32(12):i121–i127. doi: 10.1093/bioinformatics/btw255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zhang S, Zhou J, Hu H, Gong H, Chen L, Cheng C, Zeng J. A deep learning framework for modeling structural features of RNA-binding protein targets. Nucleic Acids Research. 2016;44(4):e32–e32. doi: 10.1093/nar/gkv1025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lanchantin J, Singh R, Wang B, Qi Y (2016) Deep gdashboard: Visualizing and understanding genomic sequences using deep neural networks. arXiv:1608.03644 [DOI] [PMC free article] [PubMed]
- 13.Lopez-Rincon A, Tonda A, Mendoza-Maldonado L, Mulders DGJC, Molenkamp R, Perez-Romero CA, Claassen E, Garssen J, Kraneveld AD. Classification and specific primer design for accurate detection of SARS-CoV-2 using deep learning. Scientific Reports. 2021;11(1):1–11. doi: 10.1038/s41598-020-80363-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Acera Mateos P, Balboa RF, Easteal S, Eyras E, Patel HR. Pacific: a lightweight deep-learning classifier of SARS-CoV-2 and co-infecting RNA viruses. Scientific reports. 2021;11(1):1–14. doi: 10.1038/s41598-021-82043-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Singh OP, Vallejo M, El-Badawy IM, Aysha A, Madhanagopal J, Faudzi AAM. Classification of SARS-CoV-2 and non-SARS-CoV-2 using machine learning algorithms. Computers in biology and medicine. 2021;136:104650. doi: 10.1016/j.compbiomed.2021.104650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Arslan H (2021) Machine learning methods for COVID-19 prediction using human genomic data. In: Multidisciplinary digital publishing institute proceedings, vol 74. pp 20
- 17.Korn H, Faure P. Is there chaos in the brain? II. Experimental evidence and related models. Comptes Rendus Biologies. 2003;326(9):787–840. doi: 10.1016/j.crvi.2003.09.011. [DOI] [PubMed] [Google Scholar]
- 18.Tsuda I. Chaotic itinerancy as a dynamical basis of hermeneutics in brain and mind. World Futures: Journal of General Evolution. 1991;32(2–3):167–184. doi: 10.1080/02604027.1991.9972257. [DOI] [Google Scholar]
- 19.Faure P, Korn H. Is there chaos in the brain? I. Concepts of nonlinear dynamics and methods of investigation. Comptes Rendus de l’Académie des Sciences-Series III-Sciences de la Vie. 2001;324(9):773–793. doi: 10.1016/s0764-4469(01)01377-4. [DOI] [PubMed] [Google Scholar]
- 20.Balakrishnan HN, Kathpalia A, Saha S, Nagaraj N. ChaosNet: a chaos based artificial neural network architecture for classification. Chaos: An Interdisciplinary Journal of Nonlinear Science. 2019;29(11):113125. doi: 10.1063/1.5120831. [DOI] [PubMed] [Google Scholar]
- 21.Harikrishnan NB, Nagaraj N (2020) Neurochaos inspired hybrid machine learning architecture for classification. In: 2020 international conference on signal processing and communications (SPCOM). IEEE, pp 1–5
- 22.Yoshida T, Mori H, Shigematsu H. Analytic study of chaos of the tent map: band structures, power spectra, and critical behaviors. Journal of Statistical Physics. 1983;31(2):279–308. doi: 10.1007/BF01011583. [DOI] [Google Scholar]
- 23.Lai D, Chen G, Hasler M. Distribution of the Lyapunov exponent of the chaotic skew tent map. International Journal of Bifurcation and Chaos. 1999;9(10):2059–2067. doi: 10.1142/S0218127499001498. [DOI] [Google Scholar]
- 24.Li C, Luo G, Qin K, Li C. An image encryption scheme based on chaotic tent map. Nonlinear Dynamics. 2017;87(1):127–133. doi: 10.1007/s11071-016-3030-8. [DOI] [Google Scholar]
- 25.Nagaraj N (2008) Novel applications of chaos theory to coding and cryptography. PhD thesis, NIAS
- 26.Harikrishnan NB, Nagaraj N (2019) A novel chaos theory inspired neuronal architecture. In: 2019 global conference for advancement in technology (GCAT). IEEE, pp 1–6
- 27.Devaney RL, Siegel PB, Mallinckrodt AJ, McKay S. A first course in chaotic dynamical systems: theory and experiment. Computers in Physics. 1993;7(4):416–417. doi: 10.1063/1.4823195. [DOI] [Google Scholar]
- 28.Zhao W-M, Song S-H, Chen M-L, Zou D, Ma L-N, Ma Y-K, Li R-J, Hao L-L, Li C-P, Tian D-M, et al. The 2019 novel coronavirus resource. Yi chuan= Hereditas. 2020;42(2):212–221. doi: 10.16288/j.yczz.20-030. [DOI] [PubMed] [Google Scholar]
- 29.Fan R-E, Chang K-W, Hsieh C-J, Wang X-R, Lin C-J. LIBLINEAR: a library for large linear classification. Journal of Machine Learning Research. 2008;9:1871–1874. [Google Scholar]
- 30.Lam SK, Pitrou A, Seibert S (2015) Numba: a LLVM-based Python JIT compiler. In: Proceedings of the second workshop on the LLVM compiler infrastructure in HPC, LLVM ’15, New York, NY, USA. Association for Computing Machinery
- 31.Harris CR, Millman KJ, van der Walt SJ, Gommers R, Virtanen P, Cournapeau D, Wieser E, Taylor J, Berg S, Smith NJ, Kern R, Picus M, Hoyer S, van Kerkwijk MH, Brett M, Haldane A, del R’io JF, Wiebe M, Peterson P, G’erard-Marchant P, Sheppard K, Reddy T, Weckesser W, Abbasi H, Gohlke C, Oliphant TE (2020) Array programming with NumPy. Nature 585(7825):357–362 [DOI] [PMC free article] [PubMed]
- 32.Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, Vanderplas J, Passos A, Cournapeau D, Brucher M, Perrot M, Duchesnay E. Scikit-learn: Machine learning in Python. Journal of Machine Learning Research. 2011;12:2825–2830. [Google Scholar]
- 33.Oreshkin B, López PR, Lacoste A (2018) Tadam: task dependent adaptive metric for improved few-shot learning. In: Advances in neural information processing systems. pp 721–731
- 34.Qiao S, Liu C, Shen W, Yuille AL (2018) Few-shot image recognition by predicting parameters from activations. In: Proceedings of the IEEE conference on computer vision and pattern recognition. pp 7229–7238
- 35.Chen H, Das S, Morgan J, Maharatna K. An effective PSR-based arrhythmia classifier using self-similarity analysis. Biomedical Signal Processing and Control. 2021;69:102851. doi: 10.1016/j.bspc.2021.102851. [DOI] [Google Scholar]
- 36.Coronaviridae Study Group of the International, et al. The species severe acute respiratory syndrome-related coronavirus: classifying 2019-nCoV and naming it SARS-CoV-2. Nature Microbiology. 2020;5(4):536. doi: 10.1038/s41564-020-0695-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Not applicable
Accession IDs as well as acknowledgement of the genome sequence used in the classification of SARS-CoV-2 vs. SARS-CoV-1 are available in the GitHub repository: https://github.com/HarikrishnanNB/genome-classification-nl/tree/main/sequence_usage_acknowledgements.
The codes used in this research are available in the following link: https://github.com/HarikrishnanNB/genome-classification-nl.