Machine learning recognition of protein secondary structures based on two-dimensional spectroscopic descriptors

Significance

We propose and demonstrate the use of two-dimensional UV (2DUV) spectroscopic features as observable-based descriptors for a machine learning protocol aimed at discriminating protein secondary structure motifs. The 2DUV spectra viewed as grayscale images were fed into convolutional neural networks (CNNs), resulting in accurate spectrum-structure correlation model. This enables an automated secondary structure recognition with accuracies of 97% (91%) for (non-)homologous protein segments. The success of protein 2DUV descriptors for machine learning is ascribed to their unique cross-peak information that reflects couplings between electronic transitions located at different chromophores. Incorporating coupling information is crucial for connecting the descriptors to the protein structure.

Abstract

Protein secondary structure discrimination is crucial for understanding their biological function. It is not generally possible to invert spectroscopic data to yield the structure. We present a machine learning protocol which uses two-dimensional UV (2DUV) spectra as pattern recognition descriptors, aiming at automated protein secondary structure determination from spectroscopic features. Accurate secondary structure recognition is obtained for homologous (97%) and nonhomologous (91%) protein segments, randomly selected from simulated model datasets. The advantage of 2DUV descriptors over one-dimensional linear absorption and circular dichroism spectra lies in the cross-peak information that reflects interactions between local regions of the protein. Thanks to their ultrafast (∼200 fs) nature, 2DUV measurements can be used in the future to probe conformational variations in the course of protein dynamics.

Protein structures hold the key to deciphering their versatile biological functions (1). Tremendous experimental progress has been made in protein structure determination (2–4). Artificial intelligence has shown enormous potential for determining protein structures. Very recently, DeepMind has successfully predicted protein three-dimensional structure from sequences of amino acids using a machine learning (ML) model (5, 6). These approaches provide limited information about how the conformations of a protein vary in the course of many important dynamic processes, including matter transport across membrane proteins, ligand binding, and protein folding. Since dynamical characteristics of proteins ultimately shape their function (7), it is essential to incorporate protein dynamics information into the ML training in order to identify the relevant conformations at ambient conditions.

Optical signals provide a window into a variety of response properties of matter. Combined spatial and temporal resolved techniques provide a versatile set of tools for characterizing protein structures and dynamics in ambient conditions (8, 9). The interpretation of protein spectra based on protein structure and quantum chemistry calculations is a formidable task, requiring the solution of dynamic structures from sizable spectra dataset. Developing ML protocols for connecting protein spectra and conformations is highly desirable. There is a growing effort in applying data-driven ML approaches toward automated connection of molecular spectra to structures (10–13). This has motivated us to pursue ML protocols for predicting infrared and UV-visible (UV-vis) absorption spectra of proteins from their structures (14–16). Structure inversion (i.e., direct retrieval of protein structures from spectra) is more challenging and not well developed. Only limited information about matter is projected onto the subspace spanned by the transition energies and intensities available. In conventional spectroscopy measurements, much of the rich information regarding the high-dimensional configuration space of matter is not accessible. Therefore, determining three-dimensional structure of molecules from one-dimensional (1D) spectroscopic features (e.g., peaks and line shapes) is essentially a dimension augmentation process. Conventionally, accumulative chemistry knowledge and theoretical simulations are required to reveal protein structures from spectra. It is hard to connect the complexity of protein structure and dynamics using 1D spectra signals as descriptors in ML. Descriptors containing multidimensional information about protein structures (both global and local) are required to accomplish this task.

Two-dimensional (2D) four-wave mixing spectroscopies, which measure the coupling between optical transitions in the system of interest, can provide much more detailed information about molecular structures and dynamics than their 1D counterparts (17). Because 2D spectroscopies probe time-resolved responses of both global and local structures of the system, they are widely used to accomplish this task (18–22). The 2D spectroscopies project the response information onto a 2D feature space and can reach higher resolution than 1D signals. The rich information carried by 2D spectra makes the automated interpretation of signals very challenging. Since ML is most suitable for processing high-dimensional, nonlinear datasets with clear underlying principles, developing an effective ML model that can allow secondary structure recognition from 2D spectra would be a key step toward protein structure inversion from spectra.

Results and Discussion

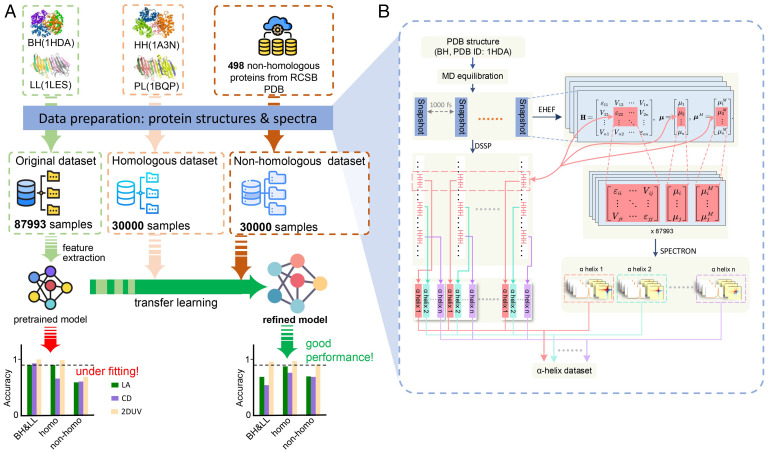
We used three datasets (Fig. 1A): 1) the original set (I), with segments with secondary structures of α-helix, β-sheet, and others (including 3₁₀-helix, π-helix, bend and coil) harvested from molecular dynamics (MD) trajectories of natural proteins bovine deoxyhemoglobin (BH; PDB ID: 1HDA) (23) and lentil lectin (LL; PDB ID: 1LES) (24); 2) the homologous set (II), with segments from human deoxyhemoglobin (PDB ID: 1A3N, homologous to BH) (25) and pea lectin (PDB ID: 1BQP, homologous to LL) (26); and 3) the nonhomologous set (III), with segments taken from 498 other proteins (PDB IDs listed in SI Appendix, Table S4). The linear absorption (LA), circular dichroism (CD), and 2DUV spectra of each segment were simulated by using an exciton model in the SPECTRON code (27). The three datasets contain 147,993 structure-spectra samples in total. Details of the dataset construction are described in Materials and Methods and SI Appendix.

Fig. 1.

Machine discrimination schemes to recognize peptide secondary structures. (A) Three sets of proteins, denoted as original (I), homologous (II), and nonhomologous (III), were used to prepare the peptide segment dataset. Using only dataset I, the pretrained model underfits the correlation between secondary structures and spectra; the performance is greatly improved by incorporating data from the other two datasets via transfer learning. The horizontal dashed lines in the bar plots denote accuracies of 90%. (B) Flowchart to generate the LA, CD, and 2DUV spectra of each peptide segment extracted from different proteins.

Because 1D and 2D spectra provide curves and grayscale images, respectively, of distributions of response intensities in the frequency domain, we applied convolutional neural networks (CNNs)—a well-established pattern recognition ML technique—to process these electronic spectra as sequences and images, respectively, based on which the structural correlations of these spectral patterns are examined (SI Appendix, Figs. S1 and S2). Using 2DUV spectra as input, the average secondary structure discrimination accuracy attained 95.1, 97.0, and 91.3% for protein segments extracted from the same protein (dataset I), from homologous protein (dataset II), and from nonhomologous protein (dataset III), respectively. 2DUV shows significant advantages for achieving our goals compared to 1D LA and CD spectra. This superior performance can be ascribed to the exciton coupling information contained in the cross-peaks of 2DUV spectra. This information is combined with excitation energies and intensities and convoluted into 1D line shapes in LA and CD. Gradient-weighted class activation mapping (grad-CAM) analysis confirms the importance of the cross-peak patterns in 2DUV for secondary structure discrimination (28).

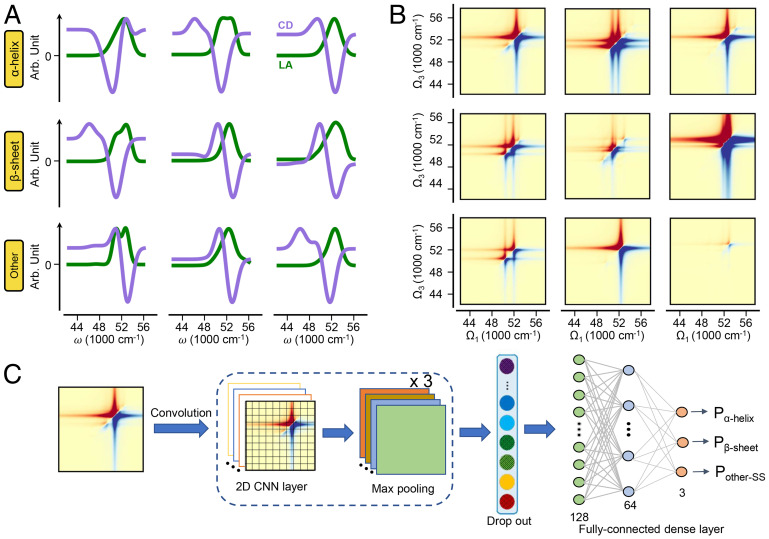
As shown in Fig. 2A, the 1D LA spectra (green lines) of peptide segments with different secondary structures are similar, with slight differences in peak widths and positions. This spectral similarity can be attributed to the congestion by signals from multiple chromophores, making the 1D spectra poorly resolved for structure discrimination. CD spectra are more informative than LA. Due to its sensitivity to exciton interaction patterns governed by the relative distances and orientations of chromophores, CD has long been used for protein secondary structure characterization (29). However, the CD signals are the differences between the absorption intensities of the opposite circular polarized incident waves, resulting in much broader and shifted peaks, as shown by the purple lines in Fig. 2A.

Fig. 2.

The 1D/2DUV spectroscopy and schematic view of the neural network for protein structure recognition. (A and B) The LA (A, green), CD (A, purple), and 2DUV (B) spectra of three randomly selected peptide segments with α-helical (first row), β-sheet (second row), and other (third row) secondary structures. (C) Schematic view of the architecture of the CNNs for secondary structure recognition from 2DUV spectra.

2DUV simultaneously represents electronic transitions (diagonal peaks) and their couplings (off-diagonal peaks) in a 2D space, giving much higher resolutions and directly illustrating the subtle distinctions in exciton couplings due to structural variations. As shown in Fig. 2B, the 2DUV spectra are much richer and, thus, more informative than the corresponding linear spectra (Fig. 2A). The simulation of 2DUV spectra requires statistical averaging of spectral patterns of individual structures, which erodes some fine features (21, 27). Moreover, 2DUV spectra of segments with the same secondary structure might possess variable spectral patterns, as shown in Fig. 2B. The three randomly selected samples from each of the secondary structure categories have different 2DUV patterns even for segments with the same secondary structure, which further complicates the analysis. It is not obvious how to extract representative spectral patterns for different secondary structures, which is required in order to establish the spectrum-structure correlation for secondary structure discrimination.

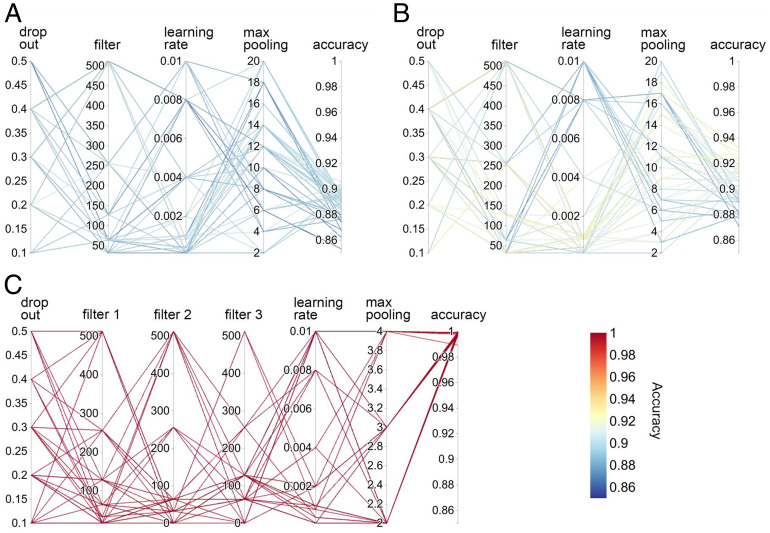
Our goal is to construct ML models that correlate the chemical and spectral information carried by the spectroscopic signals with protein secondary structures. In the first step, we constructed two 1D CNN models for LA and CD and a 2D CNN model for 2DUV to extract structure-spectra correlations. The models were first trained with the original dataset I, which was randomly split into the training, validation, and test sets with size ratios of 7:1:2. The hyperparameters—including the size of filters, learning rates, dropout ratios, and the kernel size of max pooling—were optimized using the grid search method (SI Appendix, Tables S1 and S2). Fig. 3 depicts the accuracies of secondary structure discrimination of models with various combinations of hyperparameters. For each type of model, hyperparameters such as the dropout ratio, the filter size, and the learning rate adopt a series of widely scattered values. A model was then trained and tested with each combination of hyperparameters (connected with lines), and its accuracy was reported as the color of the connecting lines. According to the color bar in Fig. 3, red lines reflect high accuracies near unity, while blue lines reflect accuracies lower than 90%. It is evident that models fed with 2DUV (Fig. 3C) perform much better than those fed with LA (Fig. 3A) and CD (Fig. 3B): the 1D model trained with LA spectra (Fig. 3A) achieved overall accuracies of 86∼91% in secondary structure discrimination, while the model trained with CD spectra (Fig. 3B) performs slightly better, reaching 87∼93% accuracies. In contrast, the 2D CNN models trained with 2DUV spectra show robust high performance of near 100% accuracy, independent of the choice of hyperparameters, as shown in Fig. 3C. The significantly higher performance of the 2D CNN models compared to the 1D models indicates that in addition to the electronic transition energies, intensities, and chiral characteristics included in the 1D spectra, the couplings between them—which are revealed only by the 2DUV spectra—are crucial for secondary structure discrimination.

Fig. 3.

Parallel coordinate plots of the hyperparameter optimization. (A and B) The 1D (LA and CD) CNNs. (C) The 2D (2DUV) CNN.

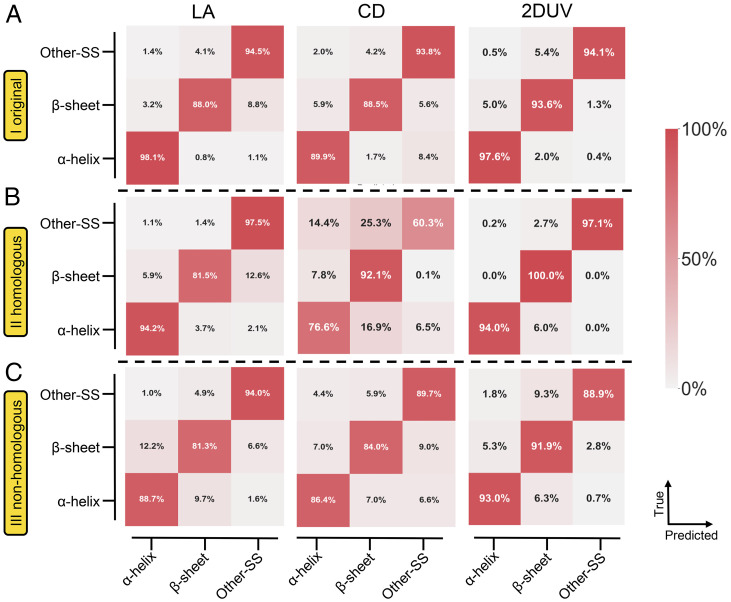
An important measure of the algorithm performance is its transferability (i.e., how the model performs on datasets other than the training set). We therefore examined the pretrained models discussed above on two new datasets: the homologous (II) and nonhomologous (III) sets. The models’ performance on the three datasets are shown by the confusion matrices in SI Appendix, Fig. S3. The vertical and horizontal axes denote the true and model-predicted labels, respectively. Although the pretrained models perform well on the original set (SI Appendix, Fig. S3A), the discrimination accuracies significantly decrease for datasets II and III (SI Appendix, Fig. S3 B and C). Specifically, the average accuracy of the LA (CD) model decreases from 98.2 (98.9) to 78.2% (66.8%), while the accuracy of the 2DUV model decreases from 100 to 98.4%. The average accuracies of the pretrained LA, CD, and 2DUV models further drop to 72.6, 73.1, and 66.4%, respectively. The lower discrimination for datasets containing new structures is expected, since the pretrained model used only spectrum-structure correlations of segments extracted from the BH and LL proteins. Spectral patterns arising from new chromophore environments in different proteins are hard to recognize.

To extend the knowledge learned from dataset I, we employed the transfer learning technique to finetune the pretrained models. In this protocol, the convolution modules (i.e., the convolution and max pooling layers) were held fixed, while the following fully connected dense layers were allowed to change (Fig. 2C). For all the 1D and 2D models, 500, 500, and 2,000 samples from datasets I, II, and III, respectively, were randomly selected. All models perform better than the pretrained ones when applied on datasets II and III. As shown in Fig. 4C, the 2D model experiences the most significant improvement, with an average accuracy of 91.3% (compared with 66.4% of the pretrained model). The performances of the LA and CD models were also improved by the transfer learning; specifically, the average accuracy of the LA model was improved from 72.6 to 88.0%, and that of the CD model was improved from 73.1 to 86.7%.

Fig. 4.

Confusion matrices of the CNN models after transfer learning to recognize secondary structures of protein segments. The vertical and horizontal axes denote the true and model-predicted categories, respectively. Each matrix element represents the ratio of samples with corresponding categorical labels. Near-unity diagonal values reflect high recognition accuracies. (A) The original set I. (B) The homologous set II. (C) The nonhomologous set III.

Even though the discrimination accuracies of the LA and CD models significantly improve with transfer learning, these models still underperform compared to the 2DUV model with 3∼5% average accuracy. The transferability to homologous dataset II is similar, as shown in Fig. 4B: the 2D model attained an average accuracy of 97.0%, which is much better than that of the models using LA (91.1%) or CD (76.3%) spectra. To summarize, either in the pretrained case or after transfer learning, the 2D model significantly outperforms its 1D counterparts.

The superiority in discriminating peptide secondary structures of the 2D compared with 1D models can be attributed to the intrinsic dimensionality advantage of the 2D spectra, where not only the excitons themselves, but also the couplings between these excitons, are given by the cross-peaks. As illustrated in the simple transition dipole coupling model, the coupling strength is sensitive to the distance and the relative orientation of the chromophores (i.e., the peptide bonds) (30). This structural dependence of the electronic coupling is then represented as cross-peak intensities in the 2DUV spectra (27). On the other hand, 2DUV also carries information buried in the LA spectra, which can be demonstrated by plotting the diagonal slice into 1D curves. The low performance of LA and CD spectra in discriminating secondary structures indicates that the exciton energy-intensity pairs in a 1D space are insufficient to construct reliable structure-spectrum correlation, which results in ambiguities in spectrum-based structure discrimination. The exciton coupling information in the 2D signals is crucial for this task.

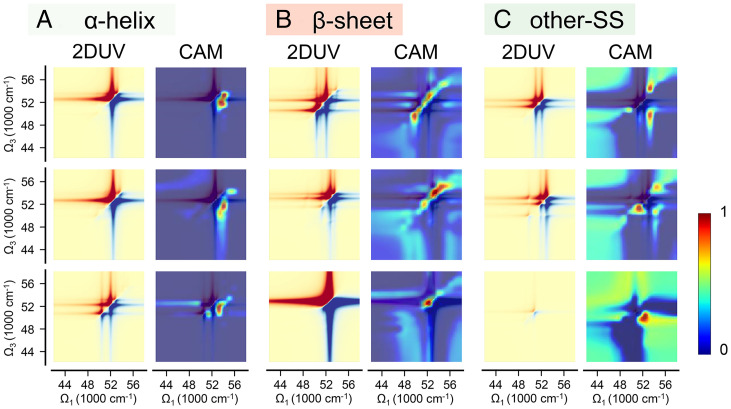
To understand why the 2DUV information is crucial for secondary structure discrimination, we have generated the grad-CAMs for typical segments (28). A grad-CAM is reconstructed from the gradients of the class target score with respect to the feature maps of the last convolution layer, which is a measure of the relative importance of the neuros in classification. The grad-CAM is a heatmap that demonstrates the region(s) of a 2DUV spectrum crucial for structure discrimination. It can also be viewed as a visual explanation of what the CNN model learned about the object. Fig. 5 depicts the 2DUV spectra and corresponding grad-CAMs of three randomly selected segments with each secondary structure category. It is evident that for all the samples shown in Fig. 5, the most important spectral features for secondary structure discrimination lie in the off-diagonal region (i.e., the cross-peaks caused by exciton coupling), which is absent in 1D LA and CD spectra. Compared to other secondary structures (Fig. 5C), for α-helices (Fig. 5A), the important spectral features lie below the diagonal line in the far UV range (52,000∼54,000 cm⁻¹) and correspond to the strong coupling between peptide excitations along the helix (21). As shown in Fig. 5B, two aspects are primarily responsible for the discrimination as β-sheets: the signals near the diagonal line in the far UV range and the clean diagonal blocks below 52,000 cm⁻¹ and above 55,000 cm⁻¹. These two 2DUV features suggest that single peptide excitations are more characteristic for β-sheets, and fewer excitons were strongly shifted by exciton coupling of their intrinsic resonance. Both arguments imply that strong coupling between peptide excitations is less common in β-sheets than in α-helices.

Fig. 5.

(Left) 2DUV spectra and corresponding grad-CAM of three randomly selected segments: (A) α-helical, (B) β-sheet, and (C) other secondary structures.

In summary, we have developed 1D and 2D CNN models using three datasets (the original set I, the homologous set II, and the nonhomologous set III) containing the LA, CD, and 2DUV spectra of nearly 148,000 protein segments to discriminate the secondary structures of peptide segments from 1D LA/CD or 2DUV spectra. With the aid of transfer learning, the 2D CNN models attained average discrimination accuracies of 95.1, 97.0, and 91.3% for the three sources of protein segments with decreasing homology to the original BH and LL protein. Compared to the 2D models trained on structure-2DUV correlations, the 1D models using LA or CD did not attain sufficient accuracy for secondary structure discrimination. The grad-CAM heatmaps revealed the important spectral regions that are crucial for secondary structure discrimination. The superiority of the 2D models stems from the exciton coupling information explicitly contained in the 2DUV spectra cross-peaks, which may not be retrieved from 1D spectra. Taking advantage of 2DUV spectroscopic features as descriptors, a ML protocol was able to automatically discriminate protein secondary structure motifs, paving the way for optical-spectroscopic monitoring, real-time structure-determination of proteins, and protein structure inversion from spectra.

Materials and Methods

Protein Segment Datasets.

To construct the original dataset I, the BH (PDB ID: 1HDA) (23) and LL (PDB ID: 1LES) (24)—consisting primarily of α-helices and β-sheets, respectively—were selected. The experimentally resolved three-dimensional structures in the Research Collaboratory for Structural Bioinformatics (RCSB) protein data bank (31) were adopted as the initial structures, followed by MD equilibrations (details in SI Appendix). Structure snapshots were harvested every 1,000 fs along the MD trajectories to avoid structural coherence. Each snapshot was scanned with the Define Secondary Structure of Protein (DSSP) (32) algorithm to extract peptide segments with pure secondary structure motifs (i.e., 28,556 α-helices, 32,439 β-sheets, and 26,998 others [87,993 in total]). The homologous set (II) and the nonhomologous set (III) were constructed with a similar procedure, with both sets consisting of 30,000 peptide segments (10,000 for each of α-helix, β-sheet, and others).

Multiscale Simulation of Peptide Electronic Spectra.

For each of the extracted peptide segments, the LA, the CD in the UV-vis region, and the 2DUV spectra were calculated using multiscale simulation schemes. As shown in Fig. 1B, each snapshot was treated by the exciton Hamiltonian with electrostatic fluctuations (EHEF) method (21) to construct the Frenkel exciton Hamiltonian and the transition electric/magnetic dipole moments. The solvation effects and intraprotein perturbations to the electronic transitions of peptide chromophores were properly incorporated by the EHEF scheme. In the meantime, using the sequencing information from the DSSP scan, the corresponding blocks of exciton Hamiltonian and transition dipoles for each peptide segment were extracted. This electronic structure and response information was then fed to the SPECTRON code (27) to simulate the LA, CD, and 2DUV spectra for each segment.

The signals were collected in the 42,000∼58,000 cm⁻¹ (238∼172 nm) frequency regime, where the peptide bond $\pi \to {\pi }^{*}$ and $n\to {\pi }^{*}$ transitions dominate the UV spectra, along with weaker contributions from the $B_b$, $B_a$, and $L_a$ transitions of the aromatic side chains (33–35). Here, we have applied a very small broadening factor of 250 cm⁻¹ in generating the spectra with Lorentzian line shapes, so as to avoid the long tails of Lorentzian line shapes and the strong overlaps between different photo-response signals (which might cause ambiguity in data analysis). Future work will be done with Gaussian line shapes to test the convergency of our results. The LA and CD spectra were recorded with a frequency resolution of 10 cm⁻¹, resulting in a $1600\times 1$ representation of the spectra. The 2DUV spectra were simulated by a k_I four-wave mixing procedure, with all pulses having parallel polarizations (27). The signals were collected with resolutions of 1,000 cm⁻¹ in both the ${\text{Ω}}_1$ and ${\text{Ω}}_3$ dimensions (see SI Appendix, section S1 for details), resulting in a $161\times 161$ representation for each 2DUV spectrum. In the end, for each segment in datasets I, II, and III, an LA spectrum, a CD spectrum, and a 2DUV spectrum were generated. The peptide segments, together with the electronic spectra, comprise the dataset (∼148,000 samples) used in this work.

CNN Models and Spectra Descriptors.

The discrimination of the peptide secondary structures from their LA, CD, or 2DUV spectra is expressed as a supervised classification problem: the model takes the spectral data as input and discriminates the secondary structure of the corresponding segment. We concentrate on the two most common secondary structures, α-helix and β-sheet, as two categories and categorize all the other secondary structures as “other.” Thus, the model maps the spectral data to one of the three categories.

We have used 1D CNNs to correlate the LA and CD spectra with secondary structures (SI Appendix, Fig. S1). The models consist of an input layer that directly adopts the linear spectra with dimensions of $1600\times 1$; the input layer is followed by two convolution modules, each containing a convolution layer with the rectified linear unit activation (36) and a max pooling layer. A dropout layer is used to regularize the output of the convolution module and pass it to two fully connected dense layers. The classification targets were output by a final softmax layer. Backpropagation and the Adam optimizer (37) were employed to train the model.

Similar to the linear spectra, a 2D CNN was used to discriminate secondary structures form the 2DUV spectra. The difference lies in the convolution module, where three convolution modules were used, each containing a convolution layer and a max pooling layer. The 2DUV signals $S({\text{Ω}}_1,{\text{Ω}}_3)$ were normalized as

$$\overline{S}({\mathrm{\Omega }}_1,{\mathrm{\Omega }}_3)=\frac{S({\mathrm{\Omega }}_1,{\mathrm{\Omega }}_3)-\mu }{\sigma },$$ [1]

where $\mu$ and $\sigma$ are the average and SD of the signals of the whole training set, respectively. The normalized signals were then clipped to the $\left[-2, 2\right]$ interval, which contains more than 97% of the spectral patterns. The renormalization and clipping of the original data accelerate the ML analysis by a factor of 2 without affecting qualitative conclusions. This renormalization simply rescales the absolute intensities using a single set of factors ($\mu$ and $\sigma$) and does not change the relative intensities between samples; tests on the original spectra generate the same results. Benchmarks conducted with spectral images at lower resolutions (of $81\times 81$ and $41\times 41$) have produced, qualitatively, the same results.

Transfer Learning to Improve Transferability.

We have simulated some practical scenarios of secondary structure discrimination from spectra, where knowledge of only a few “typical” systems were available. These can be extended to achieve broader scopes. Here, we used the original dataset (I) to construct spectra-secondary structure correlations (the pretrained model) and generalized this knowledge by the transfer learning technique to other proteins (i.e., the homologous [II] and the nonhomologous [III] datasets). To refine the pretrained model, we kept the convolution modules fixed, tuning the following layers with new datasets consisting of randomly selected samples from datasets I, II, and III.

Data Availability

All protein PDB IDs used in this work are listed in SI Appendix; previously published models and data are available in DCAIKU (http://dcaiku.com:13000/).