Spontaneous magnetization of collisionless plasma

Significance

Astronomical observations indicate that dynamically important magnetic fields are ubiquitous in the Universe, while their origin remains a profound mystery. This work provides a paradigm for understanding the origin of cosmic magnetism by taking into account the effects of the microphysics of collisionless plasmas on macroscopic astrophysical processes. We demonstrate that the first magnetic fields can be spontaneously generated in the Universe by generic motions of astrophysical turbulence through kinetic plasma physics, and cosmic plasmas are thereby ubiquitously magnetized. Our theoretical and numerical results set the stage for determining how these “seed” magnetic fields are further amplified by the turbulent dynamo (another central and long-standing question) and thus advance a fully self-consistent explanation of cosmic magnetogenesis.

Abstract

We study within a fully kinetic framework the generation of “seed” magnetic fields through the Weibel instability, driven in an initially unmagnetized plasma by a large-scale shear force. We develop an analytical model that describes the development of thermal pressure anisotropy via phase mixing, the ensuing exponential growth of magnetic fields in the linear Weibel stage, and the saturation of the Weibel instability when the seed magnetic fields become strong enough to instigate gyromotion of particles and thereby inhibit their free-streaming. The predicted scaling dependencies of the saturated fields on key parameters (e.g., ratio of system scale to electron skin depth and forcing amplitude) are confirmed by two-dimensional and three-dimensional particle-in-cell simulations of an electron–positron plasma. This work demonstrates the spontaneous magnetization of a collisionless plasma through large-scale motions as simple as a shear flow and therefore has important implications for magnetogenesis in dilute astrophysical systems.

The origin and evolution of cosmic magnetism remains one of the most profound mysteries in astrophysics and cosmology (1, 2). Observations of Faraday rotation, Zeeman splitting, and synchrotron emission suggest pervasive ∼µ G magnetic fields in our Galaxy and in the intracluster medium (ICM) of galaxy clusters (3–5). It is widely believed (6–8) that such dynamically important magnetic fields first arose as weak “seed” fields generated by cosmic batteries, subsequently amplified to currently observed levels by the turbulent dynamo—a fundamental plasma process that converts the mechanical energy of plasma motions into magnetic energy through electromagnetic induction. However, neither the origin problem—what are the physical mechanisms underpinning these batteries—nor the dynamo problem—how magnetic fields are amplified and sustained by turbulent plasma motions—are well understood.

There are two broad perspectives on the origin of cosmic seed magnetic fields: a primordial origin and a galactic origin. In the former, seed fields are generated before recombination or the era of structure formation. The earliest seed fields can be generated by exotic early-Universe mechanisms during inflation and cosmological phase transitions (e.g., refs. 9–11). At later times during the radiation-dominated era, seed fields can be produced through plasma fluctuations (12) or nonzero vorticity (13, 14) [the well-known Biermann battery (15)]. These mechanisms potentially explain the pervasiveness of magnetic fields, but with predicted amplitudes that are typically weak ($\sim {10}^{-20} \text{G}$) (16–19). Scenarios based on a galactic origin postulate that seed fields are generated through gravitational collapse or collision-related events occurring during structure formation and stellar evolution in the early Universe (at redshift $z\sim 10$). In this scenario, seed fields are generated by various fluid or plasma-kinetic instabilities, such as the magneto-rotational (Balbus–Hawley) instability (20) in accretion disks, the Rayleigh–Taylor instability (21) in stars and supernova remnants, the Kelvin–Helmholtz instability (22–25) at the shear surface of astrophysical jets, and the Weibel instability (26, 27) in collisionless shocks. The Biermann battery, aside from operating due to cosmological-scale vorticity, can also create seed fields in rotating stars (15, 28). Such seed fields, generated locally within stars or galaxies, are typically much stronger than the primordial seed fields and can potentially be transported into and diluted throughout the intergalactic medium (IGM) or early ICM by powerful galactic winds or jets (29–31). However, to what extent these mechanisms can contribute to the global magnetization of the ICM and IGM is still unclear (10, 11, 32).

Among the above-mentioned instabilities, the Weibel instability is particularly versatile. In an unmagnetized, collisionless plasma, its only requirement is directional anisotropy in the thermal motions of the charged particles—an essential feature of dilute astrophysical plasmas such as the IGM and ICM—and can produce seed fields with near-equipartition strength, albeit on microscopic plasma-inertial length scales (26, 27, 33). As a plausible key ingredient of magnetogenesis (34, 35), the Weibel instability has been studied extensively in contexts typically with a counter-streaming configuration, such as collisionless shocks occurring in both the relativistic (36–38) and subrelativistic (39, 40) regimes, in the large interpenetrating structures of intergalactic plasmas (34, 35), and in laser-plasma experiments (41, 42). Despite the fact that the Weibel instability can be easily triggered through thermal anisotropy alone, its role in a global context (beyond local shocks), such as low-Mach-number turbulence in galaxy clusters and in the IGM, has not been considered. Such contexts, however, are important to the magnetogenesis problem because of their relevance to turbulent dynamo processes (43).

Once formed, seed magnetic fields are thought to be amplified and sustained by the turbulent plasma dynamo after reionization, when the baryonic material in the universe becomes electrically conducting. Previous dynamo studies—whether conducted within the framework of magnetohydrodynamics (43–45) or, more recently, using a kinetic description (46–48)—assumed the existence of a seed field as an initial condition and thus did not address its origin. The possibility that, in a collisionless plasma (e.g., the IGM/ICM), the turbulent motions of dynamo may themselves give rise to seed fields, and thus magnetize the plasma noninductively, has not been adequately explored. This idea presents intriguing questions that have not yet been answered; namely, how, exactly, are seed fields generated by generic large-scale motions? What are the strength and morphology of these self-consistently produced seed fields? Can they seed the plasma dynamo, thereby yielding a fully ab initio solution to the problem of magnetogenesis?

In this work, we aim to understand how an initially unmagnetized plasma may magnetize itself through kinetic instabilities arising self-consistently under the action of large-scale flows, which are ubiquitous and driven by a variety of large-scale processes in astrophysical environments. In unmagnetized, collisionless environments, the plasma flows are not of a purely fluid nature; instead, they are subject to phase mixing and Landau damping. As we will show, these cause the plasma-distribution function to become anisotropic in velocity space, thereby providing free energy for microscopic instabilities, such as Weibel, to grow rapidly on top of the slowly varying macroscopic flows. The Weibel instability produces fluctuations that extract free energy from the thermal anisotropy and generate kinetic-scale seed magnetic fields. As the Weibel magnetic field grows, the plasma becomes magnetized, leading to the saturation of the instability and modifying the macroscopic transport properties of the turbulence.

At plasma-kinetic scales, any macroscopic flow may be viewed locally as a shear flow and/or a compressional flow. In this paper, we focus on how an externally driven shear flow can spontaneously magnetize the plasma. We adopt a fully kinetic framework, in which the kinetic physics of both particle species is treated self-consistently. The sequence of events through which the plasma becomes magnetized involves multiple stages, each of which we consider in detail. In the following sections, we present an analytical model describing this phenomenon, which we then show is supported by first-principles numerical simulations. Fundamentally, our calculations show that a large-scale shear flow provides an efficient mechanism for the self-magnetization of astrophysical plasmas.

Theory

Formulation of the Problem and Dimensionless Parameters.

Consider a three-dimensional (3D) system initialized with a uniform static Maxwellian plasma and negligible electromagnetic fields. The plasma has both negative and positive charges; a subscript s is added to quantities to represent these two species ($s\in \{e,i\}$ for an electron–ion plasma and $s\in \{e,p\}$ for an electron–positron plasma). Each species is represented by its distribution function in phase space $f_s(t,\mathit{x},\mathit{v})$, mass m_s, and temperature T_s. We limit our discussion to the subrelativistic regime, in which the thermal and flow velocities of both species are much smaller than the speed of light c. In this limit, the bulk flow velocity ${\mathit{U}}_s(t,\mathit{x})\equiv ({\displaystyle \int {\text{d}}^3}\mathit{v}\hspace{0.17em}\mathit{v}{f}_s)/n_s(t,\mathit{x})$, where $n_s(t,\mathit{x})\equiv {\displaystyle \int {\text{d}}^3}\mathit{v}\hspace{0.17em}{f}_s$ is the density, and the thermal pressure tensor, ${\mathrm{P}}_s(t,\mathit{x})\equiv {\displaystyle \int {\text{d}}^3}\mathit{v}\hspace{0.17em}{m}_s(\mathit{v}-{\mathit{U}}_s)(\mathit{v}-{\mathit{U}}_s)f_s$, are two basic quantities characterizing the bulk and thermal motions of the plasma, respectively.

In this initially unmagnetized Maxwellian system, we consider a shear flow driven continuously by a time-independent external body force ${\mathit{F}}_{\text{ext},s}(x)=m_s\mathit{a}(\mathit{x})$.* The force is in the $\widehat{\text{y}}$ direction with a sinusoidal spatial variation in the $\widehat{\text{x}}$ direction, giving rise to a species-independent acceleration $\mathit{a}(x)=a_0\sin (2\pi x/L)\widehat{\mathit{y}}$, where a₀ is the constant amplitude of the acceleration, and L is the system scale.

We define three time-dependent dimensionless parameters to represent the evolution of the system’s energetics. The first is the Mach number $M_s\equiv \sqrt{\langle U_s^2\rangle }/v_{\text{th}s}$, where $U_s=\left|{\mathit{U}}_s\right|$, $v_{\text{th}s}\equiv \sqrt{T_s(t=0)/m_s}$ is the initial thermal speed, and $\langle \dots \rangle$ denotes a volume average. The Mach number squared $M_s^2\approx \langle P_{\text{bulk},s}\rangle /\langle P_s\rangle$, where $P_{\text{bulk},s}\equiv m_s{n}_s{U}_s^2$ is twice the bulk kinetic energy density (ram pressure) and $P_s\equiv n_s{T}_s\approx m_s{n}_s{v}_{\text{th}s}^2$ is the thermal pressure of plasma, the latter approximation being accurate if the temperature T_s does not change significantly over time.

The second dimensionless quantity is the thermal pressure anisotropy, ${\mathrm{\Delta }}_s\equiv \sqrt{\langle {(P_{\text{max},s}/P_{\perp ,s})}^2\rangle }-1$, where $P_{\text{max},s}$ is the maximum eigenvalue of the local thermal pressure tensor ${\mathrm{P}}_s$, and $P_{\perp ,s}$ is the average of the other two eigenvalues associated with the two directions perpendicular to that of $P_{\text{max},s}$. Under the assumption of small pressure anisotropy ($P_s\approx P_{\perp ,s}$), we have ${\mathrm{\Delta }}_s\approx \langle \mathrm{\Delta }{P}_s\rangle /\langle P_s\rangle$, where $\mathrm{\Delta }{P}_s\equiv P_{\text{max},s}-P_{\perp ,s}$ represents the free-energy density stored in pressure anisotropy. Our definition of pressure anisotropy is different from the commonly used definition in terms of $P_{\perp }$ and $P_{\parallel }$ based on a preferred magnetic-field direction. In the absence of magnetic fields, we identify the local maximum thermal-pressure component and use it as a preferred direction.

Finally, the third dimensionless quantity is the inverse plasma beta, ${\beta }_s^{-1}$, where ${\beta }_s\equiv \langle P_s\rangle /\langle B^2/8\pi \rangle$ and $B(t,\mathit{x})$ is the magnetic-field strength. It represents the magnetic energy density normalized to the thermal pressure and is thus the main quantitative characteristic we use to diagnose the growth of magnetic fields. It is effectively zero when the magnetic field is initially negligible. By analyzing the evolution of $M_s^2$, Δ_s, and ${\beta }_s^{-1}$, we learn the energy partition among different energy reservoirs. In the following subsections, we describe distinct stages of the evolution as the system is continuously driven by the external shear force.

Unmagnetized Stage.

In the unmagnetized stage, the electromagnetic fields are negligible. The system can thus be described by the following nonrelativistic Vlasov equation for each species, where the only acceleration is supplied by the external force:^†

$$\frac{\partial f_s}{\partial t}+v_x\frac{\partial f_s}{\partial x}+a_0\sin \left(\frac{2\pi }{L}x\right)\frac{\partial f_s}{\partial v_y}=0.$$ [1]

This unmagnetized system is one-dimensional in position space, and so the convective term, $\mathit{v}\hspace{0.17em}·\hspace{0.17em}\nabla f_s$, reduces to $v_x{\partial }_x{f}_s$. The exact solution of Eq. 1 can be obtained by the method of characteristics:

$$\begin{array}{ll}\hfill & f_s(t,x,\mathit{v})=f_{\text{M},s}\left(\sqrt{v_x^2+v_z^2+{\widetilde{v_y}}^2}\right),\hfill \\ \hfill & \widetilde{v_y}\equiv v_y+\frac{L{a}_0}{2\pi v_x}\left[\cos \left(\frac{2\pi }{L}x\right)-\cos \left(\frac{2\pi }{L}(x-v_{x}t)\right)\right]\text{}.\hfill \end{array}$$ [2]

Here, $f_{\text{M},s}$ is the initial Maxwellian distribution for each species $f_s(0,x,\mathit{v})=f_{\text{M},s}(|\mathit{v}|)\hspace{0.17em}\hspace{0.17em}\equiv \hspace{0.17em}\hspace{0.17em}{n}_{0s}/{(\sqrt{2\pi }{v}_{\text{th}s})}^3\hspace{0.17em}\hspace{0.17em}\exp (-|\mathit{v}{|}^2/2v_{\text{th}s}^2)$, where $n_{0s}$ is the initial density. Under the normalization $\widehat{t}=t{v}_{\text{th}s}/L,\hspace{0.17em}\widehat{\mathit{v}}=\mathit{v}/v_{\text{th}s},\hspace{0.17em}\widehat{x}=x/L$, and ${\widehat{a}}_0=a_{0}L/v_{\text{th}s}^2$, Eq. 1 can be reduced to the dimensionless form ${\partial }_{\widehat{t}}{f}_s+\widehat{v_x}{\partial }_{\widehat{x}}{f}_s+{\widehat{a}}_0\sin (2\pi \widehat{x}){\partial }_{\widehat{v_y}}{f}_s=0$; this form shows that ${\widehat{a}}_0$ is the only dimensionless free parameter controlling the overall dynamics. In this solution, f_s remains Maxwellian in v_z, and, therefore, one of the eigenvectors of the local pressure tensor ${\mathrm{P}}_s$ is fixed in the z-direction with its corresponding eigenvalue $P_{zz,s}$. The other two eigenvectors corresponding to the largest and smallest eigenvalues of ${\mathrm{P}}_s$, denoted as $P_{\text{max},s}$ and $P_{\text{min},s}$, are thus in the x–y plane.

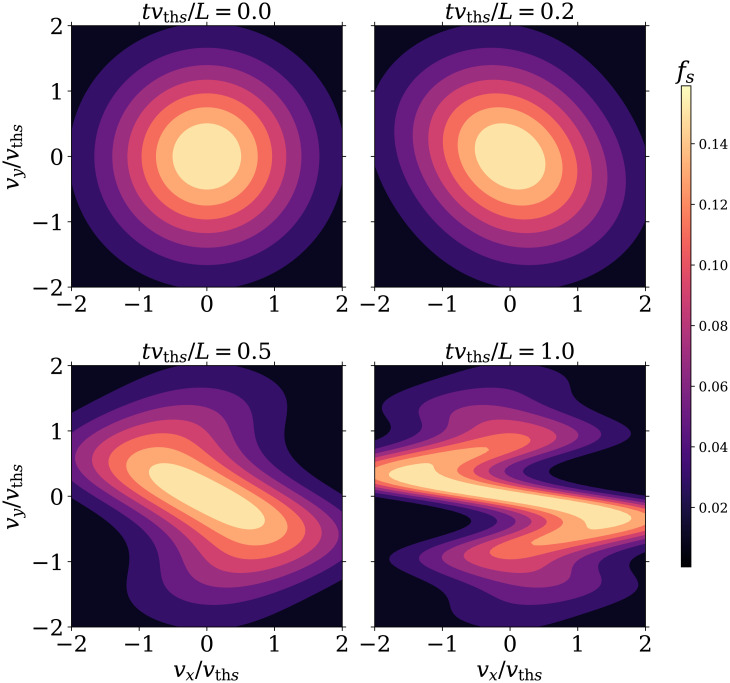
In Fig. 1, we show a visualization of the evolution of f_s (Eq. 2) integrated over v_z in the v_x-v_y phase space for the choice ${\widehat{a}}_0=0.2{\pi }^2\approx 2$. The solution is plotted at x = 0, where the maximum shear occurs. The sinusoidal acceleration a gives rise to an x-dependent bulk flow ${\mathit{U}}_s=U_s(t,x)\widehat{\mathit{y}}$. The transport of this nonuniform y-momentum is carried by particles streaming in the x direction with their thermal speeds. This gives rise to the phase-mixing feature indicated in Fig. 1 by the distortion of f_s in velocity space. The anisotropy developed in f_s leads to the generation of thermal pressure anisotropy, ${\mathrm{\Delta }}_s(t)$—a purely kinetic phenomenon, which would be absent if the plasma were a collisional fluid.

Fig. 1.

Contours of f_s (Eq. 2) integrated over v_z at different moments of time. The location x = 0 with maximum shear is chosen, and ${\widehat{a}}_0=0.2{\pi }^2$. The distribution is distorted by the phase mixing of momentum.

To obtain the early-time behavior, we can take the second-order Taylor expansion of Eq. 2 for $\mathrm{ϵ}\equiv t{v}_{\text{th}s}/L\ll 1$; the obtained f_s at positions with maximum shear is found to be a multivariate normal distribution and becomes tri-Maxwellian in the coordinate system, in which the axes are along the principal axes of ${\mathrm{P}}_s$ (SI Appendix, section 1A). In this limit, the evolution of $M_s(t)$ and ${\mathrm{\Delta }}_s(t)$ are:

$$M_s(t)=\frac{1}{\sqrt{2}}{\widehat{a}}_0\frac{t{v}_{\text{th}s}}{L}+\mathcal{O}({\mathrm{ϵ}}^3),$$ [3]

$${\mathrm{\Delta }}_s(t)=\frac{3\pi }{2\sqrt{2}}{\widehat{a}}_0{\left(\frac{t{v}_{\text{th}s}}{L}\right)}^2+\mathcal{O}({\mathrm{ϵ}}^3).$$ [4]

Both M_s and Δ_s increase on the thermal-crossing time scale, $L/v_{\text{th}s}$, of their corresponding species. Up to second order in ϵ, the bulk flow velocity, obtained by taking the first moment of Eq. 2, is simply $U_s(x,t)\widehat{\mathit{y}}=\mathit{a}(x)t$—identical to the fluid-level behavior for constant acceleration by a constant external force.

At later times, the Mach number M_s (calculated by taking the first moment of Eq. 2) asymptotes to a constant value; this occurs due to phase mixing of the particles in the x direction. One can estimate the steady-state value of M_s by noting that the average particle will accelerate until it drifts across the characteristic length scale of the box in the x direction and the local sign of the external force changes. This takes a time $\approx L/(2\pi v_{\text{th}s})$, during which the particles will accelerate to a characteristic bulk flow speed of $U_s^{\text{sat}}\approx a_{0}L/(2\pi v_{\text{th}s})$.^‡ This provides us with a saturated Mach number for each species of

$$M_s^{\text{sat}}\equiv \frac{U_s^{\text{sat}}}{v_{\text{th}s}}\approx \frac{a_{0}L}{v_{\text{th}s}^{2}2\pi }=\frac{{\widehat{a}}_0}{2\pi }.$$ [5]

We denote by τ₀ ($\approx 1/2\pi$) the moment of time that $M_s^{\text{sat}}$ is reached, normalized to $L/v_{\text{th}s}$. Eq. 5 indicates that the dimensionless parameter ${\widehat{a}}_0$ represents the characteristic Mach number of the system.

This estimation of $M_s^{\text{sat}}$ is predicated on the fact that the electromagnetic field remains negligible up until the saturation time. Realistically, however, the Weibel instability will be triggered by the developing pressure anisotropy and generate magnetic fields strong enough to affect the evolution of the background flow and the pressure anisotropy on a short time scale (which we refer to as ${\tau }_{\text{lin}}$ and introduce in the next subsection). In most astrophysical environments, the time scale for the growth of the Weibel magnetic fields is asymptotically small compared to the fluid time scale ($L/v_{\text{th}s}$)—we refer to this as the asymptotic regime. In this regime, the unmagnetized solution (Eq. 2), which does not contain the physics of Weibel instability, is only valid at very early times (on the fluid time scale) of the evolution $t{v}_{\text{th}s}/L\ll 1$, during which the expressions for $M_s(t)$ and ${\mathrm{\Delta }}_s(t)$ (Eq. 3 and Eq. 4) are good approximations.

Linear Weibel Stage.

To describe the rapid growth of Weibel magnetic fields on the slowly evolving (driven shear-flow) background, we use the unmagnetized solution, Eq. 2, as the background equilibrium, based on which we perform linear theory of the Weibel instability. Because the growth rate of this instability is proportional to the plasma frequency, ${\omega }_{\text{p}s}$, of each species, the electron Weibel instability is much faster than that of ions. We thus consider only the electron Weibel instability, triggered by the electron pressure anisotropy Δ_e (the following discussion, and, in particular, the derived scaling laws, also applies to an electron–positron plasma); the interested reader is referred to SI Appendix, section 1 for a detailed derivation.

In the asymptotic regime, the magnetic growth rate, set by the most unstable mode, is found to scale as

$${\gamma }_B\equiv \frac{\text{d}\ln B}{\text{d}t}\sim {\mathrm{\Delta }}_e^{3/2}{\omega }_{\text{p}e}\frac{v_{\text{th}e}}{c},$$ [6]

corresponding to the wavenumber

$$k_{\text{w}}\simeq {\mathrm{\Delta }}_e^{1/2}/d_e,$$ [7]

where $d_e\equiv c/{\omega }_{\text{p}e}$ is the electron skin depth. These scalings are the same as the canonical electron Weibel instability assuming a bi-Maxwellian plasma (33).

Given the time-scale separation ${\gamma }_B\gg {\partial }_t{\mathrm{\Delta }}_e/{\mathrm{\Delta }}_e\sim {\partial }_t{\gamma }_B/{\gamma }_B\sim v_{\text{th}e}/L$, we can integrate Eq. 6 to obtain the evolution of the magnetic field. Assuming a constant mean thermal pressure of the system, the time evolution of ${\beta }_e^{-1}$ (representing magnetic energy) can then be written as

$${\beta }_e^{-1}\simeq {\beta }_0^{-1}\exp \left[\frac{{\widehat{a}}_0^{3/2}}{2}{\left(\frac{t{v}_{\text{th}e}}{L}\right)}^4\frac{L}{d_e}\right]\text{},$$ [8]

where ${\beta }_0^{-1}$ is determined by the initial magnetic-field perturbation at $k_{\text{w}}$. This equation features an important length ratio, $L/d_e$; the length-scale separation $L/d_e\gg 1$ is equivalent to the time-scale separation ${\omega }_{\text{p}s}^{-1}(c/v_{\text{th}e})\ll L/v_{\text{th}e}$, the same as the separation required to perform this linear theory (${\gamma }_B\gg {\partial }_t{\mathrm{\Delta }}_e/{\mathrm{\Delta }}_e$) with a factor of ${\mathrm{\Delta }}_e^{3/2}$ difference.

Because of the superexponential growth of the Weibel instability in our system, nonlinear effects occur very soon after the exponent in Eq. 8 becomes of order unity (with logarithmic corrections due to the initial value of β_e and the exact number of e-folds). At this point, the increasingly rapid depletion of the free energy by the Weibel instability balances its supply through phase mixing, whereupon Eq. 8 is no longer valid. We denote this moment of time corresponding to the end of the linear Weibel stage, normalized to $L/v_{\text{th}e}$, as ${\tau }_{\text{lin}}$. At ${\tau }_{\text{lin}}$, the exponent in Eq. 8 reaching order unity yields the scaling ${\tau }_{\text{lin}}\sim {\left(L/d_e\right)}^{-1/4}{\widehat{a}}_0^{-3/8}$. The dependence of Δ_e on $L/d_e$ and ${\widehat{a}}_0$ follows from Eq. 4:

$${\mathrm{\Delta }}_e({\tau }_{\text{lin}})\sim {\left(\frac{L}{d_e}\right)}^{-1/2}{\widehat{a}}_0^{1/4},$$ [9]

which is essential for estimating the saturation level of Weibel magnetic fields, as we now explain.

Saturation of Weibel Instability.

At ${\tau }_{\text{lin}}$, Δ_e reaches its maximum value, and the width of the forming Weibel filaments (the wavenumber of the Weibel modes) is determined by the value of ${\mathrm{\Delta }}_e({\tau }_{\text{lin}})$ (Eq. 7). After ${\tau }_{\text{lin}}$, the electron Weibel instability enters its nonlinear stage, during which we expect the anisotropy Δ_e, and thus the growth rate γ_B, to decrease rapidly as the free energy is converted into magnetic energy. However, the length scale of the Weibel filaments should not change significantly in this stage, instead remaining similar to that set by ${\mathrm{\Delta }}_e({\tau }_{\text{lin}})$. This is because the magnetic growth rate during the nonlinear stage is small compared to that of the linear stage. Although the wavenumber of the most unstable mode decreases together with Δ_e, we do not expect it to acquire much energy (an expectation confirmed by our simulation results discussed in Numerical Experiment). Accordingly, the magnetic-energy-containing scale should remain similar to that achieved at the end of linear stage, when the magnetic growth rate is maximal and the Weibel filaments are fully formed. Other processes that can change the length scale of Weibel fields, such as the tilting of filaments due to the background shear flow and the coalescence of filaments, occur on time scales much longer than the inverse Weibel growth rate and can thus be neglected before Weibel saturation occurs.

As the magnetic field becomes stronger, it affects the trajectories of particles and gradually magnetizes them. Eventually, the electron Larmor radius, ρ_e, becomes comparable to the length scale of the magnetic field, $k_{\text{w}}^{-1}$, at which point electrons are “trapped” in the Weibel filaments. This particle-trapping condition, $k_{\text{w}}{\rho }_e\sim 1$, is commonly believed to lead to the saturation of the electron Weibel instability (e.g., refs. 33 and 49). It follows from Eq. 7 and Eq. 9 that the dependence of $k_{\text{w}}{d}_e$ on $L/d_e$ and ${\widehat{a}}_0$ satisfies

$$k_{\text{w}}{d}_e\sim {\left(\frac{L}{d_e}\right)}^{-1/4}{\widehat{a}}_0^{1/8}.$$ [10]

Thus, the dominant Weibel wavelength, ${\lambda }_{\text{w}}=2\pi /k_{\text{w}}$, is a hybrid scale, intermediate between L and d_e:

$${\lambda }_{\text{w}}\sim L^{1/4}{d}_e^{3/4}{\widehat{a}}_0^{-1/8}.$$ [11]

The average electron Larmor radius can be estimated as ${\rho }_e\simeq {\beta }_e^{1/2}{d}_e$; Together with Eq. 7, the trapping condition, $k_{\text{w}}{\rho }_e\sim 1$, provides the estimate of the value of ${\beta }_e^{-1}$ at saturation ${\beta }_{e,\text{sat}}^{-1}\sim {\mathrm{\Delta }}_e({\tau }_{\text{lin}})$. Combined with Eq. 9, this expression becomes

$${\beta }_{e,\text{sat}}^{-1}\sim {\left(\frac{L}{d_e}\right)}^{-1/2}{\widehat{a}}_0^{1/4}.$$ [12]

Eq. 11 and Eq. 12 provide the main deliverable of this study—the scaling dependence of the length scale [$\propto {(k_{\text{w}}{d}_e)}^{-1}$] and amplitude ($\propto {\beta }_{e,\text{sat}}^{-1}$) of the saturated seed magnetic fields on the two key dimensionless parameters: ${\widehat{a}}_0$ and $L/d_e$. The ${\widehat{a}}_0$ parameter is determined by the shear rate of the system, and $L/d_e$ quantifies the separation between fluid and kinetic dynamics in the system.

Our model is predictive in the asymptotic regime of large-scale separation, in which the short-time ($t{v}_{\text{th}}/L\mathrm{\lesssim }0.1$) approximation of the unmagnetized solution (Eqs. 3 and 4 and Eqs. 6 and 7) must be valid during the growth of the Weibel seed fields (at $t{v}_{\text{th}}/L\simeq {\tau }_{\text{lin}}$), i.e., ${\tau }_{\text{lin}}\mathrm{\lesssim }0.1$. (We found that the deviation between the second-order expansion and the full solution becomes noticeable at $t{v}_{\text{th}}/L\approx 0.1$.) The weak scaling dependence of ${\tau }_{\text{lin}}\sim {(L/d_e)}^{-1/4}$ then suggests that a significantly larger-scale separation, $L/d_e\mathrm{\gtrsim }{10}^4$, is required to access the deep asymptotic regime, as pertains to astrophysical environments. In regimes lacking such sufficient scale separation—e.g., systems achievable in numerical simulations and laboratory laser experiments—our model is unable to provide definite scaling laws. This is because systems with relatively small $L/d_e$ lack sufficient time-scale separation; i.e., at the moment when the Weibel magnetic fields are rapidly growing, f_s already deviates significantly from a Maxwellian distribution and possesses a complex form (e.g., Fig. 1, Lower). Therefore, explicit analytical expressions for Δ_e, γ_B, and $k_{\text{w}}$ do not exist in those nonasymptotic regimes. In order to apply our model to systems with finite values of $L/d_e$, and to test it with direct numerical simulations, we follow the same theoretical arguments used in this section, while setting undetermined power-law indices for the counterparts of Eqs. 4–7, based on which we derive the scalings of $k_{\text{w}}$ and ${\beta }_{e,\text{sat}}^{-1}$ in the nonasymptotic regime (as functions of undetermined exponents). The detailed derivation is shown in SI Appendix, section 2, and its numerical validation is shown in SI Appendix, section 4.

Numerical Experiment

Simulation Setup.

To test our model, we perform first-principles particle-in-cell simulations using the code ZELTRON (50) of an initially unmagnetized plasma driven by an external shearing force. Due to the high computational cost inherent to this problem, our simulations are performed using an electron–positron plasma ($s\in \{e,p\}$) . In the case that the external force causes the same body acceleration to both species, giving rise to a hydrodynamic flow, the evolution of an electron–positron system should be similar to an electron–proton plasma within the characteristic electron time scale (before the subsequent ion Weibel instability becomes active). In the remainder of the paper, we drop the subscript s and use $v_{\text{th}}$ and ${\omega }_{\text{p}}$ to represent thermal velocity and plasma frequency for both electrons and positrons. We set the initial temperatures to $\theta \equiv T/m_e{c}^2=1/16$ (so that the thermal motions of the particles are subrelativistic). The thermal velocity is $v_{\text{th}}\equiv \sqrt{T/m_e}=\sqrt{\theta }c$. The system is initialized with uniform Maxwellian distributions and no electromagnetic fields and is continuously driven by an external mechanical force ${\mathit{F}}_{\text{ext}}=m_e{a}_0\sin (2\pi x/L)\widehat{\mathit{y}}$. We parameterize the acceleration amplitude $a_0=S_0({\pi }^2{\theta }_e{c}^2/L)$, where S₀ is a parameter we control in the simulations and is related to the normalized forcing amplitude as $S_0={\widehat{a}}_0/{\pi }^2$. We analyze in detail one single representative case: a 3D run with $L/d_e=128$ and $S_0=0.2$. These values of $L/d_e$ and S₀ allow us to have both a separation between the fluid-scale and Weibel dynamics and a long enough time interval to test our predictions for the unmagnetized stage.

Time Evolution of Key Parameters.

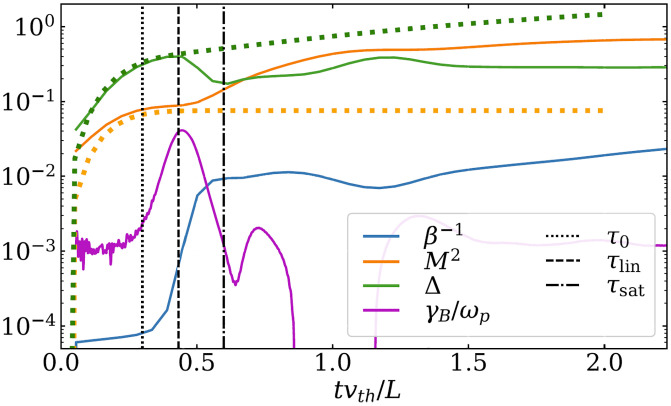
The measured Mach number M, pressure anisotropy Δ, and plasma beta β are identical between the two species and are therefore written without a species subscript. Fig. 2 compares the time evolution of M², Δ, ${\beta }^{-1}$, and ${\gamma }_B/{\omega }_{\text{p}}$. The evolution of the system can be divided into four stages: the initial unmagnetized stage, the linear Weibel stage ($t{v}_{\text{th}}/L\mathrm{\lesssim }{\tau }_{\text{lin}}$), the nonlinear Weibel stage (${\tau }_{\text{lin}}<t{v}_{\text{th}}/L\le {\tau }_{\text{sat}}$), and a prolonged stage after the saturation of Weibel instability ($t{v}_{\text{th}}/L>{\tau }_{\text{sat}}$) . We describe each distinct stage qualitatively to reveal the physical picture of the whole process.

Fig. 2.

Time evolution of M², Δ, ${\beta }^{-1}$, and ${\gamma }_B/{\omega }_{\text{p}}$. Dotted lines show the analytical results calculated with the unmagnetized solution Eq. 2.

Growth of pressure anisotropy during the unmagnetized stage.

In the unmagnetized stage, the measured evolution of M(t) and $\mathrm{\Delta }(t)$ (shown in Fig. 2) agrees reasonably well with the analytical prediction obtained by numerically integrating the exact solution of f_e in Eq. 2 (shown by the dotted curves). The slight departure from the prediction at very early times is due to numerical noise from the finite number of particles. The development of thermal pressure anisotropy Δ is due to the phase mixing of particles and is a purely kinetic feature of the collisionless plasma. We have predicted that, in an unmagnetized plasma, the bulk flow velocity, and thus M, should saturate due to phase mixing. This is indeed observed in the numerical results as the M² curve reaches a plateau after τ₀ ($\approx 0.25$; dotted vertical line).

Growth of magnetic fields during the linear Weibel stage.

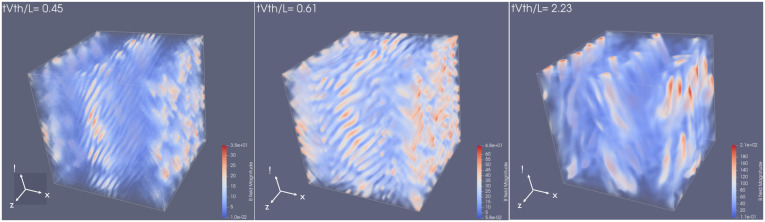
With the development of pressure anisotropy (Δ), the magnetic fields, and thus ${\beta }^{-1}$, start to grow rapidly as a result of the Weibel instability. Fig. 2 shows that in this linear Weibel stage, the measured magnetic growth rate, ${\gamma }_B\equiv \text{d}\ln B/\text{d}t$, also increases with time, suggesting a superexponential growth of magnetic fields. Magnetic fields with clear Weibel-type filamentary structures emerge on $\sim d_e$ scales from the initial random noise (Fig. 3, Left).

Fig. 3.

Visualization of magnetic-field amplitude at ${\tau }_{\text{lin}}$ (Left), ${\tau }_{\text{sat}}$ (Center), and the end (Right) of the simulation.

We identify a noteworthy moment of time, ${\tau }_{\text{lin}}$ ($\approx 0.45$; vertical dashed line in Fig. 2), when the system’s dynamics change in a qualitative manner. This is the time at which both Δ and γ_B reach their maxima and then start a sharp downturn, while M² deviates from the plateau and starts to increase again. The ${\beta }^{-1}$ continues to grow, but at a relatively smaller rate. At ${\tau }_{\text{lin}}$, both Δ and M² begin to depart from the (unmagnetized) analytical solution. These observations suggest that ${\tau }_{\text{lin}}$ is the moment at which the Weibel magnetic fields have reached a magnitude sufficient to affect the dynamics of the plasma—i.e., nonlinear effects become important.

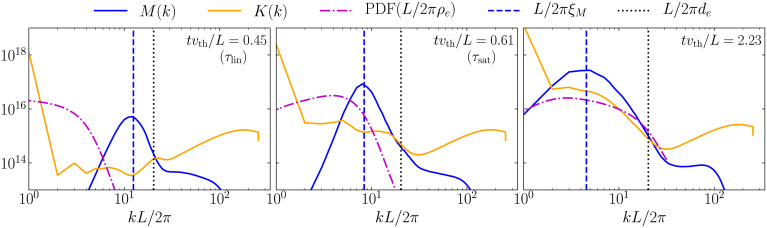
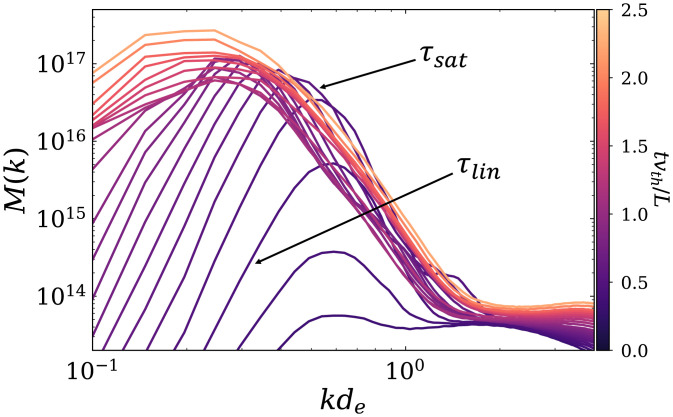
Power spectra of fluctuations (integrated isotropically in wavenumber [k] space) at ${\tau }_{\text{lin}}$ are shown in Fig. 4, Left. The power spectrum of the bulk flow, K(k), is concentrated at the system scale where the flow is driven. In contrast, the power spectrum of the magnetic field, M(k), peaks at $\sim d_e$ scale, consistent with the structure of the magnetic filaments shown in Fig. 3, Left. We define the magnetic-energy-containing scale (shown by the blue vertical dashed line in Fig. 4) as ${\xi }_M\equiv {\displaystyle \int \text{d}}k\hspace{0.17em}{k}^{-1}M(k)/{\displaystyle \int \text{d}}k\hspace{0.17em}M(k)$, which is expected to relate to the wavenumber of the most unstable Weibel modes as $k_{\text{w}}{\xi }_M\sim 1$. The dashed magenta curve shows the probability density function (PDF) of electron Larmor radius, ${\rho }_e\equiv m_e{v}_{\text{th}}c/(eB)$, where $v_{\text{th}}$ and B correspond to the local temperature and magnetic field on the numerical grid. The local temperature is calculated by averaging the three diagonal elements of the local thermal pressure tensor. At ${\tau }_{\text{lin}}$, the plasma remains unmagnetized as the Larmor radii of the majority of particles are generally of order $L/2\pi$, substantially larger than the scale of the magnetic field ξ_M. The evolution of the magnetic spectrum is shown in Fig. 5. In the linear Weibel stage, the amplitude of the spectrum increases rapidly, while its peak has a slight shift to the larger wavenumbers, consistent with the increase of Δ during this stage.

Fig. 4.

Magnetic (blue) and kinetic (orange) energy spectra at ${\tau }_{\text{lin}}$ (Left), ${\tau }_{\text{sat}}$ (Center), and the end (Right) of the simulation. The electron skin depth d_e (dotted vertical lines), magnetic energy integral scale ξ_M (dashed vertical lines), and the PDF of Larmor radius ρ_e (magenta dashed curve) are shown for reference.

Fig. 5.

Time evolution of magnetic energy spectrum.

Saturation of Weibel instability during the nonlinear stage.

After ${\tau }_{\text{lin}}$, the Weibel instability enters its nonlinear stage, in which the Weibel magnetic fields are strong enough to affect the particle trajectories and affect the overall plasma dynamics. The pressure anisotropy Δ decreases as its free energy is depleted by the Weibel instability, resulting in a drop in γ_B (Fig. 2). The nonlinear Weibel instability saturates at the moment of time that we denote as ${\tau }_{\text{sat}}$ ($\approx 0.61$) . At this time, ${\beta }^{-1}$ saturates (at the value that we call ${\beta }_{\text{sat}}^{-1}$), γ_B drops to a minuscule value, and Δ reaches its local minimum because the depletion of free energy in pressure anisotropy stops as Weibel instability saturates. We use the local minimum of Δ in simulations to identify ${\tau }_{\text{sat}}$.

The configuration of magnetic fields at ${\tau }_{\text{sat}}$ is shown in Fig. 3, Center. The filamentary structures become more prominent with stronger field amplitudes, and the filaments become progressively tilted due to the large-scale shear flow along the y axis. The spectra during this stage are shown in Fig. 4, Center. The characteristic scale of the magnetic field ξ_M has increased by about 50% as a combined effect of the decreasing unstable wavenumber due to the decreasing Δ and the tilting of filaments. The relatively modest increase in ξ_M justifies our assumption in Theory that the length scale of magnetic fields at ${\tau }_{\text{sat}}$ is similar to that at ${\tau }_{\text{lin}}$. In contrast, the magnetic energy has increased by more than an order of magnitude between ${\tau }_{\text{lin}}$ and ${\tau }_{\text{sat}}$. This rapid growth of the magnetic field’s amplitude and the slow change of its characteristic length scale during the nonlinear Weibel stage are illustrated in Fig. 5. Next, we observe that some bulk kinetic energy develops near the scale of the magnetic field (kinetic scales), corresponding to bulk motions of the filaments. However, the energy of these motions is subdominant to the magnetic energy at those scales. No strong turbulent cascade develops, and the bulk flow remains concentrated at the macroscopic system scale.

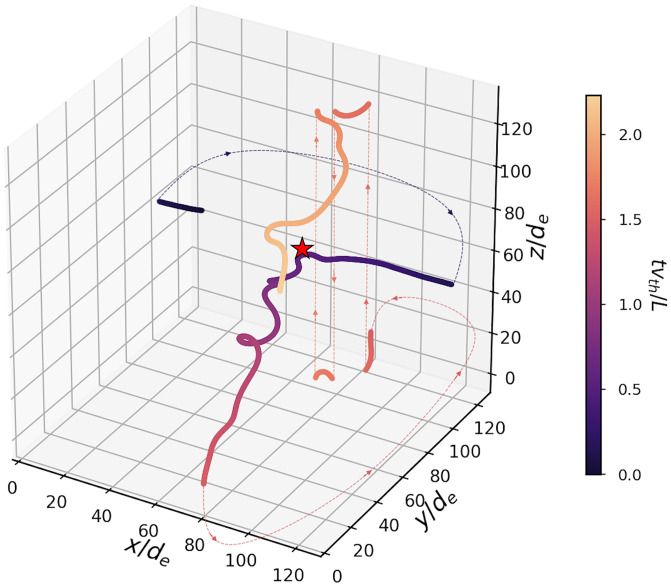
The Larmor radii of a significant fraction of particles at ${\tau }_{\text{sat}}$ become smaller than the scale of magnetic fields ξ_M, meaning that those particles are magnetized by the Weibel magnetic fields. The magnetization of the plasma is also reflected in the trajectories of particles. Fig. 6 shows a representative trajectory of an arbitrarily chosen particle. The particle initially streams freely along the x and z directions, while being pushed by the external force in the $\pm y$ direction. After $t{v}_{\text{th}}/L={\tau }_{\text{sat}}$, the particle is trapped in the magnetic filaments in the y and z directions, while its transport in the x direction is suppressed. This particle trapping leads to the suppression of the y-momentum transport in the x direction, and hence to a dramatic reduction of phase mixing. As a result, the Mach number M starts to increase again rapidly around this time, driven by the external force, while the pressure anisotropy Δ remains fluctuating at the same level because the free energy stops being replenished by phase mixing. The above evidence from spectra and particle trajectories suggests that the saturation of the Weibel instability that we observe is caused by the trapping of particles—i.e., it occurs when the condition $k_{\text{w}}{\rho }_e\sim 1$ is met—a standard criterion widely considered by previous studies (e.g., refs. 33 and 49).

Fig. 6.

Typical trajectory of a particle. The red star indicates the particle’s position at ${\tau }_{\text{sat}}$. The dotted lines indicate how the particle transits the periodic box.

Long-term evolution of Weibel magnetic fields.

After the saturation of the Weibel instability, on time scales of order $L/v_{\text{th}},\hspace{0.17em}{\beta }^{-1}$ fluctuates around ${\beta }_{\text{sat}}^{-1}$, M keeps increasing, and Δ starts to increase again due to the external forcing (Fig. 2). The saturated magnetic filaments are tilted and stretched by the shear flow until they become aligned in the direction of the shear flow (along the y axis), as shown in Fig. 3, Right. Alongside their interaction with the shear flow, the magnetic filaments also undergo a prolonged stage of coalescence with each other (51–53), during which the coherence length of magnetic fields increases. This can be seen from the shift of the power spectrum of magnetic fields to smaller wavenumbers (shown in Fig. 5). From $t{v}_{\text{th}}/L={\tau }_{\text{sat}}$ to the end of simulation (with a time interval of about $1.6L/v_{\text{th}}$), the energy-containing scale of the magnetic field grows to approach the system scale, at which magnetic energy accumulates. Fig. 4, Right shows the spectra at $t{v}_{\text{th}}/L=2.23$. At this late time, the bulk kinetic energy increases at the scale of filaments, but remains subdominant, except at the system scale. Because of the combination of the slight increase of magnetic energy due to the transient inductive amplification by the shear flow and the growth of the magnetic-field length scale ξ_M through filament coalescence, more particles become magnetized (shown by the PDF of Larmor radii compared to the scale of ξ_M) .

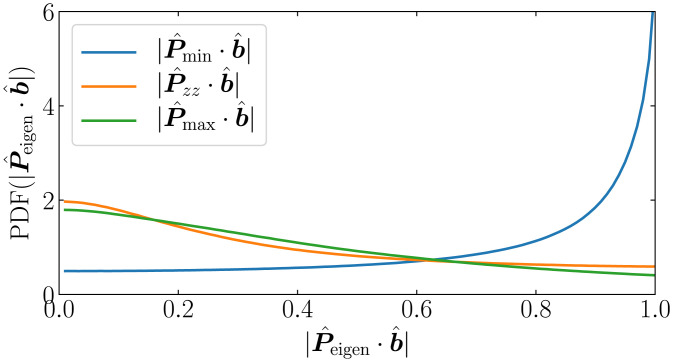
The increasing magnetization can also be quantified by the alignment between the eigenvectors of the pressure tensor $\mathrm{P}$ and the local magnetic-field unit vector $\widehat{\text{b}}$. We denote ${\widehat{\mathit{P}}}_{\text{min}},\hspace{0.17em}{\widehat{\mathit{P}}}_{zz}$, and ${\widehat{\mathit{P}}}_{\text{max}}$ as the three eigenvectors corresponding to the three eigenvalues $P_{\text{min}}<P_{zz}<P_{\text{max}}$ of $\mathrm{P}$. Fig. 7 shows the PDFs of the alignments $|{\widehat{\mathit{P}}}_{\text{eigen}}\hspace{0.17em}·\hspace{0.17em}\widehat{\mathit{b}}|$, where ${\widehat{\mathit{P}}}_{\text{eigen}}\in \{{\widehat{\mathit{P}}}_{\text{min}},{\widehat{\mathit{P}}}_{zz},{\widehat{\mathit{P}}}_{\text{max}}\}$, at the end of the simulation ($t{v}_{\text{th}}/L=2.23$) . The magnetic field is primarily aligned with ${\widehat{\mathit{P}}}_{\text{min}}$, while the PDFs of its alignment with the other two directions are very broad and similar to each other. These statistics result from the magnetization of the particles, manifested via the approximate conservation of the first adiabatic invariant $\mu \equiv P_{\perp B}/nB$, where $P_{\perp B}$ is the thermal pressure perpendicular to the magnetic field. As B increases, the conservation of μ leads to a biased increase of $P_{\perp B}$, and so the direction of the smallest pressure should correspond to the magnetic-field direction. This is displayed by the measured large $|{\widehat{\mathit{P}}}_{\text{min}}\hspace{0.17em}·\hspace{0.17em}\widehat{\mathit{b}}|$. Magnetized plasmas are approximately gyrotropic perpendicular to the magnetic field, consistent with the similar statistics of $|{\widehat{\mathit{P}}}_{zz}\hspace{0.17em}·\hspace{0.17em}\widehat{\mathit{b}}|$ and $|{\widehat{\mathit{P}}}_{\text{max}}\hspace{0.17em}·\hspace{0.17em}\widehat{\mathit{b}}|$. The magnetization of a significant fraction of the plasma particles is crucial for the coalescence of seed-field filaments, where magnetic reconnection is essential (51–53), and for the further amplification of the seed fields by the turbulent dynamo.

Fig. 7.

PDF of the alignment of magnetic-field direction $\widehat{\text{b}}$ with the thermal-pressure eigenvectors ${\widehat{\mathit{P}}}_{\text{eigen}}\in \{{\widehat{\mathit{P}}}_{\text{min}},{\widehat{\mathit{P}}}_{zz},{\widehat{\mathit{P}}}_{\text{max}}\}$, measured at $t{v}_{\text{th}}/L=2.23$.

Scaling Dependence of Saturated Seed Fields.

The numerical results from the fiducial run show qualitative agreement with our model at each distinct stage. In order to test our model quantitatively, parameter scans on the two key parameters, S₀ and $L/d_e$, are required. As we discussed at the end of Theory, a large-scale separation ($L/d_e\mathrm{\gtrsim }{10}^4$) is necessary to access the deep asymptotic regime and test the predictive scalings (Eq. 5 and Eqs. 9–12) of our model. This is difficult to achieve because of the associated large computational cost, even for two-dimensional (2D) domains. Therefore, we perform parameter scans in the nonasymptotic regime (both in 2D and 3D) and compare those numerical results with a modified (nonasymptotic) version of our theory (SI Appendix, section 2). The detailed study of the parameter scans is reported in SI Appendix. The simulation details are described in SI Appendix, section 3. The analysis of the scaling laws of key quantities (Δ, ${\beta }^{-1}$, and γ_B) at critical moments in time (${\tau }_{\text{lin}}$ and ${\tau }_{\text{sat}}$) is shown in SI Appendix, section 4, and a time-scale analysis justifying the validity of our numerical results to support our theory is performed in SI Appendix, section 5.

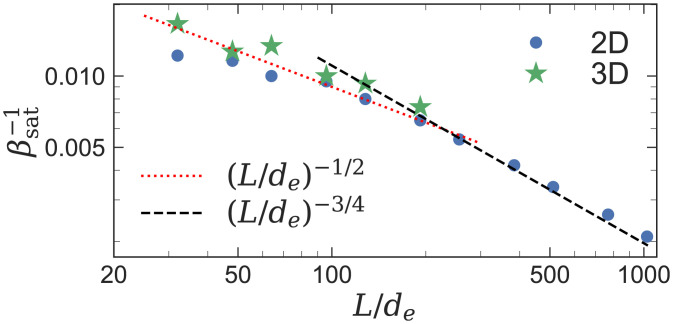
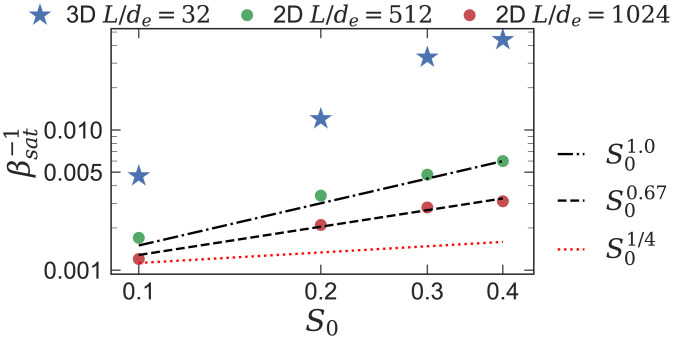
The highlight of these runs is the scaling dependence of the saturated inverse beta, ${\beta }_{\text{sat}}^{-1}$, on $L/d_e$ and S₀. Depending on whether the Weibel instability occurs before or after the bulk flow reaches the plateau (i.e., whether ${\tau }_{\text{lin}}$ is smaller or larger than τ₀), the nonasymptotic range can be divided into the preplateau regime (for $L/d_e\mathrm{\gtrsim }200$) and the postplateau regime (for $L/d_e\mathrm{\lesssim }200$) . In our modified theory, we expect ${\beta }_{\text{sat}}^{-1}\sim {(L/d_e)}^{-4/3}$ in the preplateau regime and ${\beta }_{\text{sat}}^{-1}\sim {(L/d_e)}^{-1/2}$ in the postplateau regime. This is directly confirmed by the numerical results shown in Fig. 8. The dependence on S₀ is more difficult to test in our numerical results. For runs with varying S₀, the background evolution of M and Δ for the unmagnetized plasma differs, and the transition between the preplateau and postplateau regimes occurs at different values of $L/d_e$, rendering the application of our scaling theory nontrivial. We are thus only able to predict the dependence of ${\beta }_{\text{sat}}^{-1}$ on S₀ for systems with asymptotically large $L/d_e$: ${\beta }_{\text{sat}}^{-1}\sim S_0^{1/4}$ (Eq. 12). Although we are not able to perform simulations deep in this asymptotic regime, a clear trend is shown in Fig. 9 that the measured scalings approach the $S_0^{1/4}$ prediction with increasing $L/d_e$.

Fig. 8.

Saturated inverse beta ${\beta }_{\text{sat}}^{-1}$ versus $L/d_e$ for 2D and 3D runs with varying $L/d_e$ and fixed $S_0=0.2$.

Fig. 9.

Saturated inverse beta ${\beta }_{\text{sat}}^{-1}$ versus S₀ for 2D and 3D runs with varying S₀.

In summary, the good quantitative agreement between the numerical results (shown in SI Appendix, section 4) and the predicted scalings in the nonasymptotic regime (derived in SI Appendix, section 2) supports our analytical model and its main deliverable (Eq. 11 and Eq. 12) in the asymptotic regime.

Discussion

This paper provides a demonstration and quantitative description of the spontaneous magnetization of collisionless plasma under the action of a shear flow. The primary kinetic instability that produces the seed magnetic fields is identified as the Weibel instability. We predict that in the regime with an asymptotically large time- and length-scale separation, quantified by $L/d_e$ (ratio of system scale to electron skin depth), the saturated seed magnetic fields are expected to have a characteristic length scale ${\lambda }_{\text{w}}\sim L^{1/4}{d}_e^{3/4}{\widehat{a}}_0^{-1/8}$ (Eq. 11) and lead to a saturated inverse beta ${\beta }_{e,\text{sat}}^{-1}\sim {(L/d_e)}^{-1/2}{\widehat{a}}_0^{1/4}$ (Eq. 12), where ${\widehat{a}}_0$ is the normalized acceleration driving the macroscopic shear flow. The relatively weak ${(L/d_e)}^{-1/2}$ dependence of ${\beta }_{e,\text{sat}}^{-1}$ implies that in very large astrophysical systems, the Weibel instability generates much stronger seed fields than those thought to be produced by the Biermann battery, for which ${\beta }_{\text{sat}}^{-1}\propto L^{-2}$ (54, 55). After saturation, the Weibel filaments undergo long-term evolution that sees their scale increase gradually toward the system size through coalescence.

The Weibel instability has been historically analyzed within the context of gamma-ray bursts (GRBs) in counter-streaming flows (37, 41, 42) or collisionless shocks (36, 38–40), in which the external drive is strong and/or the Mach number is high. In this work, however, we consider a weakly driven, large-scale shear flow. This constitutes an important step in establishing a connection with a broader set of astrophysical applications beyond shock physics, such as low-Mach-number turbulence in galaxy clusters and in the IGM. The production of magnetic fields has also been studied in the configuration of counter-streaming flows through the kinetic Kelvin–Helmholtz instability (22–25) and of differential rotation through electron instabilities (56, 57). By contrast, rather than initialize a configuration that is supercritical to the instabilities of interest, we instead start with a stable equilibrium and drive the system gradually toward becoming marginally unstable to the relevant kinetic instability (in this case, the Weibel). Despite the drastic difference of physical regimes, the Weibel instability in a large-scale shear flow shares qualitative similarities to that in the context of GRBs, such as the saturation due to plasma magnetization (particle trapping) and the subsequent inverse cascade through filament coalescence (58).

It is important to note that ion kinetic physics is not taken into account in this study. With the development of ion thermal pressure anisotropy, the ion Weibel instability can, in principle, also be triggered and produce seed magnetic fields on a time scale $\sim {\omega }_{\text{p}i}^{-1}$ and a length scale $\sim d_i$, where $d_i=c/{\omega }_{\text{p}i}$ is the ion skin depth. However, when the ion Weibel instability becomes active, the electron Weibel instability should already be saturated and the electrons already magnetized. In this high-β system, various electron-pressure-anisotropy instabilities are expected to play a role [e.g., electron firehose and whistler (59)], and it is not clear how these electron-scale instabilities might interplay with the ion Weibel instability [or, for that matter, subsequent ion-pressure-anisotropy instabilities, like firehose and mirror (60–62)]. We defer the inclusion of ion kinetic physics to future work.

In the meantime, it is worth applying our results to an actual astrophysical system, if only suggestively. For example, in the hot and dilute ICM, the scale of observed macroscopic turbulent motions is $L\mathrm{\gtrsim }10 \text{kpc}$, while the electron skin depth may be estimated from the observed electron density as $d_e\sim {10}^{-12} \text{pc}$. This gives a typical scale separation of $L/d_e\mathrm{\gtrsim }{10}^{16}$. For this ratio, Eq. 12 leads us to expect the saturated seed magnetic fields produced by the electron Weibel instability to give ${\beta }_{\text{sat}}\sim {(L/d_e)}^{1/2}\sim {10}^8$. Under typical cluster conditions, this value of ${\beta }_{\text{sat}}$ corresponds to an $\sim 0.1 \text{nG}$ magnetic field. Despite the relatively small scale of this field, its amplitude is notable because the Weibel’s main competitor, the Biermann battery, produces fields that are much weaker, at $\sim {10}^{-20} \text{G}$ under typical cluster conditions (15, 63). Interestingly, configurations that give rise to Biermann fields—misalignment of plasma density and pressure gradients—have been shown to be unstable to the Weibel instability as well; the ensuing strong small-scale seed fields are radically different from their more conventional Biermann origin (64, 65).

Despite their initially small (electron) scales, we argue that the saturated Weibel seed fields—whose morphology is that of flux ropes—can inverse-cascade to larger scales through magnetic reconnection (51–53, 66–68). Although a substantial fraction of the magnetic energy is released in this process and converts into plasma’s kinetic energy, the plasma heating effect is not significant due to the high plasma β of the system. This inverse cascade should reach the scale at which the reconnection time scale of the seed fields becomes comparable to the nonlinear eddy turnover time scale of the turbulent flow. Above this critical scale, the coalescence of Weibel seed fields may be expected to be replaced by amplification of those fields through the turbulent dynamo. The feasibility of this scenario will be addressed in a separate publication.

We note that another important alternative origin of seed magnetic fields is the galactic origin, whereby the seed magnetic fields were first produced in stars or accretion disks in galaxies and then injected into the early ICM or IGM by galactic winds (29–31). This conjecture is supported indirectly by the observation of early enrichment of galaxy clusters by metals (69), but faces a challenge in dispersing these fields throughout the cluster volume. We note that the galactic origin of seed fields and the Weibel origin explored in this work are not mutually exclusive. The main deliverable of this work is that there is, in fact, no need to resort to any specific astrophysical process to generate seed fields and spread them into the ICM and IGM: Simple (and ubiquitous) shear flows are sufficient to magnetize cosmic plasmas.

This work provides the first step in the building of a paradigm for understanding magnetogenesis in the Universe.^§ It quantitatively describes the emergence and evolution of seed magnetic fields that arise self-consistently from generic motions (shear flows) that can also support a turbulent dynamo. Future investigations are required to determine how such seed fields can be amplified by astrophysical turbulence to dynamically important levels on cosmologically short time scales (71). This paradigm will provide a fully self-consistent explanation for the origin and prevalence of cosmic magnetism—one of the most important science drivers of upcoming radio telescopes, such as the Square Kilometer Array.

Data Availability

HDF5 and txt replication data have been deposited in the Harvard Dataverse (https://doi.org/10.7910/DVN/OMQUDX) (72).