Significance
For over a century, it has been known that the ratio of the nuclear and cytoplasm volumes (NC ratio), rather than the separate volumes, is constant among cells of many types of organisms. Changes of the NC ratio are associated with cancerous transformations, suggesting that the ratio has physiological importance. Notably, the dominant regulatory mechanism of the NC ratio has not been identified. Here, we use physical estimates of the forces implicated in nuclear volume determination and show that they are dominated by the osmotic pressure of actively transported proteins. Inspired by this, we formulate a minimal model for the cytoplasmic and nuclear volumes that predicts the NC ratio and the factors that modulate it, in agreement with published experiments.
Keywords: nuclear volume, mechanobiology, biological physics
Abstract
The volume of the cell nucleus varies across cell types and species and is commonly thought to be determined by the size of the genome and degree of chromatin compaction. However, this notion has been challenged over the years by much experimental evidence. Here, we consider the physical condition of mechanical force balance as a determining condition of the nuclear volume and use quantitative, order-of-magnitude analysis to estimate the forces from different sources of nuclear and cytoplasmic pressure. Our estimates suggest that the dominant pressure within the nucleus and cytoplasm of nonstriated muscle cells originates from the osmotic pressure of proteins and RNA molecules that are localized to the nucleus or cytoplasm by out-of-equilibrium, active nucleocytoplasmic transport rather than from chromatin or its associated ions. This motivates us to formulate a physical model for the ratio of the cell and nuclear volumes in which osmotic pressures of localized proteins determine the relative volumes. In accordance with unexplained observations that are a century old, our model predicts that the ratio of the cell and nuclear volumes is a constant, robust to a wide variety of biochemical and biophysical manipulations, and is changed only if gene expression or nucleocytoplasmic transport is modulated.
1. Introduction
The nucleus, which is the largest organelle in the cell, regulates the expression of genes (1) via transcription of DNA found in the chromatin (a complex of DNA polymer and histone proteins), protects genes from mechanical and biochemical damage (2, 3), and controls their environment (1). Furthermore, nuclear size is related to chromatin organization (4), and changes of the nuclear size accompany cell differentiation, development, and disease (5). However, despite the effect of nuclear volume changes on chromatin organization, the associated biophysical mechanisms that determine it are not well understood. Recently, Cantwell and Nurse (6) reviewed the biological factors that are implicated in nuclear size determination: cell size, cytoplasmic factors, the LINC complex, transcription and RNA processing, nucleocytoplasmic transport, and nuclear envelope (NE) expansion. The goal of the present work is to translate these biological factors into quantifiable physical quantities, in particular the force balance between the nucleus and cytoplasm that, in mechanical (but not necessarily thermodynamic) equilibrium, relates the nuclear and cytoplasmic volumes. Our calculations show that in nonstriated muscle cells, the primary forces are due to the osmotic pressures of proteins and RNA molecules preferentially localized to the nucleus and cytoplasm and that this implies that under many conditions, the ratio of the nuclear and cytoplasmic volumes in these cells is a constant—an observation that was first made over 100 y ago (7) and has been further quantified in more recent studies (6).
As noted in the biological review (6), several experiments suggest that the chromatin content of the nucleus does not determine its size, in yeasts (8, 9), Caenorhabditis elegans (10), and vertebrates (11, 12). This conclusion disagrees with the widely accepted, qualitative nucleoskeletal theory that hypothesizes that the degree of chromatin compaction by the cellular machinery is the determining factor of nuclear size. This implies that nuclear size should sensitively depend on chromatin content (13), which is assumed to completely fill the nuclear volume. This assumption is directly refuted by some imaging experiments that observed that the chromatin does not always fill the entire volume of the nucleus (2, 14, 15). These experiments, together with others reviewed in ref. 6, indicate that the popular nucleoskeletal theory does not adequately describe the biophysical mechanisms that underlie nuclear size determination.
In this paper, we present a comparison of the possible biophysical forces that may determine the volume of the nucleus. We relate the biological factors reviewed by Cantwell and Nurse (6), as well as the size of the genome, to five potentially significant forces that originate from different components of the nucleus and cytoplasm: 1) osmotic pressure of the chromatin polymers, 2) osmotic pressure of counterions that balance the chromatin charge, 3) elastic forces of the cytoskeleton, 4) osmotic pressures of solutes (proteins and RNA molecules) that are preferentially localized (due to active transport) to the cytoplasm or nucleoplasm, and 5) NE tension. Each of these forces is theoretically derived and quantified using published biological data. Our estimates suggest that in the common scenario where the NE is not stretched and in cell types other than striated muscle (where directional forces are important), the osmotic pressure of preferentially localized, large-molecule solutes (proteins, RNA) in the nucleus is the dominant force whose balance with that of the cytoplasm determines the ratio of the nuclear and cytoplasmic volumes. Motivated by this result, we formulate a minimal biophysical model that relates both the volumes of the cell and the nucleus, in many cell types (but not striated muscle), to mechanical equilibria across the plasma membrane and NE. Our model predicts that for relaxed (i.e., not taut) NE, the volumes of the cell and the nucleus are proportional even when various biophysical factors (e.g., osmotic pressure, cellular adhesion, genome size) are varied. This result agrees with a biological observation that is more than a century old (6, 7), which underlies a popular, clinical screening technique for cancer cells, for which the proportion between the cell and nuclear volumes deviates from specific values (16). Besides suggesting a mechanistic explanation for the proportionality of cell and nuclear volumes, our physical theory highlights the potential importance of currently underestimated effects of protein and RNA localization (via nucleocytoplasmic transport) in nuclear mechanics. Our results and predictions may impact several different fields, including medicine, cellular biology, and nuclear mechanobiology.
We begin by reviewing the forces that influence the volume of the nucleus and quantifying their effects using physical theory. The various estimates are compared and the conditions for which the cell and nuclear volumes are proportional are elucidated. Finally, we discuss the relation of the theory to various experiments.
2. Forces Involved in Nuclear Volume Determination
Experiments show that the NE is viscoelastic and, over long timescales, behaves as a two-dimensional fluid (17, 18). This implies that over sufficiently long timescales and specifically in steady state, lateral flows of NE molecules relax to zero any tension gradients; that effect, known as Marangoni convection, is predicted by physical theories of two-dimensional fluids (19). In the case of the NE, these flows involve the molecular components of the membranes and lamina (20).
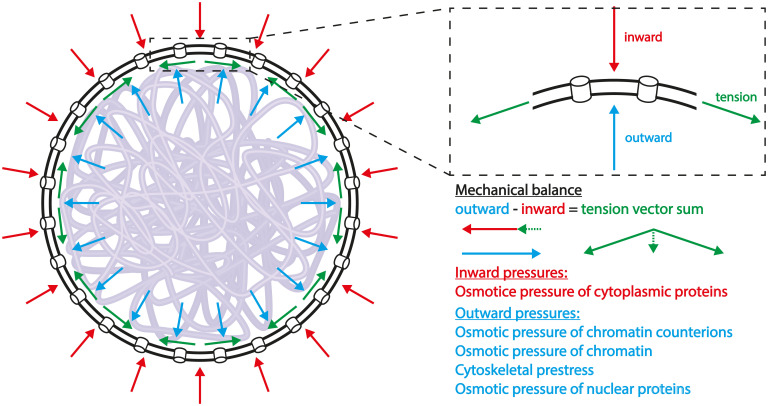
Furthermore, in steady state, the shape of the nucleus does not change, which indicates that the forces exerted on the two sides of the NE are balanced by the NE tension, as we now explain. Any imbalance of the inward and outward pressures and the NE lateral stresses (related to tension) would change the volume of the nucleus by facilitating flow of fluid either into or out of the nucleus through the nuclear pore complexes (NPCs) that are embedded in the NE. Mathematically, this force balance can be written in terms of the following equation, which is analogous to the Young–Laplace equation:
| [1] |
where is the local pressure gradient across the NE, σn is the NE tension, and H is the local mean curvature of the NE. Eq. 1 is valid for any two-dimensional fluid layer and can be derived by minimization of energy similar to the one that appears in section 2.2. of ref. 21, even for a pressure difference that can change locally across the area of the layer instead of a constant pressure. Eq. 1 applies locally for any unit area of the NE. While the mean curvature and the local pressure gradient across the NE may generally vary in the lateral directions, the tension does not, due to the viscoelastic nature of the NE and Marangoni flows (19, 20).
There are two types of forces that can be exerted on the two sides of the NE to determine the local pressure difference: 1) isotropic forces, which usually originate from cytoplasmic and nuclear pressures, and 2) nonisotropic forces, which may originate in various effects such as contractility of the stress fibers in adhered cells (22) or nonuniform tethers of the NE to cytoskeletal or “solid” structures in certain regions of the nucleus. If all of the forces that are exerted on the two sides of the NE are isotropic, the local pressure difference is constant across the area of the NE. In that case, Eq. 1 implies that in steady state (in which the tension is uniform), the mean curvature is constant; namely, the nucleus is spherical. In contrast, nonisotropic forces result in nonuniform mean curvature and nonspherical nuclei.
In the subsections below, we estimate the order of magnitude of the different possible physical contributions to the pressure difference (both isotropic and nonisotropic) across the NE and relate them to the biological structures and functions discussed in ref. 6. To demonstrate the generality of our estimates, we consider nuclei of two eukaryotic organisms from different biological kingdoms, humans (animalia) and the fission yeast Schizosaccharomyces pombe (fungi); our estimates of the various forces in the two species are summarized in Table 1. We show that for many cell types (but not for directional, striated muscle cells), the dominant contribution to originates from osmotic pressure, which is an isotropic force. For this reason and for simplicity, we consider the case that all the forces are isotropic. In that case, the nuclei are spherical and Eq. 1 for the balance of the pressures and NE tension can be written in simpler terms as the following equation that describes the entire area of the NE globally rather than locally (Fig. 1):
| [2] |
where and are respectively the sums of all the outward and inward isotropic forces (pressures), σn is the NE tension, and R is the radius of the nucleus; the effect of nonisotropic forces, which may lead to nonspherical nuclei and necessitate the use of the more general force balance of Eq. 1, is explored in 4. Discussion.
Table 1.
Order of magnitude estimates of the contributions of different nuclear and cytoplasmic components to the inward and outward pressures that are exerted on the nucleus of nonstriated muscle cells
| Species/source of pressure |
Chromatin polymer, Pa |
Chromatin counterions, Pa |
Cytoskeletal elasticity, Pa |
Cytoplasmic proteins, Pa |
Nucleoplasmic proteins, Pa |
|---|---|---|---|---|---|
| Human | 30 | 300 | 500 | 8,000 | 8,000 |
| Fission yeast | 1.5 | 20 | 500 | 8,000 | 8,000 |
Order of magnitude estimates of the contributions of different nuclear and cytoplasmic components to the inward and outward pressures that are exerted on the nucleus of nonstriated muscle cells. In striated muscle cells, the cytoskeletal stress is directional and may exceed hundred of kilopascals during contraction, making it the dominant contribution in that case, which is outside of the scope of this paper.
Fig. 1.
Force balance diagram of a spherical nucleus. The NE, depicted by two concentric black circles, representing the outer and inner (that in most species is attached to a lamin layer) NE membranes, perforated by channels (representing the nuclear pore complexes), envelopes the chromatin (semitransparent purple curve). The red arrows represent the sum of the inward pressures that tend to compress the nucleus and the blue arrows represent the sum of the outward pressures that tend to expand the nucleus. In the case where the outward pressures are larger than the inward pressures, the difference of the pressure is balanced by NE tension, depicted by green arrows whose resultant (vector sum) gives rise to an inward force, which limits the expansion of the nucleus.
2.1. Polymer Model of the Osmotic Pressure of the Chromatin.
Polymer physics predicts that the chromatin macromolecule has a thermodynamically preferred radius that it would occupy if not constrained in any way; this is known as the radius of gyration and denoted by Rg. If the radius of the nucleus R is smaller than Rg, then the chromatin is confined by the NE to a volume that is smaller than its preferred volume, which results in an outward osmotic pressure pp exerted by the chromatin on the inner side of the NE. This contribution to the outward pressure increases with the size of the genome, if the size of the nucleus remains the same. The radius of gyration of a chromatin macromolecule is determined by the length of the DNA molecule that constitutes it, its degree of compaction in the chromatin fiber, and the persistence length of the chromatin fiber. In addition to these, self-attraction or repulsion (including steric, excluded volume) of the chromatin fiber results in different dependence of Rg on the genome size. For example, self-attraction can lead to chromatin collapse (as in refs. 23 and 24). Since we are interested in identifying the dominant forces, we estimate an upper bound on the possible values of Rg and subsequently on the pressures pp. This occurs for the case where the chromatin fiber is in a “good solvent,” namely with chromatin–chromatin steric repulsion that is larger than its self-attraction, so that the radius of gyration is then maximal (25).
In that situation, the radius of gyration of a chromatin macromolecule is (25), where is the persistence length of the chromatin, and L is the contour length of the chromatin. L is related to the number of DNA base pairs in the chromatin Nbp and its average packing ratio Rp, defined as the length of a chromatin fiber (in nanometers) per kilobase of DNA (i.e., the fiber length containing in both the wound and linker DNA, 1,000 bp [kb]) (26), by the expression . Both the packing ratio of the chromatin fiber and its persistence length depend on the structure of the chromatin fiber, which is generally not uniform (27). However, different experimental measurements and theoretical estimates of the packing ratio and persistence length result in a range of 7 to 11 nm/kb for the packing ratio and to 180 nm for its persistence length (26, 28). Because we are interested in calculating an upper bound for the pressure, we choose the parameters that yield the maximal radius of gyration: a persistence length of 180 nm and a packing ratio of 11 nm/kb. Furthermore, we treat the entire genome as one chromosome (chromatin macromolecule) instead of as made up of multiple chromosomes, which simplifies the calculation and results in a slightly increased pressure (in the spirit of finding an upper bound); this is because the preferred volume of a chromosome, Vp, scales as , so that the preferred volume of two concatenated chromatin molecules is larger than the sum of the preferred volumes of the two separate chromatin molecules, since .
When the entire genome is treated as one chromatin macromolecule, the contour length of the chromatin molecule is calculated directly from the genome size and the average packing ratio of the chromatin. The diploid S. pombe genome comprises 27.6 Mbp of DNA (29), which gives rise to a contour length of ∼300 µm, while the diploid human genome comprises 6.4 Gbp (30), which gives rise to a contour length of ∼70 mm. Substitution of the contour lengths of human and yeast chromatin and the persistence length of the chromatin yields chromatin radii of gyration of ∼400 µm and 15 µm, respectively. Both of these values are significantly larger than their respective nuclear radii of 6.2 µm and 1.6 µm, calculated from respective nuclear volumes of (31) and (8) for idealized spherical nuclei. Therefore, in both cases the confinement of the chromatin (assumed to be in a good solvent for the calculation of an upper bound) in the nucleus will contribute an outward pressure. For such a polymer, with radius of gyration Rg confined in a sphere of radius , the compression energy is given from polymer physics theory by , where is the thermal energy (32). The pressure pp is then given by the negative derivative of the compression energy with respect to the volume of the nucleus, , which results in the following expression:
| [3] |
Substitution of the values of V, R, and Rg for the two species results in an order of magnitude estimates for the outward pressure due to confinement of the chromatin polymer of 30 Pa for human nuclei and 1.5 Pa for S. pombe cells. As we show below, these upper-bound values are still far below the pressures due to preferentially localized proteins (Table 1).
We note that we treated the chromatin as a neutral polymer while, in fact, it is negatively charged. This treatment is justified because the screening length (the decay length of the electrostatic interactions in electrolyte solution) in cellular systems is nm (33), which is very small compared with the polymer radius of gyration and the nuclear size. However, the net electric charge of the chromatin can contribute to the outward pressure indirectly, due to the localization of counterions in the vicinity of the chromatin, as we now discuss.
2.2. Osmotic Pressure of the Chromatin Counterions.
Chromatin is a complex of a negatively charged DNA polymer that links and is wrapped around positively charged histone proteins. Due to the steric and polymeric constraints involved, chromatin is not neutral, but has a net negative charge. As a result, the chromatin macromolecule is surrounded by a “cloud” of soluble, positive counterions that neutralize its charge by being localized within the nucleus despite being able to diffuse through the NPC (34). Theoretical studies of analogous solutions of charged colloids (35) suggest that depending on the detailed molecular structure and charge of the chromatin and the concentration of electrolytes in the nucleoplasm, the cloud of counterions may be either highly localized near the chromatin fiber or dispersed within the nucleoplasm. Localized counterions are constrained to move together with the chromatin and thus present a negligible contribution to the osmotic pressure. On the other hand, the contribution of dispersed counterions can be significant, similar, in the limiting case, to that of an ideal gas, in which all the counterions can collide with the NE.
Since we are interested in an upper-bound, order of magnitude estimate of the contribution of the counterions to the osmotic pressure, we consider the limiting case in which the counterions are dispersed within the nucleoplasm and contribute to the pressure as an ideal gas. In this limit, the concentration of counterions is uniform within the nucleoplasm and is determined by two conditions. The first one is equality of electrochemical potentials, across the NE, of each of the different species of soluble ions. The ions diffuse from the nucleus to the cytoplasm (and vice versa) via the nuclear pore complexes, which allows them to reach chemical equilibrium; this would not be the case if the NE contained active, ion pumps that directly transport ions between the cytoplasm and nucleoplasm (36). The second condition is that the cytoplasm and nucleoplasm are each to a very good approximation electro-neutral, which arises from minimization of electrostatic energy (34). In a simple model for an isolated nucleus in a salt solution that includes one type of monovalent cation, one type of monovalent anion, and a negatively charged polyelectrolyte (chromatin) that is confined to the nucleus, these two conditions give rise to the following expression for the outward pressure of the chromatin counterions pc (SI Appendix, section 1):
| [4] |
where is the thermal energy, Nch is the overall charge of the chromatin in units of electron charges, csalt is the intracellular salt concentration, and V is the nuclear volume. It is important to note that we do not include the charged macromolecules localized to the cytoplasm and their counterions, such as those associated with the negatively charged cytoskeleton (37) or the negatively charged lipids within the plasma membrane. As we now explain, such confined cytoplasmic charges are expected to counterbalance and hence decrease the predicted net outward pressure of the counterions confined to the nucleus. Since we seek an upper-bound estimate of the net outward pressure due to the counterions, we can ignore such localized, charged macromolecules. This allows us to obtain the tractable expression for the net outward pressure in Eq. 4.
Charge neutrality means that the positive counterions of the cytoskeleton and lipid membranes are confined to the cytoplasm and increase the osmotic pressure within it. This increase in the osmotic pressure of the cytoplasm decreases the difference between the nucleoplasm osmotic pressure and cytoplasm osmotic pressure, which is the net outward osmotic pressure we estimate. Therefore, our model, which does not include the confined charges of the cytoplasm, gives an upper-bound estimate of the osmotic pressure difference between the nucleus and cytoplasm.
Furthermore, our model approximates the volume of the cytoplasm as being much larger than the volume of the nucleus. This limit also leads to a reduced pressure within the cytoskeleton that only increases the estimate of the net outward pressure. When the volume of the cytoplasm is larger than the nuclear volume, but not infinitely larger, the effect that increases the osmotic pressure within the cytoplasm is related to the release of some salt ion pairs from the nucleus: The elevated concentration of nuclear counterions changes the electrochemical potential within the nucleus and causes some salt ion pairs (anion and cation) to be released from the nucleus to the cytoplasm (34) where their entropy is larger; this effect is included in the Gibbs–Donnan model that we use in SI Appendix, section 2. The displaced salt ion pairs would increase the osmotic pressure in the cytoplasm, thus decreasing our estimate of the net, outward osmotic pressure difference across the NE. In the spirit of finding an upper-bound estimate, our approximation of the volume of the cytoplasm as being much larger than that of the nucleus implies that the additional cytoplasmic osmotic pressure of the displaced ion pairs is negligible. This is because the number of released ion pairs, which is proportional to the finite nuclear volume, is delocalized within the much, much larger volume of the cytoplasm.
Importantly, because our model considers the volume of the cytoplasm to be much larger than that of the nucleus and for our upper-bound estimate free of cytoplasmically confined charges, it is appropriate for an isolated nucleus in a salt solution. For such isolated nuclei, the only counterions in the fluid surrounding the nuclei are those that originate in the phospholipids of the outer nuclear NE membrane, which are localized in the vicinity of the membrane (38). Furthermore, the contribution of these counterions to the osmotic pressure of the surrounding fluid is roughly balanced by the contribution of the counterions originating in the phospholipids that compose the inner nuclear membrane (which are similarly localized in the vicinity of the membrane). Therefore, the effect of the NE membranes on the net difference between the osmotic pressures of counterions in the nuclear compartment and outer-nuclear compartment is negligible. We discuss the relevance of our model and Eq. 4 to experiments on isolated nuclei in 4. Discussion.
We present further support to our conclusion that Eq. 4 provides an upper bound to the net outward difference across the NE, of the osmotic pressures of the counterions, in SI Appendix, section 2. There, we introduce a more detailed model that treats the finite volume of the cytoplasm—including the charges confined to it—as larger (but not infinitely larger) than the nuclear volume. This model does not provide a tractable expression such as Eq. 4, but can nonetheless be solved numerically; SI Appendix, Fig. S1 shows that indeed, the net outward osmotic pressure of the counterions in a finite cytoplasmic volume is smaller than the one obtained by Eq. 4 for an effectively infinite cytoplasmic volume. Thus, our simple estimate of the ion effects, which we now calculate, provides an upper bound to the difference of the nuclear and cytoplasmic pressures.
To calculate the net charge of the chromatin, Nch, we calculate the number of histone proteins based on the genome size (6.4 Gbp in human cells and 27.6 Mbp in S. pombe cells) (29, 30) and a typical nucleosome density of one per 200 bp (39). We then subtract the total positive charge of all the histones, where the charge of a single histone octamer is 220 electron charges (39), from the negative charge of the DNA (based on a negative charge of 2 electron charges per base pair) for both the linker DNA and the nucleosomal DNA. This results in a total chromatin charge of electron charges for humans and for S. pombe. We substitute these values into Eq. 4, along with a typical intracellular salt concentration of mM (30, 40) and nuclear volumes [∼1,000 (31) for human nuclei and ∼17 for S. pombe nuclei (8)], which results in an approximate upper bound for the pc of the two species: 300 Pa for humans and 20 Pa for yeasts. As shown in Table 1, these values are much smaller than those associated with the localized proteins.
2.3. Cytoskeletal Prestress.
The nucleus is tethered to the cytoskeleton by the LINC complex (41), which is embedded in the NE. This couples mechanical forces in the cytoskeleton and the NE, so that these forces may contribute to either outward or inward pressures.
The steady-state mechanical force within the cytoskeleton, which is generated by the contractility of the actin–myosin network, is known as prestress (42). In mechanical equilibrium that characterizes the steady state, the prestress is balanced by the stresses within the nucleus and the surroundings of the cell. The magnitude of the prestress depends on the type of cell, its inherent contractility, and the stiffness of the surroundings of the cell (extracellular matrix or substrate), against which the cell contracts (43, 44).
Furthermore, since the cellular cytoskeleton is heterogeneous, so is the prestress within it. Therefore, to estimate the mechanical forces exerted by the cytoskeleton on the nucleus, the magnitude of the prestress in the vicinity of the nucleus is relevant. Measurements in both fibroblasts (45, 46) and airway smooth muscle cells (47) reveal that the prestress may reach magnitudes of kilopascals at the periphery of cells but at their centers, where nuclei are located, the prestress is of the order of hundreds of pascals or lower. This may be explained by the fact that, in both nonmuscle (48) and smooth muscle cells (49), the contractile actomyosin network is denser at the cortex that is attached to the plasma membrane; thus, the majority of the internal stresses are generated at the cell periphery. However, in these types of cells, where the nucleus is surrounded by cytoskeleton that is less dense than the cortex, the order of magnitude of the pressure exerted on the NE by the cytoskeleton is only of the order of hundreds of pascals; accordingly, we estimate the upper bound for the prestress exerted on the nucleus by 500 Pa. This force is directed outward, from the nucleus to the cytoplasm due to the contractility of the cytoskeleton that is adhered to proteins localized near the cell membrane on one side and to the nucleus on the other. Presumably, the prestress in yeast cells, whose cytoskeleton is not connected to an extracellular matrix, is smaller than that in human cells so that 500 Pa is also an upper bound for the prestress exerted on the yeast nucleus.
Our estimate of a cytoskeletal stress exerted on the nucleus of at most a few hundred pascals is not appropriate for striated muscle cells, where the vast majority of the actin and of the myosin is localized to the myofibrils that are adjacent and linked to the nuclei (50, 51). Therefore, the stress exerted on nuclei in striated muscle cells may be much larger. Naturally, this stress varies as the muscle cell contracts and it is highly directional, in contrast to isotropic forces. To estimate the magnitude of this stress, we divide the directional force a muscle cell can generate by its cross-sectional area, which results in uniaxial stresses that may exceed hundreds of kilopascals (52, 53).
As we show in the subsection below, the estimated magnitude of the prestress in the vicinity of the nucleus, in nonstriated muscle cells, is negligible compared to the contributions of the osmotic pressure of proteins that are preferentially localized by active, nucleocytoplasmic transport. This is not the case for striated muscle cells, to which, as we mention below, our model does not apply.
2.4. Osmotic Pressures of Proteins Preferentially Localized to the Cytoplasm and Nucleoplasm.
The average concentration of cellular proteins in human and yeast cells is about 4.3 mM (54), which in a homogeneous, ideal solution contributes kPa to the osmotic pressure of the solution. However, as we now explain, not all of these kPa of osmotic pressure are contributed to the inward or outward pressure of the respective compartment of the proteins. Since about 80% of the proteins are preferentially localized (55), the results of SI Appendix, section 3, which are explained below, indicate that the osmotic pressures of the localized proteins in the cytoplasm and nucleoplasm are of the order of 8 kPa.
The distribution in the two compartments of proteins that can freely cross the NE by passive diffusion through the NPCs is determined by equilibrium thermodynamics. This dictates that the chemical potentials and hence, in the ideal solution limit, the concentrations of such protein species across the NE are equal, so that their contributions to the osmotic pressures of the two compartments are equal. Thus, no imbalance of the inward or outward pressure can ever result from passively diffusing proteins. An active, nonequilibrium process is thus required to preferentially localize proteins to either compartment and prevent their free exchange, so that these proteins contribute to the net osmotic pressure imbalance that drives fluid flow, which effectively determines the nuclear to cytoplasmic volume ratio.
Nucleocytoplasmic transport is an active, out-of-equilibrium process that preferentially localizes proteins to either the cytoplasmic or the nucleoplasmic compartment (e.g., related to nonequilibrium Ran-GTP gradients) (56–58). Localization of a protein to a given compartment means that the steady-state concentration of this protein in that compartment is larger than its concentration in the other. This can be seen from the condition (for equal fluxes in steady state) that the protein concentration flux into the nucleus must equal the protein concentration flux out of the nucleus. In the spirit of first-order kinetics, the equal flux condition is quantified as , where ki and ke are the nuclear import and export rates of a given protein species, respectively, and cc and cn are its respective cytoplasmic and nucleoplasmic concentrations. Under conditions of chemical equilibrium, the absence of active protein transport implies the two rates are equal, ki = ke, since both are determined by diffusion through the nuclear pores; this implies that cc = cn. However, active transport can result in unequal import and export rates, which results in unequal concentrations in the nucleus and cytoplasm, —i.e., preferential localization of certain proteins to one of those compartments. This argument is further quantified in SI Appendix, section 3. The osmotic pressures of the preferentially localized proteins in the nucleus and cytoplasm are not equal, in contrast to equilibrium. As we show, those contributions are indeed dominant in nonstriated muscle cells (Table 1) where the difference in osmotic pressures must, in general, be balanced by the surface tension of the NE as in Eq. 2.
However, in many cases, the NE is relaxed (2.5. NE Tension and 4. Discussion) with effectively zero tension. Mechanical equilibrium then dictates that the sum of the contributions of all the localized proteins to the inward and outward pressures must be equal (3. Model and Results). Deviations from the equality of inward and outward pressures, such as may be caused by production of new proteins (59), induce fluid flow that changes the nuclear volume and restores the equality of pressures. This is contrasted with the equilibrium case where proteins passively diffuse through the NPC and reach equal concentrations, in which their inward and outward pressures are equalized by flow of proteins rather than fluid. Thus, in the equilibrium case, nuclear volume changes are not induced by soluble molecules that can freely diffuse through the NPC.
An estimate of the fraction of preferentially localized proteins (due to nonequilibrium transport) relative to the total number of proteins is given by a study of Xenopus laevis oocytes that shows that 83% of cellular proteins are preferentially localized to either the cytoplasm or the nucleoplasm (55). This was determined by physical separation of the nucleus and cytoplasm, which is possible due to the large size of the X. laevis oocyte nucleus. Determining this for other cell types with smaller nuclei is difficult because most nuclear fractionation protocols require the use of detergents that damage the NE and mix the nucleoplasm and cytoplasm (55). However, since the localization of proteins is usually associated with their function, one can expect that the homologs of the X. laevis proteins in yeast and human cells are similarly localized. We thus expect that the percentage of localized proteins in yeast and human cells is also of the order of 80%. In the nonequilibrium situation, in the special case that the NE is relaxed, the inward/outward pressures are equal to the osmotic pressure of a protein solution, whose concentration is the average, cellular concentration of all localized proteins (SI Appendix, section 3). Therefore, we estimate that 80% of the aforementioned 10 kPa of the overall osmotic pressure of all proteins is due to the preferentially localized proteins so that the nuclear and cytoplasmic osmotic pressures are about 8 kPa each.
It is important to note that the actual contribution of the localized proteins to the inward and outward pressures may be less than the estimate of 8 kPa due to a number of factors. First, preferential localization, rather than complete localization, results in a lower net contribution of the protein species to the inward and outward pressure (SI Appendix, section 3). Second, the estimate of 80% localized proteins refers to the percentage of the protein species rather than to the number of proteins. Furthermore, this quantity was measured in the special cell type of oocytes rather than somatic cells. Therefore, the actual contribution in somatic cells may be smaller. Third, attractive interactions between proteins, such as those that lead to their oligomerization and polymerization, reduce their contribution to the osmotic pressure in a way that is not captured by the ideal solution approximation for the osmotic pressure. The last factor may decrease the osmotic pressure of the proteins by tens of percent, but is not expected to decrease it by orders of magnitude. This is because of the reversible nature of interactions between intracellular proteins, which are rarely covalent. Therefore, even when proteins polymerize into large networks, these networks coexist with large reservoir of monomers and small oligomers. This is predicted by theoretical studies of self-assembling proteins (60) and observed for the actin cytoskeleton, in which more than 50% of the actin molecules are soluble (61). For this reason, formation of the cytoskeleton, which may comprise 5 to 10% of the proteins in vertebrate cells (62), cannot decrease the osmotic pressure of the cytoplasm by more than that percentage. If we take into account oligomerization of noncytoskeletal proteins into small and large complexes, we estimate that the reduction of osmotic pressure due to interactions is of the order of tens of percent, but not orders of magnitude.
Due to the factors discussed above, our estimate of an 8-kPa contribution of the localized proteins to the inward and outward pressures should be considered as an upper limit. Nonetheless, even if this estimate is reduced by an order of magnitude to 0.8 kPa, it is still much larger than all the other contributions that appear in Table 1 for nonstriated muscle cells. This strongly suggests that the pressures due to localized proteins are the major factors that relate nuclear and cell volumes in such cells. We now use these ideas to formulate a quantitative model for the volumes of these cells and their nuclei in 3. Model and Results, where we also discuss their proportionality. Before that, we briefly discuss NE tension in terms of its nonlinear mechanical response to expansion of its area.
2.5. NE Tension.
The Young–Laplace law expresses how the tension of the NE (resultant of the vector forces in the plane of the membrane; Fig. 1) results in a net inward force that, in mechanical equilibrium, balances the total net outward pressure exerted on the NE. The NE comprises two lipid membranes and, in animal cells, a meshwork of semiflexible filamentous proteins (lamina) (63, 64). Since the mechanical response of both the lipid membranes and the semiflexible polymers to stretching is highly nonlinear and stiffens with increasing expansive strain (65, 66), these properties are expected to be reflected in the mechanical response of the NE: When the nuclear volume is relatively small (as can be the case in a hypertonic environment), the NE is relaxed and undulated (67), and expansion reduces only the entropy of the undulations and is typically small (68, 69). In contrast, when the nuclear volume is relatively large (hypotonic environment), the NE is taut. This expansion of the NE changes the conformations of its constituents (e.g., packing density of lipids or lamin fiber structure), thus raising the NE energy and increasing its tension. Therefore, following the theoretical description in ref. 67, we approximate the NE tension σ in its relaxed state by σ = 0 and in its taut state (when the nuclear radius exceeds a characteristic radius ) by a positive value of σ, which itself depends on the amount of stretching and is thus a function of the nuclear radius R. The characteristic radius Rc is determined by the number of molecules (e.g., lipids, lamin proteins) that comprise the NE and the molecular details of the NE structure. The detailed dependence of Rc on the number of molecules, as well as the dependence of σ on the nuclear radius R, for , involves many molecular details of the NE, which are outside of the scope of this paper. However, the relaxed and taut states can easily be distinguished experimentally, since the relaxed NE is undulated and is therefore less spherical than the taut NE, which is smooth (67).
3. Model and Results
Table 1 summarizes the order of magnitude estimates of the different inward and outward pressures discussed above and suggests that in many cells, the dominant contributions are the osmotic pressures due to localized proteins in the cytoplasm and nucleoplasm. These osmotic pressures are estimated to be about an order of magnitude larger than inward or outward pressures from the other sources, which themselves were upper bounds. This motivates us to consider a minimal model for determination of the volumes of the cell and the nucleus that includes the osmotic pressures due to soluble factors but neglects the effects of chromatin and cytoskeleton. While the chromatin and cytoskeleton may help control the cellular and nuclear shapes, their relatively small pressures perturb only the volumes of the cytoplasm and nucleoplasm determined by mechanical balance of osmotic pressures of the soluble factors across the NE and the plasma membrane.
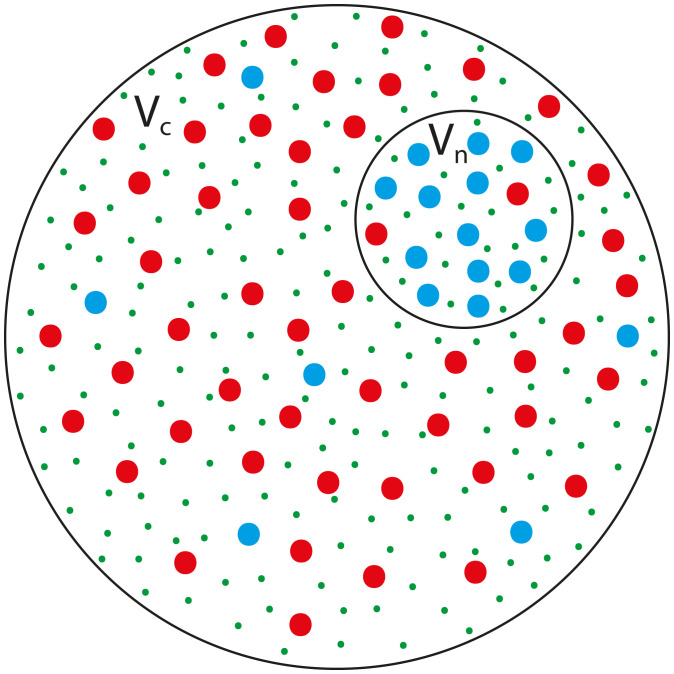
Our steady-state model considers two nested compartments (cytoplasm and nucleus) that contain both localized (large proteins and RNA that are actively transported, as discussed above) and nonlocalized solutes (small molecules/proteins and ions that freely diffuse through the nuclear pores) (Fig. 2). During steady state (e.g., interphase in nondividing cells), the volumes of the compartments are constant in time, which implies that they are in mechanical equilibrium, but not necessarily thermodynamic equilibrium. The outer (plasma) membrane separates the cytoplasm from the extracellular environment and allows, at sufficiently long timescales, free flow of water and regulated transport of ions via pumps and channels, but prevents free diffusion of large solutes. In animal cells, the lateral stress of the plasma membrane is much smaller than the intracellular pressure so that it is unlikely that the plasma membrane can passively balance osmotic pressure differences across it (31). It has been suggested that mechanosensitive ion pumps in the plasma membrane set the fluxes of ions across the membrane to actively balance the osmotic pressures in the cytoplasm and the cell buffer (36). This may not be true in the case of plants and fungi, where a rigid cell wall encapsulates the plasma membrane and mechanically supports intracellular pressure that may be larger than the extracellular one (e.g., turgor pressure) (70).
Fig. 2.
A schematic cartoon of the proposed model. Two black circles represent membranes that delineate two compartments, the cytoplasm whose volume is Vc and the nucleoplasm whose volume is Vn. The outer circle represents the plasma membrane that separates the cytoplasm from the extracellular environment and does not allow free diffusion of large solutes (large red and blue dots); steady-state exchange of small molecules and ions with the cellular environment via active pumps regulates the concentration of those small solutes or ions (small green dots) that may also passively diffuse through channels. The inner circle represents the nuclear envelope, a semipermeable double membrane (that in some species is attached to a nuclear lamina) that separates the cytoplasm and the nucleoplasm and allows free diffusion of small solutes (small green dots) but not of large solutes (large red and blue dots) through the nuclear pores. Due to the free diffusion of the small solutes through the nuclear pores, their concentration in the two compartments is the same. In contrast, the large solutes that are transported across the NE by active mechanisms are not equally distributed in the nucleus and cytoplasm. The species of large solutes represented by the blue dots are preferentially localized to the nucleoplasm while the species of large solutes that are represented by the red dots are preferentially localized to the cytoplasm. This situation is treated in SI Appendix, section 4, and in the main text we treat a minimal model where the localization is complete; as we show in SI Appendix, the two cases yield similar results.
In contrast to the outer membrane, the inner membrane (NE) that separates the cytoplasm and nucleoplasm is a semipermeable membrane that allows free flow of water and free diffusion of small solutes (e.g., small molecules/proteins and ions) through the NPCs, without any active transport via pumps. As explained above, larger solutes (e.g., proteins, RNA) are actively transported through the NPCs and thus are preferentially localized to one of the compartments.
In our model, we account for the nucleocytoplasmic transport by considering the simple situation of a single species of solute molecules that are “confined” to the cytoplasm and solute molecules confined to the nucleoplasm. Neither species can cross the NPCs. These solutes are completely localized to their respective compartments, and their number is thus conserved within each compartment. This approach is justified in SI Appendix, section 4, where we show that it yields the same results as the realistic case where a multitude of protein species are only preferentially localized rather than completely localized; for clarity, we present in the main text this minimal model that is easier to solve.
Mechanical equilibrium across a spherically shaped membrane (plasma or NE) is described by Eq. 2. In the case of the NE of nonstriated muscle cells, the pressures on the left-hand side of Eq. 2 are dominated by the osmotic pressures of the various preferentially localized solutes. Since the small, nonlocalized solutes can freely diffuse across the NE, their osmotic pressures on the two sides are equal and cancel each other on the left-hand side of Eq. 2. Thus, only the contributions of the completely localized, large solutes remain, which depend on , and the free volumes of the cytoplasm and the nucleoplasm. For spherical nuclei, this force balance is described by the following equation, which is derived from Eq. 2:
| [5] |
where σn is the NE tension, R is the radius of the spherical nucleus, is the thermal energy, Vn and Vc are the respective volumes of the nucleoplasm and cytoplasm, and and are their respective minimal volumes (the total volume of all nonsolvent molecules in the compartment). The free volumes, and are used here and in the rest of this paper to calculate concentrations to account for the steric, excluded volume interactions among the solutes, whose overall volume may be significant (31).
While the nonlocalized, small solutes (small molecules and ions) that freely diffuse across the NE through the NPCs do not play a role in determining mechanical force balance across the NE, this is not the case for the plasma membrane. The mechanical balance across the plasma membrane involves the difference of the osmotic pressure of the extracellular environment and the total osmotic pressure in the cytoplasm, which has contributions from both localized and nonlocalized solutes. To find the total osmotic pressure in the cytoplasm, we must first determine the total number of solutes within it. The small, diffusive, nonlocalized solutes in the cell are found in both the cytoplasm and nucleoplasm. We denote the numbers of nonlocalized solutes found in each respectively by Nc and Nn and define their total number: . Since these small solutes can freely cross the NE, they are in chemical equilibrium, so that in the dilute limit, their freely diffusing concentrations in the cytoplasm and nucleoplasm are equal, as are their contributions to the osmotic pressures of the cytoplasm and nucleoplasm, so that . This equation and the equation for the total number of nonlocalized, small solutes, , can be solved to give the number of nonlocalized, small solutes in each compartment:
| [6] |
| [7] |
Henceforth, for brevity, we refer to these as small solutes and omit the word nonlocalized.
Similar to the NE, mechanical balance across the plasma membrane is written for a spherical cell as
| [8] |
where σp is the tension of the plasma membrane and associated structures (e.g., cortex, cell wall), Rp is the radius of the cell, and C is the concentration of solutes in the extracellular compartment. As explained above, in animal cells the plasma membrane includes mechanosensitive ion pumps that regulate the total number of small, cellular solutes, N by controlling the fluxes of ions into and out of the cell, such that to a first approximation, (36). This may not be generally true in other types of cells. Using Eq. 6 for Nc, we can explicitly write the osmotic pressure in the cytoplasm, which is , in terms of the total number of cytoplasmic nonlocalized and completely localized solutes, so that Eq. 8 for the mechanical equilibrium of the plasma membrane becomes
| [9] |
Eqs. 5 and 9 relate the volume of the cytoplasm and that of the nucleoplasm to the NE and plasma membrane tensions σn and σp, respectively. Since there are two equations and four variables (two volumes and two tensions), this system of equations cannot be solved uniquely to determine the volumes of the cytoplasm and nucleoplasm without additional equations that relate the tensions to the rest of the variables. As explained in 2.5. NE tension, σn is a nonlinear function of the nuclear size, whose exact form depends on molecular details of the NE. However, due to the nonlinear, elastic properties of the NE, when the area of the NE (hence the nuclear radius) is smaller than a characteristic value, the NE is relaxed and its tension is negligible. In this important case, which we consider in the subsection below, Eq. 5 implies an important relationship between the volumes Vc and Vn. The case where the NE is taut (its area is larger than the characteristic value) is considered in 4. Discussion.
3.1. Cytoplasmic and Nuclear Volumes Are Proportional for a Relaxed NE () in the Ideal Solution Limit.
For , Eq. 5 indicates that the ratio between the free volumes of the cytoplasm and nucleoplasm is equal to the ratio of the numbers of completely localized solutes in their respective compartments:
| [10] |
In the “ideal solution” limit where the minimal (steric, excluded) volumes and are negligible compared with the cytoplasmic and nuclear volumes respectively, Eq. 10 predicts that the ratio of the nuclear and cytoplasmic volumes is simply proportional to the ratio of the numbers of completely localized, large solutes in each. This is thus independent of genome size, cytoskeletal properties, and electrostatics of the cell, consistent with the observation that unless the nucleocytoplasmic transport or protein expression is changed, the volume ratios of the nucleus and cytoplasm are constants (6). Of course, this ideal solution is only a gross approximation since the minimal volumes of the cytoplasm and nucleoplasm may be of the same order of magnitude as the entire volumes of each of the compartments (31). However, in SI Appendix, section 5, we show that even if the minimal volumes are included, the ratio of the two volumes is still a constant, in the approximation that the volumes of the nondiffusive structures (e.g., cytoskeleton and chromatin) are negligible compared to the total volume of their respective compartments. As our estimates presented in SI Appendix, section 5 show, this is indeed the common biological case. Therefore, we henceforth focus on the case where and so that and are well approximated by Vc and Vn, respectively. The detailed results for the case where and are included are presented in SI Appendix, section 5 and yield the same qualitative conclusion. Importantly, the prediction that the ratio equals is independent of the tension σp of the plasma membrane and cortex or cell wall. If, in addition to a relaxed NE (), the plasma membrane and cortex (or cell wall) are also relaxed (), an explicit solution for Eqs. 5 and 9 can be obtained. The plasma membrane may be relaxed in animal cells where presumably mechanosensitive ion pumps in the plasma membrane regulate ion fluxes such that is maintained.
In that case and in the ideal solution limit, Eq. 10, together with Eq. 9 for the mechanical balance of the plasma membrane, determines the volumes of the cytoplasm and nucleoplasm for the case where and :
| [11] |
| [12] |
where N is the total number of nonlocalized, small solutes, and is the total number of completely localized, large solutes (in both the cytoplasm and nucleoplasm).
4. Discussion
The quantitative estimates of the various contributions to the pressures of the nucleus and cytoplasm, and the physics-based model that predicts the proportionality of the nuclear and cytoplasmic volumes for many common cases are a physical and quantitative parallel to the qualitative, biology-based discussion in ref. 6. Our estimates of the pressures include the contributions of diffusive solutes and nondiffusive structures such as the chromatin and cytoskeleton. We show that in nonstriated muscle cells, the factors that determine the mechanical balance across the NE are the osmotic pressures of proteins preferentially localized to either the cytoplasm or the nucleus (due to active transport). In striated muscle cells, the stress generated by contraction of the sarcomeres may periodically change (e.g., in cardiomyocytes) and exceed the magnitude of the osmotic pressures in its peak; thus, including the effect of sarcomere contraction on nuclear volume requires detailed dynamic modeling that is outside of the scope of this paper. However, for other types of cells we can neglect the pressures that originate in the chromatin or cytoskeleton, which are estimated (Table 1) to be about an order of magnitude smaller, at least, than the pressures of the solutes (71). It is important to note that our estimates for the osmotic pressures of the preferentially localized proteins are based on a mean-field model that neglects the fluctuations of the protein concentrations in the two compartments. The magnitude of the fluctuations of the osmotic pressures scales with the magnitude of the fluctuations of protein concentrations. These fluctuations, relative to the average protein concentrations (for each protein species), decrease as the inverse of the square root of the number of proteins involved (72). Since the typical respective numbers of proteins in yeast and mammalian cells are of the order of 108 and 1010 proteins (30) and, as argued in 2.4. Osmotic Pressures of Proteins Preferentially Localized to the Cytoplasm and Nucleoplasm, most of them are preferentially localized, we conclude that the fluctuations of the osmotic pressures are in yeast and in mammalian cells; both are smaller than 1 Pa. This is much smaller than the difference between our estimate of the magnitude of the localized proteins’ osmotic pressures and the rest of the contributions, which are of the order of hundreds of pascals or smaller. Therefore, fluctuations are not expected to change the qualitative predictions of our model.
The force balances we consider, [5] and [9], have a simple solution for the case that the NE and plasma membrane (together with its associated layers, the cell cortex or cell wall) are relaxed, for which the volumes of the cytoplasm and nucleoplasm are respectively given by Eqs. 11 and 12. Furthermore, our model predicts that even if the NE is relaxed while the plasma membrane is not, the ratio of the volume of the nucleoplasm, Vn, and the volume of the cytoplasm, Vc, is then approximately equal to the ratio of the numbers of localized proteins in each compartment, respectively: . This prediction suggests that as long as the NE is relaxed, the nucleoplasm-to-cytoplasm volume ratio (NC ratio) is governed almost exclusively by the active, nucleocytoplasmic transport of proteins and RNA molecules to and from the cytoplasm and nucleoplasm. Biophysical or biochemical perturbations of the cell or its environment that do not change nucleocytoplasmic transport, such as osmolarity of the cellular environment or variations in the amount of chromatin, will not change the NC ratio as long as the NE remains relaxed, in agreement with multiple experiments (4, 8, 9, 31, 67). In contrast, we predict that genetic or chemical perturbations of components implicated in nucleocytoplasmic transport will change the NC ratio, in agreement with recent findings (6, 8, 73–77). The implication of nucleocytoplasmic transport as the main governing factor of the NC ratio may also explain how indirect biological effects reviewed in ref. 6, such as cytoplasmic factors, transcription and RNA processing, and the LINC complex, can affect nuclear size. Cytoplasmic factors, transcription, and RNA processing are responsible for the presence of the large solutes that are localized by nucleocytoplasmic transport, while some of the components of the LINC complex are implicated in the nucleocytoplasmic transport itself (78).
Our model also predicts that manipulations that change the abundance of nuclear or cytoplasmic soluble components contributing to the osmotic pressure may change the NC ratio. For example, depolymerization of the cytoskeleton, which may constitute 5 to 10% of the cellular proteins (62), can increase the osmotic pressure by tens of percent by increasing the amount of soluble proteins. Accordingly, this is expected to decrease the NC ratio by a similar magnitude, in agreement with experimental observations (79).
Importantly, when the NE is relaxed, the predictions of our theory are valid even when the nucleus is not spherical due to the action of nonisotropic forces (e.g., from stress fibers in adhered cells or tethers of the NE to solid nuclear structures). This is because when the NE is relaxed, in both Eqs. 1 and 2, which then are approximately identical. In other words, when , the shape of the nucleus does not enter the force balance equation (to lowest order) and does not affect the predicted volumes. In that case, we predict that the small (compared to the osmotic pressure of localized proteins), nonisotropic forces determine nuclear shape, while the pressure differences, dominated by the osmotic pressures, determine nuclear volume. This prediction for nonspherical nuclei agrees with the experimental observation that the NC ratio was maintained in adhered cells despite changes of the substrate area (31), and stiffness (80), which modified both the nuclear and cellular shapes and volumes.
In fact, the robustness of the NC ratio to various biophysical and biochemical perturbations is an observation that is more than a century old (7). It has been observed in a wide variety of organisms, but was not explained mechanistically (6) as we have now proposed. The ubiquity of the constancy of the NC ratio suggests that in most physiological scenarios, the NE is relaxed, a property that may be favored because it reduces nuclear rupture (81) and subsequent DNA damage (20). However, in nonphysiological, laboratory conditions, our theory predicts that it is possible for the NE to become taut, for example, under hypotonic conditions (67). Eq. 12, which predicts the nuclear volume for the case of relaxed NE and plasma membrane together with its associated layers, suggests that the nuclear volume increases with decreasing osmolarity of the extracellular environment. As the volume of the nucleus increases, the surface area of the NE must increase as well, eventually stretching the NE and rendering it taut. In that case, the NE tension becomes important, and for spherical nuclei, the volumes of the cytoplasm and nucleoplasm, and the NE tension, are related by Eq. 5, together with the expressions for the minimal volumes and given in SI Appendix, section 5. If the plasma membrane tension, as well as the relation between the nuclear radius and the NE tension , are known or experimentally measured, these equations can be solved to predict the volumes of the cytoplasm and nucleoplasm as a function of the extracellular osmolarity C. The NC ratio is then not constant (even if the plasma membrane is relaxed). For nonspherical nuclei, such as in adhered cells, the equations are more complex since, as described by Eq. 1, the mechanical balance that relates the cytoplasmic and nuclear volumes depends on the nuclear shape and is thus no longer independent of the nonisotropic forces. In either case, the NC ratio is expected to depend on the extracellular osmolarity C rather than being constant, as is indeed observed in cells in hypotonic conditions (67).
Although predicting the dependence of the NE tension on the nuclear radius, , is outside of the scope of our work, our discussion in 2.5. NE tension provides a qualitative prediction regarding the transition between the relaxed and taut regimes of the NE. As explained there, the mechanical properties of the NE are highly nonlinear: In the relaxed state, stretching the NE mainly suppresses undulations while in the taut regime, stretching the NE increases the separation between the molecules that constitute the NE. The transition between these two regimes occurs when the NE first becomes smooth, a state in which the area of the NE is proportional to the amount of NE components, which are in their native, unstretched molecular conformation. This implies that the NE area at which this transition happens scales with the amount of the NE components. We therefore expect that inhibition of the production of NE components may promote a transition of the NE to a taut state, thereby limiting nuclear growth and changing the NC ratio. Indeed, inhibition of nuclear growth due to lack of NE components was observed in mutant fission yeast cells, whose nuclear export of RNA and lipid production were both inhibited (74), and in an extract of X. laevis nuclei that expanded in response to titration (addition) of lamin proteins (82). The fact that both of these experiments represent nonphysiological conditions (defective nuclear export and absence of cytoplasm) also supports the idea that in most physiological conditions the NE is relaxed.
In addition, the estimates and model presented in this paper provide insights into experiments conducted on isolated nuclei (55, 67, 83). In this case, there is no outer membrane and the volume of the spherical nucleus is determined exclusively by the force balance across the NE, which is described by Eq. 2. Moreover, since nuclear extraction protocols commonly use detergents that perforate the NE (55), they are expected to decrease or even abolish the osmotic pressure of localized proteins. In this case, the next largest contribution to intranuclear pressure is either osmotic pressure of chromatin counterions or the pressure of the compressed chromatin, depending on the nucleus and buffer conditions. This intranuclear pressure is balanced by either the osmotic pressure of the buffer (e.g., due to large crowders excluded from the isolated nucleus) or NE tension. Some experiments with isolated nuclei (84) show that an increase of the buffer salt concentration causes the nuclei to shrink, which is consistent with the predictions of Eq. 4 for the intranuclear pressure due to chromatin counterions, for the case that this pressure is larger than the compression pressure of the chromatin. Other experiments show that the addition of small crowders that can cross the NE causes the nucleus to shrink more drastically than the addition of salt (67). Based on the interpretations of the authors of ref. 67, such crowders compress the chromatin, which is consistent with the case for which the dominant intranuclear pressure originates from compression of chromatin—and not the osmotic pressure of its counterions. Importantly, compression of DNA by crowders was demonstrated in molecular dynamics simulations (85).
Our theory can be directly tested by measurements (79) of the total number of large solutes that are localized to the cytoplasm and nucleoplasm, and , and comparing the ratio of the cytoplasm and nucleoplasm volumes to the ratio of and . However, accurate measurements of and are experimentally challenging because nuclear fractionation protocols commonly use detergents that perforate the NE membranes, thereby mixing the nucleoplasm and the cytoplasm (55). In X. laevis oocytes, the large sizes of the nucleus and the cell allow the nucleus to be removed mechanically without perturbing the NE membranes (55). This may potentially allow measurements of the nuclear and cytoplasmic protein concentrations using mass spectroscopy and calculation of the values of and (SI Appendix, section 4), thus providing a quantitative test of our predictions. Furthermore, qualitative tests of our theory can be conducted by changing the localization of abundant, large soluble proteins by fusing them with nuclear localization signals or nuclear export signals; our theory predicts that in this case the NC ratio will then increase or decrease, respectively. In addition, cellular events that change the proteome and its localization, such as stress conditions (86), can also be used to test our ideas, if the overall effect on protein localization of these events is known.
In conclusion, we have used a physical theory to estimate the order of magnitude of the inward and outward pressures originating in various mechanisms. In contrast to the widespread notion that the dominant contribution to the nuclear pressure results from the chromatin (which is widely believed to be the primary determinant of nuclear volume), our analysis suggests that localization of proteins and RNA molecules in the cytoplasm and nucleoplasm by active, nucleocytoplasmic transport is responsible for the dominant contributions to the inward and outward pressures and hence determines the NC ratio. Motivated by this, we formulated a predictive model for the volume of the nucleus that is based on the osmotic pressure of the preferentially localized, soluble molecules rather than the mechanical properties of large complexes such as the chromatin and cytoskeleton. While these structures may contribute important nonisotropic forces that modulate nuclear shape, they do not determine its volume. Our minimal model predicts that the ratio of the volumes of the nucleoplasm and cytoplasm is robust to a wide variety of biophysical and biochemical perturbations, an unexplained observation that is more than a century old. Beyond the prediction of the constant NC ratio, our work may impact the field of nuclear mechanobiology, since it highlights the potential role of osmotic pressures of the localized, soluble molecules and delineates the distinct response of the nucleus to isotropic and nonisotropic forces. This also suggests that the mechanical response of the nucleus, which has so far been attributed to either the lamina or chromatin (69, 87), should be analyzed more carefully to acknowledge the contributions of osmotic pressures to nuclear mechanics.
Supplementary Material
Acknowledgments
We are grateful to Omar Adame Arana, Ram Adar, Gaurav Bajpai, Dennis Discher, Ming Guo, Hagen Hofmann, Jerome Irianto, Paul Janmey, Amit Kumar, Emmanuel Levy, Dana Lorber, Matthieu Piel, Tsvi Tlusty, and Talila Volk for valuable discussions. We are especially grateful to Michael Elbaum for his critical reading of the manuscript and helpful comments. This research was supported by a Volkswagen Foundation grant, a Weizmann-Curie grant, the Fern and Manfred Steinfeld Professorial Chair, the Benoziyo Endowment Fund for Advancement of Science, the Henry Krenter Institute for Biomedical Imaging and Genomics, the Harold Perlman family, and a Pearlman grant.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2118301119/-/DCSupplemental.
Data Availability
All study data are included in this article and/or SI Appendix.
Note Added in Proof
While this paper was under review, a relevant, independent study was publicly shared as a preprint [88]. That study experimentally follows changes of cellular and nuclear volumes of yeast cells as the osmolarity of their media is manipulated. The experimental data fit an expression similar to the one presented in 3. Model and Results. Furthermore, the preprint presents experimental data in which inhibition of nuclear export leads to an increase of the NC ratio, which supports the main conclusion of the present paper.
References
- 1.Dundr M., Misteli T., Functional architecture in the cell nucleus. Biochem. J. 356, 297–310 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Dahl K. N., Kahn S. M., Wilson K. L., Discher D. E., The nuclear envelope lamina network has elasticity and a compressibility limit suggestive of a molecular shock absorber. J. Cell Sci. 117, 4779–4786 (2004). [DOI] [PubMed] [Google Scholar]
- 3.Irianto J., et al., DNA damage follows repair factor depletion and portends genome variation in cancer cells after pore migration. Curr. Biol. 27, 210–223 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Irianto J., et al., Osmotic challenge drives rapid and reversible chromatin condensation in chondrocytes. Biophys. J. 104, 759–769 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Jevtić P., Edens L. J., Vuković L. D., Levy D. L., Sizing and shaping the nucleus: Mechanisms and significance. Curr. Opin. Cell Biol. 28, 16–27 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cantwell H., Nurse P., Unravelling nuclear size control. Curr. Genet. 65, 1281–1285 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.von Hertwig R., Über Korrelation von Zell-und Kerngröße und ihre Bedeutung für die geschlechtliche Differenzeierung und die Teilung der Zelle. Biologisches Centralblatt 23, 49–62 (1903). [Google Scholar]
- 8.Neumann F. R., Nurse P., Nuclear size control in fission yeast. J. Cell Biol. 179, 593–600 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Jorgensen P., et al., The size of the nucleus increases as yeast cells grow. Mol. Biol. Cell 18, 3523–3532 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hara Y., Kimura A., Cell-size-dependent spindle elongation in the Caenorhabditis elegans early embryo. Curr. Biol. 19, 1549–1554 (2009). [DOI] [PubMed] [Google Scholar]
- 11.Harris H., The reactivation of the red cell nucleus. J. Cell Sci. 2, 23–32 (1967). [DOI] [PubMed] [Google Scholar]
- 12.Gurdon J. B., Injected nuclei in frog oocytes: Fate, enlargement, and chromatin dispersal. J. Embryol. Exp. Morphol. 36, 523–540 (1976). [PubMed] [Google Scholar]
- 13.Cavalier-Smith T., Skeletal DNA and the evolution of genome size. Annu. Rev. Biophys. Bioeng. 11, 273–302 (1982). [DOI] [PubMed] [Google Scholar]
- 14.Amiad-Pavlov D., et al., Live imaging of chromatin distribution reveals novel principles of nuclear architecture and chromatin compartmentalization. Sci. Adv. 7, eabf6251 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Popken J., et al., Reprogramming of fibroblast nuclei in cloned bovine embryos involves major structural remodeling with both striking similarities and differences to nuclear phenotypes of in vitro fertilized embryos. Nucleus 5, 555–589 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Rosenthal D. L., Wojcik E. M., Kurtycz D. F. I., The Paris System for Reporting Urinary Cytology (Springer, 2016). [DOI] [PubMed] [Google Scholar]
- 17.Dahl K. N., Engler A. J., Pajerowski J. D., Discher D. E., Power-law rheology of isolated nuclei with deformation mapping of nuclear substructures. Biophys. J. 89, 2855–2864 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Swift J., et al., Nuclear lamin-A scales with tissue stiffness and enhances matrix-directed differentiation. Science 341, 1240104 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Oron A., Davis S. H., Bankoff S. G., Long-scale evolution of thin liquid films. Rev. Mod. Phys. 69, 931 (1997). [Google Scholar]
- 20.Deviri D., Discher D. E., Safran S. A., Rupture dynamics and chromatin herniation in deformed nuclei. Biophys. J. 113, 1060–1071 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Safran S. A., Statistical Thermodynamics of Surfaces, Interfaces, and Membranes (CRC Press, 2018). [Google Scholar]
- 22.Neelam S., Hayes P. R., Zhang Q., Dickinson R. B., Lele T. P., Vertical uniformity of cells and nuclei in epithelial monolayers. Sci. Rep. 6, 1–10 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Adame-Arana O., Safran S. A., Confined polymers in a poor solvent: The role of bonding to the surface. Macromolecules 54, 4760–4768 (2021). [Google Scholar]
- 24.Bajpai G., Pavlov D. A., Volk T., Safran S., Mesoscale phase separation of chromatin in the nucleus. Biophys. J. 118, 549a (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.De Gennes P.-G., Gennes P.-G., Scaling Concepts in Polymer Physics (Cornell University Press, 1979). [Google Scholar]
- 26.Dekker J., Rippe K., Dekker M., Kleckner N., Capturing chromosome conformation. Science 295, 1306–1311 (2002). [DOI] [PubMed] [Google Scholar]
- 27.Ou H. D., et al., Chromemt: Visualizing 3d chromatin structure and compaction in interphase and mitotic cells. Science 357, eaag0025 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Langowski J., Polymer chain models of DNA and chromatin. Eur. Phys. J. E Soft Matter 19, 241–249 (2006). [DOI] [PubMed] [Google Scholar]
- 29.Wood V., et al., The genome sequence of Schizosaccharomyces pombe. Nature 415, 871–880 (2002). [DOI] [PubMed] [Google Scholar]
- 30.Milo R., Phillips R., Cell Biology by the Numbers (Garland Science, 2015). [Google Scholar]
- 31.Guo M., et al., Cell volume change through water efflux impacts cell stiffness and stem cell fate. Proc. Natl. Acad. Sci. U.S.A. 114, E8618–E8627 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Cacciuto A., Luijten E., Self-avoiding flexible polymers under spherical confinement. Nano Lett. 6, 901–905 (2006). [DOI] [PubMed] [Google Scholar]
- 33.Phillips R., Kondev J., Theriot J., Garcia H. G., Orme N., Physical Biology of the Cell (Garland Science, 2012). [Google Scholar]
- 34.Overbeek J. T., The Donnan equilibrium. Prog. Biophys. Biophys. Chem. 6, 57–84 (1956). [PubMed] [Google Scholar]
- 35.Philipse A., Vrij A., The Donnan equilibrium: I. On the thermodynamic foundation of the Donnan equation of state. J. Phys. Condens. Matter 23, 194106 (2011). [DOI] [PubMed] [Google Scholar]
- 36.Adar R. M., Safran S. A., Active volume regulation in adhered cells. Proc. Natl. Acad. Sci. U.S.A. 117, 5604–5609 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Janmey P. A., Slochower D. R., Wang Y.-H., Wen Q., Cebers A., Polyelectrolyte properties of filamentous biopolymers and their consequences in biological fluids. Soft Matter 10, 1439–1449 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Andelman D., “Introduction to electrostatics in soft and biological matter” in Soft Condensed Matter Physics in Molecular and Cell Biology, Poon W. C. K., Andelman D., Eds. (Taylor & Francis, 2006), vol. 6, pp. 97–122. [Google Scholar]
- 39.Schiessel H., The physics of chromatin. J. Phys. Condens. Matter 15, R699 (2003). [DOI] [PubMed] [Google Scholar]
- 40.Rothe M., Höfer M., K+-fluxes and growth of Schizosaccharomyces pombe at various external k+-concentrations. Folia Microbiol. (Praha) 39, 543–545 (1994).8550018 [Google Scholar]
- 41.Crisp M., et al., Coupling of the nucleus and cytoplasm: Role of the LINC complex. J. Cell Biol. 172, 41–53 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ingber D. E., Cellular mechanotransduction: Putting all the pieces together again. FASEB J. 20, 811–827 (2006). [DOI] [PubMed] [Google Scholar]
- 43.Polte T. R., Eichler G. S., Wang N., Ingber D. E., Extracellular matrix controls myosin light chain phosphorylation and cell contractility through modulation of cell shape and cytoskeletal prestress. Am. J. Physiol. Cell Physiol. 286, C518–C528 (2004). [DOI] [PubMed] [Google Scholar]
- 44.Chowdhury F., Huang B., Wang N., Cytoskeletal prestress: The cellular hallmark in mechanobiology and mechanomedicine. Cytoskeleton (Hoboken) 78, 249–276 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Canović E. P., et al., Biomechanical imaging of cell stiffness and prestress with subcellular resolution. Biomech. Model. Mechanobiol. 13, 665–678 (2014). [DOI] [PubMed] [Google Scholar]
- 46.Schierbaum N., Rheinlaender J., Schäffer T. E., Combined atomic force microscopy (AFM) and traction force microscopy (TFM) reveals a correlation between viscoelastic material properties and contractile prestress of living cells. Soft Matter 15, 1721–1729 (2019). [DOI] [PubMed] [Google Scholar]
- 47.Park C. Y., et al., Mapping the cytoskeletal prestress. Am. J. Physiol. Cell Physiol. 298, C1245–C1252 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Svitkina T. M., Actin cell cortex: Structure and molecular organization. Trends Cell Biol. 30, 556–565 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Gunst S. J., Zhang W., Actin cytoskeletal dynamics in smooth muscle: A new paradigm for the regulation of smooth muscle contraction. Am. J. Physiol. Cell Physiol. 295, C576–C587 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Folker E. S., Baylies M. K., Nuclear positioning in muscle development and disease. Front. Physiol. 4, 363 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Heffler J., et al., A balance between intermediate filaments and microtubules maintains nuclear architecture in the cardiomyocyte. Circ. Res. 126, e10–e26 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Close R. I., Dynamic properties of mammalian skeletal muscles. Physiol. Rev. 52, 129–197 (1972). [DOI] [PubMed] [Google Scholar]
- 53.Linke W. A., Popov V. I., Pollack G. H., Passive and active tension in single cardiac myofibrils. Biophys. J. 67, 782–792 (1994). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Milo R., What is the total number of protein molecules per cell volume? A call to rethink some published values. BioEssays 35, 1050–1055 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Wühr M., et al., The nuclear proteome of a vertebrate. Curr. Biol. 25, 2663–2671 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Kopito R. B., Elbaum M., Reversibility in nucleocytoplasmic transport. Proc. Natl. Acad. Sci. U.S.A. 104, 12743–12748 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Kim S., Elbaum M., A simple kinetic model with explicit predictions for nuclear transport. Biophys. J. 105, 565–569 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Kim S., Elbaum M., Enzymatically driven transport: A kinetic theory for nuclear export. Biophys. J. 105, 1997–2005 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Wu Y., Pegoraro A. F., Weitz D. A., Janmey P., Sun S. X., The correlation between cell and nucleus size is explained by an eukaryotic cell growth model. PLoS Comput. Biol. 18, e1009400 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Deviri D., Safran S. A., Equilibrium size distribution and phase separation of multivalent, molecular assemblies in dilute solution. Soft Matter 16, 5458–5469 (2020). [DOI] [PubMed] [Google Scholar]
- 61.McGrath J. L., Tardy Y., Dewey C. F. Jr., Meister J. J., Hartwig J. H., Simultaneous measurements of actin filament turnover, filament fraction, and monomer diffusion in endothelial cells. Biophys. J. 75, 2070–2078 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Cooper G. M., Hausman R. E., The Cell: A Molecular Approach (ASM Press, Washington, DC, 2007), vol. 4. [Google Scholar]
- 63.Hetzer M. W., The nuclear envelope. Cold Spring Harb. Perspect. Biol. 2, a000539 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Gruenbaum Y., Margalit A., Goldman R. D., Shumaker D. K., Wilson K. L., The nuclear lamina comes of age. Nat. Rev. Mol. Cell Biol. 6, 21–31 (2005). [DOI] [PubMed] [Google Scholar]
- 65.Helfrich W. S. R. M., Servuss R.-M., Undulations, steric interaction and cohesion of fluid membranes. Il Nuovo Cimento D 3, 137–151 (1984). [Google Scholar]
- 66.Sapra K. Tanuj, et al., Nonlinear mechanics of lamin filaments and the meshwork topology build an emergent nuclear lamina. Nat. Commun. 11, 1–14 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Finan J. D., Chalut K. J., Wax A., Guilak F., Nonlinear osmotic properties of the cell nucleus. Ann. Biomed. Eng. 37, 477 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Evans E., Rawicz W., Entropy-driven tension and bending elasticity in condensed-fluid membranes. Phys. Rev. Lett. 64, 2094–2097 (1990). [DOI] [PubMed] [Google Scholar]
- 69.Stephens A. D., Banigan E. J., Adam S. A., Goldman R. D., Marko J. F., Chromatin and lamin a determine two different mechanical response regimes of the cell nucleus. Mol. Biol. Cell 28, 1984–1996 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Steudle E., Zimmermann U., Lüttge U., Effect of turgor pressure and cell size on the wall elasticity of plant cells. Plant Physiol. 59, 285–289 (1977). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Efremov A. K., Hovan L., Yan J., Nucleus size and its effect on the chromatin structure in living cells bioRxiv [Preprint] (2021). https://www.biorxiv.org/content/10.1101/2021.07.27.453925v2.full.pdf (Accessed 1 May 2022).
- 72.Landau L. D., Lifshitz E. M., Statistical Physics (Elsevier, 2013), vol. 5. [Google Scholar]
- 73.Mukherjee R. N., Chen P., Levy D. L., Recent advances in understanding nuclear size and shape. Nucleus 7, 167–186 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Kume K., et al., A systematic genomic screen implicates nucleocytoplasmic transport and membrane growth in nuclear size control. PLoS Genet. 13, e1006767 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Vuković L. D., Jevtić P., Zhang Z., Stohr B. A., Levy D. L., Nuclear size is sensitive to ntf2 protein levels in a manner dependent on ran binding. J. Cell Sci. 129, 1115–1127 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Ganguly A., et al., Perturbation of nucleo-cytoplasmic transport affects size of nucleus and nucleolus in human cells. FEBS Lett. 590, 631–643 (2016). [DOI] [PubMed] [Google Scholar]
- 77.Brownlee C., Heald R., Importin α partitioning to the plasma membrane regulates intracellular scaling. Cell 176, 805–815.e8 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Jahed Z., Soheilypour M., Peyro M., Mofrad M. R., The LINC and NPC relationship - It’s complicated! J. Cell Sci. 129, 3219–3229 (2016). [DOI] [PubMed] [Google Scholar]
- 79.Kim K., Guck J., The relative densities of cytoplasm and nuclear compartments are robust against strong perturbation. Biophys. J. 119, 1946–1957 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Buxboim A., et al., Coordinated increase of nuclear tension and lamin-A with matrix stiffness outcompetes lamin-B receptor that favors soft tissue phenotypes. Mol. Biol. Cell 28, 3333–3348 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Deviri D., et al., Scaling laws indicate distinct nucleation mechanisms of holes in the nuclear lamina. Nat. Phys. 15, 823–829 (2019). https://www.biorxiv.org/content/10.1101/2021.07.30.454418v1.full.pdf accessed: May 1st 2022. [Google Scholar]
- 82.Levy D. L., Heald R., Nuclear size is regulated by importin α and Ntf2 in Xenopus. Cell 143, 288–298 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Bhargava M. M., Halvorson H. O., Isolation of nuclei from yeast. J. Cell Biol. 49, 423–429 (1971). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Beel A. J., Matteï P.-J., Kornberg R. D., Mitotic chromosome condensation driven by a volume phase transition. bioRxiv [Preprint] (2021). https://www.biorxiv.org/content/10.1101/2021.07.30.454418v1.full.pdf (Accessed 1 May 2022).
- 85.Kumar A., Swain P., Mulder B. M., Chaudhuri D., Impact of crowders on the morphology of bacterial chromosomes. Europhys. Lett. 128, 68003 (2020). [Google Scholar]
- 86.Kose S., Imamoto N., Nucleocytoplasmic transport under stress conditions and its role in hsp70 chaperone systems. Biochim. Biophys. Acta 1840, 2953–2960 (2014). [DOI] [PubMed] [Google Scholar]
- 87.Hobson C. M., et al., Correlating nuclear morphology and external force with combined atomic force microscopy and light sheet imaging separates roles of chromatin and lamin a/c in nuclear mechanics. Mol. Biol. Cell 31, 1788–1801 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Lemiere J., Real-Calderon P., Holt L., Fai T., Chang F., Control of nuclear size by osmotic forces in Schizosaccharomyces pombe. bioRxiv [Preprint] (2021). https://www.biorxiv.org/content/10.1101/2021.12.05.471221v2.full.pdf (Accessed 1 May 2022). [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in this article and/or SI Appendix.