Bayesian group sequential enrichment designs based on adaptive regression of response and survival time on baseline biomarkers

Abstract

Precision medicine relies on the idea that, for a particular targeted agent, only a subpopulation of patients is sensitive to it and thus may benefit from it therapeutically. In practice, it is often assumed based on preclinical data that a treatment-sensitive subpopulation is known, and moreover that the agent is substantively efficacious in that subpopulation. Due to important differences between preclinical settings and human biology, however, data from patients treated with a new targeted agent often show that one or both of these assumptions are false. This paper provides a Bayesian randomized group sequential enrichment design that compares an experimental treatment to a control based on survival time and uses early response as an ancillary outcome to assist with adaptive variable selection and enrichment. Initially, the design enrolls patients under broad eligibility criteria. At each interim decision, submodels for regression of response and survival time on a baseline covariate vector and treatment are fit; variable selection is used to identify a covariate subvector that characterizes treatment-sensitive patients and determines a personalized benefit index, and comparative superiority and futility decisions are made. Enrollment of each cohort is restricted to the most recent adaptively identified treatment-sensitive patients. Group sequential decision cutoffs are calibrated to control overall type I error and account for the adaptive enrollment restriction. The design provides a basis for precision medicine by identifying a treatment-sensitive subpopulation, if it exists, and determining whether the experimental treatment is superior to the control in that subpopulation. A simulation study shows that the proposed design reliably identifies a sensitive subpopulation, yields much higher generalized power compared to several existing enrichment designs and a conventional all-comers group sequential design, and is robust.

1 |. INTRODUCTION

Physicians routinely make treatment decisions by accounting for the fact that any treatment’s effects are modulated by known prognostic covariates such as age or disease severity. Precision medicine is motivated by the idea that heterogeneity of patient response to an experimental treatment, E, may be due to biological covariates that modify the effects of E at the cellular or molecular level. If differences in drug effects are due to genes or proteins that affect drug-metabolizing enzymes, drug-specific transporters, or cell surface markers targeted by E, then only a subset of “E-sensitive” patients defined by biological covariates, such as gene or protein expression, may respond favorably to E. Precision medicine uses biological cariates to restrict administration of drug to an identified subset of E-sensitive patients, avoiding futile use of E in nonsensitive patients unlikely to benefit from E.

As examples, 70–90% of hypertension patients respond to ACE inhibitors, and beta 2-agonists for asthma work for 30–60% of patients (Abrahams and Silver, 2009). In such settings, traditional clinical trial designs with broad eligibility criteria may be dysfunctional. A trial design assuming homogeneity may show a small estimated E effect because the estimate is an average of positive outcomes of an E-sensitive subpopulation and negative outcomes of non-E-sensitive patients. Assuming homogeneity thus may lead to the incorrect inference that a new drug is ineffective for all patients, when in fact it is effective in a subgroup of E-sensitive patients.

An efficient approach to evaluating a new targeted agent is a clinical trial that uses an enrichment design that focuses on E-sensitive patients (FDA, 2012). Most existing enrichment designs assume that an E-sensitive subgroup is known, based on preclinical studies or limited phase II trial data, and enroll patients according to predetermined eligibility criteria (Brannath et al., 2009; Jenkins et al., 2011; Mehta et al., 2014; Kimani et al., 2015; Rosenblum et al., 2016; Uozumi and Hamada, 2017). Because this assumption is often incorrect, key problems are how to use biological covariates to (1) determine whether an E-sensitive subgroup exists, and if so identify it, and (2) determine whether E provides an improvement over a standard control therapy, C, in the subgroup. Simon and Simon (2013) proposed the adaptive enrichment design, which restricts entry to an E-sensitive patient subgroup that is modified adaptively based on interim data. They considered group sequential (GS) trials, defined an E-sensitive subgroup using a cutoff for a numerical biomarker, and focused on cutpoint optimization and power comparisons of adaptive versus nonadaptive enrichment designs. Freidlin and Simon (2005) and Freidlin et al. (2010) proposed an adaptive signature design for a binary endpoint and used machine learning to select E-sensitive patients.

In this paper, we propose a GS adaptive enrichment design, AED, based on a time-to-event variable, Y, and an early response indicator, Z, with adaptive variable selection and enrichment. We are motivated by the facts that long-term events are rarely observed early in the trial, but Z is observed much sooner and may be related to treatment, covariates x, and Y. AED exploits these relationships to start adaptive enrichment early in the trial. We assume a Bayesian model with the distribution of Y a mixture over responders and nonresponders, including regression models for the probability of Z and Y on x. We define a personalized benefit index (PBI) to be a predictive probability that a patient with a given x will benefit more from E than from C. Both regression models are updated at each interim analysis by performing covariate selection, refitting the models using the newly selected subvector of x to define E-sensitive patients, and using this to update the PBI and eligibility criteria. Weights between the response and survival time components of the PBI are changed adaptively, with more weight given to survival time as the trial progresses.

Our proposed AED makes three major contributions. First, we develop a covariate selection method to characterize E-sensitive patients based on both Z and Y. Second, we define a PBI based on both endpoints to quantify the comparative E-versus-C benefit of a patient with given x, and we use this to define an adaptive enrichment rule. Third, we propose a Bayesian GS design based on this structure, including a new test statistic that accounts for the sequentially adaptive variable selection and resulting modification of the enrichment rule during the trial.

Our proposed AED is motivated by a clinical trial to investigate the effect of a novel PI3K pathway inhibitor (E) combined with olaparib for treating high-grade serous or BRCA-mutant ovarian cancer patients. Olaparib is a potent inhibitor of poly(ADP-ribose) polymerase (PARP), an enzyme involved in base-excision repair of single-strand DNA breaks. Treatment with olaparib can lead to tumor regression by a process known as synthetic lethality, which is a result of the accumulation of unrepaired DNA double-strand breaks and an unsupportable increase of genomic instability in the cancer cells. The PI3K pathway is involved in cellular proliferation and is often upregulated in high-grade serous ovarian cancer. The aim of combining PARP and PI3K pathway inhibition is to generate a synergistic treatment effect. The statistical challenge for this trial is that clinicians expect that only a subgroup of patients will benefit from E. The study has two closely related objectives. The first objective is to identify a genomic signature that predicts clinical response to E + olaparib. Mutational analysis is performed using the sequencing platform Sequenom MassARRAY. Ten mutations related to PARP and PI3K pathway will be used as biomarkers, x, for identifying a genomic signature characterizing an E-sensitive subgroup. The second objective is to evaluate whether E + olaparib is more effective than the standard treatment, cisplatin combined with paclitaxel (C) in the identified sensitive subgroup. Treatment efficacy is characterized by objective response (Z) and progression free survival time (Y). Thus, our proposed AED addresses the data structure and goals of this trial.

The remainder of the paper is organized as follows. In Section 2, we describe the mixture model for the short-term and long-term endpoints and present the GS procedure for performing adaptive variable selection, modifying the enrichment criterion, and doing treatment comparison. The proposed AED’s performance is evaluated and compared to existing methods by simulation in Section 3. We close with a discussion in Section 4.

2 |. DESIGN STRUCTURE

We consider a comparative clinical trial with patients randomized to E (G = 1) or C (G = 0) in a fixed ratio. For each patient, we assume that a covariate vector $\mathbf{x}\in {ℝ}^p$ is available at enrollment and a short-term response indicator Z and time-to-event endpoint Y are observed. In cancer trials, Z may be the indicator of ≥50% shrinkage of a solid tumor at 12 weeks compared to baseline, and Y typically is overall survival or progression-free survival time. For right censoring of Y at follow-up time U when the data are evaluated for interim decision-making, we define the observed event time Y⁰ = min(Y,U) and event indicator δ = I(Y ≤ U).

In treatment arm G = 0 or 1, denote π(x, G, θ_Z) = Pr(Z = 1|G, x, θ_Z), and let h_G(y|x, Z, θ_Y) denote the hazard function of Y at time y for a patient with covariates x and response indicator Z, where θ_Z and θ_Y are the model parameter vectors. At each decision in the GS design, our proposed design adaptively selects two subvectors of x to identify patients expected to benefit more from E than C in terms of Z or Y. The first subvector, x_z, is identified by doing variable selection in the regression model for (Z | G, x), based on the difference in response probabilities, Δ_Z(x, θ_Z) = π(x, 1, θ_Z) − π(x, 0, θ_Z). The parametric function Δ_z(x, θ_z) generalizes the indicator function f(x) = [π(x, 1) > π(x, 0)] used by Simon and Simon (2013) to define an enrichment subset. The second subvector, x_Y, is identified by doing variable selection in the regression model for (Y | Z, G, x), based on the hazard ratio Δ_Y(x, θ_Y) = h₁(y|x, Z, θ_Y)∕h₀(y|x, Z, θ_Y), for y > 0. While x_z and x_y may not be identical, they may share common terms, since a covariate predictive of a higher tumor response probability often is predictive of longer survival. To account for association, selection of x_Z and x_Y is not done independently, but rather are based on correlated vectors of latent variable selection indicators. This is described in Section 2.2.

Our design enrolls a maximum of N patients sequentially in cohorts of sizes C₁,...,C_K, with ${\sum }_{k=1}^K{c}_k=N$. The schema of the design is shown in Figure 1. The design uses a Bayesian GS test procedure including both superiority and futility stopping rules for comparing E to C in the most recently identified E-sensitive subset. The trial begins by enrolling patients under broad eligibility criteria for the first cohort of c₁ patients. When the first cohort has been enrolled and its patients’ outcomes have been evaluated, the subvectors x_Z and x_Y of x are chosen and used to compute a PBI, given formally in Section 2.3. The PBI is used to define the subgroup of E-sensitive patients, and the comparative tests are defined in terms of the E-sensitive patients. These tests possibly may terminate the trial due to either superiority or futility, but if the trial is not stopped early then only E-sensitive patients are enrolled in the second cohort. This process of identifying (x_Z, x_Y), computing the PBI, defining the set of E-sensitive patients, and performing the tests is repeated group sequentially until the end of the trial. If the maximum sample size N is reached, a final analysis is done when the last patient has been enrolled and his/her follow-up completed.

FIGURE 1.

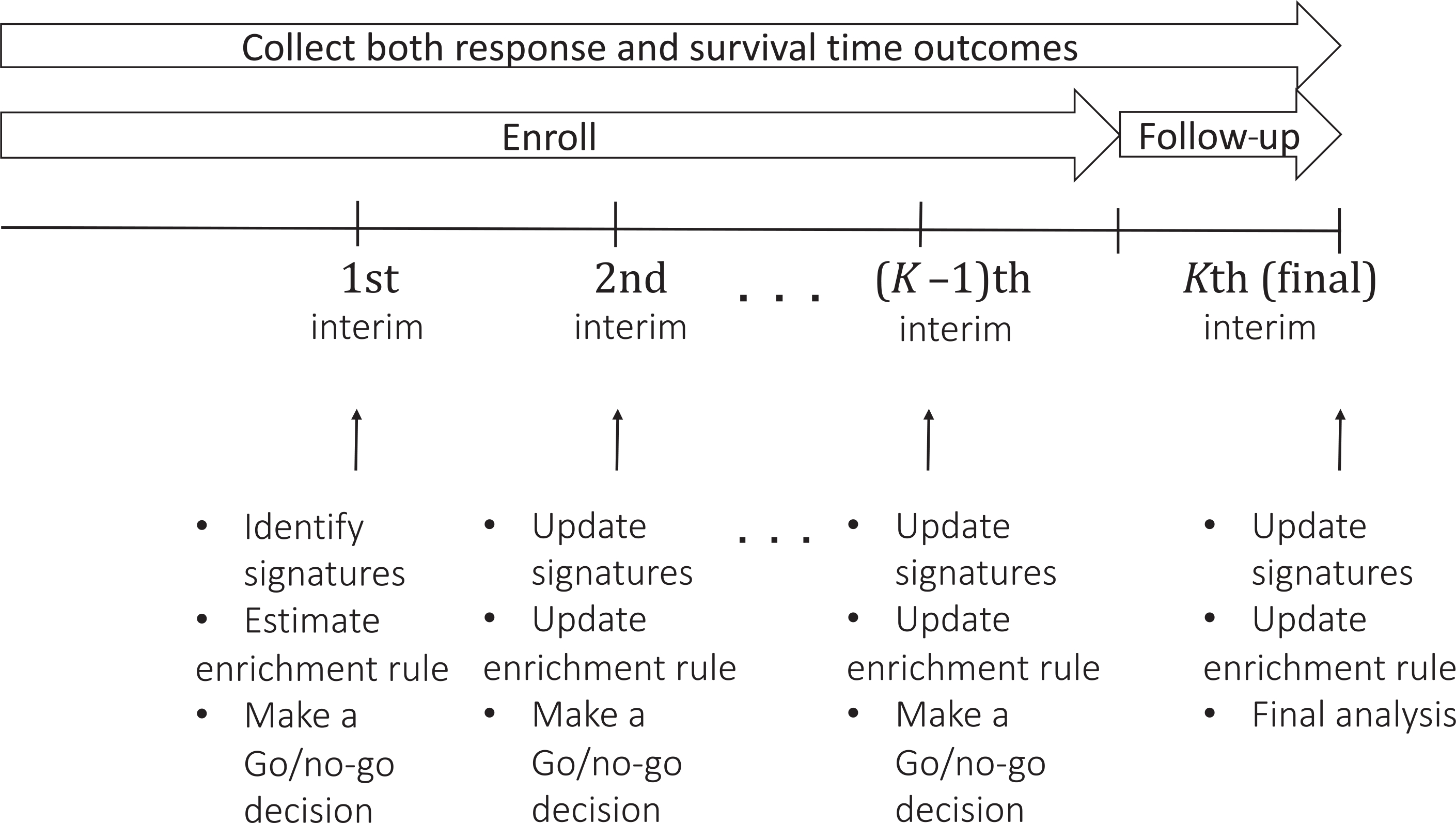
Schema of the proposed design

Below, we provide details of the probability model for (x, G, Z, Y), how sequentially adaptive variable selection and enrichment are done, and the Bayesian GS decision-making procedure.

2.1 |. Probability model

We construct a joint probability model for (Y, Z | G, x) as a mixture of the conditional distribution of (Y | Z, G, x) weighted by the marginal distribution of (Z | G, x) We will assume that Z always is observed before Y. However, if Y may be observed before Z can be evaluated, which can arise when dealing with rapidly fatal diseases, then a model elaboration is needed. We provide this, similarly to the mixture model of Inoue et al. (2002), in Web Appendix A.

For the marginal distribution of (Z ∣ x, G) we assume a probit model $\pi \left({\mathbf{x}}_i,G_i,{\theta }_Z\right)=\mathrm{\Phi }\left({\tilde{x}}_i^{\top }{\mathbf{\beta }}_Z+G_i{\tilde{x}}_i^{\top }{\mathbf{\gamma }}_Z\right)$, where i = 1, ..., n, indexes patients, Φ(·) denotes the standard normal cumulative distribution function, $\tilde{x}={\left(1,{\mathbf{x}}^{\top }\right)}^{\top }$ and ${\theta }_Z={\left({\mathbf{\beta }}_Z^{\top },{\mathbf{\gamma }}_Z^{\top }\right)}^{\top }$ is the regression coefficient parameter vector. Thus, β_Z is the vector of covariate main effects and γ_Z = (γ_Z,0, γ_Z,1, ..., γ_Z,p)^⊤ is the vector of additional E-versus-C treatment-covariate interactions, with the main experimental versus control effect γ_Z,0 Denoting Z_n = (Z₁, ... , Z_n), G_n = (G₁, ... , G_n) and ${\mathbb{X}}_n={\left({\mathit{x}}_1,...,{\mathit{x}}_n\right)}^{\top }$, the marginal likelihood of Z for the first n patients is

$$\begin{gathered} {\mathcal{L}}_n\left({\mathbf{Z}}_n,{\mathbf{G}}_n,{\mathbb{X}}_n,{\theta }_Z\right)=\prod _{i=1}^n\mathrm{\Phi }{\left({\tilde{\mathit{x}}}_i^{\top }{\mathit{\beta }}_Z+G_i{\tilde{\mathit{x}}}_i^{\top }{\mathbf{\gamma }}_Z\right)}^{Z_i} \\ \times {\left\{1-\mathrm{\Phi }\left({\tilde{\mathit{x}}}_i^{\top }{\mathit{\beta }}_Z+G_i{\tilde{\mathit{x}}}_i^{\top }{\mathbf{\gamma }}_Z\right)\right\}}^{1-Z_i}. \end{gathered}$$

For the conditional distribution of (Y | Z, G, x) we assume a proportional piecewise exponential (PE) hazard model (Sinha et al., 1999; McKeague and Tighiouart, 2000; Ibrahim et al., 2005; Kim et al., 2007). We first specify a partition of the time axis into M intervals s I_m = (τ_m−1, τ_m] for m = 1, ... , M, with a fixed time grid {τ₀, τ₁, ... , τ_M}such that 0=τ₀ < τ₁ <⋯< ∞ The assumed proportional PE hazard function is

$$\begin{array}{l}h\left(y\mid Z,G,\mathbf{x},{\mathit{\theta }}_Y\right)={\varphi }_m\exp \left({\mathit{x}}^{\top }{\mathit{\beta }}_Y+G{\tilde{x}}^{\top }{\mathit{\gamma }}_Y+{\alpha }_{Y}Z\right)\\ \times I\left(y\in {\text{I}}_m\right),m=1,...,M,\end{array}$$

with ${\mathit{\theta }}_Y={\left({\varphi }_1,...,{\varphi }_M,{\mathit{\beta }}_Y^{\top },{\mathit{\gamma }}_Y^{\top },{\alpha }_Y\right)}^{\top }$ the parameter vector, where ϕ_m > 0 is the hazard on the mth subinterval and α_Y is the main effect of response (Z = 1) on the hazard of Y. For each m = 1, ... , M, we define y_m = τ_m−1 if y ≤ τ_m−1, y_m = y if τ_m−1 < y ≤ τ_m and y_m = τ_m if y > τ_m. Given this definition of y_m, the resulting PE cdf is

$$\begin{gathered} F\left(y\mid Z,G,\mathit{x},{\mathit{\theta }}_Y\right)=1-\exp \{-\sum _{m=1}^M{\varphi }_m\left(y_m-{\tau }_{m-1}\right) \\ \times \exp \left({\mathit{x}}^{\top }{\mathit{\beta }}_Y+G{\tilde{x}}^{\top }{\mathit{\gamma }}_Y+{\alpha }_{Y}Z\right)\} \end{gathered}$$

for y > 0.

Denote ${\mathit{Y}}_n^o=\left(Y_1^o,...,Y_n^o\right)$, δ_n = (δ₁, ... , δ_n), and ${\mathcal{O}}_n=\left({\mathbf{Z}}_n,{\mathbf{Y}}_n^o,{\mathit{\delta }}_n\right)$, the observed data from the first n patients in the trial. The joint likelihood function of the short-term endpoint Z and long-term endpoint Y is

$$\begin{array}{l}{\mathcal{L}}_n\left({\mathcal{O}}_n,{\mathbf{G}}_n,{\mathbb{X}}_n,{\mathit{\theta }}_Z,{\mathit{\theta }}_Y\right)\hfill \\ ={\mathcal{L}}_n\left({\mathbf{Z}}_n,{\mathbf{G}}_n,{\mathbb{X}}_n,{\mathit{\theta }}_Z\right)\prod _{i=1}^n{\left\{f\left(Y_i^o\mid Z_i,G_i,{\mathit{x}}_i,{\mathit{\theta }}_Y\right)\right\}}^{{\delta }_i}\hfill \\ \times {\left\{1-F\left(Y_i^o\mid Z_i,G_i,{\mathit{x}}_i,{\mathit{\theta }}_Y\right)\right\}}^{1-{\delta }_i},\hfill \end{array}$$ (1)

where f(Y|Z, G, x, θ_Y) is the conditional density function of Y. The marginal likelihood function of Y is obtained by averaging the joint likelihood function of (Y, Z) over Z. We do Bayesian posterior computation. For θ_Z, as in Albert and Chib (1993), using data augmentation, based on the iid latent real-valued variables ${\tilde{Z}}_1,...,{\tilde{Z}}_n$, with Z_i = 1 if and only if ${\tilde{Z}}_i>0$ and Z_i = 0 otherwise. We assume ${\tilde{Z}}_i\mid G_i,{\mathit{x}}_i,{\mathit{\theta }}_Z~\mathcal{N}\left({\tilde{x}}_i^{\top }{\mathit{\beta }}_Z+G_i{\tilde{x}}_i^{\top }{\mathit{\gamma }}_Z,1\right)$ with prior ${\mathit{\theta }}_Z={\left({\mathit{\beta }}_Z^{\top },{\mathit{\gamma }}_Z^{\top }\right)}^{\top }~\mathcal{N}\left({\mathit{\mu }}_Z,{\text{Σ}}_Z\right)$, where μ_Z and Σ_Z are prespecified hyperparameters, and the normal variance is set equal to 1 to ensure identifiability. In our simulations, we assume vague normal priors with zero mean vector and diagonal covariance matrix with large diagonal elements 10⁶. An alternative approach is to use a logistic model, rather than the probit model. In this case, Bayesian posterior computation can be carried out efficiently using data augmentation based on the Polya–Gamma latent variable (Polson et al., 2013). For θ_Y, we assume a normal prior on both ${\left({\mathit{\beta }}_Y^{\top },{\mathit{\gamma }}_Y^{\top }\right)}^{\top }$ and α_Y and independent gamma distributions on ϕ = (ϕ₁, ... , ϕ_M), as follows: ${\left({\mathit{\beta }}_Y^{\top },{\mathit{\gamma }}_Y^{\top }\right)}^{\top }~\mathcal{N}\left({\mathit{\mu }}_Y,{\text{Σ}}_Y\right)$, ${\alpha }_Y~\mathcal{N}\left(a,{\sigma }_a^2\right)$ and ${\varphi }_m~\mathrm{Gamma}\left(c{\varphi }_m^{*},c\right)$, m = 1, ... , M, where μ_Y, Σ_Y, a, σ_a, c and ${\varphi }_m^{*}$, m = 1, ... , M are prespecified hyperparameters and Gamma(g₁, g₂) denotes a gamma random variable with shape parameter g₁ and rate parameter g₂.

2.2 |. Sequentially adaptive variable selection

A key goal is to identify subvectors of x that identify patients more likely to benefit from E. We do this by performing joint variable selection on x in each of the submodels for (Y | Z, G, x) and (Z | G, x), exploiting treatment–covariate interactions. The joint variable selections are based on correlated latent covariate inclusion variables that account for the possibility that a covariate predictive of one outcome may also be predictive of the other. In the joint likelihood function of Z and Y given in (1), for each t = Z or Y, let ψ_t denote the regression coefficient vector, excluding the intercept, so ψ_Z = (β_Z,₁, ... , β_Z,P, γ_Z,₀, γ_Z,₁, ... , γ_Z,_p) and ψ_Y = (β_Y,1, ... , β_Y,p, γ_Y,0, γ_Y,1, ... , γ_Y,p). If needed, we will use ψ_Z,0 to denote the regression intercept parameter for Z.

For each submodel, t = Z or Y, we perform Bayesian variable selection assuming spike-and-slab prior on ψ_t (Mitchell and Beauchamp, 1988; George and McCulloch, 1993; Ishwaran et al., 2005). This uses sparse posterior coefficient estimates to determine which variables to include in the submodel’s linear component. For each t, let λ_t = (λ_t,1, ... , λ_t,2p+1)^T be a vector of latent variable selection indicators corresponding to (x, G, Gx) in the linear term. The jth variable in (x, G, Gx) is included in the submodel for outcome t if λ_t,j = 1 and excluded if λ_t,j = 0.We restrict the variable selection algorithm in each submodel so that, if the interaction term Gx_j is included, then the main effect term x_j corresponding to Gx_j and G also must be included. This is known as the strong hierarchy interaction constraint (Liu et al., 2015).

Because some covariates may be predictive of treatment effects on both Z and Y, it is not appropriate to select subvectors x_Z and x_Y independently using the regression submodels for (Z | G, x) and (Y | Z, G, x). We thus endow λ_Z and λ_Y with a joint distribution, to borrow information about covariate effects on Z and Y, and refer to variable selection using (λ_Z, λ_Y) as “joint variable selection.” To account for correlation, we assume a bivariate Bernoulli distribution for (λ_Z,j, λ_Y,j), for j = 1,...,2p + 1. Denote p_Z,j = Pr(λ_Z,j = 1) and P_Y,j = Pr(λ_Y,j = 1), the marginal probabilities that the jth variable is included in the submodel for (Z |G, x) and (Y | Z, G, x), respectively, and let

$${\rho }_j=\frac{\mathrm{Pr}\left({\lambda }_{Y,j}=1,{\lambda }_{Z,j}=1\right)/\mathrm{Pr}\left({\lambda }_{Y,j}=0,{\lambda }_{Z,j}=1\right)}{\mathrm{Pr}\left({\lambda }_{Y,j}=1,{\lambda }_{Z,j}=0\right)/\mathrm{Pr}\left({\lambda }_{Y,j}=0,{\lambda }_{Z,j}=0\right)}$$

denote the odds ratio for the jth pair of latent variables. Thus, ρ_j is the ratio of the odds of λ_Z,j = 1 given λ_Y,j = 1 and the odds of λ_Z,j = 1 given λ_Y,j = 0. We denote by $\mathcal{B}\left(p_{Z,j},p_{Y,j},{\rho }_j\right)$ the joint Bernoulli distribution of (λ_Z,j, λ_Y,j). A detailed description is given in Web Appendix B.

Our spike-and-slab prior model used for the joint variable selection is

$$\begin{array}{l}{\psi }_{Z,j}\mid {\lambda }_{Z,j}~\left(1-{\lambda }_{Z,j}\right)\mathcal{N}\left(0,{\tau }_{Z,j}^2\right)+{\lambda }_{Z,j}\mathcal{N}\left(0,u_{Z,j}^2{\tau }_{Z,j}^2\right),\\ j=1,...,2p+1\end{array}$$ (2)

$$\begin{array}{l}{\psi }_{Y,j}\mid {\lambda }_{Y,j}~\left(1-{\lambda }_{Y,j}\right)\mathcal{N}\left(0,{\tau }_{Y,j}^2\right)+{\lambda }_{Y,j}\mathcal{N}\left(0,u_{Y,j}^2{\tau }_{Y,j}^2\right),\\ j=1,...,2p+1,\end{array}$$ (3)

where u_Z,j, ${\tau }_{Z,j}^2$, u_Y,j, ${\tau }_{Y,j}^2$, j = 1, ... , 2P + 1 are prespecified hyperparameters. We choose large u_Z,j and small τ_Z,j in (2) so that λ_Z,j = 1 implies that a nonzero estimate of ψ_Z,j is included, whereas λ_Z,j = 0 implies that the covariate corresponding to ψ_Z,j has negligible effect on Z. Similar choices are applied to (3) to obtain sparse vectors of coefficient estimates for Y. The latent indicator variables are assumed to follow the prior distributions $\left({\lambda }_{Z,j},{\lambda }_{Y,j}\right)\mid p_{Z,j},p_{Y,j},{\rho }_j~\mathcal{B}\left(p_{Z,j},p_{Y,j},{\rho }_j\right)$ for j = 1,...,p + 1 and λ_Z,j ~ Bernoulli(p_Z,j) and λ_Y,j ~ Bernoulli(p_Y,j), for j = p + 2,...,2p + 1. To ensure the strong hierarchical property, we impose the constraints

$$\begin{array}{l}{p}_{Z,j}=p_{Z,j-p-1}{p}_{Z,p+1}\min \left\{p_{Z,j-p-1},p_{Z,p+1}\right\},\\ j=p+2,...,2p+1\end{array}$$

$$\begin{array}{l}{p}_{Y,j}=p_{Y,j-p-1}{p}_{Y,p+1}\min \left\{p_{Y,j-p-1},p_{Y,p+1}\right\},\\ j=p+2,...,2p+1.\end{array}$$ (5)

Thus, the main effects are correlated through the bivariate Bernoulli distribution and the interactions follow the strong hierarchy property through (4) and (5). We specify prior distributions for the remaining parameters as follows:

$$\begin{array}{l}{\psi }_{Z,0}~\mathcal{N}\left(u_0,{\tau }_0^2\right),{\alpha }_Y~\mathcal{N}\left(u_a,{\tau }_a^2\right),\\ {\varphi }_m~\mathrm{Gamma}\left(\tilde{c}{\tilde{\varphi }}_m,\tilde{c}\right),m=1,...,M,\\ p_{Z,j}~\mathrm{Beta}\left(l_{Z1,j},l_{Z2,j}\right),p_{Y,j}~\mathrm{Beta}\left(l_{Y1,j},l_{Y2,j}\right),\\ \log {\rho }_j~\mathcal{N}\left(r_{1j},r_{2j}\right),j=1,...,p+1,\end{array}$$

where u₀, τ₀, u_a, τ_a, $\tilde{c}$, ${\tilde{\varphi }}_m$, m = 1, ... , M, l_Z1,j, l_Z2,j, l_Y1,j, l_Y2,j, r_1j, and r_2j, j = 1,...,p + 1, are prespecified hyperparameters. Details of the Monte Carlo Markov chain computations for the joint variable selection are given in Web Appendix C.

We have considered correlated indicator variables for inclusion of covariates in models for Z and Y, for each variable in {x, G, Gx}, but our construction assumes that the predictors are independent. If desired, the joint variable selection algorithm can be extended to the case where the predictors may be correlated. As in George and McCulloch (1993), we may generalize the distributions to be the multivariate normal priors

$$\begin{array}{l}{\mathit{\psi }}_Z\mid {\mathit{\lambda }}_Z~{\mathcal{N}}_{2p+1}\left(\mathbf{0},{\mathbf{D}}_{\lambda }\mathbf{R}{\mathbf{D}}_{\lambda }\right)\text{and}{\mathit{\psi }}_Y\mid {\mathit{\lambda }}_Y\\ ~{\mathcal{N}}_{2p+1}\left(\mathbf{0},{\tilde{\mathbf{D}}}_{\lambda }\tilde{\mathbf{R}}{\tilde{\mathbf{D}}}_{\lambda }\right),\end{array}$$

where D_λ is a diagonal matrix with a_jτ_Z,j, j = 1,...,2p + 1 with a_j = 1 if λ_Z,j = 0 and a_j = u_Z,J if λ_Z,J = 1, and ${\tilde{\mathbf{D}}}_{\lambda }$ is a diagonal matrix with ${\tilde{a}}_j{\tau }_{Y,j}$, j = 1,..., 2p + 1 with ${\tilde{a}}_j=1$ if λ_Y,j = 0 and ${\tilde{a}}_j=u_{Y,j}$ if λ_Y,j = 1 Thus, R and $\tilde{\mathbf{R}}$ are the prior correlation matrices for ψ_Z|λ_Z and ψ_Y|λ_Y. If the predictors in {x, G, Gx} are correlated, the prior correlation matrix may be specified to be proportional to (X^TX)⁻¹, where X denotes the design matrix, implying that the prior correlation is the same as the design correlation.

During the trial, joint variable selection is performed at each interim stage to obtain the subvectors x_Z and x_Y. While this procedure may miss informative covariates in x_Y early in the trial, due to an insufficient number of observed events for Y, as the trial progresses the probabilities of identifying truly important covariates with interactive effects increase. Thus, it is important to repeatedly reselect x_z and x_y as new data become available for each GS decision.

2.3 |. Adaptive enrichment

Recall that the latent indicator variables λ_Z and λ_Y identify covariates included in the regression submodels for (Z | G, x,) and (Y | Z, G, x), which are used to make adaptive GS decisions. For each cohort k = 1,...,K, let d_k be the accumulated number of events (i.e., $Y_i=Y_i^0$) at the time when the kth adaptive enrichment is performed, and let $n_k={\sum }_{j=1}^k{c}_j$ be the total number of patients enrolled in the first k cohorts. Let ${\mathcal{D}}_k=\{\left(Y_i^0,{\delta }_i,Z_i,G_i,{\mathit{x}}_i\right)$ be the accumulated data and ${\mathit{x}}_Z^{(k)}$ and ${\mathit{x}}_Y^{(k)}$ the selected subvectors at the kth interim decision. We define the PBI for a patient with covariate vector x as

$$\begin{array}{l}\Omega \left(\mathit{x}\mid {\mathcal{D}}_k\right)=\left(1-{\omega }_k\right)\mathrm{Pr}\left\{{\Delta }_Z\left({\mathit{x}}_Z^{(k)},{\theta }_Z\right)>{ϵ}_1\mid {\mathcal{D}}_k\right\}\\ +{\omega }_k\mathrm{Pr}\left\{{\mathrm{\Delta }}_Y\left({\mathit{x}}_Y^{(k)},{\theta }_Y\right)<{ϵ}_2\mid {\mathcal{D}}_k\right\},\end{array}$$ (6)

where the weight is ω_k = d_k∕n_k. Thus, the PBI is a weighted average of the posterior probabilities that a patient with covariates x will benefit from E more than C, defined in terms of the comparative treatment effect parameters ${\mathrm{\Delta }}_Z\left({\mathit{x}}_Z^{(k)},{\mathit{\theta }}_Z\right)$ and ${\mathrm{\Delta }}_Y\left({\mathit{x}}_Y^{(k)},{\mathit{\theta }}_Y\right)$ The PBI depends on x only through the selected subvectors ${\mathit{x}}_Z^{(k)}$ and ${\mathit{x}}_Y^{(k)}$ that is, $\Omega \left(\mathit{x}\mid {\mathcal{D}}_k\right)=\Omega \left({\mathit{x}}_Z^{(k)},{\mathit{x}}_Y^{(k)}\mid {\mathcal{D}}_k\right)$. The cutoffs ∊₁ and ∊₂ are design parameters specified to quantify minimal clinically significant improvements in response probability and survival, respectively. Early in the trial, when there are few observed event times, the PBI will depend on Z more than on Y for identification of patients who potentially may benefit from E. As more events occur, the weight ω_k for the survival hazard ratio component in (6) becomes larger and the weight (1 – ω_k) for the response probability difference becomes smaller, so the PBI depends more on the survival time data. To use the PBI for decision-making, we consider a patient with biomarker profile x to be eligible for enrollment into the k + 1st cohort of the trial if their PBI is sufficiently large, formalized by the rule

$$\Omega \left(\mathit{x}\mid {\mathcal{D}}_k\right)=\Omega \left({\mathit{x}}_Z^{(k)},{\mathit{x}}_Y^{(k)}\mid {\mathcal{D}}_k\right)>v{\left(\frac{n_k}{N}\right)}^g$$ (7)

for k= 1, ... , K − 1, where ν > 0 and g > 0 are prespecified design parameters. A practical method for determining ν and g is provided in Web Appendix D. This type of adaptive probability threshold was used previously by Zhou et al. (2017). Thus, at this stage of the trial, the set of E-sensitive patients is defined adaptively as those having covariate vectors satisfying the eligibility condition (7), which depends on the most recently selected subvectors ${\mathit{x}}_Z^{(k)}$ and ${\mathit{x}}_Y^{(k)}$. If the trial is not stopped early, when the Kth cohort’s outcomes have been evaluated at the end of the final follow up period, the PBI = Ω(x| D_k) is updated and used as a basis for the final tests. |

2.4 |. Bayesian sequential monitoring rules

To specify Bayesian decision criteria, we use the treatment effect averaged over the enriched trial population, which still may contain a wide spectrum of patients. The kth interim decisions are based on D_k, which consists of the accumulated data from k successive cohorts. Patients within each cohort are homogeneous since they satisfy the same eligibility criteria, but patients may be heterogeneous between cohorts since different cohorts may have different eligibility criteria because the variable selection is repeated and the PBI is refined during the trial. To make GS decisions for superiority or futility based on treatment effects on Y, the rules used by the design follow the same logical structure as those of a conventional GS test, with one important difference. Prior to each test, the set of E-sensitive patients first must be determined in order to use the most recently selected ${\mathit{x}}_Z^{(k)}$ and ${\mathit{x}}_Y^{(k)}$ to define the test statistics and to determine the enrollment criteria for the next cohort if the trial is continued. Let

$${\mathcal{X}}_k=\left\{\mathit{x}:\text{Ω}\left({\mathit{x}}_Z^{(k)},{\mathit{x}}_Y^{(k)}\mid {\mathcal{D}}_k\right)>v{\left(n_k/N\right)}^g\right\}$$

denote the set of the covariates satisfying the eligibility criteria used for the k + 1st cohort. At this point in the trial, we define the covariate-averaged long-term outcome treatment effect to be

$$T_{Y,k}(\theta )={\int }_{{\mathcal{X}}_k}{\mathrm{\Delta }}_Y\left({\mathit{x}}_Y^{(k)},{\mathit{\theta }}_Y\right){\widehat{p}}_k\left({\mathit{x}}_Y^{(k)}\right)d{\mathit{x}}_Y^{(k)},$$

where ${\widehat{p}}_k\left({\mathit{x}}_Y^{(k)}\right)$ denotes the empirical distribution of ${\mathit{x}}_Y^{(k)}$ on the set ${\mathcal{X}}_k$. Since these expectations are computed over the selected enrichment set ${\mathcal{X}}_k$, that is, the patients who are expected to benefit more from E than C in the kth cohort, T_Y,k(θ) is a treatment effect in the sense of precision medicine. Note that E is more effective than C for patients with $\mathit{x}\in {\mathcal{X}}_k$ if T_Y,k(θ) is sufficiently small.

To define GS test statistics, we must account for the fact that, due to adaptive enrichment, there are k heterogeneous cohorts at the kth analysis, and the empirical distribution ${\widehat{p}}_k\left({\mathit{x}}_Y^{(k)}\right)$ changes with k as new data are obtained. Thus, denoting the number of events in the jth cohort by e_j, we define the test statistic at the kth analysis as the weighted average of the treatment effects, ${\overline{T}}_{Y,k}(\theta )={\sum }_{j=1}^k{w}_{Y,j}{T}_{Y,j}(\theta )$ where the jth weight is $w_{Y,j}=e_j/{\sum }_{l=1}^k{e}_l$ (Lehmacher and Wassmer, 1999). Note that T_Y,k(θ) is calculated based on the data observed at the interim time. As Y is a time-to-event endpoint, T_Y,k(θ) must be updated at each later interim decision time. Let b₁ denote the hazard ratio (e.g., ≤ 1) under which E is deemed superior to C in the long-term endpoint Y, and let b₂ denote the hazard ratio (e.g., ≥ 1) under which E is deemed inferior to C. The values of (b_1, b₂) typically are prespecified by the clinicians. Let (B_1, B₂) be prespecified probability cutoffs obtained by preliminary simulation-based calibration. A practical procedure to calibrate the values of (B_1, B₂) is provided in Web Appendix E. For the interim analysis at each k= 1, ..., K − 1, the decision rules are as follows:

1. Superiority: Stop the trial for superiority of E over C in ${\mathcal{X}}_k$ if $\mathrm{Pr}\left\{{\overline{T}}_{Y,k}(\mathit{\theta })<b_1\mid {\mathcal{D}}_k\right\}>B_1$.

2. Futility: Stop the trial for futility of E over C in ${\mathcal{X}}_k$ if $\mathrm{Pr}\left\{{\overline{T}}_{Y,k}(\mathit{\theta })>b_2\mid {\mathcal{D}}_k\right\}>B_2$.

3. Final Decision: If the trial is not stopped early, at the last analysis (k = K), conclude that E is superior to C in the final E-sensitive subset ${\mathcal{X}}_K$ if $\mathrm{Pr}\{{\overline{T}}_{Y,K}(\mathit{\theta })<b_1\mid {\mathcal{D}}_K\}>B_1$, and otherwise conclude that E is not superior to C in ${\mathcal{X}}_K$.

An important practical issue during the process of constructing a design is deciding when to begin the adaptive enrichment. This depends on several factors, including the number of covariates, their information-to-noise ratio, the percentage of sensitive patients, the treatment difference between sensitive and insensitive patients, and the variances of the outcomes Z and Y. In practice, logistical limitations will often limit the number of interim decisions to 1, 2, or 3. Based on these considerations, as a rule of thumb, a reasonable time to initiate the adaptive enrichment is after 1/3 to 1/2 of the maximum number of patients has been enrolled.

If desired, at each interim analysis, the following additional futility stopping rule may be included to account for the possibility that only a very small percentage of patients may benefit from E. For a prespecified lower threshold 0 < q < 1 based on practical considerations, the futility rule stops the trial if the estimated proportion of E-sensitive patients in the trial is < q. We use q = 0.10 in the simulation study and recommend to use a value in the range 0.01 – 0.10 in practice.

At the end of the trial, identification of the final E-sensitive subset ${\mathcal{X}}_K$ based on PBI involves all covariates, because the Bayesian variable selection method based on the spike-and-slab prior does not necessarily drop covariates with little or no contribution to identify ${\mathcal{X}}_K$. To facilitate practical use, one can simplify the E-sensitive subset identification rule by dropping covariates that have low posterior probability (i.e., < 0.10) of being selected in the prediction model of (Y, Z).

3 |. SIMULATION STUDY

This section summarizes results of a simulation study to evaluate the operating characteristics (OCs) of AED and compare it to several published enrichment designs. We assumed maximum sample size 400, with patients accrued according to a Poisson process with rate 100 per year, and each patient randomized fairly to receive E or C. Up to two interim analyses were performed at 200 and 300 patients, with a final analysis 1 year after the last patient was enrolled. We considered 10 biomarkers, x = (x₁, ... , x₁₀) each either with or without an interaction effect, to define the E-sensitive subpopulation. While AED handles both continuous and categorical biomarkers, to facilitate presentation and interpretation of the simulation results, we considered only binary biomarkers with values 1 (marker positive) or 0 (marker negative).

We considered seven scenarios, described in Table 1. Scenario 1 is a null case where E is not effective for any patients, and there are no E-sensitive patients. For E-sensitive patients, we set the hazard ratio of E to C at several values Δ_Y < 1 and set several differences of Δ_Y > 0 between the response rates of E and C. For E-insensitive patients, we set Δ_Y ≥ 1 and Δ_Z ≤ 0. Numerical values of Δ_Z and Δ_Y are nonlinear functions of the regression parameters, x, and G. Technical details given in Web Appendix F.

TABLE 1.

Simulation scenarios

		E-sensitive				Non-E-sensitive
Seen.	x of E-sensitive patients	πE	${\tilde{\mu }}_E$	ΔY	ΔZ	πE	${\tilde{\mu }}_E$	ΔY	ΔZ
1	No E-sensitive patients	0.50	0.817	1	0	0.50	0.817	1	0
2	x1 = 1	0.65	2.593	0.49	0.19	0.46	0.585	1.220	−0.040
3	x1 = x2 = 1	0.65	2.768	0.60	0.23	0.40	0.586	1.300	−0.073
4	x1 = 1, x2 = 0	0.65	2.342	0.59	0.19	0.387	0.536	1.983	−0.073
5	x1 = x2 = x3 = 1	0.65	2.233	0.60	0.21	0.373	0.404	1.566	−0.141
6	x1 = x2 = 1, x3 = 0	0.65	2.236	0.60	0.19	0.300	0.225	2.247	−0.171
7	x1 = 1, x2 = x3 = 0	0.65	2.233	0.59	0.17	0.234	0.136	3.459	−0.236

In each scenario, the covariate values are given that define an E-sensitive subgroup and true values of the response probability π_E, median survival ${\tilde{\mu }}_E$, Δ_Y = hazard ratio between E and C, and Δ_Z = response probability difference between E and C are given for each subgroup determined by x. The subscript E of π_E and ${\tilde{\mu }}_E$ denotes the experimental treatment

We generated Z from a Bernoulli distribution with response probability given by

$$\begin{array}{l}\pi \left(\mathit{x},G,{\theta }_Z\right)=\mathrm{\Phi }\{{\beta }_{Z,0}+\sum _{j=1}^{10}{\beta }_{Z,j}{x}_j\\ +G\left({\gamma }_{Z,0}+\sum _{j=1}^{10}{\gamma }_{Z,j}{x}_j\right)\},\end{array}$$ (8)

and generated Y based on the hazard function

$$\begin{array}{l}h\left(y\mid Z=z,G,\mathit{x},{\mathit{\theta }}_Y\right)=h_0(y)\exp \{\sum _{j=1}^{10}{\beta }_{Y,j}{x}_j\\ +G\left({\gamma }_{Y,0}+\sum _{j=1}^{10}{\gamma }_{Y,j}{x}_j\right)+{\alpha }_{Y}Z\},\end{array}$$ (9)

where h₀(y) is the baseline hazard, assumed to follow a Weibull distribution with scale parameter 1 and shape parameter 0.6 to obtain a decreasing hazard. We chose values of the regression parameters in Equations (8) and (9) so that patients with different x respond differently to E. Web Appendix F provides numerical values of the parameters for each simulation scenario. In scenarios 2–7, we considered three E-sensitive patient prevalences: 65%, 50%, and 35%.

We set the overall type I error rate to 0.05, with b₁ = b₂ = 1 for GS monitoring. We used ∊₁ = 0 and ∊₂ = 1 to define the PBI, set the design parameters υ = 0.766 and g = 0.352 for the eligibility criteria, after calibrating these numerical values by preliminary simulations, and set q = 0.10, so that the trial is stopped if less than 10% of patients are E-sensitive. We compared AED with four designs: (1) a GS enrichment design, called GSED (Magnusson and Turnbull, 2013), that selects a “sensitive” subgroup at the first interim test based on one prespecified dichotomized biomarker; (2) a GS design, called InterAdapt (Rosenblum et al., 2016), that allows interim early stopping by a test (i) for superiority or futility in the “sensitive” subgroup or (ii) for superiority of the entire group; (3) the adaptive enrichment design proposed by Simon and Simon (2017), which we call “Simon,” and (4) an “all-comers GS design,” called CGS. To focus on the contribution of adaptive enrichment in AED, CGS is identical to AED with the one exception that CGS does not perform adaptive enrichment. Because both the GSED and InterAdapt designs require prespecified “sensitive” and “insensitive” subgroups based on a prechosen biomarker, in our simulations we used x₁ to dichotomize the patient population into these two subgroups.

To compare the designs, we calculated the generalized power (GP), defined as the probability that the design correctly (1) identifies the sensitive subpopulation and (2) rejects H₀ ∶ Δ_Y(x, θ) ≥ 1 when H₀ actually is not true with Δ_Y(x, θ) < 1, that is when E is superior to C in the E-sensitive subgroup. GP is very different from conventional power, which ignores the adaptive signature identification process and is computed under the assumption that the sensitive subgroup is known. The GP is more relevant because it reflects the actual statistical decisions, and numerical values of GP and power often are very different. If a subgroup assumed to be sensitive by a design is incorrect, then the GP = 0. GP is useful for precision medicine because it quantifies how well a complex sequentially adaptive decision-making process performs to optimize a targeted therapy.

Table 2 summarizes the simulation results for each design based on 1000 simulated trials in each scenario considered. In scenario 1, where E is ineffective for all patients, all designs preserve the nominal type I error rate 0.05, with the small exception that InterAdapt has type I error rate 0.06. Scenarios 2–7 are cases where E is effective for a particular subgroup of patients. Each of these scenarios has three subcases, with 65%, 50%, or 35% sensitive patients in cohort 1. In contrast, the tabled numerical percentages for cohorts 2 and 3 are consequences of the adaptive enrichment decisions of AED, so they are design OCs and not assumed simulation study parameters.

TABLE 2.

GP of the AED and comparator designs under seven scenarios, with survival time following a Weibull distribution with deceasing hazard

Scenario	Percentage sensitive patients in cohort			Generalized power
	First	Second	Third	AED	GSED	InterAdapt	Simon	CGS
1	0	0	0	NA	NA	NA	NA	NA
2	0.65	0.88	0.89	0.79	0.45	0.65	0.63	0.61
	0.50	0.81	0.81	0.73	0.41	0.65	0.36	0.46
	0.35	0.70	0.72	0.73	0.36	0.62	0.20	0.27
3	0.65	0.83	0.84	0.65	0	0	0.49	0.49
	0.50	0.77	0.77	0.63	0	0	0.28	0.43
	0.35	0.65	0.65	0.56	0	0	0.13	0.36
4	0.65	0.81	0.81	0.68	0	0	0.50	0.49
	0.50	0.66	0.68	0.66	0	0	0.32	0.39
	0.35	0.57	0.58	0.64	0	0	0.15	0.21
5	0.65	0.83	0.90	0.51	0	0	0.22	0.16
	0.50	0.80	0.81	0.50	0	0	0.18	0.15
	0.35	0.72	0.74	0.44	0	0	0.14	0.12
6	0.65	0.93	0.93	0.71	0	0	0.36	0.20
	0.50	0.88	0.89	0.63	0	0	0.22	0.06
	0.35	0.81	0.83	0.59	0	0	0.11	0.05
7	0.65	0.93	0.94	0.84	0	0	0.58	0.03
	0.50	0.90	0.91	0.81	0	0	0.32	0.01
	0.35	0.83	0.87	0.77	0	0	0.22	0.01

Each trial was simulated 1000 times. In each case, the proportion of sensitive patients for the first cohort is an assumed fixed true value 0.65, 0.50, or 0.35, while the numerical values for the second and third cohorts are statistics resulting from the adaptive enrichment, computed as means across the simulations

Table 2 shows that AED has much higher GP than all other designs in most scenarios. The many GP values of 0 for GSED and InterAdapt are due to the fact that both designs prespecify a sensitive subgroup, and if this subgroup is incorrect, then the GP = 0, which occurs in scenarios 3–7. Simon performs better than GSED and InterAdapt because Simon adaptively enriches and identifies sensitive patients. CGS yields similar GP as Simon in most scenarios (except scenarios 6 and 7) because CGS as defined here is a refined group sequential design, which uses the same model and decision rules as AED to select covariates, identify a sensitive subgroup, and test the treatment effect in the identified subgroup. As noted earlier, to evaluate the adaptive enrichment effect of AED, the only difference between CGS and AED is that CGS does not perform adaptive enrichment. AED outperforms both Simon and CGS with 20–40 percentage points higher GP. The much larger GP of AED stems from its adaptive enrichment of E-sensitive patients based on both short-term Z and long-term Y, and the fact that AED refines the sensitive subgroup repeatedly throughout the GS process. Because the first cohort of AED enrolls all comers, in any case the percentage of sensitive patients enrolled in the first cohort is approximately the population prevalence of sensitive patients. Since AED enriches the identified sensitive patient subgroup in all subsequent cohorts, this results in increasingly higher percentages of sensitive patients in cohorts 2 and 3. For example, in Scenario 2, the percentage of truly sensitive patients is the population value 65%, but thereafter the percentages of enrolled sensitive patients increase greatly, to 88% and 89% in cohorts 2 and 3. These high adaptive enrichment rates also make AED stop earlier for superiority compared with the other designs. As seen in Web Table 2 of Web Appendix G, AED is more likely than CGS to correctly conclude that E is more effective than C in the identified sensitive subgroup, and stop the trial early for superiority, and AED also is less likely to incorrectly stop the trial for futility when E actually is effective for the sensitive subgroup (scenarios 2–7).

To evaluate clinical benefit for future patients provided by each of the designs, in Table 3 we report ratios of the 90th, 50th, and 10th percentiles of the survival time distributions for future patients who are considered sensitive based on the rule specified by the design at the end of the trial. We simulated 1000 future patients and treated them with either E or C based on the trial’s final conclusion, so they received E if H₀ was rejected at the end of the trial, or C if H₀ was not rejected. In Table 3, each ratio for each percentile for each design is computed as the simulation average of the future survival time distribution percentile for the design, divided by the corresponding simulation average percentile resulting from the all-comers GS design. The average (range) of median survival time, MST = 50th percentile, ratios for future patients with AED were 2.14 (1.34–4.22); with GSED were 1.13 (0.75–2.11); with InterAdapt were 1.20 (0.97–1.85); and with Simon were 1.20 (0.85–2.72). Thus, in terms of survival compared to CGS, the AED provides the greatest benefit for future patients among the four enrichment designs considered. However, the clinical benefit for all enrolled patients during an adaptive enrichment trial is the average effect from the mixture of treatment-sensitive patients and treatment-insensitive patients after the randomization. The MST of patients enrolled during the trial thus does not show a substantial gain in survival benefit from using enrichment designs, and thus it is not useful to demonstrate clinical benefit.

TABLE 3.

Ratios of the 90th, 50th, and 10th percentiles of the survival time distributions for future patients after using each design, compared to the percentiles for the all-comers GS design

Scenario	Percentage sensitive patients in First cohort	Ratio of 90th, 50th, and 10th percentiles of future patients’ survival times, versus the all-comers GS design
		AED	GSED	InterAdapt	Simon
1	0	1,1,1	1,1,1	0.99, 1, 1	1,1,1
2	0.65	1.44, 1.44, 1.44	1.30, 1.30, 1.30	0.97, 0.98, 0.98	1.15, 1.14, 1.14
	0.50	1.69, 1.68, 1.68	1.19, 1.20, 1.20	1.09, 1.08, 1.09	1.05, 1.05, 1.05
	0.35	2.03, 2.04, 2.04	1.20, 1.22, 1.22	1.19, 1.19, 1.19	0.98, 0.98, 0.98
3	0.65	1.33, 1.34, 1.33	0.76, 0.75, 0.74	1.09, 1.09, 1.09	0.91, 0.91, 0.91
	0.50	1.41, 1.43, 1.42	0.80, 0.78, 0.78	1.03, 1.03, 1.03	0.98, 0.98, 0.98
	0.35	1.46, 1.49, 1.49	0.90, 0.88, 0.88	0.98, 0.97, 0.97	0.86, 0.85, 0.86
4	0.65	1.34, 1.35, 1.31	0.78, 0.76, 0.74	1.09, 1.09, 1.07	1.13, 1.13, 1.11
	0.50	1.41, 1.42, 1.37	0.83, 0.81, 0.80	1.16, 1.17, 1.13	1.12, 1.13, 1.11
	0.35	1.52, 1.55, 1.49	0.97, 0.97, 0.95	1.26, 1.28, 1.22	1.01, 1.02, 1.03
5	0.65	2.06, 2.10, 2.00	1.02, 1.00, 0.97	1.17, 1.17, 1.16	1.17, 1.18, 1.16
	0.50	1.85, 1.90, 1.84	0.98, 0.96, 0.95	1.12, 1.13, 1.11	1.09, 1.10, 1.10
	0.35	1.69, 1.76, 1.72	0.95, 0.93, 0.93	1.01, 1.02, 1.01	1.01, 1.01, 1.02
6	0.65	3.48, 3.54, 3.17	1.56, 1.51, 1.39	1.62, 1.63, 1.53	1.67, 1.69, 1.59
	0.50	2.96, 3.06, 2.84	1.23, 1.21, 1.15	1.29, 1.30, 1.26	1.18, 1.20, 1.18
	0.35	2.40, 2.53, 2.42	1.06, 1.05, 1.03	1.09, 1.10, 1.09	1.09, 1.11, 1.11
7	0.65	4.13, 4.22, 3.32	2.12, 2.11, 1.71	1.83, 1.85, 1.60	2.66, 2.72, 2.24
	0.50	3.05, 3.18, 2.72	1.61, 1.62, 1.43	1.35, 1.37, 1.28	1.37, 1.43, 1.37
	0.35	2.39, 2.53, 2.31	1.26, 1.28, 1.21	1.12, 1.13, 1.10	0.98, 1.02, 1.07

Survival times were assumed to follow a Weibull distribution with deceasing hazard. Each trial was simulated 1000 times

To examine robustness, Web Appendix H shows results for the AED when Y is generated from a Weibull distribution with scale parameter 1 and shape parameter 2 to obtain an increasing hazard and also when Y follows a log-logistic distribution with a ∩-shaped hazard. The results are similar to those in Table 2, where Y follows a Weibull distribution with decreasing hazard.

We further investigated the performance of AED when (1) the maximum sample size is 800; (2) there are 50 covariates, that is, x₁,..., x₅₀, G, Gx₁,..., Gx₅₀ are included in each regression model; (3) an additional main effect of a covariate is added, for example, in scenario 2 where x₁ has a main and an interaction effect, the main effect of x₂ is added but an associated interaction effect of x₂ with treatment is not included; (4) a covariate effect associated with Y but not with Z was considered; (5) there are no treatment–covariate interactions; (6) different design parameters were used to enrich the patient population; and (7) different sparsity parameters were used. The results are summarized in Web Appendix I, suggesting that in general AED is robust. For example, when there are no treatment–covariate interactions, and thus no E-sensitive subgroup, GP is the same as conventional power. AED performs well and has OCs similar to those of CGS.

4 |. DISCUSSION

We have proposed a Bayesian GS adaptive enrichment design, AED, for a comparative clinical trial that does covariate selection, adaptive enrichment, and treatment comparison. By repeating covariate selection at each GS decision point to take advantage of the accumulating data, the design is able to update the eligibility criteria by restricting enrollment to the most recently determined E-sensitive subgroup that is likely to benefit, based on a personal benefit index computed using both early response and survival time. Compared to the three enrichment designs of Magnusson and Turnbull (2013), Rosenblum et al. (2016), and Simon and Simon (2017), and an all-comers GS design that is identical to AED in all ways except that it does not do enrichment, the proposed AED has much higher GP across a range of scenarios. The AED also provides much greater benefit to future patients in terms of survival time. These substantial improvements over existing adaptive enrichment designs may be attributed to the AED’s adaptive biomarker selection and the effectiveness of its adaptive enrichment rule based on each patient’s covariate-based PBI. By exploiting this structure, the AED greatly magnifies the signal in the patient covariate vector and boosts the GP for correctly identifying a sensitive subgroup and detecting a true treatment advance over standard therapy, if it exists. AED is also more ethical in that it reduces the probability of enrolling E-insensitive patients who are unlikely to benefit.

A practical limitation of AED is that it is not scalable to handle high-dimensional x in a scientifically valid and clinically ethical way. Our simulations show that, with sample sizes of several hundred patents, AED can accommodate settings where x has dimension up to 50. In such settings, AED obtains good GP figures for realistic alternative hazard ratios. To implement AED, the investigators must do a preliminary biomarker screening, based on preclinical or early clinical data, to obtain x of dimension small enough to be handled practically by AED. Another practical issue is deciding when the adaptive enrichment should begin. This depends on the number of covariates, their information-to-noise ratio, the percentage of sensitive patients, the treatment difference between sensitive and insensitive patients, and the variances of the outcomes Z and Y. Since several of these factors can be estimated during the trial, a useful future research problem may be to construct a rule for use during the trial, which is defined as a function of these known and estimated quantities and the planned maximum number of GS decisions, that decides when to begin the adaptive enrichment.

DATA AVAILABILITY STATEMENT

Data sharing is not applicable to this article as no datasets were generated or analyzed in this paper.