Rules of Physical Mathematics Govern Intrinsically Disordered Proteins

Abstract

In stark contrast to foldable proteins with a unique folded state, intrinsically disordered proteins and regions (IDPs) persist in perpetually disordered ensembles. Yet an IDP ensemble has conformational features—even when averaged—that are specific to its sequence. In fact, subtle changes in an IDP sequence can modulate its conformational features and its function. Recent advances in theoretical physics reveal a set of elegant mathematical expressions that describe the intricate relationships among IDP sequences, their ensemble conformations, and the regulation of their biological functions. These equations also describe the molecular properties of IDP sequences that predict similarities and dissimilarities in their functions and facilitate classification of sequences by function, an unmet challenge to traditional bioinformatics. These physical sequence-patterning metrics offer a promising new avenue for advancing synthetic biology at a time when multiple novel functional modes mediated by IDPs are emerging.

1. INTRODUCTION

Intrinsically disordered proteins and regions (collectively termed IDPs in this review, except in Section 4.3), do not fold into unique folded structures. However, the absence of unique structures does not mean that IDP conformations are featureless (92) or that IDPs lack functions (29). In fact, they can have conformational signatures specific to their sequences, and these features may be responsible for their specific functions. The defining features can range from such broad and simple observables as radius and scaling exponent (109) to detailed interresidue distance profiles (19, 46, 63), structure factors (5, 63, 64, 77), and other measures of ensemble properties (17, 36, 53, 59). These specific features must be encoded in the sequence, but how do we unlock that code? The answer to the question of how—at first—seems just as complicated as the sequence-structure puzzle of folded proteins that perplexed protein biology for decades. Yet we can turn the disorder of IDPs to our advantage. First, the high degree of disorder allows averaging over different degrees of freedom with few constraints, facilitating models that are analytically tractable. Second, electrostatics plays a prominent role in determining IDP conformations (19, 20, 43, 44, 61, 62, 67, 93). Thanks to decades of advances in theoretical polymer physics (70), the electrostatics can now be incorporated into analytically tractable models. The same analytical framework also helps us gain insight into IDP functions. The formalism relating an IDP sequence to its conformational features—embedded in an analytical framework based on physicochemical models—is termed the physical mathematics (PM) of IDPs.

PM can provide fundamental insights into issues of IDP biophysics, from deciphering the rules of IDP regulation and formulating principles for sequence design to detecting evolutionary trends. First, principles derived from closed-form mathematical expressions can decouple the complex interplay between biological and chemical regulation (Figure 1). Biological regulators (BRs), for the purposes of this review, include posttranslational modifications (PTMs), alternate splicing, and mutations that can change the composition and placement of amino acids in IDP sequences. The coupling of sequence changes (due to BRs) to environmental conditions [chemical regulators (CRs)] such as salinity, temperature, pH, and crowding can be complicated. However, mathematical formulas that describe sequences and their responses to CRs can reveal these complex relationships. Second, understanding the intertwined effects of BRs and CRs can help in designing novel sequences and tuning solution conditions to favor desired conformations. Third, PM provides metrics that can help classify functionally similar IDPs. Functionally similar IDPs can have low sequence homology (51), rendering functional classification challenging using traditional bioinformatic tools.

Figure 1.

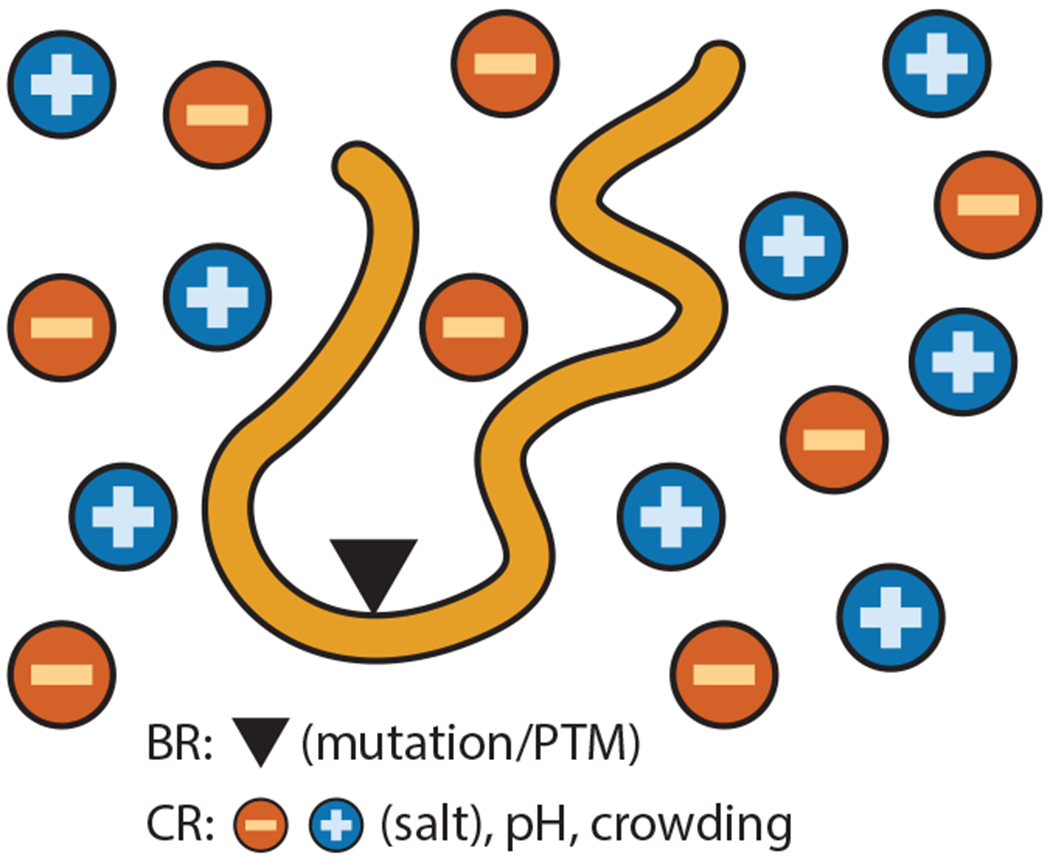
Interplay between BRs (e.g., mutations or PTMs that directly change the sequence) and CRs (e.g., changes in solution conditions) can be complex and lead to a combinatorial explosion, requiring a PM-based approach. Abbreviations: BR, biological regulator; CR, chemical regulator; PM, physical mathematics; PTM, posttranslational modification.

Mathematical relationships involving sequence, rather than composition alone, provide foundational insights that are not otherwise possible. For example, to fully appreciate the combination of BRs and CRs, we need to analyze numerous IDP sequences under diverse solution conditions. This causes a combinatorial explosion that is difficult to handle using computational tools. Likewise, understanding IDP functions often requires analyzing multiple long sequences (lengths greater than 500 amino acids; see 6) across diverse species, which is well beyond the capacities of current all-atom simulations. Coarse-grained simulations of IDPs (16, 21–25, 40, 71, 79, 89, 98) are being developed to address such challenges, particularly to model the emerging role of IDPs in forming biomolecular condensates via liquid–liquid phase separation. However, these simulations—although highly insightful and necessary to benchmark analytical theory—are not yet capable of describing functions of IDPs other than formation of condensates. Even coarse-grained simulations are not always feasible in the face of the combinatorial explosion involved in simulating IDP sequences under diverse solution conditions, nor can they simulate the large collections of long proteins that are typically needed to model evolutionary trends. Newly developed deep-learning tools (2, 49) built for predicting protein structures cannot predict ensembles and thus are not suitable for modeling IDPs. In fact, AlphaFold—not surprisingly—tends to yield very low-confidence structures when applied to IDPs (80).

Simple physics-based polymer models have revealed general principles in protein science (12–15, 34, 35, 50, 66, 81, 84, 88, 94, 95, 108). The analytical tractability of these models relies on two major simplifying assumptions. First, sequence complexity is reduced either by a homopolymer assumption (all amino acids are identical) or by adopting models with at most two different types of amino acids, for example, hydrophobic and polar. The second assumption—even in models with both hydrophobic and polar amino acids, or models with different flavors of monomers—often ignores the exact sequence positioning of the amino acids. Neglecting exact positioning is equivalent to averaging over multiple different sequences, assuming that the disorder is annealed (28, 38, 41, 83). Building physical models amenable to analytical treatments while respecting the exact placement of amino acids (sequence patterning) is challenging, despite its importance. The new era of PM of IDPs addresses this challenge (57) and is the focus of this review.

2. SEQUENCE-BASED METRICS CAN DESCRIBE THE CONFORMATIONS OF AN INTRINSICALLY DISORDERED PROTEIN AND REGION SEQUENCE

2.1. Brief Background on Homopolymer Theory and Applications to Intrinsically Disordered Proteins and Regions

We first define a few terms. The ensemble average radius of gyration, R_g, defined as $R_{\text{g}}=\sqrt{\langle r_{\text{g}}^2\rangle }$ (where ⟨..⟩ denotes the ensemble average and r_g refers to the radius of gyration for a given conformation), is typically used to describe the overall size of a polymer. Similarly, another useful metric for size is ensemble average end-to-end distance, R_ee, defined as $R_{\text{ee}}=\sqrt{\langle r_{\text{ee}}^2\rangle }$, where r_ee is the stochastic value of the end-to-end distance for a given conformation. In polymer theory, for a homopolymer without any interactions (also termed a Gaussian chain), R_g and R_ee are related: $\langle r_{\text{g}}^2\rangle =\langle r_{\text{ee}}^2\rangle /6=Nbl/6$, where N is the number of monomers, b is the bond length, and l is the Kuhn length. The Kuhn length is a measure of the correlation in the direction of connecting bonds between different monomers (or amino acids, in the case of IDPs). For a protein, typical values are b = 3.8 Å and l = 8 Å (43, 111). Kuhn length can also vary between different amino acids. However, a uniform value of Kuhn length is a reasonable approximation for typical protein sequences. The scaling of R_g is the hallmark of Gaussian chain behavior and is generalized as R_g ∝ N^ν, where ν = 1/2 recovers the Gaussian chain reference (27).

Any polymer with a dimension such as R_g less than the corresponding dimension of the Gaussian chain is considered to be collapsed. In common parlance, ν ≈ 1/3 is also termed a globule. A polymer is considered to be expanded when the dimension is greater than that of the Gaussian chain. IDP sequences tend to be enriched in charged amino acids (compared with the sequences of foldable proteins). Consistent with this statistical observation, early works found that charge composition can provide rules of thumb for distinguishing the globule and expanded states (61) and can influence several measures of IDP sizes, including R_g, R_ee, and ν (43, 62).

2.2. Intrinsically Disordered Protein and Region Conformations Depend on Charge Patterning

Charge composition gives the number of charges, but it gives no information about the placement of the charges in the sequence. Consider the two sequences shown in Figure 2. They have the same composition, or number of positive and negative charges, but the charges are distributed in different sequence orders, called patternings or decorations. Srivastava & Muthukumar (97) demonstrated that polymers with the same charge composition but different charge patternings can differ significantly in their sizes. More recently, Das & Pappu (19) revisited the role of charge decoration by simulating 30 sequences, each having 25 glutamic acids (with −1 charge each) and 25 lysines (with +1 charge each) distributed in different orders. They found that sequences with well-mixed or alternating positive and negative charges (similar to the top sequence in Figure 2) tend to have greater dimensions compared with sequences where positive and negative charges are segregated in blocks (similar to the bottom sequence in Figure 2). They defined an empirical charge-segregation metric to quantify this intuitive expectation (19). Thirumalai and colleagues (5) have also performed coarse-grained simulations to highlight the observation that charge composition alone is not sufficient to describe the subtle features of IDP conformations. The effects of varying charge patterning while keeping the same composition have also been observed in IDP functions (6, 72, 90). Intriguingly, the fact that sequence patterning alters conformation of the denatured state (of foldable proteins) has also been shown to be critical for function (10).

Figure 2.

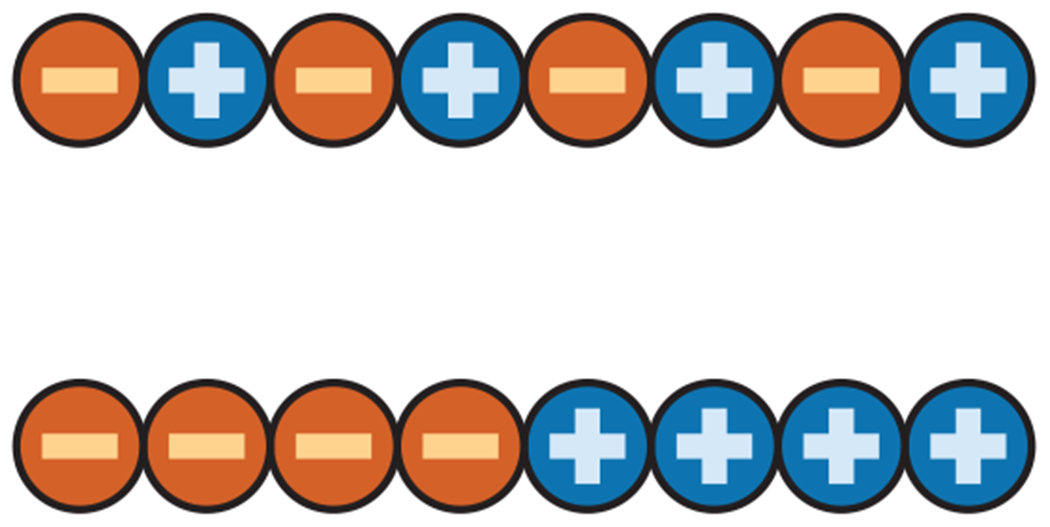
The SCD metric (the same as Q in Equation 2) is a measure of the patterning of positive and negative charges. Two sequences (top, bottom) can have the same number of positive and negative charges (composition) but differences in patterning, reflected in their differing SCDs. Blocky sequences (bottom) tend to have lower SCDs compared with sequences where charges are more dispersed (top). Abbreviation: SCD, sequence charge decoration. Figure adapted with permission from Reference 33.

2.2.1. The sequence charge decoration metric can describe the global dimensions of intrinsically disordered proteins and regions.

Recent advance in heteropolymer theory provide an analytical framework for determining the ensemble average end-to-end distance R_ee of a heteropolymer as a function of its sequence of charged monomers (amino acids, glutamic acid, aspartic acid, lysine, and arginine for proteins). The theory builds on a coarse-grained energy function with four essential ingredients (I1, I2, I3, and I4): I1 is the connectivity of monomers in the polymer; I2 is the two-body short-range interaction, which can be attractive or repulsive; I3 is the three-body short-range repulsive interaction; and I4 is the long-range electrostatic interaction among charged monomers (Figure 3). The three-body repulsive interaction is needed to avoid polymer collapse when the two-body interaction and electrostatics are highly attractive. The detailed form of the Hamiltonian (H) can be found in References 31 and 46.

Figure 3.

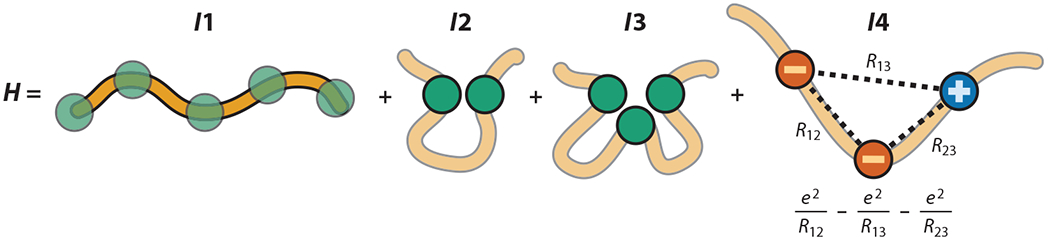
The energy function (H) of an analytical framework for determining the R_ee of a sequence that includes charged monomers accounts for chain connectivity (I1), two-body (I2) and three-body (I3) short-range interactions, and long-range electrostatic interactions (I4). The exact functional form of H can be found in References 31 and 46.

In this derivation, the effective $\langle r_{\mathrm{ee}}^2\rangle$ is $\langle r_{\mathrm{ee}}^2\rangle =Nb{l}_{\text{r}}$, where l_r is the renormalized Kuhn length, which is different from the bare Kuhn length l. The details of sequence specificity are effectively captured by l_r. This technique, originally developed by Edwards & Singh (30), provides analytical tractability. It has been used in work on homopolymers, including polyelectrolytes (PEs) (32, 39, 68). The ratio of the two Kuhn lengths is defined as a dimensionless variable: x = l_r/l. For the Gaussian chain reference state, x is equal to unity. x will deviate from unity due to the composition and patterning of amino acids. The ranges of x provide different regimes of IDP conformation, such as coil-like (x ≈ 1), globule (x ≪ 1), and expanded (x ≫ 1). An analytical expression for F(x), the free energy as a function of x, can be written by explicitly incorporating the sequence patterning as described by Equations 1 and 2:

$$\beta F(x)=\frac{3}{2}(x-\ln x)+{\left(\frac{3}{2\pi }\right)}^{3/2}\frac{\text{Ω}}{x^{3/2}}+{\omega }_3{\left(\frac{3}{2\pi }\right)}^3\frac{B}{2x^3}+\frac{l_{\text{b}}}{l}\frac{Q}{x^{1/2}}\sqrt{\frac{6}{\pi }},$$ 1.

where Ω, Q, and B contain details of the sequence and are given by

$$\begin{gathered} \text{Ω}=\frac{1}{N}\sum _{m=2}^N\sum _{n=1}^{m-1}{\omega }_{m,n}{(m-n)}^{-1/2}, \\ Q=\frac{1}{N}\sum _{m=2}^N\sum _{n=1}^{m-1}{q}_m{q}_n{(m-n)}^{1/2}, \\ B=\frac{1}{N}\sum _{p=3}^N\sum _{m=2}^{p-1}\sum _{n=1}^{m-1}\frac{(p-n)}{{[(p-m)(m-n)]}^{3/2}}, \end{gathered}$$ 2.

where l_b is the Bjerrum length, assumed to be l_b = 7.2 Å (298/T), and T is the absolute temperature. The first term defining the free energy F is the entropy respecting chain connectivity (I1 in Figure 2). The terms for Ω, B, and Q represent the contributions of interactions I2, I3, and I4, respectively (Figure 2). For a two-body residue pair (m, n, representing residue numbers), the specific short-range (or excluded volume) interaction parameter is given by ω_{m, n}, while ω₃ is the three-body repulsive interaction parameter, which is assumed to be independent of amino acid type.

For a given sequence, Q is calculated from the sum in Equation 2 by assigning a negative charge (q = −1) to glutamic and aspartic acids and a positive charge (q = 1) to lysines and arginines. Histidines can also be assigned a charge of 0.5 if desired. Thus, Q explicitly accounts for sequence charge decoration (SCD). Two sequences with the same charge composition but different charge patterning will have different values of SCD. Reference 85 provides a detailed derivation of the SCD metric. Sequences with highly segregated positive and negative charges tend to have lower SCD values, and thus smaller sizes, compared with sequences with well-dispersed positive and negative charges. For example, the alternating and blocky sequences in Figure 2 have SCD values of −0.45 and −2.02, respectively. SCD captures the overall size variation of the sequences reported by Das & Pappu (19) when compared with the dimensions (R_g) generated by all-atom Monte Carlo (55) (Figure 4a) and coarse-grained molecular dynamics simulations (65). Equations 1 and 2 provide a formalism to directly estimate the size of a chain if the two-body interaction parameters ω_{m, n} and three-body repulsive parameter ω₃ values are known. Given a sequence with a high proportion of charged residues, as in the Das & Pappu sequences, it is reasonable to replace the two-body short-range interaction with a constant term (i.e., ω_{m, n} ≈ ω₂). Figure 4b shows end-to-end distance as a function of mean-field ω₂ for a fixed value of ω₃ = 0.1 (for this typical choice of ω₃, see Reference 31). The difference in charge patterning (captured by SCD) is manifest in the chain dimensions between two sequences having the same charge composition (25 glutamic acids and 25 lysines) but different patterning (Figure 2). The variation in ω₂ can be attributed to changes in temperature or local solution condition inside the cell that can happen due to weak nonspecific interactions (103). Figure 4 also shows that changing ω₂ can cause a chain to undergo a sharp transition in conformation.

Figure 4.

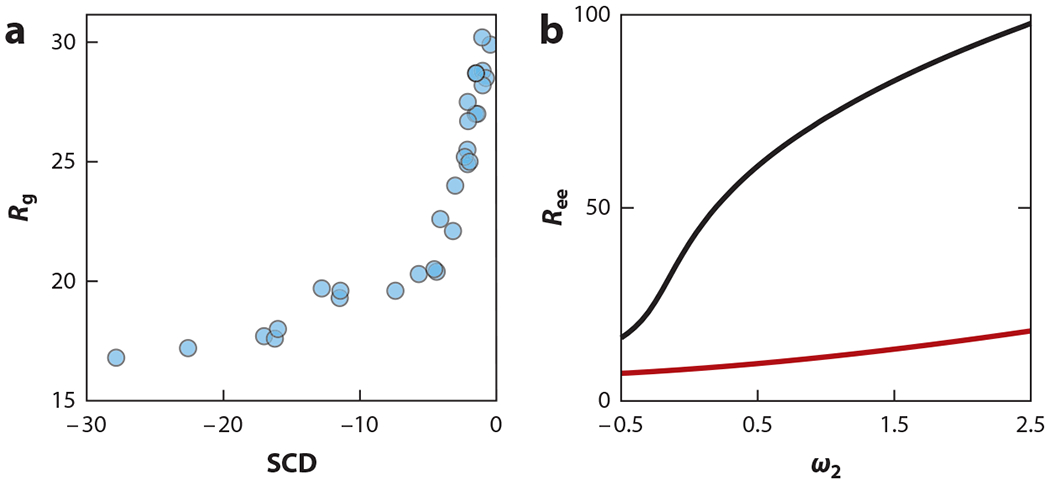
(a) SCD captures variations in size (R_g in angstroms) obtained from all-atom Monte Carlo simulations for 30 sequences, each having 25 Es and 25 Ks arranged in different orders. (b) Equations 1 and 2 can be used to predict the size (R_ee = ⟨$r_{\mathrm{ee}}^2$⟩^1/2 in angstroms) dependence on ω₂ (proxy for temperature or solution conditions) for a typical choice of ω₃ = 0.1, b = 3.8 Å, and l = 8 Å, l_b = 7.2 Å. The difference between the black curve (representing a sequence with alternating Es and Ks) and the red curve (a sequence with a block of 25 Es followed by 25 Ks) highlights the effect of charge patterning revealed by the SCD embedded in the Equation 2. Abbreviations: E, glutamic acid; K, lysine; SCD, sequence charge decoration.

2.2.2. Heuristic derivation of the sequence charge decoration metric.

The functional form of the SCD metric can be appreciated with a scaling argument. The variational calculation stipulates a quantity I, defined as $I=\langle r_{\text{ee}}^2(H_{\text{r}}-H_{\text{t}})\rangle -\langle r_{\text{ee}}^2\rangle \langle (H_{\text{r}}-H_{\text{t}})\rangle =0(30,85)$, where H_r is the Hamiltonian renormalized with the Gaussian form having effective bond length l_r, and H_t is the total form. The electrostatic contribution of the total Hamiltonian, defined as $H_{\text{t}}^{\text{el}}$, can be written as $H_{\text{t}}^{\text{el}}=\sum _{m,n}{q}_m{q}_n/\left|R_{m,n}\right|$ (ignoring constants). We also note the decomposition $r_{\text{ee}}^2=r_{n,m}^2+r_{m,n}^2+r_{n,1}^2$. With these two relationships, the relevant term in I from the electrostatics becomes

$$\sum _{m,n}{q}_m{q}_n\langle r_{m,n}^2\frac{1}{\left|r_{m,n}\right|}\rangle \propto \sum _{m,n}{q}_m{q}_n\langle \left|r_{m,n}\right|\rangle \propto \sum _{m,n}{q}_m{q}_n{(m-n)}^{1/2},$$ 3.

where the last equality uses Gaussian chain (random walk) statistics, [〈|$r_{m,n}^2$|〉]^1/2 = (m – n)^1/2, neglecting all of the prefactors. For rigorous derivations, readers should consult Reference 85. SCD captures long-range correlations in the sequence, unlike the charge patterning metric κ (not to be confused with the inverse Debye length introduced below) introduced by Das & Pappu (19). For this reason, the two charge patterning metrics—although broadly correlated (85)—can differ in their ability to capture trends such as R_g variance in sequences having the same charge composition but different patterning (55).

2.3. Noncharge Patterning Can Also Influence the Sizes of Intrinsically Disordered Proteins and Regions

Equations 1 and 2 also provide a framework for modeling the sequence specificity of noncharged amino acids by choosing interaction parameters ω_{m, n} (between any residue pair m and n) without assuming the constant ω₂ described above. Zheng, Mittal, and colleagues (110) recently adopted a normalized hydrophobicity score λ_i for each amino acid i to estimate ω_{m, n} = λ_m + λ_n. The new metric, which they called sequence hydropathy decoration (SHD), has been combined with SCD to predict scaling exponents ν and R_g for multiple sequences and benchmarked against coarse-grained simulations. The correlations between theoretically predicted and simulated values of ν were optimized to modify Ω and define SHD as

$$\text{SHD}=\frac{1}{N}\sum _{m=2}^N\sum _{n=1}^{m-1}{\omega }_{m,n}{(m-n)}^{\beta },$$ 4.

with β = −1, in contrast to β = −1/2 originally derived in Equation 2 (85). Zheng, Mittal, and colleagues’ definition of SHD (with β = −1 instead of β = −1/2), along with their parameterization scheme of ω_{m, n} = λ_m + λ_n, yielded a sequence-dependent equation to predict ν and R_g as

$$\nu =-0.0423\text{SHD}+0.0074\text{SCD}+0.701;R_{\text{g}}={\left[\frac{\gamma (\gamma +1)}{2(\gamma +2\nu )(\gamma +2\nu +1)}\right]}^{1/2}{(bl)}^{1/2}{N}^{\nu },$$ 5.

where γ ≈ 1.1615 (37), b = 3.8 Å, and l = 8 Å. Reference 110 provides more details and comparisons with simulation data. Other noncharge patterning metrics—such as local hydrophobic clustering (HpC) (10) and local asymmetry in aromatic residues (Ω_aro) (64)—have also been used to design sequences. Future studies are needed to test and improve the choice of the ω_{m, n} parameter set by using the variational formalism given by Equations 1 and 2. There are several advantages of using this general formalism: (a) First-principle patterning metrics describe local and long-range correlations in sequence, unlike other intuitive local metrics such as HpC (10), κ (19), and Ω_aro (64); (b) chain dimensions and size can be directly predicted and compared (similar to Figure 2; see 85) against experiment and/or simulation beyond just seeking the size–metric correlation shown in Figure 4a; and (c) both electrostatic and nonelectrostatic interactions can be coupled in one framework, avoiding ad hoc fitting parameters to weight SHD and SCD.

2.4. Sequence Decoration Matrices Can Provide Detailed Conformational Features

Global metrics of chain dimensions such as R_ee and R_g and/or the scaling exponent ν are typically used to describe protein sizes (36, 43, 77). Internal distance profiles, defined as $\langle {(r_i-r_j)}^2\rangle =\langle r_{i,j}^2\rangle$ between any two amino acids i and j can provide conformational features beyond R_ee, R_g, and ν. For homopolymers, such profiles are mostly redundant because homopolymers display fractal-like behavior with an approximate scaling relation $\langle {(r_i-r_j)}^2\rangle \propto |i-j{|}^{2\nu }$. In contrast, heteropolymers such as IDPs display strong heterogeneity in their internal distance profiles (19, 63) and may exhibit more nuanced features.

Recent progress in PM provides a framework for computing these ensemble average distances—besides global dimensions—as functions of sequence. The internal distance profiles are calculated as $\langle {(r_i-r_j)}^2\rangle =|i-j|b{l}_{\text{r}}(i,j)$, where l_r(i, j) is the residue pair (i, j)-specific renormalized Kuhn length, analogous to the calculation of 〈$r_{\mathrm{ee}}^2$〉 given above. These distances can be written in terms of a nondimensionalized quantity, x_i,j = l_r(i, j)/l, with a corresponding free energy function, F(x_i,j) (46):

$$\beta F(x_{i,j})=\frac{3}{2}(x_{i,j}-\ln x_{i,j})+{\left(\frac{3}{2\pi }\right)}^{3/2}\frac{{\text{SHDM}}_{i,j}}{x_{i,j}^{3/2}}+{\left(\frac{3}{2\pi }\right)}^3\frac{{\omega }_3{T}_{i,j}}{2(i-j)x_{i,j}^3}+\frac{l_{\text{b}}}{l}\sqrt{\frac{6}{\pi }}\frac{{\text{SCDM}}_{i,j}}{x_{i,j}^{1/2}}.$$ 6.

Equation 6 is a generalization of Equation 1 with four terms that account for the physical contributions of I1, I2, I3, and I4 shown in Figure 3. The charge patterning is encoded by a specific metric SCDM_i,j for a given residue pair i, j, for which the internal distance is to be computed. Consequently, the general formalism yields an SCD matrix (SCDM) with elements SCDM_i,j given by

$$\begin{gathered} {\text{SCDM}}_{i,j}=\frac{1}{(i-j)}[\sum _{m=j}^i\sum _{n=1}^{j-1}{q}_m{q}_n\frac{{(m-j)}^2}{{(m-n)}^{3/2}}+\sum _{m=j+1}^i\sum _{n=j}^{m-1}{q}_m{q}_n{(m-n)}^{1/2} \\ +\sum _{m=i+1}^N\sum _{n=1}^{j-1}{q}_m{q}_n\frac{{(i-j)}^2}{{(m-n)}^{3/2}}+\sum _{m=i+1}^N\sum _{n=j}^i{q}_m{q}_n\frac{{(i-n)}^2}{{(m-n)}^{3/2}}]. \end{gathered}$$ 7.

It is instructive to note that SCD, defined above, is just one element of the SCDM, and is only applicable to describing R_ee. Notably, we have SCDM_{i = N,j = 1} = SCD (assuming N ≈ N − 1, which is reasonable for large N).

The noncharged patterning can be similarly generalized by creating an SHD matrix (SHDM) defined as

$$\begin{gathered} {\text{SHDM}}_{i,j}=\frac{1}{(i-j)}[\sum _{m=j}^i\sum _{n=1}^{j-1}{\omega }_{m,n}\frac{{(m-j)}^2}{{(m-n)}^{5/2}}+\sum _{m=j+1}^i\sum _{n=j}^{m-1}{\omega }_{m,n}{(m-n)}^{-1/2} \\ +\sum _{m=i+1}^N\sum _{n=1}^{j-1}{\omega }_{m,n}\frac{{(i-j)}^2}{{(m-n)}^{5/2}}+\sum _{m=i+1}^N\sum _{n=j}^i{\omega }_{m,n}\frac{{(i-n)}^2}{{(m-n)}^{5/2}}]. \end{gathered}$$ 8.

The derivation of a high-dimensional SCDM and SHDM also shows the power of variational calculation that is not limited to computing a scalar metric such as SCD; a single charge patterning metric (κ, defined in 19; not to be confused with the inverse Debye length); or SHD, local hydropathy cluster (HpC) (10), and Ω_aro (64).

The detailed expression for the three-body repulsion denoted by T_i,j, omitted here for brevity, can be found in Reference 46. This formalism provides a framework for quantitatively estimating the effects of electrostatics for highly charged sequences by assuming ω_m,n ≈ ω₂. Within this approximation, the role of charge patterning on local dimensions is exclusively modeled by the SCDM. For a given value of ω₂, ω₃ and a pair of residues i, j, the free energy equation, Equation 6, is minimized to determine x_i,j,min. The ensemble average distance (R_i,j) between these two residues i, j is calculated using $R_{i,j}^2=\langle r_{i,j}^2\rangle =|i-j|bl{x}_{i,j,\min }$.

Figure 5 shows distance maps under zero-salt conditions for two different IDP sequences with specific values of ω₂ and ω₃. The best estimates for ω₂ and ω₃ were obtained by matching the values of 〈(r_i − r_j)²〉 generated in an all-atom simulation. The details of the protocol for determining ω₂ and ω₃ are given in Reference 46. Reasonable agreement between analytical theory and the all-atom simulation, noted in Figure 5, shows that the SCDM can reveal the prominent features of distance maps from the placement of charges in the sequence. It is interesting to note that different residue pairs—within the same chain—can exhibit different conformations, even as different as expanded and collapsed (Figure 5; 46, figure 4). Approaches rooted in homopolymer models ignore variations in these local features. A recent mathematical model supported by coarse-grained simulation has also shown independence of the distribution of R_ee and R_g for IDPs (96), in stark contrast to homopolymer predictions and highlighting limits of homopolymer-centric models.

Figure 5.

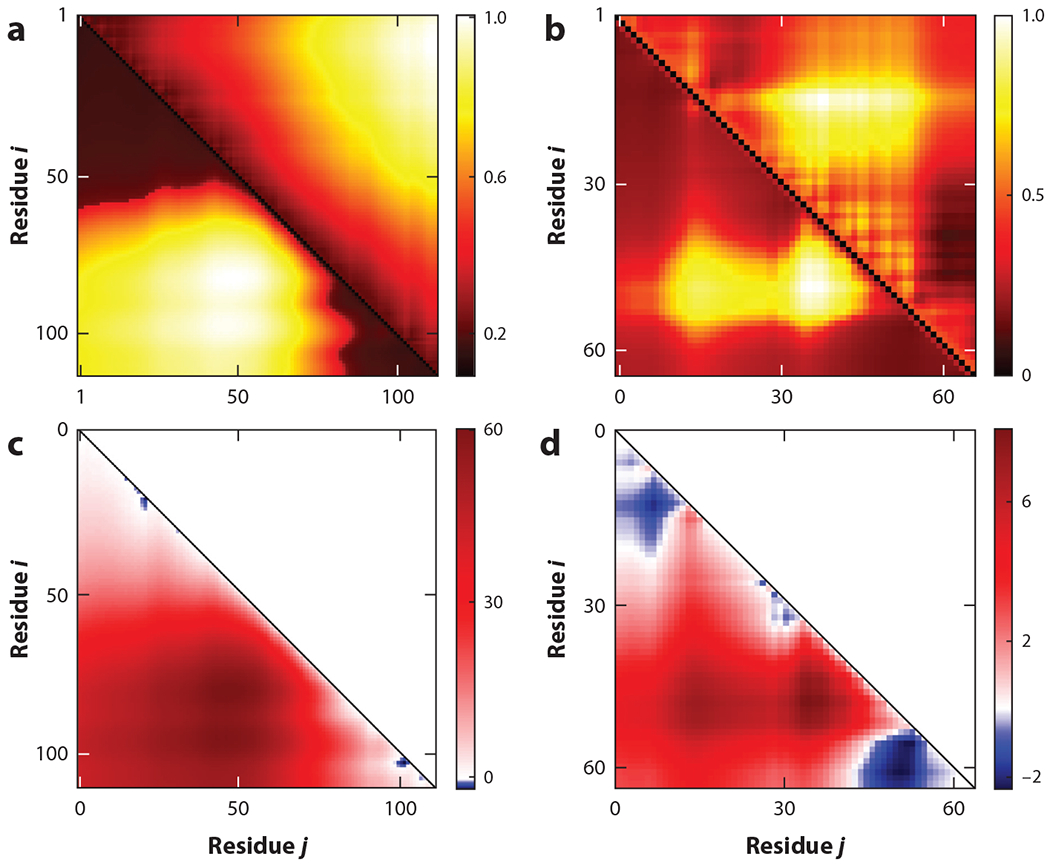
Equation 6 provides distance maps quantified by x_i,j values (lower triangles) for two intrinsically disordered protein and region sequences: (a) prothymosin-α and (b) DP00877. Color coding denotes the different values of x_i,j (normalized between 0 and 1) for residue pairs i, j (x and y axes). The noncharge parameters ω₃ and ω₂ were obtained to best match the all-atom simulation data of x_i,j shown in the upper triangle (for details, see Reference 46). (c, d ) The most expanded regions (bright yellow) in distance maps in panels a and b correspond to the bright red (repulsive) regions in the respective sequence charge decoration matrix maps shown for (c) prothymosin-α and (d ) DP00877. Figure adapted from Reference 46 with permission from AIP Publishing.

Maps of the SCDM can be generated from sequence charge information even when ω₃ and ω₂ values are not known. These graphs can provide critical information about the sets of amino acid residue pairs that experience repulsive (or attractive) electrostatic interactions, which expand (or compact) the chain. Figure 5c,d shows the electrostatic contributions to the intrachain interaction topology (quantified by the SCDM) for two IDPs (for which the distance maps are shown in Figure 5a,b). The most repulsive regions correspond to the most expanded regions in the distance maps. This feature of SCDM maps has proven useful for functional classifications (see Section 4.3).

3. INTRINSICALLY DISORDERED PROTEIN AND REGION CONFORMATIONS ARE SENSITIVE TO BIOLOGICAL AND CHEMICAL REGULATORS

3.1. Physical Mathematics Can Identify Phosphorylation Hot Spots

PTMs such as phosphorylation can alter IDP sequences by adding negatively charged phosphate groups to neutral amino acids such as serine and threonine (3). How do these modifications alter IDP conformations? Equation 6 provides a framework for predicting PTM-induced changes in SCDMs and consequent changes in internal distance profiles. Figure 6 illustrates phosphorylation-induced conformational changes for the wild-type (WT) IDP P0A8H9 and its two variants S2T15 and S54S56. The first variant, S2T15, is modified by adding negative charges (to mimic the effect of phosphorylation) at amino acids 2 and 15 in the WT sequence. The second variant, S54S56, has negative charges at residues 54 and 56 in the WT sequence. Differences in distance maps between the WT and the variants show phosphorylation can significantly alter distance profiles. Furthermore, it is evident that the choice of phosphorylation site matters. Both the S54S56 and S2T15 variants have the same charge composition, with near identical patterning except at two amino acids. These differences—due to the long-range nature of electrostatics—are enough to significantly alter the SCDMs, resulting in vastly different distance maps. Figure 6a,b shows changes in the distance maps that arise from the changes in the SCDMs. These distance maps largely agree with the results from the all-atom simulations. There are also noticeable disagreements that could be due to finer details of the all-atom simulation that the coarse-grained energy function (H) ignores.

Figure 6.

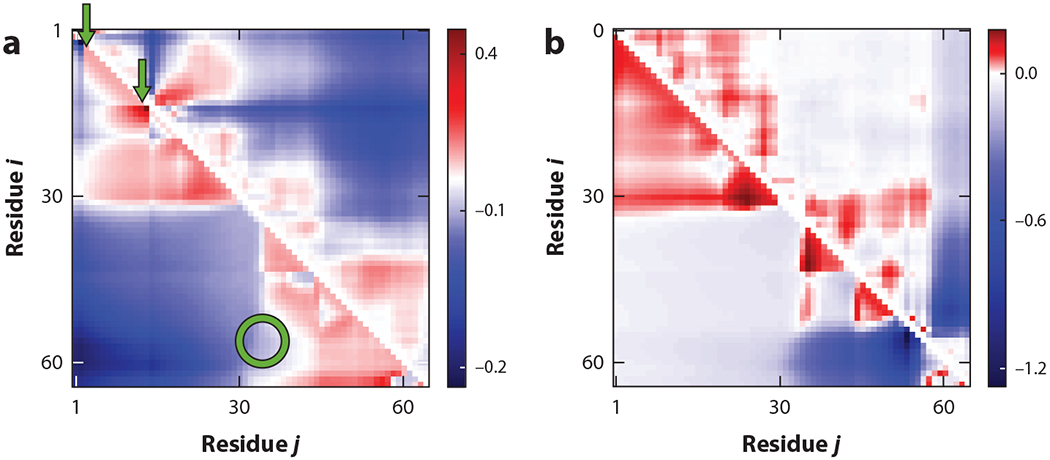
Intrinsically disordered proteins and regions have hot spots for phosphorylation. Distance profiles, given by sequence-specific x_i,j (relating to ⟨$r_{i,j}^2$⟩) for amino acid pairs i, j, for two different phosphorylated forms, (a) S2T15 and (b) S54S56, of the wild-type protein P0A8H9 show that specific phosphorylation sites induce drastic conformational changes at all scales. Positive (red) and negative (blue) differences are evident in these heat maps. Theoretical results (lower triangles) exhibit trends similar to the all-atom simulation results (upper triangles). The arrows point to sequence sites of phosphorylation that can generate changes in distances among sites that are remote in the sequence (circle). Figure adapted from Reference 46 with permission from AIP Publishing.

The results of phosphorylating different residues in the WT IDP P0A8H9 also show that IDPs propagate phosphorylation signals to distant parts of the sequence. For example, modifications at residue numbers 2 and 15 (Figure 6a) can induce changes far away. PM provides a formalism to search through numerous combinations of phosphorylation sites to identify those hot spots that can induce drastic changes locally and/or far from the site of the modification.

3.2. Intrinsically Disordered Protein and Region Conformations Are Sensitive to Salt

The dimensions of charged polymers depend on salt concentration (an example of a CR). Consider a PE consisting of charged monomers of only one type—either positive or negative. For a PE-like IDP, the electrostatics is purely repulsive; consequently, added salt will screen the repulsions, and the chain will become more compact. However, IDPs are typically polyampholytes with both positive and negative charges present in the same sequence. Would polyampholytic IDPs contract or expand with salt? The salt dependence can be modeled by a screened Coulomb potential within a Debye-Huckle formalism with an analytical solution. First, we present the salt dependence of the end-to-end distance (R_ee) of an IDP. The electrostatics contribution (Q in Equation 2) is modified to Q′ as a function of salt. Specifically, Q′ is expressed in terms of κ, the inverse Debye length is defined as κ² = 8πl_bc_s, and c_s is the salt concentration (for the exact expression of Q′, see 45, equation 3).

To predict whether an IDP will expand or collapse with the addition of salt, Q′ can be expanded in the limit of zero salt, i.e., small κl, as

$$Q^{\prime }\approx \frac{1}{2}\sqrt{\frac{6\pi }{x}}\frac{1}{N}\sum _{m=2}^N\sum _{n=1}^{m-1}{q}_m{q}_n\sqrt{m-n}-(\kappa l)\frac{\pi }{2}\frac{1}{N}\sum _{m=2}^N\sum _{n=1}^{m-1}{q}_m{q}_n(m-n)+\dots \mathcal{H}.\mathcal{O}.,$$ 9.

where $\mathcal{H}.\mathcal{O}.$ are higher-order terms in κl. The first term can be identified as the SCD (ignoring constants) expected for the end-to-end distance. The second term yields a new sequence charge patterning metric (SCD_{low salt}) (see Reference 45, equations 4 and 5) defined as

$${\text{SCD}}_{\text{low salt}}=\frac{1}{N}\sum _{m=2}^N\sum _{n=1}^{m-1}{q}_m{q}_n(m-n).$$ 10.

In the vicinity of zero salt, if SCD_{low salt} is positive (negative), the ensemble average end-to-end distance will shrink (expand) upon the addition of salt. An immediate consequence is that two IDPs with identical charge compositions but different patternings can have different responses to salt due to the different signs of SCD_{low salt}. Reference 45 provides examples of this. The trend predicted by the SCD_{low salt} metric agrees with the single-molecule Förster resonance energy transfer measurements of Schuler and colleagues (67) on a limited set of four proteins: CspTm, integrase, and the N-terminal and C-terminal ends of prothymosin-α. However, the salt dependence of charged–polar and polar–polar interactions can cause deviations from the simple trend based on the sign of SCD_{low salt} alone. Another important physical contribution, which we do not discuss, is the salting-out effect—as proposed by Zheng and colleagues (104)—that can modulate salt-dependent shape changes in IDP sequences.

The discussion above shows the role of SCD_{low salt} in determining sequence-specific, salt-dependent responses in end-to-end distances. The strong variation noted among specific residue pair distance profiles suggests that the trends observed for end-to-end distances may not be representative of the entire chain. Beyond just the end-to-end distance, the salt dependence of internal distances is also revealed by the salt-dependent (i.e., κl) SCDM, defined as ${\mathrm{SCDM}}_{i,j}(\kappa l)=Q_{i,j}^{\prime }/(i-j)$; salt-dependent $Q_{i,j}^{\prime }$ is defined in Reference 46 (equations 4 and 5).

Expanding near zero salt, an SCDM matrix of low-salt metrics defined as SCDM_{low salt} (analogous to SCD_{low salt}, defined above for the end-to-end distance) is given by

$$\begin{gathered} {\text{SCDM}}_{\text{low salt},i,j}=\frac{1}{(i-j)}[\sum _{m=j}^i\sum _{n=1}^{j-1}{q}_m{q}_n\frac{{(m-j)}^2}{(m-n)}+\sum _{m=j+1}^i\sum _{n=j}^{m-1}{q}_m{q}_n(m-n) \\ +\sum _{m=i+1}^N\sum _{n=1}^{j-1}{q}_m{q}_n\frac{{(i-j)}^2}{(m-n)}+\sum _{m=i+1}^N\sum _{n=j}^i{q}_m{q}_n\frac{{(i-n)}^2}{(m-n)}]. \end{gathered}$$ 11.

Positive (negative) values of SCDM_{low salt,i,j} would cause ensemble average 〈$r_{i,j}^2$〉 to shrink (expand) with the addition of salt. An intriguing outcome of this is that some sequences may have both positive and negative elements in their SCDM_{low salt}, implying drastically different responses to salt at different distances. Figure 7 shows an example of an SCDM_{low salt} map for protein P0A8H9 with positive values in some regions expected to shrink—in contrast to other regions expected to expand—upon addition of salt near the zero-salt regime. Differential salt response between different pairs of amino acid residues (in the context of the full protein) have been experimentally observed by Schuler and colleagues (67). Hofmann and colleagues (102) also reported different salt responses for different segments of the full protein. However, we emphasize that theoretical predictions based on SCDM_{low salt} are purely within the Debye-Hückle approximation. Deviations from these predictions may also occur for additional driving forces, such as polar-charge and salting-out effects not included in this review. As expected, i = N, j = 1, and N ≈ (N − 1) yield SCD_{low salt} in Equation 10.

Figure 7.

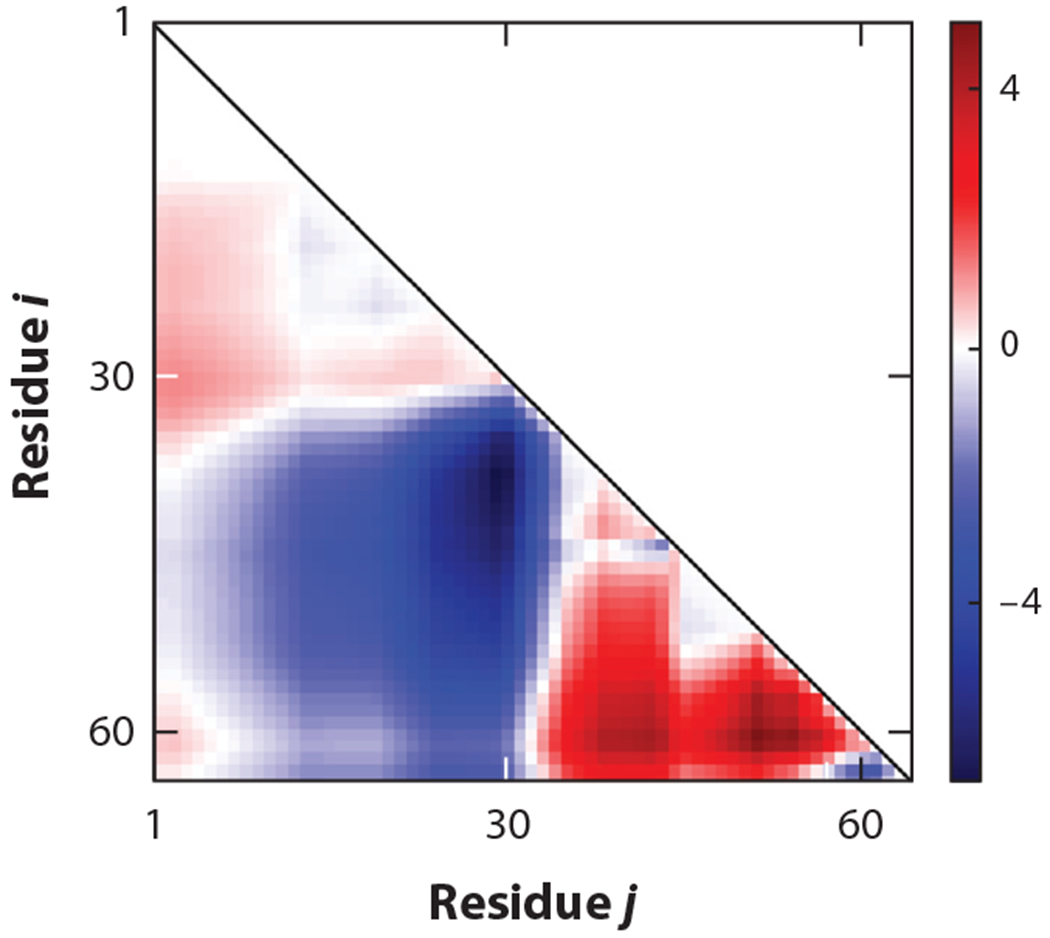
Residue pair–specific distances can have varying salt responses. Elements of SCDM_{low salt} (calculated using Equation 11) corresponding to different residue pairs (in the x and y axes) are shown for protein P0A8H9. The red regions denote positive values of the matrix elements, implying that the addition of salt near the zero-salt limit will shrink the distances among the respective residue pairs, while the blue regions denote pairs of amino acids for which the distances will expand upon addition of salt. Abbreviation: SCDM, sequence charge decoration matrix.

4. PHYSICAL MATHEMATICS MODELS FOR INTRINSICALLY DISORDERED PROTEIN AND REGION FUNCTIONS

PM is increasingly being used in modeling the functional features of IDPs. IDPs participate in many biological processes, from signaling and cellular differentiation to formation of membraneless organelles. Many of these functions rely on interactions among multiple copies of the same IDP or between IDPs and other macromolecules in disordered modes. Many of these modes of interaction are amenable to approximate models with closed-form solutions.

4.1. Analytical Models Predict Sequence-Dependent Phase Separation

Solutions of IDPs, either by themselves or in association with other macromolecules, can phase separate into protein-rich and dilute liquid phases. This phenomenon, known as liquid–liquid phase separation (LLPS), is emerging as a key mechanism in the formation of membraneless organelles and in numerous biological functions (4, 8, 42, 48, 52, 82, 91). In many such examples, IDPs in a homogeneous phase will phase separate below a critical temperature T_c. Below T_c, for a range of bulk protein densities, the solution will coexist in both the protein-rich and dilute phases, yielding a phase coexistence curve. Experiments are beginning to measure sequence-dependent T_cs and phase coexistence curves by modulating the amino acid composition or by shuffling the amino acid patterning at a fixed composition (11, 64, 72, 87, 100). In a seminal work, Chan and colleagues (56) developed a theoretical formalism using the random phase approximation (RPA; detailed below) to determine T_c as a function of sequence charge patterning. The sequence dependence of RPA theory explained remarkably well experimentally observed differences in phase-separation propensities, and their salt dependence, between two sequences: WT Ddx4 protein and its charge-scrambled (CS) version (64, 72). The CS version, created by keeping the same composition as in the WT but dispersing charges more evenly, did not phase separate, in contrast to the WT sequence. The theory of Chan and colleagues was the first of its kind to successfully explain the sequence dependence of an IDP’s propensity for phase separation. Figure 8 shows an application of the same theory to contrasting the phase separation propensity of the two different phosphorylated versions of P0A8H9 discussed above. The theory predicts that the phase separation propensity of the S54S56 variant is higher than that of the S2T15 variant, indicating the critical role of phosphorylation hot spots in determining LLPS. Both modifications have same charge composition but different patterning.

Figure 8.

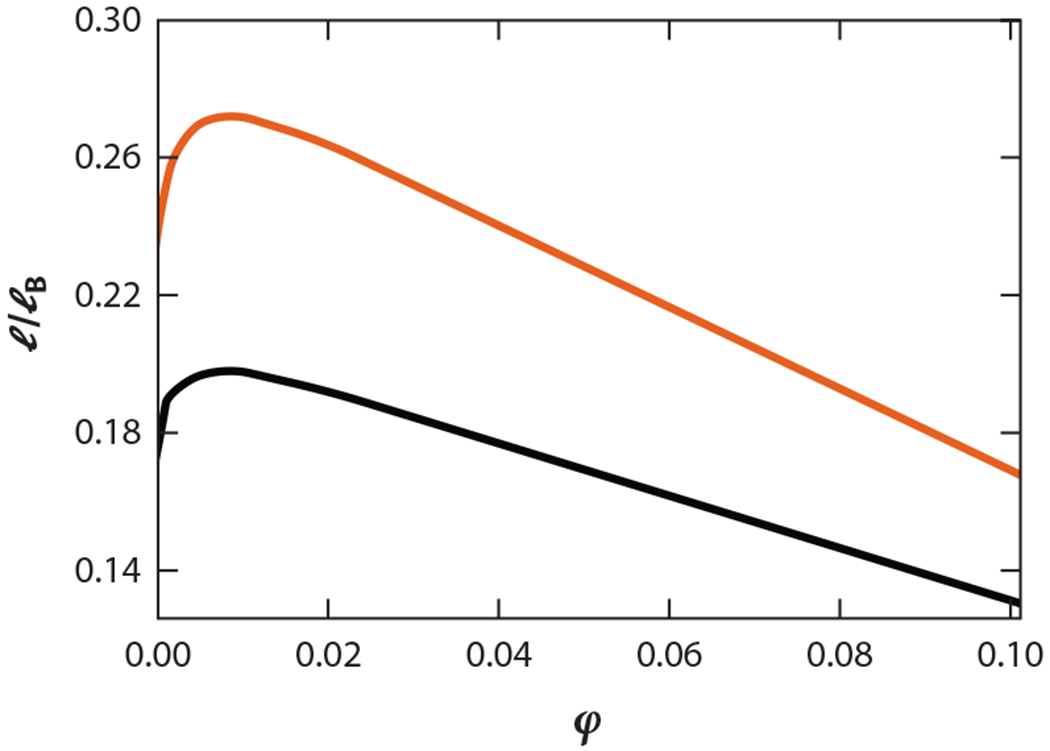
Phosphorylation hot spots can influence the propensity to phase separate. Phase diagrams (density ϕ in the x axis and dimensionless temperature l/l_b in the y axis) of two different phosphorylated versions (S54S56 in orange and S2T15 in black) of the wild-type protein P0A8H9 have been computed using the theory of Chan and colleagues (56). This theory predicts that two sequences with the same charge composition but with different patterning can have different critical points and propensities to phase separate. The effect of phosphorylation has been modeled by introducing a minus charge at the site of phosphorylation.

4.1.1. Simple explanation of random phase approximation and its improvement.

Models of phase separation must account for two key elements: the presence of multiple chains interacting with one another and the connectivity of each individual chain. The RPA formalism introduces field variables {ϕ} corresponding to the density of monomers and describing the presence of multiple chains. These variables are not directly constrained by chain connectivity. Variables {R}, describing the single-chain conformational ensemble, in contrast, must respect the connectivity of the monomers. The central aim of RPA is to account for an effective field (a function of {ϕ}) experienced by a single chain due to the presence of other chains. Consequently, the distribution of conformations {R} depends on {ϕ}, and {ϕ} itself is a function of {R}. For analytical tractability, RPA makes a simplifying approximation by neglecting higher-order fluctuations in {ϕ}, which is reasonable when densities are not too low. As part of this simplification, any explicit dependence of {R} on {ϕ} is ignored, and contributions from {ϕ} are kept only to the second order. This simplification allows chain connectivity to be accounted for within the simplest framework of a Gaussian chain. The simplified RPA predicts that the T_c of a PE (an IDP with only one type of charge) will increase with the length of the PE, contradicting earlier theoretical results, which had predicted that T_c saturates with increased chain length (70). A modified RPA called renormalized Gaussian RPA (rG-RPA) adopts a self-consistent formalism in which correlations in {ϕ} are calculated using a single-chain conformational ensemble {R}, which in turn depends on {ϕ} (54). This modification incorporates single-chain conformations correctly in building models for multichain interactions. rG-RPA recovers the correct limiting results for PE phase behavior. Furthermore, rG-RPA is able to explain differences in phase-separation propensities in WT and CS forms of Ddx4, capturing the sequence effect. A unified analytical framework such as rG-RPA demonstrates the power of first-principle PM models that can describe both polyampholyte and PE phase behavior (54). It is also important to note that the sequence-specific RPA formalism—despite the assumptions of weak fluctuations—is different from purely mean-field Flory-Huggins theory (for the interaction term), which completely neglects spatial dependence and fails to capture sequence specificity, providing another example of the importance of PM.

4.1.2. Unresolved issues.

There are still many caveats to rG-RPA. First, the theory assumes a uniform dielectric constant, even in the presence of salt. Recent work from the Chan group (23, 101) has addressed this issue and has shown that the approximation may cause modest deviations but not major changes. Second, extensions of the rG-RPA models are needed to describe the combinations of charge and noncharge patterning in chains that have charges, π, and hydrophobic interactions (23, 64, 72). Coarse-grained simulations are being developed with different interaction parameters to explain experimental data (23, 64, 99). Insights gained from these simulations may help to further advance first-principles analytical theory using rG-RPA. It is also important to develop PM models to estimate the effect of neglecting fluctuations beyond the second order, which are expected to be important in systems at low densities. At present, strong fluctuations are modeled by numerical solutions of stochastic differential equations using a self-consistent field theory formalism (18, 65). However, the quantitative, sequence-specific effects of these corrections are still unclear. For calculating the phase diagrams of PEs, in analytical calculations where higher-order terms to infinite order were approximately added within a closure relation (69), corrections beyond RPA were found to be insignificant compared with other terms (70). Improved models of the actual temperature dependence of the interaction parameters are also needed to address the lower critical solution temperatures, where proteins phase separate upon increases in temperature (26). Analytical models are needed to delineate the competition between liquid and other phases (such as solids and gels) that dictate the properties of condensates (7, 86).

4.1.3. Single-chain and many-chain physics can be related.

The success of rG-RPA also highlights the importance of single-chain conformations in predicting multichain phase behavior. The apparent interdependence between single-chain and multichain physics, inspired by earlier homopolymer results, has been elucidated in recent work. First, Lin & Chan (55) showed that the T_cs predicted using RPA [for Das & Pappu (19) sequences] strongly correlate with the SCD values for the single chain. Consistent with their observation, S54S56 has lower SCD and a higher propensity to phase separate (Figure 8) compared with S2T15 even though both sequences have same charge composition. Mittal and colleagues (24) performed coarse-grained simulations to establish the relationships between the temperature dependence of single-chain conformations and phase diagrams. Pappu and colleagues (108) have quantitatively shown how the temperature dependence of single-chain conformations can be used to predict solution phase diagrams. More recently, Lindorff-Larsen and colleagues (99) optimized a coarse-grained model against single-chain biophysical properties to predict multichain phase separation. Rana and colleagues (76) made an intriguing observation that normalized SCD can approximately determine competition between phase separation and aggregation in coarse-grained models of disordered proteins. These and other experimental studies (64, 78) highlight the importance of studying single-chain behavior to advance our understanding of solution behavior.

4.2. A Joint Sequence Charge Decoration Metric Describes Complexation Between Two Chains

Complexation is a frequent mode of protein–protein interaction. Much of the dimeric complexation of proteins leads to the formation of ordered structures. Schuler and colleagues (9) demonstrated a novel interaction mechanism in which two dissimilar IDPs can form a fully disordered complex. Their coarse-grained simulations show that simple electrostatics modeled by Debye-Hückle theory is sufficient to capture experimentally observed conformational features. Chan and colleagues (1) provided an analytical theory to quantify the binding constant between identical or dissimilar (A and B) pairs of IDPs. Intriguingly, the theory finds a metric, joint SCD (jSCD), that correlates with the binding constant. jSCD is defined as

$$\text{jSCD}(\{q_A,q_B\})=-\frac{1}{2N_A{N}_B}\sum _{s,t=1}^{N_A}\sum _{l,m=1}^{N_B}{q}_s^A{q}_t^A{q}_l^B{q}_m^B{[|s-t|+|l-m|]}^{1/2},$$ 12.

where $\{q_A\}$ is the sequence of charged amino acids in chain A, and {q_B} is that of chain B. Reference 1 provides the derivation of jSCD and its application to different pairs of heteropolymer sequences. Coacervation of polycation and polyanion chains—a limiting case of the example studied by Schuler and colleagues—is attracting a lot of interest in studies of synthetic polymers (60, 74). An interesting problem arises at the interface of complexation and phase separation. Recent work by Chan and colleagues (58) provided a mathematical model to couple the two processes and compare the results with experiments.

4.3. Charge Decoration Metrics Can Be Useful for Functional Annotation

Functionally similar intrinsically disordered regions (IDRs)—disordered segments between two structured regions—can have low sequence similarity detectable by traditional sequence alignment algorithms. Consequently, sequence and/or structure alignments, which are traditionally applied to predicting the functions of folded proteins, are not useful for predicting functionally similar IDRs. How then do we classify functionally similar IDRs? Is it possible to identify functional similarities among IDRs by finding similarities in their sequence decoration metrics, even when they are not similar in sequence alignments? Large-scale bioinformatic analyses have found underlying molecular features that are hidden in sequences but can be used to discern functionally similar proteins (105). Given that the SCDM can provide a high-dimensional representation of the charged patterning of a protein, it is natural to test the ability of SCDMs to classify IDPs (47, 73).

Further motivation for using SCDMs in discerning functional classes comes from two observations: (a) SCDMs have the ability to describe subtle features of conformations, and (b) conformational features can be similar among homologous IDPs (75). Indeed, high-dimensional features embedded in the SCDM can be used to distinguish functional and nonfunctional proteins within the Ste50 protein family (47). Ste50 is an IDR between two folded domains (107). It is critical to cell growth and shape. Moses and colleagues (107) classified five IDRs in functional and nonfunctional categories based on cell growth, shape, and basal protein expression. The five IDRs are the WT Ste50 from Saccharomyces cerevisiae; the doubly phosphorylated version of that WT; the WT Ste50 from a different organism, Lachancea kluyveri; and two other, unrelated IDRs, RAD26 and Pex5. The SCDM-based classification scheme is consistent with the experimental classification scheme (see Reference 47 for more).

Briefly, the classification algorithm proceeds in a few steps (47): (a) An IDR’s SCDM is first binarized to capture the repulsive or attractive nature of the electrostatics interactions, (b) binarized SCDMs (bSCDMs) are properly resized to compare proteins of different sizes, and (c) these bSCDMs are subsequently decomposed using principal component analysis to keep only the essential features and avoid any spurious information that may cause an artifact. The same algorithm was also reasonably successful in functionally classifying two other protein families: (a) protein family PSC, which is critical in chromatin remodeling (6), and (b) the RAM region of the Notch receptor (90). Each of these three proteins is highly charged, which justifies the use of the SCDM for functional classification while neglecting the contribution of other interactions (embedded in the SHDM). However, for IDPs with fewer charges, SHDM metrics in combination with the SCDM may be important for functional predictions. Recent work from Moses and colleagues (105, 106) revealed multiple molecular features—different from the patterning metrics noted above—that can be used to rescue and predict function.

SUMMARY POINTS.

1. The PM of IDPs describes rules of regulation that control IDP conformations.

2. Models for describing single-chain conformations inform the multichain physics of phase separation.

3. The physical mathematical relationships of IDPs provide insights into biological functions.

4. Physical mathematical equations—balancing accuracy and efficiency—overcome combinatorial challenges that may impede design strategies for new polymers or proteins.

FUTURE ISSUES.

1. Further improvement in electrostatic modeling is needed to include the roles of degree of ionization (of charged moieties) and of charge–dipole and dipole–dipole interactions. Furthermore, to improve the predictability of the conformational properties of single chains, transferable nonelectrostatics interaction parameters that can be combined with electrostatic models are needed.

2. Models for sequence-dependent phase separations are needed to account for noncharge interactions, strong fluctuations at low density, and lower critical solution temperatures. Existing theoretical platforms can be used to learn about the competition between LLPS and other physical processes such as gelation, aggregation, and complexation for which analytical models exist.

3. Efforts to build functional classification algorithms for IDPs are limited by the small numbers of data on IDP functions now available for suitable comparisons. More experimental measurements with designed variants are needed for building algorithms beyond the SCDM and for developing new patterning metrics (such as SHDMs that describe noncharge amino acids), as well as including molecular features beyond patterning metrics.