Abstract
The timing of self-initiated actions shows large variability even when they are executed in stable, well-learned sequences. Could this mix of reliability and stochasticity arise within the same neural circuit? We trained rats to perform a stereotyped sequence of self-initiated actions and recorded neural ensemble activity in secondary motor cortex (M2), which is known to reflect trial-by-trial action-timing fluctuations. Using hidden Markov models, we established a dictionary between activity patterns and actions. We then showed that metastable attractors, representing activity patterns with a reliable sequential structure and large transition timing variability, could be produced by reciprocally coupling a high-dimensional recurrent network and a low-dimensional feedforward one. Transitions between attractors relied on correlated variability in this mesoscale feedback loop, predicting a specific structure of low-dimensional correlations that were empirically verified in M2 recordings. Our results suggest a novel mesoscale network motif based on correlated variability supporting naturalistic animal behavior.
eTOC blurb
Self-initiated actions in freely moving rats can be predicted by specific ensemble activity patterns in the secondary motor cortex (M2). Variability in action timing can be explained by metastable attractors in a network model of M2. Transitions between attractors are generated by low-dimensional correlated variability, empirically verified in M2.
1. Introduction
When interacting with a complex environment, animals generate naturalistic behavior in the form of self-initiated action sequences, originating from the interplay between external cues and the internal dynamics of the animal. Self-initiated behavior exhibits variability both in its temporal dimension (when to act) and in its spatial features (which actions to choose, in which order) (Berman et al. 2016, Wiltschko et al. 2015, Markowitz et al. 2018). Large trial-to-trial variability has been observed in action timing, where transitions between consecutive actions are well described by a Poisson process (Killeen & Fetterman, 1988). Recent studies in C. elegans (Linderman et al. 2019), Drosophila (Berman et al. 2016) and rodents (Wiltschko et al. 2015, Markowitz et al. 2018) demonstrated that the spatiotemporal dynamics of self-initiated action sequences can be captured by state space models, based on an underlying Markov process. These analyses revealed a repertoire of behavioral motifs typically numbering in the hundreds, leading to a combinatorial explosion in the number of action sequences. Such a large behavioral landscape poses a formidable challenge for investigating the neural underpinnings of behavioral variability. A promising approach to tame the curse of dimensionality is to reduce the lexical variability in the behavioral repertoire, by using a task where the set of actions is rewarded when executed in a fixed order, yet retaining variability in action timing (Murakami et al. 2014, 2017), a hallmark of self-initiated behavior (Killeen & Fetterman, 1988).
Previous studies in rodents have identified the secondary motor cortex (M2) as part of a distributed network involved in motor planning, working memory (Li et al. 2016) and self-initiated tasks (Murakami et al. 2014, 2017). During delay periods in decision-making tasks, trial-averaged population activity in M2 displays clear features of attractor dynamics, with two discrete attractors encoding the animal’s upcoming choice (Inagaki et al. 2019). Are attractor dynamics in M2 confined to delay period activity? Here, we investigate the hypothesis that attractor dynamics can capture the activity of M2 neural circuits in a more naturalistic behavioral setting where a freely moving animal performs sequences of self-initiated behavior. In particular, we sought to uncover a correspondence between M2 neural activity patterns and upcoming self-initiated actions.
Because self-initiated action sequences are characterized by large trial-to-trial temporal variability in transition timing, they cannot be directly aligned across trials without the use of time-warping methods, hampering the applicability of traditional trial-averaged measures of neural activity. A principled framework to tackle this issue is to model single-trial neural population dynamics using hidden Markov models (HMMs) (Rabiner, 1989). These state space models can identify hidden states from population activity patterns in single trials, and have been successfully deployed in a variety of tasks and species from C. elegans (Linderman et al. 2019) to rodents (Jones et al. 2007, Mazzucato et al. 2015, Maboudi et al. 2018, La Camera et al. 2019), primates (Gat & Tishby, 1993; Abeles et al. 1995, Ponce-Alvarez et al. 2012, Engel et al. 2016) and humans (Baldassano et al. 2017, Taghia et al. 2018). Hidden Markov models segment single-trial population activity into sequences in an unsupervised manner by inferring hidden states from multi-neuron firing patterns. Within each pattern, neurons fire at an approximately constant firing rate for intervals typically lasting hundreds of milliseconds.
Previous work showed that the activity patterns, revealed by hidden Markov models, can be interpreted as metastable attractors, arising from recurrent dynamics in local cortical circuits (Miller & Katz 2010, Mazzucato et al. 2015). Metastable attractors are produced in biologically plausible network models (Deco & Hugues 2012, Litwin-Kumar & Doiron 2012) and have been used to elucidate features of sensory processing (Miller & Katz 2010, Mazzucato et al. 2015), working memory (Amit & Brunel, 1997) and expectation (Mazzucato et al. 2019), and to explain state-dependent modulations of neural variability (Deco & Hugues 2012, Litwin-Kumar & Doiron 2012, Mazzucato et al. 2016). However, while previous models are capable of generating sequential activity (Sompolinsky & Kanter 1986, Kleinfeld 1986, Miller & Katz 2010; Pereira & Brunel 2020), they are hindered by a fundamental trade-off between sequence reproducibility and trial-to-trial temporal variability. Namely, they can endogenously generate either reliable sequences without temporal variability (Sompolinsky & Kanter 1986, Kleinfeld 1986, Pereira & Brunel 2020) or, instead, sequences with large temporal variability but unreliable order (Litwin-Kumar & Doiron 2012; Mazzucato et al. 2015, Treves 2005). Thus, existing models are incapable of generating reproducible sequences of metastable attractors, characterized by large trial-to-trial variability in attractor dwell times.
Here, we addressed these issues in a waiting task (Murakami et al. 2014, 2017) in which freely moving rats performed many repetitions of a sequence of self-initiated actions leading to a water reward. The identity and order of actions in the sequence was fixed by the task reward contingencies (i.e., producing out-of-sequence actions yielded no rewards), yet action timing retained large trial-to-trial variability (Murakami et al. 2014, 2017). We found that M2 population activity during the task could be well modeled by an HMM that established a dictionary between self-initiated actions and neural patterns. To explain the neural mechanism generating reproducible yet temporally variable sequences of patterns, we propose that transitions between attractors are driven by low-dimensional correlated variability. This can be produced by reciprocally connecting a high dimensional recurrent network and a low-dimensional feedforward network. Attractors in the high-dimensional network represent the neural patterns inferred from M2 population activity. Previous experiments showed that recurrent circuits between cortical areas like M2 and subcortical areas such as thalamus (Guo et al. 2018, 2017) and basal ganglia nuclei (Hélie et al. 2015, Desmurget & Turner 2010, Nakajima et al. 2019) are necessary to sustain attractor dynamics and produce motor sequences, and we suggest that cortical-subcortical circuits might correspond to our high- and low-dimensional network interaction. This mechanistic model predicts a specific structure of noise correlations (to be low-dimensional and aligned between consecutive states in the sequence of neural activations), which we confirmed in the empirical data. While previous work showed that low-dimensional (differential) correlations in sensory cortex may be detrimental for accurately encoding external stimuli (Moreno-Bote et al. 2014), our results demonstrate that, surprisingly, they are essential for a motor circuit to produce stable yet temporally variable self-initiated action sequences.
2. Results
2.1. Ensemble activity in M2 unfolds through reliable pattern sequences
To elucidate the circuit mechanism underlying self-initiated actions we trained animals on a waiting task. In the waiting task, freely moving rats were trained to perform a sequence of self-initiated actions to obtain a water reward. Animals engaged in the trial by inserting their snout into a wait port, where, after a 400 ms delay, a first auditory tone signaled the beginning of the waiting epoch. Two alternative options were made available: i) waiting for a second tone, delivered at random times, then move to the Reward port to collect a large water amount (henceforth referred to as “patient” trials); or ii) terminating the trial at any moment before the second tone, then move to a reward port to collect a small amount of water (henceforth referred to as “impatient” trials). In either case, rewards were collected by withdrawing the snout from the wait port and poking into the reward port; thus, patient and impatient trials shared the same action sequence (Fig. 1a). The intervals between consecutive actions show large trial-to-trial variability with right-skewed distributions (Fig. 1b and Fig. S1a), suggestive of a potential stochastic mechanism underlying their action timing (Killeen & Fetterman 1988).
Figure 1: Waiting task and M2 pattern sequences.
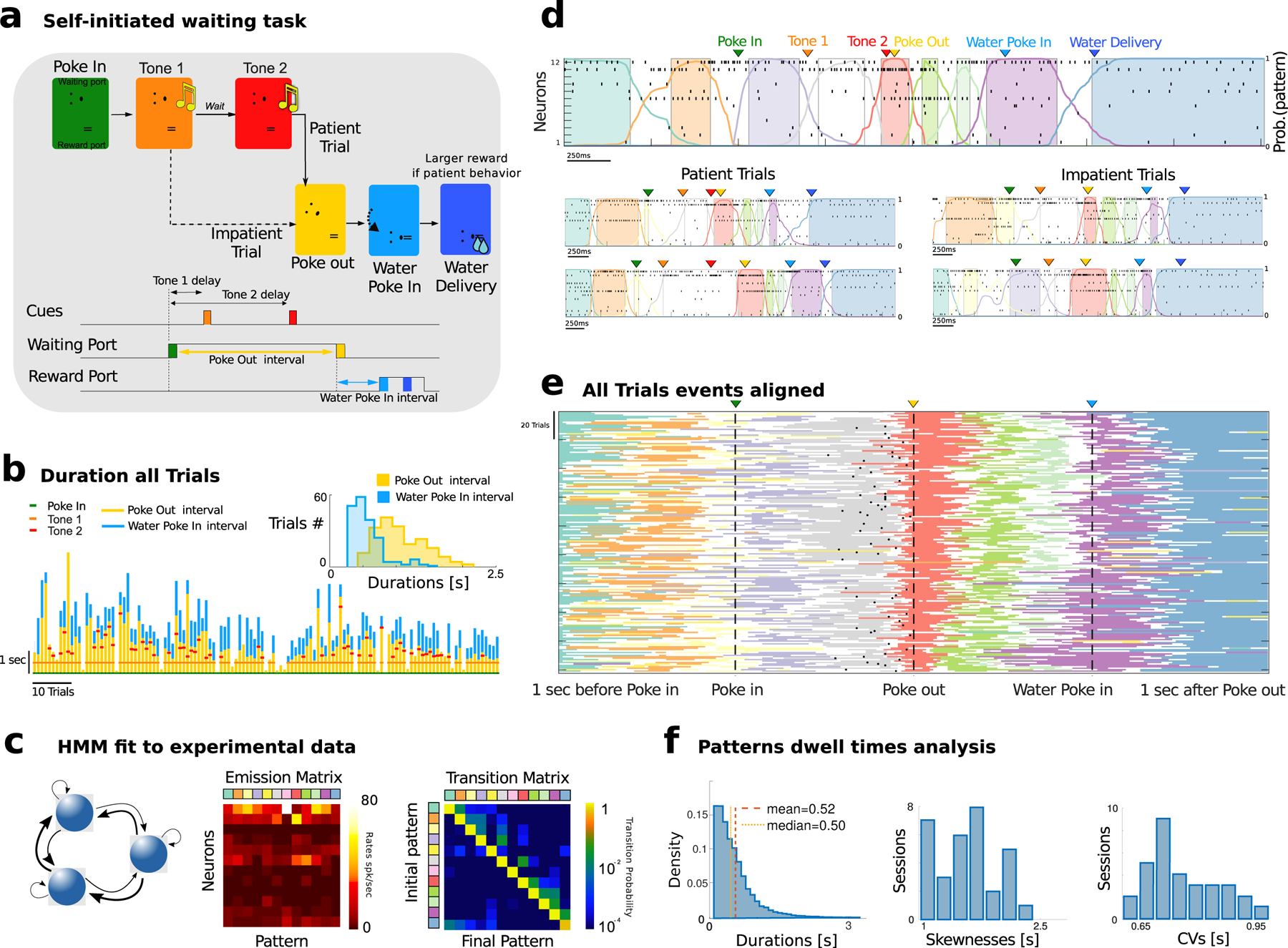
a) Schematic of task events. A rat self-initiated the waiting task by poking into a Wait port (Poke In), where tone 1 was played (after 400 ms), and, after a variable delay, a different tone 2 was played. The animal could decide to Poke Out of the Wait port at any time (after tone 2 in patient trials; between tone 1 and 2 in impatient trials) and move to the Reward port (Water Poke In) to receive a water reward (large and small for patient and impatient trials, respectively). Bottom: schedule of trial events. Three events (PI, PO, WPI) are triggered by self-initiated actions with respective interevents interval highlighted. b) Waiting behavior in a representative session. Tick marks represent event times (see legend). Vertical bars indicate waiting times for Poke Out and Water Poke In (yellow and cyan, respectively). When the red tick (second Tone) is not present, that marks an impatient trial. Inset: Interevent interval distribution for self-initiated actions ([PO - PI] and [WPI - PO], yellow and cyan, respectively). c) Neural pattern inference via Hidden Markov Model (HMM). An HMM (left, schematics) is fit to a representative session in d, returning a set of neural patterns (Emission Matrix, center) and a Transition Probability Matrix (TPM, right). Each pattern is a population firing rate vector (columns in the Emission Matrix). The TPM returns the probability for a transition between two patterns to occur. d) Representative trials from one ensemble of 12 simultaneously recorded M2 neurons during patient (top and bottom left) and impatient (bottom right) trials. Top: spike rasters with latent patterns extracted via HMM (colored curves represent pattern posterior probability; colored areas indicate intervals where a pattern was detected with probability exceeding 80%). e) All trials from the representative session (each row corresponds to a trial). Individual trials have been time-stretched to align to five different events (1 s before Poke In, Poke In, Poke Out, Water Poke In, 1s after Poke Out). All trials display a stereotyped pattern sequence. Color-coded lines represent stretched intervals where patterns were detected (same as colored intervals in d). Black tick marks represent tone 2 onset in patient trials only, while impatient trials are displayed but tone 2 is not reported. f) Left: Histogram of pattern dwell times for all patterns across all trials in the representative session reveal right-skewed distributions (we excluded the first and last pattern in the sequence, whose duration artificially depends on trial interval segmentation). Skewness and coefficient of variability (CV) of pattern dwell time distributions reveal large trial-to-trial variability (33 sessions).
To uncover the neural correlates of self-initiated actions, we recorded ensemble spike trains from the secondary motor cortex (M2, from N = 6 – 20 neurons per session, 9.9 ± 3.6 on average across 33 recorded sessions) of rats engaged in the waiting task (Murakami et al. 2014, 2017). We found that single-trial ensemble neural activity in M2 consistently unfolded through reliable sequences of hidden or latent neural patterns, inferred via a hidden Markov model (HMM, see Fig. 1c and Fig. S2). This latent variable model posits that ensemble activity in a given time bin is determined (and emitted) by one of a few unobservable latent activity patterns, represented by a vector of ensemble firing rates (depicted column-wise in the “emission matrix”). In the next time bin, the ensemble may either dwell in the current pattern or transition to a different pattern, with probabilities given by rows of the “transition matrix.” Stochastic transitions between patterns occur at random times according to an underlying Markov chain (i.e., transitions solely depend on the current pattern), and neurons discharge as Poisson processes with pattern-dependent firing rates. The number of patterns in each session was selected via an unsupervised cross-validation procedure (10.2 ± 0.6 across 33 sessions, which ranged from 6 to 22 patterns, Fig. S2a; see Methods) and did not depend on ensemble size (Fig. S2b). The identity and order of inferred patterns were remarkably consistent within each session even across patient and impatient trials. Fig. 1d shows five example raster plots where the sequence of states unfolds through the trial while Fig. 1e shows the sequence of states in all the trials of the same session (Fig. S3). The average pattern dwell time was 0.52 ± 0.13 s (mean ± sd across all sessions, dwell time was defined as intervals where the HMM posterior probability was above 80%, see Methods and Fig. 1f; median and interquartile dwell time was 0.42(0.36, 0.49)), in agreement with previous findings in other cortical areas (Mazzucato et al. 2015). Transition intervals between consecutive states lasted 0.14 ± 0.06 s, thus significantly shorter than state durations. Such long dwell times, which are greater than typical single neuron time constants, suggest that the observed patterns may be an emergent property of the collective circuit dynamics within M2 and reciprocally connected brain regions. Crucially, even though the identity and order of patterns within a sequence were highly consistent across trials, pattern dwell times showed large-trial to trial variability, characterized by right-skewed distributions (Fig. 1f–Fig. S2c, coefficient of variability CV= 0.76 ± 0.10 and skewness 1.60 ± 0.46). This temporal heterogeneity suggests that a stochastic mechanism may contribute to driving transitions between consecutive patterns within a sequence.
2.2. Robustness of pattern inference
We performed a series of control analyses aimed at testing the robustness of our pattern sequence model. We first examined how much single-cell autocorrelation and pairwise correlations contributed to the pattern sequence detection. To do so, first we performed a cross-validation analysis comparing the data to two surrogate datasets (Fig. 2a) (Maboudi et al. 2018). In the “circular-shuffled” surrogate dataset, we circularly shifted bins for each neuron within a trial (i.e., row-wise), thus destroying pairwise correlations but preserving single-cell autocorrelations. In the “swap-shuffled” surrogate dataset, we randomly permuted population activity across bins within a trial (i.e., column–wise), thus preserving instantaneous pairwise correlations but destroying autocorrelations. We found that the cross-validated likelihood of held-out trials for an HMM trained on the real dataset was significantly larger compared to an HMM trained on surrogate datasets (Figs. S2f to S2h, empirical vs. circular shuffled: p = 6.5×10−7; vs. swap shuffled: p = 5.4×10−7, signed-rank test). When we destroyed autocorrelations, the model entirely failed to detect pattern transitions, leaving only one pattern (Fig. 2b to 2c, p = 5.4×10−7). When destroying pairwise correlations, the model still detected multiple patterns whose number was in the same range as the model trained on the empirical data (Fig. 2c, p = 0.19). However, pattern detection was significantly less confident than in empirical data (Fig. 2b, Fig. 2c, p = 3.2×10−6); moreover, inferred pattern sequences were significantly sparser and more similar across trials in the data compared to the surrogate datasets (Fig. 2c, p = 2.7 × 10−6, Fig. S2d and Fig. S4). We concluded that single-cell autocorrelations, but not pairwise correlations, played an important role in extracting pattern sequences. Moreover, pattern sequences were not driven by the most active neuron in the ensemble but they are a robust collective property of the whole ensemble dynamics (comparison of HMM fits to the empirical data with surrogate datasets obtained by removing neurons with the highest activity revealed no significant differences, Figs. S4b to S4f).
Figure 2: Robustness of pattern inference.
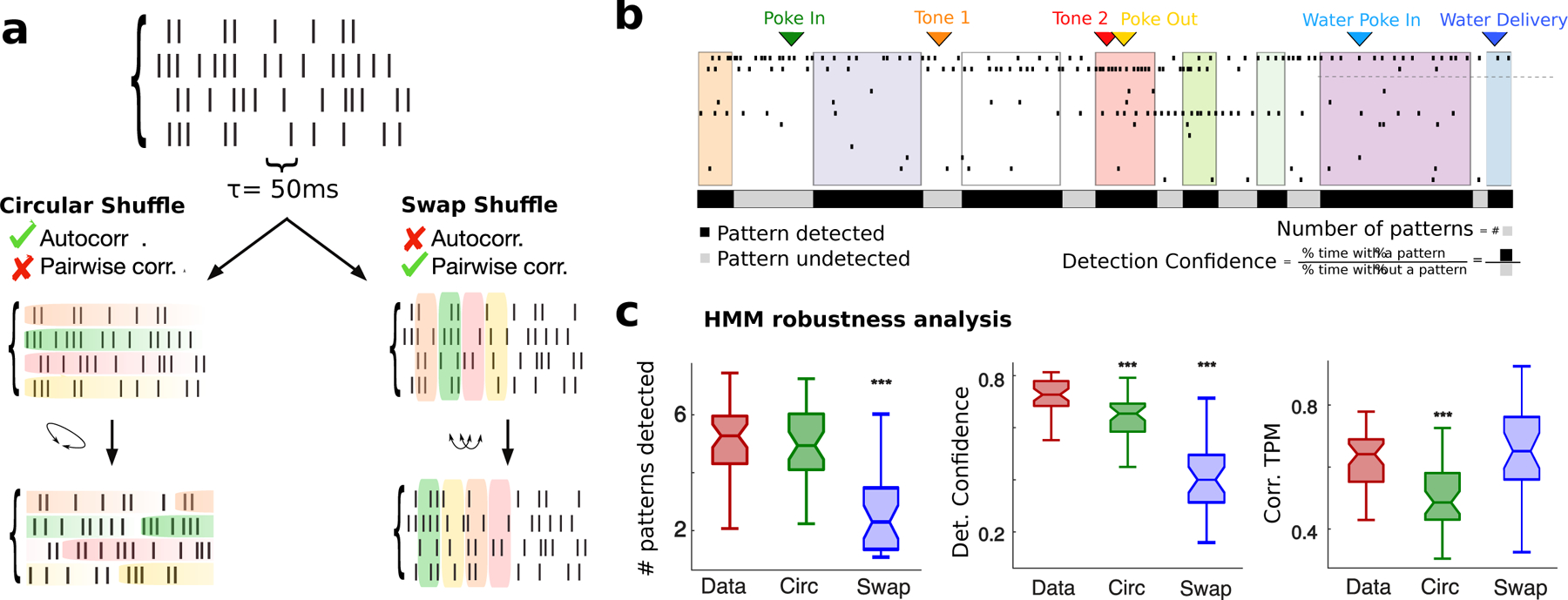
a) Schematic of shuffled procedure to create surrogate datasets: Circular Shuffle (left) preserved single-cell autocorrelations and destroyed pairwise correlations; Swap Shuffle (right) preserved pairwise correlations and destroyed autocorrelations. c) Representative trial showing detection confidence measure (same color-coded notation as in Fig. 1; black and grey bars: fraction of trial duration where patterns were detected with probability larger or smaller than 80%, respectively. d) HMM robustness analyses. Left: Average number of patterns in each trial for empirical and surrogate datasets. Center: Pattern detection confidence, estimated as fraction of time across all trials where patterns were detected with probability exceeding 80%. Right: Consistence of pattern sequence, estimated as Pearson correlation coefficients between single-trial estimates of “symbolic” TPMs encoding the sequence identity (see Methods methods:comparison). b-d: signed-rank tests between empirical and shuffled datasets, * = p < 0.05, ** = p < 0.01, *** = p < 0.001.
In additional control analyses, we found that the observed neural pattern sequences reflected an underlying discrete process and were not an artifact of the HMM inference. A Gaussian Process Factor Analysis (GPFA, see Fig. S5 and STAR Methods) (Engel et al. 2016, Byron et al. 2009, Churchland & Abbott 2012) revealed abrupt transitions in the time course of GPFA latent factors separating long and approximately constant epochs with long-tailed dwell time distributions (Fig. S5), closely matching the discrete HMM state sequences; and a strong bimodality of GPFA latent factors, consistent with underlying discrete states (Engel et al. 2016).
2.3. Patterns arise from dense and distributed neural representations
How do pattern sequences emerge from neural activity? Patterns formed separate clusters tiling population activity space, with between-cluster distances being significantly larger than within-cluster distances (Fig. 3a, Wilcoxon rank-sum test, p < 10−20). Most neurons were active in several patterns, leading to dense neural representations, where overlaps between patterns (0.41 ± 0.22, defined as Pearson correlation between firing rate vectors) were significantly larger than expected solely on the basis of the underlying firing rate distribution (Fig. 3b, p < 3 × 10–18, t-test). We found that the vast majority of neurons (88 ± 2 %) had firing rates significantly modulated across patterns (Fig. 3c). While 12 ± 2% of neurons were not modulated and 14 ± 2% had 2 different firing rates across patterns (bistable neurons), we found that 74 ± 2% of neurons were “multistable”, namely, they attained 3 or more firing rates across all patterns, in agreement with previous findings (Mazzucato et al. 2015). In particular, neurons attained on average 3.22 ± 1.17 different firing rates across patterns underscoring a distributed code of neural patterns across the neural population, Fig. 3c and Fig. S2i. Such multistability was more pronounced in the empirical data compared to the circular and swap shuffled datasets (Fig. S4a, Kolmogorov-Smirnov test: empirical vs. circular shuffle, p = 5.9×10−6, empirical vs. circular shuffle, p = 1.4 × 10−33), suggesting that multistability is a property of ensemble dynamics beyond single neuron autocorrelations and pairwise correlations. Furthermore, we found no linear dependence between a single cell multistability property and its average firing rate (Pearson correlation R2 = 0.11, p = 0.20), thus suggesting that multistability is unrelated to a cell’s average firing rate. We concluded that most M2 neurons participated in the pattern sequences, suggesting that M2 neural populations can support dense and distributed representations characterized by mixed selectivity to several patterns.
Figure 3: Dense and distributed population code in M2.
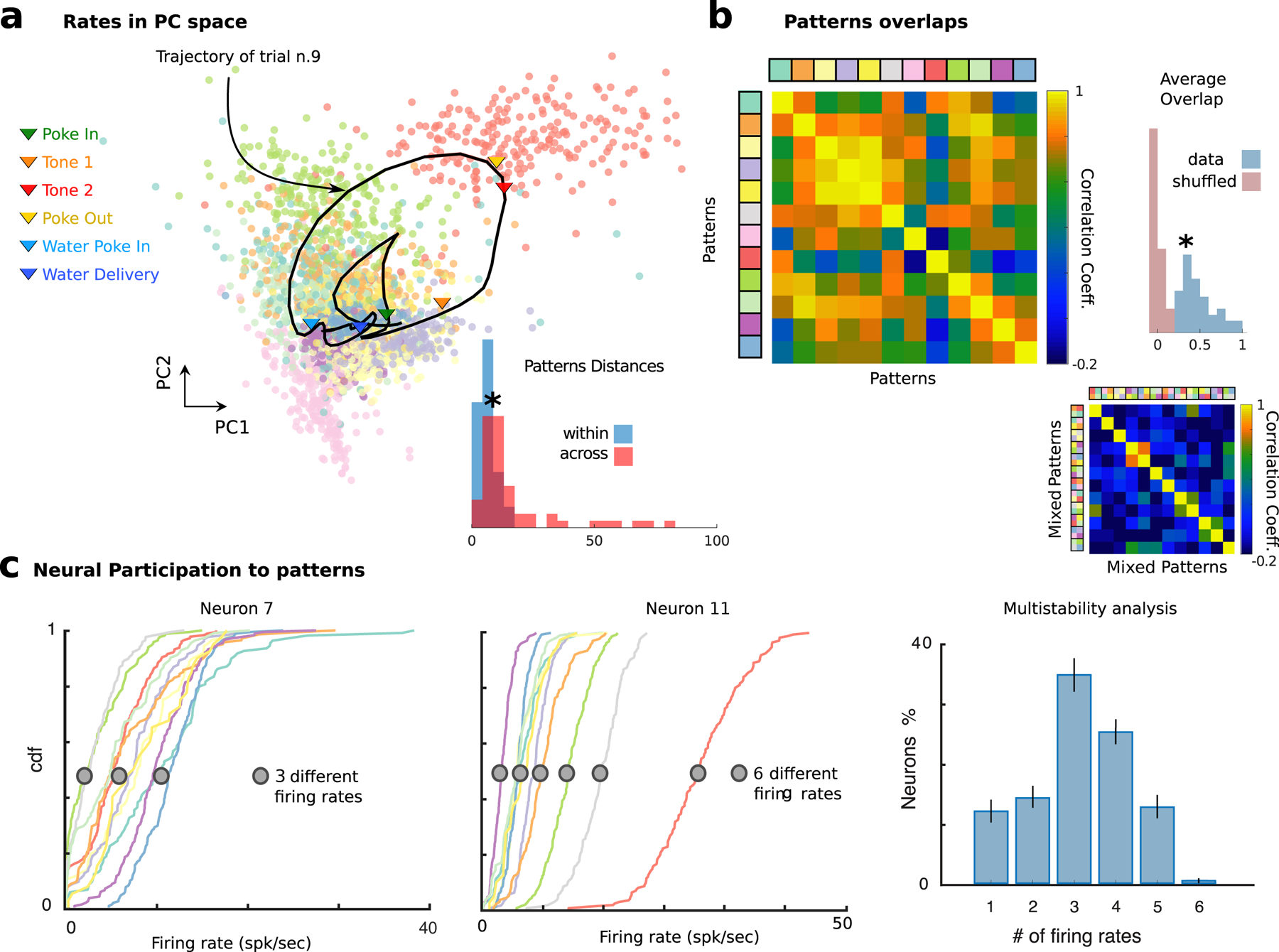
a) Neural patterns cluster in Principal Component space (all trials from the representative session in Fig. 1; color-coded dots represent patterns in single trials; one representative trial smoothed trajectory obtained by averaging neural activity in a sliding window of 600ms; arrows show events onsets along trajectory). Inset: Distribution of within- and across-cluster distances between patterns (ranksum test p < 2.0 × 10−7). Colors of different patterns are consistent with previous and following figures where the same example session is analyzed. b) Pearson correlation matrix between patterns reveals significantly larger overlaps in the empirical data (top left: representative session) compared to those found when drawing random patterns from the empirical firing rate distribution (bottom right). In this case the average firing rate of individual neurons in each pattern and trial was randomly drawn from the firing rate distribution of all neurons across all patterns in the same trial. Inset: Distribution of pattern correlations for empirical (blue) versus shuffled datasets (red). c) Single neuron firing rates are modulated by pattern sequences. Left: Cumulative firing rate distributions conditioned on patterns (color-coded as a) and Fig. 1d) for two neurons from the representative ensemble, revealing 3 and 6 significantly different firing rates across patterns, respectively (see Methods sec. 3.4 and Fig. S2i). Right: Number of different firing rates per neuron revealed multistable dynamics where 87 ± 2% of neurons had activities modulated by patterns.
2.4. Pattern onsets predict self-initiated actions
What kind of information about self-initiated behavior can be decoded from M2 pattern sequences? The statistical structures of neural patterns and action sequences shared remarkable similarities: single-trial consistency of identity and order of actions/patterns within a session, yet right-skewed distributions of timing intervals across trials (Fig. 1e and Fig. S3). We thus hypothesized that the onset of specific neural patterns could be causally involved with and therefore predictive of the timing and identity of upcoming self-initiated actions.
To test this hypothesis, we aimed to establish a cross-validated dictionary between actions and neural patterns, which we did by tagging the onset of specific patterns with the actions they most strongly predicted (Fig. 4a). This automated tagging method showed that, even though both pattern onsets and actions occurred at highly variable times in different trials, action onset times were reliably preceded by specific patterns onset on a sub-second scale (−99(−293, 28)ms, median (interquartile interval) between pattern onset and tagged action). In correct trials, defined as those in which a visit to the waiting port was followed directly by a movement to the reward port (both patient and impatient types, 67 ±16% fraction of trials per session, see Fig. 1a), the cross-validated accuracy of predicting actions from neural patterns was very high (Fig. 4c). Trials with other action sequences, where the animal behaved erratically, were deemed as incorrect trials (Fig. 4c and Fig. S6).
Figure 4: Predicting self-initiated actions from neural pattern onsets.
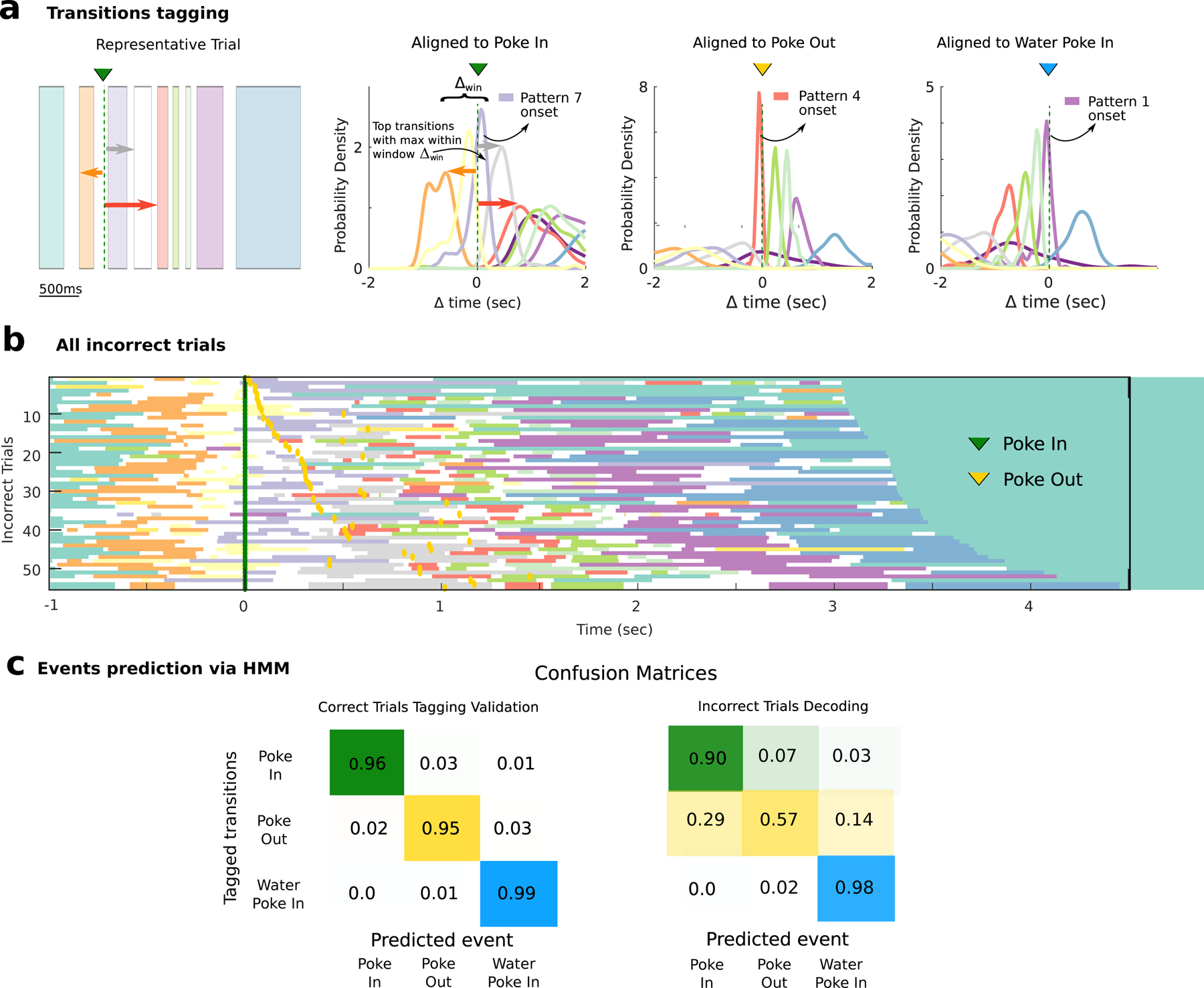
a) Schematic of pattern/action dictionary. Left: For each action in a correct trial (left: representative trial from Fig. 1d), pattern onsets are aligned to that action (Poke In in this example). The pattern whose median onset occurs within an interval Δwin = [−0.5, 0.1] s aligned to the action, and whose distribution has the smallest dispersion, is tagged to that action (color-coded curves are distributions of action-aligned pattern onsets from all correct trials in the representative session in Fig. 1). b) In incorrect trials (55 trials from the same representative session; time t = 0 aligned to Poke In), the same patterns as in correct trials are detected (cf. Fig. 1e), but they concatenate in different sequences. c) Predicting self-initiated actions from pattern onsets. Left panel: In correct trials (split into training and test sets), using a pattern-action dictionary established on the training set (procedure in panel a), action onsets are predicted on test trials (confusion matrix: cross validated prediction accuracy averaged across 33 sessions; hits: correct action predicted within an interval of [−0.1, 0.5] s aligned to pattern onset). Right panel: In incorrect trials, actions onsets are predicted based on the cross-validated dictionary established in correct trials.
To assess the significance of the action/pattern dictionary, we aimed at testing whether pattern onsets could correctly predict actions performed during incorrect trials ( 32.5 ± 15.8%, see Fig. 4b and Fig. S6), based on the dictionary learned solely from correct trials. Pattern sequences in correct trials were more correlated (0.520 ± 0.108, mean ± sd Pearson correlation across sessions) than in incorrect trials (0.398 ± 0.076; t-test, p < 10−5). The correlation between sequences in correct trials and those in incorrect trials (0.395 ± 0.096) was similar to the correlation found in incorrect trials (t-test, p = 0.88). This is consistent with the fact that correct (Fig. 1e) and incorrect trials (Fig. 4b) both begin with a Poke In/Poke Out then start diverging. Nevertheless, when using the cross-validated action/pattern dictionary learned on correct trials, we were able to correctly predict which actions the animal would perform in incorrect trials (Fig. 4b to Fig. 4c).
Perhaps surprisingly, we found that single neurons in M2 were not responsive to sensory stimuli (auditory tones 1 and 2: 6 and 4 responsive neurons across 328 neurons). Moreover, it was not possible to discriminate patient vs. impatient conditions from modulations of population firing rates (from a decoding analysis, Fig. S6f) nor from the distribution of pattern dwell times (Kolmogorov-Smirnov test, p > 0.05 in 95% of the sessions), reflecting the consistency of action timing distributions between the two conditions ( p > 0.05 in 95% of the sessions). These results are consistent with the hypothesis that M2 neural activity reliably encodes for the animal’s actions, regardless of whether these actions are performed in a patient or impatient trial. Indeed, both conditions involved the same action sequence, encoded in a reliable neural pattern sequence occurring in both condition. These results suggest that M2 activity mostly reflected stochasticity in action timing from trial to trial, regardless of whether a trial was classified as patient or impatient. We thus concluded that the spatiotemporal variability observed in M2 population activity in single trials is consistent with a mechanism whereby specific pattern onsets anticipate self-initiated actions.
2.5. Correlated variability generates sequences of metastable attractors
What is a possible circuit mechanism underlying the observed pattern sequences? We aimed at capturing three main features of the empirical data: ( I) Long lived neural patterns (0.5s on average, Fig. 1f), suggesting they originate from attractor dynamics; ( II) Right-skewed pattern dwell time distributions (see Fig. 1f), suggesting that transitions may be noise-driven (see e.g., (Gardiner et al. 1985)); ( III) Highly reliable sequences across trials (Fig. 1e and Fig. S3). We thus sought a mechanistic model generating reliable sequences of long-lived attractors with noise-driven transitions between attractors.
The crucial ingredient driving transitions between patterns in the model entails constraining population activity fluctuations along a low-dimensional manifold within a high-dimensional of activity space. We achieved this by embedding a low-rank term in the synaptic couplings.
We modeled population activity in M2 as arising from a recurrent network of rate units governed by the following dynamics:
| (2.1) |
where ui and are post-synaptic currents and single-neuron current-to-rate transfer functions representing the activity of M2 neurons (fit to the empirical data in M2, Fig. 5a, Fig. S7). We hypothesized that patterns originated from p discrete attractors ƞμ, for μ = 1,…, p, stored in the symmetric synaptic couplings (f and g are threshold functions, see Methods and (Pereira & Brunel 2018)), consistent with experimental evidence supporting discrete attractor dynamics in M2 (Schmitt et al. 2017, Guo et al. 2017, Inagaki et al. 2019). Because we sought to generate transitions stochastically, the model operates in a regime where the attractors ƞμ were stable in the absence of the second term JF (Fig. S7c). Transitions between attractors, giving rise to sequences, originate from the asymmetric term in (Eq. (2.1)), henceforth referred to as correlated variability term. This term generates stochastic dynamics via the noise ζ (t). We will discuss below the mechanistic origin of this term.
Figure 5: Attractor model of pattern sequences.
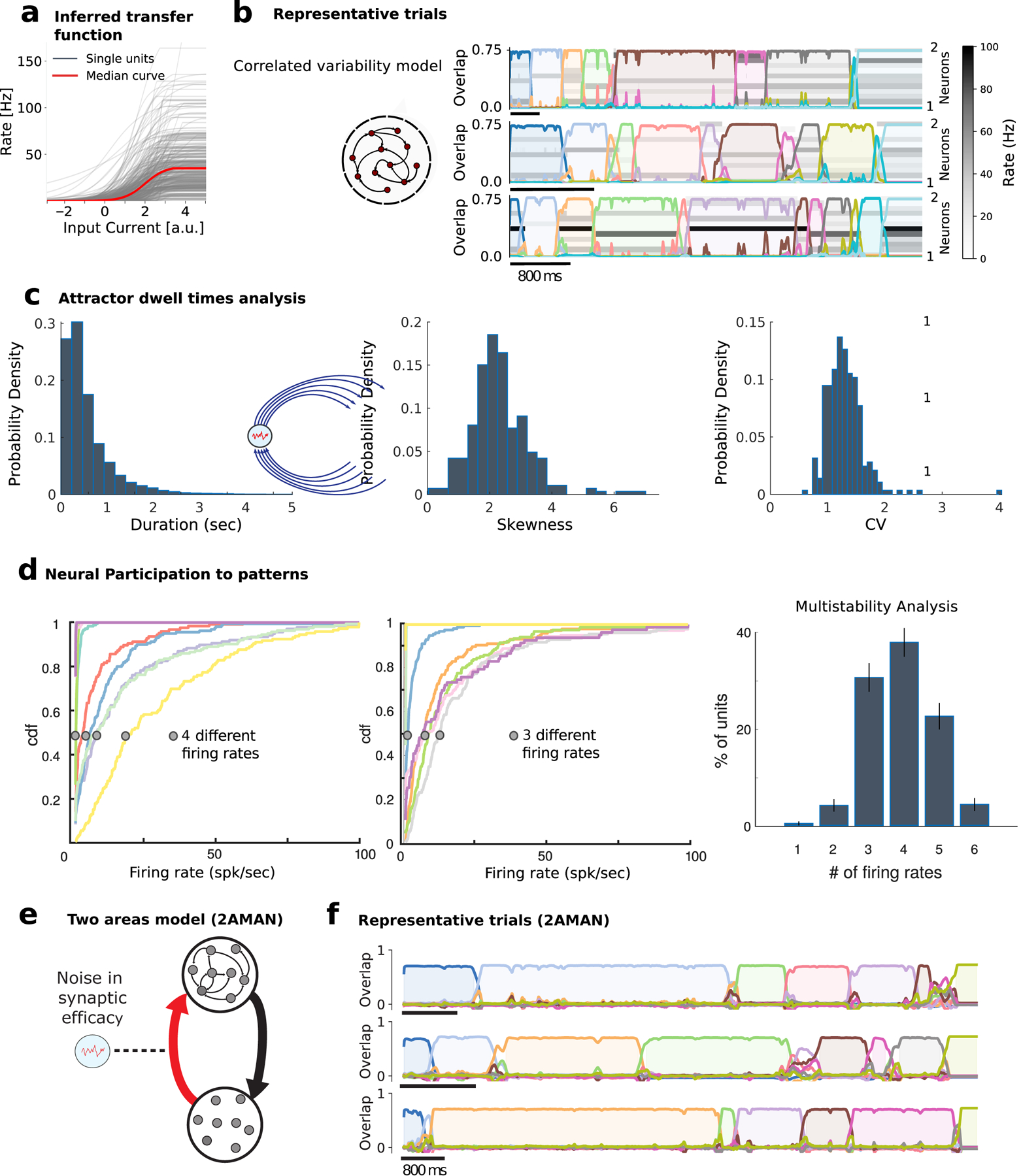
a) Distribution of empirical single-cell current-to-rate transfer functions ϕi inferred from the data (328 neurons from 33 sessions), used as transfer functions in the recurrent network model (see Methods). b) The correlated variability model Sec. 2.6 generates reliable sequences of long-lived attractors with large trial-to-trial variability in attractor dwell times (representative trials: rows represent the activity of 12 neurons randomly sampled from the network; color-coded curves represent time course of overlaps (see Eq. (3.10)) between population activity and each attractor; detected attractors are color-shaded). c) Histogram of attractor dwell times across trials in the representative network of b) reveals right-skewed distributions (left, we excluded the first and last pattern in the sequence, whose duration artificially depends on trial interval segmentation). Skewness (center) and coefficient of variability (CV, right) of pattern dwell time distributions reveal large trial-to-trial variability (33 simulated networks). The same plots, generated by means of states individuated in the model via a HMM fit on the model simulated neural traces, are shown in Fig. S9a. d) Single neuron firing rates are modulated by pattern sequences in the model. Cumulative firing rate distributions conditioned on attractors (color-coded as in b)) for two representative neurons in the model, revealing 2 and 3 significantly different firing rates across attractors, respectively (see Methods Sec. 3.4). Inset: Number of different firing rates per neuron revealed multistable dynamics where 99 ±1% of neurons had activities modulated by patterns. c) Two-area model schematic. Fluctuations in the synaptic efficacy depend only on the pre-synaptic terminals at area Y (see Eq. (3.15)), and therefore on the fluctuations on the synaptic efficacy of the Y→M2 synapses. d) Three example trials of the two-area model dynamics. As our analytical calculations predict, it produces meta-stable attractor dynamics that quantitatively match our phenomenological model and the data (dwell times distribution not shown). Parameters are the same as in Table 1. The additional parameters take values NY = 1000, AY←M2 = 0.12, and AM2←Y = 1. Area Y’s input-output transfer function is the rectifier linear function ϕ(x) = [x –1]+.
The correlated variability term constrains population activity fluctuations onto a low-dimensional manifold within activity space, whose dimension is bounded by the number p of attractors, thus much smaller than the number of neurons N. The effect of this term is to generate population activity fluctuations which are correlated across neurons. Within a large range of parameters (Fig. S7d), the network model met all our objectives: ( I) long-lived attractors matching the empirical data (average dwell time in Fig. 5b fit to the representative session in Fig. 1) emerging from the network’s collective dynamics; ( II) Right-skewed dwell time distributions (Fig. 5c); ( III) highly reliable attractor sequences (in ~ 4% of trials the model generates the wrong sequence of patterns, reminiscent of the incorrect trials in the empirical data). Since attractors would be stable in the absence of noise ζ (t) (Fig. S7c), transitions between attractors were entirely noise-driven in this model.
Furthermore, we found that single-neuron firing rate distributions were heterogeneous (Fig. 5d), similar to the empirical ones (Fig. 3c). In particular, most neurons participated in the sequential dynamics, attaining on average 3.8 ± 0.9 different firing rates across patterns, explaining the single-neuron multistability properties observed in M2 neural data (Fig. 5c, see also (Mazzucato et al. 2015)). When compared to traditional attractor models with sparse activations (Tsodyks & Feigel’man 1988), multistability was accompanied with a more dense code Fig. S8. We conclude that metastable attractor dynamics in our model captured the lexically stable yet temporally variable features of pattern sequences observed in the empirical data.
2.6. Correlated variability originates in a mesoscale feedback loop
The crucial ingredient driving transitions between patterns in the model (see Eq. (2.1)) entails restricting fluctuations along a low-dimensional manifold within activity space. We achieved this by embedding a low-rank noise term in the synaptic connectivity architecture of the neural circuit. What is the circuit origin of these couplings? We found that this low-rank structure naturally arises from a two-area model, describing a feedback loop between a large recurrent circuit representing M2 and a small feedforward circuit (provisionally denoted as Y):
| (2.2) |
Here, ui represent the activity of M2 neurons (same as in Eq. (2.1)), and ri represent activities of neurons in area Y (see model schematic in Fig. 5e). The latter area is smaller ( NY ≪ N) and faster (τY <τ), and lacks recurrent couplings, suggesting it may correspond to a subcortical circuit. The asymmetric term J F in Eq. (2.1), which generates stochastic transitions between otherwise stable attractors, originates from the reciprocal couplings WY←M 2 and W M 2←Y between M2 and area Y in Sec. 2.6, its temporal dependence arising from fluctuations in the synaptic efficacy of the Y → M2 synapses (see Methods and Fig. 5e). The reciprocal connections WY←M 2 and WM 2←Y in this two-area model can be integrated out when dynamics in area Y are faster than in M2 (τY <τ) (Reinhold et al. 2015, Jaramillo et al. 2019). The two-area mesoscale model (2AMAN) in Sec. 2.6 is then mathematically equivalent to the effective dynamics in Eq. (2.1), whose recurrent couplings are augmented to include an asymmetric term JF, inherited from the reciprocal loop. In the Methods section we show how the mean and variance of the noise term ζ (t) in Eq. (2.1) capture, respectively, the strength and the variability of the couplings in the feedback loop between M2 and area Y. Its time dependence arises from fluctuations in the synaptic efficacy assuming area Y is small. This variability in the synaptic efficacy may emerge from different but not-exclusive cellular mechanisms such as short term plasticity (Tsodyks et al. 1998) or stochastic synaptic vesicle release (Dobrunz & Stevens 1997). Network simulations of our two-area model confirm our mathematical results (see Fig. 5f).
2.7. Correlated variability is necessary to explain temporal variability in attractor networks
Is it possible to generate the observed pattern sequences with alternative mechanisms, in the absence of correlated variability? We varied symmetric ( JS) and asymmetric ( JF) synaptic coupling strength but with no noise ( ζ (t) = const in Eq. (2.1)), generating either decaying activity, or stable attractors, or sequences of attractors (Fig. S7c). However, all these alternative models failed to capture crucial aspects of the data. Namely, dwell times distributions were short and they showed no trial-to-trial variability, thus being incompatible with the observed patterns (Fig. 1f).
We then attempted to rescue these models by driving the network with increasing levels of private noise, namely, external noise, independent for each neuron (Fig. S8d, see Methods). This led to small amounts of trial-to-trial variability in dwell times, but was still qualitatively different from the empirical data. Increasing the private noise level beyond a critical value destroyed sequential activity (Fig. S8e).
We reasoned that the difficulty in generating long-lived, right-skewed distributions of dwell times in this alternative class of models was due to the fact that transitions were not driven by noise, but by the deterministic asymmetric term JF. Adding private noise did not qualitatively change variability, due to the high dimensionality of the stochastic component. Private noise induces independent fluctuations in each neuron; however, in order to drive transitions from one attractor to the next one within a sequence, these fluctuations have to align along one specific direction in the N-dimensional space of activities. The probability that independent fluctuations align in a specific direction vanishes in the limit of large networks, explaining why in the private noise model transitions cannot be driven by noise. We thus concluded that correlated variability, in the context of attractor networks, was necessary to reproduce the right-skewed distribution of pattern dwell time observed in the data.
2.8. Low-dimensional variability of M2 pattern sequences
Our recurrent network model (see Eq. (2.1)) entails a specific hypothesis for the mechanism underlying the observed sequences: transitions between consecutive attractors are generated by correlated variability. We reasoned that, if this was the mechanism at play in driving sequences, then two clear predictions should be borne out in the neural population data. First, the correlated variability term in Eq. (2.1) predicts that population activity fluctuations within a given pattern (color-shaded intervals in Fig. 5b), henceforth referred to as “noise correlations”, lie within a subspace whose dimension is much smaller than that expected by chance (Fig. 6a, dimensionality in the model vs. shuffled surrogate dataset, ranksum test, p < 10−15). Second, the sequential structure of the correlated variability term in Eq. (2.1) implies that noise correlation directions for attractors that occur in consecutive order within a sequence should be co-aligned. A canonical correlation analysis showed that in the correlated variability model the alignment across attractor (measured using the top K principal components of the noise correlations, where K is its dimensionality) was much larger than expected by chance (Fig. 6b, alignment in the model vs. shuffled surrogate dataset, ranksum test, p < 10−5). More specifically, we found that the strongest alignment occurred between consecutive patterns within a sequence, compared to those occurring further apart (Fig. 6b and Fig. S9, ranksum test, p < 10–20).
Figure 6: Low-dimensional variability in models and data.
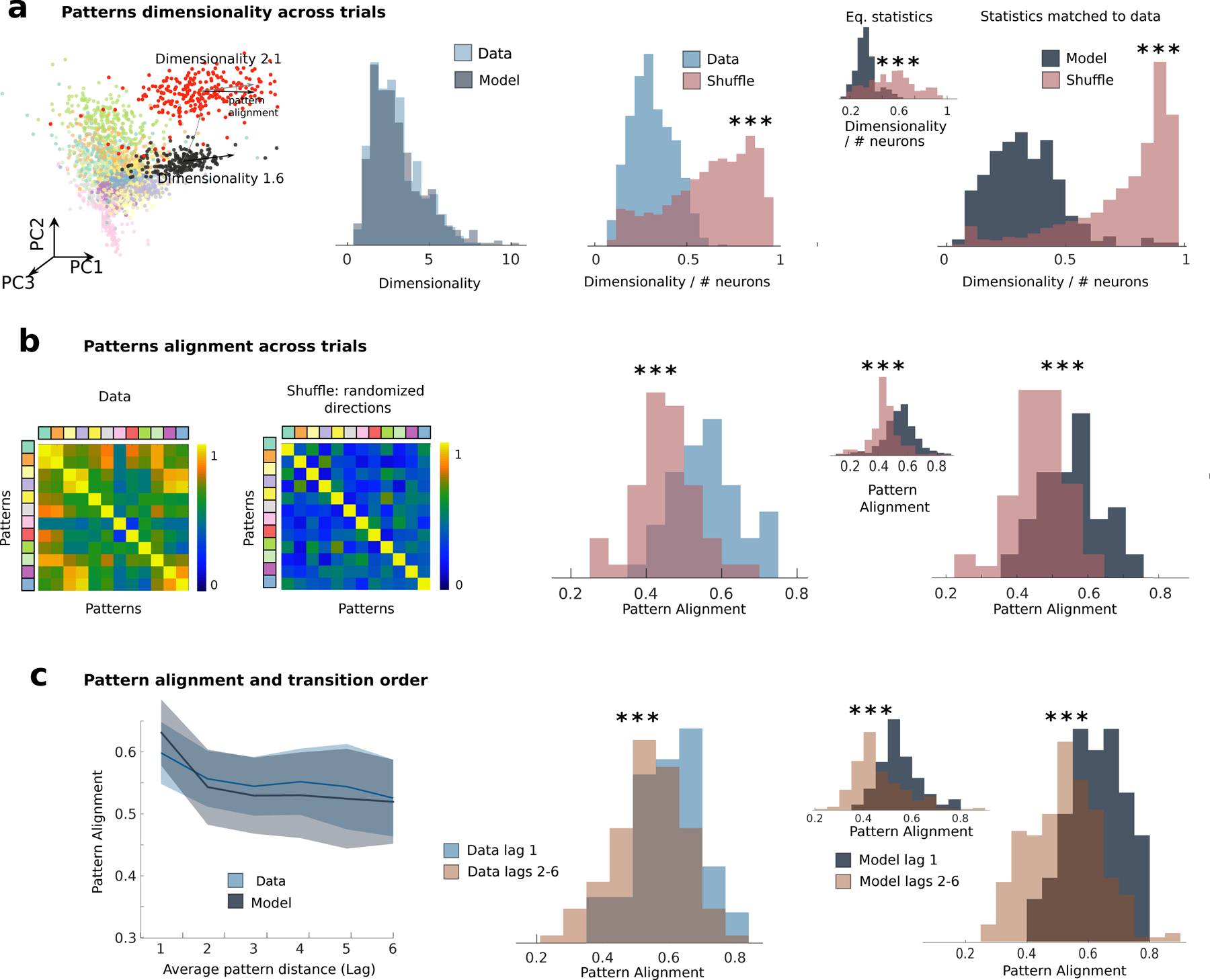
a) Comparison of dimensionality of pattern-conditioned noise correlations in the data (blue) and the model (grey) reveals low-dimensional population activity fluctuations, significantly smaller than expected by chance (red, shuffled datasets). In the shuffle dataset the firing rate of each neuron in each state and trial was randomly sampled from the the empirical distributions of firing rates for all states and trials in the same session. From left to right: first panel, representative session as in Fig. 1); second panel, summary across 33 sessions from the data and the model; third panel, fractional dimensionality in the data; fourth panel: model dimensionality estimated by matching ensemble sizes and number trials to data across 33 simulated sessions; inset: dimensionality estimated from N=10000 neurons in 33 simulated sessions. b) Pattern-conditioned noise correlations are highly aligned between patterns in the data. Alignment between top canonical correlation vectors (blue, data; gray, model) is larger than between random principal component directions (red). c) Left: Alignment of noise correlations between each pattern and patterns occurring at lag n in the sequence (e.g., n =1 represents patterns immediately preceding or following the reference pattern) in the model (grey) and in the data (blue). Pattern alignments are significantly larger for patterns at one lag compared to patterns at longer lags. All panels: * = p < 0.05, *** = p < 0.001. The same plots in panels a-c, generated by means of states individuated in the model via a HMM fit on the model’s simulated neural traces, are shown in Figs. S9b to S9d.
Having established strong statistical features regarding low-dimensional, aligned noise correlations, we tested whether the structure of correlations predicted by the model was observed in the M2 neural ensemble data. We defined noise correlations in the empirical data as population activity fluctuations around each neural pattern inferred from the HMM fit (Fig. 6a). Applying the same analyses to the data that were run on the model, we found that indeed empirical noise correlations around each neural pattern had lower dimension than expected by chance, and closely matched the dimensionality predicted by the model (Fig. 6a). CCA further revealed that noise correlations were highly aligned between patterns, significantly above the alignment expected by chance (Fig. 6b, rank-sum test p = 1.70×10−4). Finally, directions of variability were more aligned between consecutive patterns, compared to patterns further apart in the sequence, (rank-sum test, p < 10−14; see Fig. 6c and Fig. S9). Thus, the features of the noise correlations in the neural ensemble data were strongly consistent with the predictions from the correlated variability model.
3. Discussion
Our results establish a correspondence between self-initiated actions and discrete pattern sequences in secondary motor cortex (M2). We found that population activity in M2 during a self-initiated waiting task unfolded through a sequence of patterns, with each pattern reliably predicting the onset of upcoming actions. We interpreted the observed patterns as metastable attractors emerging from the recurrent dynamics of a two-area neural circuit. The model was capable of robustly generating reliable sequences of metastable attractors recapitulating the properties of the dynamics found in the empirical behavioral and neural data. We propose a neural mechanism explaining the variability in attractor dwell times as originating from correlated variability in a two-area model. The model predicts that population activity fluctuations around each attractor (i.e., “noise correlations”) are highly aligned between attractors and constrained to lie on a low-dimensional subspace, and we confirmed these predictions in the empirical neural (M2) data. Our work establishes a mechanistic framework for investigating the neural underpinnings of self-initiated actions and demonstrates a novel link between correlated variability and attractor dynamics.
3.1. Evidence for discrete attractor dynamics in cortex
Attractors are characterized by long periods where neural ensembles discharge persistently at approximately constant firing rate (defining a neural pattern) punctuated by relatively abrupt transitions to a different relatively constant pattern. Evidence for attractors was reported in temporal (Fuster & Jervey 1981, Miyashita 1988) and frontal areas in primates (Fuster & Alexander 1971, Funahashi et al. 1989) and rodents (Erlich et al. 2011, Schmitt et al. 2017, Guo et al. 2017, Inagaki et al. 2019), and in rodent sensory cortex (Jones et al. 2007, Ponce-Alvarez et al. 2012, Mazzucato et al. 2015).
Experimental evidence for stimulus-driven sequences of metastable attractors was previously found in primate frontal areas (Gat & Tishby 1993, Abeles et al. 1995, Seidemann et al. 1996) and rodent sensory areas (Jones et al. 2007). Random sequences were also observed during ongoing periods (Mazzucato et al. 2015, 2016, Engel et al. 2016). In all those cases, and consistent with our results, state dwell times showed large trial-to-trial variability captured by Markovian dynamics (i.e., right-skewed distributions), suggesting an underlying stochastic process driving transitions (Miller & Katz 2010, Mazzucato et al. 2015, 2019). A novel feature of our results is that the reliable sequence of metastable attractors is not driven by external stimuli, but rather is internally generated.
3.2. Neural circuits underlying pattern sequences
The main features of M2 ensemble activity explained by our network models were the reliable identity and order of long-lived neural patterns occurring in a sequence, and the large trial-to-trial variability of pattern dwell times. Both features can be robustly attained when transitions between attractors arise from correlated variability. For an extended comparison with other mechanistic models of attractor sequences see Table S1.
How does our two-area mesoscale attractor network (2AMAN) model architecture map onto specific neural circuits? Previous work showed, using inactivation experiments, that the stochastic component in action timing variability originated in M2 (Murakami et al. 2017). Our 2AMAN model relies on a small and fast network lacking recurrent couplings, representing a subcortical circuit connected to M2, such as the areas that comprise its basal ganglia or thalamic nuclei, as suggested by recent perturbation experiments (Guo et al. 2017, Schmitt et al. 2017). Although a larger mesoscale network may underlie sequence generation, including cortex, thalamus, and basal ganglia (Kawai et al. 2015, Hélie et al. 2015, Desmurget & Turner 2010, Nakajima et al. 2019, Markowitz et al. 2018, Murray et al. 2017, Nakajima et al. 2019, Kao et al. 2005) or a distributed mesoscale network (Svoboda & Li 2018).
A large amount of evidence implicated preparatory activity in rodent M2, specifically the anterolateral motor cortex, in action and movement planning both in forced-choice tasks (Erlich et al. 2011, Li et al. 2015, Chen et al. 2017, Sul et al. 2011, Inagaki et al. 2019, Guo et al. 2014) as well as self-initiated tasks (Murakami et al., 2014, 2017). The pattern sequences we uncovered in M2 were consistent with the features of preparatory activity (Jin & Costa 2015): a precise dictionary linked specific patterns to actions; pattern onset reliably predicted action onset; and action timing variability strongly correlated with pattern onset variability.
3.3. Correlated variability in sensory vs. motor processing
The main conceptual innovation in our 2AMAN model is the introduction of low-dimensional correlated variability driving reliable sequences with variable timing. Similar “motor noise correlations” have been recently reported during vocal babbling in juvenile songbirds (Darshan et al. 2017). Low-dimensional correlated variability has been widely reported in sensory cortex, where it may carry information about the animal’s behavioral state (McGinley et al. 2015, Cohen & Maunsell 2009, Huang et al. 2019) or movements (Niell & Stryker 2010, Polack et al. 2013, Stringer et al. 2018, Musall et al. 2019, Salkoff et al. 2019). It has been proposed that low-dimensional correlated variability in sensory cortex may be detrimental to sensory processing as it may limit a network’s information processing capability (Moreno-Bote et al. 2014). Here, we found that low-dimensional correlated fluctuations in a motor area are the crucial mechanism enabling neuronal sequences to unfold with variable timing. It is likely that variable timing is an adaptive feature of motor behavior to avoid predation or competition, or to explore the temporal aspects of a given behavior independently of the choices of actions. We speculate that exploration could allow learning of proper timing by a search in timing space independent of action selection and vice-versa, as may be the case in songbirds (Kao et al. 2005, Goldberg & Fee 2011, Darshan et al. 2017). Our results thus suggest that low-dimensional correlations are essential for motor generation.
3.4. Action timing variability and M2 activity
Here, we provided new evidence suggesting that M2 is involved in generating self-initiated actions and, crucially, show how variability in M2 population dynamics could generate the variability in self-initiated behavior. Our previous studies showed that most of the variance in waiting times of impatient trials is of stochastic origin, although a small fraction is of deterministic origin and could be interpreted as a trial-history-dependent bias in waiting times (Murakami et al. 2014, 2017), likely originating in the prefrontal cortex (PFC). Waiting time itself, however, was encoded only in M2 activity but not in PFC, consistent with the parsimonious hypothesis that the stochasticity in waiting time originates in a circuit that includes M2 itself. These results thus provide strong evidence for our interpretation that M2 circuits are directly involved in the decision of which action to plan and when to act, generating the stochasticity in self-initiated action timing. More generally, these results support a combined PFC-M2-subcortical picture leading to the decision to act: PFC providing a deterministic choice bias, which is translated into an actual choice signal by a downstream circuit including M2, injecting stochastic trial-to-trial variability via a subcortical feedback loop.
STAR Methods
RESOURCE AVAILABILITY
Lead contact
Further information and requests for resources should be directed to and will be fulfilled by the Lead Contacts, Zachary Mainen (zmainen@neuro.fchampalimaud.org) and Luca Mazzucato (lmazzuca@uoregon.edu).
Materials availability
This study did not generate new unique reagents.
Data and code availability
The code for simulating the network model is available at the following GitHub repository https://github.com/ulisespereira/sequences-attractors-M2. Data or data analysis scripts are available upon reasonable request from the lead contacts.
EXPERIMENTAL MODEL AND SUBJECT DETAILS
All procedures involving animals were either carried out in accordance with US National Institutes of Health standards and approved by Cold Spring Harbor Laboratory Institutional Animal Care and Use Committee or in accordance with European Union Directive 86/609/EEC and approved by Direção-Geral de Veterinária. Experiments were performed on 37 male adult Long-Evans hooded rats. Rats had free access to food, but water was restricted to the behavioral session and 20–30 additional min per day. Animals were involved in previous procedures.
Behavioral task
Rats were trained on the self-initiated waiting task (Fig. 1a) in a behavioral box containing a Wait port at the center and a Reward port at the side (entry/ exit from ports were detected via infrared photo-beam). Rats self-initiated a trial by poking into the Wait port (“Poke In”). If the rat stayed in the Wait port for T1 delay (0.4s), the first tone played (tone 1; 6 or 14 kHz tone), signaling availability of reward in the Reward port. If the rat waited in the Wait port after tone 1, then tone 2 was played after a T2 delay (14 or 6 kHz, different from tone 1). If the rat visited the Reward port after tone 2, a large water reward (40 μl) was delivered after a 0.5s delay (patient trial). If the rat poked out after tone 1 but before tone 2, and visited the Reward port, a small water reward (10 μl) was delivered after a 0.5s delay (impatient trial). The rat had to visit the Reward port within 2s after the poke out to collect rewards. These trials were referred to as “correct trials;” trials were the animal performed different action sequences were deemed “incorrect trials.” If the rat poked out before tone 1, no rewards were made available. Re-entrance to the Wait port was discourage with a brief noise burst. T2 delay was drawn from an exponential distribution, with minimum value 0.7s and mean adjusted to achieve patient trials in one third of the session. After reward delivery, an inter-trial interval (ITI) started during which white noise played. The time from the Poke In to the ITI end was held constant, so that the rat could not increase reward collection by leaving the Wait port fast with the goal to start the next trial early. The optimal strategy was thus to always wait for tone 2. To test whether neuronal responses depended on a specific action, 3 rats were trained on two variants of the task. In these experiments, a different behavioral box contained a Reward port, a nose-poke Wait port, and a lever-press Wait port. Blocks of nose-poke trials and lever-press trials were interleaved in each session. In the nose-poke block, the rat was to perform the same task as above. In the lever-press block, task rules were the same but the rat had to wait for the tones by keeping the lever pressed. The wrong action (nose-poke waiting in the lever-press block and vice versa) was not rewarded and classified as “incorrect trials.” 5 animals were trained on only the delay variant of the task. 3 animals where trained on both variants (delay and lever). We restricted the statistics of recordings to sessions where 6 or more neurons were simultaneously recorded. Upon applying such criteria a total of 33 sessions including 33 delay blocks and 21 lever blocks were analyzed across 8 animals. Each block last for 70–100 trials. Transitions between the blocks were not signaled. 33 sessions (7 rats) were recorded, see (Murakami et al. 2014) for extensive details.
Electrophysiological data
Rats were implanted with a drive containing 10–24 movable tetrodes targeted to the M2 (3.2–4.7 mm anterior to and 1.5–2.0 mm lateral to Bregma). Electrical signals were amplified and recorded using the NSpike data acquisition system (L.M. Frank, University of California, San Francisco, and J. MacArthur, Harvard University Electronic Instrument Design Lab). Multiple single units were isolated offline by manually clustering spike features derived from the waveforms of recorded putative units using MCLUST software (A.D. Redish, University of Minnesota). Tetrode depths were adjusted before or after each recording session in order to sample an independent population of neurons across sessions. See (Murakami et al. 2014) for details.
METHOD DETAILS
Pattern sequence estimation
A Hidden Markov Model (HMM) analysis was used to detect neural pattern sequences from simultaneously recorded activity of ensemble neurons. Here, we briefly describe the method used and refer to Refs.(Mazzucato et al. 2015, 2019) for details. According to the HMM, the network activity is in one of M hidden “patterns” at each given time. A pattern is a firing rate vector ri (m) (the “emission matrix”, Fig. 1c), where i = 1,…, N is the neuron index and m = 1,…, M identifies the pattern. In each pattern, neurons discharge as stationary Poisson processes conditional on the pattern’s firing rates ri (m). Stochastic transitions between patterns occur according to a Markov chain with transition matrix (TPM, Fig. 1c) Tmn, whose elements represent the probability of transitioning from pattern m to n at each given time. We segmented trials in 5 ms bins, and the observation of either yi (t) = 1 (spike) or yi (t) = 0 (no spike) was assigned to a bin at time t for the i-th neuron (Bernoulli approximation); if in a given bin more than one neuron fired, a single spike was randomly assigned to one of the active neurons. A single HMM was fit to all correct trials per session, yielding emission probilities and transition probabilities between patterns, optimized via the Baum-Welch algorithm with a fixed number of hidden patterns M (iterative maximum likelihood estimate of parameters and latent patterns given the observed spike trains).
The number of patterns M is a model hyperparameter, optimized using the following model selection procedure (Engel et al. 2016). In each session, we used K-fold cross-validation (with K = 20) to train an HMM on (K –1) – folds and estimate the log-likelihood of the held-out trials LL (M) as a function of number of patterns M in the fit (see Fig. S2). The held-out LL (M) increases with M, until reaching a plateau. We selected the number of patterns M * for which the incremental increase LL (M +1) – LL (M) had the largest drop (the point of largest curvature) before the plateau (Satopaa et al. 2011a). For control, we performed model selection using an alternative method, the Bayesian Information Criterion (Mazzucato et al. 2019), obtaining comparable results (not shown).
To gain further insight into the structure of the model selection algorithm, we performed a post-hoc comparison between the parameters optimized on the training set for each value of M (number of patterns), across the cross-validation K-folds. In particular, we estimated the similarity between the optimized features (emission and transition matrices ) in the k1 -th fold and the k2 –th fold for given M, according to the following congruence C (k1, k2) measure (Tomasi & Bro 2006):
where N is the ensemble size, is the normalized emission for pattern m, and is the normalized transition matrix . Features were matched across folds using the stable matching algorithm (Gale & Shapley, 2013). If the two folds yielded identical parameters, one would find C (k1, k2) = 1. A congruence above 0.8 signals good quantitative agreement between different folds, whereas congruence below 0.6 suggests a poor similarity among folds (Williams et al. 2018). We calculated the average congruence across all fold pairs for given M and verified that the number M * of patterns selected with the cross-validation procedure above corresponded to the elbow in the congruence curve (see Fig. S2a). For larger number of patterns, average congruence typically fell below 0.8.
The Baum-Welch algorithm only guarantees reaching a local rather than global maximum of the likelihood. Hence, for each session, after selecting the number of pattern M * as above, we ran 20 independent HMM fits on the whole session, with random initial guesses for emission and transition probabilities, and kept the best fit for all subsequent analyses. The winning HMM model was used to infer the posterior probabilities of the patterns at each given time p (m, t) from the data. Only those patterns with probability exceeding 80% in at least 50 consecutive ms were retained (henceforth denoted simply as patterns, Fig. 1d). This procedure eliminates patterns that appear only very transiently and with low probability, also reducing the chance of over-fitting. Pattern dwell time distributions (Fig. 1f) within each session were estimated from the empirical distribution of interval times where a pattern’s probability was above 80%. Lowering the value of 50ms would extend the distribution of pattern dwell times towards zero (cf. Fig. 1f) reducing the mean of such a distribution, although the characteristic tail and long transitions would remain as a hallmark of the underlying neural processes.
HMM robustness to neural population subsampling
We compared the HMM analysis of the full empirical dataset with two datasets obtained by removing specific neurons in each session. The two datasets were obtained as follows. For each session we computed the average firing rate for each neuron across all trials without taking HMM states into account, Fig. S4b. Then in one case (first dataset) we removed the neuron with the highest firing rate and run the HMM analysis again, this is labelled ”high” in Fig. S4c. In the second case we removed the neuron with median firing rate and similarly run the HMM analysis, ”median” case in Fig. S4d. Examples of the outcome of the HMM fit on the example session excluding respectively the top firing and median firing neuron are shown in Figs. S4c to S4d. The HMM fits to the subsampled statistics were in astounding agreement with the HMM fit to the full population underscoring the robustness of the HMM method even for small population sizes. In our statistics the average number of neurons per session was 9.9 ± 3.3. This robustness was captured by several metrics Figs. S4e to S4f. The number of states individuated selected by the HMM was remarkably similar across all sessions Fig. S4e, both concerning the number of states selected by our crossvalidation procedure and the number of states retained by our selection criteria, cf. Methods 4.3. Similarly properties related to the sequence of states (i.e., number of states per sequence, average state duraction and fraction of time for each trial occupied by states with a 80% posterior probability) were all remarkably similar with no significant difference across all sessions Fig. S4f.
Comparison with surrogate datasets
We compared the HMM analysis of the empirical dataset with two surrogate datasets, obtained with the following shuffled procedure (Fig. 2, (Maboudi et al. 2018)). In the “circular” shuffle, each neuron’s binned spike counts were circularly shifted within-trial randomly (row-wise circular shift), preserving autocorrelations but destroying pairwise correlations. In the “swap” shuffle, packets of binned population spike counts were randomly permuted in time (column-wise swap), preserving pairwise correlations but reducing autocorrelations. Each packet consisted of 10 binned spikecount vectors amounting to a total time of 50ms as each bin was of 5ms. For comparison of the real dataset with shuffled ones, we adopted the same K-fold cross-validation procedure as above, where an HMM was fit on training sets and the posterior probabilities p (m, t) of patterns were inferred from observations in the held-out trials (test set).
From the pattern posterior probabilities inferred on held-outs, we estimated several observables for comparison between real and shuffled datasets. Pattern detection confidence was estimated as the fraction of a trial length where a pattern was detected with high confidence ( p (m, t) > 80%).
Sparseness of transitions was estimated as the average Gini coefficient of TPMs obtained from the K training sets. The TPM returns the probability for a transition between two patterns to occur (see Sec. S4.3), therefore a sparser TPM suggests a more robust sequence unfolding. We also estimated the across-trials sequence similarity as follows. In a trial where patterns were detected above 80% in a certain consecutive order, we compiled a “symbolic” TPM, whose diagonal element were set equal to the number of non-consecutive occurrences of pattern m, and off-diagonal element was set equal to the number of n → m transitions observed; finally each row was normalized: . E.g., the pattern sequence 1, 2, 3,1, 2 is in one-to-one correspondence to the symbolic TPM
Sequence similarity was defined as the trial-averaged Pearson correlation between T (sym).
In the data, we define the overlaps q between N-dimensional vectors ri and si describing inferredpatterns as the correlation coefficient
where σ (r) is the standard deviation of r i.
Single neuron multistability
To assess how single-neuron activity was modulated across different patterns, local (i.e., single-trial) firing rate estimates for neuron i given a pattern m were obtained from the maximization step of the Baum-Welch algorithm
| (3.1) |
Where yi (t) are the neuron’s observations in the current trial of length T. To determine whether a neuron’s conditional firing rate distributions differed across patterns (Fig. 3c), we performed a non-parametric one-way ANOVA (unbalanced Kruskal-Wallis, p¡0.05). A post-hoc multiple-comparison rank analysis (with Bonferroni correction) revealed the smallest number of significantly different firing rate distributions across patterns. Given a p value pmn for the pairwise post hoc comparison between patterns m and n, we considered the symmetric M × M matrix S with elements Smn = 0 if the rates were different ( pmn < 0.05 / M) and Smn = 1 otherwise. For example, consider the case of 3 patterns and the following S matrix, where patterns were sorted by firing rates:
Firing rates of patterns 1 and 2 were not significantly different, but they were different from pattern 3 firing rate. Hence, in this case we classified the neurons as multistable with 2 different firing rates across patterns (Mazzucato et al. 2015).
Tagging pattern onsets to self-initiated actions
The HMM analysis yields a posterior probability distribution p (m, t) for the neural pattern m at time t. At any time we identified the active pattern when . When this criterion was not met by any pattern then no pattern was assigned, cf. Fig. 1d. The onset time of a specific pattern was identified as the first time where . Transitions of several patterns appeared in close proximity to specific events (Fig. 4a), we thus developed a method to tag pattern onsets to specific events. Specifically we tagged onset of a given pattern with one of three actions (Poke In, Poke Out, Water Poke In, respectively, for poking in and out of the Wait port and poking in to the Reward port) with the following procedure. For each session we analyzed all correct trials. We first realigned trials to the specific event recomputing the times of occurrences of all pattern onsets with respect to the event. In each session we analyzed all transitions to patterns which occurred in at least 70% of correct trials. This returned a distribution of times for the onset times of pattern .
If the average of the distribution , we tagged the pattern to the event. When multiple transitions matched our criteria, we selected the one with minimum inter-quartile . This procedure returned patterns tagged with specific actions for each trial (cf. Fig. 4c) and tagged one or more patterns in 82% of the sessions. Wherever a pattern was tagged it appeared on average in 90% of the session’s trials. We name pattern onset times {tPI, tPO, tWPI } respectively for the actions Poke In, Poke Out and Water Poke In.
Decoding actions from pattern onsets
We reversed the pattern tagging procedure to decode actions from pattern onsets. Transitions were tagged to actions using correct trials (training set) using the procedure above, then actions were decoded from pattern onsets using incorrect trials (test set). The decoding procedure follows these steps: for every trial, given an action time taction and the tagged pattern onset times , we classified the action according to
When no patterns passed this criteria the action was not labelled. This procedure labelled 63% of all actions. This procedure labelled 63% of all actions (at least one pattern was tagged to actions in 82% of the sessions). Whenever a pattern was tagged to an action, the pattern appeared in 90% (on average) of the session’s trials. The tagging procedure was therefore robust, and we believe that it could significantly improved in future experiments with the availability of larger populations of simultaneously recorded neurons. For each session and all tagged actions we estimated a confusion matrix of our decoding procedure (cf. Fig. 4c) by comparing the true actions (rows of the confusion matrix) with their predicted labels (columns of the confusion matrix). The confusion matrix across all sessions was obtained by averaging confusion matrices for individual sessions. In order to show, in our analysis, the statistics of non-classified actions despite tagged states being present in the trial, we performed a second analysis. We limited the statistics of sessions and trials to those where all three actions had corresponding tagged patterns. In such sessions each tagged transition could be misclassified with a different action or with no action at all. Thus, it was possible to uniformly report the statistics comparing the relative occurrence of the prediction of an action versus no-action; confusion matrices for these reduced statistics are reported in Fig. S6d.
Noise correlation analysis
To assess trial-to-trial variability in population activity we measured the neural dimensionality of population activity fluctuations around each pattern. We first estimated the noise covariance Cij (m), namely, the covariance conditioned on intervals where pattern m occurred (the time window with posterior probability ≥ 80% in each trial):
| (3.2) |
where NT is the number of trials in the session and i, j = 1,…, N index neurons. The superscript T denotes vector transposition. In each trial a and window the average firing rate in pattern m was computed from eq:hmmrate. We then computed the dimensionality d (m) of population activity fluctuations around pattern m as the participation ratio (Abbott et al. 2011, Mazzucato et al. 2016):
| (3.3) |
where λi are the eigenvalues of the covariance matrix for i = 1,…, N neurons (Abbott et al. 2011, Mazzucato et al. 2016). This measure is bounded by the ensemble size N and captures the number of directions, in neural space, across which variability is spread over.
To test the hypothesis that trial-to-trial variability is constrained within a lower dimensional subspace, we proceeded as follows. For each neural pattern m, we considered the first K Principal Components {PC1,…, PCK }m of C (m) in methods:cm, where K is the integer minor or equal to the average of d (m) across the M patterns within each session: . This represents the across-patterns average dimensionality of noise correlations within a session. Using a Canonical Correlation Analysis we then estimated the canonical variables between and for pairs of patterns m1 and m2, obtaining the respective correlation coefficients ρ/j between the K canonical variables, j ∈ {1..K}. Alignment A(m1, m2) was then defined as the average correlation coefficient between the canonical variables , cf. Fig. 6b.
To compute the shuffled statistics for Fig. 6 and similar, we proceeded as follows. In the case of the dimensionality (Fig. 6a) we created random ensambles of pattern activities by shuffling (using random permutations) neural activities within a session across all patterns and neurons. In the case of the of the pattern alignment (Fig. 6b) we computed the shuffled statistics by computing canonical correlation coefficients not between top principal components of two patterns (as many as individuated by the average dimensionality described above in each session) but rather between random principal components directions. In such a way the plots highlight how top principal components of pattern correlations are aligned between two patterns against the null hypothesis of random alignment between any two principal components of the same patterns.
Firing rate modulations by stimuli and conditions
Single cell responses to tones.
To estimate single neuron responses to the tone we performed a t-test for responses of individual neurons before and after the two tones from the spike count vector, across trials, before and after the sensory stimulus in a window of 50ms. We retained only trials where no other event (e.g., Poke Out) was present within a 100ms window from the onset of the stimulus.
Decoding of condition.
We sought to decode patient vs impatient trials from the time course of neural activity. We started by computing spikecount vectors binning spikes of neural activity through a non-overlapping moving window of 50ms. In each trial we considered the neural activity from 1sec before Poke In until 1.5sec after Water Poke In. We then labelled each spikecount vector respectively as ”patient” or ”impatient” if they belonged to a trial where the animal displayed the corresponding behavior. Finally we used a neural classifier (linear or SVM) trained on all spikecount vectors (Fig. S6f). In the SVM case several kernels yielded similar results, displayed are results for a Gaussian kernel.
GPFA fit to neural data
A Gaussian Process Factor Analysis (GPFA (Byron et al. 2009)) represents a continuous latent space model where hidden factors underlying the dynamics smoothly unfold through time giving rise to neural activity. GPFA posits that population activity is generated by an underlying continuous and low dimensional Gaussian process. By its nature, the GPFA aims to fit a continuous latent trajectory to population activity, as opposed to the HMM’s discrete nature of sudden transitions between long-dwelling states. Although this hypothesis may theoretically provide an alternative explanation for our results, we discovered that the time course of the GPFA latent factors closely matched the HMM discrete pattern sequences.
The number of latent variables Nfactors for each session was identified by means of a 3-fold crossvalidation procedure and selected by means of choosing the point of maximum curvature in the crossvalidation curve, identically to the criterion used to identify the number of HMM states. Here we used the knee locator algorithm described in (Satopaa et al. 2011b) with sensitivity parameter s = 1. Once the number of latent variables was assessed for each session, a GPFA model with the corresponding number of variables was fit.
The application of the GPFA method resulted in a time series for each of the Nfactors in each trial which were underlying neural dynamics. These time series are displayed in Fig. S5a for the example session considered in Fig. 1b to Fig. 1e. To aid visualization, for each factor (in each of the top 5 panels) we time warped the temporal dynamics in each trial to visualize it across all trials of the session. The characteristic trend of latent factors in this session shows how the onset of different actions is characterized by strong modulations of a subset of latent factors, capturing sudden changes in the neural dynamics they fit. This hints to a discrete rather than continuous feature of the latent space underlying neural dynamics. We visualized the trajectory of latent factors in their PC space Fig. S5b confirming a similar signature. The marginal distribution of PC 1 and PC 2 are shown in the plots at margin.
Network model
In this section we describe the correlated variability model generating reliable sequences of metastable attractors (see Eq. (2.1)), whose dynamics is ruled by the current-based formulation of the standard rate model (Grossberg 1969, Miller & Fumarola 2012):
| (3.4) |
The firing rates are analog positive variables given by the transformation of synaptic currents to rates by the input-output transfer function ϕi (ui). Transfer functions ϕi were inferred from the empirical firing rate distribution of M2 single neurons (see below inferring_transfer_function). The parameter τ corresponds to the single neuron time constant. We set the M2 symmetric connectivity to be sparse (Mason et al. 1991, Markram et al. 1997, Holmgren et al. 2003, Thomson & Lamy 2007, Lefort et al. 2009). Our connectivity consists of two terms, traditionally referred to as the symmetric term and the asymmetric term (Domany et al. 1995). The symmetric term reads
| (3.5) |
where t he variable represents the structural connectivity of the M2 local circuit, modeled as an Erdos-Renyi graph where with probability c. The normalization constant Nc corresponds to the average number of connections to a neuron; AS is the overall strength of the symmetric term. For any nonzero synaptic connection (i.e., cij = 1), the strength of the synaptic weight is given by . The variables are distributed as , where are normally distributed, i.e., . The functions f and g are given by the step functions
| (3.6) |
Therefore, the pair of binary random patterns and are correlated. We assume that , which constrains one of the two parameters of g. This constrain does not apply to f (i.e., ), and in our model the function f is biased towards inhibition (i.e., ). While is symmetric only if f = g, we choose to keep the terminology ‘symmetric’ for this term for consistency with early work in networks of binary neurons (Sompolinsky & Kanter 1986, Kleinfeld 1986, Herz et al. 1989, Domany et al. 1995).
The correlated variability term in Eq. (3.4) is comprised by the asymmetric matrix which is is given by
| (3.7) |
where the rank p of the matrix is much lower than the number of neurons N in the network. Hence, this term induces low-dimensional correlated fluctuations across neurons, driven by the Ornstein-Uhlenbeck process ζ (t) given by
| (3.8) |
where , and are the timescale, mean and variance of the process, respectively. For a derivation of these parameters see the next section.
In Sec. 2.7, we compared the correlated variability model (see Eq. (3.4)) to a private noise model
| (3.9) |
where term is additive white Gaussian noise with mean zero and variance representing private noise, independently drawn for each neuron. Here, the asymmetric part of the synaptic couplings is constant, proportional to the parameter , unlike the time varying asymmetric term in Eq. (3.4).
As a measure of the pattern retrieval (Fig. 5), we used overlaps, defined as the Pearson correlation between the instantaneous firing rate and the nonlinear transformation of a given pattern (Pereira & Brunel, 2018; Gillett et al., 2020)
| (3.10) |
Two-area mesoscale model
In this section, we show how to obtain the network model in Eq. (2.1), starting from the two-area network in Sec. 2.6, whose dynamics is governed by
| (3.11) |
In Fig. 5e a schematic of the two-area network model is shown. The first equation describes the dynamics of N neurons in area M2, with the notations as in Eq. (3.4). The second term represents the firing rates of NY neurons in area Y, where we assume . We approximate area Y dynamics as linear. The projections from M2 to area Y are structured similarly as M2 recurrent connections in Eq. (3.5), i.e.,
| (3.12) |
although there are two important differences. First, since the number of neurons in M2 and area Y are N and NY respectively, then is a rectangular matrix with dimensions NY×N. Second, projections from Y to M2 are dense. The right vectors in the outer product inside the sum in Eq. (3.12), , are the same vectors as the right vectors in the Eq. (3.5). The left vectors in the outer product are different than , but have the same statistics than , i.e. where , are normally distributed . Therefore, when M2 activity is in the μth attractor, since the μth overlap is order one, the activity is mostly projected along the direction in area Y. The parameter AY ←M 2 corresponds to the overall strength of the M 2 → Y projections.
We assume the activity of area Y is fast with respect to , replacing Sec. 3.4 by its steady state
| (3.13) |
Similarly to the M2 →Y projections, the feedback projections Y →M2 in Sec. 3.4 are given by
| (3.14) |
The variable represents the synaptic efficacies from Y to M 2, which in our model fluctuate in time. The parameter AM2←Y corresponds to the overall strength of the Y → M 2 projections. Fluctuations in the synaptic efficacy are pervasive. They can be the product of several different cellular mechanisms as for example short term depression (Tsodyks & Markram 1997) or variability in the synaptic vesicle release (Dobrunz & Stevens 1997). In this work, we consider a simple model for capturing the temporal fluctuations in the synaptic efficacy given by a noisy linear dynamics below
| (3.15) |
Here τs corresponds to the time-scale of the fluctuations in the synaptic efficacy, is the variance of these fluctuations, and is a Gaussian random variable with mean zero and variance one. In our model, changes on synaptic efficacy of the Y →M2 projections depend on fluctuations of pre-synaptic neurons in area Y given by the variable .
The input current to M2 due to the feedback loop between M2 and area Y is approximately
| (3.16) |
Here, we used the fact that has mean and finite variance σ2, when averaged over an ensemble of of patterns y and fluctuations of the synaptic efficacies in Eq. (3.15). The variable ω (t) represents the normalized fluctuations with mean zero and unit variance, and a finite autocovariance time-scale. Therefore, the matrix in Eq. (2.1) corresponds to the effective connectivity arising from the feedback loop between M2 and area Y given by
| (3.17) |
which has rank . Assuming , the fluctuations in Sec. 3.4 are order 1. We account for both the strength and the variability in the M2 →Y and Y →M2 projections, via the Ornstein-Uhlenbeck process ζ (t) in Eq. (3.8). Notice that τζ is the effective time-scale of the temporal fluctuations in the sum over Y neurons in Sec. 3.4. Its mean and variance control, respectively, the strength and the variability of the effective asymmetric couplings obtained after integrating out the dynamics in area Y. The variance is inversely proportional to the size of the neural population in area Y. Network simulations of our two-area model confirm our mathematical results (see Fig. 5f).
Inferring the transfer function from data
For inferring the input-output transfer function from in vivo recordings we adapted a method proposed in (Lim et al. 2015) to our hidden Markov model analysis. Briefly, for each session, the empirical distribution of mean firing rates across patterns and neurons is constructed. As in (Lim et al. 2015), we assumed normally distributed synaptic input currents. By rank-matching the firing rates to a standardized normal distribution we obtained the empirical current-to-rate transfer function (see Fig. S7). Similarly to (Pereira & Brunel 2018), for each recorded unit we fit this curve with a sigmoidal function
| (3.18) |
If input currents produced firing rates in transfer:1 larger than a neuron’s maximal firing rate Rmax, then the correspding firing rates were set to Rmax. Using the above procedure we inferred a distribution of parameters , one from each recorded unit (Fig. 5a). For conveying the diversity in the transfer functions inferred from data, in our model we randomly sampled with replacement 10000 samples from the parameter distribution above.
Network simulations
For the network simulations of the correlated variability model in Figs. 5 and Fig. 6, the parameter values used are listed in Table 1. The number of sessions and trials per session are matched to those in the empirical data. The number of attractors in each session, e.g., p (see Eq. (3.5)) are taken to be the same as the number of patterns inferred in each empirical session using the HMM. An attractor was detected in the model when the overlap between network activity and the attractor is larger than 0.4.
Table 1:
Network parameters.
| Model parameters | ||
|---|---|---|
| Parameter | Value | comment |
| c | 0.1 | connectivity sparsity |
| N | 10000 | network size |
| q f | 0.65 | potentiation offset for f |
| x f | 1.7 | potentiation/depression threshold for f |
| x g | 1.7 | potentiation/depression threshold for g |
| A S | 3 | strength of the symmetric connectivity |
| 0.65 | mean of the synaptic noise | |
| σζ | 0.65 | standard deviation of the synaptic noise |
| τζ | 20ms | synaptic noise time constant |
| σ p | 0 | standard deviation of the private noise |
| τ | 20ms | single neuron time constant |
For the network simulations of the private noise model in Figs. S7c to S7d the parameter are the same as in Table 1 except AS = 1, σζ = 0, and σ p = 0.2. An attractor was detected in the model when the overlap between network activity and the attractor is larger than 0.2.
The simulations where performed using custom Python scripts.
HMM fit to network model simulations
To verify our framework and the properties of our model, we fit a HMM model to the network simulations of the model and recomputed the same plots of Figs. 5 to 6 reported in Fig. S9. Neural activities in the model are of a continuous nature (rate based simulations) therefore we fit a gaussian HMM as follows. We run simulations of the model by matching the statistical properties of empirical data (see Sec. 3.4). For each simulated session we sampled a number of neurons equal to the one in the recordings. We then convolved neural activities with a gaussian filter of short duration (sd 60ms). We experienced this to be necessary to obtain a reliable convergence of the HMM. We selected the number of states in the model and fit the simulated neural population activities for each session with the HMM by means of a expectation-maximization algorithm. This fit returned the identity of the state generating the neural activity. On these statistics we then run the analysis of Figs. 5 to 6 to obtain the metrics shown in Fig. S9.
QUANTIFICATION AND STATISTICAL ANALYSIS
Data analyses was performed with custom-written software using MATLAB (Mathworks) and Python. No statistical methods were used to pre-determine sample sizes, but sample sizes were similar to previous studies (Erlich et al. 2011, Guo et al. 2014). All summary statistics are mean ± sd across 33 sessions, unless otherwise stated.
Supplementary Material
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Experimental models: Organisms/strains | ||
| Long-Evans hooded rats. | Harlan | Le/CpbHsd |
| Software and algorithms | ||
| MATLAB | MathWorks | MATLAB R2019a |
| Python version 3.7 | Python | https://www.python.org/ |
| Custom code for network simulations | This paper | https://github.com/ulisespereira/sequences-attractors-M2 |
| MClust-3.5 | A. David Radish, University of Minnesota | http://redishlab.neuroscience.umn.edu/MClust/MClust.html |
| Other | ||
| Behavior control system: BControl | Carlos D. Brody, Princeton University | https://brodylabwiki.princeton.edu/bcontrol/index.php/Main_Page |
| Tetrode wire | P.Reid | Polyimide-insulated nichrome 0.0005’’ diameter |
| NSpike data acquisition system | L.M. Frank, University of California, San Francisco, and J. MacArthur, Harvard University Electronic Instrument Design Lab |
http://nspike.sourceforge.net/ |
Highlights.
Behavioral sequences in freely moving rats revealed large variability in action timing.
Actions were preceded by onset of specific neural patterns in secondary motor cortex.
Metastable attractors in a network model can explain the origin of timing variability.
Transitions between attractors are driven by low-dimensional correlated variability.
Acknowledgments
We would like to thank Fanny Cazettes, Nick Steinmetz, Dennis Nestvogel and Yonathan Loewenstein for discussions. We thank in particular Laureline Logiaco, James M. Murray and Nicolas Brunel for suggestions on the network model. L.M. was supported by a National Institute of Deafness and Other Communication Disorders Grant K25-DC013557, by National Institute of Neurological Disorders and Stroke Grant R01-NS118461 (BRAIN Initiative), and by a Swartz Foundation Award 66438. Z.F.M. was supported by the European Research Council (671251).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Declaration of Interests
The authors declare no competing interests.
References
- Abbott LF, Rajan K & Sompolinsky H (2011), Interactions between Intrinsic and Stimulus-Evoked Activity in Recurrent Neural Networks, Oxford University Press, chapter 4. [Google Scholar]
- Abeles M (1991), Corticonics, New York: Cambridge University Press. [Google Scholar]
- Abeles M, Bergman H, Gat I, Meilijson I, Seidemann E, Tishby N & Vaadia E (1995), ‘Cortical activity flips among quasi-stationary states’, Proc Natl Acad Sci USA 92, 8616–8620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amit DJ & Brunel N (1997), ‘Model of global spontaneous activity and local structured activity during delay periods in the cerebral cortex’, Cereb Cortex 7(3), 237–52. [DOI] [PubMed] [Google Scholar]
- Baldassano C, Chen J, Zadbood A, Pillow JW, Hasson U & Norman KA (2017), ‘Discovering event structure in continuous narrative perception and memory’, Neuron 95(3), 709–721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berman GJ, Bialek W & Shaevitz JW (2016), ‘Predictability and hierarchy in drosophila behavior’, Proceedings of the National Academy of Sciences 113(42), 11943–11948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Byron MY, Cunningham JP, Santhanam G, Ryu SI, Shenoy KV & Sahani M (2009), Gaussian-process factor analysis for low-dimensional single-trial analysis of neural population activity, in ‘Advances in neural information processing systems’, pp. 1881–1888. [DOI] [PMC free article] [PubMed]
- Chen T-W, Li N, Daie K & Svoboda K (2017), ‘A map of anticipatory activity in mouse motor cortex’, Neuron 94(4), 866–879. [DOI] [PubMed] [Google Scholar]
- Churchland MM & Abbott LF (2012), ‘Two layers of neural variability’, Nat Neurosci 15(11), 1472–4. [DOI] [PubMed] [Google Scholar]
- Cohen MR & Maunsell JH (2009), ‘Attention improves performance primarily by reducing interneuronal correlations’, Nature neuroscience 12(12), 1594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darshan R, Wood WE, Peters S, Leblois A & Hansel D (2017), ‘A canonical neural mechanism for behavioral variability’, Nature communications 8, 15415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deco G & Hugues E (2012), ‘Neural network mechanisms underlying stimulus driven variability reduction’, PLoS Comput Biol 8(3), e1002395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dehaene S, Changeux J-P & Nadal J-P (1987), ‘Neural networks that learn temporal sequences by selection’, Proceedings of the National Academy of Sciences 84(9), 2727–2731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desmurget M & Turner RS (2010), ‘Motor sequences and the basal ganglia: kinematics, not habits’, Journal of Neuroscience 30(22), 7685–7690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diesmann M, Gewaltig MO & Aertsen A (1999), ‘Stable propagation of synchronous spiking in cortical neural networks’, Nature 402, 529–533. [DOI] [PubMed] [Google Scholar]
- Dobrunz LE & Stevens CF (1997), ‘Heterogeneity of release probability, facilitation, and depletion at central synapses’, Neuron 18(6), 995–1008. [DOI] [PubMed] [Google Scholar]
- Domany E, Hemmen J. v. & Schulten K (1995), Models of Neural Networks I, Springer. [Google Scholar]
- Engel TA, Steinmetz NA, Gieselmann MA, Thiele A, Moore T & Boahen K (2016), ‘Selective modulation of cortical state during spatial attention’, Science 354(6316), 1140–1144. [DOI] [PubMed] [Google Scholar]
- Erlich JC, Bialek M & Brody CD (2011), ‘A cortical substrate for memory-guided orienting in the rat’, Neuron 72(2), 330–343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fiete IR, Senn W, Wang CZ & Hahnloser RH (2010), ‘Spike-time-dependent plasticity and heterosynaptic competition organize networks to produce long scale-free sequences of neural activity’, Neuron 65(4), 563–576. [DOI] [PubMed] [Google Scholar]
- Funahashi S, Bruce CJ & Goldman-Rakic PS (1989), ‘Mnemonic coding of visual space in the monkey’s dorsolateral prefrontal cortex’, Journal of neurophysiology 61(2), 331–349. [DOI] [PubMed] [Google Scholar]
- Fuster JM & Alexander GE (1971), ‘Neuron activity related to short-term memory’, Science 173(3997), 652–654. [DOI] [PubMed] [Google Scholar]
- Fuster JM & Jervey JP (1981), ‘Inferotemporal neurons distinguish and retain behaviorally relevant features of visual stimuli’, Science 212(4497), 952–955. [DOI] [PubMed] [Google Scholar]
- Gale D & Shapley LS (2013), ‘College admissions and the stability of marriage’, The American Mathematical Monthly 120(5), 386–391. [Google Scholar]
- Gardiner CW et al. (1985), Handbook of stochastic methods, Vol. 3, springer; Berlin. [Google Scholar]
- Gat I & Tishby N (1993), Statistical modeling of cell assemblies activities in associative cortex of behaving monkeys, in ‘Advances in neural information processing systems’, pp. 945–952.
- Gillett M, Pereira U & Brunel N (2020), ‘Characteristics of sequential activity in networks with temporally asymmetric hebbian learning’, Proceedings of the National Academy of Sciences 117(47), 29948–29958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldberg JH & Fee MS (2011), ‘Vocal babbling in songbirds requires the basal ganglia-recipient motor thalamus but not the basal ganglia’, Journal of neurophysiology 105(6), 2729–2739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grossberg S (1969), ‘On learning and energy-entropy dependence in recurrent and nonrecurrent signed networks’, journal of Statistical Physics 1(2), 319–350. [Google Scholar]
- Guo K, Yamawaki N, Svoboda K & Shepherd GM (2018), ‘Anterolateral motor cortex connects with a medial subdivision of ventromedial thalamus through cell type-specific circuits, forming an excitatory thalamo-cortico-thalamic loop via layer 1 apical tuft dendrites of layer 5b pyramidal tract type neurons’, Journal of Neuroscience 38(41), 8787–8797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo ZV, Inagaki HK, Daie K, Druckmann S, Gerfen CR & Svoboda K (2017), ‘Maintenance of persistent activity in a frontal thalamocortical loop’, Nature 545(7653), 181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo ZV, Li N, Huber D, Ophir E, Gutnisky D, Ting JT, Feng G & Svoboda K (2014), ‘Flow of cortical activity underlying a tactile decision in mice’, Neuron 81(1), 179–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hahnloser RH, Kozhevnikov AA & Fee MS (2002), ‘An ultra-sparse code underliesthe generation of neural sequences in a songbird’, Nature 419(6902), 65. [DOI] [PubMed] [Google Scholar]
- Hélie S, Ell SW & Ashby FG (2015), ‘Learning robust cortico-cortical associations with the basal ganglia: an integrative review’, Cortex 64, 123–135. [DOI] [PubMed] [Google Scholar]
- Herz A, Sulzer B, Kühn R & Van Hemmen J (1989), ‘Hebbian learning reconsidered: Representation of static and dynamic objects in associative neural nets’, Biological cybernetics 60(6), 457–467. [DOI] [PubMed] [Google Scholar]
- Holmgren C, Harkany T, Svennenfors B & Zilberter Y (2003), ‘Pyramidal cell communication within local networks in layer 2/3 of rat neocortex’, The Journal of physiology 551(1), 139–153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang C, Ruff DA, Pyle R, Rosenbaum R, Cohen MR & Doiron B (2019), ‘Circuit models of low-dimensional shared variability in cortical networks’, Neuron 101(2), 337–348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Inagaki HK, Fontolan L, Romani S & Svoboda K (2019), ‘Discrete attractor dynamics underlies persistent activity in the frontal cortex’, Nature 566(7743), 212–217. [DOI] [PubMed] [Google Scholar]
- Jaramillo J, Mejias JF & Wang X-J (2019), ‘Engagement of pulvino-cortical feedforward and feedback pathways in cognitive computations’, Neuron 101(2), 321–336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin X & Costa RM (2015), ‘Shaping action sequences in basal ganglia circuits’, Current opinion in neurobiology 33, 188–196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones LM, Fontanini A, Sadacca BF, Miller P & Katz DB (2007), ‘Natural stimuli evoke dynamic sequences of states in sensory cortical ensembles’, Proc Natl Acad Sci U S A 104(47), 18772–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jun JK & Jin DZ (2007), ‘Development of neural circuitry for precise temporal sequences through spontaneous activity, axon remodeling, and synaptic plasticity’, PloS one 2(8), e723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kao MH, Doupe AJ & Brainard MS (2005), ‘Contributions of an avian basal ganglia–forebrain circuit to real-time modulation of song’, Nature 433(7026), 638. [DOI] [PubMed] [Google Scholar]
- Kawai R, Markman T, Poddar R, Ko R, Fantana AL, Dhawale AK, Kampff AR & Ölveczky BP (2015), ‘Motor cortex is required for learning but not for executing a motor skill’, Neuron 86(3), 800–812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Killeen PR & Fetterman JG (1988), ‘A behavioral theory of timing.’, Psychological review 95(2), 274. [DOI] [PubMed] [Google Scholar]
- Kleinfeld D (1986), ‘Sequential state generation by model neural networks.’, Proceedings of the National Academy of Sciences of the United States of America 83(24), 9469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- La Camera G, Fontanini A & Mazzucato L (2019), ‘Cortical computations via metastable activity’, arXiv preprint arXiv:1906.07777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lefort S, Tomm C, Sarria J-CF & Petersen CC (2009), ‘The excitatory neuronal network of the c2 barrel column in mouse primary somatosensory cortex’, Neuron 61(2), 301–316. [DOI] [PubMed] [Google Scholar]
- Li N, Chen T-W, Guo ZV, Gerfen CR & Svoboda K (2015), ‘A motor cortex circuit for motor planning and movement’, Nature 519(7541), 51. [DOI] [PubMed] [Google Scholar]
- Li N, Daie K, Svoboda K & Druckmann S (2016), ‘Robust neuronal dynamics in premotor cortex during motor planning’, Nature 532(7600), 459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lim S, McKee JL, Woloszyn L, Amit Y, Freedman DJ, Sheinberg DL & Brunel N (2015), ‘Inferring learning rules from distributions of firing rates in cortical neurons’, Nature neuroscience 18(12), 1804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linderman SW, Nichols AL, Blei DM, Zimmer M & Paninski L (2019), ‘Hierarchical recurrent state space models reveal discrete and continuous dynamics of neural activity in c. elegans’, bioRxiv p. 621540. [Google Scholar]
- Litwin-Kumar A & Doiron B (2012), ‘Slow dynamics and high variability in balanced cortical networks with clustered connections’, Nat Neurosci 15(11), 1498–505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu JK & Buonomano DV (2009), ‘Embedding multiple trajectories in simulated recurrent neural networks in a self-organizing manner’, Journal of Neuroscience 29(42), 13172–13181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maboudi K, Ackermann E, de Jong LW, Pfeiffer BE, Foster D, Diba K & Kemere C (2018), ‘Uncovering temporal structure in hippocampal output patterns’, eLife 7, e34467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markowitz JE, Gillis WF, Beron CC, Neufeld SQ, Robertson K, Bhagat ND, Peterson RE., Peterson E., Hyun M., Linderman SW. et al. (2018), ‘The striatum organizes 3d behavior via moment-to-moment action selection’, Cell. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markram H, Lübke J, Frotscher M, Roth A & Sakmann B (1997), ‘Physiology and anatomy of synaptic connections between thick tufted pyramidal neurones in the developing rat neocortex.’, The Journal of physiology 500(2), 409–440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mason A, Nicoll A & Stratford K (1991), ‘Synaptic transmission between individual pyramidal neurons of the rat visual cortex in vitro’, Journal of Neuroscience 11(1), 72–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazzucato L, Fontanini A & La Camera G (2015), ‘Dynamics of multistable states during ongoing and evoked cortical activity’, The Journal of Neuroscience 35(21), 8214–8231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazzucato L, Fontanini A & La Camera G (2016), ‘Stimuli reduce the dimensionality of cortical activity’, Frontiers in systems neuroscience 10, 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazzucato L, La Camera G & Fontanini A (2019), ‘Expectation-induced modulation of metastable activity underlies faster coding of sensory stimuli’, Nature neuroscience p. 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGinley MJ, Vinck M, Reimer J, Batista-Brito R, Zagha E, Cadwell CR, Tolias AS, ardin JA & McCormick DA (2015), ‘Waking state: rapid variations modulate neural and behavioral responses’, Neuron 87(6), 1143–1161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller KD & Fumarola F (2012), ‘Mathematical equivalence of two common forms of firing rate models of neural networks’, Neural computation 24(1), 25–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller P & Katz DB (2010), ‘Stochastic transitions between neural states in taste processing and decision-making’, J Neurosci 30(7), 2559–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miyashita Y (1988), ‘Neuronal correlate of visual associative long-term memory in the primate temporal cortex’, Nature 335(6193), 817. [DOI] [PubMed] [Google Scholar]
- Mongillo G, Amit DJ & Brunel N (2003), ‘Retrospective and prospective persistent activity induced by hebbian learning in a recurrent cortical network’, European Journal of Neuroscience 18(7), 2011–2024. [DOI] [PubMed] [Google Scholar]
- Moreno-Bote R, Beck J, Kanitscheider I, Pitkow X, Latham P & Pouget A (2014), ‘Information-limiting correlations’, Nature neuroscience 17(10), 1410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murakami M, Shteingart H, Loewenstein Y & Mainen ZF (2017), ‘Distinct sources of deterministic and stochastic components of action timing decisions in rodent frontal cortex’, Neuron 94(4), 908–919. [DOI] [PubMed] [Google Scholar]
- Murakami M, Vicente MI, Costa GM & Mainen ZF (2014), ‘Neural antecedents of self-initiated actions in secondary motor cortex’, Nature neuroscience 17(11), 1574. [DOI] [PubMed] [Google Scholar]
- Murray JM et al. (2017), ‘Learning multiple variable-speed sequences in striatum via cortical tutoring’, Elife 6, e26084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Musall S, Kaufman MT, Juavinett AL, Gluf S & Churchland AK (2019), ‘Single-trial neural dynamics are dominated by richly varied movements’, bioRxiv p. 308288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nádasdy Z, Hirase H, Czurkó A, Csicsvari J & Buzsáki G (1999), ‘Replay and time compression of recurring spike sequences in the hippocampus’, Journal of Neuroscience 19(21), 9497–9507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakajima M, Schmitt LI & Halassa MM (2019), ‘Prefrontal cortex regulates sensory filtering through a basal ganglia-to-thalamus pathway’, Neuron. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niell CM & Stryker MP (2010), ‘Modulation of visual responses by behavioral state in mouse visual cortex’, Neuron 65(4), 472–479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pereira U & Brunel N (2018), ‘Attractor dynamics in networks with learning rules inferred from in vivo data’, Neuron 99(1), 227–238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pereira U & Brunel N (2020), ‘Unsupervised learning of persistent and sequential activity’, Frontiers in Computational Neuroscience 13, 97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polack P-O, Friedman J & Golshani P (2013), ‘Cellular mechanisms of brain state–dependent gain modulation in visual cortex’, Nature neuroscience 16(9), 1331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ponce-Alvarez A, Nacher V, Luna R, Riehle A & Romo R (2012), ‘Dynamics of cortical neuronal ensembles transit from decision making to storage for later report’, J Neurosci 32(35), 11956–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rabiner LR (1989), ‘A tutorial on hidden markov models and selected applications in speech recognition’, Proceedings of the IEEE 77, 257–286. [Google Scholar]
- Rajan K, Harvey CD & Tank DW (2016), ‘Recurrent network models of sequence generation and memory’, Neuron 90(1), 128–142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reinhold K, Lien AD & Scanziani M (2015), ‘Distinct recurrent versus afferent dynamics in cortical visual processing’, Nature neuroscience 18(12), 1789. [DOI] [PubMed] [Google Scholar]
- Salkoff DB, Zagha E, McCarthy E & McCormick DA (2019), ‘Movement and performance predict widespread cortical activity in a visual detection task’, bioRxiv p. 709642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satopaa V, Albrecht J, Irwin D & Raghavan B (2011a), Finding a ”kneedle” in a haystack: Detecting knee points in system behavior, in ‘2011 31st International Conference on Distributed Computing Systems Workshops’, pp. 166–171. [Google Scholar]
- Satopaa V, Albrecht J, Irwin D & Raghavan B (2011b), Finding a” kneedle” in a haystack: Detecting knee points in system behavior, in ‘2011 31st international conference on distributed computing systems workshops’, IEEE, pp. 166–171. [Google Scholar]
- Schmitt LI, Wimmer RD, Nakajima M, Happ M, Mofakham S & Halassa MM (2017), ‘Thalamic amplification of cortical connectivity sustains attentional control’, Nature 545(7653), 219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seidemann E, Meilijson I, Abeles M, Bergman H & Vaadia E (1996), ‘Simultaneously recorded single units in the frontal cortex go through sequences of discrete and stable states in monkeys performing a delayed localization task’, J Neurosci 16(2), 752–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sompolinsky H & Kanter I (1986), ‘Temporal association in asymmetric neural networks’, Physical review letters 57(22), 2861. [DOI] [PubMed] [Google Scholar]
- Stringer C, Pachitariu M, Steinmetz N, Reddy CB, Carandini M & Harris KD (2018), ‘Spontaneous behaviors drive multidimensional, brain-wide population activity’, BioRxiv p. 306019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sul JH, Jo S, Lee D & Jung MW (2011), ‘Role of rodent secondary motor cortex in value-based action selection’, Nature neuroscience 14(9), 1202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Svoboda K & Li N (2018), ‘Neural mechanisms of movement planning: motor cortex and beyond’, Current opinion in neurobiology 49, 33–41. [DOI] [PubMed] [Google Scholar]
- Taghia J, Cai W, Ryali S, Kochalka J, Nicholas J, Chen T & Menon V (2018), ‘Uncovering hidden brain state dynamics that regulate performance and decision-making during cognition’, Nature communications 9(1), 2505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomson AM & Lamy C (2007), ‘Functional maps of neocortical local circuitry’, Frontiers in neuroscience 1, 2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomasi G & Bro R (2006), ‘A comparison of algorithms for fitting the parafac model’, Computational Statistics & Data Analysis 50(7), 1700–1734. [Google Scholar]
- Treves A (2005), ‘Frontal latching networks: a possible neural basis for infinite recursion’, Cognitive neuropsychology 22(3–4), 276–291. [DOI] [PubMed] [Google Scholar]
- Tsodyks M, Pawelzik K & Markram H (1998), ‘Neural networks with dynamic synapses’, Neural computation 10(4), 821–835. [DOI] [PubMed] [Google Scholar]
- Tsodyks MV & Feigel’man MV (1988), ‘The enhanced storage capacity in neural networks with low activity level’, EPL (Europhysics Letters) 6(2), 101. [Google Scholar]
- Tsodyks MV & Markram H (1997), ‘The neural code between neocortical pyramidal neurons depends on neurotransmitter release probability’, Proceedings of the national academy of sciences 94(2), 719–723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams AH, Kim TH, Wang F, Vyas S, Ryu SI, Shenoy KV, Schnitzer M, Kolda TG & Ganguli S (2018), ‘Unsupervised discovery of demixed, low-dimensional neural dynamics across multiple timescales through tensor component analysis’, Neuron 98(6), 1099–1115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiltschko AB, Johnson MJ, Iurilli G, Peterson RE, Katon JM, Pashkovski SL, Abraira VE., Adams RP. & Datta SR. (2015), ‘Mapping sub-second structure in mouse behavior’, Neuron 88(6), 1121–1135. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The code for simulating the network model is available at the following GitHub repository https://github.com/ulisespereira/sequences-attractors-M2. Data or data analysis scripts are available upon reasonable request from the lead contacts.


