Optimal vaccine roll-out strategies including social distancing for pandemics

Summary

Non-pharmacological interventions (NPIs), principally social distancing, in combination with effective vaccines, aspire to develop a protective immunity shield against pandemics and particularly against the COVID-19 pandemic. In this study, an agent-based network model with small-world topology is employed to find optimal policies against pandemics, including social distancing and vaccination strategies. The agents’ states are characterized by a variation of the SEIR model (susceptible, exposed, infected, recovered). To explore optimal policies, an equation-free method is proposed to solve the inverse problem of calibrating an agent’s infection rate with respect to the vaccination efficacy. The results show that prioritizing the first vaccine dose in combination with mild social restrictions, is sufficient to control the pandemic, with respect to the number of deaths. Moreover, for the same mild number of social contacts, we find an optimal vaccination ratio of 0.85 between older people of ages $>65$ compared to younger ones.

Graphical abstract

Highlights

• •An epidemic model on networks is developed including lockdowns and vaccination strategies
• •An equation-free method is used to compute the microscopic infection rate
• •First dose prioritization controls the pandemic under mild contact restrictions
• •There is an optimum ratio of vaccinating ages >65 over the younger ones of 0.85

Health sciences; Virology; Public health

Introduction

Non-pharmacological interventions (NPIs), such as social distancing, stay-at-home, and lockdowns, have been considered the main strategy of governments to hinder the spread of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) and to control the stress on the health systems: to limit the occupation number in hospitals, as well as the overall death toll in 2020 (Haug et al., 2020; Paital et al., 2020; Bendavid et al., 2021). The availability of vaccines against SARS-CoV-2 allowed new possibilities to control the pandemic and aspired to develop effective protection against the virus transmission. By the end of 2020, a variety of vaccines were introduced with different immunization efficacies (Maier et al., 2021; Das et al., 2021). The vaccination process varied widely among countries, with different vaccination rates per day over the entire population without a common protocol (Maier et al., 2021; Israel.gov.health, 2021; Robert.Koch.Institute, 2021; greece.gov, 2021). Until November 29, 2021, more than 264 million infections with 5.26 million deaths have been reported worldwide, while more than nine billion doses have been vaccinated (WHO, 2021).

Limitations on the vaccine availability as well as the limited capability of health systems raise the question of how a country can design a successful vaccination deployment plan. The suitable combination of first or second-dose strategies that result in the lowest number of deaths is an open problem. Moreover, the vaccination age stratification is another pressing problem (Bubar et al., 2021): older people show dramatically more severe SARS-CoV-2 courses of disease (Logunov et al., 2020, 2021), which demands their prioritization in the vaccine administration. At the same time, younger individuals with increased mobility and a lifestyle with more contacts are potentially powerful transmitters of the virus. Therefore, decreasing the infection in the latter group should have a strong impact on the pandemic dynamics and in consequence on the expected number of deaths. Importantly, recent studies support that vaccination planning cannot be successful in the absence of NPIs (Moore et al., 2021).

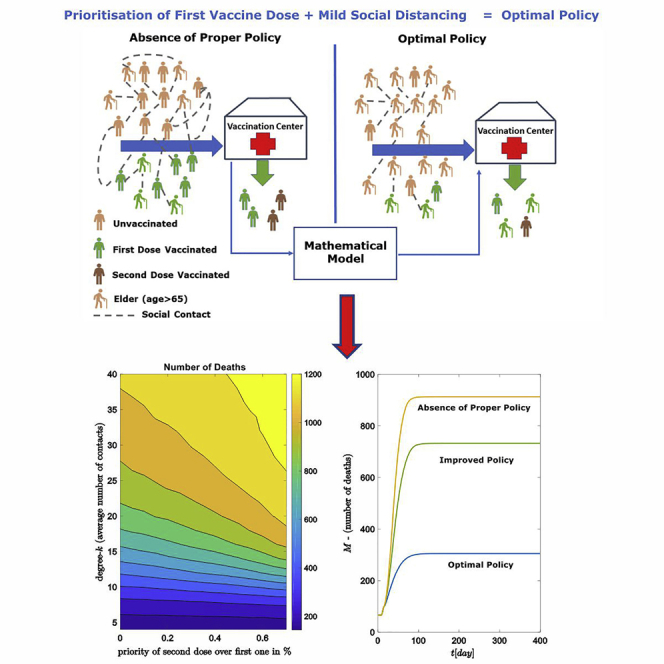
In this study, we evaluate the effect of different vaccination policies in the context of different vaccination dose strategies, social distancing, and vaccination targets based on the age distributions (see Figure 1). By using a network-based epidemic model (Salathé et al., 2010; Reppas et al., 2010, 2015; Siettos, 2011; Eames et al., 2015; Zhang et al., 2015; Siettos et al., 2015; Mata, 2021), we demonstrate the interplay of the aforementioned factors in designing an effective vaccination strategy. In section: Materials and methods, the epidemic model is developed and presented and a methodology to calibrate individual infection rates with respect to vaccination efficacy is proposed. This is achieved by using equation-free techniques (Gear et al., 2003, 2005; Zagaris et al., 2009; Kevrekidis and Samaey, 2009; Spiliotis and Siettos, 2011; Reppas et al., 2010; Siettos, 2011; Marschler et al., 2014; Siettos et al., 2015; Sieber et al., 2018; Siettos and Russo, 2022) by coupling agent-based models with numerical methods such as Newton-Raphson. Moreover, we show how the network connectivity (which serves as an approximation of the social distancing NPIs) combined with different vaccination strategies affect the epidemic development. Finally, in section: Results we analyze the vaccination efficacy by considering both the age distribution for selecting the vaccination targets along with the application of NPIs. The results show that giving priority to unvaccinated people (i.e., prioritizing the first dose and delaying the second dose), is sufficient to control the pandemic when mild social distancing (medium number of contacts) is implemented. We found that combined with the implementation of mild NPIs the optimal vaccination strategy is to choose for the vaccinated subjects a ratio of 0.85 for elder people of ages $>65$ over the younger ones. Therefore, we can state that the implementation of mild NPIs supports any vaccination planning toward controlling the epidemic.

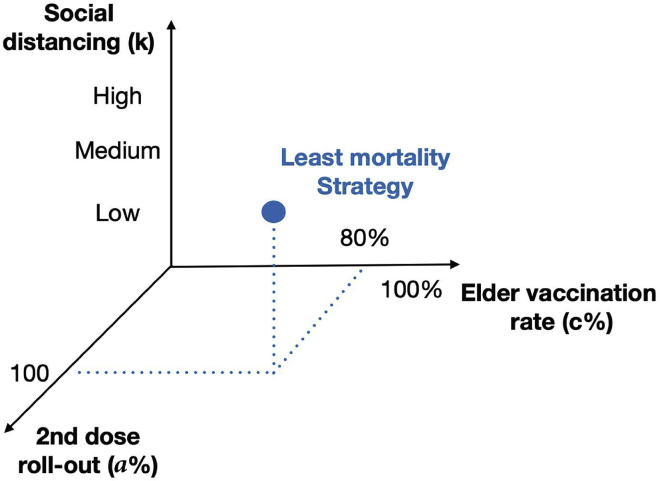
Figure 1.

Strategies for minimizing the expected number of deaths

Combining policies: the first/second vaccine dose, the age stratification, and the social distancing, in order to mitigate the SARS-CoV-2 impact. The optimal combination (blue marker) of policies leads to a minimum number of expected deaths.

Materials and methods

Agent-based epidemic model on networks for designing vaccination policies on non-pharmacological interventions

To study the SARS-CoV-2 epidemic dynamics, a discrete agent-based model on the complex network has been developed, extending (Syga et al., 2021), see Figure 2A. Each node in the network represents an individual agent with undirected edges as social contacts, see Figure 2B. The network is constructed in the following way: Initially, the nodes are positioned in a ring-like structure and every node is connected with its k nearest neighbors, and secondly, rewiring every link to a randomly chosen node with probability $p_{\text{net}}$ (Watts and Strogatz, 1998). The (connectivity) degree of each node is defined as the number of links to other nodes and represents the number of social contacts. Each agent can have 5 states S, E, I, R, M: susceptible or healthy, exposed to virus, infected (asymptomatic or not), recovered (which cannot be re-infected anymore), and finally the state of death (mortality) (Anastassopoulou et al., 2020; Calafiore et al., 2020; Foy et al., 2021). Every time step of the agent-based model corresponds to a day. Depending on the vaccination roll-out policy, a specific constant number of susceptible individuals (per day) who have received either the first or second dose enhanced their resistance to SARS-CoV-2 infection. At each time step, each $i-$ th individual in the healthy-susceptible state becomes exposed with probability

$$P_i=1-{\left(1-p_i^{\text{inf}}\right)}^{I_i}$$ (Equation 1)

where $I_i$ is the number of infected neighbors of the i susceptible individual. The variable $p_i^{\text{inf}}$ expresses the infection probability in the presence of one infected social contact. Thus, the term ${\left(1-p_i^{\text{inf}}\right)}^{I_i}$ describes the probability of no infection in the presence of $I_i$ infected contacts.

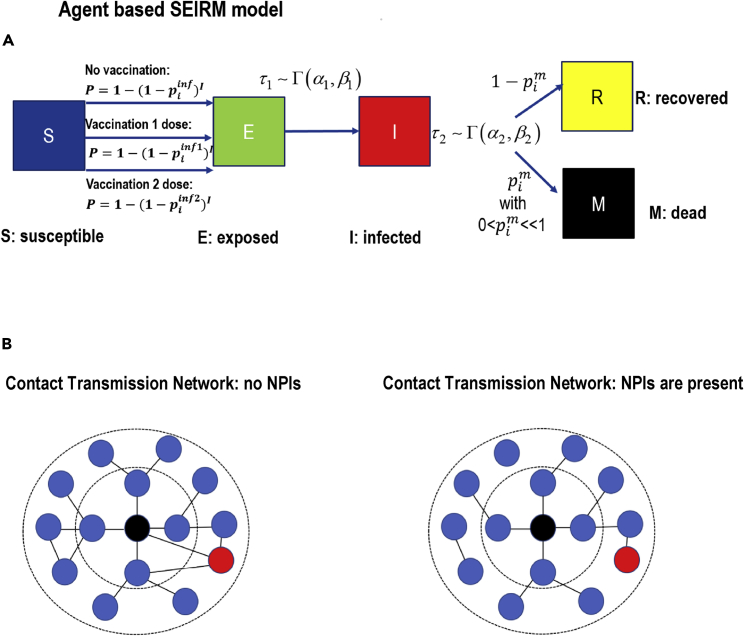
Figure 2.

Agent-based model schematics

(A) Representative figure of the model. A susceptible agent (S) becomes exposed (E) with probability P, see Equation (1). The probability P depends on the infection rate $p_i^{\text{inf}}$. A Vaccinated agent shows higher resistance to infection by decreasing the infection rate: $p_i^{\text{inf}2}<p_i^{\text{inf}1}<p_i^{\text{inf}}$ where $p_i^{inf1}$ and $p_i^{inf2}$ stands for first/second dose, respectively. Then, after time τ (which is chosen from $\text{Γ}$ distribution) the exposed become infected (I). Finally the agent recovers (R) with probability $\left(1-p_i^m\right)$, $0<p_i^m\ll 1$ or passes away (M).

(B) For representative reasons we show a simplification of contact networks (blue circles represent healthy individuals, red circles depict infected individuals, while the central black circle represents the $i-$ th agent we refer to) in the absence (left) or in the presence (right) of NPIs. In the latter case, the main difference is the reduction of contacts which corresponds to the reduction of the k parameter (mean connectivity degree) in the small-world structure.

The probability $P_i=P_i\left(p_i^{\text{inf}}\right)$ is an increasing function with respect to the variable $p_i^{\text{inf}}$, with $P_i\left(0\right)=0$ and $P_i\left(1\right)=1$. Unvaccinated susceptible agents have the same constant probability $p_i^{\text{inf}}$, while vaccinated individuals have a smaller probability $p_i^{\text{inf}1}$ or $p_i^{\text{inf}2}$. The probability $p_i^{\text{inf}1}$ is used 10 days after the first dose while and $p_i^{\text{inf}2}$ is used after a second dose has been applied (after 30 days from the first dose). The new values of $p_i^{\text{inf}}$ depend on the efficacy of the type of vaccine and have been calculated a priori, which is presented in section: Equation-free method for the inverse problem: estimating the individual infection probability for a given vaccine efficacy.

After being exposed, the agents change their states from susceptible to exposed and a waiting time ${\tau }_E$ (waiting time before the agent becomes infectious) is assigned which is drawn from a $\text{Γ}$ distribution (Syga et al., 2021; Linton et al., 2020) that is, ${\tau }_E\sim \text{Γ}\left(a_E,b_E\right)$, where $a_E,b_E$ denote the parameters of the $\text{Γ}$ distribution. In each time step, the waiting time ${\tau }_E$ is reduced by 1, that is, ${\tau }_E={\tau }_E-1$ and ${\tau }_E>0$. The first time step when ${\tau }_E<0$ the disease progress, and the exposed individual gets infected. Then a new waiting time ${\tau }_I$ is assigned, ${\tau }_I\sim \text{Γ}\left(a_I,b_I\right)$, drawn from the $\text{Γ}$ distribution. Similarly, at each time step, the ${\tau }_I$ is decreased by 1, that is, ${\tau }_I={\tau }_I-1$. In the model, vaccinated people can still be infected, but with a lower transmission probability.

Finally, the transition from infection to recovery or to death depends on the age and on the administration of the vaccination. Specifically, in the model the first time when ${\tau }_I<0$ the node changes state in the following way: with small probability $p_i^m$ the infected agent dies (mortality), or in the opposite case (with probability $1-p_i^m$) the agent recovers and cannot be infected anymore. The value of $p_i^m$ is defined in the following way: if the i-th individual is less than 65 years old then independently of the vaccination the probability of dying is $p_i^m=0.005$. In the opposite case that is, age $>$ 65 then the unvaccinated people have the probability of dying $p_i^m=0.13$, while in the vaccinated case the $p_i^m$ decreases to $p_i^m=0.008$. The values of $p_i^m$ were computed from the available data of Germany for a period starting January 2020, until the end of May 2021 (Robert.Koch.Institute, 2021; Statista, 2021).

The parameters of $\text{Γ}$-distributed waiting times were inferred from COVID-19 disease characteristics, as these have been found to fit optimally (Syga et al., 2021; Linton et al., 2020) the real waiting times. Specifically for the exposed state ${\tau }_E\sim \text{Γ}\left(a_E,b_E\right)$ and ${\tau }_I\sim \text{Γ}\left(a_I,b_I\right)$, where $a_E=9,b_E=1/3$ and $a_I=100/3,b_I=3/10$. For these parameters of the $\text{Γ}$ distribution, the mean value is three and one, respectively, and the standard deviation is and 10 and $\sqrt{3}$, respectively. In the next section, a systematical methodology is proposed in order to estimate the infection probability $p_i^{\text{inf}1}$ or $p_i^{\text{inf}2}$ for vaccinated individuals.

Agent-based simulations to compute the individual infection probability depending on vaccination efficacy

After vaccination, the agents increase their resistance to infection, which implies a lower probability compared to $p_i^{\text{inf}}$. The values for vaccinated are $p_i^{\text{inf}1}$ (first dose) or $p_i^{\text{inf}2}$ (second dose). The values of these probabilities depend on the efficacy of the applied vaccine and their computation is an open problem for the epidemic modeling for which a solution is suggested in section: Equation-free method for the inverse problem: estimating the individual infection probability for a given vaccine efficacy. The concept behind our approximation for estimating the $p_i^{\text{inf}1}$ or $p_i^{\text{inf}2}$, is that we mimic the clinical process in the agent-based model (see Vaccine efficacy in clinical trials) to obtain an estimation for the efficacy (Logunov et al., 2021). For this, our agent-based model is used as timestepper or discrete-time map (Reppas et al., 2010; Siettos, 2011; Marschler et al., 2014; Kevrekidis and Samaey, 2009; Spiliotis and Siettos, 2011; Russo et al., 2020), which defines the input of $x=p_i^{\text{inf}}$ and output $e={\text{Φ}}_T\left(x\right)$, the reproduced efficacy. Using an equation-free methodology (Kevrekidis and Samaey, 2009; Reppas et al., 2010; Spiliotis and Siettos, 2011; Marschler et al., 2014) a numerical method (i.e., Newton Raphson scheme) is wrapped around the map $e={\text{Φ}}_T\left(x\right)$ to find the demanded value $x=p_i^{\text{inf}}$ numerically.

Vaccine efficacy in clinical trials

In order to define a vaccine’s efficacy in clinical trials (Logunov et al., 2021), individuals are separated into two groups: the vaccine recipients and the placebo recipients. After a time period, the odds ratio ($R_O$) is defined as the fraction of the proportion of vaccinated people who developed COVID-19, divided by the proportion of COVID-19 developed from the placebo recipients (Logunov et al., 2021). Specifically, if l is the number of vaccinated participants who developed COVID-19 and b is the number of all vaccinated participants, then the ratio $\frac{l}{b}$ is the proportion of COVID-19 in the sample of vaccinated people. Clearly, a larger vaccine efficacy results in low values of the ratio $\frac{l}{b}$ that is, $\frac{l}{b}\approx 0$. Similarly, if c is the number of placebo recipients with COVID-19, and d is the total number of placebo recipients then the $\frac{c}{d}$ is the percentage of individuals with COVID-19 in the sample of placebo recipients. The odds ratio is given by

$$R_O=\frac{l/b}{c/d}$$ (Equation 2)

and the efficacy e of the vaccination is defined as

$$e=1-R_O.$$ (Equation 3)

If the vaccine is highly effective then $\frac{l}{b}\approx 0\Rightarrow R_O\approx 0\Rightarrow e\approx 1-0=1$. However, for low efficacy we obtain: $\frac{l}{b}\approx \frac{c}{d}\Rightarrow R_O\approx 1\Rightarrow e=1-R_O\approx 1-1=0$.

For instance, in the case of the Sputnik vaccine trial (Logunov et al., 2021) which involved almost 21,000 participants, 14,964 and 4902 participants received the second dose and placebo, respectively (Logunov et al., 2021). According to (Logunov et al., 2021) (Table 2 there in) 21 days after the first dose, 14 and 62 participants from the truly vaccinated and placebo sample were infected, respectively. Then the odds ratio is written $R_O=\frac{14/14964}{62/4902}=0.0845$, results in efficacy $e=1-0.0845=0.915$.

Equation-free method for the inverse problem: Estimating the individual infection probability for a given vaccine efficacy

In this section we address the question, how the individual infection probability $p_i^{\text{inf}}$ can be computed for a given vaccination efficacy. Depending on the vaccine efficacy we expect a decrease in the probability of infection or more precisely the transition from $S\to E$, that is, a decrease of the $p_i^{\text{inf}}$ in Equation (1).

In the computational agent-based model, two samples of vaccination recipients and not vaccinated agents are randomly chosen. For each vaccinated agent i, the individual infection probability $p_i^{\text{inf}}$ is computed and results in a new value $p_i^{\text{inf}1}$ or $p_i^{\text{inf}2}$. The aim of the following equation-free computations is to determine this value. The value of $p_i^{\text{inf}}$ for the unvaccinated sample stays unchanged. Starting with an initial guess for the new value of parameter $p_i^{\text{inf}}$, at each time step the model evolves (i.e., $S_t\to S_{t+1}$, $E_t\to E_{t+1}$ and so forth). After a short time period of $T=100$ steps (days) the ratio $R_O$ and the efficacy $e=1-R_O$ are determined implicitly from the samples of vaccinated and not vaccinated agents in the exact same way as in section: Vaccine efficacy in clinical trials that is,

$$e={\text{Φ}}_{T=100}\left(A,p^{\text{inf}}\right)=1-R_O=1-\frac{\left(\frac{N_{\text{infected}}^{\text{vac}}}{N_{\text{vac}}}\right)}{\left(\frac{N_{\text{infected}}^{\text{unv}}}{N_{\text{unv}}}\right)}$$ (Equation 4)

where the values $N_{\text{infected}}^{\text{vac}}$ and $N_{\text{infected}}^{\text{unv}}$ represent the total number of infected agents from the samples of vaccinated after time $T=100$ (with population $N_{\text{vac}}$) and not vaccinated agent, respectively (with population $N_{\text{unv}}$). The final value e is calculated by averaging over the ensemble of $N_{\text{sample}}$ identical copies.

For a network with constant structure, the above procedure defines a map from infection probability $p_i^{\text{inf}}$ to efficacy e, that is, ${\text{Φ}}_T:\left[\mathrm{0,1}\right]\to \mathbb{R}$:

$$e={\text{Φ}}_T\left(A,p^{\text{inf}}\right)$$ (Equation 5)

where A is the adjacency matrix of the network that contains all information about the structural topology (degree distribution, clustering, path length, and so forth) and the variable $p_i^{\text{inf}}$ has to be determined in order to get the efficacy $e=e_0$. This means, the following equation has to be solved

$$e_0={\text{Φ}}_T\left(A,p^{\text{inf}}\right)\iff e_0-{\text{Φ}}_T\left(A,p^{\text{inf}}\right)=0\iff G\left(p^{\text{inf}}\right)=0$$ (Equation 6)

with $G\left(p^{\text{inf}}\right)=e_0-{\text{Φ}}_T\left(A,p^{\text{inf}}\right)$. The above equation can be solved numerically using the Newton- Raphson method or an alternative iterative algorithm. The derivative of G required for the Newton method can be approximated using the difference quotient

$$G^{\prime }\left(p^{\text{inf}}\right)\approx \frac{G\left(p^{\text{inf}}+\Delta p\right)-G\left(p^{\text{inf}}\right)}{\Delta p}=-\frac{{\text{Φ}}_T\left(A,p^{\text{inf}}+\Delta p\right)-{\text{Φ}}_T\left(A,p^{\text{inf}}\right)}{\Delta p}.$$ (Equation 7)

For different values of $e_0$ the solutions $p^{\text{inf}}$ of Equation (6) define the discretized inverse function $p^{\text{inf}}={\text{Φ}}_T^{-1}\left(A,e_0\right)$ of the map ${\text{Φ}}_T$ in Equation (5) and results in the value $p_i^{\text{inf}1}$ or $p_i^{\text{inf}2}$. For the initial value of the Newton method, a previously calculated solution is used.

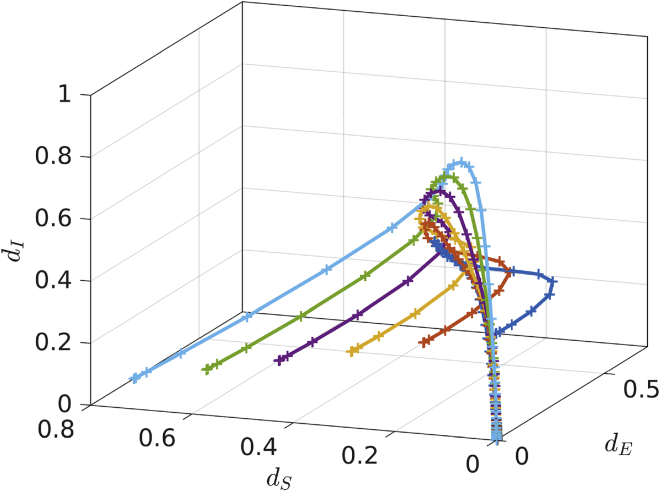
The main assumption for the equation-free approach is that a macroscopic description for the detailed agent-based model dynamics exists which results in a closed-form of a few macroscopic variables (Gear et al., 2003, 2005; Zagaris et al., 2009; Kevrekidis and Samaey, 2009; Spiliotis and Siettos, 2011; Reppas et al., 2010; Siettos, 2011; Marschler et al., 2014; Siettos and Russo, 2022). In systems where a macroscopic description exists, there is a timescale separation between the microscopic and the macroscopic behavior. This means that there is a fast convergence to a low-dimensional slow manifold which describes the macroscopic dynamics. This is demonstrated in Figure 3 which depicts the system behavior that quickly converges to a slow manifold. The macroscopic variables are the expected values of densities (susceptible, exposed, infected, and deaths) of the network realizations. The individual state of an agent represents the microscopic state of the system. Independently of the initial random agent’s states (microscopic system description), the system evolves quickly toward a slow manifold (Siettos, 2011), see Figure 3.

Figure 3.

Low-dimensional slow manifold for the macroscopic dynamics

Fast convergence to a slow manifold: Starting with different random microscopic initializations for the agents' states, the dynamics of the macroscopic densities $d_I$, $d_S$ and $d_E$ (infected, susceptible and exposed), converge to one dimensional manifold.

The map from the macroscopic densities to a microscopic system realization (also called lifting operator (Gear et al., 2003, 2005; Kevrekidis and Samaey, 2009; Zagaris et al., 2009; Reppas et al., 2010; Spiliotis and Siettos, 2011; Siettos, 2011; Marschler et al., 2014; Siettos and Russo, 2022)) is achieved by producing random assignments of the 5 state variables (S, E, I, R, M), consistent with the given macroscopic densities. In detail, this is conducted by choosing randomly a number $n_x$ of arbitrary agents in the network, with $n_x=[d_x\cdot N]$. Here $d_x$ is the macroscopic density of the state x where $x\in \left\{\text{S},\text{ E},\text{ I},\text{ R},\text{ M}\right\}$, N is the total number of agents and $[\cdot ]$ represents the integer part.

The projection from the microscopic agent’s realizations, back to the macroscopic system description, known as restriction operator (Gear et al., 2003; Kevrekidis and Samaey, 2009), is achieved by computing the macroscopic densities that is, counting all the agents in the network with the same individual state (i.e., S or I and so forth) divided with the total number of agents.

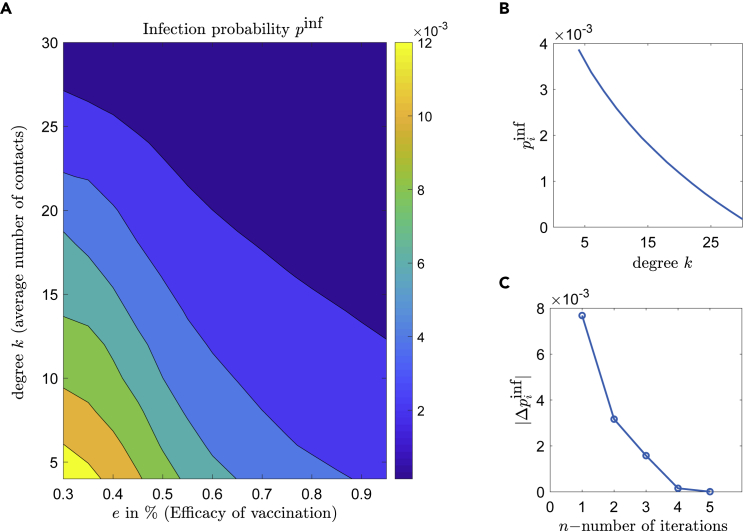
The macroscopic efficacy depends implicitly on the macroscopic densities. The implicit Equation (6) is solved for the infection probability by the Newton-Raphson method. The solutions of Equation (6) for different parameters depend on the network structure (i.e., degree k and network rewiring probability $p_{\text{net}}$). Figure 4A shows the values of $x=p_i^{\text{inf}}$ with respect to the different levels of efficacy e and connectivity-degree k, (with constant rewiring probability $p_{\text{net}}=0.005$). Figure 4B shows a monotonically decreasing behavior of $x=p_i^{\text{inf}}$ with respect to the local degree k (keeping the efficacy constant to $e_0=0.9$). Figure 4C depicts the convergence of Newton-Raphson algorithm for Equation (6), using the approximated derivative of Equation (7) for $e_0=0.9,k=10$.

Figure 4.

Estimating the infection probability using equation-free-methods

(A) The infection probability $p^{\text{inf}}$ with respect to the efficacy $e_0$ and the mean k-degree (number of social contacts), resulting from Equation (6).

(B) The values of $p_{\text{inf}}$ for $e_0=0.9$ resulting from Equation (6) for all degrees.

(C) The difference $\left|\text{Δ}{p}_i^{\text{inf}}\right|$ over the number of iterations for the Newton-Raphson, for $k=10$ contacts.

Results

For all simulations, a population with a total number of $N={10}^5$ agents is used. The network rewiring probability is chosen to be $p_{\text{net}}=0.005$ (Watts and Strogatz, 1998). Different vaccination rates of 10, 500, and 1000 doses/day (which correspond to a percentage of $0.01\text{\%},0.5\text{\%}$ and $1\text{\%}$ of the total population) are studied. The infection probability $p_i^{\text{inf}}$ for vaccinated people is adapted to both efficacy e and local connectivity k according to the section: Equation-free method for the inverse problem: estimating the individual infection probability for a given vaccine efficacy. An unvaccinated agent/person has the infection probability $p_i^{\text{inf}}=0.02$ (Syga et al., 2021), which is described with $e=0$.

Initially, the vaccination strategy with respect to the priority of the first or second dose is investigated, assuming a constant rate of vaccinations per day. As the vaccination policy involves a second dose after about a month, the question arises: which priority should be used to vaccinate people with the first or second dose in order to decrease the number of deaths. This has to be optimized depending on a given social distancing measure of low, medium, or high number of contacts. To deal with this problem a percentage a (a in %), is defined on the daily rate for the second dose. For example, in case of 100 vaccinations per day, a percentage $a=10\text{\%}$ means that 90 people get the first dose and 10 will get also the second dose. In the following simulations, a first dose results in 50% efficacy to protect against the virus while the second dose result in an efficacy of 90%.

The second scenario investigates how prioritizing the age to select people for a first dose for medium and high efficacy vaccination processes to minimize the number of deaths. The minimization problem depends also on a given social distancing measures: low, medium, or high number of contacts. Two groups with different ages are defined. Group A contains individuals with age over 65 and represents 20% of the population. Group B contains all people with age less than 65 years. The ratio c expresses the priority between the two age groups. We define the parameter c as the percentage of the group A older than 65 years who get vaccinated per day. For example in a constant window of 100 daily injections, if $c=0.3$, then 30 individuals belong to group A (older than 65 years) and the remaining 70 belong to group B (i.e., prioritization for the vaccination is given to group B).

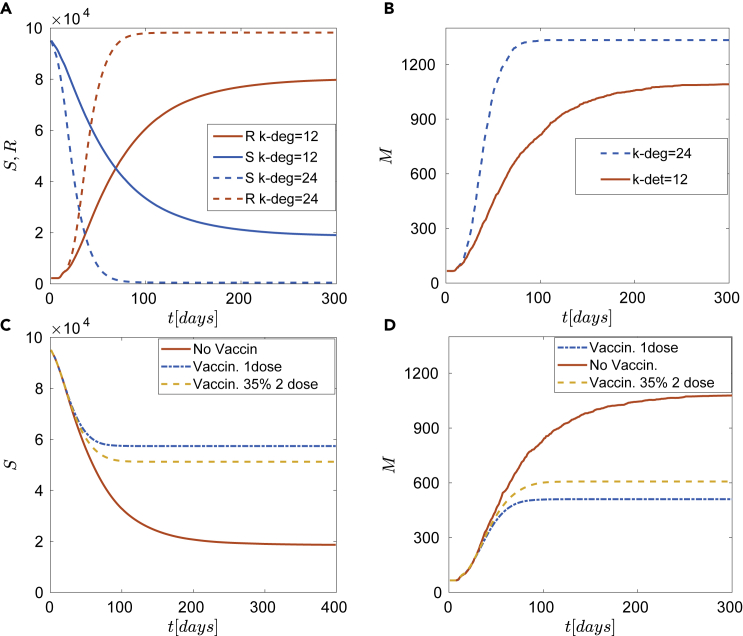
In all simulations, the expected number of deaths is calculated as a mean value of 128 identical realizations of the model. Figure 5 depicts four different scenarios with a constant vaccination rate of 1000 doses/day. The simplest case of the epidemic dynamics without vaccination is shown in Figures 5A and 5B. The well-known case of fast pandemic expansion ($k=24$ in Figures 5A and 5B) resulting from a large number of contacts is highlighted. The susceptible population in case of $k=24$ (dash line) decays to zero within 100 days and similarly, the expected number of deaths converges to a large number of approximately 1300. This might bring the health care system to collapse. Figures 5C and 5D show the vaccination effects in the case of $k=12$ contacts on average for each agent, for different policies: first dose (dashed-dotted in Figures 5C and 5D), 65% per day receives the first dose, and the remaining 35% a second dose (i.e., in a constant vaccination rate of $w=1000$ doses per day, 650 are newly vaccinated individuals and 350 receive a 2nd dose) also the case without vaccination is depicted for comparison. These results stress the clear advantage of an optimal vaccination strategy in combination with social distancing.

Figure 5.

Epidemic dynamics for different NPIs and vaccination policies

(A) Without vaccination. Time series of susceptible (S) and recovered (R) for different local connectivities $k=12$ and $k=24$.

(B) The expected number of deaths (without vaccination) for different local connectivities, $k=12$ and $k=24$.

(C and D) Epidemic dynamics for different vaccination policies for local connectivity $k=12$. Solid red line corresponds to no vaccination, dashed-dotted line to one dose and dashed line to $a=35\text{\%}$ under the assumption of constant number w = 1000 vaccinations per day. (C) Time series of susceptible (S). (D) The expected number of deaths (M) for local connectivity k = 12 reveals a more efficient policy of one dose.

First and second dose vaccination policy under low daily roll-out injection rate

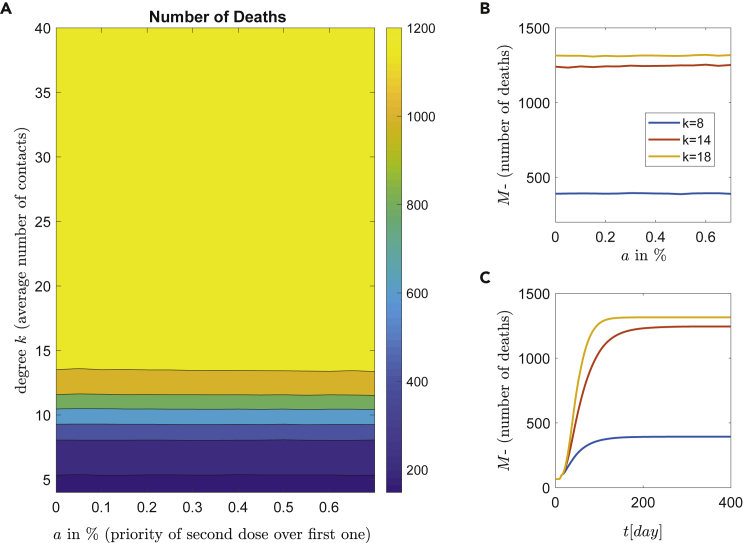
First, a low number of daily vaccinations is studied. Each day a constant number of 10 people/day is vaccinated, which corresponds to 0.01% of the whole population (roll-out rate). The expected number of deaths with respect to the parameter a and the NPIs is depicted in Figure 6A. Clearly, for a very low number of vaccinations per day (i.e., $w=10$ vaccinations/day), only the contact restrictions (lockdown) can reduce the expected number of deaths. Three representative degrees (contacts) $k=8,k=14,k=18$ are shown in Figure 6B with respect to the percentage of first or double doses and the corresponding average time series are depicted in Figure 6C.

Figure 6.

Epidemic dynamics for low roll-out vaccination rate

Simulations of the epidemic model with respect to the vaccination strategies and NPIs. Each day a constant ratio of 0.01% of the population per day (10 people) is vaccinated.

(A) The number of deaths with respect to the degree k (social contacts) and percentage a, of people who received a second dose. There are well defined regions of different behaviors with major contribution of high mortality (yellow).

(B) The effect of NPIs (contact restrictions) with respect to the first or second dose strategy. Three representative degrees $k=\mathrm{8,14,18}$ are shown.

(C) Time series of the number of deaths for constant mixture $a=0.35$ and for degrees $k=8$, $k=14$ and $k=18$.

The almost constant lines in Figure 6B reveal the independence of the number of deaths with respect to dosing. In a nutshell, for low vaccination roll-out (i.e., $w=10$ doses/day) the dosing policy has no impact on the virus spread and the subsequent deaths. Finally, due to the small number of daily vaccinations, the dynamics is dominated from social connections and (unfortunately) for $k>13$ the expected number of deaths remains high. The desirable scenario with a low number of deaths is achieved only in a narrow area below $k=8$ or $k=9$ degrees (contacts), which is very difficult to be achieved practically.

A single-dose vaccination policy is sufficient to control the epidemic for large roll-out rates

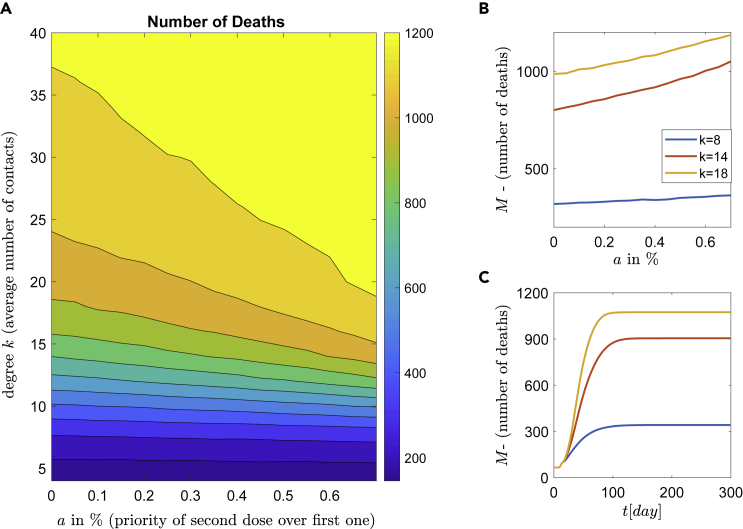
In this section, a different scenario of a vaccination scheme with an increased number of vaccinations is studied. Every day a constant number of 500 people, which corresponds to 0.5% of the population, are vaccinated. The average dynamics (over the ensemble of 128 realizations) with respect to the parameter a and the (connectivity) degree k are shown in Figure 7A. The mean value of the number of deaths (over the ensemble of 128 realizations, i.e., $N_{\text{sample}}=128$) with respect to parameter a for three representative degrees $k=8$, $k=14$ and $k=18$ is shown in Figure 7B, while in Figure 7C the corresponding time series of the number of death (in average) for constant mixture a = 0.35 and for degree $k=8$, $k=14$ and $k=18$ are shown.

Figure 7.

Epidemic dynamics for medium roll-out vaccination rate

Simulations of the epidemic model with respect to the vaccination strategies and NPIs.

(A) constant number of $w=500$ people representing 0.5% of the population (roll-out rate) is vaccinated per day. The percentage $a\text{\%}$ describes the proportion of people who get the second dose and increase the infection resistance.

(B)The efficacy of NPIs with respect to the first or second dose. Three representative degrees (social contacts) $k=\mathrm{8,14,18}$ are shown.

(C) Time series of the number of deaths for constant mixture $a=0.35$ and for degrees $k=8$, $k=14$ and $k=18$.

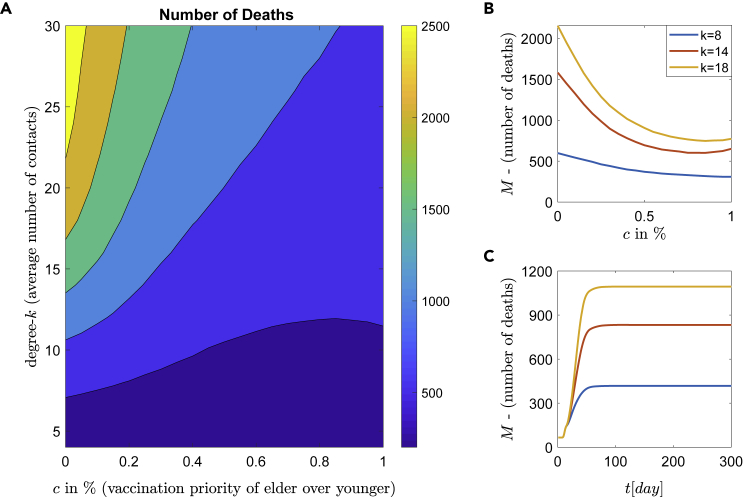
The results in Figure 7A show the number of deaths depending on the degree k and the percentage of the second dose. This leads to a (coarse) separation of the domain into zones of the expected number of deaths. This can be categorized into three zones of low (deep blue), medium (blue-green), and high (orange-yellow) number of deaths. The expected number of deaths monotonically increases with respect to parameter a (see, Figure 7B), meaning that independently of the degree k (contacts), the best policy is the one where priority is given to all unvaccinated first (i.e., $a\approx 0$). Additionally, the increase of parameter a has strong negative impact as with this quantity the expected number of death increases dramatically. For example, the curve with the mean degree of $k=14$ (Figure 7B), starts at $a=0$ with around 800 deaths and increases monotonically until 1100 for $a=0.7$. The optimal solution (minimum value) is obtained at $a\approx 0$ (precisely $a=0.04$), while the 95% confidence interval (CI) for this number of contacts was calculated as (0.002, 0.1).

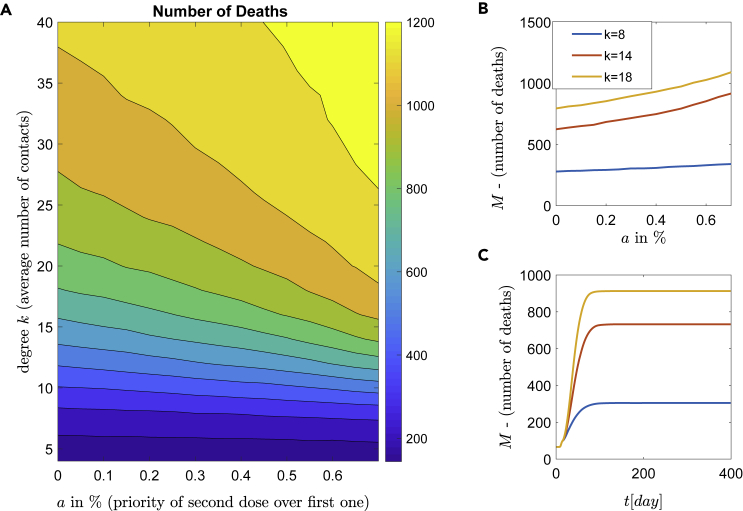
Similar behavior is obtained when the daily vaccination rate is 1% ($w=1000$ vaccinations/day), and again the best policy is to use the vaccine first for all unvaccinated people (i.e., $a\approx 0$, see also Table 1) and vaccinate a second dose later. Likewise, the dynamic behavior can be categorized in three coarse zones of low, medium and high numbers of deaths (see Figure 8). As expected, compared to the 0.5% vaccination rate (i.e., $w=500$ vaccinations/day), the higher number of vaccinations reduces the number of deaths. The comparison between the two zones with high mortality (light, normal and dark yellow) in Figures 7A and 8A, respectively, reveals that in the case of the vaccination rate 0.5%, the zone with high mortality corresponds to 60% of the whole area, while in the case of vaccination rate of 1%, this zone corresponds to 40% of the whole area. Furthermore, comparing Figures 7C and 8C for the number of contacts $k=18$, the number of deaths is about 1074 and 912, respectively. This is a reduction of 15%, while for $k=14$ the number of deaths is 905 and 732, respectively, resulting in a reduction of 19%.

Table 1.

Computed values for parameters a and c which correspond to the optimal policy, and for roll-out window w = 1000 doses/day, along with their 95% CI

Number of contacts (degree $k$)	Computed value of the parameter $a$	95% confidence interval for the parameter $a$
$k$ = 8 contacts per person	$a=$ 0.078	$a$$\in$ (0, 0.365)
$k$ = 14 contacts per person	$a=$ 0.036	$a$$\in$ (0, 0.15)
$k$ = 18 contacts per person	$a$ = 0.0387	$a$$\in$ (0, 0.165)

Number of contacts (degree $k$)	Computed value of the parameter $c$	95% confidence interval for the parameter $c$
$k$ = 14 contacts per person	$c$ = 0.85	$c$$\in$ (0.75, 1)

Figure 8.

Epidemic dynamics for highly roll-out vaccination rate

Simulations of the epidemic model with respect to the vaccination strategies and NPIs. Daily, $w=1000$ people (representing 1% of the population) are vaccinated.

(B) The efficacy of NPIs with respect to the first or second dose. Three representative degrees (social contacts) $k=\mathrm{8,14,18}$ are shown.

(C) Time series of the number of deaths for constant mixture $a=0.3$ five and for degrees $k=8$, $k=14$ and $k=18$.

Importantly, the first dose prioritization has also great social impact in the sense that even with a high contact number, that is, with a degree $15<k<22$ (no strict lockdown), see also (Ioannidis et al., 2021), the expected number of deaths remains low. In contrast, transitioning into the yellow zone, when $a\in [0.6,0.7]$ and $k=20$, where a large number of deaths (about 1000) can be observed. To conclude, the policy choice of a second dose instead of prioritizing the first dose vaccination of all unvaccinated people, increases the expected number of deaths dramatically.

There exists an optimal age-dependent vaccination policy

The next fundamental question regarding the policies against the SARS-CoV-2 pandemic is about the age priority for the daily vaccinations. The previous simulation results in section: A single-dose vaccination policy is sufficient to control the epidemic for large roll-out rates for the first/second dose prioritization showed that prioritizing the first dose is optimum to reduce the COVID mortality. Consequently, we studied the age priority problem for this case. Further choices are a high-efficacy vaccination of $e_0=0.7$, and a vaccination rate of 1% per day.

The population has been separated into two groups: group A (age > 65, representing 20% of the whole population) and group B (age < 65) contains the remaining 80% of the population. The parameter c shows the percentage of vaccinated people from group A with respect to the amount w of people being vaccinated per day. High values of c (i.e., $c\to 1$) show prioritization of the elder group A (age > 65), see also section: Results.

Depending on the two parameters c and the connectivity degree k, the number of deaths, averaged over the sample of $N_{sample}=128$ realizations, is shown in Figure 9A. The dynamic behavior can be categorized into different zones of strategies according to the resulting mortality. As shown in Figure 9A, there are 6 different zones depicted with dark blue, blue and light blue, green or cyan, and the narrow yellow zones (dark and light yellow) with the last two associated with the highest mortality. It is clear that higher values of c, which means: high priority to vaccinate elder people, lead to low mortality.

Figure 9.

Epidemic dynamics with respect to the age priority

Simulations of the epidemic model with respect to the age priority and with a combination of NPIs. Each day a constant number of 1000 people (roll-out window) are vaccinated with one dose of $e_0=0.7$ efficacy. The parameter $c\text{\%}$ describes the percentage of elder people (age>65) which are daily vaccinated.

(A) The number of deaths with respect to the degree k (social contacts) and the percentage c. The diagram separates the domain into different zones of strategies according to resulting mortality.

(B) The expected number of deaths with respect to the c% of. Three representative degrees $k=\mathrm{8,14,18}$ are shown.

(C) Time series of the number of deaths for $c=0.85$ and for degree $k=\mathrm{8,14,18}$.

It is crucial to mention that low mortality can be achieved even for a high number of contacts. For example, in Figure 9A the blue areas of low mortality exist for all ranges of degrees (contacts) and importantly, even with degree k over 25 (for $c>0.7$).

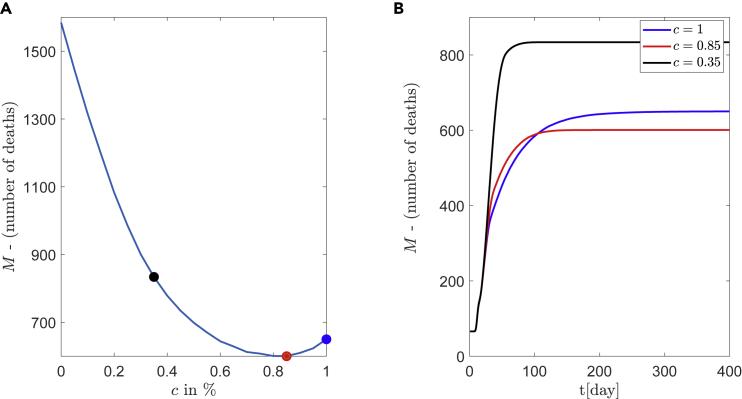
Another interesting result is the non-monotonous behavior of the mortality for a medium connectivity regime with respect to the parameter c. This is depicted in 9(B), for degrees $k=14$ and $k=18$, where a global minimum is achieved at $c\approx 0.85$. A more detailed illustration is given in Figure 10, for the degree $k=14$. The expected number of deaths for $c=0.35$, $c=0.85$ and $c=1$ are marked with filled circles and results in 833, 600, and 648 deaths, respectively. The optimal policy for this medium social distancing is at $c=0.85$ within a 95% CI: (0.75, 1), and not at $c=1$ which corresponds to “first the older” policy (the typical governmental policy).

Figure 10.

Existence of optimal policy, prioritizing people of ages > 65

Simulations of epidemic model for medium number of contacts $k=14$.

(A) The parameter c describes the percentage of elder people (age>65) who are vaccinated per day. A clear minimum appears at $c=0.85$ instead of $c=1.$

(B) Corresponding curves for $c=0.35$, $c=0.85$ (corresponds to minimum number of deaths) and $c=1$.

Finally, Figure 10A demonstrates the importance of the best policy assessment, where depending on the chosen policy, the mortality varies from 600 (for $c=0.85$) to 1582 (for $c=0$).

Discussion

In this work, using the concrete example of COVID-19, we studied how pandemic mortality is affected first by the vaccination policy and second by social distancing. A large-scale agent-based model with SEIRM dynamics has been used on complex small-world networks. This combination allowed to design of vaccination strategies (i.e., prioritization of first dose policy and age stratification) to further suggest how to reduce the expected number of deaths.

A systematic methodology has been developed to estimate the reduction in the infection probability for vaccinated individuals, from the given vaccine efficacy. This has been achieved by simulating clinical trial processes of efficacy estimation and subsequently by wrapping around the model methods of numerical analysis (e.g., Newton-Raphson). The proposed method is an equation-free approach (Kevrekidis and Samaey, 2009; Proctor et al., 2014) because it computes the infection probability from a given vaccine efficacy (the vaccination process), without having an explicit equation for the Newton-Raphson scheme.

Suggestions of vaccination strategy with priority to first dose

The analysis showed clearly that the optimal vaccination strategy is the first dose prioritization. The expected number of deaths varies significantly under social distancing measures. Prioritizing the first vaccine dose across the whole population (delaying thus the second dose) is sufficient to control the pandemic, in terms of COVID-19 deaths, only for mild social distancing measures (low-medium number of contacts, see Figures 7 and 8). The effectivity of the vaccine is described in the model with the efficacy parameter, which makes the approach independent from a specific type of vaccine. Therefore, it is possible to adjust the model to different types of vaccines by adapting this parameter.

Remarkably, a similar result has been obtained from the analysis of (Maier et al., 2021; Silva et al., 2021) using detailed models of differential equations. In (Maier et al., 2021) the authors showed that delaying the second vaccine dose is expected to prevent COVID-19 deaths in a four to five-digit range. However, their analysis does not consider social distancing measures as the present study. The agent-based formulation used in our paper is in particular suited to describe the dependence of social contacts on complex networks. The typical problem of analyzing agent-based models has been overcome by using equation-free techniques.

The presented analysis highlights the strong dependence of the expected number of deaths on social distancing. Figures 7 and 8 show the drawback of high connectivity (degree $k>30$), where even with the optimal strategy of one dose, the expected number of deaths has almost the double amount compared to mild connectivity (i.e., $k=15$). In addition, mild to higher connectivity increases the sensitivity of the number of deaths on the roll-out policy. For example in Figure 8 with connectivity $k\approx 20$ the expected deaths range from $\approx 600$ ($a=0$) to $\approx 1000$ ($a=0.7$). Moore et al. studied multiple scenarios of NPIs relaxation and vaccine characteristics (Moore et al., 2021). Similar to the results presented in our work, they showed that vaccination alone is insufficient to suppress the outbreak (Moore et al., 2021). Specifically, in the absence of NPIs, they reported that even with high vaccination efficacy the reproduction number will be larger than one (in their case study $\approx 1.58$). Furthermore, they reported that after the end of the vaccination program, the expected removal of all NPIs predicts more than 20,000 deaths in the UK.

Suggestion of vaccination strategy with age priority

Using a first dose strategy, the age vaccination priority was investigated. Interestingly, the results revealed the existence of non-monotonic behavior for mild social distancing measures. The minimal expected number of deaths is obtained by the vaccination strategy of 85% for people over 65 years, and the remaining percentage is from the younger group. This result is robust for first-dose vaccine efficacies above 50%. A similar result has been obtained in a previous study by Matrajt et al. (2021), where a detailed age-stratified continuous model had been used in combination with optimization algorithms to estimate an optimal vaccine strategy. When minimizing with respect to the number of deaths, the authors found in the mentioned study that for low vaccine efficacy, it is optimal to vaccinate older groups first. For higher vaccine efficacy, they suggest a change in the vaccination strategy to prioritizing high-transmission individuals (younger people) (Matrajt et al., 2021). Additionally, Bubar et al. (2021) used a similar mathematical model to investigate age-stratified prioritization strategies and concluded similarly. They found for the choice of the objective function to minimize the years of life loss, that the vaccination should be prioritized for adults above 60 years (Bubar et al., 2021).

Limitations of the study

The inherent complexity of the SARS-CoV-2 pandemic implies that our assumptions might be too restrictive. Furthermore, the model does not distinguish between asymptomatic and symptomatic infection rates, which may affect the network dynamics (Russo et al., 2020; Mayorga et al., 2020). For example in Lombardy, Italy which was the epicenter of the outbreak in Europe during the first wave, it had been determined (Russo et al., 2020) that the actual cumulative number of asymptomatic cases was 15 times the confirmed cumulative number of registered infection cases.

Furthermore, the simulations are made for the expected number of deaths without considering other possible NPIs (i.e., masks, school regulations, hand hygiene, and so forth). In addition, side effects of NPIs which can increase the number of deaths are not included in our model. For example in the case of very restricted NPIs (which corresponds to very low degrees k), the following harmful side effects are reported (Bendavid et al., 2021): hunger, drug overdoses, postponed surgeries, and generally missed health services. For example, delayed diagnosis of cancer and suboptimal care may have a strong impact on the population of patients with cancer (Patt et al., 2020). Additionally, in a long-term view, the air pollution especially in big cities enhances COVID mortality: A positive correlation between the pollution of nanoparticles and increased number of SARS-CoV-2 viral attachment in respiratory epithelial cells is reported (Paital and Agrawal, 2021; Paital and Das, 2021; Mousazadeh et al., 2021).

Conclusions and outlook

As the final concluding remark, we stress that the analysis of the model proposes an alternative to the strongly restricted NPIs, as mild social distancing measures (low-medium amount of contacts) simultaneously with an optimal vaccine policy can decrease sufficiently the expected number of deaths.

A possible future extension could be the use of more realistic structures of networks and the impact on the emergent pandemic dynamics. The use of household structures in the connectivity, the dominant heterogeneity factor (Hilton and Keeling, 2019), could contribute to a more realistic modeling. Detailed demographic data such as age structure and age-specific fatalities (Dudel et al., 2020), as well as mobility variations during pandemic (Basellini et al., 2021), will also improve the modeling.

Another research direction is the investigation of the parameter-dependent network dynamics (infection rates, efficacy, density of connections). Using equation-free methods in conjunction with numerical bifurcation analysis tools for multi-scale agent-based problems (Kevrekidis and Samaey, 2009; Reppas et al., 2010; Spiliotis and Siettos, 2011; Siettos et al., 2016), will finally help to predict signs or early warnings for upcoming pandemic waves.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and algorithms
MATLAB2020a	MathWorks	https://de.mathworks.com

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by Prof. Haralampos Hatzikirou, e-mail: haralampos.hatzikirou@ku.ac.ae.

Materials availability

This study did not generate new materials.

Method details

In Materials and methods a detailed description of the methodology is contained.

Quantification and statistical analysis

The confidence intervals for the minimise parameters (a and c) were calculated and provided collectively in Table 1.

Published: July 15, 2022

Data and code availability

No data was collected for this study. All results were produced from numerical simulations. The MATLAB codes used for simulations and analyses can be requested from the lead contact.