Excited-State Vibronic Dynamics of Bacteriorhodopsin from Two-Dimensional Electronic Photon Echo Spectroscopy and Multiconfigurational Quantum Chemistry

Abstract

Owing to the ultrafast time scale of the photoinduced reaction and high degree of spectral overlap among the reactant, product, and excited electronic states in bacteriorhodopsin (bR), it has been a challenge for traditional spectroscopies to resolve the interplay between vibrational dynamics and electronic processes occurring in the retinal chromophore of bR. Here, we employ ultrafast two-dimensional electronic photon echo spectroscopy to follow the early excited-state dynamics of bR preceding the isomerization. We detect an early periodic photoinduced absorptive signal that, employing a hybrid multiconfigurational quantum/molecular mechanical model of bR, we attribute to periodic mixing of the first and second electronic excited states (S₁ and S₂, respectively). This recurrent interaction between S₁ and S₂, induced by a bond length alternation of the retinal chromohore, supports the hypothesis that the ultrafast photoisomerization in bR is initiated by a process involving coupled nuclear and electronic motion on three different electronic states.

Graphical Abstract

The double-bond photoisomerization of the protonated Schiff base of all-trans retinal (rPSBAT) is the light energy conversion process fueling the bacteriorhodopsin (bR) proton pumping cycle.¹ This process is thought to involve ethylenic (i.e., C=C) stretches acting in concert with out-of-plane and twisting vibrational modes identified as the main components of the isomerization coordinate.² Recent ultrafast time-resolved spectroscopic and X-ray investigations of bR isomerization^3–6 have indeed identified a number of such modes associated with the excited-state nuclear dynamics; albeit, the x-ray studies were conducted at high excitation conditions⁵ that questions assigning the observed structural changes to biologically important processes.⁷ The motions involved are best inferred from the ultrafast spectroscopic studies conducted under biologically relevant excitation conditions. These nuclear dynamics are known to direct the molecular population along the first singlet excited-state (S₁) potential energy surface (PES), ultimately leading to formation of the J photoproduct ground state (S₀) after decay at an S₁/S₀ conical intersection (CI).

A number of computational and experimental studies^8–10 have proposed a three-state mechanistic model for bR photoisomerization that involves the second excited state (S₂). This is in contrast to the mechanistic model of visual rhodopsins, which employ the 11-cis stereoisomer of the retinal chromophore, where a two-state model involving only the S₀ and S₁ appears to apply.^2,11,12 Most studies that have proposed the three-state model cite the slower excited-state dynamics of bR compared to those of visual rhodopsins such as bovine rhodopsin (Rh) as evidence for the involvement of the S₂ state, which acts to create a barrier on S₁.¹³ This behavior has also been found in other, slower reacting, microbial rhodopsins such as the sensory rhodopsin from Anabaena, channelrhodopsin-2, and rPSBAT in solution.^14–16 However, despite numerous spectroscopic investigations with high temporal resolution,^10,17–22 there has been no direct experimental observation of the participation of S₂ in the excited-state dynamics of bR. This is likely due to the congested spectral dynamics, which limits the effective resolution of spectroscopic measurements in the most readily accessible resonant spectral window.

Two-dimensional electronic photon echo (2DPE) spectroscopy^23–25 is particularly well suited for studying systems for which absorption spectra are congested, and such a multidimensional spectroscopic approach has found considerable application in the study of pigment–protein complexes with multiple chromophores^26–33 and synthetic model analogues.^34–36 While bR contains only a single chromophore, as a result of its ultrafast photochemistry, spectral features from the initial S₀ rPSBAT (the reactive excited state) and the distorted 13-cis chromophore (early S₀ photointermediates) show considerable temporal and spectral overlap (see Figure 1). Moreover, for Franck–Condon transitions (i.e., vertical excitations) that populate excited vibrational states on the S₁ PES, the dynamics resulting from the corresponding vibrational wavepacket preparation are uniquely accessible to 2D spectroscopy and can be observed only under resonant excitation. The advantages of multidimensional spectroscopy applied to such photoreactive systems were recently demonstrated for interconverting merocyanine isomers,³⁷ where unique reactive dynamics and isomer formation were observed as a result of the greater resolution provided by the multidimensional experiment.

Figure 1.

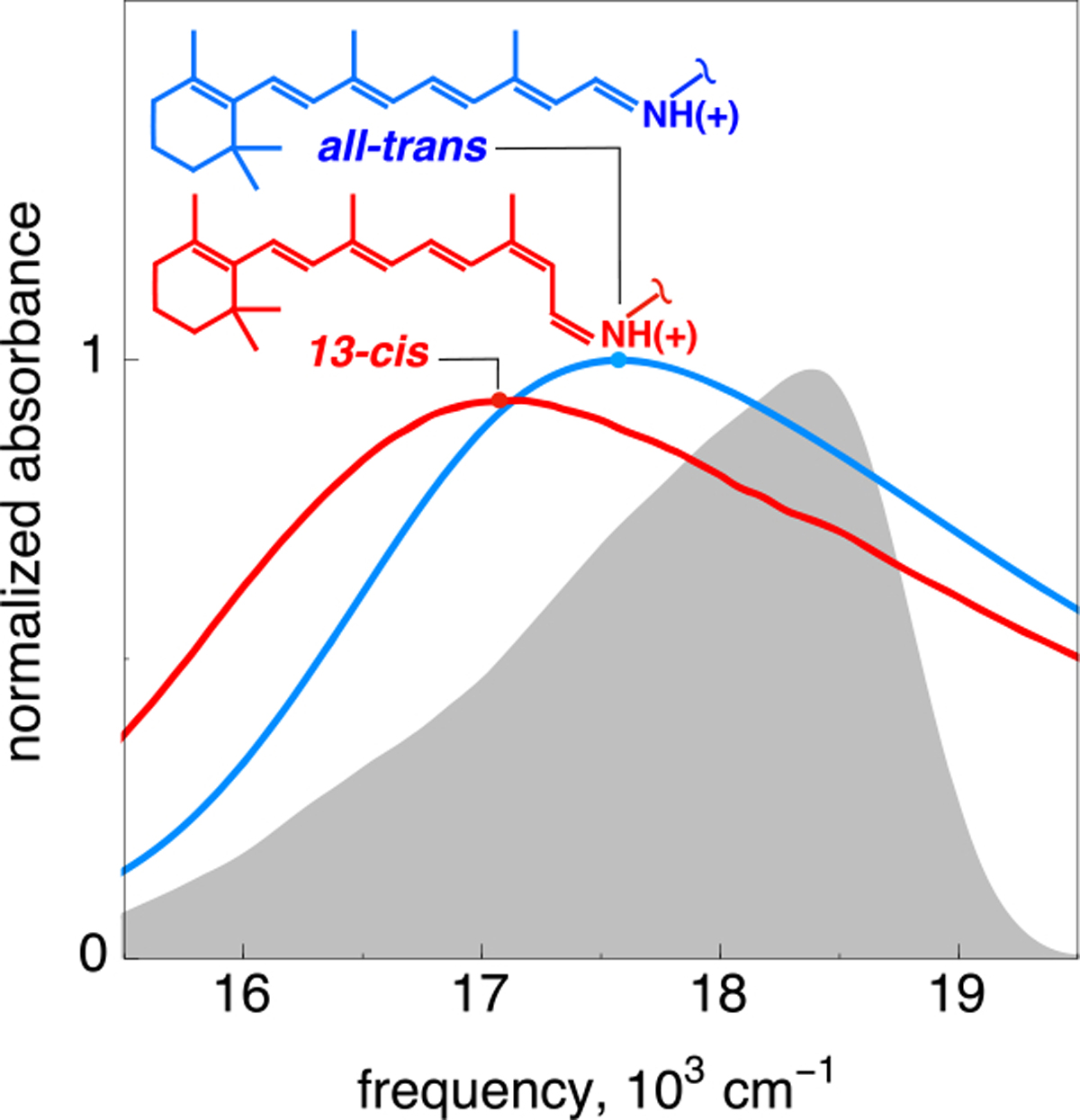
Absorption spectra of the light-adapted all-trans configuration of the bR chromophore (blue) and its 13-cis primary isolable photoproduct K (red), showing both the featureless linear absorption spectra and considerable spectral overlap between the reactant and primary photoproduct states. The laser spectrum is colored gray. The top Lewis structures display a broken N–C_ε single bond linking the chromophore to the protein cavity.

Here, we apply 2DPE spectroscopy with broadband resonant pulses to bR photoisomerization and resolve dynamics associated with distinct chromophore excitation frequencies corresponding to a strongly coupled ~1000 cm⁻¹ vibronic transition. The resulting spectral evolution reveals periodic coherent changes in the electronic character of the excited-state population implicating state mixing events recurring three times over the first 100 fs following photoexcitation. An ab initio multiconfigurational quantum mechanical/molecular mechanical (QM/MM) computational model of bR is employed to investigate the origin of these events. Our investigation complements, in a fundamental way, a recently reported non-adiabatic dynamics study³⁸ focusing on events occurring at longer time scales (beyond 100 fs).

In contrast to the featureless linear absorption spectrum in Figure 1, the real part of the 2DPE response shows clear signatures of vibronic coupling^39,40 immediately upon photoexcitation and persisting for ~100 fs. In the 2D spectrum at a waiting time t₂ of 5 fs (see Figure 2, and Figure S3 for all real-value 2D spectra), these vibronic features manifest as clear on-diagonal peaks at the linear absorption maximum of ~17500 cm⁻¹ and at a higher frequency of ~18500 cm⁻¹, with an associated cross peak below the diagonal. While not visible in the linear absorption spectrum at room temperature, a higher-energy shoulder with ~1000 cm⁻¹ splitting from the absorption maximum has been observed previously in low-temperature studies of bR,⁴¹ consistent with the features observed in the 2D spectra. This frequency is consistent with a methyl rock or out-of-plane hydrogen wag and is a vibration readily observed in resonance Raman scattering of bR.^42–45 These results corroborate recent transient absorption experiments that also restored excited-state vibrational dynamics predominantly in the <1000 cm⁻¹ region.^3,4 Femtosecond pump–probe experiments have also revealed excited-state oscillations due to coherent vibrations at frequencies in the range of ~800–1600 cm⁻¹.^10,18

Figure 2.

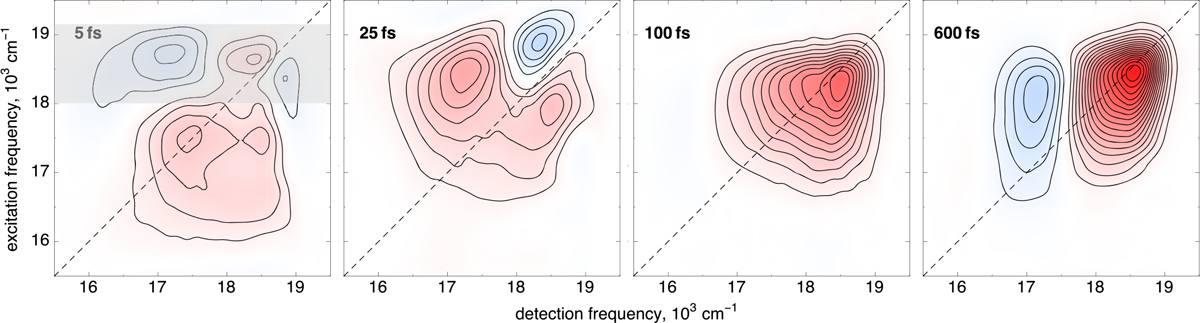
Real-value 2DPE spectra of bR at select waiting times. Immediately following excitation, vibronic coupling of ~1000 cm⁻¹ is observed between the absorption maximum of 17500 cm⁻¹ and a higher-frequency shoulder at 18500 cm⁻¹, and an associated cross peak is observed below the diagonal. Above the diagonal, large-amplitude oscillatory dynamics persist for ~100 fs, commensurate with excitation of the high-energy vibronic transition, as highlighted with a translucent gray bar in the 2D spectrum at a waiting time of 5 fs. For waiting times (t₂) of ≥100 fs, spectral diffusion results in broad homogeneous features, and photoproduct formation at the conventional differential absorption maximum of the J photointermediate is observed on a 600 fs time scale.

In addition to the vibronic features mentioned above, we observe a broad absorptive response commensurate with excitation of the high-frequency shoulder, visible in the t₂ = 5 fs 2D spectrum in Figure 2 as the blue contours above the diagonal. This absorptive feature spans a 16000–18000 cm⁻¹ spectral region and is observed only as a result of excitation of the ~18500 cm⁻¹ vibronic transition. Spectral features related to this vibronic transition persist for the first 100 fs following photoexcitation before the onset of spectral diffusion results in a more homogeneous response, seen as the broad, featureless bleach that dominates the 2DPE spectrum at a t₂ of 100 fs. Then, on the time scale of the formation of the canonical J photointermediate (which is a red-shifted, vibrationally hot precursor of the isolable primary photointermediate K of Figure 1), an absorptive band red-shifted relative to the bleach response appears, consistent with the transient absorption kinetics observed previously.^4,17

The spectral dynamics associated with the vibronic features above the diagonal are shown in Figure 3, where pump frequency-resolved dynamics are generated through integration over the excitation frequencies associated with the high-energy vibronic transition at 18500 ± 500 cm⁻¹, which allows for the isolation of excitation frequency effects without compromising temporal resolution, as would narrowband transient absorption experiments. Excitation of the vibronic shoulder at ~18500 cm⁻¹ reveals large-amplitude oscillations spanning the 16000–18000 cm⁻¹ range that are clearly resolved over the first ~100 fs. Absorptive signals dominate the spectral response at three particular waiting times, namely, 10, 40, and 75 fs.

Figure 3.

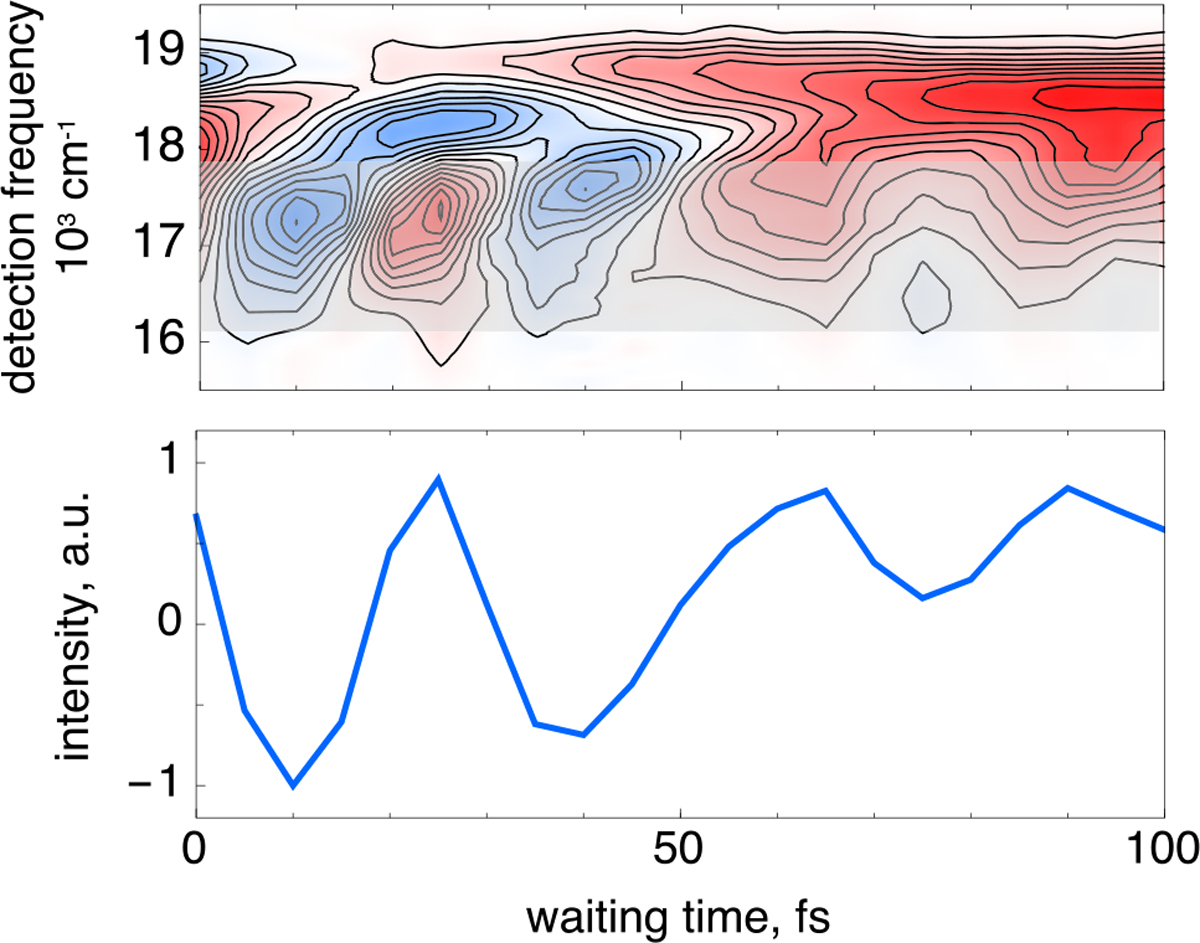
Waiting time dynamics associated with excitation of the high-frequency vibronic shoulder over the range shown in Figure 2. Broad, large-amplitude oscillatory dynamics are observed over the first 100 fs following photoexcitation (top). These plots are produced by integration of the 2D spectra over the excitation frequencies from 18000 to 19000 cm⁻¹ (see the gray highlighted region in the first panel of Figure 2). Spectral integration of the gray translucent region in the top panel shows significant absorptive features centered at waiting times of approximately 10, 40, and 75 fs (bottom).

The large amplitude, broad spectral response, and unique temporal dynamics correlated with excitation of the high-frequency vibronic shoulder all implicate chromophore dynamics occurring immediately on the excited-state potential energy surface, preceding the large twisting deformation of the isomerizing double bond that occurs on the characteristic ~500 fs time scale.

To interpret the observed bR spectral dynamics, we constructed a QM/MM model of the protein starting from its light-adapted crystallographic structure (Protein Data Bank entry 1C3W)⁴⁶ and incorporating the rPSBAT chromophore (see Figure 4A). The model S₀ equilibrium structure was then used as a starting point to propagate a 100 fs trajectory on the spectroscopically allowed S₁ PES with zero initial velocities. In this way, we ensure that the time evolution is exclusively due to the S₁ force field driving the initial motion of the excited-state population. The trajectory is assumed to represent the center of the population relaxing out of the Franck–Condon point. Such an assumption was tested for similar models^47,48 and is justified by the fact that such a time scale is insufficient for complete vibrational dephasing. The calculation was run using the affordable CASSCF/AMBER level of theory, but energies at each step of the trajectory are then re-evaluated at the more accurate CASPT2/AMBER level using the 6–31G* basis set. In Figure 4B, we show the energy profiles for S₀ and the relevant excited states. In Figure 4C, we plot the evolution of the bond length alternation (BLA) coordinate along the trajectory. The BLA is a stretching coordinate (i.e., a combination of stretching modes) that describes the simultaneous expansion of the double bonds and contraction of single bonds of rPSBAT; the BLA is mathematically defined as the difference between the average of formal single (e.g., C₁₄–C₁₅) and double (e.g., C₁₃=C₁₄) bond lengths. We find that the BLA dominates the relaxation motion, as indicated by the large changes in the BLA value shown in Figure 4C. We note that not all bonds stretch at identical frequencies (see Figure S5, where the C15=N bond can clearly be seen oscillating at a higher frequency), but most bond lengths along the backbone do follow the periodicity of the BLA mode. Meanwhile, changes in the out-of-plane modes such as methyl rock and torsion are present but much smaller (see Figure S5). This is in agreement with earlier experimental^10,42–45 and computational¹³ studies of bR that have shown that the initial response of bR is dominated by stretching modes. From an inspection of Figure 4C, it is apparent that the BLA displays oscillations remarkably close in frequency to the oscillations seen in the periodic features described in the 2D spectral evolution above the diagonal. Indeed, the BLA coordinate oscillates three times over the first 100 fs and has an amplitude greater than or equal to zero approximately 0–5, 25–35, and 55–60 fs after excitation. From the energy profiles of Figure 4B, it is immediately evident that the oscillations modulate the gap between different electronic states. Most relevant for the discussion presented here is the modulation of the energy gap between S₂ and S₁. As displayed in Figure 4C, the S₂–S₁ gap closely follows the BLA modulation and reaches a maximum when the BLA value is small (i.e., negative) and a minimum when the BLA value is near zero (i.e., when the single and double bond lengths along the chromophore backbone are similar). This indicates that, at positive BLA values, the S₂ and S₁ energy surfaces would approach each other. Such vibronic coupling would therefore be enhanced by larger oscillations causing the BLA value to shift above 0 Å or by some other vibrational component that would induce a decrease in the S₂–S₁ gap. Figure S6 shows that the electronic character of S1 and S₂ is certainly coupled, with the difference in the charge transfer character oscillating periodically. While this oscillation is not clearly aligned with the BLA, it does very closely follow the oscillations in the C15=N bond length (compare the middles of Figure S5 and S6). Such oscillations in the charge transfer character will also be enhanced by additional vibrational energy, as well as the S₂–S₁ energy gap that follows the BLA.

Figure 4.

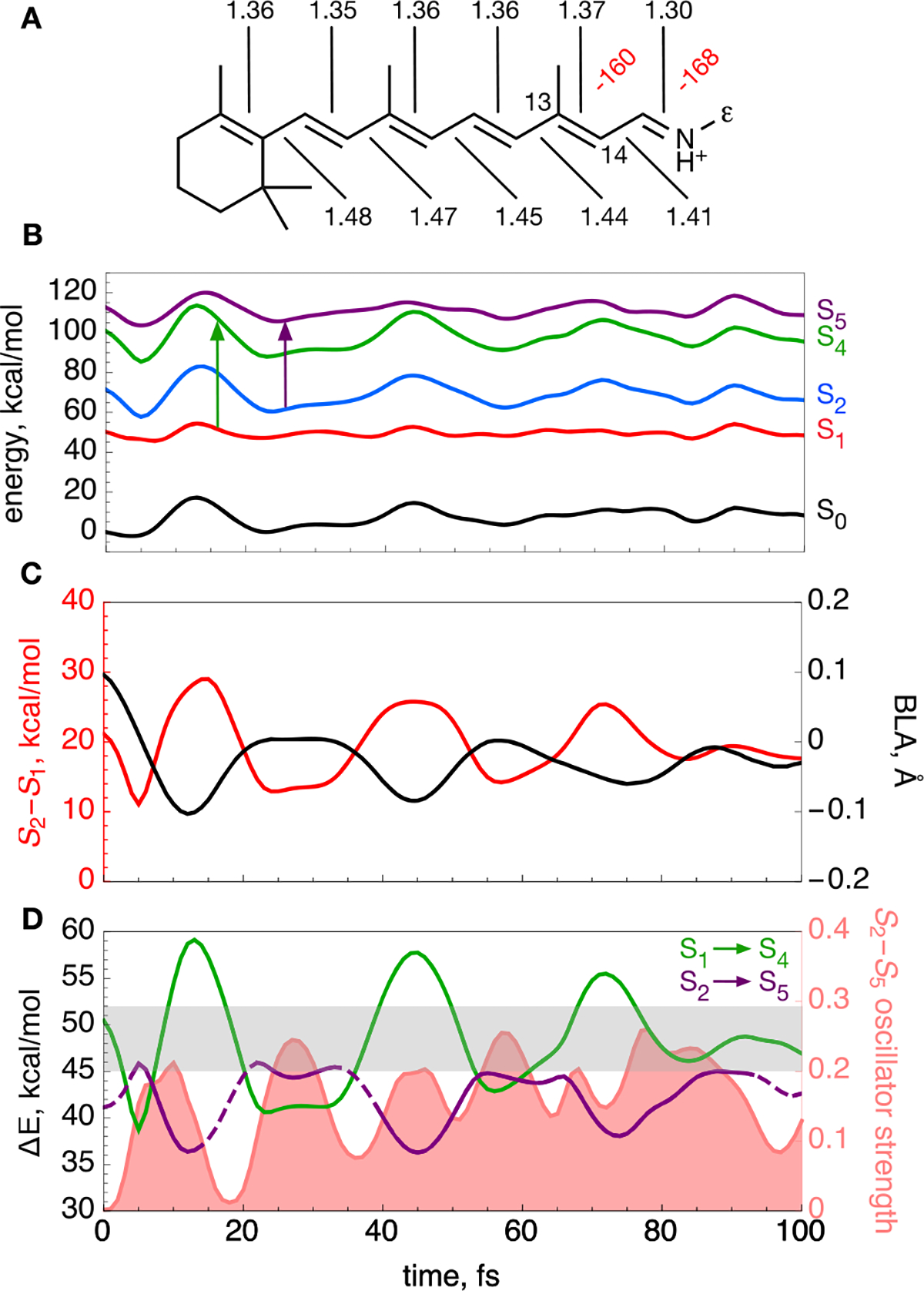
Computational modeling of bR. (A) Computed equilibrium structure of bR rPSBAT. Backbone dihedral angles twisted more than 10° are labeled in red. Bond lengths along the conjugated backbone are labeled in black (in angstroms). The ε indicates the C_ε atom. (B) S₀–S₂, S₄, and S₅ CASPT2/AMBER energy profiles (black, red, blue, green, and purple lines, respectively) along the S₁ trajectory released from the S₀ equilibrium structure. The vertical arrows indicate the investigated electronic transitions. (C) Evolution of the BLA coordinate (black line) describing the elongation of double bonds coupled with shortening of single bonds along the trajectory. Also shown is the S₂–S₁ energy gap (red). (D) Evolution of the S₁ → S₄ and S₂ → S₅ energy gaps along the trajectory (green and purple lines, respectively). The lines are dashed when the oscillator strength of the corresponding transition has an oscillator strength of <0.1. The S₂ → S₅ oscillator strength is shown as the light red area. The experimental detection window is shaded in gray in the graph. Note that the S₁ → S₅ and S₂ → S₄ transitions have a low oscillator strength along the entire trajectory.

On the basis of the results described above, we propose possible explanations for the origin of the observed 16000–18000 cm⁻¹ dynamics (Figure 3). We hypothesize that such off-diagonal peaks reflect transient and recursive excited-state absorption activity. Therefore, the periodic appearance and disappearance of the signal must be due to oscillations in the energy and/or electronic character of the corresponding transition. In the computational bR model, we find two bright transitions falling within the experimental detection window of 16000–18000 cm⁻¹. Figure 4D shows the computed S₁ → S₄ and S₂ → S₅ excitation energy progression (see arrows in Figure 4B). The S₁ → S₄ excitation energy varies significantly as a function of BLA, increasing from ~40 to ~57.5 kcal/mol (i.e., from ~14000 to ~20000 cm⁻¹). During each oscillation, the S₄–S₁ energy gap quickly passes (1–2 fs) through the experimental observation window but then remains for 10 fs substantially off resonance with values well above 18000 cm⁻¹. According to these simulations, passages through the experimental window would occur six times, at approximately 10, 20, 40, 50, 70, and 80 fs, in contrast with the experimentally detected signal that smoothly oscillates once every ~30 fs. On the other hand, the S₂ → S₅ transition appears to better fit the periodicity of the observed spectral dynamics and will occur only once per BLA cycle with a frequency similar to the BLA. This transition also has a large oscillator strength when its energy is in the experimental window (see the bottom of Figure S6). Therefore, we assign the experimentally detected fundamental absorption to be most likely originating from the S₂ → S₅ transition and not from the S₁ → S₄ transition. We note here that the instrument response function of 15 fs may not fully resolve the S₁ → S₄ contributions to the modulation. It is also worth noting that the S₅–S₄ energy difference, as well as their electronic character, is strongly modulated by the BLA mode (Figure S6, middle). However, despite these oscillations, the S₁ to S₅ oscillator strength remains small throughout the trajectory (Figure S6, bottom).

During the simulated excited-state dynamics, we also see a periodic ~25% decrease in the S₁–S₀ energy gap, which reaches a minimum value close to 30 kcal/mol at 12, 45, and 77 fs (Figure S6, top) and therefore reproduces the periodicity of the observed off-diagonal signals. This suggests that non-adiabatic decay from S₁ to S₀ may take place at these times even though the system is still not twisted and therefore far from the canonical (90° twisted) CI. This may even provide an explanation for the spectroscopic signal observed in Figure 3. However, the S₁–S₀ energy gap, even if reduced further by vibrational excitation yielding a more negative BLA value, remains large and unlikely to allow for decay. Such an S₁ decay hypothesis is also inconsistent with the fact that the observed signal appears periodically instead of building up due to formation of a ground-state species.

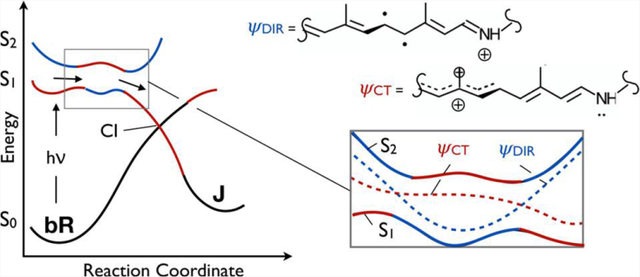
Of the possibilities mentioned above, therefore, absorption from S₂ to S₅ seems to be most consistent with the results of 2D spectroscopy. How is it possible to observe an absorption from S₂ when only S₁ is initially populated? The S₂ state must be populated by part of the S₁ population, or the S₁ and S₂ states must exchange their original electronic character during the excited-state progression. In a non-adiabatic description of the S₂–S₁ interaction, these possibilities represent alternative descriptions of the same event. As anticipated above, when S₂ and S₁ are close in energy (i.e., at 5, 24, and 57 fs, preceding the spectroscopic signals by ~5–15 fs), the tendency to couple increases. Accordingly, at the Franck–Condon point, S₁ has charge transfer character (ψ_CT) and S₂ has a diradical character (ψ_DiR). However, both the energy gaps and the electronic character of the S₁ PES and S₂ are modulated by bond stretching/BLA modes. It is therefore likely that, for a vibrationally excited population, the S₂ and S₁ mix when they are closer to degeneracy. In panels A and B of Figure 5, we schematically illustrate an increase in the level of mixing of the two electronic surfaces (non-adiabatic states) when passing from a large to a small S₂–S₁ energy gap. The mixing, in turn, induces larger variations in the electronic character, as the population traveling on the adiabatic S₁ PES acquires the electronic character of the S₂ state (i.e., as if it were populating S₂ in that region). These computations indicate that the S₂ and S₁ crossing probability would be maximal when the BLA value reaches a maximum. This is also exactly when the transition from S₂ (i.e., from a state with a ψ_DIR dominating character) to S₅ is brightest and within the experimental detection range.

Figure 5.

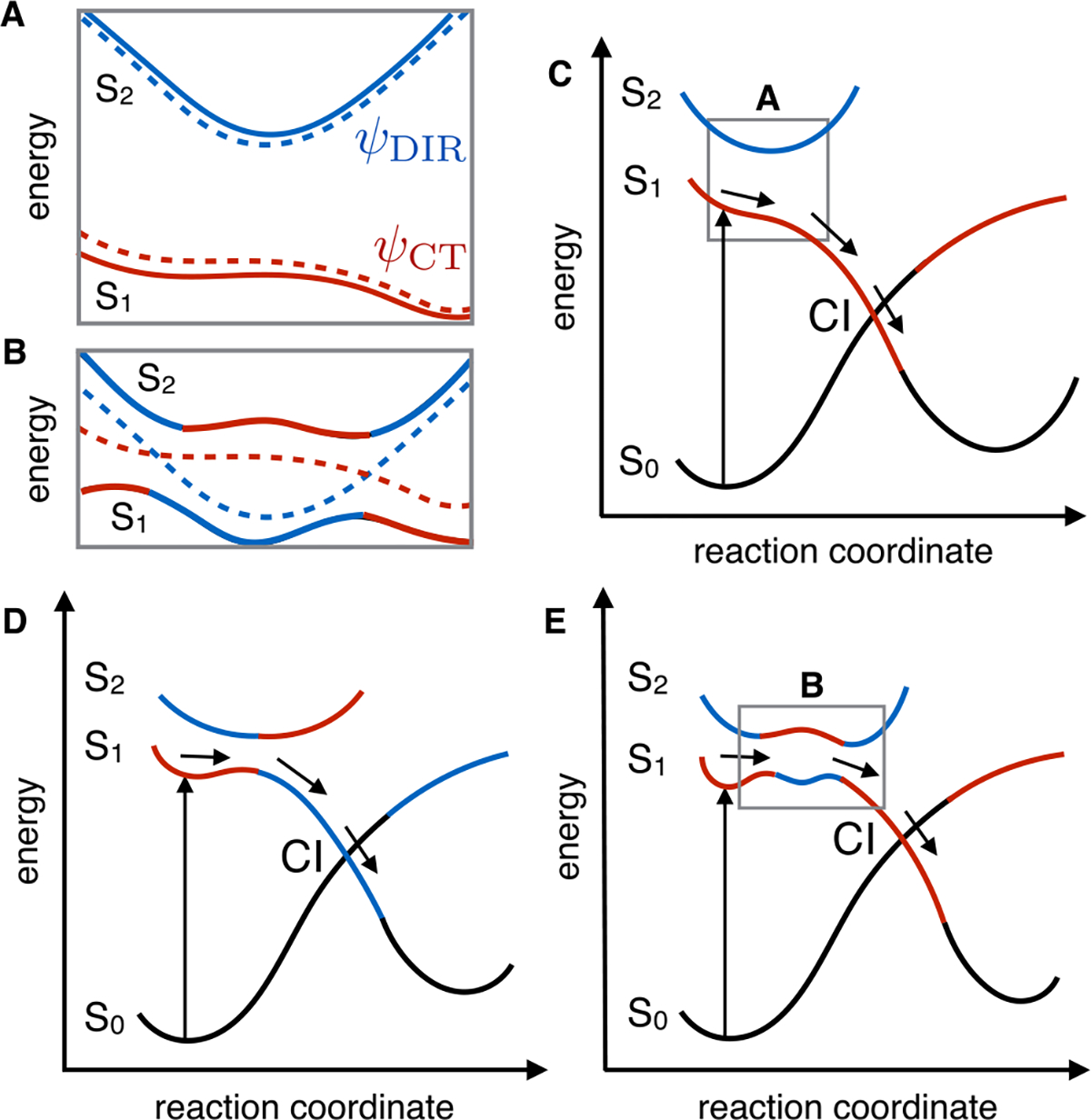
Schematic representation of the photochemical isomerization path in bR. (A) ψ_CT and ψ_Dir non-adiabatic states (dashed lines) corresponding to charge transfer (red) and diradical (blue) electronic character, respectively. The ψ₂ and ψ₁ adiabatic states (full lines) associated with the S₁ and S₂ PESes are seen as linear combinations of the non-adiabatic states. (B) Schematic illustration of the consequence of the stabilization of the diradical non-adiabatic state with respect to the charge transfer non-adiabatic state, leading to a reduction in the S₂–S₁ energy gap. (C) Conventional two-state model, where S₂ does not participate in the photoisomerization. (D) Conventional three-state model. (E) Model that emerged from this work, where mixing of the S₂ and S₁ surfaces as a result of the BLA dynamics produces a rugged excited PES prior to the conical intersection.

The QM/MM trajectory analysis thus provides a potential explanation for the experimentally observed spectral dynamics. This same analysis provides a basis for explaining why the signal only appears when bR is excited at the vibronic shoulder at ~18500 cm⁻¹. Absorption at ~17500 cm⁻¹ (the linear absorption maximum) would result in dynamics similar to the computed trajectories, where the release from the Franck–Condon point leads to S₂–S₁ states not less than 9 kcal/mol apart (see Figure 4) and thus too far to cause a strong mixing of the associated wave functions. Such an energy gap is expected to yield only a modest mixing of the ψ_CT and ψ_mR characters, as shown in Figure S6. However, in the limiting case of an S₂ stabilization large enough to induce an S₂ and S₁ crossing (more precisely, the intersection of the ψ_CT and ψ_DIR non-adiabatic energy surfaces), a strong increase in the oscillator strength of the S₁ → S₅ transition would be observed (which is nearly forbidden if the S₁ state retains its character). The computational limits of the approach presented here, which represents the best compromise possible when a CASPT2/MM level of theory is required to obtain realistic excitation energies, prevents a complete analysis of the effect of the excitation of specific vibrational modes. Thus, we must hypothesize that upon excitation of the vibronic peak at ~18500 cm⁻¹, the additional vibrational excess energy would flow into modes prompting larger oscillations in the S₂–S₁ energy gap, thus inducing a stronger electronic-state mixing/crossing. The experimental observations indicate that these modes have 945 and 1634 cm⁻¹ components. Remarkably, such frequencies correspond to periods of ~35 and ~20 fs, respectively, and are therefore close to the computed oscillation periods for the energy gap and oscillator strengths of the S₂–S₁ transition (see Figure 4D). As mentioned above, a ~35 fs period is also close to the average period displayed by the BLA mode that also appears to couple with out-of-plane wagging modes (see Figure S5).

There are currently two mechanistic models proposed for the photoisomerization of the chromophore in retinal proteins. The two-state model of Figure 5C has been proposed for the extremely fast photoisomerization of Rh featuring an S₁ lifetime on the order of 50 fs.^12,49,50 In contrast, the three-state model of Figure 5D describes the bR photoisomerization involving a slower progression toward the S₁/S₀ CI and an S₁ lifetime of ~500 fs. While the two-state model does not include S₂ at all, in the original three-state model S₂ forms an avoided crossing with the S₁ state that results in a barrier on the S₁ energy surface as well as a change in character of the wave function from ψ_CT to ψ_DIR along the reaction coordinate. The experimental and computational data presented in this work support a three-state mechanistic model of bR photoisomerization that appears to be fundamentally different from the model depicted in Figure 5D. As is apparent from comparison of panels D and E of Figure 5, these models are initially similar as they imply that the S₂ PES carrying the diradical character is stabilized during the early relaxation of the S₁ population until an S₂/S₁ avoided crossing is reached. At the avoided crossing, the ψ_CT and ψ_DIR wave function character would exchange, making the populated state S₂-like. However, the experiments and computations in this work suggest that the S₂-like ψ_dir character does not ultimately carry out the isomerization, as shown in Figure 5D. In that case, the S₂ → S₅ absorption would persist throughout the excited-state lifetime of the molecule. Therefore, the two models in panels D and E of Figure 5 diverge along the reaction coordinate leading to the S₁/S₀ CI controlling excited-state decay and photoproduct formation. As established elsewhere for bR, Rh, and other microbial and animal rhodopsins,^13,47,48,51 such a CI invariably corresponds to a crossing between S₀ and the same S₁ that had charge transfer character at the Franck–Condon region. It is thus apparent that the motion along the C₁₃=C₁₄ twisting coordinate must destabilize the S₂ state and restore the ψ_CT character along the S₁ PES. Thus, while the presence of a first S₂/S₁ avoided crossing would justify, in both mechanistic models, the observed slower isomerization of bR compared to Rh, at least a second avoided crossing is expected to occur before the S₁/S₀ CI is reached (see Figure 5B for a non-adiabatic representation of the exchange in electronic character in the framed region of Figure 5E). In fact, oscillations in the relative energy gap between S₂ and S₁ (which have even been shown to cross in simulations of photoisomerization in other microbial rhodopsins⁵²) would result in a rugged excited-state PES driving a slower photoisomerization reaction.

These results indicate that during the early stage of the light energy conversion process in bR, the excited-state population may access the ψ_DIR electronic character periodically during the initial 100 fs and before significant C₁₃=C₁₄ twisting takes place. This would be detected only when bR is excited at the vibronic shoulder due to the vibrational excess energy funneled into modes capable of further decreasing the S₂–S₁ energy gap, driving changes in the excited-state character of the wave function. Finally, it must be noted that the proposed three-state model in Figure 5E can be smoothly transformed into the two-state model of Figure 5C through an increasing destabilization of S₂ with respect to S₁. This can be realized by comparing the schematic representations of the energy profiles associated with the pure (non-adiabatic) ψ_CT and ψ_DIR states in panels A and B of Figure 5. Owing to the different electronic character (and charge distribution) of these states, we conclude that the evolutionary optimization of the chromophore cavity by either changes in amino acid composition or associated changes in cavity structure may modulate the S₂–S₁ energy gap and, as a consequence, the mechanistic model controlling the photoisomerization as well as the formation of a fluorescent species. In other words, the observed and simulated vibronic dynamics would correspond to a preparatory stage resulting in the production of the photocycle fluorescent intermediate I and, after S₁ decay, in the formation of photoproduct J preceding K.

MATERIALS AND METHODS

Sample Preparation.

Bacteriorhodopsin trimers in lipid nanodiscs were prepared and characterized as described previously.⁴ Bacteriorhodopsin was initially solubilized with 4% (w/v) Triton X-100 from a washed purple membrane isolated from Halobacterium salinarum cultures. MSP1E3D1 expression and purification were carried out as described previously.⁵³ For incorporation of bR in nanodiscs, the solubilized bR and MSP1E3D1 were mixed with 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) lipids (Avanti Polar Lipids, Inc.) solubilized in 100 mM cholate to a final bR:MSP1E3D1:lipid molar ratio of 3:2:100. The buffer for the nanodisc self-assembly and the following size-exclusion chromatography consisted of 10 mM Tris-HCl and 0.1 M NaCl at pH 7.4 and 20 °C. The mixture was incubated for 30 min. Subsequently, the detergent was removed by treatment for 3 h at room temperature with 500 mg of wet Biobeads SM-2 (Bio-Rad) per milliliter of solution, with gentle agitation to keep the beads suspended. Beads were removed by centrifugal filtration. Self-assembled nanodiscs were concentrated, filtered through 0.22 μm filters, and injected onto a Superdex 200 10/300 GL column (GE Healthcare) run at 0.5 mL/min at room temperature with collection of 2 min fractions. Peak elution was monitored at 280 and 565 nm. The final sample was resuspended in 100 mM MES and 500 mM NaCl (pH 6.0) and kept at room temperature for all subsequent measurements.

2D Spectroscopy.

Photon echo spectra⁵⁴ of the isomerization dynamics of retinal in bR were recorded using 12 fs pulses having an energy of 7 nJ/beam.⁵⁵ The local oscillator was attenuated by OD 1.8, with a temporal delay of ~400 fs introduced by the optical path length of the OD filter itself. The coherence time t₁ was scanned over the range [−128, 128] fs in 1.6 fs steps, and 100 scans were averaged per t₁ delay. Precise determination of the LO delay (and therefore phasing) was performed by comparison of the pump–probe response to the heterodyne echo about t₁ = t₂ = 0, measured sequentially in the 2DPE spectrometer. 2D spectra were subsequently recorded for population times between 0 and 150 fs in 5 fs intervals and coarse-grained sampling of longer waiting times thereafter. A 100 cm⁻¹ square moving average has been applied to the data.

QM/MM Calculations.

The bR QM/MM model was constructed starting from its crystal structure (Protein Data Bank entry 1C3W).⁴⁶ Details regarding the model construction and optimization are provided in the Supporting Information. Geometry optimizations and excited-state dynamics were performed at the two-root state-averaged complete-active-space self-consistent-field (CASSCF) level of theory with a 6–31G* basis set, accounting for the effect of the protein using the AMBER force field. Energies were then re-evaluated at the six-root complete-active-space second-order perturbation theory (CASPT2)/AMBER level of theory.