Abstract
Blebs are pressure-driven protrusions that have been observed in cells undergoing apoptosis, cytokinesis, or migration, including tumor cells that use blebs to escape their organs of origin. Here, we present a minimal 1D model of bleb-driven cell motion that combines a simple mechanical model with turnover kinetics of the actin cortex and adhesions between the membrane and the cortex. The deterministic version of this model is used to study the properties of individual blebbing events. We further introduce stochastic turnover of the adhesions, which allows for spontaneous initiation of repeated blebbing events, thus leading to sustained cell travel. We explore how the main parameters of the system control the properties of the blebbing events and the speed of cell travel. Finally, we derive a further simplification by deriving a Langevin approximation to this stochastic model.
Significance
Bleb-driven migration requires spontaneous, repeated blebbing. This study presents a simple model of cell motility using blebs, and introduces stochastic fluctuations to the membrane-cortex adhesions that can lead to sustained unidirectional motion. The model presented allows us to identify the determinants of the distance traveled by cells employing blebs.
Introduction
Blebs are cellular protrusions that appear as smooth spherical expansions of the membrane formed when it separates from the underlying actin cortex (see Fig. 1, top), driven by hydrostatic pressure generated in the cytoplasm by the contractile actomyosin cortex (1, 2, 3). They were originally associated with cells undergoing apoptosis, but have also been observed in cytokinesis and in migrating cells. Many cell types can use protrusions such as blebs for motility, including mammalian tumor cells (4), which can use blebs to force their way through the endothelium and invade new tissues, and metastatic cells, which can use blebs to escape antitumor treatments that rely on protease inhibitors (2). Pressure-driven expansion is faster than lamellipodial protrusion and, since such protrusions have no cortex, can occur in any direction and adapt to the shape of the extracellular environment. There are also data to suggest that such growth requires less energy than lamellipodium formation (2).
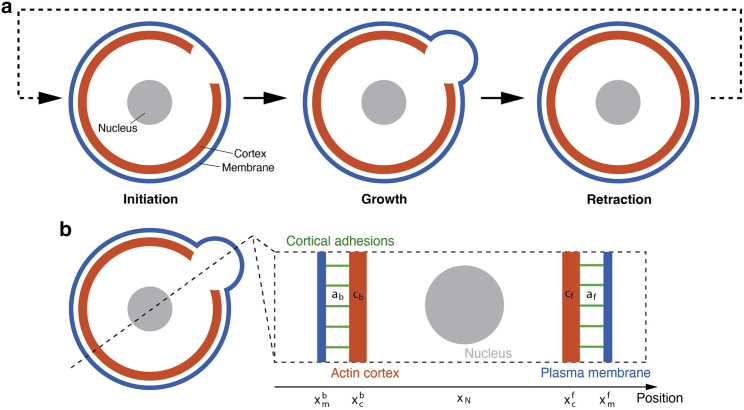
Figure 1.
(Top) Schematic figure of cell blebbing mechanism. Stochastically induced local detachment of cortex-membrane linking proteins drives the membrane expansion. By reconnecting the cortex-membrane attachment, the inflation retracts back to the steady state. (Bottom) Schematic figure of our bleb-driven cell migration model in 1D. Local bleb formation dynamics (5) at both ends are coupled with the mechanical model of the whole cell.
The life cycle of the bleb can be divided into three steps: initiation, growth, and retraction. Two mechanisms have been proposed for initiation: a local decrease in membrane-cortex attachment or a local rupture of the cortex. They could also be functioning together (1). Both of these have been observed experimentally in both motile and nonmotile blebbing cells (2). The bleb initially appears devoid of filamentous actin and grows as cytoplasmic fluid fills the protrusion. Bleb inflation is thought to be driven by intracellular pressure transients generated by myosin II contraction of the actin cortex (6). Over time, the actin cortex reassembles at the bleb plasma membrane and drives cortex retraction: once expansion ceases, ERM (Ezrin, Radixin, Moesin) proteins (responsible for cortex-membrane adhesion) are recruited to the membrane, followed by actin, actin-bundling proteins, and lastly contractile proteins (6). In migrating cells, retraction does not always occur since movement depends on a stable bleb, and instead the cell body moves forward as a result of contraction at the rear of the cell (1). In such cells, a new bleb often forms after cortex repolymerization under the membrane (2).
Biochemically, cortex composition is dominated by actin, actin-bundling proteins, and myosin II. High myosin II activity is critical for the formation of blebs (7). The cortex is linked to the membrane by ERM proteins, which can switch from an inactivated closed conformation to an active open conformation that exposes an actin binding site and a membrane-targeting domain (6). Thus, a decrease in membrane-cortex attachment corresponds to ERM proteins returning to the closed conformation. The actin cortex that remains at the base of the bleb is disassembled by the constitutive turnover of actin (2). An important question in bleb dynamics is how cortex reassembly begins. One possibility with some experimental support is that cortex assembly is constitutive, but slow compared with bleb expansion, so that it can only catch up when the expansion slows down (6).
An important aspect of bleb initiation and growth is that it can be localized to just a part of the cell, so that different parts of the cell can be mechanically isolated (as they often are chemically) (8). The precise mechanisms that determine where a bleb is initiated during migration are not known. However, observations suggest that asymmetries in the membrane-cortex attachment could play a role in determining the cell front: in Walker carcinosarcoma cells, the level of Ezrin (a member of the ERM family) is elevated at the back of the cell, and reduced at the leading edge, facilitating bleb formation in the front of the cell (2,9). Understanding the formation of pressure-driven protrusions and their part in cell travel is important as treatments are developed for pathologies where cells may employ this type of migration, such as cancer (2) and immune deficiencies. The precise mechanics of this are not well understood.
In this paper, we present a simple reduced stochastic model of blebbing that can simulate continuous cell movement. The model consists of a 1D mechanical model in which the front, back, and central (nucleus) position are tracked, together with a turnover model for the actin cortex and adhesion molecules at the front and the back. The breakage and formation of adhesion bonds are stochastic, so that blebs are initiated spontaneously either at the front or back of the cell. Although our model was initially conceived as a reduced model of blebbing in general, recent experimental evidence suggests that cells can undergo blebbing in a narrow 1D channel (10,11) for which our model should be directly applicable.
There have been many previous modeling studies on blebbing that focus on different aspects of this phenomenon. In a series of papers, Woolley and co-workers have developed a continuum mechanical model of blebs based on the assumption of axisymmetric geometry (12, 13, 14, 15). These papers focus primarily on membrane and cortical mechanics. On the other hand, in (16,17) the authors introduce a 2D mechanical model of immersed boundary type wherein membrane and cortical structures interact with the cytosolic and extracellular fluids. In contrast to the above models, which focus on mechanical and geometric aspects of cell blebbing, (5) focuses on the turnover kinetics of the cortex and adhesions. Cortical and adhesion densities defined at each point of the membrane satisfy an equation expressing their turnover. These protein densities are coupled to a simple mechanical model of the membrane. The analysis and simulations of all of the above models are confined mostly to the growth and retraction of a single blebbing event.
In this paper, we introduce a simple model of pressure-driven cell migration model in 1D, which connects subcellular adhesion process and cell migration dynamics. We neglect the geometry of the bleb and focus on how intrinsic noise from molecular interaction of cortex components can generate stochastic membrane-cortex separation, which allows cells to migrate by hydrostatic pressure. In our model, the cell configuration is described by five coordinate locations in one dimension: the cortical and membrane positions at the front and back, and the position of the nucleus. At the front and back of the cell, cortical and adhesion densities that undergo turnover are defined. The adhesion kinetics in particular is stochastic, making it possible for the cell to initiate spontaneous blebbing events. The incorporation of this stochastic initiation mechanism allows for the simulation of repeated blebbing events and thus continuous cell movement. In its simplicity, our mechanical model is analogous to (18,19), where models of low Reynolds number swimmers of Purcell type (20) are adapted to study cell blebbing. The focus of their study, however, is on the mechanical and hydrodynamical aspects of blebbing, especially as they relate to swimming efficiency.
There have been a handful of modeling studies in which the full blebbing cycle has been studied, much like our study here. In (21), the authors incorporate bleb initiation into their axisymmetric mechanical model (12,13, 14, 15) by randomly selecting a bleb location over the surface of the cell from a given probability distribution. Bleb initiation thus does not arise from an internal dynamical process. Arguably the most ambitious effort in incorporating cell biological details in a computational model of blebbing motility is that of (22), in which the authors develop an agent-based model of both membrane and cortex and their attachment to the underlying substrate, incorporating stochasticity in several different processes. Our model is much simpler and does not match (22) in its biophysical realism. However, the simplicity of our model allows for a more extensive parameter study and a clearer conceptual understanding of the mechanisms that may allow blebbing to lead to cell motility.
We also point out that, although the aim of this study is to clarify the properties of cell blebbing, the reduced nature of the model may make it applicable to other modes of pressure-driven cell migration more generally. For example, in (3) it is suggested that lamellipodial protrusions are pressure driven, and not driven by actin polymerization.
In the next section (Methods), we describe our model setup. We first describe our differential equation model, which is formed by combining a turnover model of based on (5) with a mechanical model similar to (23). In the model from (5) the position of the cell is fixed, which is clearly not suitable for our purposes of modeling persistent movement. We allow our cell to move by introducing coordinates at the front and back position of the cell, as well as the position of the nucleus. At the front and back of the cells, cortical and adhesion density experience turnover (5). Much like the model in (5), this model exhibits excitable behavior but also exhibits other dynamical behaviors as studied in the Results. We also study the distance the cell travels when a blebbing event is induced.
Our parametric study indicates the importance of the membrane water permeability and myosin contraction to bleb formation. Sufficient water permeability and an appropriate level of myosin contraction is needed for the system to reside within the excitable regime. When water permeability is too low or when myosin contraction is too high or too low, the deterministic system loses its excitability, making it difficult to generate blebs.
The above deterministic model is only capable of generating one blebbing event under an external perturbation, particularly in the excitable regime. As described in the Methods section, we further introduce stochastic fluctuations to the membrane-cortex adhesion density by taking into account the fact that these links are finite in number. This results in a stochastic hybrid system (24,25). This stochasticity leads to spontaneous blebbing events, which can lead to unidirectional motion in the presence of a parametric bias between the front and back of the cells. The stochastic bleb initiations are correlated with the kinetics of the membrane and the actin cortex, in contrast to (21). Our model of bleb-based motility thus constitutes a dynamical system (an excitable system) in which the cell is stochastically kicked out the basin of attraction of the sedentary state. This is similar to the spontaneous generation of action potentials through the fluctuation of opening and closing of ion channels, as studied in (24).
To highlight the importance of stochastic fluctuations in our model, we highlight two observations. First, we find that bleb-driven cell migration is possible even when the underlying deterministic dynamical system is in the bistable regime. In the deterministic regime, the bleb never heals, but in the stochastic case the bleb will be stochastically driven to heal, thereby making migration possible. This implies that the cell can utilize a wider parameter range for bleb-driven motility. Second, the frequency of blebbing is a major contributor to speed, which is determined by the escape probability from basin of attraction of the steady state. This, again, is a feature that is clearly absent in the deterministic system.
We conclude this section with a study of the statistics of the blebbing events using a renewal process approximation. We derive a Langevin equation of cell migration by matching the asymptotic moments of the approximation process. We conclude our paper with a discussion of our results and future directions.
Methods
We model the cell as a 1D strip in a narrow channel. This is the situation that corresponds to the experiments of (10,11). We do, however, believe that our model captures essential features of blebbing more generally, especially as the cell moves in confined environments.
Consider a bounded interval in which the cell lies , where is the front membrane position and is the back membrane position. In the intracellular region between these two points, the unknowns are the fluid velocity u and hydrostatic pressure p, which we will assume to be spatially constant. Other unknown quantities are the adhesion density a, cortex thickness c, the cortical positions at the front and back , and the nucleus location . The adhesion and cortex densities (a and c), are defined at the front and back of the cell, denoted by , , , and . A schematic diagram for our model is given in Fig. 1 (bottom).
Assembly and turnover
We model the cortex thickness c, following (5), assuming simple first-order kinetics,
| (1) |
where ω governs cortex assembly, and assumes that a new cortex requires adhesion to a nearby membrane. The second term describes cortex turnover, with rate r. In this context, c is interpreted as a combination of density and spatial thickness, with arbitrary units.
The cortex is attached to the membrane via ERM proteins. We refer to the effect of these proteins as “adhesions.” We use the model of (5), employing similar first-order kinetics for the adhesion assembly and turnover, and three additional assumptions: 1) adhesion assembly saturates at high cortex thickness; 2) adhesion attachment requires proximity between cortex and membrane, with characteristic distance δ, that describes the “reach” of the adhesion molecules; and 3) adhesion detachment is force dependent, with characteristic breaking force . These considerations lead to
| (2) |
where and are the adhesion assembly and turnover rates, respectively, and is the cortex thickness at which adhesion assembly is half-maximal. The numerator follows from the assumption that adhesions collectively behave like springs with Hookean stiffness κ. Note that adhesion turnover is significantly faster than cortex turnover, leading to a separation of timescales.
Equations 1 and 2 are the same at the front and back of the cell, with the appropriate superscripts.
Mechanics
We assume that the pressure p inside the cell and the fluid velocity u are both constant in space. At the front membrane position , we have the following condition:
| (3) |
The above equation states that the difference in pressure across the membrane at the front is balanced by the adhesion and membrane forces. The exterior pressure is given by , where is a drag coefficient. The pressure is the pressure in the far field, which we take to be the same in the far front and far back of the cell. Since the pressure is defined only up to a constant, we may take without loss of generality. The drag coefficient represents the resistance of the exterior fluid to flow, and was used previously in (23). The adhesion force acts between the cortex and the membrane, modeled as a spring force whose spring constant is proportional to the adhesion density . The membrane force is modeled as a spring connecting the membrane and the nucleus position, with a natural length of l. Likewise, force balance at the back membrane is given by:
| (4) |
At the front and back membranes, we also impose the following conditions:
| (5) |
| (6) |
The fluid velocity u is spatially uniform (but varying in time), an immediate consequence of our assumption that the fluid in the narrow channel is a 1D incompressible fluid. The difference in the membrane velocity and the fluid velocity u is given by the transmembrane water flow. This transmembrane water flow in turn is proportional to the difference in pressure across the membrane interface, as given in Eqs. 3 and 4, where ζ is the water permeability coefficient.
At the cortex, we have the following force balance equations:
| (7) |
| (8) |
Here, we have assumed that the cortex experiences a drag force with respect to the underlying substrate, whose strength is proportional of the cortical density . This drag force is balanced by the adhesion forces between the cortex and membrane and the force between the nucleus and cortex. We attribute the latter to the force generated by the actin cytoskeletal network that permeates the cytosol, which is continuous with the actin cortex underlying the membrane. In our simple model, the actin network generates a force between the center, which we assume to be the nucleus, and the actin cortex residing close to the front and back of the cell. This force is assumed to be Hookean. We model this as a Hookean spring force whose spring constant is proportional to the cortical density , with the coefficient σ controlling the strength of actomyosin contractility. The position of the cell nucleus satisfies the following equation
| (9) |
where the nucleus is assumed to experience a drag force with respect to the substrate with drag coefficient . The spring force connecting the nucleus and the membrane positions are required for the model cell to maintain a stable fixed length at rest. The inclusion of the nucleus in the model is motivated by observations of the importance of nuclear mechanics for confined cell movement (26). From the point of view of model behavior, the presence of the nucleus allows for the front and back to be less tightly coupled. Nuclear positioning is controlled by cytoskeletal elements and the microtubules in particular (27), and we attribute the spring-like force between nucleus and membrane to these structures in a simplified manner. The incorporation of rest length is a reflection of the assumed rigidity of the microtubular network.
The above model satisfies the following power identity:
| (10) |
The above equality is a statement of power balance. The first line is an expression for the power exerted by the spring forces, and the second line represents viscous and frictional dissipation. The adhesion and cortical densities , , change in time according to Eqs. 1 and 2, but let us replace these values by constants , in the above expression (i.e., we consider a model in which the adhesion and cortical densities are constant). Then, we will have:
| (11) |
The above relation is a statement that the elastic energy of the system decreases in time, and shows that the cell should eventually come to a full stop. The above calculation shows that the dynamics of the adhesions and the cortex is crucial for the model exhibits nontrivial dynamics.
Physical parameters are summarized in Table 1
Table 1.
Model parameters
| Symbol | Dimensions | Meaning |
|---|---|---|
| Ω | (A.U.) μm2 s −1 | cortex assembly rate constant |
| R | s−1 | cortex turnover rate constant |
| μm−2 s−1 | adhesion assembly rate | |
| s−1 | adhesion turnover rate | |
| (A.U.) | cortex thickness at half-maximal adhesion | |
| Δ | Μm | adhesion length between cortex and membrane |
| Κ | pN μm−1 | adhesion spring constant |
| pN | adhesion breaking strength | |
| Pa | pressure far from the cell | |
| Pa μm−1 | hydrostatic pressure scale | |
| Pa s μm−1 | fluid drag constant | |
| Ζ | μm s−1 Pa−1 | water permeability constant |
| Σ | Pa (A.U)−1μm−1 | actin-myosin contractility |
| L | Μm | membrane rest length |
| Pa s μm−1 (A.U) −1 | cortex drag factor | |
| Pa s μm−1 | nucleus drag factor |
Nondimensionalization and parameter estimates
First, we can simplify the fluid equations as follows: subtracting Eq. 3 from Eq. 4, we get that
| (12) |
We nondimensionalize the system choosing characteristic cortex thickness , characteristic density of adhesions ( μm−2 s−1 (8)), characteristic time s (28), characteristic length μm (29), characteristic pressure ( Pa μm−1 (8)), and characteristic fluid velocity . This results in the nondimensional system:
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
with 10 nondimensional parameters defined in Table 2. Note that we use the same labels for all quantities for simplicity, but these are now nondimensional. Many of the parameters were already estimated in (5). For the remaining parameters, we obtain estimates based on matching the cell velocity with that reported in (30). In subsequent sections, we will vary and within a specified range to determine their impact on model behavior. The parameters and are set to a small positive value as shown in Table 2 unless indicated otherwise. Indeed, setting and to 0 does not lead to appreciably different results in our computations. We note that, if we set , Eq. 15 becomes a constraint that implicitly determines u as an algebraic constraint; an explicit equation for u can be obtained by taking the time derivative of (15) and plugging in (16, 17, 18, 19, 20) in the resulting equation. The behavior of the model with respect to larger values of and is briefly discussed at the end of the Results section.
Table 2.
Nondimensional parameters
| Symbol | Definition | Interpretation | Estimate | Source |
|---|---|---|---|---|
| cortex intensity | (5) | |||
| ϵ | ratio of cortex turnover and adhesion rates | 0.1 | (5) | |
| D | adhesion reach | (5) | ||
| F | adhesion bond strength | (5) | ||
| pressure relative to adhesion strength | (5) | |||
| M | myosin contractility relative to adhesion strength | (5) | ||
| fluid drag relative to adhesion strength | see text | |||
| ratio of cortex turnover rate and mechanical changes rate | see text | |||
| drag on cortex relative to adhesion strength | see text | |||
| drag on nucleus relative to adhesion strength | see text |
Stochastic model formulation
We now look at modifying the model system, (13), (14), (15), (16), (17), (18), (19), (20), to include stochastic effects in the adhesion density. Individual adhesion proteins have two possible conformations: open (when they tether the membrane and cortex together) and closed (when they do not). To formulate the stochastic model, we think of the adhesion dynamics as a birth-death process, with proteins changing conformation so that as the system evolves it may increase or decrease the number of proteins attached and hence the adhesion density. We let , where α is the per-protein adhesion density and k is the number of proteins, and we replace Eq. 14 with a Markov chain where the probabilities that a new protein will be attached or detached given by g and h respectively, where
| (21) |
| (22) |
To begin the simulation, we choose an initial, or “base,” number of adhesion proteins to be the number of adhesions at steady state and use that to determine α, which is then kept constant. The steady state is computed using the deterministic system. To observe the cell blebbing cycle, it is necessary for the initial condition to be chosen so that the system starts close to the deterministic steady state. The stochastic simulations are then run using a continuous-time Gillespie’s algorithm to update the number of adhesions attached as the system progresses:
-
1.Possible events:
-
•: adhesion forms ()
-
•: adhesion breaks ()
-
•
-
2.Rates:
-
•
-
•
-
•
-
3.
-
4.
Time until next event ,
| (23) |
At each , update the integral using the trapezium rule and check the equality. When it holds, go on.
-
5.
is selected with probability
| (24) |
to update .
-
6.
Update all other variables.
Results
Deterministic model
The model, (13), (14), (15), (16), (17), (18), (19), (20), combines the mechanisms of membrane-cortex interaction (force-sensitive adhesion, cortex contractility, cortex turnover) with force balance in the cell (fluid pressure, membrane, and cortex tension). Numerical simulations of the model reveal several classes of dynamics: stable nonblebbing states, stationary blebbing, and bleb-driven migration. Note that, throughout this section, parameters are the same on both sides of the cell. Without loss of generality, we focus on the effect of perturbations from steady state on the front side, which will then be the “leading edge” of the cell.
For a bleb to form, enough adhesions have to break so that the membrane and cortex will detach. In the blebbing parameter regime, a large enough perturbation to the steady state, by breaking the adhesions (lowering ), leads to a large excursion of the cortical density and results in cell movement. The system thus exhibits excitable behavior, as was documented in (5). A small perturbation, however, will not lead to bleb formation and subsequent movement. In the nonblebbing parameter regime, even if all adhesions are removed, the system returns to steady state without the membrane separating enough from the cortex for the cortex to depolymerize before adhesions reappear. This is a monostable regime, in which the system always returns to steady state after a perturbation of even large size.
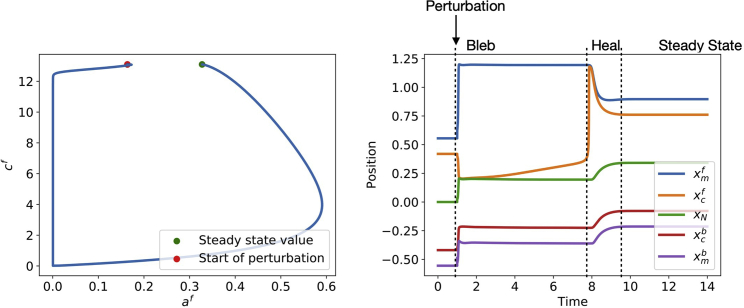
A sample simulation for the bleb-driven migration case is shown in Fig. 2, obtained by setting the system to steady state, and generating a perturbation at the front of the cell by removing 50% of the adhesions. When this perturbation is significant (enough adhesions are removed), as in the case shown in Fig. 2, the remaining adhesions are destroyed and the cortex depolymerizes. This leads to the membrane detaching from the cortex and protruding. This initial expansion is very rapid compared with the full life cycle of the bleb, in line with measurements in (8). The adhesions subsequently accumulate under the protruding membrane and the cortex is able to reattach and thicken. Cortex contraction then drives the bleb to heal, returning the system to equilibrium. It is important to note that, while a and c will return to the same initial steady state after the bleb heals, the positions of the membrane, cortex, and nucleus will have a new steady state. This is because these positions do not have a reference location (in contrast, for example, to (5)), but rather a reference distance between the various points (in other words, any parallel translation of a steady state will yield a steady state).
Figure 2.
Deterministic bleb-driven migration. Plots of a sample simulation with a perturbed initial condition (, where is the value of at steady state). (Left) versus trajectory. (Right) Membrane, cortex, and nucleus positions. Parameters used here are , , , , , , , , , and .
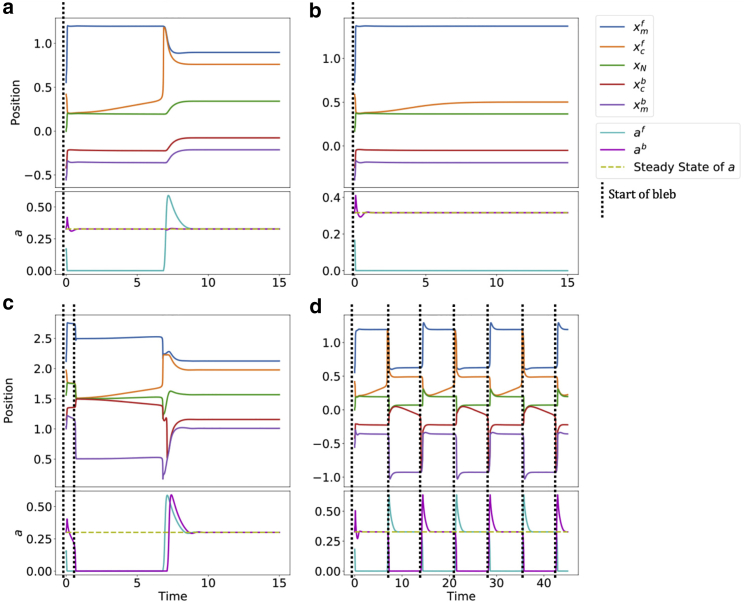
In the blebbing regime we observe four qualitatively different behaviors, as shown in Fig. 3: bleb formation and healing on the side of the perturbation (Fig. 3 a), a bleb forming but never healing (Fig. 3 b), a bleb on one side propagating to induce a bleb on the other side (Fig. 3 c), or an oscillation where blebs alternate from front to back (Fig. 3 d). These behaviors are summarized in Fig. 4.
Figure 3.
Various deterministic model behaviors. (a) Single bleb that heals shown in Fig. 2. (b) Bleb forms but never heals (). This is the bistable regime. (c) Front bleb drives a secondary bleb at the back (). (d) Oscillatory blebbing events alternating from front to back (). Sample paths are initiated at the perturbed . Other parameters are the same as in Fig. 2.
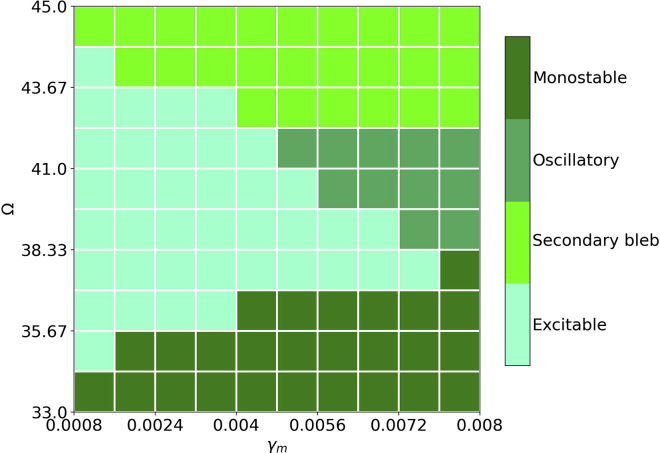
Figure 4.
Phase diagram of the deterministic model over the plane of the cortex intensity and the inverse of water permeability . Other parameters are the same as Fig. 2.
We can recover most model behaviors by varying the cortex assembly rate , and the inverse permeability of the cell membrane . The transitions between behaviors as these parameters are varied are shown in Fig. 4. We first observe that a sufficiently high value of is necessary for the system to be in the blebbing regime (be it excitable, osicllatory, or the secondary bleb regime). We may understand this as follows. When is small, the steady-state value of the cortex is small (see Eq. 13), thus making it easier for the system to go back to steady state after an initial perturbation. Given this quick recovery, there is not enough time for the cortex to detach from the membrane to form a bleb.
A sufficiently small value of (greater membrane water permeability) is needed for the cell to reside in the excitable regime. A larger value of pushes the cell into a monostable regime, an oscillatory regime, or a regime in which secondary blebs are seen. Larger values of implies that both tend to follow the same velocity u (see Eqs. 16 and 17). Another way to understand this is through incompressibility. If water permeability is low, then the length of the cell should stay roughly constant, which implies that the front and back of the cell must move at roughly the same velocity. For small values of , this has a stabilizing effect; a perturbation on the front side is stabilized by the back side which is not experiencing a perturbation. For larger values of wherein the system is in the blebbing regime, perturbation at the front will tend to lead to blebbing on the back side as well. We point out that this kind of oscillatory behavior has been previously observed for protrusions in fibroblasts which, like blebs, are devoid of actin (31).
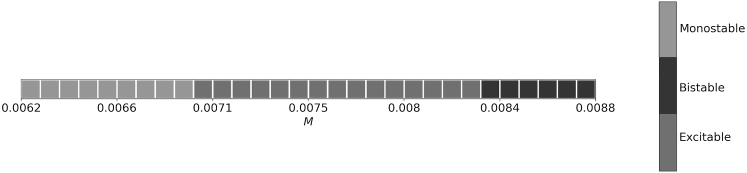
Myosin contractility, M, plays a major role in bleb formation and cell travel. As can be seen in Fig. 5 if M is too low, the system is nonblebbing, in line with experimental evidence (32). When M is above a critical value, the system reaches a blebbing state. There is a second critical value of M, above which the system is bistable; a bleb will form but will not heal. The adhesions do not reform under the membrane, and the system reaches a new steady state with one side of the membrane permanently detached as shown in Fig. 3 b.
Figure 5.
Phase diagram of the deterministic model as M is varied. Other parameters are the same as Fig. 2.
Similar behaviors can be observed by varying the cortical kinetic parameters D and F. We find that, if D or F are too small, the system becomes bistable, with a second steady state such that the bleb will not heal (see Fig. 3 b). This can be simply explained: if the reach of adhesion molecules is too small, adhesions between membrane and cortex cannot reform; similarly, if F is too small, bonds that do reform are weak and the bleb cannot heal. An increase in does not lead to larger blebs, although it does lead to greater displacement.
We next examine how the time course, size, and total displacement per bleb event varies with the parameters of the system by varying each parameter one by one while fixing the others. Based on this study, we make the predictions shown in Table 3. We find that, as adhesion reach D increases, healing accelerates—the membrane-cortex distance needed for reattachment is wider, allowing for faster recruitment of adhesions. Similarly, decreases in M lead to faster healing. Increases in lead to smaller bleb size, as the overall force pushing the membrane outward decreases.
Table 3.
Model predictions for experimental perturbations
| Perturbation | Parameter | Prediction |
|---|---|---|
| Decrease adhesion strength | Smaller blebs | |
| Increase myosin contractility | Slower bleb healing | |
| Increase molecular size of adhesion molecules | Faster healing |
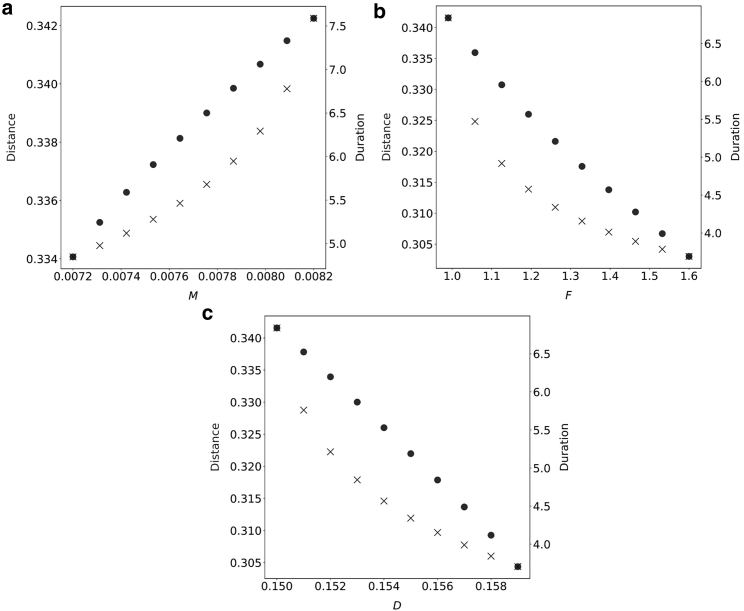
In Fig. 6 we plot the dependence of travel distance and duration on the parameters M, F, and D. Further parameter studies on travel distance can be found in the supporting material. As M increases in the excitable regime, both the travel distance and bleb duration increase. Stronger myosin contraction tends to pull the cortex away from the membrane and thus leads to a longer bleb duration. Although the bleb travel distance does increase, this change is about 10% and thus smaller in proportion than the change in duration. In this sense, we may say that an increase in M in fact decreases the velocity of the cell. The effect of D and F is similar in the sense that the change in duration is much larger proportionally than the change in total bleb travel distance. As D decreases, the total displacement of the cell increases, and bleb healing is slower. It is clear that, if the adhesion reach is very large, it is easy (and fast) for the adhesions to reform and the cortex to reattach compared with when the adhesion reach is small. However, if D becomes too small, the system reaches a stable nonblebbing state. Similarly, as F decreases, the total displacement of the cell increases, and bleb healing slows down.
Figure 6.
Traveling distance and duration for individual blebbing event with various parameters. Other parameters are the same as Fig. 2. Note that only parameters in the excitable regime are considered.
While variations on the drag in the cortex and nucleus ( and , respectively) do not affect the cell’s ability to form a bleb, and the system will remain in the blebbing or nonblebbing regime based on the other parameters, variations in drag can affect the distance traveled. If either drag parameter becomes too large, the net displacement of the cell becomes negligible, even if the bleb does form. Furthermore, changes in and can decouple the front and back of the cell, eliminating bleb propagation between the front and back.
Stochastic model
Here, we consider a stochastic model in which the adhesions are modeled as being discrete, as described in the Methods section.
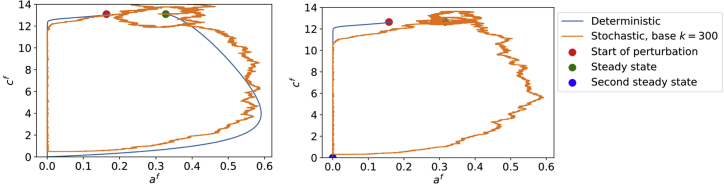
In contrast with the deterministic system, the stochastic system does not require an initial perturbation to generate a bleb, but can instead be set initially to the steady state of the deterministic system. Then, eventually, stochastic fluctuations make the adhesion density become low enough for the membrane and cortex to detach and the system to form a bleb. An example is shown in Fig. 7 (left) overlayed on a deterministic simulation for reference.
Figure 7.
Sample stochastic simulation, starting at steady state, with the deterministic case shown for reference. (Left) Parameters are the same as Fig. 2. (Right) .
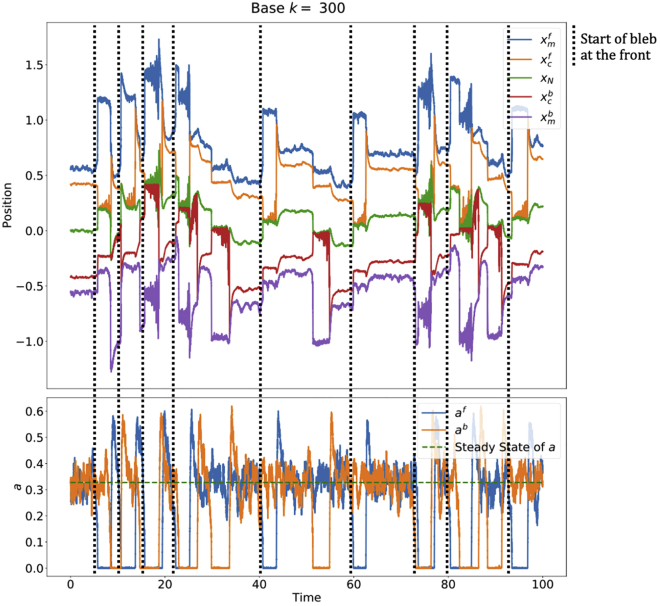
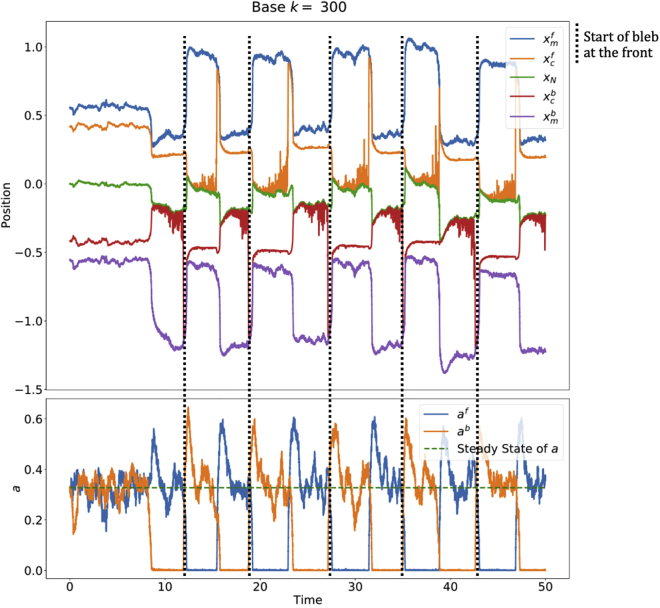
A full sample simulation is shown in Fig. 8. Since the system is symmetric between the front and the back, both sides are equally likely to form a bleb, so that, in the long run, the cell does not have an overall displacement ( for long simulation times).
Figure 8.
Stochastic simulation, starting at steady state. Parameters are the same as Fig. 2.
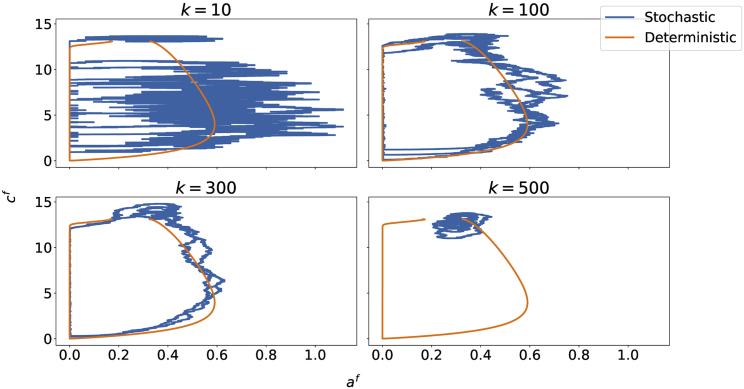
To start the stochastic simulation, we first set the system to steady state using the deterministic model to compute the starting values. As laid out in the Methods section, we then let , where α is constant and k is the number of attached proteins. The choice of initial k, is key to the frequency of bleb formation, as illustrated in Fig. 9: if the base value of k is too small, adhesions are removed too easily and the system becomes erratic; if the base value of k is too large, the adhesions never decrease enough for the membrane and cortex to detach and for a bleb to form. We choose a value of k in line with measurements of protein density at the membrane (33).
Figure 9.
Stochastic simulation compared with the deterministic case for various choices of initial number of attached proteins k (). Parameters are the same as Fig. 2.
Model behaviors
In this section, we discuss the differences in system behavior in the stochastic and deterministic regimes.
Recall that, in the deterministic regime, cell travel was accomplished in the excitable regime but not in the bistable regime. In the stochastic regime, bistability (Fig. 3 b) is not a deterrent for the cell to travel, as the system is able to escape also the basin of attraction of the second steady state, as seen in Fig. 7 (right). Then, even for parameter regimes which would be bistable in the deterministic case, we still get sustained blebbing in the stochastic case. This means, for example, that the values of M for which sustained travel is possible extends from the excitable into the bistable regime as shown in Fig. 5.
We find that the onset of oscillations, as shown in Fig. 3 d, shifts when we make the system stochastic. We showed in Fig. 4 that increases in make the system oscillatory. The onset of these oscillations requires a higher value of in the stochastic regime than in the deterministic regime. The reason for this is as follows: in the oscillatory regime, simulations suggest that a stable fixed point and a stable limit cycle coexist. The generation of this limit cycle should be traceable to a subcritical Hopf bifurcation, possibly through a canard explosion (34). When the value of is small, the stable limit cycle is too close to the stable steady state in the deterministic phase plane. A noisy periodic trajectory along the deterministic stable limit cycle will then fall into the basin of the stable steady state, thus aborting the oscillatory dynamics. As is increased, the distance between the stable limit cycle and steady state is increased, and the oscillatory dynamics can persist. A sample stochastic oscillatory simulation is shown in Fig. 10.
Figure 10.
Stochastic simulation in the oscillatory regime, starting at steady state. Here, , while other parameters are the same as Fig. 2.
Introducing bias
The system, as simulated in Fig. 8, is symmetric, so that the cell does not exhibit net displacements over a long time. Thus, in order to get a net movement, we bias the cell so that it is more likely to bleb at the front by making the front excitable and the back monostable in the corresponding deterministic system (the choice of front and back is arbitrary). Then, only the front side will retain the ability to bleb, and the cell will be able to sustain travel in that specific direction.
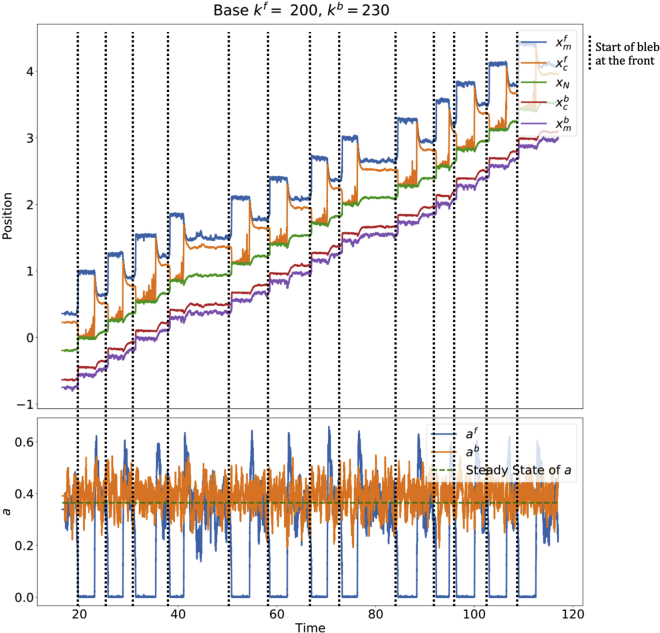
There are multiple theories regarding the polarization of a blebbing cell. One such theory suggests that there are fewer ERM proteins at the side where the bleb forms (3,9). In our model, this corresponds to having a different, smaller number of attached proteins at the front compared with the back (), under the assumption that the adhesion constant α is equal on both sides. To determine the regime (monostable or excitable/bistable) on each side we use the deterministic system and modify appropriate parameters so that the adhesion densities at the front and back of the cell at steady state are different (). It is then expected that the side with the smaller deterministic steady state value of a (and hence smaller initial k) will be more likely to produce a bleb. Indeed, in examples that we have checked, for steady states with smaller value of steady-state value of a, a smaller perturbation in a was sufficient for the solution to leave the steady state (for example, in Fig. 11, the size of perturbation necessary to generate a bleb is smaller at the front than at the back). In particular, we choose the parameters with the front in the excitable regime (blebbing) and the back in the monostable regime (nonblebbing) as determined in the deterministic setting. At the excitable side (front), noise allows the system to escape the basin of attraction of the steady state, while at the monostable side (back) the basin of attraction cannot be escaped. We emphasize that the biased deterministic simulations still require a manual perturbation for the system to initiate a bleb and travel.
Figure 11.
Biased stochastic simulation, starting at steady state. , . Other parameters are the same as Fig. 2. Note that the simulation is first run as deterministic to steady state.
To bias the cell, we change the values of some of the parameters so that they are different at the front and back of the cell (this effectively breaks the symmetry of the system). Since we found that M, F, and D control the overall distance traveled, we test these parameters to bias the cell by choosing , etc. A sample polarized simulation is shown in Fig. 11. Varying the parameters at the front and back to get different bias magnitudes showed that if is less than 4% bigger than the system does not yield a clear cell polarization.
Determinants of distance traveled
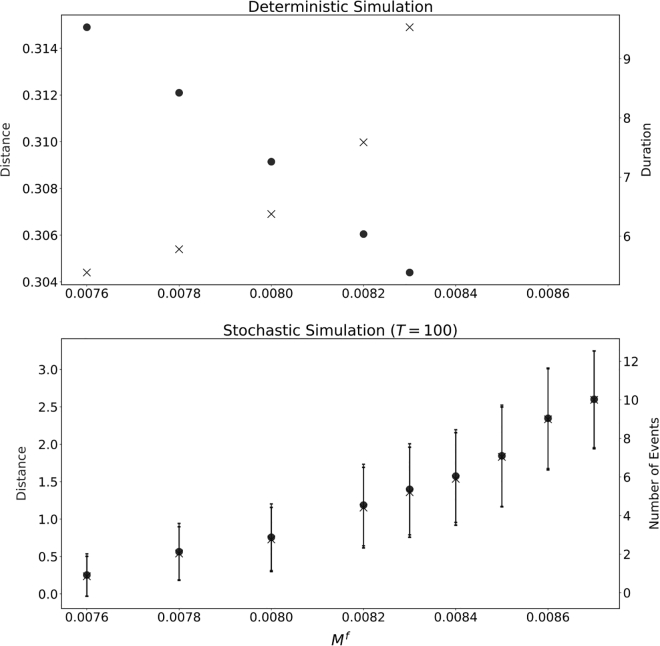
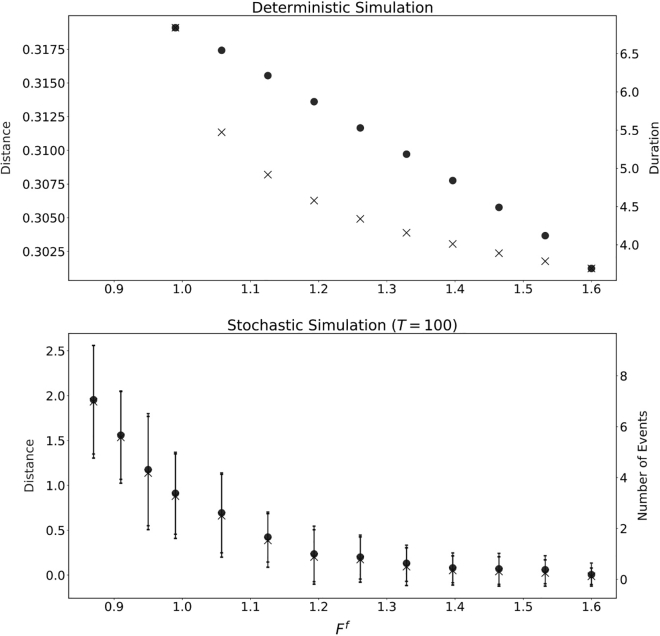
Let us now consider the biased system in the deterministic case, such that the front is excitable and the back is monostable. As discussed in the previous section, low values of M lead to a nonblebbing state, while increasing M takes the system first into the excitable (blebbing) regime and then into the bistable regime (see also Fig. 5). Simulations show that this trend holds for the front myosin strength as well. Within the excitable regime, as shown in Fig. 12 (top), leads to an increase in bleb duration much like the case studied in Fig. 6. The change in travel distance is minimal as is varied is minimal. Thus, the speed per blebbing event decreases with an increase .
Figure 12.
(Top) Distance traveled and event time for a single bleb in the deterministic case as varies. (Bottom) Average and standard deviation of total distance traveled for time and number of blebbing events for the stochastic case as varies with . The time step was set at and the initial number of adhesions was set to . Parameters are as in Fig. 2.
In the stochastic case, however, the overall speed of the cell increases with , as shown in Fig. 12 (bottom). We find that, even though individual events take longer, as seen in the deterministic simulations, the frequency of blebbing also increases in the stochastic simulations, so that the cell travels further. A larger value of leads to a smaller value of the steady-state value of the adhesion density , thus making the basin of attraction of the stable state smaller with respect to perturbations in .
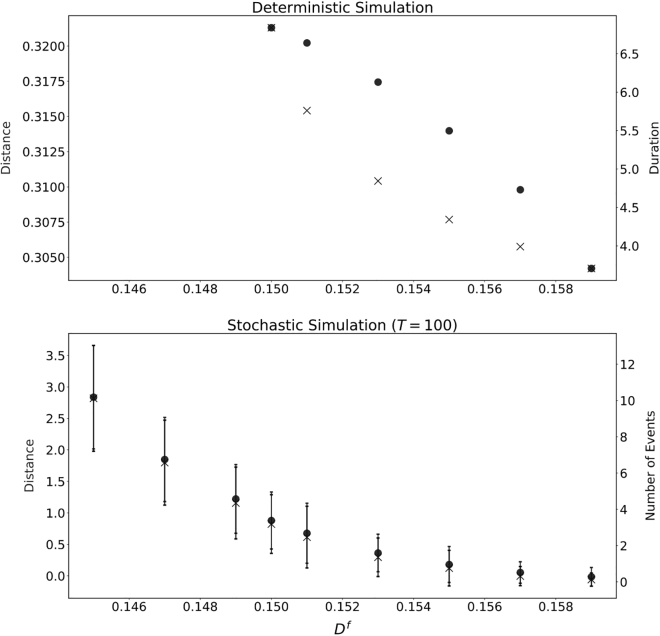
If we bias the cell by modifying F or D instead (, or ), decreases in or still lead to increases in the distance traveled in a single event (Figs. 6, 13, top, and 14, top). However, the increase in distance is much smaller in the biased case. For changes in F or D, the event duration does not change much between the biased and unbiased settings. Decreasing or any further would lead to the bistable regime. In the stochastic case, cell velocity increases as or decreases, as shown in Figs. 13 (bottom) and 14 (bottom).
Figure 13.
(Top) Distance traveled and event time for a single bleb in the deterministic case as varies. (Bottom) Average and standard deviation of total distance traveled for time and number of blebbing events for the stochastic case as varies with . The time step was set at and the initial number of adhesions was set to . Parameters are as in Fig. 2.
Figure 14.
Parameters are as in Fig. 2. (Top) Distance traveled and event time for a single bleb in the deterministic case as varies. (Bottom) Average and standard deviation of total distance traveled for time and number of blebbing events for the stochastic case as varies with . The time step was set at and the initial number of adhesions was set to .
Approximation of biased stochastic model
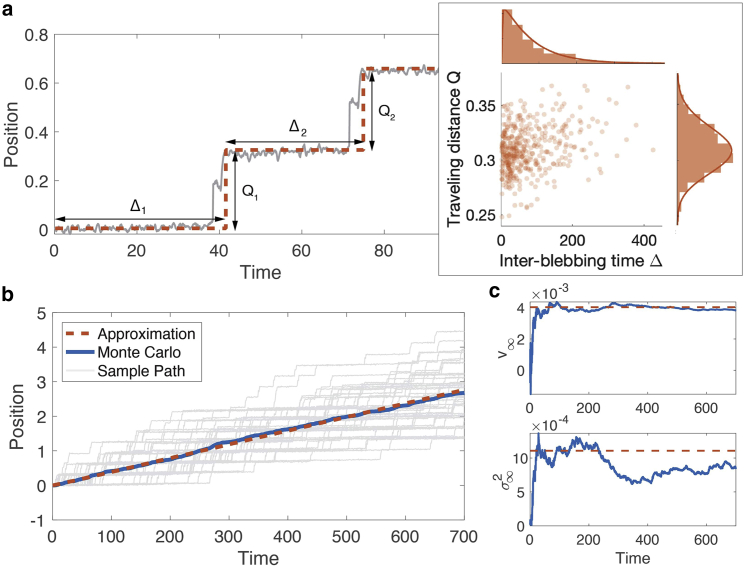
One important feature of the biased stochastic model is that the bleb expansion period takes place in a very short timescale compared with the overall span of bleb formation, as seen in Fig. 15 a. Such series of events can be approximated by a renewal process (35,36). A single bleb event consists of two random variables: the interblebbing time and the traveling distance Q. Let us label the bleb events by . We collect the statistics of from a total of sample paths whose initial condition is at the steady state of the deterministic model. Results show that the statistics of are approximately independent and identically distributed for all n. This is because each bleb event is generated by stochastically escaping the same deterministic basin of attraction, as shown in Fig. 7. Another observation is that and are almost uncorrelated:
Figure 15.
Approximation of the biased stochastic model. (a) Nucleus position is approximated by a renewal process with interblebbing time and traveling distance for . The statistics of the first bleb event and the following events (red dots) are independent and identically distributed. (b) Average nucleus position as a function of time. The first moment of the original process (blue curve) comes from averaging a total of 48 sample paths (gray curves). Corresponding curves for the approximation processes (red-dotted curve) are computed by numerically solving Eq. 5 in supporting material for . (c) Time-averaged speed (top) and variance (bottom) of the original process is compared with the asymptotic speed and variance of the approximation process by Eqs. 26 and 27. Parameters used here are and , and the others are the same as Fig. 2.
We thus assume that the two random variables are independent even for the same n. We approximate the discrete statistics of the random variables by continuous gamma distributions. That is, the distributions of the random variables take the form
where is the gamma distribution with shape and scale . Therefore, our assumptions imply that
for all . We estimate by the maximum likelihood estimation, as depicted in the subpanel of Fig. 15 a. Introducing the blebbing time
then the nucleus position is approximated by the renewal process
| (25) |
where is the Heaviside function giving one if otherwise zero. Note that the time-averaged speed and variance of the approximation process can be written in terms of the bleb statistics
| (26) |
and
| (27) |
as derived in the supporting materials. Therefore, the asymptotic behavior of the approximation process can be matched by the following stochastic differential equation
| (28) |
where is a Wiener process.
Numerical comparison in Fig. 15 b shows that the first moments of the original stochastic model and our approximation are in good agreement. In particular, the asymptotic slope for both processes converges to the value in Eq. 26 as .
Conclusion
The model presented here considers the bleb formation and healing cycle together with the mechanics of the system to produce bleb-driven cell migration in a reduced 1D model. We investigate the size of the blebs, the time from formation to healing, and the distance traveled in individual blebbing events. The stochastic model allows sustained cell travel by repeated blebbing.
We find that myosin contractility, and the molecular reach and strength of adhesions, determine the distance traveled by the cell with a single bleb (Fig. 6). Our model makes predictions about how the distance traveled changes with experimental perturbations, such as changes in myosin contractility that could be induced by changes in blebbistatin (32).
We also investigate the effect of varying biophysical parameters on bleb size and healing time. In this case, we find that changes in the molecular reach of adhesions, in the nondimensional parameter D, affect the time taken for the bleb to heal as in (5). In contrast with the results in (5), where increases in M abolish blebbing, increases in myosin contractility in our model lead to a case where the bleb forms, but never heals (see Fig. 3 b, Fig. 5). We also find that a sufficiently high water permeability is a crucial parameter for cell bleb-driven cell migration to be possible (Fig 4), a conclusion that is supported by recent experimental evidence (11).
In contrast to the deterministic model, the stochastic version of the model allows for sustained travel, wherein the intrinsic stochasticity accorded by the finiteness of the adhesion links leads to repeated blebbing events. Here, the front and back of the cells are in different parametric regimes so that the cell is given a bias. When the front end of the cell is excitable, a sufficiently strong stochastic perturbation is amplified to generate a bleb at the front. An increase in lengthens the duration of the bleb event with a small change in the total travel distance per bleb event, thus leading to a decrease in speed. In the stochastic case, however, the basin of attraction of the steady state becomes smaller, which leads to a greater frequency of blebbing events, making the cell travel faster. Interestingly, excitability in the narrow sense is not strictly necessary for persistent travel. Indeed, it is also possible for the stochastic model to generate sustained travel in the bistable case, as the system can produce enough noise to escape both basins of attraction in tandem (see Fig. 12). This increases the range of parameters over which the cell is able to sustain persistent travel.
We point out that what we observe is sustained travel under an externally applied bias. Our model, by itself, does not seem to be capable of polarization through symmetry breaking. The mathematical reason for this is that, after each bleb, the model returns to the steady state and thus forgets in which direction the cell had blebbed. Most models of cell polarization require intracellular signaling cascades (37) that our model does not consider. It would be interesting for future directions to combine cell polarization models with our cell blebbing model.
From a theoretical perspective, we studied a stochastic hybrid system that combines a deterministic system (cell migration dynamics) with a Markov chain on a discrete space (adhesion protein assembly and turnover). The stochasticity of the Markov process leads to spontaneous excitation (cell bleb event) in which the system escapes from the deterministic basin of attraction of the stable steady state. Such escape time problems have been studied in the context of cellular neuroscience by applying Kramer’s rate theory (38,39) and the large deviation theory (40,24,41). Instead of the analytic approximations, we directly obtain the escape time distribution by Monte Carlo simulation and focus on analyzing the resulting behavior driven by the series of excitation events.
Furthermore, we derive a simple effective stochastic differential equation of bleb-driven cell migration (Eq. 28) by approximating our stochastic model with a renewal process and calculating its asymptotic velocity and variance (Eqs. 26 and 27). These kinematic parameters are determined by the statistics of the bleb size and the interblebbing time, which can be obtained directly from experimental data. Thus, this gives us a method to compare the theoretical result generated from biophysical parameters with experimental data.
There are recent experiments of bleb-driven cell migration in 1D channels for which our model is directly applicable (10,11). Blebbing is confined to the front and back ends of the cell in this context, and this situation is well captured by our model. Insofar as blebbing is seen in this 1D situation, our model can be regarded as a simple theoretical model that captures some of the essential features of blebbing.
It is, however, clear that one of the greatest limitations of our model is that it is 1D. In our 1D model, the blebs only form at the front and the back. In the case of a 2D or 3D model, blebs can form along any position along the membrane, and the spatial extent of the bleb that forms will influence the dynamics. Papers (12, 13, 14, 15) have considered the cortical and membrane mechanical aspects of this issue and (16, 17, 18, 19) have focused on the intracellular and extracellular hydrodynamic aspects of this problem. It is hoped that the 2D or 3D situation can also be studied using a similar framework of an excitable dynamical system combined with a suitable mechanical model, coupled with random perturbations arising from molecular noise. Indeed, (5) performs simulation on a spatially extended version of the model, although their simulations are deterministic. Combining a spatially extended excitable model with stochasticity will result in a stochastic partial differential equation, which is generally difficult both from an analytical and computational points of view.
Author contributions
M.J.M.-L., H.K., and Y.M. designed the research, developed and analyzed the model, and wrote the article.
Declaration of interests
The authors declare no competing interests.
Acknowledgments
This work was supported by the Simons Foundation (Math + X grant) to H.K. and Y.M., and by NSF DMS-2042144 awarded to Y.M.
Editor: Mark Alber.
Footnotes
Additional studies on the effect of parameters on total bleb displacement and the derivation of the asymptotic approximation process can be found in the supporting material. It can be found online at https://doi.org/10.1016/j.bpj.2022.04.016.
Supporting material
References
- 1.Paluch E.K., Raz E. The role and regulation of blebs in cell migration. Curr. Opin. Cell Biol. 2013;25:582–590. doi: 10.1016/j.ceb.2013.05.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Charras G.T., Paluch E., Paluch E.K. Blebs lead the way: how to migrate without lamellipodia. Nat. Rev. Mol. Cell Biol. 2008;9:730–736. doi: 10.1038/nrm2453. [DOI] [PubMed] [Google Scholar]
- 3.Zatulovskiy E., Tyson R., et al. Kay R.R. Bleb-driven chemotaxis of Dictyostelium cells. J. Cell Biol. 2014;204:1027–1044. doi: 10.1083/jcb.201306147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Fackler O.T., Grosse R. Cell motility through plasma membrane blebbing. J. Cell Biol. 2008;181:879–884. doi: 10.1083/jcb.200802081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Manakova K., Yan H., et al. Allard J. Cell surface mechanochemistry and the determinants of bleb formation, healing, and travel velocity. Biophysical J. 2016;110:1636–1647. doi: 10.1016/j.bpj.2016.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Charras G.T., Hu C.-K., et al. Mitchison T.J. Reassembly of contractile actin cortex in cell blebs. J. Cell Biol. 2006;175:477–490. doi: 10.1083/jcb.200602085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Schaks M., Giannone G., Rottner K. Actin dynamics in cell migration. Essays Biochem. 2019;63:483–495. doi: 10.1042/ebc20190015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Charras G.T., Coughlin M., et al. Mahadevan L. Life and times of a cellular bleb. Biophysical J. 2008;94:1836–1853. doi: 10.1529/biophysj.107.113605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ruprecht V., Wieser S., et al. Heisenberg C.-P. Cortical contractility triggers a stochastic switch to fast amoeboid cell motility. Cell. 2015;160:673–685. doi: 10.1016/j.cell.2015.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Holle A.W., Govindan Kutty Devi N., et al. Spatz J.P. Cancer cells invade confined microchannels via a self-directed mesenchymal-to-amoeboid transition. Nano Lett. 2019;19:2280–2290. doi: 10.1021/acs.nanolett.8b04720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zhao R., Cui S., et al. Konstantopoulos K. Hydraulic resistance induces cell phenotypic transition in confinement. Sci. Adv. 2021;7:eabg4934. doi: 10.1126/sciadv.abg4934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Woolley T.E., Gaffney E.A., et al. Goriely A. Cellular blebs: pressure-driven, axisymmetric, membrane protrusions. Biomech. Model. Mechan. 2014;13:463–476. doi: 10.1007/s10237-013-0509-9. [DOI] [PubMed] [Google Scholar]
- 13.Woolley T.E., Gaffney E.A., et al. Goriely A. Three mechanical models for blebbing and multi-blebbing. IMA J. Appl. Math. 2014;79:636–660. doi: 10.1093/imamat/hxu028. [DOI] [Google Scholar]
- 14.Woolley T.E., Gaffney E.A., et al. Goriely A. Global contraction or local growth, bleb shape depends on more than just cell structure. J. Theor. Biol. 2015;380:83–97. doi: 10.1016/j.jtbi.2015.04.023. http://www.sciencedirect.com/science/article/pii/S002251931500199X [DOI] [PubMed] [Google Scholar]
- 15.Woolley T.E., Gaffney E.A., Goriely A. Membrane shrinkage and cortex remodelling are predicted to work in harmony to retract blebs. Roy. Soc. Open Sci. 2015;2:150184. doi: 10.1098/rsos.150184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Strychalski W., Guy R.D. A computational model of bleb formation. Math. Med. Biol. 2013;30:115–130. doi: 10.1093/imammb/dqr030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Strychalski W., Guy R.D. Intracellular pressure dynamics in blebbing cells. Biophysical J. 2016;110:1168–1179. doi: 10.1016/j.bpj.2016.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wang Q., Hu J., Othmer H. Natural Locomotion in Fluids and on Surfaces. Springer; 2012. Models of low reynolds number swimmers inspired by cell blebbing; pp. 185–195. [Google Scholar]
- 19.Wang Q., Othmer H.G. Analysis of a model microswimmer with applications to blebbing cells and mini-robots. J. Math. Biol. 2018;76:1699–1763. doi: 10.1007/s00285-018-1225-y. [DOI] [PubMed] [Google Scholar]
- 20.Purcell E.M. Life at low Reynolds number. Am. J. Phys. 1977;45:3–11. doi: 10.1119/1.10903. [DOI] [Google Scholar]
- 21.Woolley T.E., Gaffney E.A., Goriely A. Random blebbing motion: a simple model linking cell structural properties to migration characteristics. Phys. Rev. E. 2017;96:012409. doi: 10.1103/physreve.96.012409. [DOI] [PubMed] [Google Scholar]
- 22.Tozluoğlu M., Tournier A.L., et al. Sahai E. Matrix geometry determines optimal cancer cell migration strategy and modulates response to interventions. Nat. Cell. Biol. 2013;15:751–762. doi: 10.1038/ncb2775. [DOI] [PubMed] [Google Scholar]
- 23.Li Y., Yao L., et al. Sun S.X. On the energy efficiency of cell migration in diverse physical environments. PNAS. 2019;116:23894–23900. doi: 10.1073/pnas.1907625116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Newby J.M., Bressloff P.C., Keener J.P. Breakdown of fast-slow analysis in an excitable system with channel noise. Phys. Rev. Lett. 2013;111:128101. doi: 10.1103/physrevlett.111.128101. [DOI] [PubMed] [Google Scholar]
- 25.Bressloff P.C. Vol. 41. Springer; 2014. Stochastic Processes in Cell Biology; pp. 608–614. [Google Scholar]
- 26.Xia Y., Pfeifer C.R., Discher D.E. Nuclear mechanics during and after constricted migration. Acta Mechanica Sinica. 2019;35:299–308. doi: 10.1007/s10409-018-00836-9. [DOI] [Google Scholar]
- 27.Gundersen G.G., Worman H., Worman H.J. Nuclear positioning. Cell. 2013;152:1376–1389. doi: 10.1016/j.cell.2013.02.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Fritzsche M., Thorogate R., Charras G. Quantitative analysis of Ezrin turnover dynamics in the actin cortex. Biophysical J. 2014;106:343–353. doi: 10.1016/j.bpj.2013.11.4499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tasnim H., Fricke G.M., et al. Moses M.E. Quantitative Measurement of naïve T cell association with Dendritic cells, Frcs, and Blood Vesselsin lymph nodes. Front. Immunol. 2018;9:1–13. doi: 10.3389/fimmu.2018.01571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Robertson T.F., Chengappa P., et al. Burkhardt J.K. Lymphocyte egress signal sphingosine-1-phosphate promotes ERM-guided, bleb-based migration. J. Cell Biol. 2021;220:777–780. doi: 10.1083/jcb.202007182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Paluch E., Piel M., et al. Sykes C. Cortical actomyosin breakage triggers shape oscillations in cells and cell fragments. Biophysical J. 2005;89:724–733. doi: 10.1529/biophysj.105.060590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tinevez J.-Y., Schulze U., et al. Paluch E. Role of cortical tension in bleb growth. PNAS. 2009;106:18581–18586. doi: 10.1073/pnas.0903353106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Smith E.M., Hennen J., et al. Mueller J.D. In situ quantification of protein binding to the plasma membrane. Biophysical J. 2015;108:2648–2657. doi: 10.1016/j.bpj.2015.04.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Desroches M., Guckenheimer J., et al. Wechselberger M. Mixed-mode oscillations with multiple time scales. Siam Rev. 2012;54:211–288. doi: 10.1137/100791233. [DOI] [Google Scholar]
- 35.Doob J.L. Renewal theory from the point of view of the theory of probability. Trans. Am. Math. Soc. 1948;63:422–438. doi: 10.1090/s0002-9947-1948-0025098-8. [DOI] [Google Scholar]
- 36.Bressloff P.C., Kim H. Search-and-capture model of cytoneme-mediated morphogen gradient formation. Phys. Rev. E. 2019;99:052401. doi: 10.1103/physreve.99.052401. [DOI] [PubMed] [Google Scholar]
- 37.Rappel W.-J., Edelstein-Keshet L. Mechanisms of cell polarization. Curr. Opin. Syst. Biol. 2017;3:43–53. doi: 10.1016/j.coisb.2017.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Keener J.P., Newby J.M. Perturbation analysis of spontaneous action potential initiation by stochastic ion channels. Phys. Rev. E. 2011;84:011918. doi: 10.1103/physreve.84.011918. [DOI] [PubMed] [Google Scholar]
- 39.Khovanov I., Polovinkin A.V., Polovinkin A., Luchinsky D.G., Luchinsky D., McClintock P.V.E., McClintock P. Noise-induced escape in an excitable system. Phys. Rev. E. 2013;87:032116. doi: 10.1103/physreve.87.032116. [DOI] [Google Scholar]
- 40.Schuss Z. Vol. 170. Springer Science & Business Media; 2009. pp. 339–398. (Theory and Applications of Stochastic Processes: An Analytical Approach). [Google Scholar]
- 41.Freidlin M.I., Wentzell A.D. Springer; 1998. Random Perturbations of Dynamical Systems; p. 189. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.