Abstract
Photonic neural networks perform brain-inspired computations using photons instead of electrons to achieve substantially improved computing performance. However, existing architectures can only handle data with regular structures but fail to generalize to graph-structured data beyond Euclidean space. Here, we propose the diffractive graph neural network (DGNN), an all-optical graph representation learning architecture based on the diffractive photonic computing units (DPUs) and on-chip optical devices to address this limitation. Specifically, the graph node attributes are encoded into strip optical waveguides, transformed by DPUs, and aggregated by optical couplers to extract their feature representations. DGNN captures complex dependencies among node neighborhoods during the light-speed optical message passing over graph structures. We demonstrate the applications of DGNN for node and graph-level classification tasks with benchmark databases and achieve superior performance. Our work opens up a new direction for designing application-specific integrated photonic circuits for high-efficiency processing large-scale graph data structures using deep learning.
The diffractive photonic processor is used to construct graph neural networks for processing graph-structured data optically.
INTRODUCTION
Deep learning technologies (1) have achieved enormous advances in a wide range of artificial intelligence (AI) applications, including computer vision (2), speech recognition (3), natural language processing (4), autonomous vehicles (5), biomedical science (6), etc. The core is to leverage multilayer neural networks to learn hierarchical and complicated abstracts from big data, driven by the continuous development of integrated electronic computing platforms, such as central processing units (7), graphics processing units (GPUs) (8), tensor processing units (9), and field-programmable gate arrays (10). However, the electronic computing performance is approaching its physical limit and faces large difficulties to keep pace with the increase in demand of AI development, which is a common plight in a broad range of applications requiring large-scale deep neural models. In recent years, there has been growing research of interest in photonic computing to use photons as the computing medium to construct photonic neural networks using its advanced properties of high parallelism, minimal power consumption, and light-speed signal processing.
Numerous photonic neural network architectures have been proposed to facilitate complex neuro-inspired computations (11, 12), such as diffractive neural networks (13–19), optical interference neural networks (20, 21), photonic spiking neural networks (22, 23), and photonic reservoir computing (24, 25). Existing architectures have been most successful in processing data with regular structures in the form of vectors or grid-like images. Nevertheless, various scientific fields analyze data beyond such underlying Euclidean domain. As typical representatives, graph-structured data, which encode rich relationships (i.e., edges) between entities (i.e., nodes) within complex systems, are ubiquitous in the real world, ranging from chemical molecules (26) to brain networks (27). To process the graph-structured data, graph neural networks (GNNs) (28–32) have been developed as a broad new class of approaches that are able to integrate local node features and graph topology for representation learning. Among these models, message passing–based GNNs have major advantages of flexibility and efficiency by generating neural messages at graph nodes and passing along edges to their neighbors for feature updates. It has been successfully applied in many graph-based applications, including molecule property prediction (26), drug discovery (33), skeleton-based human action recognition (34), spatiotemporal forecasting (35), etc. However, how to effectively take advantage of photonic computing to benefit graph-based deep learning still remains largely unexplored.
Here, we propose the diffractive GNN (DGNN), a novel photonic GNN architecture that can perform optical message passing over graph-structured data. DGNN is built upon the foundation of integrated diffractive photonic computing units (DPUs) for generating the optical node features. Each DPU comprises the successive diffractive layers implemented with metalines (36, 37) to transform the node attributes into optical neural messages, where the strip optical waveguides are deployed to encode the input node attributes and output the transformed results. The optical neural messages sent from node neighborhoods are aggregated using optical couplers. In DGNN architecture (Fig. 1), the DPUs can be cascaded horizontally to enlarge the receptive field to capture complex dependencies from the arbitrary size of neighboring nodes. Besides, the DPUs can also be stacked vertically to extract higher-dimensional optical node features for increasing its learning capacity, inspired by the multihead strategy used in numerous modern deep learning models, e.g., transformer (38) and graph attention networks (30). On the basis of this scalable optical message passing scheme, we first demonstrate the semisupervised node classification task, where the DGNN-extracted optical node features are fed into an optical or electronic output classifier to determine the node category. The results show that our optical DGNN achieves competitive and even superior classification performance with respect to the electronic GNNs on both synthetic graph models and three real-world graph benchmark datasets, i.e., two citation networks and one Amazon copurchase graph. Furthermore, DGNN also supports graph-level classification, where the additional DPUs are used to aggregate all-optical node features into a graph-level representation for classification. The results on skeleton-based human action recognition demonstrate the effectiveness of our architecture for the task of graph classification.
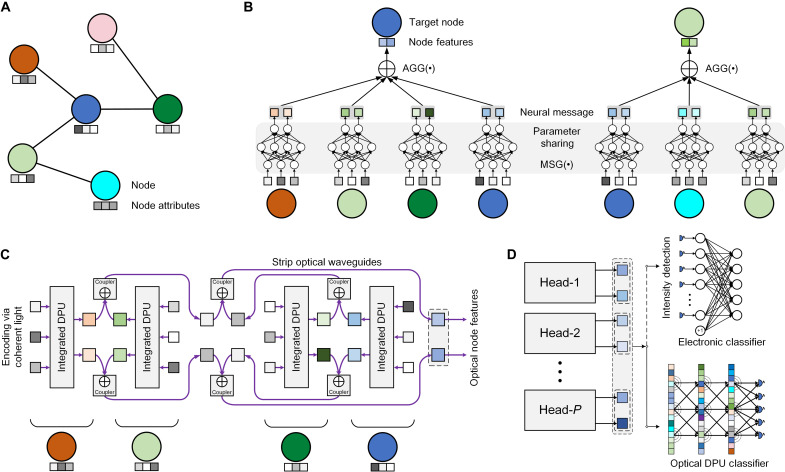
Fig. 1. The architecture of optical DGNN.
(A) An exemplar graph with six nodes and five edges. Each node has 3D attributes. (B) The schematic illustration of a single round message passing of the GNN for target graph nodes, including the feature transformation and aggregation. (C) An all-optical architecture illustration for graph representation learning, where node features are encoded into amplitude or phase of the light in optical waveguides and transformed by the integrated DPUs. The transformed optical node features are aggregated using the optical couplers. The architecture is scalable for large graphs with a large number of nodes. (D) A multihead strategy is adopted to extract high-dimensional optical node features, based on which the node and graph classification tasks are performed using either electronic or optical DPU classifier, resulting in the DGNN-E or DGNN-O architecture. Each head is a structure similar to (C) that produces 2D optical features.
RESULTS
General GNN design principle
A graph structure of N nodes is represented as a tuple G = (V, ℰ, A), where is the node set with i denoting the node indices, ℰ ⊆ V × V is the edge set, and A∈ℝN×N is the adjacency matrix encoding the connection between graph nodes. Figure 1A shows a toy example of a graph with six nodes, where each node vi ∈ V is attached with a three-dimensional (3D) attribute xi. One prominent and powerful approach in most existing GNNs to learn effective node representations is the message passing scheme (28–31), as depicted in Fig. 1B. Each node aggregates neural messages sent from local neighborhoods during each iteration l (l = 1, …, L) of the message passing procedure
| (1) |
| (2) |
where is the neural message of jth node, N(i) is the neighboring node indices of node vi, is the updated features of node vi after l iterations of message passing, is the initial node attributes, MSG(l)( · ) is a neural network shared across graph nodes to perform the feature transformation and generate neural messages, and AGG(l)( · ) is a function that aggregates messages sent from local neighborhoods. To generate the graph-level representation hG, a read-out function Read − out( · ) can be applied to aggregate all node features into a vector after L rounds of message passing
| (3) |
With the extracted node/graph-level features, we can perform node/graph-level classification task by feeding the features to the output classifier and jointly learn model parameters via the end-to-end error backpropagation training method. In the following, we elaborate the design of DGNN to implement these critical operations using on-chip optical devices and modules.
DGNN architecture for optical message passing
The DGNN architecture is illustrated in Fig. 1 (C and D), which comprises all-optical devices and modules to implement the MSG( · ), AGG( · ), and Read − out( · ) functions in Eqs. 1 to 3. Specifically, the input node attributes are encoded by modulating the amplitude or phase of the coherent light, which can be realized via on-chip optical modulators, e.g., Mach-Zehnder interferometers (MZIs) (20). The input optical field of each node attribute passes through a single-mode waveguide with transverse-electric polarization and is coupled into the integrated DPU module. The DPU module achieves the MSG( · ) function using successive layers of 1D metalines as the diffractive layers to modulate the input optical field (see Materials and Methods and figs. S1 to S4). The metaline is a 1D etched rectangle silica slot array in the silicon membrane of silicon-on-insulator (SOI) substrate that forms as diffractive meta-atoms. The modulation coefficients of a diffractive meta-atom in metaline are determined by the height and width of the slot (see fig. S1). The neural message of each node is generated by coupling the output optical field of DPU with the single-mode or tapered output waveguides (see Materials and Methods and figs. S5 to S7), where the number of optical waveguides m determines the message dimensionality. We set m = 2 to avoid the waveguide crossing during the aggregation of neural information from neighboring nodes in this work, which can be scaled to arbitrary size in principle for further increasing the learning capability (see fig. S8).
The AGG( · ) function is realized by the optical Y-coupler (see Fig. 1C), where the feature aggregation of 2D optical neural messages over two nodes would not cause the waveguide crossing. Thus, the architecture can aggregate information from arbitrary size of neighborhood by stacking the building block of DPU horizontally. The only waveguide crossing happens during the injection of light from the coherent source to DPU modules (see fig. S9), which can be well-addressed by the existing waveguide crossing technology to minimize the signal cross-talk and energy loss (39). To further enhance the expressive power of 2D node features, P independent heads can be vertically stacked in parallel as shown in Fig. 1D to produce 2P-dimensional optical features for graph nodes following the multihead strategy. Besides, the procedure of a single round optical message passing for feature updating can be further stacked to perform multiple rounds of message passing.
To enable graph-level learning, the read-out function Read − out( · ) can be realized by applying additional DPUs to aggregate all multihead optical node features into the optical graph features. First, each head of a graph node in Fig. 1D for producing optical node features is cascaded with a read-out DPU with two input waveguides and two output waveguides. Then, we aggregate the updated 2P-dimensional optical node features of all nodes over each independent head using the optical Y-coupler to perform a two-by-two optical aggregation, which obtains the 2P-dimensional optical graph features. By feeding the extracted node/graph-level features into the output optical or electronic classifier, corresponding to the DGNN-O or DGNN-E, respectively, the node/graph classification tasks are performed. The modulation coefficients of all diffractive meta-atoms are jointly optimized via the end-to-end error backpropagation training method.
Node classification using semisupervised learning
We apply the DGNN for semisupervised node classification, which is one of the major AI tasks that GNNs have achieved notable success so far. Given the graph where each node is attached with vector-based attributes and a subset of graph node labels, the node classification task is to infer the labels for the remaining nodes. To scale-up GNNs for tackling large graph datasets, we adopt the PPRGo (31) model to directly capture the high-order neighborhood information with a single AGG( · ) process (see Materials and Methods). This avoids the exponential neighborhood expansion problem during the multiple rounds of message passing and eliminates the nonlinear transition function. For each target node vi, we use the DPU to implement MSG(xi) and then aggregate optical features of nodes with the top-k largest scores according to its personalized PageRank vector. After the training process of DGNN with the DPU settings detailed in Materials and Methods, the optical modulation coefficients are optimized, and the slot width of diffractive meta-atoms in the metalines are determined. We validate the superior classification performance of the DGNN on both the synthetic graph data and three real-world large-scale graph datasets, i.e., Cora-ML (40), Citeseer (41), and Amazon Photo (42), using both photonic finite-difference time-domain (FDTD) and analytical model evaluation.
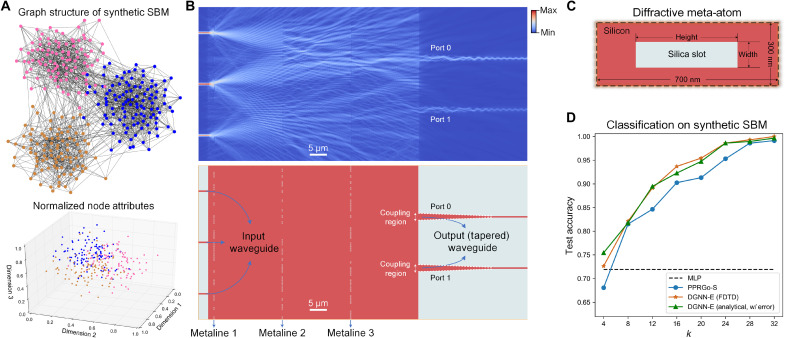
The synthetic graph in Fig. 2A is generated using the stochastic block model (SBM) (43) to simplify the task and reduce the computational complexity for FDTD evaluation (see Materials and Methods). In this example, the DGNN is trained by configuring a single head, i.e., P = 1, that generates a 2D neural message for each target node from a 3D node attribute. The layout of the DPU module is shown in Fig. 2B(bottom), which includes the corresponding input and output tapered or single-mode waveguides and three layers of metalines. Each metaline has 150 diffractive meta-atoms, with each meta-atom size of 300 nm (see Fig. 2C). We set the binary modulation for meta-atoms with every three consecutive elements to be the same, i.e., the same silica slot width and height, to consider the fabrication capability of existing silicon photonics foundry (see Materials and Methods) and reduce the modulation error of the analytical model with respect to FDTD (see fig. S2). The comparisons of output optical neural message of DPU module between the analytical model and FDTD are evaluated in figs. S3 and S4. Figure 2B(top) shows the optical field propagation of the DPU module using FDTD evaluation for an exemplar node, where the amplitude of input light source mode in three input waveguides represents the node attributes, i.e., the 0.7674, 0.8795, and 0.6225, from top to down, respectively.
Fig. 2. Semisupervised node classification on a synthetic graph.
(A) Top: The synthetic SBM graph with 300 nodes, where different colors denote different communities, i.e., categories. Bottom: The 3D node attributes of different communities are generated from different multivariate Gaussian distributions and normalized to [0,1]. (B) Top: The electric field of the DPU evaluated with FDTD that performs the MSG( · ) function on a target node of the synthetic SBM. Bottom: The corresponding DPU module is implemented in the silicon membrane of the SOI chip. The beginning core widths of tapered and single-mode output waveguides are set to be 2 μm and 500 nm, respectively. (C) The geometric diagram of the diffractive meta-atom that is formed by etching the rectangle silica slot in the silicon membrane of SOI substrate. (D) Classification accuracy of DGNN-E under different top-k nodes for feature aggregation with comparisons to MLP and PPRGo electronic models.
We use the DGNN-E for node classification of the synthetic graph that feeds the intensity detection of the calculated optical node features to an electronic fully connected layer, where the numbers of input nodes and output neurons are equivalent to the feature dimension and category number, respectively. We further update each node’s representation by aggregating features with different k values to retrain the output electronic classifier for validating the effectiveness of the optical node representation. The classification results of DGNN-E with single-mode and tapered output waveguide under different k values are shown in Fig. 2D and fig. S5, respectively. With the optimization of taper angle (see Materials and Methods), each tapered output waveguide couples larger regions, i.e., 2 μm, of the output optical field for improving the DPU power transmission rate without decreasing the classification performance. Besides, Fig. 2D shows that the DGNN-E evaluated with FDTD achieves comparable performances with respect to the analytical model with system errors included (see Materials and Methods), and both are competitive or superior to the electronic PPRGo-S GNNs and multilayer perceptrons (MLPs) under the same number of learnable parameters. Performing computations with complex-valued optical fields, i.e., photons carrying both amplitude and phase information, extends an orthogonal dimension for each operation and can introduce advanced properties to our architecture. Numerous researches (44–47) have verified that the complex-valued neural networks enable the capabilities of faster learning (45), richer feature representation (45, 46), and better generalization characteristics (47) than the real-valued counterpart networks. It has also been demonstrated that complex-valued photonic neural networks can achieve higher learning capability and model performance (21, 48). In DGNN, the DPU modules extract the complex-valued optical node representations to facilitate the node classification task.
On real-world benchmark graph databases, we construct the DGNN architecture by setting the top-k node number for feature aggregation to 8 and the head number to 4, i.e., k = 8, P = 4. Thus, each node generates 8D optical features in total, two dimensions for each head, from the preprocessed node attributes (see Materials and Methods and table S1). For the DGNN-E with electronic output classifier, the intensity of optical features detected with photodetectors is fed into an electronic fully connected layer, similar to the process on the synthetic graph. For the DGNN-O with optical output classifier, the eight output waveguides of optical features are directly coupled with a classifier DPU module composed of six diffractive layers with other settings the same as the DPU modules for generating optical neural messages. The classification results are detected by the photodetectors, each corresponding to one category, where the category of input is determined by finding the target photodetector with the maximum detected optical signal (13).
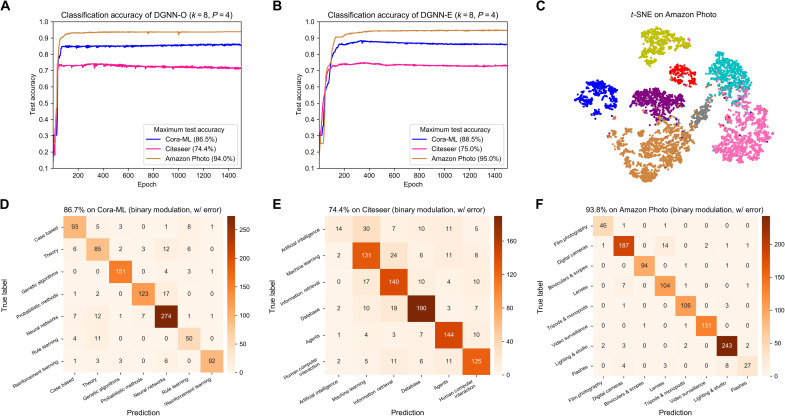
We report in Table 1 the analytical test accuracies of semisupervised node classification, i.e., the transductive learning, of DGNN on three benchmark graphs and compare them to electronic computing approaches of linear principal components analysis (PCA), nonlinear MLPs, and nonlinear PPRGo GNNs, including PPRGo-S and PPRGo-WS (see Materials and Methods). Both the MLP and feature transformation of PPRGo are configured using fully connected neural networks with two hidden layers and settings to have the same number of learnable parameters. The test accuracy convergence plots of DGNN-O and DGNN-E are shown in Fig. 3 (A and B, respectively). Besides, we also evaluate the DGNN-E using binary diffractive modulations with system errors by including the different amounts of Gaussian noise in fig. S10. Although the convergences fluctuate because of the rounding operation, the retraining scheme can be adopted to achieve stability and obtain even higher accuracy by fixing the learned modulation coefficient and retraining the output classifier. The confusion matrices of test results using binary diffractive modulation with a system error, implemented by including the standard deviation (SD) of 0.3 of Gaussian noise, on three benchmark databases are shown in Fig. 3 (D to F), which achieves test accuracies of 86.7, 74.4, and 93.8% on Cora-ML, Citeseer, and Amazon Photo, respectively. Overall, the results in Table 1 reveal the following facts: (i) Models that exploit the graph structure substantially outperform models that ignore the graph structure; (ii) the all-optical inference of DGNN-O achieves competitive performance with the PPRGo-S; (iii) DGNN-E achieves 1.3% higher classification accuracy than PPRGo-S on the Cora-ML database, showing that the optical modules of DGNN for implementing MSG( · ) and AGG( · ) are even more effective than the electronic message passing; and (iv) as the feature aggregation is essentially a low-pass filter (49) that can suppress the noise to a certain extent, the binary diffractive modulation with system error included also achieves competitive performance on all the graph benchmarks, demonstrating the robustness of architecture to system noise.
Table 1. Semisupervised node classification results on three benchmark graphs.
The classification accuracy (%) of DGNN architecture are obtained by setting k = 8 and P = 4.
| Dataset | Cora-ML | Citeseer | Amazon Photo |
| PCA | 79.4 | 70.9 | 90.6 |
| MLP | 81.5 | 71.3 | 93.1 |
| PPRGo-S | 87.2 | 74.3 | 95.0 |
| PPRGo-WS | 88.2 | 75.9 | 95.1 |
| DGNN-O | 86.5 | 74.4 | 94.0 |
| DGNN-E | 88.5 | 75.0 | 95.0 |
| DGNN-E (binary modulation, with error) |
86.7 | 74.4 | 93.8 |
Fig. 3. Semisupervised node classification on three benchmark graph databases.
(A) Test accuracy convergence plots of DGNN-O with optical DPU output classifier. (B) Test accuracy convergence plots of DGNN-E with electronic output classifier. (C) t-distributed stochastic neighbor embedding (t-SNE) visualization of node representations of DGNN-E on the Amazon Photo dataset. (D to F) Confusion matrices of DGNN-E classification result on three graphs with binary modulation and system errors by including Gaussian noise with an SD of 0.3.
Furthermore, we conduct ablation studies of DGNN-E architecture on the neighborhood size k for feature aggregation and the number of heads P for the output classifier (fig. S11). Note that k = 1 refers to the architecture without message passing, which degenerates to the plain diffractive neural network (13). By increasing k from 1 to 8, the test accuracy on Cora-ML monotonically increases and gains over 9% compared with the diffractive neural network (fig. S11A), demonstrating the functionality of feature aggregation for node classification. Besides, the multihead scheme substantially improves the test accuracy by generating a higher dimension of optical features (fig. S11B). We also demonstrate that input node attributes can be flexibly encoded into the amplitude or phase of input optical fields with comparable model performance (fig. S11C). In addition, the importance of diffractive modulation for performing the feature transformation is shown in fig. S11 (D and E). We further evaluate the classification performance of DGNN-E with respect to the individual geometric parameters of DPUs on the Cora-ML graph database, including the number of diffractive layers, the distance between successive diffractive layers, and the number of meta-atoms per diffractive layer (see fig. S12). The results demonstrate the robustness of DGNN-E with respect to the geometric parameters of DPUs within a large range, which indicates that the computing region size of DPU modules has the potential to be further optimized for improving the integration density. To visualize the generated optical feature representations for all graph nodes, we apply the t-distributed stochastic neighbor embedding (t-SNE) (50) on the detected intensity values of optical node features for DGNN-E with k = 8 and P = 4. As illustrated in Fig. 3C and fig. S13, the t-SNE plots show that the node features exhibit discernible clustering across different classes in the projected 2D space, verifying the effectiveness of the optical implementations of MSG( · ) and AGG( · ) functions in DGNN architecture. In addition to semisupervised transductive learning, we also evaluate the inductive reasoning aptitude of DGNN (see Materials and Methods). The inductive node classification results on the three benchmarks are shown in fig. S14 and table S2, where DGNN still outperforms or achieves competitive performance with the electronic counterpart.
Graph classification for skeleton-based human action recognition
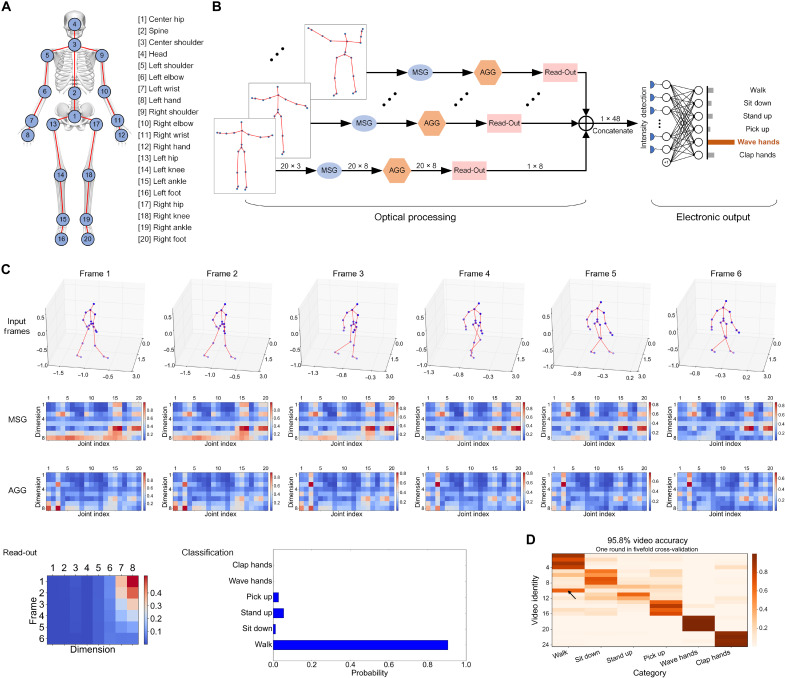
We validate the performance of DGNN on graph-level classification by applying it for the task of skeleton-based human action recognition. The skeleton data are sequences of frames with each frame containing a set of 3D joint coordinates of the target recorded by sensors, with which the task is to predict the category of action in each sequence. In this work, we adopt the UTKinect-Action3D database (51) for evaluation, which contains the RGB, depth, and skeleton videos of 10 participants performing each action two times that are captured by a single stationary Kinect V1 at a frame rate of 30 frames/s. Here, we select 6 of 10 types of actions from the skeleton-based data, including walk, sit down, stand up, pick up, wave hands, and clap hands. The graph structure of a skeleton is shown in Fig. 4A, which contains the (x, y, and z) locations of 20 joints at each frame.
Fig. 4. Graph classification of the DGNN on the task of action recognition.
(A) Graph structure of skeleton data captured by Kinect V1. (B) The schematic of DGNN architecture for skeleton-based human action recognition. (C) Visualizing results of a selected subsequence from the test set for performing the action category of the walk. The normalized amplitude of each frame processed after optical MSG( · ), AGG( · ), the L2-normalized intensity values after optical Read − Out( · ), and the classification result are shown. (D) The inference results of all the test subsequences in one round of fivefold cross-validation. The arrow indicated slot is the only misclassified video of the database.
The workflow of DGNN architecture is illustrated in Fig. 4B. We implement the MSG( · ) and AGG( · ) functions using four heads that generate an 8D optical node feature for each joint, where the neural messages at each joint are aggregated from their direct neighbors. At each skeleton frame, the head is cascaded with a DPU to perform Read − out( · ) that aggregates all node features into an 8D optical graph feature. Similar to the previous work (16), we divide each sequence with a length of M into numbers of subsequences with the same length of n (n ≪ M). Then, n graph-level representations are concatenated to be fed into the output classifier for action recognition of the subsequence. We set n = 6 in this study, resulting 48D optical features for each subsequence, which are fed into an electronic fully connected neural network layer to determine the subsequence category. The video category is obtained by applying the winner-takes-all strategy (16, 25) on all video subsequences. To ensure the credibility of the evaluation, we perform fivefold cross-validation on the 20 participants with six actions, i.e., 120 videos and 2512 subsequences, and report the average subsequence accuracy and video accuracy.
Our DGNN architecture achieves test subsequence accuracy of 83.3% and video accuracy of 90.0%, verifying the effectiveness of the proposed method on graph-level learning. We visualize the results of subsequence action recognition for the categories of the walk and wave hands, as shown in Fig. 4C and fig. S15, respectively. It is obvious that the optical MSG( · ), AGG( · ), and Read − Out( · ) functions learn substantially different patterns for these two categories of actions. Specifically, taking the feature maps obtained by MSG( · ) as a close look, the DGNN learns the largest intensity values for the joint of index 16 and 20, corresponding to the left foot and right foot, respectively, for the action category of walking, but the joint of index 8, corresponding to the left hand, for the action category of waving hands. This can be interpreted as the critical of the joints for recognizing these two actions, which is consistent with the human consciousness. In Fig. 4D, the categorical voting matrix of one round in fivefold cross-validation, corresponding to 95.8% video accuracy, is provided to visualize the classification results on all the test subsequences. The percentage of votes for the six actions in each test video is calculated, and the videos are reordered so that the diagonal blocks of the matrix represent the correct classification. The test result shows that only one video, indicated by the arrow, is misclassified.
DISCUSSION
Scarce training labels
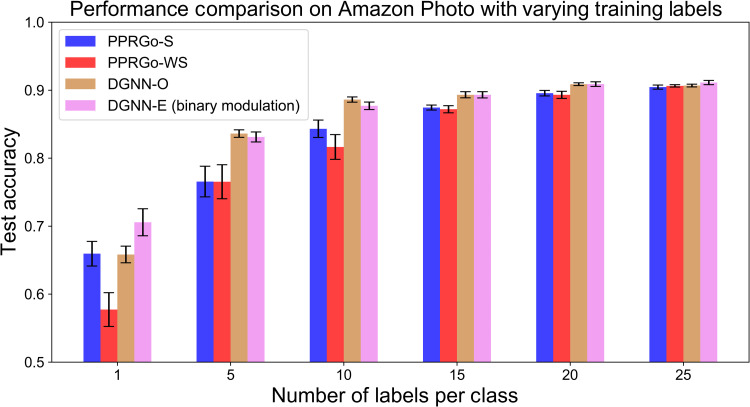
We analyze the effectiveness of DGNN under the limited size of training labels, which is a common case in semisupervised learning. With the same architecture settings, we compare the performance of DGNN with respect to the baselines of electronic models under different sizes of training labels, including 1, 5, 10, 15, 20, and 25 labels per class. We plot the bar graph of test accuracy with error bars by performing 10 times evaluations for each size of training label in Fig. 5. The mean values of the results are shown in table S3, where binarizing the diffractive modulation layer facilitates overcoming the local minimum problem during the network training and improves the classification accuracy. The DGNN architecture outperforms all baselines for all label-scarce settings, especially at the small training-set size, e.g., only one label per class, which demonstrates the higher generalization ability with respect to other electronic computing approaches.
Fig. 5. Classification on Amazon Photo with scarce training labels.
Performance of architecture under different training-set sizes is evaluated. The DGNN architecture consistently outperforms the electronic PPRGo GNN model, which demonstrates its superior robustness and generalization ability.
DPU with tapered output waveguides
Tapered waveguides are used to couple larger regions of output optical fields to the output ports of integrated DPU. The improved coupling efficiency of the tapered output waveguide enables the photodetectors to receive more optical power and increases the signal-to-noise ratio (SNR) during the photoelectric conversion. Higher SNR provides a higher quality of input signals to the classifier and ensures the stability of the classification tasks. The quantitative evaluations of the output energy distribution and model performance of tapered and single-mode waveguides are shown in fig. S6. we use the FDTD to evaluate the power distribution of optical features on the test nodes of synthetic SBM graph with the trained DGNN-E models. The beginning core widths of tapered output waveguides are optimized and set to be 2 μm (see Materials and Methods and fig. S7) instead of 500 nm used in the single-mode output waveguides. For each test graph node, the power transmission rate of DPU is obtained by calculating the proportion of the output power of two ports with respect to the input light source power, with which the frequency histogram of transmission rate on all graph nodes are obtained (see fig. S6, A and B). The average power transmission rate of DPU with tapered output waveguide is 2.01%, which is ~5.6 times higher than the single-mode output waveguide of 0.36%.
With the estimated power transmission rate of DPU, we evaluated the photocurrent SNR of the on-chip photodetector, formula detailed in Materials and Methods, under different input light source powers (see fig. S6C). We further evaluated the test accuracy of the DGNN-E model with respect to the SNR, under the top-k neighboring node setting of 16, by including the photodetector noise to the node features and retraining the electronic classifier (fig. S6D). Increasing the input light source power and the power transmission rate of DPU improves the photocurrent SNR and achieves more stable model performance on the synthetic SBM graph. In this work, the PPRGo model with a single round of message passing is adopted to directly capture the high-order neighborhood information. The computing energy efficiency of DGNN is calculated on the basis of the input light source power of 10 mW, which achieves the sufficient photocurrent SNR of 34.6 and 20.2 dB with the tapered and single-mode output waveguides, corresponding to the model test accuracy of ~94.4 and ~92.3%, respectively.
Computing precision of DPU
The quantization bits, determining the computing precision of DPU, can be inferred from the photocurrent SNR. In digital signal processing, the quantization error is introduced during the quantization of analog-to-digital converter. Assuming that the signal has a uniform distribution covering all quantization levels, the signal–to–quantization noise ratio can be formulated as SQNR = 20log10(2Q) = 6.02Q dB, where Q represents the number of quantization bits. Therefore, the photocurrent SNR of 34.6 dB using tapered output waveguides with 10 mW of input light source power corresponds to ~6 quantization bits.
Computing density and energy efficiency
It is worth noting that once the DGNN architecture design is optimized and fabricated physically, the on-chip optical devices for the computation of node and graph representations as well as the optical output classifier during the inference are all passive. Such the inference process for graph-based AI tasks is processed at the speed of light, limited only by the input data modulation and output detection rates, and consumes little energy compared with electronic GNNs. To be specific, assuming that the DGNN transforms n-dimensional attributes into the m-dimensional optical neural messages for each node with MSG( · ), aggregates optical features of k nodes with AGG( · ), and stacks P heads for a C-class classification task. Therefore, the MSG( · ) module of each node contains an n × m weight matrix for each node, the AGG( · ) module in each head contains the sum of k nodes of m-dimensional vectors, and the classifier contains an mP × C weight matrix. Therefore, each inference cycle of DGNN contains (2nmk + mk)P operations (OPs) for feature extractions and 2mPC operations for the classification, i.e., having the total operations of (2nk + k + 2C)mP. Considering a 30-GHz data modulation and photodetection rate based on the existing silicon photonic foundry (52), the computing speed of DGNN is (6nk + 3k + 6C)mP × 1010 OPs/s. Assuming the typical light source power of 10 mW, the energy efficiency of DGNN is (6nk + 3k + 6C)mP × 1012 OPs/J. For the node classification settings with n = 20, m = 2, k = 8, P = 4, C = 8, the computing speed is 82.6 TOP/s (Tera-Operations/s) and energy efficiency is 8.26 POP/s (Peta-Operations/s) per watt. For the DPU module in Fig. 2 with a computing region size of 61.5 μm by 45 μm, performing the MSG( · ) function with a 3× 2 weight matrix, the computing density is 130 TOP/s per square millimeter. The corresponding implementation of the same 3×2 weight matrix using the on-chip MZI photonic devices would require the computing region size of 300 μm by 200 μm that is ~21.7 times larger, assuming each MZI with a size of 100 μm by 100 μm (21). Notice that the energy efficiency and computing density of the state-of-the-art GPU Tesla V100 are 100 GOP/s per watt and 37 GOP/s (Giga-Operations/s) per square millimeter, respectively (53). DGNN architecture achieves more than four orders of magnitude improvements on energy efficiency and more than three orders of magnitude improvements on computing speed.
Scalability of architecture
The proposed DGNN architecture performs AGG( · ) only once to directly consider high-order node features, which avoids the exponential neighborhood expansion issue in extracting long-range neighborhood information and facilitates the scalability for learning larger graphs. In principle, the head number of architectures can be scaled to arbitrary size, and the basic DPU modules, e.g., in Fig. 1C, can be horizontally stacked and interconnected with Y-couplers and strip waveguides to aggregate optical neural messages from the arbitrary size of neighborhoods. Moreover, the architecture has the flexibility to extend with multiple rounds of optical message passing by further stacking DPU modules. The DPU module can be scaled up by increasing the numbers of metaline layers and meta-atoms at each layer, and the input and output numbers of the DPU can be scaled up with additional optical modulators and waveguide crossings, e.g., in fig. S8. The working wavelength of our architecture can be extended from a single wavelength to multiple wavelengths for further enhancing the computing throughput. The accumulation of system error can be alleviated by retraining the output classifier, e.g., in fig. S10. Besides, the in situ training approach (16) can also be applied to address the system errors and improve the training efficiency by developing the on-chip DPU modules with programmable modulation coefficients, e.g., using a 1D indium tin oxide for modulation (54).
Limitations and future works
In this study, the optical feature aggregation in DGNN is realized using the 2 by 1 optical Y-coupler with a combining ratio of 50 : 50, which does not support the assigning of different weights for different neighboring nodes, i.e., the weighted sum. Although the average feature aggregation has already achieved remarkable performance in both node- and graph-level classification tasks, message passing with weighted sum could further boost the model capacity and can be implemented using the on-chip amplitude modulator, e.g., phase changing materials (22). Another limitation is that the proposed DGNN architecture uses a linear model for optical message passing. Although existing works have demonstrated the possibility of implementing the optical nonlinear activation functions (55, 56), the nonlinear operation is not critical in GNNs as studied in the previous work (49). This can be proved by the remarkable model performance that DGNN has already achieved in the real-world benchmark datasets. For example, DGNN almost achieves the state-of-the-art performance on Amazon Photo under large scarce training labels and significantly outperforms the electronic GNNs under the scarce label settings. Therefore, including nonlinear activation function in DGNN is left for future work as the potential to further enhance the model learning capability.
In summary, we take the first step to present the optical deep learning architecture, i.e., DGNN, that can perform the all-optical graph representation learning over the graph-structured data for the high-accurate node- and graph-level classification tasks. The architecture is designed using the integrated DPU for extracting optical neural messages of graph nodes and on-chip optical devices for passing and aggregating the messages. We verify the functionalities of DGNN with both the analytical and FDTD evaluations. The results demonstrate the comparable and even superior classification performance than the electronic GNN and achieve orders of magnitude improvement on computing performance than the electronic computing platform. We expect that our work will inspire the future development of advanced optical deep learning architectures with integrated photonic circuits beyond the Euclidean domain for high-efficient graph representation learning.
MATERIALS AND METHODS
PPRGo GNN model
PPRGo (31) implements the MSG( · ) with a neural network to transform node attributes and performs a single round AGG( · ) for each target node to directly aggregate information from the top-k neighboring nodes ordered by the nodes’ personalized PageRank score. The personalized PageRank matrix is analytically defined as: , where α ∈ (0,1] is the teleport probability of personalized PageRank, is the symmetric normalized adjacency matrix with added self-loops, A denotes the adjacency matrix, D denotes the degree matrix, and I denotes the identity matrix. The ith row of Π, denoted by Πi, is the personalized PageRank scores of all the graph nodes with respect to node vi. PPRGo performs the AGG( · ) for node vi by only summing the features of nodes that are the top-k largest entries in Πi, where the aggregated node features are fed to the output classifier to predict the label of node vi. Note that the calculation of Πi is a procedure of data preprocessing, which only needs to be calculated once and can be implemented with fast algorithms (31). We applied two variants of PPRGo, i.e., the PPRGo-S and PPRGo-WS (see Table 1). PPRGo-S uses the aggregator that directly sums up the neighboring features. In contrast, PPRGo-WS uses the aggregator that performs the weighted sum of neighboring features according to the personalized PageRank scores.
Generating the synthetic graphs
The SBM (43) is a widely used generative graph model in network analysis. We evaluated the effectiveness of our all-optical graph representation learning by generating the synthetic SBM graph with 300 nodes to reduce the computational complexity and the requirement of computing resources during the architecture evaluation using FDTD. Specifically, the 300 nodes were assigned to three communities (categories), and node attributes of each community were generated from the corresponding 3D multivariate Gaussian distribution. The simplest SBM has two parameters p and q, corresponding to intraclass link probability and interclass link probability, respectively, with the graph generation rule as follows
| (4) |
where yi and yj denote the category of nodes vi and vj, respectively, with aij as the indicator variable for the edge connection of two graph nodes. In this work, we set p = 0.1 and q = 0.005. We randomly selected five labeled nodes per category for training, and the left 285 nodes were used for the test. The generated graph is illustrated in Fig. 2A.
Preprocessing of benchmark graphs for node classification
Cora-ML and Citeseer are the document cocitation networks in which each node represents a document and edges are citations between them. Amazon Photo is a segment of the Amazon copurchase graph (42), where nodes represent goods and edges denote that the two goods are frequently bought together. All three graphs have node attributes encoded by bag-of-words. Following previous works for node classification on benchmark graphs (57), we randomly selected 1000 nodes as the test set for each benchmark dataset with the remaining nodes for training. To reduce the number of input strip waveguides for the DPU, we adopted the PCA to preprocess the node attributes and reduce their dimensions. We set the dimension of the node attribute to be 20, and the values were scaled to be compatible with the optical system, i.e., encoding the node attributes into either the amplitude (rescale to [0,1]) or phase (rescale to [0,2π)) of coherent optical waves. The overview of dataset statistics is summarized in table S1.
DPU settings
The integrated DPU uses the successive layers of diffractive metalines to modulate the optical wavefront. Each metaline comprises diffractive meta-atoms, i.e., the array of rectangle silica slots etched in the silicon membrane of SOI substrate, as shown in fig. S1A. The height and width of a slot determine the phase and amplitude modulation coefficients of a diffractive meta-atom. We adopted the Rayleigh-Sommerfeld diffraction for analytical modeling the optical wave propagation and modulation (13), and the FDTD evaluations were performed via Lumerical FDTD software (Lumerical Inc.). The working wavelength of our architecture was set to be 1550 nm. To facilitate the training of DPU and improve the modulation accuracy, we used the subwavelength height for the silica slot and fixed it to be 400 nm, with which the silica slot width was optimized within [0, 100] nm under the fixed slot period of 300 nm, corresponding to the optimizing of the phase modulation range of [0, 1.55] rad (see figs. S1, B and C). Moreover, considering the fabrication capability of existing silicon photonics foundry and to reduce the modeling deviation, we also adopted the binary modulation that the width of the slot was quantized to take value from {0,100} nm and set the slot width of every three consecutive meta-atoms to be the same. The input and output planes were divided into regular intervals with the numbers equivalent to the numbers of input and output waveguides, where each waveguide was placed at the central position of each interval.
In the task of node classification, we set the DPU module to have three and four layers of metalines with a layer distance of 20 and 100 μm, respectively, to perform the feature transformation for the synthetic and benchmark databases, respectively; each metaline comprised 150 and 600 meta-atoms, respectively, corresponding to the metaline length of 45 and 180 μm, respectively. The input and output planes were coupled with 3 input waveguides and 2 output waveguides, respectively, for the synthetic database and 20 input waveguides and 2 or 8 output waveguides, respectively, for the benchmark database. Besides, for the benchmark database, the output classifier DPU module of DGNN-O architecture was set to have six layers of metalines with other settings the same as the feature transformation DPU module. In the task of skeleton-based human action recognition, the feature transformation DPU module was set to have six layers of metalines and three input optical waveguides for encoding 3D joint coordinates with other settings the same as the node classification on real-world graphs. Similarly, the read-out function of each head was implemented with the DPU module with five layers of metalines.
Training details of DGNN
All DGNN models were numerically implemented and trained on the basis of Python (v3.6.8) and TensorFlow (v1.12.0, Google), and the PCA was implemented using Scikit-learn (v 0.23.2). The diffractive wave propagation was analytically modeled with the Rayleigh-Sommerfeld diffraction model implemented using the angular spectrum method (13). The modulation coefficients of diffractive layers were optimized during the training, where the phase modulation coefficient of each diffractive meta-atom was correlated with amplitude modulation coefficients and determined by the slot width (see fig. S1C). We adopted the Adam optimizer (58) to perform the gradient descent and error backpropagation. The loss function of DGNN-E was the softmax cross-entropy between the electronic output and the one-hot ground-truth labels, while the loss function of DGNN-O was the mean squared error between the detected intensity values on the output plane and the target, i.e., 1 for the position of the target detection region and 0 for the others regions. The learning rate was set to 0.1, 0.01, and 0.005 for the node classification with DGNN-O, node classification with DGNN-E, and skeleton-based human action recognition, respectively. The retraining procedure used a learning rate of 0.1. We used the full-batch training fashion in the node classification, while the batch size was set to 32 in the task of skeleton-based action recognition. Besides, for training DGNN-E with binary modulation, the modulation coefficient of each meta-atom was computed with an extra rounding operation.
Optimizing the taper angle of output waveguides
The taper angle of output waveguides was optimized on the basis of the evaluation of both classification accuracy of DGNN-E and power transmission rate of DPU (see fig. S7). We search the optimal taper angle by fixing the length of tapered output waveguides to 20 μm and varying the input width of tapered waveguides from 1 to 8 μm with a step size of 1 μm, corresponding to the taper angle from ~0.7° to ~10.6°. Notice that 500-nm input width corresponds to the single-mode waveguide with a taper angle of 0°. For each input width setting, the DGNN-E is retrained and tested on the synthetic SBM graph to evaluate the model classification accuracy (see fig. S7A). To obtain the averaged power transmission rates of DPU (see fig. S7B), we set the input light source power of 10 mW and calculate the proportion of the output power of two ports with respect to the input power for each test graph node using FDTD, with which the frequency histogram of power transmission rate on all graph nodes is obtained (see fig. S7C). With the difference of DPU structure and coupling efficiency of tapered output waveguides under different taper angles, the results demonstrate that the optimal input width of tapered output waveguides is 2 μm, corresponding to the taper angle of ~2.1°, which achieves the model test accuracy of 93.7% and power transmission rate of 2.01%.
Photocurrent SNR
The photocurrent SNR of the on-chip photodetector can be formulated as (59)
| (5) |
where represents the mean square, i.e., the power, of signal photocurrent Is; , , and represent the power of the typical photodetector noise sources, including thermal noise, shot noise, and dark current readout noise, respectively. Given the bandwidth (B) of the photodetector receiver, which is negatively correlated to the response time, the noise sources can be formulated as
| (6) |
where represents the power spectral density of thermal noise, which is independent of the light frequency, with the Boltzmann’s constant k, the absolute temperature T, and the load resistance R; represents the power spectral density of shot noise with the electron charge q and the signal photocurrent Is; represents the power spectral density of dark current readout noise, modeled as the white noise, with the electron charge q and the dark current Id. Given the input source power P and the averaged power transmission rate β of DPU without considering the insertion loss of waveguide circuits, the averaged photocurrents of signals can be represented as: Is = β × Responsivity × P. By substituting Eq. 6 to Eq. 5, we have
| (7) |
During the calculation, we set the typical room temperature T = 293 K and the standard load resistance R = 50 ohms. According to the process design kits of Chongqing United Microelectronics Center silicon photonics foundry (52), the device parameters of on-chip Germanium photodetector are as follows: Responsivity = 0.9 A/W, Id = 50 nA, B = 30 GHz, under the working wavelength of 1550 nm.
Training details of electronic models
Similarly, all implementations of electronic models were based on Python (v3.6.8), TensorFlow (v1.12.0, Google), and Scikit-learn (v 0.23.2). The PCA classification results were obtained using a linear classifier to the preprocessed node attributes. The MLPs were configured using two hidden layers with the Rectified Linear Unit (ReLU) or tanh nonlinear activation function. The size of the second hidden layer was set to be 8, and the size of the first hidden layer was adjusted to make the model have the same number of learnable parameters as DGNN-E. The electronic PPRGo GNNs used the MLP for implementing the feature transformation. All the electronic models used the softmax cross-entropy between predictions and targets as the loss function. The learnable parameters were optimized using an Adam optimizer with a learning rate of 0.01 and a training epoch of 10000.
Transductive learning and inductive learning
In the task of semisupervised node classification, which is also termed transductive learning, all the nodes and the graph structure are available. While in supervised learning, i.e., inductive learning, all the test node are unavailable. For the inductive learning in this work, all 1000 test nodes, including their features and graph structures, are unseen during the training. In other words, we delete all test nodes with their associated edges to obtain the training set. During the test, we recover the original graph to perform the inference.
Analytical modeling of DPU with system errors
To reduce the modulation deviations between the analytical model and FDTD due to the uncontinuous change of parameters between adjacent meta-atoms, every three consecutive meta-atoms in the metalines was restricted to be the same (see fig. S2). Other error sources that cause the model deviations include the mutual coupling between adjacent meta-atoms, the reflection between metalines, and the fabrication errors during the semiconductor process. During the evaluation, we modeled the system error by including the Gaussian noise with an SD of 0.3 to the trained phase modulation coefficients and the amplitude modulation coefficients. Moreover, the architecture still performs well even under more significant Gaussian noise, demonstrating its robustness to the system errors (see fig. S10).
Fabrication process for photonic metalines
We considered the fabrication capability of the existing silicon photonics foundry (52) during the design and evaluation of DGNN architecture. The fabrication process for diffractive metalines of DPU can be based on silicon photonic semiconductor fabrication techniques, including the photoresist coating, deep ultraviolet (DUV) exposure, developing, etching, photoresist removal, and top cladding (see fig. S16). The metalines are composed of rectangular silica slot arrays etched on SOI substrate, which can be fabricated using silicon photonic semiconductor fabrication techniques, e.g., the DUV lithography process. The top layer of the start SOI wafer is 220-nm-thick silicon. The prepared wafer is covered with the photoresist by spin coating and prebaked to drive off excess photoresist solvent. Then, the photoresist is exposed to the intense ultraviolet light pattern determined by the target structure. The DUV exposure allows the photoresist on the top of the slot arrays to be removed by developing, and the silicon is etched in areas without photoresist with wet etchants or plasma etchants. Last, the rest photoresist is removed with resist stripper or ashing process, and the chip is cladded with silica through plasma-enhanced chemical vapor deposition to protect the structures.
Acknowledgments
Funding: This work is supported by the National Natural Science Foundation of China (No. 62088102 and No. 61932022), the National Key Research and Development Program of China (No. 2020AA0105500 and No. 2021ZD0109902), and the Tsinghua University Initiative Scientific Research Program.
Author contributions: Q.D., X.L., and H.X. initiated and supervised the project. X. L., R.Y., and T.Y. conceived and designed the research. T.Y. and R.Y. implemented the algorithm and conducted the numerical experiments. R.Y., T.Y., and Z.Z. processed the data. X.L., R.Y., T.Y., and Z.Z. analyzed and interpreted the results. All authors prepared the manuscript and discussed the research.
Competing interests: Q.D., X.L., R.Y., T.Y., and H.X. are inventors on a patent application related to this work filed by Tsinghua University. The authors declare that they have no other competing interests.
Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials.
Supplementary Materials
This PDF file includes:
Figs. S1 to S16
Tables S1 to S3
REFERENCES AND NOTES
- 1.LeCun Y., Bengio Y., Hinton G., Deep learning. Nature 521, 436–444 (2015). [DOI] [PubMed] [Google Scholar]
- 2.K. He, X. Zhang, S. Ren, J. Sun, Deep residual learning for image recognition, in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR, 2016), pp. 770–778. [Google Scholar]
- 3.Hinton G., Deng L., Yu D., Dahl G. E., Mohamed A.-r., Jaitly N., Senior A., Vanhoucke V., Nguyen P., Sainath T. N., Kingsbury B., Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups. IEEE Signal Process. Mag. 29, 82–97 (2012). [Google Scholar]
- 4.D. Bahdanau, K. Cho, Y. Bengio, Neural machine translation by jointly learning to align and translate, in International Conference on Learning Representations (ICLR, 2015). [Google Scholar]
- 5.V. Rausch, A. Hansen, E. Solowjow, C. Liu, E. Kreuzer, J. K. Hedrick, Learning a deep neural net policy for end-to-end control of autonomous vehicles, in 2017 American Control Conference (ACC) (IEEE, 2017), pp. 4914–4919. [Google Scholar]
- 6.Baldi P., Deep learning in biomedical data science. Annu. Rev. Biomed. Data Sci. 1, 181–205 (2018). [Google Scholar]
- 7.Moore G. E., Cramming more components onto integrated circuits. Proc. IEEE 86, 82–85 (1998). [Google Scholar]
- 8.Krizhevsky A., Sutskever I., Hinton G. E., Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 1, 1097–1105 (2012). [Google Scholar]
- 9.N. P. Jouppi, C. Young, N. Patil, D. Patterson, G. Agrawal, R. Bajwa, S. Bates, S. Bhatia, N. Boden, A. Borchers, R. Boyle, P.-l. Cantin, C. Chao, C. Clark, J. Coriell, M. Daley, M. Dau, J. Dean, B. Gelb, T. V. Ghaemmaghami, R. Gottipati, W. Gulland, R. Hagmann, C. R. Ho, D. Hogberg, J. Hu, R. Hundt, D. Hurt, J. Ibarz, A. Jaffey, A. Jaworski, A. Kaplan, H. Khaitan, A. Koch, N. Kumar, S. Lacy, J. Laudon, J. Law, D. Le, C. Leary, Z. Liu, K. Lucke, A. Lundin, G. MacKean, A. Maggiore, M. Mahony, K. Miller, R. Nagarajan, R. Narayanaswami, R. Ni, K. Nix, T. Norrie, M. Omernick, N. Penukonda, A. Phelps, J. Ross, M. Ross, A. Salek, E. Samadiani, C. Severn, G. Sizikov, M. Snelham, J. Souter, D. Steinberg, A. Swing, M. Tan, G. Thorson, B. Tian, H. Toma, E. Tuttle, V. Vasudevan, R. Walter, W. Wang, E. Wilcox, D. H. Yoon, In-datacenter performance analysis of a tensor processing unit, in Proceedings of the 44th Annual International Symposium on Computer Architecture (ACM, 2017), pp. 1–12. [Google Scholar]
- 10.C. Zhang, P. Li, G. Sun, Y. Guan, B. Xiao, J. Cong, Optimizing FPGA-based accelerator design for deep convolutional neural networks, in Proceedings of the 2015 ACM/SIGDA International Symposium on Field-programmable Gate Arrays (ACM, 2015), pp. 161–170. [Google Scholar]
- 11.Wetzstein G., Ozcan A., Gigan S., Fan S., Englund D., Soljačić M., Denz C., Miller D. A. B., Psaltis D., Inference in artificial intelligence with deep optics and photonics. Nature 588, 39–47 (2020). [DOI] [PubMed] [Google Scholar]
- 12.Shastri B. J., Tait A. N., de Lima T. F., Pernice W. H. P., Bhaskaran H., Wright C. D., Prucnal P. R., Photonics for artificial intelligence and neuromorphic computing. Nat. Photonics 15, 102–114 (2021). [Google Scholar]
- 13.Lin X., Rivenson Y., Yardimci N. T., Veli M., Luo Y., Jarrahi M., Ozcan A., All-optical machine learning using diffractive deep neural networks. Science 361, 1004–1008 (2018). [DOI] [PubMed] [Google Scholar]
- 14.Yan T., Wu J., Zhou T., Xie H., Xu F., Fan J., Fang L., Lin X., Dai Q., Fourier-space diffractive deep neural network. Phys. Rev. Lett. 123, 023901 (2019). [DOI] [PubMed] [Google Scholar]
- 15.Li J., Mengu D., Yardimci N. T., Luo Y., Li X., Veli M., Rivenson Y., Jarrahi M., Ozcan A., Spectrally encoded single-pixel machine vision using diffractive networks. Sci. Adv. 7, eabd7690 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhou T., Lin X., Wu J., Chen Y., Xie H., Li Y., Fan J., Wu H., Fang L., Dai Q., Large-scale neuromorphic optoelectronic computing with a reconfigurable diffractive processing unit. Nat. Photonics 15, 367–373 (2021). [Google Scholar]
- 17.Chang J., Sitzmann V., Dun X., Heidrich W., Wetzstein G., Hybrid optical-electronic convolutional neural networks with optimized diffractive optics for image classification. Sci. Rep. 8, 1–10 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bueno J., Maktoobi S., Froehly L., Fischer I., Jacquot M., Larger L., Brunner D., Reinforcement learning in a large-scale photonic recurrent neural network. Optica 5, 756–760 (2018). [Google Scholar]
- 19.Goi E., Chen X., Zhang Q., Cumming B. P., Schoenhardt S., Luan H., Gu M., Nanoprinted high-neuron-density optical linear perceptrons performing near-infrared inference on a CMOS chip. Light Sci. Appl. 10, 1–11 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Shen Y., Harris N. C., Skirlo S., Prabhu M., Baehr-Jones T., Hochberg M., Sun X., Zhao S., Larochelle H., Englund D., Soljačić M., Deep learning with coherent nanophotonic circuits. Nat. Photonics 11, 441–446 (2017). [Google Scholar]
- 21.Zhang H., Gu M., Jiang X. D., Thompson J., Cai H., Paesani S., Santagati R., Laing A., Zhang Y., Yung M. H., Shi Y. Z., Muhammad F. K., Lo G. Q., Luo X. S., Dong B., Kwong D. L., Kwek L. C., Liu A. Q., An optical neural chip for implementing complex-valued neural network. Nat. Commun. 12, 1–11 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Feldmann J., Youngblood N., Wright C. D., Bhaskaran H., Pernice W. H. P., All-optical spiking neurosynaptic networks with self-learning capabilities. Nature 569, 208–214 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chakraborty I., Saha G., Roy K., Photonic in-memory computing primitive for spiking neural networks using phase-change materials. Phys. Rev. Appl. 11, 014063 (2019). [Google Scholar]
- 24.Larger L., Baylón-Fuentes A., Martinenghi R., Udaltsov V. S., Chembo Y. K., Jacquot M., High-speed photonic reservoir computing using a time-delay-based architecture: Million words per second classification. Phys. Rev. X. 7, 011015 (2017). [Google Scholar]
- 25.Antonik P., Marsal N., Brunner D., Rontani D., Human action recognition with a large-scale brain-inspired photonic computer. Nat. Mach. Intell. 1, 530–537 (2019). [Google Scholar]
- 26.Duvenaud D., Maclaurin D., Aguilera-Iparraguirre J., Gómez-Bombarelli R., Hirzel T., Aspuru-Guzik A., Adams R. P., Convolutional networks on graphs for learning molecular fingerprints. Adv. Neural Inf. Process. Syst. 28, 2224–2232 (2015). [Google Scholar]
- 27.C. Hu, L. Cheng, J. Sepulcre, G. El Fakhri, Y. M. Lu, Q. Li, Matched signal detection on graphs: Theory and application to brain network classification, in International Conference on Information Processing in Medical Imaging (Springer, 2013), pp. 1–12. [DOI] [PubMed] [Google Scholar]
- 28.T. N. Kipf, M. Welling, Semi-supervised classification with graph convolutional networks, in International Conference on Learning Representations (ICLR, 2017). [Google Scholar]
- 29.J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals, G. E. Dahl, Neural message passing for quantum chemistry, in International Conference on Machine Learning (PMLR, 2017), pp. 1263–1272. [Google Scholar]
- 30.P. Veličković, G. Cucurull, A. Casanova, A. Romero, P. Lio, Y. Bengio, Graph attention networks, in International Conference on Learning Representations (ICLR, 2018). [Google Scholar]
- 31.A. Bojchevski, J. Klicpera, B. Perozzi, A. Kapoor, M. Blais, B. Rózemberczki, M. Lukasik, S. Günnemann, Scaling graph neural networks with approximate pagerank, in Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (ACM, 2020), pp. 2464–2473. [Google Scholar]
- 32.Vignac C., Loukas A., Frossard P., Building powerful and equivariant graph neural networks with structural message-passing. Adv. Neural Inf. Process. Syst. 33, 14143–14155 (2020). [Google Scholar]
- 33.C. Zang, F. Wang, MoFlow: An invertible flow model for generating molecular graphs, in Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (ACM, 2020), pp. 617–626. [Google Scholar]
- 34.S. Yan, Y. Xiong, D. Lin, Spatial temporal graph convolutional networks for skeleton-based action recognition, in Thirty-second AAAI Conference on Artificial Intelligence (AAAI, 2018), pp. 7444–7452. [Google Scholar]
- 35.Y. Li, R. Yu, C. Shahabi, Y. Liu, Diffusion convolutional recurrent neural network: Data-driven traffic forecasting, in International Conference on Learning Representations (ICLR, 2018). [Google Scholar]
- 36.Wang Z., Li T., Soman A., Mao D., Kananen T., Gu T., On-chip wavefront shaping with dielectric metasurface. Nat. Commun. 10, 1–7 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zarei S., Marzban M.-r., Khavasi A., Integrated photonic neural network based on silicon metalines. Opt. Express 28, 36668–36684 (2020). [DOI] [PubMed] [Google Scholar]
- 38.Vaswani A., Shazeer N., Parmar N., Uszkoreit J., Jones L., Gomez A. N., Kaiser Ł., Polosukhin I., Attention is all you need. Adv. Neural Inf. Process. Syst. 30, 5998–6008 (2017). [Google Scholar]
- 39.Wu S., Mu X., Cheng L., Mao S., Fu H., State-of-the-art and perspectives on silicon waveguide crossings: A review. Micromachines 11, 326 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.A. Bojchevski, S. Günnemann, Deep gaussian embedding of graphs: Unsupervised inductive learning via ranking, in International Conference on Learning Representations (ICLR, 2018). [Google Scholar]
- 41.Sen P., Namata G., Bilgic M., Getoor L., Galligher B., Eliassi-Rad T., Collective classification in network data. AI Magazine 29, 93–93 (2008). [Google Scholar]
- 42.O. Shchur, M. Mumme, A. Bojchevski, S. Günnemann, Pitfalls of graph neural network evaluation. arXiv:1811.05868 [cs.LG] (14 November 2018).
- 43.Holland P. W., Laskey K. B., Leinhardt S., Stochastic blockmodels: First steps. Soc. Networks 5, 109–137 (1983). [Google Scholar]
- 44.C. Trabelsi, O. Bilaniuk, Y. Zhang, D. Serdyuk, S. Subramanian, J. F. Santos, S. Mehri, N. Rostamzadeh, Y. Bengio, C. J. Pal, Deep complex networks, in International Conference on Learning Representations (ICLR, 2018). [Google Scholar]
- 45.D. P. Reichert, T. Serre, Neuronal synchrony in complex-valued deep networks, in International Conference on Learning Representations (ICLR, 2014). [Google Scholar]
- 46.Wisdom S., Powers T., Hershey J., Le Roux J., Atlas L., Full-capacity unitary recurrent neural networks. Adv. Neural Inf. Process. Syst. 29, (2016). [Google Scholar]
- 47.Hirose A., Yoshida S., Generalization characteristics of complex-valued feedforward neural networks in relation to signal coherence. IEEE Trans. Neural Netw. Learn. Syst. 23, 541–551 (2012). [DOI] [PubMed] [Google Scholar]
- 48.Dou H., Deng Y., Yan T., Wu H., Lin X., Dai Q., Residual D2NN: Training diffractive deep neural networks via learnable light shortcuts. Optics Lett. 45, 2688–2691 (2020). [DOI] [PubMed] [Google Scholar]
- 49.F. Wu, A. Souza, T. Zhang, C. Fifty, T. Yu, K. Weinberger, Simplifying graph convolutional networks, in International Conference on Machine Learning (PMLR, 2019), pp. 6861–6871. [Google Scholar]
- 50.Van der Maaten L., Hinton G., Visualizing data using t-SNE. J. Mach. Learn. Res. 9, 2579–2605 (2008). [Google Scholar]
- 51.L. Xia, C.-C. Chen, J. K. Aggarwal, View invariant human action recognition using histograms of 3D joints, in 2012 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops (IEEE, 2012), pp. 20–27. [Google Scholar]
- 52.https://service.cumec.cn/.
- 53.Yao P., Wu H., Gao B., Tang J., Zhang Q., Zhang W., Yang J. J., Qian H., Fully hardware-implemented memristor convolutional neural network. Nature 577, 641–646 (2020). [DOI] [PubMed] [Google Scholar]
- 54.Forouzmand A., Salary M. M., Shirmanesh G. K., Sokhoyan R., Atwater H. A., Mosallaei H., Tunable all-dielectric metasurface for phase modulation of the reflected and transmitted light via permittivity tuning of indium tin oxide. Nanophotonics 8, 415–427 (2019). [Google Scholar]
- 55.Huang C., Jha A., De Lima T. F., Tait A. N., Shastri B. J., Prucnal P. R., On-chip programmable nonlinear optical signal processor and its applications. IEEE J. Sel. Top. Quantum Electron. 27, 1–11 (2020). [Google Scholar]
- 56.Williamson I. A., Hughes T. W., Minkov M., Bartlett B., Pai S., Fan S., Reprogrammable electro-optic nonlinear activation functions for optical neural networks. IEEE J. Sel. Top. Quantum Electron. 26, 1–12 (2020). [Google Scholar]
- 57.Y. Rong, W. Huang, T. Xu, J. Huang, Dropedge: Towards deep graph convolutional networks on node classification, in International Conference on Learning Representations (ICLR, 2019). [Google Scholar]
- 58.D. P. Kingma, J. Ba, Adam: A method for stochastic optimization, in International Conference on Learning Representations (ICLR, 2015). [Google Scholar]
- 59.R. Hui, Photodetectors in Introduction to Fiber-optic Communications (Academic Press, ed. 1, 2019), pp. 125–154. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figs. S1 to S16
Tables S1 to S3