Investigating the A_n+1B_nX_3n+1 Homologous Series: A New Platform for Studying Magnetic Praseodymium Based Intermetallics

Abstract

The recent discovery of the A_n+1B_nX_3n+1 (A = lanthanide, B = transition metal, X = tetrel) homologous series provides a new platform to study the structure–property relationships of highly correlated electron systems. Several members of Ce_n+1Co_nGe_3n+1 (n = 1, 4, 5, 6, and ∞) show evidence of heavy electron behavior with complex magnetic interactions. While the Ce analogues have been investigated, only n = 1, 2, and ∞ of Pr_n+1Co_nGe_3n+1 have been synthesized, with n = 1 and 2 showing a nonsinglet magnetic ground state. The Pr analogues can provide a platform for direct comparison of highly correlated behavior. In this perspective, we discuss the impetus for synthesizing the Pr_n+1Co_nGe_3n+1 members and present the structural characterization of the n = 3 and n = 4 members. We lay the foundation for future investigations of the Pr_n+1Co_nGe_3n+1 family of compounds and highlight the importance of complementary methods to characterize new quantum materials.

1. Introduction

The discovery of novel emergent electronic states in magnetic highly correlated quantum materials^1,2 is necessary to advance next generation technologies.³ These states allow the stabilization of a number of quasi-particles that can be taken advantage of for new technologies or advance our understanding of important physical phenomena, such as Majorana fermions in topological insulators for quantum computing,^4,5 Weyl fermionic states in topological semimetals to study magnetotransport phenomena,⁶ and other highly correlated states.^3,4,7−9 Herein, we focus on heavy fermions and their quantum critical points, around which unconventional superconductivity has been observed.^10,11 From a materials perspective, our goals are to (1) connect highly correlated physics to the structural and electronic features of a material, (2) identify and synthesize quantum materials, and (3) understand the synthesis of quantum materials. These goals aim to discover new platforms of compounds with magnetic and transport properties that can be tuned to study quantum critical points.¹⁰ While external parameters such as temperature, pressure, and magnetic field are necessary in these investigations, additional parameters such as dimensionality and the structural environment of magnetic ions can enrich our understanding of structure–property relationships.

Occasionally, homologous series, families of related compounds with a chemical formula that changes as a function of an integer, are discovered that allow a robust method of tuning physical properties through discrete variations in chemical structure and composition. These families can be built from intergrowth structures, where each member is rationalized as an assembly of known crystal structures. In recent decades, several intermetallic homologous series have been discovered such as Ce_nMIn_3n+2,^12,13 Th₂(Au_xSi_1–x)[AuAl₂]_nSi₂,¹⁴ Ce(PdAl)_n,¹⁵ and [LnGe₂]_n[LnLi₂Ge]_m.^16,17 The nature of a homologous series makes them specially systematic to study complex phenomena as linked to their repeating structural motifs, thus allowing novel connections to be drawn between chemical structure and properties in ways dissimilar compounds cannot achieve. The Ln_2–yZn₄As₄·n(LnAs) (Ln = La–Nd, Sm, and Gd) series built from [LnAs] and [Zn₂As₂] slabs¹⁸ is an example of band gap tuning as a function of structure. Here, there is a gradual increase in electron density at the band gap as a function of the [LaAs] slabs’ thickness, directly attributed to the change in structure and composition. Ce_nMIn_3n+2 (n = 1, 2, and ∞; M = Co, Rh, and Ir) offered new potential in studying magnetically mediated superconductivity in the CeIn₃ parent structure,¹⁹ CeMIn₅,^20,21 and Ce₂MIn₈²² by considering the role of the CeIn₃ and MIn₂ layers and transition metal substitution. To evaluate the highly correlated nature of compounds, the Sommerfeld coefficient (γ), the electronic contribution to specific heat, and a measure of heavy electron behavior can be obtained from the following equation: C_p = γT + αT³, where T is the temperature and α is the phonon contribution to the specific heat. With application of pressure, the antiferromagnets emerge into a superconducting phase,¹³ with an enhanced Sommerfeld coefficient of γ ∼ 400 mJ/mol K² for Ce_nRhIn_3n+2 (n = 1 and 2) and γ ∼ 700 mJ/mol K² for Ce_nIrIn_3n+2 (n = 1 and 2) and, most prominently, with the antiferromagnetic CeIn₃ (T_N = 10 K) becoming superconducting with 27.5 kbar. The properties of this family of compounds led to the linking of dimensionality, in addition to the evaluation of the significance of the Ce local cuboctahedral environment on the influence of magnetic correlation. Given a new intermetallic homologous series, we present a robust platform to demonstrate the potential for the discovery of new phenomena and the study of exotic and emergent behavior as a function of dimensionality.

2. A_n+1Co_nGe_3n+1

The A_n+1B_nX_3n+1 homologous series (A = lanthanide, B = transition metal, X = tetrel)²³ holds promise as a new platform to study highly correlated emergent phenomena. The progression of the series can be understood as systematic additions of BaNiSn₃/AuCu₃-type disordered subunits intergrown with CeNiSi₂-type subunits, where odd and even members crystallize in the orthorhombic Cmcm and Cmmm space groups, respectively. For each n member of the series, n – 1 BaNiSn₃/AuCu₃-type subunits are stacked along the b direction between CeNiSi₂-type subunits, where the sequential stacking of BaNiSn₃/AuCu₃ subunits separates the CeNiSi₂ subunits as a function of n. Therefore, the homologous series provides a systematic platform to study the effects of changing dimensionality and local environment on magnetism and electronic structure.

Ce_n+1Co_nGe_3n+1 compounds n = 1,²⁴ 4,^25,26 5,²⁷ 6,²⁸ and ∞²⁹ have been reported and can be used to study the interplay of local 4f¹ electron systems and conduction electrons. Ce³⁺ ions are odd spin systems that follow Kramer’s theorem, which guarantees the formation of a doublet electronic ground state outside of an applied magnetic field due to the presence of time reversal symmetry. At sufficiently low temperatures, the doublet ground state allows for local 4f and conduction electron hybridization that results in the emergence of the magnetic Kondo effect, manifesting as heavy electron behavior, and eventually a valence transition from Ce³⁺ to Ce⁴⁺.³⁰ As illustrated by the Doniach model,³¹ Kondo interactions are in direct competition with Ruderman–Kittel–Kasuya–Yosida (RKKY) interactions dependent upon the strength of magnetic exchange interactions, making compounds that exhibit both heavy electron behavior and magnetic ordering exciting platforms for studying quantum critical points. All characterized members of the Ce_n+1Co_nGe_3n+1 family, n = 1, 4, 5, 6, and ∞, show evidence of heavy electron behavior, and the n = 4, 5, 6, and ∞ members demonstrate complex anisotropic competition between antiferromagnetic and ferromagnetic states.

The n = 1 member, CeCo_0.89Ge₂, is a Kondo compound (T_K > 200 K) with no magnetic ordering down to 1.5 K.³²⁻³⁴ However, patterns have emerged in the properties of the Ce_n+1Co_nGe_3n+1 family for n = 4–6. The anisotropic magnetic properties of Ce₅Co_4+xGe₁₃, Ce₆Co_5+xGe₁₆, and Ce₇Co_6+xGe₁₉ are similar to one another. Two of the five magnetic transitions of the n = 6 member overlap with two of the transitions in the n = 4 member, with the remaining three transitions overlapping with the transitions found in the n = 5 member, most likely due to their related local environments.²⁶⁻²⁸ The n = ∞ member, CeCoGe₃, is a Kondo antiferromagnet (T_K ∼ 100 K) with three magnetic transitions at T = 21 K, T = 12 K, and T = 8 K³⁵ that resemble the anisotropy of the other n members. The presence of CeCoGe₃ in this series is particularly exciting, as the noncentrosymmetric superconductor has recently been theoretically predicted to be topologically nontrivial.³⁶⁻³⁸

Topological phases containing local inversion symmetry breaking such as UTe₂^39,40 and CeRh₂As₂^41,42 have gathered much attention in recent years. As such, the CeCoGe₃ sublattice in Ce_n+1Co_nGe_3n+1 creates a unique opportunity to understand the structure–property relationships of local inversion symmetry breaking on the bulk properties of a material as a function of n.^43,44 With evidence of highly correlated phenomena, complex magnetism, and the potential for topological behavior, the Ce_n+1Co_nGe_3n+1 family of compounds are candidates to study new states of matter, such as Weyl–Kondo semimetals,^7,45 through the addition of CeCoGe₃ layers. The potential of the A_n+1B_nX_3n+1 series is not limited to the Ce analogues, as the physical properties of Pr based intermetallic compounds have garnered increasing interest over the past three decades.

3. Pr_n+1Co_nGe_3n+1

Ce and Pr behave fundamentally differently due to their respective 4f¹ and 4f² electronic configurations. For example, CeAlGe is an incommensurate antiferromagnetic type-I Weyl semimetal,⁴⁶ whereas PrAlGe exhibits type-II Weyl semimetal behavior with an anomalous Hall conductivity of ∼680 Ω^–1 cm^–1 due to a ferromagnetic spin–glass-like ordering at 15 K.^47,48 Observations of Weyl fermions through angle resolved photoelectron spectroscopy measurements and the intrinsic anomalous Hall response confirmed these differences in physical properties.^49,50 Additionally, Si substitution in PrAlGe_1–xSi_x (0 < x < 1) has shown tunable anomalous Hall effects, demonstrating the interplay between scattering mechanism and topological state. Magnetoresistance sensitivity was also shown to increase by as much as 100% from PrAlSi to PrAlGe.⁵¹

The 4f electronic ground states are responsible for differences in physical properties through changes in their interaction with conduction electrons. While Ce³⁺ ions follow Kramer’s theorem, Pr³⁺ ions have an even number of 4f electrons and are classified as non-Kramer’s ions. Here, the doublet ground state is no longer protected by time reversal symmetry, resulting in many Pr compounds adopting a singlet ground state and, thus, having neither heavy electron behavior nor magnetic ordering; for example, PrCoGe₃ is non-Kondo with no magnetic ordering.⁵² However, the point group symmetry of the local environment of non-Kramer’s ions affords another path to achieving a doublet or quasi-doublet ground state through crystal electric field (CEF) splitting, inspiring the study of quantum fluctuations in spin systems and exotic quadrupolar phenomena.⁵³ Crystal field schemes of Pr atoms in cubic environments have been the primary focus of the highly correlated behavior in Pr systems due to their predilection toward doublet ground states. The CEF stabilized non-Kramer’s doublet ground state results in a two-channel Kondo effect through electric quadrupolar ordering.⁵⁴ Electric quadrupolar ordering has led to identification of new quantum critical points,⁵⁵ non-Fermi liquid behavior,⁵⁶ and unconventional superconductivity.⁵⁷ PrInAg₂^58,59 was the first heavy electron Pr compound discovered with the second largest Sommerfeld coefficient identified (γ ∼ 6.5 J/mol K²). Later, a large family of heavy superconducting compounds, PrM₂X₂₀ (M = Ti and V with X = Al;⁵⁶ M = Ir and Rh with X = Zn;^60,61 M = Ni with X = Cd⁶²), was identified where the different M and X could be varied to tune the superconducting transition temperatures, quadrupolar order, and magnetic order.

Nonetheless, compounds with lower Pr point symmetry have recently shown that heavy electron behavior of a similar magnitude can be observed in quasi-doublet states. In PrSi,⁶³ ferromagnetic ordering is observed despite a singlet ground state, due to quasi-doublet formation via a singlet ground state to singlet first excited state transition with a difference in energy of ΔT = 9 K. Low-lying crystal field excitations with ΔT = 12 K were also used to justify the elevated Sommerfeld coefficient of Pr₂Rh₃Ge₅, γ ∼ 81 mJ/mol K².⁶⁴ The singlet–singlet quasi-doublets (ΔT = 63.9 K) in PrPdAl⁶⁵ were recently found to result in a raised Sommerfeld coefficient of γ ∼ 940 mJ/mol K². With these examples and others, such as Pr₃Rh₄Sn₁₃ (γ ∼ 761 mJ/mol K²)⁶⁶ and Pr₅Ir₄Sn₁₀ (γ ∼ 500 mJ/mol K²),^67,68 there is mounting interest in Pr based intermetallic compounds with noncubic point symmetries and highly correlated behavior that, when coupled with the modularity of a homologous series, supports investigation of the Pr_n+1Co_nGe_3n+1 series.

In the Pr_n+1Co_nGe_3n+1 series, n = 1, 2, and ∞ members have been reported. PrCo_1–xGe₂, n = 1, has one antiferromagnetic transition at 5 K and a potential metamagnetic transition in the low-field magnetization.⁶⁹ For Pr₃Co_2+xGe₇,⁷⁰n = 2, magnetic susceptibility data at 0.1 T shows two antiferromagnetic transitions at 5.3 and 9.3 K and three metamagnetic transitions below an applied field of 3 T. These transitions seem to be suppressed with the introduction of Sn in Pr₃Co_2+xGe_7–ySn_y,⁷⁰ with only two metamagnetic transitions occurring at applied fields of <1 T. Both phases are far below the expected magnetization for Pr, approaching 1 μ_B/mol-Pr at 7 T and 4 K; however, the effective magnetic moment for Pr₃Co_2+xGe_7–ySn_y (μ_eff = 3.81 μ_B/Pr) is above the theoretical spin only moment of Pr³⁺ (3.58 μ_B/Pr³⁺). For comparison, Pr₃Ni_2–xSn₇⁷¹ has similar behavior, with a single metamagnetic transition occurring below 2 T and 2 K. With the identification of two newly synthesized members of the Pr_n+1Co_nGe_3n+1 series, n = 3 and n = 4, we now have a platform to demonstrate the tunability of this series for future work (Figure 1).

Figure 1.

(a) Aggregate crystals containing Pr₅Co_4+xGe_13–ySn_y before etching and (b) a fragment after etching. (c) Plates of Pr₄Co_3+xGe_10–ySn_y.

The n = 3 member Pr₄Co_3+xGe_10–ySn_y (see Figure 2 for structural representation and Table S1 for crystallographic data) is isostructural to Eu₂Ni_2–xSn₅ (Eu₄Ni_4–xSn₁₀, Cmcm).⁷² The atomic positions for both structures are shown in Table S2. Pr₄Co_3+xGe_10–ySn_y can be described as a stacking of CeNiSi₂ alternating with two slabs of BaNiSn₃/AuCu₃. The main differences between the Eu₄Ni_4–xSn₁₀ and Pr₄Co_3+xGe_10–ySn_y structures are (1) the complexity of the disorder and (2) the relative occupancy of the transition metals in the disordered components. In Eu₄Ni_4–xSn₁₀, the disorder is composed of two components: AuCu₃ and BaNiSn₃ in one orientation. In contrast, the Pr₄Co_3+xGe_10–ySn_y structure is composed of three disordered components, which are AuCu₃ and two orientations of BaNiSn₃ (right side up and down relative to the b axis).

Figure 2.

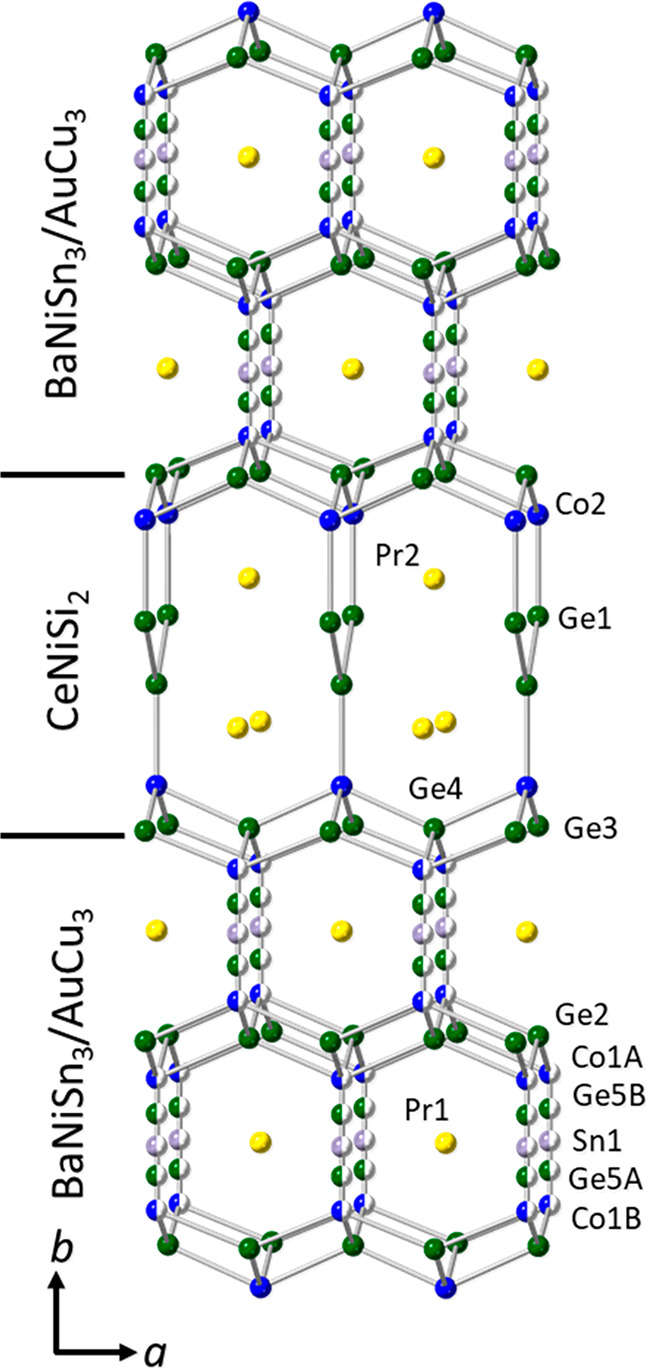
Crystal structure of Pr₄Co_3+xGe_10–ySn_y, where yellow, blue, green, and gray spheres represent Pr, Co, Ge, and Sn, respectively.

Pr₅Co_4+xGe_13–ySn_y (Figure 3 and Tables S1 and S3) of the Ce₅Co₄Ge₁₃ structure type²⁵ can be described as a Co incorporated Nb₅Ga₁₃-type structure composed of AlB₂, BaNiSn₃, and BaNiSn₃/AuCu₃ subunits. The use of AlB₂ subunits is analogous to CeNiSi₂, resulting in a stacking pattern of three BaNiSn₃/AuCu₃ subunits separated by one CeNiSi₂ subunit. In the report of Ce₅Co₄Ge₁₃, a disordered model with BaNiSn₃/AuCu₃ subunits was suggested, as a logical explanation of the observed residual electron densities. This disorder is also observed in the published structure of Ce₅Co_4+xGe_13–ySn_y²⁶ and in the model of Pr₅Co_4+xGe_13–ySn_y presented in this manuscript. Like Pr₄Co_3+xGe_10–ySn_y, there are also reduced Co occupancies relative to the Ge occupancies within the disordered components.

Figure 3.

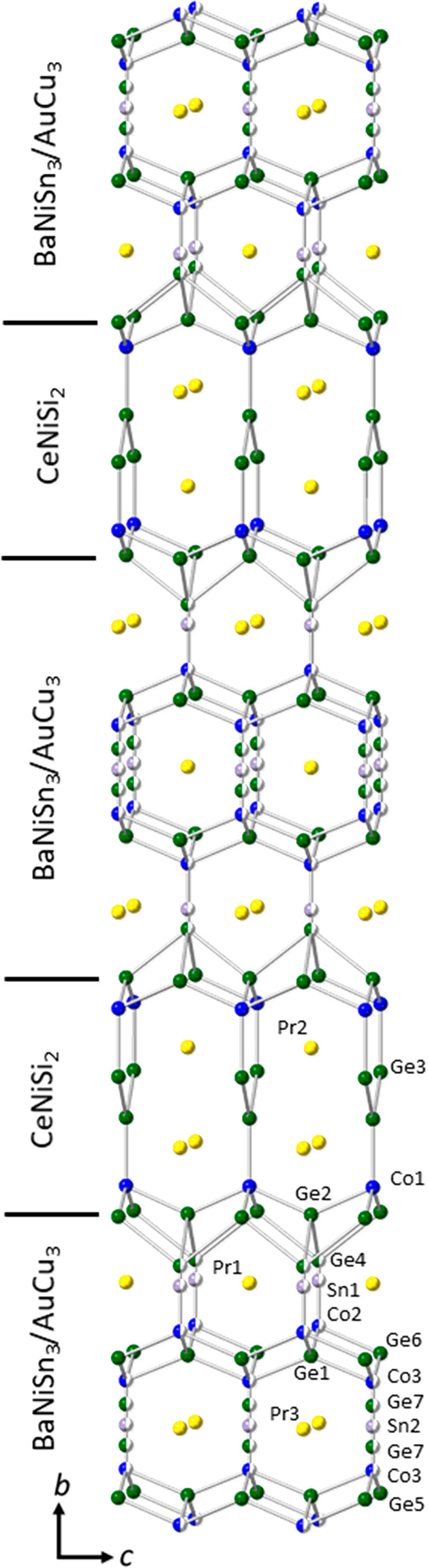
Crystal structure of Pr₅Co_4+xGe_13–ySn_y, where yellow, blue, green, and gray spheres represent Pr, Co, Ge, and Sn, respectively.

4. Challenges and Future Outlook

While single crystal diffraction provides great insights into the crystal structure, it is imperative to know if the single crystal is truly representative of the entire batch of crystals grown. With powder diffraction, the experiment can confirm the purity and homogeneity of the crystalline sample. For Pr₄Co_3+xGe_10–ySn_y, while the structural models obtained through single crystal X-ray diffraction are in good agreement with measured intensities, significant differences arise when compared to the bulk sample, revealing the challenges of using coherent scattering methods to model disorder. The local environment of the Pr1 site has, based on single crystal models, five potential configurations over a length of approximately 5 Å which extends diffraction techniques to the limits of their capabilities when considering the similar X-ray scattering cross sections of Co and Ge, the similar contact distances seen in the literature from Co–Co, Co–Ge, and Ge–Ge contacts depending on the covalency, and the similar bonding behaviors of Sn and Ge. Thus, despite the acceptable refinement statistics and reasonable crystal chemistry of the Pr₄Co_3+xGe_10–ySn_y model obtained from single crystal diffraction, the model must be refined further. While in many circumstances single crystal X-ray and powder diffraction are satisfactory to obtain exceptional models of disordered crystal structures,⁷³ for the future of quantum materials, drawing attention to the use of complementary structure techniques for their characterization is extremely important. The electronic contributions of minor structural defects can result in significant differences in physical properties. The structural investigations of heavy fermion compound Ce₂RhIn₈ are a model learning tool in how complementary structure techniques come together.⁷⁴ Incongruencies in Bragg peak intensities observed in X-ray powder diffraction inspired electron diffraction experiments ultimately leading to high-resolution synchrotron X-ray reciprocal space mapping of single crystals and high-resolution neutron powder diffraction experiments that identified unexpected two-phase mosaic disorder in a crystal structure otherwise believed to be ordered. The identification of complex disorder in Ce₂RhIn₈ went on to be used to rationalize the physical properties of other related heavy electron materials⁷⁵⁻⁷⁸ and inspire more detailed synthetic investigations,⁷⁹ again underscoring the importance of thorough structural characterization.

A similar approach could be used for the Pr_n+1Co_nGe_3n+1 homologous series to clarify the number of apparent disorder configurations in the BaNiSn₃/AuCu₃-type subunits through short-range correlations, address the peak broadening of the (2 0 0) and (0 0 2) reflections, and identify the cause of non-Bragg scattering at the 10° to 11° 2θ range using long-range correlations. Techniques such as pair distribution function, neutron diffraction methods, electron microscopy, and electron diffraction methods provide alternative views of a material that, taken together, work to elucidate the structure of compounds from local disorder at specific atomic sites to macroscopic disorder such as stacking faults and mosaicity effects.

We have successfully synthesized two members of the Pr_n+1Co_nGe_3n+1 homologous series: Pr₄Co_3+xGe_10–ySn_y and Pr₅Co_4+xGe_13–ySn_y. However, phase pure synthesis of a single homologous series member remains a significant challenge. Due to the similar stoichiometries based on the relative elemental ratios of the Pr_n+1Co_nGe_3n+1 series members, altering the reactant ratios proved ineffective. As such, our remaining option has been to refine the temperature profile, but without comprehensive ternary or quaternary phase diagrams, there is little guidance for this approach. Unexpectedly, raising the Sn concentration of the reaction has been the most successful method of obtaining phase pure homologous series members, despite producing the byproduct Pr₂Co₃Ge₅. This is similar to recent findings regarding Y₄RuGe₈.⁸⁰ The possibility of altering the flux concentration to isolate different n members presents a promising new method of reaction tuning that has inspired an investigation into in situ X-ray powder diffraction methods⁸¹⁻⁸³ and thermal analysis^84,85 to understand how changing flux conditions influence the formation of homologous series members and other related phases.^86,87

Despite these structural challenges, the Pr_n+1Co_nGe_3n+1 series presents new opportunities for 4f² electron systems. Uncovering potential correlative effects between different crystallographic Pr sites, dimensionality, and local environment could impact local 4f hybridization with conduction electrons. Thus, there is strong motivation to measure the physical properties of the Pr_n+1Co_nGe_3n+1 homologous series. Due diligence in developing new structural models of quantum materials is equally as important to the quantum community as their physical properties. We keep these considerations in mind for the synthesis of the Pr_n+1Co_nGe_3n+1 homologous series, as understanding the Pr local environment is extremely important to relating crystal electric field to electronic and magnetic behavior at the intersection of topological materials and highly correlated electron systems.

5. Methods

5.1. Synthesis

Pr₄Co_3+xGe_10–ySn_y and Pr₅Co_4+xGe_13–ySn_y were prepared using the flux growth method with tin as a metallic flux. The elements were combined in the ratio 3 Pr:2 Co:7 Ge:50 Sn and 3 Pr:2 Co:7 Ge:20 Sn, respectively, with the weight of the Pr₄Co_3+xGe_10–ySn_y reactants being 0.50 g, Sn flux 2.80 g Pr₅Co_4+xGe_13–ySn_y reactants’ weight 0.25 g, and Sn flux 0.56 g. The elements were transferred to an alumina Canfield crucible⁸⁸ and sealed in fused silica tubes under ∼1/3 atm of Ar gas. The Pr₅Co_4+xGe_13–ySn_y ampule was placed in a programmable furnace at 300 °C and heated to 1175 °C at the rate 100 °C/h. The sample dwelled at 1175 °C for 24 h and was cooled to 815 °C at the rate 3 °C/h, where it dwelled for approximately 6 h before removal and centrifugation of excess Sn flux. Residual flux was removed via etching in dilute HCl. A layered aggregate of plates, approximately 2 mm × 4 mm × 7 mm in size, composed of Pr₃Co_2+xGe_7–ySn_y, Pr₄Co_3+xGe_10–ySn_y, and Pr₅Co_4+xGe_13–ySn_y was obtained. The Pr₄Co_3+xGe_10–ySn_y reaction followed similar parameters with a 4 h dwell time at 1175 °C and a 30 h dwell time at 815 °C. One large platelike crystal of Pr₄Co_3+xGe_10–ySn_y, 1 mm × 3 mm × 4 mm in size, and some polyhedral shaped crystals of Pr₂Co₃Ge₅, approximately 1 mm × 2 mm × 2 mm in size, were obtained. Single crystals of Pr₄Co_3+xGe_10–ySn_y and Pr₅Co_4+xGe_13–ySn_y were cut from their respective samples. The Pr₄Co_3+xGe_10–ySn_y method was reproduced with a modified temperature profile for comparison to the synthesis of Pr₅Co_4+xGe_13–ySn_y, where the dwell time at 1175 °C was increased to 24 h, and the sample was removed from the furnace upon reaching 815 °C with less than 1 h of dwell time. From this sample, Pr₂Co₃Ge₅ was obtained as a dominant product. Small platelike crystals below 1 mm × 1 mm × 1 mm in size were also observed.

5.2. Laboratory Powder X-ray Diffraction

Powder X-ray diffraction data was collected on an aggregate containing Pr₃Co_2+xGe_7–ySn_y, Pr₄Co_3+xGe_10–ySn_y, and Pr₅Co_4+xGe_13–ySn_y using a Bruker D8 Advance diffractometer operating at 40 kV/30 mA with Cu Kα radiation (λ = 1.54184 Å) equipped with a LYNXEYE detector. Data was collected in the 2θ range from 5.0° to 90°. Laboratory powder X-ray diffraction was performed on the aggregate sample that was used to collect Pr₅Co_4+xGe_13–ySn_y single crystal data, and it was determined that the sample contained an intergrown mixture of series members; however, the presence of more than a single n member made accurate phase identification extremely difficult due to overlapping Bragg reflections and air scattering present in the laboratory powder diffraction. To overcome this problem, high-resolution powder diffraction data was collected at beamline 11-BM at the Advanced Photon Source of Argonne National Laboratory, where a combination of using a transmission mode, analyzer crystals, and high photon flux resulted in far higher signal-to-noise ratios.

5.3. High-Resolution Powder X-ray Diffraction

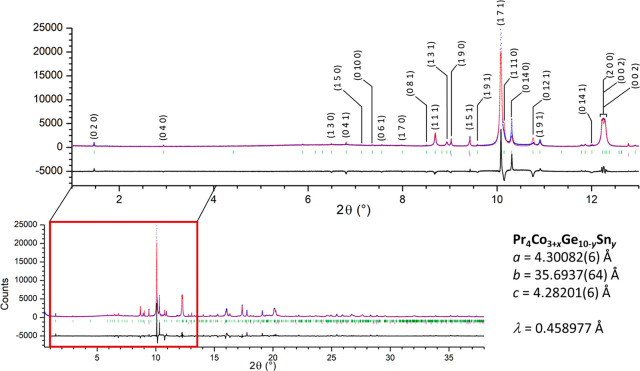
High-resolution powder X-ray diffraction data (λ = 0.458977 Å) was collected in the 2θ range from 0.5° to 43.5° for Pr₅Co_4+xGe_13–ySn_y and from 0.5° to 48.8° for Pr₄Co_3+xGe_10–ySn_y at the 11-BM beamline at the Advanced Photon Source of Argonne National Laboratory. All data modeling was carried out using TOPAS-Academic software. A two-phase Rietveld refinement using data collected on a ground fragment of the single phase plate of Pr₄Co_3+xGe_10–ySn_y and Sn (Figure 4) was able to account for all visible Bragg reflections, showing the sample is phase pure. However, mismatched intensities and non-Bragg scattering reveal a more complex story than captured through single crystal methods. The intensities of the (0 2 0), (1 7 1), (1 11 0), and (0 14 0) reflections are different than the calculated model. Given the platelike morphology of crystals grown from this series and the large anisotropy of the lattice parameters, intensity corrections were attempted by considering the preferred orientation of different combinations of the following reflection families: (0 2n 0), (1 2n–1 0), (0 2n–1 1), and (1 2n–1 1), but the improvements on the refinement were insignificant. Anisotropic strain broadening was also evaluated with little improvement to the refinement. As all mismatched intensities have dependence on the b crystallographic direction, attempts were made to alter the disorder model obtained through single crystal diffraction. While the intensities were improved considerably, the resulting structural model disagreed with the compositions obtained from elemental analysis and single crystal models.

Figure 4.

High-resolution synchrotron X-ray powder diffraction collected at 11-BM at the Advanced Photon Source of Pr₄Co_3+xGe_10–ySn_y shown in blue (λ = 0.458977 Å). The calculated fit from Rietveld refinement is shown in red, with the difference plot shown in black. Green and purple tick marks indicate Pr₄Co_3+xGe_10–ySn_y and Sn reflections, respectively. Labeled reflections are those with mismatched intensities.

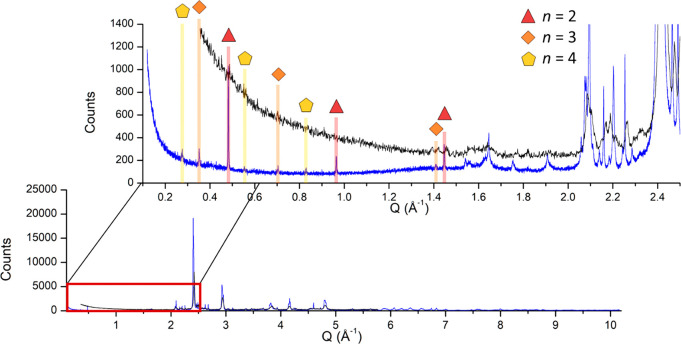
One factor that could be impacting the accuracy of the single crystal structure refinement is the lack of visibility for the (0 2 0) reflection. Due to the large b axis of Pr₄Co_3+xGe_10–ySn_y, the (0 2 0) reflection appears at a low 2θ angle of 4.56° (Mo Kα, λ = 0.71073 Å). This is outside the 2θ collection range 10.06° to 59.74° due to shadowing from the beam stop either fully or partially blocking this reflection. Since the disorder is strongly correlated to the (0 2n 0) reflections, the (0 2 0) reflection is particularly sensitive to changes in the structural model. Without this reflection, the single crystal model lacks key intensity information against which to refine the structural model. This is an additional challenge when working with compounds with very large unit cells, especially when blocked reflections are critical to regions of disorder. Due to the mixed phase nature of the sample containing Pr₅Co_4+xGe_13–ySn_y, a Pawley refinement was performed. From this data, low-angle (0 2n 0) reflections were visible (Figure 5), which were critical in identifying the members of the Pr_n+1Co_nGe_3n+1 series due to their strong correlation with the systematically elongated b axis of the series. Yet, without a single phase sample we were limited in our ability to refine the crystal structure against the bulk powder diffraction pattern through Rietveld refinement. Instead, a Pawley refinement revealed a mixed phase system of n = 2, 3, and 4 (Table 1). Although the lattice parameters obtained for Pr₃Co_2+xGe_7–ySn_y and Pr₅Co_4+xGe_13–ySn_y agree with single crystal data,⁷⁰ overlapping Bragg reflections remain a challenge with clear deviations in the refined a and c lattice parameters of Pr₄Co_3+xGe_10–ySn_y from single crystal data and phase pure powder diffraction. From here, obtaining phase pure samples will be the only way to validate the homogeneity of the disorder observed in the single crystal model for Pr₅Co_4+xGe_13–ySn_y.

Figure 5.

Comparison of laboratory (black, λ = 1.5406 Å) and high-resolution synchrotron (blue, λ = 0.458977 Å) X-ray powder diffraction data taken at 11-BM at the Advanced Photon Source. Colored lines and shapes indicate the (0 2n 0) reflections used to identify members of the homologous series Pr₃Co_2+xGe_7–ySn_y (blue triangle), Pr₄Co_3+xGe_10–ySn_y (yellow diamond), and Pr₅Co_4+xGe_13–ySn_y (red pentagon).

Table 1. Lattice Parameters Obtained from the Pawley Refinement of Pr₅Co_4+xGe_13–ySn_y.

	Space Group	a (Å)	b (Å)	c (Å)	V (Å3)
Pr3Co2+xGe7–ySny	Cmmm	4.25340(3)	26.0705(20)	4.29152(3)	475.881(7)
Pr4Co3+xGe10–ySny	Cmcm	4.36710(14)	35.6931(63)	4.20920(14)	656.113(34)
Pr5Co4+xGe13–ySny	Cmmm	4.28048(5)	45.4234(67)	4.30056(7)	836.175(21)

5.4. Single Crystal X-ray Diffraction

Single crystal X-ray diffraction data was obtained at room temperature using a Bruker D8 Quest Kappa single crystal X-ray diffractometer, equipped with an IμS microfocus source (Mo Kα, λ = 0.71073 Å), HELIOS optics monochromator, and PHOTON II CPAD detector. The Bruker SAINT program was used to integrate the diffraction data, and the intensities were corrected for absorption via a multiscan method implemented in SADABS 2016/2.⁸⁹ Preliminary starting models were generated using the intrinsic phasing methods in SHELXT⁹⁰ and subsequently anisotropically refined (full-matrix least-squares on F²) using SHELXL.⁹¹ Details of both structure refinements can be found in Tables S1–S3. Single crystals of Pr₄Co_3+xGe_10–ySn_y (0.01 mm × 0.01 mm × 0.02 mm) and Pr₅Co_4+xGe_13–ySn_y (0.02 mm × 0.12 mm × 0.14 mm) were cut from their respective samples and mounted on glass fibers using two-part epoxy.

The crystal structure of Pr₄Co_3+xGe_10–ySn_y was preliminarily modeled in the noncentrosymmetric space group Amm2. However, additional symmetries were detected using the ADDSYM function in PLATON, resulting in the final selection of the centrosymmetric space group Cmcm, in agreement with the Eu₄Co_4–xSn₁₀ structure type. In contrast to the Eu₄Co_4–xSn₁₀ structure type, additional electron densities of 5.43 e^–/ų and 4.53 e^–/ų were observed in the Pr1 local environment at (0 0.6408 0) and (0 0.7082 0), respectively. To address the observed intensities, an additional Co1B–Ge1B dimer was added. In accordance with the elemental analysis results indicating the presence of Sn incorporation, the Sn1 site was considered, leading to marginally improved refinement statistics relative to the assignment of a Ge atom. Additionally, when compared to the lattice parameters of Pr₄Co_3+xGe₁₀ grown in In flux (a = 4.2831(7) Å, b = 35.497(8) Å, c = 4.2533(10) Å), there is a difference in the b lattice parameter of approximately 0.3 Å corresponding to the incorporation of Sn. This effect was observed in Pr₃Co_2+xGe_7–ySn_y and Pr₃Co_2+xGe₇ as well. The Sn incorporation in the presence of Sn flux agrees with observations from Ce_n+1Co_nGe_3n+1–ySn_y (n = 4, 5, and 6). At this point in the refinement, Co vacancies had not been considered, but a hole of −5.46 e^–/ų was observed on the Co1A site. Thus, the Co1A, Co1B, and Co2 site occupancies were allowed to refine freely, resulting in a reduction in occupancy from ∼66% to ∼58% for Co1A, from ∼7.8% to ∼5.0% for Co1B, and from unity to 99% for Co2. The corresponding Ge sites’ occupancy saw an increase from ∼66% to ∼67% for Ge1A and from ∼7.8% to ∼8.4% for Ge1B. The fully occupied Co2 site and vacancies on the Co1A and Co1B sites agree with the crystal structure determination of Eu₄Ni_4–xSn₁₀.

The crystal structure of Pr₅Co_4+xGe_13–ySn_y was found to crystallize in the orthorhombic space group Cmmm. The disorder modeled in this structure is in extremely good agreement with the refinement of Ce₅Co_4+xGe_13–ySn_y, with the Pr1 local environment consisting of one Co2–Ge4 dimer representing the BaNiSn₃ structure type complemented by the Sn1 site representing the AuCu₃ structure type and the Pr3 local environment consisting of two complementary Co3–Ge7 dimers with the Sn2 site occupying the remainder of the configurations. Unlike Ce₅Co_4+xGe_13–ySn_y, upon refining the weighting scheme, a negative electron density of −6.00 e^–/ų was observed on the Co3 site in the Pr3 local environment. To address this, the Co3 occupancy was allowed to refine freely, where its occupancy reduced from ∼35% to ∼28%. From here, the occupancies of Co1 of the Pr2 local environment and Co2 of the Pr1 local environment were refined freely, resulting in an occupancy of approximately 99% for Co1 and a reduction the Co2 occupancy from ∼87% to ∼83%. The Co1 occupancy was fixed to unity, but the Co2 and Co3 vacancies were retained. The freely refined Co2 and Co3 sites resulted in an occupancy increase from 87% to 88% for Ge4 and from 35% to 37% for Ge7.

5.5. Elemental Analysis

Single crystals of Pr₄Co₃Ge_10–ySn_y and Pr₅Co₄Ge_13–ySn_y were analyzed using energy dispersive (X-ray) spectroscopy on a VERSA 3D focused ion beam scanning electron microscope with an acceleration voltage of 20 kV. The weight percentages obtained from EDS (normalized to Pr) resulted in the atomic formulas Pr_4.00(2)Co_3.22(1)Ge_9.34(7)Sn_0.66(1) and Pr_5.00(3)Co_4.38(1)Ge_12.27(5)Sn_0.44(2), which are comparable to the single crystal refinement formulas Pr₄Co_3.25(3)Ge_9.50(1)Sn_0.469(4) and Pr₅Co_4.22(2)Ge_12.48(1)Sn_0.519(7), respectively.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c02152.

• Additional details on the disorder model of Pr₄Co_3+xGe_10–ySn_y and Pr₅Co_4+xGe_13–ySn_y, the full structure refinement details of Pr₄Co_3+xGe_10–ySn_y and Pr₅Co_4+xGe_13–ySn_y (Table S1), a comparison of atomic positions for Pr₄Co_3+xGe_10–ySn_y and Eu₄Ni_4–xSn₁₀ (Table S2), and a comparison of atomic positions for Pr₅Co₄Ge_13–ySn_y and Ce₅Co_4+xGe_13–ySn_y (Table S3) (PDF)

• CIF data for Pr₄Co_3+xGe_10–ySn_y (CIF)

• CIF data for Pr₅Co_4+xGe_13–ySn_y(CIF)

The authors declare no competing financial interest.