Meta-matching as a simple framework to translate phenotypic predictive models from big to small data

Abstract

We propose a simple framework – meta-matching – to translate predictive models from large-scale datasets to new unseen non-brain-imaging phenotypes in small-scale studies. The key consideration is that a unique phenotype from a boutique study likely correlates with (but is not the same as) related phenotypes in some large-scale dataset. Meta-matching exploits these correlations to boost prediction in the boutique study. We apply meta-matching to predict non-brain-imaging phenotypes from resting-state functional connectivity. Using the UK Biobank (N=36,848) and HCP (N=1,019) datasets, we demonstrate that meta-matching can greatly boost the prediction of new phenotypes in small independent datasets in many scenarios. For example, translating a UK Biobank model to 100 HCP participants yields an 8-fold improvement in variance explained with an average absolute gain of 4.0% (min=−0.2%, max=16.0%) across 35 phenotypes. With a growing number of large-scale datasets collecting increasingly diverse phenotypes, our results represent a lower bound on the potential of meta-matching.

1. INTRODUCTION

Individual-level prediction is a fundamental goal in systems neuroscience and is important for precision medicine^1–4. Therefore, there is growing interest in leveraging brain imaging data to predict non-brain-imaging phenotypes (e.g., fluid intelligence or clinical outcomes) in individual participants. To date however, most prediction studies are underpowered, including less than a few hundred participants. This has led to systemic issues related to low reproducibility and inflated prediction performance^5–8. Prediction performance can greatly improve when training models with well-powered samples^9–12. The advent of large-scale population-level human neuroscience datasets (e.g., UK Biobank, ABCD) is therefore critical to improving the performance and reproducibility of individual-level prediction. However, when studying clinical populations or addressing focused neuroscience topics, small-scale datasets are often unavoidable. Here, we propose a simple framework to effectively translate predictive models from large-scale datasets to new non-brain-imaging phenotypes (from hereon shortened to ‘phenotypes’) in small data.

More specifically, given a large-scale brain imaging dataset (N > 10,000) with multiple phenotypes, we seek to translate models trained from the large dataset to new unseen phenotypes in a small independent dataset (N ≤ 200). We emphasize that the large and small datasets are independent. Furthermore, phenotypes in the small independent dataset do not have to overlap with those in the large dataset. In machine learning, this problem is known as meta-learning, learning-to-learn or lifelong learning^13–16 and is also closely related to transfer learning^17–19. For example, meta-learning can be applied to a large dataset (e.g., one million natural images) to train a deep neural network (DNN) to recognize multiple object categories (e.g., furniture and humans). The DNN can then be adapted to recognize a new, unseen object category (e.g., birds) with a limited set of samples^20–22. By learning a common representation across many object categories, meta-learning is able to adapt the DNN to a new object category with relatively few examples^21–23.

The key observation underpinning our meta-learning approach is that the vast majority of phenotypes are not independent, but are inter-correlated (Figure S1). Indeed, previous studies have discovered a relatively small number of components that link brain imaging data and an entire host of phenotypes, such as cognition, mental health, demographics and other health attributes^24–27. Therefore, a unique phenotype X examined by a small-scale boutique study is probably correlated with (but not the same as) a particular phenotype Y in some pre-existing large-scale population dataset. Consequently, a machine learning model that has been trained on phenotype Y in the large-scale dataset might be readily translated to phenotype X in the boutique study. In other words, meta-learning can be instantiated in human neuroscience by exploiting this existing correlation structure, a process we refer to as ‘meta-matching’.

Meta-matching can be broadly applied to different types of magnetic resonance imaging (MRI) data. Here, we focused on the use of resting-state functional connectivity (RSFC) to predict phenotypes. RSFC measures the synchrony of resting-state functional MRI signals between brain regions^28–30, while participants lie at rest without any ‘extrinsic’ task. RSFC has provided important insights into human brain organization across health and disease^31–35. Given any brain parcellation atlas^36–39, a whole brain RSFC matrix can be computed for each participant. Each entry in the RSFC matrix reflects the functional coupling strength between two brain parcels. In recent years, there is increasing interest in the use of RSFC for predicting phenotypes (e.g., age or cognition) of individual participants, i.e., functional connectivity fingerprint^40–45. Thus, our study will utilize RSFC-based phenotypic prediction to illustrate the power and field-wide utility of meta-matching.

To summarize, we proposed meta-matching, a simple framework to exploit large-scale brain imaging datasets for boosting RSFC-based prediction of new, unseen phenotypes in small datasets. The meta-matching framework is highly flexible and can be coupled with any machine learning algorithm. Here, we considered kernel ridge regression (KRR) and fully connected deep neural network (DNN), which we have previously demonstrated to work well for RSFC-based behavioral and demographics prediction¹¹. We developed two classes of meta-matching algorithms: basic and advanced. Our approach was evaluated using 36,848 participants from the UK Biobank^25,46 and 1,019 participants from the Human Connectome Project⁴⁷.

2. RESULTS

2.1. UK Biobank experimental setup

We utilized 55 × 55 resting-state functional connectivity (RSFC) matrices from 36,848 participants and 67 phenotypes from the UK Biobank⁴⁶. The 67 phenotypes were winnowed down from an initial list of 3,937 phenotypes by a systematic procedure that excluded brain variables, binary variables (except sex), repeated measures and measures missing from too many participants. Phenotypes that were not predictable even with 1000 participants were also excluded; note that these 1000 participants were excluded from the 36,848 participants. See Methods for more details.

The data was randomly divided into training (N = 26,848; 33 phenotypes) and test (N = 10,000; 34 phenotypes) meta-sets (Figure 1A). No participant or phenotype overlapped across the training and test meta-sets. Figure 1B shows the absolute Pearson’s correlations between the training and test phenotypes. The test meta-set was further split into K participants (K-shot; K = 10, 20, 50, 100, 200) and remaining 10,000-K participants. The group of K participants served to mimic traditional small-N studies.

Figure 1. Experimental setup for meta-matching in the UK Biobank.

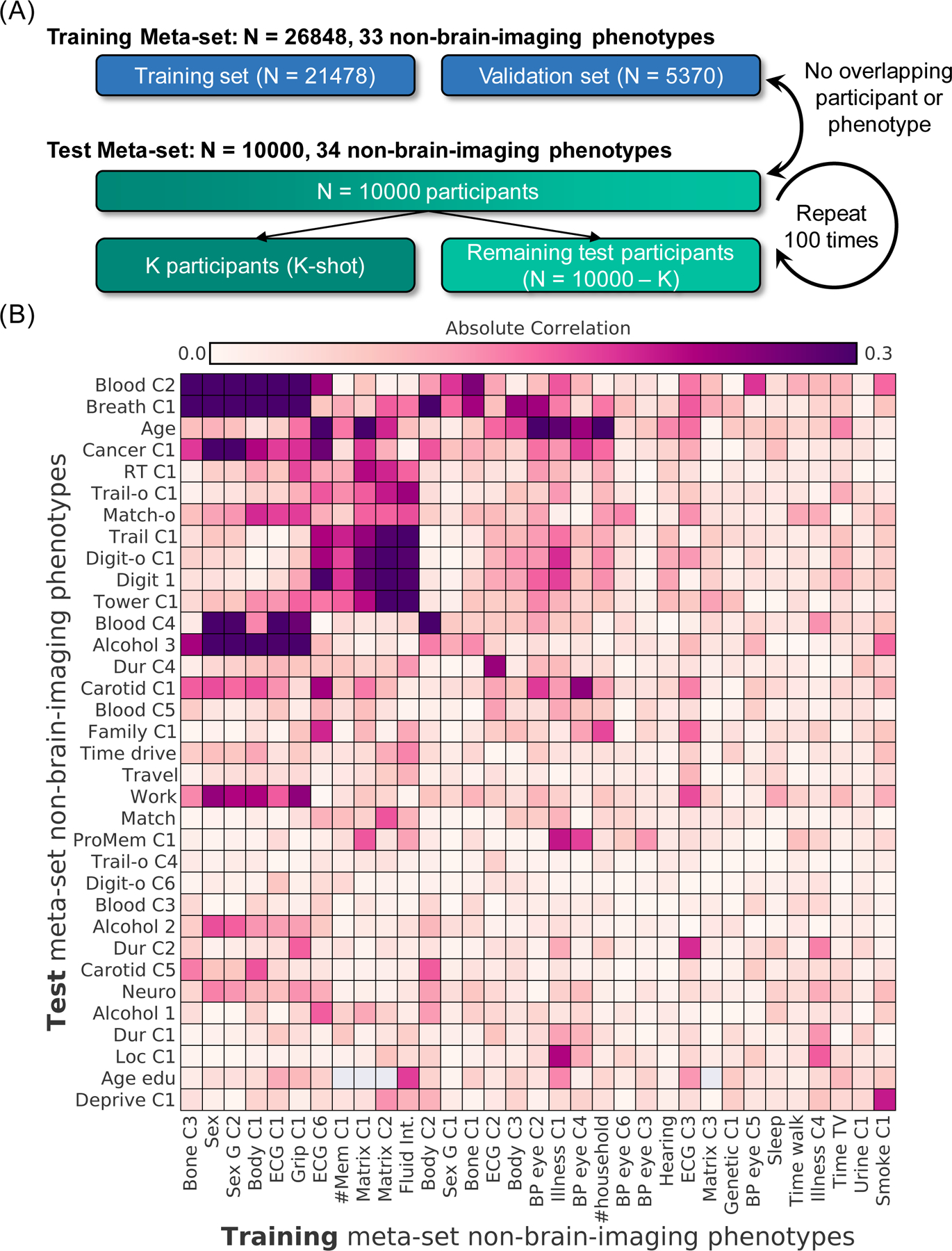
The goal of meta-matching is to translate predictive models from big datasets to new unseen phenotypes in independent small datasets. (A) The UK Biobank dataset (Jan 2020 release) was divided into a training meta-set comprising 26,848 participants and 33 phenotypes, and a test meta-set comprising independent 10,000 participants and 34 other phenotypes. It is important to emphasize that no participant or phenotype overlapped between training and test meta-sets. The test meta-set was in turn split into K participants (K = 10, 20, 50, 100, 200) and remaining 10,000-K participants. The group of K participants mimicked studies with traditionally common sample sizes. This split was repeated 100 times for robustness. (B) Absolute Pearson’s correlations between phenotypes in training and test metasets. Each row represents one test meta-set phenotype. Each column represents one training meta-set phenotype. Figures S2 and S3 show correlation plots for phenotypes within training and test meta-sets. Dictionary of phenotypes is found in Tables S1 and S2.

For each phenotype in the test meta-set, a classical machine learning baseline (KRR) was trained on the RSFC matrices of the K participants and applied to the remaining 10,000 – K participants. Hyperparameters were tuned on the K participants. We note that small-N studies obviously do not have access to the remaining 10,000 – K participants. However, in our experiments, we utilized a large sample of participants (10,000 – K) to accurately establish the performance of the classical machine learning baseline. We repeated this procedure 100 times (each with different sample of K participants) to ensure robustness of the results⁴⁸.

KRR was chosen as a baseline because of the small number of hyperparameters, which made it suitable for small-N studies. We have also previously demonstrated that KRR and deep neural networks can achieve comparable prediction performance in functional connectivity prediction of behavior and demographics in both small-scale and large-scale datasets¹¹.

2.2. Basic meta-matching outperforms classical KRR

The meta-matching framework is highly flexible and can be instantiated with different machine learning algorithms. Here, we considered KRR and fully connected DNN, which we have previously demonstrated to work well for RSFC-based behavioral and demographics prediction¹¹. We considered two classes of meta-matching algorithms: basic and advanced (Figure 2).

Figure 2. Application of basic and advanced meta-matching to the UK Biobank.

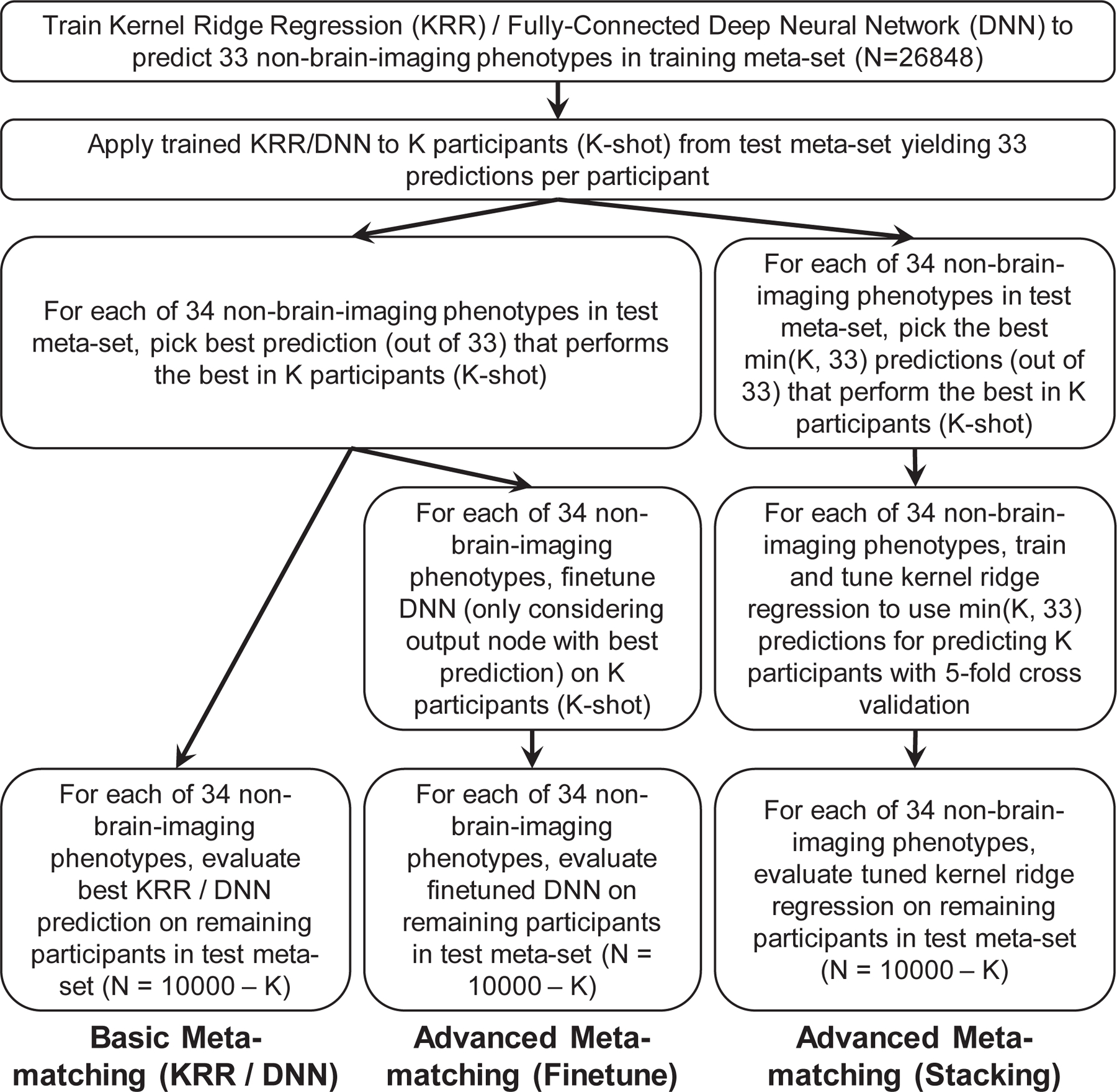
The meta-matching framework can be instantiated using different machine learning algorithms. Here, we incorporated kernel ridge regression (KRR) and fully-connected feedforward deep neural network (DNN) within the meta-matching framework. We proposed two classes of meta-matching algorithms: basic and advanced. In the case of basic meta-matching, we considered two variants: basic meta-matching (KRR) and basic meta-matching (DNN). In the case of advanced meta-matching, we considered two variants: advanced meta-matching (finetune) and advanced meta-matching (stacking). Both advanced meta-matching variants utilized the DNN. See text for more details.

In ‘basic meta-matching (KRR)’, for each phenotype in the training meta-set, we trained a kernel ridge regression (KRR) model to predict the phenotype from the RSFC matrices. We then applied the 33 trained KRR models to the RSFC of the K participants (from the test meta-set), yielding 33 predictions per participant. For each test meta-set phenotype, we picked the prediction (out of 33 predictions) that predicted the test meta-set phenotype the best in the K participants. The corresponding KRR model (yielding this best prediction) was used to predict the test phenotype in the remaining 10,000 – K participants. We also repeated the above procedure using a generic fully connected feedforward DNN instead of KRR, yielding the ‘basic meta-matching (DNN)’ algorithm. The only difference is that instead of training 33 DNNs (which would require too much computational time), a single 33-output DNN was utilized. See Methods for details.

Figure 3A shows the prediction accuracies (Pearson’s correlation coefficient) averaged across 34 phenotypes and 10,000 – K participants in the test meta-set. The boxplots represent 100 random repeats of K participants (K-shot). Bootstrapping was utilized to derive p values (Figure 3B; Figure S4; see Methods). Multiple comparisons were corrected using false discovery rate (FDR, q < 0.05). Both basic meta-matching algorithms were significantly better than the classical (KRR) approach across all sample sizes (Figure 3B). The improvements were large. For example, in the case of 20-shot (a typical sample size for many fMRI studies), basic meta-matching (DNN) was more than 100% better than classical (KRR): 0.124 ± 0.016 (mean ± std) versus 0.052 ± 0.007. Indeed, classical (KRR) required 200 participants before achieving an accuracy (0.120 ± 0.005) comparable to basic meta-matching (DNN) with 20 participants.

Figure 3. Meta-matching reliably outperforms predictions from classical kernel ridge regression (KRR) in the UK Biobank.

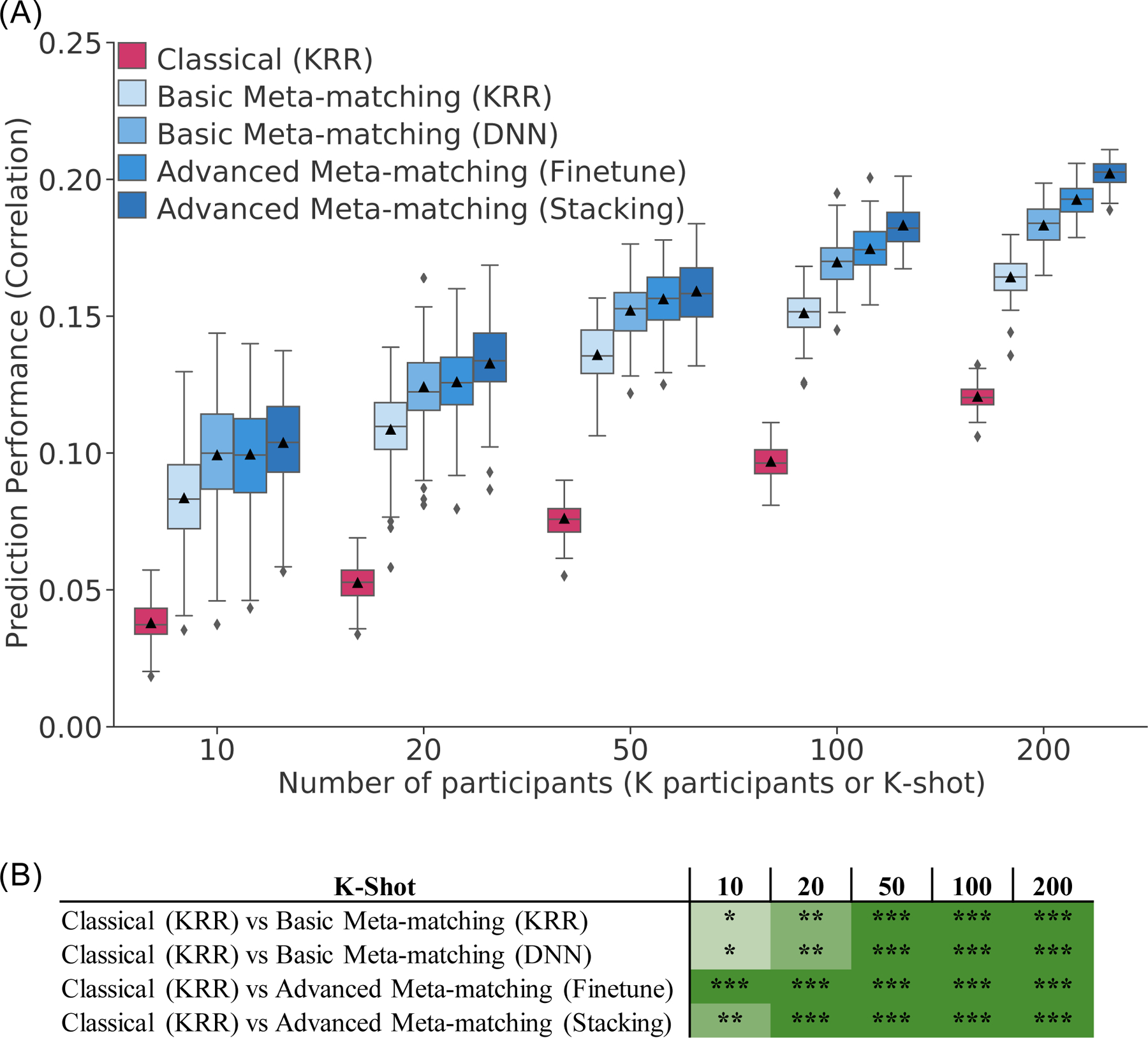
(A) Prediction performance (Pearson’s correlation) averaged across 34 phenotypes in the test meta-set (N = 10,000 – K). The K participants were used to train and tune the models (Figure 2). Boxplots represent variability across 100 random repeats of K participants (Figure 1A). Whiskers represent 1.5 inter-quartile range. (B) Statistical difference between the prediction performance (Pearson’s correlation) of classical (KRR) baseline and meta-matching algorithms. P values were calculated based on a two-sided bootstrapping procedure (see Methods). “*” indicates p < 0.05 and statistical significance after multiple comparisons correction (FDR q < 0.05). “**” indicates p < 0.001 and statistical significance after multiple comparisons correction (FDR q < 0.05). “***” indicates p < 0.00001 and statistical significance after multiple comparisons correction (FDR q < 0.05). “n.s.” indicates no statistical significance (p ≥ 0.05) or did not survive FDR correction. Green color indicates that meta-matching methods were statistically better than classical (KRR). The actual p values and statistical comparisons among all algorithms are found in Figure S4. Prediction performance measured using coefficient of determination (COD) is found in Figure S5.

When utilizing coefficient of determinant (COD) as a metric of prediction performance (Figures S5 and S6), all algorithms performed poorly (COD ≤ 0) when there were 20 or less participants (K = 10 or 20), suggesting worse than chance prediction. When there were at least 50 participants (K ≥ 50), basic meta-matching algorithms became substantially better than classical (KRR) approach. However, the improvement was only statistically significant starting from around 100–200 participants.

To summarize, basic meta-matching performed well even with 10 participants if the goal was ‘relative’ prediction (i.e., Pearson’s correlation⁴⁹). However, if the goal was ‘absolute’ prediction (i.e., COD⁷), then basic meta-matching required at least 100 participants to work well.

2.3. Advanced meta-matching provides further improvement

We have demonstrated that basic meta-matching led to significant improvement over the classical (KRR) baseline. However, in practice, there might be significant differences between the training and test meta-sets, so simply picking the best phenotypic prediction model from the training meta-set might not generalize well to the test meta-set. Thus, we proposed two additional meta-matching approaches: ‘advanced meta-matching (finetune)’ and ‘advanced meta-matching (stacking)’.

As illustrated in Figure 2, the procedure for advanced meta-matching (finetune) is similar to basic meta-matching (DNN). Briefly, we trained a single DNN (with 33 outputs) on the training meta-set. We then applied the 33-output DNN to the K participants and picked the best DNN model for each test phenotype (out of 34 phenotypes). We then finetuned the top two layers of the DNN using the K participants before applying the finetuned model to the remaining 10,000 – K participants. See Methods for details. This approach can be thought of as complementing basic meta-matching with a simple form of transfer learning⁵⁰.

In the case of advanced meta-matching (stacking), we trained a single DNN (with 33 outputs) on the training meta-set. We then applied the 33-output DNN to the K participants, yielding 33 predictions per participant. The top M predictions are then used as features for predicting the phenotype of interest in the K participants using KRR. To reduce overfitting, M is set to be the minimum of 33 and K. For example, for the 10-shot scenario, M is set to be 10. For the 50-shot scenario, M is set to be 33. The DNN (which was trained on the training meta-set) and KRR models (which were trained on the K participants) were then applied to the remaining 10,000 – K participants. See Methods for details. This approach can be thought of as complementing basic meta-matching with the classic stacking strategy^51,52.

Figure 3A shows the prediction accuracies (Pearson’s correlation coefficient) averaged across 34 phenotypes and 10,000 – K participants in the test meta-set. Both advanced meta-matching algorithms exhibited large and statistically significant improvements over classical (KRR) approach across all sample sizes (Figure 3B). For example, in the case of 20-shot, advanced meta-matching (stacking) was more than 100% better than classical (KRR): 0.133 ± 0.014 (mean ± std) versus 0.053 ± 0.007. Among the meta-matching algorithms, the advanced meta-matching algorithms were numerically better than the basic meta-matching algorithms from 20-shot onwards, but statistical significance was not achieved until around 100-shot onwards (Figure S4B).

In the case of variance explained as measured by COD (Figures S5 and S6), all algorithms performed poorly (COD ≤ 0) when there were less than 50 participants (K < 50), suggesting chance or worse than chance prediction. From 50-shot onwards, advanced meta-matching algorithms became statistically better than classical (KRR) approach (Figures S5B and S6B). The improvements were substantial. For example, in the case of 100-shot, advanced meta-matching (stacking) was 400% better than classical (KRR): 0.053 ± 0.005 (mean ± std) versus 0.010 ± 0.004. Among the meta-matching algorithms, the advanced meta-matching algorithms were numerically better than the basic meta-matching algorithms from 100-shot onwards, but statistical significance was not achieved until 200-shot (Figure S6B).

To summarize, advanced meta-matching performed well even with 10 participants if the goal was ‘relative’ prediction (i.e., Pearson’s correlation⁴⁹). However, if the goal was ‘absolute’ prediction (i.e., COD⁷), then advanced meta-matching required at least 50 participants to work well.

2.4. Correlations between phenotypes drive improvements

Despite the substantial advantage of meta-matching over classical (KRR), not every phenotype benefited from meta-matching. For example, in the case of 100-shot, the average performance (Pearson’s correlation) of classical (KRR) and advanced meta-matching (stacking) were 0.097 ± 0.006 (mean ± std) and 0.183 ± 0.007, respectively. This represented an average absolute gain of 0.086 (min = −0.023, max = 0.266) across 34 test phenotypes. In the case of COD, there was an average absolute gain of 0.043 (min = −0.012, max = 0.268) across test 34 phenotypes.

Figures 4 illustrates the 100-shot prediction performance (Pearson’s correlation coefficient) of four test meta-set phenotypes across all approaches. Figure S7 shows the same plot for COD. For three of the phenotypes (average weekly beer plus cider intake, symbol digit substitution and matrix pattern completion), meta-matching demonstrated substantial improvements over classical (KRR). In the case of the last phenotype (time spent driving per day), meta-matching did not yield any statistically significant improvement.

Figure 4. Examples of phenotypic prediction performance in the test meta-set (N = 9,900) in the case of 100-shot learning.

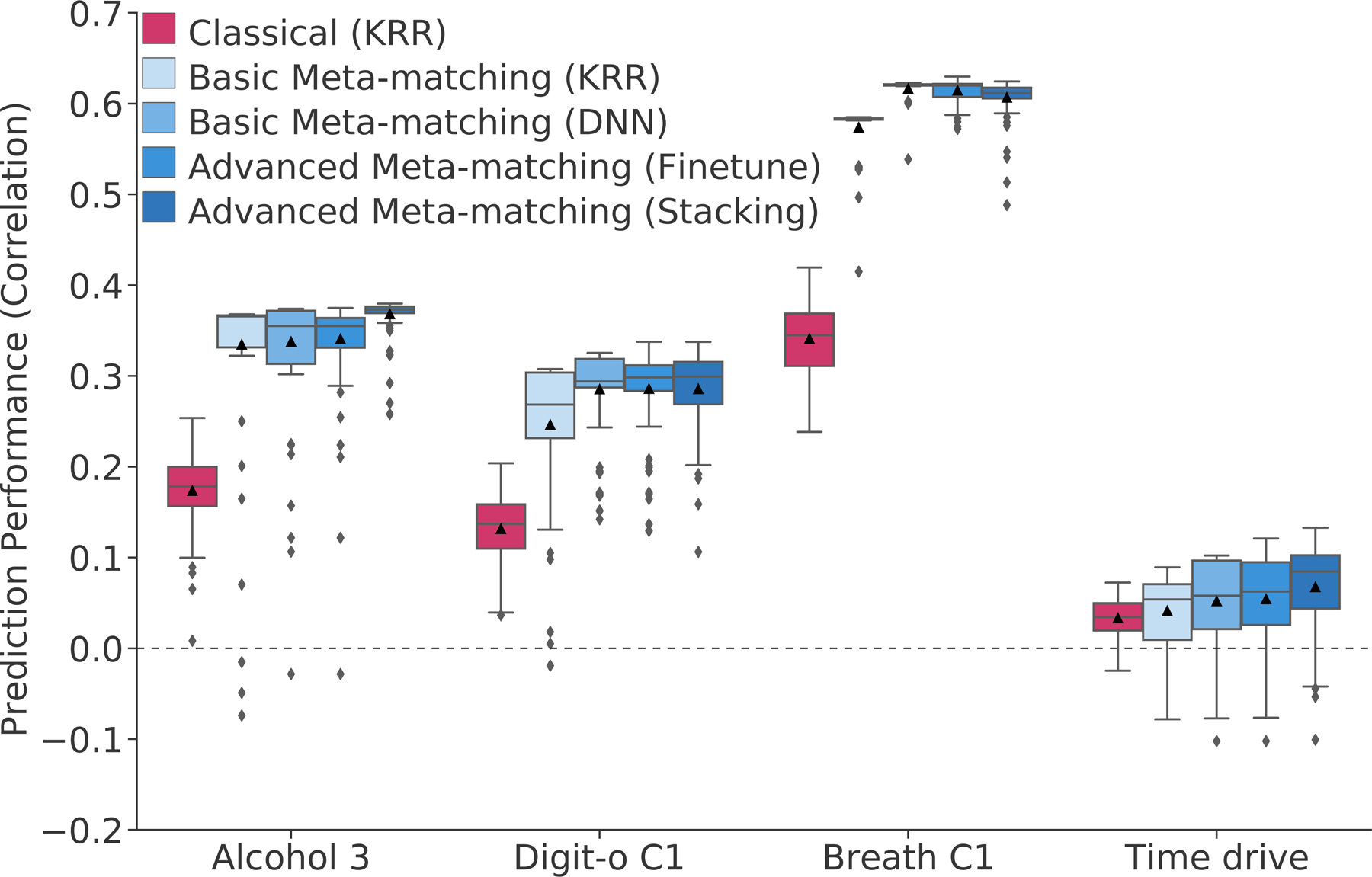
Here, prediction performance was measured using Pearson’s correlation. “Alcohol 3” (average weekly beer plus cider intake) was most frequently matched to “Bone C3” (bone-densitometry of heel principal component 3). “Digit-o C1” (symbol digit substitution online principal component 1) was most frequently matched to “Matrix C1” (matrix pattern completion principal component 1). “Breath C1” (spirometry principal component 1) was most frequently matched to “Grip C1” (hand grip strength principal component 1). “Time drive” (Time spent driving per day) was most frequently matched to “BP eye C3” (blood pressure & eye measures principal component 3). For each boxplot, the horizontal line indicates the median and the black triangle indicates the mean. The bottom and top edges of the box indicate the 25th and 75th percentiles respectively. Whiskers correspond to 1.5 times the interquartile range. Outliers are defined as data points beyond 1.5 times the interquartile range. Figure S7 shows an equivalent figure using coefficient of determination (COD) as the prediction performance measure.

Given that meta-matching exploits correlations among phenotypes, we hypothesized that variability in prediction improvements were driven by inter-phenotype correlations between the training and test meta-sets (Figures 1B & S1B). Figure 5 shows the performance improvement (Pearson’s correlation) as a function of the maximum correlation between each test phenotype and training phenotypes. Figure S8 shows the same plot for COD. As expected, test phenotypes with stronger correlations with at least one training phenotype led to greater prediction improvement with meta-matching. Despite the small number of participants employed in the K-shot scenarios, Figure S9 shows that most of the time, meta-matching was able to select training phenotypes that were strongly correlated with the test phenotypes. Interestingly, phenotypes that were better predicted by classical (KRR) also benefited more from meta-matching (Figures S10 and S11).

Figure 5. Prediction improvements were driven by correlations between training and test meta-set phenotypes.

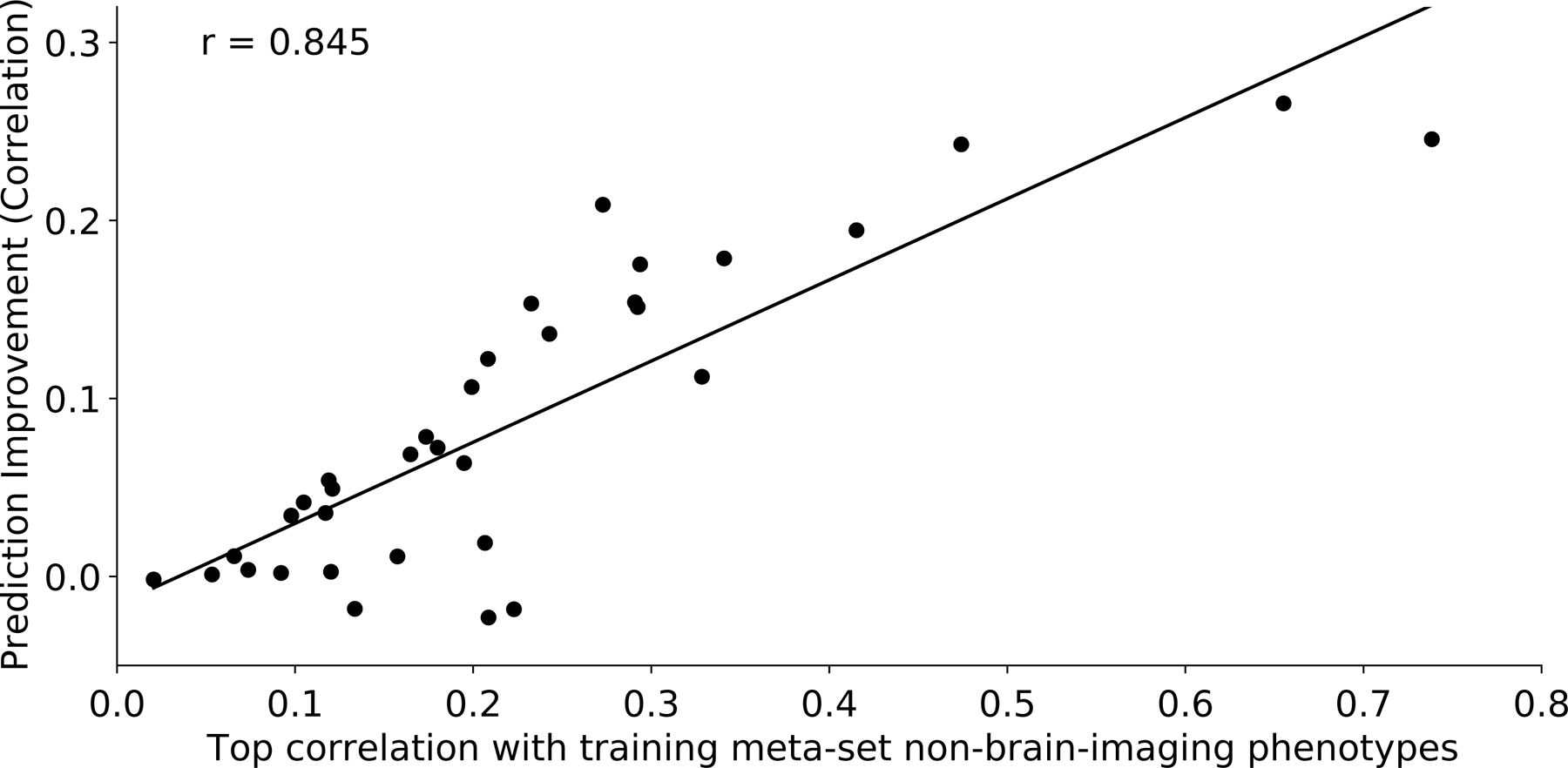
Vertical axis shows the prediction improvement of advanced meta-matching (stacking) with respect to classical (KRR) baseline under the 100-shot scenario. Prediction performance was measured using Pearson’s correlation. Each dot represents a test meta-set phenotype. Horizontal axis shows each test phenotype’s top absolute Pearson’s correlation with phenotypes in the training meta-set. Test phenotypes with stronger correlations with at least one training phenotype led to greater prediction improvement with meta-matching. Similar conclusions were obtained with coefficient of determination (Figure S8).

2.5. Human Connectome Project (HCP) experiment setup

The previous analysis (Figure 3) suggests that meta-matching can perform well in the UK Biobank. However, both training and test meta-sets were drawn from the same dataset. To demonstrate that meta-matching can generalize well to a completely new dataset from a different MRI scanner with distinct demographics and pre-processing, we considered data from the Human Connectome Project (HCP⁴⁷). There were several important differences between the HCP and UK Biobank, including age (22 to 35 in the HCP versus 40 to 69 in the UK Biobank), preprocessing (grayordinate combined surface-volume coordinate system in the HCP versus MNI152 coordinate system in the UK Biobank) and scanners (highly customized Skyra scanner in the HCP versus ‘off-the-shelf’ Skyra scanners in the UK Biobank).

We note that 55 × 55 RSFC matrices were not available in the HCP dataset, so the following analyses utilized 419 × 419 RSFC matrices from both UK Biobank and HCP. The training meta-set comprised 36,847 UK Biobank participants with 419 × 419 RSFC matrices and 67 phenotypes (Figure 6A). The test meta-set comprised 1,019 HCP participants with 419 × 419 RSFC matrices and 35 phenotypes (Figure 6A). The 35 HCP phenotypes were winnowed down from 58 phenotypes by excluding phenotypes that were not predictable in the full HCP dataset (see Methods for more details). Given that KRR was applied to the entire HCP dataset to select the final set of phenotypes, we note that this procedure is biased in favor of the KRR baseline.

Figure 6. Experiment setup for meta-matching in the Human Connectome Project (HCP).

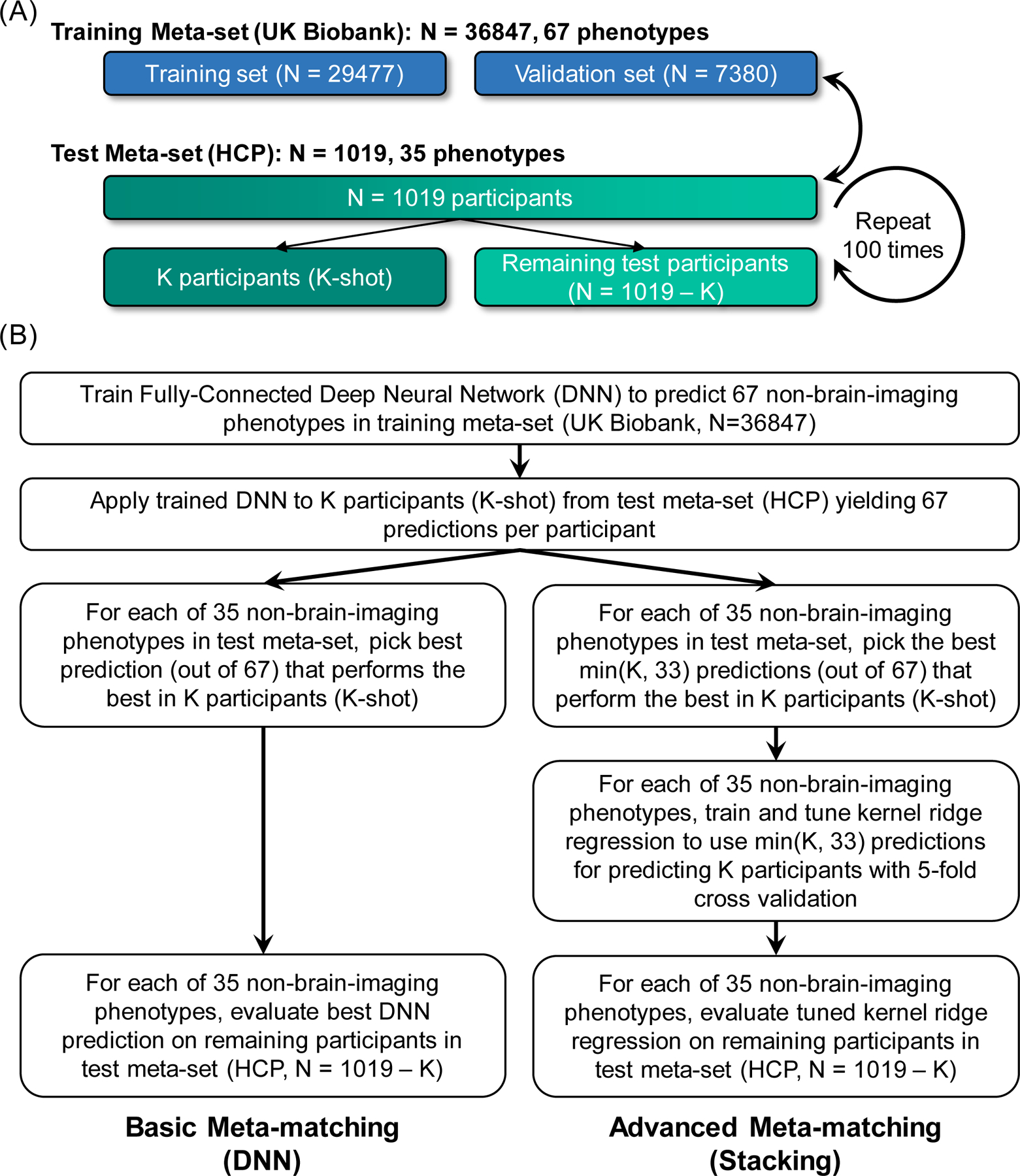
(A) The training meta-set comprised 36,847 UK Biobank participants and 67 phenotypes. The test meta-set comprised 1,019 HCP participants and 36 phenotypes. It is important to emphasize that no participant or phenotype overlapped between training and test meta-sets. The test meta-set was in turn split into K participants (K = 10, 20, 50, 100, 200) and remaining 1,019-K participants. This split was repeated 100 times for robustness. (B) Application of basic and advanced meta-matching to the HCP dataset. Here, we considered basic meta-matching (DNN) and advanced meta-matching (stacking).

Overall, the experimental setup (Figure 6) was the same as the UK Biobank analyses (Figures 1 and 2), except for the choice of training and test meta-sets. In addition, basic meta-matching (DNN) and advanced meta-matching (stacking) were the most promising approaches among the basic and advanced meta-matching approaches respectively in the UK Biobank (Figure 3), so we will focus on these two approaches.

2.6. Meta-matching outperforms classical KRR in the HCP

Figure 7A shows the prediction accuracies (Pearson’s correlation coefficient) averaged across 35 phenotypes and 1,019 – K participants in the HCP test meta-set. The boxplots represent 100 random repeats of K participants (K-shot). Bootstrapping was used to derive p values (Figure 7B; Figure S12; see Methods). Multiple comparisons were corrected using false discovery rate (FDR, q < 0.05). The results were very similar to experiment 1. Both meta-matching algorithms were significantly better than the classical (KRR) approach for 20-shot and above (Figure 7B). The improvements were large. For example, in the case of 20-shot (a typical sample size for many fMRI studies), basic meta-matching (DNN) was more than 100% better than classical (KRR): 0.123 ± 0.028 (mean ± std) versus 0.047 ± 0.016. Advanced meta-matching (stacking) was numerically (but not statistically) better than basic meta-matching (DNN).

Figure 7. Meta-matching reliably outperforms classical kernel ridge regression (KRR) in the HCP.

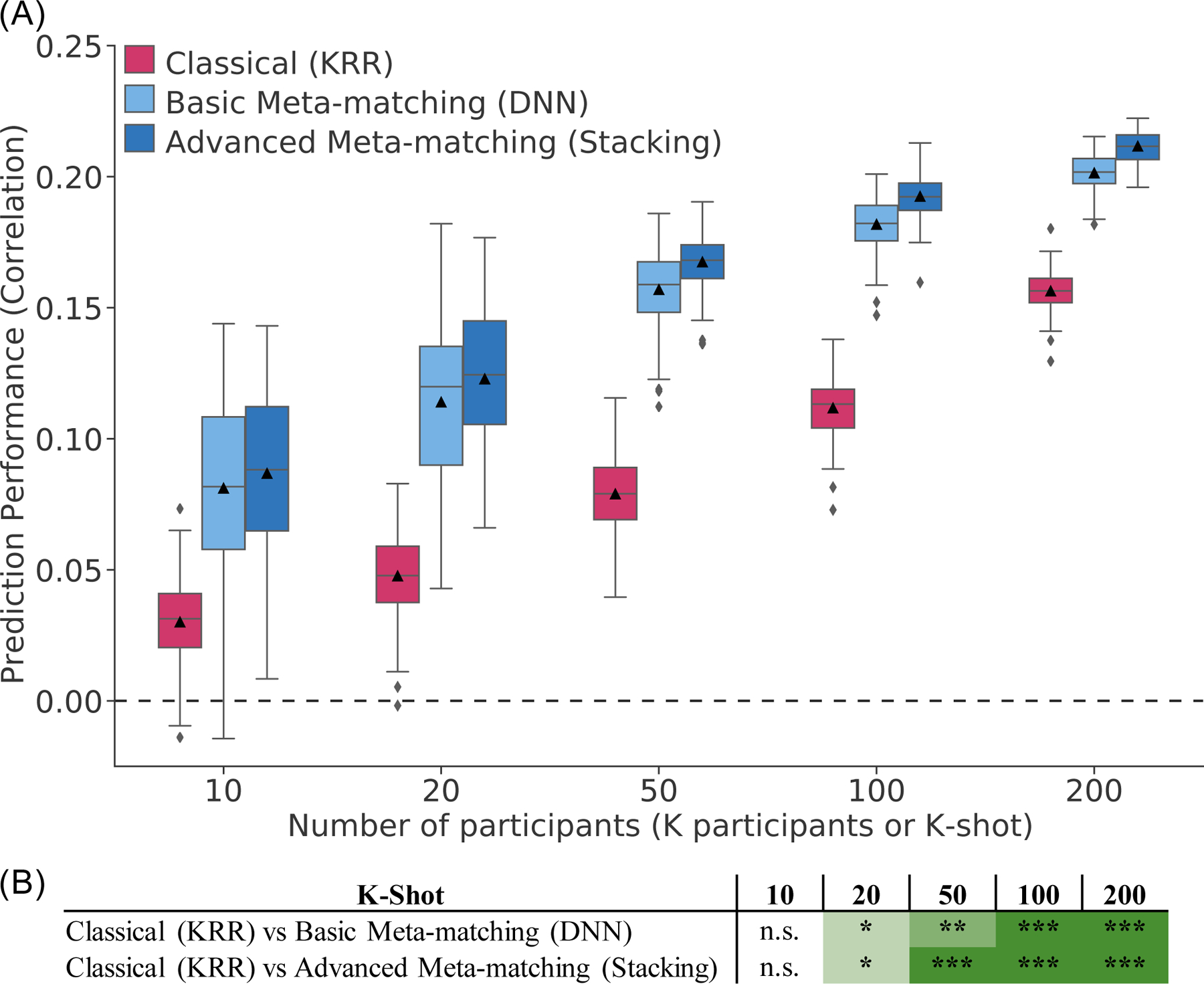
(A) Prediction performance (Pearson’s correlation) averaged across 35 phenotypes in the test meta-set (N = 1,019 – K). The K participants were used to train and tune the models (Figure 6B). Boxplots represent variability across 100 random repeats of K participants (Figure 6A). For each boxplot, the horizontal line indicates the median and the black triangle indicates the mean. The bottom and top edges of the box indicate the 25th and 75th percentiles respectively. Whiskers correspond to 1.5 times the interquartile range. Outliers are defined as data points beyond 1.5 times the interquartile range. (B) Statistical difference between the prediction performance (Pearson’s correlation) of classical (KRR) baseline and meta-matching algorithms. P values were calculated based on a two-sided bootstrapping procedure (see Methods). “*” indicates p < 0.05 and statistical significance after multiple comparisons correction (FDR q < 0.05). “**” indicates p < 0.001 and statistical significance after multiple comparisons correction (FDR q < 0.05). “***” indicates p < 0.00001 and statistical significance after multiple comparisons correction (FDR q < 0.05). “n.s.” indicates no statistical significance (p ≥ 0.05) or did not survive FDR correction. The actual p values and statistical comparisons among all algorithms are found in Figure S12. Prediction performance measured using coefficient of determination (COD) is found in Figure S13. Green color indicates that meta-matching methods were statistically better than classical (KRR).

In the case of explained variance measured by COD (Figures S13 and S14), all algorithms performed poorly (COD ≤ 0) when there were 10 participants (K = 10), suggesting worse than chance prediction. When there were at least 50 participants (K ≥ 50), basic meta-matching (DNN) became substantially better than classical (KRR) approach. However, the improvement was only statistically significant when there were at least 100 participants (K ≥ 100). On the other hand, advanced meta-matching (stacking) was statistically better than classical (KRR) when there were at least 20 participants (K ≥ 20). Again, the improvements were substantial. For example, in the case of 100-shot, advanced meta-matching (stacking) was 800% better than classical (KRR): 0.045 ± 0.005 (mean ± std) versus 0.005 ± 0.006.

However, similar to the UK Biobank, despite the substantial advantage of meta-matching over classical (KRR), not every phenotype benefited from meta-matching. For example, in the case of 100-shot, the average performance (Pearson’s correlation) of classical (KRR) and advanced meta-matching (stacking) were 0.112 ± 0.011 (mean ± std) and 0.192 ± 0.008. This represented an average absolute gain of 0.081 (min = −0.029, max = 0.189) across 35 test phenotypes. In the case of COD, there was an average absolute gain of 0.040 (min = −0.002, max = 0.160) across 35 test phenotypes.

2.7. Interpreting meta-matching with the Haufe transform

The primary goal of our study is to improve phenotypic prediction. However, a pertinent question is whether interpretation of the resulting meta-matching models might be biased by pre-trained predictive models. Most previous studies have interpreted the regression weights or selected features of predictive models, which could be highly misleading⁵³. Here, we consider the Haufe’s transform⁵³ that yields a positive (or negative) predictive-feature value for each RSFC edge. A positive (or negative) predictive-feature value indicates that higher RSFC for the edge was associated with the predictive model predicting greater (or lower) value for the phenotype. We refer to the outputs of the Haufe transform as predictive network features (PNFs).

We will focus on the 100-shot scenario. First, for each HCP phenotype, we derived pseudo ground truth PNFs by training a KRR model on the full HCP dataset (N = 1,019) and then applied the Haufe transform to the KRR model. We then computed PNFs for various approaches to compare against the ground truth. In the case of classical (KRR), we trained the KRR model on 100 random HCP participants (i.e., 100-shot) and then computed the PNFs. In the case of basic meta-matching (DNN) and advanced meta-matching (stacking), we translated the trained UK Biobank model on the 100 HCP participants using meta-matching and then computed the PNFs. We also computed PNFs by applying the Haufe transform to the trained UK Biobank model using UK Biobank RSFC data and the best phenotype selected by basic meta-matching (DNN), which we will refer to as ‘basic meta-matching (DNN) training’. We then correlated the resulting PNFs with the ground-truth PNFs. This procedure was repeated 100 times and correlations with the ground truth was averaged across the 100 repetitions.

It is important to note that the pseudo ground truth was derived using KRR, which is therefore biased towards classical (KRR). Nevertheless, as shown in Figure 8, we found that advanced meta-matching (stacking) was numerically closer to the ‘ground truth’ than the PNFs from classical (KRR), although the difference was not statistically significant. On the other hand, PNFs from advanced meta-matching (stacking) was statistically closer to the pseudo ground truth than basic meta-matching (DNN) and basic meta-matching (DNN) training.

Figure 8. Agreement (correlation) of predictive network features with pseudo ground truth in the HCP dataset.

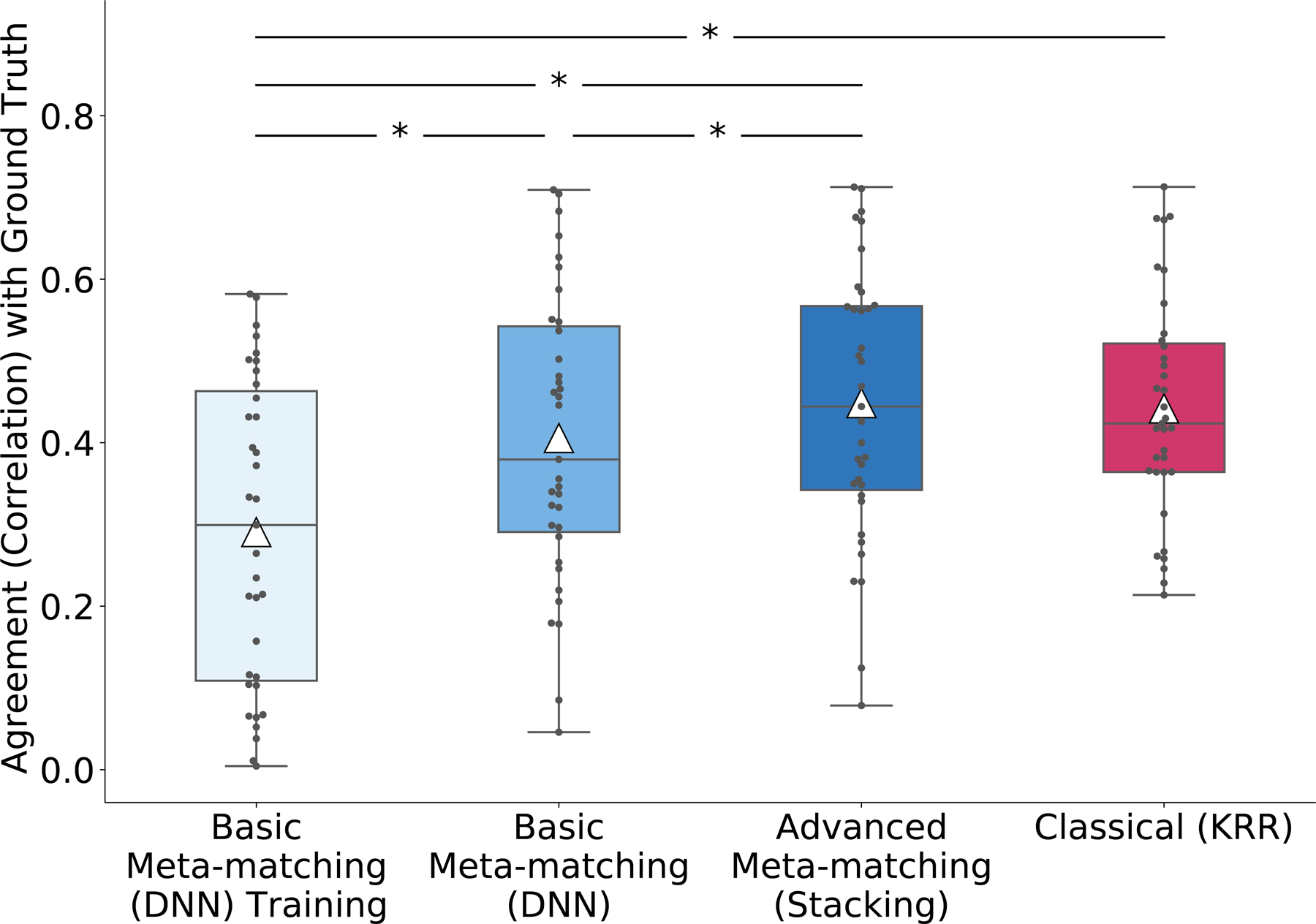
For both meta-matching (stacking) and classical (KRR), the Haufe transform⁵³ was utilized to estimate predictive network features (PNFs) in the 100-shot scenario (N = 100). Pseudo ground truth PNFs were generated by applying the Haufe transform to a KRR model trained from the full HCP dataset (N = 1,019). PNFs was also estimated for basic meta-matching (DNN) training based on the UK Biobank (N = 29,477). We found that the PNFs derived from meta-matching (stacking) and classical (KRR) achieved similar agreement with pseudo ground truth. For each boxplot, the horizontal line indicates the median and the black triangle indicates the mean. The bottom and top edges of the box indicate the 25th and 75th percentiles respectively. Whiskers correspond to 1.5 times the interquartile range. Outliers are defined as data points beyond 1.5 times the interquartile range.

3. DISCUSSION

In this study, we proposed ‘meta-matching’, a simple framework to effectively translate predictive models from large-scale datasets to new phenotypes in small data. Using a large sample of almost 40,000 participants from the UK Biobank, we demonstrated that meta-matching can dramatically boost prediction performance in the small-sample scenario. We also demonstrated that the DNN trained on the UK Biobank can be translated well to the HCP dataset from a different scanner with different demographics and preprocessing. Overall, our results suggest that meta-matching will be extremely helpful for boosting the predictive power in small-scale boutique studies focusing on specific neuroscience questions or clinical populations.

3.1. Interpretation of meta-matching

Given that meta-matching exploits correlations among phenotypes, the prediction mechanism might potentially be non-causal. However, we note that the primary goal of this study is to improve phenotypic prediction. There are many applications, where prediction performance is inherently useful^1,54 even if the prediction is achieved via potentially non-causal routes. For example, antidepressants take at least four weeks to start working and less than 50% of patients respond well to the first drug prescribed to them. Therefore, improving the ability to predict the best depression treatment is clinically useful even if the prediction mechanism is potentially ‘confounded’.

Furthermore, exploiting phenotypic correlations for prediction does not imply that the prediction is necessarily confounded. Related behaviors (e.g., negative affect, low mood, anxiety, etc) are often correlated because of common underlying neurobiology. Exploiting such correlational structure to improve prediction is entirely appropriate. For example, translating a negative affect predictive model from a large-scale database to improve anxiety prediction in patients with post-traumatic stress disorder should not be considered as confounding.

There are situations where phenotypic correlations should be considered confounds, but whether a variable is a confound or not, is highly dependent on the goal of a study. For example, age is causally related to Alzheimer’s Disease dementia. However, if a study is interested in dementia risks above and beyond aging, then age becomes a confound. Therefore, all observational studies (including studies using meta-matching) should carefully consider what are confounds (or not) on a case-by-case manner. Overall, we believe that handling confounds in meta-matching, while an important consideration, is no different from other observational studies.

To illustrate how confounding phenotypes might be handled in meta-matching, let us focus on advanced meta-matching (stacking). If a researcher believes a-priori that a particular training phenotype (e.g., age) is a confound for the prediction of a test phenotype (e.g., Alzheimer’s Disease), then the researcher can regress the training phenotype (e.g., age) from the variables in the training meta-set before training. The researcher can also regress the predicted training phenotype (e.g., predicted age) from the other predicted variables in the K participants (in the test meta-set) before performing stacking. Alternatively, the stacking model can be interpreted (e.g., using the Haufe transform) to infer the extent to which different training phenotypes (e.g., age) contributed to the prediction of the test phenotype (e.g., AD). The researcher can then reason whether the prediction mechanism is confounded or not in the specific application.

Our results (Figure 8) also suggest that meta-matching models are not less interpretable than classical approaches in terms of predictive network features extracted by the Haufe transform. However, both classical (KRR) and advanced meta-matching (stacking) only exhibited moderate similarity with the pseudo ground truth (correlation ≈ 0.4), suggesting that interpreting predictive models built on small datasets remains an open research question not just in neuroscience but also in machine learning.

Finally, it is worth noting that the Haufe transform was developed to interpret linear predictive (discriminative) models, so it is directly applicable to KRR given our choice of a linear kernel. Application of the Haufe transform to advanced meta-matching (stacking) is equivalent to seeking a linear interpretation of the nonlinear model⁵³ (see equation 8 of reference), which might therefore provide an incomplete interpretation.

3.2. Meta-matching model 1.0

The full UK Biobank DNN model (trained with 36,847 participants and 67 phenotypes) is made publicly available as part of this study. We will refer to this model as ‘meta-matching model 1.0’. To illustrate its use, let us consider a hypothetical new study with 100 participants.

The researcher should first validate the meta-matching approach on their data by adapting meta-matching model 1.0 on 80 random participants (using meta-matching stacking) and testing on the remaining 20 participants. This procedure can be repeated multiple times and an average performance can be computed. Assuming the resulting prediction performance is satisfactory, the researcher can then move on to the next step, which is dependent on the goal of the researcher.

If the goal is to obtain prediction for the 100 participants, for each participant, the researcher can first translate the meta-matching model to the other 99 participants (i.e., 99-shot) and then use the model to predict the phenotype of the left-out participant. On the other hand, if the goal is to predict new participants beyond the 100 participants, the researcher can adapt the meta-matching model to all 100 participants (i.e., 100-shot). This final adapted model can then be applied to new participants beyond the 100 participants. Furthermore, the researcher can also interpret the final adapted model for new insights into the brain, e.g., by using the Haufe transform⁵³.

3.3. Absolute versus relative prediction performance

We note that a variety of prediction performance measures have been utilized in the literature. For studies interested in relative ranking^41,49, Pearson’s correlation is a common performance metric. We showed that if Pearson’s correlation was used as a performance metric, meta-matching performed very well even with as few as 10 participants (Figure 3). Thus, if the experimenter’s goal is relative ranking, then our experiments suggest that meta-matching is superior regardless of sample sizes.

However, others have strongly argued in favor of absolute prediction performance⁷. In this scenario, COD is a common performance metric that measures variance explained by the predictive algorithm. In the case of the UK Biobank, advanced meta-matching dramatically outperformed classical (KRR) in terms of COD, when there were at least 50 participants (Figure S5). In the case of the HCP dataset, advanced meta-matching dramatically outperformed classical (KRR) in terms of COD, when there were at least 20 participants (Figure S14). Thus, our experiments suggest that absolute prediction is unlikely to be successful with less than 20 participants and should not be considered a realistic goal.

3.4. Limitations & future work

Although the core idea behind meta-matching is to exploit correlations among phenotypes, we note that the resulting algorithms leverage on several closely related ideas in machine learning, including meta-learning, multi-task learning and transfer learning¹⁷. For example, the use of a single neural network to predict all phenotypes simultaneously is known as multi-task learning⁵⁵. The finetuning component of advanced meta-matching (finetune) can be thought of as a simple version of network-based transfer learning⁵⁰. Similarly, advanced meta-matching (stacking) seeks to exploit the benefits of ‘averaging’ predictions^51,52 on top of the core idea of meta-matching. However, it is worth noting that the largest gain in performance (e.g., K = 100-shot in Figures 3 and 7) comes from the core idea of meta-matching. The additional machine learning techniques (e.g., finetuning and stacking) do further boost performance, but at a smaller magnitude. Nevertheless, it is possible that more advanced machine learning approaches can further boost performance. This is a promising avenue for future work.

Because meta-matching exploits correlations between training and test meta-sets, the amount of prediction improvement strongly relied on the strongest correlations between the test phenotype and training phenotypes (Figure 5). Consequently, not all phenotypes benefited from meta-matching. For example, in the case of 100-shot in the HCP dataset, the prediction performance of advanced meta-matching (stacking) was numerically worse for 4 of the 35 phenotypes (in the case of Pearson’s correlation) and 2 of the 35 phenotypes (in the case of COD). However, it is important to note that this limitation exists for all meta-learning and transfer learning algorithms – model transfer is easier if the source and target domains are more similar; performance will degrade if source and target domains are very different.

While initial large-scale projects target young healthy adults, a growing number of large-scale population-level datasets are targeting different populations, including elderly, children, lifespan and different disorders. These newer datasets will likely include rarer phenotypes specific to the target populations. This suggests that phenotypic diversity will continue to grow, which would increase the probability of some phenotypes in some large-scale datasets being correlated with a new phenotype of interest in a smaller dataset. An example of future work would be to develop a meta-matching model based on the ABCD dataset, which includes mental health symptoms, such as the child behavioral checklist (CBCL).

We also note that the UK Biobank does have a large number of mental health measures. However, many of these measures are binary yes/no questions, which might not be sufficiently ‘rich’ for imaging-based prediction. Consequently, these measures were filtered out in our current study. Recent studies have begun to synthesize more meaningful mental health summary measures that are better correlated with brain imaging features⁵⁶. As future work, we hope to build on such efforts, which would allow us to either include these mental health summary measures into an omnibus meta-matching model (that predict a wider variety of phenotypes) or to build a meta-matching model specialized for mental health. Nevertheless, it is likely the case that some rare phenotypes will not be able to benefit from meta-matching.

4. METHODS

4.1. Datasets

This study utilized data from two datasets: the UK Biobank^25,46 and the Human Connectome Project⁴⁷. Our analyses were approved by the National University of Singapore Institutional Review Board.

The UK Biobank (under UK Biobank resource application 25163) is a population epidemiology study with 500,000 adults (age 40–69) recruited between 2006 and 2010⁴⁶. A subset of 100,000 participants is being recruited for multimodal imaging, including brain MRI, e.g., structural MRI and resting-state fMRI (rs-fMRI) from 2016 to 2022^25,46,57,58. A wide range of non-brain-imaging phenotypes was acquired for each participant. Here, we considered the January 2020 release of 37,848 participants with structural MRI and rs-fMRI. Structural MRI (1.0mm isotropic) and rs-fMRI (2.4mm isotropic) were acquired at four imaging centers (Bristol, Cheadle Manchester, Newcastle, and Reading) with harmonized Siemens 3T Skyra MRI scanners. Each participant has one rs-fMRI run with 490 frames (6 minutes) and a TR of 0.735s.

The Human Connectome Project (HCP) S1200 release comprised 1,094 young healthy adults (age 22 to 35) with preprocessed rs-fMRI data^59–61. A number of non-brain-imaging phenotypes was acquired for each participant. For each participant, structural MRI (0.7mm isotropic) and rs-fMRI (2mm isotropic) were acquired at Washington University at St. Louis with a customized Siemens 3T Connectome Skyra MRI scanner. Each participant has two rs-fMRI sessions. Each session has two rs-fMRI runs with 1200 frames (14.4 minutes) each and a TR of 0.72s.

4.2. Brain imaging data

In the case of the UK Biobank analyses (Figures 1 to 5), we utilized 55 × 55 RSFC (partial correlation⁶²) matrices from data-field 25753 of the UK Biobank^25,58. Data-field 25753 RSFC had 100 whole-brain spatial independent component analysis (ICA) derived components⁶³. After the removal of 45 artifactual components, as indicated by the UKB team, 55 components were left²⁵. Data-field 25753 contains two instances, first imaging visit (instance 2) and first repeat imaging visit (instance 3). The first imaging visit (instance 2) had RSFC data for 37,848 participants, while the first repeat imaging visit (instance 3) only had RSFC data for 1,493 participants. Here, we only considered RSFC from the first imaging visit (instance 2).

In the case of the analyses exploring model translation from the UK Biobank to the HCP (Figures 6 to 8), 55 × 55 RSFC matrices were not available in the HCP. Therefore, we considered 419 × 419 RSFC (Pearson’s correlation) matrices for both UK Biobank and HCP, consistent with previous studies from our group^11,35,44. The 419 × 419 RSFC matrices were computed using 400 cortical⁶⁴ and 19 sub-cortical⁶⁵ parcels. In the case of the UK Biobank, ICA-FIX pre-processed volumetric rs-fMRI timeseries data⁵⁸ was projected to MNI152 2mm template space. The timeseries were averaged within each cortical and each subcortical parcel. Pearson’s correlations were computed to generate the 419 × 419 RSFC matrices. In the case of the HCP, we utilized ICA-FIX MSMALL timeseries in the grayordinate (combined surface and subcortical volumetric) space⁶⁶. The timeseries were averaged within each cortical and each subcortical parcel. Pearson’s correlations were computed to generate the 419 × 419 RSFC matrices.

4.3. RSFC-based prediction setup

Our meta-matching framework is highly flexible and can be instantiated with different machine learning algorithms. Here, we considered kernel ridge regression (KRR) and fully-connected feedforward deep neural network (DNN), which we have previously demonstrated to work well for RSFC-based behavioral and demographics prediction¹¹. As discussed in the previous section, each RSFC matrix was a symmetric N x N matrix, where N is the number of independent components or parcels. Here, N = 55 (Figures 1 to 5) or 419 (Figures 6 to 8). Each element represented the degree of statistical dependencies between two brain components. The lower triangular elements of the RSFC matrix of each participant were then vectorized and used as input features for KRR and DNN to predict individuals’ phenotypes.

Kernel ridge regression⁶⁷ is a non-parametric machine learning algorithm. This method is a natural choice as we previously demonstrated that KRR achieved similar prediction performance as several deep neural networks (DNNs) for the goal of RSFC-based behavioral and demographics prediction¹¹. Roughly speaking, KRR predicts the phenotype (e.g., fluid intelligence) of a test participant by the weighted average of all training participants’ phenotypes (e.g., fluid intelligence). The weights in the weighted average are determined by the similarity (i.e., kernel) between the test participant and training participants. In this study, similarity between two participants was defined as the Pearson’s correlation between the vectorized lower triangular elements of their RSFC matrices. KRR also contains an $l_2$ regularization term as part of the loss function to reduce overfitting. The hyperparameter λ is used to control the strength of the $l_2$ regularization^11,67.

A fully-connected feedforward deep neural network (DNN) is one of the most classical DNNs⁶⁸. We previously demonstrated that the feedforward DNN and KRR could achieve similar performance for RSFC-based behavioral and demographics prediction¹¹. In this study, the DNN was trained based on the vectorized lower triangular elements of the RSFC matrix as input features and output the prediction of one or more non-brain-imaging phenotypes. The DNN consists of several fully connected layers. Each node (except input layer nodes) is connected to all nodes in the previous layer. The values at each node is the weighted sum of node values from the previous layer. For example, the value of each node in the first hidden layer is the weighted sum of all input FC values. The outputs of the hidden layer nodes go through a nonlinear activation function, Rectified Linear Units (ReLU;$f\left(x\right)=max\left(0,x\right)$). The output layer is linear. More details about hyperparameter tuning (e.g., number of layers and number of nodes per layer) are found in Supplemental Methods S1. We note that traditional deep convolutional neural networks are invalid for RSFC matrices, so are not utilized.

4.4. Non-brain-imaging phenotype selection in the UK Biobank

In the case of the UK Biobank, to obtain the final set of 67 non-brain-imaging phenotypes, we began by extracting all 3,937 unique phenotypes available to us under UK Biobank resource application 25163. We then performed three stages of selection and processing:

1. In the first stage, we

   • Removed non-continuous and non-integer data fields (date and time converted to float), except for sex.
   • Removed Brain MRI phenotypes (category ID 100).
   • Removed first repeat imaging visit (instance 3).
   • Removed first two instances (instance 0 and 1) if first imaging visit (instance 2) exists and first imaging visit (instance 2) participants were more than double of participants from instance 0 or 1.
   • Removed first instance (instance 0) if only the first two instances (instance 0 and 1) exist, and instance 1 participants were more than double of participants from instance 0.
   • Removed phenotypes for which less than 2000 participants had RSFC data.
   • Removed behaviors with the same value for more than 80% of participants.
     After the first stage of filtering, we were left with 701 phenotypes.
2. We should not expect every phenotype to be predictable by RSFC. Therefore, in the second stage, our goal was to remove phenotypes that could not be well predicted even with large number of participants. More specifically,

   • We randomly selected 1000 participants from 37,848 participants. These 1000 participants were completely excluded from the main experiments (Figure 1A).
   • Using these 1000 participants, kernel ridge regression (KRR) was utilized to predict each of the 701 phenotypes using RSFC. To ensure robustness, we performed 100 random repeats of training, validation, and testing (60%, 20%, and 20%). For each repeat, KRR was trained on the training set and hyperparameters were tuned on the validation set. We then evaluated the trained KRR on the test set. phenotypes with an average test prediction performance (Pearson’s correlation) less than 0.1 were removed.
     At the end of this second stage, 265 phenotypes were left. The list of selected and removed UK Biobank phenotypes can be found in Supplemental Methods S2.

3. Many of the remaining phenotypes were highly correlated. For example, the bone density measurements of different body parts were highly correlated. Principal component analysis (PCA) was performed separately on each subgroup of highly similar phenotypes in the 1000-participant sample. Similarity was evaluated based on the UK Biobank-provided categories of item sets (i.e., items under the same category were considered highly similar). PCAs were not applied to 18 phenotypes (out of 265 phenotypes), which were not similar to other phenotypes. For the purpose of carrying out PCA, missing values were filled in with the EM algorithm⁶⁹. For each PCA, we kept enough components to explain 95% of the variance in the data or 6 components, whichever is lower. Overall, the PCA step reduced the 247 phenotypes (out of 265 phenotypes) to 93 phenotypes. We then repeated the previous step (stage 2) on these 93 phenotypes, resulting in 49 phenotypes with prediction performance (Pearson’s correlation) larger than 0.1. Adding back the 18 phenotypes that were not processed by PCA, we ended up with 67 phenotypes utilized in this manuscript. For the UK Biobank analyses (Figures 1 to 5), this PCA procedure was also applied separately to the training and test meta-sets. For model translation from UK Biobank to HCP (Figures 6 to 8), the PCA procedure was applied to all 36,848 participants.

The final list of the phenotypes for UK Biobank is found in Tables S1 and S2.

4.5. Non-brain-imaging phenotype selection in the HCP

In the case of HCP, we considered 58 non-brain-imaging phenotypes across cognition, emotion and personality, consistent with our previous studies^11,44,70. Of the 1,094 HCP participants, 1,019 participants had all 58 non-brain-imaging phenotypes. We performed KRR and 10-fold inner-loop nested cross-validation to predict each phenotype separately using RSFC. To ensure robustness, we performed 100 random repetitions of the 10-fold nested cross-validation procedure. Phenotypes with an average prediction performance (Pearson’s correlation, averaged across 10 folds and 100 random repetitions) greater than 0.1 were retained, yielding 35 phenotypes. The final list of 35 phenotypes is found in Table S3. Given that KRR was applied to the entire HCP dataset to select phenotypes, we note that this procedure is biased in favor of the KRR baseline. Therefore, the superior prediction performance of meta-matching (Figure 7) was even more noteworthy.

4.6. Data split scheme in the UK Biobank analyses

For the UK Biobank analyses (Figures 1 to 5), we considered 36,848 participants with 55 × 55 RSFC matrices and 67 phenotypes. As illustrated in Figure 1A, we randomly split the data into two meta-sets: training meta-set with 26,848 participants and 33 phenotypes, and test meta-set with 10,000 participants and 34 phenotypes. There was no overlap between the participants and phenotypes across the two meta-set. Figure 1B shows the Pearson’s correlations between the training and test phenotypes. Figures S2 and S3 show correlation plots for phenotypes within training and test meta-sets.

For the training meta-set, we further randomly split it into a training set with 21,478 participants (80% of 26,848 participants) and validation set with 5370 participants (20% of 26,848 participants). For the test meta-set, we randomly split 10,000 participants into K participants (K-shot) and 10,000 – K participants, where K had a value of 10, 20, 50, 100, and 200. The group of K participants mimicked traditional small-N studies. Each random K-shot split was repeated 100 times to ensure stability.

Z-normalization (transforming each variable to have zero mean and unit variance) was applied to the phenotypes. In the case of the training meta-set, z-normalization was performed by using the mean and standard deviation computed from the training set within the training meta-set. In the case of the test meta-set, for each of the 100 repeats of the K-shot learning, the mean and standard deviation were computed from the K participants and subsequently applied to the full test meta-set.

4.7. Data split scheme in the HCP analyses

To translate predictive models from the UK Biobank to HCP, the test meta-set comprised 1,019 HCP participants with 419 × 419 RSFC matrices and 35 phenotypes (Figure 6A). The training meta-set comprised 36,847 participants with 419 × 419 RSFC matrices and 67 phenotypes from the UK Biobank. We further split the training meta-set into a training set with 29,477 participants (80% of 36,847 participants) and a validation set with 7,380 participants (20% of 36,847 participants). For the test meta-set, we randomly split 1,019 participants into K participants (K-shot) and 1,019 – K participants, where K had a value of 10, 20, 50, 100, and 200. The group of K participants mimicked traditional small-N studies. Each random K-shot split was repeated 100 times to ensure stability. Similar to the UK Biobank analyses, z-normalization was applied to the phenotypes.

4.8. Classical Kernel Ridge Regression (KRR) Baseline

For the classical (KRR) baseline, we performed K-shot learning for each non-brain-imaging phenotype in the test meta-set, using K participants from the random split (Figures 1A and 6A). More specifically, for each phenotype, we performed 5-fold cross-validation on the K participants using different values of the hyperparameter λ (that controlled the strength of the $l_2$ regularization). To choose the best hyperparameter, prediction performance was evaluated using the coefficient of determination (COD). The best hyperparameter λ was used to train the KRR model using all K participants. The trained KRR model was then applied to the remaining test participants, i.e., N = 10,000 - K in the case of Figures 1 to 5 and N = 1,019 - K in the case of Figures 6 to 8. Prediction performance in the 10,000 - K (or 1,019 - K) test participants was measured using Pearson’s correlation and COD. This procedure was repeated for each of the 100 random subsets of K participants.

Note that when applied to the 10,000 - K (or 1,019 - K) participants, COD was defined as $1-\frac{{\sum }_i{\left(y_i-{\widehat{y}}_i\right)}^2}{{\sum }_i{\left(y_i-\overline{y}\right)}^2}$, where $y_i$ was the true target variable of the $i$-th participant (among the 10,000 - K participants), ${\widehat{y}}_i$ was the predicted target variable of the $i$-th participant and $\overline{y}$ was the mean target variable in the training set (K participants). The best possible value for COD was 1. It was possible for COD to be less than 0, in which case, we were better off not using any imaging data for prediction. Instead, we could simply predict using the mean target variable in the training set, which would yield a COD of 0.

4.9. Basic meta-matching

The meta-matching framework is highly flexible and can be instantiated with different machine learning algorithms. Here, we incorporated kernel ridge regression (KRR) and fully-connected feedforward deep neural network (DNN) within the meta-matching framework. We proposed two classes of meta-matching algorithms: basic and advanced. In the case of basic meta-matching, we considered two variants: “basic meta-matching (KRR)” and “basic meta-matching (DNN)” (Figures 2 and 6B).

To ease our explanation of basic meta-matching, we will focus on the experimental setup for the UK Biobank analysis (Figures 1 to 5). In the case of basic meta-matching (KRR), we first trained a KRR to predict each training non-brain-imaging phenotype from RSFC. We used the training set (N = 21,478) within the training meta-set for training and validation set (N = 5,370) within the training meta-set for hyperparameter tuning. The hyperparameter λ was selected via a simple grid search. There were 33 phenotypes, so we ended up with 33 trained KRR models from the training meta-set. Second, we applied the 33 trained KRR models to K participants (K-shot) from the test meta-set, yielding 33 predictions per participant. Third, for each test phenotype (out of 34 phenotypes), we picked the best KRR model (out of 33 models) that performed the best (as measured by COD) on the K participants. Finally, for each test phenotype, we applied the best KRR model to the remaining participants in the test meta-set (N = 10,000 – K). Prediction performance in the 10,000 – K participants was measured using Pearson’s correlation and COD. To ensure robustness, the K-shot procedure was repeated 100 times, each with a different set of K participants.

In the case of basic meta-matching (DNN), we first trained one single DNN to predict all 33 training phenotypes from RSFC. In other words, the DNN outputs 33 predictions simultaneously. The motivation for a single multi-output DNN is to avoid the need to train and tune 33 single-output DNNs. We used the training set (N = 21478) within the training meta-set for training and validation set (N = 5370) within the training meta-set for hyperparameter tuning. Details of the hyperparameter tuning is found in Supplementary Methods S1. Second, we applied the trained DNN to the K participants (K-shot) from the test meta-set, yielding 33 different phenotypical predictions for each given participant. Third, for each test phenotype (out of 34 phenotypes), we picked the best output DNN node (out of 33 output nodes) that generated the best prediction (as measured by COD) for the K participants. Finally, for each test phenotype, we applied the predictions from the best DNN output node on the remaining 10,000 – K participants in the test meta-set. Prediction performance in the 10,000 – K participants was measured using Pearson’s correlation and COD. To ensure robustness, the K-shot procedure was repeated 100 times, each with a different set of K participants.

4.10. Advanced meta-matching

There might be significant differences between the training and test meta-sets. Therefore, simply picking the best non-brain-imaging phenotypic prediction model estimated from the training meta-set might not generalize well to the test meta-set. Thus, we proposed two additional meta-matching approaches: “advanced meta-matching (finetune)” and “advanced meta-matching (stacking)” (Figures 2 and 6B).

To ease our explanation of advanced meta-matching, we will focus on the experimental setup for the UK Biobank analysis (Figures 1 to 5). In the case of advanced meta-matching (finetune), we used the same multi-output DNN from basic meta-matching (DNN). Like before, for each test phenotype (out of 34 phenotypes), we picked the best output DNN node (out of 33 output nodes) that generated the best prediction (as measured by COD) for the K participants. We retained this best output node (while removing the remaining 32 nodes) and finetuned the DNN using the K participants (K-shot). More specifically, the K participants were randomly divided into training and validation sets using a 4:1 ratio. The training set was used to finetune the weights of the last two layers of the DNN, while the remaining weights were frozen. The validation set was used to determine the stopping criterion (in terms of the number of training epochs). The finetuned DNN was applied to the remaining 10,000 – K participants in the test meta-set. We note that the finetuning procedure was repeated separately for each of 33 test phenotypes. Prediction performance in the 10,000 – K participants was measured using Pearson’s correlation and COD. To ensure robustness, the K-shot procedure was repeated 100 times, each with a different set of K participants. More details about the finetuning procedure can be found in Supplementary Methods S3.

In the case of advanced meta-matching (stacking), we used the same multi-output DNN from basic meta-matching (DNN). The DNN was applied to the K participants (K-shot) from the test meta-set, yielding 33 predictions per participant. For each test phenotype (out of 34 phenotypes), the best M predictions (as measured by COD) were selected. To reduce overfitting, M was set to be the minimum of K and 33. Thus, if K was smaller than 33, we considered the top K outputs from the multi-output DNN. If K was larger than 33, we considered all 33 outputs of the multi-output DNN. We then trained a kernel ridge regression (KRR) model using the M DNN outputs to predict the phenotype of interest in the K participants. The hyperparameter λ was tuned using grid search and 5-fold cross-validation on the K participants. The optimal λ was then used to train a final KRR model using all K participants. Finally, the KRR model was applied to the remaining 10,000 – K participants in the test meta-set. We note that this “stacking” procedure was repeated separately for each of 33 test phenotypes. Prediction performance in the 10,000 – K participants was measured using Pearson’s correlation and COD. To ensure robustness, the K-shot procedure was repeated 100 times, each with a different set of K participants.

4.11. DNN implementation

The DNN was implemented using PyTorch⁷¹ and computed on NVIDIA Titan Xp GPUs using CUDA. More details about hyperparameter tuning are found in Supplementary Methods S1. More details about DNN finetuning are found in Supplementary Methods S3.

4.12. Statistical tests

To evaluate whether differences between algorithms were statistically significant, we adapted a bootstrapping approach developed for cross-validation procedures⁷² (see page 85 of reference). To ease our explanation of the bootstrapping procedure, we will focus on the experimental setup for the UK Biobank analysis (Figures 1 to 5).

More specifically, we performed bootstrap sampling 1,000 times. For each bootstrap sample, we randomly picked K participants with replacement, while the remaining 10,000 – K participants were used as test participants. Thus, the main difference between our main experiments (100 repeats of K-shot learning in Figure 2A) and the bootstrapping procedure is that the bootstrapping procedure sampled participants with replacement, so the K bootstrapped participants might not be unique. For each of the 1,000 bootstrapped samples, we applied classical (KRR) baseline, basic meta-matching (KRR), basic meta-matching (DNN) and advanced meta-matching (stacking), thus yielding 1,000 bootstrapped samples of COD and Pearson’s correlation (computed from the remaining 10,000 – K participants). Bootstrapping was not performed for advanced meta-matching (finetune) because 1000 bootstrap samples would have required 60 days of compute time (on a single GPU).

Statistical significance for COD and Pearson’s correlation were calculated separately. For ease of explanation, let us focus on COD. The procedure for Pearson’s correlation was exactly the same, except we replaced COD with Pearson’s correlation in the computation. To compute the statistical difference between advanced meta-matching (finetune) and another algorithm X, we first fitted a Gaussian distribution to the 1,000 bootstrapped samples of COD from algorithm X, yielding a cumulative distribution function (CDF_X). Suppose the average COD of advanced meta-matching (finetune) across the 100 random repeats of K-shot learning was µ. Then the p value was given by 2 * CDF(µ) if µ is less than the mean of the bootstrap distribution, or 2 * (1 - CDF(µ)) if µ is larger than the mean of bootstrap distribution.

When computing the statistical difference between two algorithms X and Y with 1000 bootstrapped samples each, we first fitted a Gaussian distribution to the 1,000 bootstrapped samples of COD from algorithm X, yielding a cumulative distribution function (CDF_X). This was repeated for algorithm Y, yielding a cumulative distribution function (CDF_Y). Let the average COD of algorithm X (and Y) across the 100 random repeats of K-shot learning be µ_X (and µ_Y). We can then compute a p value by comparing µ_X with CDF_X and a p value by comparing µ_Y with CDF_Y. The larger of the two p values was reported.

P values were computed between all pairs of algorithms. Multiple comparisons were corrected using false discovery rate (FDR, q < 0.05). FDR was applied to all K-shots and across all pairs of algorithms.

4.13. Haufe transform

To evaluate the interpretability of meta-matching models, we performed Haufe transform⁵³ with HCP and UK Biobank dataset. For a predictive model with functional connectivity (FC) as input and feature or phenotype as output, Haufe transform computes a positive (or negative) value for each FC edge (one element of FC matrix) and feature pair. A positive (or negative) value indicates that higher FC value was associated with predicting greater (or lower) feature value. We refer to the output of the Haufe transform described as predictive network features (PNFs).

We applied Haufe transform to various methods. First, we derived “ground truth” PNFs by training a kernel ridge regression model on full HCP dataset (N = 1019). For each HCP phenotypes (out of 35 phenotypes), we first trained a kernel ridge regression (KRR) with 5 fold cross-validation to get the best hyperparameter (lambda) on 1,019 HCP participants. Then we applied the KRR trained on 1,019 participants to predict the HCP phenotypes on 1,019 participants. Finally, we computed the covariance between the phenotype prediction (vector of 1×1,019) and value of each functional connectivity (FC) edge or element (vector of 1×1,019). For every phenotype and FC edge pair, we will have covariance value. The final PNFs is in shape of 87571 times 35, where 87571 is the number of elements in 419 by 419 FC (419 * 418 / 2) and 35 is number of HCP phenotypes.

In the case of PNFs for “Classical (KRR)”, for each HCP phenotype (out of 35 phenotypes), we trained KRR model on 100 randomly split HCP participants (from 1,019 participants) with 5 folds cross-validation to get the best hyperparameter (lambda) on these 100 HCP participants. Then we applied the KRR trained on 100 participants to predict the HCP phenotypes on 100 participants. Finally, we computed the covariance between the phenotype prediction (vector of 1×100) and value of each functional connectivity (FC) edge or element (vector of 1×100). For every phenotype and FC edge pair, we will have covariance value. We got PNFs in shape of 87571 times 35. Due to the randomness of random split, we performed the whole process 100 times with different random split of 100 from 1,019 participants. We averaged the PNFs of 100 times random splits (87571 times 35 times 100, averaged along 100). Finally, we have the PNFs for “Classical (KRR)” with shape of 87571 times 35.

In the case of PNFs for “Basic Meta-matching (DNN)” and “Advanced Meta-matching (stacking)”, for each HCP phenotype (out of 35 phenotypes), we applied the trained basic / advanced meta-matching model (trained on whole UK Biobank datasets with 36,847 participants and 67 phenotypes) for prediction on 100 randomly split HCP participants (from 1,019 participants). The 100 randomly split participants are the same 100 participants in PNFs calculation for “Classical (KRR)”. We computed the covariance between the phenotype prediction (vector of 1×100) and value of each functional connectivity (FC) edge or element (vector of 1×100). For every phenotype and FC edge pair, we will have covariance value. We got PNFs in shape of 87571 times 35. We performed same 100 repeats of random split of 100 from 1,019 participants as PNFs calculation for “Classical (KRR)”. We averaged the PNFs of 100 times random splits (87571 times 35 times 100, averaged along 100). Finally, we have the PNFs for “Basic Meta-matching (DNN)” and “Advanced Meta-matching (stacking)” with shape of 87571 times 35.

In the case of PNFs for “Basic Meta-matching (DNN) Training”, we trained DNN to predict 67 phenotypes of UK Biobank on training set of UK Biobank (N = 29,477 which is 80% of UK Biobank full 36,847 participants). We applied the trained DNN to predict 67 phenotypes on training set of UK Biobank (same N = 29,477). Then we computed the covariance between the phenotype prediction (vector of 1×29,477) and value of each functional connectivity (FC) edge or element (vector of 1×29,477). For every phenotype and FC edge pair, we will have covariance value. We got PNFs in shape of 87571 times 67. This PNFs is on UK Biobank dataset. For each of HCP phenotype (out of 35 phenotypes), we checked their best matched phenotypes in UK Biobank datasets with the trained basic meta-matching FNN, and we selected the matched UK Biobank phenotype’s PNFs as the PNFs for this HCP phenotype. Finally, we have the PNFs for “Basic Meta-matching (DNN) Training” with shape of 87571 times 35.

4.14. Computational costs of meta-matching

Meta-matching comprises two stages: training on the training meta-set and meta-matching on new non-brain-imaging phenotypes in the K participants (K-shot). Training and hyperparameter tuning on the training meta-set is slow, but only has to be performed once. For example, in our study, training the DNN with automatic hyperparameter tuning using the HORD algorithm^73–75 on a single graphics processing unit (GPU) took about 2 days. In the case of both basic meta-matching algorithms, meta-matching on new non-brain-imaging phenotypes is extremely fast because it only requires forward passes through a neural network (in the case of DNN) or matrix multiplications (in the case of KRR). More specifically, the second stage for basic meta-matching algorithms took less than 0.1 second for a single test meta-set phenotype and one K-shot. In the case of advanced meta-matching (stacking), there is an additional step of training a KRR model on the K participants. Nevertheless, the second stage for advanced meta-matching (stacking) only took 0.5 second for a single meta-set phenotype and one K-shot. On the other hand, the computational cost for finetuning the DNN for advanced meta-matching (finetune) is a lot more substantial, requiring about ~30 seconds for a single test meta-set phenotype and one K-shot. Although 30 seconds might seem quite fast, repeating the K-shot 100 times for all values of K and 34 meta-set phenotypes required 6 full days of computational time.

4.15. Data availability

This study utilized publicly available data from the UK Biobank (https://www.ukbiobank.ac.uk/) and HCP (https://www.humanconnectome.org/). Data can be accessed via data use agreements.

4.15. Code availability

Code for the classical (KRR) baseline and meta-matching algorithms can be found here (https://github.com/ThomasYeoLab/CBIG/tree/master/stable_projects/predict_phenotypes/He2022_MM). The trained models for meta-matching (i.e., Meta-matching model 1.0) are also publicly available (https://github.com/ThomasYeoLab/Meta_matching_models). The code was reviewed by two co-authors (LA and PC) before merging into the GitHub repository to reduce the chance of coding errors.