On selection bias in comparison measures of smartphone-generated population mobility: an illustration of no-bias conditions with a commercial data source

Abstract

Purpose:

Passively generated cell-phone location (“mobility”) data originally intended for commercial use has become frequently used in epidemiologic research, notably during the COVID-19 pandemic to study the impact of physical-distancing recommendations on aggregate population behavior (e.g., average daily mobility). Given the opaque nature of how individuals are selected into these datasets, researchers have cautioned that their use may give rise to selection bias, yet little guidance exists for assessing this potential threat to validity in mobility-data research. Through an example analysis of cell-phone-derived mobility data, we present a set of conditions to guide the assessment of selection bias in measures comparing aggregate mobility patterns over time and between groups.

Methods:

We specifically consider bias in measures comparing group-level mobility in the same group (difference, ratio, percent difference) and between groups (difference in differences, ratio of ratios, ratio of percent differences). We illustrate no-bias conditions in these measures through an example comparing block-group-level mobility between income groups in U.S. metro areas before (January 1^st-March 10, 2020) and after (March 11^th-April 19^th, 2020) the day COVID-19 was declared a pandemic.

Results:

Within-group contrasts describing mobility over time, especially for the higher-income decile, were expected to be most resistant to bias during the example study period.

Conclusions:

The presented conditions can be used to assess the susceptibility to selection bias of group-level measures comparing mobility. Importantly, they can be used even without knowledge of the degree of bias in each group at each time point. We further highlight links between no-bias principles originating in epidemiology and economics, showing that certain assumptions (e.g., parallel trends) can apply to biases beyond their original application.

INTRODUCTION

Epidemiologists conducting descriptive and etiologic research may rely on unconventional measures of population behavior derived from ‘big data.’^1–3 One recent example in the early months of the COVID-19 pandemic was the urgent need to understand the impact of physical-distancing recommendations on population behavior. Researchers^3–11 and journalists^12–14 used data derived from cell phone GPS to quantify population movement at the aggregate level. Such passively generated location (“mobility”) data have become more available as a result of the emergent data-collection paradigm wherein global-position-system (GPS) traces of consenting users are collected by certain cell-phone apps which then send location data to commercial firms.^10,15 These firms, such as Safegraph or Cuebiq, then mask, aggregate, or anonymize the data in some way and make them available for commercial or research purposes.^16–18

Epidemiologists and population-health scientists interested in characterizing the relationship between community mobility and health may see both the promise and the pitfalls of the use of such ‘big data’.^10,15 On the one hand, mobility data can have a high degree of measurement accuracy and a large sample size at a comparatively low cost. On the other hand, researchers may be wary that use of the data may give rise to biased estimates.^19–21 This concern is relevant whether community mobility is the target for inference (e.g., describing differential response to public-health efforts to influence mobility²²) or community mobility is an ecologic exposure in relation to a separate population-health outcome.⁸

A specific concern is selection bias,^10,23 which occurs when the parameter of interest in a target population differs from its estimate in the dataset available for analysis.^24,25 Research using mobility data may be particularly prone to selection bias. For one, the way observations arrive into the dataset is often opaque.²⁶ Some firms inform users that their data may be aggregated for research or commercial purposes.¹⁸ Many firms, though, do not disclose which specific apps send them data, leading to uncertainty regarding who ends up in the analysis dataset.^16–18 A second challenge is that selection occurs both between and within individuals. Not every individual in the target population may ever use an app that sends data to one of these firms. Further, those who do use these apps may only do so for certain periods of time, so only part of their daily mobility may be sampled. Considering these challenges, selection bias may threaten the validity of research using mobility data unless the target population is the analysis dataset itself.

An encouraging nuance, however, is that the presence of bias when using these data sources for epidemiologic purposes will depend on the research question and the measure used to answer that question. Specifically, bias in comparison measures (e.g., those that compare a mobility measure between groups or between time points or both) can depend on both the measure used and its scale, whether the scale is relative (as in a ratio) or absolute (as in a difference).^25,27,28 Relative comparison measures are useful for considering the strength of a comparison, while absolute comparison measures are useful for understanding the overall magnitude or burden of a comparison.^27,29,30 It has long been documented in epidemiology that selection bias will only distort an odds ratio—a relative measure—if selection proportions differ by both exposure and disease.²⁴ However, the same condition does not necessarily apply for the risk ratio³¹—another relative measure—or the risk difference²⁵—an absolute measure.

To inform no-bias conditions for absolute measures, the econometrics literature offers guidance, specifically the extensive literature on the difference in differences.^32,33 In its classic formulation, a difference-in-differences analysis assumes that the linear difference between the outcome variable across time periods would have been the same between groups were it not for an intervention or treatment.³² This parallel-trends assumption is typically used in studies aiming to estimate causal effects, relaxing an otherwise stricter assumption of no unmeasured confounding. The same parallel-trends assumption may be useful for relaxing assumptions related to selection bias, but its utility for biases beyond those pertaining to causal inference is not commonly presented. (As a note on terminology, selection bias is sometimes used in economics to describe what epidemiologists call confounding. See page 264 of Modern Epidemiology 4^th Edition (ME4)³⁴ and Heckman [1985³⁵, 1990³⁶] for historical examples. Here, we use the term as defined above, and we do not distinguish between selection bias for descriptive versus effect measures.³⁷) Given the range of disciplines using mobile-phone-generated mobility data, from public health and epidemiology¹⁰ to social sciences³⁸ and transportation research,^1,15 the research community would benefit from an overview of no-bias conditions inspired by both the epidemiologic and econometric traditions.

In this paper, we present conditions under which selection bias is not expected to be a threat to valid conclusions when commercially derived mobile-phone data are used to compare population mobility patterns. In an example analysis using Cuebiq® data, we describe no-bias conditions in six measures making group-level comparisons. Three of the measures (the difference, ratio, and percent difference) make within-group comparisons, and the other three (the difference in differences, ratio of ratios, and ratio of percent differences) compare within-group contrasts between groups. We consider the plausibility of each no-bias condition in a step-by-step process. We conclude by noting that certain assumptions, including the parallel trends of the difference in differences, can apply for biases beyond those for which they were initially developed. Epidemiologists and other researchers using mobility data can use these conditions to guide the choice of measures used to answer their research question and more clearly articulate assumptions regarding the presence of selection bias in those measures.

METHODS

Target population and data sources

We first describe the conditions for no bias. Then, through an example analysis, we highlight how researchers can use these conditions to make more informed conclusions about study validity with respect to selection bias. The goal of our example study is to compare the change in Census block-group-level aggregate mobility between the top and bottom deciles of median household income in U.S. metro areas before and after March 11, 2020, when WHO declared a global pandemic. That is, the outcome of interest is population mobility, and the exposures under study are the income groups and time periods. The target population is the 21,670 United States metro block groups in either the top 10^th percentile of median household income for their state (j=1; n = 10,815 block groups) or the bottom 10^th percentile (j=0; n = 10,855 block groups). Household income is defined by the 2014–2018 American Community Survey. We estimate mobility in this population using Cuebiq aggregated mobile phone location data, which are collected by select smartphone apps from about 15 million people anonymous users who opted in to data collection for research purposes through a GDPR and CCPA compliant framework. Cuebiq data have been used by journalists and researchers during the COVID-19 pandemic.^5,7,13,14 For each device in their sample, Cuebiq calculates a mobility index, derived from the base-19 logarithm of the daily distance the device travels. The mobility index is bounded by 0 and 5.³⁹ We were provided the median mobility index, henceforth mobility index, summarized by home census block group. Home is defined where the device is observed most often at night.

Notation and definitions of absolute and relative measures

We calculate the estimated mean mobility index, denoted as ${\widehat{Y}}_{j,t}$, in each income group over two time periods: before (t=0; January 1, 2020—March 10, 2020) and after March 11, 2020 (t=1; March 11, 2020—April 19, 2020). Note that we use ${\widehat{Y}}_{j,t}$ to denote the estimated mean mobility index, but it could refer to any estimated summary measure (e.g., mean distance traveled) in any group j at time t. To compare group-level mobility over time within the same group, we estimate the difference $\left({\widehat{D}}_j\right)$, the ratio $\left({\widehat{R}}_j\right)$, and the percent difference $\left({\widehat{PD}}_j\right)$. To compare within-group changes between groups, we estimate the difference in differences $(\widehat{DlD})$, the ratio of ratios $(\widehat{ROR})$, and the ratio of percent differences $(\widehat{RPD})$. The difference and the difference in differences are absolute measures; they keep the units of their constituent measures. The ratio, the percent difference, the ratio of ratios, and the ratio of percent differences are relative measures; their units cancel.

In Table 1, we define these estimated measures (those with the hat notation) in terms of their estimands (without the hat notation) in the target population and corresponding bias factors. Selection bias is often defined in terms of selection probabilities.²⁴ Following the measurement-error literature,^28,40,29,44 we use bias-factor notation because our focus is the bias of a continuous group-level summary measure, which is not easily expressed as a function of the proportion of underlying study participants, as in selection probabilities. The additive bias factor, α_j,t, is defined as ${\alpha }_{j,t}={\widehat{Y}}_{j,t}-Y_{j,t}$. The multiplicative bias factor, β_j,t, is defined as ${\beta }_{j,t}=\frac{{\widehat{Y}}_{j,t}}{Y_{j,t}}$. Estimated measures describing a contrast on the absolute scale are defined with α_j,t, and estimated measures describing a contrast on the relative scale are defined with β_j,t. In the main text, we assume that the sample is constant once it is drawn and thus do not conceptualize the estimates or the bias factors as random variables. In the appendix, we consider the estimates as varying between imagined study replications.

Table 1.

Definitions of the measures and their estimates defined with bias factors.

Measure name	Scale	Estimand	Estimateb
Linear difference, Dj	Absolute	Dj = Yj,1 − Yj,0	${\widehat{D}}_j={\widehat{Y}}_{j,1}-{\widehat{Y}}_{j,0}=\left(Y_{j,1}+{\alpha }_{j,1}\right)-\left(Y_{j,0}+{\alpha }_{j,0}\right)$
Ratio, Rj	Relative	$R_j=\frac{Y_{j,1}}{Y_{j,0}}$	${\widehat{R}}_j=\frac{{\widehat{Y}}_{j,1}}{{\widehat{Y}}_{j,0}}=\frac{Y_{j,1}*{\beta }_{j,1}}{Y_{j,0}*{\beta }_{j,0}}$
Percent difference,a PDj	Relative	$P{D}_j=\frac{Y_{j,1}}{Y_{j,0}}-1$	${\widehat{PD}}_j=\frac{{\widehat{Y}}_{j,1}}{{\widehat{Y}}_{j,0}}-1=\frac{Y_{j,1}*{\beta }_{j,1}}{Y_{j,0}*{\beta }_{j,0}}-1$
Difference in differences, DD	Absolute	DiD = (Y1,1 − Y1,0) − (Y0,1 − Y0,0)	$$\begin{gathered} \widehat{DlD}=\left({\widehat{Y}}_{1,1}-{\widehat{Y}}_{1,0}\right)-\left({\widehat{Y}}_{0,1}-{\widehat{Y}}_{0,0}\right) \\ =(\left(Y_{1,1}+{\alpha }_{1,1}\right)-\left(Y_{1,0}+{\alpha }_{1,0}\right))-(\left(Y_{0,1}+{\alpha }_{0,1}\right)-\left(Y_{0,0}+{\alpha }_{0,0}\right)) \end{gathered}$$
Ratio of ratios, RR	Relative	$RoR=\frac{\frac{Y_{1.1}}{Y_{1,0}}}{\frac{Y_{0,1}}{Y_{0,0}}}$	$\widehat{ROR}=\frac{\frac{{\widehat{Y}}_{1,1}}{{\widehat{Y}}_{1,0}}}{\frac{{\widehat{Y}}_{0,1}}{{\widehat{Y}}_{0,0}}}=\frac{\frac{Y_{1,1}*{\beta }_{1,1}}{Y_{1,0}*{\beta }_{1,0}}}{\frac{Y_{0,1}*{\beta }_{0,1}}{Y_{0,0}*{\beta }_{0,0}}}$
Ratio of percent differences, RPD	Relative	$RPD=\frac{\frac{Y_{1,1}}{Y_{1,0}}-1}{\frac{Y_{0,1}}{Y_{0,0}}-1}$	$\widehat{RPD}=\frac{\frac{{\widehat{Y}}_{1,1}}{{\widehat{Y}}_{1,0}}-1}{\frac{{\widehat{Y}}_{0,1}}{{\widehat{Y}}_{0,0}}-1}=\frac{\frac{Y_{1,1}*{\beta }_{1,1}}{Y_{1,0}*{\beta }_{1,0}}-1}{\frac{Y_{0,1}*{\beta }_{0,1}}{Y_{0,0}*{\beta }_{0,0}}-1}$

^aWe omit the 100% multiplier for simplicity of notation; it does not affect conclusions.

^bFor expressions involving the relative bias factor, we stipulate that β_j,t ≠ 0 so that the adjacent Y_j,t does not drop out of the expression, creating unusual results.

Conditions for no bias

Adapting the definition above,²⁵ selection bias would arise if the summary measure as estimated by the Cuebiq data differed from the corresponding parameter in the broader target population. We assume the source of the systematic error is the selection process (who is in the sample?) and not measurement (how is mobility measured?). In the discussion, we comment on how the same conditions can apply for systematic measurement error.

Table 2 and Figure 1 present the conditions for no bias in the summary measures, with progressively less strict assumptions from Conditions 1 to Conditions 4.1 and 4.2. The conditions are sufficient but not necessary. We algebraically justify these conditions in Web Appendix 1. In Web Appendix 2, we consider the conditions when the bias factors are viewed as random variables. In our formulation, estimators for absolute measures are statistically unbiased by linearity of expectation, and estimators for relative measures are statistically consistent but not necessarily statistically unbiased because the expectation of a quotient of two random variables is not in general the quotient of their expectations.⁴¹ Condition 1 states that all values of ${\widehat{Y}}_{j,t}$ are unbiased, a strict condition. Condition 2 allows bias in ${\widehat{Y}}_{j,t}$ but states that the bias is equivalent between all groups and time periods. If Condition 2 is met on the absolute scale, then all absolute measures (${\widehat{D}}_j$ and $\widehat{DlD}$) are unbiased, and if it is met on the relative scale, then all relative measures (${\widehat{R}}_j$, ${\widehat{PD}}_j$, $\widehat{ROR}$, and $\widehat{RPD}$) are unbiased.

Table 2.

Conditions sufficient for measures to be unbiased.

Number	Descriptiona	Scale	Notationb	Sufficient for these summary measures to be unbiased.
1	There is no bias in any group in any time period.	Absolute	α0,0 = α0,1 = α1,0 = α1,1 = 0.	${\widehat{D}}_j$, $\widehat{DıD}$
		Relative	β0,0 = β0,1 = β1,0 = β1,1 = 1.	${\widehat{R}}_j$, ${\widehat{PD}}_j$, $\widehat{ROR}$, $\widehat{RPD}$
2	Bias is the same in all groups and time periods.	Absolute	α0,0 = α0,1 = α1,0 = α1,1 = α.	${\widehat{D}}_j$, $\widehat{DıD}$
		Relative	0 ≠ β0,0 = β0,1 = β1,0 = β1,1 = β.	${\widehat{R}}_j$, ${\widehat{PD}}_j$, $\widehat{ROR}$, $\widehat{RPD}$
3.1.	Bias is the same between time periods within group.	Absolute	α0,0 = α0,1 = α0,t, and α1,0 = α1,1 = α1,t.	${\widehat{D}}_j$, $\widehat{DıD}$
		Relative	0 ≠ β0,0 = β0,1 = β0,t, and 0 ≠ β1,0 = β1,1 = β1,t.	${\widehat{R}}_j$, ${\widehat{PD}}_j$, $\widehat{ROR}$, $\widehat{RPD}$
3.2.	Bias is the same between groups within time period.	Absolute	α0,0 = α1,0 = αj,0, and α0,1 = α1,1 = αj,1.	$\widehat{DıD}$
		Relative	0 ≠ β0,0 = β1,0 = βj,0, and 0 ≠ β0,1 = β1,1 = βj,1.	$\widehat{ROR}$
4.1.	The between-time-period trend in bias is the same between groups.	Absolute	α1,1 − α1,0 − α0,1 − α0,0 = αj,1 − αj,0.	$\widehat{DıD}$
		Relative	$\frac{{\beta }_{1,1}}{{\beta }_{1,0}}=\frac{{\beta }_{0,1}}{{\beta }_{0,0}}=\frac{{\beta }_{j,1}}{{\beta }_{j,0}}$.	$\widehat{ROR}$
4.2.	The between-group trend in bias is the same between time periods.	Absolute	α1,1 − α0,1 − α1,0 − α0,0 = α1,t − α0,t.	$\widehat{DıD}$
		Relative	$\frac{{\beta }_{1,1}}{{\beta }_{0,1}}=\frac{{\beta }_{1,0}}{{\beta }_{0,0}}=\frac{{\beta }_{1,t}}{{\beta }_{0,t}}$.	$\widehat{ROR}$
5	Neither the between-time-period trend in bias is the same between groups, nor is the between-group trend in bias the same between time periods.	Absolute	α1,1 − α1,0 ≠ α0,1 − α0,0 and α1,1 − α0,1 ≠ α1,0 − α0,0.	None
		Relative	$\frac{{\beta }_{1,1}}{{\beta }_{1,0}}\ne \frac{{\beta }_{0,1}}{{\beta }_{0,0}},\text{ and }\frac{{\beta }_{1,1}}{{\beta }_{0,1}}\ne \frac{{\beta }_{1,0}}{{\beta }_{0,0}}$.	None

^aThe meaning of the word trend in conditions 4.1. and 4.2 depends on the scale. Please refer to the notation for further precision.

^bFor expressions involving the multiplicative bias factor, we stipulate that β_j,t ≠ 0 so that the adjacent Y_j,t does not drop out of the expression, creating unusual results.

Figure 1.

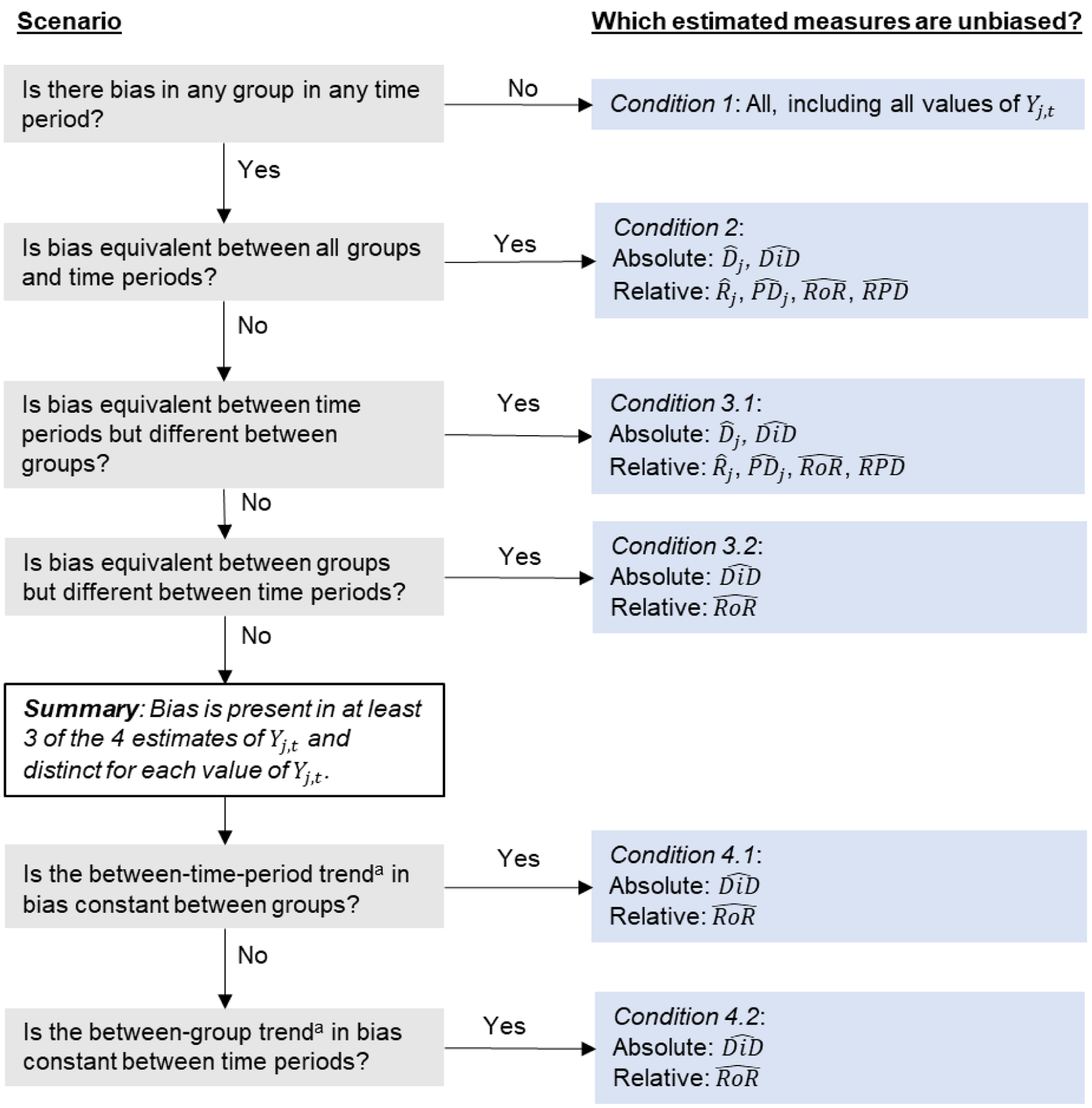
Flow chart of the bias patterns.

^aThe precise meaning of the word trend in Conditions 4.1 and 4.2 depends on the scale. Please refer to the notation in Table 2 for further precision.

Under Conditions 3.1 and 3.2, bias may vary between groups or between time periods, but not both. If Condition 3.1 is met on the absolute scale, then all absolute measures are unbiased, and if it is met on the relative scale, then all relative measures are unbiased. Under Condition 3.2, bias differs between time periods but is equivalent between groups. If this pattern is met additively, then only $\widehat{DlD}$ is unbiased, and if met multiplicatively, then only $\widehat{ROR}$ is unbiased.

Under Conditions 4.1 and 4.2, bias is distinct in each of the four group-time combinations, but either the between-time-period trend in bias is constant between groups (4.1), or the between-group trend in bias is constant between time periods (4.2). If Condition 4.1 is met on the absolute scale, then only the $\widehat{DlD}$ is expected to be unbiased. This condition is the classic parallel-trends assumption in difference-in-differences analyses.³² Meanwhile, if Condition 4.1 is met on the relative scale, then only $\widehat{ROR}$ is unbiased. If Condition 4.2 is met on the absolute scale, then $\widehat{DlD}$ is again expected to be unbiased, as justified by the same difference-in-differences assumptions. If Condition 4.2 is met on the relative scale, then only $\widehat{ROR}$, but not $\widehat{RPD}$, is expected to be unbiased. Note that Conditions 4.1 and 4.2 suffice for $\widehat{ROR}$ but not for $\widehat{RPD}$ because the ratio of ratios is a cross-product ratio,⁴² so it is invertible like an odds ratio,^43,47 whereas the ratio of percent differences, like a risk ratio, is not generally invertible.

Finally, if bias is distinct for each value of ${\widehat{Y}}_{j,t}$, and there is neither a constant temporal trend in bias between groups nor a constant between-group trend in bias between time periods, then no measures are expected to be unbiased.

RESULTS

The estimated mean daily mobility index by group is presented in Figure 2. The estimated summary measures and the least restrictive condition(s) under which they are unbiased are also presented in Table 3. Between January 1^st and March 10^th of 2020, the top 10^th percentile had an average mobility index of 3.88, which fell to 1.74 between March 11^th and April 19^th. Meanwhile, the bottom 10^th percentile had an average mobility index of 3.77 before March 11^th and 3.14 thereafter.

Figure 2.

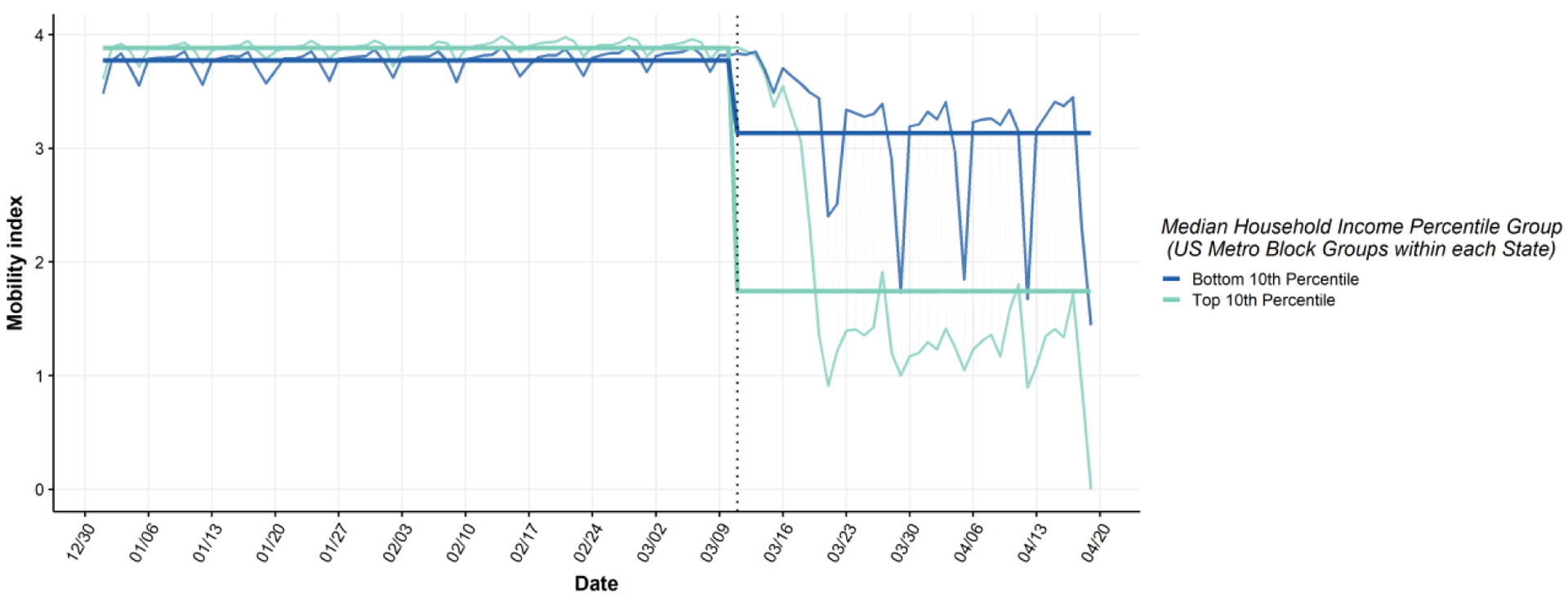
Daily mobility index among US metro block groups in the top and bottom 10^th percentile of median household income before (January 1^st-March 10^th) and after (March 11^th-April 19^th) the WHO declaration of COVID-19 as a global pandemic. Household income is defined by the 2014–2018 American Community Survey.

Table 3.

Comparing estimated mean mobility index within and between groups in US metro block groups in the top 10^th and bottom 10^th state-specific percentiles before (January 1, 2020-March 1, 2020) and after (March 11, 2020-April 19, 2020) the WHO announced a global pandemic.

	Estimated mean mobility in each time point		Within-group estimated measures			Between-group estimated measures
	t=0	t=1	${\widehat{D}}_j$	${\widehat{R}}_j$	${\widehat{PD}}_j$	$\widehat{DıD}$	$\widehat{ROR}$	$\widehat{RPD}$
Top 10th percentile, j = 1	3.88	1.74	−2.14	0.45	−55.2%	−1.51	0.54	3.27
Bottom 10th percentile, j = 0	3.77	3.14	−0.64	0.83	−16.9%
Least strict condition(s) sufficient for unbiasedness	1	1	3.1	3.1	3.1	4.1, 4.2	4.1, 4.2	3.1

Following the stepwise process in Figure 1, we consider the plausibility of each condition. The mobility measures by group and time period are only unbiased—stated circularly—if they are unbiased (Condition 1). Smartphone adoption has risen to about 80% in the United States,⁴⁴ but unequal access persists both to the devices themselves⁴⁸ and to the high-speed networks they rely on.⁴⁵ Thus, at the outset, we expect that there may have been bias in at least one group during at least one period, ruling out Condition 1.

Measures comparing time periods or groups have less strict no-bias conditions. Differential access to smartphones between income groups also suggests that neither Condition 2 nor Condition 3.2 is met. One may plausibly assume, however, that any bias in the mobility index between income groups was stable over time within group (Condition 3.1), given the short timeframe of the study (January 1, 2020-April 19, 2020). If so, then in each group the estimated difference (${\widehat{D}}_1=-2.14$; ${\widehat{D}}_0=-0.64$), ratio (${\widehat{R}}_1=0.45$; ${\widehat{R}}_0=0.83$), and percent difference (${\widehat{PD}}_1=55.2\%$; ${\widehat{PD}}_0=16.9\%$) would be valid. On the other hand, the pandemic initially had a strikingly disparate economic impact.^46,47 Unexpected job loss combined with limited savings⁴⁸ may have resulted in difficulty paying phone bills for the lower-income group during this time period.⁴⁹ As a result, Condition 3.1. is more plausible for the high-income decile. Still, for this short period, Condition 3.1 is defensible even for the low-income decile, as major phone carriers and lenders were encouraged by the Federal Communication Commission and the Federal Reserve to offer leniency on payment plans in March and April of 2020.^50,51

To assess the validity of the between-group measures, we consider Conditions 4.1 and 4.2, which are less stringent than Conditions 3.1 and 3.2. The plausibility of these conditions for this example again largely depends on the extent to which smartphone use was disrupted in the low-income group after March 11^th. We assume the disruption was negligible for this short study period and thus that the discrepancy in bias between groups was constant over time (Condition 4.2), meaning the difference-in-differences $\widehat{(DlD}=-1.51)$ and the ratio of ratios $(\widehat{RoR}=0.54)$ would have been valid.

Summarizing, for this study, we expect the three measures comparing mobility over time in the high-income decile (${\widehat{D}}_1=-2.14$; ${\widehat{R}}_1=0.45$; ${\widehat{PD}}_1=-55.2\%$) are the least susceptible to selection bias. Even if Cuebiq’s sample is biased at each time point in the high-income group, if the bias was constant over time (Condition 3.1), as is plausible given the pandemic’s limited immediate economic impact on the high-income group, then these estimates would be valid. For reasons mentioned, we are cautiously confident in the validity of the between-group contrast measures ($\widehat{DlD}=-1.51$; $\widehat{RoR}=0.54$; $\widehat{RPD}=3.27$) and the within-group contrasts for the lower-income decile (${\widehat{D}}_0=-0.64$; ${\widehat{R}}_0=0.83$; ${\widehat{PD}}_1=-16.9\%$).

DISCUSSION

Passive cell-phone-generated location (“mobility”) data have become commonly used in epidemiologic research and practice, most prominently for COVID-19 epidemiology.^6,8–11 Beyond COVID-19, additional epidemiologic topics include migration patterns following severe weather,⁵² active transportation,¹⁵ and other health-relevant topics.³⁸ Making inference on the relationship between an aggregate population behavior (e.g., average daily mobility) and a health outcome requires clarity on the validity of the measures derived from data sources not originally intended for epidemiological research. In this paper, we use the example of cell-phone mobility to describe assumptions needed to make unbiased estimates of certain measures describing population behavior from a source of big data, with attention to the problem of differential selection into the big dataset. Informed by no-bias principles in epidemiology and economics,^25,31,32 we specifically described a set of conditions that can be used to guide the assessment of selection bias in measures comparing aggregate mobility patterns.

A practical advantage of the conditions is that they can be used to consider the presence of bias in comparison measures even if the degree of bias is not known in any of the groups under study at any time. In our example, we did not know the true population parameter for any of the four values of this mobility index in the group-by-time contingency table. Acquiring that knowledge would have required information on the movement patterns of all individuals in our target population of the 21,670 United States metro block groups in the two income deciles over the course of the study period, or at least a representative summary measure known to be correct. That information was not feasible to collect. We thus used the stepwise process highlighted in Figure 1 to consider which comparison measures may suffer least from selection bias. In this example, we reasoned that within-group measures comparing mobility over time in the higher-income decile were probably least resistant to bias and thus could choose to calculate these measures and present this rationale, assumptions, and conclusions accordingly.

In addition to helping to guide the choice of measure to answer the research question, consideration of these conditions can help readers critically evaluate existing journalism and literature using mobility data. In their early reporting on the pandemic, The New York Times reported relative changes in mobility patterns using a percent difference.¹⁴ As they implied, the relative measure is less susceptible to bias than if they had reported group-specific absolute measures over time.⁶ This manuscript offers justification for their approach; Condition 3.1 would suffice. Researchers have also used comparison measures when describing changes in mobility over the course of the pandemic.^6,9 Jay and colleagues used a difference-in-differences approach to assess changes in population mobility between groups using Safegraph data.⁶ As in our analysis, the time period of that study was fairly short (January 6^th-May 3^rd, 2020). Thus, either Condition 4.1 or Condition 4.2 is likely to have been met, suggesting the DiD estimate was robust to selection bias.

As noted in the introduction, the presented conditions are not new. Some have long been used in epidemiology,^25,31 while others have a history of use in economics.³² By presenting them together in this manner, we hope to emphasize links between the conditions and that their principles can apply for biases beyond those for which they were developed. On page 321 of ME 4,²⁴ the expression of the odds ratio with inverse-selection weights in Equation 14–2 is analogous to the definition of the ratio-of-ratios estimate in this manuscript’s Table 1. Both are cross-product ratios^42,53 with multiplicative factors applied in each of the four cells of the contingency table. Conditions 3.1, 3.2, 4.1, and 4.2 are variations of the axiom that there is only bias in an odds ratio when selection is associated with both exposure and outcome.^24,25,31 Alternatively stated, these conditions are sufficient for the overall selection bias factor in ME4’s Equation 14–1 to be one (“…no bias occurs if the selection bias factor is one [p. 322].”).

Perhaps a more novel insight is our illustration that the parallel-trends assumption from difference-in-differences analyses can be used to reason with selection bias. The DiD approach is typically used to relax no-confounding assumptions related to causal inference.³⁷ Our presentation shows that the core principle of the DiD—that bias can cancel when two differences are taken—can also apply when the bias in view is selection bias rather than confounding. Conditions 4.1 and 4.2 also underscore that the above-noted adage from epidemiology, that bias in an odds ratio only manifests when selection is associated with both exposure and outcome,^24,25,31 essentially invokes the parallel-trends assumption of the DiD on a different scale. This point is also illustrated by Athey and Imbens, whose change-in-changes model relaxes the additive-scale-dependence of the DiD.⁵⁴

Although not the present focus, the no-bias conditions may also be useful for addressing measurement error⁵⁵ in research using mobile-phone data. For example, Hunter and colleagues used passively generated location data to classify and quantify walking behavior.⁷ Suppose walking were measured with systematic error, but that this bias did not differ additively between income groups or time periods. If so, then Condition 2 would apply, and the corresponding additive summary measures comparing walking within and between groups would be valid.

In summary, skepticism regarding selection bias is certainly warranted when using passively generated mobility data. Nevertheless, certain comparison measures may be rather resistant to bias. Researchers across disciplines using mobile-phone-generated data may use these conditions to guide the choice of comparison measure and to assess the susceptibility of those measures to selection bias.