Abstract
Objectives
Characterizing features of the viral rebound trajectories and identifying host, virological, and immunological factors that are predictive of the viral rebound trajectories are central to HIV cure research. We investigate if key features of HIV viral decay and CD4 trajectories during antiretroviral therapy (ART) are associated with characteristics of HIV viral rebound following ART interruption.
Methods
Nonlinear mixed effect (NLME) models are used to model viral load trajectories before and following ART interruption, incorporating left censoring due to lower detection limits of viral load assays. A stochastic approximation EM (SAEM) algorithm is used for parameter estimation and inference. To circumvent the computational intensity associated with maximizing the joint likelihood, we propose an easy-to-implement three-step method.
Results
We evaluate the performance of the proposed method through simulation studies and apply it to data from the Zurich Primary HIV Infection Study. We find that some key features of viral load during ART (e.g., viral decay rate) are significantly associated with important characteristics of viral rebound following ART interruption (e.g., viral set point).
Conclusions
The proposed three-step method works well. We have shown that key features of viral decay during ART may be associated with important features of viral rebound following ART interruption.
Keywords: censoring, HIV/AIDS studies, longitudinal data, stochastic approximation EM (SAEM) algorithm
Introduction
Characterizing features of the viral rebound trajectories and identifying host, virological, and immunological factors that are predictive of the viral rebound trajectories are central to HIV cure research (Julg et al. 2019; Li, Smith, and Mellors 2015; Richman et al. 2009). After the initiation of an antiretroviral therapy (ART), viral loads typically decline over time and subsequently drop below the assay’s detection limit, i.e., the viral loads may be left censored. If the ART is discontinued, viral loads usually rise rapidly to peak values, then decrease and stabilize at a level commonly referred to as a viral set point. There are many barriers to curing HIV. Efforts have been focusing on either a functional cure (lowering viral set points) or a sterilizing cure (eliminating all HIV-infected cells), with the former being a more realistic goal (Rouzioux, Hocqueloux, and Sáez-Cirión 2015).
To date, a number of biomarkers have been found to be predictive of the timing of viral rebound or viral set point after treatment interruption including ART initiation during acute/early HIV infection (Namazi et al. 2018; Von Wyl et al. 2011), pre-ATI (analytic treatment interruption) CA-RNA (cell-associated RNA) levels (Li et al. 2016), and T-cell exhaustion markers measured prior to ART (Hurst et al., 2015). So far, to the best of our knowledge, most studies focused on predictors that reflect values at a single time point (e.g., age at the start of treatment interruption), or provide simple summaries of observed values over history (e.g., nadir CD4 count, changes in numbers of cytotoxic T-lymphocytes) (Bing et al. 2020; Conway, Perelson, and Li 2019; Oxenius et al. 2002; Wang et al. 2020). Here we investigate the effect of longitudinal biomarkers on features of viral rebound, leveraging rich information from the Zurich Primary HIV Infection Study, where viral load and CD4 cell counts were measured longitudinally since seroconversion.
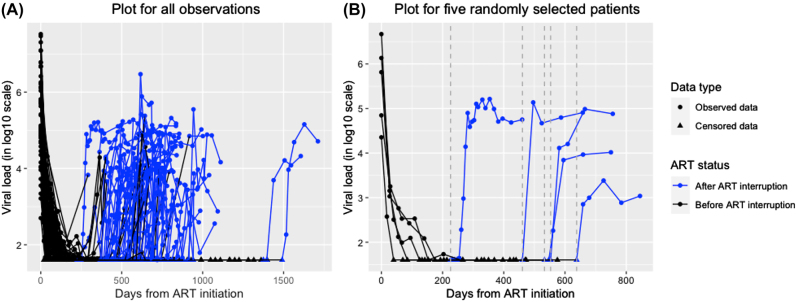
The Zurich Primary HIV Infection Study consists of participants presenting with acute or recent HIV-1 infection between November 2002 and July 2008. This study was described in details in Gianella et al. (2011). In brief, acutely and recently HIV-1 infected individuals were offered immediate standard first line combination ART (cART) according to treatment recommendations of that time (Thompson et al. 2010), and after at least one year of viral suppression below detection limits ( 50 HIV-1 RNA copies/mL of plasma), they could elect to stop therapy. Reinitiation of cART was based on CD4 count criteria of that time. Figure 1 shows entire viral load (HIV-1 RNA copies/mL of plasma, in log10-scale) trajectories during ART and following ART interruption for all subjects and for 5 randomly selected subjects respectively (for data following ART interruption, we only show the first 36 weeks of data because viral load levels typically stabilize before then). We see that viral loads decline rapidly during ART and then may rebound quickly following ART interruption, and that viral loads after reaching peak points during rebound exhibit large variations between subjects. Our main objective is to study if key features of viral decay during ART, such as individual-specific viral decay rates, are associated with important characteristics of viral rebound following ART interruption, such as individual-specific viral rebound rates or set points.
Figure 1:
Viral load (log10-scale) trajectories before and following ART interruption. Left censored values are denoted by triangle dots on the bottom horizontal line with the censored values imputed by the detection limit. Observed values are denoted by circle dots. Data during ART are in black, and data following ART interruption are in blue. The dashed vertical lines in gray indicate times when the ART was interrupted. Figure (A) shows data from all subjects, and Figure (B) shows data from 5 randomly selected subjects.
Mixed effects models are well-suited to model longitudinal data with large variations between individual viral load trajectories, since random effects in the models can be used to incorporate the between-individual variations, as well as individual-specific inference. To model viral load trajectories during ART, Wu and Ding (1999) proposed nonlinear mixed effects (NLME) models based on reasonable biological arguments, and the proposed exponential decay models have been shown to fit viral load data during ART very well. For viral rebound trajectories following ART interruption, Wang et al. (2020) proposed a different NLME model where the key features of viral rebounds are represented by the model parameters. Thus, here we use these two NLME models to model viral load before and after ART interruptions respectively. Mixed effects models with left censored responses have also been studied in the literature (Hughes 1999; Vaida, Fitzgerald, and DeGruttola 2007; Vaida and Liu 2009; Wu 2002).
Statistical inference for NLME models is typically based on the likelihood method (Wu 2009). Due to unobservable random effects and nonlinearity of the models, exact likelihood estimation based on the numerical integration methods or Monte Carlo expectation-maximization (MCEM) algorithm can be computationally intensive and may suffer from convergence problems (Wu 2009). A widely used and computationally more efficient approximate method is the linearization method of Lindstrom and Bates (Lindstrom and Bates 1990), but its performance can be less satisfactory in some cases (Comets, Lavenu, and Lavielle 2017). Here we consider the stochastic approximation expectation-maximization (SAEM) algorithm for parameter estimation and inference of NLME models (Comets, Lavenu, and Lavielle 2017; Delyon, Lavielle, and Moulines 1999; Samson, Lavielle, and Mentré 2006). The SAEM algorithm is computationally more efficient than the MCEM algorithm and it performs well in the sense of producing reasonable estimates and fast convergence.
In this article, we consider three mixed effects models: two NLME models with left censored responses – one NLME model for viral dynamics during ART and another NLME model for viral rebound following ART interruption, and a linear mixed effects (LME) model for CD4 data during ART. The three models are linked through shared random effects. To reduce the computational burden, we fit the three models separately based on a three-step method, using the SAEM algorithm. We use a parametric bootstrap method to obtain standard errors of all parameter estimates and incorporate estimation uncertainty from separate model fittings. Our contributions are: (i) to our knowledge, our work is the first to study the relationship between viral declines during ART and viral rebound after ART based on NLME models; (ii) the proposed three-step method is simple, and can be implemented with existing software; (iii) the proposed method is based on exact likelihood method, so there is no concern about approximation accuracies as in other approximate methods such as linearization methods, and it is also computationally feasible; and (iv) the proposed method performs well, as shown in simulations, and clearly outperforms a common naive method that uses an imputed value for censored observations and model-based standard errors.
The article is organized as follows. In Section 2, we describe the models motivated by the real dataset, and we propose a three-step method for parameter estimation. Section 3 presents a comprehensive data analysis. The proposed method is evaluated in Section 4 via simulations. We conclude the article with some discussion in Section 5.
Models for data before and following ART interruption
In this section, we first consider an NLME model for viral decay and an LME model for CD4 trajectories during ART. Then, the random effects in these two models, which summarize individual-specific CD4 and viral load trajectories, are used as “covariates” in the viral rebound NLME model following ART interruption. Our goal is to exam if the individual-specific viral rebound characteristics following ART interruption are associated with individual-specific CD4 and viral load profiles during ART.
Models for viral load and CD4 during ART
First, we model viral load trajectories during ART. Let Y ij be the (log10-transformed) viral load value (in copies/mL) of individual i measured at time t ij during ART. Let y ij be the observed value of Y ij , and let , i = 1, 2, …, n, j = 1, 2, …, n i . We use similar notation for other variables. The values of Y may be left censored due to the assay’s lower detection limit. Based on possible virus elimination and production processes, Wu and Ding (1999) showed that the viral load trajectories during ART typically exhibit exponential decay patterns and may be modelled by NLME models.
A general NLME model can be written as follows:
| (1) |
where g(⋅) is a known nonlinear function, x ij is a vector containing covariates including time, η is a vector containing fixed effect parameters, contains random effects, contains within-individual random errors, and B and Σ i are covariance matrices. The random effects b i and the random errors e i are assumed to be independent. When the function g(⋅) is a linear function, the NLME model (1) reduces to an LME model. It is common to assume that the within-individual errors are conditionally independent given the random effects, i.e., , where is the n i × n i identity matrix.
For the viral load data during ART, as shown in Figure 1, we consider the following NLME model (Wu and Ding 1999)
| (2) |
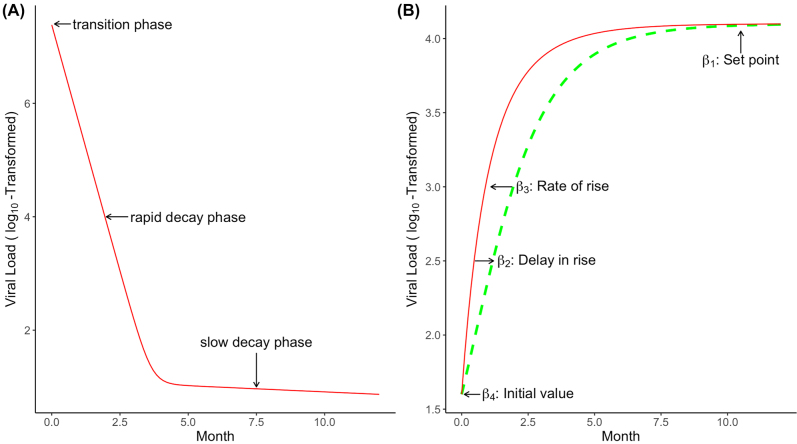
where are random effects, λ 1 is the first-phase viral decay rate, which corresponds to the rapid decay phase reflecting decay of productively, long-lived and/or latently infected cells, λ 2 is the second-phase viral decay rate during ART, which corresponds to the slow decay phase reflecting decay of long-lived and/or latently infected cells and other residual infected cells, is typical viral load value at the start of ART. This NLME model is rooted from a biological compartment model describing the interaction between HIV and its host cells and has been shown to provide a good fit to the viral decay phase after ART initiation (Wu and Ding 1999). Figure 2A shows the viral decline profile for a typical subject based on model (2). Random effects are introduced to each parameter to incorporate large variations between individuals. As shown in Figure 1, some viral load values are left censored or below the detection limit. In estimating the parameters in the above NLME model, the censored viral load values must be taken into account to avoid biased results (Hughes 1999; Wu 2002).
Figure 2:
Viral load trajectories during and after ART.
(A) A schematic illustration of viral dynamics profiles during ART based on model (2). (B) A schematic illustration of viral rebound profiles following ART interruption based on model (5).
In addition to viral loads, CD4 cell count during ART may be also associated with viral rebounds, due to the known association between CD4 and viral load. The observed CD4 values are highly variable, reflecting both short-term biological variation and measurement error. To address measurement errors in the observed CD4 values, we may model the observed CD4 longitudinal data empirically to estimate true CD4 values. Specifically, let z ij be the observed CD4 cell count (in cells/mm3) of individual i measured at time t ij , i = 1, 2, …, n, j = 1, 2, …, m i . We may consider the following general LME model for CD4 data
| (3) |
where vectors u ij and v ij contain covariates including time, vector α contains fixed effect parameters, vector a i contains random effects with a i ∼ N(0, A), is the assumed (unobserved) true CD4 value whose corresponding observed error-prone value is z ij based on the classical measurement error model, and ɛ ij is the measurement error, with ɛ ij ’s are . We may take appropriate transformations of the observed CD4 values, such as a log-transformation or a -transformation so that the transformed data are more compatible with the normality and constant variance assumptions. We compare different models based on observed/predicted plots, normal QQ-plots, and residual plots (see Appendix), as well as the simplicity of the model and its interpretation. We find that a -transformation of CD4 provides satisfactory results since it produces similar results as the log-transformation and it is widely used in the analysis of datasets from the AIDS Clinical Trials Group network (ACTG) (see, e.g., Noubary and Hughes 2012).
Note that the general LME model (3) includes nonparametric mixed effects models which may be useful if the CD4 trajectories are complicated without clear patterns, since we can use a basis-based approach to approximate the nonparametric mixed model by an LME model (Wu 2009). Thus, the general LME model (3) is quite flexible for modelling complex CD4 longitudinal data.
For the motivating dataset shown in Section 1, we considered several empirical polynomial LME models for CD4 data during ART. We find that the following simple empirical LME model fits the CD4 data reasonably well (see Appendix)
| (4) |
where are fixed effects and are random effects. More complex models, such as a quadratic LME model with α 3i = α 3 + a 3i , do not improve the model fit substantially but they are more complex and less stable. Thus, we choose the simpler LME model (4) for the (square root transformed) CD4 data.
A viral rebound model following ART interruption
We now model viral rebound data following ART interruption. Let w ij be the (log10-transformed) viral load value of individual i measured at time , , where is the time since ART interruption (not since the start of ART). After ART interruption, the viral load trajectories typically rise to a peak value followed by a decrease to a viral load set point. Wang et al. (2020) proposed an NLME model with a flexible functional form to capture this non-linear trajectory and provide biological insights regarding the rebound process. In comparison to non-parametric modeling approaches such as the use of penalized smoothing splines (Zhao et al. 2021), key features of viral rebound trajectories are represented by the parameters in the model, which provides a means to assess the covariate effects on each of these model parameters and allows us to identify critical pre-ATI predictors for these features directly. Comparison of this parametric NLME model to a dynamic viral model (Prague et al. 2019) found that both modeling approaches led to good individual fits and consistent conclusions regarding the features of the viral rebound process (Bing et al. 2020).
Following Wang et al. (2020) (with minor modification), we consider the following NLME model for modelling the viral rebound following ART interruption
| (5) |
| (6) |
where vector contains individual-specific parameters, vector contains fixed effect parameters, R i is a 4 × q * design matrix contains covariates, and contains random effects with G being a covariance matrix, and ξ ij is within-individual random error. We assume that the random effects τ i and the random error ξ ij are independent, and ξ ij are i.i.d. . Here the modification from Wang et al. (2020) is to replace the term that describes the decline of the viral load from peak to set-point by a constant parameter. The reason for this modification is that our viral load data after their peaks during rebound exhibit large between-subject variations without a clear pattern, so the parameter in the original model of Wang et al. (2020) that characterizes the ‘dip’ after the leak may not be estimated well; including such parameter in the model may also lead to non-convergences issues. In our current setting, we focus on modeling the rate of rise and viral set points. While the simplification with a constant term in the above model limits our ability to estimate the peak and the decline from the peak, it provides a good fit to the data and allows the parameters of primary interest (rate of rise and viral set point) to be estimated well.
Note that the above NLME model (5) and (6) may be viewed as a two-stage model: In stage 1, model (5) describes the viral rebound trajectories within an individual; and in stage 2, model (6) assumes that the between-individual variations in the individual-specific parameters in model (5) may be partially explained by covariates in R i as well as random effects τ i .
The parameters in NLME model (5) have the following attractive interpretations (Wang et al. 2020): parameter β 1i represents set point after rebound, parameter β 2i and β 3i respectively characterize the timing and rate of rise in viral rebound, and parameter β 4i denotes initial viral load value at the start of rebound. Figure 2B shows the viral load rebound profile for a typical subject based on model (5). Therefore, each of the four parameters denotes an important characteristic of the viral rebound trajectories following ART interruption.
As noted in Section 1, our main objective is to assess if key features of viral load or CD4 trajectories after ART initiation may be associated with important characteristics of viral rebounds following ART interruption. We may use the second-stage model (6) to evaluate such possible associations. Note that the random effects b i in NLME model (2) for viral load data during ART may be viewed as individual-specific characteristics of the viral load trajectories during ART. Thus, we may use the random effects b i as “covariates” in the rebound model (6) to see if these “covariates” may partially explain the large variations in the individual-specific parameters β i during viral rebound. Similarly, we may consider the random effects a i in the CD4 model (4) during ART and use them as possible “covariates” in the NLME model (6) for viral load following ART interruption. Specifically, in the NLME model for viral rebound, we may consider the following second-stage model for (6)
| (7) |
where β k ’s are fixed effects parameters, γ kl ’s are fixed effect parameters associated with the corresponding random effects respectively, and v * i denotes other baseline covariates.
For the motivating dataset shown in Figure 1, the sample size is small. In this case, we may simplify the second-stage model (7) to reduce the number of parameters and only focus on the key features of viral decay and viral rebound. For example, to see if the initial viral decay rate λ 1i = λ 1 + b 3i in NLME model (2) during ART may be associated with the values of setpoints β 1i after viral rebound, we may consider the following second-stage model
| (8) |
Then, testing H 0: γ 13 = 0 vs. H 1: γ 13 ≠ 0 allows us to assess possible association between b 3i and β 1i . Similarly, we can evaluate other possible associations.
Parameter estimation and inference
In the previous section, we describe two NLME models and an LME model for viral load and CD4 longitudinal data before and following ART interruption respectively. A challenge in data analysis is that some viral loads are left censored in the later period during ART and in the early period after ART interruption. In other words, both NLME models for viral loads must incorporate left censored data. In this section, we consider a likelihood method for parameter estimation and inference, incorporating left censoring. Note that we may consider the (joint) likelihood for all observed data under the three models. However, such a unified approach can be computationally very intensive, as will be discussed later in this section. To circumvent the computational burden, here we consider likelihood methods for the three models separately, but accounting for shared random effects linking these models. Then we propose a simple three-step method for parameter estimation and inference.
We first consider the NLME model (2) for viral dynamics during ART. Suppose that the lower detection limit of viral load is d i for subject i, i.e., viral load values smaller than d i cannot be observed. The observed value of viral load y ij for individual i at time t ij can then be written as , where c ij is the censoring indicator such that is observed if c ij = 0 and y ij is left censored if c ij = 1, i = 1, 2, …, n; j = 1, 2, …, n i . Let , let denote the observed components of , and let y cen,i denote the censored components of y i . The observed data of viral load before ART interruption are . Let f(⋅) denote a generic density function and F(⋅) denote the corresponding cumulative density function (cdf). Let θ 1 be the collection of all unknown parameters in the NLME model (2). The likelihood for the observed viral load data during ART based on the NLME model (2) can be written as
We see that the likelihood L o ( θ 1) involves an intractable integration, since the dimension of (y cen,i , b i ) is high and the model is nonlinear.
To evaluate L o ( θ 1), a commonly used method is the MCEM algorithm (Wei and Tanner 1990), treating the left censored values y cen,i and random effects b i as “missing data” (Hughes 1999; Wu 2002). Specifically, the E-step at the kth EM iteration can be written as
where is the parameter estimate from previous EM iteration (k = 1, 2, …). To evaluate in the E-step, we can use Monte Carlo methods to simulate a large number of “missing data” (y cen,i , b i ) from the conditional distribution , and then approximate by the empirical mean based on the simulated values. This simulation step can be implemented by Gibbs sampler along with rejection sampling methods or the importance sampling method or other Markov Chain Monte Carlo (MCMC) methods (Wu 2009). The M-step can be based on the Newton-Raphson method. This MCEM algorithm can be computationally intensive since the dimension of the “missing data” (y cen,i , b i ) can be high, so simulating large numbers from the conditional distribution can be very slow.
Alternatively, a computationally more efficient method than the MCEM algorithm is the stochastic approximation EM (SAEM) algorithm (Delyon, Lavielle, and Moulines 1999). The SAEM algorithm replaces the E-step of the MCEM algorithm by a single draw from the conditional distribution based on an MCMC method, and then use a stochastic approximation to update . Delyon, Lavielle, and Moulines (1999) shows theoretically that SAEM converges to a (local) maximum of the likelihood under general conditions. The SAEM algorithm for NLME models has been implemented in the software “Monolix” (Comets, Lavenu, and Lavielle 2017; Kuhn and Lavielle 2005). Samson, Lavielle, and Mentré (2006) extends the SAEM method to NLME models with left censoring, based on simulating the left-censored values y cen,i from a right-truncated Gaussian distribution based on the Gibbs sampling in the E-step of the SAEM algorithm.
Similarly, the foregoing SAEM method can be used for the NLME model (5) and (6) for viral rebound data following ART interruption. In fact, we may consider the SAEM algorithm for all three models simultaneously based on the joint likelihood of all observed data. However, such a joint likelihood method can be difficult to implement and computationally extremely intensive, since the dimension of the “missing data” (y cen,i , w cen,i , b i , τ i , a i ) is very high so even a single simulation using an MCMC method can be computationally over-whelming, where w cen,i denotes the censored components of . Therefore, here we propose to use SAEM for each NLME model with left censoring separately to reduce the computation burden. Specifically, we propose the following three-step (TS) method:
-
–
Step 1: For data during ART, fit the NLME model (2) for viral load with censoring using the above SAEM algorithm and fit the LME model for CD4 using the standard method respectively, and then obtain the maximum likelihood estimates (MLEs) of the fixed parameters and the empirical Bayes estimates of the random effects, and , respectively;
-
–
Step 2: For viral rebound data following ART interruption, fit the NLME model (5) with left censoring using the above SAEM algorithm, with the random effects a i and b i in the second-stage model (7) substituted by their empirical Bayes estimates and from Step 1;
-
–
Step 3: Obtain the standard errors of the parameter estimates based on a (parametric) bootstrap method, which incorporates the estimation uncertainty of random effect estimates and in Step 1.
The parametric bootstrap method works as follows:
Simulate CD4 and viral load data with left censoring, based on the fitted LME and two NLME models using the above three-step method, where the model parameters are replaced by their estimates.
For the simulated CD4 and viral load data, fit all three models again using the above three-step method and obtain all parameter estimates.
Repeat the above process B times (say, B = 100), we obtain B estimates for each parameter. The sample standard deviation of these B estimates of each parameter is the parametric bootstrap estimate of standard error of the corresponding parameter estimate.
The above bootstrap method incorporates the estimation uncertainty of the parameter and random effect estimates in the TS method with separate model fitting, so it should produce more reliable standard errors of the parameter estimates than those from separate model fitting. Note that, in Step 2 of the above TS method, we use the empirical Bayes estimates of the random effects. An alternative approach is to sample from the posterior distribution of the random effects, but this approach may introduce additional variability from the sampling.
Results of data analysis
In this section, we analyze the dataset shown in Figure 1 using the proposed TS method and a naive (NV) method, which still uses the SAEM algorithm but the censored values are substituted by half the detection limit and inference is based on model-based standard errors. There are 75 patients in the study. Viral loads and CD4 are repeatedly measured on patients during ART and following ART interruption, with the longest time of 58.4 months and shortest time of 16.73 months. After ART interruption, viral load usually increases to a peak within 6–10 weeks, then decrease to a stable level over a time scale of months. Therefore, we restrict our attention to data within week 36 (9 months). We excluded individuals with 2 or less repeated measurements either during ART or following ART interruption (n = 5) or individuals with un-suppressed viral load values at the first time point following ART interruption (n = 4). For remaining viral load data during ART, the minimum number of repeated measurements is 5, and the maximum number of repeated measurements is 19, with an average number of repeated measurements being 9.32. For viral load data following ART interruption, the minimum number of repeated measurements is 3, and the maximum number of repeated measurements is 23, with an average number of repeated measurements being 6.63. The proportions of viral load measurements that are left censored (below the detection limit) before or after ART interruption are 59.6% or 23.9%, respectively. From Figure 1, we can see that the viral load trajectories during ART exhibit clear patterns of viral decay. Following ART interruption, the viral loads rebound quickly, but their trajectories become complicated after reaching peak points, with substantial between-subject variations.
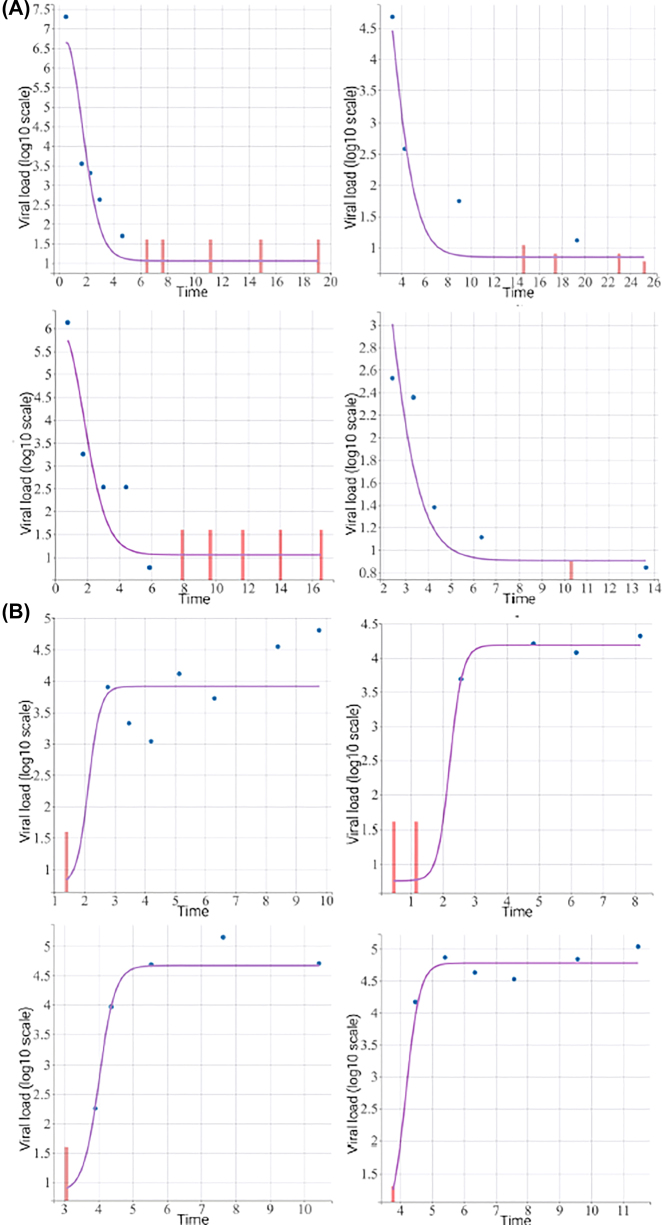
For viral load data during ART, we fit the NLME model (2) of Wu and Ding (Wu and Ding 1999), with left-censored data addressed by the SAEM method. The bi-exponential decay NLME model (2) fits the viral load data very well. Figure 3A (top four figures) shows the fitted values vs. the corresponding observed values for four randomly selected subjects during ART. For the CD4 data during ART, the CD4 trajectories do not appear to exhibit clear patterns, with large between-subject variations, possibly due to substantial measurement errors. However, there seems an overall upward trend. Thus, we fit the LME model (4) to the CD4 data, which captures a rough upward trend before ART interruption.
Figure 3:
Observed and fitted viral load trajectories before (top four figures) and following (bottom four figures) ART interruption for 4 randomly selected subjects respectively. The red vertical bars represent left-censored viral loads.
For viral load data following ART interruption, we consider the following NLME model
| (9) |
where β 1i is the viral set point during rebound and the random effects (b 1i , b 2i , b 3i , b 4i , a 1i , a 2i ) are defined in model (7) (e.g., b 3i is the random effect associated with the initial viral decay rate λ 1i during viral decay before ART interruption). We again address left-censored data by the SAEM method. We use the parametric bootstrap method with B = 100 to estimate the standard errors of all the fixed effect parameter estimates. This NLME model for viral rebound also fits the data reasonably well. Figure 3B (bottom four figures) shows the fitted values vs. the corresponding observed values for four randomly selected subjects during viral rebound.
Table 1 shows parameter estimation results for models (2) and (9) (the time unit in data analysis is month). We see that parameters γ 13 and γ 14, which link the initial viral decay rates λ 1i and λ 2i during ART to viral setpoints β 1i following ART interruption for individual i, suggest an association among these features (p-value = 0.029 and < 0.001 respectively). Specifically, the initial viral decay rates during ART appears to be negatively associated with the viral setpoints following ART interruption: the faster the viral decay after start of ART, the lower the setpoints following ART interruption. In addition, the second-phase viral decay rates during ART appears to be negatively associated with the viral setpoints following ART interruption: the faster the viral decay in the slow decay phase during ART, the lower the setpoints following ART interruption. The naive method produces similar estimates but different standard errors (we only show naive SE in Table 1 since naive estimates are similar). We will evaluate the two methods via simulation in the next section.
Table 1:
Parameter estimates with a second-stage model for setpoint β 1i .
| Parameter | Estimate | Naive SE | Bootstrap SE | z-Value | p-Value |
|---|---|---|---|---|---|
| P 1 | 11.258 | 0.283 | 0.167 | 67.449 | 0.000 |
| λ 1 | 4.790 | 0.380 | 0.362 | 13.244 | 0.000 |
| P 2 | 3.271 | 0.117 | 0.206 | 15.872 | 0.000 |
| λ 2 | 0.225 | 0.027 | 0.019 | 11.788 | 0.000 |
| α 1 | 0.087 | 0.007 | 0.017 | 5.178 | 0.000 |
| α 2 | 24.080 | 0.517 | 0.438 | 54.985 | 0.000 |
| β 1 | 2.828 | 0.161 | 0.243 | 11.651 | 0.000 |
| γ 11 | 0.144 | 0.073 | 0.075 | 1.911 | 0.056 |
| γ 12 | −0.027 | 0.559 | 0.755 | −0.035 | 0.972 |
| γ 13 | −0.252 | 0.079 | 0.116 | −2.177 | 0.029 |
| γ 14 | −97.574 | 50.944 | 26.294 | −3.711 | 0.000 |
| γ 15 | −0.026 | 0.033 | 0.035 | −0.728 | 0.467 |
| γ 16 | 0.811 | 1.290 | 4.291 | 0.189 | 0.850 |
| β 2 | 1.588 | 1.308 | 0.694 | 2.289 | 0.022 |
| β 3 | 3.360 | 1.614 | 0.828 | 4.056 | 0.000 |
| β 4 | 0.783 | 0.119 | 0.151 | 5.195 | 0.000 |
Naive SE is the standard error based on separate model fitting without bootstrap, z-Value is the ratio of estimate/bootstrap SE, and p-Value is based on the z-Value and the standard normal tail probability for a two-sided test.
We may also consider the following second stage model associated with the NLME model (9) for viral rebound following ART interruption:
| (10) |
The analysis results are presented in Table 2. We see that the rate of rise during viral rebound following ART interruption β 3i appears to be negatively correlated with initial viral decay rate (γ 33) and positively correlated with initial viral load values (γ 31). That is, the faster the initial viral decline during ART or the lower the initial viral loads, the slower the viral rising following ART interruption.
Table 2:
Parameter estimates with a second-stage model for rebound rate β 3i .
| Parameter | Estimate | Naive SE | Bootstrap SE | z-Value | p-Value |
|---|---|---|---|---|---|
| P 1 | 11.258 | 0.283 | 0.204 | 55.176 | 0.000 |
| λ 1 | 4.790 | 0.380 | 0.236 | 20.321 | 0.000 |
| P 2 | 3.271 | 0.117 | 0.167 | 19.575 | 0.000 |
| λ 2 | 0.225 | 0.027 | 0.019 | 11.627 | 0.000 |
| α 1 | 0.087 | 0.007 | 0.011 | 7.765 | 0.000 |
| α 2 | 24.080 | 0.517 | 0.518 | 46.456 | 0.000 |
| β 1 | 2.946 | 0.375 | 0.127 | 23.196 | 0.000 |
| β 2 | 1.542 | 1.040 | 0.419 | 3.680 | 0.000 |
| β 3 | 3.280 | – | 0.448 | 7.327 | 0.000 |
| γ 31 | 0.837 | 0.053 | 0.211 | 3.971 | 0.000 |
| γ 32 | −4.589 | 0.177 | 2.691 | −1.705 | 0.088 |
| γ 33 | −1.110 | 0.008 | 0.317 | −3.501 | 0.000 |
| γ 34 | −221.564 | 12.712 | 116.409 | −1.903 | 0.057 |
| γ 35 | −0.106 | 0.023 | 0.109 | −0.969 | 0.333 |
| γ 36 | −0.090 | 0.445 | 8.458 | −0.011 | 0.991 |
| β 4 | 0.772 | 0.448 | 0.057 | 13.625 | 0.000 |
Naive SE is the standard error based on separate model fitting without bootstrap, z-Value is the ratio of estimate/bootstrap SE, and p-Value is based on the z-Value and the standard normal tail probability for a two-sided test. A naive SE is unavailable, possibly due to parameters being unidentifiable.
In summary, the analysis results show that some key characteristics of the viral load trajectories during ART, especially the initial viral decay rates after the start of ART, appear to be associated with some important features of the viral rebound following ART interruption, such as viral setpoints and rates of viral rising. The CD4 data during ART do not seem to be associated with important features of the viral rebound following ART interruption.
Simulation study
In this section, we conduct extensive simulations to evaluate the proposed TS method and compare it with the naive method used in data analysis. We choose similar NLME models to those in the data analysis section, but we omit the CD4 model for simplicity. The true values of the model parameters are set to be similar to those estimated in the data analysis section. The sample size is set to be n = 50 individuals. For the within-individual longitudinal measurements, to mimic the real dataset, for half the sample we choose 10 repeated measurements during ART and 9 repeated measurements following ART interruption, while for the remaining half the sample we choose 11 repeated measurements during ART and 11 repeated measurements following ART interruption. The measurement times are chosen to be similar to those in the real dataset. Two sets of measurement times during ART are t 1 = (0.5, 1.6, 2.3, 3, 4.6, 6.5, 7.6, 11.2, 14.9, 19.1) and t 2 = (0.5, 0.7, 1.7, 3, 4.4, 5.9, 7.9, 9.6, 11.7, 14, 16.5). Two sets of measurement times following ART interruption are and .
We generate the viral load data during ART based on the following NLME model
| (11) |
where e ij i.i.d. and . The true values are P 1 = 17.0, P 2 = 2.6, λ 1 = 4, λ 2 = 0.05, and σ 1 = 0.5. The detection limit is set to be d = 1.60. For the viral load data following ART interruption, we generate the data based on the following NLME model
where b 3i is the random effect from model (11), , and τ i ∼ N(0, G). The true parameter values are β 1 = 3.2, β 2 = 5.6, β 3 = 10, β 4 = 1, γ 3 = 1, σ 3 = 0.5,
We evaluate the proposed TS method based on bias, mean square error (MSE), and coverage rates of 95% confidence intervals. For a parameter β and its estimate , the bias and root MSE (rMSE) are defined as , and the coverage rate is the proportion of confidence intervals which covers the true value. We compare the TS method to a naive method which replaces censored viral loads by half the detection limits and uses the model-based standard errors for inference. For the TS method, the number of bootstrap samples is B = 100. The simulations are repeated 100 times. While a larger number of repetitions may be more desirable, the computation involving bootstrap is intensive and the 100 repetitions results seem sufficient to allow us to make reasonable conclusions (Morris, White, and Crowther 2019).
The simulation results are shown in Table 3. We see that the proposed TS method performs quite well and clearly outperforms the naive method: estimates based on the TS method are approximately unbiased with estimated coverage probabilities close to the nominal level 0.95, while estimates based on the naive method may sometimes produce biased results with estimated coverage probabilities way below the nominal level 0.95. Despite the simulation results, both methods seem to produce similar results on the real data analysis in the previous section. Note that the SE’s based on the naive method maybe underestimate the true variation since the naive method ignores the uncertainties of the censored values and the separate NLME model fitting, therefore the naive method may lead to smaller MSE’s but lower coverage probabilities. On the other hand, the proposed TS method incorporates the uncertainty of the censored values by the SAEM algorithm and the separate NLME model fitting by bootstrap, so it may lead to larger MSE’s but correct coverage probabilities.
Table 3:
Simulation results.
| Parameter | True value | Method | Estimate | SE | Bias | rMSE | Coverage |
|---|---|---|---|---|---|---|---|
| P 1 | 17.0 | TS | 17.097 | 0.425 | 0.097 | 0.435 | 0.95 |
| Naive | 17.088 | 0.257 | 0.088 | 0.272 | 0.91 | ||
| λ 1 | 4.0 | TS | 4.092 | 0.240 | 0.092 | 0.257 | 0.91 |
| Naive | 4.137 | 0.216 | 0.137 | 0.256 | 0.91 | ||
| P 2 | 2.6 | TS | 2.794 | 0.398 | 0.194 | 0.442 | 0.95 |
| Naive | 2.222 | 0.111 | −0.378 | 0.394 | 0.39 | ||
| λ 2 | 0.1 | TS | 0.040 | 0.081 | −0.010 | 0.081 | 0.95 |
| Naive | 0.029 | 0.009 | −0.021 | 0.023 | 0.40 | ||
| β 1 | 3.2 | TS | 3.267 | 0.140 | 0.067 | 0.155 | 0.95 |
| Naive | 3.324 | 0.130 | 0.124 | 0.180 | 0.86 | ||
| γ 3 | 1.0 | TS | 0.986 | 0.096 | −0.014 | 0.097 | 0.94 |
| Naive | 0.999 | 0.083 | −0.001 | 0.083 | 0.92 | ||
| β 2 | 5.6 | TS | 5.588 | 1.187 | −0.012 | 1.187 | 0.94 |
| Naive | 6.370 | 1.354 | 0.770 | 1.558 | 0.84 | ||
| β 3 | 10.0 | TS | 10.079 | 2.062 | 0.079 | 2.064 | 0.94 |
| Naive | 11.170 | 2.650 | 1.170 | 2.897 | 0.88 | ||
| β 4 | 1.0 | TS | 0.930 | 0.092 | −0.070 | 0.115 | 0.85 |
| Naive | 0.861 | 0.072 | −0.139 | 0.157 | 0.62 |
Since the performance of MLEs of mixed effects models depends both on the sample size and the number of repeated measurements, we also conduct another simulation study by choosing more frequent repeated measurements, with other true parameter values remaining the same. The measurement times are chosen to be close to those in the real dataset with additional measurement times in between. Specifically, the new set of measurement times during ART are chosen to be t 1 = (0.4, 1.2, 1.6, 2.1, 3.2, 4.6, 5.3, 7.8, 10.4, 13.4, 17), and the new set of measurement times following ART interruption are chosen to be (0, 0.6, 0.8, 1.2, 1.4, 1.7, 1.9, 2.1, 2.6, 3.1, 3.8, 4.5, 5.4, 6). The simulation results are shown in Table 4. The proposed TS method again outperforms the naive method.
Table 4:
Simulation results with more frequent repeated measurements.
| Parameter | True value | Method | Estimate | SE | Bias | rMSE | Coverage |
|---|---|---|---|---|---|---|---|
| P 1 | 17.0 | TS | 16.820 | 0.733 | −0.180 | 0.755 | 0.93 |
| Naive | 16.981 | 0.259 | −0.019 | 0.260 | 0.89 | ||
| λ 1 | 4.0 | TS | 4.011 | 0.288 | 0.011 | 0.288 | 0.92 |
| Naive | 4.103 | 0.202 | 0.103 | 0.227 | 0.85 | ||
| P 2 | 2.6 | TS | 2.968 | 0.705 | 0.368 | 0.796 | 0.95 |
| Naive | 2.273 | 0.142 | −0.327 | 0.357 | 0.51 | ||
| λ 2 | 0.1 | TS | 0.096 | 0.186 | 0.046 | 0.191 | 0.95 |
| Naive | 0.041 | 0.012 | −0.009 | 0.015 | 0.34 | ||
| β 1 | 3.2 | TS | 3.223 | 0.132 | 0.023 | 0.134 | 0.94 |
| Naive | 3.304 | 0.121 | 0.104 | 0.159 | 0.87 | ||
| γ 3 | 1.0 | TS | 0.986 | 0.095 | −0.014 | 0.096 | 0.97 |
| Naive | 0.996 | 0.089 | −0.004 | 0.089 | 0.96 | ||
| β 2 | 5.6 | TS | 5.553 | 0.873 | −0.047 | 0.874 | 0.95 |
| Naive | 6.258 | 0.676 | 0.658 | 0.943 | 0.79 | ||
| β 3 | 10.0 | TS | 9.757 | 1.460 | −0.243 | 1.481 | 0.96 |
| Naive | 10.715 | 1.166 | 0.715 | 1.368 | 0.82 | ||
| β 4 | 1.0 | TS | 0.980 | 0.079 | −0.020 | 0.081 | 0.88 |
| Naive | 0.886 | 0.048 | −0.114 | 0.124 | 0.63 |
Conclusions and discussion
We have shown that key features of viral decay during ART may be associated with important features of viral rebound following ART interruption. For example, the faster the viral decay after start of ART, the lower the setpoints following ART interruption. Such a finding may provide insights into HIV cure research. Recent findings suggest that HIV-1 latent reservoir is primarily established near the time of ART initiation (Abrahams et al. 2019); interventions in addition to ART to inhibit the formation of latent reservoir may subsequently lead to a lower viral set point – a key goal of the HIV functional cure. A limitation of our dataset is that the sample size is somewhat small.
In the future, if we are able to obtain a larger dataset, we may be able to identify more interesting associations between features of viral decay and viral rebound. Another issue is the frequencies of the repeated measurements within each individual. If the longitudinal data were collected more frequently over time, the mixed effects model parameters might be estimated more accurately in the sense of possibly smaller standard errors, allowing us to identify more interesting associations. It would also be of interest to investigate optimal study design, e.g., how to schedule measurement times, to improve efficiency of data analysis.
We have considered two NLME models with left censoring and an LME model, and we estimate the model parameters separately using an SAEM algorithm and a bootstrap method, called a three-step method. Similar ideas have appeared in the context of measurement error literature (Carroll et al. 2006). A major advantage of the proposed three-step method is that it is easy to implement and is computationally efficient. A disadvantage is that the parameter estimates may not be most efficient if the assumed models hold, since the model parameters are estimated separately. In addition, other possible useful covariates, such as the time from viral suppression to ART interruption, are not included in the models in order to keep the models relatively simple, and the possible association between the random effects in the viral load models and the CD4 model is ignored for simplicity, due to small sample sizes. One may also consider simultaneous likelihood inference based on the joint likelihood of all three models via an Monte Carlo EM algorithm (e.g., Wu 2009), but such a method can be computationally very intensive and may encounter convergence issues, since the dimensions of unobservable random effects and censored values are high. Alternatively, we may consider approximate joint likelihood inferences based on the so-called h-likelihood (Lee, Nelder, and Pawitan 2017) or based on Laplace approximations (Vonesh et al. 2002), but the accuracy of these approximations could be a potential issue. Another promising approach is to use Bayesian methods (e.g., Dey, Chen, and Chang 1997; Huang et al. 2018), which will be investigated separately.
In this article, we have focused on studying the associations among the individual viral dynamic characteristics during ART and following ART interruption, such as the individual viral decay rates and setpoints. Another important direction is to study the association between the individual viral dynamic characteristics during ART and times to viral rebound or times to setpoints after ART is stopped. For example, are individuals with faster viral declines during ART associated with slower viral rebounds after the therapy is stopped? Such questions may be answered using joint inference for an NLME model for viral dynamics during ART and a time-to-event model such as a Cox proportional hazards model. There is an extensive literature on joint models for longitudinal and survival data and modelling times to viral rebound (e.g., Conway, Perelson, and Li 2019; Hill et al. 2016; Yu, Wu, and Gilbert 2018). We will explore this direction separately.
The models can be extended in different ways. For example, we may consider semiparametric NLME models for viral rebound data since the viral rebound trajectories after reaching peak points may not be easily modelled parametrically due to large between-individual variations without clear patterns. In the article, we have assumed that the left censored viral loads follow the same distribution as the observed viral loads. Such an assumption is not testable based on the observed data. We may consider an approach which does not make such assumption, e.g., treating the censored values as point masses as in Yu, Wu, and Gilbert (2018).
Appendix: Model selection and diagnostics
In this section, we consider model selection and diagnostics for CD4 models. These viral load models are well studied in the literature (e.g., Wang et al. 2020; Wu and Ding 1999; Wu 2009). For the CD4 data, we considered log-transformation and square root transformation so that the transformed data are more compatible with the normality and constant variance assumptions. We find that these two transformations lead to similar results. More complex transformations, such as those based on the Box-Cox transformations, do not appear to improve the results substantially, and they are harder to interpret. Therefore, in the paper, we choose the square root transformation of CD4 counts since it is widely used in ACTG data analyses.
For CD4 model selections, since the CD4 model is secondary in the paper and CD4 data are measured with errors, we focus on the simplicity and goodness-of-fit of the candidate models. We find that a simple LME model captures the main features of the CD4 trajectories and it also fits the observed CD4 data reasonably well, i.e., in the paper, we choose the CD4 model:
where CD4 ij is the original CD4 count for subject i measured at time t ij , α k ’s are fixed effects, and a ki ’s are random effects. Note that this simple CD4 model may also be interpreted as a classic measurement error model, where may be interpreted as the unobserved true (transformed) CD4 value for subject i at time t ij . The AIC (BIC) values for the CD4 models with a quadratic term (and a random effect) and without a quadratic term are 2690 (2733) and 2733 (2759), respectively. Thus, adding a quadratic term does not appear to improve the model substantially but it may make the model more complicated and less stable.
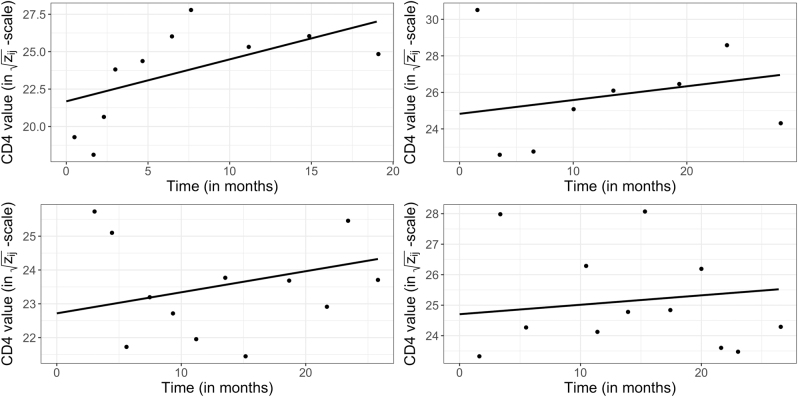
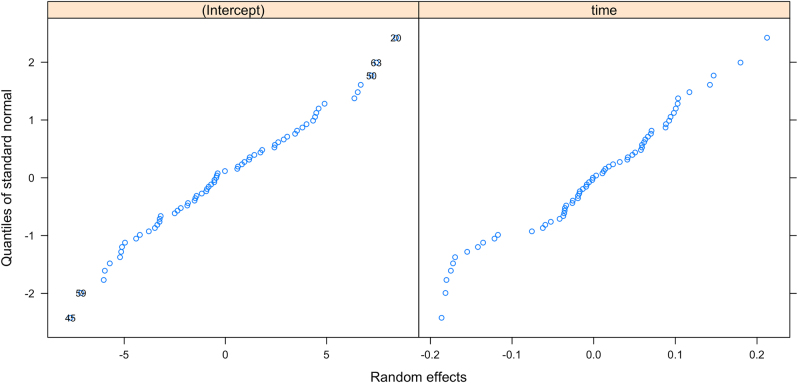
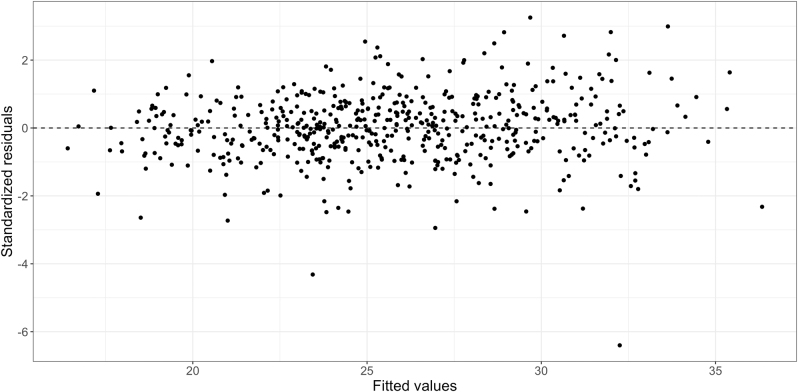
Figure 4 shows the observed/fitted CD4 values for four randomly selected subjects. We see that the CD4 model captures the main features of the CD4 trajectories. Figure 5 shows the normal QQ-plots for the estimated random effects in the intercepts and slopes of the CD4 model. We see that the normality assumptions are mostly reasonable. Figure 6 shows the overall residual plots of the CD4 model. These model diagnostics indicate that the simple CD4 model is a reasonable choice.
Figure 4:
Observed/fitted CD4 values for four randomly selected subjects. The solid lines represent individual fitted CD4 models, and the dots represent observed CD4 values.
Figure 5:
Normal QQ-plots for random effects in intercepts and slopes in the CD4 model.
Figure 6:
Residual plot for the CD4 model.
Footnotes
Research funding: We gratefully acknowledge grants from US National Institute of Allergy and Infectious Diseases P01 AI131385, R01 AI136947, an Ebert Career Development Award from Harvard Pilgrim Health Care Institute and Harvard Medical School, and the Natural Sciences and Engineering Research Council of Canada (NSERC) discovery grant 22R80742, and Swiss National Science Foundation, 179571.
References
- Abrahams M. R., Joseph S. B., Garrett N., Tyers L., Moeser M., Archin N., Council O. D., Matten D., Zhou S., Doolabh D., Anthony C., Goonetilleke N., Abdool Karim S., Margolis D. M., Pond S. K., Williamson C., Swanstrom R. The Replication-competent HIV-1 Latent Reservoir is Primarily Established Near the Time of Therapy Initiation. Science Translational Medicine . 2019;11:1–11. doi: 10.1126/scitranslmed.aaw5589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bing A., Hu Y., Prague M., Hill A. L., Li J. Z., Bosch R. J., DeGruttola V., Wang R. Comparison of Empirical and Dynamic Models for HIV Viral Load Rebound after Treatment Interruption. Statistical Communications in Infectious Diseases . 2020;12:20190021. doi: 10.1515/scid-2019-0021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carroll R. J., Ruppert D., Stefanski L. A., Crainiceanu C. M. Measurement Error in Nonlinear Models: a Modern Perspective . 2nd ed. New York: Chapman and Hall/CRC; 2006. [Google Scholar]
- Comets E., Lavenu A., Lavielle M. Parameter Estimation in Nonlinear Mixed Effect Models Using Saemix, an R Implementation of the SAEM Algorithm. Journal of Statistical Software. 2017;80:i03–41. doi: 10.18637/jss.v080.i03. [DOI] [Google Scholar]
- Conway J. M., Perelson A. S., Li J. Z. Predictions of Time to HIV Viral Rebound Following ART Suspension that Incorporate Personal Biomarkers. PLoS Computational Biology. 2019;15:e1007229. doi: 10.1371/journal.pcbi.1007229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delyon B., Lavielle M., Moulines E. Convergence of a Stochastic Approximation Version of the EM Algorithm. Annals of Statistics. 1999;27:94–128. doi: 10.1214/aos/1018031103. [DOI] [Google Scholar]
- Dey D. K., Chen M.-H., Chang H. Bayesian Approach for Nonlinear Random Effects Models. Biometrics . 1997;53:1239–52. doi: 10.2307/2533493. [DOI] [Google Scholar]
- Gianella S., von Wyl V., Fischer M., Niederoest B., Battegay M., Bernasconi E., Cavassini M., Rauch A., Hirschel B., Vernazza P., Weber R., Joos B., Günthard H. F., The Swiss HIV Cohort Study Effect of Early Antiretroviral Therapy during Primary HIV-1 Infection on Cell-Associated HIV-1 DNA and Plasma HIV-1 RNA. Antiviral Therapy. 2011;16:535–45. doi: 10.3851/imp1776. [DOI] [PubMed] [Google Scholar]
- Hill A. L., Rosenbloom D. I., Goldstein E., Hanhauser E., Kuritzkes D. R., Siliciano R. F., Henrich T. J. Real-time Predictions of Reservoir Size and Rebound Time during Antiretroviral Therapy Interruption Trials for HIV. PLoS Pathogens. 2016;12:e1005535. doi: 10.1371/journal.ppat.1005535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Y., Lu X., Chen J., Liang J., Zangmeister M. Joint Model-based Clustering of Nonlinear Longitudinal Trajectories and Associated Time-to-event Data Analysis, Linked by Latent Class Membership: With Application to AIDS Clinical Studies. Lifetime Data Analysis. 2018;24:699–718. doi: 10.1007/s10985-017-9409-0. [DOI] [PubMed] [Google Scholar]
- Hughes J. P. Mixed Effects Models with Censored Data with Application to HIV RNA Levels. Biometrics. 1999;55:625–9. doi: 10.1111/j.0006-341x.1999.00625.x. [DOI] [PubMed] [Google Scholar]
- Hurst J., Hoffmann M., Pace M., Williams J. P., Thornhill J., Hamlyn E., Meyerowitz J., Willberg C., Koelsch K. K., Robinson N., Brown H., Fisher M., Kinloch S., Cooper D. A., Schechter M., Tambussi G., Fidler S., Babiker A., Weber J., Kelleher A. D., Phillips R. E., Frater J. Immunological Biomarkers Predict HIV-1 Viral Rebound after Treatment Interruption. Nature Communications. 2015;6:8495. doi: 10.1038/ncomms9495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Julg B., Dee L., Ananworanich J., Barouch D. H., Bar K., Caskey M., Colby D. J., Dawson L., Dong K. L., Dubé K., Eron J., Frater J., Gandhi R. T., Geleziunas R., Goulder P., Hanna G. J., Jefferys R., Johnston R., Kuritzkes D., Li J. Z., Likhitwonnawut U., van Lunzen J., Martinez-Picado J., Miller V., Montaner L. J. Recommendations for Analytical Antiretroviral Treatment Interruptions in HIV Research Trials—Report of a Consensus Meeting. The Lancet HIV. 2019;6:e259–e268. doi: 10.1016/s2352-3018(19)30052-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhn E., Lavielle M. Maximum Likelihood Estimation in Nonlinear Mixed Effects Models. Computational Statistics & Data Analysis. 2005;49:1020–38. doi: 10.1016/j.csda.2004.07.002. [DOI] [Google Scholar]
- Lee Y., Nelder J., Pawitan Y. Generalized Linear Models with Random Effects: Unified Analysis via h-likelihood. 2nd ed. Vol. 153. Boca Raton: CRC Press/Taylor & Francis Group; 2017. [Google Scholar]
- Li J., Etemad B., Ahmed H., Aga E., Bosch R. J., Mellors J. W., Kuritzkes D. R., Lederman M. M., Para M., Gandhi R. T. The Size of the Expressed HIV Reservoir Predicts Timing of Viral Rebound after Treatment Interruption. AIDS. 2016;30:1–353. doi: 10.1097/qad.0000000000000953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J. Z., Smith D. M., Mellors J. W. The Critical Roles of Treatment Interruption Studies and Biomarker Identification in the Search for an HIV Cure. AIDS. 2015;29:1429. doi: 10.1097/qad.0000000000000658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindstrom M. J., Bates D. M. Nonlinear Mixed Effects Models for Repeated Measures Data. Biometrics. 1990;46:673–87. doi: 10.2307/2532087. [DOI] [PubMed] [Google Scholar]
- Morris T. P., White I. R., Crowther M. J. Using Simulation Studies to Evaluate Statistical Methods. Statistics in Medicine. 2019;38:2074–102. doi: 10.1002/sim.8086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Namazi G., Fajnzylber J. M., Aga E., Bosch R. J., Acosta E. P., Sharaf R., Hartogensis W., Jacobson J. M., Connick E., Volberding P., Skiest D., Margolis D., Sneller M. C., Little S. J., Gianella S., Smith D. M., Kuritzkes D. R., Gulick R. M., Mellors J. W., Mehraj V., Gandhi R. T., Mitsuyasu R., Schooley R. T., Henry K., Tebas P., Deeks S. G. The Control of HIV after Antiretroviral Medication Pause (CHAMP) Study: Posttreatment Controllers Identified from 14 Clinical Studies. The Journal of infectious diseases. 2018;218:1954–63. doi: 10.1093/infdis/jiy479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noubary F., Hughes M. D. Factors Affecting Timing of Antiretroviral Treatment Initiation Based on Monitoring CD4 Counts. Journal of acquired immune deficiency syndromes. 2012;61:326. doi: 10.1097/qai.0b013e31826be75e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oxenius A., McLean A. R., Fischer M., Price D. A., Dawson S. J., Hafner R., Schneider C., Joller H., Hirschel B., Phillips R. E., Weber R., Günthard H. F. Human Immunodeficiency Virus-Specific CD8+ T-cell Responses Do Not Predict Viral Growth and Clearance Rates during Structured Intermittent Antiretroviral Therapy. Journal of Virology. 2002;76:10169–76. doi: 10.1128/jvi.76.20.10169-10176.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prague M., Gerold J. M., Balelli I., Pasin C., Li J. Z., Barouch D. H., Whitney J. B., Hill A. L. Viral Rebound Kinetics Following Single and Combination Immunotherapy for HIV/SIV. . 2019 BioRxiv: 700401. [Google Scholar]
- Richman D. D., Margolis D. M., Delaney M., Greene W. C., Hazuda D., Pomerantz R. J. The Challenge of Finding a Cure for HIV Infection. Science. 2009;323:1304–7. doi: 10.1126/science.1165706. [DOI] [PubMed] [Google Scholar]
- Rouzioux C., Hocqueloux L., Sáez-Cirión A. Posttreatment Controllers: What Do They Tell Us? Current Opinion in HIV and AIDS. 2015;10:29–34. doi: 10.1097/coh.0000000000000123. [DOI] [PubMed] [Google Scholar]
- Samson A., Lavielle M., Mentré F. Extension of the SAEM Algorithm to Left-Censored Data in Nonlinear Mixed-Effects Model: Application to HIV Dynamics Model. Computational Statistics & Data Analysis. 2006;51:1562–74. doi: 10.1016/j.csda.2006.05.007. [DOI] [Google Scholar]
- Thompson M. A., Aberg J. A., Cahn P., Montaner J. S., Rizzardini G., Telenti A., Gatell J. M., Günthard H. F., Hammer S. M., Hirsch M. S., Jacobsen D. M., Reiss P., Richman D. D., Volberding P. A., Yeni P., Schooley R. T. Antiretroviral Treatment of Adult HIV Infection: 2010 Recommendations of the International AIDS Society–USA Panel. JAMA. 2010;304:321–33. doi: 10.1001/jama.2010.1004. [DOI] [PubMed] [Google Scholar]
- Vaida F., Fitzgerald A. P., DeGruttola V. Efficient Hybrid EM for Linear and Nonlinear Mixed Effects Models with Censored Response. Computational Statistics & Data Analysis. 2007;51:5718–30. doi: 10.1016/j.csda.2006.09.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaida F., Liu L. Fast Implementation for Normal Mixed Effects Models with Censored Response. Journal of Computational & Graphical Statistics. 2009;18:797–817. doi: 10.1198/jcgs.2009.07130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Von Wyl V., Gianella S., Fischer M., Niederoest B., Kuster H., Battegay M., Bernasconi E., Cavassini M., Rauch A., Hirschel B., Vernazza P., Weber R., Joos B., Günthard H. F. Early Antiretroviral Therapy During Primary HIV-1 Infection Results in a Transient Reduction of the Viral Setpoint upon Treatment Interruption. PLoS One. 2011;6:e27463. doi: 10.1371/journal.pone.0027463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vonesh E. F., Wang H., Nie L., Majumdar D. Conditional Second-order Generalized Estimating Equations for Generalized Linear and Nonlinear Mixed-effects Models. Journal of the American Statistical Association. 2002;97:271–83. doi: 10.1198/016214502753479400. [DOI] [Google Scholar]
- Wang R., Bing A., Wang C., Hu Y., Bosch R. J., DeGruttola V. A Flexible Nonlinear Mixed Effects Model for HIV Viral Load Rebound after Treatment Interruption. Statistics in Medicine. 2020;39:2051–66. doi: 10.1002/sim.8529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei G. C., Tanner M. A. A Monte Carlo Implementation of the EM Algorithm and the Poor Man’s Data Augmentation Algorithms. Journal of the American Statistical Association. 1990;85:699–704. doi: 10.1080/01621459.1990.10474930. [DOI] [Google Scholar]
- Wu H., Ding A. A. Population HIV-1 Dynamics In Vivo: Applicable Models and Inferential Tools for Virological Data from Aids Clinical Trials. Biometrics. 1999;55:410–8. doi: 10.1111/j.0006-341x.1999.00410.x. [DOI] [PubMed] [Google Scholar]
- Wu L. A Joint Model for Nonlinear Mixed-effects Models with Censoring and Covariates Measured with Error, with Application to AIDS Studies. Journal of the American Statistical Association. 2002;97:955–64. doi: 10.1198/016214502388618744. [DOI] [Google Scholar]
- Wu L. Mixed Effects Models for Complex Data. Boca Raton: Chapman & Hall/CRC Press; 2009. [Google Scholar]
- Yu T., Wu L., Gilbert P. B. A Joint Model for Mixed and Truncated Longitudinal Data and Survival Data, with Application to HIV Vaccine Studies. Biostatistics. 2018;19:374–90. doi: 10.1093/biostatistics/kxx047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao L., Chen T., Novitsky V., Wang R. Joint Penalized Spline Modeling of Multivariate Longitudinal Data, with Application to HIV-1 RNA Load Levels and CD4 Cell Counts. Biometrics. 2021;77:1061–74. doi: 10.1111/biom.13339. [DOI] [PubMed] [Google Scholar]