Novel, User-Friendly Experimental and Analysis Strategies for Fast Voltammetry: Next Generation FSCAV with Artificial Neural Networks

Abstract

Fast-scan adsorption-controlled voltammetry (FSCAV) was recently derived from fast-scan cyclic voltammetry to estimate the absolute concentrations of neurotransmitters by using the innate adsorption properties of carbon fiber microelectrodes. This technique has improved our knowledge of serotonin dynamics in vivo. However, the analysis of FSCAV data is laborious and technically challenging. First, each electrode requires post-experimental in vitro calibration. Second, current analysis methods are semi-manual and time-consuming and require a steep learning curve. Finally, the calibration methods used do not adapt to nonlinear electrode responses. In this work, we provide freely accessible computational solutions to these issues. First, we design an artificial neural network (ANN) and train it with a large data set (calibrations from 140 electrodes by six different researchers) to achieve calibration-free estimations and improve predictive error. We discuss the power of the ANN to obtain a low predictive error without electrode-specific calibrations as a function of being able to predict the sensitivity of the electrode. We use the ANN to successfully predict the absolute serotonin concentrations of real in vivo data. Finally, we create a fast and user-friendly, fully automated analysis web platform to simplify and reduce the expertise required for the postanalysis of FSCAV signals.

Introduction

Measuring and analyzing the brain’s chemicals is of critical importance for better understanding and treating brain disorders. A suite of different sensing modalities exist to measure brain chemicals. Fast-scan cyclic voltammetry (FSCV) at carbon fiber microelectrodes (CFMs) is a particularly powerful tool, offering high selectivity, sensitivity, and excellent spatiotemporal resolution.¹ FSCV has been used for decades to provide information about the real-time chemical dynamics of neuromodulators in models where the neurotransmitter is electrically, optically, pharmacologically, or behaviorally stimulated.²⁻⁵ In the absence of a rapid change in concentration, FSCV is not highly informative. This is because a large capacitive background current (a consequence of scanning > 10 V s^–1) must be subtracted out to see underlying Faradaic changes.⁶ This necessity for background subtraction means that basal or ambient neurotransmitter levels cannot be estimated with FSCV. In response to this limitation, fast-scan controlled-adsorption voltammetry (FSCAV) has been developed. The technique uses the innate adsorption properties of CFMs to estimate the equilibrium concentration of analytes on the electrode surface.⁷⁻⁹ The technique was previously used for the study of tonic changes of dopamine ex vivo(10) and in vivo.¹¹ In our group, we are interested in studying in vivo serotonin dynamics. With FSCAV, we have investigated the differences in ambient serotonin in different brain regions,¹² in male and female mice,¹³ and under various drug challenges.^8,14

FSCAV has greatly expanded the scope of information afforded by fast voltammetry. However, for FSCAV, each electrode requires a post-experimental in vitro calibration to account for large differences in the response across electrodes. This is a time-consuming effort with potential for experiment loss (if the electrode is lost post experiment). Pre-experimental calibration is also possible,⁶ but due to carbon surface modifications, the sensitivity during the in vivo experiment is greatly modified.¹⁵ Additionally, electrode responses can be nonlinear, which makes the estimation of concentration challenging. A final difficulty is that our current, semi-manual FSCAV analysis method is cumbersome, time-consuming and technically demanding.

There are a variety of strategies that can be utilized to improve these analysis challenges.¹⁶⁻²⁰ Artificial neural networks (ANNs) are particularly attractive due to their ability to learn from big data sets, their capabilities to fit nonlinear data, and high accuracy of predictions. ANNs are machine learning models that resemble biological neural networks. The models comprise different units that connect to each other, apply activation functions to the inputs and generate analysis outputs. The training process consists of iteratively modifying the weights of the units to fit labeled (such as concentration) data.²¹ ANNs have been used to accurately classify in vitro and in vivo FSCV dopamine signals.^19,22 Here, for the first time, we apply ANNs to serotonin FSCAV analysis.

First, we designed an ANN with specific input features from FSCAV voltammograms. We trained this network in two ways (with 1 calibration and 140 post-calibrations from six different researchers) and found that the predictive error of the ANNs greatly was improved versus linear regression but not improved by the increased input number of calibrations. Then, we created a second ANN that was informed by the entire voltammogram. This model did not need calibration and showed improved predictive error. We discuss this ANN’s capacity to achieve calibration-free analysis as a function of being able to predict background current from the full voltammogram and thus utilized the network to successfully predict absolute serotonin concentrations of real in vivo data. Finally, we created a time-saving and user-friendly, fully automated FSCAV analysis platform, freely available on the web and built on our previously developed web app for FSCV analysis (http://analysis-kid.hashemilab.com/).²³ The open-source code is also available, under an MIT license, at https://github.com/sermeor/The-Analysis-Kid.

Experimental Section

Animals and Surgical Procedures

Mice (C57BL/6J) (Jackson Laboratory, Bar Harbor, ME, USA) were injected with a 25% urethane solution based on mouse weight (7 μL/g). Following anesthesia administration, the mouse was placed into a stereotaxic system (David Kopf Instruments, Tujunga, CA, USA) where body temperature was maintained via a heating pad (Braintree Scientific, Braintree, MA, USA). Three holes were drilled into the skull of the mouse based off coordinates from the mouse brain atlas.²⁴ The working electrode was placed in the CA2 region of the hippocampus (CA2: −2.91, +3.35, −2.5) the stimulating electrode (insulated stainless-steel, diameter 0.2 mm, untwisted, Plastics One, Roanoke, VA, USA) was placed in the medial forebrain bundle (−1.58, +1.00, −4.80), and a pseudo Ag|AgCl reference electrode was placed in the opposite hemisphere of the brain. Stimulation was accomplished via linear constant current stimulus isolator (NL800A Neurolog, Medical Systems Corp, Great Neck, NY, USA) with the following parameters: 60 Hz, 360 μA each, 2 ms in width, and 2 s in length. Stimulations were used to verify serotonin release such that the electrode was in the vicinity of serotonin terminals. Animal use followed NIH guidelines and complied with the University of South Carolina Institutional Animal Care and Use Committee under an approved protocol.

Microelectrode Fabrication

CFMs were made individually by aspirating a single carbon fiber (Goodfellow Corporation, PA, USA) into a 0.6 mm × 0.4 mm glass capillary (A-M Systems, Inc., Sequim, WA, USA). The capillary was then pulled by a vertical puller (Narishige, Tokyo, Japan) to create a seal. The carbon fiber was then trimmed to 150 ± 5 μm. Liquion (LQ-1105, 5% by weight Nafion) (New Castle, DE, USA) was electrodeposited onto the surface of the carbon fiber by dipping and applying a constant potential of +1.0 V for 30 s. The electrode was then dried at 70 °C for 10 min and used after 24 h.

Data Collection and Analysis

FSCAV was performed using a Dagan Potentiostat, (Dagan Corporation, Minneapolis, NM, USA), National Instruments multifunction device USB-6341 (National Instruments, Austin, TX, USA), WCCV 4.0 software (Knowmad Technologies LLC, Tucson, AZ, USA), a Pine Research headstage (Pine Research Instrumentation, Durham, NC, USA), and a precision analog switch (ADG419, Analog Devices, Norwood, MA, United States). Data filtering (zero phase, butterworth, 2 kHz low-pass) and signal smoothing were done within WCCV software. The experimental procedure has three steps. First, the “Jackson” waveform (+0.2 to +1.0 to −0.1 to +0.2 V, 1000 V/s)²⁵ was applied at a frequency of 100 Hz for 2 s to minimize adsorption of serotonin followed by a 10 s holding potential (0.2 V) to allow serotonin to preconcentrate at the carbon surface, and finally with 18 s of waveform application to acquire the signal of interest. The third cyclic voltammogram (CV) was then used to estimate the concentration of serotonin.

Computational Methods

FSCAV Measurement Methods

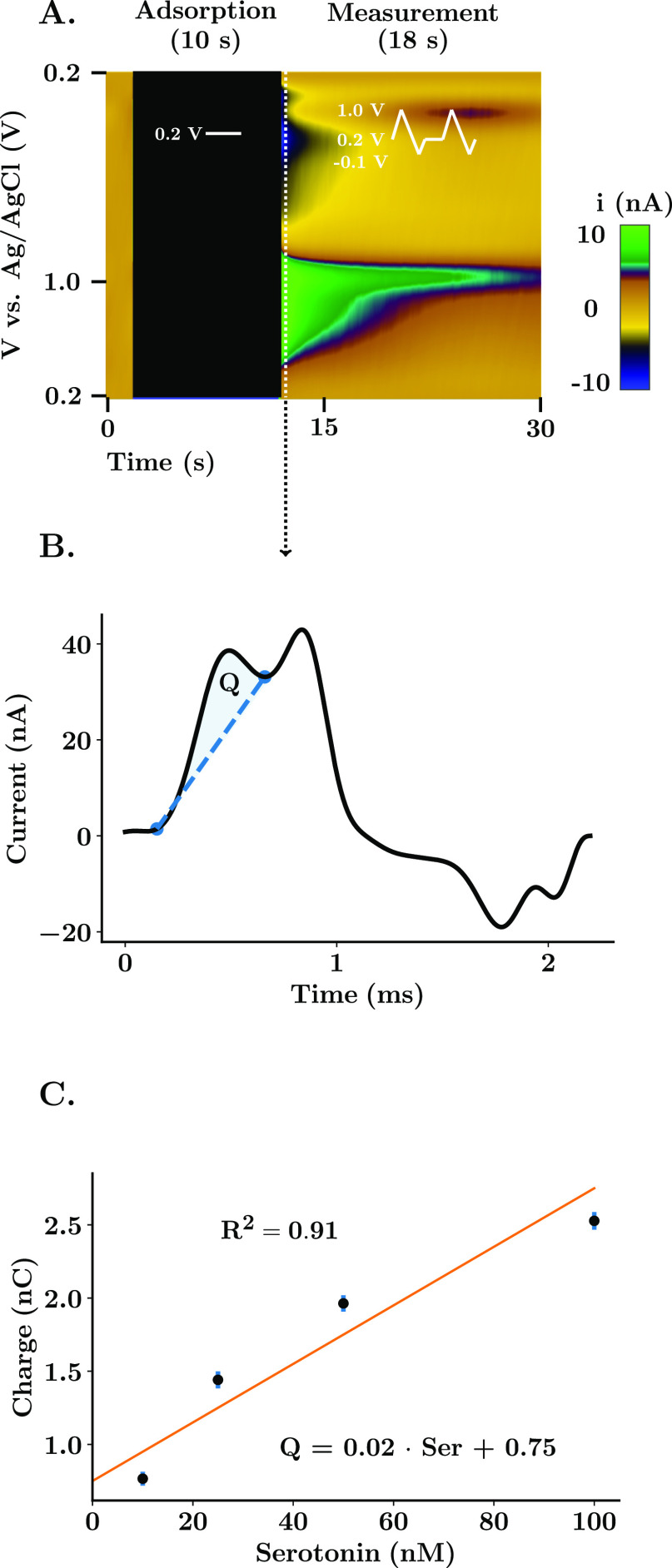
Limits of integration to estimate the charge of the Faradaic peak and maximum amplitude from FSCAV serotonin CVs were obtained using custom-designed automatic local minima and local maxima algorithms implemented in The Analysis Kid.²³ Charge of the Faradaic peak was calculated using Simpson’s rule. The first integration point was normalized to have a current value of zero to avoid subtraction of area between the negative and positive currents of the CVs. A linear regression was obtained between the two integration points to obtain the baseline used to measure the Faradaic charge. This minimized the interference from the capacitive peak. Linear regression models from post-calibrations were obtained using linear least squares between concentration labels and estimated the charge of the serotonin Faradaic peak. Figure 1 shows this calibration process. The coefficient of determination (R² = 0.91) and the standard error of the estimate (SEE = 10.70 nM) were used as parameters to assess the goodness of fit.

Figure 1.

Experimental and calibration strategy for FSCAV. (A) Representative color plot of a FSCAV serotonin acquisition in the CA2 region of the hippocampus. The procedure is composed of three steps: an initial 2 s where the waveform is applied (100 Hz) to minimize adsorption, followed by 10 s of holding potential (0.2 V) and finished with 18 s of conventional cycling to acquire the signal of interest. (B) Third cyclic voltammogram following the application of the voltage waveform. The Faradaic charge (Q) is the result of the integration between the serotonin peak and a baseline between integration points that minimizes the interference of the capacitive peak present at 1.0 V. (C) In vitro post-calibration curve. A linear regression is used to obtain a relationship between the integrated charge and the concentration of serotonin in solution. Scatter points and error bars show the mean ± standard deviation of 15 repetitions per concentration. R² indicates the goodness of fit.

Artificial Neural Networks

ANNs were designed and trained using TensorFlow and Keras in Python 3.6.²⁶ All neural networks were designed to function as regression models; the final layer consists of a unity continuous node which predicts serotonin concentration from the input features. All nodes were fully connected (dense layers).

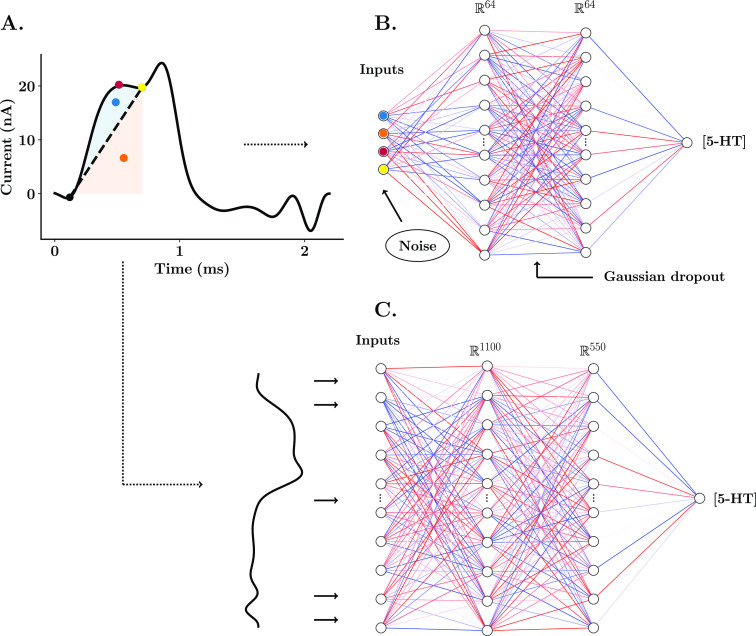
Single electrode models were designed with four input parameters from the Faradaic peak for serotonin: charge above baseline, charge below baseline, maximum amplitude, and valley point between the Faradaic and the capacitive peak (see Figure 2). The structure of the neural network consisted of one input layer (4 nodes), two hidden layers (64 nodes), and one output later (1 node). The standardized neural network was inputted with all the samples from the serotonin CV (1100 samples, 2.2 ms acquired at a frequency of 500 kHz). In this case, the ANN was designed with one input layer (1100 input features, the sample size of the serotonin CV), two hidden layers (1100 nodes and 550 nodes, respectively), and one output layer (1 output feature). All input features for all models used during training and prediction were standardized to have a mean of 0 and a standard deviation of 1. All nodes of the ANN were set to have a rectified linear activation function, given in eq 1

1

y is the output and X is the vector of inputs of each node.²⁷

Figure 2.

Schematic of ANNs for the training and estimation of tonic concentration of serotonin. (A) FSCAV serotonin CV from an in vivo acquisition in the CA2 region of the hippocampus of a mouse. Each of the features used as inputs of the single electrode NN model are color-marked: the maximum amplitude of the Faradaic peak (red), charge above baseline (blue), baseline charge (orange), and valley point between the Faradaic peak and capacitive peak (yellow). (B) Structure of the shallow neural network for predictions from a single electrode post-calibration. (C) Structure of the shallow neural network for standardized predictions across electrodes.³⁴

The training sets for the ANN consisted of electrode post-calibrations for four tris-buffered serotonin solutions (10, 25, 50, and 100 nM). Fifteen repetitions were taken for each of the solutions. Electrode-specific models were trained with one post-calibration (60 CVs). Gaussian noise with a default standard deviation of 0.25 was added as a regularization layer (only active during training). Additionally, a Gaussian dropout layer with a default dropout rate of 0.2 was added between the ANN hidden layers. These two mechanisms mitigate overfitting of the neural networks when only a small data set is available. The pretrained model and standardized model were trained with 140 post-calibrations of electrodes made and calibrated by six different researchers. For the pretrained model, training features for each individual post-calibration used during pretraining were standardized to have a mean of 0 and a standard deviation of 1. Training and validation splits were set a to 9:1 ratio. The Adam optimizer,²⁸ with a default learning rate of 0.001, was used to train all neural networks. The root-mean-square error (RMSE) between predicted and true serotonin concentration values was used as the cost function of the fitting process. The number of iterations was set to 200 for electrode-specific models (single electrode and pretrained model). Fine-tuning of the pretrained model consisted of 100 epochs with a set learning rate of 0.0001. The standardized model was trained with a k-fold cross validation of five train and test splits. Once trained, the neural networks were exported to JavaScript to be deployed on The Analysis Kid.

The web application allows the import of FSCAV data as CVs with the Faradaic peak of interest (commonly, the third CV for serotonin after waveform reapplication) in text or spreadsheet format. The interface is separated into two sections: fitting and prediction. In the fitting section, the user imports the post-calibration acquisition when using electrode-specific post-calibrations and assigns a concentration label to them. A regression model is then selected to fit the calibration data to the concentration labels, including the conventional linear regression and the two electrode-specific ANNs described here. An extensive configuration panel allows the user to select the model and tune training hyperparameters (learning rate, ANN layer size, standard deviation of Gaussian noise, number of epochs, patience, minimum delta and dropout rate). The application also allows evaluating the fitting via graphing of experimental data with the best line of fit (linear regression) or true versus predicted value plot. The standardized neural network does not require electrode-specific fitting, and therefore, the user can proceed directly to the prediction window.

In the prediction section, the user imports the files from an in vivo experiment, and the model fitting selected is used to predict serotonin ambient concentration from the imported files. The predictions can then be graphed as serotonin versus imported file or exported into a spreadsheet.

Statistical Analyses

Statistical significance is defined as p < 0.05. All statistical tests are performed using Python 3.6 SciPy²⁹ and MATLAB 2020b. Distribution of samples is shown as mean ± SEM if not stated otherwise. Error of model predictions is shown as the RMSE between true and predicted concentrations. FSCAV post-calibrations and in vivo predictions of serotonin were tested for significance using analysis of variance (ANOVA) and Tukey–Kramer post-hoc multiple comparisons. See the Supporting Information for a full description of the statistical analyses.

Results and Discussion

ANNs as Predictive Models for Absolute Serotonin Concentrations

FSCV has been used for decades to measure complex chemical dynamics in vivo. FSCAV is a newly developed method that reports ambient analyte levels. Unlike FSCV, FSCAV calibration techniques do not have optimal prediction capabilities. As it stands, electrode-specific linear regressions are used to relate Faradaic signal (charge) to concentration in a beaker post experiment. These calibrations are required for FSCAV because we have found significant variability in sensitivity, limit of detection, and saturation between electrodes.^8,14 These differences primarily stem from inconsistencies between carbon surfaces that change the adsorption profile of analytes. The error in measurement between electrodes is much less for FSCV than FSCAV (individual calibrations are often not needed for FSCV and are replaced with a standard calibration factor). We believe this is because the greatly reduced absorption time in FSCV means that analyte adsorption is to the most thermodynamically favorable sites. Once these more favorable sites are maxed out, more complex adsorption profiles come into play, which is then manifested in the increased error between electrodes with several seconds adsorption time (FSCAV). Electrode-specific post-calibrations are burdensome, and in some cases, in vivo signals are invalidated because electrodes become unusable (e.g. broken) after the experiment. Another limitation of a post-calibration procedure is the regression model itself. In Figure 1C, the calibration is nonlinear and using such a fit creates inaccuracies. While a simple solution to fit such a nonlinear relationship would be a higher order regression model (e.g. quadratic), this approach will still necessitate individual post-calibrations.

In this work, we use supervised machine learning models to simplify the process of accurate calibration. Specifically, we chose shallow ANNs (with only one or two hidden layers) because they are able to adapt to nonlinear responses and variability of electrodes and do not require large data sets for training.³⁰ The following describes the design and validation of our neural networks.

We first tested whether our model’s predictive error could be improved with training with large data sets. We created two different models based on a shallow neural network using the same architecture and different training schemes.

The first ANN, which we coin “the single electrode model”, was uniquely trained with a single post-calibration. Due to the small size of the data set, Gaussian noise (default standard deviation of 0.25 after normalization) and Gaussian dropout (default rate of 0.2) were used during training to mitigate overfitting. The second ANN, which we call “the pretrained model”, was first trained with 140 post-calibrations of electrodes from six different researchers and then finely tuned (trained again for a limited number of iterations) for a particular electrode used for an in vivo experiment.

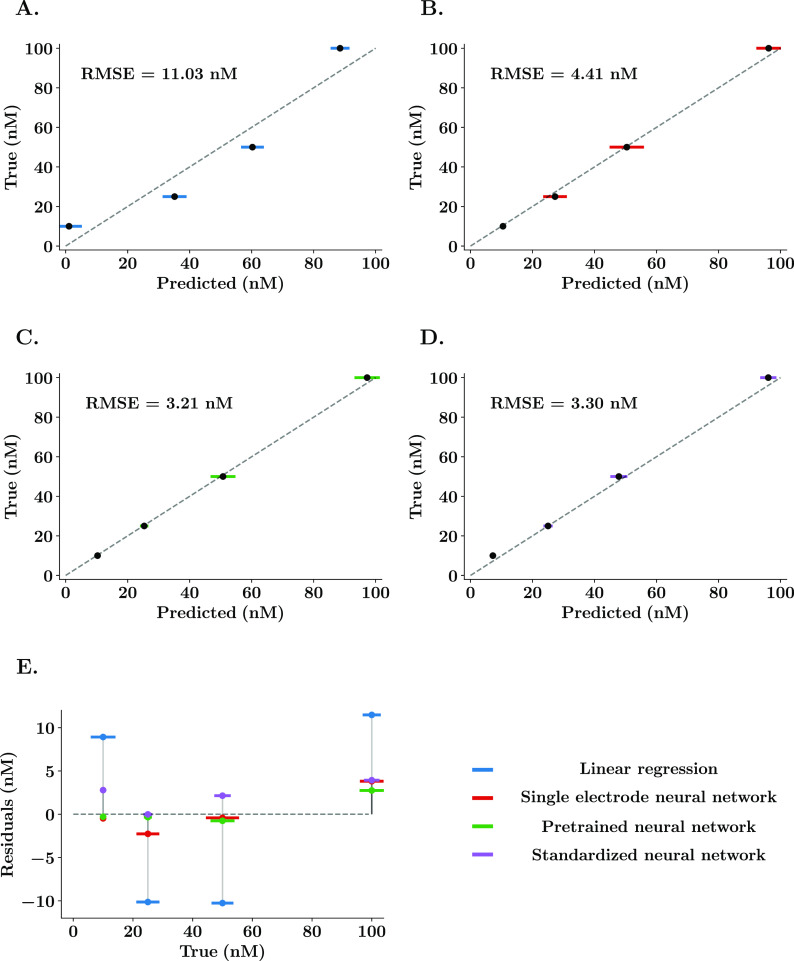
Figure 2B shows the structure of the neural network. A single node output layer allows the prediction of a continuous variable which represents absolute serotonin concentration. The input features, shown in Figure 2A for a representative serotonin CV, were selected via scatter plots (see the Supporting Information) after finding a high positive correlation to serotonin concentration. Figure 3 shows true versus predicted values of a representative post-calibration using a linear regression (Figure 3A) and the ANN with 1 post-calibration (Figure 3B) and the ANN with 140 post-calibrations (Figure 3C). Figure 3E shows the superposed mean and standard deviation (n = 15 repetitions) of the residuals of predictions for all models where the differences of residuals between the linear regression and the ANN models are clearly distinguishable.

Figure 3.

Representative comparisons between linear regression and neural network predictions of serotonin in vitro. (A–D) True vs predicted values of a representative serotonin post-calibration using the model determined by the color. Error bars (colored) denote the standard deviation of 15 repetitions for each solution concentration. The gray dashed line represents the ideal predictions. (E) Residuals vs true values for both linear and neural network regressions. The neural network without pretraining (red) was trained for a limit of 300 epochs and a learning rate of 0.001. Pretraining (green) consisted of training the neural network with 140 normalized post-calibrations from different electrodes. After that, the model is finely tuned with the electrode-specific post-calibration. The standardized neural network (purple) was trained with the whole data set and using all the data points of the CVs as input features.

It is clear from Figure 3E that the neural network mean predictions are closer to the ideal predictions than a linear regression. The comparison analysis was performed for five representative electrodes. The error of the estimate was found to be significantly higher when using the linear regression compared to the single electrode ANN model (post-hoc test, RMSE = 8.82 ± 1.06 nM vs 4.22 ± 0.33 nM, p = 0.0023) and the pretrained ANN model (post-hoc test, RMSE = 8.82 ± 1.06 nM vs 2.80 ± 0.54 nM, p = 0.0002), while no difference was found between the two single electrode ANN models (post-hoc test, RMSE = 2.80 ± 0.54 nM vs 4.33 ± 0.47 nM, p = 0.5449). Importantly, no significant effect of the model used was found in the measured standard deviation of the repetitions for the same solution (two-way ANOVA on standard deviation, F = 0.35, p = 0.8427), suggesting that the reduction of predicted error is a result of a better model fit and not a reduction of the variability between measurements, which could indicate that the ANNs are overfitting.

Neural network models for regression are therefore able to better fit the nonlinear response of the electrode and provide a more accurate estimation of ambient concentration of serotonin solutions. However, we found no improvement by training the ANN with many data sets. This is because using specific features from the CV does not allow the model to learn the complex ways that the signal can change. Additionally, electrode-specific training for both methods used is, however, still required and remains a major limitation of the FSCAV calibration process. Thus, we next designed an ANN to predict concentration from the whole CV, allowing for calibration-free analysis.

We call this model “the standardized neural network”. We used a large data set and neural complexity of the ANN to account for the differences in sensitivity across electrodes. In Figure 2C, the standard ANN was designed with one input layer of 1100 features to input all the data points of a serotonin CV (acquired at 500 kHz for 2.2 ms). The first hidden layer also matches the size of the inputs, while the second hidden layer has a 50% reduction in nodes. This model was trained with 140 post-calibrations of approximately 60 CVs each (15 repetitions of four serotonin concentrations: 10, 25, 50, and 100 nM). More information on the training and test results is in the Supporting Information. Figure 3D shows true versus predicted values for the same representative post-calibration as used in Figure 3A–C. The prediction results appear analogous to those obtained using electrode-specific neural networks. The predictive error is significantly lower than the one obtained using the linear regression (post-hoc test, RMSE = 8.82 ± 1.06 nM vs 4.33 ± 0.81 nM, p = 0.0029) and not significantly different from those obtained using the single electrode neural network models (post-hoc test, RMSE = 4.22 ± 0.33 nM vs 4.33 ± 0.81 nM, p = 0.9996; post-hoc test, RMSE = 2.80 ± 0.54 nM vs 4.33 ± 0.81 nM, p = 0.4869).

Importantly, the standardized neural network does not require a post-calibration experiment to predict the specific response of the electrode to known changes in concentration by learning the response from 140 previously used electrodes. This is likely because the neural network model is able to learn and recognize the variability in the shape of the CV due to mass transport, electrode manufacture, and adsorption differences between experiments. This allows the complex model to predict the sensitivity of the electrode being used based on the shape and amplitude of all the features in the FSCAV cyclic voltammogram.

Next, we propose why our ANN is able to predict concentrations across electrodes with different sensitivities.

Background Current as a Predictive Feature for Sensitivity

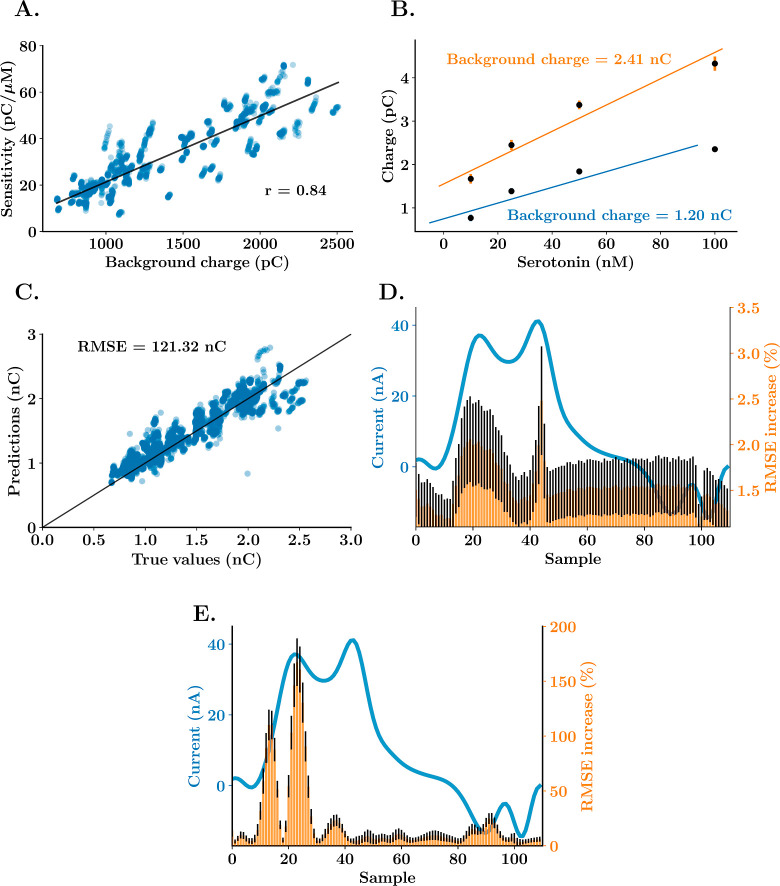
We asked why our ANN can function across electrodes with different sensitivities. Previous FSCV studies have correlated some features of the background capacitive current to electrode sensitivity.³¹⁻³³ Here, we find a robust positive linear correlation between the FSCAV capacitive current after the adsorption period (10 s) and the electrode sensitivity (Figure 4). In Figure 4A, the area under the forward sweep of the waveform of the background CV of 106 electrodes was plotted versus their sensitivity to serotonin after background subtraction and a r coefficient of 0.84 confirms linear correlation. In Figure 4B, the regression fittings for two representative electrodes are plotted versus their background charges illustrating clearly that a higher background current correlates well with more sensitivity (orange).

Figure 4.

Background charge correlation to FSCAV sensitivity for the detection of serotonin. (A) Sensitivity vs average background charge scatter graph for 106 electrodes, Pearson’s correlation coefficient between both parameters and best fit regression line (black). (B) Linear regression calibrations (regression line and average ± standard deviation) and average background current charges for two representative electrodes from the data set in part (A). (C) True vs predicted values of background current from the test data set (20% of the whole data set) for the last k-fold of the neural network training. The vertical line shows the ideal response, where true values are equal to predicted values. (D, E) Representative example of a CV of 100 nM serotonin solution (blue) and mean ± SEM percentage of increase of RMSE (n = 10 trainings, 100 repetitions per training) after each of the time samples in the CVs are replaced with a standardized random value across the whole data set for the ANN that predicts background current (part D) and serotonin concentration (part E). Values of average and standard deviation are shown in groups of 10 samples.

In principle then, including the background current as an input feature could further improve the prediction capabilities of our standardized neural network. To test this hypothesis, we included the area under the curve of the background current for each acquisition in the input data set. The input layer was then set to 1101 features (all the samples of the CV and the estimation of the background), and the rest of the neural network structure and training paradigm were kept identical to the previous model. No statistical significance was found between the testing performance of the standardized neural network with and without the addition of the charge of the background current (k-fold cross validation with n = 5 train and test split, t-test difference between means, RMSE = 3.84 ± 0.24 nM vs 4.10 ± 0.48 nM, p = 0.6452). We thought this outcome was likely because the standardized neural networks are able to estimate the sensitivity of the electrode directly from the Faradaic CV. To test this idea, the standardized neural network was trained to predict the background current of the electrode and indeed predicted background current from the background-subtracted CV with a low predictive error (Figure 4C). The most significant samples to achieve this low predictive error are the ones from the switching peak and serotonin oxidation peak, as shown in the sensitivity analysis in Figure 4D. Here, each CV data point was replaced with a standardized random value during training (a value that falls within the distribution of samples). An increase in the RMSE of the test predictions means that the sample is important for the neural network to predict background current. The serotonin oxidation peak and the switching peak considerably increase the error of prediction of background current when set constant, meaning that they are critical parameters for the neural network to predict the background current. Figure 4E shows this same sensitivity analysis for our ANN that predicts serotonin concentration. Here, only the serotonin oxidation peak samples increased the predictive error.

Therefore, our ANN is able to predict concentrations across electrodes with different sensitivities because information-rich CVs can predict background current, this current is in turn correlated to the sensitivity of electrodes. We next use our ANN for real in vivo data.

Neural Network In Vivo Predictions

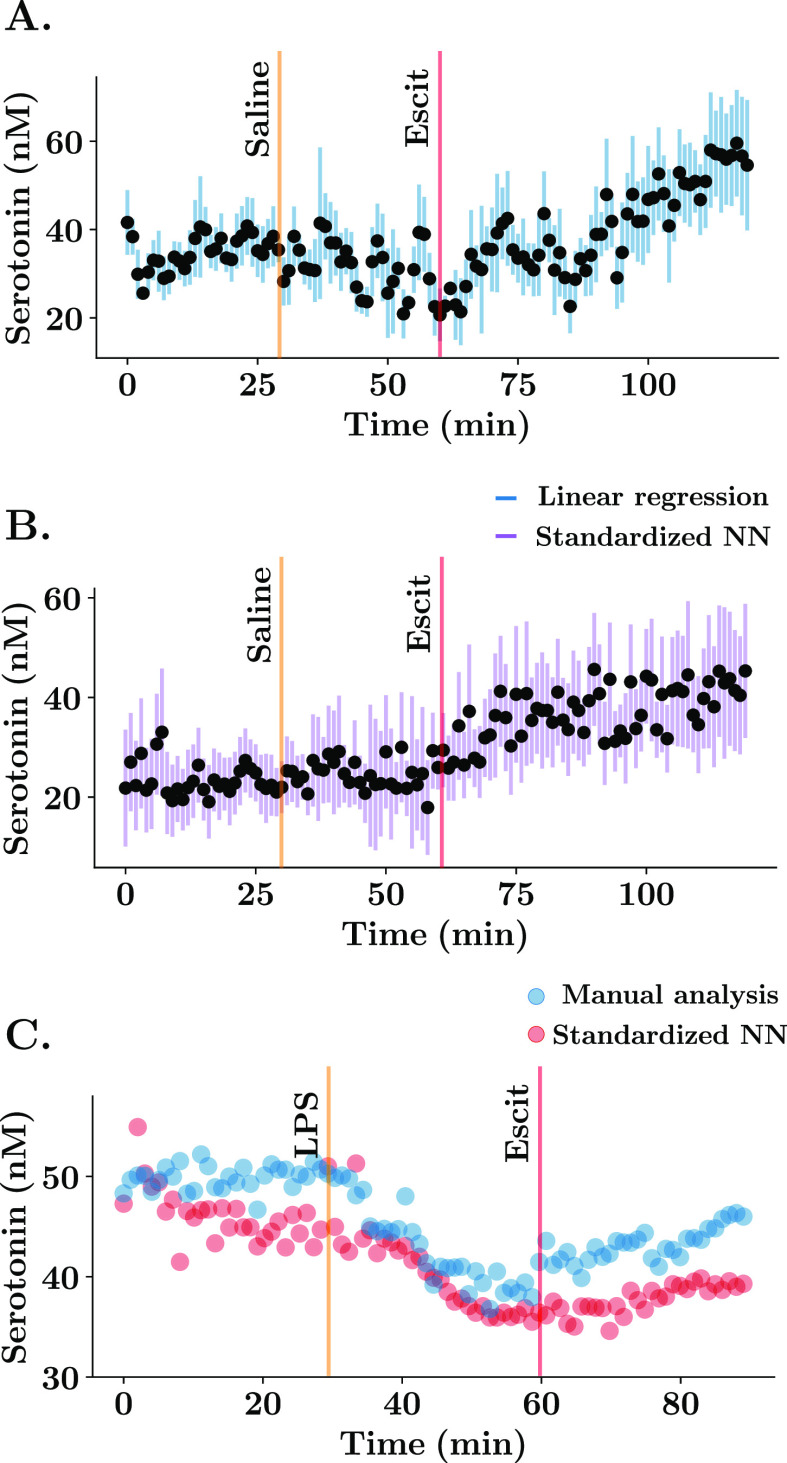
Thus far, our investigations have been using data collected in vitro, and clearly there are differences between CVs collected in vitro and in vivo due to the complex in vivo matrix.⁸ To study the predictive power of our standardized ANN in vivo, we compared a data set analyzed via linear regression (Figure 5A) to the same data set analyzed by the ANN. In this experiment, serotonin was measured in the hippocampus of five mice for 30 min, and at this point, a saline injection was administered, and 30 min after that, an agent thought to increase serotonin levels, a selective serotonin reuptake inhibitor (SSRI), escitalopram (ESCIT) was administered, and files were collected for a further 60 min. Figure 5A uses post-calibrations for all five electrodes and shows that serotonin levels (average ± SEM) increase after SSRI. Figure 5B is an analysis of the same data set with our calibration-free ANN. A repeated measures ANOVA and paired multiple comparisons were performed for all concentration values with factors being treatment (within groups) and regression model applied. First, there was a significant change in basal serotonin 120 min after SSRI injection with respect to the control state (post-hoc paired tests, linear regression: 34.91 ± 5.59 nM vs 53.75 ± 14.76 nM, p = 0.0314; neural networks: 23.46 ± 7.14 nM vs 45.32 ± 13.46 nM, p = 0.0257). The average basal concentration for the first 30 min is not significantly different between both predictions (post-hoc test, [serotonin] = 34.91 ± 5.59 nM vs 23.46 ± 7.14 nM, p = 0.5731) and neither is the concentration at later time points between both predictions (post-hoc test at 120 min, [serotonin] = 53.75 ± 14.76 nM vs 45.32 ± 13.46 nM, p = 0.6841). This finding is very exciting given the similar values yet significantly more simple analysis (i.e. calibration free).

Figure 5.

Comparison between linear regression and standardized neural network for in vivo serotonin ambient predictions. (A,B) Mean ± SEM (n = 5 animals) concentration vs time trace of basal serotonin recorded in the CA2 region of the hippocampus. In part A, the calibration was performed using an electrode-specific post-calibration. In (B), the predictions were obtained from the standardized neural network by feeding the totality of the CV to the model. Mice were injected with a saline solution at 30 min and the SSRI, escitalopram (ESCIT) (10 mg/kg) solution at 60 min. (C) Representative concentration vs time FSCAV acquisition in the CA2 region of the hippocampus using manual analysis (blue) and the automatic calibration using standardized neural networks (red). Mouse was injected with a lipopolysaccharide solution (0.2 mg/kg) at 30 min and ESCIT (10 mg/kg) solution at 60 min.

Finally, we compared a previously semi-manual single data set analysis (where the charge was calculated for each CV by a person, rather than automatically as in Figure 5A) to the same data set analyzed by our ANN (Figure 5C). In this experiment the mouse was given lipopolysaccharide,¹⁴ which correlated to a decrease in serotonin, followed by SSRI, after which the serotonin levels increased. Here, our ANN was also able to well replicate the hand analysis. Importantly, the ANN performs this analysis in less than a second, whereas this single data typically takes a researcher >2 h (in addition to several hours for a post-calibration) and has potential for human error.

Automatic Analysis of FSCAV Cyclic Voltammograms

We incorporated our new ANN algorithms in a detached application for automated analysis of FSCAV data as part of our existing web application analysis of FSCV data, The Analysis Kid.²³ The algorithms were designed to minimize the time required to obtain a calibration model and predictions for in vivo data. First, local minima algorithms estimate the integration points and maximum amplitude of the serotonin Faradaic peak from the uploaded CVs, as depicted in Figure 1B. The application also allows the manual setting of the integration points via a graphical interface. There is an option to upload post-calibration CVs for linear regressions for analysis of different analytes (ANN is developed for serotonin only at this stage). Pretrained ANN models were designed and trained with TensorFlow in Python and deployed in the web application using the TensorFlow.js API. Linear regression fittings are shown in the web application as depicted in Figure 1C, with an estimation of R² and SEE. The user can also see the predicted versus true concentration labels using the predictive model for both linear regression and ANN predictions.

Once a satisfactory calibration model has been obtained, a prediction panel allows the user to upload in vivo CVs to estimate concentration. The predicted concentration versus file number is then plotted in the web application. Finally, both fitting parameters and/or predictions of concentration can be exported into a spreadsheet. TensorFlow ANN models can be exported in a JSON format and opened in different software programs (e.g. Python’s TensorFlow architecture).

The main novelty of this calibration method resides in the fact that it can be fully automated online without the use of specific software, and it uses new machine learning models that are tested to provide more accurate predictions in vitro.

Conclusions

FSCAV was recently derived from FSCV to estimate absolute concentrations of neurotransmitters by using the innate adsorption properties of CFMs. In this work, we developed new computational techniques to improve the analysis of the technique and ease of use. An ANN, the standard neural network, was designed to provide calibration-free predictions and reduced predictive error. We discussed the power of this ANN to obtain a low predictive error without electrode-specific calibrations, concluding this is likely because it is able to predict the sensitivity of the electrode. We then used the ANN to successfully predict absolute serotonin concentrations of real in vivo data and reproduce the results obtained with electrode-specific predictions. Finally, we created an open-source and fully automated analysis web platform to simplify and reduce the expertise required for the postanalysis of FSCAV signals.

Glossary

Abbreviations

FSCV

fast-scan cyclic voltammetry

FSCAV

fast-scan controlled-adsorption voltammetry

5-HT

5-hydroxytryptamine

AUC

area under the curve

RMSE

root-mean-square error

SEE

standard error of the estimate

SEM

standard error of the mean

ANN

artificial neural network

NN

neural network

CV

cyclic voltammogram

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsmeasuresciau.1c00060.

• Link to the code repository, scatter analysis of CV features, importance of the features for the ANN, training results, and full statistical analyses of in vitro and in vivo FSCAV predictions (PDF)

Author Contributions

S.M. gathered and processed the data set and developed the web application, M.V. and S.M. developed the ANNs for FSCAV calibration, and N.R. developed an initial classification ANN for FSCAV. C.W. and L.H. acquired the in vivo serotonin data. P.H., S.M., C.W. and M.V. wrote the manuscript. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The CAMS Lectureship Award, NSF CAREER award 1654111, and NIH R01 MH106563 (all P.H.) supported this work.

The authors declare no competing financial interest.