ON THE CONTROL OF PSYCHOLOGICAL NETWORKS

Abstract

The combination of network theory and network psychometric methods have opened up a variety of new ways to conceptualize and study psychological disorders. The idea of psychological disorders as dynamic systems has sparked interest in developing interventions based on results of network analytic tools. However, simply estimating a network model is not sufficient for determining which symptoms might be most effective to intervene upon, nor is it sufficient for determining the potential efficacy of any given intervention. In this paper, we attempt to remedy this gap by introducing fundamental concepts of control theory to both psychometricians and applied psychologists. We introduce two controllability statistics to the psychometric literature, average and modal controllability, to facilitate selecting the best set of intervention targets. Following this introduction, we show how intervention scientists can probe the effects of both theoretical and empirical interventions on networks derived from real data and demonstrate how simulations can account for intervention cost and the desire to reduce specific symptoms. Every step is based on rich clinical EMA data from a sample of subjects undergoing treatment for complicated grief, with a focus on the outcome suicidal ideation. All methods are implemented in an open-source R package netcontrol, and complete code for replicating the analyses in this manuscript are available online.

1. Introduction

Common cause models of psychopathology posit that correlations between symptoms arise from an underlying disease entity (e.g., coughing, fever, and Koplik spots co-occur due to the measles virus). Although this common cause model is clearly appropriate for some diseases such as those caused by pathogens, the utility of this perspective for psychopathology has been increasingly questioned (Borsboom, 2008; Kendler, Zachar, & Craver, 2011). In contrast, the network theory of psychopathology posits that psychological disorders can be described as sets of causally interacting symptoms (Borsboom, 2017; Cramer, Waldorp, van der Maas, & Borsboom, 2010). Under this framework, psychopathology is an emergent property constructed from dynamic interactions among symptoms and other related problems (Kendler et al., 2011; Radden, 2018). This theoretical stance is grounded in insights drawn from philosophy of psychiatry, network science, systems science, and historical calls for greater complexity in clinical psychology and, in recent years, has generated a rapidly growing body of applied research (Robinaugh, Hoekstra, Toner, & Borsboom, 2019).

Researchers working within the network approach to psychopathology have relied heavily on network psychometrics: a class of statistical models derived from diverse fields (e.g., statistical mechanics) that seeks to model relations between symptoms (Epskamp, 2017). Researchers using these methods often focus their analyses on identifying “central” symptoms strongly interconnected within the symptom network. The hope is that such analyses may identify symptoms that play an important causal role in the maintenance of the disorder and, thus, may be an important target for treatment (Contreras, Nieto, Valiente, Espinosa, & Vazquez, 2019; Fried et al., 2017). Although early network studies often assessed cross-sectional (i.e., between-subject) data, there has been a growing focus on examining temporal (i.e. within-subject) data, as this level of analysis is better aligned with the within-person hypotheses about disease etiology and treatment that are the focus of network theory (Jordan, Winer, & Salem, 2020). It is posited that targeted treatment of “central” symptoms in these temporal networks (i.e., those exhibiting strong temporal associations with other symptoms) will produce considerable downstream improvement in other symptoms, a position that is consistent with how many clinicians think about mental disorder treatment (Kim & Ahn, 2002). Clinical trials testing this idea are already underway (Levine & Leucht, 2016).

Unfortunately, due to their chaotic nature, predicting how complex, dynamical systems will respond to intervention is exceedingly difficult and there is no guarantee that treatments targeting central symptoms will actually offer the hypothesized benefits outlined above. In this paper, we propose that control theory, a well-established mathematical discipline, provides a better, data-driven way to identify optimal treatment targets while also equipping us to evaluate the theoretical efficacy of proposed interventions using estimated network structures.¹ We will begin by introducing readers to network psychometrics and to the core concepts in control theory. After these primers, we introduce optimal control methods and demonstrate in two simple simulated examples how these control theory methods can be applied to psychological data. We then further illustrate the clinical utility of control theory by using it in a series of simulation studies to (a) examine single target interventions, (b) evaluate multiple interventions applied simultaneously and (c) simulate empirical interventions. We conclude by discussing the limitations of this approach and the steps needed in future research to fully realize the potential of control theory within psychological science.

2. Introduction to Network Psychometrics and Control Theory

The first step to any application of control theory is that of system identification (Ljung, 1999). In traditional control theory settings such as manufacturing or engineering, the systems in question are often known a priori, such as a production line. In the case of psychopathology, the dynamics governing the relations between symptoms overtime are unknown, and must be determined. In a network psychometric framework, we construct a psychological network. A psychological network consists of nodes, representing the symptoms or problems under study, and edges, representing some kind of relation between the symptoms, be it causal or statistical. Edges may represent relations among symptoms within a single individual over time or the between-subject relations among symptoms in a group of individuals. Consider the network presented in Fig. 1 estimated using multilevel integrated vector autoregressive models (ML-VARI; Bringmann et al., 2013; Epskamp, Waldorp, Mõttus, & Borsboom, 2018; Shumway & Stoffer, 2017) using ecological momentary assessment (EMA) data of symptoms from 8 subjects during treatment for complicated grief (For details on why multilevel integrated VAR is used, see Supplementary Materials). Complicated grief is a bereavement-specific syndrome characterized by persistent, intense, and impairing grief-related thoughts, emotions, and behaviors. Nodes in the network represent 9 core symptoms of complicated grief as well as thoughts about suicide. Edges represent the relation between the change in a symptom from time t − 1 to t and the change in another symptom from time t to time t + 1, controlling for all other lagged relations. Because relations are temporal and differ in magnitude, the resulting edges are both directed and weighted. That is, they provide information about both the direction of the temporal association (e.g., change in thoughts about the future predicts change in emotional pain, but not vice versa) and the strength of that association (e.g., the association from suicidal ideation to thoughts about the loved one is stronger than the reverse).

Figure 1. Symptom Dynamics of Complicated Grief.

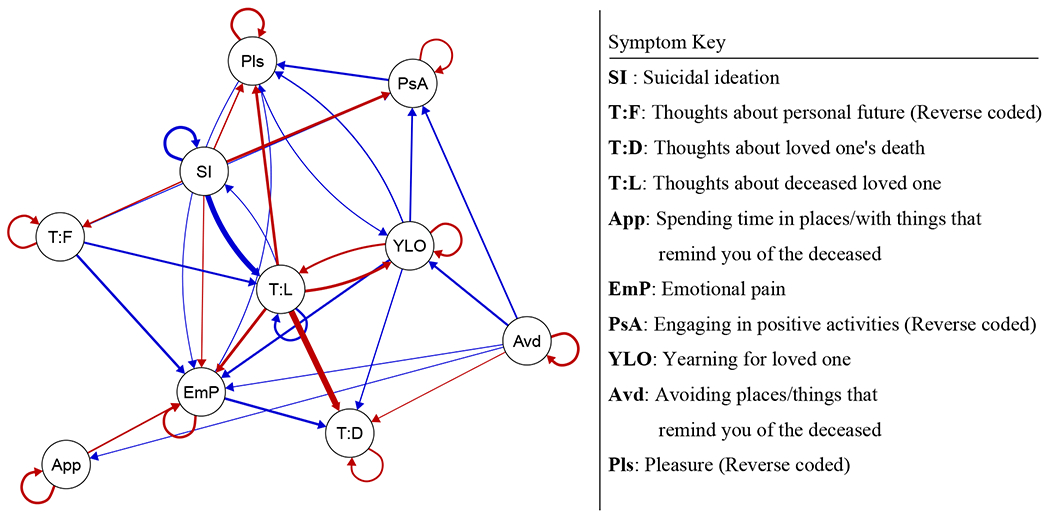
Blue edges represent positive relations, red represents negative relations. Autoregressive effects were rescaled to improve edge contrast, and edges with absolute values below .05 were omitted from the visualization. Note that this network represents the lagged relation between the changes in symptom values (i.e., the use of an integrated VAR) rather than the lagged relations between the symptom values themselves. .

Importantly, a network model-informed intervention requires more than just estimating network structure. The behavior of a dynamical system, such as the ones proposed by network psychometric models, can be difficult to predict on the basis of the network structure alone. An intervention does not have just an instantaneous effect, rather that instantaneous treatment effect will propagate over time throughout the system, which in turn can change the overall impact of the intervention. To understand the impact of interventions on a dynamical system, an approach that goes beyond structure to examine how the complex dynamics of the system will be affected over time is required. Control theory provides one such toolkit.

2.1. Primer on Control Theory

Control theory is a mathematical discipline concerned with the control of dynamic systems. It was first developed to improve manufacturing outcomes. For example, helping to determine the series of inputs to a manufacturing plant that optimize production while minimizing cost. Since its development, control theory has emerged as an important area of research in diverse areas of science. In this section, we will introduce several fundamental concepts of control theory with a focus on its application in psychopathology. To make this introduction as accessible as possible, we will primarily use terminology from psychology and network science and will include equivalent terms from control theory parenthetically and in bold italics (e.g., psychological term (control theory term)). To further assist translation, a glossary of control theory terms and their equivalent concepts in psychology appears in Table 1.

Table 1.

Glossary of Control Theory Terms, Psychological Equivalent, and Definition

Control Theory	Psychological Equivalent	Definition
Physical plant	Psychological system	The dynamical system that is being controlled
Control inputs	Interventions/treatments	Intentional inputs to the system
Disturbance	Disturbance	Random inputs to the system (not measurement error)
Error	Measurement Error	Random error due to measurement (doesn’t impact the system)
State	Symptom value	The (possibly unobserved) values of the variables in the system
Observation	Measurement / Item	The observed measurement of a variable in the system
Energy	Cost of intervention	The overall cost of applying control inputs

Notably, we are not the first to propose applying control theory to psychological research. Hyland (1987) applied principles of control theory to theoretical models of depression, while Carver and Scheier (1998) and Johnson, Chang, and Lord (2006) examined how control theory principles map onto self-regulation, cognition, and behavior. Other researchers have applied control theory principles to adaptive intervention designs. For example, Molenaar (1987), Sinclair and Molenaar (2008) and Molenaar (2010) demonstrated how optimal control methods can be used to individualize psychotherapeutical trajectories. Rivera, Pew, and Collins (2007) likewise described how to apply control theory to model and assess adaptive interventions on single target variables. In perhaps the most comprehensive application, Rivera, Hekler, Savage, and Downs (2018) used a sophisticated form of control called model predictive control (MPC) in two separate interventions with sedentary, overweight adults and pregnant women (for further discussion of the utility of MPC, see our Future Directions section). Finally, there is a related large literature on adaptive interventions (Collins, Murphy, & Bierman, 2004; Collins et al., 2004; Nahum-Shani et al., 2018), which is a considerably broader topic than just control theory, and addresses key considerations for both study and intervention design.

Prior applications of control theory have primarily focused on either theoretical implications or single target behavioral interventions (e.g. an intervention to increase walking in sedentary adults (Rivera et al., 2018)). With the development of network psychometrics and the expansion of intensive longitudinal data collection, there is a growing opportunity for more complex applications of control theory: applications which promise to not only tailor existing interventions to individual needs, but also to improve our understanding of psychological disorders by identifying both core controllable symptoms and heterogeneity in these symptoms and their response to treatment. Accordingly, our introduction to control theory will focus on its for application in these growing areas of research.

2.2. Defining The Control System

There are many possible system types, including continuous time, non-linear, time-varying, and stochastic systems. Here, it is important to note the distinction between a system in the control theory sense, and a model in the statistical sense. A data model (or statistical model) is a representation of the data. A control system is a combination of the data model and defined set of control inputs. In our case, the aforementioned VARI model is being used to represent the dynamics governing the set of symptoms, and the control system we present below is an elaboration of that model which includes control inputs.

One of the simplest types of system is the discrete linear time-invariant system (DLTI). These control systems operate over discrete time units, have no non-linear components (and can thus be represented entirely using linear algebra), and the system dynamics do not change over time (hence time-invariant). This type is well-suited for both representing network psychometric models (such as the a VARI model depicted in Fig. 1) and for illustrating control theory techniques. As such, we focus on DLTIs in this paper (for more information about system identification, including the rationale for why we chose the ML-VARI model as the system of interest in this paper, see SM).

DLTI systems take the following form:

$$\begin{gathered} {\mathbf{\text{x}}}_{t+1}={\mathbf{\text{Ax}}}_t+{\mathbf{\text{Bu}}}_t \\ {\mathbf{\text{y}}}_t={\mathbf{\text{Cx}}}_t \end{gathered}$$ (1)

where x_t is a vector of p symptom (state) values at time t, A is the p × p coefficient matrix governing their dynamics, and B is a p × l matrix mapping l interventions (control inputs) u_t to the p symptoms. y_t is the vector of the observed measurements of the symptoms (observations) at time t while C is a matrix that maps the true values of symptoms x_t to the observed measurements y_t. If one specifies that C = I (I being the identity matrix) then y_t = x_t.

Although Eq. 1 is very similar to a vector autoregressive model at lag-1 that currently dominates the within-subjects network literature in psychopathology (Bringmann et al., 2013; Robinaugh, Haslbeck, et al., 2019), there are three important differences: (a) the inclusion of the control inputs u_t, (b) the addition of an observation equation (i.e. y_t = Cx_t), and (c) the lack of a disturbance term (ε_t in Eq. 1). The inclusion of control inputs is a necessity, though it is important to note they are additive inputs. The observation equation will feel familiar to readers versed in latent variable modeling, as it maps indicators (the observed measurements) to underlying states. To simplify our exposition, we make the assumption of complete observability throughout this manuscript (C = I). This assumption implies that there are no latent variables and that the observed variables are perfectly reliable, which is a problematic assumption when considering psychological constructs. Fortunately, more general forms of the C matrix can be specified to allow for latent x with manifest indicators y. Using more general forms of C requires testing for observability, or the ability to reconstruct the latent variables x from the measured indicators y. For a more detailed discussion of observability, see Preumont (1997).

Finally, in the original manufacturing context of control theory the absence of a disturbance term is defensible as disturbances are rare. In psychological systems, regular random disturbances are to be expected. Fortunately, however, if the random disturbance has an expected value of 0 and is uncorrelated in time (i.e., white noise), then disturbances can be ignored when considering optimal control inputs (Molenaar, 2010). The assumption of a white noise disturbance term is common across many time series and longitudinal models used in psychology and crucially relies on an assumption that any temporal dependence is explicitly modeled. Relaxing this assumption and allowing for time-correlated disturbances is the purview of stochastic control theory (See Åström (2006) for a introduction), a topic of relevance to psychological research, but not one we will address here. To demonstrate the robustness of these methods to disturbances, we generate white noise disturbances for each of our simulations.

3. Using Control Theory to Select Intervention Targets.

With our system specified, we can now identify which symptoms are the best intervention targets. For example, in our complicated grief network, it would be beneficial to know whether a targeted intervention to reduce, say, emotional pain is more effective than an intervention to increase positive engagement. However, the mere specification of the system is not sufficient to determine how an intervention will perform, as the performance of an intervention is entirely dependent on how it interacts with the dynamical system that it effects. Control theory provides tools to directly quantify the theoretical impacts of a targeted intervention in the form of controllability centrality measures. To begin, let us make some simplifying assumptions that reduce notational burden. First, let C = I. This reduces the system in Eq. 1 to

$${\mathbf{x}}_{t+1}=\mathbf{A}{\mathbf{\text{x}}}_t+\mathbf{B}{\mathbf{\text{u}}}_t.$$ (2)

The matrix B describes how a set of interventions impacts the symptom values. From this system, we compute the controllability Gramian W_∞, which is the solution to the following Lyapunov equation in the case of a discrete time-invariant linear system (Lewis, Vrabie, & Syrmos, 2012):

$${\mathbf{W}}_{\infty }-\mathbf{A}{\mathbf{W}}_{\infty }{\mathbf{A}}^{\prime }=\mathbf{B}{\mathbf{B}}^{\prime }$$ (3)

where ′ is the transpose operator.

The controllability Gramian is related to efficacy of a given intervention with respect its impact on the entire system. Eigenvectors with large eigenvalues define directions in the space of x that are easier for a given intervention to move the system in (Summers, Cortesi, & Lygeros, 2016).

Critically, the controllability Gramian refers to the controllability of the entire system using the set of treatments specified in B. As such, we can easily use the controllability Gramian to assess how efficiently the system can be controlled by specific symptoms. Let B = I. In this case, each intervention defined in B is the intervention on a single symptom. Therefore, the value on the diagonal of the controllability Gramian when B = I quantifies the effect that intervening on each symptom individually has on the rest of the system (Summers et al., 2016). This controllability metric is called average controllability², which provides a direct measure of how efficient it is to target a given symptom for intervention, relative to the efficiency of targeting other symptoms in the symptom. An intervention that targets a high average controllability symptom will lead to more change in the system overall than an equivalently strong intervention that targets a symptom with lower controllability. Importantly, these are relative differences, and average controllability does not indicate that an intervention will have a strong or clinically meaningful effect. We elaborate on this point later in Section 4.1.

Average controllability of individual symptoms is strongly associated with the network statistic of strength (the sum of the outgoing or incoming edge weights for a given node), which is commonly used when discussing intervention targets in psychological networks (Fried et al., 2017). However, average controllability holds three advantages over strength as a metric of symptom importance. First, whereas strength is concerned with network structure, average controllability is focused on the effect of a theoretical intervention, thereby more directly reflecting the ultimate end goal of identifying intervenable symptoms. Second, average controllability incorporates both the directionality of edges and the sign of edges into a single value per node. In contrast, strength is typically calculated using either outgoing or incoming edges and does not account for the sign of edge weights (i.e., they take the absolute value). Failing to account for path signs can result in underestimating suppression effects, where a symptom that has high out-degree is not as effective to intervene upon as a symptom with lower out-degree, simply because the high out-degree symptom has a mixture of positive and negative effects. Finally, average controllability is modular (Summers et al., 2016), meaning that, if one were interested in intervening on only k symptoms, then the best set of symptoms to intervene on are the k symptoms with the greatest average controllability. This guarantees that symptoms chosen on the basis of high average controllability should be as effective when intervened upon simultaneously as when they are intervened upon separately in isolation. In contrast, symptoms chosen on the basis of strength are more likely to be less effective intervention targets when intervened upon together.

There is an important nuance to the use of average controllability applied to individual symptoms. The average controllability of an individual symptom assumes that it is possible to intervene on that symptom in isolation. This is analogous to the reasoning behind using node strength to identify individual symptom importance. However, as mentioned above, average controllability is calculated on the level of interventions, and the same advantages that average controllability has at the symptom level apply to average controllability calculated with multi-symptom interventions. The modular property of average controllability implies that the most effective set of multi-symptom interventions (in terms of moving the system overall) are the set of interventions with the highest average controllability.

A second controllability metric is modal controllability (Hamdan & Nayfeh, 1989). Whereas average controllability quantifies the efficiency of intervening on a symptom relative to intervening on other symptoms in a total symptom reduction sense, modal controllability quantifies the “reach” of intervening on a given symptom. The “modal” in modal controllability refers to the modes of the underlying dynamical system. Roughly speaking, modes refer to the independent directions a system can move in and are the dynamical systems analog to the orthogonal components of a principal components analysis in cross-sectional data.³ For example, a single-symptom intervention that targets a symptom with low modal controllability would be more restricted in the ways it can change other symptoms relative to a single-symptom intervention targeting a high modal controllability symptom. Because interventions targeting high modal controllability symptoms can effect the system in more ways, such interventions are also more likely to impact ”hard-to-reach” symptoms that are less centrally located in the psychometric network. Like with average controllability, modal controllability of a symptom assumes that the symptom can be intervened on in isolation and modal controllability can be calculated for multi-symptom interventions.

To calculate modal controllability, let λ_j be the jth eigenvalue of A and ν_ij be the ith entry on the jth eigenvector. The modal controllability of symptom i is then (Pasqualetti, Zampieri, & Bullo, 2014):

$${\varphi }_i=\sum _{j=1}^n\left(1-{\left|{\lambda }_j\right|}^2\right){\left|{\nu }_{ij}\right|}^2$$ (4)

where n is the number of symptoms and |·| is the modulo operator for complex numbers. Modal controllability is submodular rather than modular (Pasqualetti et al., 2014), which means that determining the set of interventions that maximize modal controllability is not a simple matter of choosing the k interventions with the greatest modal controllability. However a greedy optimization approach will result in a near optimal solution (pg. 4 Summers et al., 2016).

We emphasize that average and modal controllability can be used not only to assess interventions on single symptoms, but also broader intervention strategies that target multiple symptoms. This is especially useful in the context of predefined interventions, where the goal is not to determine which symptoms are best to target, but rather to determine which interventions (out of many) are most effective in reducing symptoms overall. Here again, we would stress that this is a significant advantage of controllability metrics over indices of node centrality, which only provide information about a single node in isolation and cannot be used to describe the impact of a multi-target intervention, something that is almost certainly required in any real-world treatment context. Finally, in the Supplementary Materials, we describe a statistical testing approach for evaluating how the rank ordering of symptoms or interventions with respect to controllability measures generalize from a sample to the population.

4. Using Control Theory to Simulate Treatments

The identification of treatment targets is only one advantage of a control theory approach. A second advantage is that control theory provides the opportunity to evaluate how well interventions might perform, even before empirical studies such as randomized controlled trials are carried out. We can achieve this aim using optimal control methods that seek to determine a sequence of control inputs (i.e. interventions) that will drive a system to a desired end state with minimum cost. To introduce these methods, we will review three key concepts: tests of controllability, cost functions, and optimal control.

4.1. Testing Controllability

One fundamental question is whether a given system is controllable. Is it possible to control the trajectory of all the symptoms over time, given a set of interventions and the dynamics of the system? Note that controllability does not refer to the ability to control a single symptom. Rather, it refers to the ability to control the entire system from a single symptom or set of symptoms. A system is controllable if given A and B, for any desired final state $\widehat{\mathbf{\text{x}}}$, there exists a series of interventions (control inputs) such that ${\mathbf{\text{x}}}_{\widehat{t}}=\widehat{\mathbf{\text{x}}}$ for some $\widehat{t}>0$. Although this property is important to evaluate, it doesn’t reflect the practicality of controlling the system. A system can be mathematically controllable, but require an unreasonable amount of time or intervention strength. Conversely, a system might not be mathematically controllable, but a given intervention still proves to be effective at reducing symptoms by a clinically relevant degree. Evaluating the controllability of a system provides useful diagnostic measures, but further steps are necessary to evaluate the actual effect of a given intervention. There are two approaches to assessing controllability that we present here, the first being a classical test of controllability and the second being a descriptive approach using indirect effect calculations.

To test if a system is controllable, one can construct the following matrix:

$$\mathcal{C}=\left[\mathbf{\text{B}},\mathbf{\text{AB}},{\mathbf{\text{A}}}^2\mathbf{\text{B}},\dots ,{\mathbf{\text{A}}}^{\mathbf{\text{n}}-1}\mathbf{\text{B}}\right]$$ (5)

where n is the number of variables in the system. The system is controllable if $\mathcal{C}$ has full row-rank $\text{rank}\left(\mathcal{C}\right)=n$. When we consider a single intervention that reduces the symptom of complicated grief with the highest average controllability (i.e., suicidal ideation), we find that the system is not controllable, as $\mathcal{C}$ is not full rank. This implies that the intervention targeting suicidal ideation is not capable of reducing all symptoms to 0, even if applied at full strength over an infinite amount of time.

For an alternative and perhaps more intuitive approach to examining controllability, we can take advantage of the fact that AⁱB represents the effect of the interventions described in B after i timesteps. Therefore

$${\mathbf{E}}_{\infty }=\mathbf{B}+\sum _{i=1}^{\infty }{\mathbf{A}}^i\mathbf{B}$$ (6)

is a p × l matrix where entry E_∞[ij] represents the total effect of intervention j on symptom i if the intervention is applied once at time i = 0. This matrix provides a practical look at the overall effect of an intervention and can indicate whether an intervention will be effective at changing a given symptom.

Now, consider an intervention for complicated grief that only targets suicidal ideation. We can calculate the intervention effect for this single target intervention E_∞, which is presented in Table 2.

Table 2.

Total Potential Intervention Effect

Symptom	Suicidal Ideation	Thoughts: Loved One	Yearning: Loved One	Approach	Thoughts: Death	Emotional Pain	Avoidance	Thoughts: Future	Pleasure	Positive Activities
Treatment Effect	−2.09	−0.63	0.10	−0.05	0.138	0.123	−0.01	0.08	0.13	0.15

Table 2 indicates that a single intervention that initially reduces suicidal ideation by 1 point, will lead to a total reduction over time of 2.09 points for suicidal ideation and 0.63 points for thoughts: loved ones. However, the same intervention would lead to, for example, an increase in yearning: loved ones of 0.1. As this intervention reduces some symptoms while increasing others, this system (i.e., complicated grief) cannot be controlled by a single intervention that targets suicidal ideation.

If a single symptom intervention on suicidal ideation failed to achieve control of the system, the next question is: What is the minimal set of interventions that is sufficient to control the system? Unfortunately, there is no simple solution to this problem. Determining this set exactly (actuator placement) is computationally intractable (indeed, an NP-hard problem, Olshevsky, 2014a), though there are algorithms that find a set of control inputs that render the system controllable (Olshevsky, 2014a, 2014b). There are practical barriers as well. First, it might be impossible to directly intervene on some symptoms. For example, in Cognitive Behavioral Therapy, interventions target emotional symptoms only indirectly via interventions on cognition or behavior. Second, it is unlikely that any given intervention will only directly impact a specific symptom or subset of symptoms, with other symptoms only impacted indirectly. Instead, interventions likely directly effect many symptoms within a system to varying degrees of strength. We illustrate the impact of assuming a highly specific intervention vs one with more broad effects in Section 5.1.

4.2. The Cost Function

To this point, the tools we have described for evaluating the effect of an intervention do not account for the cost of the intervention. Both approaches we have considered (controllability indices and tests of mathematical controllability) operate under the assumption that an intervention can be arbitrarily applied at any strength. These tools are useful, as they provide evaluations of the potential efficacy of an intervention. However, they do not provide any guidance as to the optimal implementation of a given intervention. In order to apply control in any practical context, we first need to define how costly our interventions are. To do this, we use a cost function. A general form of the cost function that provides analytic solutions is that of a linear-quadratic regulator (Lewis et al., 2012):

$$J_t=\frac{1}{2}{{\mathbf{x}}^{\prime }}_T{\mathbf{S}}_T{\mathbf{x}}_T+\frac{1}{2}\sum _{k=t}^{T-1}\left({{\mathbf{x}}^{\prime }}_k\mathbf{Q}{\mathbf{x}}_k+{{\mathbf{\text{u}}}^{\prime }}_k\mathbf{R}{\mathbf{u}}_k\right)$$ (7)

where T is the final timepoint. Many cost functions in the context of control theory are similar to the general linear-quadratic regulator, as this form is particularly amenable to analytic solutions to the control problem. In practice, choice of the cost function depends on the nature of the control problem. Here, we are seeking to minimize symptom values.

In the above cost function, the matrices S_T, Q and R have important substantive interpretations. S_T is a p × p positive (semi) definite matrix that provides the relative weighting of the final values of each symptom. For example, S_T = I places equal importance on each symptom. Off-diagonal elements of S_T place more importance on reducing collections of symptoms together, instead of considering each symptom as making an independent contribution to the cost function. Q_k is a p × p positive (semi) definite matrix specifying the relative importance of each symptom at each timepoint. For simplicity’s sake, here Q is time-invariant but could vary over time. Finally R is a l × l positive (semi) definite matrix specifying the relative cost of each intervention. As with Q, R can vary over time. By manipulating S_T, Q and R, researchers can examine the theoretical performance of their intervention set under a variety of settings.

Many cost functions in the context of control theory are similar to the general linear-quadratic regulator, as this form is particularly amenable to analytic solutions to the control problem. In practice, choice of the cost function depends on the nature of the control problem. Here, we are seeking to minimize symptom values both by the final timepoint (where symptoms’ importance are represented by S_T) and during the period of control ( where symptoms’ importance are represented by Q), while keeping cost of the intervention minimal (with cost of each intervention represented by R). As such, this function is a reasonable choice for the control problem at hand.

4.2.1. Determining Cost Parameters

Unlike parameters that govern dynamics (i.e., A and B), which could be inferred as part of system identification, the parameters of the cost function J must be defined by the analyst. There are several considerations for this definition:

• Relative Weighting - Each of the matrices S_T, Q_t and R contribute to the total cost, and when specifying them, the analyst must consider the relative weighting both within and between matrices carefully. For example, if S_T and Q_t are I while R = 10I, then the cost of applying interventions will be weighted more heavily than the values of symptoms.

• Scaling - If symptoms are measured on a different scale (i.e., one symptom is on a 1-7 point scale, the next a 1-5 point scale), this will affect how the control parameters function. For example, weighting the importance in the S_T matrix of 1-5 symptom and a 1-7 symptom equally (e.g., diagonal entries of S_T equal 1 for those symptoms) will result in the symptoms having unequal importance, as the scaling is different.

• Timeframe - The relative weights of R vs. S_T and Q_t will affect the timescale of the intervention strategy. If R makes much more of a contribution to cost than symptoms do, then an ”optimal” intervention strategy might be to apply the intervention at very low strength, which requires a longer intervention period. Alternatively, if cost of interventions is not weighted strongly, then the intervention might be applied too strongly or too quickly.

• Intervention Strength - The combination of S_T, Q and R with the scaling of the observed variables ultimately determines the scaling of the optimal control inputs u_t, which in the setting of interventions we refer to as intervention strength. It is important to chose the cost parameters so the estimated intervention strength is interpretable, which depends on the precise nature of the intervention. For example, if an intervention is a set of CBT sessions in a given month, a reasonable scale for intervention strength would be from 0 (no sessions) to 8 (two sessions a week). A 0-8 scale would not be reasonable for an intervention defined as either a 60 minute or 30 minute session. There, a 0 (no session) to 1 (60 minute session) scale might be more appropriate. ⁴

There are no clear cut rules for setting the control parameter values. The precise values that an analyst chooses will be dependent on the data and purpose at hand. We emphasize that the choice of values is not an inferential process, as they do not depend on the data generating process but rather reflect the desired goals of applying control.

4.3. Optimal Control

With our cost function J_t defined and parameter values set, we can now determine the optimal series of control inputs (u_t) that minimizes the cost function J_t over a finite time horizon T. We do not present derivations here, but for a thorough treatment see Lewis et al. (2012). First, we must compute an intermediate series of weighting matrices:

$${\mathbf{S}}_t={\mathbf{A}}^{\prime }{\left({\mathbf{S}}_{t+1}^{-1}+\mathbf{B}{\mathbf{R}}^{-1}{\mathbf{B}}^{\prime }\right)}^{-1}\mathbf{A}+\mathbf{Q}.$$ (8)

Note that S_t is defined with recursion forward in time, where the value of S_t at time T is the a priori defined S_T. The above expression for S_t is referred to as a Riccati equation in the control theory literature.

With S_t computed for every t ∈ 1 … T, we can then compute a set of matrices that allow us to inform our intervention strategy based on the current symptom values (Kalman gain sequence):

$${\mathbf{K}}_t={\left({\mathbf{B}}^{\prime }{\mathbf{S}}_{t+1}\mathbf{B}+\mathbf{R}\right)}^{-1}{\mathbf{B}}^{\prime }{\mathbf{S}}_{t+1}\mathbf{A}$$ (9)

and finally the optimal sequence of intervention strengths

$${\mathbf{\text{u}}}_t=-{\mathbf{K}}_t{\mathbf{\text{x}}}_t.$$ (10)

Note that the optimal sequence of control inputs are computed on the basis of the observed sequence of x. In other words, the optimal sequence of interventions is a closed feedback loop, as the values of x_t inform the control inputs u_t. Importantly, this differs from open loop controls, which can be used to drive systems to predefined endpoints instead of minimizing the cost function J_t. However, because open loop controls do not take into account the current value of the symptoms, they are not robust to any deviation off of the expected trajectory, making them unsuitable for controlling an inherently noisy and measurement error prone system like that of a psychological disorder.

4.4. Two Simple Control Examples

To demonstrate the use of optimal control methods, we first apply them in two simple simulated examples: an easy-to-control system (System 1) and a difficult-to-control system (System 2). Both systems have three variables (A, B, and C), white noise disturbances (randomly generated once and applied to both System 1 and System 2), and a single intervention that is applied to variable A. S_T and Q are both I, and R = 100I. The VARI networks for both systems, the control inputs, and the variable time series appear in Figure 2. In both cases, the starting values for all three variables was set at 20 (on a wholly arbitrary scale). The key differences between System 1 and System 2 are the presence of a suppressing effect from C to B and the negative autoregressive effect on B, both of which render System 2 more difficult to control than System 1.

Figure 2.

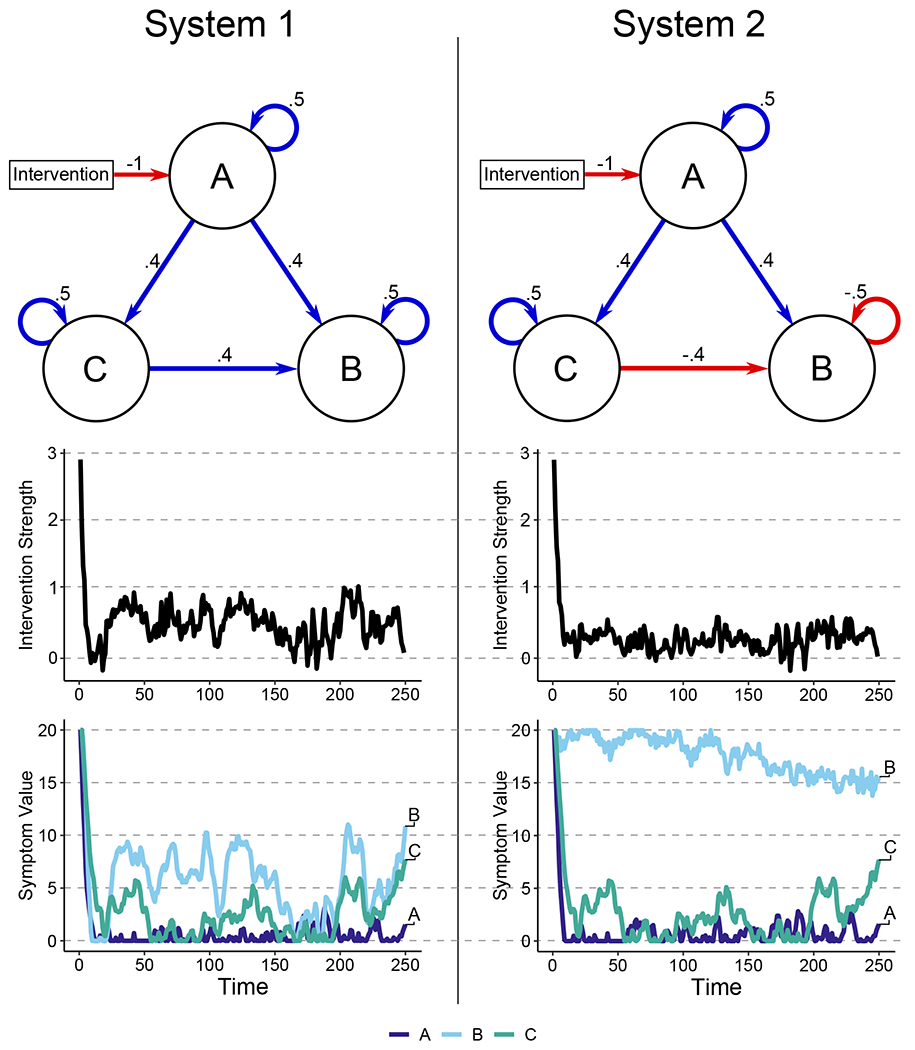
Networks, Intervention and Variable Values for Systems 1 and 2. Networks represent dynamics operating on change (as in Figure 1). Both systems were subjected to the same series of disturbances, which was generated as white noise.

These simulations illustrate two important points. First, this form of closed-loop feedback control is fairly robust to disturbances. In both systems, even with disturbances, control successfully minimized variable A and further reduced the value of variable C, keeping both fairly low across time. Second, a system can be controllable in an absolute sense but not controllable in a practical sense. In the difficult-to-control System 2, our interventions had minimal effect. Even though variable A was positively associated with variable B in System 2, the negative relation between C and B partially suppresses the A-to-C relation, and the negative autoregressive effect of B further dampens any interventions that impact B through A. This is the case even though both System 1 and 2 are “controllable,” as indicated by the previously described rank test for controllability. Examining the total intervention strength for both systems, an intervention that reduces variable A by 1 would lead to a total reduction in variable B of 2.88 in System 1 but only .1 in System 2, an order of magnitude different. In other words, even though System 2 could be controlled with very high cost and/or over a very long timeframe, it is not controllable in a practical sense.

5. Illustrating the Clinical Utility of Control Theory

5.1. Controlling Psychological Networks via Single-Target Intervention

Now that we have established that closed-loop interventions work in principle in simple simulated systems, we turn back to the VARI model of complicated grief symptoms estimated from empirical data. Although the network psychometric modeling literature has often focused on identifying symptoms thought to have the largest potential impact on other symptoms, another potential goal of these models could be to identify the specific symptoms most amenable to intervention. The simplest scenario is an intervention that targets a single symptom. In analyses described in detail in the supplementary materials, we identified suicidal ideation as the symptom with the highest average controllability (indicating that suicidal ideation is the most effective single symptom to reduce, see Supplementary Materials for details ). In Section 4.1 we showed that a suicidal ideation-only intervention was not capable of controlling the entire system. Here, we demonstrate what that means in practice.

To begin setting up the matrices that form the cost function for this simulation, we assume that (a) no symptom is more important to reduce than any other and (b) this importance does not change over the course of treatment. This implies that S_T = Q = I⁵ and when R = aI, where a is a positive number chosen to ensure that intervention is not unrealistically strong. The control input matrix B is, for a single symptom intervention targeting suicidal ideation, a 10 × 1 vector of 0s, with the exception of the element corresponding to suicidal ideation, which is set to 1. Our dynamics matrix A is taken from the group network of complicated grief symptoms (Fig. 1), see Supplementary Materials for more details. We add in a small amount of random disturbance to each symptom at each timepoint, sampled independently from a Normal(0, .1) distribution. In the following simulations, all symptoms will start at their middle value (3 for suicidal ideation and 5 for every other symptom), and are restricted in their ranges from 0 to the symptom maximum (5 for suicidal ideation, 7 for all other symptoms). Finally, intervention strength (control inputs) are restricted to be positive or zero. This restriction prevents the case where the optimal control would involve increasing symptoms by applying an “anti-intervention.”

For a single-symptom intervention targeting suicidal ideation, the control input matrix B is a 10 × 1 vector of 0s, with the exception of the element corresponding to suicidal ideation, which is set to 1. Previously, we noted that a psychological intervention, even one explicitly designed to reduce a single symptom, is unlikely to have no direct effects on any other symptoms. For example, in the case of talk-therapies, common factors such as therapeutic alliance are likely to impact a wide range of symptoms. Similarly, pharmaceutical interventions target biological systems involved in many behavioral outcomes. To reflect this, we can modify the suicidal ideation-targeted intervention to be a “heavy handed” intervention: one that targets a specific symptom but directly reduces other symptoms as well. Figure 3 Panel A shows what optimal control looks like when the treatment reduces only suicidal ideation by 1 point per unit of intervention strength. In contrast, Panel B shows what optimal control looks like when the intervention reduces suicidal ideation by 1 point per unit of intervention strength, and all other symptoms by .1 point per unit of intervention strength. Panel A allows us to assess the impact of reducing a single symptom (in this case suicidal ideation), but the “heavy handed” intervention depicted in Panel B is likely closer to a real-world psychological intervention.

Figure 3.

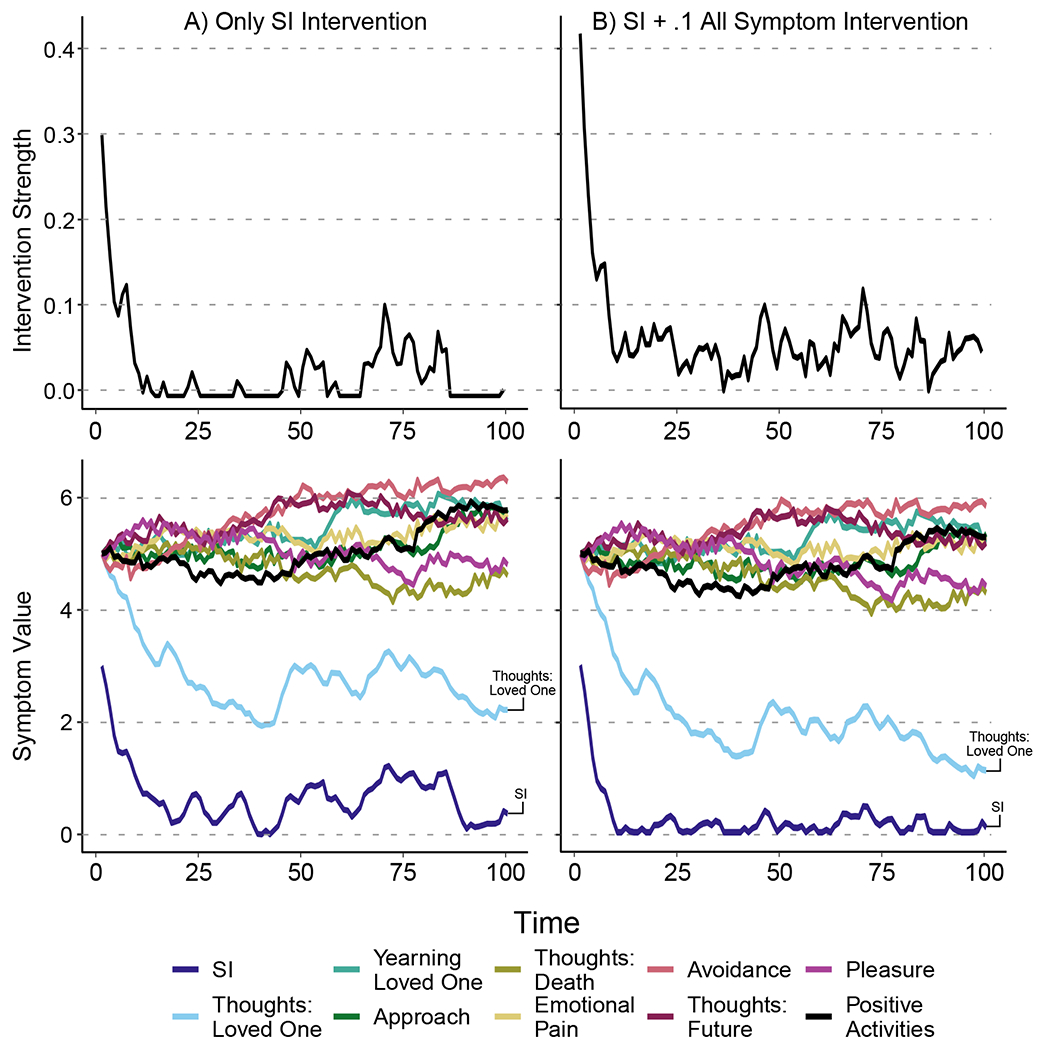
Intervention strength and symptom values when (A) intervening on only suicidal ideation with strength of 1 and (B), when intervening on suicidal ideation with a strength of 1, and all other symptoms with a strength of .1. Note that the same sequence of random disturbances were applied to each simulation. Results show that the broader intervention in Panel B leads to more reduction in suicidal ideation and thoughts: loved ones than the single target intervention in Panel A. Additionally, the broad nature of the intervention in Panel B only reduced the spread of symptoms other than suicidal ideation and thoughts: loved ones slightly more than the single target intervention in Panel A.

First, let us examine the symptoms’ behavior and the intervention’s magnitude over the course of 100 timepoints. R is set to 100I, which (in this example) restricted the maximum intervention strength to an approximately .3 point reduction of suicidal ideation for the intervention that targets only suicidal ideation (Panel A) and .4 for the intervention that targets suicidal ideation and all other symptoms (Panel B).

There are three key features to note in Figure 3. First, both types of interventions were initially applied at a high strength (.3 in Panel A and .425 in Panel B), then was applied at lower strength for the rest of the intervention period. In Panel A, the single target intervention, there were periods of 0 intervention strength, while in Panel B, intervention strength was non-zero across the intervention period. This was due to the broader intervention being used to control non-target symptoms. Second, both thoughts: loved ones and suicidal ideation showed a greater reduction and less variance when the intervention reduced all symptoms slightly (Panel B) relative to single target intervention (Panel A). Finally, in Panel B relative to Panel A, the remaining symptoms had a smaller spread in their trajectories, while the majority of the remaining symptoms did not show meaningful reductions.

Although suicidal ideation was the symptom with the highest average controllability for both within- and between-subject networks, the symptom trajectories in Fig. 3 show that an intervention that solely or primarily targets suicidal ideation mainly reduces suicidal ideation and thoughts: loved ones, while other symptoms were effectively unchanged. These results highlight two crucial points. First, controllability metrics indicate how efficiently interventions targeting single symptoms will impact the whole system relative to targeting other symptoms. Second, although controllability metrics can help us identify the most impactful symptoms, they indicate little about the magnitude of the impacts from such an intervention. Selecting intervention targets is important, but evaluating these interventions is necessary to gain a genuine understanding of their impact. This example also illustrates how control theory can guide the application of maintenance interventions. For example, the optimal sequence of control inputs applied the intervention around timepoint 75 after a period of relatively low intervention strength, in response to the slight trend upwards seen in suicidal ideation and thoughts: loved ones.

Overall, our simulations suggest that applying single target interventions can be effective in reducing the targeted symptom, but are less likely to meaningfully impact all symptoms, even when the intervention has small direct effects on non-targeted symptoms. However, it is unlikely that a single intervention is all that a therapist has on hand. Instead, several interventions would be available which could be applied simultaneously, a situation we cover next.

5.2. Controlling Networks via Multiple-Target Interventions

Suppose Intervention A targets suicidal ideation, Intervention B targets positive activities (reverse coded so that reductions correspond to increases in enjoyment of positive activities), and Intervention C targets thoughts: future. In this example, all three interventions also reduce non-targeted symptoms by .1. The B matrix for these interventions is shown in Table 3.

Table 3.

B Matrix for Interventions A, B and C.

	Intervention
	A	B	C
Suicidal Ideation	−1	−.1	−.1
Thoughts: Loved One	−.1	−.1	−.1
Thoughts: Future	−.1	−.1	−1
Avoidance	−.1	−.1	−.1
Thoughts: Death	−.1	−.1	−.1
Positive Activities	−.1	−1	−.1
Yearning: Loved One	−.1	−.1	−.1
Approach	−.1	−.1	−.1
Pleasure	−.1	−.1	−.1
Emotional Pain	−.1	−.1	−.1

We apply these three interventions simultaneously, with all symptoms being weighted equally, and all interventions having the same cost (e.g. R = 100I). Figure 4 shows the intervention strength and symptom trajectories in this case.

Figure 4.

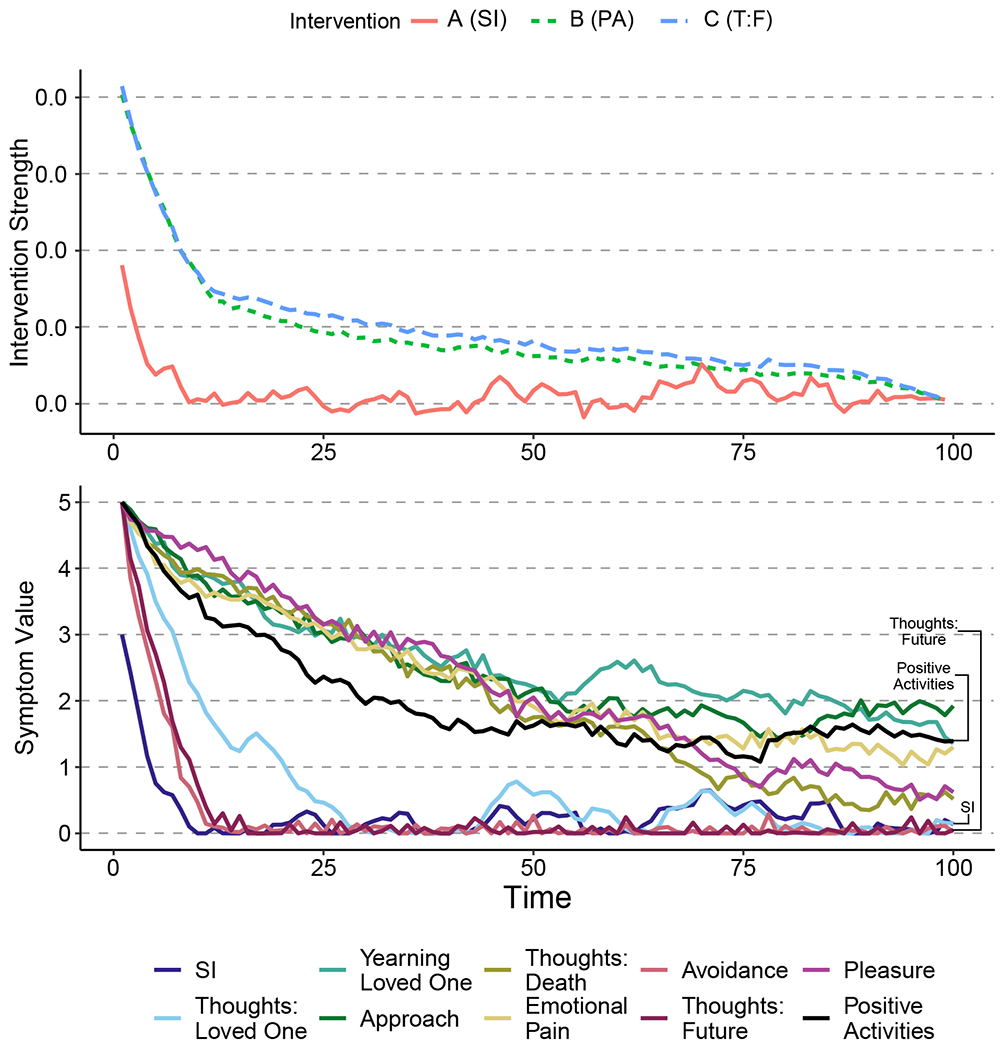
Intervention Strength and Symptom Values for Interventions A, B and C. Intervention A primarily targets suicidal ideation, Intervention B primarily targets positive activities (reverse coded), and Intervention C primarily targets. thoughts: future. The simulataneous application of these interventions led to a reduction to 0 for both suicidal ideation and thoughts: future, and a ~ 3.75 reduction in positive activities (reverse coded).

First, Figure 4 indicates that when these three interventions are applied simultaneously, all symptoms can be meaningfully reduced within the given timeframe. Second, the interventions are not applied equally strongly. Intervention A is applied with the weakest strength throughout the timeframe, while Interventions B and C are applied with similar strength throughout the timeframe. Third, this set of interventions only reduced suicidal ideation, thoughts: loved ones, thoughts: future and avoidance to near 0. All other symptoms were reduced by ~ 3 to ~ 4.5 points. This is notable as positive activities was the specific target of Intervention B, yet was not successfully reduced to 0.

This example evaluates three very simple interventions: real-life interventions such as cognitive behavioral therapy almost certainly include at least two more important complications. First, not all treatments are equally costly, in different meanings of costly. Pharmacological interventions are less resource intensive than weekly psychotherapy targeting the intense and pervasive negative emotions that characterize complicated grief, but may come with stronger side-effects. Second, the impact on safety and well being is not the same across symptoms: any clinician would prefer to remove suicidal ideation from the clinical picture as quickly as possible, even if that meant delaying an intervention on other important, but less immediately harmful, grief-related symptoms. This means we may want to use control theory to optimize control of one specific symptom rather than the whole system, such as suicidal ideation. Fortunately, the control theory framework explicitly allows one to account for these considerations.

5.3. Changing Symptom Importance and Intervention Cost

Take again the set of three interventions (A, B, C) from the previous example. We apply three modifications to showcase the possibilities that the control theory framework offers. First, we prioritize quickly reducing and maintaining minimal levels of suicidal ideation, given its greater threat to patient safety. Second, we also illustrate the effect of different intervention costs: we set Intervention A to cost twice as much as Intervention B, and Intervention C to cost half as much as Intervention B. Third, we model the scenario where Interventions A and B are difficult or impossible to apply together (e.g., two pharmacological interventions that interact poorly, or two intensive behavioral interventions). Our S_T, Q and R matrices are presented below.

$${\mathbf{S}}_T=\left[\begin{array}{cccccccccc}10& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 1\end{array}\right]$$ (11)

$$\mathbf{Q}=\left[\begin{array}{cccccccccc}5& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& .5& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& .5& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& .5& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& .5& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& .5& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& .5& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& .5& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& .5& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& .5\end{array}\right]$$ (12)

where for both S_T and Q, the first column/row corresponds to suicidal ideation.

$$\mathbf{R}=a\left[\begin{array}{ccc}2& 0& 2\\ 0& 1& 0\\ 0& 0& .5\end{array}\right]$$ (13)

where the rows/columns are ordered, A, B, C. This R matrix puts our assumptions about relative cost of interventions into rigorous form. The 1 corresponds to B being half as expensive as A, while the .5 corresponds to C being a quarter as expensive as A. The 2 on the off-diagonal specifies that there are additional costs to implementing intervention A and C at the same time (analogous to two medications having negative interactions) To keep intervention strengths from being unrealistically high, a = 2500.

Fig. 5 shows the symptom trajectories and intervention strengths for this control setup. Changing the control parameters led to these interventions being applied quite differently than in Figure 4. First, the fact that Intervention A and C are difficult to apply together is reflected in how these two interventions were applied. There is a spike in the strength of Intervention C around time 10, and there is a spike in the strength of Intervention A around time 65. Both interventions were applied at a very low level throughout the remainder of the timeframe. Second, even though SI was set as the most important symptom to reduce, the inability to apply all three interventions simultaneously resulted in SI being reduced at a slower rate than that shown in Fig. 4. Finally, while the same sets of symptoms as in Fig. 4 were reduced to near 0, the remaining symptoms were not reduced as much overall as in 5.

Figure 5. Symptom Values and Intervention Strength for Interventions A, B, C with Unequal Symptom Importance and Intervention Costs.

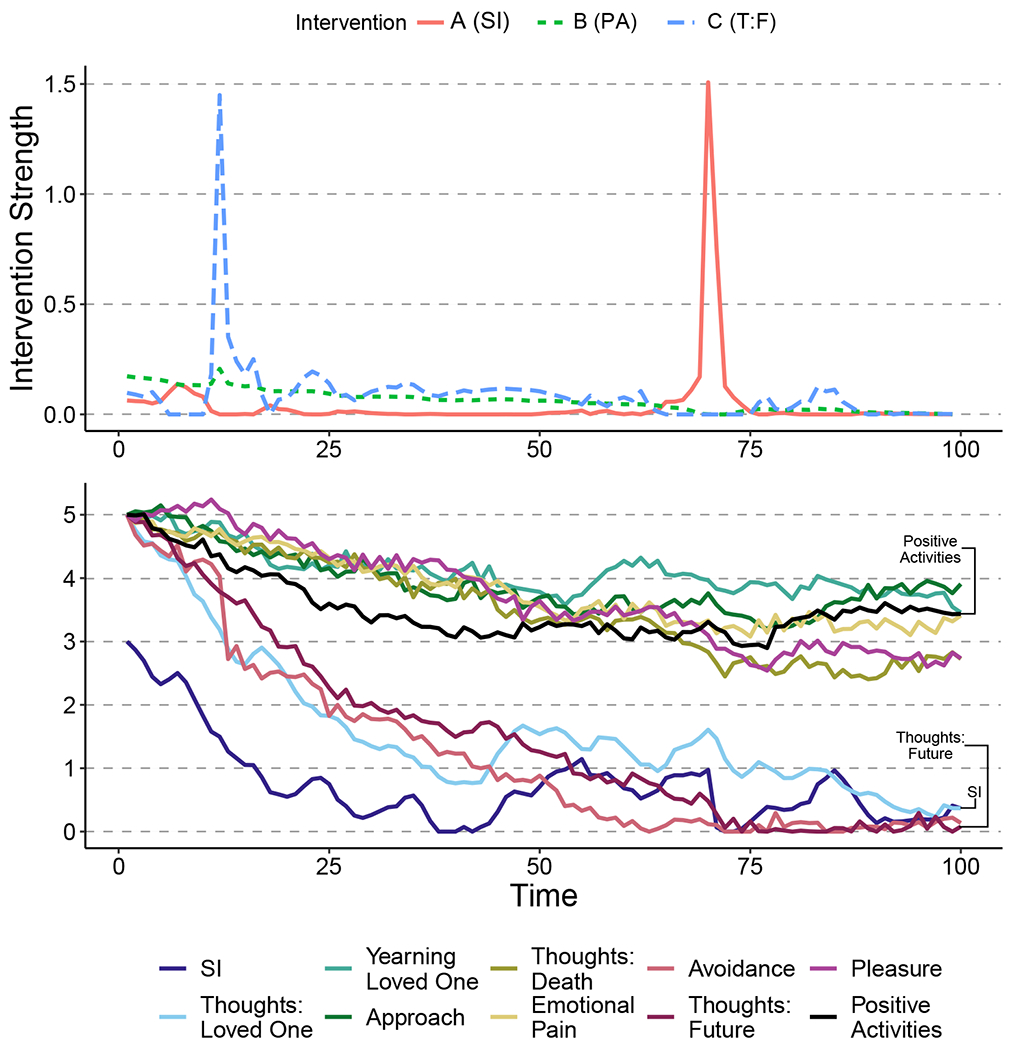
Note: Interventions A and C have been specified to be incompatible (i.e. applying them simultaneously costs more than applying both separately). The simultaneous application of these interventions led to a similar reduction to 0 for both suicidal ideation and thoughts: future as in Fig. 4, but only a ~ 1.5 point reduction in positive activities (reverse coded) (compared to a 3.75 reduction seen in Fig. 4).

In these examples we have been evaluating interventions that have been proposed on the basis of controllability statistics. However, it is common that we have a priori knowledge on the efficacy of real-world interventions. In the next section, we simulate the effects of the complicated grief treatment intervention of Shear (2010) that was given to our sample of patients.

6. Discussion

The use of network psychometric models to inform intervention design is a promising aim for clinical research, but one that requires new mathematical tools if it is to be realized. In this paper, we introduced several fundamental concepts from control theory, such as controllability centrality and optimal control, and illustrated via examples how they can improve intervention evaluation and design. All examples used EMA data from a sample of subjects undergoing treatment for complicated grief; this allowed us to firmly embed the methodology discussed in a practical, real-world empirical example. Below, we summarize our substantive findings and propose future directions for methodological research in control theory and network psychometrics.

6.1. Controlling Psychological Networks: The Empirical Case of Complicated Grief

Our analyses, although meant principally to demonstrate methodology, revealed several interesting features of complicated grief and its treatment. Suicidal ideation and thoughts about one’s deceased loved one had the highest average controllability (as seen in Section 2 of the Supplementary Materials), suggesting that intervening on those two symptoms in the present sample would be more effective at changing the system of complicated grief as a whole than would intervening on other symptoms. An analysis of single symptom interventions showed that targeting suicidal ideation was indeed the most effective single symptom intervention. However, it also showed that this single-symptom intervention was not successful at reducing all other symptoms to zero. Indeed, most symptoms were relatively unaffected. This suggests that the dynamic system that underlies complicated grief is not solely driven by any one symptom, and that single symptom interventions may not be effective at treating the disorder’s gestalt.

Modeling and comparing multiple interventions sets (A, B, C) shed further light on the structure of complicated grief. In the first set of interventions, Intervention A (targeting the symptoms of suicidal ideation and thoughts: loved one) was more effective, in terms of intervention cost to total reduction in symptoms, relative to Interventions B or C when applied separately. However, when applied in tandem, Interventions A, B and C together led to much better treatment outcomes: reducing all symptoms of complicated grief. Finally, in Section 4 of the Supplementary Materials, we simulated how the empirical treatment that the subjects were undergoing, a structured psychological therapy focused on accepting the loved one’s death– would impact subjects symptoms when applied optimally. We found that the simulated “empirical” treatment appeared primarily impact patients’ preoccupation with thoughts of the deceased loved one while also significantly reducing suicidal ideation in the process.

These substantive conclusions should be interpreted in light of a number of limitations. First, there are only eight subjects present in the analysis, each of whom not only met criteria for complicated grief, but also reported persistent suicidal thoughts, limiting the generalizability of our findings. Second, all simulations were performed under the assumption that the group-level dynamics were a reasonable estimate for each subject in the population, an assumption that is unlikely to hold. Third, the treatment effect was modeled within the ML-VARI as a 0/1 indicator, which does not reflect the fact that the treatment had multiple phases. This choice, made to simplify the control theory modeling of the treatment effect, likely also reduces our power to detect treatment effects that varied over the stages of the intervention. Finally, and most importantly, although we used an integrated VAR(1,1) model to model symptom trajectories as a non-stationary process, it is unlikely that this model truly represents the causal dynamics underlying the disorder, a significant limitation to which we will return.

6.2. Methodological Challenges and Future Directions

In this paper, we aimed to introduce control theory as a valuable tool for identifying intervention targets and understanding the behavior of a psychological system undergoing intervention. Below, we more fully discuss limitations in the presented approach, briefly introduce more modern control theory methods, and identify future research directions that may radically improve the application of control theory to psychology.

6.2.1. The Importance of System Identification

Like any methodological approach, control theory can only be as effective as the information it is provided. If the system to which one is applying control theory fails to capture the important dynamics of the real-world psychological system, the methods we have presented here will be ill-equipped to inform intervention. Accordingly, how one decides to model a psychological process will have major consequences for control theory applications.

In the network psychometric literature, the most commonly used time-series model, the VAR model, assumes stationarity. That is, it assumes that the means and variances of the time series are stable across time. In this paper, we used the VARI model, assuming that time series of symptom values are non-stationary, but that the change in symptom values from timepoint to timepoint is stationary. This ensured that the symptoms followed a unit-root process, allowing their trajectories to be permanently altered by interventions. This is vital, as a stationary VAR process is inherently mean reverting: no amount of intervention will permanently shift the expected symptom values away from the model-defined mean. Future research in the area of longitudinal psychometric network modeling should focus on modeling systems of symptoms in a way that allows disturbances (e.g., interventions) to impact the data-generating process directly. Such work will be especially important for researchers aiming to inform treatment. A state-space modeling approach is particularly amenable to this, as non-stationary processes can be modelled at the latent state level, while stationary error processes can be modeled at the indicator level. State-space modeling also allows for non-linear processes, an area where control theorists have developed several approaches for optimizing interventions.

An alternative approach to system identification than the one presented here would to work not from data-based models, but from theory-based models. In recent years, several researchers have argued for the benefits of formalizing theories in clinical psychology as mathematical or computational models (e.g. Burger et al., 2019; Fried, 2020; Haslbeck, Ryan, Robinaugh, Waldorp, & Borsboom, 2019; Robinaugh, Haslbeck, et al., 2019). These formal theories often take the form of a causal network that aims to capture the dynamic processes that give rise to psychopathology. Although we herein demonstrated the use of control theory methods on networks derived from real data, there is no reason why the methods we used could not be applied to understanding the dynamics of a formal model. Indeed, we consider this to be a novel and promising application of control theory for psychological science. However, just as with models derived from empirical data, it is important to remember that the application of control theory will only be successful to the extent that the formal theory is an adequate representation of the target system of interest. Accordingly, it will be critical for theorists to develop strong formal theories if this approach is to be successful.

6.2.2. The Importance of Measurement and Measurement Error

The systems modeled in this paper were assumed, for the sake of simplicity, to have a white noise disturbance component. White noise error processes do not impact the optimal control estimates for linear systems (Molenaar, 1987). More complex error processes (e.g., the temporally correlated noise commonly found in psychological data) can be be addressed through the use of stochastic control theory. However there are other sources of error than disturbances, with measurement error being a major concern for any psychological dataset. Studying how measurement error impacts statistical models of psychological data is a time-honored tradition in psychometrics and control theory should be no exception. Some control theory literature does touch on measurement error (i.e. Schultz, 1964), but measurement error is particularly salient for clinical psychopathology research. Most recent applications of control theory to human behavior have observable outcomes (e.g., walking measured by actigraphy), and are less susceptible to measurement error. The measurement of psychological symptoms however typically relies on self-reported assessments of symptom severity/frequency, which are more susceptible to error, making it vital to evaluate effects of measurement error on control outcomes. One promising but currently underutilized way to account for measurement error in network psychometric is latent variable network modelling (Epskamp, Rhemtulla, & Borsboom, 2017), which should be further developed for longitudinal network modelling of non-stationary processes.

In addition to error in symptom measurement, there also likely to be error in intervention strength measurement. The strength of an intervention is not simply the immediate impact on symptoms, but also needs to take into account how the intervention interacts with subject specific dynamics. The consequences of this type of measurement error are especially salient in our present context, as psychological interventions have direct impacts on the lives and health of patients. The issue of how best to measure intervention strength is a relatively novel one for clinical psychology, but one that is critical to evaluating the expected impact of the intervention on systems of interest. Future control theory applications should examine how measurement error in the estimate of system dynamics, control inputs, and symptom observation during intervention may all bias conclusions.

6.2.3. The Future of Control Theory in Psychology

In this paper we aimed to provide an accessible introduction to control theory by focusing on a relatively straightforward set of analyses. However, the field of control theory is much broader than just these analyses and more complex analyses are available to help address challenges that are likely to be faced in applying this work within clinical psychology. For example, the analyses performed in this paper restricted symptoms values to a particular range and required interventions to be positive. Binary control inputs, or control inputs that have bounds, are referred to in the control theory literature as saturated control inputs. These restrictions led to interpretable trajectories and intervention regimes above, but can have large impacts on system behavior and are thus not completely optimal. When applying control theory to psychology, inputs and outputs will likely always be bounded/saturated, which necessitates more complex methods than we have used here when optimal performance is desired.

The constraint issue can be resolved using hybrid model predictive control (HMPC; Bemporad & Morari, 1999), which not only allows for constraints on both control inputs and state values, but also for categorical control inputs and state values. HMPC also brings with it the advantages of model predictive control, in that it can be applied to non-linear systems and allows for non-quadratic forms of the cost function. However, model predictive control approaches do not guarantee an optimal sequence of interventions and systems as it can be computationally difficult to determine the control laws for many variables (Kouvaritakis & Cannon, 2015). Nonetheless, psychological data is likely to be more amenable to model predictive control in practice, because there may be less need for rapid online control calculations such as in an engineering context. This would avoid some of the computational issues associated with applying this approach to high-dimensional data with a high sampling frequency.

Another challenge likely to be faced in clinical psychology is the possibility for time-delayed effects. Our intervention’s effects were modeled as instantaneous, with an intervention at time t causing a change in symptoms at time t. In reality, psychological interventions may not have such instantaneous effects. For example, an intervention reducing grief-related avoidance behavior may take weeks before it is accepted and adhered to by a patient. Such time-delayed effects, like saturated inputs, change how optimal controls should be calculated. Future research in this area should focus on bringing time-delayed control methods into control theory applications in psychology, as this would improve the external validity of the approach.

Perhaps the most important step in applying control theory within clinical psychology will be to move toward applying these methods using within person-specific networks. In Section 5.1 we estimated the intervention effect at the group-level, assuming homogeneity in treatment response. Although interventions will likely have at least some common effect, the response of any single participant to any single intervention is likely heterogeneous. One solution is to explicitly estimate individualized treatment effects. However, there are several important considerations to note. First, the amount of data per person needed to estimate individual treatment effects is far greater than that needed when estimating group-level treatment. Second, estimation of an individual intervention effect requires collecting data before treatment for that given individual, which complicates optimally controlling the intervention applications for that person. Nonetheless, modeling individual treatment effects and applying them in a control setting could potentially improve the personalization of psychological interventions.

Finally, we would like to stress the importance of cross-validation in future applications of control theory that compares simulated and empirical interventions. The methods and results presented in this paper take a simulation approach to evaluating the implied efficacy of interventions on psychological networks. This allows for formalized predictions of treatment response, without having to evaluate the treatment in an empirical study. A vital next step would be to compare these formalized predictions from the simulations to the actual treatment response in a new intervention study with a different sample of individuals. As mentioned above, this enables researchers to cross-validate their interventions. Any mismatch between the simulation-implied treatment effect and the empirical (observed) treatment effect would help reveal issues in modeling, data collection, or other threats to inference.

6.3. Conclusion

Control theory holds great promise for improving the development and evaluation of psychological interventions. Control theory as a field is more generally well developed; as such, future applications of control theory to psychology can benefit from many already existing tools. Although there are some unique challenges that psychological data also present, solving these challenges offers new opportunities to provide clinical science with more accurate predictions and stronger interventions that account for heterogeneity in both treatment and treatment response. In particular, control theory opens up new possibilities for personalized treatment strategies, where interventions could be applied based on the unique dynamics of a given patient. More work is clearly necessary, but we hope that applying control theory to the intervention sciences will ultimately improve people’s real-life experiences and outcomes across a diversity of interventions, be they medical treatments, mental health management, or behavioral interventions.