Concealable physically unclonable function chip with a memristor array

Abstract

A physically unclonable function (PUF) is a creditable and lightweight solution to the mistrust in billions of Internet of Things devices. Because of this remarkable importance, PUF need to be immune to multifarious attack means. Making the PUF concealable is considered an effective countermeasure but it is not feasible for existing PUF designs. The bottleneck is finding a reproducible randomness source that supports repeatable concealment and accurate recovery of the PUF data. In this work, we experimentally demonstrate a concealable PUF at the chip level with an integrated memristor array and peripherals. The correlated filamentary switching characteristic of the hafnium oxide (HfO_x)-based memristor is used to achieve PUF concealment/recovery with SET/RESET operations efficiently. PUF recovery with a zero-bit error rate and remarkable attack resistance are achieved simultaneously with negligible circuit overhead. This concealable PUF provides a promising opportunity to build memristive hardware systems with effective security in the near future.

A memristor-based physically unclonable function chip is demonstrated to be concealable with high reliability and security.

INTRODUCTION

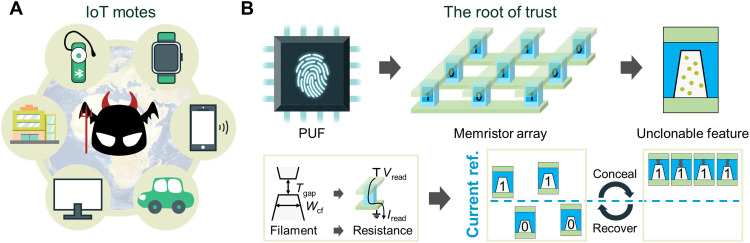
The expansion of the Internet of Things (IoT) has led to the exponential growth of electronic devices and considerable concern about hardware security, which is threatened by hardware piracy, counterfeiting, and Trojan implantation from unknown supply chains (Fig. 1A). Unauthenticated and unqualified devices sneaking into the market will cause immeasurable economic loss and sensitive information leakage. This serious situation highlights the impending need for trusted device identification. A physically unclonable function (PUF) is a feasible solution to the root of trust for IoT devices (1–4). A PUF usually leverages static randomness in a physical circuit to generate PUF keys. These keys are inherent, unpredictable, chip specific, and thus analogous to human fingerprints (5–7). Cloning PUFs without any awareness of these keys is impossible even if someone exactly replicates the same manufacturing process and PUF generation algorithm. These attractive features enable the PUF to be the foundation of trustworthy identification as a lightweight security primitive (8–11).

Fig. 1. Introduction of hardware security.

(A) Worldwide, IoT devices are under various threats, including being hacked, physically attacked, and counterfeited by malicious and unorthodox parties. (B) The function and mechanism of PUFs for hardware security. PUFs provide an electronic fingerprint for device identification and data encryption. A memristor crossbar array can be implemented for PUF chips, as each memristor inherently has unclonable features in the morphology of its conductive filament (CF) (e.g., filament width W_cf and filament gap length T_gap). This random feature can be easily extracted through a read operation to generate PUF data. Furthermore, programming memristors can realize effective concealment and recovery of the data to achieve higher security.

However, the development of attack means still poses an enormous threat to the current security system. Secret information (i.e., PUF data) can be stolen through advanced microprobing attack and sophisticated analysis methods with leaked side-channel information (12–16). Therefore, a PUF with random and noncloning features is far from sufficient to guarantee security. This vulnerability is rooted in the fact that PUF data are physically accessible, as the data are represented by detectable and unchangeable circuit features, and the system works with regularity. Therefore, a secure PUF is heavily desired to counter the aforementioned attack means by having the following features: (i) PUF data are concealed and thus physically unavailable when the PUF is not called and can be recovered when the PUF is called, and (ii) the performance of the PUF is random enough to conceal the system’s regularity. We define a PUF with these two important features as a concealable PUF, which offers strengthened security by being immune to illegal circuitry detection and side channel eavesdropping (17).

PUFs are traditionally designed with the complementary metal-oxide semiconductor (CMOS) technique, which leverages mismatches in grouped transistors caused by manufacturing variations (18–23). Once changed, the mismatch patterns (i.e., PUF data) are irrecoverable, so these CMOS-based PUFs cannot be physically concealed. As a result, to achieve sufficient attack resistance, the secure system relies on a probing detection circuit to sense the damage on the top metal, an extensive redundant circuit to confuse the layout analysis, and a power management circuit to nullify side-channel leakage (24–26). All these circuits need to be meticulously devised and are area-consuming. In addition, CMOS PUF techniques are demanding in terms of process conditions and are likely to provide inadequate randomness.

In contrast, memristors are considered a more suitable randomness source for PUFs due to their appealing characteristics (e.g., inherent stochasticity and high density) and notable variation (27). With a compact crossbar array structure, the randomness in the conductance distribution (7, 28–31), switching delay (32, 33), and probabilistic switching (34, 35) have been used to produce highly random and reliable PUFs. Furthermore, memristive randomness has been demonstrated to be effective in obfuscating side-channel performance (36, 37), and one-time recovery of the random conductance distribution has been realized with a 15% error rate (38). These studies indicate that memristors are promising for bringing stronger security to hardware systems. However, the implementation of a concealable memristive PUF still faces the following difficult challenges: (i) A crucial characteristic of the memristor has not been found to support the repetitive and reliable recovery of PUF data, and (ii) a concealing scheme should be developed to implement efficient and secure concealing of PUF data. Because of these challenges, the existing memristive PUFs storing data by distinct resistance states cannot realize data concealment. In this case, attackers can access these private data using microprobes with minor effort. As a result, the security of memristive PUFs thus far is based on a fallback assumption that hackers cannot physically access the PUF chips, which is becoming less convincing and lowers the likelihood of their use in practical IoT applications.

In this work, we propose a concealable PUF with a compact memristor array (Fig. 1B). After initialization by the FORMING-RESET operation, memristors form conductive filaments (CFs) inside with random morphologies, which determine device conductivity and are used as the unclonable feature to characterize PUFs. Memristors with different conductance values are compared with a fixed reference to represent PUF data. Excellent randomness is demonstrated for this PUF by achieving 50.3% average uniformity, 49.9% average diffusion, and 50.5% average uniqueness. The highly random feature of memristor devices, as well as the corresponding PUF data, can be dynamically concealed and recovered. To conceal the PUF data, the memristors are programmed to have a high conductance state so that CFs are extended with newly generated oxygen vacancies (Vo); thus, the critical feature (i.e., filament morphology or device conductivity) is successfully concealed. In this case, the correct PUF data are inaccessible, and the comparison method produces unmeaningful results with a bias close to 1. On the other hand, by clearing those additional Vo with the RESET operation, CFs can recover to their original states with acceptable errors to reproduce the correct PUF data. In other words, to implement efficient recovery, the RESET operation can be applied to neutralize the effects caused by the SET operation, and thus, notable similarity or correlation can be found between the conductance values obtained after RESET and the initial states.

We demonstrate this idea at the integrated chip level, successfully achieving the hiding of more than 70% of PUF keys and a 0% bit error rate (BER) for recovery. Compared with the previous work (38), which develops a PUF-based provable key destruction scheme, this work implements a concealable PUF by achieving repeatable concealment and accurate recovery of the PUF data based on a newly found filamentary switching characteristic. Furthermore, PUF concealment and recovery inject intrinsic uncertainty into the side channel of the whole security system, making the system performance unanalyzable and immune to noninvasive attacks. Therefore, in addition to basic device-to-device (D2D) randomness, the concealable PUF fully exploits the cycle-to-cycle (C2C) correlation of memristors to efficiently address the major challenge faced by the memristive PUF community, illuminating its prospect with unprecedented security.

RESULTS

Memristor-based PUF system design

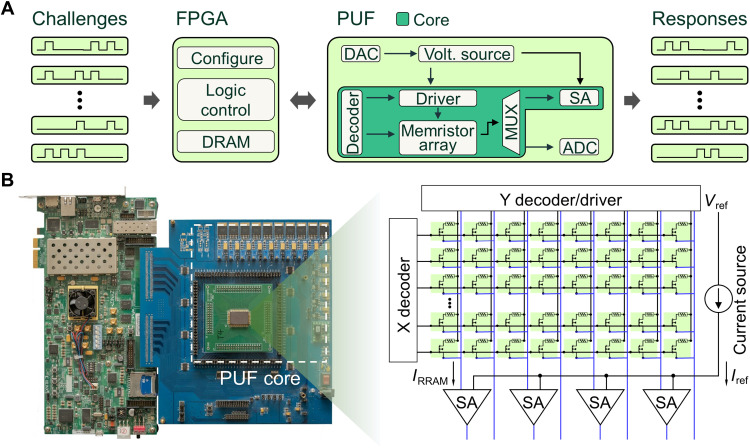
A hardware system is designed with a memristor PUF chip, a customized printed circuit board (PCB), and a field-programmable gate array (FPGA) evaluation board to demonstrate the concealable memristive PUF (Fig. 2A). The chip implements the core of this PUF system, including a memristor crossbar array, peripheral drivers, and high-resolution read circuits. Programming the memristor array provides essential entropy (e.g., randomness in the conductance state) for PUF key generation. The randomness derives from physical processes and is of extremely high quality. However, considering the small difference between the current sensed from the memristor array and the reference, on-chip and high-resolution read circuits are highly required. Otherwise, the entropy cannot be fully extracted, leading to 0/1-biased and spatially correlated PUF keys. For this purpose, we design an offset-tolerant sense amplifier (SA) that supports reliable amplification of current differences as small as 3.8 nA (39). In this PUF chip, offset-tolerant SAs are placed in parallel, and a shared voltage-controlled current source is taken as the reference. Compared with an off-chip current source, an on-chip source enables more precise adjustment of the reference and generates a reference with better stability. Therefore, with all of the essential analog circuits on chip, experiments can provide more accurate, meaningful, and convincing evaluation results for memristor-based PUFs. The digital parts of a PUF (e.g., PUF key generation algorithm, register configuration, and other logic controls) are fulfilled externally by the FPGA, making the system more flexible for various PUF implementations and further optimizations. In addition, for test convenience (e.g., to evaluate the C2C correlation), programmable voltage sources and an analog-to-digital converter (ADC) are integrated onboard to measure the accurate conductance value of the memristor.

Fig. 2. Memristor-based PUF system.

(A) The architecture of the memristor-based PUF system. The FPGA communicates with the customized PCB through the FPGA Mezzanine Card (FMC) interface. The FPGA receives instructions (e.g., generating, concealing, and reading the PUF) with a specific challenge from the PC and sends control signals to the PUF chip, onboard digital-to-analog converter (DAC), and ADC. The readout results from the memristor array are sent back to the FPGA for postprocessing and then output as the response to the challenge. (B) Photograph of the PUF system. ZC706 FPGA evaluation board from Xilinx is used. The chip contains an 8-kb memristor array and supports parallel operation for up to eight memristor devices.

The input and output of a PUF are typically named challenge and response, respectively. For this system, the challenge is the sequence number of PUF keys, and the response is the corresponding digital readout result from the memristor array. Figure 2B shows a photograph of the whole system and a schematic of the PUF chip (see Materials and Methods for the system and the PUF chip details).

Device characterization for memristor

HfO_x-based memristors exhibit appealing resistive switching characteristics by controlling the formation and rupture of internal CFs. The conductivity of CFs is determined by a number of factors, such as the Vo distribution morphology. As a result, when a memristor array is programmed, the stochastic generation and recombination of Vo in the HfO_x layer will certainly cause D2D variation. For example, fig. S1C illustrates the wide conductance distribution of 1024 memristors programmed with one SET/RESET pulse. This D2D variation found in memristor arrays has been theoretically and mathematically studied and is encouraging for PUF key generation (40–42).

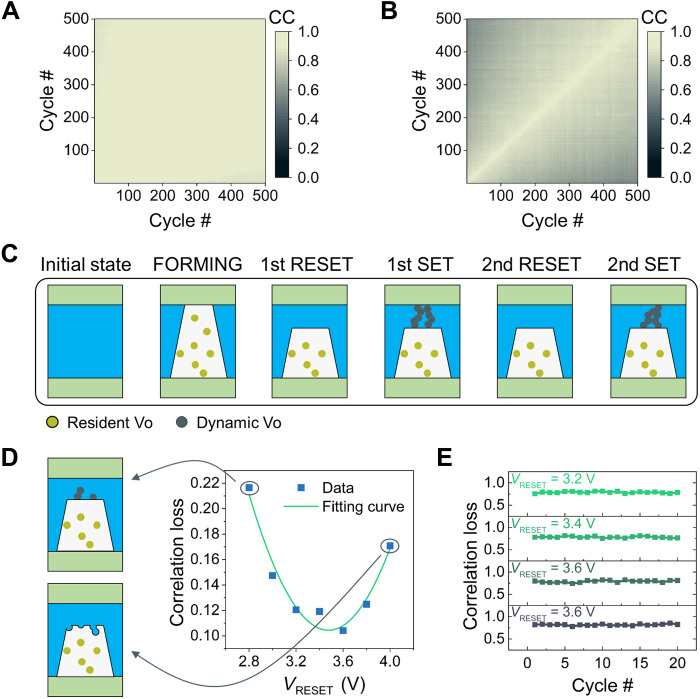
In addition to the well-known D2D variation, we find that the conductance values measured in different switching cycles can be correlated, and we define this correlation as the C2C correlation. For instance, when a memristor is programmed with SET/RESET cycles, its conductance value changes within its own distinct ranges (fig. S2). The variation range is correlated with the conductance value obtained in the first cycle. To further demonstrate the C2C correlation, the same experiment is implemented with 1024 memristors. The conductance values measured after RESET and SET are separately recorded, and the correlation coefficients (CCs) between cycles are calculated (see Materials and Methods for the detailed calculation of CCs). For the conductance values measured after RESET, a strong correlation with a CC greater than 80% is found in the 500th cycle (Fig. 3A), while for the conductance values measured after SET, the correlation degrades markedly over cycles (Fig. 3B). More directly, fig. S3 shows the colormaps of conductance distributions obtained after consecutive SET/RESET cycles, from which uniform patterns can be obtained after RESET, but the patterns obtained after SET are more variable. This C2C correlation found in a memristor array ensures that the original conductance distribution can be partly reproduced by a soft RESET pulse after being obfuscated by a soft SET pulse but not vice versa.

Fig. 3. Correlated filamentary switching characteristics.

(A) The CC matrix of the resistance distribution measured after RESET between cycles. (B) The correlation matrix of the resistance distribution measured after SET between cycles. A CC higher than 0.8, which means a strong correlation, is shown in white, and the color gradually fades to black as the CC decreases. (C) Illustration of the proposed model to explain the correlated filamentary switching found in the HfO_x-based memristor. The resident Vo (yellow dots) form the foundation of CF (white background), which is insensitive to soft SET and RESET operations, while the dynamic Vo (gray dots) in the gap can be iteratively erased and generated with the same SET/RESET voltage. (D) The estimated correlation loss between the original resistance distribution (after the first RESET) and the distribution measured after the 21st RESET. The experiment is implemented with variable RESET voltage and SET voltage fixed at 2.2 V. The large correlation loss found at low and high RESET voltages can be explained by the proposed model as under-RESET (top left inset) and over-RESET (bottom left inset), respectively. (E) The change in estimated correlation loss between the original resistance distribution and the distribution measured after SET in different cycles.

To explain this correlated filamentary switching phenomenon, we propose a model of the evolution of CFs (Fig. 3C). The CFs include a resident part and a dynamic part. Vo tend to be more stable in the resident part than in the dynamic part. The resident part forms a tough connection to the bottom electrode. The possible reasons include higher immigration and recombination barriers, and the region is less affected by the applied electric field. Therefore, a soft but sufficiently strong RESET pulse can erase the dynamic part but has a negligible impact on the resident part. This explains why a strong correlation can be found in the conductance values measured after RESET, which is mainly determined by the changeless resident part with reasonable variation. On the other hand, a SET pulse will regenerate dynamic Vo in the CF gap to form brand-new conductive paths with a highly random morphology. The varied paths produce different barriers for electron transport from the cathode to the anode. Therefore, the conductance distribution measured after SET is less correlated among cycles. This model is supported by atomic-scale numerical simulation with the kinetic Monte Carlo (KMC) method (see Materials and Methods for the KMC simulation details). In the KMC simulation, the newly generated dynamic Vo are gradually recombined under a RESET electric field, followed by the recombination of residual Vo, as shown in fig. S4 (A and B). With a fixed pulse width, there is a narrow range for the RESET voltage to achieve a 100% recombination rate of dynamic Vo while keeping the residual part unchanged (fig. S4C). This delicate balance between SET and RESET ensures that the KMC simulation reproduces the correlated filamentary switching phenomenon (fig. S5).

Therefore, SET/RESET voltages play critical roles in achieving this balance. A RESET voltage that is too weak cannot form a steady CF gap and thus leaves several dynamic Vo as electron traps, while a RESET voltage that is too strong will cause unexpected erosion of the resident part of the CF (fig. S6). The slight bias accumulating over cycles will lead to the total failure of conductance recovery. This is also experimentally verified by calculating the correlation loss in 20 switching cycles with a sweeping RESET voltage and fixed SET voltage, as shown in Fig. 3D (see Materials and Methods for the detailed calculation of correlation loss). Furthermore, the high correlation loss found on the SET side demonstrates that the hiding of conductance data can be efficiently realized by one SET pulse (Fig. 3E).

Concealable PUF design

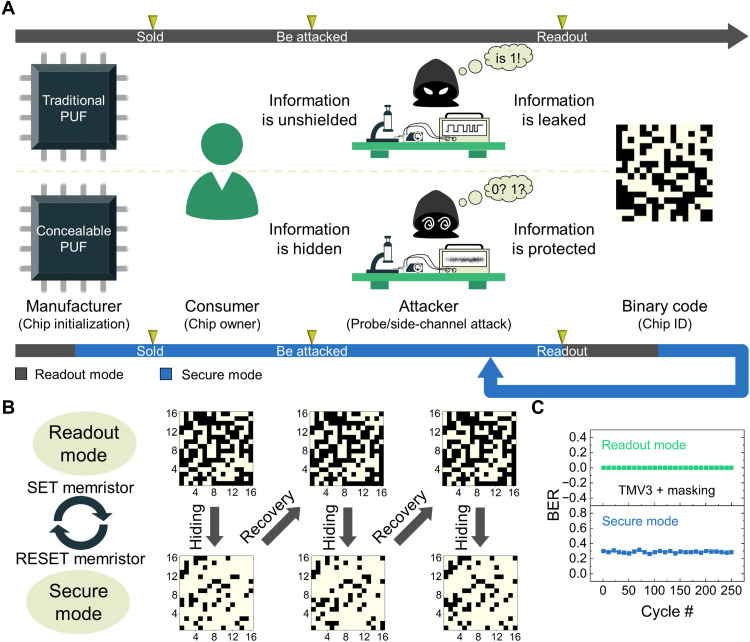
The aforementioned characteristics enable us to implement a concealable memristive PUF with considerable enhancement in security. Figure 4A illustrates the timeline for a PUF chip from manufacturing to practical application. In the first stage, the chip is initialized by the manufacturer to generate electronic fingerprints from inherent uncertainty in the physical entity. To realize this, we leverage the D2D variation in conductance values of the memristors (43, 44). Initially, FORMING and RESET operations are applied to the memristor array to obtain a random conductance distribution. Then, those memristors are selected in sequence, and their conductance values are compared with an on-chip reference. The PUF generation algorithm is given by the following equation

$$P_{n,m}=\{\begin{array}{c}1 \text{if} I_{n,m}>I_{\text{ref}}\\ 0 \text{if} I_{n,m}<I_{\text{ref}}\end{array}$$ (1)

Fig. 4. Implementation of the concealable memristive PUF.

(A) The illustrated timeline of a PUF chip from manufacturing to practical use. Traditional PUF and concealable PUF are compared. The line shown in blue indicates that the PUF is in secure mode so that an attacker cannot obtain meaningful data with either invasive or noninvasive attack methods. When receiving legal access requests, the concealable PUF recovers its data for readout and then conceals them again when the readout is completed. (B) The implementation and demonstration of a concealable memristive PUF. Readout mode and secure mode can be easily achieved by RESET and SET memristors with one pulse, respectively. Consecutive concealing and recovery of 16 × 16 data from a memristor array is presented. 1 and 0 are shown in white and black, respectively. (C) The change in BER with incremental concealing-recovery cycles. TMV3 and masking techniques are used here to prevent the PUF from producing error bits in readout mode.

Here, I_n,m is the readout current from the memristor located in the nth row and mth column of the array. I_ref is the reference current. P_n,m is the correspondingly generated PUF bit. If the memristor has a higher (or lower) conductance value than the reference, then it has a value of 1 (or 0) for the PUF. To ensure unbiased data, a search scheme is developed to determine the reference value so that it is very close to the median of the conductance distribution (see Materials and Methods for the details). In this way, the PUF keys have a close-to-0.5 uniformity (e.g., the average is 0.503) and pass the National Institute of Standards and Technology (NIST) test (fig. S7A and table S1). In addition, the notable D2D variation leads to a highly random conductance distribution as the filaments in each memristor device are formed stochastically and independently, which also guarantees the excellent diffusion and uniqueness of the proposed PUF (figs. S7B and S8). The average of the diffusion and the uniqueness is 49.9 and 50.5%, respectively.

After being initialized, the PUF chip is sold and can be invoked to prove the legal identity for its owner. However, the PUF chip could be maliciously attacked at some points. For a traditional unconcealable PUF, if attackers have unhindered access to the chip, they could steal the PUF information with a certain analysis method. This will induce terrible results, as the attackers can easily impersonate the owner without any awareness. In contrast, our concealable PUF whose data are normally hidden can provide effective protection against such attacks.

Figure 4B illustrates the operation scheme of our concealable PUF. Data can be concealed and recovered efficiently with one SET and RESET pulse, respectively, because of the introduced C2C correlation. This scheme allows us to hide data into pure 1 in theory by programming memristors into higher conductance states and reproduce data by programming memristors back to the origin states. However, it is possible for some memristors with minor changes in their conductance values to produce 0 in the secure mode. Note that the successful concealment of most of the data is enough to prohibit the PUF from producing meaningful information in any actual applications, and regenerating the original data based on this highly incomplete information is impossible. In addition, it is also possible for some memristors whose conductance values are close to the reference to produce error PUF bits after recovery. To improve the reliability, temporal majority voting (TMV) and masking techniques are used, as illustrated in fig. S9A (see Materials and Methods for the technique details). Figure 4C and fig. S9B show the change in BER with incremental concealing/recovery cycles. With TMV3 and masking techniques, the data can be reliably recovered, as no error bit is found in readout mode. Meanwhile, the BER approaches 30% in secure mode, which means that the produced data cannot be used in practice for correct identification. The prices (e.g., power consumption and delay) of performing a read operation with a TMVx postprocess circuit are summarized in table S2. The adoption of TMV3 results in a 3× power consumption and delay, which mainly consumed by the SA working for three clock periods, but leads to a substantial reduction in BER. Furthermore, the use of TMV3 is much more efficient and effective than using a tradition error correction code circuit (45).

Attack resistance analysis

If a malicious party gets ahold of the PUF chip, then he or she may access the hidden data by means of microprobes and try recovering the original data by either brute force attack or correlation analysis attack. This possible situation makes it necessary to evaluate the security of our concealable PUF based on the assumption that the hidden data are available to attackers through invasive attacks. The box plot in Fig. 5A shows the conditional probability of a valid bit v_i being a under the precondition that its corresponding hidden value h_i being b [i.e., Pr (v_i = a | h_i = b)]. As both h_i and v_i are binary values, a and b equal 0 or 1. Furthermore, the conditional min-entropy can measure the min-entropy preserved in the valid data {v_i} after all hidden data {h_i} have been known by an attacker. For example, the conditional min-entropy equal to 0 means that the attacker can easily figure out {v_i} based on {h_i}, and the conditional min-entropy equal to 1 means that {h_i} do not leak any information about {v_i}. The conditional min-entropy can be calculated by the following equation (46)

$$H_{\infty }(v_i \mid h_i)=-\text{log}\{E_{b\leftarrow h_i}[{\text{max}}_a\text{Pr}(v_i=a \mid h_i=b)]\}$$ (2)

Fig. 5. Attack resistance analysis of the concealable memristive PUF.

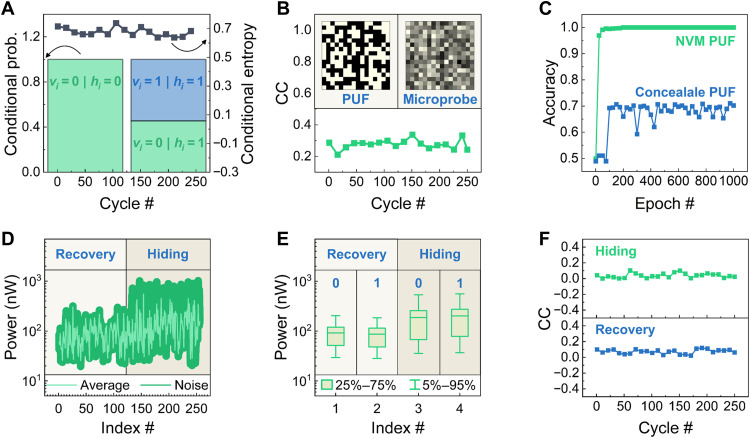
(A) The conditional probability (the height of the box, corresponding to the left y axis) of the situation indicated by the label in box and the change of the conditional min-entropy (point plot, corresponding to the right y axis) with incremental concealing-recovery cycles. v_i is the ith PUF bit, and h_i is the value after the bit is concealed. (B) The change in CC between binary PUF data (top left inset) and analog resistance values measured in secure mode (top right inset). (C) The change of prediction accuracy with incremental training epoch for traditional NVM PUF, whose data are steadily stored by distinct high and low conductance states, and the developed concealable PUF. (D) The power track during the recovery and concealing of a 128-bit ID. The result is collected from multiple concealing-recovery cycles (dark green), and only the power consumption in the memristor array is considered. (E) The distribution of power consumption in the memristor array for the recovery and hiding of one PUF bit. (F) The change in CCs between power consumption and PUF bits in the recovery (top) and concealing (bottom) processes.

The conditional min-entropy fluctuates about 0.7 with incremental concealing-recovery cycles, indicating that if an attacker has access to the hidden data and plans to break the PUF with 128-bit key length in a brute-force way, then the probability of him successfully hitting the correct key is less than 2^{–128 × 0.7} = 10⁻²⁷. With a supercomputer whose processing speed exceeds 2 × 10⁵ TFlop/s, it would take hundreds of years to go through all the probabilities, which is highly impractical in reality.

The assumption also allows attackers to perform attacks in an analog way by analyzing the correlation between valid PUF data and the conductance distribution in secure mode (Fig. 5B). The conductance pattern obtained from secure mode by microprobes is disordered, and CC is less than 0.4 in 250 cycles. Multilayer fully connected perceptron (MLP) can capture the slight correlation between challenges and responses of a PUF and was demonstrated effective to break a complex PUF (47, 48). Therefore, to further demonstrate the resistance against machine learning attack, we use a MLP to perform such an attack on both our concealable PUF and a traditional nonvolatile memory (NVM) PUF (see Materials and Methods for the neural network details). Figure 5C shows that the trained neural network predicts recovered PUF data with 70% accuracy, which is far from enough to break our PUF. In contrast, the neural network can be correctly trained to break traditional NVM PUFs, where a correlation is found between valid PUF data and the conductance values.

Side-channel attack analyzes the side-channel behavior (e.g., power consumption) of a security chip to break the internal PUF in a noninvasive way. However, the intrinsic noise in a memristor array is a natural defense against this form of attack and is fully exploited in this work. Figure 5D shows the power track for the memristor array during the recovery and concealing of a 128-bit PUF key in different cycles, where large noise can be observed because of the variation in memristors’ conductance values. The power consumption for the recovery and concealing of one PUF bit varies within a fairly wide range, and negligible correlation is found such that no information is leaked during these processes, as shown in Fig. 5 (E and F). In addition, we develop a method to further exploit this intrinsic noise by injecting it into the side channel of the whole system to avoid attackers starting side-channel attacks from the CMOS part (fig. S10). When the security chip receives an encryption or identification instruction, the PUF keys stored in the concealable PUF are recovered, read out, and then concealed again. In general, attacks can be carried out when those PUF keys are written into registers, and the system performs identification or encryption algorithms with pure CMOS circuits. However, by holding the read voltage of the PUF module, the variation in the memristor’s conductance value leads to a noisy power signal detected from an external node, and thus, the original regularity is completely submerged. In this way, the inherent uncertainty of the concealable PUF is exploited to provide excellent resistance against side-channel attack for security chips without extra circuit overhead.

DISCUSSION

The successful demonstration of the concealable PUF leads to tremendous immunity against prevailing attacks, and the utilization of the special memristive features avoids onerous circuit design. Important metrics of the proposed memristive PUF are summarized and compared to different PUF devices in table S3. Overall speaking, our memristive PUF shows considerable advantages due to the high integration density and intrinsic variation of our memristor devices, as well as the PUF design method. Furthermore, our concealable PUF is implemented in integrated system level with a memristive PUF chip and on-chip read/control circuits, which guarantees more credible, valuable, and convincing results. Besides, compared with the previous works, our work makes a breakthrough by achieving efficient, effective, and repeatable concealing and recovery of PUF data.

We further study and analyze the stability of the concealable PUF. First, temperature stability is an important metric for a PUF system. To analyze this, the PUF system is tested at high temperature up to 100°C, and the resistance distribution is found moving toward lower values (fig. S11A). This movement leads to a mismatch between the preset reference value and the changed resistance values, and the BER increases to 4.5% at 100°C (fig. S11B). On the other hand, the change of temperature has neglected impact on the PUF concealability, as the BER for secure mode remains close to 50% at all cases. To minimize the effect of temperature (i.e., to improve the temperature stability), a median detector circuit can be adopted to generate temperature-dependent reference (49). Furthermore, the PUF stability against aging can be evaluated by its retention and duration. In this work, we verify that the PUF can be correctly recovered 16 hours after being concealed and demonstrate the PUF having 0% BER during the first 250 switching cycles. The C2C variation of our memristor device could result in the occurrence of error bits if the cycle number keeps increasing because of the change of the SET/RESET balanced condition. Further enhancing the stability of the concealable PUF by improving the uniformity of the memristor device and adopting postprocessing circuit will solve this issue.

In summary, we have designed a concealable memristive PUF and demonstrated it with an integrated PUF system. The correlated filamentary switching found in an HfO_x-based memristor is fully exploited to realize the concealing and recovery of PUF in an efficient way. An innovative filamentary switching model is also studied and verified with KMC method. The reliability of the PUF can be improved to achieve zero BER for data recovery and successful hiding of 70% information. This concealable feature, combined with the intrinsic noise in memristor arrays, enables the PUF to effectively resist both invasive and noninvasive attacks, which are the major threats to modern hardware security. Consequently, the concealable PUF provides a creditable solution to the root of trust for IoT devices and is the essential primitive in implementing various security systems with enhanced security and minimum circuit overhead.

MATERIALS AND METHODS

PUF chip and PUF system

The PUF chip contains an 8-kb memristor array (i.e., 64 rows and 128 columns), taking the typical one transistor–one memristor unit as the basic PUF unit. The selected transistor has a width of 1 μm and a length of 0.5 μm, and the size of the memristor is 0.5 μm by 0.5 μm. The memristor uses a TiN/TaO_x/HfO_x/TiN material stack and is integrated between M4 and M5 (fig. S1A). Furthermore, fig. S1B shows the top view of the fabricated PUF chip and layout details. The chip is fabricated with standard 130-nm CMOS technology and takes up 427 μm by 352 μm in total.

The PUF system relies on FPGA to configure the registers of the digital-to-analog converter (DAC) and PUF chip to realize the programming of memristors with controllable pulse conditions and addresses. FPGA also implements important functions for the PUF system. (i) FPGA preprocesses the received challenge, which is originally the sequence number of PUF keys and ultimately decodes it into the addresses of arrayed memristors. For example, if the challenge is 1, then FPGA configures the row address as 0x00 and the column address sweeping from 0x00 to 0x80. (ii) FPGA implements a search algorithm for the reference and postprocessing techniques such as TMV and masking. (iii) The FPGA implements PUF generation, concealing, recovery, and readout functions by sending corresponding operation instructions (e.g., FORMING, SET, RESET, and READ) to specific memristors.

Calculation method for C2C correlation and correlation loss

To evaluate the correlated filamentary switching characteristic of our HfO_x-based memristor, 1024 memristors are consecutively SET and RESET for 500 cycles. The voltage condition for SET is V_WL = 2.0 V, V_BL = 2.2 V, and V_SL is grounded; the voltage condition for RESET is V_WL = 4.0 V, V_SL = 3.6 V, and V_BL is grounded. After the nth RESET, the conductance distribution is recoded as {G^R}_n, and the CCs between {G^R} are calculated by the following equation to obtain Fig. 3A

$$\mathrm{\rho }=\frac{1}{N-1}{\displaystyle {\sum }_{i=1}^N}\left(\frac{A_i-{\mathrm{\mu }}_A}{{\mathrm{\sigma }}_A}\right)\left(\frac{B_i-{\mathrm{\mu }}_B}{{\mathrm{\sigma }}_B}\right)$$ (3)

Here, A and B are the input sequences with lengths equal to N (e.g., {G^R}₅₀₀ and {G^R}). μ and σ are the mean value and SD of the sequence, respectively. Similarly, the conductance distribution after the nth SET is recoded as {G^S}_n, and the CCs are calculated in the same way to obtain Fig. 3B.

To estimate the correlation loss, which is defined as 1 minus the CC, {G^R}₁ and {G^R}₂₀ are input into the function to obtain Fig. 3D. {G^R}₁ and {G^S}_i, where i ranges from 1 to 20, are input into the function to obtain Fig. 3E.

KMC simulation

The KMC simulation includes two phases, namely, the forming phase and cycling phase, to simulate the Vo behavior in the HfO_x layer and to support our proposed model. To generate an event (i.e., to refresh the Vo distribution), the electric potential distribution, current density distribution, thermal distribution, and Vo generation/migration/recombination probabilities are calculated in sequence, and a random number is generated to determine which event takes place (50). Specifically, the electric potential and current distributions are calculated using Kirchhoff laws; the thermal distribution is solved by Fourier’s heat conductance equation; and the probabilities for events are estimated with the electric field modified Arrhenius equation. After completing FORMING and RESET, those Vo that form direct conductive paths with the cathode are defined as resident Vo, and those Vo in the gap are defined as dynamic Vo.

We first construct a CF with random morphology and 20 dynamic Vo in the gap. Then, a RESET electric field is applied to the device, and the average consumed times for the recombination of each Vo are recorded to obtain fig. S4. The time taken up with each happened event is estimated as follows

$$t=-\frac{\text{log}(r)}{f \times P_{\text{sum}}}$$ (4)

Here, r is a uniformly distributed random number in the interval (0,1). f is the atomic vibration frequency. P_sum is the sum of the probabilities for all possible events.

In the forming phase, Vo gradually accumulates from scratch to reach a preset target for the conductance value. In each switching cycle, a SET or RESET operation is defined to include a fixed number of events N (e.g., the N for SET and RESET are 200 in this experiment). After each operation is completed, the updated Vo distribution is recorded, and the resident part is highlighted in white to obtain figs. S5 and S6.

Determination of the on-chip reference

The reference is supplied by an on-chip voltage-controlled current source, which can be precisely adjusted by configuring corresponding registers. The determination of the reference depends on the conductance distribution obtained after the first RESET to achieve uniform random numbers. A search loop is designed with FPGA as follows: (i) Set up an initial value for the reference current and the expected range of the uniformity (e.g., 50% ± σ); (ii) read out PUF keys and calculate the uniformity; (iii) if the ratio is in the preset range, then stop the iteration as the current reference value is very close to the median of the distribution; otherwise, if the ratio is higher (or lower) than the required value, increase (or decrease) the reference current and repeat step ii.

TMV and masking techniques

The TMVx technique uses x memristors to represent one PUF bit (fig. S7A) (51). In the PUF enrollment stage, x PUF bits are separately generated from x neighboring memristors. The PUF bit generated from the first memristor is XOR with all these bits to generate helpful data. In the future readout stage, x PUF bits are read out from these memristors again, and some bits could flip because of inevitable variation. The bits are bitwise XOR with the help data, and the majority in the results is produced as the PUF response.

To implement the masking technique, PUF bits are read out multiple times in the enrollment stage. Those bits with a high error rate (e.g., 1% in this work) are masked and thus do not contribute to the PUF. Specifically, in this work, the masking technique is performed on the basis of the TMV technique.

Neural network for correlation analysis attack

We use a 16 × 200 × 1 multilayer perceptron network with a sigmoid activation function to implement the correlation analysis attack. The network is first trained with 102,400 groups of experimental data. Each group of data contains an analog resistance value and a corresponding PUF bit. The resistance value is converted into a digital value with 16-bit length and then input into the network, and the PUF bit is the target for the network training. The backpropagation algorithm is used in this training process. After the training is completed, another 12,800 groups of data are used as the test set to evaluate the prediction accuracy.

Supplementary Materials

This PDF file includes:

Figs. S1 to S11

Tables S1 to S3

References