Conventional finite element models estimate the strength of metastatic human vertebrae despite alterations of the bone’s tissue and structure

Abstract

Introduction:

Pathologic vertebral fractures are a major clinical concern in the management of cancer patients with metastatic spine disease. These fractures are a direct consequence of the effect of bone metastases on the anatomy and structure of the vertebral bone. The goals of this study were twofold. First, we evaluated the effect of lytic, blastic and mixed (both lytic and blastic) metastases on the bone structure, on its material properties, and on the overall vertebral strength. Second, we tested the ability of bone mineral content (BMC) measurements and standard FE methodologies to predict the strength of real metastatic vertebral bodies.

Methods:

Fifty-seven vertebral bodies from eleven cadaver spines containing lytic, blastic, and mixed metastatic lesions from donors with breast, esophageal, kidney, lung, or prostate cancer were scanned using micro-computed tomography (μCT). Based on radiographic review, twelve vertebrae were selected for nanoindentation testing, while the remaining forty-five vertebrae were used for assessing their compressive strength. The μCT reconstruction was exploited to measure the vertebral BMC and to establish two finite element models. 1) a micro finite element (μFE) model derived at an image resolution of 24.5 μm and 2) homogenized FE (hFE) model derived at a resolution of 0.98 mm. Statistical analyses were conducted to measure the effect of the bone metastases on BV/TV, indentation modulus (Eit), ratio of plastic/total work (WPl/Wtot), and in vitro vertebral strength (Fexp). The predictive value of BMC, μFE stiffness, and hFE strength were evaluated against the in vitro measurements.

Results:

Blastic vertebral bodies exhibit significantly higher BV/TV compared to the mixed (p = 0.0205) and lytic (p = 0.0216) vertebral bodies. No significant differences were found between lytic and mixed vertebrae (p = 0.7584). Blastic bone tissue exhibited a 5.8% lower median Eit (p < 0.001) and a 3.3% lower median Wpl/ Wtot (p < 0.001) compared to non-involved bone tissue. No significant differences were measured between lytic and non-involved bone tissues. Fexp ranged from 1.9 to 13.8 kN, was strongly associated with hFE strength (R2=0.78, p < 0.001) and moderately associated with BMC (R2=0.66, p < 0.001) and μFE stiffness (R2=0.66, p < 0.001), independently of the lesion type.

Discussion:

Our findings show that tumour-induced osteoblastic metastases lead to slightly, but significantly lower bone tissue properties compared to controls, while osteolytic lesions appear to have a negligible impact. These effects may be attributed to the lower mineralization and woven nature of bone forming in blastic lesions whilst the material properties of bone in osteolytic vertebrae appeared little changed. The moderate association between BMC- and FE-based predictions to fracture strength suggest that vertebral strength is affected by the changes of bone mass induced by the metastatic lesions, rather than altered tissue properties. In a broader context, standard hFE approaches generated from CTs at clinical resolution are robust to the lesion type when predicting vertebral strength. These findings open the door for the development of FE-based prediction tools that overcomes the limitations of BMC in accounting for shape and size of the metastatic lesions. Such tools may help clinicians to decide whether a patient needs the prophylactic fixation of an impending fracture.

1. Introduction

Cancer forms a major cause of morbidity and mortality across the world, with an estimated 18.1 million new cases and 9.6 million cancer-related deaths in 2018 [1]. Recent improvements in cancer treatment have prolonged the lives of many patients, leading to a large number of patients being at risk of developing bone metastases at advanced stages of the disease [2]. The spine is one of the most frequent site for bone metastases [3,4]. Bone metastases are categorized depending on how they interfere with the normal bone remodeling. Lytic lesions are characterized by the rarefaction of the bone network and the creation of lytic foci, while blastic lesions consist in the uncontrolled formation of immature and poor quality bone. A mixed metastatic vertebra would present both lytic and blastic phenotypes [5,6].

Pathological vertebral fractures (PVF), caused when the lesioned vertebra can no longer sustain physiological loads [7–10], are an integral part of spinal adverse events and occur in 15–20% of patients with spinal bone metastases [11]. PVF cause pain and immobility [12], resulting in severe impairment of quality of life, increased health costs [4,13,14], and are directly associated with significant shortening of the patient’s survival [12,15]. Once fractured, further collapse of the vertebral body may cause loss of vertebral height, kyphoscoliosis and restrictive lung disease [16,17]. The most dreaded complication associated with PVF is metastatic epidural spinal cord compression, which can cause paraplegia or quadriplegia. Systemic therapy and local radiation may halt tumour progression, but they do not restore the strength of the diseased vertebra. In fact, radiotherapy is known to increase fracture risk [18].

The impact of spinal metastasis on the anatomic integrity of the vertebral column can be imaged with MRI and CT [17,19–24]. Altered geometry, destruction of the pedicles, pain, age, anatomic location, lesion type, activity levels, radiographic alignment, previous vertebral body collapses and the application of radiotherapy have been identified as predictors of fracture risk [25]. Unfortunately, the implications on the stability of the spinal column and its risk to undergo catastrophic failure have been difficult to quantify with any kind of precision [16,26–28]. The Fracture Risk Assessment Tool (FRAX) uses demographic information such as age, vertebral height, prior fracture, and BMD to predict risk of fracture [29]. FRAX demonstrated limited fracture prediction in breast [30] and prostate cancer cohorts [31,32]. The spinal instability neoplastic score (SINS) was developed specifically for patients with spinal bone metastases [33]. It categorizes PVF risk based on vertebral level, pain, lesion, bone quality, radiographic alignment, vertebral body collapse and postero-lateral spinal element involvement. However, the reproducibility of its imaging components is poor [27]. When assessed by members of the Spinal Oncology Study Group, which developed SINS, kappa scores for inter-observer agreement were (0.244, 0.456, 0.462, and 0.492) for bone quality, alignment, vertebral body collapse, and postero-lateral involvement, respectively. Hence, although widely used clinically to predict the degree of spinal instability, its prognostic utility for predicting PVF [18,34,35] remains controversial [36,37]. It is therefore imperative that clinicians are provided with a reliable tool allowing to predict the risk of PVF in patients with metastatic spine disease in order to induce the appropriate treatment.

In silico (virtual) tests via finite element (FE) models are increasingly used in orthopedic research. Depending on the resolution of the available CT-images, two distinct FE approaches can be utilized. At high resolutions, one approach is to establish a μFE model by first segmenting the bone voxels from an image followed by their direct conversion into hexahedral finite elements. This approach explicitly accounts for the bone micro-structure and is therefore especially interesting to simulate the behavior of pathological bony architectures. The main drawback of μFE is that such simulations quickly lead to models with several millions of degrees of freedom, enforcing the use of specialised FE solvers and high-performance computing systems. Furthermore, the high-resolution imaging techniques required for this type of simulation is currently limited to the peripheral skeleton for in vivo applications. Nevertheless, μFE models are considered today’s gold standard for in silico stiffness estimation [38,39]. A more clinically relevant approach is the homogenized finite element (hFE) model, where the element size is orders of magnitude larger than the underlying micro-structure. Each hFE element implicitly accounts for underlying bone micro-structure by scaling its mechanical properties to the surrounding mixture of bone, bone marrow and background [40,41]. hFE models have gained substantial interest in clinics, as they can be directly generated from clinical CT data, are easily solved on standard desktop computers, and were shown to predict fracture risk in cohort studies [42,43].

FE models provided unique insights into the effect of a range of simulated osteolytic defects on the failure strength of cadaver vertebra [44–49]. In recent in vivo studies, clinical CT based hFE models were even used to evaluate the strength of lytic vertebrae [50,51]. However, as encouraging as these studies are, there exists a number of caveats before clinical application. For instance, up to 20% of the breast cancer patients present blastic or mixed lesions, not just lytic ones [52]. While metastases impact the bone architecture, they likely affect its tissue properties as well [53,54]. Whether FE models can accurately predict the strength of any metastatic vertebrae has yet to be verified.

This study first investigated the effect of bone metastases (lytic, blastic or mixed) on the vertebral structure, the bone tissue properties, and on the overall vertebral strength. Second, we tested the ability of bone mineral content (BMC) measurements and standard FE methodologies to predict the strength of metastatic vertebral bodies. For this purpose, 57 thoracic and lumbar cadaver vertebral bodies obtained from 11 donors with prostate, breast, kidney, lung and esophageal primary tumours were scanned with μCT, separated in two sub groups with 12 samples to be processed for nanoindentation and 45 samples for in vitro compression tests. Fig. 1 provides a graphical overview of the study.

Fig. 1.

Study overview. Fifty-seven metastatic vertebral bodies (A) were scanned with μCT (B). Based on CT images, metastatic regions were identified (C). Nanoindentation measurements (D) were performed on a subset of 12 samples. The remaining 45 samples were compressed to failure in the laboratory with a testing setup allowing the free collapse of the vertebral body thanks to a ball joint (E). The image data from the same sample subset was processed to generate micro finite element models (F) and, after coarsening to clinical resolution, homogenized finite element models (G). Finally, the micro-mechanical parameters were analysed and the in silico results were compared to the experimental data. The colours in (C) correspond to non-involved (gray), lytic (red) and blastic (black) areas. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

2. Materials and methods

2.1. Sample selection

Eleven cadaver spines (3 female, 8 male, age 49 y to 71 y, mean 54 y) were obtained through the Anatomy Gifts Registry (Hanover, MD) from donors with known history of solid primary tumours (3 breast, 3 lung, 2 prostate, 2 kidney, 1 esophageal). Donor demographics are presented in Table 1. As part of the exclusion criteria, none of the donors underwent radiotherapy within a 3-month period prior to death. Each spine was inserted into a radiolucent imaging chamber filled with saline solution followed by degassing for 8 h at 37 °C. Using a clinical CT scanner (Aquilion 64, Canon Medical System (formerly Toshiba Medical), USA), all spines were imaged using standard spine imaging protocol (125 kV, 60 ms, ROI: 8.0 in., matrix size: 512, slice thickness: 500 μm, 396 μm in-plane resolution). Based on the radiological review, fifty-seven vertebrae confirmed to present metastatic bone lesions were selected for this study.

Table 1.

Donor demographics summarising primary tumour, age, race (black/caucasian), sex, height and weight.

Spine ID	Primary	Age	Race	Sex	Height [cm]	Weight [kg]
A	Prostate	55	C	M	183	68
B	Prostate	71	C	M	188	68
C	Lung	53	C	M	175	86
D	Breast	59	C	F	170	79
E	Lung	60	B	M	183	82
F	Lung	49	B	M	178	68
G	Esophageal	52	C	M	170	127
H	Breast	60	C	F	165	68
I	Kidney	71	C	M	170	54
J	Kidney	56	C	M	180	79
K	Breast	60	C	F	163	41

2.2. Sample preparation

The spines were first dissected free of all soft tissues. Each selected vertebra was separated from its spine by cutting through the adjacent discs, followed by sectioning of the pedicles in the coronal plane to remove the posterior elements. Once completed, a diamond coated band-saw (Exakt 300, Exakt Technologies, Inc., Germany) was used to section both endplates under constant water irrigation. While doing so, the transverse plane of the vertebral bodies was defined so that the maximal vertebral section height could be generated. This process resulted in plano-parallel vertebral body sections ranging from 12 mm to 25 mm in height. To assess the parallelism of the surfaces, the specimen’s height was measured at four locations (anterior, posterior, left and right) using a mechanical caliper (Mitutoyo 530 (150 mm, 0.01 mm accuracy), Japan). Samples with a difference in height larger than 0.1 mm were polished (LaboPol-20, Struers, Denmark) until inter-measurement differences were less than 0.1 mm.

2.3. Micro CT and metastases classification

Each vertebral section was scanned with μCT (μCT100, Scanco Medical, Switzerland) at 24.5 μm isotropic voxel size (tube voltage: 70 kV, tube current: 200 μA, integration time: 500 ms). High-frequency noise contained in the images was reduced with a Gauss filter (Sigma: 0.8, Support: 1) [55,56] and a custom script (IPL, Scanco Medical, Switzerland) was used to generate a mask separating each vertebra from its background. For each image, the BMC within that mask was computed.

The optimal bone segmentation threshold for each μCT image was computed based on an adaptive threshold algorithm [57,58]. The computed segmentation thresholds of all individual measurements were averaged and the mean value (429 ± 56 mgHA/cm3) was selected to segment all samples. The resulting segmented μCT images were used for the computation of the overall (i.e. cortical + trabecular regions) bone volume fraction (BV/TV) of the samples and for generating the μFE models. Finally, the μCT images were reviewed by three clinicians, an orthopedic surgeon and two radiologists, for the radiographic appearance of the bone. Using a consensus table, each sample was graded as either lytic, blastic or mixed. For each sample, the lesions were only outlined as the definition of the boundaries is delicate. Pixel-wise segmentation of the lesions would not have been possible with a regular thresholding procedure because the gray-value of the metastatic tissue is similar to non-involved bone. A large manual effort or advanced machine learning techniques prone to errors given the small, heterogeneous data-set would have been required. As a consequence, the exact metastatic volumes were not measured.

2.4. Nanoindentations of the metastatic and non-involved bone tissues

Twelve samples, randomly selected to undergo nanoindentation measurements, were further processed using a diamond coated bandsaw to obtain 3 mm thick parallel sections (Exakt 300, EXAKT Technologies, Inc., Germany). Following the procedure described in [59], the sections were infiltrated with methylmethacrylate (MMA). Each embedded section was cut to fit the nanoindenter sample holder and a micro-milling system (Polycut ultra-miller, Reichert-Jung, Germany) was used to ensure the specimen’s parallel surface with respect to the specimen holder. To remove scratches caused by the micro-milling process, the surface was polished (LabPol-5, Streuers, Denmark) with a silicon carbide paper (P4000, Struers, Denmark), finished with a 1 μm diamond paste [60], cleaned in an ultrasonic bath (Type 88,169, Bioblock Scientific AG, Switzerland) for five minutes to ensure that no residue particles remained on the surface and dried at room temperature for 24 h before measurement.

An Ultra Nanoindentation Tester (CSM instruments, Switzerland) was used to perform indentation measurements (Berkovic tip geometry, depth: 1 μm, loading speed: 100 mN/min, unloading speed: 400 mN/ min, holding time: 30 s) [61]. Following the findings by Wolfram et al. [62], thirty-two indentation points were defined on bone trabecule located within each region (lytic, blastic or non-involved), resulting in 787 indentation measurements in total. Within each selected region, eight distinct trabeculae were identified, with four measurements performed in the transverse and four measurements in the axial direction of the trabecula. For both directions, two measurements were performed in the inner region of the trabecula and two in the outer region. For highly blastic regions, these locations could not appropriately be defined, and thus the indentations were evenly spread out over the entire blastic region. For some highly lytic regions, the trabeculae were completely resorbed (e.g. Fig. 3 (A)). In these cases, the nanoindentations were performed in the bone trabeculae surrounding the bone cavity. For each measurement, the indentation modulus (Eit), the elastic (Wel), the plastic (Wpl) and the total indentation work (Wtot) were computed. The fraction Wpl/Wtot can be interpreted as a measure of ductility, low values (towards 0) suggesting a brittle and high values (towards 1) suggesting a ductile material.

Fig. 3.

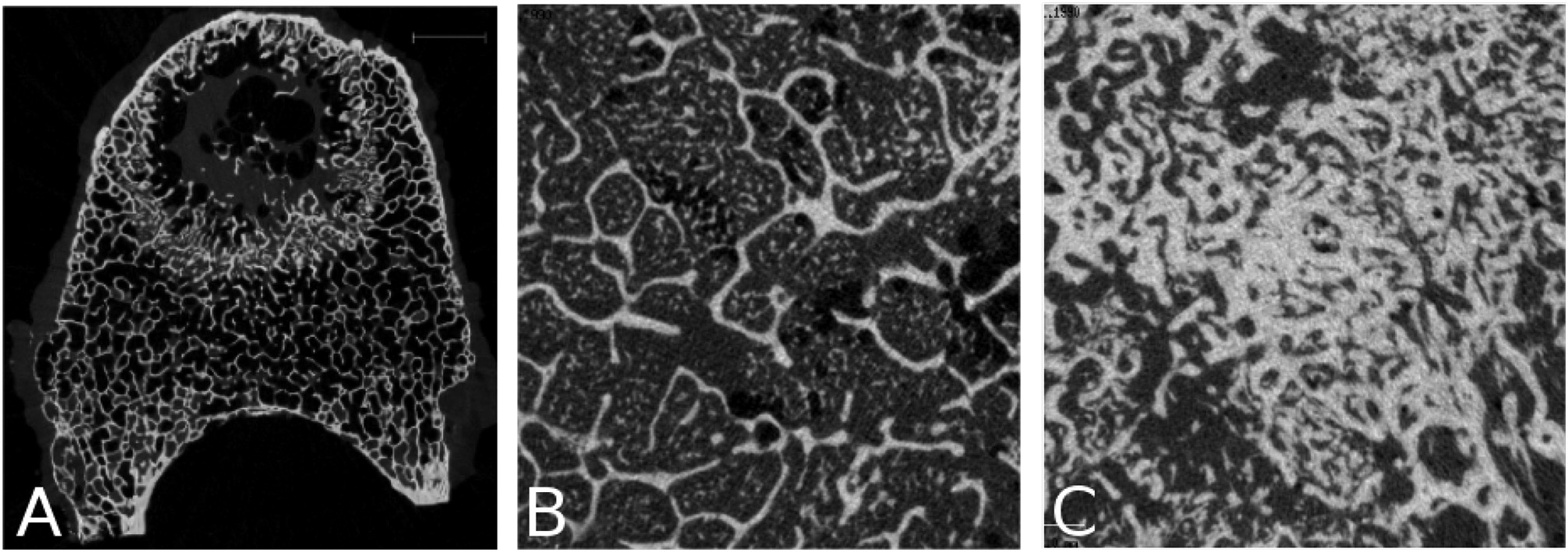
Close-up on the observed alterations. (A) Osteolytic lesions sometimes lead to lytic foci (lung primary, C 209), (B) “islands” of mineralized tissue were often seen in the bone marrow of vertebrae with blastic metastases (prostate primary, B 280), (C) blastic lesions resulted in a very dense trabecular network (prostate primary, A 180).

2.5. Mechanical testing

Prior to mechanical testing, the vertebral levels allocated for mechanical testing (n = 45) were equilibrated in 0.9% NaCl saline solution for one hour at room temperature. Based on the protocol described by Dall’Ara et al. [63], a fracture was induced by compressing the vertebral body between two steel plates mounted on a servo-hydraulic compression system (858 Mini Bionix II, MTS, Eden Prairie, USA). Both steel plates had their contact surfaces sandblasted to prevent the sample from sliding during the compression test. The caudal plate was rigidly fixed to the construct. The cranial plate was mounted to the loading mechanism via a ball joint.

To induce an anterior wedge-shaped fracture, the specimen’s center of mass was computed from the μCT images and digitally shifted anteriorly by a distance equal to 10% of the antero-posterior width of the bottom surface. The resulting position and outer contour of the bottom surface were printed on a sheet of paper and placed on the testing system to allow for the precise positioning of the sample (Fig. 1.E) [63]. The cranial load plate was lowered until a tare load of 25 N was recorded to confirm the contact. A uniaxial displacement was applied at a rate of 5 mm/min [40,55] until failure was registered or the maximum force (15 kN) of the MTS built-in load cell (model: 662.20D-04) was reached. The outcome of the testing procedure was the vertebral strength (Fexp), defined as the maximum measured compressive force.

Seven samples were excluded from the statistical analysis as they could not be fractured because their strength exceeded the limit of the load cell.

2.6. Generation of the linear μFE models

The bone voxels of the segmented μCT images (Section 2.3) were, after removal of non-connected structures, converted into linear eight-node hexahedral finite elements, yielding on average 316 million elements per sample. Young’s modulus was set to 10 GPa and Poisson’s ratio to 0.3 [62].

The nodes of the caudal surface were set as fully constrained. To limit the degrees of freedom of the model, the nodes of the cranial surface were set to allow motion only along the loading direction. The μFE models were solved for stiffness (KμFE) using Parosol [64,65] on a Linux based cluster (16 Intel Xeon E5 cores, 256 GB RAM), resulting in a mean computation time of six hours per sample. The outcome of the μFE models was the in silico sample stiffness (KμFE).

Four samples were excluded from the statistical analysis as they could not be processed due to RAM limitations on our system.

2.7. Generation of the non-linear homogenized FE models

The hFE model generation is based on a method first described by Chevalier et al. [55]. Pahr et al. [66] validated this modelling approach for vertebral bodies with various degrees of osteoporosis using the testing protocol defined by Dall’Ara et al. [63].

First, all negative BMD values in the masked μCT images (Section 2.3) were clipped to zero to prevent negative local BMD values caused by air bubbles. The corrected BMD images were down-sampled to 0.98 mm isotropic voxel size to mimic the resolution of clinical CT images. This voxel size was chosen as it represents a worst-case clinical CT resolution, it shortens the computation times for potential clinical applications and is similar to the 1 mm element size employed by the only FDA-approved clinical use for FEA modelling of vertebral strength (VirtuOst, O.N.Diagnostics Inc., USA, http://ondiagnostics.com). The resulting voxels were converted into eight-node hexahedral finite elements. Each element was assigned a local BV/TV, computed by dividing the element BMD with the mean tissue BMD of the entire volume (BMD_tissue = 684 mgHA/cm³). Each voxel was then assigned a fixed transverse isotropy with the main direction along the cranio-caudal axis of the vertebra (fabric eigenvalues: 1.249, 0.894, 0.894) [55].

The constitutive law and material constants were taken from Pahr et al. [66]. In brief, an anisotropic, time-dependent, BV/TV-based constitutive law was implemented as an Abaqus (V.6.13, Dassault Systems, France) user material (UMAT). The law includes linear elasticity, yielding and plasticity with the accumulation of damage and irreversible strains.

To replicate the experimental boundary conditions, the nodes of the caudal surface were constrained in all directions. The nodes of the cranial surface were kinematically coupled to a virtual ball joint. Loading conditions were prescribed with a uniform axial displacement at a rate of 5 mm/min applied to the ball joint. The models were solved using six 3.2 GHz cores and lasted approximately thirty minutes per simulation. The outcome of the hFE models was a predicted value of the in silico sample strength (FhFE).

2.8. Statistical analysis

All statistical analyses were performed in JMP pro (14, SAS, NC). All reported p values are two-tailed with an alpha level set to 0.05. Univariate statistics were used to summarise the specimen’s demographics, bone properties, indentation properties, measured vertebral strength, and FE predicted vertebral strength. Descriptive statistics were used to test whether 1) the overall BV/TV values, 2) indention parameters (Eit and Wpl/Wtot), and 3) the measured vertebral strength (Fexp), were non-normally distributed.

The sampling of multiple vertebrae per spine for mechanical testing (45 vertebrae from 11 spines) and the selection of multiple indentation sites for each of the additional twelve vertebrae, can introduce noneindependence (clustering) of the data. For example, strength values for vertebrae obtained from the same spine could be correlated due to anatomical and genetic factors. Linear mixed model (LMM) analysis [67] was used to test for the effect of multiple indentation sites, with lesion type entered as a fixed variable, Eit or Wpl/Wtot entered as the outcome variables, and Spine ID (indicating the spine from which the vertebral levels were obtained (Table 1)), set as a random variable.

LMM analysis was similarly applied to test for the effect of selecting multiple vertebrae per spine on the association between 1) BMC, 2) KμFE, and 3) FhFE, entered as fixed effects, with Spine ID entered as a random variable. The measured strength (Fexp), entered as the outcome variable.

Based on the findings of the LMM analysis, Kruskal–Wallis one-way ANOVA was used to test for the effect of bone lesion classification on differences in the indentation parameters, Eit and Wpl/Wtot. Steel-Dwass analysis was used for posthoc comparisons within each grouping. We applied regression analysis to test for the association of 1) BMC, 2) KμFE, 3) FhFE, with the measured strength (Fexp).

3. Results

3.1. Influence of the metastases on the bone structure

Fig. 2 presents axial μCT slices and photographs of typical lytic, mixed, and blastic vertebrae. Additionally, μCT mid-planes and planar projections of all samples are provided as supplementary material. Vertebrae classified as osteolytic generally presented a thinning of the cortex and rarefaction of the trabeculae through the entire vertebra, but focal bone loss (cavities) was also found (Fig. 3 A). Vertebrae classified as blastic were characterized by an overall increased bone density (Figs. 2C, 3C). Local scleroses could also be observed in vertebrae classified as mixed (Fig. 2B). Finally, mineralized tissue was sometimes found in the inter-trabecular space (Fig. 3 B). Descriptive statistics revealed BV/TV to be non-normally distributed (Shapiro-Wilk W test, Osteoblastic: p = 0.0036, Mixed: p = 0.0404, Osteolytic: p = 0.0201). Lesion classification significantly affected the BV/TV values between the lesion groups (Kruskal-Wallis test: χ2 = 12.08, p = 0.0024). Post-test analysis (Steel-Dwass all-pairs test) revealed vertebrae with osteoblastic lesions to exhibit significantly higher BV/TV values compared to vertebrae with mixed (p = 0.0205) and osteolytic (p = 0.0216) lesions. No such statistically significant differences were found between the osteolytic and mixed lesions vertebrae (p = 0.7584).

Fig. 2.

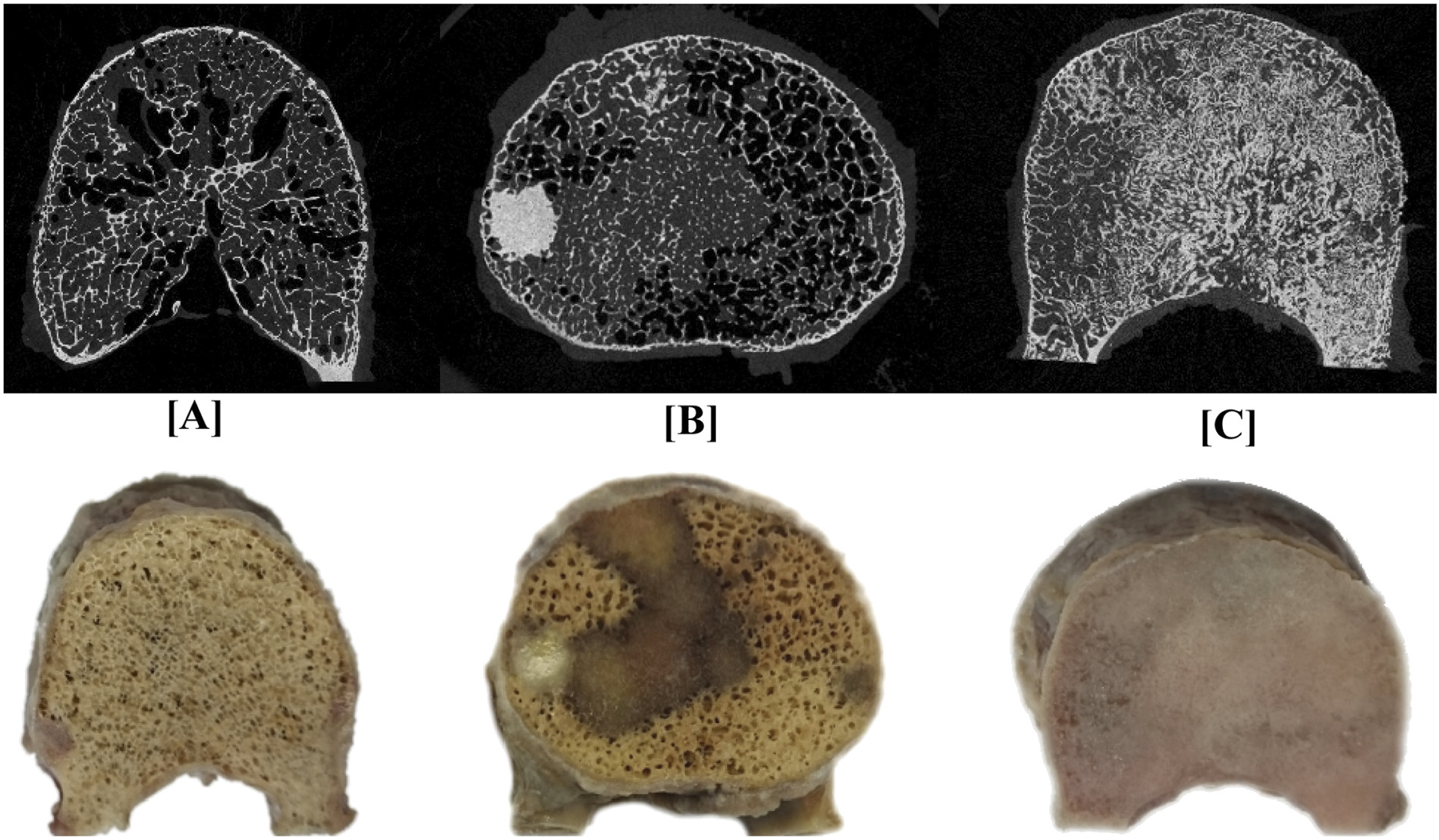
A pictorial illustration of μCT axial images of vertebral bodies containing (A) osteolytic (lung primary, F 250), (B) mixed (breast primary, D 168) and (C) osteoblastic (breast primary, H 217) metastases. The row below provides photograph of the corresponding vertebral bodies.

3.2. Influence of the metastases on the bone tissue properties

A total of 787 indentation points were measured with 328 measurements performed in trabecular bone regions with no radiological evidence of metastatic involvement, 366 measurements in osteoblastic regions, and 93 measurements in osteolytic regions. Table 3 summarizes the type of lesion measured on each sample.

Fig. 4 presents a graphical summary of the distribution of the indentation modulus (Eit) and the ratio of plastic to total work (Wpl/Wtot). Eit and Wpl/Wtot were found to be non-normally distributed (Shapiro-Wilk W test, p < 0.001 respectively), yielding a median (Q1-Q3) of 14.30 (12.42–16.43) GPa for Eit and 0.79 (0.77–0.82) for Wpl/Wtot.

Fig. 4.

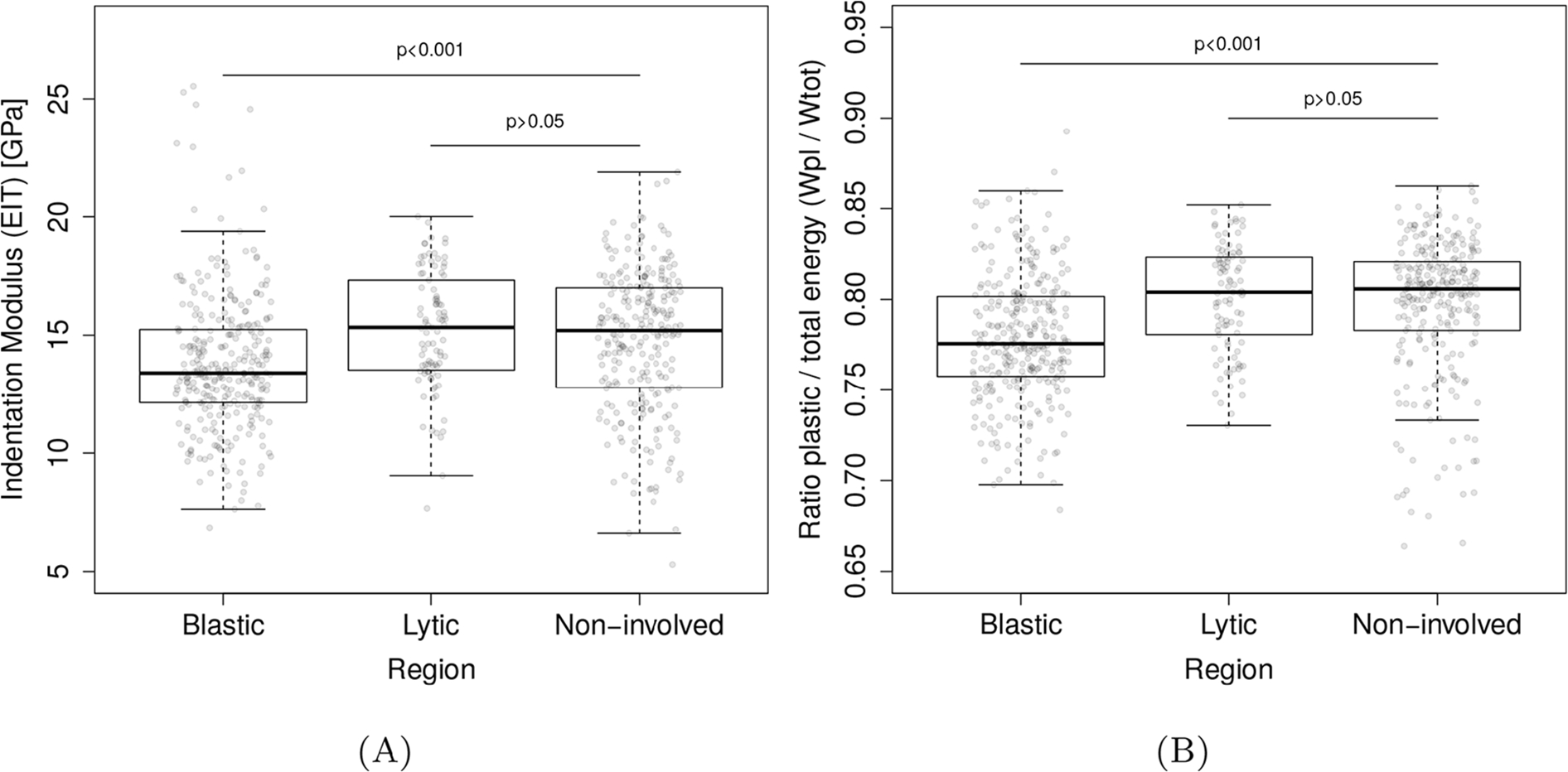
Nanoindentation results per lesion type. For both indentation modulus (Eit) and ratio of total to plastic work (Wpl/Wtot), the blastic bone showed significantly lower values compared of non-involved bone. No such statistical differences were found for similar comparison with osteolytic bone.

LMM analysis revealed Spine ID to have no significant effect on the association between bone lesion type and either Eit (Wald p = 0.063) or Wpl/Wtot (Wald p = 0.058). Kruskal-Wallis test revealed a statistically significant difference between the lesion groups for Eit (χ2 = 35.28, p < 0.001) and for Wpl/Wtot (χ2 = 58.25, p < 0.001). Post-hoc analysis (Steel-Dwass all-pairs test) demonstrated that, compared to non-involved and osteolytic bone tissues, osteoblastic bone tissue exhibited a 5.8% lower median Eit value (P < 0.001) and a 3.3% lower median Wpl/Wtot value (P < 0.001). We found no statistically significant differences for either Eit or Wpl/Wtot between non-involved bone tissue and bone tissue surrounding osteolytic lesions (p = 0.441 and p = 0.7998, respectively).

3.3. Influence of the metastases on the experimental vertebral strength

Fig. 5 presents typical loading curves and the mechanical integrity of the samples based on the lesion group. The corresponding numerical values are summarized in Table 4.

Fig. 5.

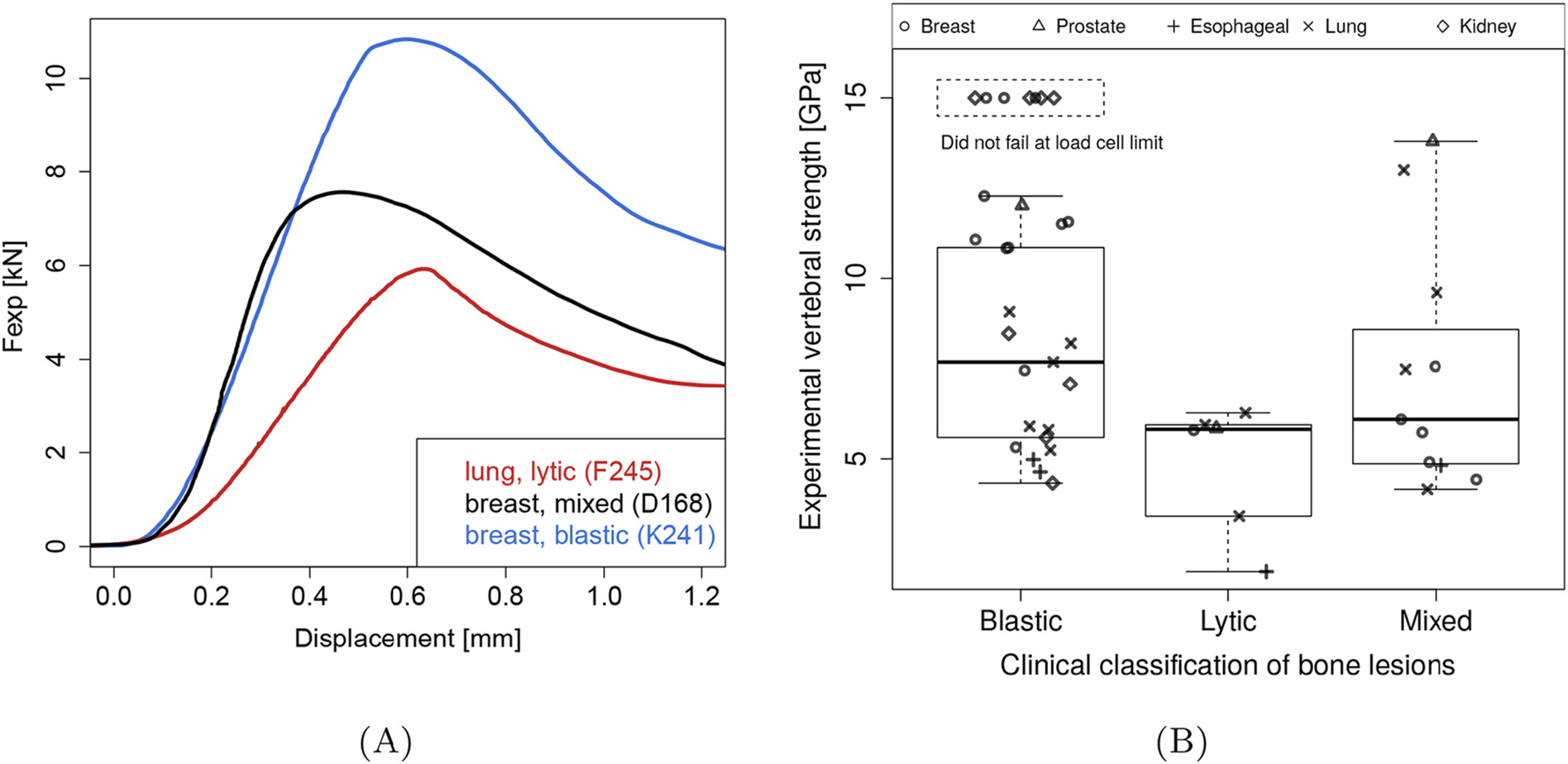
(A) Typical experimental load-displacement curves for lytic, mixed, and blastic vertebral bodies, the number in the legend identifies the samples (Table 4). (B) Vertebral bodies containing osteoblastic metastases showed significantly higher Fexp than those containing mixed or osteolytic lesions.

Table 4.

Overview of the investigated vertebral bodies: ID combines the spine ID and the sample ID where the spine ID specifies the origin vertebral column (Table 1), vertebral level, metastatic lesion type, bone volume ratio (BV/TV), experimental strength (Fexp), μFE stiffness (KμFE), bone mineral content (BMC) and hFE strength (FhFE). Missing entries represent samples that did not fail during experimental testing or μFE simulations that could not be solved due to insufficient RAM on our system (256 GB).

ID	Level	Type	BV/TV	Fexp [kN]	KμFE [kN/mm]	BMC [mgHa]	FhFE [kN]
A180	L1	Blastic	0.36	–	–	13,072.43	27.93
A181	T9	Blastic	0.41	–	–	6664.84	21.63
A183	T10	Blastic	0.44	–	–	7709.67	22.66
A185	L4	Blastic	0.47	–	–	15,242.64	45.51
B280	T11	Blastic	0.23	8.48	59.78	5671.98	13.17
B283	T12	Blastic	0.14	7.08	36.36	3943.31	7.09
B284	T7	Blastic	0.14	4.33	26.02	2290.62	4.63
B286	T10	Blastic	0.16	5.59	40.03	3224.38	6.18
C201	L2	Blastic	0.19	8.21	39.21	4453.95	8.31
C202	T6	Lytic	0.19	6.27	43.81	1698.79	5.66
C203	T10	Mixed	0.20	7.49	47.83	3032.91	8.34
C207	L4	Mixed	0.21	9.61	52.51	4649.90	8.97
C208	T11	Blastic	0.21	7.69	48.37	3591.92	8.80
C212	L5	Mixed	0.27	12.99	42.00	5901.75	14.35
C213	L3	Blastic	0.20	9.08	55.45	3899.27	9.11
D164	T11	Mixed	0.13	4.91	27.91	2395.72	4.74
D168	L3	Mixed	0.15	7.57	50.58	3201.55	6.88
D171	L5	Blastic	0.16	7.46	48.42	3884.66	6.20
D172	T10	Mixed	0.12	4.43	25.79	1849.35	3.82
D175	L1	Lytic	0.14	5.79	33.70	2757.27	4.83
D191	L2	Mixed	0.14	6.09	30.84	3753.34	5.49
E265	L1	Blastic	0.18	5.80	37.36	3758.41	8.78
E266	T12	Blastic	0.19	5.90	43.30	3901.26	9.96
E290	T9	Blastic	0.19	5.24	32.96	2809.90	7.38
F245	L3	Lytic	0.16	5.94	38.06	3712.16	6.60
F246	T10	Mixed	0.13	4.16	32.71	1832.54	4.93
F250	T9	Lytic	0.12	3.42	29.04	1633.02	4.59
G194	L5	Mixed	0.24	13.78	157.33	4603.28	15.41
G195	T5	Lytic	0.23	5.84	83.08	1390.29	5.99
G197	L4	Blastic	0.18	12.01	76.70	4748.03	10.16
H217	L1	Blastic	0.41	–	128.53	6934.06	21.26
H229	L5	Blastic	0.38	–	110.41	7109.02	13.62
H233	L4	Blastic	0.33	11.50	90.87	6336.46	10.95
H234	T9	Mixed	0.25	5.73	49.97	3426.46	8.20
H237	T12	Blastic	0.34	11.56	100.44	6006.08	14.29
H238	T8	Blastic	0.21	5.32	45.91	2888.37	9.69
I225	T11	Lytic	0.09	1.89	21.00	973.10	3.26
J293	L1	Blastic	0.15	4.98	28.59	4413.45	6.60
J294	T10	Blastic	0.13	4.64	30.94	2515.80	5.17
J302	T6	Mixed	0.13	4.82	36.78	1396.17	3.92
K241	L3	Blastic	0.37	10.85	95.82	5576.22	12.22
K269	L1	Blastic	0.38	10.83	85.41	5666.50	13.69
K270	T12	Blastic	0.39	12.27	105.82	4268.17	13.45
K273	L4	Blastic	0.39	–	150.09	4263.83	16.19
K274	T11	Blastic	0.39	11.07	85.41	3971.01	11.78

Fexp was found to be non-normally distributed (Shapiro-Wilk W test p = 0.028) with a median (Q1-Q3) strength value of 5.82 (3.03–6.02) kN for the osteolytic vertebrae, 5.91 (4.72–8.08) kN for the mixed lesions vertebrae and 10.83 (5.85–14.00) kN for osteoblastic vertebrae.

Kruskal-Wallis test revealed a statistically significant difference in Fexp between the lesion groups (χ2 = 9.8, p = 0.0074). Post-test analysis (Steel-Dwass all-pairs test) showed vertebrae with osteoblastic lesions to exhibit higher median Fexp compared to vertebrae containing mixed (86.1%, p = 0.0250) and osteolytic (86.1%, p = 0.0115) lesions. We did not find such significant differences between vertebrae with mixed and osteolytic bone lesions.

3.4. Can BMC and FEA accurately predict vertebral strength despite the metastases?

Fig. 6 illustrates the association of Fexp with the specimen’s (a) BMC, (b) KμFE, and (c) FhFE. LMM analysis revealed spine ID to have no significant effect on the strength of the association MC significant effect on the strength of the association (p = 0.090), KμFE (p = 0.225) and FhFE (p = 0.161).

Fig. 6.

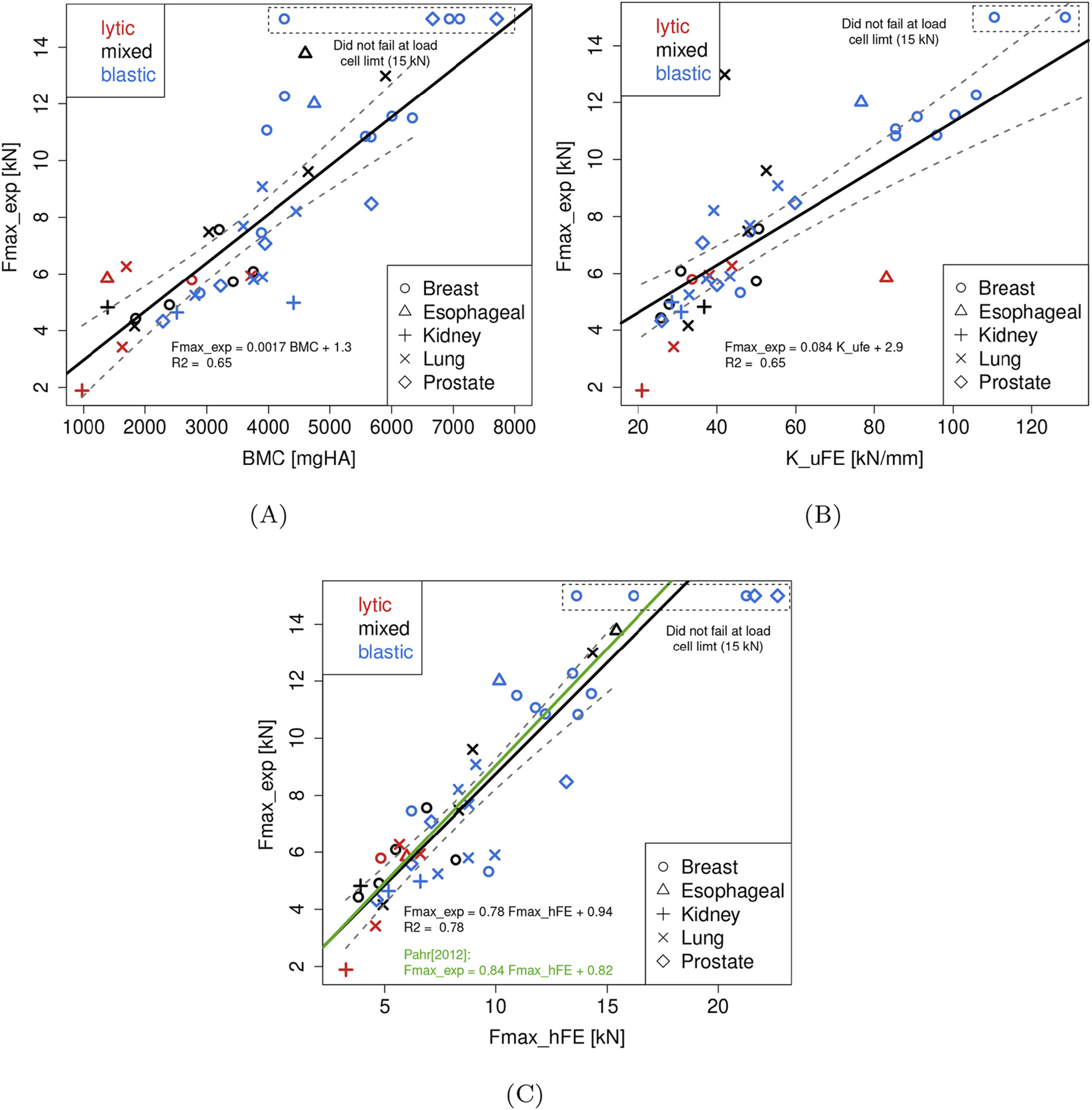
Linear relationships established between the in vitro strength (Fexp) and (A) bone mineral content (BMC), (B) μFE stiffness (KμFE), and (C) hFE strength (FhFE). The black line represents the linear regression through all data points specified by the equation given within the individual plots. The gray band around the regression lines represent the 95% confidence interval. Additionally in (B), the green line represents the linear regression reported by [66] for cancer-free vertebrae. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Ordinary least regression analysis established that BMC values were moderately associated with Fexp (F(1, 36) = 131.33, p < 0.001) with the variation in BMC explaining 66% of the variation in Fexp (Fig. 6 (a)). μFE predicted stiffness (KμFE) values were moderately associated with Fexp ((F(1, 36) = 70.174, p < 0.001) with the variation in KμFE explaining 66% of the variation in Fexp (Fig. 6 (b)). By comparison, hFE predicted strength (FhFE) values were strongly associated with Fexp (F(1, 36) = 131.32, p < 0.001) with the variation in FhFE explaining 78% of the variation in Fexp (Fig. 6 (c)). The linear regressions established between Fexp and BMC, KμFE, and FhFE for each lesion group is presented Table 2. These numbers tend to confirm the robustness of the hFE approach in predicting Fexp. Regression analysis for BMC and μFE models showed lesion phenotype specific differences in the model’s prediction strength (Table 4), with both variables showing a weak association for osteolytic vertebrae. Interpretation of the models for the osteolytic and mixed lesion phenotype however has to be done with care due to the relatively low number of specimens in both groups as compared to the osteoblastic group.

Table 2.

Results of the linear regressions between vertebral strength (Fexp), bone mineral content (BMC), μFE stiffness (KμFE), and hFE strength (FhFE) for all, lytic, blastic, and mixed samples. Based on these numbers, hFE models seem to predict vertebral strength better than the other methods and is more robust to the type of lesion.

Variable	B	SE	β	95% CI for B	R2	P
Fmax_hFE
Intercept	0.938	0.72		−0.292 – 2.169
F_hFE (kN)	0.781	0.078		0.641 – 0.919	0.78	<0.001
Clinical classification with Fmax_hFE
Intercept	1.205	0.72		−0.273 – 2.68
F_hFE	0.779	0.078	0.883	0.620 – 0.937	0.77	<.0001
Lesion classification
Blastic	−0.487	0.396	0.098	−1.293 – 0.319		0.228
Mixed	−0.094	0.479	0.016	−0.879 – 0.806		0.947
Lytic	−0.241	0.512	0.041	−1.283 – 0.319		0.641
K_μFE
Intercept	2.945			1.723 – 4.166
K_μFE (kN/mm)	0.08	0.010		0.063 – 0.104	0.66	<.0001
Clinical classification with K_μFE
Intercept	3.540	0.580		2.359 – 4.727		<.0001
K_μFE	0.082	0.009	0.797	0.063 – 0.100	0.73	<.0001
Lesion classification					0.76	0.0146
Blastic	−0.225	0.426	−0.045	−1.093 – 0.643		0.602
Mixed	−1.158	0.487	−0.111	−1.759 – 0.412		0.2158
Lytic	−1.667	0.533	−0.286	−2.702 – 0.633		0.0025
BMC with K_μFE
Intercept		0.531		−0.539 – 1.618
K_μFE	0.0542	0.008	0.527	0.0382 – 0.0702		<.0001
BMC	0.5395	0.0002	0.5257	0.0008 – 0.0014		<.0001

4. Discussion

The first aim of this study was to employ μCT, nanoindentations, and compression tests to evaluate the impact of tumour-induced bone metastases on the structure, tissue-level, and organ-level mechanical properties of human vertebral bone obtained from donors with solid tumours. The second aim was to evaluate the ability of BMC and CT-based FE models, generated at high and clinical resolutions, to predict the measured compressive strength of pathologic cadaver vertebrae containing osteolytic, osteoblastic and mixed bone lesions.

4.1. Effect of the metastases on the bone structure and tissue

Osteolytic vertebrae (lung, kidney, or breast cancer) exhibited the lowest BV/TV of the three lesion groups, indicative of the lesion mediated rarefaction of the vertebral bone network. As reported in the literature, infiltration of vertebral bone with osteolytic bone metastasis resulted in the degradation of the trabecular bone microarchitecture, the creation of osteolytic foci within this network, and destruction of a significant portion of the cortex Hojjat and Whyne [68]; Nazarian et al. [53]; Tamada et al. [54].

At the tissue level, osteolytic metastases were reported to affect the organisation of collagen fibers [69–71], mineral phase and crystal size [70,72], and to degrade collagen cross-linkage [73] in a murine model, without impacting the indentation modulus and hardness compared to healthy bone [69,73]. These results are surprising because such alterations would be expected to affect bone tissue material properties. Yet, using human samples, we found no significant difference between lytic and non-involved tissue in terms of Eit and Wpl/Wtot ratio. These findings suggest that the reduced strength of osteolytic vertebrae is predominantly due to the rarefaction of the bone architecture (lower BV/TV) rather than changes in the tissue properties. Osteoblastic vertebrae (breast, kidney, lung, esophageal, or prostate cancer) exhibited higher median BV/TV values, (+53%) compared to vertebrae with mixed or osteolytic lesions. Trabeculae in these samples appeared abnormally thick and interconnected, sometimes without clear preferred orientation. This visual impression is confirmed by previous μCT studies [53,54] reporting high BV/TV values (20–50%) with a significantly higher number of bone trabeculae, trabecular surface, but a lower degree of structural anisotropy [54], when compared to healthy bone. Remarkably, several of the osteoblastic vertebrae in our study showed sub-regions with up to 90% BV/TV, indicating an almost compact bone.

Despite an increase in bone volume and osteoid deposition [54], blastic bone is of inferior quality: we measured a 5.8% lower Eit and a 3.3% lower Wpl/Wtot compared to lytic and non-involved bone. Other authors reported a 19.2% lower indentation modulus and 17.9% lower hardness in a murine model [70]. The lower intrinsic properties can be explained the high amount of new, less mineralized tissue and unorganised, woven collagen structure [74,75] likely induced by tumourderived growth factors [76] rather than mechanical stimuli. Assuming constant yield strains across BV/TV, a decrease in tissue elastic modulus (−5.8%) would lead to a similar reduction in yield stress. Yet, blastic vertebrae were significantly stronger the lytic and mixed ones (up to +700% in strength). These findings suggest that the increased strength of osteoblastic vertebrae is predominantly due to the densification of the bone architecture (higher BV/TV) despite lower tissue properties.

Based on these results, the difference in tissue properties plays a minor role on vertebral strength compared to bone mass. We thus chose to employ a standard BV/TV-driven constitutive law and material constants obtained from healthy bone tissue for the finite element simulations in this study.

4.2. Effect of the metastases on the in vitro strength

The osteoblastic vertebrae demonstrated markedly higher strength and BMC values compared to vertebrae with mixed (a median increase of 36.7% and 26.9% respectively) and osteolytic (a median increase of 34.5% and 137.5% respectively) lesions. Independent of the lesion phenotype, BMC values were moderately associated with Fexp (R2 = 0.65), which is in close agreement with correlations obtained with none-pathologic human vertebrae [77]. Interestingly, vertebrae with mixed lesions showed little difference in strength compared to lytic samples (+2% median), despite a markedly higher BMC (+87.1% median). These findings may 1) help explaining the difficulties in assessing the effect of mixed lesions on the vertebral strength based on the radiological appearance alone and 2) suggest that the strength of mixed vertebrae is predominantly determined by the location of the osteolytic lesions.

Previous studies have evaluated the effect of tumour size, shape and location based on non-pathologic vertebrae with artificial, continuous defects [46–48,78–81]. An artificial cavity cannot not mimic an array of smaller, diffused lytic lesions, or a blastic metastasis. To the best of our knowledge, our study is the first one to quantify the effect of real bone metastases on the strength of human vertebral bodies.

4.3. Predictions of in vitro strength

Homogenized FE models were shown to predict vertebral strength better than purely densitometric measures such as BMC, in part by accounting for the 3D distribution of bone mass [60]. Our findings go one step further and demonstrate that homogenized FE modelling can reliably predict the strength of the pathologic vertebrae, without having to adapt the material model to the type of metastasis. In a previous work, Pahr et al. [66] validated the modelling approach against normal to osteoporotic vertebral bodies. Interestingly, both the slope and the intercept of their linear regression are within the 95% confidence interval of our values, with a similar coefficient of determination (R2 = 0.77 [66] vs. R2 = 0.78). These findings reaffirm the importance of incorporating the spatial contribution of the bone architecture for predicting the strength of bone, pathological or not.

Surprisingly, however, the μFE simulation, which explicitly accounts for the bone architecture, yielded only a moderate association between KμFE and Fexp (R2= 0.65). Contrary to FhFE, KμFE was less strongly related to the strength of the lytic vertebrae compared to that of the blastic or mixed ones (Table 2). We posit that a reason for such difference is the uniaxial loading condition. Contrary to the hFE model, we were not able to replicate the ball joint of the experimental setup because of the high number of degrees of freedom involved in the μFE simulation. As stiffness is measured for very small displacements, a major impact was not expected. An additional source of discrepancy is the sensitivity to the segmentation threshold. Set slightly too high, it can disconnect thin trabeculae in the μFE model and artificially lower KμFE. Larger vertebrae would also appear thinner, but are less likely to disconnect. Similarly, a threshold set too low would close the tight trabecular gaps of the blastic metastases. Finally, a more mechanistic explanation is that lytic lesions affect the strain distribution within trabeculae causing significant variation in local mechanics and early initiation of buckling in the experiments [68,82].

In several of the osteoblastic vertebrae, we observed calcified structures within the marrow spaces (e.g. Fig. 3 B). Although we performed no histological examination, these structures may originate from osteoid depositions or cartilage mineralization, likely the result of the lesion mediated disruption of the normal skeletal homeostasis. At the given μCT resolution, most of them seem disconnected from the main trabecular architecture indicating that they do not contribute to bone stability and were thus removed from the μFE models. Although such depositions cannot be distinguished on clinical CT (or down-scaled μCTs in our case), they contribute to the measured mineral content. Given these structures’ unclear contribution to bone strength, the standard interpretation that increased mineral content leads to stronger bone must be made with care in the context of bone metastases. Still, the hFE approach was robust enough to yield equivalent strength predictions as for cancer-free vertebral bodies Pahr et al. [66].

Previously, studies using FE models for predicting vertebral strength in vivo based on clinical CT images of cancer patients [50,51] assumed that finite elements models validated on healthy vertebrae would be able to predict the strength of metastatic vertebrae as well. To the best of our knowledge, this is the first study to actually validate the FE models on real metastatic vertebral bodies, despite alterations of bone mass, structure, and tissue properties.

4.4. Justification for the testing protocol

Studies on the effect of the intervertebral disc on the structural response of spines have yielded conflicting results. In non-pathologic spines, the state of the intervertebral disc was reported to affect the strength of the vertebral body [83–85], as well as its failure pattern [86,87]. In spine segments with mechanically simulated large single osteolytic defect, Whyne et al. [88] reported disc degenerative state to have little effect on vertebral bulging under compression. By contrast, Alkalay and Harrigan [44] showed that the deformation pattern within the endplate and disc was affected by the lytic defect. Given these conflicting reports and the need to guarantee controlled loading and boundary conditions for testing and consequent modelling Dall’Ara et al. [63], we decided to remove the intervertebral discs to better isolate the lesion’s impact on the vertebral strength.

This decision leaves only two testing options: endplate embedding in a rigid resin [55] or endplate removal [63]. Using CT-based hFE models, we have previously demonstrated that 1) the two techniques result in the same strength [89] and 2) models with embedded endplates provide good prediction of the strength of vertebrae loaded experimentally via their intervertebral discs [90]. Removing the endplates and intervertebral discs allows us to capture strength variation, without having to deal with the disc or embedding material. Finally, although there is a clinical agreement regarding the importance of the posterior elements in the stability and risk of fracture of pathologic spines [91], the effect of lesion phenotype on the structural integrity of the posterior elements remains unstudied. Thus it is unclear how the stability of the spine segment would be affected. Given the lack of information, we decided to section the pedicles and focus the study on the vertebral body. Although our test configuration does not fully capture the structural response of the vertebrae in the context of a spine unit, it is fully justified, given the aims of the study. Numerous studies have performed in vitro testing of vertebrae with artificial defects using more elaborated setups [46–48,78–81]. However, the diverse experimental setups (e.g. high loading rates versus quasi-static loading) make a direct comparison to these studies difficult. Choosing a well-controlled and proven testing protocol allowed, despite its limitations, a comparison with similar experiments performed on cancer-free samples Dall’Ara et al. [63]; Pahr et al. [66].

4.5. Justification for generating the hFE models from μCT

In order to identify and select levels with bone metastases, we did image the full spines using clinical CT ex vivo. The FE models, however, were derived from the μCT scans of the vertebral bodies. While the μFE models require the high-resolution CTs, hFE models could have been generated from clinical CTs. However, the clinical CT images were performed on the intact vertebral columns, and were acquired without calibration phantom rendering a conversion of native Hounsfield units into to BMD values impossible without additional assumptions. On the other hand, the μCT acquisitions were calibrated and performed on vertebral sections prepared for the experiments (intervertebral discs and endplates removed). To compare experimental and μFE values to clinical CT based hFE predictions, we would have had to downscale and register the μCT images to find the correct vertebral section in the clinical CT, which would have been prone to errors. Finally, average densitometric variables such as BMD correlate highly between μCT and clinical CT [92]. In summary, using the coarsened μCT to generate the hFE model allowed for a direct, simple, and reproducible model generation and BMD evaluation.

4.6. Limitations

Our study has several limitations, other than those associated with the in vitro testing of cadaver spines. Although we had access to the donor’s medical history, including identification of primary cancer, surgical, chemotherapy, and medication, we received little information regarding radiotherapy treatments and, if so, what levels were treated. Radiotherapy, highly prevalent in this patient population, is increasingly recognised as a risk factor for PVF [18,93,94]. In a study of gamma-irradiated (31 kGy) human cancellous allograft bone, [95] reported a reduction of up to 66% in bone strength while no significant effects were observed for the stiffness of the bone. Although the radiation dose absorbed by a patient during radiotherapy is lower by more than two orders of magnitude than the one employed by Schwiedrzik et al., we cannot rule out that some of the outliers in the present dataset may have been caused by previous radiotherapy treatments.

With the study sample classified predominately as osteoblastic, we had limited number of vertebrae classified as osteolytic or with mixed lesions. Combined with the large variation in strength values for each group, we had a reduced statistical power for comparisons between the lesion phenotypes. We still provided the correlations per group for information, but more samples are needed in each group before drawing conclusions.

Finally, we did not present experimental values for vertebral stiffness. The reason for this omission was that we were not able to produce perfectly parallel sections during sample preparation, which would have affected the stiffness measurements. However, since the clinical interest is to estimate fracture risk, strength seems to be the essential variable to focus on. Therefore, and to avoid misinterpretations, we decided to exclude the experimental stiffness from the evaluation.

4.7. Conclusions

In conclusion, this novel study shows that indentation properties of osteoblastic bone are slightly lower compared to osteolytic or normal regions. Although experimental confirmation, for instance by Raman spectroscopy, will become necessary, this small reduction may be attributed to the lower mineralization and woven nature of the new bone formed in blastic regions. However, this difference in tissue properties plays a secondary role on vertebral strength compared to bone mass. As a consequence, standard homogenized FEA successfully predicts the strength of vertebral bodies without having to adapt the material model to the metastases. Compared to BMC, FEA accounts for the position, shape and size of lytic or blastic lesions and delivers improved strength prediction. Given that FEA can detect individuals at risk of fracture in a clinical setup [96], the hope is to develop a similar tool to help the clinicians decide whether a metastatic patient is at risk of fracture and needs prophylactic surgery [97].

Supplementary Material

Appendix-A

Appendix A

Table 3. Lesion type measured by nanoindentation. The column ID combines the spine ID and the sample ID. Marks between parentheses were not measured due to absence of trabecular structure at the given location.