Summary
Decreasing projection views to a lower X-ray radiation dose usually leads to severe streak artifacts. To improve image quality from sparse-view data, a multi-domain integrative Swin transformer network (MIST-net) was developed and is reported in this article. First, MIST-net incorporated lavish domain features from data, residual data, image, and residual image using flexible network architectures, where a residual data and residual image sub-network was considered as a data consistency module to eliminate interpolation and reconstruction errors. Second, a trainable edge enhancement filter was incorporated to detect and protect image edges. Third, a high-quality reconstruction Swin transformer (i.e., Recformer) was designed to capture image global features. The experimental results on numerical and real cardiac clinical datasets with 48 views demonstrated that our proposed MIST-net provided better image quality with more small features and sharp edges than other competitors.
Keywords: computed tomography, inverse problems, deep learning, transformer, multiple domains
Highlights
-
•
A multi-domain integrative Swin transformer was proposed for spare-data imaging
-
•
A trainable image edge enhancement filter recovers sharp image edges and features
-
•
A modified vision transformer first demonstrates its great potential in tomography
-
•
Patient clinical cardiac and numerical data demonstrate our MIST power
The bigger picture
Decreasing projection views to a lower X-ray radiation dose usually leads to severe streak artifacts. To improve reconstructed image quality from sparse-view data, we develop a multi-domain integrative Swin transformer (MIST) network in this study. The proposed MIST-net incorporates lavish domain features from data, residual data, image, and residual image using flexible network architectures, which help deeply mine the data and image features. To detect image features and protect image edges, the trainable edge enhancement filter is further incorporated to the network for improving encode-decode ability. A high-quality reconstruction transformer was designed to improve the ability of global feature extraction. Our results from both simulation and real cardiac data demonstrated the great potential of MIST.
A multi-domain integrative Swin transformer network (MIST-net) demonstrates feasibility, advantages, and great potential in sparse-view tomographic reconstruction. MIST-net mainly integrates data, image, residual data, and residual image domain information into a unified model with a trainable edge enhancement filter and advanced transformer AI technique to realize ultra-sparse-data (48 views) high-fidelity imaging.
Introduction
Computed tomography (CT) has been widely used in medical diagnosis and industrial detection fields because of its excellent imaging ability.1 Especially in 2020, CT became an essential technology to detect and diagnose coronavirus disease 2019 (COVID-19).2 Although CT scans provide practical and accurate diagnostic results, they are also increasingly harmful to human bodies with radiation dose.3 An effective approach to reduce radiation dose is sparse-view CT reconstruction,4,5 in which only part of the projection data are used for image reconstruction. In this case, traditional reconstruction algorithms such as filtered back-projection (FBP)6 lead to serious streaking artifacts as well as low image quality.
Since the emergence of artificial intelligence,7, 8, 9 many deep learning-based methods have been developed to improve the quality of sparse-view CT reconstruction.10, 11, 12 They can be divided into three categories: image domain restoration,13 dual-domain restoration,14,15 and iterative reconstruction methods.16,17 Image domain restoration methods are also called post-processing methods. They directly process low-quality images as the input and ground truth as output of network, which means that this kind of methods do not need raw data. The typical reconstruction networks include FBPConvNet,13 DenseNet deconvolution network (DDNet),11 and residual encoder-decoder convolutional neural network (RED-CNN).10 In addition, Xie et al.18 used a generative adversarial network (GAN) to remove limited-angle artifacts. Wang et al.19 presented a limited-angle CT image reconstruction algorithm based on a U-net convolutional neural network, which can effectively eliminate noise and artifacts while preserving image structures. As there are no projection data playing the game, it is difficult to accurately recover image details and features with streak artifact removal.
The dual-domain deep reconstruction methods usually concentrate to reconstruct high-quality images by considering both projection and image domains simultaneously. For example, Hu et al.20 proposed a hybrid domain neural network (HDNet), which recovered projection and image information successively. Liu et al.21 presented a lightweight structure using spatial correlation. Zhang et al.22 designed a hybrid-domain convolutional neural network for limited-angle CT. Wu et al.23 presented a dual-domain residual-based optimization network (DRONE), which performed well in edge preservation and detail recovery. The dual-domain network can be also applied to three-dimensional (3D) reconstruction.24 However, the final images may suffer from secondary artifacts because the errors of projection interpolation are usually introduced.
Inspired by the classic iteration reconstruction, deep reconstruction networks can also be designed as unfolding deep iterative reconstruction. Cheng et al.25 accelerated iterative reconstruction with the help of deep learning. Chen et al.26 presented a learned experts’ assessment-based reconstruction network (LEARN) for sparse-view data reconstruction. Zhang et al.27 extended the LEARN model to a dual-domain version, named LEARN++. Xiang et al.28 proposed a fast iterative shrinkage thresholding algorithm (FISTA) for inverse imaging problems. Unrolling iterative reconstruction methods can suppress noise and artifacts to improve image quality. Nevertheless, iterative reconstruction methods need huge GPU memory, which leads to difficulty working with 3D geometry.
In this work, we propose a multi-domain integrative Swin transformer network (MIST-net) to reconstruct high-quality CT images from sparse-view projections. Broadly, our network architecture consists of three key components: initial recovery, data consistency correction, and high-fidelity reconstruction. In the initial recovery, a data extension encoder-decoder block is first used to extend sparse-view data by deep interpolation. Then, an end-to-end edge enhancement reconstruction sub-network reconstructed the initial image for sparse artifact removal and image edge preservation. However, the projection domain interpolation may introduce errors to further generate unexpected artifacts. Therefore, the data consistency module, which consists of two residual sub-networks (one for residual projection estimation, the other for residual image correction), was introduced to reduce errors and improve structural details. Although convolutional neural network (CNN)-based deep learning reconstruction methods have provided good performance, they cannot learn global and long-range image information interaction well because of the locality of convolution operator.29,30 Fortunately, transformers31 have such ability for modeling long-range information and show good performance in natural language processing (NLP) tasks.31, 32, 33 The proposal of the vision transformer (VIT)34 shows that transformers can take place of convolutions in some image processing tasks.35, 36, 37 Therefore, we introduce a hierarchical vision transformer using shifted windows (Swin)37 in a high-fidelity reconstruction module to capture long-range dependencies.
Compared with developed CNN-based deep networks for sparse-view reconstruction in the past few years, our MIST-net is innovative in several aspects. First, an encode-decode38 structure is used in the initial recovery module to extract deep features in both data and image domains simultaneously. Specifically, an edge enhancement reconstruction network in the image domain was designed to recover the image edge. Second, both data residual and image residual networks are used in data consistency module to eliminate errors in both projection and image domains, which contribute to artifact reduction and subtle structure recovery. Third, a modified Swin reconstruction transformer (Recformer) extracts both shallow and deep features in the image domain to ensure final reconstruction results.
The organization of the paper is as follows. First, the main reconstruction results from our MIST and competitors are reported. We also implement a detailed ablation study including numerical and real cardiac data to show the advantages of our MIST-net. We further perform noise analysis experiments to verify robustness of the model. We then discuss our results and make conclusions of this work. In the Experimental procedures section, we introduce basic theories and then describe our proposed MIST-net carefully.
Results
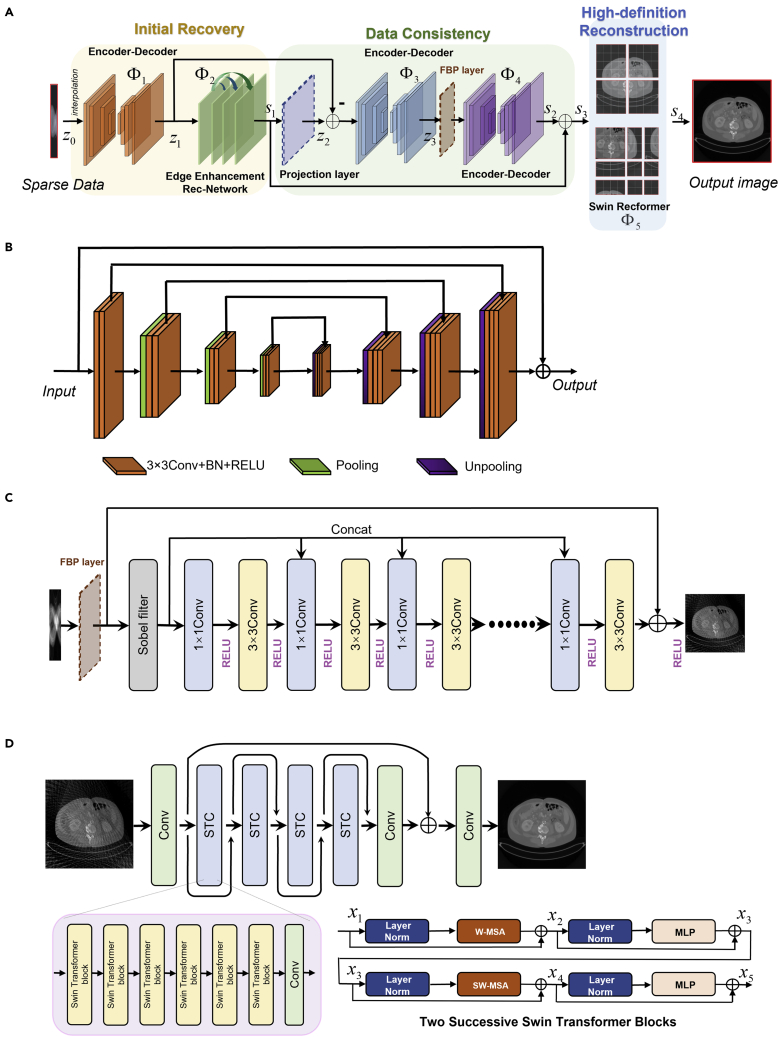
In this study, we developed a multi-domain integrative Swin transformer network to reconstruct CT images from ultra-sparse view projections. To obtain initial recovery images, two CNN-based sub-networks in both projection domain and image domain were designed. Then, we designed a dual-domain residual network to eliminate errors and noise. Our proposed Swin reconstruction transformer (i.e., Recformer) sub-network refined intermediate results. Figure 1 demonstrates the overall architecture of our MIST-net; more details can be found in the Experimental procedures.
Figure 1.
The overall architecture of our proposed MIST-net
(A) The pipeline of the proposed MIST-net.
(B and C) Our network has three modules: initial recovery, data consistency, and high-definition reconstruction; (B) the encoder-decoder block with similar U-net architecture; (C) the edge enhancement reconstruction sub-network for recovering an initially reconstructed CT image.
(D) The Swin Recformer network to reconstruct a high-quality image.
Our model was designed and trained in Python using the PyTorch framework. All experiments were run on a PC with 48G NVIDIA RTX A6000 GPU, Intel Xeon Gold 6242R CPU at 3.10 GHz and 128 GB random-access memory (RAM). The configuration of the training network is as follows. Our network was trained by the Adam optimizer, and the learning rate was set to 0.00025. The number of epochs was 50, and batch size was 1. FBPConvNet,13 HDNet,20 DDNet,11 FISTA,28 and LEARN26 are treated as comparisons. The root-mean-square error (RMSE), peak signal-to-noise ratio (PSNR), and structure similarity index (SSIM) are introduced to quantitatively assess reconstruction results. Our code is publicly released at https://zenodo.org/record/6368099.
Simulated data result
To validate the feasibility of our proposed network, we trained and tested our model on 2016 NIH-AAPM-Mayo Low-Dose CT Grand Challenge datasets.39 The datasets come from Siemens Somatom Definition CT scanners at 120 kVp and 200 mAs. To generalize our model to real datasets, we rearranged datasets with all scanning and configuration parameters being consistent with following real cardiac CT datasets. Specifically, the distances from the X-ray source to the system isocenter and detector are set as 53.85 and 103.68 cm. The number of detector units and views are set to 880 and 2,200 respectively. The size of reconstructed CT images is 512 × 512 pixels. Finally, a total number of 4,665 sinograms of 2,200 × 880 pixels were acquired from 10 patients at a normal dose setting, where 4,274 sinograms of 8 patients were used for network training and the remaining 391 sinograms from other 2 patients for network testing. Our operation to obtain sparse data is as follows: for every sinogram of 2,200 × 880 pixels, we sample every 30 views until 48 × 880 pixels have been collected. That means our sampled projection data can only cover 235.6 degrees. We also sample every 10 views to obtain a projection of 144 × 880 pixels, which is used as a projection label.
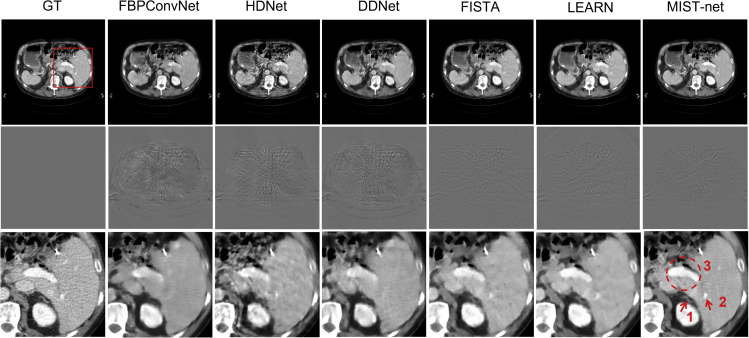
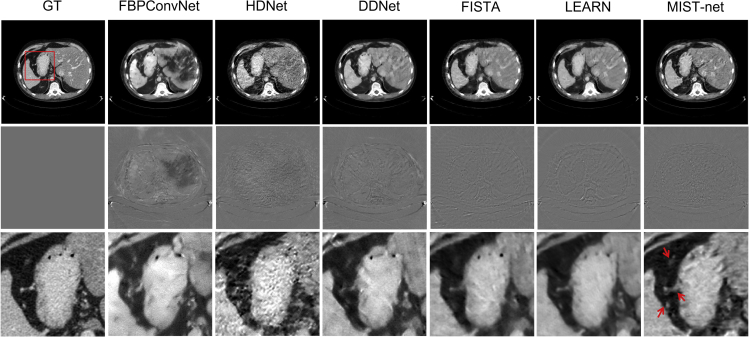
Figures 2 and 3 demonstrated the representative reconstruction results with cases 1 and 2 from patients 1 and 2 of different reconstruction networks. It was clearly observed that FBPConvNet removed most of the artifacts caused by sparse views, but the image boundaries and details were further destroyed. HDNet obtained better images, but it leads to excessive image smoothing. DDNet was able to recover some image details, but its results still contained a few unacceptable artifacts. Unlike the above-mentioned methods, FISTA and LEARN, two advanced unrolled deep reconstruction methods, have better performance in sparse-view reconstruction because they can effectively improve image quality with richer details and clearer edges. However, some tiny features were still lost. In contrast to competitors, our MIST-net improved image quality with the best details and edges.
Figure 2.
Visualizations of sparse-view reconstruction in case 1 by using different methods
The first through seventh columns represent ground truth (GT), FBPConvNet, HDNet, DDNet, FISTA, LEARN, and MIST-net counterparts from 48 views. The second row shows the difference images relative to the GT, and the third row represents the extracted region of interest (ROI) from first row images. The display windows for the reconstructed and difference images are [−160 240] HU and [−90 90] HU.
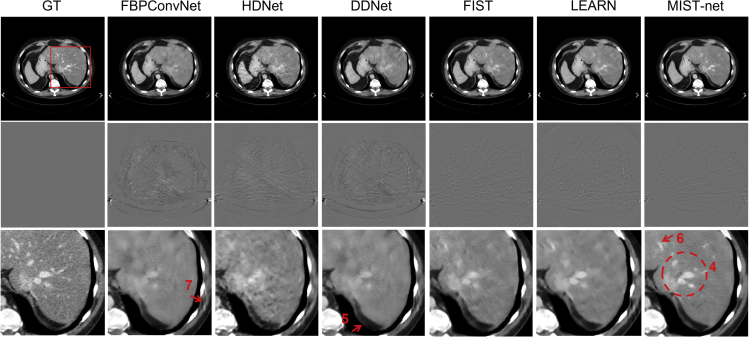
Figure 3.
Visualizations of sparse-view reconstruction in case 2 by using different methods
The first through seventh columns represent ground truth, FBPConvNet, HDNet, DDNet, FISTA, LEARN, and MIST-net counterparts from 48 views. The second row shows the difference images relative to the GT, and the third row shows the magnification ROIs. The display windows for the reconstructed and difference images are [−160 240] HU and [−90 90] HU.
To display advantages of MIST-net, the regions of interests (ROIs) were extracted and magnified in Figures 2 and 3. First, one can see that the magnified structures marked by arrows 1 and 2 were badly blurred and destroyed by FBPConvNet, HDNet, and DDNet in Figure 2. In contrast to FBPConvNet, HDNet, and DDNet, FISTA and LEARN achieved better images. However, FISTA-net and LEARN results were still inferior to our MIST network. Besides, FBPConvNet, HDNet, and DDNet missed details and over-smoothened tissue edges in circle 3. Compared with FBPConvNet, HDNet, and DDNet, FISTA-net and LEARN almost eliminated artifacts and achieved better images. However, it was still found that the structure of tissue was slightly fuzzy, which exposed its weakness on edge recovery. On contrary, our MIST-net obtained the best reconstructed result with clear edges and rich details in the image region indicated circle 3.
On the other hand, the image structure indicated by circle 4 in Figure 3 demonstrated the advantages of MIST-net in terms of structural fidelity. The image feature highlighted by circle 4 was almost lost or damaged by FBPConvNet, HDNet, and DDNet. FISTA and LEARN could retain a few structural features, but they were still blurry. In addition, the feature with arrow 5 showed that DDNet and FBPConvNet produced a gray intensity shift, while FISTA, LEARN, and MIST-net can address this problem. To further explain the superiority of our MIST-net in terms of fine texture retain, the easily overlooked details marked with arrows 6 and 7 are emphasized in Figure 3. With these highlight structures, it can be inferred that FBPConvNet, HDNet, and DDNet smeared small image features. FISTA and LEARN recovered some image features missed by the above-mentioned methods, but the finer image features such as that indicated by the arrow 6 were destroyed. As a result, compared with other methods, MIST-net achieved the best results that look quite similar to ground truth. More reconstruction experimental results can be found in Appendix A in Supplemental experimental procedures (see Figure S1).
We also made a quantitative evaluation of all methods, and the results are quantified in Table 1. It was observed that our MIST network produced better results than the FBPConvNet, HDNet, DDNet, FISTA, and LEARN methods. Table 1 demonstrates that FBPConvNet and DDNet achieved the worst performance in PSNR, SSIM, and RMSE, which indicated that the performance of post-processing methods was severely affected by sparse-view artifacts. Compared with FBPConvNet, concentrating only on image domain, HDNet stacked two U-net structures respectively in both projection and image domains. HDNet had better scores than FBPConvNet, which benefits from the effectiveness of hybrid domain processing. Meanwhile, FISTA and LEARN certainly outperformed FBPConvNet, HDNet, and DDNet in all evaluations because of iterative processing. In Table 1, our proposed MIST-net method has the smallest RMSEs and the biggest PSNRs and SSIMs compared with those competitors. These quantitative results validated the advantages of the proposed MIST-net, demonstrating the best performance. More statistical quantitative results from all simulation testing datasets are given in Table 2, and they demonstrate that our MIST-net can obtain the best performance. Finally, we also performed the experiments with more views (i.e., 64 views), and the results are given in Appendices A and B of Supplemental experimental procedures (Figure S2; Table S1).
Table 1.
Quantitative evaluation of 48 projection reconstruction results from two simulated cases
| Views | FBPConvNet | HDNet | DDNet | FISTA | LEARN | MIST-net | ||
|---|---|---|---|---|---|---|---|---|
| 48 | RMSE↓ | case 1 | 27.1508 | 24.1323 | 24.6031 | 18.1993 | 18.0470 | 16.2775 |
| case 2 | 28.7080 | 22.4121 | 29.1107 | 17.7193 | 17.5947 | 15.8242 | ||
| PSNR↑ | case 1 | 38.3953 | 39.4190 | 39.2512 | 41.8699 | 41.9429 | 42.8392 | |
| case 2 | 37.0957 | 39.2461 | 36.9747 | 41.2868 | 41.8392 | 42.2693 | ||
| SSIM↑ | case 1 | 0.9573 | 0.9625 | 0.9602 | 0.9744 | 0.9760 | 0.9800 | |
| case 2 | 0.9647 | 0.9672 | 0.9635 | 0.9752 | 0.9784 | 0.9818 |
Table 2.
Quantitative evaluation of 48 projection reconstruction results from simulated testing datasets
| Views | Methods | RMSE | PSNR | SSIM |
|---|---|---|---|---|
| 48 | FBPConvNet | |||
| HDNet | ||||
| DDNet | ||||
| FISTA | ||||
| LEARN | ||||
| MIST-net |
Clinical cardiac validation
To further verify the performance of MIST-net, the real dataset used by Yu et al.40 was used. The curved cylindrical detector contains 880 units, and there are 2,200 views with a full scan. The diameter of field of view (FOV) covers 49.8 × 49.8 cm2, with an image matrix of 512 × 512 pixels. The distance from the X-ray source to the system isocenter and the detector array were 53.85 and 103.68 cm. Because we trained the reconstruction network using American Association of Physicists in Medicine datasets, here, we transferred the trained network to evaluate reconstruction performance using real dataset, which can be also benefit to evaluate the generalization ability of our model. We also extracted 48 views from short scan to test our MIST-net for sparse-view CT imaging. It is worth mentioning that the data distribution of real datasets is different from simulated datasets. Thus, we pre-processed clinical cardiac dataset to keep its data distribution consistent with that of training datasets. Specifically, we first normalized the clinical dataset and then mapped it to the distribution of numerical simulated data.
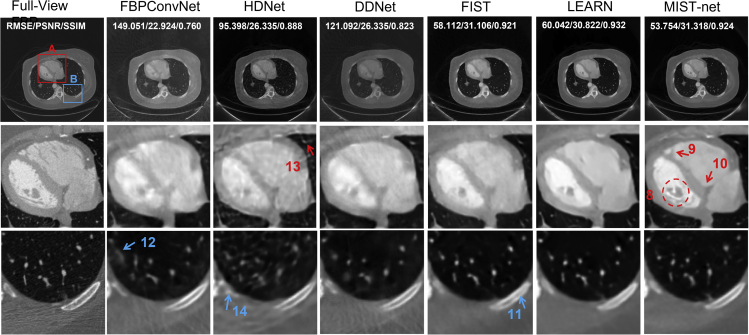
Figure 4 shows reconstruction results from 48 views using different reconstruction methods. The full-view FBP reconstruction also contained some noise and short-scan artifacts.41 Compared with these competitors, our proposed MIST-net achieved the best reconstruction results. Firstly, as shown in circle 8, MIST-net achieved the structure closest to the ground truth, which adequately embodies the advantages of MIST-net in terms of structural fidelity. In addition, the image feature marked by arrow 9 was not recovered by FBPConvNet, HDNet, DDNet, FISTA, and LEARN, but the proposed MIST recovered the structure, which showed that MIST-net was good at details and feature recovery. Again, MIST-net reconstructed clearer image edges and showed finer structures. The clearest edges indicated by arrow 10, which cannot be obviously reconstructed by other competitors, strongly confirmed the advantages of the proposed MIST-net. On the contrary, the edges in the reconstructed images were hard to distinguish from FBPConvNet, HDNet, and DDNet. FISTA and LEARN provided a better reconstruction in arrow 10, but the details were still compromised. Furthermore, the feature indicated by arrow 11 was destroyed from FISTA-net.
Figure 4.
Clinical cardiac CT reconstructions from sparse-view data by using different networks
The first through seventh columns stand for the FBP reconstruction from full-view data, FBPConvNet, HDNet, DDNet, FISTA, LEARN, and MIST-net counterparts from 48 views. The second and third rows show ROIs. The display windows for the reconstructed images are [−800 1,000] HU.
Compared with our proposed model, other non-iterative methods performed unsatisfactorily. Obviously, FBPConvNet could not recover the image structure indicated by arrow 12. Benefiting from a dual-domain design, HDNet suppressed most of artifacts and noise, but it still caused fuzziness as well as sparse-view artifacts, which are clearly indicated by arrows 13 and 14. Furthermore, benefiting from the iterative mechanism, the reconstructed image from FISTA and LEARN were better than those obtained by FBPConvNet, HDNet, and DDNet. In edge restoration, FISTA and LEARN were still worse than our proposed network. The real experiments further demonstrated that the proposed network performed consistently better than the other competitors in practice. They also demonstrated the power of the transformer in the sparse-view CT reconstruction.
Ablation exploration and generalization analysis
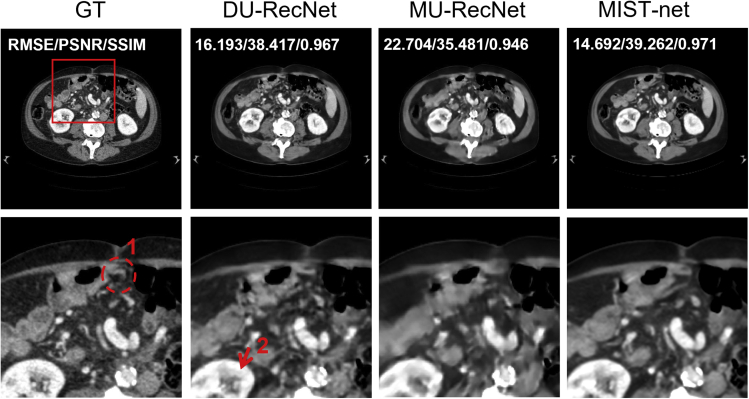
For analyzing and benchmarking the proposed network MIST-net, we further focused on ablation explorations to validate the effectiveness of different modules. First, the DU-RecNet represents a simplified MIST-net that uses two encoder-decoder blocks to replace the edge enhancement reconstruction sub-network and Swin Recformer sub-network. The MU-RecNet denoted the modified DU-RecNet by removing data consistency module. All networks were trained in the same way. As shown in Figure 5, the residual domain processing is helpful for artifact reduction and detail recovery. Regarding circle 1 and arrow 2 results, DU-RecNet could recover better features than MU-RecNet, as the residual domain sub-network was designed to eliminate interpolation errors. The RMSE, PSNR, and SSIM results further explained advantage of residual domain sub-network.
Figure 5.
Reconstruction results in case 3
The first through third columns represent ground truth and reconstructions from DU-RecNet and MU-RecNet counterparts with 48 views. The second row shows the ROIs. The display window for the reconstructed images is [−160 240] HU.
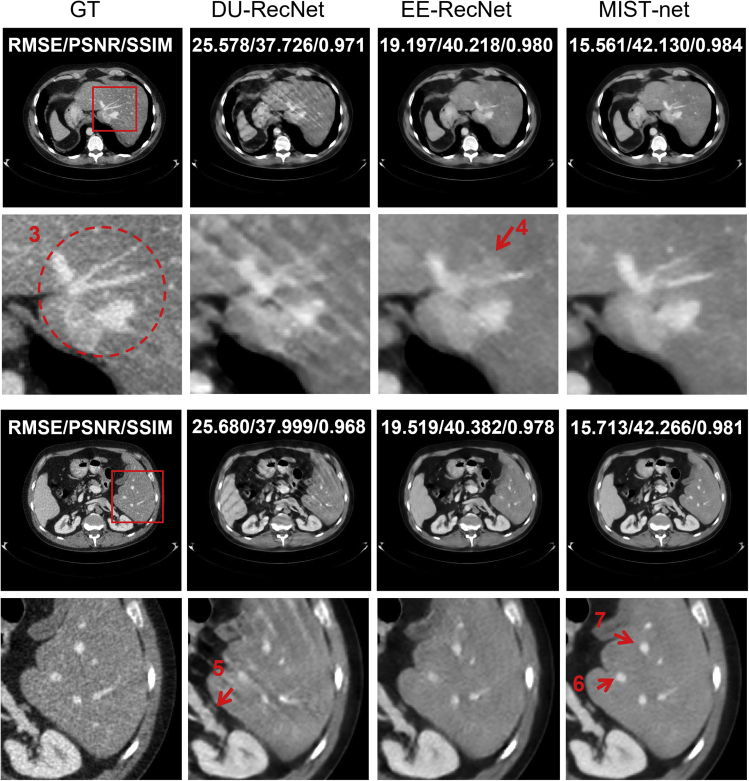
We also constructed an EE-RecNet to verify the effectiveness of the edge enhancement reconstruction network. Compared with DU-RecNet, EE-RecNet only added the edge enhancement reconstruction network. The architecture of EE-RecNet was similar to MIST-net, except that the final Swin Recformer network was replaced by a U-net. Figure 6 shows reconstruction results from DU-RecNet, EE-RecNet, and MIST-net. As shown at the top of Figure 6 (case 4), DU-RecNet result contained a few artifacts due to sparse-view down-sampling. The edge enhancement reconstruction module indeed reduces artifacts in the image domain and helps overcome edge over-smoothness. Additionally, we found that image region marked with circle 3 was destroyed by DU-RecNet. Both EE-RecNet and MIST-net reconstructed the general outline, but EE-RecNet lost some details with arrow 4. Furthermore, from the bottom of Figure 6 (case 5), one observes that Swin transformer was also important for high-contrast structural recovery, low-contrast feature reconstruction, and textural detail preservation. The detail indicated by arrow 5 was blurred by DU-RecNet, while MIST-net could reconstruct it well. In addition, features marked by arrows 6 and 7 were very similar to the ground truth, but they were blurry in the images reconstructed by DU-RecNet and EE-RecNet. The RMSE, PSNR, and SSIM metrics were computed to confirm the gain with the edge enhancement reconstruction sub-network. The quantitative results in terms of RMSE, PSNR, and SSIM have clearly illustrated the merits of our proposed MIST-net.
Figure 6.
Comparison of different networks reconstruction results in cases 4 (top) and 5 (bottom)
The first through fourth columns represent ground truth and reconstructions from DU-RecNet, EE-RecNet, and MIST-net counterparts from 48 views. The second row of each part shows the ROIs. The display window for the reconstructed images is [−160 240] HU.
The statistical quantitative evaluations of ablation experiments were computed in terms of RMSE, PSNR, and SSIM, and their results were summarized in Table 3. It can be seen that our MIST-net can obtain the best quantitative statistical results in terms of mean and SD than other networks.
Table 3.
Quantitative evaluation of ablation experiments
| Views | Network | RMSE | PSNR | SSIM |
|---|---|---|---|---|
| 48 | DU-RecNet | |||
| MU-RecNet | ||||
| EE-RecNet | ||||
| MIST-net |
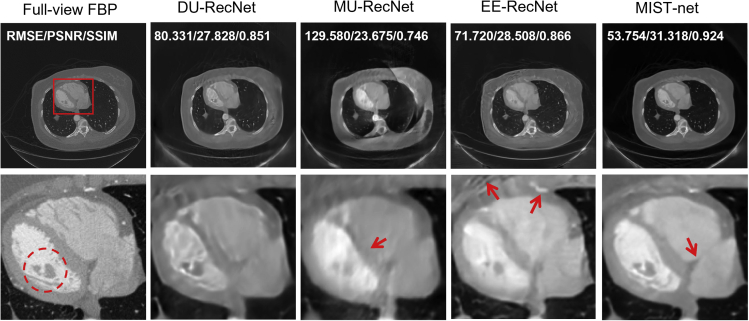
To demonstrate the influence of different modules, we also did an ablation experiment on the real cardiac CT dataset. Figure 7 shows the clinical cardiac reconstructed images from 48 views using relative methods. The performance of MU-RecNet was compromised, and the edges and details were hard to distinguish. DU-RecNet reconstructed observed features but still caused hazy edges, which are clearly indicated by an arrow in Figure 7. EE-RecNet recovered details but produced sparse-view artifacts. Compared with competitors, MIST-net delivered the best image quality and evaluation indicators.
Figure 7.
Comparison of different networks reconstruction results in the real dataset
The first through fifth columns stand for the FBP reconstruction from full-view data, DU-RecNet, MU-RecNet, EE-RecNet, and MIST-net counterparts from 48 views. The second row shows ROIs. The display windows for the reconstructed images are [−800 1,000] HU.
To demonstrate the advantages of our MIST-net with similar parameters and memory, we design a pure CNN structure as a baseline, which uses five ResUnets to replace all parts of the procedure. Then, we study the effect of edge enhance sub-network and dual transformers with similar parameters. The result can be found in Table 4. The “Baseline + Edge-Enhance” is similar to the overall structure of EE-RecNet except for the number of parameters. Compared with MIST-net, “Baseline + Dual-SwinRec” uses Swin transformer in both the edge enhancement sub-network and the last reconstruction block. With similar parameters, Table 4 shows that both edge enhancement Rec-Network and Swin transformer play important roles in controlling image quality.
Table 4.
Comparison between ablation candidates with similar size
| Networks | RMSE | PSNR | SSIM | Number of Parameters |
|---|---|---|---|---|
| Baseline | ||||
| +Edge-Enhance | ||||
| +Dual-SwinRec | ||||
| MIST-net |
To further verify the effect of Swin-Recformer in the last module, we designed Swin-Recformer modules of different complexity and introduced MIST-Tiny (MIST-T), MIST-Small (MIST-S), MIST-Base (MIST-B), and MIST-Large (MIST-L). The design of their initial recovery and data consistency blocks is exactly the same, and the difference is only in the Swin transformer module. In this paper, we use MIST-B as the proposed MIST-net. The architecture hyper-parameters of these model variants are as follows:
-
•
MIST-T: C = 96, layer numbers = {2,2,6,2}, head numbers = {3,6,12,24}
-
•
MIST-S: C = 96, layer numbers = {2,2,18,2}, head numbers = {3,6,12,24}
-
•
MIST-B: C = 96, layer numbers = {6,6,6,6}, head numbers = {6,6,6,6}
-
•
MIST-L: C = 96, layer numbers = {8,8,8,8}, head numbers = {8,8,8,8}
where C is the channel number of hidden layers in the first stage. The quantitative evaluation and number of parameters are listed in Table 5. The experimental results show that MIST-B achieved the best results. In addition, we observed that larger model (MIST-L) leads to worse results, possibly because of overfitting.
Table 5.
Comparison between Swin Recformer modules of different computational complexity
| Views | Network | RMSE | PSNR | SSIM | Number of Parameters |
|---|---|---|---|---|---|
| 48 | MIST-T | ||||
| MIST-S | |||||
| MIST-B | |||||
| MIST-L |
We also study residual data in the data consistency module. As shown in Figure 1A (i.e. in our network structure), the residual data is inputted to the encoder-decoder block . As a comparison, we use as an input and make an interpolation network. The quantitative analysis can be found in Table 6. The results demonstrated that works better as residual data inputted to .
Table 6.
Comparison between different designs of residual data
| Residual Data | RMSE | PSNR | SSIM |
|---|---|---|---|
The generalization ability is also an important issue for deep learning-based image reconstruction in practice. In this study, Gaussian noise was added to the images, where the mean and variance are set as 0 and 0.01. Then, the noisy images were used to verify the ability of reconstruction models against noise attacks during the testing process. Figure 8 showed the reconstructed results with different networks. The structures marked with the arrows show that details were blurred by noise using FBPConvNet, HDNet, DDNet, FISTA, and LEARN. Our proposed MIST-net can obtain better image quality than other competitors. The more detailed noise experimental results are given in Appendix C of Supplemental experimental procedures (see Figure S3).
Figure 8.
The generalization of different deep reconstruction networks against noise on simulation datasets
The first through 7th columns stand for the ground truth, FBPConvNet, HDNet, DDNet, FISTA, LEARN, and MIST-net counterparts from 48 views. The first through third rows represent reconstructed results, difference images, and the magnified ROIs.
Discussion
Deep learning has attracted rapidly increasing attention in the field of medical image analysis. Since 2016, convolutional neural network-based deep learning techniques have been extensively developed for tomographic imaging with sparse data, some of which were already approved by commercial scanners and translated into clinical practice. Although CNN-based deep learning is impressive, it cannot learn global and long-range image information interaction well, because of the locality of convolution operation (e.g. 3 3 or 5 5 region), with the further result that this kind of method fails to capture global structures and features of tomographic imaging. Fortunately, the vision transformer can convert an image into a sequence to enhance capability of long-range modeling, which is also one of the inspirations for this paper.
In this study we presented a multi-domain integrative Swin transformer network for sparse-view CT reconstruction. Our primary contribution is that we first presented a multi-domain integrative Swin transformer network and then used it for sparse-view tomographic reconstruction. Our MIST-net reconstructs tomographic images with sparse data, where both projection and image domains are respectively responsible for repairing projection data and restoring images in the initial sub-network reconstruction stage. Then, both residual projection and residual image domain sub-networks are used to eliminate measurement errors and make the data consistent. To retain features and enhance the edge of the tomographic image, an edge enhancement sub-network is introduced to avoid over-smoothness and edge blurring. More important, we proposed a Recformer (a novelty transformer) sub-network to capture global features and structures of tomographic imaging. Our work first demonstrated the feasibility of transformer-based tomographic imaging with sparse data as well extinguished reconstruction performance. The results showed that the proposed network could effectively reduce streaking artifacts caused by sparse-view projection and recover image features and details.
We verified our approach with both simulated and clinical datasets, showing that it outperforms CNN-based methods such as FBPConvNet, DDNet, HDNet, FISTA, and LEARN. FBPConvNet and DDNet represent the performance of image post-processing methods. HDNet, as a dual domain-based deep reconstruction method, encoded projection domain and image domain information simultaneously. FISTA and LEARN are unrolled iterative deep learning methods, and they provide state-of-the-art reconstruction results. Compared with competitors, our MIST-net achieved the best quantitative performance. We also compare the complexity and runtime of all competitors (see Table S2). Our network runs faster than LEARN and DDNet. Compared with HDNet, the advantages are also obvious because HDNet needs to train two networks separately, which makes the training process more complicated. Compared with FBPConvNet, because our network is larger, the comparison does not seem fair. To address this issue, we designed MIST-Tiny (10.4M) in subsequent ablation experiments. MIST-Tiny has a similar size as FBPConvNet (9.8M) and HDNet (9.8M × 2) and still shows relatively good performance. Compared with FISTA and LEARN, as they are iterative methods, the small number of parameters is a major feature. However, multiple projection and back-projection operations cause a huge computational footprint, which makes it difficult to apply to clinical practice. Thus, we cannot rely on network parameters to judge which is good or bad between our network and iterative methods. In ablation experiments, we have verified the effectiveness of proposed modules under the condition of consistent parameters, and we performed ablation studies on the Swin module alone. It is worth noting that the performance of MIST-Large is degraded compared with standard MIST-Base. The possible reason is that the larger model leads to overfitting. Finally, Gaussian noise experiments further exhibited better generalization ability of MIST-net over competitors.
Our work first demonstrated the feasibility of transformer-based tomographic imaging with sparse data as well extinguished reconstruction performance. In the future, the transformer can be introduced into unrolled iterative reconstruction. As mentioned above, the computational cost of unrolled methods depends on the number of iterations (i.e., projection and back-projection operations). Thus, the easiest way to reduce the amount of computation is to reduce the number of iterations. However, for a simple CNN, it is difficult to train well with a small number of iterations. By introducing the transformer, the reconstruction network can capture long-range information and become easier to train than pure CNN. For example, the iterative method of CNN and transformer may get good results with fewer iterations (e.g., 5 or 7 iterations).
Although the proposed network has demonstrated good performance in sparse-view tomographic reconstruction, there are still some issues that need to be addressed. First, the proposed method incurs more computational and memory cost than pure CNN-based methods, which is a challenge of transformed-based applications in medical imaging. Second, transformers had strict requirements on input image size because of position encoding, which limits the flexibility of transformer-based deep reconstruction. Therefore, we did not use Swin transformers in our projection domain, because the size of sparse-view projection is always different. In addition, the transformer requires large datasets to show the unique advantages. However, medical image datasets with labels are scarce. We plan to extend our method to iterative reconstruction and explore the feasibility of our MIST-net with a self-supervised strategy42 for limited-angle CT43 and low-dose CT.44 In summary, in this paper we present a MIST-net reconstruction model, which will encourage transformer-based applications in medical imaging.
Experimental procedures
Resource availability
Lead contact
Weiwen Wu, PhD (email: wuweiw7@mail.sysu.edu.cn).
Materials availability
The library used in this study is made publicly available via Zenodo (https://zenodo.org/record/6368099).
Methodology
CT imaging model
The ideal mathematical model of CT imaging can be expressed as a discrete linear system:
| (Equation 1) |
where x represents a reconstructed CT image, and it can be expressed as . stands for the measured projection data, and it can be written as . stands for projection noise, and is a CT system matrix, which contains Q×P elements. Because of the noise in y, the solution of Equation 1 can be obtained by minimizing the following objective function:
| (Equation 2) |
where stands for the Frobenius norm. The ART or SART are usually used to minimize Equation 2.45 However, solving x directly from a very sparse projection data y is an under-determined inverse problem, which may lead to the poor reconstructed image quality with streak artifacts. Thus, in traditional analytical methods, a regularization term representing prior knowledge is usually introduced to obtain better reconstruction result; then we have
| (Equation 3) |
There are two components in Equation 3, the fidelity term and the regulation prior knowledge term . The hyper-parameter is designed to balance these two components. Different reconstruction methods correspond to different regularization priors, such as total variation46,47 and dictionary learning.43,48,49
Multi-domain integrative network
In the projection domain, the main work is to complement and restore the sparse-view sinograms. For example, Dong et al.50 completed the missing data with U-net architecture, then a typical network further refined the raw image reconstructed from completed projections. The benefit of the projection domain deep neural network is that it can reduce the data error from the view of detector measurement. However, the interpolated projection with deep neural networks may introduce wrong measurement and further result in false-positive and false-negative diagnosis results. Unfortunately, the false results are also difficult to correct even if by a high-fidelity post-processing image domain network. To overcome this challenge, the residual data domain sub-network is first considered to correct the data inconsistency of the initial reconstructed image. Indeed, the stage is beneficial to correct original data errors to overcome the data inconsistency. Furthermore, one residual image domain sub-network further improves the reconstruction performance. Finally, Swin transformer architecture can deeply characterize various latent features of the reconstructed image to capture local and global information of image-self.
Edge detection operator
The edges of images are among the most important features, conveying a wealth of internal information, especially in medical images; for example, the edges of tumors are key in diagnosing if they are benign or malignant. In this work, we introduced a Sobel filter51 to overcome the problem of excessive edge smoothing. The Sobel operator belonged to the orthogonal gradient operator, and its gradient corresponded to the first derivative. For a continuous function , where (a, b) indicates the position point, the gradient can further be expressed as a vector:
| (Equation 4) |
| (Equation 5) |
| (Equation 6) |
where and stand for the magnitude and direction angle of . The partial derivatives needed to be calculated for each pixel point by using the Equation 6. The original Sobel operator contains a 3 × 3 vertical filter and a 3 × 3 horizontal filter, which has a maximum response to the vertical edge and the level edge, respectively.
Liang et al.52 proposed an edge enhancement-based densely connected network (EDCNN) and achieved good performance in low-dose CT denoising. Sharifrazi et al.53 applied Sobel filters to achieve accurate detection of COVID-19 patients from CT images. Compared with other edge operators, the mechanism of Sobel is the differential of two rows or two columns, and it can fully enhance elements on both sides, which makes the edge seem more obvious. In this work, in addition to the level and vertical filter, we further add a diagonal filter to our network in.52
Vision transformers
The transformer was first proposed for natural language processing. The transformer was similar to an encoder-decoder structure which consists of multi-head self-attention blocks, normalization layers, and point-wise feedforward networks. The vision transformer, proposed by Dosovitskiy et al.,34 can be considered the first vision transformer backbone for image classification. The VIT demonstrated the effectiveness of transformer in CV tasks, although it required huge parameters and memory because the global computation led to quadratic complexity. To reduce the use of GPU memory and the number of calculation parameters, the Swin transformer37 computed self-attention within local windows. The computational complexity of a global multi-head self-attention (MSA) module and a window based on image patches with the size of n × n are respectively recorded as and , where n2, C, and M are the number of pixels in an image patch, the channel number of the hidden layers, and window size, respectively. To solve the global modeling problem caused by local windows, the Swin transformer designed a shifted window to strengthen the connection between adjacent windows. Because of its impressive performance, the transformer has also been introduced to medical image processing. Chen et al.54 proposed TransUNet, which claimed to be the first transformer-based medical image segmentation network. Recently, Eformer used self-attention and depth-wise convolution for better local context capture in medical image denoising.55 Our novel network MIST-net was developed to explore transformers in sparse-view data reconstruction. Again, we designed a Swin Recformer sub-network by combining the Swin transformer and convolution layer to make full use of both shallow and deep features.
MIST-net
Figure 1 illustrates the flowchart of our proposed MIST-net. There are three key components: initial recovery, data consistency, and high-definition reconstruction. Both initial recovery and data consistency have two sub-networks; one works in radon domain and the other was designed within images domain. We will describe each sub-network, and more network details can be found in Appendix D of Supplemental experimental procedures (see Tables S3–S5).
Initial recovery module
The architecture of this module is shown in Figure 1. The first block of this module is an encoder-decoder block with a linear interpolation at the beginning. This part is designed to restore spare-view projection data to full-view projection data . This is achieved by a projection domain sub-network . At the first layer of initial reconstruction is the network-based image reconstruction (i.e., FBP layer). An edge enhancement reconstruction sub-network was used to process the FBP layer output and further obtain a clearer and faithful image s1. The initial recovery module can be expressed as follows:
| (Equation 7) |
where represents the reconstruction sub-network from the initial recovery module.
Data consistency module
The errors are always introduced in projections and images because the interpolation in the radon domain cannot accurately predict the missing original data. In addition, the following reconstruction sub-network in the images domain may result in false positive and negative results. These errors may cause the secondary artifacts to compromise the quality of images. The data consistency module consists of two parts: the projection residual processing sub-network and the image residual processing sub-network . Here, we use two encoder-decoder blocks to handle residual data. The re-sampled residual data from can be expressed as , where represents the projection data from the image s1. The estimated projection data residual of the data consistency module is expressed as
| (Equation 8) |
In addition to the data difference computed by the trained data residual network according to (Equation 5), there is also an image difference between the output of the initial recovery module and desired image. Here, the image residual processing sub-network was further used to reduce the data inconsistency. The output of the image residual processing sub-network is as follows:
| (Equation 9) |
Then, we can get the middle reconstruction output by adding the output of initial recovery module to the results of data consistency module; we have that
| (Equation 10) |
High-definition reconstruction module
The sparse-view projection may lead to serious streaking artifacts in CT images, especially when the number of views is extremely scanty. The function of this module is similar to post-processing methods that learn mappings from poor images to clear images. In traditional image super-resolution and denoising tasks, SwinIR56 has achieved great success by using the Swin transformer as a backbone. In this part, we propose a hybrid architecture called Swin Recformer, which is based on both convolution layers and Swin transformer layers to implement the image reconstruction task. As shown in Figure 1D, the Swin Recformer contains convolutional layers, Swin transformer mixed convolution (STC), units and a few residual connections. Each STC unit consists of six transformer layers as well as one convolutional layer.
In this section, we will provide architecture details of the STC unit. An STC unit contains six Swin transformer layers and a 3 × 3 convolution layer. The Swin transformer block contains 2 core designs, which are described below. First, the Swin transformer designed a non-overlapping window-based multi-head self-attention (W-MSA) block, which can learn the long-range information correlation in a small-size window region (e.g., a 16 × 16 feature map). Second, the shifted window-based multi-head self-attention (SW-MSA) block adds shifted windows to improve interactions between different windows. In the lower right of the Figure 1D, two successive Swin transformer blocks are presented. Each Swin transformer block is successively composed of LN layer, multi-head self-attention mechanism, residual connection, and MLP. The W-MSA mechanism and the SW-MSA mechanism make up two adjacent transformer blocks. With the shifted window partitioning design, consecutive Swin transformer blocks are computed as follows:
| (Equation 11) |
| (Equation 12) |
| (Equation 13) |
| (Equation 14) |
where and denote the output features of the W-MSA/SW-MSA module and the MLP module for block , respectively; W-MSA and SW-MSA denote window-based multi-head self-attention using regular and shifted window partitioning configurations, respectively. As for the traditional transformer methods, self-attention is computed as follows:
| (Equation 15) |
where are the query, key, and value matrices; d is the query/key dimension; and M2 is the number of patches in a window. Because the relative position along each axis lies in the range [−M + 1, M − 1], we parameterize a smaller sized bias matrix , and values in are taken from . After six Swin transformer blocks, a 3 × 3 convolutional layer was added to enhance the feature. Between adjacent STC units, a residual connection was used to aggregate feature maps generated from transformer and convolution.
Loss functions
For sparse-view CT reconstruction, we optimize the parameters of MIST-net by minimizing the dual-domain mean square error (MSE). It can be written as follows:
| (Equation 16) |
where is the image MSE term. and stand for the label and output images, respectively. is the projection MSE, where and represent projection label and output. is a weighting factor; here it was set as 0.1.
Acknowledgments
This work was partially supported by the Shenzhen Science and Technology Program (grants GXWD20201231165807008 and 20200825113400001); the Natural Science Foundation of Guangdong Province, China (2022A1515011384); and the National Natural Science Foundation of China (62101606,81702198).
Author contributions
J.P. proposed the reconstruction method, debugged code, carried out experiments, and wrote the draft manuscript. H.Z. provided beneficial suggestions for revision. Weifei Wu and Z.G. commented on the paper and provided valuable suggestions. Weiwen Wu initialized and supervised the project, debugged code, and further revised the draft.
Declaration of interests
The authors declare no competing interests.
Published: April 22, 2022
Footnotes
Supplemental information can be found online at https://doi.org/10.1016/j.patter.2022.100498.
Supplemental information
Data and code availability
All original code has been publicly released on https://zenodo.org/record/6368099. This paper analyses existing public data. These data are available at: https://www.aapm.org/GrandChallenge/LowDoseCT/.
References
- 1.Bakator M., Radosav D. Deep learning and medical diagnosis: a review of literature. Multimodal Tech. Interact. 2018;2:47. [Google Scholar]
- 2.Long C., Xu H., Shen Q., Zhang X., Fan B., Wang C., Zeng B., Li Z., Li X., Li H. Diagnosis of the Coronavirus disease (COVID-19): rRT-PCR or CT? Eur. J. Radiol. 2020;126:108961. doi: 10.1016/j.ejrad.2020.108961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Brenner D.J., Hall E.J. Computed tomography—an increasing source of radiation exposure. N. Engl. J. Med. 2007;357:2277–2284. doi: 10.1056/NEJMra072149. [DOI] [PubMed] [Google Scholar]
- 4.Bian J., Siewerdsen J.H., Han X., Sidky E.Y., Prince J.L., Pelizzari C.A., Pan X. Evaluation of sparse-view reconstruction from flat-panel-detector cone-beam CT. Phys. Med. Biol. 2010;55:6575. doi: 10.1088/0031-9155/55/22/001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bian J., Wang J., Han X., Sidky E.Y., Shao L., Pan X. Optimization-based image reconstruction from sparse-view data in offset-detector CBCT. Phys. Med. Biol. 2012;58:205. doi: 10.1088/0031-9155/58/2/205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Katsevich A. Theoretically exact filtered backprojection-type inversion algorithm for spiral CT. SIAM J. Appl. Math. 2002;62:2012–2026. [Google Scholar]
- 7.Litjens G., Kooi T., Bejnordi B.E., Setio A.A.A., Ciompi F., Ghafoorian M., Van Der Laak J.A., Van Ginneken B., Sánchez C.I. A survey on deep learning in medical image analysis. Med. Image Anal. 2017;42:60–88. doi: 10.1016/j.media.2017.07.005. [DOI] [PubMed] [Google Scholar]
- 8.Niu C., Zhang J., Wang G., Liang J. Computer Vision – ECCV 2020: 16th European Conference. Springer; 2020. Gatcluster: self-supervised Gaussian-attention network for image clustering; pp. 735–751. [Google Scholar]
- 9.Niu C., Cong W., Fan F.-L., Shan H., Li M., Liang J., Wang G. Low-dimensional manifold constrained disentanglement network for metal artifact reduction. IEEE Trans. Radiat. Plasma Med. Sci. 2021 doi: 10.1109/TRPMS.2021.3122071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chen H., Zhang Y., Kalra M.K., Lin F., Chen Y., Liao P., Zhou J., Wang G. Low-dose CT with a residual encoder-decoder convolutional neural network. IEEE Trans. Med. Imaging. 2017;36:2524–2535. doi: 10.1109/TMI.2017.2715284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zhang Z., Liang X., Dong X., Xie Y., Cao G. A sparse-view CT reconstruction method based on combination of DenseNet and deconvolution. IEEE Trans. Med. Imaging. 2018;37:1407–1417. doi: 10.1109/TMI.2018.2823338. [DOI] [PubMed] [Google Scholar]
- 12.Wang G., Ye J.C., De Man B. Deep learning for tomographic image reconstruction. Nat. Machine Intelligence. 2020;2:737–748. [Google Scholar]
- 13.Kyong Hwan J., McCann M.T., Froustey E., Unser M. Deep convolutional neural network for inverse problems in imaging. IEEE Trans. Image Process. 2017;26:4509–4522. doi: 10.1109/TIP.2017.2713099. [DOI] [PubMed] [Google Scholar]
- 14.Bertram M., Rose G., Schafer D., Wiegert J., Aach T. IEEE; 2004. Directional Interpolation of Sparsely Sampled Cone-Beam CT Sinogram Data; pp. 928–931. [Google Scholar]
- 15.Liu J., Ma J., Zhang Y., Chen Y., Yang J., Shu H., Luo L., Coatrieux G., Yang W., Feng Q. Discriminative feature representation to improve projection data inconsistency for low dose CT imaging. IEEE Trans. Med. Imaging. 2017;36:2499–2509. doi: 10.1109/TMI.2017.2739841. [DOI] [PubMed] [Google Scholar]
- 16.Yu W., Wang C., Huang M. Edge-preserving reconstruction from sparse projections of limited-angle computed tomography using ℓ 0-regularized gradient prior. Rev. Scientific Instr. 2017;88:043703. doi: 10.1063/1.4981132. [DOI] [PubMed] [Google Scholar]
- 17.Humphries T., Winn J., Faridani A. Superiorized algorithm for reconstruction of CT images from sparse-view and limited-angle polyenergetic data. Phys. Med. Biol. 2017;62:6762. doi: 10.1088/1361-6560/aa7c2d. [DOI] [PubMed] [Google Scholar]
- 18.Xie S., Xu H., Li H. IEEE; 2019. Artifact Removal Using GAN Network for Limited-Angle CT Reconstruction; pp. 1–4. [Google Scholar]
- 19.Wang J., Liang J., Cheng J., Guo Y., Zeng L. Deep learning based image reconstruction algorithm for limited-angle translational computed tomography. PLoS One. 2020;15:e0226963. doi: 10.1371/journal.pone.0226963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hu D., Liu J., Lv T., Zhao Q., Zhang Y., Quan G., Feng J., Chen Y., Luo L. Hybrid-domain neural network processing for sparse-view CT reconstruction. IEEE Trans. Radiat. Plasma Med. Sci. 2021;5:88–98. doi: 10.1109/trpms.2020.3011413. [DOI] [Google Scholar]
- 21.Liu Y., Deng K., Sun C., Yang H. A lightweight structure aimed to utilize spatial correlation for sparse-view CT reconstruction. arXiv. 2021 doi: 10.48550/arXiv.2101.07613. Preprint at. [DOI] [Google Scholar]
- 22.Zhang Q., Hu Z., Jiang C., Zheng H., Ge Y., Liang D. Artifact removal using a hybrid-domain convolutional neural network for limited-angle computed tomography imaging. Phys. Med. Biol. 2020;65:155010. doi: 10.1088/1361-6560/ab9066. [DOI] [PubMed] [Google Scholar]
- 23.Wu W., Hu D., Niu C., Yu H., Vardhanabhuti V., Wang G. DRONE: dual-domain residual-based optimization NEtwork for sparse-view CT reconstruction. IEEE Trans. Med. Imaging. 2021;40:3002–3014. doi: 10.1109/TMI.2021.3078067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zheng A., Gao H., Zhang L., Xing Y. A dual-domain deep learning-based reconstruction method for fully 3D sparse data helical CT. Phys. Med. Biol. 2020;65:245030. doi: 10.1088/1361-6560/ab8fc1. [DOI] [PubMed] [Google Scholar]
- 25.Cheng L., Ahn S., Ross S.G., Qian H., De Man B. International Conference on Fully Three-Dimensional Image Reconstruction in Radiology and Nuclear Medicine. 2017. Accelerated iterative image reconstruction using a deep learning based leapfrogging strategy; pp. 715–720. [Google Scholar]
- 26.Chen H., Zhang Y., Chen Y., Zhang J., Zhang W., Sun H., Lv Y., Liao P., Zhou J., Wang G. LEARN: Learned experts’ assessment-based reconstruction network for sparse-data CT. IEEE Trans. Med. Imaging. 2018;37:1333–1347. doi: 10.1109/TMI.2018.2805692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Zhang Y., Chen H., Xia W., Chen Y., Liu B., Liu Y., Sun H., Zhou J. LEARN++: recurrent dual-domain reconstruction network for compressed sensing CT. arXiv. 2020 doi: 10.48550/arXiv.2012.06983. Preprint at. [DOI] [Google Scholar]
- 28.Xiang J., Dong Y., Yang Y. FISTA-Net: learning A fast iterative shrinkage thresholding network for inverse problems in imaging. IEEE Trans. Med. Imaging. 2021;40:1329–1339. doi: 10.1109/TMI.2021.3054167. [DOI] [PubMed] [Google Scholar]
- 29.Bello I., Zoph B., Vaswani A., Shlens J., Le Q.V. 2019 IEEE/CVF International Conference on Computer Vision (ICCV) IEEE; 2019. Attention augmented convolutional networks; pp. 3286–3295. [Google Scholar]
- 30.Cordonnier J.-B., Loukas A., Jaggi M. On the relationship between self-attention and convolutional layers. arXiv. 2019 doi: 10.48550/arXiv.1911.03584. Preprint at. [DOI] [Google Scholar]
- 31.Vaswani A., Shazeer N., Parmar N., Uszkoreit J., Jones L., Gomez A.N., Kaiser Ł., Polosukhin I. Attention Is All You Need. arXiv. 2017:5998–6008. doi: 10.48550/arXiv.1706.03762pp. Preprint at. [DOI] [Google Scholar]
- 32.Radford A., Wu J., Child R., Luan D., Amodei D., Sutskever I. Language models are unsupervised multitask learners. OpenAI blog. 2019;1:9. [Google Scholar]
- 33.Otter D.W., Medina J.R., Kalita J.K. A survey of the usages of deep learning for natural language processing. IEEE Trans. Neural Netw. Learn. Syst. 2020;32:604–624. doi: 10.1109/TNNLS.2020.2979670. [DOI] [PubMed] [Google Scholar]
- 34.Dosovitskiy A., Beyer L., Kolesnikov A., Weissenborn D., Zhai X., Unterthiner T., Dehghani M., Minderer M., Heigold G., Gelly S. An image is worth 16x16 words: transformers for image recognition at scale. arXiv. 2020 doi: 10.48550/arXiv.2010.11929. Preprint at. [DOI] [Google Scholar]
- 35.Arnab A., Dehghani M., Heigold G., Sun C., Lučić M., Schmid C. Vivit: a video vision transformer. arXiv. 2021 doi: 10.48550/arXiv.2103.15691. Preprint at. [DOI] [Google Scholar]
- 36.Zhou H.-Y., Guo J., Zhang Y., Yu L., Wang L., Yu Y. nnFormer: interleaved transformer for volumetric segmentation. arXiv. 2021 doi: 10.48550/arXiv.2109.03201. Preprint at. [DOI] [Google Scholar]
- 37.Liu Z., Lin Y., Cao Y., Hu H., Wei Y., Zhang Z., Lin S., Guo B. Swin transformer: Hierarchical vision transformer using shifted windows. arXiv. 2021 doi: 10.48550/arXiv.2103.14030. Preprint at. [DOI] [Google Scholar]
- 38.Ronneberger O., Fischer P., Brox T. Springer; 2015. U-net: Convolutional Networks for Biomedical Image Segmentation; pp. 234–241. [Google Scholar]
- 39.AAPM challenge. https://www.aapm.org/GrandChallenge/LowDoseCT/
- 40.Yu H., Wang G., Hsieh J., Entrikin D.W., Ellis S., Liu B., Carr J.J. Compressive sensing–Based interior tomography. Preliminary Clin. Appl. 2011;35:762. doi: 10.1097/RCT.0b013e318231c578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Zeng G. The fan-beam short-scan FBP algorithm is not exact. Phys. Med. Biol. 2015;60:N131. doi: 10.1088/0031-9155/60/8/N131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Niu C., Wang G., Yan P., Hahn J., Lai Y., Jia X., Krishna A., Mueller K., Badal A., Myers K. Noise entangled GAN for low-dose CT simulation. arXiv. 2021 doi: 10.48550/arXiv.2102.09615. Preprint at. [DOI] [Google Scholar]
- 43.Xu M., Hu D., Luo F., Liu F., Wang S., Wu W. Limited-angle X-ray CT reconstruction using image gradient ℓ₀-norm with dictionary learning. IEEE Trans. Radiat. Plasma Med. Sci. 2020;5:78–87. [Google Scholar]
- 44.Wu W., Zhang Y., Wang Q., Liu F., Chen P., Yu H. Low-dose spectral CT reconstruction using image gradient ℓ0–norm and tensor dictionary. Appl. Math. Model. 2018;63:538–557. doi: 10.1016/j.apm.2018.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Wu W., Yu H., Gong C., Liu F. Swinging multi-source industrial CT systems for aperiodic dynamic imaging. Opt. Express. 2017;25:24215–24235. doi: 10.1364/OE.25.024215. [DOI] [PubMed] [Google Scholar]
- 46.Yu H., Wang G. Compressed sensing based interior tomography. Phys. Med. Biol. 2009;54:2791. doi: 10.1088/0031-9155/54/9/014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Wu W., Hu D., An K., Wang S., Luo F. A high-quality photon-counting CT technique based on weight adaptive total-variation and image-spectral tensor factorization for small animals imaging. IEEE Trans. Instrum. Meas. 2020;70:1–14. [Google Scholar]
- 48.Shen Y., Li J., Zhu Z., Cao W., Song Y. Image reconstruction algorithm from compressed sensing measurements by dictionary learning. Neurocomputing. 2015;151:1153–1162. [Google Scholar]
- 49.Zha Z., Liu X., Zhang X., Chen Y., Tang L., Bai Y., Wang Q., Shang Z. Compressed sensing image reconstruction via adaptive sparse nonlocal regularization. Vis. Comput. 2018;34:117–137. [Google Scholar]
- 50.Dong J., Fu J., He Z. A deep learning reconstruction framework for X-ray computed tomography with incomplete data. PLoS One. 2019;14:e0224426. doi: 10.1371/journal.pone.0224426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Sobel I., Feldman G. 1968. A 3x3 isotropic gradient operator for image processing; pp. 271–272. a talk Stanford Artif. Project. [Google Scholar]
- 52.Liang T., Jin Y., Li Y., Wang T. IEEE; 2020. EDCNN: Edge Enhancement-Based Densely Connected Network with Compound Loss for Low-Dose CT Denoising; pp. 193–198. [Google Scholar]
- 53.Sharifrazi D., Alizadehsani R., Roshanzamir M., Joloudari J.H., Shoeibi A., Jafari M., Hussain S., Sani Z.A., Hasanzadeh F., Khozeimeh F. Fusion of convolution neural network, support vector machine and Sobel filter for accurate detection of COVID-19 patients using X-ray images. Biomed. Signal Process. Control. 2021;68:102622. doi: 10.1016/j.bspc.2021.102622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Chen J., Lu Y., Yu Q., Luo X., Adeli E., Wang Y., Lu L., Yuille A.L., Zhou Y. Transunet: transformers make strong encoders for medical image segmentation. arXiv. 2021 doi: 10.48550/arXiv.2102.04306. Preprint at. [DOI] [Google Scholar]
- 55.Luthra A., Sulakhe H., Mittal T., Iyer A., Yadav S. Eformer: edge enhancement based transformer for medical image denoising. arXiv. 2021 doi: 10.48550/arXiv.2109.08044. Preprint at. [DOI] [Google Scholar]
- 56.Liang J., Cao J., Sun G., Zhang K., Van Gool L., Timofte R. SwinIR: image restoration using swin transformer. arXiv. 2021:1833–1844. doi: 10.48550/arXiv.2108.10257. Preprint at. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All original code has been publicly released on https://zenodo.org/record/6368099. This paper analyses existing public data. These data are available at: https://www.aapm.org/GrandChallenge/LowDoseCT/.