Summary
Determining the effect of vaccine-induced immune response on disease risk is an important goal of vaccinology. Typically, immune correlates analyses are conducted prospectively with immune response measured shortly after vaccination and subsequent disease status regressed on immune response. In outbreaks and rare disease settings, collecting samples from all vaccinees is not feasible. The test negative design is a retrospective design used to measure vaccine efficacy where symptomatic individuals who present at a clinic are assessed for relevant disease (cases) or some other disease (controls) and vaccination status ascertained. This article proposes that test negative vaccinees have immune response to vaccine assessed both for relevant (e.g., Ebola) and irrelevant (e.g., vector) proteins. If the latter immune response is unaffected by active (Ebola) infection, and is correlated with the relevant immune response, it can serve as a proxy for the immune response of interest proximal to infection. We show that logistic regression using imputed immune response as the covariate and case disease as outcome can estimate the prospective immune response slope and detail the assumptions needed for unbiased inference. The method is evaluated by simulation under various scenarios including constant and decaying immune response. A simulated dataset motivated by ring vaccination for an ongoing Ebola outbreak is analyzed.
Keywords: Imputation; Likelihood, Logisitic regression; Regression calibration
1. Introduction
The test negative design is a kind of case–control study used to estimate vaccine efficacy (Fukushima and Hirota, 2017). Originally proposed for pneumococcal vaccination Broome and others (1980), it has been used extensively for influenza vaccine see Jackson and Nelson (2013) as well as rotavirus vaccine (Boom and others, 2010). The basic design uses symptomatic subjects who come to a clinic with symptoms that could be either the vaccine preventable case disease (say Ebola) or a different control disease (non-Ebola). Vaccination status is ascertained and vaccine efficacy (VE) calculated as one minus the odds of vaccine among cases divided by the odds of vaccine among controls. This equals the prospective vaccine efficacy due to the invariance of the odds ratio for prospective or case–control sampling. The test negative study requires that all symptomatic vaccinees have the same probability of a clinic visit, an analogous condition for the symptomatic unvaccinated subjects, and that exposure be the same for all vaccinated and unvaccinated subjects. Numerous authors have investigated the sensitivity of the test negative design to these assumptions Sullivan and others (2016), Westreich and Hudgens (2016), Fukushima and Hirota (2017), and Lewnard and others (2018).
An important goal in vaccine development is to evaluate how vaccine-induced immune response correlates with risk of disease, known as a “correlate of risk” (Qin and others, 2007). Identification of a specific immune response that is associated with low disease risk provides a target for vaccine development. A common approach to evaluate immune correlates is to measure immune response to the vaccine shortly after vaccination determine who gets infected during prospective follow-up and then use logistic regression to predict the probability of disease as a function of measured immune response. Ideally, such an approach would be used in outbreak settings, see Halloran and others (2020), but at times it may not be feasible to prospectively collect samples. In addition, for rare diseases in non-outbreak settings, an enormous number of samples may need to be collected for traditional correlates analysis. In other settings, the durability of a vaccine is of interest and thus the immune response at the time of exposure is of interest though this may be many years after vaccination.
This article details an approach to immune correlates analysis under a test negative design using samples collected from vaccinees proximal to exposure. To fix ideas, consider the rVSV vaccine for Ebola which induces an immune response to Ebola antigens say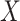 
as well as to the Vesicular Stomatitis Vaccine (VSV) vector, say 
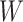. Naively, one might measure 
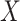among the symptomatic vaccinees who visit a clinic and fit a logistic regression with outcome being Ebola and covariate 
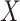. The problem is that Ebola immune response is likely massive in those with Ebola infection. What we really want is the pure vaccine-induced 
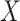just prior to exposure in both Ebola cases and controls. As a proxy, we can use 
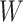at the clinic visit which should be similar to 
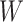at exposure. Provided 
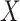and 
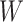are correlated, we can use 
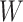to impute the vaccine-induced 
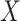at exposure. We can then fit a logistic regression with Ebola as the outcome using the expectation of 
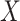conditional on 
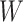, say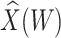 
, as the covariate; also known as regression calibration. If the time interval from vaccination to exposure is relatively long, the substantial decay of the immune response over time may need to be addressed. This can be accomplished either by stratification, or flexible parametric modeling of risk over study time, provided the disease is rare. We evaluate the performance of the method via simulation and illustrate its use by a simulated dataset meant to reflect the recent Ebola outbreak in the Democratic Republic of the Congo where the rVSV Ebola vaccine was deployed using ring vaccination.
2. Formulation and models
2.1. Constant immune response
An important goal in vaccine development is to assess how immune response to the vaccine,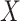 
, is associated with the risk of infection/disease 
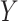. In a randomized trial, vaccinees 
have an immune response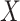 
measured shortly after vaccination. For now, assume that 
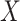does not change. Volunteers are followed for a period of time 
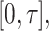and disease status is recorded. With a test negative design, we need both the case disease and a different (control) disease for reference while the undiseased are not used. We thus define the disease of interest (case), a different disease (control), or undiseased which we denote by 
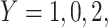respectively. We need three possibilities for later use in a test negative design. If both diseases are acquired, we use the case disease. We assume that among vaccinees
 |
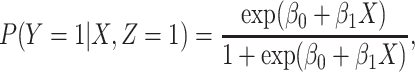(2.1) |
and that
 |
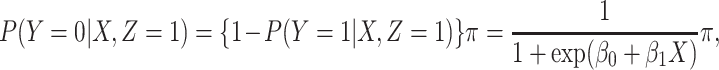(2.2) |
where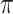 
is the conditional probability that a vaccinee who avoids the case disease develops the control disease. Note that 
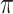is assumed free of 
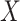as it should not have an effect on acquiring the control disease. An immune correlates analysis relating risk of disease to immune response can be conducted by fitting (2.1) in vaccinees using as outcome the indicator that 
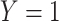(versus 
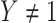). For developmental simplicity, we do not incorporate baseline covariates in (2.1) though one can.
For certain settings,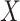 
may not be measured shortly after vaccination. For rare diseases it may be prohibitively costly, or in outbreak settings it may not be logistically feasible. In other settings, the durability of a vaccine is unknown and thus 
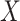at exposure is of interest even though it may be many years since vaccination. Or in outbreak settings, it may not be logistically feasible to draw samples. In all these situations, a correlates analysis using the immune response proximal to exposure would be of great interest.
A design that collects information proximal to exposure is the test negative which takes symptomatic patients (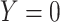
or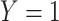 
) who present at a clinic and tests them for the disease of interest and records vaccination status. Those testing positive are classified as cases (
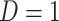) while those testing negative are classified as controls (
). Formally,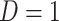 
if 
and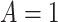 
, while 
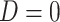if 
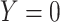, and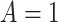 
, where 
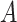is the indicator a person with either disease (i.e., 
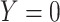or 1) arrives at the clinic. Overall vaccine efficacy is estimated as
 |
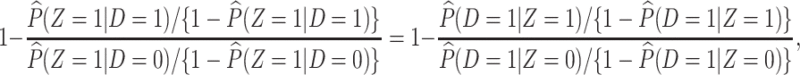(2.3) |
where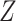 
is the vaccine indicator see Guolo (2008). The second equality follows from the invariance of the odds to prospective and retrospective sampling. The test negative design can be much more efficient than a prospective study, but does require more assumptions.
Suppose, we somehow knew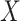 
in all vaccinees who arrived at the clinic. Let 
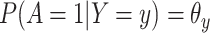be the arrival probability for an symptomatic vaccinee with disease status 
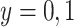. Based on (2.1) and (2.2), we can derive the probability that a symptomatic vaccinee who arrives at the clinic has the case disease:
 |
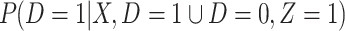(2.4) |
 |
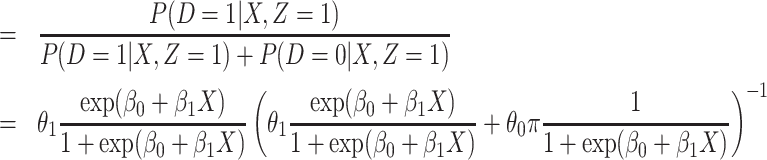(2.5) |
 |
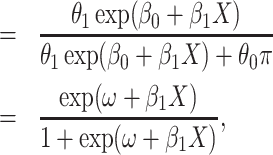(2.6) |
where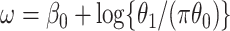 
. Thus, if we fit a simple logistic regression model with 
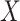as covariate among vaccinees in the clinic, we can recover the slope 
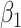from (2.1). Note that this obtains even if we allow cases and controls to have different arrival probabilities. The usual test negative design requires 
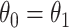for all vaccinees. We next consider the actual setting where 
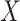must be derived from measurements at arrival. Figuring out how to get 
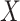from test negative data is the major contribution of this article.
In practice, we can measure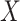 
when subjects arrive at the clinic, say 
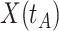where 
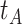is the arrival time. Naively fitting (2.6) using the clinic 
is problematic. For vaccinees who present with the control disease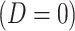 
, 
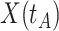should be close to 
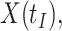where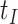 
is just prior to infection as control disease should have little effect on the vaccine-induced immune response to the relevant vaccine antigen. But the vaccinated who present with the disease of interest 
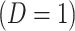are likely to have quite high 
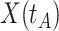due to active infection. So 
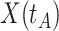at arrival is different from 
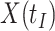for vaccinees with 
.
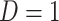However, certain vaccines (e.g., vector based vaccines) also induce an immune response to irrelevant antigens (e.g., the vector), say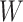 
, which should be relatively unaffected by active infection. To fix ideas, suppose that 
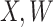achieve stable values shortly after vaccination and remain constant in 
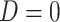diseased controls. If 
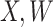are correlated prior to exposure, then one could predict the unadulterated 
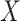at exposure using the 
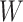at presentation. One could then use 
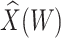, the imputed immune response to relevant vaccine antigens at exposure, in lieu of 
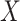. This works if 
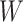is unaffected by case or control disease and 
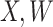are unaffected by control disease. But these requirements can be weakened. Suppose that for both groups, we observe 
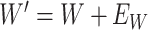and for those with control disease we observe 
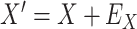where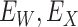 
are errors (which can be correlated and have non-zero means). Thus 
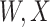are the pre-infection values while 
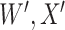are the values observed at the clinic when subjects are diseased. If 
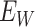differs for case and control disease, however, the control model fitted on 
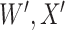does not apply to cases and a more complex approach would be required.
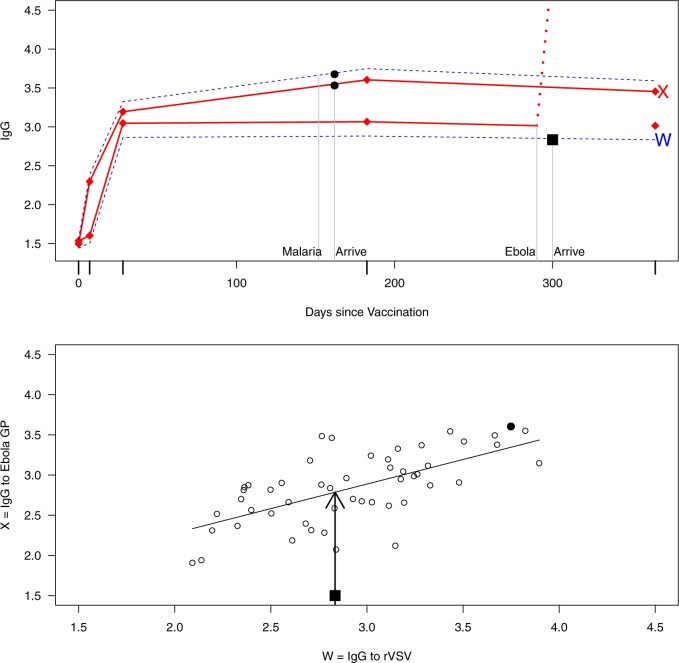
This strategy is displayed in Figure 1. The diamonds are actual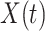 
while the two solid bent lines are linear interpolations of the IgG antibody response to the outside of the Ebola virus i.e., Ebola glycoprotein (GP) following rVSV vaccination from two randomly selected subjects in Prevail 1, an immunogenicity trial of the rVSV vaccine Kennedy and others (2016). Immune response was measured at baseline, 1 week, 1 month, 6 months, and 1 year (diamonds). While IgG response to vector 
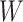was not measured, we illustrate interpolated hypothetical values by the dashed bent lines. We pretend that these two subjects were infected, with, respectively, malaria and Ebola. They became symptomatic and arrived at a clinic a few days after productive exposure. The 
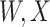values for the malaria patient at arrival are similar to the values at exposure, but for the Ebola patient, only 
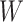is similar at exposure and arrival while 
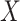(dashed line) is massive from active Ebola infection., The bottom panel illustrates hypothetical data with a correlation of 0.70 between 
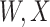that might have been obtained from a sample of vaccinated controls who arrived at the clinic. From this relationship, we can impute 
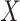at infection for the Ebola patient.
Fig. 1.
Top panel: IgG immune responses over time for two vaccinated volunteers from Prevail 1. The solid bent line is the linear interpolation of X = IgG to Ebola GP measured at weeks 0, 1, 4, 26, and 52 (red diamonds). The dotted red line is hypothetical X to reflect Ebola infection. The dashed bent line is hypothetical W=IgG to rVSV vector. The subject infected with malaria arrives with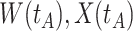 
similar to those at infection. Only 
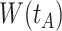is similar to the value prior to infection for the Ebola infected volunteer. Bottom panel: a scatter plot of 
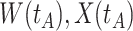for the controls (circles) with imputation of 
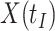for the Ebola case (solid square).
More formally, from the controls we can fit the model
 |
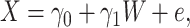(2.7) |
where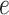 
is an error term. Using the estimated parameters, we impute 
,
 |
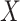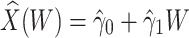and fit the logistic regression model in the symptomatic vaccinees
 |
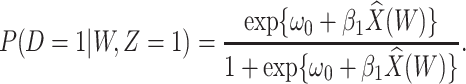(2.8) |
This imputation is known as regression calibration and is a simple way to correct for measurement error in a covariate. Note that we impute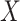 
even in the vaccinated controls where 
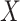is known and thus treat both cases and controls in the same way. Using imputation in all those with 
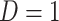and 
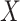directly in all those with 
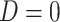leads to substantial bias. Because we use 
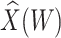, which is estimated instead of 
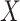, which is fixed, standard errors from standard software fitting (2.8) are likely too small. A simple remedy is to use the bootstrap or use derived standard errors, see Rosner and others (1990).
Instead of using an imputed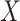 
for regression calibration, one can perform a correlates analysis using 
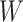directly. While 
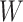is not part of the mechanism of protection, “correlates” analyses are often done with immune responses that may not be causal but are presumably related to the causal mechanism. As an example, smallpox vaccination involves scraping the arm with antigen. A vaccine “take” is recorded if a pox forms. While the scar itself does not protect, it is a proxy for a robust relevant immune response to the vaccine and risk of disease by scar or “take” is of interest even though it is clearly a non-mechanistic correlate of risk using the nomenclature of Plotkin and Gilbert (2012). Use of 
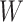directly is simple, avoids the measurement error issue, requires no imputation, and has slightly better power than use of imputed 
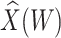, as we will see. Use of 
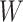by itself, however, is not easily interpretable unless as a proxy for vaccine “take,” i.e., 
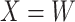is binary and 
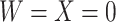is like being unvaccinated.
2.2. Waning immune response
The above development is appropriate if the immune responses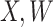 
are stable during the followup period for the cohort study. In general, antibody decay over time and the above approach can lead to bias. To see this, suppose that nearly everyone was vaccinated prior to an outbreak which exploded and then waned so the risk of the case disease decreased over time, coinciding with the antibody decay. Further suppose that the control disease rate was constant over time. Then even if 
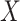was unrelated to 
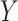we would associate low 
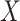with low risk and we would tend to estimate a positive 
. And the problem is even more complicated as, in general, people will be vaccinated at various times and the case disease rate might vary with time.
Let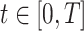 
be the time since the start of the test negative study. To develop the time varying 
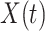setting more formally, we will assume that the hazard for a case disease arriving at time 
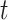with covariate 
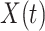is given by
 |
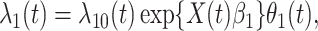(2.9) |
where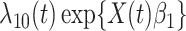 
is the hazard for case disease a little before 
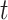and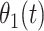 
is the probability of arriving at the clinic at time 
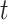, given a case infection just prior to 
.
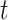We analogously assume that the hazard for the control disease is independent of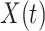 
and arbitrary, as is the instantaneous probability of arriving. Thus, the hazard for a person with control disease arriving at the clinic is
 |
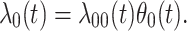Recall that the probability of an event in a small interval [t,t+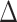
), given no event prior to 
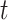, is approximately 
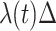for an arbitrary hazard function 
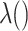. Under a “rare” disease assumption, we can calculate the probability that a given vaccinee who showed up at time 
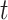was a case as
 |
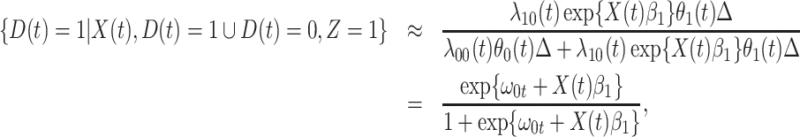(2.10) |
where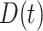 
is the indicator of case disease for an arrival at time 
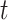and
 |
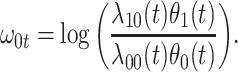Now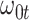 
could be constant. One way this can happen is if 
and 
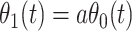so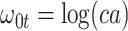 
. If so, we can simply fit logistic regression to the 
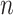data points 
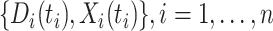. In general, 
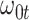will not be constant so that
 |
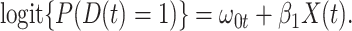(2.11) |
We might specify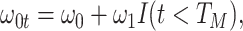 
where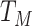 
is say the median followup time. Or we could fit a quadratic function of log(t). In practice, different approaches to specify 
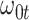could be tried and the best one selected. Note that we only need know (or impute) 
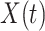at the time of arrival to the clinic for each vaccinee.
3. Assumptions
The above approaches recover the prospective slope f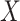or 
or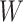 
if the model assumptions are met. In this section, we delineate the assumptions when 
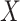is known for all, constant after time 
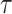, the logistic-type model 
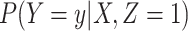is correctly specified, and there is independence between exposure and 
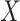. The major issue is thus whether vaccinated cases (controls) arrive with fixed probability 
(
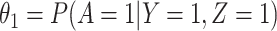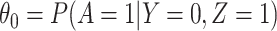). Or equivalently, whether those who arrive are a representative sample of cases and controls respectively. We allow 
.
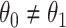1. The vaccinees who arrive with the control disease provide a representative sample of the distribution of immune response among those vaccinated without the case disease.
This follows if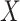 
has no impact on the probability of acquiring the control disease and no impact on the probability of arriving at the clinic so 
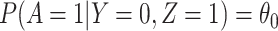. Note we can allow 
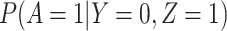to depend on latent or measured disease stratus or baseline covariates as long as they independent of 
.
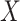2. The vaccinees who arrive with the case disease provide a representative sample of the distribution of immune response among those vaccinated with the case disease.
 |
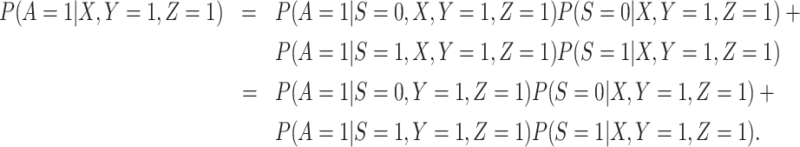(3.12) |
The last equality follows if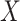 
has no additional impact on 
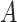given severity which seems a reasonable assumption. Using the last equality, we can see that 
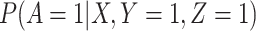does not depend on 
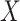if either 
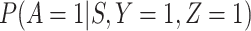is free of 
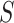or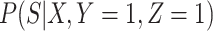 
is free of 
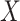. We discuss each in turn.
Now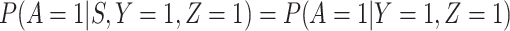 
if severity does not impact health seeking behavior. This might occur if all cases are equally encouraged to arrive at a clinic and all cases are equally compliant, or if the severity gradient is modest enough that it does not change behavior.
Next consider when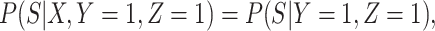 
i.e.,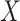 
has no impact on severity given a vaccinee is infected. While this obtains if the vaccine’s mechanism of action is all-or-none, it is a weaker condition. An all-or-none vaccine implies that the distribution of severity is unchanged by vaccination so that 
, where 
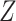is the vaccine indicator. But we only require 
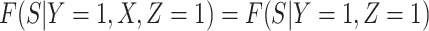which allows 
.
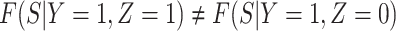If neither assumption is plausible but case disease severity is observed, there is a remedy provided disease follows the prospective logistic regression model:
 |
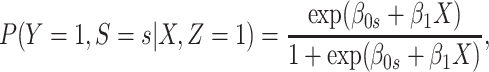(3.13) |
for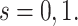 
Then even if 
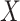affects the arrival probability through the observable disease severity, recovery of 
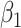using data 
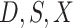follows from arguments analogous to those used to derive (2.6). One can show that (3.13) implies the distribution of disease severity among the vaccinated infecteds, 
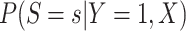, varies with 
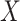reflecting a kind of disease modifying vaccine.
These conditions can be relaxed using baseline covariates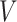 
. If the prospective model (2.1) controls for confounding by specifying 
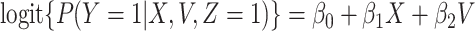, then the above arguments go through, even if the arrival probabilities satisfy 
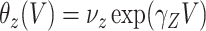. One can show that 
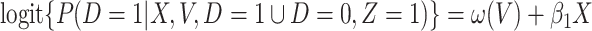with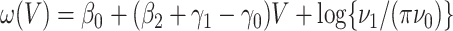 
, and thus 
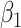remains the coeffience for 
.
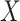To summarize, assuming the verity of (3.12) and a correctly specified model for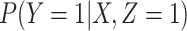 
, we can recover 
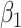even if 
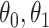depend on 
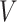unless disease severity is unobservable, 
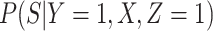depends on 
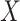, and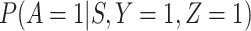 
depends on 
.
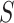4. Simulations
4.1. Constant immune response
We illustrate performance for the simple case where antibody does not decay. We prospectively generate data for vaccinees which are then sampled retrospectively as in a test negative design. We assume a population of size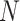 
vaccinees and generate the case disease according to
 |
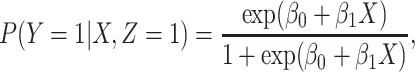and sequentially generate control disease among the case uninfecteds as
 |
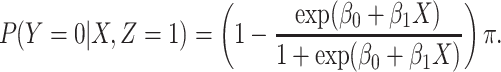We specify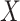 
as Gaussian with mean= 3.00 and standard deviation =0.50 as in the Prevail 1 vaccine trial Kennedy and others (2016). We generate
 |
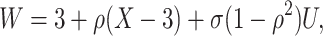where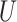 
is standard normal. Thus, 
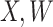are bivariate normal with common mean 3.00, common standard deviation 0.50, and correlation 
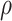. We set 
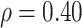, 0.70, and 1.00. For reference, a study estimated a correlation of 0.70 between ELISA OD immune response readouts for VSV proteins (W) and Ebola proteins (X) at 56 days post vaccination Poetsch and others (2018).
We specify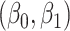 
as (
5.51, 0.00), (
4.05, 
0.60), and (
1.12, 
1.81). These correspond to no, modest, and strong effects of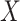 
. To help interpret 
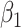, the ratios of risk of case disease for the 1st versus 8th octile of 
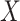are 1, 2, and 10, respectively, for 
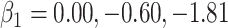. We set the conditional risk of control disease as 
, 
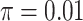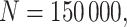and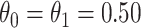 
so that vaccinated cases and controls arrive with equal probability.
We evaluate estimation of the model
 |
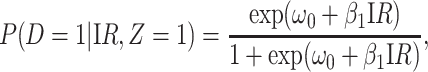(4.14) |
where IR, the immune response, is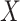 
, 
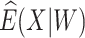, or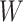 
Table 1 presents the results using 10 000 simulated studies per scenario. Columns 4 and 5 provide the sample mean and variance of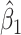 
. Column 6 reports the rejection rate for the two-sided 
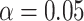Wald test using the Monte Carlo standard error over the 10 000 simulated studies. We see that we have power of around 100% to test the effect of IR when 
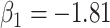for all scenarios, while for 
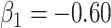we need a correlation of 0.70 to approach 80% power. The type I error rate seems consistent with the 
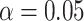used for testing.
Table 1.
Simulated performance of logistic regression using different covariates for IR immune response;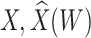 
, or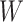 
. Sample statistics for different parameters estimates are presented. 
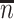is the average number of symptomatic vaccinees who arrive and 
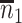the average number of vaccinees who arrive with the case disease. 1000 test negative designs are simulated for each row. The last row has 
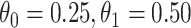all other rows have 
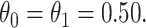Each row is based on 10 000 simulated studies.
|
|
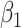
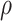
IR |
|
|
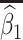
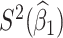
% Reject |
|
|
|---|---|---|---|---|---|---|---|
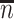
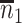
| 0.000 | 1.000 |
|
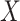
0.002 |
0.019 | 0.053 | 1049 | 302 |
0.600 |
1.000 |
|
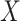
0.602 |
0.024 | 0.973 | 972 | 225 |
1.810 |
1.000 |
|
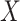
1.821 |
0.040 | 1.000 | 908 | 160 |
| 0.000 | 0.700 |
|
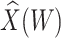
0.001 |
0.040 | 0.048 | 1048 | 302 |
0.600 |
0.700 |
|
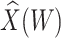
0.605 |
0.049 | 0.786 | 973 | 225 |
1.810 |
0.700 |
|
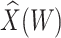
1.826 |
0.076 | 1.000 | 909 | 160 |
| 0.000 | 0.400 |
|
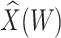
0.003 | 0.122 | 0.049 | 1049 | 302 |
0.600 |
0.400 |
|
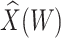
0.603 |
0.152 | 0.332 | 973 | 225 |
1.810 |
0.400 |
|
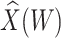
1.827 |
0.232 | 0.974 | 909 | 160 |
| 0.000 | 0.700 |
|
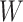
0.001 |
0.020 | 0.048 | 1048 | 302 |
0.600 |
0.700 |
|
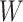
0.423 |
0.024 | 0.790 | 973 | 225 |
1.810 |
0.700 |
|
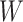
1.274 |
0.035 | 1.000 | 909 | 160 |
| 0.000 | 0.400 |
|
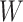
0.001 | 0.019 | 0.048 | 1049 | 302 |
0.600 |
0.400 |
|
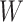
0.239 |
0.023 | 0.344 | 973 | 225 |
1.810 |
0.400 |
|
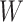
0.725 |
0.032 | 0.984 | 909 | 160 |
0.600 |
1.000 |
|
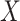
0.604 |
0.031 | 0.938 | 599 | 225 |
Regression calibration recovers the true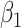 
even with 
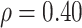. In the Appendix, we derive the correct (marginalized) probability of 
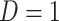given 
under our assumptions. We show that this curve as a function of 
(with slope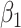 
) is virtually identical to the regression calibration curve (with the same slope 
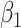), irrespective of 
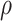. This fidelity explains the excellent recovery of 
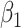with regression calibration. Regression calibration does become more biased as 
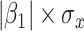increases, but for these simulations, 
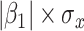is relatively small, Follmann and others (1999).
Intuitively, as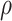 
decreases estimation becomes more difficult. For 
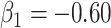, the variance for 
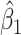under regression calibration is 0.024, 0.049, and 0.152 for 
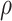= 1.00, 0.70, and 0.40, respectively. So the variance roughly doubles as 
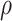goes from 1.00 to 0.70 and triples as 
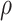goes from 0.70 to 0.40. In contrast, with direct use of 
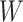the variance of 
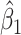stays constant at about 0.023 or 0.024 for all 
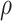with 
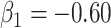. The use of 
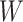in lieu of 
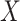, of course, leads to a smaller estimate of 
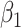but this is counterbalanced by the smaller variance. The upshot is that the power for testing 
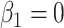is nearly identical for regression calibration and direct use of 
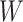for all scenarios.
In the Appendix, we provide additional simulations with sample sizes 1/10th and 10 times that of Table 1. The three approaches have less power and more variability with the smaller sample size and the opposite with larger sample size. Regression calibration continues to be nearly unbiased for the larger sample size, though it has some bias for the smaller sample size.
The above simulations were conducted under the standard assumptions of the test negative design. In the final row, we set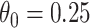 
while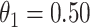 
so that vaccinees with the control disease have half the arrival probability of the vaccinated cases, which violates the standard test negative assumption. We set 
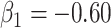and evaluate 
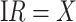so that the second line of Table 1, which has 
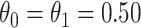provides a reference. As expected, we see the estimate of 
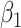is still unbiased, though the variance for 
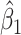is slightly increased due to fewer control vaccinees.
4.2. Waning immune response
In this subsection, we provide a brief evaluation of the model (2.11). To focus on the issue of antibody decay, we assume that 
is measured without error, and that everyone with either disease arrives at a clinic. We specify the instantaneous conditional risk for control disease using a Weibull hazard,
 |
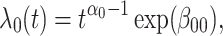where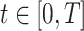 
is the time since start of the test negative study. When 
(
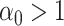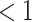) the hazard is increasing (decreasing). The instantaneous conditional risk of case disease is specified as
 |
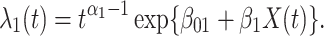For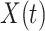 
, we specify linear antibody decay according to a random effects model. For person 
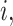the decay is
 |
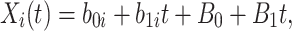where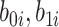 
are independent normals with mean 0 and standard deviations 
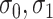, respectively. The parameter 
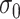reflects both natural variation in immune response to vaccination as well as variation in vaccination times as those vaccinated long ago would tend to have smaller 
.
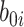We generate times to case and control disease by the inverse cumulative distribution function method where we generate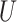 
, a uniform [0,1] random variable and then determine the disease arrival time 
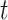that solves 
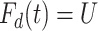for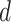 
= 0,1. For the case disease, this is solved by numerically minimizing 
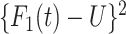. For subjects who experience both case and control events, we use the first and discard the second. We set 
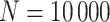vaccinees and follow subjects until we observe 1000 first events.
For all scenarios, we set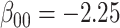 
, (
, and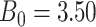 
. Our reference case is 
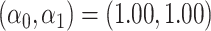, or constant risk of each disease and 
, 
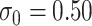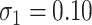. We then vary these parameters to see their impact on performance. The hazards and distribution of arrival times are graphed in the Supplementary material available at Biostatistics online.
We evaluate two different modeling strategies for (2.11). The first is to treat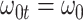 
as fixed with no dependence on time. The second is to evaluate five models and pick the one with the best Akaike Information Criterion (AIC). The five models are to treat 
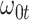as constant (1), linear in 
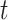(2), quadratic in 
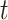(3), linear in 
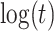(4), and quadratic in 
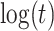. This second strategy is meant to mimic how a data analyst might address a non-constant 
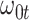. To summarize performance, we calculate the sample mean and variance for the estimate of 
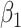under modeling strategies 1 and 2. We also report the modal model choice of strategy 2 and the number of times that modal choice was chosen. Additionally, we report the number of cases and controls for the last data set.
Table 2 presents the summary results. We see that both modeling strategies 1 and 2 recover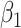 
very well for scenario 1, our reference, and scenario 2, where 
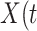) has more variability and a steeper mean decline. Both scenarios 1 and 2 have constant hazards for both case and control disease. For non-constant hazards, modeling strategy 1 is biased with bias of around 
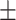10%. Modeling strategy 2 has minimal bias for non-constant hazards and picks 
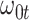as a linear function of 
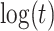in about 70–80% of the simulations using the AIC criterion.
Table 2.
Performance of logistic regression based strategies for dealing with the nuisance function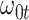 
. Strategy 1: Fix 
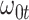at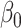 
. Strategy 2: Choose 
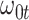based on AIC. The sample average and variance over the simulations are given for 
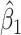under the two strategies. AIC choice reports the modal choice for strategy 2 while 
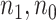are the number of cases and controls for the last simulated dataset. The true value of 
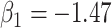. Each row is based on 1000 simulated studies.
| Strategy 1 | Strategy 2 | AIC | # times | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenario |
|
|
|
|
|
|
|
|
|
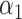
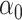
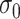
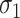
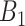
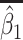
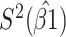
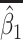
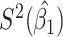
Choice | Chosen |
|
|
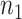
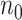
| 1 | 1.00 | 1.00 | 0.5 | 0.1 |
0.5 |
1.47 |
0.0204 |
1.47 |
0.0209 | 1 | 735 | 426 | 574 |
| 2 | 1.00 | 1.00 | 1.0 | 0.5 |
1.0 |
1.48 |
0.0100 |
1.48 |
0.0102 | 1 | 693 | 629 | 371 |
| 3 | 1.25 | 0.75 | 0.5 | 0.1 |
0.5 |
1.59 |
0.0268 |
1.48 |
0.0271 | 4 | 738 | 235 | 765 |
| 4 | 0.75 | 1.25 | 0.5 | 0.1 |
0.5 |
1.35 |
0.0213 |
1.48 |
0.0239 | 4 | 780 | 618 | 382 |
| 5 | 1.50 | 0.50 | 0.5 | 0.1 |
0.5 |
1.61 |
0.0858 |
1.49 |
0.0927 | 4 | 770 | 66 | 934 |
| 6 | 0.50 | 1.50 | 0.5 | 0.1 |
0.5 |
1.29 |
0.0324 |
1.48 |
0.0392 | 4 | 828 | 829 | 171 |
Strictly speaking, (2.10) obtains under a “rare” disease assumption. In the above simulations, 10% of the vaccinees acquired disease with no noticeable bias. We did further simulations and did observe about 7% bias for scenario 2 with 30% disease acquisition.
5. Example
In the 2018–2020, outbreak of Ebola in the Democratic Republic of the Congo a ring vaccination campaign was conducted. Local surveillance teams kept track of new Ebola cases which were then relayed to a WHO vaccination team that vaccinated the contacts and contacts of contacts of the index case. Several hundred thousand at risk people were thus vaccinated. Following vaccination, the vaccinees were monitored and encouraged to visit an Ebola transit/treatment center once any symptoms developed. The ring campaign used the rVSV vaccine which is estimated to have quite high efficacy though breakthrough infections occur, WHO (2019) and Henao-Restrepo and others (2015). The durability of the vaccine and the impact of immune response on risk of disease are unknown. Prospectively collecting samples in all vaccinees for correlates analysis has not been done.
To illustrate our approach, we simulate a dataset meant to loosely approximate a large Ebola ring vaccination campaign with a vaccine whose substantial efficacy is modulated by immune response. We assume that each person’s immune response is relatively stable over time. We assume 150 000 at risk subjects are vaccinated and generate case and control infections as in the previous section with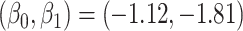 
. We set 
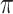, the conditional risk of control disease (e.g., malaria) equal to 0.005 and assume that vaccinated subjects arrive at the transit center with fixed probability 
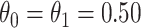, as one might expect from regular monitoring and encouragement. Note that with regular monitoring of all subjects in a ring, the assumption that 
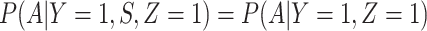for vaccinees may hold, thus even if rVSV does modify disease, the estimated risk of disease as a function of immune response should be unbiased.
To provide additional context, we assume 300 000 unvaccinated subjects are at risk (e.g., have first or second degree contact with an Ebola case) and generate case infections with probability 0.01. We generate control infections from this set with conditional probability 0.005 just as for the vaccinated. We assume that the unvaccinated contacts arrive with probability 0.25 for both case and control disease, irrespective of severity. Finally, we assume that 20% of the arrivals occur within 35 days of contact with an Ebola case. For vaccinees, this should ensure a relatively stable vaccine-induced immune response at arrival.
For this single simulated dataset, a total of 114 unvaccinated contacts of Ebola cases arrived at least 35 days post contact. The proportion with Ebola Virus Disease (EVD) was 0.69. In contrast, 127 vaccinated contacts of an Ebola case arrived at least 35 days post contact with an EVD proportion of 0.28. Thus the overall test negative VE for these late arrivals is estimated as
 |
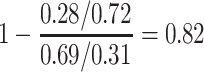The above VE estimate is unbiased under the standard test negative assumptions that vaccinees (unvaccinated) have fixed probability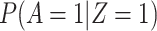 
(
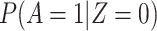) of arriving at a transit center, irrespective of true disease status, disease severity, and equal exposure of vaccinees and unvaccinated. This latter assumption may be questioned in a ring study where the vaccinees are all known contacts of a case.
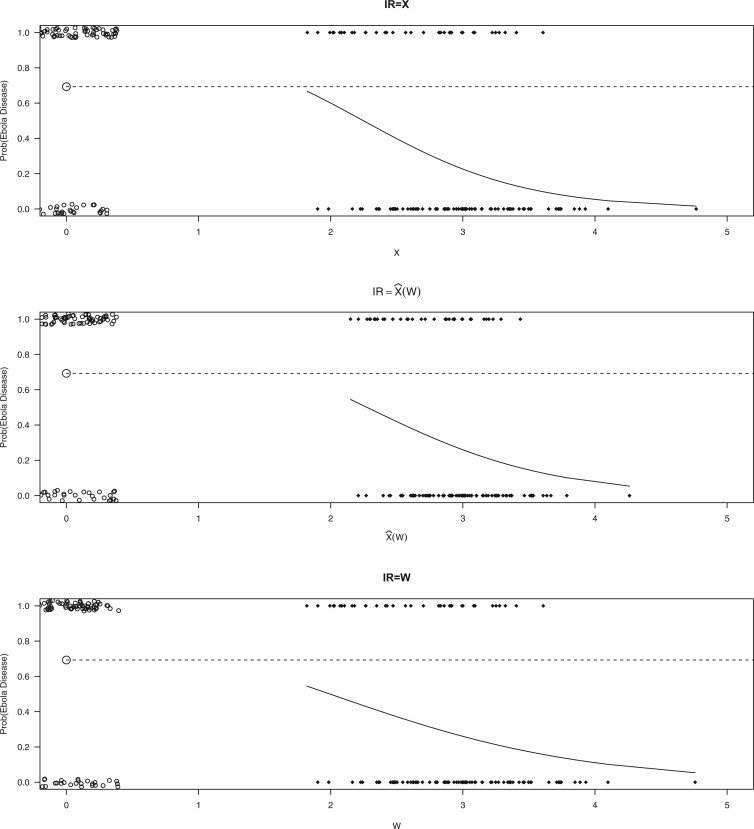
Figure 2 displays the data, jittered for the unvaccinated for whom we set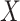 
to 0, along with the fitted logistic regression model 
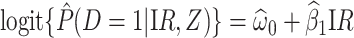where 
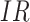is the immune response covariate, 
, 
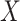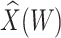, or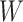 
. For the unvaccinated, we draw a dashed line at the observed Ebola disease rate of 0.69 for reference. Table 3 provides the estimated parameters. We see that, as expected, using 
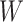results in a smaller 
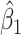than use of 
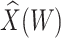and that the Wald statistic for testing 
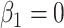for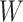 
is identical to the Wald statistic based on 
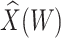, when we use the naive standard error. We also provide the bootstrap standard error and Wald statistic for regression calibration based on 1000 resamples. The resultant standard errors are slightly larger than the naive standard errors. The two-sided p-values for testing an effect of 
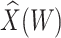and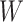 
on disease are, respectively, 0.02 and 0.01. Recall that the estimates of 
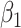are unbiased even if the arrival probability for vaccinees depends on latent severity, provided the vaccine has an all-or-none mechanism. Estimates of 
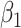are also unbiased even if the vaccine modifies latent disease severity, provided the arrival probability is the same for all vaccinees with the case disease.
Fig. 2.
Simulated data to illustrate an immune correlates analysis based on a test negative design for the 2018–2020 Ebola outbreak in the DRC. Unvaccinated subjects’ data are given by jittered open circles near x-axis near 0 and whose Ebola disease rate of 0.69 is given by the dashed line. Vaccinated subjects’ data are given by diamonds. The estimated probability of disease for vaccinees is given by the solid curve. The three panels correspond to using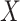 
, 
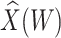, and 
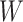as the immune response, respectively.
Table 3.
Parameter estimates for a simulated data set with 114 unvaccinated and 127 vaccinated subjects. We evaluate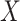 
, 
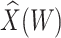, and 
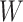as the immune response covariate.
IR =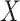 
|
IR=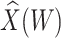
|
IR= 
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| parm | est | se | Wald | est | se
|
Wald
|
se
|
Wald
|
est | se | wald |
|
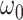
3.68 | 1.28 | 2.86 | 3.28 | 1.68 | 1.95 | 1.70 | 1.93 | 2.07 | 1.20 | 1.72 |
|
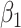
1.64 |
0.46 |
3.54 |
1.45 |
0.58 |
2.49 |
0.60 |
2.40 |
1.04 |
0.42 |
2.49 |
Naive standard errors, 
Bootstrap standard errors
To help interpret the magnitude of the effect of the imputed immune response on risk of disease, we can compare the ratio of the risk of disease at the 10th versus 90th percentile of the observed distribution of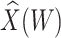 
. These percentiles are 2.51 and 3.39, respectively, with associated probabilities of disease of 0.42 and 0.16 for these late vaccinated arrivals. Thus the risk is roughly 2.5 times greater at the 10th versus 90th percentile of 
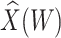indicating a substantial effect of antibody on EVD risk.
6. Discussion
This research arose from the design of an immune correlates study using test negative data for the 2018–2020 Democratic Republic of the Congo (DRC) Ebola outbreak. The main contribution of this article is the idea that an estimate of the effect of the relevant immune response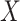 
on the risk of disease can be estimated by using an irrelevant immune response 
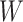. We use the proxy 
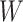to impute 
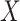based on a prediction model that is estimated in vaccinated controls using samples collected upon arrival at a clinic. The method extends to settings where antibody substantially decays over time. Simulations demonstrated the feasibility of the proposed methods.
This approach applies beyond Ebola. The key requirement is that the vaccine of interest produce irrelevant immune responses that will be unaffected by the disease of interest, and that these immune responses are correlated with the immune response of interest. One such application is for extremely rare diseases such as the prevention of Zika-induced congenital birth defects. Suppose Puerto Rico begins Zika vaccination in 2025 and an outbreak sweeps the island in 2040. Since Zika-induced birth defects are rare, a prospective immune correlates design would require long-term storage of samples from hundreds of thousands of women just after vaccination. Furthermore, the values collected in 2025 onward would not address the question of the immune response at Zika exposure in 2040. But using the methods of this article we could sample cases (mothers of children with birth defects who are antibody positive for non-vaccine Zika antigens) and controls (mothers of children with birth defects who are antibody negative for non-vaccine Zika antigens). We could then apply a test negative design to assess overall VE and also perform an immune correlates analysis with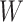 
and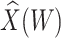 
, providing that a 
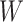that predicts 
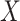were available.
We focused on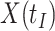 
or the immune response proximal to infection. However, traditional immune correlates analyses focus on 
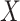shortly after vaccination. Our methods for time constant immune response directly apply as here 
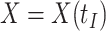. If antibody decay occurs, one could in principle apply (2.10) with 
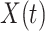replaced by 
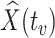, the predicted value of 
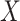shortly after vaccination. This would require the development of models to predict 
.
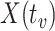The biggest challenge in this approach is whether the biology is amenable. Some vaccines won’t induce a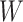 
at all. Other times, even if 
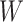is induced the correlation may be too weak for this method to work. This may be more of a problem with pre-existing immunity to either the antigens of the vaccine or the vector. On the other hand, it is not really required that 
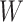be an immune response to the vector. What is required is the existence of covariates 
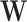that predict 
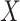among vaccinees and that 
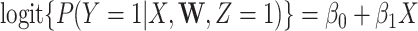. Development of such methods is left to future work.
Supplementary Material
Acknowledgments
This work utilized the computational resources of the NIH HPC Biowulf cluster (http://hpc.nih.gov). We thank Jing Qin and Michael Fay for helpful comments.
Conflict of Interest: None declared.
7. Software
The code to reproduce the example is given at https://github.com/follmand/Test-Negative-Immune-Correlates.
Supplementary materials
Supplementary material is available at http://biostatistics.oxfordjournals.org.
References
- Boom, J. A., Tate, J. E., Sahni, L. C., Rench, M. A., Hull, J. J., Gentsch, J. R., Patel, M. M., Baker, C. J. and Parashar, U. D. (2010). Effectiveness of pentavalent rotavirus vaccine in a large urban population in the United States. Pediatrics 125, e199–e207. [DOI] [PubMed] [Google Scholar]
- Broome, C. V., Facklam, R. R. and Fraser, D. W. (1980). Pneumococcal disease after pneumococcal vaccination: an alternative method to estimate the efficacy of pneumococcal vaccine. New England Journal of Medicine 303, 549–552. [DOI] [PubMed] [Google Scholar]
- Follmann, D. A., Hunsberger, S. A. and Albert, P. S. (1999). Repeated probit regression when covariates are measured with error. Biometrics, 55, 403–409. [DOI] [PubMed] [Google Scholar]
- Fukushima, W. and Hirota, Y. (2017). Basic principles of test-negative design in evaluating influenza vaccine effectiveness. Vaccine 35, 4796–4800. [DOI] [PubMed] [Google Scholar]
- Guolo, A. (2008). A flexible approach to measurement error correction in case–control studies. Biometrics 64, 1207–1214. [DOI] [PubMed] [Google Scholar]
- Halloran, M. E., Longini, I. M. and Gilbert, P. B. (2020). Designing a study of correlates of risk for Ebola vaccination. American Journal of Epidemiology 189, 747–754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henao-Restrepo, A. M., Longini, I. M., Egger, M., Dean, N. E., Edmunds, W. J., Camacho, A., Carroll, M. W., Doumbia, M, Draguez, B., Duraffour, S.et al. (2015). Efficacy and effectiveness of an RVSV-vectored vaccine expressing Ebola surface glycoprotein: interim results from the guinea ring vaccination cluster-randomised trial. The Lancet 386, 857–866. [DOI] [PubMed] [Google Scholar]
- Jackson, M. L. and Nelson, J. C. (2013). The test-negative design for estimating influenza vaccine effectiveness. Vaccine 31, 2165–2168. [DOI] [PubMed] [Google Scholar]
- Kennedy, S. B., Neaton, J. D., Lane, H. C., Kieh, M. W. S., Massaquoi, M. B. F., Touchette, N. A., Nason, M. C., Follmann, D. A., Boley, F. K., Johnson, M. P.et al. (2016). Implementation of an Ebola virus disease vaccine clinical trial during the Ebola epidemic in Liberia: design, procedures, and challenges. Clinical Trials, 13, 49–56. [DOI] [PubMed] [Google Scholar]
- Lewnard, J. A., Tedijanto, C., Cowling, B. J. and Lipsitch, M. (2018). Measurement of vaccine direct effects under the test-negative design. American Journal of Epidemiology 187, 2686–2697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plotkin, S. A. and Gilbert, P. B. (2012). Nomenclature for immune correlates of protection after vaccination. Clinical Infectious Diseases 54, 1615–1617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poetsch, J. H., Dahlke, C., Zinser, M. E., Kasonta, R., Lunemann, S., Rechtien, A., Ly, M. L., Stubbe, H. C., Krähling, V., Biedenkopf, N.et al. (2018). Detectable vesicular stomatitis virus (VSV)-specific humoral and cellular immune responses following VSV-Ebola virus vaccination in humans. The Journal of Infectious Diseases 219, 556–561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin, L., Gilbert, P. B., Corey, L., McElrath, M. J. and Self, S. G. (2007). A framework for assessing immunological correlates of protection in vaccine trials. The Journal of Infectious Diseases 196, 1304–1312. [DOI] [PubMed] [Google Scholar]
- Rosner, B., Spiegelman, D. and Willett, W. C. (1990). Correction of logistic regression relative risk estimates and confidence intervals for measurement error: the case of multiple covariates measured with error. American Journal of Epidemiology 132, 734–745. [DOI] [PubMed] [Google Scholar]
- Sullivan, S. G., Tchetgen Tchetgen, E. J. and Cowling, B. J. (2016). Theoretical basis of the test-negative study design for assessment of influenza vaccine effectiveness. American Journal of Epidemiology 184, 345–353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westreich, D. and Hudgens, M. G. (2016). Invited commentary: beware the test-negative design. American Journal of Epidemiology 184, 354–356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- WHO. (2019). Preliminary Results on the Efficacy of rVSV-ZEBOV-GP Ebola Vaccine using the Ring Vaccination Strategy in the Control of an Ebola Outbreak in the Democratic Republic of the Congo: An Example of Integration of Research into Epidemic Response. https://reliefweb.int/report/democratic-republic-congo/preliminary-results-efficacy-rvsv-zebov-gp-ebola-vaccine-using-ring.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.