Subcritical escape waves in schooling fish

Abstract

Theoretical physics predicts optimal information processing in living systems near transitions (or pseudo-critical points) in their collective dynamics. However, focusing on potential benefits of proximity to a critical point, such as maximal sensitivity to perturbations and fast dissemination of information, commonly disregards possible costs of criticality in the noisy, dynamic environmental contexts of biological systems. Here, we find that startle cascades in fish schools are subcritical (not maximally responsive to environmental cues) and that distance to criticality decreases when perceived risk increases. Considering individuals’ costs related to two detection error types, associated to both true and false alarms, we argue that being subcritical, and modulating distance to criticality, can be understood as managing a trade-off between sensitivity and robustness according to the riskiness and noisiness of the environment. Our work emphasizes the need for an individual-based and context-dependent perspective on criticality and collective information processing and motivates future questions about the evolutionary forces that brought about a particular trade-off.

Social spreading of escape behavior is suppressed in fish schools, reducing false alarms at the cost of lower responsiveness.

INTRODUCTION

Biological systems process information about their environment to detect and appropriately react to changes within it. In many such systems, such as gene regulatory networks (1), neuronal networks (2, 3), or animal groups (4, 5), biological function relies on distributed processing of information through the collective dynamics of interacting, potentially heterogeneous, components or agents. This collective information processing is often considered optimal at or close to a critical point (3, 6), where statistical physics predicts maximal sensitivity of the collective dynamics to small differences in an external perturbation and fast transmission of information across arbitrarily large systems.

Critical points in the parameter space of a multiagent system mark points of collective instability, which exhibit a qualitative change in the aggregate dynamics, corresponding to a phase transition in an infinite system (6–9). In biological systems, which typically have many fewer components than those studied in statistical physics, pseudo-critical points provide a finite-size analog that similarly exhibits maximal sensitivity. Throughout this work, when referring to criticality, we refer to this finite-size equivalent.

The changes in collective behavior associated with a critical point can have important functional and behavioral consequences for biological systems, such as the transition of disordered movement of individuals into coordinated marching in locust nymphs at a critical density (10). For similar reasons, criticality is studied in other biological contexts, such as neural activity, brain networks (8, 11–14), gene regulatory networks (15), and collective cell behavior (16).

For animal collectives, signatures of near criticality have been observed in bird flocks (17), mammals (7), insects (18, 19), and fish schools (20), while theoretical models have investigated maximal sensitivity at the critical regime (21–24). Predominantly, these studies considered the system’s maximal sensitivity or flexibility or the appearance of long-ranged correlations within it as possible benefits of criticality to animals within collectives (25). However, while individuals within animal groups can benefit from social information provided by others (26), environmental and internal noise may also result in individuals making erroneous decisions, resulting in them providing misleading social cues (27, 28). Sharing the imperfect information of many agents can therefore not only increase each individual’s likelihood to be informed about environmental changes (e.g., the presence of a predator) but also may risk an increase in false or irrelevant information being propagated, especially in fast behavioral decisions (29). Thus, collective biological systems face a trade-off between filtering out noise and remaining sensitive to relevant, potentially sparse information.

Here, we investigate whether and how being critical (or at a context-dependent distance from criticality) manages this trade-off in a specific biological system, namely, escape waves in schools of juvenile fish (golden shiners, Notemigonus crysoleucas) (27, 28, 30). These fish form coordinated schools in response to high mortality from predation risk in the wild and, as an escape behavior, show a startle response that spreads socially (31, 32).

This system lets us explore core aspects of previous studies of criticality in biological systems, namely, (i) quantifying where in parameter space the particular system operates with respect to a critical point, which includes finding an aggregate variable (called an order parameter in physics) that identifies the transition best [e.g., average marching direction in case of the swarming locust (10, 33)]; (ii) functional benefits of operating near criticality (23, 24, 34, 35); and (iii) revealing the mechanisms enabling biological systems to control and adapt their critical behavior to ensure proper function (7, 36–38). Recognizing that group-level optima suggested by criticality may not be evolutionarily stable with respect to individual-level adaptation (24), we also consider the individual-level impact of a specific collective behavior.

Avalanche processes, like escape waves, are important to the collective dynamics of many biological systems, including spike avalanches in neuronal networks and disease transmission in human or animal populations (12, 14, 39–42). In such processes, local changes in the state of individual units (i.e., spiking of a neuron or infection of an individual) can trigger similar changes in its neighbors. Avalanche dynamics can transition from the supercritical regime in which local changes propagate through the entire group to the subcritical regime where change remains local. Across many living systems, we have evidence that the degree of behavioral spreading is regulated. In neural cultures, adding biochemical regulators that modify excitation and inhibition can force the system to supercritical and subcritical states (11), while in macaques, key individuals influence how conflict spreads through a colony (7).

In golden shiners, the strength of behavioral spreading was found to be controlled by their spatial structure, predominantly defined via school density (28). Here, using a data-driven computational approach, we investigate the hypothesis that there is a critical density exhibiting features of optimal information processing in this collective escape response and study whether it can be reached via this density-based mechanism and what different distances to criticality imply for the individual fish. Our results suggest that the costs of being critical—such as susceptibility to noise and associated energetic, and/or time, costs—may play an important role in animal groups and should be considered alongside the benefits. Overall, our work highlights how regulating distance to criticality can manage the trade-off between robustness and sensitivity according to environmental context.

RESULTS

Modeling experimental cascade size distributions

Our data come from two previous studies of startle cascades (initiated by randomly occurring single startles) in quasi–two-dimensional (2D) schools of juvenile golden shiners (N. crysoleucas) (27, 28) [details in Materials and Methods and refer to the supplementary materials of (27) for a video of a startle cascade]. This study uses data from (28) of fish schools (N = 40) under two experimental conditions differing in group members’ perceived risk of the environment, namely, before and after an alarm substance was sprayed on the water surface which increases perceived risk. Following (28), we call these conditions “baseline” and “alarmed” [for larger groups from (27), see section S3.8].

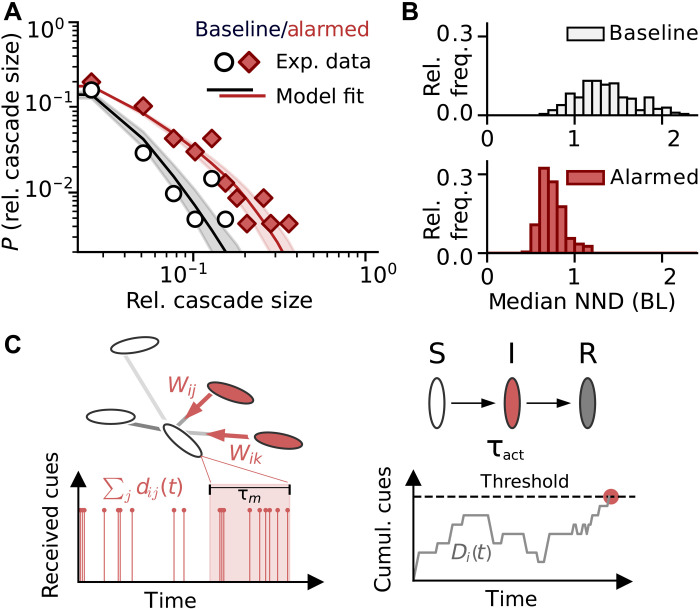
The data contain n = 206 (baseline) and n = 232 (alarmed) detected startle cascades, and Figure 1 summarizes relevant experimental observations from (28): The observed distribution of relative cascade sizes (number of individuals that startle within a certain spatial and temporal interval from each other after an initial startle event as a fraction of group size; diamond and circles, Fig. 1A) indicates that, on average, schools in the alarmed condition exhibit larger cascades than those in the baseline. In addition, the alarmed condition exhibits higher average spatial density at cascade initiation (Fig. 1B), characterized by a lower median nearest neighbor distance (NND) measured in body lengths (BL), a measure which an individual may be able to perceive, and potentially control, through its social behavior.

Fig. 1. Experimental data and computational model.

Key aspects of the baseline and alarmed experimental datasets from (28) (differing in group members’ perceived environmental risk) and model calibration via fitting of the cascade size distribution: (A) Observed cascade size distributions (data points). For increased perceived risk (alarmed, red diamonds), a larger average cascade size is observed. Distributions are summarizing n = 206 (baseline) and n = 232 (alarmed) observations of startle cascades. Our model (solid line) is calibrated on observed cascade sizes via a log-likelihood approach. Solid lines show distributions of relative cascade size obtained from 10,000 model runs with shaded areas indicating the credible interval of the model fit. For more details on the model, refer to Materials and Methods, Fig. 2, and section S2. (B) Histograms characterizing school densities in the datasets via median nearest neighbor distance (NND). For the alarmed condition (red, higher perceived risk), fish are closer to one another. (C) Scheme of SIR-type model dynamics: Observation of social cues over time triggers individual startling response mediated by strength of network links (w_ij) and individual responsiveness (threshold).

A central finding in (28) is that the observed increase in average cascade size cannot be explained by a change in individual responsiveness alone. Rather, the modulation of group structure, as captured here by NND, is essential to explain this increase [see also previous theoretical work (43, 44)]. Here, we aim to systematically study this structure-based control mechanism of spreading behavior. However, because it is not possible to freely control the density of fish schools in experiments without strongly interfering with the system, and thus potentially losing any biological or ecological relevance, direct observations are limited and unevenly distributed across school densities. Instead, by using simulations from an empirically calibrated model of startle cascades, we can generate well-founded hypotheses about structure-based control in this system, and the remainder of this work explores this approach. Note that, while the lack of system-wide cascades in the observed data is already suggestive of a subcritical state in both experimental conditions (see Fig. 1A), the observed distributions alone do not allow us to quantify distance to a potential critical point in collective startle dynamics and the role of group density and individual sensitivity in controlling this distance, which we will use the computational model for.

In (27), startle cascades in golden shiners were shown to agree best with the predictions of a complex fractional contagion process spreading on statistically inferred interaction networks. Here, we use a closely related model framework, as previously outlined in (28). In both model formulations, the nodes of the network represent individual fish, and the static weighted directed network links represent influence of one individual’s startle behavior on that of another.

The social influence (link weight) is obtained from data regarding each individual’s first response (startle/no startle) to an initial random startle because this has the clearest causal relationship between the perception of the social cue (the initial startle) and the response. We estimate link strength from the positions and orientations of individuals via a logistic regression of these data using the two features identified in (27) and (28) as being most predictive of startle response, logarithmic interindividual Euclidean distance and a ranked visual property (see Materials and Methods for more details on network construction).

In our model, the node behavior [adopted from a general behavioral contagion model (45, 46) that relies on internal evidence accumulation similar to drift-diffusion models (47, 48)] can be summarized as follows: An individual integrates stochastic activation cues that it receives from its startling neighbors over time at rates proportional to social influence and itself will startle when the amount of accumulated cues surpasses its response threshold [see Materials and Methods for a detailed description of the SIR (susceptible-infected-recovered)–type model and Fig. 1C for a model schematic]. We fit the individual response threshold to best predict the experimentally observed cascade sizes for each dataset via a maximum-likelihood approach (see fig. S6 for a plot of the log likelihood). Figure 1A shows the resulting fit of the experimental data for these optimal thresholds.

Predicting cascades beyond observed school densities

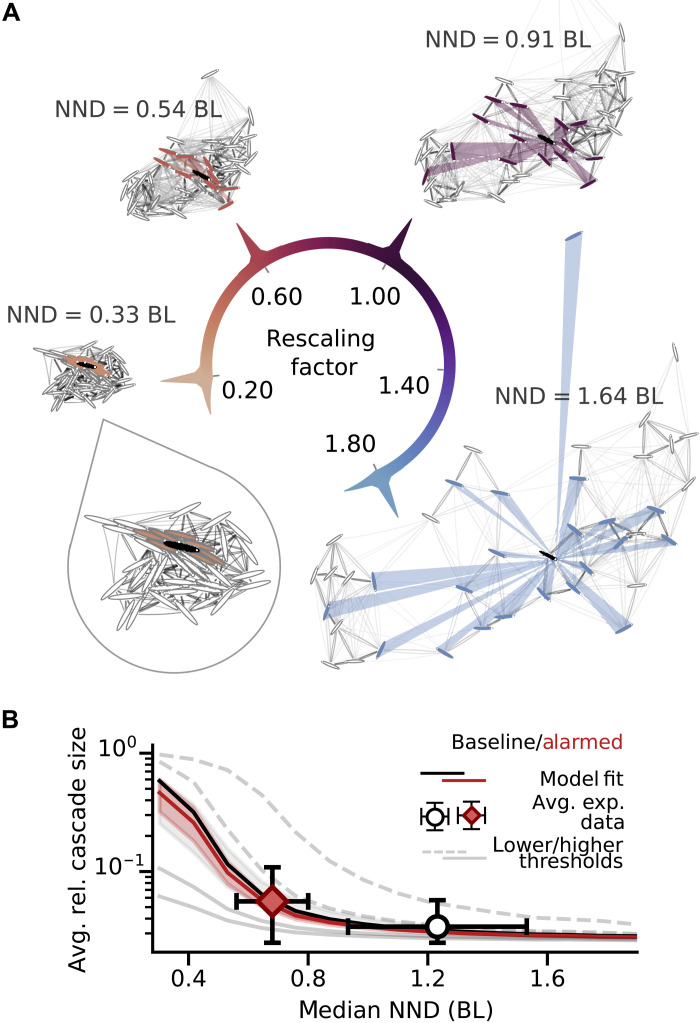
The underlying spatial positions of individuals associate interaction networks with a certain median NND. Networks from experimental data are therefore limited to school densities as depicted in Fig. 1B. To predict cascades for other densities, we construct additional networks by rescaling positional data from experimental trials as illustrated in Fig. 2A. Rescaling changes interindividual distances, resulting in altered values of median NND (noted next to each school) and visual interactions. Individuals are approximated as ellipses whose visual fields are obtained semianalytically (see Materials and Methods and section S3.1, demonstrating the validity of this approximation). Overlaps of individuals are avoided via automated minimal adjustment of rescaled positions and orientations.

Fig. 2. Predicting cascade sizes across densities via a data-driven computational approach.

(A) Examples of interaction networks obtained from rescaled position data for one experimental startle event with rescaling factors λ ∈ (0.2,0.6,1.0,1.8). The corresponding median NND is noted next to each network. The darkness of lines between individuals represent link strength (>0.01 only, to keep the figure comprehensible). An example visual field [rays originating from a focal individual (black) hitting visible neighbors (colored)] illustrates decrease in number of visible neighbors with increasing density due to occlusions. (B) Model predictions of average relative cascade size (lines) for different response thresholds [high values (solid lines) to low values (dashed lines)] show transition from local to global cascades with decreasing NND. Experimental observations from Fig. 1, summarized here as averages ± 1 SD (error bars, truncated below at 1/N = 0.025 because we use one initial startler and cascades cannot be smaller than this), are best predicted by the black and red curves, respectively, corresponding to the threshold value obtained via fitting the full cascade size distribution (Fig. 1A). Shaded areas are credible intervals of the model fit (gray, baseline; red, alarmed).

Figure 2A illustrates the density dependence of visual fields and resulting interaction networks. A focal individual (black) has links to individuals occupying above 0.02 radians in its visual field [colored ellipses, threshold based on visual limits identified in (49) and as used in (27); other visual thresholds do not affect main results, see section S3.4]. Because visibility is not necessarily reciprocal, networks are directed and asymmetric. Link weight decreases with increasing interindividual distance (see Materials and Methods and Eq. 2) and is indicated by link darkness, with darker lines corresponding to stronger links. Overall, with increasing density, the interaction networks have fewer but stronger links (see the Supplementary Materials for more details on network properties).

The black and red lines in Fig. 2B show the dependence of relative average cascade size (which we call group responsiveness) following one initial startle on median NND as predicted by the model using rescaled networks and best-fitting response thresholds, while gray lines are for lower (dashed) and higher (solid) threshold values. For context, the dots and error bars summarize the data from Fig. 1 by their average value ± 1 SD.

For all threshold values, the model predicts increasing group responsiveness with decreasing NND. Note that the existence of a full transition from local (close to zero group responsiveness) to global cascades (group responsiveness of 1) with decreasing NND is not certain for this specific type of model based on visual interactions, as shown by the solid gray lines in Fig. 2. It is rather the result of the specific density dependencies of several interacting effects: (i) Average link strength increases with decreasing NND by construction (see Eq. 2), which increases the group responsiveness. Assuming that we could decrease interindividual distances indefinitely while keeping the number of links constant, this dependence would ensure that we reach a transition to global cascades. However, this effect combines with two others caused by the individuals’ physical bodies: (ii) The bodies represent a lower limit to NND (where, in the extreme, it becomes physically impossible to move two bodies closer together), thus providing an effective upper limit to average link strength; and (iii) the number of links decreases with decreasing NND due to occlusions [see fig. S5 and (43)].

Estimation of criticality indicates subcritical behavior

Phase transitions become well defined only in infinite systems, while in finite systems such as ours, the transition between the alternate global states becomes more gradual as system size decreases (9). Still, effects of the transition, such as increased sensitivity, persist near the infinite-size critical point. In this section, we investigate whether the empirically calibrated model (Fig. 2, red and black lines) exhibits a maximum in sensitivity indicating a critical point within the accessible range of densities, and if so, where the densities of the observed schools are located with respect to it.

While in classical physical systems, this sensitivity refers to the change in order parameter for a small change in an external field (a perturbation), for biological systems, one may study the change induced by a single individual’s behavior (7). Considering initial startle events as perturbations and number of initial startlers as perturbation strength, we analogously define the school’s collective sensitivity (Δc) as the difference between the group responsiveness (measured by average relative cascade size) to one (c₁) and two (c₂) initial startles (Δc = c₂ − c₁). The maximal collective sensitivity is our functionally relevant indicator of near criticality in analogy to maximal susceptibility to a weak external perturbation acting as a characteristic feature of the pseudo-critical point in finite systems in classical statistical mechanics (50).

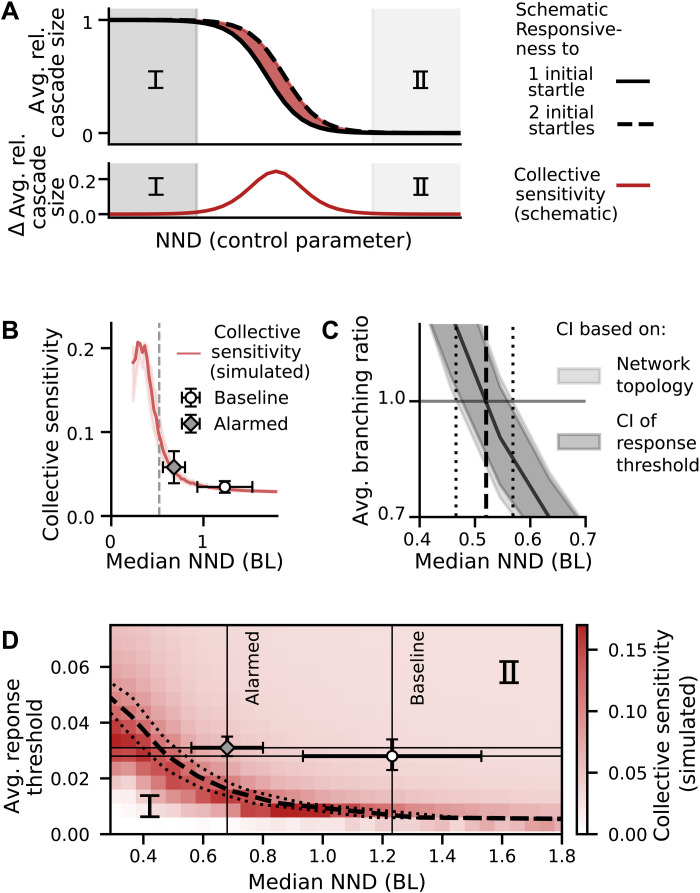
To motivate the biological relevance of this measure, Fig. 3A schematically depicts a transition from local to global cascades in our finite system for one and two initial startlers. Let us assume that the number of initial startles contains information about the environment (e.g., likelihood of imminent threat). Far away from the transition, any perturbation (i.e., one or two initial startlers) will either cause (almost) the entire system to respond [(i) supercritical regime, dark gray background, group responsiveness one] or will cause no response at all [(ii) subcritical regime, vanishing group responsiveness, light gray background]. Thus, the number of initial startlers (perturbation strength) cannot be inferred from collective response in these regimes, and the initial information is lost. Around the critical point (white background), responses of all sizes occur. Here, small differences in perturbation strength (one or two initial startles) lead to different average relative cascade sizes. The associated increase in collective sensitivity as depicted in the bottom of Fig. 3A is generally thought to benefit collective information processing. Here, increased sensitivity may allow different collective responses to a predator and/or to a noise cue and thus permits filtering, enabling large cascades to be triggered only by sufficiently strong cues.

Fig. 3. Estimating criticality via maximum sensitivity.

(A) Schematic sketch of transition to illustrate the concept behind (B) and (C). Top: Group responsiveness (average relative cascade size) to one and two initial startlers only differs around the transition (white background), which may enable different collective responses to noise and relevant cues. In both gray areas (I marks the supercritical regime, and II marks the subcritical regime), any cue triggers the same response, making distinction impossible. Bottom: Collective sensitivity, defined as the difference between the group responsiveness to two and one initial startles, shows a peak at the transition. (B) Collective sensitivity as a function of median NND, model predictions averaged over all networks. Shaded areas mark the credible interval of the model fit (see fig. S6). Lines end at low NND where physical bodies limit density. The observed spreading is subcritical with the alarmed condition closer to criticality than the baseline condition as shown by markers with error bars representing simulation result averages over original scale networks (error bars indicate 1 SD). (C) Average branching ratio of fitted model from averaging over networks in bins of median NND (shaded light gray area: ±1 SD, capturing variance in network topology). The confidence interval (CI) of the branching ratio due to uncertainty in the model fit (CI of the response threshold) is indicated in dark gray and comparable to the CI based on the variance in network topology (light gray). Dashed vertical line indicates where b = 1 [also included in (B)]; dotted line indicates uncertainty due to variance in network topology). (D) Collective sensitivity as a function of median NND and average individual response threshold shows a peak close to the analytically estimated critical line [b = 1, line styles as in (C)], separating the subcritical (I) and supercritical (II) regimes. Markers with error bars show averages over simulations on original scale networks and represent the observed schools’ average behavior.

We measure the collective sensitivity via simulations of cascades initiated by two or one initial startles. While the experimental data only contain cascades initiated by one individual using the empirically calibrated model, we can trigger any number of initial startles (see Materials and Methods and fig. S11 for other possible definitions of collective sensitivity, which show a similar qualitative behavior). Figure 3B depicts the dependence of the collective sensitivity on NND, obtained from averaging simulation results over all rescaled networks. The line ends around NND ≈ 0.3 BL, where constructing 2D networks of higher density is impossible (without assuming a highly ordered closest packing of ellipses) because of the physical bodies being not allowed to overlap. We find that maximum sensitivity (roughly 0.2 difference in group responsiveness) occurs at an NND of about 0.3 to 0.4 BL, which coincides approximately with these highest densities.

The data points in Fig. 3B indicate averages over trials (±1 SD) of the collective sensitivity obtained from simulations on the original scale networks. They thus characterize the behavior of the schools under the two different experimental conditions. The error bars of these data points are large due to the large range of observed school densities (refer to fig. S25 for a figure with the raw data). The two experimental datasets have an average collective sensitivity of 0.035 ± 0.007 (baseline) and 0.058 ± 0.019 (alarmed) at average median NND of 1.23 ± 0.3 BL and 0.68 ± 0.12 BL, respectively. Thus, their sensitivity could be increased by a factor of 5.9 and 3.4, respectively, by becoming critical. Instead, the observed schools are, on average, subcritical, with NND large enough that cascades on average stay local. In addition, we observe that while schools do get closer to criticality when perceived risk is higher, the physical bodies act as a lower limit for NND, which prevents the school from becoming maximally sensitive by density modulation alone (this also holds for other measures of density, as shown in fig. S25, and may extend to 3D schools, as discussed in section S3.3).

Regulation of distance to criticality

Next, we explore whether an additional change of individuals’ responsiveness (quantified by the average response threshold) can move the school to or across a critical manifold. Although (28) found no significant change in individual responsiveness resulting from a higher perceived environmental risk, these findings may not extend to multisensory cues or noisy environments (51, 52). In Fig. 3C, the collective sensitivity is plotted for varying both NND and the average response threshold and shows one clear band of maximum values.

To verify that the observed maximum in sensitivity is caused by a critical instability, we derive a branching ratio measure as an analytical estimate of the critical point in an infinite system (7). The average branching ratio b describes how small initial startling cascades, on average, tend to grow (b > 1) or shrink (b < 1), with b = 1 marking the transition between these two distinct aggregate behaviors (and corresponding to a true phase transition in an infinite system; for details, refer to Materials and Methods). Note that we use the branching ratio only as an additional indicator of the location of the critical point and not to fit a low-dimensional branching process model (53).

The black dashed line in Fig. 3C marks this analytically estimated critical line (b = 1) separating the subcritical [(I) b < 1] and supercritical [(II) b > 1] regime (for the full dependency of the average branching ratio on NND and average response threshold, refer to fig. S14). The estimate of the location of the critical line obtained from the analytically derived branching ratio (i.e., b = 1) and the location of the simulated maximum sensitivity agree well. The remaining differences in their locations in the 2D parameter space of median NND and individual response threshold are likely due to simplifying assumptions made in the derivation of the branching ratio and finite-size effects [see Materials and Methods and (54)].

The data points with error bars indicate the areas in parameter space that best describe experimental datasets (horizontal bar, average density ± 1 SD; vertical bar, optimal parameter fit and credible interval; see table S1). Figure 3B is thus a cross section of this plot at the horizontal lines. Following the vertical lines, we see that a decrease of average response threshold could bring the schools to criticality without a density change, but the necessary threshold values lie outside of the credible intervals. Overall, a density change can move the school toward the transition, and a change of individual responsiveness could even allow crossing to the supercritical regime (bottom left corner). Yet, experimentally observed densities at both levels of perceived risk (in the absence of a real predator) are not located at a maximum of any sensitivity measure (fig. S11).

Individual costs and benefits of criticality

Having established that fish schools could cross the transition but remain subcritical in experiments, we next examine the potential benefits of (sub)criticality in this system and interpret the consequences to individual fish using a hypothetical model of visual predator detection in different environmental contexts. In addition to constructing a biologically informed and testable hypothesis for the origins of the observed subcriticality, our goal with this approach is to illustrate and encourage an individual-based and context-dependent view of criticality beyond the maximization of a single group-level property [e.g., sensitivity (24)].

Golden shiners live in fission-fusion populations with fluctuating group membership (32). Given that fish likely do not consistently occupy certain positions in the school, we interpret the average relative cascade size as the probability that an individual fish will startle given some number of initial startlers. For example, if cascades initiated by one startle, on average, reach 40% of the school, then any fish has an average probability of 40% to respond to a single initial startle.

Figure 3B can thus be interpreted as the difference in individual response probability to one and two initial startlers. Thus, the closer the school’s NND is to the approximated critical point (b = 1), the better the individual fish’s average response distinguishes numbers of initial startlers. The relevant distinction in this escape context is, however, whether the cascade was triggered by the detection of a predator, or not, because this determines the optimal behavior for the individual. Ideally, all fish would escape when there is a predator (true positive) and not do so otherwise (true negative), but because of ambiguous cues (both environmental and social), two types of errors arise: False positives occur when an individual startles in the absence of a predator and false negatives when it fails to startle in the presence of a predator (55, 56).

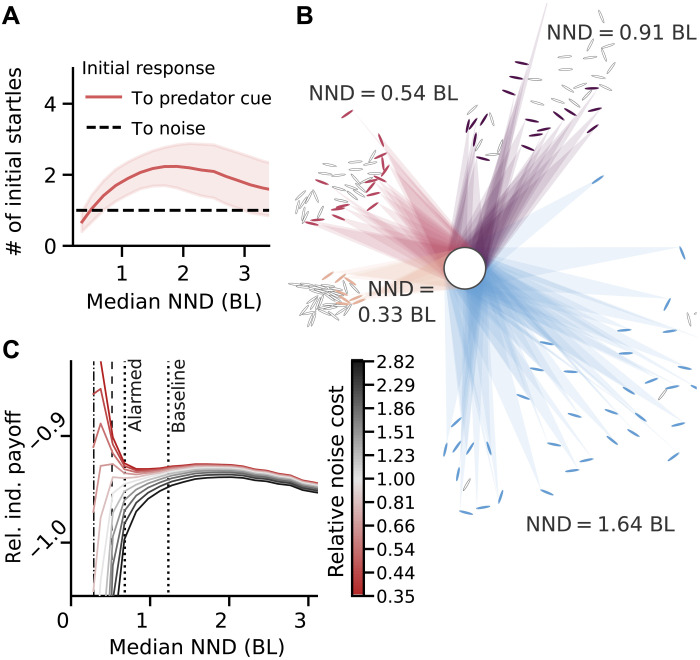
Because there are presently no data regarding predation of golden shiner fish by predators in noisy environments, here, we use a hypothetical initial reaction of the school either to the appearance of a predator (predator cue) or to the noise in the environment (noise cue). We simulate the likelihood of false positives and false negatives for different distances to criticality via average cascade sizes triggered by cue type–dependent numbers of initial startles (details are provided below). The simulated final fraction of the group responding to a noise cue or not responding to a predator cue gives the individual’s probability of a false positive or a false negative, respectively (see fig. S19). Figure 4A shows the assumed number of initial startlers for each type of cue. To simulate false positives, cascades were initiated by one randomly chosen individual (dashed line). The number of initial startlers for a predator cue (solid line, Fig. 4A) is determined by the school’s modeled ability to visually detect a predator as illustrated in Fig. 4B for changing school density. The predator (white circle with a diameter of 3 BL at equal distance to school borders) can be seen by all colored individuals (ellipses). Shaded triangles illustrate the visual perception of the predator by the school (rays emitted from individuals’ eyes hitting the predator). Because collective information processing is most beneficial for low signal-to-noise ratios (57), we consider a cryptic predator, where only a small fraction of those individuals for which the predator is not occluded also reacts to it with a startle (general results are independent of the exact value of this fraction, p_detect; see fig. S20). While occlusions limit detectability at low NND, the decrease of initial response to a predator at high NND in Fig. 4A is due to an upper distance limit on the visibility of the predator.

Fig. 4. Hypothetical predator detection model reveals distance to criticality can manage trade-off between two types of errors.

(A) Initial response to predator and noise cue as function of school’s median NND. Initial predator response is given by a fixed fraction of the average number of individuals that can see the predator. (B) Visual predator detection for schools adjusted to have different median NND (stated next to each school). Colored individuals are able to see the predator (white circle). Shaded areas illustrate the visual field similar to Fig. 2A. (C) Relative payoff for an individual in a school in different environments (characterized by relative noise cost) as function of school’s median NND. Averages of experimentally observed school densities are indicated (dotted vertical lines) as well as the estimates of the critical point [b = 1 (dashed line) and maximum sensitivity (black dash-dotted vertical line)]. Depending on the environment, different values of NND (i.e., different distances from criticality) maximize payoff. In risky environments (red), being highly responsive is more important than filtering, while in very noisy low-risk environments, being critical is detrimental to the payoff (black curves). For intermediate values of relative noise cost (light gray/red), there are two maxima: one based on maximum sensitivity at criticality (left) and one based on maximum personal visual access to the predator (right). Parameters: p_detect = 0.1, d_pred = 10 BL, and d_max = 40 BL.

To compare the benefits of different distances from criticality, we introduce the relative individual payoff. This measure adds up the costs of errors (loss of energy and time due to false positives and risk of death or injury due to false negatives) weighted by their likelihood of occurrence in a certain environment, which we obtain from simulations as described above.

The relative noise cost captures both the riskiness and the noise level of the environment. High values correspond to a noisy and/or low-predation environment, where most of the sensory cues are nonthreatening, while low values correspond to environments with high predation and/or very low noise, where sensory cues have a high likelihood to represent actual threats (for a detailed description, refer to Materials and Methods). Thus, noisy environments are characterized by low signal-to-noise ratio, where, e.g., visual cues on the presence of a cryptic predator are difficult to distinguish from other environmental fluctuations.

Figure 4C shows the relative payoff for an individual in a school of N = 40 fish for different relative noise cost. One observes three different kinds of dependency on NND:

1) For relatively safe and/or noisy environments (black curves), a single optimum appears at low density (NND ≈ 2 BL). Its exact position depends on the predator distance and assumed maximal detection distance of an individual (see fig. S23A for a version with maxima at the observed averages of the experimental dataset, marked by dotted vertical lines here). For these environments, near criticality decreases the payoff to individuals, dominated by the costs of false positives. The optimal spatial configuration (an intermediate NND) maximizes visual access to personal information about a potential predator while keeping social information relatively low and corresponds roughly to the maximum in Fig. 4A.

2) For environments with high predation and/or low noise (red curves), near criticality increases the relative payoff to individuals, which is dominated by the costs of false negatives. In these environments, depending on p_detect, the maximal relative payoff lies either near the estimated critical point or past it in the inaccessible supercritical regime, where overall responsiveness is maximized (see Fig. 3A and fig. S24). Under these conditions, individual response relies almost completely on social information.

3) Only for intermediate relative noise cost (light gray to light red), near criticality yields the maximal payoff for the individual. Here, individuals can benefit from the behavioral contagion process’ increased sensitivity to the number of initial startlers seen in Fig. 3 (and fig. S11). In all other scenarios, the benefit of an increased collective sensitivity near criticality is outweighed by either the increased false positive rate and decreased visual accessibility of the environment (compared to higher NND) or the decreased true positive rate (compared to lower NND). Only by including the sensory constraints on visual predator detection via the varying number of initial startles do we find the second maximum in the relative payoff in addition to the maximum near criticality.

Changing the parameters of visual predator detection can shift the visual access–based maximum (see figs. S20 and S22), and we find that, on average, baseline and alarmed datasets (indicated by dotted vertical lines) could optimize individual payoff according to the perceived riskiness of the environment, with the baseline condition corresponding to a higher and the alarmed condition to a lower relative noise cost (see fig. S23A).

DISCUSSION

We set out to (i) investigate criticality in the context of escape waves in animal groups and where the experimentally observed fish schools operate with respect to it (i.e., their distance to criticality); (ii) understand potential functional benefits of near criticality, especially with respect to the trade-off between robustness to noise versus sensitivity to environmental cues; and (iii) determine which individual or structural features control a group’s distance to criticality. We combined experimental observations of alarms spreading through groups of juvenile golden shiners at two different average school densities with a computational model to predict the average collective response across school densities. We identified a critical density at which transition from predominantly local to global cascades occurs. However, under two experimental conditions, the spreading of escape waves within the school is, on average, subcritical, with the schools in the alarmed condition being closer to the transition, answering (i).

Addressing (ii), we show that the critical manifold exhibits a high sensitivity to small differences in perturbation strength (number of initial startlers). Investigating biologically relevant functional benefits of near criticality for the individual fish, we considered the costs associated with two possible decision errors, namely, false positives and false negatives. Using simulated average cascade sizes and visual predator detection to infer individual’s relative payoffs, we find that depending on the type of environment, near criticality may be beneficial or detrimental to individuals and that by changing their distance to criticality fish within a school can manage the trade-off between robustness and sensitivity according to their current environment. In addition, this focus on visual predator detection identifies a potential trade-off between the acquisition of accurate personal and social information about the environment for the individual, where, with increasing density, the individual’s private information about the environment decreases because of occlusions, but the social information increases because of stronger interactions within the group.

Regarding (iii), we find that school density and individual responsiveness control the school’s distance to criticality. Under the experimental conditions, the upper limit to school density due to the fishs’ physical bodies prevents the schools from moving past the critical manifold to a supercritical state via modulation of density alone, potentially increasing robustness of contagion dynamics to density fluctuations. However, we show that increasing individual sensitivity allows a transition to supercritical spreading.

We study false alarms in a laboratory environment with fish that were bred in captivity without real predators. To improve our relative payoff measure, future experiments with real predators are needed to test and calibrate the underlying hypothesized model of visual predator detection. While we assume the initialization of a cascade by a certain number of fish at one point in time, the presence of an actual predator likely represents a temporally extended cue, which may cause additional (nonsocial) startles based on personal information and thus increase the average cascade size.

In insect swarms, it has been argued that large groups under natural conditions appear to operate near criticality (18), yet small groups under laboratory conditions do not (58, 59). Whereas many questions remain open regarding the role of environmental factors driving the observed collective movement of such swarms under natural conditions, it is possible that analogous effects could be observed in fish schools, with changes to the number of individuals and/or fluctuations in the natural environment, driving the system closer to, or potentially past, the critical state. Studies of larger groups under similar (laboratory) conditions could test whether there exists a trend of decreasing distance to criticality with increasing group size that we see when comparing the results of the fitted model on original-scale networks based on data from (28) and (27). In addition, fish raised in nonlaboratory conditions may, however, develop different thresholds or interactions. Further investigations of startling cascades under ecologically relevant scenarios, including under predation threat, environmental fluctuations, and a varying number of prey individuals, will be key here (60). In general, having a larger number of observations may also allow a direct observation of the density dependence of average cascade size via the natural fluctuations in school density. Further, the use of virtual reality for animals (61) may provide the means to control the density and the number and position of initial startles in future experiments.

The nature of interactions in our model does not change with density, yet lateral-line sensory inputs could additionally influence interactions at high densities, potentially shifting the critical point. However, our previous work (28) showed that the functional form of the interactions does not change significantly for the naturally observed change of density exhibited in response to perceived risk. While our results do not preclude the possibility that other mechanisms may increase sensitivity further in high-density situations, this would not change our main finding of subcritical spreading at the observed densities.

Previously, an initial increase in density following a collective escape response has been identified as essential to escape waves in schooling fish (30). Startles may systematically change local density and thus expedite or inhibit spreading. In addition, cascades may temporarily change the group’s overall density and thus create a group-level refractory period or an increased attention to further cues. These aspects are not considered in our modeling approach because it uses static interaction networks, which has previously been shown to be an appropriate approximation due to the high speed of spreading of cascades relative to changes in the interaction network topology (27). Nevertheless, future studies should consider the full spatiotemporal dynamics. If behavioral spreading systematically influences school density, then this may indicate a regulatory mechanism of self-organized (sub)criticality, allowing the school to control their interactions to remain responsive to relevant signals while filtering noise.

While it was previously known that the spatial structure of the school influences cascade size (28, 30), we systematically explore this influence via a model, identify the critical density, and place groups observed in experiments with respect to this transition. The investigation of two different environmental conditions, and the corresponding observed change of distance to criticality, sets this study apart from previous work on criticality in animal collectives (7, 17, 18). Our estimation of individual relative payoff offers a possible explanation of the observed subcritical spreading and emphasizes the importance of combining the collective description common to statistical physics with the individual perspective often taken in biological and psychological research on decision-making.

Our modeling results suggest that the collective response of schooling fish potentially minimizes the individuals’ average cost due to detection errors by tuning the estimated trade-off of false positives and false negatives according to the perceived risk of the environment. This occurs via a change of the school’s density and thereby its distance to criticality and not primarily by being at the critical point and thus maximally distinguishing different inputs. The absence of a single optimal amplification scheme (often assumed to be exactly at the critical point) may be due to the high variability in the environment and also variability of initial responses to the same cue due to changing group compositions and interindividual differences.

On the basis of our findings, we suggest that the study of criticality in living systems and, particularly, in animal collectives, focuses not only on the possible computational benefits but also on the potential costs of amplification of irrelevant fluctuations. By presenting a concrete example of a system that makes use of different distances to criticality according to context, we emphasize the benefits of actively regulating distance to criticality according to the environmental conditions or the complexity of the computational task at hand, as also recently discussed in the context of neuroscience (62). While many studies of neuronal cascades have focused on evidence of near criticality (8, 11, 12, 63–65) or subcriticality (14, 66) in certain contexts, others have highlighted the possibility that the distance to criticality varies with changing attentional states (53, 67–70). These examples suggest a pattern of active control in the trade-off between robustness and sensitivity that could be common to many forms of collective information processing. However, while in networks of neurons, the collective behavior determines the fitness of a single organism, the evolutionary pressure forming the collective behavior of animals is thought to act on the individual (23, 24). It is therefore also possible, and a promising direction for future research, that the control of distance to criticality in animal collectives may differ systematically from that observed in neuroscience.

MATERIALS AND METHODS

Experimental data

This study uses experimental tracking data of schools of juvenile golden shiners (N. crysoleucas), as described in (28) and (27), swimming freely in a white tank with shallow water, keeping them approximately 2D. Startling cascades were initiated by randomly occurring single startle (without provision of a stimulus or presence of a predator). A startle is a fast-start movement that is identified from tracking data via a threshold on the change in kinetic energy in (28) or a speed and turning angle in (27). Startles occurring within 1 s and 50 cm from each other are considered to be part of the same cascade (28). Previous work has found that these false alarms spread indistinguishably from startles that are initiated by a real fearful tactile stimulus (27). From (28), we use data of groups before and after a natural alarm substance [Schreckstoff, a family of chondroitins released from injured fish skin, i.e., close to a successful predation event (71)] was automatically sprayed on the water surface. To increase the number of samples in the baseline condition where cascades are not occurring as frequently as in the alarmed condition, we also included those cascades from control trials (where water was sprayed on the surface instead of Schreckstoff) that happened before the spraying. For more details on the experiments and data collection, we refer the readers to the original studies (27, 28).

Behavioral contagion model

To simulate startle cascades, we use a SIR-type model of behavioral contagion based on (45, 46) and previously used in (28). An individual, represented by a node in an interaction network with edges w_ij, can be in one of three states: susceptible (swimming at base speed), active (startling), and recovered (having startled in the cascade already). At the beginning of the simulation, we set n ≥ 1 individuals to the active state, and we stop the simulation once no more active individuals remain.

The individuals’ internal dynamics are as follows: A susceptible individual i receives stochastic activation cues of fixed size d_a from active individuals j with a rate r_ij = ρ_maxw_ij proportional to their link strength in the interaction network. Because the interaction networks are based on vision, this means that the individual is only influenced by those visible to it, i.e., those with w_ij > 0. The individual internally integrates the stochastic time series of received cues, d_ij(t), equally over its recent history of length τ_m (its memory time) to obtain its current cumulative activation

$$D_i(t)=\frac{1}{K_i}{\displaystyle \sum _j}{\displaystyle {\int }_{t-{\mathrm{\tau }}_m}^t}{d}_{\mathit{\text{ij}}}(t\prime ) dt\prime$$ (1)

Here, for simplicity, we approximated the increment of the internal state by a point process with d_ij corresponding to the Dirac delta function. K_i is the number of i’s visible neighbors, making this a fractional contagion process as supported by the previous work (27). Each individual has an internal response threshold θ_i that indicates the level of socially signaled risk it tolerates before startling itself. If the cumulative activation exceeds this threshold, then the individual becomes active. After a fixed activation time τ_act, it recovers and stays that way until the end of the simulation. Response thresholds are drawn from a uniform distribution with minimum θ_min = 0 and maximum ${\mathrm{\theta }}_{\text{max}}=2\overline{\mathrm{\theta }}$ (resulting in an average response threshold of $\overline{\mathrm{\theta }}$) to account for stochasticity due to inaccessible internal states of individuals at the time of initial startle. Most parameters are fixed as in (28) (τ_act = 0.5s, ρ_max = 10³s⁻¹, d_a = 10⁻³), leaving the average response threshold $\overline{\mathrm{\theta }}$ as a single free parameter describing the individual sensitivity to social cues. Similar to (28), we fit the average response threshold to the experimental data using a maximum-likelihood approach with 10,000 simulations of a cascade per network, initiated by the same individual as experimentally observed for this network (fig. S6 and table S1). We set the finite memory to τ_m = 1 s, as link weights w_ij were obtained from the experimental data using a time window of 1 s to detect startles following an initial startle event (28); however, our general results are robust with respect to the choice of τ_m (see section S3.6).

Construction of interaction networks

Interaction networks are based on experimentally observed first responses to a single initial random startle. Previous work found that, via L1-penalized logistic regression and multimodel inference, among a variety of features of the initial startler itself (absolute features) and in relation to other within the group (comparative features), the probability of individual i to be a first responder to the initial startle of individual j can best be predicted by the log of the metric (Euclidean) distance (LMD) between individual i and j (in centimeters) and the ranked angular area (RAA) of j in the visual field of i (27, 28). Here, the RAA numbers all individuals in order of decreasing visual angle in the visual field of j, with RAA = 1 being the largest individual and RAA = N − 1 being the smallest. Here, we perform a logistic regression (n = 4018 for the baseline condition and n = 8238 for the alarmed condition) on these previously established features to determine how to construct network links from the positions and orientations of individuals. The resulting coefficients β_i can be found in table S2, and networks links are thus given by

$$w_{\mathit{\text{ij}}}={(1+\text{exp} (-{\mathrm{\beta }}_1-{\mathrm{\beta }}_2\text{LMD}-{\mathrm{\beta }}_3\text{RAA}))}^{-1}$$ (2)

For the construction of networks of different densities, we rescaled the positions of the fish and recalculated metric distances and visual fields and resulting RAAs to obtain network links via Eq. 2. Individuals were approximated as ellipses, and an automated routine [based on (72)] was used to shift and slightly turn individuals where they overlapped to ensure a 2D school. Details can be found in section S1.

We validated the ellipse approximation by comparing the networks that we obtain for the original (nonrescaled) density with the networks constructed in previous research (27) (which used ray casting and body shape reconstruction from the tracking software to calculate the visual fields). We compared the two sets based on network properties and the ability of the behavioral contagion model (see previous paragraph) to explain the observed data using these networks (section S3.1) and found good agreement.

Sensitivity

We simulate 1000 startle cascades per experimental trial and rescaling factor by setting m randomly chosen individuals to the active (startling) state and recording the number of individuals that startle before the cascade dies out. From these simulations, we obtain an average cascade size for each trial, initial condition (m), and bins of median NND by averaging over the simulation runs. Division by group size, N, yields the relative average cascade size, c_m. Subtracting the relative average cascade sizes following m initial startles from that following m + 1 initial startles gives the sensitivity shown in fig. S11, with the special case of m = 1 shown in Fig. 3B. Subtracting the relative average size of cascades triggered by one individual from that triggered by m individuals yields the sensitivity shown in fig. S11. The qualitative result does not depend on choosing initiators at random but holds for choosing them to be network neighbors as well (see fig. S11).

Branching ratio calculation

A useful measure to describe the aggregate effects of a local perturbation in a contagion model is the average branching ratio, which answers the question: In a completely susceptible (quiescent) system in which a single individual j becomes active, what is the average number of other individuals i that become active due to the direct influence of individual j? This branching ratio b describes how small initial startling cascades, on average, tend to grow or shrink. For large N, it also defines a transition between two distinct aggregate behaviors: When b < 1, startling cascades tend to die out and only affect a small fraction of the whole group, and when b > 1, cascades tend to spread through the entire group. To calculate b, we note that the average total additional activation received by individual i due to j startling is (28)

$$\mathrm{\Delta }{D}_i=d_{\mathrm{a}}{\mathrm{\rho }}_{\text{max}}{\mathrm{\tau }}_{\text{act}}\frac{w_{\mathit{\text{ij}}}}{K_i}$$ (3)

where d_a is the activation cue intensity, ρ_max is the maximum rate of receiving cues, τ_act is the activation duration, K_i is the number of i’s visible neighbors, and w_ij is the probability from the logistic regression model that i is a first responder given that individual j initially startled. As in (28), we will discretize time in 1-ms increments and set the arbitrary scale of cue intensities d_a such that d_aρ_max = 1, producing

$$\mathrm{\Delta }{D}_i={\mathrm{\tau }}_{\text{act}}\frac{w_{\mathit{\text{ij}}}}{K_i}$$ (4)

We translate this additional activation to individual i into the average number of additional startles produced by calculating the probability that this causes i’s state to go above the threshold. This is equal to ΔD_i times the probability density of i’s threshold being between D_i and D_i + ΔD_i. Because we use a constant probability density for thresholds $p({\mathrm{\theta }}_i)={\mathrm{\theta }}_{\text{max}}^{-1}$, and given ΔD_i < θ_max, the probability of i startling due to j startling is

$$p_{\mathit{\text{ij}}}=\mathrm{\Delta }{D}_i{\mathrm{\theta }}_{\text{max}}^{-1}=\frac{{\mathrm{\tau }}_{\text{act}}}{{\mathrm{\theta }}_{\text{max}}}\frac{w_{\mathit{\text{ij}}}}{K_i}$$ (5)

Then, the average number of additional individuals startled due to j’s startle is our branching ratio

$$b_j={\displaystyle \sum _i}{p}_{\mathit{\text{ij}}}=\frac{{\mathrm{\tau }}_{\text{act}}}{{\mathrm{\theta }}_{\text{max}}}{\displaystyle \sum _i}\frac{w_{\mathit{\text{ij}}}}{K_i}$$ (6)

and the average branching ratio, given that the cascade starts with a random individual j, is the measure used in this study as an analytical measure of criticality. Here, it is assumed that all neighbors of j are susceptible at the time of activation of j and that j is the only active neighbor of its network neighbors i. This assumption is best met at the beginning of a cascade and likely leads to an overestimation of the effective average branching ratio observed in simulations (73).

Relative individual payoff

Assuming individual payoffs due to different costs of false and true positives and negatives, we have derived the relative payoff, ψ, as a function of median NND to

$$\mathrm{\psi }(\text{NND})=-\frac{1}{{\mathrm{\psi }}_0}[p_{\text{fp}}(\text{NND})·\mathrm{\xi }+p_{\text{fn}}(\text{NND})]$$ (7)

(see detailed derivation in section S5.2). In Eq. 7, the relative noise cost

$$\mathrm{\xi }=\frac{{\mathrm{\rho }}_{\text{noise}}}{{\mathrm{\rho }}_{\text{pred}}}\left(\frac{{\mathrm{\kappa }}_{\text{fp}}-{\mathrm{\kappa }}_{\text{tn}}}{{\mathrm{\kappa }}_{\text{fn}}-{\mathrm{\kappa }}_{\text{tp}}}\right)$$ (8)

characterizes the environment via the costs associated with each event type (false and true positive, κ_fp ≥ 0 and κ_tp ≤ 0, as well as false and true negative, κ_fn ≥ 0 and κ_tn ≤ 0), and the rate at which predator cues, ρ_pred, and noise cues, ρ_noise, appear. The conditional probabilities of the two types of error, startling (s) in response to noise (false positives, p_fp) or not startling ($\overline{s}$) in response to a predator cue (false negatives, p_fn), are determined through simulations of average cascade sizes. Depending on the type of error, cascades are initiated by different numbers, N_init, of randomly selected individuals as follows

$$p_{\text{fp}}(\text{NND})=p(s\mid N_{\text{init}}=1,\text{NND})$$ (9)

$$p_{\text{fn}}(\text{NND})=p(\overline{s}\mid N_{\text{init}}=p_{\text{detect}}{N}_{\text{vis}}(\text{NND}),\text{NND})$$ (10)

Referring to experimental observations, where random startles occur at low rates (27) and therefore cascades where triggered by a single initial random startle, we use one initial startler to simulate false positives. False negatives are simulated as the average fraction of a school that is not part of a cascade initiated by p_detectN_vis(NND) individuals. Here, N_vis(NND) is the average number of individuals that can see a predator at distance d_pred = 10 BL from the school boundary with a maximal detection range of d_max = 40 BL, and p_detect = 0.1 characterizes the individual responsiveness to a predator cue. Average cascade sizes for noninteger numbers of initial startles are obtained by proportionally combining the results for the two integers closest to the desired value. The relative payoff is rescaled by the costs for an individual in an infinitely dilute school

$${\mathrm{\psi }}_0=\underset{\text{NND}\to \infty }{\text{lim}}[p_{\text{fp}}(\text{NND})·\mathrm{\xi }+p_{\text{fn}}(\text{NND})]=1-\frac{p_{\text{detect}-\mathrm{\xi }}}{N}$$ (11)

to highlight the influence of schooling. Qualitatively, our results are independent of the exact choice of d_pred, d_max, and p_detect (see section S5.1 and figs. S20 and S22).

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S25

Tables S1 to S3