Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2022 Jun 6;144(24):10921–10928. doi: 10.1021/jacs.2c03726

Mechanistic Insights into the Reaction of Amidines with 1,2,3-Triazines and 1,2,3,5-Tetrazines

Zhi-Chen Wu †, K N Houk ‡, Dale L Boger †,§,*, Dennis Svatunek ∥,‡,*
PMCID: PMC9228069  PMID: 35666564

Abstract

graphic file with name ja2c03726_0009.jpg

1,2,3-Triazines and 1,2,3,5-tetrazines react rapidly, efficiently, and selectively with amidines to form pyrimidines/1,3,5-triazines, exhibiting an orthogonal reactivity with 1,2,4,5-tetrazine-based conjugation chemistry. Whereas the mechanism of the reaction of the isomeric 1,2,4-triazines and 1,2,4,5-tetrazines with alkenes is well understood, the mechanism of the 1,2,3-triazine/1,2,3,5-tetrazine–amidine reaction as well as its intrinsic reactivity remains underexplored. By using 15N-labeling, kinetic investigations, and kinetic isotope effect studies, complemented by extensive computational investigations, we show that this reaction proceeds through an addition/N2 elimination/cyclization pathway, rather than the generally expected concerted or stepwise Diels–Alder/retro Diels–Alder sequence. The rate-limiting step in this transformation is the initial nucleophilic attack of an amidine on azine C4, with a subsequent energetically favored N2 elimination step compared with a disfavored stepwise formation of a Diels–Alder cycloadduct. The proposed reaction mechanism is in agreement with experimental and computational results, which explains the observed reactivity of 1,2,3-triazines and 1,2,3,5-tetrazines with amidines.

Introduction

The inverse electron demand Diels–Alder reaction of heterocyclic azadienes serves as a powerful method for the construction of highly substituted or functionalized six-membered heterocyclic systems with widespread applications, including natural product total synthesis1−3 and the divergent construction of screening libraries.4−7 In particular, the ultrafast reaction between 1,2,4,5-tetrazines and strained alkenes is now developed as a mature and widely applied bioorthogonal conjugation method in chemical biology.8−12 Previous contributions in this area resulted in the detailed establishment of the reactivity of each heterocycle class with a variety of dienophiles,13−17 and computational studies elucidated the intrinsic reactivities of these heterocycles as well as the impact of substituent effects.18−23 Specifically, we explored the cycloaddition reactions between 10 fundamental azadienes and ethylene dienophiles, revealing the origins of their different reactivities from the analysis of both orbital interactions and distortion energies.19 Due to the low energetic penalty during distortion to the transition state geometry, 1,2,4,5-tetrazines and 1,2,4-triazines have the highest reactivity among tetrazines and triazines, which is demonstrated by the superb reactivity of these two heterocycles and the extensive exploration of the bioorthogonal ligation reactions of 1,2,4,5-tetrazines.9,24,25

Recently, we systematically defined the reactivity of various 1,2,3-triazines and that of the first member of the previously unknown 1,2,3,5-tetrazines as a family of more polarized dienes in inverse electron demand Diels–Alder reactions and demonstrated their applications in the synthesis of various heterocycles including pyridines, pyrimidines, pyridazines, and 1,3,5-triazines.26−32 Specifically, we defined the outstanding reactivity between 1,2,3-triazine/1,2,3,5-tetrazine and amidines, providing nearly quantitative conversion to pyrimidines/1,3,5-triazines under mild conditions, demonstrated the exclusive C4/N1 cycloaddition selectivity, and quantitatively determined the rate constants of these reactions that meet the requirements of applicable ligation reactions. The observed orthogonal reactivity between a novel 1,2,3,5-tetrazine/amidine ligation and a traditional 1,2,4,5-tetrazine/strained alkyne ligation revealed a highly distinct reactivity between the two isomeric tetrazines.26 A similar discovery was also reported by Siegl and Vrabel, with an observed orthogonality between the 1,2,3-triazine/amidine ligation pair and the 1,2,4-triazine/trans-cyclooctene pair.33 Whereas 1,2,3,5-tetrazines/1,2,3-triazines are predictably less reactive than 1,2,4,5-tetrazines/1,2,4-triazines with ethylene dienophiles, the source of their superb intrinsic reactivity with heterodienophiles including amidines remains unclear. Our previous investigation of the reaction between 1,2,3-triazines and enamines revealed the reaction course shifting away from a concerted to a stepwise mechanism along with an improved reactivity depending on the triazine substituents as well as the reaction solvent,34 shedding light on the impact of a potential alternative reaction mechanism on the outstanding reactivity. Herein, we report our experimental and computational investigation of the mechanism and the intrinsic reactivity of the reaction between amidines and 1,2,3,5-tetrazine/1,2,3-triazines.

Results and Discussion

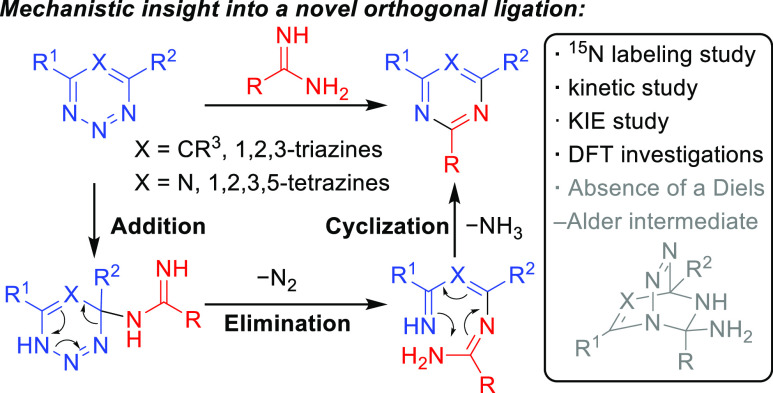
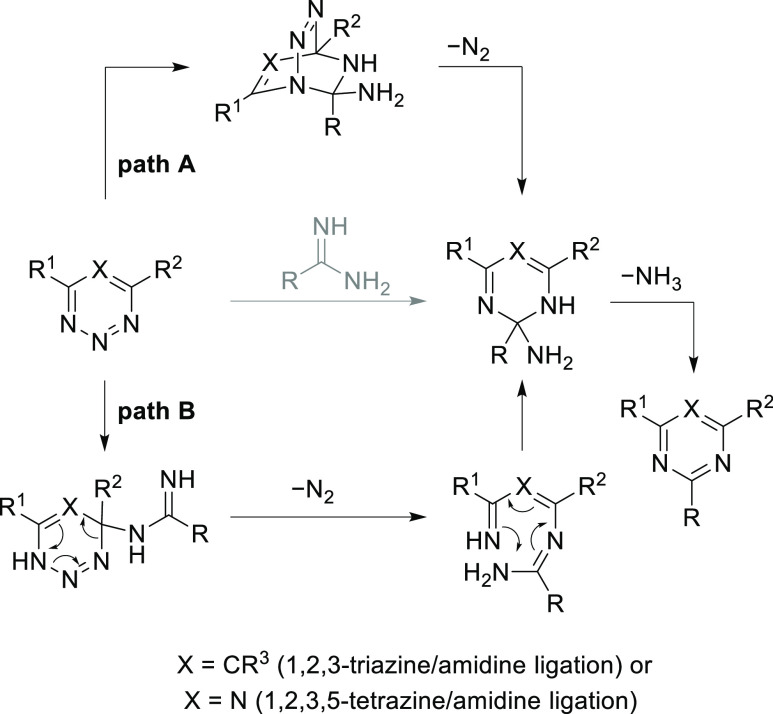
Focusing on the mechanism of the reaction between amidines and 1,2,3,5-tetrazine/1,2,3-triazines, the widely accepted pathway is a concerted or stepwise Diels–Alder reaction mechanism, which is then followed by a subsequent retro Diels–Alder reaction and elimination to provide the aromatic 1,3,5-triazine/pyrimidine products (Figure 1, path A). However, due to the increase in the polarity of both reactants, an alternative stepwise addition/N2 elimination/cyclization mechanism may also be proposed.30 Initiated by a nucleophilic attack of the amidine nitrogen on C4 of the triazine or tetrazine, the adduct could then lose dinitrogen, followed by electrocyclization and elimination to provide the same products (Figure 1, path B).

Figure 1.

Figure 1

Open in a new tab

Possible mechanisms for the reaction between 1,2,3-triazines/1,2,3,5-tetrazines with amidines including a Diels–Alder mechanism (path A) and an addition/N2 elimination/cyclization mechanism (path B).

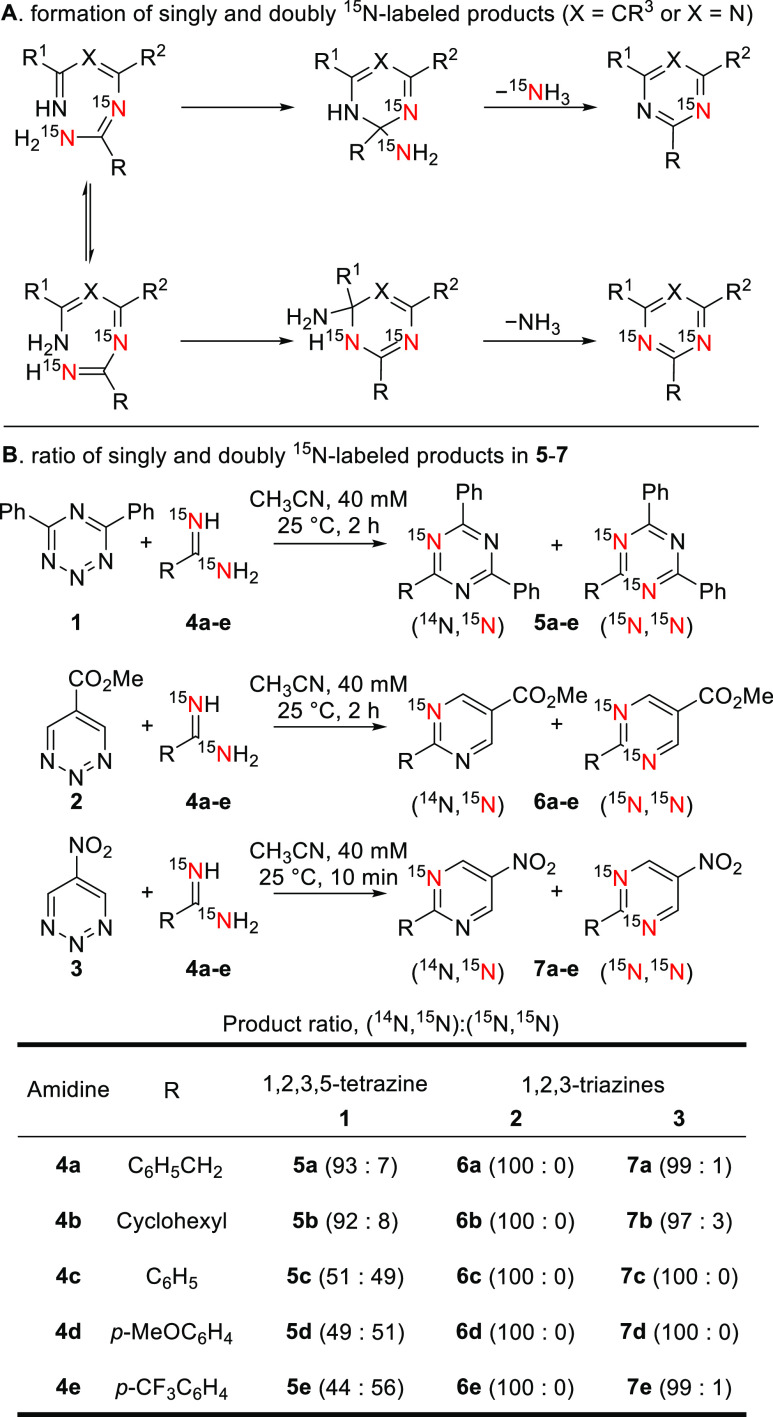
In order to investigate the mechanism of the reaction between 1,2,3,5-tetrazines/1,2,3-triazines and various amidines and distinguish between a concerted or stepwise cycloaddition mechanism (path A) versus a mechanism without the cycloadduct (path B), we expanded our previous 15N-labeling studies of the reaction of 1 or 2 with doubly 15N-labeled amidine 4a.26,30 Here, we analyzed the reaction product obtained in the reaction of doubly 15N-labeled amidines 4a-e and 1,2,3,5-tetrazine 1 or 1,2,3-triazines 2 and 3 (Figure 2). The Diels–Alder mechanism is expected to provide singly 15N-labeled products exclusively, whereas two tautomeric 1,3,5-trienes could be present in the alternative addition/N2 elimination/cyclization mechanism, providing access to both singly and doubly 15N-labeled products (Figure 2A). Similar to the reaction with non-labeled amidine counterparts, the labeling reaction was performed under mild and dilute conditions to provide 1,3,5-triazine products (5a–e) or pyrimidine products (6a–e, 7a–e) in nearly quantitative yields (86–99%, Figure S1). The ratios of singly and doubly 15N-labeled products were then determined by high-resolution mass spectrometry (HRMS). For 1,3,5-triazine products 5a–e for which a substantial quantity of doubly 15N-labeled product was observed, the second 15N incorporation ratio was further confirmed through the analysis of the 13C NMR spectra, focusing on the carbon peaks split by a 2J(13C–15N) coupling. The second 15N incorporation ratio is consistent across the two methods, with an observed <5% difference. For pyrimidines 6a–e and 7a–e, the splitting patterns of 13C signals revealed that no doubly 15N-labeled pyrimidines were observed, further confirming the results from HRMS.

Figure 2.

Figure 2

Open in a new tab

15N-labeling studies.

Whereas the reactions between tetrazine 1 and alkyl amidines 4a or 4b provided a 7–8% incorporation of the second 15N in the triazine products, the reaction between 1 and aryl amidines (4c–e) resulted in a substantial 49–56% incorporation of the second 15N. While the second, but minor, 15N incorporation in the triazine products 5a and 5b still provided an ambiguous observation that could be consistent with both mechanisms, a nearly 1:1 ratio of the two labeled products in 5c–e clearly rules out the concerted or stepwise cycloaddition mechanism, suggesting that the reaction does not progress through the cycloaddition intermediate. Notably, the ratios of labeled products were not found to be significantly impacted by either the sterics of the alkyl amidine substituents or the electronics of substituted benzamidines (5c–e). The 15N-labeling studies of the reactions between 1,2,3-triazines (2 and 3) and amidines 4a-e provided exclusively singly 15N-incorporated triazine products (6a–e and 7a–e, second 15N incorporation 0–3%), differing in the reaction outcome from the reactions of 1,2,3,5-tetrazine. The observed difference in the labeling studies is interesting and intriguing, requiring our further investigation into the reaction mechanism.

Our subsequent investigation focused on the reaction kinetics and the substituent electronic effects of the reactions to further probe the mechanism through a quantitation of reaction rates of tetrazine 1 and triazine 2 (Figure 3). The reaction of tetrazine 1 or triazine 2 with a series of para-substituted benzamidines 8a–e was monitored by 1H NMR (solvent: CD3CN/CDCl3 1:1), and conversion was determined by observing either the formation of corresponding 1,3,5-triazine or pyrimidine products or the consumption of reactants. The data acquired were observed to fit second-order reaction kinetics from which the rate constants were then determined.

Figure 3.

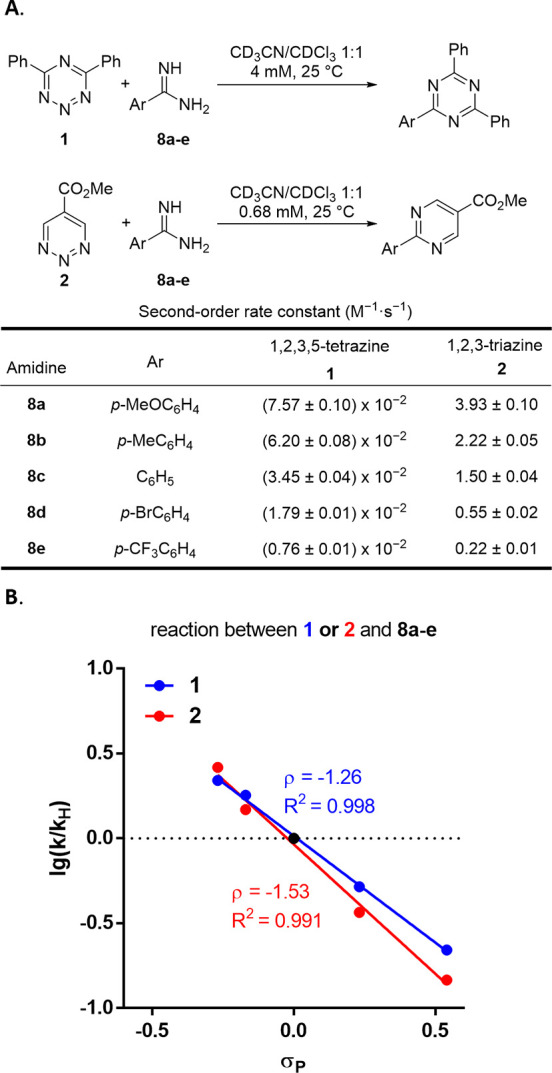
Figure 3

Open in a new tab

(A) Second-order rate constants of the reactions between tetrazine 1 or triazine 2 and amidines 8a–e. (B) Hammett plot for the reaction between 1 or 2 and 8a–e.

Through 1H NMR monitoring of the reaction, a clean formation of the products was observed without the observation of any reaction intermediates (Supporting Information, Figures S2–S11), indicating that the first step in the reaction pathway is the rate-limiting step in both the 1,2,3,5-tetrazine/amidine and 1,2,3-triazine/amidine reactions. A large electronic effect of the para-substituents on the benzamidines 8a–e on the reaction was observed; benzamidines with electron-donating substituents (8a, 8b) provided a greater reactivity and those with electron-withdrawing substituents (8d, 8e) reacted more slowly. The difference in reactivity was as large as 10- to 15-fold between the most electron-rich amidine 8a and the most electron-deficient amidine 8e. The relative reaction rates were found to fit a linear Hammett plot, where a ρ value of −1.26 was observed for 1,2,3,5-tetrazine 1, and a slightly larger ρ value of −1.53 was observed for 1,2,3-triazine 2. These observations indicate the accumulation of a partial positive charge on the amidine carbon in the transition state of the rate-determining step and support the reaction being initiated by a nucleophilic attack of the amidine nitrogen onto tetrazine 1 or triazines.

With these experimental insights in hand, we proceeded with a computational study of these systems. Using density functional theory (DFT), we employed the M06-2X density functional augmented with Grimme’s D3 dispersion correction as proposed by Grimme and co-workers.35 DFT calculations were performed using Gaussian 09 Rev D.01. def2TZVP was used as the basis set. The SMD model with acetonitrile as solvent was used to include the solvent effects. Conformer searches of all involved structures, including transition states, were conducted. A detailed description of the methods used can be found in the Supporting Information.

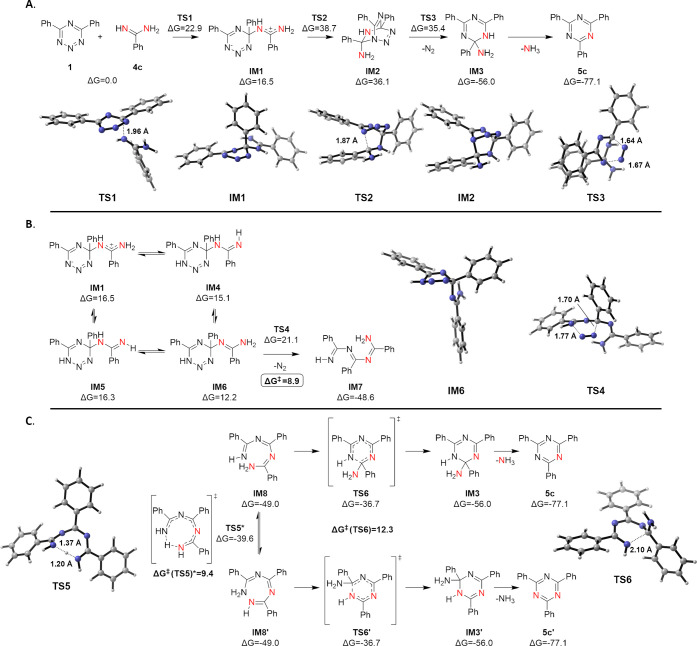
Starting with the reaction between 1 and 4c, we first investigated the Diels–Alder mechanism (Figure 4A). A concerted Diels–Alder transition state could not be located, which is not surprising given the polarized nature of both the diene and dienophile. The initial nucleophilic attack of the amidine nitrogen at C4 of tetrazine 1 has a free energy barrier of 22.9 kcal/mol (TS1), leading to a zwitterionic intermediate IM1, which is 16.5 kcal/mol higher in energy than the starting material. Formation of the second bond is highly unfavored with a transition state TS2 at 38.7 kcal/mol, and the energy of Diels–Alder product IM2 is at 36.1 kcal/mol in relation to the starting material. The subsequent retro Diels–Alder reaction is barrierless (TS3) and gives a stable intermediate IM3 accompanied by the elimination of N2, and the final product 5c is provided after elimination of NH3. For tetrazine 1, the ratio between singly and doubly 15N-labeled products in the reaction with doubly 15N-labeled amidine 4c is close to 1:1. This experimental result already excludes the Diels–Alder mechanism and is further supported by our calculations due to the high free energies encountered in this pathway.

Figure 4.

Figure 4

Open in a new tab

(A) Diels–Alder mechanism for the reaction between 1 and 4c. (B) Retro Diels–Alder step of the addition/N2 elimination/cyclization pathway between 1 and 4c. (C) Electrocyclization step of the addition/elimination/cyclization pathway between 1 and 4c. Lowest energy pathways and 3D geometries of key structures are shown. Energies are in kcal/mol relative to starting materials. *Barrier height was corrected to account for tunneling.

Next, we investigated the addition/N2 elimination/cyclization pathway. The first step is a nucleophilic attack identical to the Diels–Alder mechanism, where the zwitterionic intermediate IM1 formed is in equilibrium with three other tautomers (IM4–6, Figure 4B).

The most stable intermediate IM6 corresponds to the lowest energy transition state (TS4) among the tautomers in the subsequent retro Diels–Alder reaction to provide highly stable IM7 accompanied by the extrusion of N2. IM1, IM4, and IM5 can also undergo the retro-Diels–Alder reaction, leading to tautomers of IM7, albeit with higher barriers (see Figure S12). Amongst all the possible tautomeric and rotational isomers of IM7, isomers IM8 and IM8′ are the only ones that can react in the 6π electrocyclization (Figure 4C), which can rapidly interconvert between each other by intramolecular proton transfer through the low-energy transition state TS5 (corrected for tunneling, see Figure S14). However, these two intermediates are the same due to symmetry, and only the usage of 15N-labeled amidine 4c or amidines different from 4c as the reaction partner differentiate between these tautomers. The electrocyclization products IM3 and IM3′ are hence expected to be generated in equal amounts since both electrocyclization pathways are equivalent; a subsequent elimination of NH3 provides both singly and doubly 15N-labeled triazines 5c in a 1:1 ratio as the overall product of the reaction. Consequently, such a stepwise reaction mechanism through intermediates IM8 and IM8′ is in good agreement with our 15N-labeling studies where a 49:51 ratio was observed for product 5c. The comparison of the activation energy of all steps and the relative energy of all transition states supports the initial nucleophilic addition as the rate-limiting step, which is also in accordance with monitoring of the reaction progress between 1,2,3,5-tetrazine 1 and aryl amidines 8a–e as well as the observed Hammett relationship (Figure 3B).

A more general case was also investigated in detail in addition to the 1,2,3,5-tetrazine ligation reaction with amidine 4c to shed light on the reaction mechanism with a non-symmetrical 6π-electrocyclization precursor with two possible electrocyclization pathways. Focusing on the selectivity-determining electrocyclization step between 1 and 4a, the electrocyclization precursors IM9 and IM10 are close in energy with IM10 at a relative energy of +0.6 kcal/mol (Figure 5); the interconversion between the two tautomers is also possible through TS7. This intramolecular proton transfer is accelerated due to tunneling (Figure S14). Electrocyclization starting from IM9 through TS8 was found to be kinetically favored by −2.6 kcal/mol over the alternative TS9, resulting in the formation of IM11 as the major cyclized intermediate over IM12. The final elimination of NH3 provides both triazines 5a and 5a′, with the major product being the singly labeled product 5a under kinetic control. The predicted reaction outcome agrees with the experimental result where the reaction between 1,2,3,5-tetrazine 1 and 15N-labeled phenylacetamidine 4a provided triazine 5a in a 93:7 ratio of singly and doubly 15N-labeled products.

Figure 5.

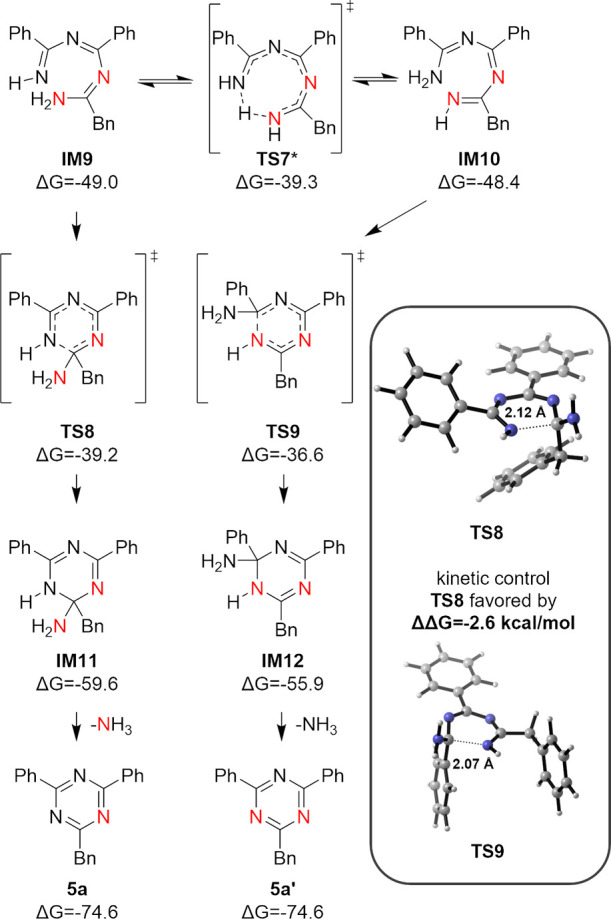
Figure 5

Open in a new tab

Electrocyclization step of the addition/N2 elimination/cyclization pathway between 1 and 4a. Lowest energy pathway and 3D geometries of key structures are shown. Energies are in kcal/mol relative to starting materials. *Barrier height was corrected to account for tunneling.

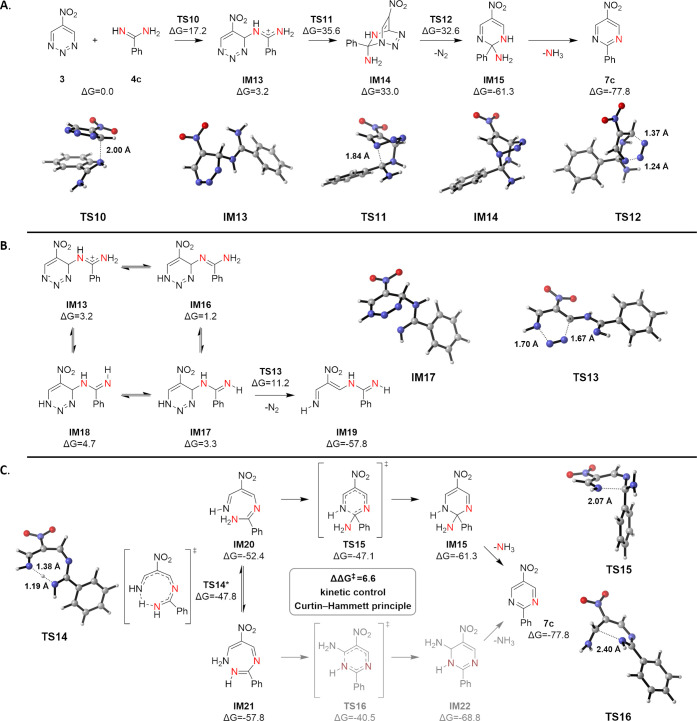
Following our studies on the reaction with 1,2,3,5-tetrazines, we then investigated the mechanism of the reaction between 1,2,3-triazine 3 and amidine 4c. Triazine 3 instead of 2 was chosen for its additional symmetry, avoiding an additional twofold increase in the already very high number of investigated conformers/tautomers. Similar to the case of 1,2,3,5-tetrazine, a concerted Diels–Alder transition state could not be located. In the stepwise Diels–Alder pathway (Figure 6A), the initial nucleophilic attack of the amidine nitrogen at C4 of triazine 3 shows a free energy barrier of 17.2 kcal/mol (TS10), leading to a zwitterionic intermediate IM13, which is 3.2 kcal/mol higher in energy than the starting materials. Formation of the second bond is highly unfavored with a transition state TS11 at 35.6 kcal/mol, and the energy of Diels–Alder product IM14 is 33.0 kcal/mol in relation to the starting material. The subsequent retro Diels–Alder reaction is barrierless (TS12) and gives a more stable intermediate IM15 accompanied by elimination of N2, and the final product 7c is provided after elimination of NH3. While the Diels–Alder pathway is in agreement with the result of 15N-labeling experiments, the rate-limiting step was found to be the formation of the Diels–Alder cycloadduct IM14, which is contradictory to the observed Hammett relationship in a similar triazine 2. The high barrier encountered in the formation of the bicyclic Diels–Alder product IM14 further supported an alternative mechanism not including the energetically highly disfavored cycloadduct.

Figure 6.

Figure 6

Open in a new tab

(A) Diels–Alder mechanism for the reaction between 3 and 4c. (B) Retro Diels–Alder step of the addition/N2 elimination/cyclization pathway between 3 and 4c. (C) Electrocyclization step of the addition/elimination/cyclization pathway between 3 and 4c. Lowest energy pathways and 3D geometries of key structures are shown. Energies are in kcal/mol relative to starting materials. *Barrier height was corrected to account for tunneling.

Next, we investigated the addition/N2 elimination/cyclization pathway. The first step is a nucleophilic attack identical to the Diels–Alder mechanism, where the formed zwitterionic intermediate IM13 was found to be in equilibrium with three other tautomers (IM16–18, Figure 6B). While all these isomers can undergo the retro Diels–Alder reaction with low barriers, the activation energy for isomer IM17 is the lowest at 11.2 kcal/mol in relation to the starting material, forming the highly stable intermediate IM19. IM13, IM16, and IM18 can also undergo dinitrogen elimination to yield isomers of IM19 (see Figure S13). Similar to the case of IM7, intermediate IM19 is also in equilibrium with a collection of isomers, including electrocyclization precursors IM20 and IM21 (Figure 6C), which are also interconvertible through intramolecular proton transfer (TS14, corrected for tunneling, see Figure S14). Although intermediate IM20 is considerably less stable than IM21, the corresponding transition state (TS15) of the electrocyclization is −6.6 kcal/mol lower in energy than the alternative TS16. Kinetic control leads to the cyclized product IM15, which gives the final product 7c after the loss of NH3. Such a reaction pathway is predicted to provide exclusive formation of the pyrimidine product containing only one of the nitrogen atoms originating from the amidine. This agrees with our labeling studies where only singly 15N-labeled 7c is observed when triazine 3 is treated with doubly 15N-labeled amidine 4c. This observation is not limited to this specific case but is a general result where singly 15N-labeled products are generated exclusively when 1,2,3-triazines 2 and 3 are treated with various 15N-labeled amidines (Figure 2). Similar to the case of 1,2,3,5-tetrazine 1, the initial nucleophilic attack was identified as the rate-limiting step, which agrees with the observed Hammett relationship for the electronically and sterically very similar triazine 2 (Figure 3B). Although both of the reaction pathways are predicted to provide exclusive singly 15N-labeled pyrimidine products, the addition/N2 elimination/cyclization mechanism is supported by the nature of the rate-limiting step and the energetically favored N2 elimination.

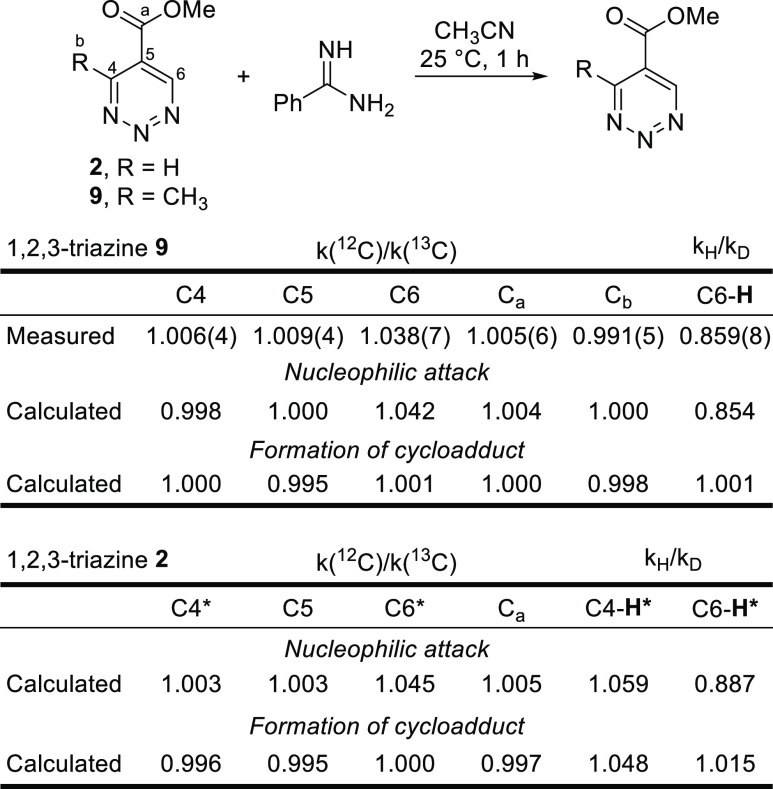
Additional studies of the kinetic isotope effect (KIE) of key atoms in the azadienes provided further insights into the reaction mechanism (Figure 7). A combined experimental and theoretical investigation of the KIE was conducted on 1,2,3-triazines, where both 12C/13C and additional H/D KIE information due to the presence of the aromatic protons on the azadiene system could be examined. Due to the symmetrical nature of 1,2,3-triazine 2, experimental measurements of H/D and 12C/13C KIE were conducted on 1,2,3-triazine 9, a previously reported32 reactive triazine with an added C4 methyl substituent, to allow their precise determination. The 12C/13C KIE of all carbons in 1,2,3-triazine 9 was determined through Singleton’s method,36 and the direct intermolecular competition method was applied for the H/D KIE determination of the triazine aromatic hydrogen. A significant primary 12C/13C KIE (1.038) of the 1,2,3-triazine C6 carbon and a strong inverse secondary H/D KIE (0.859) of the aromatic proton in triazine 9 were observed, while the 12C/13C KIE of the remaining carbons including C4 were found to be essentially 1 (1.00). The observed results are indicative of a direct bond formation of only the C6 carbon and a change in its hybridization state from sp2 to sp3 in the transition state of the rate-determining step.

Figure 7.

Figure 7

Open in a new tab

KIE studies. *For calculated KIEs, a nucleophilic attack in position 6 was used.

These results agree well with the calculated KIE for an initial nucleophilic attack at C6 (C6 12C/13C KIE = 1.042, H/D KIE = 0.854), consistent with the addition/N2 elimination/cyclization mechanism with the nucleophilic addition being the first and rate-determining step. The reaction pathway through a rate-determining formation of the cycloadduct features a calculated KIE of 1.001 for the C6 carbon, 1.000 for the C4 carbon, and 1.001 for the aromatic proton on triazine 9, which is distinct from the observed results and further indicating that it is an unlikely mechanism. For comparison, energy profiles (Supporting Information Figure S15) and theoretical KIEs were also calculated for 1,2,3-triazine 2 and resemble the results obtained with methyl 1,2,3-triazine 9.

Conclusions

Through combined experimental and computational mechanistic studies, the suspected concerted or stepwise Diels–Alder reaction pathway was ruled out as a plausible reaction mechanism for the reaction of 1,2,3-triazines/1,2,3,5-tetrazines with amidines. Instead, the results revealed that a stepwise addition/N2 elimination/cyclization pathway is a more likely mechanism. An initial nucleophilic attack of the electron-rich amidine nitrogen on the electron-deficient 1,2,3-triazine/1,2,3,5-tetrazine carbon was revealed to be the rate-determining step, which is in agreement with the calculated highest energy barrier, absence of detectable reaction intermediates, a singularly strong KIE on C6 carbon (of 9) as well as the attached proton, and the strong Hammett relationship of the para-substituents of the arylamidines on the overall reactivity with a positive charge accumulation on the amidine in the transition state.

Subsequent reaction progresses through a highly exothermic retro Diels–Alder reaction with the elimination of N2, avoiding the formation of an intermediate and unstable bicyclic Diels–Alder adduct. Incorporation of one or two amidine nitrogen atoms, as observed by 15N-labeling studies, is kinetically controlled at the 6π electrocyclization step. Electronic properties of the substituents of the triene intermediate as well as its intrinsic reactivity were found to determine the ratio of singly versus doubly labeled products. The proposed reaction mechanism provided deeper insights into this formal inverse electron demand Diels–Alder reaction as well as further understanding of the origin of the observed orthogonal reactivity between polarized heterocyclic systems (including 1,2,3,5-tetrazine and 1,2,3-triazine) and relatively non-polarized heterocyclic azadienes (including 1,2,4,5-tetrazine and 1,2,4-triazine).

Acknowledgments

This project has received funding from the National Science Foundation (CHE-1764328, K.N.H.) and National Institutes of Health (CA042056, D.L.B.). The computational results presented have been achieved using the Vienna Scientific cluster (VSC) at TU Wien and the Hoffman2 cluster at UCLA. D.S. is grateful to the Theodor Körner fund (Vienna, Austria) for financial support. The authors gratefully thank Dr. Laura Pasternack (TSRI) for the guidance on KIE and kinetic studies by NMR spectroscopy. The authors acknowledge TU Wien Bibliothek for financial support through its Open Access Funding Program.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.2c03726.

  • Computational methods and results, additional computational data, organic synthesis, reaction kinetics, labeling studies, kinetic isotope effect studies, and copies of NMR spectra (PDF)

  • Coordinates of all calculated geometries (ZIP)

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

Due to a production error, this paper was published ASAP June 6, 2022, with an error in Figure 3. The corrected version was reposted June 6, 2022.

Supplementary Material

ja2c03726_si_001.pdf (7.9MB, pdf)
ja2c03726_si_002.zip (40.9KB, zip)

References

  1. Boger D. L. Diels−Alder Reactions of Azadienes. Tetrahedron 1983, 39, 2869–2939. 10.1016/s0040-4020(01)92154-4. [DOI] [Google Scholar]
  2. Boger D. L. Diels-Alder Reactions of Heterocyclic Azadienes. Scope and Applications. Chem. Rev. 1986, 86, 781–793. 10.1021/cr00075a004. [DOI] [Google Scholar]
  3. Zhang J.; Shukla V.; Boger D. L. Inverse Electron Demand Diels–Alder Reactions of Heterocyclic Azadienes, 1-Aza-1,3-Butadienes, Cyclopropenone Ketals, and Related Systems. A Retrospective. J. Org. Chem. 2019, 84, 9397–9445. 10.1021/acs.joc.9b00834. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Moisan L.; Odermatt S.; Gombosuren N.; Carella A.; Rebek J. Synthesis of an Oxazole–Pyrrole–Piperazine Scaffold as an α-Helix Mimetic. Eur. J. Org Chem. 2008, 1673–1676. 10.1002/ejoc.200701164. [DOI] [Google Scholar]
  5. Volonterio A.; Moisan L.; Rebek J. Jr. Synthesis of Pyridazine-Based Scaffolds as α-Helix Mimetics. Org. Lett. 2007, 9, 3733–3736. 10.1021/ol701487g. [DOI] [PubMed] [Google Scholar]
  6. Biros S. M.; Moisan L.; Mann E.; Carella A.; Zhai D.; Reed J. C.; Rebek J. Jr. Heterocyclic α-helix mimetics for targeting protein-protein interactions. Bioorg. Med. Chem. Lett. 2007, 17, 4641–4645. 10.1016/j.bmcl.2007.05.075. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Lahue B. R.; Lo S.-M.; Wan Z.-K.; Woo G. H. C.; Snyder J. K. Intramolecular Inverse-Electron-Demand Diels–Alder Reactions of Imidazoles with 1,2,4-Triazines: A New Route to 1,2,3,4-Tetrahydro-1,5-naphthyridines and Related Heterocycles. J. Org. Chem. 2004, 69, 7171–7182. 10.1021/jo040193z. [DOI] [PubMed] [Google Scholar]
  8. Kamber D. N.; Nguyen S. S.; Liu F.; Briggs J. S.; Shih H.-W.; Row R. D.; Long Z. G.; Houk K. N.; Liang Y.; Prescher J. A. Isomeric triazines exhibit unique profiles of bioorthogonal reactivity. Chem. Sci. 2019, 10, 9109–9114. 10.1039/c9sc01427f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Oliveira B. L.; Guo Z.; Bernardes G. J. L. Inverse electron demand Diels-Alder reactions in chemical biology. Chem. Soc. Rev. 2017, 46, 4895–4950. 10.1039/c7cs00184c. [DOI] [PubMed] [Google Scholar]
  10. Devaraj N. K.; Weissleder R.; Hilderbrand S. A. Tetrazine-Based Cycloadditions: Application to Pretargeted Live Cell Imaging. Bioconjugate Chem. 2008, 19, 2297–2299. 10.1021/bc8004446. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Blackman M. L.; Royzen M.; Fox J. M. Tetrazine Ligation: Fast Bioconjugation Based on Inverse-Electron-Demand Diels–Alder Reactivity. J. Am. Chem. Soc. 2008, 130, 13518–13519. 10.1021/ja8053805. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Denk C.; Svatunek D.; Filip T.; Wanek T.; Lumpi D.; Fröhlich J.; Kuntner C.; Mikula H. Development of a 18F-Labeled Tetrazine with Favorable Pharmacokinetics for Bioorthogonal PET Imaging. Angew. Chem., Int. Ed. 2014, 53, 9655–9659. 10.1002/anie.201404277. [DOI] [PubMed] [Google Scholar]
  13. Carboni R. A.; Lindsey R. V. Reactions of Tetrazines with Unsaturated Compounds. A New Synthesis of Pyridazines. J. Am. Chem. Soc. 1959, 81, 4342–4346. 10.1021/ja01525a060. [DOI] [Google Scholar]
  14. Steigel A.; Sauer J. (4+2)-Cycloadditionen 6-gliedriger Heterocyclen mit Inaminen. Tetrahedron Lett. 1970, 11, 3357–3360. 10.1016/s0040-4039(01)98475-8. [DOI] [Google Scholar]
  15. Neunhoeffer H.; Bachmann M. Cycloadditionen mit 1,3,5-Triazinen. Chem. Ber. 1975, 108, 3877–3882. 10.1002/cber.19751081220. [DOI] [Google Scholar]
  16. Wilkie G. D.; Elliott G. I.; Blagg B. S. J.; Wolkenberg S. E.; Soenen D. R.; Miller M. M.; Pollack S.; Boger D. L. Intramolecular Diels–Alder and Tandem Intramolecular Diels–Alder/1,3-Dipolar Cycloaddition Reactions of 1,3,4-Oxadiazoles. J. Am. Chem. Soc. 2002, 124, 11292–11294. 10.1021/ja027533n. [DOI] [PubMed] [Google Scholar]
  17. Neunhoeffer H.; Werner G.. Reaktion von Pyridazinen mit 1-Diäthylamino-propin; Justus Liebigs Annalen der Chemie, 1973; Vol. 1973, pp 437–442. [Google Scholar]
  18. Talbot A.; Devarajan D.; Gustafson S. J.; Fernández I.; Bickelhaupt F. M.; Ess D. H. Activation-Strain Analysis Reveals Unexpected Origin of Fast Reactivity in Heteroaromatic Azadiene Inverse-Electron-Demand Diels–Alder Cycloadditions. J. Org. Chem. 2015, 80, 548–558. 10.1021/jo5025514. [DOI] [PubMed] [Google Scholar]
  19. Yang Y.-F.; Liang Y.; Liu F.; Houk K. N. Diels-Alder Reactivities of Benzene, Pyridine, and Di-, Tri-, and Tetrazines: The Roles of Geometrical Distortions and Orbital Interactions. J. Am. Chem. Soc. 2016, 138, 1660–1667. 10.1021/jacs.5b12054. [DOI] [PubMed] [Google Scholar]
  20. Liu F.; Liang Y.; Houk K. N. Bioorthogonal Cycloadditions: Computational Analysis with the Distortion/Interaction Model and Predictions of Reactivities. Acc. Chem. Res. 2017, 50, 2297–2308. 10.1021/acs.accounts.7b00265. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Liu F.; Liang Y.; Houk K. N. Theoretical Elucidation of the Origins of Substituent and Strain Effects on the Rates of Diels–Alder Reactions of 1,2,4,5-Tetrazines. J. Am. Chem. Soc. 2014, 136, 11483–11493. 10.1021/ja505569a. [DOI] [PubMed] [Google Scholar]
  22. Svatunek D.; Wilkovitsch M.; Hartmann L.; Houk K. N.; Mikula H. Uncovering the Key Role of Distortion in Bioorthogonal Tetrazine Tools That Defy the Reactivity/Stability Trade-Off. J. Am. Chem. Soc. 2022, 144, 8171–8177. 10.1021/jacs.2c01056. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Svatunek D.; Denk C.; Mikula H. A computational model to predict the Diels–Alder reactivity of aryl/alkyl-substituted tetrazines. Monatsh. Chem. 2018, 149, 833–837. 10.1007/s00706-017-2110-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Choi J. Y.; Lee B. C. Click Reaction: An Applicable Radiolabeling Method for Molecular Imaging. Nucl. Med. Mol. Imag. 2015, 49, 258–267. 10.1007/s13139-015-0377-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Kuba W.; Wilkovitsch M.; Carlson J. C. T.; Mikula H. Tetrazine-Based Cycloadditions in Click Chemistry. Sci. Synth. 2021, 1, 577. [Google Scholar]
  26. Wu Z.-C.; Boger D. L. Characterization, and Cycloaddition Reactivity of a Monocyclic Aromatic 1,2,3,5-Tetrazine. J. Am. Chem. Soc. 2019, 141, 16388–16397. 10.1021/jacs.9b07744. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Anderson E. D.; Boger D. L. Inverse Electron Demand Diels–Alder Reactions of 1,2,3-Triazines: Pronounced Substituent Effects on Reactivity and Cycloaddition Scope. J. Am. Chem. Soc. 2011, 133, 12285–12292. 10.1021/ja204856a. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Anderson E. D.; Boger D. L. Scope of the Inverse Electron Demand Diels–Alder Reactions of 1,2,3-Triazine. Org. Lett. 2011, 13, 2492–2494. 10.1021/ol2007428. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Anderson E. D.; Duerfeldt A. S.; Zhu K.; Glinkerman C. M.; Boger D. L. Cycloadditions of Noncomplementary Substituted 1,2,3-Triazine. Org. Lett. 2014, 16, 5084–5087. 10.1021/ol502436n. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Glinkerman C. M.; Boger D. L. Cycloadditions of 1,2,3-Triazines Bearing C5-Electron Donating Substituents: Robust Pyrimidine Synthesis. Org. Lett. 2015, 17, 4002–4005. 10.1021/acs.orglett.5b01870. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Glinkerman C. M.; Boger D. L. Characterization, and Rapid Cycloadditions of 5-Nitro-1,2,3-triazine. Org. Lett. 2018, 20, 2628–2631. 10.1021/acs.orglett.8b00825. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Quiñones R. E.; Wu Z.-C.; Boger D. L. Reaction Scope of Methyl 1,2,3-Triazine-5-carboxylate with Amidines and the Impact of C4/C6 Substitution. J. Org. Chem. 2021, 86, 13465–13474. 10.1021/acs.joc.1c01553. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Siegl S. J.; Vrabel M. Probing the Scope of the Amidine-1,2,3-triazine Cycloaddition as a Prospective Click Ligation Method. Eur. J. Org Chem. 2018, 2018, 5081–5085. 10.1002/ejoc.201800530. [DOI] [Google Scholar]
  34. Yang Y.-F.; Yu P.; Houk K. N. Computational Exploration of Concerted and Zwitterionic Mechanisms of Diels-Alder Reactions between 1,2,3-Triazines and Enamines and Acceleration by Hydrogen-Bonding Solvents. J. Am. Chem. Soc. 2017, 139, 18213–18221. 10.1021/jacs.7b08325. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Goerigk L.; Hansen A.; Bauer C.; Ehrlich S.; Najibi A.; Grimme S. A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions. Phys. Chem. Chem. Phys. 2017, 19, 32184–32215. 10.1039/c7cp04913g. [DOI] [PubMed] [Google Scholar]
  36. Singleton D. A.; Thomas A. A. High-Precision Simultaneous Determination of Multiple Small Kinetic Isotope Effects at Natural Abundance. J. Am. Chem. Soc. 1995, 117, 9357–9358. 10.1021/ja00141a030. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja2c03726_si_001.pdf (7.9MB, pdf)
ja2c03726_si_002.zip (40.9KB, zip)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES