Abstract

Although a large percentage of eukaryotic proteomes consist of proteins with multiple domains, not much is known about their assembly mechanism, especially those with intricate native state architectures. Some have a complex topology in which the structural elements along the sequence are interwoven in such a manner that the domains cannot be separated by cutting at any location along the sequence. Such proteins are multiply connected multidomain proteins (MMPs) with the three-domain (NMP, LID, and CORE) phosphotransferase enzyme adenylate kinase (ADK) being an example. We devised a coarse-grained model to simulate ADK folding initiated by changing either the temperature or guanidinium chloride (GdmCl) concentration. The simulations reproduce the experimentally measured melting temperatures (associated with two equilibrium transitions), FRET efficiency as a function of GdmCl concentration, and the folding times quantitatively. Although the NMP domain orders independently, cooperative interactions between the LID and the CORE domains are required for complete assembly of the enzyme. Kinetic simulations show that, on the collapse time scale, multiple interconnected metastable states are populated, attesting to the folding heterogeneity. The network of kinetically connected states reveals that the CORE domain folds only after the NMP and LID domains, reflecting the interwoven nature of the chain topology.
Short abstract
In the ADK enzyme, the NMP domain folds independently. Both thermodynamics and kinetics show that cooperative interactions between the LID and CORE domains are needed for assembly of ADK.
Introduction
It is estimated that nearly 70% of eukaryotic proteins consist of multiple domains.1 They are involved in a wide array of functions, such as allosteric signaling (for example, hemoglobin and the bacterial chaperonin GroEL), passive elasticity of muscle (titin), and cargo transport by motors (dynein). Despite the inherent difficulties in identifying domains in proteins, a perusal of their structures shows that there is a great deal of diversity in their architectures.1 For example, the giant titin protein is a heteropolymer made of thousands of β-sheet single-domain immunoglobulin (Ig) proteins that are connected by linkers. Pioneering single-molecule pulling experiments2 on the polyprotein Ign established that it unfolds one domain at a time. It is likely that refolding, upon force quench, also proceeds by the formation of the native state, one domain at a time. Therefore, titin might assemble by preformed monomer units. We refer to polyproteins, such as Ign, as simply connected multidomain proteins (SMPs) because they can be partitioned into individual subunits by merely excising the linkers. Another example of SMP, the ankyrin repeat, is shown in Figure 1A (Protein Data Bank ID: 3TWT). The amino acid residues, and the associated secondary structural elements (SSEs), in the SMPs are “one-dimensionally contiguous”.3 In contrast, in multiply connected multidomain proteins (MMPs), the sequences are intertwined in such a manner that their structures cannot be dissected into independently folding subunits. Thus, topologically, the domains cannot be cut in such a manner that they follow the sequence in a continuous linear manner, as is the case in SMPs. An example of an MMP is the T4 lysozyme whose folding cooperativity was shown, using pulling experiments,4 to reflect the discontinuity in the connectivity of the SSEs in which a portion of the N-terminal sequence is part of the C-terminal domain. The connectivity of domains in terms of sequence is even more complicated in adenylate kinase (ADK), the protein of interest in this study, shown in Figure 1B (Protein Data Bank ID: 4AKE). According to the Wetlaufer3 classification, the domains in ADK are discontinuous with respect to the sequence and the connectivity of the SSEs. The rules linking the topology of the folded state of the MMPs are hard to anticipate based solely on the connectivity of sequence and SSEs. The problem is exacerbated because, with the exception of very few studies,4−6 there is a paucity of detailed experimental studies that have dissected the folding pathways of MMPs.
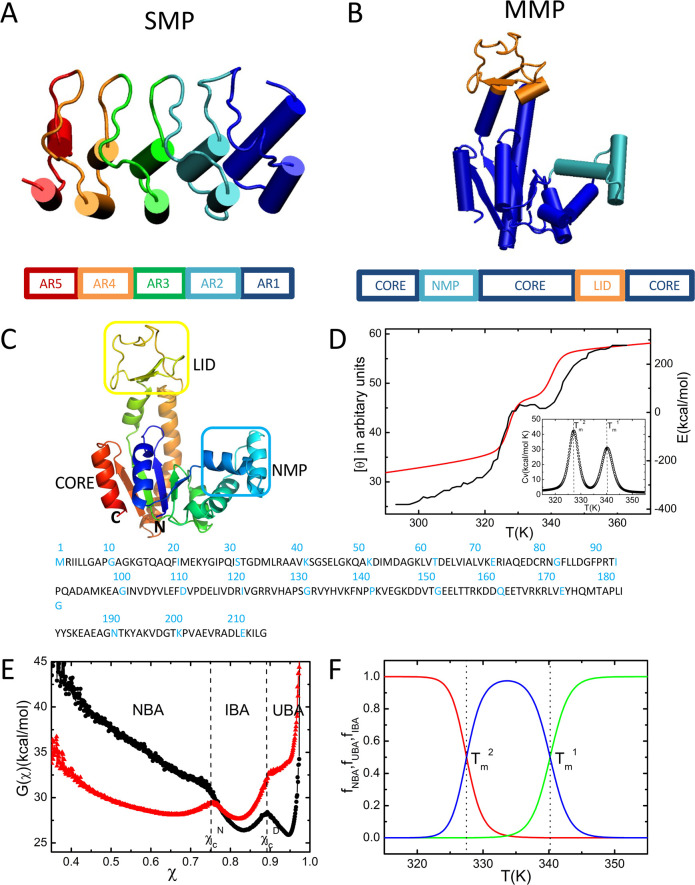
Figure 1.
Structure, sequence,
and folding thermodynamics. (A) Cartoon representation
of the ankyrin repeat (PDB ID: 3TWT), an example for SMP. (B) Cartoon representation
of ADK (PDB ID: 4AKE), an example for MMP. (C) Ribbon diagram representation of ADK.
The N and C termini are indicated. The simulated sequence is shown
below. (D) Temperature dependence of the CD signal (black line) extracted
from experiments18 and the simulated total
energy (red line) as a function of temperature. The inset shows the
calculated heat capacity as a function of temperature. (E) Free energy
profiles at  (black) and
(black) and  (red) as a function of the structural overlap
function, χ (see eq 5). The values
(red) as a function of the structural overlap
function, χ (see eq 5). The values 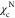 and
and 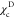 are used to separate
the global equilibrium
states, which are the native basin of attraction (NBA), intermediate
basin of attraction (IBA), and unfolded basin of attraction (UBA).
(F) Temperature dependence of the fraction of molecules in the NBA
(red), UBA (green), and IBA (blue).
are used to separate
the global equilibrium
states, which are the native basin of attraction (NBA), intermediate
basin of attraction (IBA), and unfolded basin of attraction (UBA).
(F) Temperature dependence of the fraction of molecules in the NBA
(red), UBA (green), and IBA (blue).
In a series of most insightful experiments, Haas and co-workers reported the steps involved in the folding of Escherichia coli ADK, triggered by varying the guanidinium chloride (GdmCl) concentration.6−8 One of their key findings is that the collapse of ADK is fast, but the formation of secondary structural elements is slow.7 In a subsequent double kinetics experiments,6 they further established that structure formation in the CORE domain (Figure 1B) is slow upon denaturant quenching. More recently, Haran and co-workers used single-molecule fluorescence resonance energy transfer (smFRET) experiments5 to generate equilibrium trajectories at a fixed [GdmCl] concentration. Their results, which were analyzed by a hidden Markov model (HMM) analysis at different [GdmCl] values, suggest that folding occurs by the kinetic partitioning mechanism in which there are multiple metastable states in the folding landscape of ADK. The direct flux to the folded state from the unfolded ensemble (referred to as the partition factor elsewhere9) is only Φ ≈ 0.02,10 which implies that the majority of the molecules fold by first populating one of the (roughly six obtained from HMM analysis at 0.65 M [GdmCl]) metastable states. Surprisingly, they found that connectivity between the states and the associated fluxes between them could be tuned by altering the denaturant concentration. Their experiments showed that the folding landscape of ADK is not only rugged but is also malleable to changes in the external conditions. Although qualitatively similar results have been found in the folding of PDZ3,11 a 110-residue protein with a topology much simpler than that of ADK, the intricate topology of the MMP renders the folding of the latter more complicated.
The structure of the 214-residue ADK consists of three domains: the NMP domain, the LID domain, and the CORE domain (Figure 1C).12 The NMP domain spans residues 30–59 (indicated by the blue square in Figure 1C) and the LID domain consists of residues 122–159 (indicated by the yellow square), and the rest of the residues (1–29, 60–121, and 160–214) belong to the CORE domain. Sequence penetration across the native structure is vividly illustrated in ADK by noting that the N-terminal residues, 1–29, are part of the CORE domain comprising C-terminal residues. Contacts formed between N-terminal and C-terminal residues are labeled in the contact map of ADK in Figure S1.
Here, we investigate thermal and denaturant-dependent folding of ADK using simulations based on the self-organized polymer model with side chains (SOP-SC) and the molecular transfer model (MTM),13−15 under conditions that closely mimic those used in the experiments.5,6,10 Coarse-grained model simulations, without side chains, were used to investigate folding cooperativity and multiple routes to the native state in ADK by thermal folding and unfolding.16,17 After demonstrating that our simulations quantitatively reproduce many experimental measurements, we show that cooperative interactions between the LID and CORE domains, with folding of the former being slave to partial ordering of the latter, are required for ADK self-assembly. In contrast, the NMP domain folds independently at a higher temperature (or denaturant concentration) than the other two domains. The enhanced cooperative interactions between the LID and the CORE domains arise due to the discontinuous nature of the latter. The network of states linking the unfolded to the folded state, both at equilibrium and during refolding upon temperature quench, is multiply connected and shows that folding must occur by parallel pathways. The late stage of folding involves interaction between a reentrant helix in the CORE domain that forms contact with elements in the N-terminal CORE domain. The methods used here are transferable for investigating the folding of other MMPs.
Results
Simulations Predict Thermal Denaturation Accurately
The circular dichroism
(CD) spectrum shows that ADK undergoes two
cooperative transitions, one at 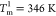 and the other at
and the other at 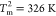 (18) (Figure 1D, black line). In
order to assess if the simulations reproduce the observed thermal
melting profile, we used replica-exchange molecular dynamics (REMD)19−21 and low-friction Langevin dynamics22 in
order to calculate the melting profiles. The temperature-dependent
total energy E, which mirrors the CD signal, also
shows two cooperative transitions (Figure 1D, red line). The corresponding melting temperatures,
identified by the peaks in the heat capacity, Cv, are at
(18) (Figure 1D, black line). In
order to assess if the simulations reproduce the observed thermal
melting profile, we used replica-exchange molecular dynamics (REMD)19−21 and low-friction Langevin dynamics22 in
order to calculate the melting profiles. The temperature-dependent
total energy E, which mirrors the CD signal, also
shows two cooperative transitions (Figure 1D, red line). The corresponding melting temperatures,
identified by the peaks in the heat capacity, Cv, are at 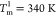 ,
,  (see
the inset of Figure 1D). The values of Tm’s obtained
from our simulations and experiments are
in excellent agreement with each other. This is remarkable given that
no parameter in the SOP-SC model was adjusted to obtain agreement
with experiments.
(see
the inset of Figure 1D). The values of Tm’s obtained
from our simulations and experiments are
in excellent agreement with each other. This is remarkable given that
no parameter in the SOP-SC model was adjusted to obtain agreement
with experiments.
Three State Folding
The temperature-dependent
profiles
of E and Cv demonstrate that ADK folds globally in a three-state manner.
The free energy profile, G(χ), as a function
of the overlap function, χ given in eq 5, at 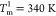 and
and  (Figure 1E), shows three states,
which represent the NBA (native
basin of attraction), UBA (unfolded basin of attraction), and the
IBA (intermediate basin of attraction, i.e., IEQ). The conformations are grouped into three basins based
on the χ values, shown by the black vertical dashed lines in Figure 1E. If
(Figure 1E), shows three states,
which represent the NBA (native
basin of attraction), UBA (unfolded basin of attraction), and the
IBA (intermediate basin of attraction, i.e., IEQ). The conformations are grouped into three basins based
on the χ values, shown by the black vertical dashed lines in Figure 1E. If 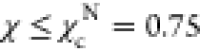 , the conformations
are classified as belonging
to the NBA. Conformations with
, the conformations
are classified as belonging
to the NBA. Conformations with 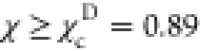 belong to the UBA, and the rest of the
conformations represent IBA (IEQ). At
belong to the UBA, and the rest of the
conformations represent IBA (IEQ). At  ,
the NBA is unstable while IEQ and the
unfolded state have similar stabilities (Figure 1E, black line). At
,
the NBA is unstable while IEQ and the
unfolded state have similar stabilities (Figure 1E, black line). At  ,
ADK transitions between the NBA and IBA
while the UBA is unstable (Figure 1E, red line). Additional structural details of the IEQ state are shown in Figure S2.
,
ADK transitions between the NBA and IBA
while the UBA is unstable (Figure 1E, red line). Additional structural details of the IEQ state are shown in Figure S2.
In Figure 1F, we plot the fraction of molecules in the NBA, fNBA([0], T) (the first argument indicates
the value of the denaturant concentration); in the UBA, fUBA([0], T); and in the IBA, fIBA([0], T). The temperature
dependencies of fUBA([0], T) (green curve in Figure 1F) and fNBA([0], T) (shown in red in Figure 1F) show that ADK unfolds and folds cooperatively at the two
melting temperatures. At  , the value of fNBA([0], T) is negligible,
reflecting the cooperative
transition between the IBA and UBA. Using fIBA([0], T) = fUBA([0], T) = 0.5, we obtained
, the value of fNBA([0], T) is negligible,
reflecting the cooperative
transition between the IBA and UBA. Using fIBA([0], T) = fUBA([0], T) = 0.5, we obtained  , which coincides with the peak in the heat
capacity (inset in Figure 1D) . At low temperatures, the value of fUBA([0], T) is negligible, suggesting that
ADK undergoes a cooperative transition between the NBA and the IBA.
Using fIBA([0], T) = fNBA([0], T) = 0.5, we obtained
, which coincides with the peak in the heat
capacity (inset in Figure 1D) . At low temperatures, the value of fUBA([0], T) is negligible, suggesting that
ADK undergoes a cooperative transition between the NBA and the IBA.
Using fIBA([0], T) = fNBA([0], T) = 0.5, we obtained  ,
which also agrees with the peak in Cv.
,
which also agrees with the peak in Cv.
Equilibrium Folding of the Domains
The average fraction
of native contacts in each domain, QNMP, QLID, and QCORE, as a function of temperature (Figure 2A), shows that the NMP and the LID domains
fold in a two-state manner with the melting temperature,  and
and  . In contrast, the CORE domain folds in
a three-state manner. The two melting temperatures, extracted from
the temperature dependence of
. In contrast, the CORE domain folds in
a three-state manner. The two melting temperatures, extracted from
the temperature dependence of 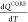 , show that the ordering
of this domain
reflects the two transition temperatures in the heat capacity and
the total energy (Figure 1D). It follows that the incremental assembly of the CORE domain,
across both the melting temperatures, is the reason that ADK globally
folds in three stages.
, show that the ordering
of this domain
reflects the two transition temperatures in the heat capacity and
the total energy (Figure 1D). It follows that the incremental assembly of the CORE domain,
across both the melting temperatures, is the reason that ADK globally
folds in three stages.
Figure 2.
Temperature-dependent connectivity of metastable states.
(A) Fraction
of native contacts in each domain, QNMP, QLID, and QCORE, as a function of temperature. The inset shows the temperature dependence
of  . (B) Distributions of the fraction of native
contacts within the three domains P(QNMP), P(QLID), and P(QCORE) at
. (B) Distributions of the fraction of native
contacts within the three domains P(QNMP), P(QLID), and P(QCORE) at 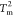 (left) and
(left) and  (right). (C) Network of thermodynamically
connected substates at
(right). (C) Network of thermodynamically
connected substates at 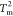 . The numbers on the
arrows are the transition
times from one substate to another substate. (D) Same as part C except
it is calculated at
. The numbers on the
arrows are the transition
times from one substate to another substate. (D) Same as part C except
it is calculated at  .
.
A more nuanced picture of the folding thermodynamics emerges from
the distributions of QNMP, QLID, and QCORE at  and
and  shown in Figure 2B. If
shown in Figure 2B. If 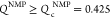 , the NMP domain
is predominantly folded
, the NMP domain
is predominantly folded
otherwise it is unfolded (compare
the left and right panels in the upper panels in Figure 2B). The data in Figure 2A,B show that the NMP domain
forms before the LID and CORE domains become structured, as the temperature
is decreased. Similarly, if 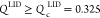 , the LID substructure adopts nativelike
conformations (see the middle panels in Figure 2B). P(QNMP) [P(QLID)] is bimodal at
, the LID substructure adopts nativelike
conformations (see the middle panels in Figure 2B). P(QNMP) [P(QLID)] is bimodal at 
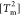 (Figure 2B), which is consistent with the interpretation that
both of the domains fold in an almost all-or-none manner, albeit at
different melting temperatures. The lower melting temperature of the
LID domain shows that it is thermodynamically less stable than the
NMP domain, which accords well with single-molecule pulling experiments.23 If
(Figure 2B), which is consistent with the interpretation that
both of the domains fold in an almost all-or-none manner, albeit at
different melting temperatures. The lower melting temperature of the
LID domain shows that it is thermodynamically less stable than the
NMP domain, which accords well with single-molecule pulling experiments.23 If 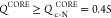 , the CORE domain is in the native state.
If the inequality
, the CORE domain is in the native state.
If the inequality 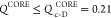 is satisfied, the CORE domain is in the
unfolded state. In the intermediate state, we find that 0.21 < QCORE < 0.45 (see the bottom panels in Figure 2B). Two-dimensional
free energy profiles G(Qα, Qβ) (α and β are
the appropriate domain labels) in Figure S3 illustrate the cooperativity between the LID and CORE domains at
the two melting temperatures.
is satisfied, the CORE domain is in the
unfolded state. In the intermediate state, we find that 0.21 < QCORE < 0.45 (see the bottom panels in Figure 2B). Two-dimensional
free energy profiles G(Qα, Qβ) (α and β are
the appropriate domain labels) in Figure S3 illustrate the cooperativity between the LID and CORE domains at
the two melting temperatures.
Network of Connected Substates
The NMP and LID domains exhibit two statelike transitions as T is varied whereas the CORE domain ordering is best described using three states labeled as U, I, and N (Figure 2A). Thus, from a thermodynamic perspective, we could describe the formation of ADK using 2 × 2 × 3 = 12 substates. They are S1(UUU), S2(UUI), S3(UUN), S4(UNU), S5(UNI), S6(UNN), S7(NUU), S8(NUI), S9(NUN), S10(NNU), S11(NNI), and S12(NNN). The first letter in the parentheses represents the state of the NMP domain, the second letter the state of the LID domain, and the third letter the state of the CORE domain.
We first determined the percentages of the substates in each global state obtained in the simulations by generating 28 folding trajectories. The conformations that are sampled were grouped into the 12 substates (S1–S12) and the 3 global states (UG, IG, and NG). The percentages are determined from the number of each substate in each global state. Out of the total 12 substates, only 7 substates are significantly populated. We find that the global native state is a superposition of the substate S9 (7.3%) and S12 (92.7%), which we write as NG = 7.3%·S9 + 92.7%·S12. Similarly, the globally unfolded state is decomposed as UG = 92.8%·S1 + 7.2%·S7. For the global intermediate state, we find IG = 1.1%·S2 + 97.8%·S8 + 1.1%·S11.
We then performed a flux analysis among these substates at the
two melting temperatures ( and
and 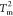 ) to assess the complexity of the network
connectivity in the thermodynamic folding landscape. At the lower
melting temperature,
) to assess the complexity of the network
connectivity in the thermodynamic folding landscape. At the lower
melting temperature,  , the equilibrium flux
predominantly flows
through the substates S9, S12 and S2, S8, S11 (Figure 2C). Considering their global structural features,
the network shows that ADK transitions primarily between NG and IG. The numbers on the
arrows are the transition times from one substate to another substate.
At the higher melting temperature
, the equilibrium flux
predominantly flows
through the substates S9, S12 and S2, S8, S11 (Figure 2C). Considering their global structural features,
the network shows that ADK transitions primarily between NG and IG. The numbers on the
arrows are the transition times from one substate to another substate.
At the higher melting temperature  , the network connectivity involves predominantly
the substates S2, S8 and S1, S7 (Figure 2D). By mapping to the global structural features,
we find that ADK transitions back and forth between IG and UG at the higher melting
temperature.
, the network connectivity involves predominantly
the substates S2, S8 and S1, S7 (Figure 2D). By mapping to the global structural features,
we find that ADK transitions back and forth between IG and UG at the higher melting
temperature.
Chemical Denaturation
In order to
compare with experiments
directly, we first used the molecular transfer model (MTM)13 to simulate the effects of GdmCl on the equilibrium
properties. Following our previous studies,13−15 we chose a
simulation temperature, Ts, at which the
calculated free energy difference between the native state (NG) and the unfolded state (UG), ΔGNU(Ts) (= 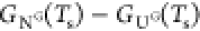 ) and the measured free energy ΔGNU(TE) at TE (= 293 K) coincide. The use of ΔGNU(Ts) = ΔGNU(TE) (in water)
to fix Ts is equivalent to choosing the
overall reference free energy scale in the simulations. For ADK, ΔGNU(TE = 293 K) =
−9.8 kcal/mol at [C] = 0,18 which results in Ts = 322 K.
Except for the choice of Ts, no other
parameter is adjusted to obtain agreement with experiments for any
property.
) and the measured free energy ΔGNU(TE) at TE (= 293 K) coincide. The use of ΔGNU(Ts) = ΔGNU(TE) (in water)
to fix Ts is equivalent to choosing the
overall reference free energy scale in the simulations. For ADK, ΔGNU(TE = 293 K) =
−9.8 kcal/mol at [C] = 0,18 which results in Ts = 322 K.
Except for the choice of Ts, no other
parameter is adjusted to obtain agreement with experiments for any
property.
With Ts = 322 K fixed,
we first computed the FRET efficiency as a function of [GdmCl] for ADK (Figure 3A). The FRET efficiency of a protein conformation was calculated
using  , where Ree is
the end-to-end distance, and R0 = 49 Å.
In the experiments, residues 73, 203 were labeled.24 The agreement between the computed (thick black line) and
the measured (black dots)5 FRET efficiencies
is excellent. The derivative of the computed FRET efficiency with
respect to [GdmCl] (inset of Figure 3A) also shows signs of the two thermodynamic
transitions as the denaturant concentration is increased, which accords
well with our thermal unfolding calculations. The midpoint concentration
for the major transition is
, where Ree is
the end-to-end distance, and R0 = 49 Å.
In the experiments, residues 73, 203 were labeled.24 The agreement between the computed (thick black line) and
the measured (black dots)5 FRET efficiencies
is excellent. The derivative of the computed FRET efficiency with
respect to [GdmCl] (inset of Figure 3A) also shows signs of the two thermodynamic
transitions as the denaturant concentration is increased, which accords
well with our thermal unfolding calculations. The midpoint concentration
for the major transition is  , which agrees well with the measured result.24 The predicted midpoint concentration for the
second transition is at
, which agrees well with the measured result.24 The predicted midpoint concentration for the
second transition is at 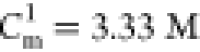 , which has not been observed in experiments.
The values for the FRET efficiency for the structures in the UBA are
roughly constant as [GdmCl] changes (green line in Figure 3A) whereas the values
for the FRET efficiency for the structures in the NBA decrease substantially
as [GdmCl] increases (red line in Figure 3A).
, which has not been observed in experiments.
The values for the FRET efficiency for the structures in the UBA are
roughly constant as [GdmCl] changes (green line in Figure 3A) whereas the values
for the FRET efficiency for the structures in the NBA decrease substantially
as [GdmCl] increases (red line in Figure 3A).
Figure 3.
Effect of GdmCl on ADK
folding. (A) Comparison of the calculated
(thick black line) and experimental measurements5 (black dots) of the FRET efficiencies as a function of
[GdmCl], the GdmCl concentration. The inset shows
the derivative of the calculated FRET efficiency, which clearly indicates
that there are two distinct transitions. Decomposition of the FRET
efficiency for the structures in the NBA (red), UBA (green), and IBA
(blue). (B) Comparison of experimental measurements of the FRET efficiencies
(black dots)5 and the calculated fraction
of ADK molecules in the NBA (red), UBA (green), and IBA (blue) as
a function of [GdmCl]. The comparison shows that
below ∼0.8 M the experimental FRET efficiency coincides with
the calculated values for ADK molecules that are predominantly in
the NBA, which is consistent with the plot in part A. In the range
0.8 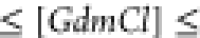 2
M molecules, both the NBA and IBA contribute
to the FRET efficiency. (C) Fraction of native contacts in each domain, QNMP, QLID, and QCORE, as a function of [GdmCl]. The inset shows the denaturant dependence of
2
M molecules, both the NBA and IBA contribute
to the FRET efficiency. (C) Fraction of native contacts in each domain, QNMP, QLID, and QCORE, as a function of [GdmCl]. The inset shows the denaturant dependence of  . (D) Distributions of the fraction of native
contacts within the three domains P(QNMP), P(QLID), and P(QCORE) at
. (D) Distributions of the fraction of native
contacts within the three domains P(QNMP), P(QLID), and P(QCORE) at  (left) and
(left) and  (right). (E) Heat capacity versus temperature
for different values of [GdmCl]. (F) [GdmCl] dependence of the melting temperatures. The fits to the lines are
explicitly displayed. The units of B1 and B2 are K M–1. The black (red)
line is for
(right). (E) Heat capacity versus temperature
for different values of [GdmCl]. (F) [GdmCl] dependence of the melting temperatures. The fits to the lines are
explicitly displayed. The units of B1 and B2 are K M–1. The black (red)
line is for 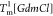 (
( ).
).
The dependence of the simulated fNBA([GdmCl], Ts) on [GdmCl] is also in excellent agreement with the measured
FRET efficiency5 (Figure 3B). As in the case of thermal denaturation,
the transition at low [GdmCl] takes place between
the NBA and the IBA. The corresponding midpoint concentration  ,
determined using fNBA([GdmCl], Ts) = fIBA([GdmCl], Ts) = 0.5
(red and blue lines in Figure 3B), is close to the experimental
value.24 The transition at high [GdmCl] occurs as the intermediate state is destabilized,
thus populating the unfolded state. Using fUBA([GdmCl], Ts) = fIBA([GdmCl], Ts) = 0.5 (green and blue lines in Figure 3B), the associated midpoint concentration
is
,
determined using fNBA([GdmCl], Ts) = fIBA([GdmCl], Ts) = 0.5
(red and blue lines in Figure 3B), is close to the experimental
value.24 The transition at high [GdmCl] occurs as the intermediate state is destabilized,
thus populating the unfolded state. Using fUBA([GdmCl], Ts) = fIBA([GdmCl], Ts) = 0.5 (green and blue lines in Figure 3B), the associated midpoint concentration
is 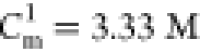 .
.
The variations in the average values of the fraction of native
contacts in the various domains (QNMP, QLID, and QCORE),
shown in Figure 3C,
as a function of [GdmCl], are very similar to the
results in Figure 2A. The distributions of QNMP, QLID, and QCORE at
the two midpoint concentrations (Figure 3D) are also qualitatively similar to the
ones calculated at the two melting temperatures (Figure 2B). However, there is a subtle
difference. In the presence of the denaturant, the range of conformations
that are accessed is broader. For example, the probability of sampling
the ordered state of LID domain (⟨QLID⟩ > 0.6) is non-negligible at  whereas it is much smaller at
whereas it is much smaller at  (compare the middle panels in Figures 2B and 3D). This subtle difference could result in the differences
in the stability of the folded ADK in the presence of GdmCl and folding
induced by lowering the temperature.
(compare the middle panels in Figures 2B and 3D). This subtle difference could result in the differences
in the stability of the folded ADK in the presence of GdmCl and folding
induced by lowering the temperature.
The heat capacity curves
at various values of [GdmCl] show that the peaks
corresponding to 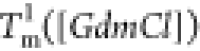 and
and 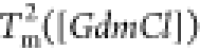 decrease as [GdmCl] increases
(Figure 3E). The decreases
in
decrease as [GdmCl] increases
(Figure 3E). The decreases
in 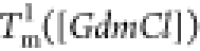 and
and 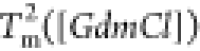 are both linear (Figure 3F). The variation
in
are both linear (Figure 3F). The variation
in 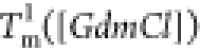 is well fitted using
is well fitted using 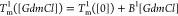 , where B1 ≈
−4.7 K/M. The variation in
, where B1 ≈
−4.7 K/M. The variation in 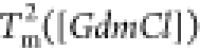 can be fitted similarly
using
can be fitted similarly
using  , where B2 ≈
−4.5 K/M.
, where B2 ≈
−4.5 K/M.
Collapse Kinetics and Folding Kinetics
To analyze the
collapse and folding kinetics, we generated 100 folding trajectories
(see the SI for details) using Brownian
dynamics simulations at T = 293 K at [GdmCl] = 0 M.25 We calculated the time-dependent
changes in the radius of gyration (⟨Rg(t)⟩ by averaging over the ensemble
of trajectories). The decay of ⟨Rg(t)⟩, which is a measure of the extent of
collapse, is fitted using a single exponential function (Figure 4B), yielding collapse
rate kc = 391 s–1, which
as we discuss below is larger than the folding kf. Thus, global compaction occurs before folding, as observed
in the experiment.26 In particular, the
distances d(28–71)(t) and d(122–159)(t) approach the native values extremely rapidly (Figure 4C), which likely
corresponds to the dead time of the experiments.26Figure S5A,C in the SI shows
that the time for the probabilities of these two distances, P(d(28–71))(t)
and P(d(122–159))(t), to exceed about 0.5 is ∼2 ms, which is on the
order of the collapse time  . Thus, global compaction occurs rapidly
upon making the conditions favorable for folding, as observed in the
experiment.26
. Thus, global compaction occurs rapidly
upon making the conditions favorable for folding, as observed in the
experiment.26
Figure 4.
Folding and collapse
kinetics. (A) Fraction of unfolded ADK molecules
as a function of time (black) calculated from the distribution of
first passage times. The red line is an exponential fit ( with τF = 5.5 ms) to the
data. (B) Kinetics of collapse monitored by the average
with τF = 5.5 ms) to the
data. (B) Kinetics of collapse monitored by the average 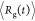 as
a function of t (black).
The fit to the data, given by a single exponential function (red line)
yields an average collapse time τc = 2.56 ms. (C)
Time-dependent changes in the distances between residues 28 and 71
(black line), 18 and 203 (red line), 122 and 159 (green line), and
36 and 129 (blue line). In the folded state, the distances between
these four pairs of residues are 11.3, 13.1, 7.6, and 26.5 Å,
respectively.
as
a function of t (black).
The fit to the data, given by a single exponential function (red line)
yields an average collapse time τc = 2.56 ms. (C)
Time-dependent changes in the distances between residues 28 and 71
(black line), 18 and 203 (red line), 122 and 159 (green line), and
36 and 129 (blue line). In the folded state, the distances between
these four pairs of residues are 11.3, 13.1, 7.6, and 26.5 Å,
respectively.
Before estimating the folding
time from simulations, we first calculated
the folding rate theoretically using  ,27,28 which gives fairly
accurate estimates for the folding times, spanning nearly 10 orders
of magnitude, for proteins of varying length.29 For ADK, N = 214, we find that
,27,28 which gives fairly
accurate estimates for the folding times, spanning nearly 10 orders
of magnitude, for proteins of varying length.29 For ADK, N = 214, we find that 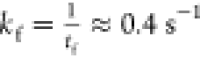 , which is in good agreement with experiments.7 From the distribution of first passage times, Pfp(s), the fraction of unfolded
molecules at time t is calculated using
, which is in good agreement with experiments.7 From the distribution of first passage times, Pfp(s), the fraction of unfolded
molecules at time t is calculated using 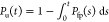 . An exponential fit,
. An exponential fit, 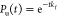 , yielded the folding
rate at [GdmCl] = 0 M, kf = 182 s–1(Figure 4A). The calculated
value is larger than the experimental value of ∼
, yielded the folding
rate at [GdmCl] = 0 M, kf = 182 s–1(Figure 4A). The calculated
value is larger than the experimental value of ∼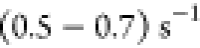 obtained by quenching the denaturant
concentration
from a high value to [GdmCl] = 0.3 M. The experimental
[GdmCl] is fairly close to
obtained by quenching the denaturant
concentration
from a high value to [GdmCl] = 0.3 M. The experimental
[GdmCl] is fairly close to  = 0.55 M. Therefore, one has to account
for the stability change so that the simulation results could be compared
to experiments directly. If the corrections due to the stability change
at 0.3 M are made (Figure S4), using the
data in Figure 3B,
we predict that kf at [GdmCl] = 0.3 M is ∼
= 0.55 M. Therefore, one has to account
for the stability change so that the simulation results could be compared
to experiments directly. If the corrections due to the stability change
at 0.3 M are made (Figure S4), using the
data in Figure 3B,
we predict that kf at [GdmCl] = 0.3 M is ∼ (details in the SI), which agrees well
with measurements.6,7
(details in the SI), which agrees well
with measurements.6,7
Heterogeneity in the Self-Assembly of ADK
The generated
folding trajectories could be used to quantitatively extract the extent
of folding heterogeneity. In particular, ensemble FRET experiments
provide data on the time-dependent changes in FRET efficiencies by
varying the positions of the FRET probes. We calculated the time dependence
of the distances between four pairs of residues: (i) the distance
between 28 and 71, which are at the ends of a 44-residue segment including
the NMP domain; (ii) the distance between residues 18 and 203, which
could be a reporter of the global folding; (iii) the distance between
residues 122 and 159, which are the ends of LID domain; and (iv) the
distance between residues 36 and 129, which reflects the closeness
of the NMP and LID domains (Figure 4C). The time-dependent changes in these distances are
well-fitted using single exponential functions, from which we obtained
the time scales for d(28–71), d(18–203), d(122–159), and d(36–129). The values are ∼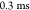 ,
∼
,
∼ ,
∼
,
∼ ,
and ∼
,
and ∼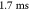 .
The corresponding rates of formation for
the NMP domain, global molecule, LID, and interface between NMP and
LID domains are 3, 472 s–1, 255 s–1, 2, 342 s–1, and 584 s–1. These
calculations show that the NMP and LID domains form early in the folding
process, and their interface forms before collapse. The distributions
of these four distances at different times, shown in Figure S5, provide a more detailed picture of the assembly
dynamics of different regions of ADK. The results in Figure S5 show that there is a great deal of dispersion in
the ordering of various parts of the ADK structure.
.
The corresponding rates of formation for
the NMP domain, global molecule, LID, and interface between NMP and
LID domains are 3, 472 s–1, 255 s–1, 2, 342 s–1, and 584 s–1. These
calculations show that the NMP and LID domains form early in the folding
process, and their interface forms before collapse. The distributions
of these four distances at different times, shown in Figure S5, provide a more detailed picture of the assembly
dynamics of different regions of ADK. The results in Figure S5 show that there is a great deal of dispersion in
the ordering of various parts of the ADK structure.
Parallel Pathways and Kinetic Intermediates
We calculated the fraction of native contacts of each domain, QNMP, QLID, and QCORE, from the 100 folding trajectories. Using these as progress variables for the folding reaction, we find that ADK folds by multiple parallel pathways. The NMP and the LID domains fold cooperatively in a two-state manner, albeit at different rates, while the CORE domain folds through 5 successive stages, which is illustrated using a sample folding trajectory at the bottom right of Figure 5. In each of these stages, the CORE domain becomes increasingly ordered with acquisition of the nativelike structure occurring in the final stage. Therefore, ADK could fold through 2 × 2 × 5 = 20 states. However, in the 100 folding trajectories, only 13 states are kinetically populated. We classify these as LL1, HL1, LH1, HH1; LL2, HL2, LH2, HH2; HL3, LH3, HH3; HH4; and HH5. The first letter in the 3-letter notation represents the state of NMP domain: “L” means that the value of QNMP is low, and the NMP domain is unfolded. “H” means that the value of QNMP is high, and the NMP domain is folded. The second letter represents the state of LID domain, and the third letter stands for the state of the CORE domain. Labels “1–5” denote different levels for the values of QCORE. LL1 is the starting unfolded state, and HH5 is the final folded state. There are 15 distinct folding pathways found in the generated folding trajectories (see Table S1 in the SI).
Figure 5.
Network of connected states accessed during folding kinetics and parallel pathways. Each state is colored according to the average fraction of the native contacts formed at each residue. Color code: blue, structured; red, unstructured. The 12 most probable folding pathways are represented by the colored arrows with the line widths representing the probability of each folding pathway. The panel on the bottom right shows one representative folding trajectory. The hierarchy of assembly of the domains is clear. The NMP and LID domains form prior to the formation of the CORE domain. A sequence of transitions (1 to 5) drive consolidation of the folded ADK.
The fluxes through the 13 states follow a complex pattern, as illustrated in Figure 5, where each state is colored according to the average fraction of native contacts formed at each residue. As observed in the single-molecule experiment,5 and in a previous coarse-grained thermally triggered folding simulation,16 the folding trajectories might involve transitions between the distinct states, thus introducing loops in the folding pathways. For simplicity, we removed these loops from the figure, and only the 12 most probable pathways are shown in Figure 5. From this folding flux diagram, we find that the early stage in the folding reaction for ADK is very plastic while the late stage is more restricted, which reflects the narrowing of the folding free energy landscape to the native state. In addition, there is a pathway that directly connects the globally unfolded state (LL1) to HH2 from which folding to the native state (HH5) occurs sequentially (Figure 5). It is likely that the fluxes through the metastable states could be altered by changing the external conditions.5
Thermal and Kinetic Networks Are Similar
To illustrate the structural similarities between the 7 thermal substates with significant populations and the 13 substates identified from the kinetic folding trajectories, we computed the average fraction of native contacts formed by every residue, fQ, for the 20 states. For each thermal substate, we searched for the kinetic state that has a high degree of correlation (exceeding 0.9) between thermal and kinetic fQ. For the thermal substates S2 and S9, we could not find suitable matching kinetic states, which means that these two substates are not sampled in the kinetic folding trajectories. The other 5 thermal states correlate with the kinetic states (Figure 6). The correlation between S8 and HL3 is very high (R = 0.99, Figure 6D). We surmise that S8 and HL3 are structurally similar (in short, S8 ∼ HL3). Likewise, we find S11 ∼ HH3 (R = 0.93, Figure 6E), S1 ∼ LL1 (R = 0.96, Figure 6A), S7 ∼ HL1 (R = 0.98, Figure 6B), and S12 ∼ HH5 (R = 0.94, Figure 6C). The high degree of correlation for the major states during folding shows that in both thermal and kinetic folding, very similar states are sampled. The connectivity between these states, which would define the folding pathways, could vary and may readily be altered by changing the [GdmCl].5
Figure 6.
Comparison between thermal and kinetic states. (A) Correlation between fQ’s for S1 and LL1. The correlation coefficient R = 0.96. (B) Correlation between fQ’s for S7 and HL1 with R = 0.98. (C) Correlation between fQ’s for S12 and HH5 with R = 0.94. (D) Correlation between fQ’s for S8 and HL3 with R = 0.99. (E) Correlation between fQ’s for S11 and HH3 with R = 0.93.
Discussion
We have shown that the strategy developed here that combines a coarse-grained SOP-SC model for the multidomain protein and a phenomenological theory that takes the effects of denaturants into account (GdmCl in the present work) accounts quantitatively for many aspects of folding of ADK, which is an example of MMP. The key results are as follows: (i) The calculated folding times, corrected for stability at the small value of [GdmCl] (= 0.3 M), are in excellent agreement with experiment. (ii) The order of events, as assessed by the time-dependent changes in the distances between specific residues (Figure 4C), reproduces the ensemble averaged FRET experiments.6 In particular, the finding that the intramolecular distance between residues 28 and 71 reaches the value in the native state extremely rapidly before any global structure acquisition accords well with experiments.6 In addition, we find that the slow steps in the consolidation of the native fold involve reduction in the distances between 36 and 129 (residues in the NMP and LID domains) and between 18 and 203 reaching the values in the folded state. Although both Q18 and A203 are in the core domain, the rate of approaching the Q18–A203 distance in the folded state is slow and occurs only upon global folding, a conclusion that is also in accord with ensemble FRET experiments.
Equilibrium Collapse under the Folding Condition
There
is considerable interest in determining the size, 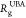 , of the structures
in the UBA under folding
conditions, determined by low denaturant concentration. The current
consensus is that the
, of the structures
in the UBA under folding
conditions, determined by low denaturant concentration. The current
consensus is that the 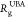 contracts
continuously as the [GdmCl] is decreased from a high
to low value (see, for example,
ref (30)). We calculated
the dependence of
contracts
continuously as the [GdmCl] is decreased from a high
to low value (see, for example,
ref (30)). We calculated
the dependence of 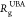 as
a function of [GdmCl] using the ensemble of conformations
that belong to only the UBA.
The results in the inset of Figure 4B show that, as expected on general grounds,
as
a function of [GdmCl] using the ensemble of conformations
that belong to only the UBA.
The results in the inset of Figure 4B show that, as expected on general grounds,  decreases
continuously from ∼57.8
to ∼49.8 Å as the denaturant concentration decreases.
This corresponds to a contraction of about 14%, relative to the size
at high [GdmCl]. It is worth noting that the percent
decrease is in line with that found in other proteins.30
decreases
continuously from ∼57.8
to ∼49.8 Å as the denaturant concentration decreases.
This corresponds to a contraction of about 14%, relative to the size
at high [GdmCl]. It is worth noting that the percent
decrease is in line with that found in other proteins.30
Cooperativity
Communication between
domains during
the assembly of ADK, as the temperature is decreased, is dramatically
different from the all-or-none behavior normally observed in ensemble
experiments in single domain proteins31−36 or in the folding of SMPs. We expect, based on the structure of
ADK (Figure 1C), that
the NMP and (possibly) the LID domains could order nearly independently
in a two-state manner because their sequences are contiguous in sequence
and in the arrangement of the secondary structural elements. This
expectation is borne out in the plots in Figure 2A, which shows that the more stable NMP domain
melts at the higher temperature  . Rao and Gosavi17 also came to similar
conclusions.
. Rao and Gosavi17 also came to similar
conclusions.
Similarly, a two-state like,
albeit with less cooperativity, is observed in the folding of the
less stable LID domain whose melting temperature is 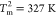 .
The near independence of their folding
is also reflected in the free energy profiles shown in Figure S3 in the SI. Comparison of Figure S3A,D shows that the NMP domain forms
independently of the LID domain. At both
.
The near independence of their folding
is also reflected in the free energy profiles shown in Figure S3 in the SI. Comparison of Figure S3A,D shows that the NMP domain forms
independently of the LID domain. At both  and
and  , the average value
of QNMP exceeds 0.5 while the value of QLID remains small until the temperature is reduced
below
, the average value
of QNMP exceeds 0.5 while the value of QLID remains small until the temperature is reduced
below 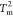 (Figure 2A). In other words, the formation of the NMP domain
does not induce order in the LID domain. Similar conclusions may be
drawn by comparing the temperature-dependent profiles for QNMP and QCORE shown
in Figure 2A and the
free energy profiles shown in Figure S3B,E. The NMP and CORE domains assemble independently, which indicates
that there is little communication between the two domains.
(Figure 2A). In other words, the formation of the NMP domain
does not induce order in the LID domain. Similar conclusions may be
drawn by comparing the temperature-dependent profiles for QNMP and QCORE shown
in Figure 2A and the
free energy profiles shown in Figure S3B,E. The NMP and CORE domains assemble independently, which indicates
that there is little communication between the two domains.
In contrast, from the perspective of both thermodynamics and kinetics,
the folding of the LID and CORE domains are intertwined. As the temperature
decreases below  , the ⟨Q⟩
for the CORE increases, and only when it reaches ∼0.5 is there
a sharp increase in ⟨Q⟩ for the LID
(see the green curve in Figure 2A). The results in Figure S3C,F also suggest that at
, the ⟨Q⟩
for the CORE increases, and only when it reaches ∼0.5 is there
a sharp increase in ⟨Q⟩ for the LID
(see the green curve in Figure 2A). The results in Figure S3C,F also suggest that at 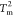 orders in the CORE
and the LID domain are
coordinated in the sense that a decrease in the free energy associated
with the CORE domain also results in an increase in the stability
of the LID domain. In other words, folding of the LID domain is slave
to acquisition of certain order in the CORE domain. The importance
of cooperative interactions between the LID and CORE domain, which
is a consequence of contacts between the reentrant secondary structural
elements in the folded state (Figure S1), was previously established17 by comparing
the equilibrium energy profiles of ADK and circular permutants. Finally,
we note that, even after folding is complete, the LID domain is less
stable compared to the other two domains.23 The decreased stability of the LID domain might be a conduit to
facilitate allosteric transitions.37,38
orders in the CORE
and the LID domain are
coordinated in the sense that a decrease in the free energy associated
with the CORE domain also results in an increase in the stability
of the LID domain. In other words, folding of the LID domain is slave
to acquisition of certain order in the CORE domain. The importance
of cooperative interactions between the LID and CORE domain, which
is a consequence of contacts between the reentrant secondary structural
elements in the folded state (Figure S1), was previously established17 by comparing
the equilibrium energy profiles of ADK and circular permutants. Finally,
we note that, even after folding is complete, the LID domain is less
stable compared to the other two domains.23 The decreased stability of the LID domain might be a conduit to
facilitate allosteric transitions.37,38
Based on optical tweezer experiments on T4 lysozyme,4 which also harbors a reentrant helix like ADK, it has been argued that cooperativity between the distant parts of the chain is needed for stability. It is tempting to speculate that interwoven discontinuous chain topology in MMPs might be an evolutionary consequence not only for stability but also for functional purposes.
Pathways
Both equilibrium, thermal melting and denaturant-induced unfolding show that multiple states are sampled as the transition from the folded state to the unfolded state occurs in ADK. In addition, the refolding kinetics reveals that an intricately connected network of metastable states is involved in the route to the folded state. The fluxes through these states are dramatically different, which suggests that refolding is heterogeneous. The heterogeneity in the folding pathway has been shown in smFRET experiments,5,10 which established that the complexity of the pathways increases as GdmCl concentration increases. The kinetic simulations further support the conclusion reached in experiments. Because smFRET uses only a one-dimensional coordinate for the structures, the metastable structures could not be determined. Our simulations (Figure 5) reveal that the folding pathways are highly complex and heterogeneous and give possibly an even more nuanced picture than that suggested based on analyses of the experimental data.5,10 We find that, at the late stages of folding (HH3 → HH4 → HH5), the contacts in the NMP and the LID domain are fully formed, but various secondary structural elements in the CORE domain have not fully folded (see the bottom right panel in Figure 5). In the HH3 → HH4 transition, the helix given in orange in Figure 1C becomes ordered, and in the HH4 → HH5 transition, the helix displayed in red in Figure 1C is acquired, resulting in an increase in QCORE (see the blue line in the sample folding trajectory in Figure 5).
Although the late stages of folding occur sequentially (HH3 → HH4 → HH5), folding pathways are heterogeneous before HH3 forms. Figure 5 vividly illustrates that there are multiple routes to the formation of HH3. In some of the pathways the LID domain forms first, but in others, the NMP domain forms before the LID domain. The network is multiply connected in the sense HH2 can be accessed through LL1 → HH2 or by the pathway LL1 → LH2 → HH2. Such a complex network of pathways through which the fluxes could dramatically change does not exist in single domain proteins or possibly in SMPs.
Rules for the Folding of Multidomain Proteins
Some general lessons about multidomain proteins emerge from the current work when integrated with previous studies. (1) The domains in the SMPs assemble almost independently with the stability being determined by interface between neighboring constructs. For instance, in the ankyrin repeat proteins (Figure 1A), folding is triggered by interaction between domains i and i + 1, which propagates until assembly is complete.39 (2) In other homo-oligomeric SMP complexes, the interactions at the interfaces contribute most to the stability, which implies that the nature of residues at the junction of domains must play a key role. From a kinetic perspective, the orientations of the domains are significant, as shown in the assembly of the allosteric tetrameric protein, l-lactate dehydrogenase.40 In these cases, the free energy of stability is approximately the sum of the individual domains and an additional gain in the interface formation with correct relative orientation. (3) In contrast, in the MMPs in which the domains are discontinuous from the sequence and SSE perspective, communication between domains is most relevant. That this is the case has been shown in pulling experiments on T4 lysozyme4 in which a reentrant helix stabilizes interaction between the two domains. Similarly, the C-terminal helix α9, the N-terminal helix α1, and the strand β3 play the analogous role in ADK (Figure S1 in the SI). We speculate that the enhanced stability due to the interwoven contacts might be needed to minimize fluctuations in the apo folded state (see Figure S1 in the pulling experiment23) in order to facilitate the closed to open transition in the LID domain, which is required for function. (4) During the refolding kinetics, the continuous domains fold before the discontinuous domains. We do not find that the CORE domain is formed before the other two. The same conclusion was reached in the refolding of the two dihydrofolate reductases41 in which the continuous adenosine loop domain always folds before the discontinuous loop domain. Despite such a stringent requirement in the order of folding of the domains, there are many metastable states that are visited during the early stages of folding (Figure 5), which attests to the plasticity of the folding landscape.5
Concluding Remarks
The general conclusion that emerges from this study is that cooperative interactions in multidomain proteins, with discontinuity in sequence and interactions between reentrant secondary structural elements that stabilize the native fold, arise late in the folding process. The early stages of folding and assembly are highly dynamic. A number of predictions, such as the dependence of the melting temperatures on [GdmCl], order of formation of the domains, and interplay between formation of the three domains, could be experimentally tested. The more subtle structural changes might require additional single-molecule experiments along the lines initiated recently.5 It is likely that similar rules also hold in the self-assembly of ion-driven folding of ribozymes (RNA molecules that function as enzymes), which are composed of many domains.42,43 In Azoarcus ribozyme, several of the domains could fold independently. However, some parts of the sequences are interwoven, and cooperative interactions between domains that harbor these domains typically occur only above the midpoint of the ion concentration (usually Mg2+). It would be interesting to use single-molecule pulling experiments4 to dissect interdomain interactions in RNA.
Methods
SOP-SC Model
We carried out simulations using the SOP-SC (self-organized polymer-side chain) model for the protein.14,44 Each residue is represented by two interaction beads with one located at the Cα position and the other at the center of mass of the side chain. The SOP-SC energy function is
| 1 |
The detailed
functional forms for VFENE, 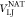 , VNEI, and
, VNEI, and 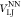 and the values
of the parameters are described
elsewhere.14
and the values
of the parameters are described
elsewhere.14
Molecular Transfer Model (MTM)
Currently the MTM is the only available computational method that accurately predicts the outcomes of experiments and provides the structural basis for folding as a function of denaturants15,45,46 and pH.47 In the MTM, whose theoretical basis is provided in a previous study,44 the effective free energy function for a protein in aqueous denaturant solution is given by
| 2 |
In eq 2, ΔG({ri}, [C]) is the free energy of transferring a given protein conformation from water to an aqueous denaturant solution with [C] being the concentration. The sum in the above equation is over all of the beads, and δg(i, [C]) is the transfer free energy of the interaction center i; αi is the solvent accessible surface area (SASA) of the interaction center i, and αGly–i–Gly is the SASA of the interaction center i in the tripeptide Gly–i–Gly. We used the procedure described previously14,44 to calculate the thermodynamic properties of proteins in the presence of denaturants.
Langevin and Brownian Dynamics Simulations
We assume that the dynamics of the protein is governed by the Langevin equation
| 3 |
where m is the mass of a bead, ζ is the friction coefficient, Fc = –∂EP({ri})/∂ri is the conformational force calculated using eq 1, and Γ is the random force with a white noise spectrum.
We performed Langevin simulations using a low friction coefficient ζ = 0.05m/τL.22 The equations of motions were integrated using the Verlet leapfrog algorithm. To enhance conformational sampling, we used replica-exchange molecular dynamics (REMD).19−21
In order to simulate the folding kinetics, we set ζ = 50m/τL, which approximately corresponds to the value in water.25 At the high ζ value, we use the Brownian dynamics algorithm48 to integrate equations of motion using
| 4 |
Data Analysis
We identify the melting temperature as
the peak position in the specific heat as a function of temperature,  .
.
The structural overlap function, 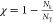 ,9 is employed
to monitor the folding/unfolding reaction, where
,9 is employed
to monitor the folding/unfolding reaction, where
 |
5 |
In eq 5, Θ(x) is the Heavyside function. If  = 2 Å, there is a contact. Nk is the number of contacts
in the kth conformation, and NT is the total number of contacts in the folded state. The
microscopic order parameter of the protein, χ, is used to distinguish
between the native, unfolded, and intermediate states.
= 2 Å, there is a contact. Nk is the number of contacts
in the kth conformation, and NT is the total number of contacts in the folded state. The
microscopic order parameter of the protein, χ, is used to distinguish
between the native, unfolded, and intermediate states.
Acknowledgments
We are grateful to Prof. Gilad Haran and Dr. David Scheerer for useful comments. Z.L. acknowledges financial support from the National Natural Science Foundation of China (11104015 and 11735005) and the China Scholarship Council (201806045049). D.T. is grateful to the National Science Foundation (CHE 19-000033) and the Collie-Welch Regents chair (F0019) for supporting this work.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acscentsci.2c00140.
The authors declare no competing financial interest.
Supplementary Material
References
- Han J. H.; Batey S.; Nickson A. A.; Teichmann S. A.; Clarke J. The folding and evolution of multidomain proteins. Nat. Rev. Mol. Cell. Bio. 2007, 8, 319–330. 10.1038/nrm2144. [DOI] [PubMed] [Google Scholar]
- Rief M.; Gautel M.; Oesterhelt F.; Fernandez J. M.; Gaub H. E. Reversible unfolding of individual titin immunoglobulin domains by AFM. Science 1997, 276, 1109–1112. 10.1126/science.276.5315.1109. [DOI] [PubMed] [Google Scholar]
- Wetlaufer D. Nucleation, Rapid Folding, and Globular Intrachain Regions in Proteins. P. Natl. Acad. Sci. USA 1973, 70, 697–701. 10.1073/pnas.70.3.697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shank E. A.; Cecconi C.; Dill J. W.; Marqusee S.; Bustamante C. The folding cooperativity of a protein is controlled by its chain topology. Nature 2010, 465, 637–U134. 10.1038/nature09021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pirchi M.; Ziv G.; Riven I.; Cohen S. S.; Zohar N.; Barak Y.; Haran G. Single-molecule fluorescence spectroscopy maps the folding landscape of a large protein. Nat. Commun. 2011, 2, 493. 10.1038/ncomms1504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishay E.; Rahamim G.; Orevi T.; Hazan G.; Amir D.; Haas E. Fast Subdomain Folding Prior to the Global Refolding Transition of E. coli Adenylate Kinase: A Double Kinetics Study. J. Mol. Biol. 2012, 423, 613–623. 10.1016/j.jmb.2012.08.001. [DOI] [PubMed] [Google Scholar]
- Ratner V.; Amir D.; Kahana E.; Haas E. Fast collapse but slow formation of secondary structure elements in the refolding transition of E. coli adenylate kinase. J. Mol. Biol. 2005, 352, 683–699. 10.1016/j.jmb.2005.06.074. [DOI] [PubMed] [Google Scholar]
- Orevi T.; Ishay E.; Pirchi M.; Jacob M.; Amir D.; Haas E. Early Closure of a Long Loop in the Refolding of Adenylate Kinase: A Possible Key Role of Non-Local Interactions in the Initial Folding Steps. J. Mol. Biol. 2009, 385, 1230–1242. 10.1016/j.jmb.2008.10.077. [DOI] [PubMed] [Google Scholar]
- Guo Z. Y.; Thirumalai D. Kinetics of Protein-Folding - Nucleation Mechanism, Time Scales, and Pathways. Biopolymers 1995, 36, 83–102. 10.1002/bip.360360108. [DOI] [Google Scholar]
- Kantaev R.; Riven I.; Goldenzweig A.; Barak Y.; Dym O.; Peleg Y.; Albeck S.; Fleishman S.; Haran G. Manipulating the Folding Landscape of a Multidomain Protein. J. Phys. Chem. B 2018, 122, 11030–11038. 10.1021/acs.jpcb.8b04834. [DOI] [PubMed] [Google Scholar]
- Liu Z. X.; Thirumalai D. Denaturants Alter the Flux through Multiple Pathways in the Folding of PDZ Domain. J. Phys. Chem. B 2018, 122, 1408–1416. 10.1021/acs.jpcb.7b11408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller C. W.; Schlauderer G. J.; Reinstein J.; Schulz G. E. Adenylate kinase motions during catalysis: An energetic counterweight balancing substrate binding. Structure 1996, 4, 147–156. 10.1016/S0969-2126(96)00018-4. [DOI] [PubMed] [Google Scholar]
- O’Brien E. P.; Ziv G.; Haran G.; Brooks B. R.; Thirumalai D. Effects of denaturants and osmolytes on proteins are accurately predicted by the molecular transfer model. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 13403–13408. 10.1073/pnas.0802113105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Z. X.; Reddy G.; O’Brien E. P.; Thirumalai D. Collapse kinetics and chevron plots from simulations of denaturant-dependent folding of globular proteins. Proc. Natl. Acad. Sci. U.S.A. 2011, 108, 7787–7792. 10.1073/pnas.1019500108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reddy G.; Liu Z. X.; Thirumalai D. Denaturant-dependent folding of GFP. Proc. Natl. Acad. Sci. U. S. A. 2012, 109, 17832–17838. 10.1073/pnas.1201808109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W. F.; Terakawa T.; Wang W.; Takada S. Energy landscape and multiroute folding of topologically complex proteins adenylate kinase and 2ouf-knot. Proc. Natl. Acad. Sci. U. S. A. 2012, 109, 17789–17794. 10.1073/pnas.1201807109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rao V.; Gosavi S. In the Multi-domain Protein Adenylate Kinase, Domain Insertion Facilitates Cooperative Folding while Accommodating Function at Domain Interfaces. Plos. Comp. Biol. 2014, 10, e1003938 10.1371/journal.pcbi.1003938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burlacu-Miron S.; Perrier V.; Gilles A. M.; Pistotnik E.; Craescu C. T. Structural and energetic factors of the increased thermal stability in a genetically engineered Escherichia coli adenylate kinase. J. Biol. Chem. 1998, 273, 19102–19107. 10.1074/jbc.273.30.19102. [DOI] [PubMed] [Google Scholar]
- Sugita Y.; Okamoto Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999, 314, 141–151. 10.1016/S0009-2614(99)01123-9. [DOI] [Google Scholar]
- Zhou R. H.; Berne B. J.; Germain R. The free energy landscape for beta hairpin folding in explicit water. Proc. Natl. Acad. Sci. U.S.A. 2001, 98, 14931–14936. 10.1073/pnas.201543998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanbonmatsu K. Y.; Garcia A. E. Structure of Met-enkephalin in explicit aqueous solution using replica exchange molecular dynamics. Proteins-Structure Function and Genetics 2002, 46, 225–234. 10.1002/prot.1167. [DOI] [PubMed] [Google Scholar]
- Honeycutt J. D.; Thirumalai D. The Nature of Folded States of Globular-Proteins. Biopolymers 1992, 32, 695–709. 10.1002/bip.360320610. [DOI] [PubMed] [Google Scholar]
- Pelz B.; Zoldak G.; Zeller F.; Zacharias M.; Rief M. Subnanometre enzyme mechanics probed by single-molecule force spectroscopy. Nat. Commun. 2016, 7, 10848. 10.1038/ncomms10848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rhoades E.; Gussakovsky E.; Haran G. Watching proteins fold one molecule at a time. Proc. Natl. Acad. Sci. U.S.A. 2003, 100, 3197–3202. 10.1073/pnas.2628068100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veitshans T.; Klimov D.; Thirumalai D. Protein folding kinetics: Timescales, pathways and energy landscapes in terms of sequence-dependent properties. Folding and Design 1997, 2, 1–22. 10.1016/S1359-0278(97)00002-3. [DOI] [PubMed] [Google Scholar]
- Ratner V.; Sinev M.; Haas E. Determination of intramolecular distance distribution during protein folding on the millisecond timescale. J. Mol. Biol. 2000, 299, 1363–1371. 10.1006/jmbi.2000.3814. [DOI] [PubMed] [Google Scholar]
- Thirumalai D. From Minimal Models to Real Proteins: Time Scales for Protein Folding Kinetics. J. Phys. I (Fr.) 1995, 5, 1457–1467. 10.1051/jp1:1995209. [DOI] [Google Scholar]
- Hyeon C.; Thirumalai D. Chain Length Determines the Folding Rates of RNA. Biophys. J. 2012, 102, L11–L13. 10.1016/j.bpj.2012.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nassar R.; Dignon G. L.; Razban R. M.; Dill K. A. The Protein Folding Problem: The Role of Theory. J. Mol. Biol. 2021, 433 (20), 167126. 10.1016/j.jmb.2021.167126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thirumalai D.; Samanta H.; Maity H.; Reddy G. Universal Nature of Collapsibility in the Context of Protein Folding and Evolution. Trends Biochem. Sci. 2019, 44, 675–687. 10.1016/j.tibs.2019.04.003. [DOI] [PubMed] [Google Scholar]
- Jackson S. E. How do proteins fold?. Folding Des 1998, 3, R81–R91. 10.1016/S1359-0278(98)00033-9. [DOI] [PubMed] [Google Scholar]
- Li M. S.; Klimov D. K.; Thirumalai D. Finite Size Effects on Thermal Denaturation of Globular Proteins. Phys. Rev. Lett. 2004, 93, 268107. 10.1103/PhysRevLett.93.268107. [DOI] [PubMed] [Google Scholar]
- Onuchic J. N.; Wolynes P. G. Theory of protein folding. Curr. Opin. Struct. Biol. 2004, 14, 70–75. 10.1016/j.sbi.2004.01.009. [DOI] [PubMed] [Google Scholar]
- Schuler B.; Eaton W. A. Protein folding studied by single-molecule FRET. Curr. Opin. Struct. Biol. 2008, 18, 16–26. 10.1016/j.sbi.2007.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dill K. A.; Bromberg S.; Yue K. Z.; Fiebig K. M.; Yee D. P.; Thomas P. D.; Chan H. S. Principles of Protein-Folding - a Perspective from Simple Exact Models. Protein Sci. 1995, 4, 561–602. 10.1002/pro.5560040401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dill K. A.; Chan H. S. From Levinthal to Pathways to Funnels. Nat. Struct. Biol. 1997, 4, 10–19. 10.1038/nsb0197-10. [DOI] [PubMed] [Google Scholar]
- Whitford P. C.; Miyashita O.; Levy Y.; Onuchic J. N. Conformational Transitions of Adenylate Kinase: Switching by Cracking. J. Mol. Biol. 2007, 366, 1661–1671. 10.1016/j.jmb.2006.11.085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schrank T.; Bolen D.; Hilser V. Proc. Natl. Acad. Sci. U. S. A. 2009, 106, 16984–17989. 10.1073/pnas.0906510106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrick D.; Ferreiro D. U.; Komives E. A. Folding landscapes of ankyrin repeat proteins: experiments meet theory. Curr. Opin. Struc. Biol. 2008, 18, 27–34. 10.1016/j.sbi.2007.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J.; Thirumalai D. Interface Residues That Drive Allosteric Transitions Also Control the Assembly of L-Lactate Dehydrogenase. J. Phys. Chem. B 2018, 122, 11195–11205. 10.1021/acs.jpcb.8b06430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Inanami T.; Terada T.; Sasai M. Folding pathway of a multidomain protein depends on its topology of domain connectivity. Proc. Natl. Acad. Sci. U. S. A. 2014, 111, 15969–15974. 10.1073/pnas.1406244111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behrouzi R.; Roh J. H.; Kilburn D.; Briber R. M.; Woodson S. A. Cooperative Tertiary Interaction Network Guides RNA Folding. Cell 2012, 149, 348–357. 10.1016/j.cell.2012.01.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Denesyuk N.; Thirumalai D. How do metal ions direct ribozyme folding?. Nat. Chem. 2015, 7, 793–801. 10.1038/nchem.2330. [DOI] [PubMed] [Google Scholar]
- Liu Z. X.; Reddy G.; Thirumalai D. Theory of the Molecular Transfer Model for Proteins with Applications to the Folding of the src-SH3 Domain. J. Phys. Chem. B 2012, 116, 6707–6716. 10.1021/jp211941b. [DOI] [PubMed] [Google Scholar]
- O’Brien E. P.; Ziv G.; Haran G.; Brooks B. R.; Thirumalai D. Effects of denaturants and osmolytes on proteins are accurately predicted by the molecular transfer model. P. Natl. Acad. Sci. USA 2008, 105, 13403–13408. 10.1073/pnas.0802113105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reddy G.; Thirumalai D. Dissecting Ubiquitin Folding Using the Self-Organized Polymer Model. J. Phys. Chem. B 2015, 119, 11358–11370. 10.1021/acs.jpcb.5b03471. [DOI] [PubMed] [Google Scholar]
- O’Brien E. P.; Brooks B. R.; Thirumalai D. Effects of pH on Proteins: Predictions for Ensemble and Single-Molecule Pulling Experiments. J. Am. Chem. Soc. 2012, 134, 979–987. 10.1021/ja206557y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ermak D. L.; Mccammon J. A. Brownian Dynamics with Hydrodynamic Interactions. J. Chem. Phys. 1978, 69, 1352–1360. 10.1063/1.436761. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.