Abstract
Studies of critically ill, hospitalized patients often follow participants and characterize daily health status using an ordinal outcome variable. Statistically, longitudinal proportional odds models are a natural choice in these settings since such models can parsimoniously summarize differences across patient groups and over time. However, when one or more of the outcome states is absorbing, the proportional odds assumption for the follow-up time parameter will likely be violated, and more flexible longitudinal models are needed. Motivated by the VIOLET Study1, a parallel-arm, randomized clinical trial of Vitamin D3 in critically ill patients, we discuss and contrast several treatment effect estimands based on time-dependent odds ratio parameters, and we detail contemporary modeling approaches. In VIOLET, the outcome is a four-level ordinal variable where the lowest ‘not alive’ state is absorbing and the highest ‘at-home’ state is nearly absorbing. We discuss flexible extensions of the proportional odds model for longitudinal data that can be used for either model-based inference, where the odds ratio estimator is taken directly from the model fit, or for model-assisted inferences, where heterogeneity across cumulative log odds dichotomizations is modeled and results are summarized to obtain an overall odds ratio estimator. We focus on direct estimation of cumulative probability model parameters using likelihood-based analysis procedures that naturally handle absorbing states. We illustrate the modeling procedures, the relative precision of model-based and model-assisted estimators, and the possible differences in the values for which the estimators are consistent through simulations and analysis of the VIOLET Study data.
Keywords: longitudinal data, ordinal responses, proportional odds, partial proportional odds, randomized clinical trial, absorbing state, marginalized models
1 |. INTRODUCTION
Ordinal health status scales are common in medical and public health research because they capture naturally ordered severity categories that reflect specific physical or mental health states. Statistical analysis of ordinal data often relies on a comparison of category frequencies or on rankings based on the outcome ordering. Comprehensive multivariable analysis is often facilitated by regression models tailored for ordinal outcomes including the proportional odds (PO) model2. With a K state ordinal response, the PO model provides a unique and ordered intercept for each of the K − 1 dichotomizations of the cumulative response distribution, while independent variable associations with the cumulative log odds are assumed to be constant across such dichotomizations. When the PO assumption is violated, or when one seeks to increase the flexibility of the model, one could adopt a partial proportional odds (PPO) model3, or a saturated model that characterizes each possible dichotomization separately. PPO models represent a measured compromise between flexibility and parsimony by permitting users to choose covariate associations that depend on the outcome dichotomization, while the other covariates have constant associations across dichotomizations of the response.
In settings where repeated measures data have been collected, longitudinal analyses can offer important advantages over cross-sectional analyses even when time-specific associations are ultimately of interest. For example, in a parallel-arm randomized clinical trial, cross-sectional estimates of intervention effects at the end of the study can be estimated with greater precision using longitudinal data analyses than with cross-sectional analyses4,5. PO models for longitudinal data have been discussed extensively, and several authors6,7,8 have developed ordinal data extensions to the generalized estimating equations (GEE) procedure for binary data9,10,11. These approaches estimate marginal model parameters, and because they are semiparametric, they only require correct specification of the exposure-response relationship, but not higher order moments of the multivariate response variable, to ensure valid inferences. Uncertainty estimates are most often calculated with robust, ‘sandwich-based’ methods9 or bootstrap methods12. In settings where one seeks to estimate marginal model parameters using likelihood-based procedures, Lee and Daniels13 proposed marginalized models for ordinal data which extend the marginalized models class originally proposed for binary response data14,15,16. Like GEE, marginalized model estimation separates the exposure-response model from higher order moment models; however, inferences are based on a likelihood which can be advantageous if one has interest in model selection, prediction, or improved robustness to missing data patterns (e.g., missing at random).
Our research is motivated by the VIOLET Study1, the analysis of which involves longitudinal ordinal response data where the PO model assumption is clearly violated; we will approach the problem with marginal PPO models. VIOLET is a parallel-arm, placebo-controlled randomized clinical trial of Vitamin D3 for treating critically ill, hospitalized patients. In the VIOLET Study data analyzed in this paper, patients were observed daily over the course of a four-week period to be in one of four ordered outcome states: 1) not alive, 2) with acute respiratory distress syndrome (ARDS) or on mechanical ventilator, 3) in the hospital but without ARDS or on a ventilator, and 4) at-home. For this four-week follow-up period, VIOLET reported the difference in the proportion of patients alive on the last day, the difference in the average number of ventilator-free days, and the difference in the average hospital length of stay, comparing Vitamin D3 and placebo arm groups. While the outcomes are irrefutably clinically important, each analysis was conducted separately and so none of them took full advantage of the ordinal and longitudinal data that were collected. The motivation for this paper is to promote flexible analyses that fully utilize ordinal and longitudinal data collected in parallel-arm randomized clinical trials. Rather than estimate conditional models (e.g., mixed models or Markov transition models) that must be summarized to obtain group contrasts that are of interest in randomized clinical trials, we extend the fully parametric, marginalized transition model, that intentionally reparametrizes the Markov structure to estimate group effects directly with a marginal model.
While longitudinal analyses of ordinal outcome states can efficiently exploit the information contained in the VIOLET Study data, they must consider an important feature of the data that to our knowledge has not been addressed extensively, namely that at least one of the outcomes states is absorbing (i.e., being in state k on day t implies being in state k for all t′ > t). Specifically, in the VIOLET Study data, the lowest state (k = 1; not alive) was absorbing, and the highest state (k = 4; at-home) probability increased over the course of follow-up and behaved to an approximation like an absorbing state. As we will show, in settings where we seek to study associations with ordinal longitudinal response data, the presence of at least one absorbing state is likely to lead to severe violations of the PO assumption over time, thus requiring an extension of the marginalized transition model from the PO specification to a PPO specification. Our overall inferential strategy is to identify models that have good fidelity to the data under study and do not necessarily rely on a restrictive model for parsimonious characterization of treatment group differences. Rather, in order to summarize “overall intervention effects” either across time or at the end of the follow-up period, we initially fit a flexible PPO model to estimate dichotomization-specific intervention effects as functions of follow-up time. Subsequently, time- and/or dichotomization-specific intervention effects are summarized to obtain estimates of pre-defined global intervention effects. Considerations for summarizing intervention effects across distinct outcome levels are similar to those of composite endpoints17 in that one must choose an appropriate weighting scheme to capture a meaningful, global intervention effect. If additional covariates are included in regression models then we can choose to construct marginal summaries through additional standardization strategies18.
This paper is organized as follows. Section 2 describes the VIOLET Study and highlights key features that motivate this line of research. Section 3 describes cumulative probability models including the PO and PPO models and parsimonious estimands for intervention effects. In Section 4, we discuss first-order marginalized transition models13, their appropriateness for estimating model parameters in the presence of absorbing states, and some of their challenges. We then describe simulation experiments that resemble VIOLET Study data analyses in Section 5. In Section 6, we return to the VIOLET Study to conduct analyses using the methods described in this paper. Finally, we conclude with a discussion in Section 7.
2 |. VIOLET STUDY OF VITAMIN D3 IN CRITICALLY ILL PATIENTS
The VIOLET Study1 was a parallel-arm, placebo-controlled randomized clinical trial of the efficacy of Vitamin D3 supplements in critically ill patients. For the purpose of this analysis, we consider data from the first four weeks of the study (with 27 follow-up days), where at each follow-up day, participants were observed to be in one of four, ordered outcome states: not alive, on mechanical ventilator or with ARDS, hospitalized, or at-home. For the remainder of the paper, we will refer to the second most severe state as Vent/ARDS. The overall goal of the intervention is to improve outcomes over the course of follow-up and particularly at the end of the follow-up period. We approach this problem using ordinal longitudinal regression models that we summarize to capture intervention effects over time or at individual follow-up times.
We consider 1351 of the 1360 participants in the VIOLET Study with follow-up data and whose baseline, pre-randomization state was Vent/ARDS or in-hospital. Baseline characteristics for participants are described elsewhere1, though the median (interquartile range) age was 58 (31, 75) years, and 36% of the participants were enrolled in the Vent/ARDS state. Figure 1 shows outcome state empirical cumulative log-odds for the placebo and intervention arms during follow-up. The log odds of being in the baseline outcome states (hospitalized or Vent/ARDS) decreased dramatically over time in both arms, and the log odds of being not alive or at-home increased. This is not surprising because death is an absorbing state, and therefore the prevalence of death must be non-decreasing over the course of follow-up. The home state is nearly absorbing as the study did not observe any transitions from the home state to either of the hospitalized or Vent/ARDS states. A total of 21 participants passed away after being discharged home. Table 1 shows day to day transition probabilities, and as we can see, beyond the absorbing death state, and the nearly absorbing at-home state, outcome states on successive days are very highly associated with one another. Ten, eight, 28, and 54 percent of all person-days were observed to be in the not alive, Vent/ARDS, in-hospital, and at-home states, respectively.
FIGURE 1.
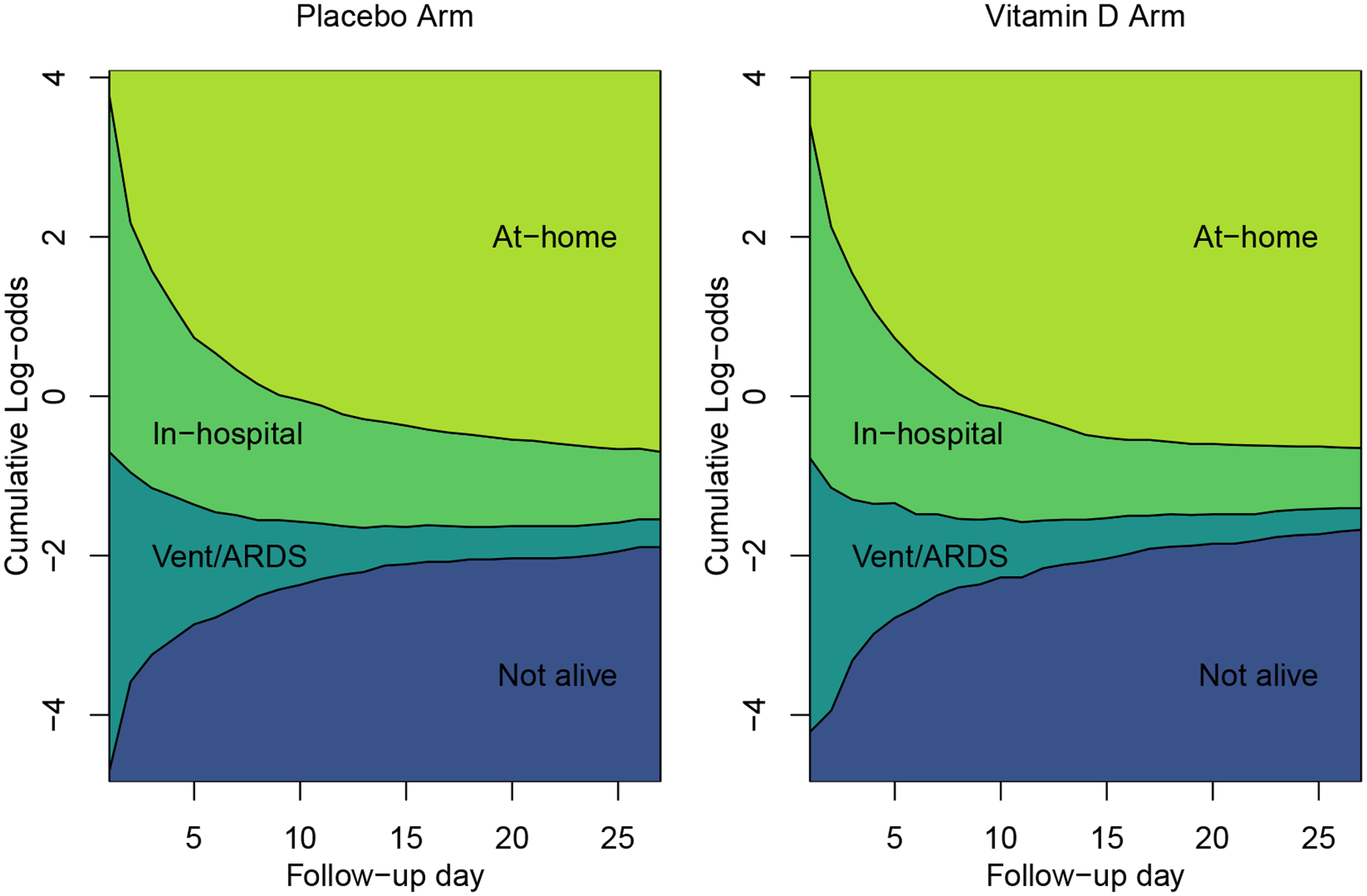
VIOLET Study data: Empirical cumulative log odds across 27 follow-up days
TABLE 1.
Day to day state transition probabilities across 1351 VIOLET Study participants
| Yi(tij−1) | |||||
|---|---|---|---|---|---|
| Yi(tij) | Not alive | Vent/ARDS | In-hospital | Home | Overall |
| Not alive | 1.000 | 0.0266 | 0.0057 | 0.0016 | 0.1024 |
| Vent/ARDS | 0.0000 | 0.8645 | 0.0029 | 0.0000 | 0.0802 |
| in-hospital | 0.0000 | 0.0936 | 0.9117 | 0.0000 | 0.2812 |
| Home | 0.0000 | 0.0153 | 0.0797 | 0.9984 | 0.5363 |
The presence of the absorbing death state combined with the nearly absorbing at-home state induces a severe violation of the PO assumption for parameters associated with study day. Under the PO assumption, the outcome association with follow-up day is captured with a single functional across outcome dichotomizations which would imply that the cumulative log-odds curves in Figure 1 would be parallel to one another. This is clearly not the case. Because the PO assumption is severely violated, PPO models will be implemented in the VIOLET Study data analysis. What is not clear from these plots is whether the treatment effect violates the PO assumption across study days; we show how to address this issue with our model specification.
3 |. CUMULATIVE PROBABILITY MODELS
For the analysis of VIOLET1, we will implement marginally-specified cumulative probability models (CPM). Let i ∈ {1, … , N} denote subject, tij ∈ {1, … , mi} denote follow-up day on visit j, Y i be a mi–vector of ordinal response values with Yi(tij) ∈ {1, … , K}, and Xi be a mi ×p design matrix with Xi(tij) a p–vector corresponding to day tij. In the VIOLET Study data, tij = j and K = 4 with k = 1 implying death and k = 4 implying the home state. The marginal CPM is given by πi(tij) = pr[Yi(tij) ≤ k | Xi(tij)] and we make the full covariate conditional mean or no interference assumption that pr[Yi(tij) ≤ k | Xi(tij)] = pr[Yi(tij) ≤ k | Xi]19,20,21.
The marginal CPM is “marginal” in the sense that it does not include observed or latent response values as independent variables in the regression model. That is, the model for the relationship between the response and the intervention indicator is separated from the model for the relationship among the responses at different follow-up times. In contrast, conditional CPMs capture the intervention-response relationship and higher order moments of the response in the same regression model. Generalized linear mixed models use latent random effects in the intervention-response regression to capture response dependence (i.e., the second moment) and higher order moments, while standard Markov, semi-Markov models, and partly conditional models22,23,24 explicitly condition on response history in the regression model for the intervention effect. Even though one could estimate these conditional models and then marginalize over the random effects distribution or response history to estimate marginal intervention effects25, the present paper studies models that deliberately reparameterize a first-order Markov model to estimate intervention effects directly while borrowing the Markov characterization in a separate response dependence model. We believe marginalized models have much potential for use in medical and public health research, and research regarding their performance in real-world settings is needed.
All estimators from the models discussed herein will be derived from the marginal CPM. While there are many ways to summarize intervention effects in a longitudinal parallel-group randomized clinical trial for ordinal response data (odds ratios, risk ratios, or risk differences) we focus on intervention effects on the odds ratio scale. In many common settings, and with careful consideration, one may convert estimates from the odds ratio scale to other scales.
3.1 |. Proportional Odds and Partial Proportional Odds Models
The marginal CPM from a longitudinal PO model is a reasonable choice for the analysis of a parallel-arm randomized clinical trial with ordinal outcomes. This logit link transformed CPM captures treatment associations with the cumulative odds using a main effect of treatment and a treatment by time interaction. We refer to this model as po1. It is given by,
| (1) |
where f1(tij) and f2(tij) are known flexible functions of study day. Importantly, in this paper we deliberately choose f1(tij) and f2(tij) to be functions that are 0 when tij = 1, so that and capture the kth intercept and the intervention effect, respectively, on the first follow-up day tij = 1. The function captures the tij–specific log odds that the response is at level k or lower in the control arm (xi = 0), and it can also be thought of as a tij–specific intercept. In this model, parameters and may be scalar or vector values depending on the functional forms of f1(tij) and f2(tij). Function quantifies the difference in the log odds between the treatment (xi = 1) and control (xi = 0) arms at tij (i.e., treatment effect). Note that does not depend on threshold k, and so the treatment effect satisfies PO assumptions even while varying over time. This model could include other non-treatment covariates and confounders though we exclude them here for simplicity.
As one can see from (1), we assume in this model that for each k < K, is constant over tij. That is, this model assumes that the time effect for xi = 0, f1(tij), satisfies the PO assumption. By examining the left panel of Figure 1, it is clear that the are not parallel over time, and so the PO assumption for f1(tij) is severely violated. To address non-proportional odds in the cumulative log odds association with f1(tij), we increase the flexibility of the model by writing it as a PPO model that relaxes the PO assumption on f1(tij). We refer to the following model,
| (2) |
as ppo1, where ck is an indicator for the dichotomization Yi(tij) ≤ k. We may think of this PPO model using concatenated, time-specific proportional-odds models where the time-specific intercepts are given by, , , and and the time-specific intervention effect (i.e., the log odds ratio) is forced to satisfy the PO assumption with .
We can increase flexibility even further by relaxing PO assumptions on xi and/or f2(tij)xi for at least one of the outcome dichotomizations. For the purpose of analyses discussed in this paper, we will permit distinct treatment by time interactions for all dichotomizations of the outcome value using the following model which we refer to as ppo2,
| (3) |
Similar to ppo1 we think of this model as a set of cross-sectional, tij–specific models that are concatenated, but in addition to dichotomization-specific intercepts, this model yields dichotomization-specific intervention effects given by, , , and . Though one could consider another model that permits non-proportional odds on , we can see from Figure 1, nearly all subjects are in the hospitalized or Vent/ARDS states on day tij = 1 of follow-up. There are effectively only two observed response states when tij = 1, and so there is no evidence to suggest a PO assumption violation at that time point.
It is important to note that while in this paper we discuss PO and PPO models for analysis of the VIOLET Study data, there is a literature on flexible and parsimonious alternatives to both models. PO models are cumulative “link” models specifically with a logit link. Other cumulative link models include the proportional hazards (log-log link) and ordered probit (probit link) models. Further, other classes of models for ordinal data include continuation ratio models, adjacent category models, and stereotype models (see e.g.,26,27,28). Among all of these model choices, the most popular is probably the cumulative probability model with the logit link (i.e., the PO model). Alternatives to the PPO model specification include location-scale models29 and trend odds models30 that parameterize non-proportional odds to be shifts not only in the means of the latent logistic distribution, but also shifts in the scales. Specifically, the trend odds model can be viewed as a PPO model but with the non-proportionality parameters (e.g., and ) constrained to be linear or at least monotonic (e.g., ). These modeling approaches are viable alternatives to the ones discussed in this paper.
3.2 |. Estimands: Parsimonious model-based and model-assisted intervention effects
Parsimonious intervention associations on day tij can be captured directly with (2). Because the association is taken directly from the model, we refer to it is as a model-based estimand and the estimator as a model-based estimator. If equation (2) is correct, this is an efficient way of estimating the intervention effect. Even if the PO assumption for the intervention effect is incorrect, one could argue that is a reasonable summary of the relationship between the intervention variable and the ordered outcome. Alternatively, we may seek to strike a balance between a parsimonious intervention association and model flexibility by defining model-assisted estimands that take a weighted average of dichotomization-specific estimates from model (3), . The weight wk(tij) is assigned to the kth dichotomization-specific intervention association and should be chosen carefully based on study goals.
Table 2 shows three distinct weighting schemes for model-assisted estimands as they could apply to the VIOLET Study. MAs(tij) uses a simple average of dichotomization-specific parameters on day tij and has been proposed previously for cross-sectional analyses of ordinal outcomes25. MA613(tij) gives relative weights of 6, 1, and 3 to the first, second and third dichotomizations, thus reflecting the value placed on each of the dichotomizations. For example, in the VIOLET Study, the MA613(tij) weighting scheme gives the intervention effect for the not alive (k = 1) versus alive (k > 1) dichotomization six times the weight of the intervention effect for the Vent/ARDS or worse (k ≤ 3) versus in-hospital or better (k > 2) dichotomization and twice the weight of the intervention effect for the in-hospital or worse (k ≤ 3) versus at-home (k = 4) dichotomization. This weighting scheme can and should be modified based on pre-specified utilities. MAp(tij) places weights that are proportional to the precision with which dichotomization-specific parameters are estimated. In addition to summarizing dichotomization-specific intervention effects to obtain the global summary at time tij, one could also summarize / average across all k and tij though such summaries are not addressed here.
TABLE 2.
Estimands for longitudinal analyses of ordinal outcome data
| Estimand | Definition | Description |
|---|---|---|
| MBppo1(tij) | Model (2) intervention parameter under PO assumption for the intervention effect | |
| MAs(tij) | Simple average of dichotomization-specific parameters from Model (3) | |
| MA613(tij) | Value-based weighting of dichotomization-specific parameters from Model (3) | |
| MAp(tij) | Precision-based weighting with proportional to the precision of the estimator from Model (3). |
MB = model-based, MA = model-assisted.
4 |. MARGINALIZED MODELS FOR ORDINAL LONGITUDINAL DATA
The , , and values from equations 1, 2, and 3, respectively, are examples of marginal CPMs. They capture the univariate distribution [Yi(tij) | Xi(tij)], while being agnostic to the joint, multivariate distribution [Y i | Xi]. To conduct a likelihood-based analysis with marginal CPMs, we need to identify higher-order, joint moments of the multivariate distribution. For the purpose of the analyses discussed here, we appeal to the first-order marginalized transition model for ordinal response data (OMTM1) proposed by Lee and Daniels13, and for ease of exposition, we will make the proportional odds assumption and will suppress the superscripts. The general form of the OMTM1 model is given by two regression equations,
where the first is a marginal cumulative logit model with Yij considered as a univariate response as described in equation (1), is a (conditional) Markov transition probability, and γkl is a log relative risk ratio parameter for the transition from state l to state k. The intercept, Δi,k[Xi(tij)], is an implicit function that links the first and second regression equations. For each subject and time, (i, tij), and at each iteration of the maximization algorithm, the K − 1 elements of {Δi,1[Xi(tij)], … , Δi,K−1[Xi(tij)]} are calculated simultaneously13. Specifically, because the marginal distribution is equal to the marginalized [over Yi(tij−1)] conditional distribution, then Δi,k[Xi(tij)] are the values that solve
| (4) |
where
is a transition probability from state g to k. Value μi,k(tij) = πi,k(tij) − πi,k−1(tij) is the marginal probability of being in state k, and πi,K (tij) = 1. When fitting these models, each step of the Newton Raphson algorithm alternates between updating (α, β, γ) and updating Δi,k[Xi(tij]. Given (α, β, γ), the Δi,k[Xi(tij)] are computed by solving the equation (4), and once the values of Δi,k[Xi(tij)] have been calculated for all (j, k), subject i’s contribution to the likelihood can be identified directly with
The first term only includes the marginal probability at the first observed timepoint μi,k(ti1) because lagged response values are unavailable, and the second term include the dependence model probability , that explicitly conditions on the lagged response value. Score and information calculations for this model are detailed in the text and web appendices of Lee and Daniels (2007)13.
4.1 |. Absorbing state: technical details
In the presence of an absorbing state, some hi,kg(tij) will take on values of 1 and 0. For example, because death (k = 1) is absorbing, hi,11(tij) = 1 and hi,k1(tij) = 0 for k > 1. Examining equation (4), we observe an important restriction on the model, namely that the marginal probability of being in an absorbing state must be non-decreasing with follow-up time, i.e., μi,1(tij) ≥ μi,1(tij−1). While this makes intuitive sense, in studies such as VIOLET, where μi,1(tij) increases slowly towards the end of the follow-up period (see Figure 1), one must ensure that the fitting algorithm, e.g., Newton-Raphson, does not jump to a set of parameter estimates that violate this restriction. This can be achieved by forcing small jump-size or by using monotonic study day functionals.
Since state k = 1 is absorbing in VIOLET, then γ11 = ∞ and γk1 = −∞ for k > 1. By examining the likelihood, one can see that if Yi(tij) = 1, then the subject i contribution to the likelihood is degenerate for all tij′ > tij. This fact implies that one would make the same inferences whether one analyzed the data by keeping all observations after an absorbing state is observed or by removing all post-absorbing state observations. If one chooses to keep all observations following an absorbing state, our experience has been that the OMTM1 fitting algorithm is able to appropriately estimate γ11 to be a large positive number and the γk1s to be large negative numbers. However, such an approach requires fixed follow-up times and a well-defined follow-up period in order to include the post absorbing state observations. Most often, one would remove all observations after an absorbing state is entered. In such cases, one must set γ11 to be an appropriately large value, say 25, and the γk1s to be appropriately large in magnitude but negative, say −25, for valid calculations of Δi,k[Xi(tij)].
Remark 1: The response dependence model described above explicitly captures each of the K × K transitions separately. Due to this flexibility, we are able to appropriately address absorbing states. In the absence of a parameter that allows the state transition model to equal one for absorbing states, the model will not be coherent at the time an absorbing state is observed. Specifically, the ordinal marginalized transition model described above captures a data generating model that applies both before and after the absorbing state has occurred.
Remark 2: If one seeks to use a semi-parametric procedure such as GEE to estimate parameters from the marginal CPM in the presence of an absorbing state, observations following absorbing state entry must be retained. Otherwise marginal state probability estimates will be biased. Though not studied extensively here, such estimators could be used to analyze the VIOLET data. We do not focus on GEE methods here primarily because our interest is in likelihood-based procedures that permit model comparison with an objective function. Further, as discussed in Lee and Daniels13, the first-order marginalized transition model has the same robustness to response dependence misspecification that GEE estimators have, namely, valid marginal CPM estimation is possible even in the presence of dependence model misspecification. Valid inferences are possible with robust standard errors31,32,33.
5 |. SIMULATIONS
We now explore the behavior of marginalized model estimators of model-based and model-assisted estimands in the presence of an absorbing state in scenarios similar to the VIOLET Study. We simulate a parallel-arm RCT of n=1000 patients with 20 equally spaced follow-up visits across a time-period that ranges from ti1 = 1 to ti20 = 10. For the purpose of generating and fitting the data, we set f1(tij) = f2(tij) = f(tij) = log10(tij) so that f(1) = 0 and f(10) = 1. Let Xi be a binary treatment indicator (1 for intervention and 0 for control), xi be the observed value, and Yi(tij) ∈ {1, 2, 3, 4} be a four level outcome variable with the lowest state k = 1 being absorbing. We generate data according to the ppo2 CPM in equation (3) with α = (−4, −1.5, 2) so that the vast majority of subjects are in states k = {2, 3} at tij = 1 [when f(tij) = 0], so that, similar to VIOLET Study data, pr[Yi(tij) ∈ {1, 4}] increases substantially and pr[Yi(tij) ∈ {2, 3}] decreases substantially over the course of follow-up. The intervention effect at f(tij = 1) = 0 is which is set to −0.1, and we fix .
To examine operating characteristics of model-based and model-assisted estimators of intervention associations over time, we vary the extent to which the PO assumption for the intervention effect is violated and the degree of response dependence in the data generating mechanism. Specifically, we examine to study no violation, moderate violation, and severe violation of the PO assumption for the intervention effect. Notice that when the ppo2 model simplifies to ppo1. Figure 2 shows the functional form for the dichotomization-specific intervention associations under the three scenarios. In the left panel, all dichotomization-specific intervention associations are equal to one another with the log odds ratio equal to −0.1 at tij = 1 and 0.1 at tij = 10. In right panel, where the PO assumption is severely violated, the intervention association differs for Yi(tij) ≤ 1, Yi(tij) ≤ 2, and Yi(tij) ≤ 3, and for Yi(tij) ≤ 3 the log odds ratio is equal to −0.1 at tij = 1 and −0.3 at tij = 10.
FIGURE 2.
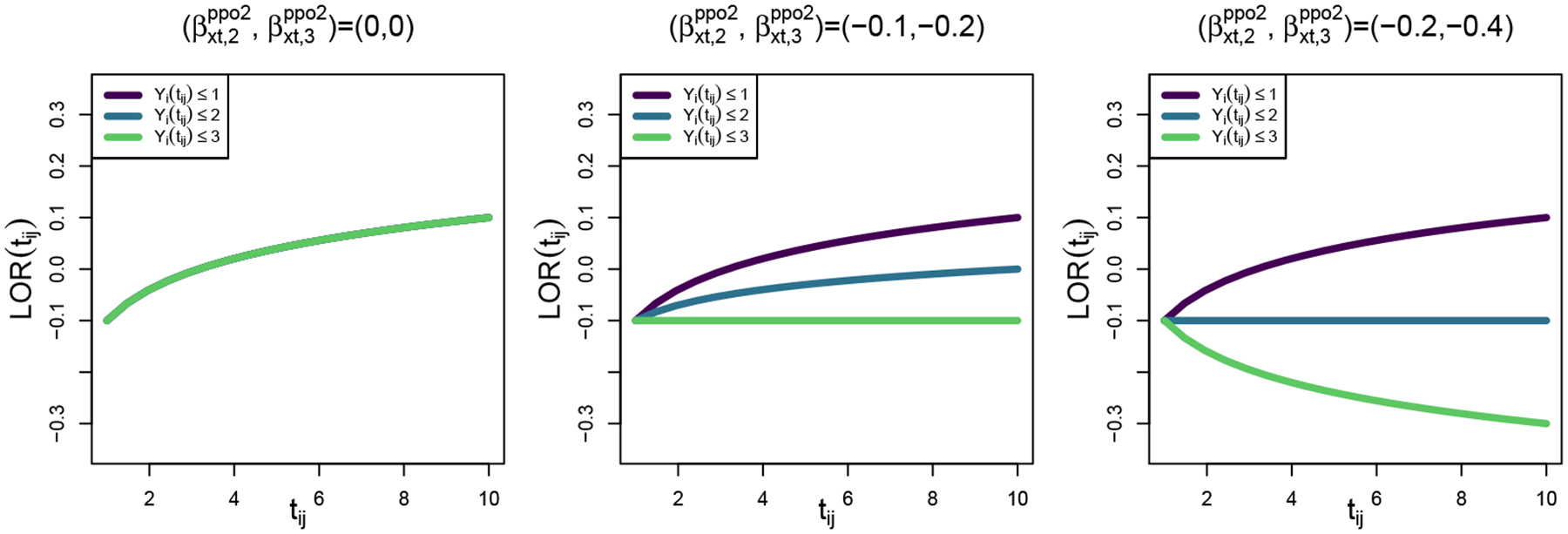
Dichotomization-specific functional form of the intervention association [i.e., log odds ratio (LOR)] across no , moderate , and severe violations of the PO assumption for the simulation studies, where subscripts 2 and 3 indicate contrasts for k = 2 and k = 3 versus k = 1.
To study the impact of response dependence on the estimators, let Γ denote the 3×3 dependence model parameter matrix with elements γkl denoting the log relative risk ratio for transitioning from state l to state k with state k = 4 being the reference state for both the response [Yi(tij)] and the lagged response [Yi(tij−1)] in the response dependence model. We study Γ values equal to and , in order to capture high and moderate degrees of response dependence, respectively, recognizing that the presence of an absorbing state itself represents a very high degree of response dependence. High values along the diagonal [e.g., (20, 7, 7) in the left matrix] induce large log relative risk ratios of remaining in the same state on successive days. We set (γ11, γ21, γ31) = (20, −20, −20) to generate the absorbing state for k = 1 where the probability of transitioning on successive days from state 1 to 1, 1 to 2, and 1 to 3 is effectively 1, 0, and 0, respectively. Table 3 shows a realization of the transition matrices from Yi(tij−1) (columns) to Yi(tij) (rows) for high and moderate response dependence with N = 5000 simulated subjects. As we can see, values along the diagonals decline when response dependence is reduced. For each of the six data generating mechanisms (none, moderate and severe violations of the PO assumption and high and moderate response dependence), we fit the data using ppo1 and ppo2 to capture the model-based and model-assisted estimates of the target estimands. We summarize results across 1000 replicates.
TABLE 3.
Transition matrices for the high and moderate response dependence settings in the simulation studies
| Yi(tij) | High Response Dependence: Yi(tij−1) | Moderate Response Dependence: Yi(tij−1) | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | |
| 1 | 1.000 | 0.020 | 0.002 | 0.012 | 1.000 | 0.024 | 0.005 | 0.010 |
| 2 | 0.000 | 0.904 | 0.017 | 0.006 | 0.000 | 0.689 | 0.057 | 0.045 |
| 3 | 0.000 | 0.002 | 0.900 | 0.010 | 0.000 | 0.068 | 0.792 | 0.072 |
| 4 | 0.000 | 0.074 | 0.081 | 0.972 | 0.000 | 0.220 | 0.146 | 0.872 |
Table 4 shows average parameter estimates, empirical standard errors, and coverage probabilities across replicates for ppo1 and ppo2 model fits in all scenarios. Notice that for all of the properly specified models [i.e., ppo2 in all scenarios and ppo1 when ], inferences appears to be approximately valid, with parameter estimates approximately unbiased and with coverage probabilities nearly equal to their 95% nominal level. In settings where the PO assumption is violated, the ppo1 model estimate for is not expected to yield the same quantity as the ppo2 estimate for . Whereas the ppo2 model is estimating the treatment by time interaction [xi · f(tij)] effect for the k ≤ 1 response dichotomization, the ppo1 model is making the PO assumption and is therefore estimating an “across-dichotomization” interaction effect. As one might expect, in the scenarios shown here, the ppo1 estimator appears to be a weighted average of dichotomization-specific treatment by time interactions from the ppo2 model fits. For example, for the scenario with high response dependence and with , the average ppo1 estimator for was −0.063, which is a weighted average of the dichotomization-specific estimates from the ppo2 model, i.e., 0.212 (k = 1), 0.212 − 0.204 = 0.008 (k = 2), and 0.212 − 0.400 = −0.188 (k = 3). However, in a setting shown in the appendix with lower response dependence, the across-replicate average ppo1 estimator was −0.297 which is not an average of the dichotomization-specific estimates. While such a scenario is highly divergent from the VIOLET Study data, it is worth being aware of and checking the extent to which the PO assumption is violated when using the ppo1 estimator.
TABLE 4.
Average parameter estimates, empirical standard errors, and coverage probabilities across 1000 replicates for model fits from ppo1 and ppo2. In all cases, data were generated from a ppo2 model and fit with ppo2 and ppo1 models. In settings where , the ppo1 model is correctly specified. When this is not the case, it is misspecified and estimated coefficients differ from ppo2 model.
| ppo2 estimates | ppo1 estimates | |||||||
|---|---|---|---|---|---|---|---|---|
| Dependence | ||||||||
| High | (0,0) | True value | −0.1 | 0.2 | 0 | 0 | −0.1 | 0.2 |
| Average Estimate | −0.101 | 0.203 | −0.004 | −0.008 | −0.101 | 0.198 | ||
| Standard Error | [0.128] | [0.183] | [0.098] | [0.128] | [0.127] | [0.159] | ||
| Coverage | (0.951) | (0.945) | (0.953) | (0.947) | (0.955) | (0.934) | ||
| (−0.1, −0.2) | True value | −0.1 | 0.2 | −0.1 | −0.2 | NA | NA | |
| Average Estimate | −0.102 | 0.205 | −0.102 | −0.203 | −0.116 | 0.068 | ||
| Standard Error | [0.127] | [0.180] | [0.097] | [0.126] | [0.126] | [0.156] | ||
| Coverage | (0.948) | (0.961) | (0.949) | (0.951) | NA | NA | ||
| (−0.2, −0.4) | True value | −0.1 | 0.2 | −0.2 | −0.4 | NA | NA | |
| Average Estimate | −0.106 | 0.212 | −0.204 | −0.400 | −0.132 | −0.063 | ||
| Standard Error | [0.123] | [0.188] | [0.095] | [0.119] | [0.122] | [0.161] | ||
| Coverage | (0.954) | (0.935) | (0.933) | (0.946) | NA | NA | ||
| Moderate | (0,0) | True value | −0.1 | 0.2 | 0 | 0 | −0.1 | 0.2 |
| Average Estimate | −0.102 | 0.200 | 0.000 | 0.000 | −0.102 | 0.200 | ||
| Standard Error | [0.114] | [0.190] | [0.090] | [0.122] | [0.113] | [0.156] | ||
| Coverage | (0.948) | (0.953) | (0.939) | (0.947) | (0.948) | (0.954) | ||
| (−0.1, −0.2) | True value | −0.1 | 0.2 | −0.1 | −0.2 | NA | NA | |
| Average Estimate | −0.097 | 0.196 | −0.101 | −0.201 | −0.120 | 0.026 | ||
| Standard Error | [0.115] | [0.186] | [0.080] | [0.113] | [0.115] | [0.158] | ||
| Coverage | (0.947) | (0.950) | (0.954) | (0.950) | NA | NA | ||
| (−0.2, −0.4) | True value | −0.1 | 0.2 | −0.2 | −0.4 | NA | NA | |
| Average Estimate | −0.101 | 0.200 | −0.201 | −0.400 | −0.146 | −0.150 | ||
| Standard Error | [0.117] | [0.192] | [0.080] | [0.110] | [0.117] | [0.163] | ||
| Coverage | (0.942) | (0.947) | (0.946) | (0.944) | NA | NA | ||
Figures 3 a and 3 b show time-specific summaries of intervention effects for the model-based and model-assisted analysis approaches. Figure 3 a corresponds to the high response dependence setting and Figure 3 b corresponds to moderate response dependence. The top-left panels of the figures show that when the proportional odds assumption for the intervention effect is met, the model-based and model-assisted approaches estimate the same quantity since all of the estimated effects are stacked on top of one another. However, when the PO assumption is not met, the estimators are consistent for distinct quantities. When response dependence is high and PO assumption violations are moderate (top central panel in Figure 3 a), the different global estimators still capture similar quantities. However, with moderate response dependence or with severe violations of the PO assumption, the estimators capture distinct quantities. In particular the model-based estimator of MBppo1(tij) not only estimates a different value at each timepoint, but it can also estimate a different trend as shown in the top right panels of Figures 3 a and 3 b.
FIGURE 3.
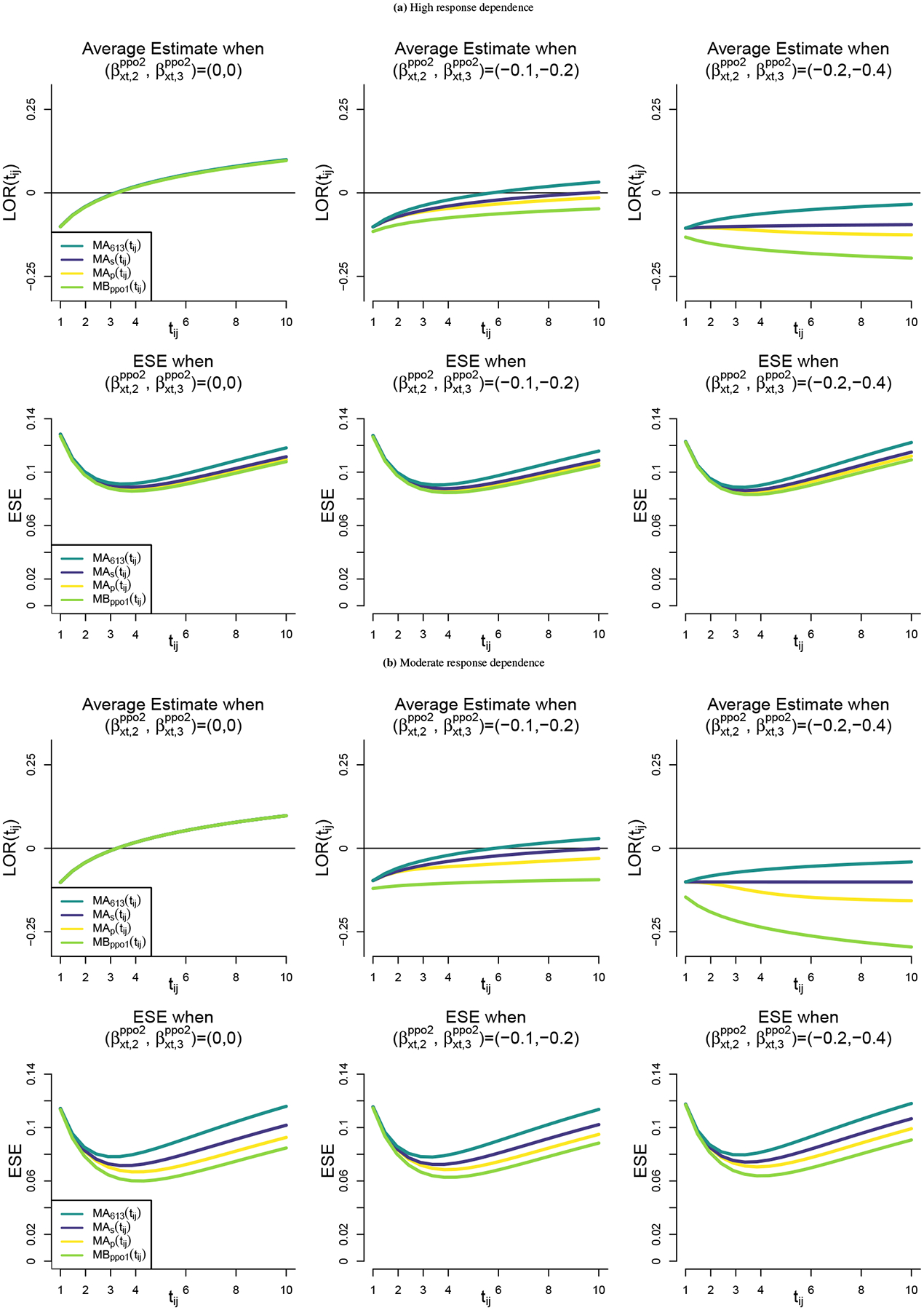
Model-based and model-assisted summaries: For high (a) and moderate (b) response dependence settings, we report averages of the tij–specific estimates of intervention effects using a global log odds ratio [LOR(tij)] and the empirical standard errors (ESE) across 1000 replicates. We includes scenarios with no violation , moderate violation , and severe violation of the proportional odds assumption for the intervention effect.
In the bottom row of panels in Figures 3 a and 3 b we observe that all estimators were most precisely estimated towards the middle of the follow-up period. In all cases, MBppo1(tij) was estimated with the greatest precision over time, followed by MAp(tij), MAs(tij), and MA613(tij). MA613(tij) was estimated with the least precision in the scenarios studied here because the estimator gives the largest weight to the intervention effect corresponding to Yi(tij) ≤ 1 which is relatively rare. The extent of precision differences among the estimators is highly related to the strength of response dependence in the data. The precision of the estimators is similar in the high response dependence settings that most closely resemble the VIOLET study data and differs substantially in the moderate response dependence data setting.
6 |. ANALYSIS
We now conduct analyses of the VIOLET Study data with the broad goal of estimating the potential benefit of Vitamin D3 administration in critically ill patients. We seek to base inferences on parsimonious intervention effects using odds ratios across outcome dichotomizations and at distinct follow-up times (tij ∈ {7, 14, 21, 27}). We fit the ppo1 and ppo2 models from equations 2 and 3, respectively, and for comparison the corresponding cross-sectional estimators from scalar response analyses that do not exploit the longitudinal structure of the data, which is commonly done in randomized clinical trials1. We then summarize the results to make inferences on the day-specific MBppo1(tij), MAs(tij), MA613(tij), and MAp(tij). In all cases, f1(tij) = f2(tij) = f(tij) is a restricted cubic spline (three degrees of freedom) on the log of follow-up day, so that f(1) = 0.
One benefit of the OMTM1 is that inference is based on an objective likelihood function, and Table 5 shows maximized likelihoods for three OMTM1 models, po1, ppo1, and ppo2 that correspond to equations 1, 2, and 3, respectively. By comparing ppo1 to po1, it is very clear (p < 0.0001) that relaxing the PO assumption on the f(tij) association is crucial for these models. This is consistent with Figure 1. However, by comparing ppo2 to ppo1, we observe insufficient evidence to suggest that relaxing the PO assumption on the xi · f(tij) interaction association improves model fit (p = 0.2677). Further, using a likelihood ratio test (not shown) on ppo1 there is insufficient evidence to suggest that the intervention is associated with the ordered outcome states over time (p = 0.2695).
TABLE 5.
VIOLET Study data analysis: Likelihood ratio tests for the po1, ppo1 and ppo2 model fits
| Model | Parameters | Log-Likelihood | p-value |
|---|---|---|---|
| po1 | 15 | −8449.51 | NA |
| ppo1 | 21 | −6185.93 | <0.0001 (vs po1) |
| ppo2 | 27 | −6182.12 | 0.2677 (vs ppo1) |
Figure 4 shows that ppo1 and ppo2 estimated the cumulative probabilities for the placebo and Vitamin D3 arms well, although upon close inspection we can see the ppo2 fit appears slightly better calibrated than ppo1. Towards the end of follow-up, ppo1 slightly overestimates log odds of being in the not alive state (k = 1) and of being in the Vent/ARDS or lower states (k ≤ 2) in the placebo arm, while it somewhat underestimates them in the Vitamin D3 arm. Further, towards the middle and end of the study, ppo2 appears to align more closely to the observed pr[Yi(tij) ≤ 3 | Xi(tij)] (right panel) than does ppo1. Overall, the added flexibility provided by ppo2 appears to improve model fit (slightly) even though it does not represent a statistically significant improvement at the two-sided 0.05 significance level.
FIGURE 4.
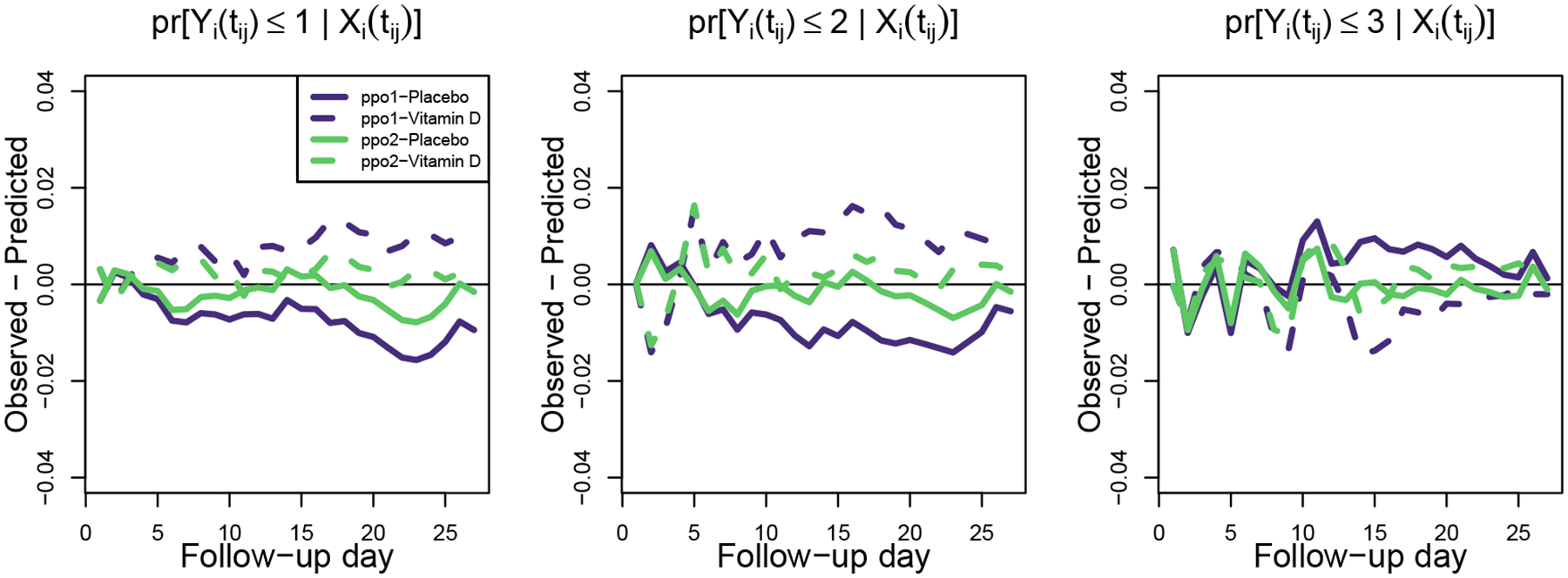
Calibrations plots for the cumulative pr[Yi(tij) ≤ k | Xi(tij)] over the 27 follow-up days. For models ppo1 and ppo2 we display the predicted minus the observed probabilities of falling at or below state k ∈ {1, 2, 3}.
The top panel of Figure 5 shows the log odds ratio (Vitamin D3 versus placebo) for each of the response dichotomizations from ppo2. As stated earlier, according to a likelihood ratio test, there is insufficient evidence to suggest that these estimates are different from one another; however, we estimated that Vitamin D3 tended to lower the odds of being in the hospital or worse state [Yi(tij) ≤ 3] across most of the follow-up period as compared to placebo, but after day 10, it increased the odds of being in the Vent/ARDS or worse states [Yi(tij) ≤ 2] and the odds of being not alive [Yi(tij) ≤ 1]. It is worth noting the difference in the precision of the three dichotomization-specific treatment effect estimators. Overall, the in-hospital or worse versus at-home dichotomization [Yi(tij) ≤ 3] was estimated with the greatest precision while the not alive versus alive [Yi(tij) ≤ 1] dichotomization was estimated with the least precision. This is caused by differences in the four outcome state prevalences over time.
FIGURE 5.
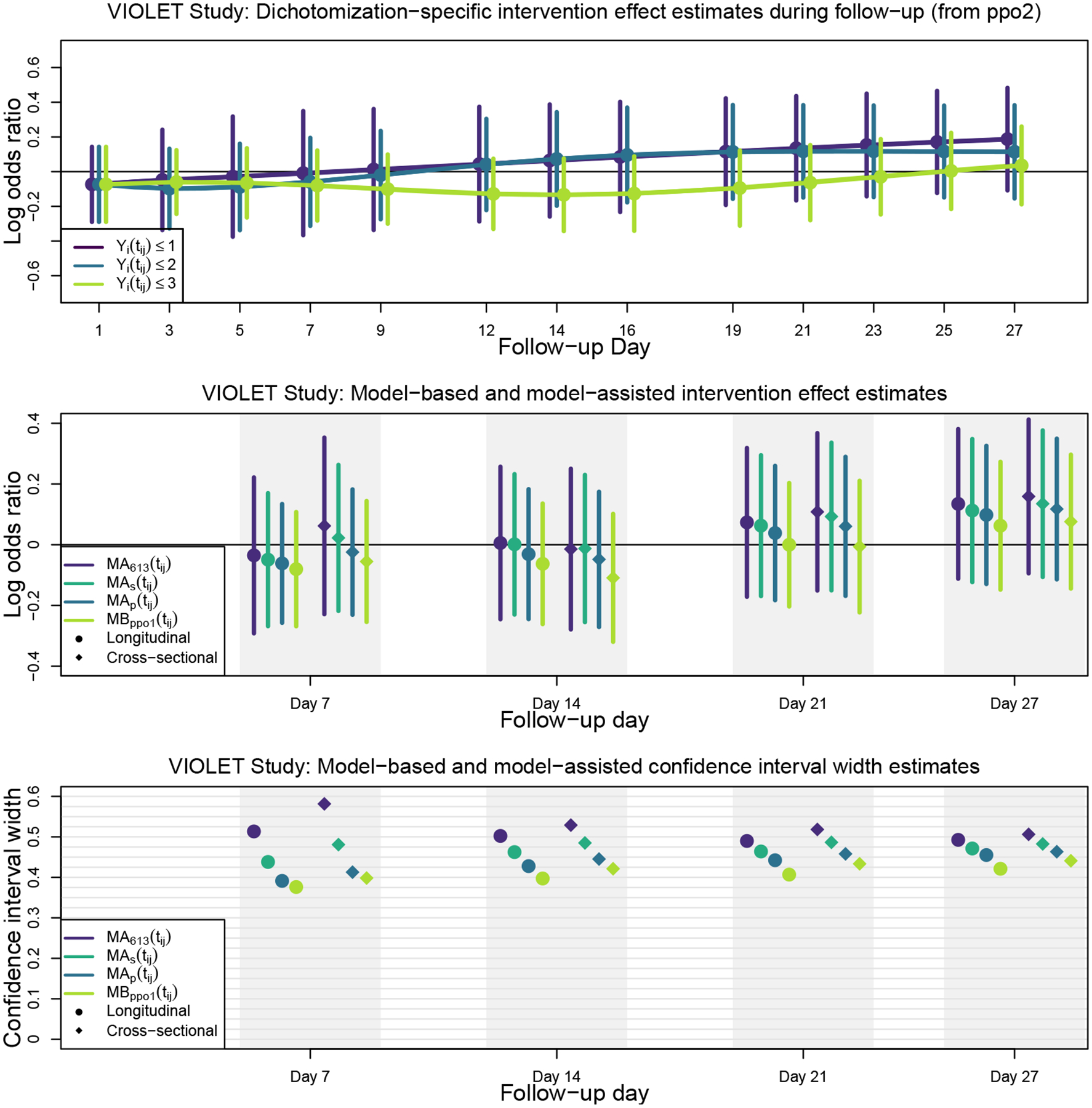
VIOLET Study results: Intervention effect estimates and confidence interval widths for model-based, model-assisted, and cross-sectional model fits
The middle panel of Figure 5 shows the estimated log odds ratios and confidence intervals for being in the lower (worse) outcome state for any of the outcome dichotomizations (Vitamin D3 versus placebo) at follow-up days 7, 14, 21, and 27. The bottom panel shows confidence interval widths. The longitudinal OMTM1 estimates are denoted with circles while corresponding cross-sectional estimates, based on conducting PO or PPO model analyses cross-sectionally at each time using the VGAM package34 in the R programming language35, are denoted with diamonds. Because the evidence suggesting non-proportional odds on the intervention effect was weak, model-based and model-assisted estimators yielded quite similar results. Similar to simulation results, the MBppo1(tij) estimator yielded the tightest confidence intervals, although the MAp(tij) was nearly as precise. Not surprisingly, the value-based weighted estimator, MA613(tij), yielded the widest confidence intervals. We also note efficiency losses when using cross-sectional estimators compared to the analogous longitudinal estimators. The estimated variances associated with cross-sectional analyses were 2% to 28% larger than they were for the corresponding longitudinal analyses, although most were in the range of 5% to 10%. Simulations shown in the Online Supplement depict scenarios where efficiency gains of longitudinal over cross-sectional analyses are more pronounced (e.g., with lower response dependence and in the presence of missing data).
7 |. DISCUSSION
We discussed model-based and model-assisted approaches to analyses of parallel-arm, longitudinal clinical trials in settings where the outcome is ordinal and at least one state is absorbing. Estimands were derived from marginal partial proportional odds (PPO) models that were made appropriately flexible to align with study goals (e.g., using splines in time). Estimation was based on ordinal, first-order marginalized transition models that capture marginal model parameters directly and are well suited to address challenges associated with absorbing outcome states. We found that when the PO assumption for the intervention parameter is correct, or even when mildly incorrect, making the PO assumption and using estimates derived from ppo1 are highly efficient. However, in realistic settings, the model-assisted estimators can be nearly as efficient as the model based-estimator when the PO assumption is correct. When the PO assumption is incorrect, model-assisted estimands may be more interpretable because the weighting scheme used to derive the weighted averages of dichotomization-specific intervention effects is explicit and can be specified by the user. Importantly, the weighting schemes can be based on study goals that either give higher weights to dichotomizations that are deemed of greater importance or that seek high estimation efficiency.
We note that one could approach this problem by fitting conditional, Markov models and then marginalizing over lagged responses to estimate marginal intervention effects25. While both marginal and conditional model approaches are reasonable, this paper seeks to estimate marginal model parameters directly. In future research, we will study the extent to which marginal intervention effects derived from conditional models agree with direct marginal model estimates over a broad range of study scenarios. In particular, it will be interesting to compare relative efficiencies and robustness under misspecification.
We believe that the modeling approaches described in this paper are broadly applicable and can be summarized to ascertain other estimands that may be of interest. A primary motivation for studying these procedures was that death was a natural outcome state for the VIOLET Study (i.e., the most severe one). However, modeling choice becomes much more nuanced when death is not a natural outcome state that clearly takes on a value at one end of the ordinal scale. For example, if one seeks to study, say an ordinal outcome scale for glucose concentration in a wearable insulin pump intervention study of participants with uncontrolled type II diabetes, then the outcome value of death does not fall naturally at one end or the other of the glucose concentration scale. That is, death could result from severe hyperglycemia or severe hypoglycemia. In such cases, it could be argued that one should view death as a competing event and then potentially examine intervention association with glucose levels conditioned on being alive.
A challenge associated with specifying the marginal CPM and response dependence models separately occurs in the presence of absorbing states. The value Δi,k[Xi(tij)] is a function that renders the first and second OMTM1 models coherent, and it must be calculated for all i, j, and k to identify the likelihood. However, if the two models are not coherent, Δi,k[Xi(tij)] cannot be calculated. As an example, if we assume that state k = 1 is absorbing, then the marginal probability of being in state 1 must never decrease with time. If, in fact, the true marginal state k = 1 probability increases very slowly, it is possible for the fitting algorithm to step to a set of parameter values that yield a decrease in the marginal state probability. In that case, the fitting procedure will fail. One must either force monotonicity in the k = 1 state probability as a function of time or one must force the fitting algorithm to take very small steps. Another challenge arises when state probabilities are low. In such circumstances, the fitting algorithm may take a step that leads to time-specific intercepts “crossing.” This, in turn, yields cumulative probabilities that appear to decrease (i.e., negative state probabilities) which also leads to the algorithm failing. For this reason, and because the procedure we described estimates (K −1)2 dependence model parameters, we are uncertain of the extent to which this fitting procedure will be able to address a large number of ordered outcome states. Finally, due to the large number of dependence model parameters being estimated, this approach may be challenged by non-stationarity of the dependence structure or a dependence structure that is modified by baseline covariates. In both cases, additional dependence model parameters are required to properly specify the model. Lee and Daniels13 discuss more parsimonious response dependence models which could be required to expand these models to other settings.
While the VIOLET Study had minimal amounts of missing follow-up data, in future work we will also seek to explore challenges associated with missing data. Even though the OMTM1 is robust to dependence model misspecification, it requires complete data, and we will need to explore the operating characteristics of the OMTM1 in the presence of absorbing states and intermittently missing data. Code used to generate and analyze data from the models described in this paper are available at https://github.com/schildjs/OMTM1/.
Supplementary Material
ACKNOWLEDGEMENTS
This research was, in part, supported by the National Institute of Health grant R01HL094786 and R01AI093234, and the National Institutes of Health (NIH) Agreement 1OT2HL156812-01. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the NIH. The authors wish to acknowledge the contributions of the Study Design and Analysis Core of the NHLBI Collaborating Network of Networks for Evaluating COVID-19 and Therapeutic Strategies (CONNECTS) Administrative Coordinating Center Science Unit, who provided valuable feedback on the manuscript and methodology, and facilitated data access. The authors thank Adit Ginde MD, Doug Hayden PhD, David Schoenfeld PhD, and Taylor Thompson MD for their assistance with this manuscript and all the PETAL Network Coordinators, Investigators, the NHLBI, and VIOLET study participants for making this work possible. This work was conducted in part using the resources of the Advanced Computing Center for Research and Education at Vanderbilt University, Nashville, TN.
Footnotes
CONFLICT OF INTEREST
None declared.
References
- 1.Ginde AA, Brower RG, Caterino JM, et al. Early High-Dose Vitamin D3 for Critically Ill, Vitamin D-Deficient Patients. N Engl J Med 2019; 381(26): 2529–2540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.McCullagh P. Regression Models for Ordinal Data. Journal of the Royal Statistical Society Series B - Methodological 1980; 42(2): 109–142. [Google Scholar]
- 3.Peterson B, Harrell F. Partial Proportional Odds Models for Ordinal Response Variables. Journal of the Royal Statistical Society Series C-Applied Statistics 1990; 39(2): 205–217. [Google Scholar]
- 4.Frison L, Pocock SJ. Repeated measures in clinical trials: analysis using mean summary statistics and its implications for design. Statistics in Medicine 1992; 11(13): 1685–1704. [DOI] [PubMed] [Google Scholar]
- 5.Yang L, Tsiatis AA. Efficiency study of estimators for a treatment effect in a pretest–posttest trial. The American Statistician 2001; 55(4): 314–321. [Google Scholar]
- 6.Heagerty P, Zeger S. Marginal regression models for clustered ordinal measurements. Journal of the American Statistical Association 1996; 91(435): 1024–1036. doi: 10.2307/2291722 [DOI] [Google Scholar]
- 7.Parsons NR, Costa ML, Achten J, Stallard N. Repeated measures proportional odds logistic regression analysis of ordinal score data in the statistical software package R. Computational Statistics & Data Analysis 2009; 53(3): 632–641. doi: 10.1016/j.csda.2008.08.004 [DOI] [Google Scholar]
- 8.Touloumis A, Agresti A, Kateri M. GEE for multinomial responses using a local odds ratios parameterization. Biometrics 2013; 69(3): 633–640. [DOI] [PubMed] [Google Scholar]
- 9.Zeger SL, Liang KY. Longitudinal data analysis for discrete and continuous outcomes. Biometrics 1986; 42(1): 121–130. [PubMed] [Google Scholar]
- 10.Lipsitz S, Laird N, Harrington D. Generalized Estimating Equations for Correlated Binary Data - Using the Odds Ratio as a Measure of Association. Biometrika 1991; 78(1): 153–160. [Google Scholar]
- 11.Carey V, Zeger S, Diggle P. Modeling Multivariate Binary Data with Alternating Logistic Regressions. Biometrika 1993; 80(3): 517–526. doi: 10.1093/biomet/80.3.517 [DOI] [Google Scholar]
- 12.Cameron AC, Gelbach JB, Miller DL. Bootstrap-based improvements for inference with clustered errors. The Review of Economics and Statistics 2008; 90(3): 414–427. [Google Scholar]
- 13.Lee K, Daniels MJ. A class of markov models for longitudinal ordinal data. Biometrics 2007; 63(4): 1060–1067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Azzalini A. Logistic regression for autocorrelated data with application to repeated measures. Biometrika 1994; 81(4): 767–775. [Google Scholar]
- 15.Heagerty P. Marginally specified logistic-normal models for longitudinal binary data. Biometrics 1999; 55(3): 688–698. doi: 10.1111/j.0006-341X.1999.00688.x [DOI] [PubMed] [Google Scholar]
- 16.Heagerty PJ. Marginalized transition models and likelihood inference for longitudinal categorical data. Biometrics 2002; 58(2): 342–351. [DOI] [PubMed] [Google Scholar]
- 17.Evans SR, Follmann D. Using Outcomes to Analyze Patients Rather than Patients to Analyze Outcomes: A Step toward Pragmatism in Benefit:risk Evaluation. Stat Biopharm Res 2016; 8(4): 386–393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hernán M, Robins J. Causal Inference: What If. Chapman & Hall/CRC. 2020. [Google Scholar]
- 19.Pepe M, Anderson G. A Cautionary Note on Inference for Marginal Regression Models with Longitudinal Data and General Correlated Response Data. Communications in Statistics-Simulation and Computation 1994; 23(4): 939–951. doi: 10.1080/03610919408813210 [DOI] [Google Scholar]
- 20.Diggle P, Diggle PJ, Heagerty P, et al. Analysis of longitudinal data. Oxford University Press. 2002. [Google Scholar]
- 21.Schildcrout JS, Heagerty PJ. Regression analysis of longitudinal binary data with time-dependent environmental covariates: bias and efficiency. Biostatistics 2005; 6(4): 633–652. [DOI] [PubMed] [Google Scholar]
- 22.Pepe MS, Heagerty P, Whitaker R. Prediction using partly conditional time-varying coefficients regression models. Biometrics 1999; 55(3): 944–950. [DOI] [PubMed] [Google Scholar]
- 23.Kurland BF, Johnson LL, Egleston BL, Diehr PH. Longitudinal Data with Follow-up Truncated by Death: Match the Analysis Method to Research Aims. Stat Sci 2009; 24(2): 211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kurland BF, Heagerty PJ. Directly parameterized regression conditioning on being alive: analysis of longitudinal data truncated by deaths. Biostatistics 2005; 6(2): 241–258. [DOI] [PubMed] [Google Scholar]
- 25.Benkeser D, Díaz I, Luedtke A, Segal J, Scharfstein D, Rosenblum M. Improving precision and power in randomized trials for COVID-19 treatments using covariate adjustment, for binary, ordinal, and time-to-event outcomes. Biometrics 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Anderson JA. Regression and ordered categorical variables. Journal of the Royal Statistical Society: Series B (Methodological) 1984; 46(1): 1–22. [Google Scholar]
- 27.Tutz G. Sequential models in categorical regression. Computational Statistics & Data Analysis 1991; 11(3): 275–295. [Google Scholar]
- 28.Agresti A. Categorical data analysis. 482. John Wiley & Sons. 2003. [Google Scholar]
- 29.Hedeker D, Berbaum M, Mermelstein R. SAS code for “Location-scale models for multilevel ordinal data: Between-and within-subjects variance modeling. Journal of Probability and Statistical Science 2006; 4: 1–20. [Google Scholar]
- 30.Capuano AW, Dawson JD. The trend odds model for ordinal data. Statistics in medicine 2013; 32(13): 2250–2261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Huber PJ. The behavior of maximum likelihood estimates under nonstandard conditions. Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Statistics 1967; 1(1): 221–233. [Google Scholar]
- 32.White H. A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity. Econometrica: journal of the Econometric Society 1980: 817–838. [Google Scholar]
- 33.Liang KY, Zeger SL. Longitudinal data analysis using generalized linear models. Biometrika 1986; 73(1): 13–22. [Google Scholar]
- 34.Yee TW. The VGAM Package for Categorical Data Analysis. Journal of Statistical Software 2010; 32(10): 1–34. [Google Scholar]
- 35.R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna, Austria: 2020. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


