Development of Force Field Parameters for the Simulation of Single- and Double-Stranded DNA Molecules and DNA–Protein Complexes

Abstract

Although molecular dynamics (MD) simulations have been used extensively to study the structural dynamics of proteins, the role of MD simulation in studies of nucleic acid based systems has been more limited. One contributing factor to this disparity is the historically lower level of accuracy of the physical models used in such simulations to describe interactions involving nucleic acids. By modifying nonbonded and torsion parameters of a force field from the Amber family of models, we recently developed force field parameters for RNA that achieve a level of accuracy comparable to that of state-of-the-art protein force fields. Here we report force field parameters for DNA, which we developed by transferring nonbonded parameters from our recently reported RNA force field and making subsequent adjustments to torsion parameters. We have also modified the backbone charges in both the RNA and DNA parameter sets to make the treatment of electrostatics compatible with our recently developed variant of the Amber protein and ion force field. We name the force field resulting from the union of these three parameter sets (the new DNA parameters, the revised RNA parameters, and the existing protein and ion parameters) DES-Amber. Extensive testing of DES-Amber indicates that it can describe the thermal stability and conformational flexibility of single- and double-stranded DNA systems with a level of accuracy comparable to or, especially for disordered systems, exceeding that of state-of-the-art nucleic acid force fields. Finally, we show that, in certain favorable cases, DES-Amber can be used for long-timescale simulations of protein–nucleic acid complexes.

Introduction

Molecular dynamics (MD) simulations have frequently been used to characterize the structural dynamics of proteins. The application of MD simulation to nucleic acid based systems, however, has received considerably less attention, and as a consequence, the energy functions and associated parameterizations (″force fields″) used in simulating nucleic acids have been subject to less development and validation than corresponding protein force fields. In recent years, however, there have been substantial improvements to both the Amber¹⁻⁴ and CHARMM⁵ family of DNA force fields, and an entirely new DNA force field based on QM data has recently been proposed to complement existing models.⁶ In the case of RNA, we recently revised the torsion and nonbonded parameters of an Amber RNA force field⁷ with an emphasis on obtaining a force field that could, with an accuracy comparable to that of state-of-the-art protein force fields, describe both single- and double-stranded RNA structures.

Here, we describe a revision of our previously published force field parameters for RNA aimed at achieving for DNA a similar level of accuracy as was obtained for simulations of single- and double-stranded RNA oligomers.⁷ As RNA and DNA are chemically very similar, we postulated that previously adjusted parameters for RNA should be largely transferable to DNA with a similar effect. Indeed, we found that after transferring the modified RNA nonbonded parameters to the DNA force field, only small adjustments to a few torsion parameters were required to make the force field suitable for DNA simulations. We also developed new parameters for the magnesium ion, a cofactor shown to often be critical for the stability of tertiary structures of nucleic acids, and for structural zinc ions, which are often found in protein motifs that bind to nucleic acids. The revised force field parameters were tested by comparing results from simulations of single-stranded (ssDNA) and double-stranded DNA (dsDNA) molecules (known to form a number of different secondary structures) to experiments. We found that the structure, dynamics, and thermodynamics of these systems were described with a level of accuracy comparable to that of state-of-the-art nucleic acid force fields. In particular, we found that this force field gives an excellent description of ssDNA structures while still providing a reasonably accurate description of dsDNA systems, with the notable exception that DES-Amber underestimates the relative stability of the BI/BII conformations.

A second, equally important aim of this work was to make our nucleic acid force field parameters compatible with our latest protein force field parameterization, which provides state-of-the-art accuracy.⁸ In this protein force field, the effect of polarization on the dielectric environment is modeled by an empirical scaling and redistribution of the net charges for ionic residues. The same approach has been followed here to develop the DNA and RNA electrostatic parameters so that these force fields can be used in combination with the protein force field. We name the force field that includes all of these parameters (the new DNA parameters, the revised RNA parameters, and the existing protein and ion parameters) DES-Amber. (We note that, in our previous work,⁸ “DES-Amber” referred to a force field consisting solely of the protein parameters.) Subsequent testing of DES-Amber in simulations of protein–DNA and protein–RNA complexes gave mixed results, yielding an accurate reproduction of the structures of some, but not all, of the complexes investigated.

Similar mixed results had been previously obtained for simulations of protein–protein complexes using the DES-Amber protein parameters.⁸ A reparameterization of the phosphate backbone nonbonded interactions was attempted; this parameterization, described in detail in the Supporting Information (SI), involved the optimization of the phosphate–water interaction by modifications of the Lennard–Jones (LJ) pair potential followed by torsion refitting based on NMR data from short ssDNA fragments. The distribution of charges on the O2′ hydroxyl group and the aromatic carbon–water interactions were also optimized to reproduce QM data and the osmotic coefficient of purine in water. The resulting force field, named DES-Amber 3.20 (from the value of the LJ σ parameter of the interaction between water and the phosphate oxygen), greatly improved the description of protein–nucleic acid complexes, though we could not achieve a consistent improvement across all systems. Although further parameter optimization may result in more consistent improvement, the simple, nonpolarizable functional form used to describe the nonbonded interactions may limit the ability of the force field to simultaneously describe with a high level of accuracy isolated proteins and nucleic acids, as well as protein–protein and protein–nucleic acid complexes, and it is possible that more sophisticated, polarizable force fields (which are outside the intended scope of this work) may be required to address this shortcoming.

Methods

Ab Initio Calculations

The previously introduced DES-Amber force field for RNA⁷ is a modification of the Amber nucleic acid force field.^1,9 In this earlier work, nucleobase charges and LJ parameters were developed based on QM calculations of nucleobase stacking and pairing, and QM torsion scans were used to develop new torsion parameters for the backbone and glycosidic torsions. For the development of a DNA force field, nucleobase nonbonded parameters are expected to be the same as in RNA, but the χ (O4′-C1′-N9-C4 in purines and O4′-C1′-N1-C6 in pyrimidines) torsion and the ζ (C3′-O3′-P′-O5′) torsion are expected to be affected to some extent by the absence of the OH2′ group. New torsion potentials were thus determined following our previous work on RNA.⁷ In vacuo potential energy surface (PES) scans of the χ torsion were performed for the four ribonucleosides. Torsion scans for the ζ torsion were performed on a model molecule mimicking the DNA backbone. QM energies were calculated at the MP2 level of theory, using local and density-fitting approximations¹⁰ with an augmented double-zeta basis set (aug-cc-pVDZ) and the COSMO model¹¹ to account for solvation effects, using the MOLPRO program.¹² The torsions were scanned between −180 and 180° in 10° increments. Each structure was relaxed at the MP2 level with a number of other dihedral angles constrained to prevent the formation of intramolecular hydrogen bonds, thus ensuring the smoothness of the potential energy surfaces. Only one-dimensional scans were performed, and the coupling between dihedral angles¹³ was not explicitly considered. The total number of terms, N, in the cosine expansion was four for the χ torsion and three for the ζ torsions. The new k_n and ϕ_n values are summarized in Table 1.

Table 1. Revised Torsion Parameters Obtained from a Fit to Torsion Energy Profiles Calculated at the MP2 Level of Theory^a.

angle	ϕ1	k1	ϕ2	k2	ϕ3	k3	ϕ4	k4
χA	–7.75	–0.5250	–4.44	1.9578	–35.39	–0.9569	–21.36	0.2058
χC	138.56	–1.0002	–31.94	2.8162	34.57	–1.1862	–53.36	0.7164
χT	–7.14	–0.1027	–2.45	2.2160	–13.96	–0.9599	–123.92	–0.2482
χG	6.19	–0.5093	–0.54	1.7381	–29.00	–0.8156	–2.69	0.2408
ζ	–154.60	–0.2379	–4.09	1.6200	–51.37	0.4252

^aTorsion angle potentials, V_ϕ, are expressed as 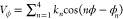. The χ torsion angle parameters were made nucleotide-specific (subscripts A, C, T, and G), while the same set of ζ torsion angle parameters was used for all nucleotides. Units are degrees for angles and kcal mol^–1 for force constants.

Assignment of Charges to the Terminal Residues

In the Amber force field, the −1.0 charge of the 3′-terminal nucleobase, which is often phosphorylated, is split between the 3′-terminal residue (−0.6921) and the 5′-terminal residue (−0.3079). This charge distribution is the result of where the residue boundaries are defined in the Amber force field and does not follow the common approach of assigning integer charges to each residue in most fixed-charge force fields for biomolecules. We maintained it in our reparameterization for consistency with the original Amber force field. We also tested a force field (which we term DES-Amber T) in which the charge of the terminal groups was adjusted to localize all of the negative charge on the 3′-terminal nucleotide. For this force field, we performed simulations of short ssDNA fragments of two to six nucleotides (see the subsection Simulated Tempering Simulations of Short ssDNA Molecules below). Although we found some differences in the conformational ensembles sampled by simulations performed using these different charge distributions, both matched the experimental J-couplings well (RMSD <1 Hz, Table S1), suggesting that both charge distributions are reasonable choices.

MD Simulations of dT₄₀

We performed MD simulations of dT₄₀ molecules starting from a structure in which all residues were in the B-DNA conformation. This structure was solvated in cubic 130³ ų water boxes containing 0.025, 0.1, 0.4, or 1.0 M NaCl. At each NaCl concentration, 100 μs of simulation at 300 K and 1 atm in the NPT ensemble was performed using the DES-Amber and the DES-Amber SF1.0 force fields. For comparison, simulations of 100 μs were also run using the Amber-bsc1 force field,¹ and simulations of 40 μs were run using the CHARMM36 force field.⁵ The persistence length L_P was calculated from 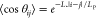, where, for a polymer formed by a chain of vectors of the same length L, θ_ij is the angle between two unit vectors i and j and |i–j| is their distance in sequence. The end-to-end distance was measured and FRET intensities were calculated assuming a Förster radius of 60 Å.¹⁴

Simulated Tempering Simulations of Short ssDNA Molecules

We performed simulated tempering simulations of 18 ssDNA molecules ranging from two to six nucleotides in length (Table S1). Each system was generated using Maestro¹⁵ and solvated in a cubic 50³ ų box containing 0.1 M NaCl. Simulations were performed using the Amber-bsc1 force field¹ and the TIP3P water model,¹⁶ the DES-Amber force field, the DES-Amber SF1.0 force field, and the DES-Amber T force field. The TIP4P-D water model¹⁷ was used in all DES-Amber simulations. The systems were first equilibrated at 300 K for 100 ps using the Desmond software,¹⁸ and production simulated tempering simulations¹⁹ of 20 μs were performed in the NPT ensemble²⁰⁻²² with 100 rungs spanning the 273–410 K range using Anton.²³ NMR J-couplings were calculated for the sugar ring protons using the Karplus relation as parameterized by Haasnoot^24,25 and compared to the J-couplings measured experimentally.²⁶⁻³⁵

Simulated Tempering Simulations of the d(GCGAAGC) Polynucleotide

We performed simulated tempering simulations of the d(GCGAAGC) polynucleotide that experimentally folds into a hairpin structure. We solvated the experimentally determined structure (PDB entry 1kr8)³⁶ in a cubic 50³ ų box of TIP4P-D water containing 1.0 M NaCl. Simulations were performed using the DES-Amber force field and the DES-Amber SF1.0 force field. The systems were first equilibrated at 300 K for 100 ps using the Desmond software, and production simulated tempering simulations of 170 μs were performed in the NPT ensemble with 100 rungs spanning the 278–410 K range using Anton. The free energy of the hairpin at 310 K was calculated as 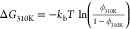, where ϕ_310K is the fraction of frames where the hairpin was folded at 310 K, computed using a dual-cutoff^37,38 of 1 and 6 Å on the heavy-atom RMSD from the experimental structure, averaged over 50 ns.

Simulated Tempering Simulations of DNA Duplex Formation

We performed simulated tempering simulations of seven complementary DNA duplexes of sequence d(CACAG), d(CGCGG), d(CGTACG), d(GAGTGAG), d(GCGC), d(GGATCC), and d(TCATGA). The double-stranded models of the seven DNA duplexes were generated with the program COOT.³⁹ Each duplex was solvated in a cubic 50³ ų box containing 0.1 M salt (Table S2). Simulations were performed using the Amber-bsc1 force field with the TIP3P water model, the DES-Amber force field, and the DES-Amber SF1.0 force field. The TIP4P-D water model was used in all DES-Amber simulations. The systems were first equilibrated at 300 K for 100 ps using the Desmond software, and production simulated tempering simulations of 500 μs were performed in the NPT ensemble with 100 rungs spanning the 278–410 K range using Anton. The fraction of frames containing B-DNA at each temperature (ϕ) was computed using a dual cutoff of 2 and 10 Å on the backbone RMSD from the ideal B-DNA conformation, averaged over 50 ns. The free energy of the B-DNA duplex at 310 K was calculated as 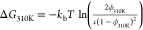, where c is the DNA concentration in the simulation box. The ″experimental″ free energy was estimated using the nearest-neighbor model of SantaLucia⁴⁰ with [Na⁺] = 0.1 M.

MD Simulations of DNA Oligomers

We performed simulations of 17 different sequences of lengths ranging from 10 to 17 amino acids (Table S4). The starting structure of each simulation was taken from the experimental structures deposited in the PDB (Table S4).⁴¹⁻⁵⁷ Three simulations were performed for the Drew–Dickerson dodecamer (DDD) starting from three different experimental structures. These simulations gave indistinguishable results, and only one is discussed in detail. Each oligomer was solvated by a 0.1 M NaCl water solution in a cubic box with a minimum distance between periodic images of 30 Å. For each system, 50 μs of MD simulation in the NPT ensemble at 300 K was performed. Five microseconds of MD simulation was also performed using the Amber-OL15 force field⁴ using theTIP3P¹⁶ and the OPC⁵⁸ water models and the Joung–Cheatham ion parameters.⁵⁹ The base-step, base-pair, and nucleobase structural parameters of the oligomers were calculated for 5000 evenly spaced frames of each simulation using the DSSR software.⁶⁰

MD Simulations of Noncanonical DNA Structures

We performed simulations of Z-DNA, two CEB2 and telomeric G-quadruplexes, and one DNA trimer. The initial structures were taken from PDB entries 4ocb,⁶¹2lpw,⁶²1jrn,⁶³ and 1bwg.⁶⁴ Five independent simulations of Z-DNA at different salt concentrations were performed with the system solvated in 0.1, 0.5, 0.75, 1.0, or 1.5 M KCl in a 70³ ų cubic box. The quadruplexes were solvated in 0.1 M KCl in a 60³ ų cubic box. The trimer was solvated in 0.15 M KCl in a 80³ ų cubic box. To equilibrate the ion distribution and allow K⁺ ions to migrate between the nucleobases, the telomeric G-quadruplex was equilibrated for 1 μs using position restraints on the nucleic acid heavy atoms with a force constant of 0.1 kcal mol^–1 Å^–1; CEB2 was equilibrated for 5 μs using position restraints on the backbone atoms with a force constant of 0.2 kcal mol^–1 Å^–1. Production runs of 50 μs (with no position restraints) were then performed for each system.

MD Simulations of Protein–Nucleic Acid Systems

We performed simulations of six protein–RNA and six protein–DNA complexes. The starting structure for each simulation was the experimental NMR or X-ray structure as found in the PDB: 2dgc,⁶⁵3jxc,⁶⁶3zhm,⁶⁷4mhg,⁶⁸1tro,⁶⁹3bdn,⁷⁰2az0,⁷¹4qoz,⁷²1urn,⁷³4qil,⁷⁴5dea,⁷⁵ and 3k5y.⁷⁶ Protein–nucleic acid complexes were solvated in a 0.1 M NaCl water solution in a cubic box with a minimum distance between periodic images of 30 Å. Production runs of 50 μs were performed for each system.

Results

Force Field Parameterization

Development of the DES-Amber Force Field Parameters for DNA

As an initial step, we incorporated into the Amber-bsc1 DNA force field the revised nucleobase LJ and electrostatic nonbonded parameters that were derived previously for RNA.⁷ For thymine, which is typically not found in RNA—as it is replaced by uracil in most cases—the Amber charges were used.

We developed two force field parameter sets: one (which we name DES-Amber) with charge scaling consistent with the previously reported DES-Amber protein and ion force field parameters and a second (which we name DES-Amber SF1.0) with no charge scaling, consistent with the previously reported DES-Amber SF1.0 protein and ion force field parameters.⁸ Our previously reported RNA parameter set⁷ did not include charge scaling and is thus part of the DES-Amber SF1.0 force field; the revised RNA parameters reported in this work, with charge scaling applied to ionic residues, are part of the DES-Amber force field. Each force field (DES-Amber and DES-Amber SF1.0) thus contains parameters for DNA, RNA, proteins, and ions. Both DES-Amber and DES-Amber SF1.0 are based on procedures similar to those used when developing the DES-Amber protein force field,⁸ with the only difference between the two parameter sets being the charge of the ionic residues, which are scaled by 0.9 in the case of DES-Amber and 1.0 (i.e., no rescaling) in the case of DES-Amber SF1.0.

Previous work has shown that glycosidic torsion parameters should not be shared between DNA and RNA molecules.⁹ We thus focused the torsion optimization on the χ (OS-CT-N-C) and ζ (CT-OS-P-OS) angles; all other torsion parameters and bonded terms were kept the same as the RNA parameters in DES-Amber SF1.0 derived previously.⁸ The torsion parameters describing the nucleotide-specific χ angles were obtained from a fit to the torsion QM energy profiles calculated at the MP2 level using MolPro.^12,77 This level of theory has been found to accurately describe torsion angles in nucleobases,⁹ and we found it to be sufficient to achieve a good level of accuracy for the parameterization of χ angles in RNA.⁷ Following previous work, single nucleosides in both C3′-endo and C2′-endo conformations were used as model compounds in the generation of χ-related torsion energies.⁹ Restraints were applied to the sugar hydroxyl group torsions to prevent the formation of intramolecular hydrogen bonds between the sugar and the nucleobase during geometry optimization. For the ζ angle, a deoxyribose N-methyl phosphate molecule was used as a model compound in the generation of torsion energies. The revised torsion parameters are reported in Table 1.

Parameterization of the Magnesium Ion

Magnesium ions are often very important for the stability of the tertiary structure of nucleic acids.^78,79 Previous studies have highlighted that, although the description of the hydrated Mg²⁺ ion appears to be satisfactory,⁸⁰ the original parameterizations for the Mg²⁺ ions in Amber⁸¹ and CHARMM are suboptimal.⁸² In both of these ion parameterizations, the ionic radius of the ion is too small, leading to the overbinding of Mg²⁺ and slow exchange of the water shell. These deficiencies could result in simulation inaccuracies, especially in cases where the process of ion binding to the phosphate backbone is important. Subsequent studies have highlighted the importance of developing water-specific ion parameters,⁵⁹ in particular for divalent ions.^83,84 We thus revised the nonbonded parameters of the Mg²⁺ ions with the aim of making them compatible with the TIP4P-D water model¹⁷ and the DES-Amber force field. We focused our parameterization on trying to achieve a balance between the affinity of the Mg²⁺ ion for water and for the negatively charged groups on proteins and nucleic acids (phosphates and carboxylates) while keeping the ionic radius close to the values estimated experimentally. Although we were able to achieve a reasonable compromise between these competing objectives for the scaled-charge version of DES-Amber, we were unable to obtain a good fit for DES-Amber SF1.0, so in this force field, the original Amber parameters⁸¹ were retained.

In our optimization of parameters for Mg²⁺, we used Mg²⁺ binding to tRNA_Phe as our benchmark system. This RNA molecule folds into a complex T-shaped structure stabilized by multiple Mg²⁺ ions.⁸⁵ In two sites, Mg²⁺ ions directly interact with the nucleotides (bridging the phosphate groups of two nucleotides), and in an additional three sites, the ions are completely solvated and only interact indirectly with the phosphate moieties through the hydration shell.^86,87 We expect that the ability to recapitulate both binding modes in a single simulation would provide an indication that the force field parameters achieve a reasonable balance between the affinity for water and the affinity for biomolecules. We were unable, however, to achieve this balance using standard combination rules for the LJ potential. We thus decided to first set pair-specific LJ interaction parameters between Mg²⁺ and water to achieve an ionic radius consistent with the experimentally determined first peak of the radial distribution function of water and Mg²⁺ and then scan for a suitable set of atomic LJ parameters for the Mg²⁺ ion that would allow us to optimally describe the different ion-interaction sites in tRNA_Phe.

Following previous work,^82,88 the LJ parameters for the Mg–O_wat interaction were first determined by performing simulations of Mg²⁺ in water, with σ parameters ranging from 2.9435 to 3.097 Å and ε ranging from 0.015 to 0.045 kcal mol^–1, ultimately choosing the parameters ε = 0.025914 kcal mol^–1 and σ = 3.004 Å, as these values best reproduced the experimental Mg–O_wat distance of 2.07–2.11 Å^89,90 and the water exchange rate of 6.7 × 10⁵ s^–1.⁹¹ Subsequently, simulations of 50–150 μs were performed starting from a tRNA_Phe structure (PDB entry 1ehz)⁸⁷ in which the six magnesium ions identified in the X-ray structure were removed and a total of 11 magnesium ions were added to the water solution together with 0.15 M KCl. Position restraints of 0.3 kcal mol^–1 Å^–1 were applied to the nucleic acid backbone to prevent the collapse of the structure when no structural magnesium ions were bound. During the simulations, the occupancy of the sites where Mg²⁺ ions were observed in the X-ray structure and the coordination sphere of the ions were monitored. We gradually increased the value of the Mg²⁺ σ from 2.77 Å, and for each increase, we tested values of the Mg²⁺ ε ranging from 0.009 to 0.002 kcal mol^–1; we found, using LJ parameters for Mg²⁺ (for all interactions except with water) of ε = 0.003000 kcal mol^–1 and σ = 3.075 Å, that after 100 μs of MD simulation starting from a tRNA_Phe structure with no Mg²⁺ ions bound, five of the six sites were occupied by Mg²⁺ ions in the correct coordination pattern (Figure 1A,B). This suggests that this set of force field parameters results in a reasonable affinity for the phosphate backbone. In the case of the sixth site, a neighboring site was occupied instead. Finally, we verified that, following equilibration of the position of the Mg2⁺ ions, the tRNA structure was also stable in the absence of position restraints (Figure S12).

Figure 1.

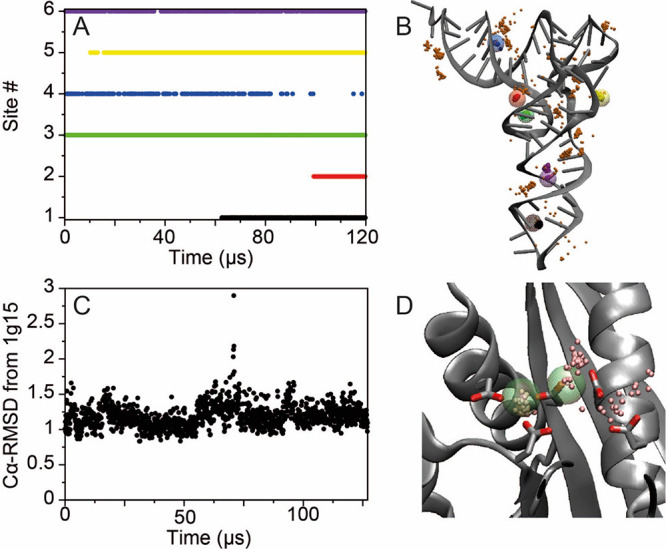
Binding of Mg²⁺ to tRNA and RNaseH. (A) Occupancy of the six Mg²⁺ sites in tRNA as a function of simulation time. After 120 μs of simulation, five of the binding sites observed experimentally⁸⁷ were occupied. (B) Mg²⁺ ion positions between 100 and 120 μs of simulation; 25 snapshots of the positions of the Mg²⁺ ions occupying the six binding sites are reported as small solid pink spheres. The positions of the crystallographic Mg²⁺ ions are highlighted as large transparent multicolored spheres. (C) Cα-RMSD in Å from the X-ray structure (PDB entry 1g15)⁹² in a 127 μs simulation of RNaseH started from the apo enzyme. (D) Snapshots of the positions of the Mg²⁺ ions from the last 20 μs of simulation (small pink spheres). The positions of the crystallographic Mn²⁺ ions are reported as large green transparent spheres.

As an additional test, we performed a simulation of the Escherichia coli ribonuclease H (RNaseH). The active site of this protein contains four negatively charged residues (Asp10, Glu48, Asp70, and Asp134) and one Mg²⁺ ion.⁹² At high Mg²⁺ concentration, binding of a second Mg2⁺ ion inactivates the enzyme. We performed a simulation starting from the apo crystal structure (PDB entry 2rn2),⁹³ in which Mg²⁺ ions are not present, in a 0.1 M MgCl and 0.1 M NaCl water solution. Position restraints were not necessary in this case, as Mg²⁺ is not required for the structural stability of the RNaseH protein. Indeed, the global protein structure was remarkably stable during the 127 μs of simulation, as indicated by the average Cα root-mean-square deviation (RMSD) of 1.2 Å with respect to the holo structure (PDB entry 1g15)⁹² (Figure 1B). After approximately 50 μs of simulation, a Mg²⁺ ion occupied one of the binding sites occupied by a divalent ion in the Mn²⁺-bound X-ray structure, and at approximately 100 μs of simulation, a second ion bound to the active site (Figure 1D). Both ions remained bound for the rest of the simulation, with the second ion being more loosely coordinated (Figure 1C), an observation that may be consistent with its lower experimentally determined affinity.⁹²

In our simulation setup for the RNaseH system, there were 18 Mg²⁺ ions in solution and 20 negatively charged residues in the protein. During the course of the simulation, Mg²⁺ ions transiently interacted with other protein residues, but despite the large number of possible interactions, only two additional persistent interactions were observed (with Glu6 and Glu154). The significance of these interactions is unclear, as the binding–unbinding kinetics are slow with respect to the timescale of the simulation, but the low number of alternative persistent interactions observed suggests that this set of Mg²⁺ parameters does not lead to strong overbinding of the magnesium ions to the negatively charged protein residues.

Single-Stranded DNA Tests

Solution Conformation of Long Single-Stranded DNA Molecules

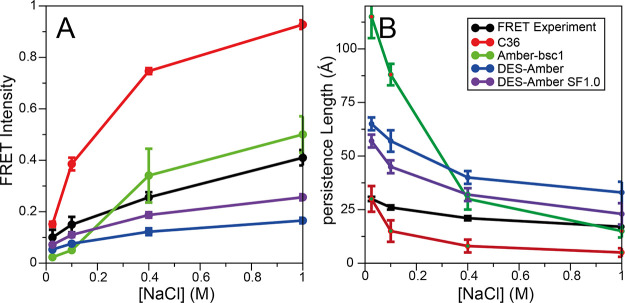
In testing DES-Amber, our first goal was to verify that the force field is capable of reproducing the conformational properties of long, disordered single-stranded nucleic acids. Previously, we have observed that simulations of a long, disordered RNA molecule (rU40) performed with the Amber and, to a lesser extent, the CHARMM force fields resulted in highly compact conformations, at odds with experimental observations, and found that this issue was resolved in the DES-Amber SF1.0 force field.⁷ For this work, we used a 40-residue poly-thymine (dT₄₀), as our test system. Although this molecule is not of particular biological significance, it is known to be mostly disordered in solution^94,95 and thus may be particularly sensitive to force field errors. With both DES-Amber and DES-Amber SF1.0, we performed 100 μs of simulation at 300 K in 0.025, 0.1, 0.4, and 1.0 M NaCl solutions; for comparison, we also performed simulations with the Amber-bsc1¹ and CHARMM36⁵ force fields. These two force fields were chosen because they are generally believed to represent the state of the art for the Amber and CHARMM family of force fields.^5,96 As a first step, for each simulation, we compared the persistence length (L_p) and the FRET intensities calculated assuming a Förster radius of 56.4 Å^14,94 (Figure 2A,B) to the reported experimental values.

Figure 2.

Comparison of calculated and experimental (A) FRET intensities and (B) persistence lengths for dT₄₀ as function of NaCl concentration for simulations run with CHARMM36 (C36, red), Amber-bsc1 (green), DES-Amber (blue), and DES-Amber SF1.0 (purple). Experimentally measured FRET intensities and persistence lengths⁹⁴ are reported in black.

At low salt concentrations, simulations with both DES-Amber and DES-Amber SF1.0 resulted in relatively expanded conformational ensembles that are generally consistent with the FRET intensity values measured experimentally at low salt concentrations,¹⁴ although the persistence length appears to be overestimated due to the prevalence of relatively rigid B-like structures. This effect was even more pronounced in the Amber-bsc1 simulations, where the conformational ensemble was dominated by the presence of a long B-like structure with an end-to-end distance of >120 Å and a persistence length of 85 Å. This finding is at odds with experimental observations indicating that dT₄₀ should be somewhat disordered, with an end-to-end distance of ∼65 Å⁹⁴ and a persistence length of 30 Å.⁹⁴ This discrepancy may be the result of a slight overfitting of torsion parameters to helical structures.

The FRET intensity and persistence length calculated from the CHARMM36 simulations were in excellent agreement with experiment at the lowest salt concentration investigated here (0.025 M, Figure 2), but at physiological salt concentrations, the simulations resulted in FRET intensities that are much higher than the experimental values due to the strong tendency of the CHARMM36 force field to collapse into molten globule structures. In simulations at high salt concentration, the extended structures observed in DES-Amber, DES-Amber SF1.0, and Amber-bsc1 had a greater tendency to collapse, resulting in a smaller persistence length and higher FRET intensities, in fair agreement with experiment. In the case of Amber-bsc1, the collapsed species in simulation were characterized by metastable hairpin structures (as indicated by the large number of base pairs that are transiently formed, Figure S1). The significance of this finding is unclear, as FRET and SAXS data suggest that poly-dT should be largely disordered in solution,^14,94,95,97 but an atomic-level structural characterization of this system using experimental approaches is difficult.⁹⁷

Overall, these results suggest that the dimensions and flexibility of the disordered state, a quantity that can be strongly affected by force field artifacts and is difficult to predict in simulation,⁷ are recapitulated reasonably well by both DES-Amber force fields. It should be noted that the DES-Amber force fields appear to underestimate the level of compaction that occurs at high salt concentration (Figure 2), which results in disordered ensembles and persistence lengths that are slightly larger than the experimental estimates, possibly due to some degree of overstabilization of B-like structures.

Solution Conformation of Short Single-Stranded DNA Molecules

To test the description of local conformational fluctuations in short ssDNA, we performed simulated tempering simulations of 18 ssDNA molecules composed of two to six nucleotides (Table S1). Each system was subjected to 20 μs of simulation using DES-Amber and DES-Amber SF1.0, and we compared the resulting ³J-couplings for the sugar ring protons, calculated using the Haasnoot Karplus equation,^24,25 to a dataset of 644 ³J-couplings measured using NMR spectroscopy (Figure 3).²⁶⁻³⁵ Using both revised force fields, most of the systems investigated had mean squared errors <1 Hz², indicating good agreement between the calculated and experimental ³J-couplings (for comparison, the average root-mean-square error of Amber-bsc1 across all systems is 1.70 Hz; Table S1). The largest deviations were observed in the H1′–H2′ ³J-coupling of the first nucleobase; the calculated coupling for this pair was often larger than the experimental value, suggesting that, in simulation, the sugar ring slightly overpopulates the S conformation.^25,26 These deviations, however, are generally not much larger than the expected accuracy of the Haasnoot parameterization of the Karplus relation, and to avoid the risk of overfitting, we refrained from performing additional tuning of the force field parameters based on these data.

Figure 3.

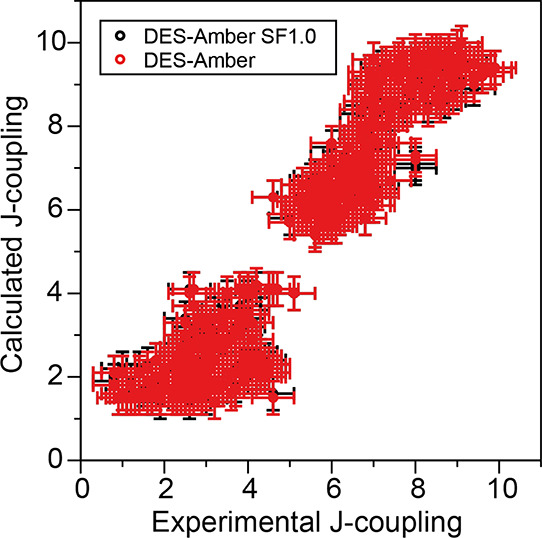
Comparison of 644 calculated and experimental J-couplings for the deoxyribose protons in 18 short ssDNA molecules, ranging from two to six nucleotides in length, in simulations using the DES-Amber (red) and DES-Amber SF1.0 (black) force fields.

Double-Stranded DNA Tests

Structure and Stability of a DNA Hairpin

Having established that DES-Amber provides a reasonable description of disordered single-stranded DNA molecules, our next goal was to test whether the force field could describe molecules that fold into a well-determined structure, such as a DNA hairpin. We performed 170 μs of simulated tempering simulations of the d(GCGAAGC) polynucleotide using DES-Amber and DES-Amber SF1.0. This sequence has been found experimentally to fold into a hairpin in solution (PDB entry 1kr8).³⁶ On the μs timescale in our simulations, the polynucleotide folded into structures with heavy-atom RMSDs of <1 Å from the experimentally determined structure (Figure 4), suggesting a folding rate roughly 2 orders of magnitude faster than that of RNA tetraloops.⁷ Similarly to what we observed for a number of RNA tetraloops, the hairpin was less stable than what is observed experimentally (the calculated ΔG_fold at 310 K was 1.3 and 1.5 kcal mol^–1 for DES-Amber and DES-Amber SF1.0, respectively, compared to the experimentally determined⁹⁸ ΔG_fold of −3.2 kcal mol^–1). This discrepancy may be the result of residual inaccuracy in the description of the nonbonded interactions.

Figure 4.

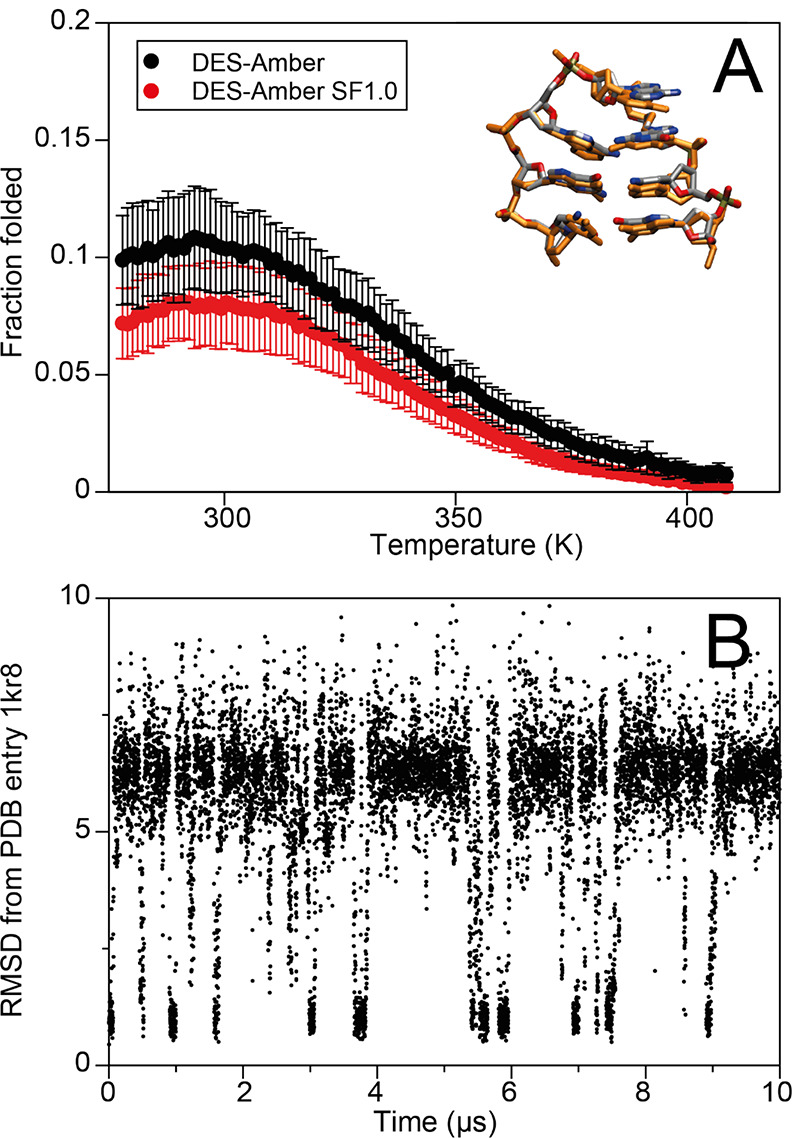
(A) Folding free energy as a function of temperature for the DNA hairpin d(GCGAAGC) with the DES-Amber (red) and DES-Amber SF1.0 (black) force fields. The structure obtained by averaging the frames between 9.2 and 9.5 μs of simulation time is shown superimposed with the experimental structure. (B) Backbone RMSD trace (Å) for the first 10 μs of the simulated tempering simulation of the d(GCGAAGC) DNA sequence performed with the DES-Amber force field.

Thermodynamic Stability of DNA Duplexes

B-DNA, as the most common double helix found in nature, is arguably the most important structure that is formed by DNA molecules. As a test of the ability of the force field to correctly identify double-stranded B-DNA as the thermodynamically most stable structure, and to recapitulate the observed experimental dependence of stability on the DNA sequence, we performed 500 μs simulated tempering simulations of seven pairs of DNA sequences with lengths ranging between four and seven nucleotides. We found that the correct B-DNA structure formed reversibly (Figure 5A and Figures S2–S4) in simulations performed with all three force fields investigated (DES-Amber, DES-Amber SF1.0, and Amber-bsc1). The B-DNA structure was also correctly identified as the thermodynamically most stable conformation at low temperatures (Figure 5B,C).

Figure 5.

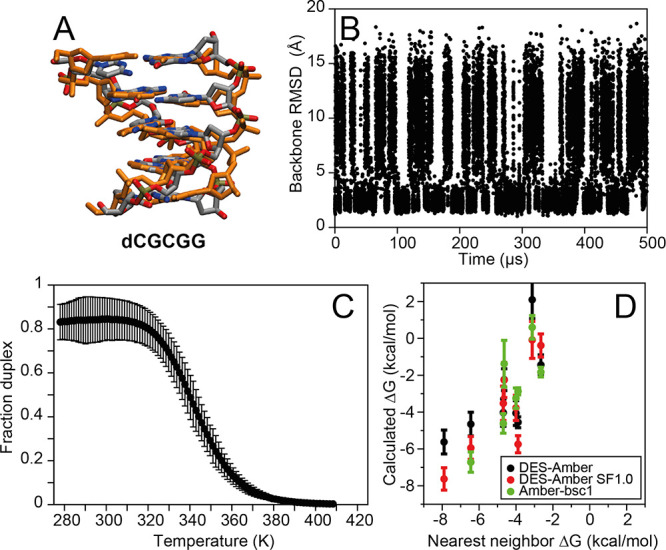
Simulated tempering simulations of short B-DNA fragments. (A) Snapshot from the d(CGCGG) simulation superimposed on a canonical B-DNA reference structure. (B) Backbone RMSD from a canonical B-DNA structure in the simulation of d(CGCGG) performed with DES-Amber. (C) Fraction of B-DNA duplex frames as a function of temperature. (D) Calculated melting free energy at 300 K for short B-DNA duplexes from simulations performed with DES-Amber, DES-Amber SF1.0, and Amber-bsc1 compared to the melting free energy predicted using a nearest-neighbor model.

Some notable differences were observed between Amber-bsc1 and the DES-Amber force fields in the non-B-DNA conformational ensembles. Whereas in DES-Amber and DES-Amber SF1.0 the two DNA oligomers were noninteracting 60–70% of the time when B-DNA was not formed, in Amber-bsc1, the two strands rarely fully separated and, when B-DNA was not formed, were bound in molten globule states with noncanonical structure 90–97% of the time (Table S3). Such states have not been reported in the literature and are probably an artifact of the tendency of this force field to form disordered structures that are overcollapsed.

There was generally a reasonable correlation between the calculated relative stability and the stability predicted by a nearest-neighbor model⁴⁰ (Figure 5D and Table S2), although the absolute stability at 310 K was systematically underestimated (by approximately 0.2 kcal mol^–1 per nucleobase for DES-Amber and 0.15 kcal mol^–1 per nucleobase for DES-Amber SF1.0 and Amber-bsc1). The origin of this discrepancy is unclear. It would be possible, in principle, to achieve much better agreement with experiment for these systems through a suitable modification of torsion parameters, as is often performed in the optimization of protein force fields.^37,99,100 We decided, however, not to pursue this route, as the simulations of short ssDNA molecules indicate that there is already a strong tendency to populate B-DNA conformations, suggesting that errors in the torsion parameters may not be responsible for the behavior observed here.

Solution Structure of Long DNA Duplexes

It is important that a DNA force field have the ability to reproduce the subtle deviations from the canonical B-DNA conformation that are induced by changes to local sequence, as these differences can be relevant for function and sequence recognition. Following previous work on DNA force field development,¹ we have performed simulations of 19 dsDNA molecules containing 10 to 17 nucleobase pairs using the DES-Amber and DES-Amber SF1.0 force fields. Each simulation was run in the NPT ensemble at 300 K for 50 μs, and the structure observed in simulation was compared to the corresponding experimentally determined structure. For all but one of the systems investigated, the DNA structure remained close to the experimental structure (Table S4), although in some cases fraying of the termini was observed. The RMSDs were comparable to those observed for Amber-bsc1 (e.g., average backbone RMSD was 2.47 Å for DES-Amber and 2.49 Å for Amber-bsc1), a force field that has been shown to describe these systems with extremely high accuracy.^1,101

A somewhat larger structural deviation from the X-ray structure was observed for d(CTTTTAAAAG) using all force fields, in particular when using DES-Amber SF1.0; this is possibly because this sequence was crystallized with seven Ca²⁺ ions bound, and these ions were not present in the MD simulation. In simulations of d(GGATATATCC) performed using DES-Amber SF1.0, the duplex dissociated. This is not entirely unexpected given that nearest-neighbor models predict this sequence to be only marginally stable at 300 K,^102,103 and our calculations of the free energy of melting of short duplexes suggest that the DES-Amber SF1.0 force field may slightly underestimate duplex stability.

Although RMSD is a useful metric for monitoring large conformational transitions such as DNA melting or the B-A transition, it is relatively insensitive to the details of the fine structure of the DNA double helix. We thus calculated average base-step and base-pair parameters, as well as structural parameters for each nucleobase. The full set of data is available in the SI. DES-Amber, DES-Amber SF 1.0, and DES-Amber 3.20 results are almost indistinguishable; this is not unexpected, as they largely share the same torsion potentials.

Previous studies have indicated that force field inaccuracies can result in the overstabilization of the γ-trans conformation, which can become the dominant conformation at long timescales.^104−106 Our structural analyses indicate that in simulations performed with the DES-Amber force fields, the γ-trans conformation is observed in the terminal base pairs 10% of the time, possibly due to occasional fraying, and 1% of the time in the rest of the sequence. (The corresponding results are 8 and 4% in Amber-bsc1 and 3 and 0.4% in Amber-OL15, respectively). The deviation of the step and pair parameters from the X-ray data was calculated for all force fields (Tables S9–S14). Although it is unclear how closely the simulation of the duplex in solution should resemble the X-ray structure, we found that the parameters in simulations performed using the DES-Amber force fields deviate from the X-ray structure by about the same amount as the reference force fields (Amber-bsc1 and Amber-OL15), suggesting that the DES-Amber force fields provide a description of the average nucleobase conformation with about the same accuracy as these state-of-the-art force fields. Averages were also calculated for the helical rise and twist per base step (Table S15). We found that, for all force fields, the calculated average rise was ∼3.35, ∼0.1 Å larger than that in the X-ray structures. The average helical twist was 33° for DES-Amber and 34° for Amber-OL15 and Amber-bsc1, values that are comparable to the 35° average value in the X-ray structures.

Finally, we analyzed in more detail the self-complementary Drew–Dickerson dodecamer (DDD) of sequence d(CGCGAATTCGCG), a system that has previously been very well-characterized by both simulations and experiments.^{5,41−43,96,107,108} In all three force fields, simulations of DDD resulted in a structure closer to the structures determined by NMR in aqueous solution (e.g., DES-Amber average RMSD was 1.93 Å from PDB entry 1duf(41) and 2.14 Å from 1naj(42)) than to the crystal structure (e.g., DES-Amber average was RMSD 2.61 Å from PDB entry 1bna(43)) (Table S4).

For the six base-step parameters (twist, roll, slide, rise, shift, and tilt),⁶⁰ we compared the values to the range of values observed in experimentally determined structures¹⁰¹ (Figure 6). All base-step parameters were well converged in 50 μs of simulation, with DES-Amber and DES-Amber SF1.0 giving almost identical results. Agreement with experiment for most of the base-step parameters was satisfactory, though the local description of the GC base step appeared to be inaccurate; this is consistent with the observation that the helical twist of the GC step appears to be underestimated in DES-Amber simulations (Tables S9–S11). Interestingly, simulations performed with Amber-bsc1, despite having an overall RMSD from the experimental structures (1.83 Å from 1duf) similar to that observed in simulations performed with DES-Amber (1.93 Å) (Table S4), typically yielded a better description of the local geometry of the GC base step. The CGCG region of the DDD dodecamer has been shown to exhibit unusual flexibility due to the population of a large fraction of the BII state at 300 K (34% for the GC step and 56% for the CG step).¹⁰⁹ The BI/BII population of these steps in the DDD simulations performed with the DES-Amber force fields was only 1% for the GC step and 3% for the CG step, whereas it was ∼30 and ∼50%, respectively, for Amber-bsc1 and Amber-OL15. More generally, we found that the BII population in the DES-Amber duplex simulations rarely exceeded a few percent, while it was almost an order of magnitude larger in simulations performed using Amber-bsc1 and Amber-OL15. This suggests that there is some imbalance in describing the relative stability of the BI and BII conformations and points to an area in which the DES-Amber force field could be improved, possibly by suitable optimization of the backbone torsions or the guanine nonbonded parameters that for this work were simply transferred, without further refinement, from the RNA parameters previously derived for the DES-Amber SF1.0 force field.

Figure 6.

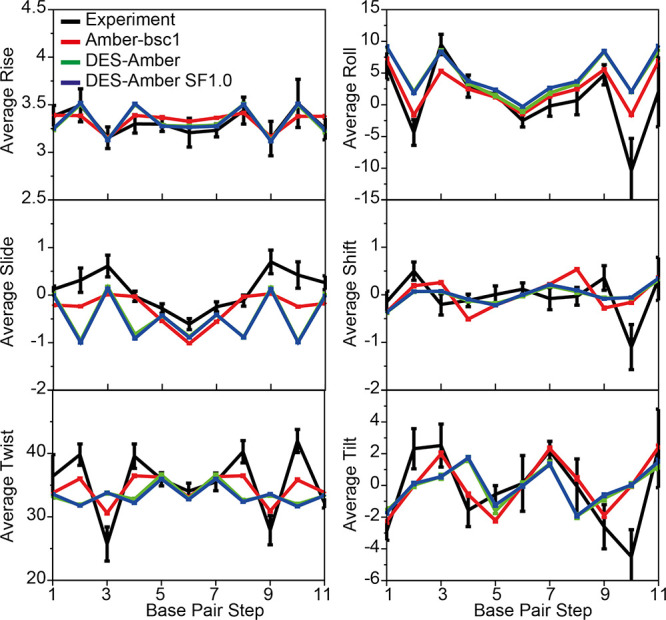
MD simulations of DDD. Comparison of the average six base-step parameters (twist, roll, slide, rise, shift, and tilt) measured in simulations performed with DES-Amber (green), DES-Amber SF1.0 (blue), and Amber-bsc1 (red) to the values observed in seven crystal and NMR structures deposited in the protein data bank (PDB entries 1bna, 2bna, 7bna, 9bna, 1naj, 1jgr, and 4c64)¹⁰¹ (black). Error bars for the experimental values report the variance of the data. Error bars for the simulated data are estimated using block averaging of the trajectory data.

Structural Stability of Noncanonical DNA Structures

Although B-DNA is the predominant form of DNA under physiological conditions, particular sequences or conditions can stabilize alternate DNA structures. We investigated the ability of DES-Amber to recapitulate some of these structures by performing simulations of (i) Z-DNA at varying salt concentrations, (ii) two DNA G-quadruplexes, and (iii) a DNA triplex.

Z-DNA is a left-handed helical form of DNA that is stabilized by GC-rich sequences containing 8-methylguanine,¹¹⁰ or 5-methyl cytosine in water/methanol solution¹¹¹ or at very high salt concentrations (>3 M NaCl).^112,113 For d(CG)_n, the Z-DNA conformation can be crystallized under physiological conditions, suggesting that it should be at least marginally stable in solution; improving the stability of this structure has been the focus of a recent Amber force field optimization.¹¹⁴ We have performed 200 μs simulations starting from a d(CGCGCGCGCGCG) Z-DNA dodecamer X-ray structure (PDB entry 4ocb)⁶¹ at salt concentrations ranging from 0.1 to 1.5 M NaCl. Simulations could not be performed at higher concentrations, as the solubility of NaCl and KCl in DES-Amber is <2 M. Simulations were fairly stable on the timescale of a few microseconds, with backbone RMSDs from the starting X-ray structure of 1–2 Å (see Figure 7A for a representative simulation at 0.75 M), but extensive fraying of the duplex terminal base pairs was observed on longer timescales in all simulations. In most cases, one-third to one-half of the initial Z-DNA base pairs were still formed at the end of the simulation (Figure S8), a result suggesting that Z-DNA is only partially stable under the simulation conditions over long timescales; this finding is consistent with the experimental observation that rather extreme conditions are required to stabilize Z-DNA in solution.

Figure 7.

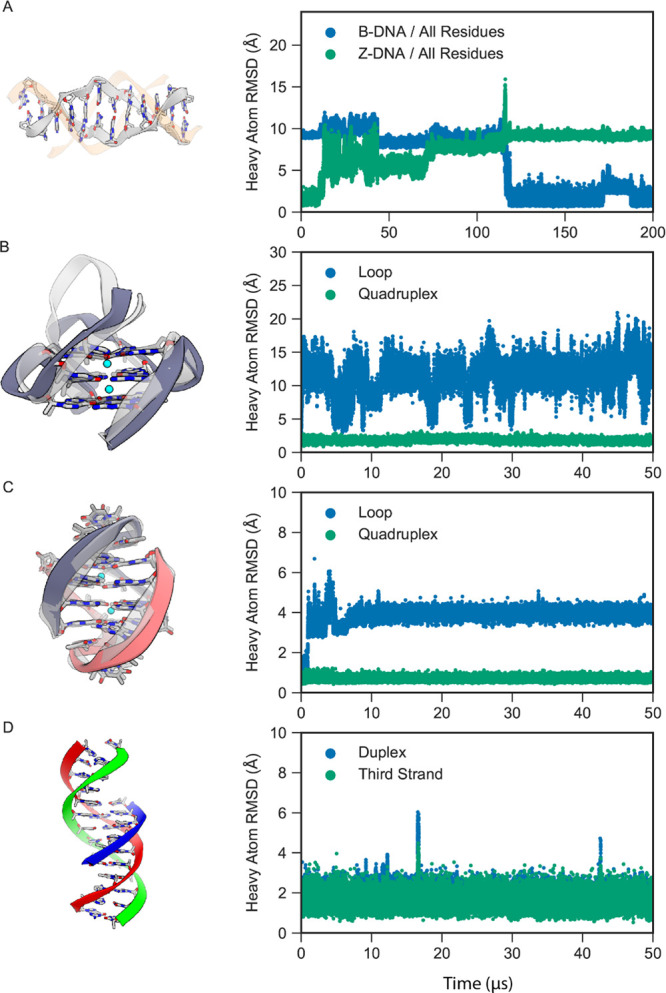
MD simulations of other forms of DNA with DES-Amber. (A) A Z-DNA dodecamer (gray) in 0.75 M KCl spontaneously transitioned to B-DNA (orange). The heavy-atom RMSDs with respect to the initial Z-DNA structure (green) and final B-DNA structure (blue) are shown on the right. (B) The CEB25 human minisatellite locus G-quadruplex, with the initial structure shown in light gray and the final structure shown in dark gray. The heavy-atom RMSDs of the loop (blue) and quadruplex (green) segments (in the reference alignment to the quadruplex core) are shown on the right. (C) The Oxytricha nova telomeric DNA G-quadruplex, with the initial structure shown in light gray and the final structure shown in dark gray and red. The heavy-atom RMSDs of the loop (blue) and quadruplex (green) segments (in the reference alignment to the quadruplex core) are shown on the right. (D) Triple-stranded DNA, with the duplex shown in red and green and the third strand in blue. The heavy-atom RMSDs of the duplex (blue) and third strand (green) (in the reference alignment of the duplex) are shown on the right.

In high-resolution X-ray structures of Z-DNA, two main backbone rotamer states (ZI and ZII) have been observed. Previous studies have shown that simulations of Z-DNA in 2 M NaCl performed with several force fields of the Amber family can populate rotamer conformations (ZI′ and ZII′) not observed in the X-ray structures.^3,4 Although the solution structure of Z-DNA in 2 M NaCl is not known, as it is only marginally stable,¹¹³ the ZI′ and ZII′ rotamers are believed to be force field artifacts.⁴ We have calculated the torsion angles from the first 2 μs of the Z-DNA simulations at 1 M NaCl (Figure S21). On this timescale and at this salt concentration, the Z-DNA structure was largely preserved in the DES-Amber simulations, and the ZI (60–65%) and ZII (30–35%) rotamers dominate. We observed a small amount of the ZI′ conformation (∼5%) and none of the ZII′ conformation.

Interestingly, in the 0.75 M simulation, the Z-DNA spontaneously transitioned to B-DNA without fully dissociating. The process began with terminal base-pair fraying, which led to the distortion of the full Z-DNA duplex after approximately 10 μs. The structure then began to adopt a B-DNA-like structure on one end, while a DNA-bubble-like structure formed in the center of the duplex. The gap formed by the bubble transiently opened and closed by the formation of mismatched base pairs over the course of 100 μs until the entire structure eventually underwent a cooperative transition to B-DNA at roughly 120 μs (Figure 7A).

Another important noncanonical structure is the G-quadruplex, a conformational form of DNA commonly found in telomeric DNA. We performed 50 μs simulations of two DNA G-quadruplexes: a repeat unit of the CEB25 human minisatellite locus (PDB entry 2lpw)⁶² and the Oxytricha nova telomeric DNA G-quadruplex (PDB entry 1jrn).⁶³ The G-quadruplex structure is generally composed of a quadruplex region stabilized by potassium ions that intercalate between four guanine bases arranged in a plane separated by loops: a single nine-nucleotide-long loop in CEB25 and two three-nucleotide-long loops in the telomeric DNA system. All crystallographic ions and water molecules were removed during simulation setup, and the systems were solvated in 0.1 M KCl. We first performed 1 μs of restrained equilibration before running the 50 μs simulations.

During equilibration, potassium ions intercalated between the guanine bases, stabilizing the complex; as a result, in both simulations, the quadruplex region was fairly stable (average heavy-atom RMSDs of 0.8 and 1.7 Å, as shown in Figure 7B,C). The loop region in CEB25, however, reversibly sampled several different conformations, including the experimentally determined structure—a result consistent with the higher degree of flexibility observed experimentally for this region.⁶² The two shorter loops in the telomeric DNA were more rigid; in all simulations, however, the ion sites at the stem–loop junction were rarely occupied, and flipping of T7 after a few microseconds of simulation induced a slight rearrangement in the loop structures, with formation of a T5–T8 and T17–T20 pair (Figure 7C). This conformation has been observed in previous studies using enhanced sampling methods.¹¹⁵ Although accurate parameterization of torsion angles can improve the loop stability, such as in the Amber-OL15 force field,⁴ it has been hypothesized that an accurate description of this loop requires a polarizable force field.¹¹⁶

Finally, we performed simulations of triple-stranded DNA (also known as H-DNA or triplex DNA). Triplex DNA is a complex formed between a B-DNA duplex and a third oligonucleotide.⁶⁴ The complex is formed by Hoogsteen base pairs¹¹⁷ and is stabilized under acidic conditions due to the pronation of cytosines to create a C-G*C+ triad.¹¹⁷ We parameterized the protonated cytosine based on our unprotonated cytosine parameters (see Methods) and simulated the d(GACTGAGAGACGTA-TACCGTCTCTCAGTC-CTCTCT) triple-stranded DNA complex⁶⁴ for 50 μs. We find that in both DES-Amber and DES-Amber SF1.0, the complex was stable on the timescale of the simulation, with marginally higher stability in DES-Amber (Figure 7D). In particular, we found that even when the B-DNA duplex underwent terminal fraying, the third strand remained stable in the major groove. These results indicate that the DES-Amber force field can accurately capture the Hoogsteen base pairing necessary for stabilizing triple-stranded DNA.

Protein–Nucleic Acid Complexes

Structural Stability of Protein–DNA Complexes

Finally, we investigated the ability of DES-Amber to maintain the structure of protein–nucleic acid complexes. This is a particularly demanding test, as it requires an accurate balance of the interactions both within and between force fields for each biomolecular component.^118,119 We selected the complexes of DNA with the GNC4 leucine zipper (PDB entry 2dgc),⁶⁵ the P22 c2 repressor (PDB entry 3jxc),⁶⁶ the Cl repressor from bacteriophage TP901-1 (PDB entry 3zhm),⁶⁷ the ETS transcriptional repressor ETV6 (PDB entry 4mhg),⁶⁸ the Trp repressor (PDB entry 1tro),⁶⁹ and the lambda repressor (PDB entry 3bdn)⁷⁰ as our test systems. Each system was run at 300 K for 50 μs using DES-Amber and DES-Amber SF1.0, and the deviation from the starting structure was measured (Figure 8).

Figure 8.

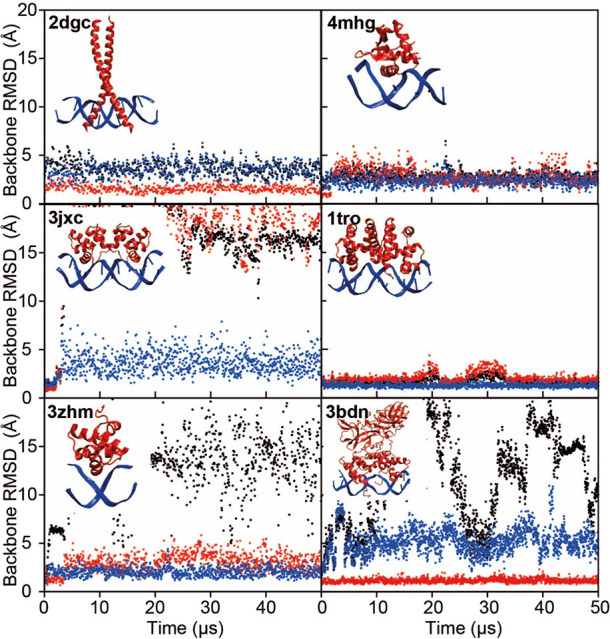
MD simulations of six protein–DNA complexes performed with the DES-Amber force field. RMSD trace as a function of simulation time for the complex (black), the protein (red), and the DNA (blue). Each panel is labeled with the PDB entry of the starting structure. The PDB structure of the complex is displayed as an inset in each plot.

The Trp repressor, GNC4 leucine zipper, and ETS transcriptional repressor ETV6 complexes were stable in both force fields throughout the 50 μs simulations. The lambda repressor–operon complex displayed a large amount of flexibility when DES-Amber SF1.0 was used, with reversible fraying at the DNA termini and reversible binding/unbinding of one of the two lambda repressor units. This complex was more stable with DES-Amber, although transient binding/unbinding was also observed in this force field.

The P22 c2 repressor and Cl repressor systems were stable only for a few microseconds, after which the complexes dissociated in both force fields. The P22 c2 repressor is a protein dimer with two independent binding sites, and dimerization is associated with the bending of the DNA operon due to a local B-DNA to B′-DNA transition.¹²⁰ In the simulation, the protein–protein dimer interface broke, leading to a straightening of the DNA double helix and disruption of the original geometry of the complex. The Cl repressor is monomeric and binds selectively to a short double-stranded DNA stretch. This complex dissociated in the simulation, although both the DNA and the repressor are structurally very stable, as indicated by the small RMSDs with respect to the starting structure for these individual pieces of the complex.

Structural Stability of Protein–RNA Complexes

We also performed simulations of a set of six protein–RNA complexes with various structures and binding modes using DES-Amber; some of these were previously investigated by Krepl et al.¹¹⁹ In particular, we conducted 50 μs of simulations of the complexes of dsRNA–B2 protein (2az0),⁷¹ tertiarily structured mRNA stem–loop, stem–loop binding protein and 3′hExoribonuclease 1 (4qoz),⁷² RNA hairpin–U1A protein (1urn),⁷³ the ROQ domain–Hmg19 stem-loop RNA (4qil),⁷⁴ RNA duplex-quadruplex junction–RGG peptide (5dea),⁷⁵ and ssRNA–Pumilio FBF-2 protein (3k5y).⁷⁶

None of the complexes dissociated, and four complexes (2az0, 4qoz, 3k5y, and 4qil) were remarkably stable for the entire 50 μs of simulation (Figure 9). We did observe, however, that a few key protein–nucleic acid interactions were unstable in the simulations. In 5dea, for example, the C- and N-terminal residues of the peptide were fairly flexible and only loosely bound, a result consistent with the NMR observation that only residues 8 to 17 are essential for binding.¹²¹ During the simulation, however, the contact between RNA and Arg10 broke; this contact is considered critical for recognition¹²¹ and is thus not expected to be broken.

Figure 9.

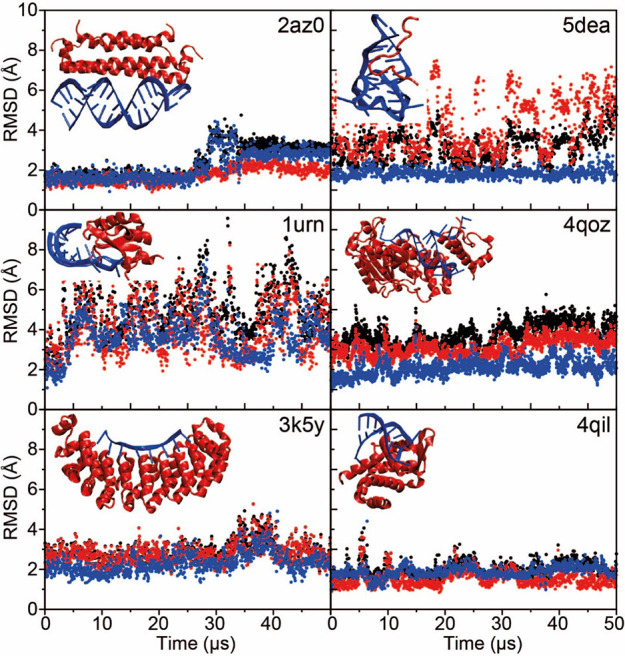
MD simulations of six protein–RNA complexes performed with the DES-Amber force field. RMSD trace as a function of simulation time for the complex (black), the protein (red), and the RNA (blue). Each panel is labeled with the PDB entry of the starting structure. The experimentally determined structure of the complex is displayed as an inset in each plot.

Overall, the protein–nucleic acid simulations performed using DES-Amber on the 50 μs timescale resulted in stable simulations for all protein–RNA complexes considered and for about half of the protein–DNA complexes. Complexes were sometimes found to be more flexible than indicated by experiment, and certain key interactions were poorly described. It is possible that, even in such cases, the simulations may still be informative, but care should be taken in the interpretation of the results.

Reparameterization of Nucleic Acid Backbone Nonbonded Parameters to Improve the Description of Protein–Nucleic Acid Complexes

Overall, we found that the DES-Amber force fields provided a fairly accurate description of nucleic acids but that their performance was less satisfactory in simulations of certain protein–nucleic acid complexes. We notice that often, in cases where the dissociation of a complex was observed, structures of the individual components (protein and nucleic acid) were reasonably well-maintained, suggesting that the main issue is related to inaccuracies in the description of nonbonded interactions at the protein–nucleic acid interface. We speculate that the use of a water model like TIP4P-D (or OPC, which has very similar parameters⁵⁸) that reduces artifacts related to overcompaction may magnify force field inaccuracies that in simulations performed with water models like TIP3P would normally be masked by the strong stabilization of compact structures. Simulations performed with TIP4P-D or OPC may thus be less forgiving toward inaccuracies in the macromolecular force field. In an attempt to improve the description of protein–nucleic acid complexes, we have performed a reparameterization, using experimental data (Figure S6), of the nonbonded parameters of the phosphate group in DES-Amber, which we had not previously optimized (see SI for a full description of these reparameterization and validation efforts). We did not attempt the same reparameterization for DES-Amber SF1.0.

The reparameterized force field, which we term DES-Amber 3.20 (from the value in Å of the σ parameter in the optimized LJ interaction between the phosphate oxygen atoms and water^122−128), is comparably accurate to DES-Amber in simulations of nucleic acids (see, e.g., Figures S5, S7, and S9), and we tested it in simulations of protein–nucleic acid complexes by performing 50 μs simulations of eight DNA–protein complexes (the six complexes listed above and two zinc fingers), as shown in Figure 8 and in Figures S13–20, and six RNA–protein complexes, as shown in Figure 9. We found that on the 50 μs timescale investigated, all the complexes studied were stable and none dissociated (Figure 10), a clear improvement compared to using DES-Amber without the reparameterization. This finding suggests that DES-Amber 3.20 may be suitable for long-timescale simulations of systems containing both proteins and nucleic acids. (The relatively large RMSD of the 3bdn complex was mostly attributable to rigid pivot motions of the two large protein domains that are not involved in DNA binding and are thus free to move in solution, but the complex itself was stable.) Although it is possible that the improved performance of DES-Amber 3.20 might be the result of having two additional parameters compared to DES-Amber (specifically, two additional, explicit LJ pairs for nucleic acid–water interactions; see SI), the improvements observed in the description of protein–nucleic acid interactions were substantial, and we recommend the use of DES-Amber 3.20 in simulations of such systems.

Figure 10.

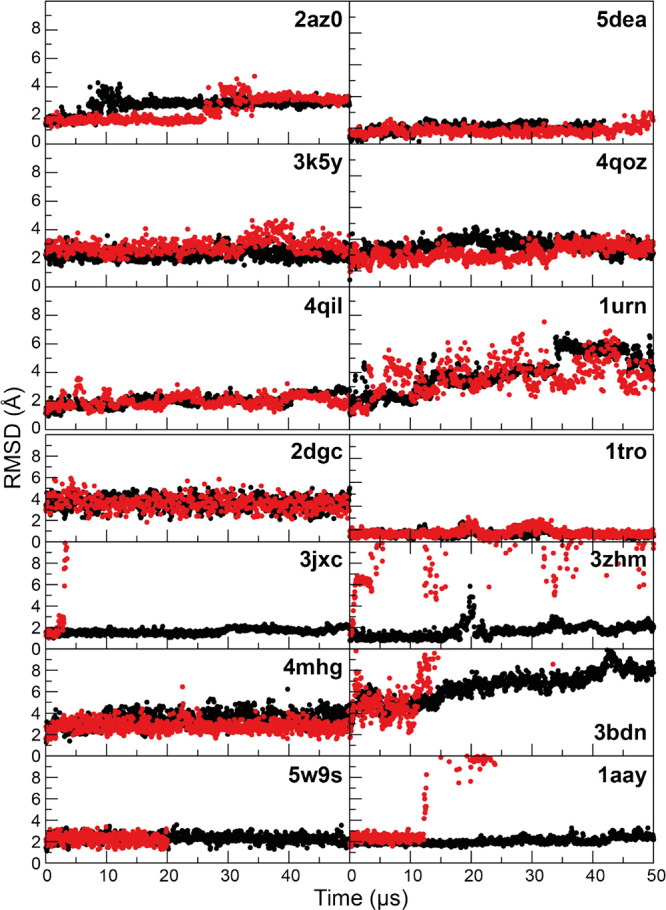
MD simulations of six protein–RNA complexes (top) and eight protein–DNA complexes (bottom) performed with the DES-Amber 3.20 (black) and DES-Amber (red). Backbone RMSD traces are reported as a function of simulation time. Flexible terminal residues and regions that were not resolved in the X-ray structures were omitted from the RMSD calculations. Each panel is labeled with the PDB entry of the starting structure.

Discussion

We have performed an optimization of the Amber DNA force field parameters using our previously reported nonbonded parameters for RNA as a starting point. We also optimized parameters for magnesium ions and structural zinc ions. The new DNA force field parameters are part of the DES-Amber force field, which also contains RNA and protein parameters, and were tested on both single- and double-stranded DNA systems. Comparison of DES-Amber simulation results to experiment indicated that, in most cases, the structure and local flexibility of both single- and double-stranded DNA systems were reproduced with a level of accuracy similar to state-of-the-art force fields, with the notable exception of the BII population, which appears to have been underestimated in the DES-Amber DNA duplex simulations.

Despite the adjustment of DNA-specific parameters, we observed that the stability of the DNA B-helix was underestimated by ∼0.1–0.2 kcal mol^–1 per nucleobase. While it would be possible to correct this deficiency by further optimizing torsion parameters, we decided against this strategy, as it appeared that structures consistent with the B-helix conformation were already well-populated in single-stranded DNA. We thus suspect that some error in the balance of base stacking and hydrogen bonding or backbone electrostatic interactions may be responsible. We also observed some deviation from experiment in the local structure of CG base pairs, a deficiency resulting from the strong repulsion between the two guanine nucleobases on opposing strands, which induced local and global distortions in the helix. Such an imbalance is also characteristic of simulations performed with other Amber force fields,^129,130 and it is unclear if a simple reparameterization of nonbonded interactions and torsion angles would be sufficient to address it or if a more sophisticated functional form might be required.

Finally, we performed a set of simulations of protein–DNA and protein–RNA complexes, with somewhat mixed results. Some complexes appeared to be well-described, while others became unstable and dissociated during simulation. Discrepancies from experiment were also observed in previous simulations of a number of protein–protein complexes.⁸ Based on the simulations presented here, this instability could not simply be ascribed to internal strain resulting from the instability of one of the biomolecular components, as in some cases of unstable complexes the isolated proteins or nucleic acids were structurally stable. To further investigate this issue, we performed an analysis of the backbone nonbonded interactions and attempted a reparameterization of the phosphate group based on experimental data (see SI). The resulting DES-Amber 3.20 force fields improved the description of the complexes while yielding results roughly equivalent to the DES-Amber force fields for systems containing nucleic acids only. To achieve these results, it was necessary to introduce two additional nonbonded pairs, which may in effect be compensating for the lack of an explicit polarization model; such adjustments may not be required in the context of a polarizable force field. Achieving an even higher degree of accuracy may require the use of more complex functional forms. Further studies will be required to fully address this issue.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.1c10971.

• Development of a generalized force field for the description of structural zinc ions compatible with DES-Amber; parameterization strategy for nonstandard residues; optimization of nucleic acid backbone nonbonded parameters against experimental data; assessment of the accuracy of DES-Amber 3.20 for DNA simulations; assessment of the accuracy of DES-Amber 3.20 for RNA simulations; simulations of short DNA oligomers and comparison to NMR J-couplings (Table S1); simulations of dsDNA reversible duplex formation (Table S2); simulations of dsDNA reversible duplex formation (Table S3); long DNA oligomers simulations (Table S4); deviations from experimental J-couplings for simulations of ssRNA tetranucleotides (Table S5); magnitude of torsion corrections from refitting based on experimental NMR J-coupling data (Table S6); modified force field parameters for DES-Amber 3.20 (Table S7); simulations of dsRNA reversible duplex formation (Table S8); DES-Amber simulations of DNA duplexes (Table S9); DES-Amber 1.0 simulations of DNA duplexes (Table S10); DES-Amber 3.20 simulations of DNA duplexes (Table S11); Amber-bsc1 simulations of DNA duplexes (Table S12); Amber-OL15 simulations in TIP3P water of DNA duplexes (Table S13); Amber-OL15 simulations in OPC water of DNA duplexes (Table S14); average helical rise and twist in simulations of DNA duplexes (Table S15); dT40 simulations (Figure S1); simulated tempering simulations of DNA duplex formation performed with the Amber-bsc1 force field (Figure S2); simulated tempering simulations of DNA duplex formation performed with the DES-Amber SF1.0 force field (Figure S3); simulated tempering simulations of DNA duplex formation performed with the DES-Amber force field (Figure S4); simulated tempering simulations of DNA duplex formation performed with the DES-Amber 3.20 force field (Figure S5); comparison of calculated and experimental osmotic coefficients for DMP, purine, cytidine, and uridine (Figure S6); comparison of the disordered states of rU40 and dT40 simulated with different force fields with FRET data (Figure S7); MD simulations of the d(CGCGCGCGCGCG) Z-DNA dodecamer at KCl concentrations ranging between 0.1 and 1.5 M (Figure S8); MD simulations of a d(CGCGCGCGCGCG) Z-DNA dodecamer performed with the DES-Amber 3.20 force field (Figure S9); MD simulations of three complex RNA folds (Figure S10); MD simulations of six proteins containing structural zinc ions (Figure S11); MD simulations of tRNA (Figure S12); MD simulations of a leucine zipper/DNA complex (Figure S13); MD simulations of the Trp-repressor/operator complex (Figure S14); MD simulations of the P22 c2 repressor protein operator complex (Figure S15); MD simulations of CI repressor in complex with the OL2 operator half-site (Figure S16); MD simulations of ETV6 bound to DNA (Figure S17); MD simulations of the λ-repressor (Figure S18); MD simulations of the zinc finger of human CXXC5 in complex with CpG DNA (Figure S19); MD simulations of the ZIF268 zinc finger-DNA complex (Figure S20); MD simulations of Z-DNA in 1 M NaCl (Figure S21); and MD simulations of complex RNA folds (Figure S22) (PDF)

The authors declare the following competing financial interest(s): This study was conducted and funded internally by D. E. Shaw Research, of which D.E.S. is the sole beneficial owner and Chief Scientist, and with which all authors are affiliated.

Notes

The MD trajectories of the simulations described in this manuscript are available for noncommercial use through contacting trajectories@deshawresearch.com. The force field parameters are available in Desmond format on GitHub: https://github.com/DEShawResearch/viparr-ffpublic. (The force field parameters are also available in Gromacs format through contacting trajectories@deshawresearch.com.)