Characterizing Mode Anharmonicity and Huang–Rhys Factors Using Models of Femtosecond Coherence Spectra

Abstract

Femtosecond laser pulses readily produce coherent quantum beats in transient–absorption spectra. These oscillatory signals often arise from molecular vibrations and therefore may contain information about the excited-state potential energy surface near the Franck–Condon region. Here, by fitting the measured spectra of two laser dyes to microscopic models of femtosecond coherence spectra (FCS) arising from molecular vibrations, we classify coherent quantum-beat signals as fundamentals or overtones and quantify their Huang–Rhys factors and anharmonicity values. We discuss the extracted Huang–Rhys factors in the context of quantum-chemical computations. This work solidifies the use of FCS for analysis of coherent quantum beats arising from molecular vibrations, which will aid studies of molecular aggregates and photosynthetic proteins.

The topography of an excited-state potential-energy surface strongly influences the photophysical, photochemical, and photobiological properties of a molecule or molecular system,^1,2 thereby impacting the development of promising device applications such as light harvesting³ or fluorescence sensing.⁴ Electronic spectra contain information regarding the topography of excited-state potential-energy surfaces,^5,6 in particular, information about the intramolecular vibrational modes of a molecule and the coupling of those modes to the electronic transition.^7,8 This information can—in principle and in practice—be extracted from measured spectra, especially near the Franck–Condon region of the potential-energy surface. Several groups, for example, have used computations and models in conjunction with steady-state electronic spectra to extract coupling parameters.^9,10 In another example, Lawless and Mathies used resonance Raman spectra to find the normalized displacement, which is related to the Huang–Rhys factor,^11,12 of each Franck–Condon active vibrational mode in Nile blue.¹³ In addition, Lee et al. extracted the reorganization energy, which is also related to the Huang–Rhys factor, of coumarin 153 from time-resolved fluorescence spectra.¹⁴ Other time-resolved spectroscopy techniques have provided similar information,¹⁵⁻²⁰ and each method has benefits and limitations.

For femtosecond transient-absorption spectroscopy, researchers have measured quantum-beat signals arising from vibrational wavepackets since the 1990s,^21,22 and these wavepackets are expected to contain topographical information about the excited electronic state near the Franck–Condon region. Photosynthetic pigment–protein complexes,²³⁻²⁵ retinal pigment–protein complexes,²⁶⁻³⁴ and laser dye molecules³⁵⁻⁴³ have been measured in detail, and other measured systems include heme proteins,⁴⁴ phytochrome pigment–protein complexes,⁴⁵⁻⁴⁷ carbon nanotubes,⁴⁸ charge–transfer systems,⁴⁹⁻⁵² polymers,⁵³ perovskite materials,⁵⁴ and molecular aggregates and crystals.⁵⁵⁻⁵⁸ Further reports analyzed how pulse chirp and temperature affect the measurement of vibrational quantum beats.⁵⁹⁻⁶³ Finally, a variety of theoretical studies have aided the interpretation of the curious phase and amplitude profiles that often characterize vibrational quantum-beat signals.⁶⁴⁻⁷⁰

Despite these efforts, quantitative information is not routinely extracted from measured vibrational quantum-beat signals in transient-absorption spectra, other than the assessment of the presence or absence of oscillations at a particular frequency. Therefore, in this contribution, we fit measured quantum-beat signals to our recently developed microscopic vibrational models of femtosecond coherence spectra (FCS),^69,70 which we define as the Fourier-domain amplitude and phase profiles, A(ω) and ϕ(ω), respectively, as a function of detection frequency, ω, for a chosen oscillation frequency, ω₀. We denote the measured spectrally resolved TA data set as S(ω,τ₂), where τ₂ is the pump–probe time interval and ω is the detection frequency axis. After Fourier transformation of the data set over the pump–probe time interval, the resultant complex-valued spectrum can be denoted as M(ω, ω₂) = 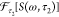, where ω₂ is the oscillation frequency axis resulting from Fourier transformation. Some previous works use FCS to refer to the spectrally integrated signal (1D vibronic spectrum), A(ω₂) = ∫|M(ω,ω₂)|dω. Our usage of FCS refers to the amplitude or phase profile of a selected oscillation frequency, ω₀, as a function of detection frequency, A(ω) = M(ω, ω₂)|_{ω2 = ω0}. Most FCS contain one or more sharp amplitude nodes and abrupt phase shifts, which can be envisioned in the 1D displaced harmonic oscillator model as arising from the features of the vibrational eigenfunctions.⁶⁹ Some previous authors on some occasions have used FCS or the related terms vibrational coherence spectroscopy (VCS) and broadband impulsive vibrational spectroscopy (BB-IVS), among others, to refer to 1D vibronic spectrum showing the amplitude of peaks as a function of oscillation frequency.^{31,38,44,67,71,72} Although in principle the amplitude of each peak in a 1D vibronic spectrum is directly related to the Huang–Rhys factor of the mode, the amplitude of a peak is also affected by an attentuation envelope arising from the pulse spectrum, the spectral phase of the pulse, and the detection wavelengths over which the signal was summed.^39,59−61 In this work, we normalize each mode before analyzing its FCS—the amplitude profile as a function of detection frequency—to characterize the anharmonicity and Huang–Rhys factor.

Here we analyze the measured FCS of representative Franck–Condon active modes for two laser dyes to demonstrate the utility and applicability of the methodology. By evaluating selected vibrational modes having a variety of amplitudes and profiles, this fitting and analysis of measured spectra serve as an experimental validation of our previous theory work, and it demonstrates how quantitative parameters could be obtained. We show that the overall shape of the FCS profile allows us to classify the signal as arising from a fundamental, overtone, or combination-band mode, and we show that the fits to the models can yield reasonable parameter values. 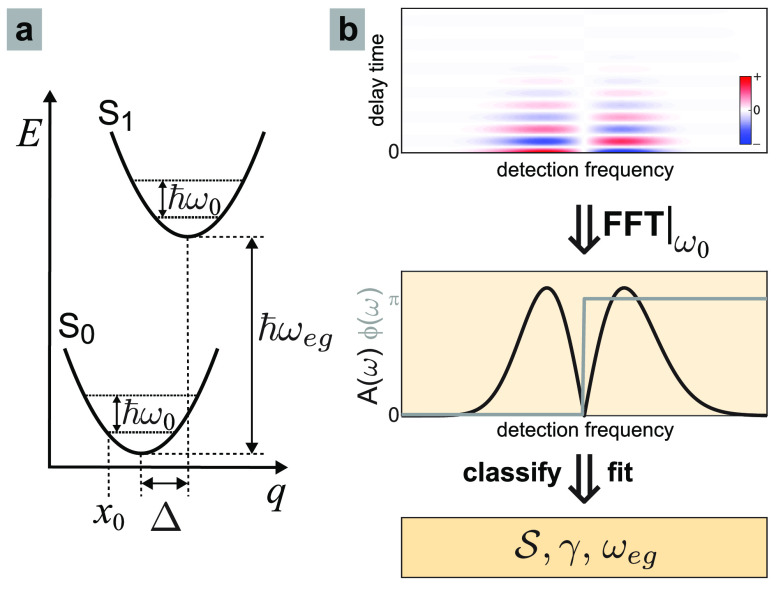Central to the analysis is the ubiquitous displaced harmonic oscillator model shown in Figure 1a. In this model,⁷³ both the ground (S₀) and excited (S₁) electronic states are harmonic potentials of frequency ω₀, offset vertically by energy ℏω_eg, and offset horizontally by a displacement Δ, which—after normalization relative to x₀, the classical turning point of the lowest-energy eigenfunction, Δ̃ = Δ/x₀—is related to the Huang–Rhys factor by 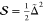. The horizontal axis, q, is the displacement coordinate of one specific normal mode.

Figure 1.

(a) Displaced harmonic oscillator model of molecular spectroscopy is characterized by vibrational frequency (ω₀), Huang–Rhys factor (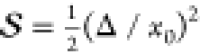), and electronic energy shift (ℏω_eg). (b) Measured vibrational quantum beat signals (top) can be Fourier transformed to produce femtosecond coherence spectra (FCS) for each mode (middle), which can then be classified as a fundamental, overtone, or combination-band mode and then fit using the appropriate model. (bottom) The fit yields the parameters 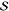and ω_eg, as well as the electronic dephasing (γ).

Previously we used a doorway–window method to develop analytic FCS expressions in terms of the normalized displacement.⁷⁰ As a simplification and generalization, here we express the fundamental (p = 1) and overtone (p = 2) FCS, respectively, directly in terms of the Huang–Rhys factor, 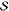, as

1

where the auxiliary functions are given by

2

In these expressions, m and n index the vibrational eigenstates of the ground and excited electronic states, respectively; ω_a,b = (E_a – E_b)/ℏ, which implicitly includes vertical offset ω_eg ; γ is a universal phenomenological dephasing parameter for the emitted optical coherence signals; and ω is the detection frequency variable. When fitting measured spectra, ω arises from the calibrated detector and ω₀ is given directly from the measured oscillation frequency of each quantum beat, and therefore, the fit parameters are limited to only the set 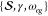. As discussed previously for the harmonic model,⁶⁹ when p = 1 (p = 2), the amplitude profile is typically characterized by two (three) peaks separated by one (two) node(s) in the amplitude FCS profiles; the profiles can be interpreted as arising from the nodes in the n = 1 or n = 2 vibrational eigenfunctions for fundamental and overtones, respectively; in the case of fundamental modes, the two peaks have at most a ∼20% difference in amplitude.

We then developed a related model in which the ground-state and excited-state potentials are displaced and harmonic but have distinct curvatures. Section S2 of the Supporting Information contains the details. We use an analytic, albeit complicated, expression for the appropriate Franck–Condon coefficients⁷³ recast in a dimensionless unit system amenable for fitting measured spectra. The Franck–Condon coefficients can then be inserted into the generic FCS expression. The result is that the fit parameters for this unequal-curvature harmonic model include 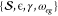. The parameter ϵ controls the relative frequencies, ω_0g = ϵ²ω_0e, where we fix ω_0e to be the measured oscillation frequency. Simulations shown in the Supporting Information reveal that ϵ ≠ 0 induces modest additional asymmetry to the two main peaks.

To quantify the anharmonicity, we also developed FCS expressions based on the displaced Morse oscillator model.⁷⁰ This model introduced parameter λ, an integer representing the number of bound vibrational eigenstates in each electronic potential, which we use as a proxy for the inverse anharmonicity. This anharmonic model can produce FCS amplitude profiles in which the peaks have extremely different amplitudes. In contrast to the relatively trim FCS expression of the harmonic model, the FCS expression we derived previously for the anharmonic model was a function of both the emission frequency variable (ω) and the oscillation frequency variable (ω₀). This prevented rapid fitting of measured spectra. Therefore, here we derived an FCS expression of the anharmonic model as a function of only ω by assuming that the wavepacket is composed primarily of the two lowest-energy vibrational eigenstates in the excited electronic state. In an anharmonic potential, this is the only combination of vibrational eigenstates that will produce oscillations at the fundamental oscillation frequency relevant to this FCS profile, ω₂ = ω_0,1. This assumption is appropriate when the normalized displacement is relatively small, Δ̃ ≲ 1, which is widely applicable to molecular systems.^8,13,14 The expression for ω₂ = ω_0,1 is

3

where the complicated auxiliary function, A_MO(λ, Δ̃, m) is given in section S1 of the Supporting Information. Even though eq 3 arises from assuming the excited-state wavepacket is composed of only two vibrational eigenfunctions, all ground-state vibrational eigenfunctions m are included, and therefore, the FCS profile can still be composed of many overlapping Lorentzian terms. Converting the normalized displacement into an effective Huang–Rhys factor, 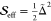, the fit parameters for the anharmonic FCS model are 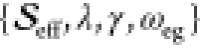. Using this convenient conversion requires some caution because—in contrast to the harmonic models—in the anharmonic model, the FCS arising from Δ̃ < 0 and Δ̃ > 0 are distinct.

Physically, eqs 1 and 3 demonstrate that each model yields a collection of Lorentzian peaks, each peak is broadened by γ and weighted by an auxiliary function, and the peaks overlap to yield lineshapes akin to those illustrated in the middle of panel b in Figure 1. A primary aim of this work is to evaluate the utility of these one-dimensional FCS models using measured spectra. An ideal prototype molecule would

• completely lack nonradiative decay mechanisms and consequently have a high fluorescence quantum yield;

• have a Stokes shift large enough to separate excited-state wavepacket signals from ground-state wavepacket signals;

• have absorption and fluorescence spectra in a wavelength range that is convenient for the femtosecond spectrometer;

• lack Duschinsky mixing,⁷⁴ which is a relative rotation between multidimensional ground-state and excited-state potential-energy surfaces, so that one-dimensional models are adequate.

One such sample seems to be rhodamine 101. Rhodamine dyes are characterized by a xanthene moiety serving as the chromophore and a benzoic-acid moiety linked at the ortho position with respect to the location of the oxygen atom in the xanthene’s central ring (see the structure in panel a of Figure 2). Rhodamine 101 has an excited-state lifetime in methanol of 4 ns⁷⁵ and a reported fluorescence quantum yield of 99% in methanol over a wide temperature range.⁷⁶ In methanol, rhodamine 101 has absorption and fluorescence maxima of 567 and 588 nm, respectively, which are well within the range of the ultrabroadband laser pulses produced by our femtosecond laser system. Furthermore, these values indicate a Stokes shift of 19 THz (630 cm^–1), which should be adequate to distinguish between coherent wavepackets on the excited and ground electronic states. The ground-state wavepackets should be suppressed because the transition-dipole moment is likely to be coordinate-independent and the ultrabroadband laser pulses encompass the absorption spectrum.^60,65,68 We found no publications reporting Duschinsky mixing in rhodamine 101. In addition to several weak peaks, the steady-state Raman spectrum displays moderate or strong peaks at 1648, 1508, 1360, and 1347 cm^–1 (49.5, 45.3, and 40.5 THz) arising from aromatic C–C stretches in the xanthene moiety, and a moderate-intensity peak at 760 cm^–1 (22.8 THz) arising from a C–H out-of-plane bending mode.⁷⁷ Prior femtosecond transient–absorption measurements have identified multiple coherent vibrational oscillations in rhodamine 101;^25,39 however, the researchers did not produce FCS profiles or compare them to a model.

Figure 2.

Results for rhodamine 101. (a) Molecular structure. (b) Measured transient-absorption spectra, with population decays subtracted from the 1 ps data set view. Absorption and fluorescence spectra displayed in violet and green, respectively, along with the laser pulse spectrum in cyan. (c) 1D vibronic spectrum. Vertical blue lines indicate peaks to be analyzed with FCS. (d) Measured (black) and fitted harmonic (red) and anharmonic (dark cyan) FCS amplitude profiles at indicated oscillation frequencies. (e) Measured (black) and unequal-curvature harmonic (orange) FCS amplitude profiles at indicated frequencies. Dashed lines in panels b, d, and e indicate absorption and fluorescence maxima.

Panel b in Figure 2 displays measured transient–absorption spectra on 1 ns and 1 ps time scales, the latter revealing the vibrational quantum beats as oscillatory signals that appear in addition to the conventional, slowly decaying ground-state bleach and stimulated emission signals. No excited-state absorption signals appear in this spectral region. Subtraction of the slowly decaying signals, Fourier transformation, and subsequent summation over all detection frequencies lead to the 1D vibronic spectrum displayed in panel c, which reveals the oscillation frequencies of the vibrational modes. There are 16 peaks above the noise: 6.3, 7.0, 10.7, 12.4, 12.9, 14.2, 18.8, 22.9, 31.4, 34.2, 36.8, 39.8, 45.4, 49.8, 85.6, and 88.8 THz. These values are largely consistent with the peak locations that can be estimated from Figure 8 in ref (39), and the peaks above 20 THz are also largely consistent with peaks in the steady-state Raman spectrum.⁷⁷ The solvent, methanol, gives rise to the peaks near 31, 85, and 88 THz.⁹⁰

To evaluate the applicability and utility of the FCS models, we focus on three modes: 6.3, 7.0, and 12.4 THz (210, 233, and 413 cm^–1). Specifically, we study the 7.0 THz mode because it is the highest amplitude, and we chose the 6.3 and 12.4 THz modes because the latter is at a frequency indicating it is potentially the overtone of the former, and careful inspection of Figure 8 from ref (39) reveals profiles for the 6.3 and 12.4 THz peaks that fit this anticipated classification. The measured FCS amplitude profiles (see black traces in panel d in Figure 2) reveal that the 6.3 and 7.0 THz modes have the two-peak/single-node profile of fundamental vibrational modes, while the 12.4 THz mode has the three-peak/two-node profile of an overtone. Despite the noise, the three-peak/two-node profile of the 12.4 THz profile was qualitatively distinct and was repeatable over multiple measurements. Consistent with these classifications is that the 12.4 THz mode has a frequency approximately double that of the 6.3 THz peak, given the estimated error of ±0.1 THz.

Having classified the three modes, we then fit each measured amplitude profile to the FCS expression for the harmonic model (red traces in panel d of Figure 2). While the fits do reproduce the main features of the measured FCS profiles, the harmonic column of Table 1 reveals that the coefficients of determination, R², are very poor, ranging from about 0.06 to 0.35, and the extracted Huang–Rhys values seem a bit high compared to those of other molecules, which ranged from less than 0.01 to 0.4.^8,13,14 Section S3 of the Supporting Information contains full fit results. Because relative peak heights that are more than about 20% asymmetric cannot be obtained with the harmonic FCS model, the quantitatively poor fits are expected for the 6.3 THz and 7.0 THz modes. One could hypothesize additional asymmetry even in a harmonic model from temperature effects because the model assumes zero temperature, while we performed the measurements at room temperature. However, Kumar and Champion showed that even for a mode at 1.2 THz, the effects of this change in temperature on the amplitude profiles are minor.⁶⁷ In contrast to the harmonic model, simulations using the anharmonic model have demonstrated the ability to have extremely asymmetric peak heights.⁷⁰ We therefore fit the FCS profiles of the 6.3 and 7.0 THz modes to the anharmonic FCS model (dark cyan traces in panel d of Figure 2). The fit errors of the 6.3 and 7.0 THz modes improved significantly, having R² values >0.95. Qualitatively, the anharmonic fits reproduce the high-frequency peaks at about 530 THz well but struggle to reproduce adequately the depth of the nodes and the height of the lower-frequency peaks at about 500 THz. For simpler comparison between the models, we converted the normalized displacement arising from the anharmonic model into an effective Huang–Rhys factor, 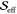, using 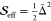. The effective Huang–Rhys factors of about 1.6 and 1.2 for the 6.3 and 7.0 THz modes, respectively, again seem too high relative to the previous reports. Unfortunately, significant geometric changes of the benzoic acid moiety for S₀ and S₁ frustrated efforts to compare the Huang–Rhys values to those arising from quantum-chemical computations. Section S3 of the Supporting Information contains details of these attempted quantum-chemical computations. The failure of the calculations reinforces the need for an alternative pathway to this information. Finally, we present the anharmonicity of the modes in Table 1 both in terms of λ_best as well as the more conventional anharmonicity value, χ, where the two are related by χ = ω₀ /(2 λ_best) .

Table 1. Fit Results of Rhodamine 101 for the Three FCS Models^a.

	harmonic		anharmonic				unequal harmonic
ω0/(2π)		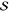R2		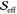λbest	χ	R2		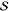ϵ	R2
6.3	0.45	0.056	1.62	11	0.29	0.988	0.14	2.10	0.991
7.0	0.41	0.354	1.22	11	0.32	0.963	0.70	1.15	0.865
12.4	0.93	0.076

^aAll values are dimensionless except ω₀ and χ, which are in units of THz.

Using the unequal-curvature harmonic model, we fit the measured spectra of the two fundamental modes of interest for rhodamine 101. Table 1 contains the fit results, and panel e in Figure 2 contains the fitted FCS. The qualitative aspects of the 6.3 THz mode fit are compelling, and the R² value of 0.991 confirms that the fit using this model is superior to the other two models. However, the best-fit value for ϵ is 2.10, indicating that the frequency of the ground-state potential is more than 4× higher than the excited-state potential. Because the value of ϵ was so large, we hypothesized this would lead to additional peaks at lower or higher frequencies. Figure S2 in the Supporting Information contains the plot of the fitted FCS extended across a much larger detection-frequency window. It reveals additional peaks at lower frequencies, notably one at about 445 THz (675 nm). Although these predicted peaks are outside our detection window, the spectrum presented in Figure 8 of ref (39) does have a peak near the predicted detection frequency, providing tentative support of the fit result, which at first glance seemed unreasonable. One possible explanation is Duschinsky mixing.⁷⁴ One can envision that the projection of an -dimensional potential-energy model having rotation between the ground and excited states onto a single coordinate would indeed make it appear as if the frequencies of the two electronic states were different.

For the 7.0 THz mode, the fit using the unequal-curvature harmonic model is significantly better than the harmonic model, but inspection of the FCS shape reveals several discrepancies for both peaks and the node. The anharmonic model provided the best fit, although the effective Huang–Rhys factor of 1.22 remained higher than anticipated.

Although rhodamine 101 seemed to have the photophysical characteristics of an ideal test molecule, the lack of computational results prevents confirmation of the unexpectedly large parameter values obtained from the fits to the models. We therefore turn to a second laser dye, cresyl violet, that has many of the ideal photophysical characteristics and is amenable to quantum-chemical computations of its vibronic modes. The structure of cresyl violet is depicted in panel a of Figure 3. Cresyl violet is one member of the 1,4-oxazine family of dyes, which have been used in dye lasers and as fluorescent labels⁷⁸⁻⁸² due in part to their favorable spectroscopic properties. Cresyl violet is a rigid, planar molecule that has four amine hydrogens. This molecule has become a standard for development of ultrafast laser spectrometers for detection of coherent quantum-beat signals.⁸³⁻⁸⁶ A notable feature of the members of this dye family is an extremely strongly coupled vibronic mode having a frequency of about 17.7 THz (590 cm^–1).²¹ Measurements and analysis have generated two competing hypotheses regarding the strong vibronic mode. One hypothesis is that the mode is extremely harmonic.^43,87 A second hypothesis is that the molecule is subject to nonadiabatic dynamics,^42,88 and the mode is, therefore, anharmonic in the adiabatic basis.⁸⁹ Here we can use the FCS models to test these hypotheses: The nonadiabatic hypothesis is supported if the anharmonic model fits the measured FCS better than both of the harmonic models. In addition, we study the 22.0 THz mode because it had the most equal-amplitude peaks representing a weak Huang–Rhys factor, and we selected the 15.6 THz because it has a similar profile as the 17.6 THz mode but without the literature attention.

Figure 3.

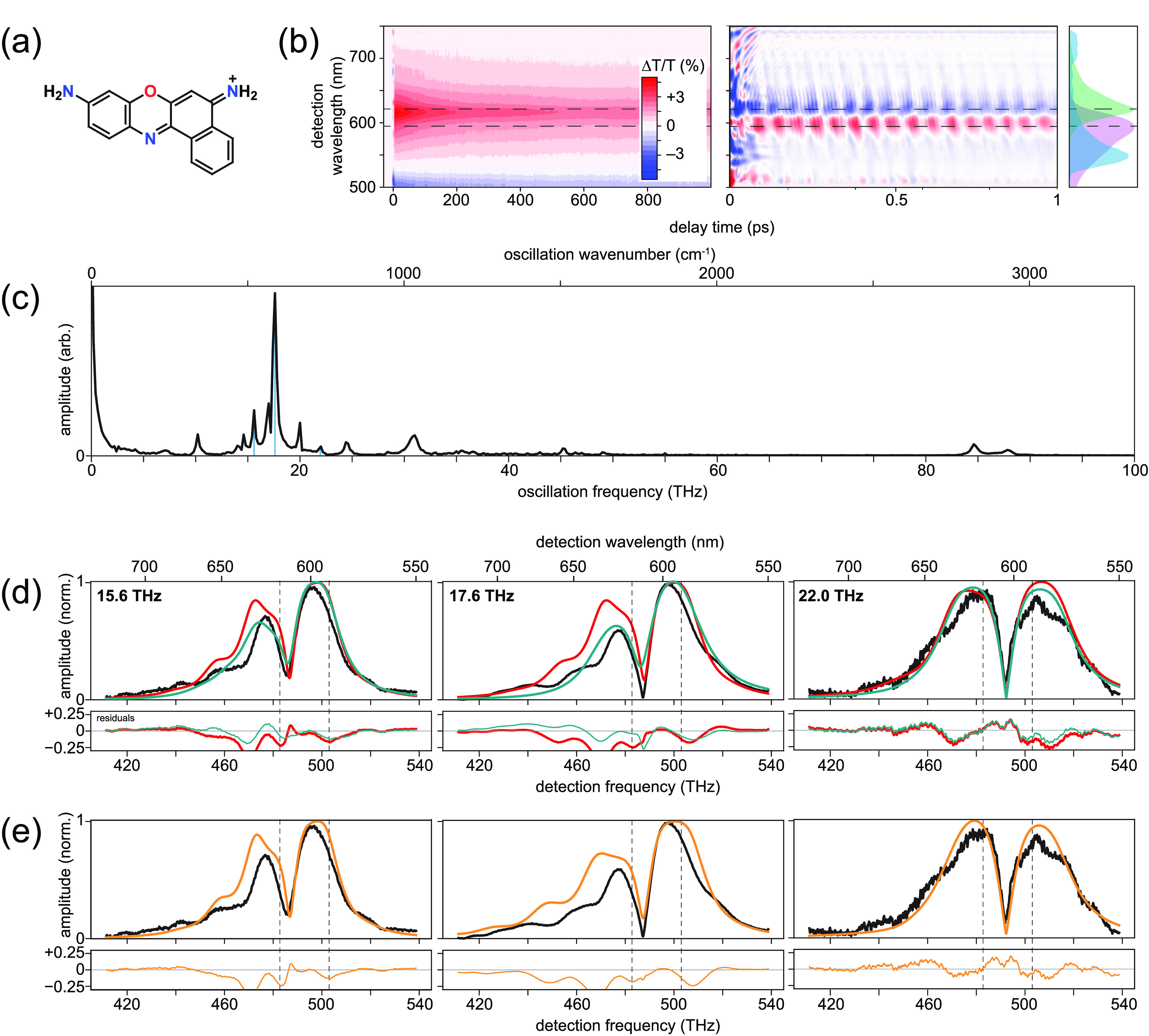
Results for cresyl violet. (a) Molecular structure. (b) Measured transient-absorption spectra, with population decays subtracted from the 1 ps data set view. Absorption and fluorescence spectra displayed in violet and green, respectively, along with the laser pulse spectrum in cyan. (c) 1D vibronic spectrum. Vertical blue lines indicate peaks to be analyzed with FCS. (d) Measured (black) and fitted harmonic (red) and anharmonic (dark cyan) FCS amplitude profiles at indicated oscillation frequencies. (e) Measured (black) and unequal-curvature harmonic (dashed orange) FCS amplitude profile at indicated frequencies. Dashed lines in panels b, d, and e indicate absorption and fluorescence maxima.

Panel b in Figure 3 displays measured transient–absorption spectra on 1 ns and 1 ps time scales, the latter revealing the vibrational quantum beats as oscillatory signals that appear in addition to the conventional, slowly decaying ground-state bleach and stimulated emission signals. An excited-state absorption band appears at detection wavelengths below about 510 nm (588 THz). Subtraction of the slowly decaying signals, Fourier transformation, and subsequent summation over all detection frequencies lead to the 1D vibronic spectrum displayed in panel c, which reveals the oscillation frequencies of the vibrational modes. There are 14 peaks above the noise: 7.2, 10.2, 14.6, 15.6, 17.0, 17.6, 20.0, 22.0, 24.4, 31.0, 45.2, 49.0, 84.6, and 87.6 THz. These values are consistent with prior spectroscopic measurements of cresyl violet,⁸³⁻⁸⁵ and again the peaks near 31, 85, and 88 THz arise from methanol.

Parallel to the rhodamine 101 analysis, we focus on three representative modes. The measured FCS displayed in black traces in panel d in Figure 3 reveal that all three modes have the two-peak/single-node profile of fundamental vibrational modes. We therefore first apply fits using the harmonic model (red traces in panel d of Figure 3). The fits detailed in Table 2 have R² ranging from 0.7 to over 0.9 and yielded extracted Huang–Rhys factors of 0.25, 0.24, and 0.01 for the 15.6, 17.6, and 22.0 THz modes, respectively. These values seem reasonable when compared to values of similar molecules;^13,14 however, the fits of the 15.6 and 17.6 THz modes struggled to reproduce the low-frequency peaks at about 470 THz. The results of the unequal-curvature harmonic model were almost identical to the harmonic model—the ϵ values were very nearly unity; hence, we do not evaluate this model further. Finally, we apply fits using the anharmonic model. This model improved the results for the 15.6 and 17.6 THz modes and produced negligible changes for the 22.0 THz mode. The R² values for all modes rise to above 0.9, and the effective Huang–Rhys parameters extracted were, respectively, 0.32, 0.15, and 0.20. These values also seem plausible.

Table 2. Fit Results of Cresyl Violet for the Three FCS Models^a.

	harmonic		anharmonic				unequal harmonic
ω0/(2π)		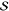R2		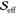λbest	χ	R2		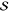ϵ	R2
15.6	0.25	0.855	0.32	5	1.56	0.947	0.27	0.98	0.856
17.6	0.24	0.710	0.15	2	4.4	0.919	0.22	1.09	0.718
22.0	0.01	0.946	0.20	28	0.4	0.951	0.00	0.95	0.955

^aAll values are dimensionless except ω₀ and χ, which are in units of THz. The value of 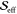for the 22.0 THz mode arises from a negative 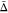value.

Because of the planarity of the cresyl violet molecule and its modest S₀–S₁ geometry changes, quantum-chemical calculations of the vibronic modes were more successful than those for rhodamine 101. Section S4 of Supporting Information contains further details. Briefly, of the 11 nonsolvent peaks observed in the 1D vibronic spectrum, 10 appear in the computations and their frequencies agree to within <10% of the measured frequencies. The very weak 22.0 THz mode did not appear in the computations, and we analyze it further below. The salient results are that the computed Huang–Rhys factors were 0.07 and 0.28 for the 15.6 and 17.6 THz modes, respectively. While quantitatively there is some disagreement between values extracted from the measurements and the computational results, the general trend is the same.

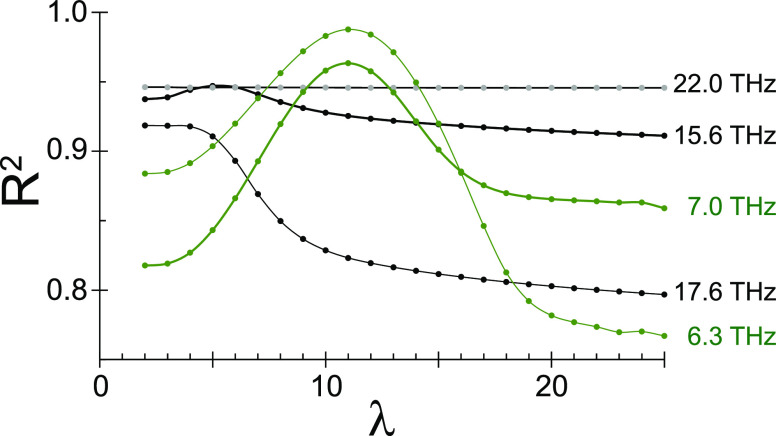
Comparing the fit results between the harmonic and anharmonic models suggests that the 22.0 THz mode is harmonic and 15.6 and 17.6 THz have some anharmonicity. To bolster this confirmation, we can inspect R²(λ), which is the coefficient of determination at each value of λ for the anharmonic model. Figure 4 displays the R²(λ) results for both molecules. In the case of a very harmonic potential, there should be negligible variation in the coefficient of determination for values of λ above a certain threshold. In contrast, an anharmonic potential should yield fits that are worse both above and below a preferred λ value. In Figure 4, the R²(λ) curves for both modes of rhodamine have maxima near λ ≈ 10, supporting the earlier assessment that these modes have significant anharmonicity. In sharp contrast to these maxima, the R²(λ) curve for the 22.0 THz mode of cresyl violet is essentially flat, having no visible maximum. The R²(λ) data sets for the 15.6 THz mode of cresyl violet displays a weak maximum at λ = 5. Finally, the R²(λ) data set for the 17.6 THz mode of cresyl violet shows a maximum at λ = 2. These data for cresyl violet support the conclusion that the 22.0 THz mode is harmonic and that the 15.6 and 17.6 THz modes have anharmonicity.

Figure 4.

Coefficient of determination dependence as a function of anharmonicity, R²(λ), for two modes of rhodamine 101 (green) and three modes of cresyl violet (black/gray). The 22.0 THz mode of cresyl violet is essentially flat, indicating no perferred value of λ.

These results contribute to the debate surrounding the strongly coupled vibronic mode (17.6 THz) of cresyl violet, using the 22.0 THz mode as an internal control. The asymmetric peak heights in the FCS profile of the 17.6 THz mode suggest that the harmonic models will fail, and indeed, these models struggle both qualitatively and quantitatively to fit the measured spectrum. In contrast, the relative symmetry of the two peaks in the FCS profile of the 22.0 THz mode suggest that the harmonic models will fit well, and this is borne out both qualitatively and quantitatively. The anharmonic model yields essentially no improvement to the fit of the 22.0 THz mode, whereas this model yields a substantial improvement for the 17.6 THz mode. Further, the R²(λ) function has a maximum at a low value of λ = 2. Taken together, these observations are inconsistent with the hypothesis that the 17.6 THz mode is strongly harmonic and support the hypothesis that this mode has significant anharmonicity. More broadly, the data presented here indicate that anharmonicity plays a key role in most of the analyzed vibrational modes. Hence, while the displaced harmonic oscillator model is very useful for pedagogical and qualitative understanding of vibrational spectroscopy signals, it seems inadequate for quantitative analysis of vibrational quantum beats in femtosecond transient–absorption spectra, which may require an anharmonic analysis such as the Morse oscillator model derived and used in this work.

In conclusion, we have refined the harmonic and anharmonic (Morse oscillator) models of FCS profiles arising from vibrational quantum beats, and we have developed a new harmonic model for the case of the ground and excited states having distinct curvatures. The harmonic models of fundamentals and overtones include explicit dependence on the Huang–Rhys factor, 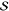, and conventional anharmonicity, χ. These models are useful for studying excited-state vibrational modes and, in particular, low-frequency excited-state vibrational modes that are challenging to study with frequency-domain vibrational spectroscopy methods such as Raman spectroscopy. The data and analyses of two laser dye samples demonstrate that combined use of the harmonic and anharmonic FCS models can provide qualitative insights into the vibrational quantum beats and the topography of the excited-state potential energy surface near the Franck–Condon region. The extracted Huang–Rhys values for three modes of cresyl violet were somewhat consistent with values produced by quantum-chemical calculations, which were restricted to the harmonic approximation. The key observable related to the extracted Huang–Rhys factors and anharmonicity is the asymmetry of the two peaks on either side of the node in the amplitude profile of the FCS. The ratio of peak heights strongly affects the values obtained for these two microscopic vibrational parameters. We conducted a preliminary analysis of three additional factors—the pump-pulse spectrum, adding a second mode, and nonzero temperature—that could potentially affect the ratio; thus far, no adjustment to the model has produced a strong effect. Therefore, future work is needed to re-evaluate the assumptions of the models to assess the accuracy of the extracted values. For example, one could consider limitations of the Condon approximation or the evolution of the system during the pump pulse. We found that an effective assessment of anharmonicity should include evaluating the coefficient of determination R²(λ), which is the dependency of the anharmonic fit on the number of bound vibrational eigenstates. Despite these promising advances, the models do not yet meet quantitative expectations. Therefore, future efforts will be needed to reassess the assumptions underlying the models and to understand additional challenges that complicated this analysis. A salient issue is to resolve any effects of using 1D models to fit data arising from measurements of a molecule having a ∼3N-dimensional potential-energy surface. We previously showed that including a second mode affects the peak widths,⁶⁹ but a future detailed study may reveal changes to the extracted Huang–Rhys factors. Furthermore, including at least one more mode would allow the introduction of a Duschinsky rotation matrix and thereby more reliably modeling spectra from molecules such as rhodamine 101. Despite the nuances, the results indicate the utility of the FCS models for studies of vibrational quantum beats in femtosecond transient-absorption spectroscopy measurements of molecules and molecular aggregates.

Methods

Laboratory Methods. We acquired rhodamine 101 (C₃₂H₃₁N₂O₃·ClO₄; Rhodamine 640 Perchlorate) and cresyl violet (C₁₆H₁₁N₃O₂·HClO₄; Cresyl Violet 670 Perchlorate) from Luxottica Exciton and dissolved each solid dye sample in anhydrous spectroscopic-grade methanol (Sigma-Aldrich). To reduce scatter, we filtered each solution using a 0.45 μm poly(ether sulfone) syringe filter (VWR) prior to optical measurements. The peak optical density (OD) was about 0.25. We used Cary 5000 and Horiba FL3-21 instruments to collect the absorption and fluorescence spectra, respectively.

The output of a commercial 1 kHz amplified Ti:sapphire laser producing ∼150 fs pulses centered at 806 nm pumped a home-built noncollinear optical parametric amplifier identical to one used in prior works.^4,91 The ultrabroadband laser pulses spanned from approximately 510 to 750 nm, and the shot-to-shot stability was ∼1% relative standard deviation. Two sets of dispersion-compensating mirror pairs adjusted the temporal dispersion of the pulse, which had a pulse duration of about 8.8 fs based on second-harmonic generation frequency-resolved optical gating measurements (see Figure S5), conducted using a 10 μm thick beta barium borate crystal (Newlight Photonics).

The pump–probe spectrometer included a computer-controlled delay stage (Newport XMS50-S) to adjust the timing of the pump pulse relative to the probe pulse, and we performed the scans with 1 fs steps to minimize the presence of scatter in the FCS profiles. The only transmissive optic was a 1 mm thick ultraviolet fused silica 10% reflective beamsplitter that was antireflection coated for 440–1020 nm on the back side (Layertec), which separated the pump and probe beams. An identical optic placed in the probe arm equalized the dispersion and created a reference beam used for balanced detection. The electronics package included a phase-locked rotary optical chopper (New Focus 3502) in the pump arm, a data-acquisition board (NI PCI-6281), and an amplified photoreceiver (New Focus 2001-FS) to implement the optimal balanced detection algorithm.⁹² The spectrally resolved detector consisted of an Andor Kymera 193i and Zyla 5.5 sCMOS camera, calibrated to an estimated ±1 nm using a linear fit to multiple peaks from an atomic lamp. We report transient-absorption spectra as percent transient transmittance, ΔT/T.

We quantify the error between the fitted, F(ω), and measured, M(ω), FCS using the coefficient of determination

4

where M̅ is the mean of the measured spectrum. We used the curve fit function of Python and SciPy to perform the nonlinear least-squares fits of the models to the measured FCS spectra.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.1c04162.

• (PDF)

The authors declare no competing financial interest.