Active cytoskeletal composites display emergent tunable contractility and restructuring

Abstract

The cytoskeleton is a model active matter system that controls processes as diverse as cell motility and mechanosensing. While both active actomyosin dynamics and actin–microtubule interactions are key to the cytoskeleton’s versatility and adaptability, an understanding of their interplay is lacking. Here, we couple microscale experiments with mechanistic modeling to elucidate how connectivity, rigidity, and force-generation affect emergent material properties in composite networks of actin, tubulin, and myosin. We use multi-spectral imaging, time-resolved differential dynamic microscopy and spatial image autocorrelation to show that ballistic contraction occurs in composites with sufficient flexibility and motor density, but that a critical fraction of microtubules is necessary to sustain controlled dynamics. The active double-network models we develop, which recapitulate our experimental findings, reveal that while percolated actomyosin networks are essential for contraction, only composites with comparable actin and microtubule densities can simultaneously resist mechanical stresses while supporting substantial restructuring. The comprehensive phase map we present not only provides important insight into the different routes the cytoskeleton can use to alter its dynamics and structure, but also serves as a much-needed blueprint for designing cytoskeleton-inspired materials that couple tunability with resilience and adaptability for diverse applications ranging from wound healing to soft robotics.

Introduction

The cytoskeleton is an active network of proteins, including semiflexible actin filaments, rigid microtubules, and motor proteins, that maintains cell structure and facilitates essential functions such as migration,^1,2 division,^3-5 and intracellular transport.^6-8 These diverse processes are driven by the cytoskeleton’s ability to actively self-organize and restructure, for example by myosin II motors actively crosslinking, pushing and pulling actin filaments.^9,10 Actomyosin interactions generate contractile forces and flow,¹¹ playing an important role in processes ranging from contractile ring formation during cell division¹² to lamellipodia adhesion during cell migration.¹³

In vitro studies of actomyosin networks show that active material properties such as contraction can only be achieved by fine-tuning the densities of actin, passive crosslinkers, and myosin.^14-20 In crosslinked actin networks, contraction only occurs for a limited range of crosslinker:actin ratios: too low (< 0.05) and the network is insufficiently connected to transmit force, while too high (>0.15) and the network becomes too rigid to respond.¹⁶ Within the active range, reported contraction rates varied by a factor of ~3. Other studies have shown that a critical motor density is required for contractility, but contraction rates do not change substantially above this density.¹⁷ Further, organized contractile dynamics and restructuring have often required confining actomyosin networks to quasi-2D geometries crowded to a surface, and have typically been limited to ~5 min of observed activity.^19,20 More recently, studies of 3D actin networks confined in vesicles have reported more prolonged actomyosin activity,^21,22 crosslinker-dependent membrane deformations,^23,24 and interactions between microtubules and actin networks.²⁵ Here, to increase the tunability, longevity, resilience, and viability of actomyosin active matter as a functional material, we couple microtubules to 3D actomyosin networks and combine experiments with modeling to systematically explore a broad parameter space of composite formulations and spatiotemporal scales. Our results also shed important new light on the role that actin–microtubule interactions play in actomyosin dynamics in the cytoskeleton.

Steric actin–microtubule interactions are integral to in vivo cytoskeleton processes.^25-29 The ability of stiff microtubules, with ~100× larger persistence length than semiflexible actin filaments (~1 mm vs. ~10 μm) to bear large compressive loads, plays an important role in balancing actomyosin contraction during cell migration.^30,31 Meanwhile, actin networks reinforce the mechanical stability of microtubules by increasing elasticity, reducing their likelihood to buckle, and limiting their growth.^25,32,33 Further, previous in vitro studies show that co-entangled actin–microtubule systems exhibit emergent mechanical properties, such as concomitant stiffness and mobility, that are not possible in single component systems,^34-36 highlighting the promise of cytoskeleton composites as a model platform for material design and engineering.

While active actomyosin systems have been extensively studied, active actin–microtubule composites remain almost entirely unexplored. We previously showed that a co-entangled composite of microtubules and actin filaments driven by myosin II exhibited surprisingly controlled and reproducible contraction in the absence of crosslinkers,³⁷ which we attributed to microtubules increasing network connectivity and providing extensile reinforcement against flow.^38,39 Here, to build on this proof-of-concept study, we couple time-resolved differential dynamic microscopy and spatial image autocorrelation with active double-network modeling to map the phase space of active dynamics to composite formulation. We reveal how the myosin-driven dynamics of varying composites evolve over long times, and connect the active dynamics to network restructuring and mechanical moduli.

Results

We create and simulate co-entangled actin–microtubule networks driven by myosin II motor activity and systematically tune the molar actin fraction (Φ_A = [actin]/([actin] + [tubulin])) and molar myosin concentration (c_M) (Fig. 1). We image composites using multi-spectral confocal microscopy (Movie S1, ESI^†) and employ differential dynamic microscopy (DDM) and spatial image autocorrelation (SIA) to quantify the active dynamics as well as the spatiotemporally varying composite structure. Further, we perform simulations of active biopolymer double-networks to understand the mechanisms underlying our experimental results and correlate measured dynamics and restructuring to mechanical properties. To determine the fraction of actin necessary to maintain activity and the fraction of microtubules necessary to maintain controlled dynamics, we vary Φ_A while holding the combined concentration of actin and tubulin fixed. To determine what range of myosin concentrations drives organized contractility over sustained periods of time, we vary the molar myosin concentration c_M from 0.12–0.48 μM and examine network dynamics over extended time periods (~45 min to several hours). We note that the protein concentrations used here are lower than those found in cells, with reported values of ~50–500, ~5–20, and ~0.5–5 μM for actin, tubulin and myosin II, respectively.^40-42 We instead honed our parameter space through ample trial-and-error testing based on previous in vitro studies of actomyosin and actin–microtubule systems that showed potential as tunable, resilient, active materials.^35,37,43 We show that increasing molar actin fraction Φ_A and myosin concentration c_M generally results in greater contraction and restructuring in both experiments and simulations (Fig. 1). However, there are important exceptions to this rule and emergent regions of the phase space that we describe below.

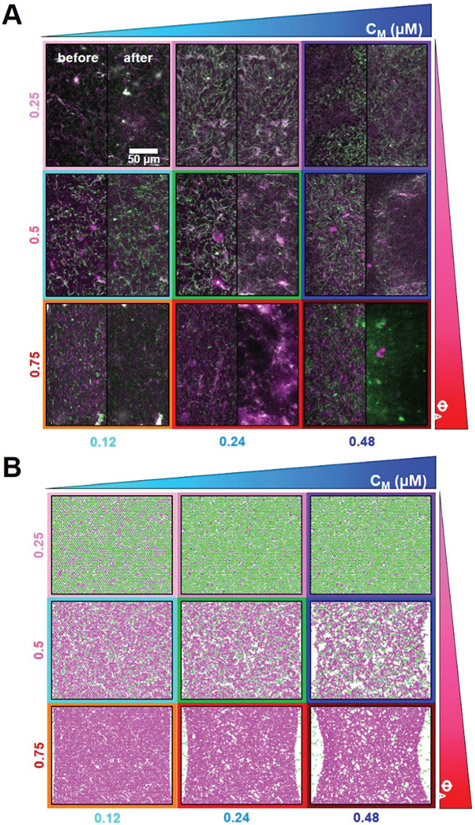
Fig. 1.

Tuning the composition of active cytoskeleton composites. (A) 256 × 128 pixel (212 × 106 μm) two-color confocal microscopy images show how composites of actin filaments (magenta) and microtubules (green) are rearranged via myosin II motor activity (Movie S1, ESI^†). In each panel, images taken at the beginning (left, before) and end (right, after) of the 45 min myosin activation are shown. Panels are ordered by increasing myosin concentration (c_M, blue) going from left to right and increasing molar fraction of actin (Φ_A, red) going from top to bottom. The colors outlining each panel match the color coding used in subsequent figures. Scale bar pertains to all images. (B) Deformation of a simulated active biopolymer double-network for parameters shown in (A). Simulations show how double-networks made of an actomyosin network (magenta) and a microtubule network (green) deform for varying concentrations of myosin and actin. As in (A), panels are ordered by increasing myosin concentration (c_M, blue) from left to right and increasing actin fraction (Φ_A, red) going from top to bottom. Simulation box size is 88 × 73 μm for all images.

To quantify active dynamics and restructuring, we perform differential dynamic microscopy (DDM) on the separate actin and microtubule channels of each time-series collected for each composition. With DDM, we determine the rate at which density fluctuations decay over time⁴⁴ (see Methods). Fig. 2A shows representative DDM image structure functions D(q, Δt) for the composite formulations shown in Fig. 1. As shown, the dependence of D(q,Δt) on the lag time Δt is similar for both actin and microtubule channels for each (Φ_A, c_M) combination, indicating synchronized movement of actin filaments and microtubules across all composites. However, the lag time at which each D(q,Δt) reaches a decorrelation plateau, signifying the time at which the composite is sufficiently decorrelated from its previous configuration, depends strongly on composition.

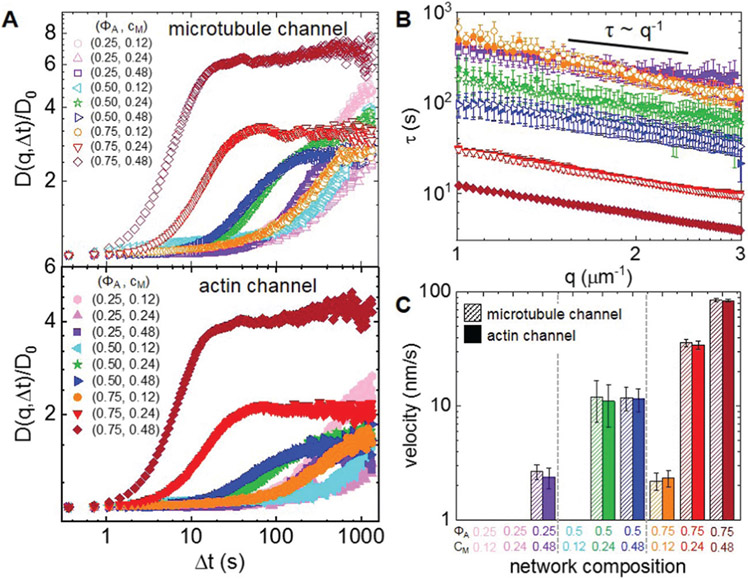
Fig. 2.

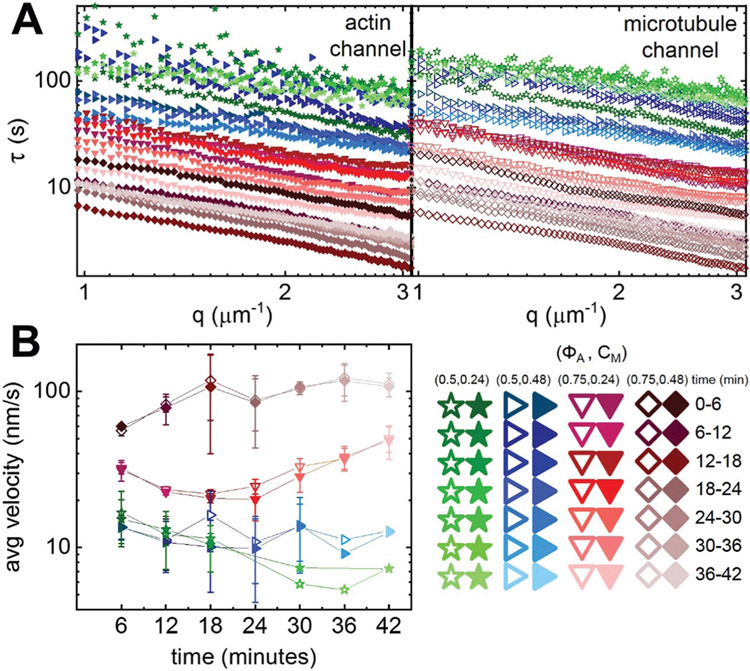
Differential dynamic microscopy shows that composite contraction dynamics can be independently tuned by the actin fraction and myosin concentration. (A) Representative image structure functions D(q, Δt) of varying active composites, normalized by the corresponding initial value D₀, at wavenumber q = 1.481 μm⁻¹. DDM is performed separately on microtubule (top, open symbols) and actin (bottom, filled symbols) time-series channels. The lag time dependence for all curves is largely indistinguishable when comparing actin and microtubule channels. For the actin channel, image structure functions of composites with lower myosin concentrations c_M (cyan left pointing triangles) and lower actin fractions Φ_A (light pink hexagons, pink upwards pointing triangles) do not reach plateaus, while those of composites with higher myosin concentrations and actin fractions reach decorrelation plateaus at varying lag times (purple squares, green stars, blue right pointing triangles, orange circles, red downwards pointing triangles, maroon diamonds). (B) Average characteristic decay time τ vs. wavenumber q for both actin (filled symbols) and microtubule (open symbols) channels for each condition that reached a plateau in (A). All curves follow τ ~ q⁻¹ scaling for q = 1–3 μm⁻¹, indicating ballistic motion. Symbol colors and shapes correspond to legends in (A). (C) Average contraction velocities k extracted from fitting τ(q) curves in (B) to τ = (kq)⁻¹. Error bars in (B) and (C) represent the standard error of values across 3–5 replicates.

D(q, Δt) curves for networks containing Φ_A < 0.5 and c_M < 0.24 μM do not exhibit plateaus within the experimental time frame, indicating undetectable movement. Data taken in the absence of myosin or blebbistatin deactivation show similar curves that lack plateaus (Fig. S1, ESI^†), verifying that the plateaus observed in the other composites arise from motor-driven dynamics (Fig. 2). Of the composites that exhibit plateaus, the lag time at which a plateau is reached markedly decreases with increasing actin fraction. Myosin concentration appears to play a less important role, though a critical c_M is required for detectable active motion.

For image structure functions that reach plateaus, we extract a characteristic decay time τ for each wavevector q (see Methods) (Fig. 2B). For all cases, τ(q) curves for actin and microtubule channels overlap, again indicating coordinated dynamics. Further, all curves approximately scale as τ ~ q⁻¹ (Table S1, ESI^†), signifying ballistic motion. The magnitude of τ(q) determines the contraction rate and depends on composite formulation. By fitting each curve to τ ~ (kq)⁻¹, we determine a composite-dependent contraction velocity, k (Fig. 2C). We find similar contraction velocities in both actin and microtubule channels for all compositions, as expected from similar τ(q) curves. The composite with (Φ_A, c_M) = (0.75,0.48) contracts the fastest at 85 ± 2 nm s⁻¹, similar but still slower than the velocity of 90 ± 20 nm s⁻¹ we measured for a 100% actin network (Φ_A = 1) with a lower myosin concentration (c_M = 0.24, Fig. S2, ESI^†). Lowering the actin fraction from Φ_A = 0.75 to 0.5 reduces the contraction speed by a factor of ~7 to ~12 nm s⁻¹, which is surprisingly unaffected by reducing the myosin concentration from c_M = 0.48 to 0.24 μM. Further lowering Φ_A or lowering c_M results in ~6× reductions in contraction velocity, with the two slower composites exhibiting similar speeds (~2.3 nm s⁻¹).

To correlate contraction dynamics with motor-driven restructuring, we analyze the spatial autocorrelation of images at uniformly distributed time-points throughout each time-series (see Methods) (Fig. 3). For a specific image in a time-series, the autocorrelation g(r) determines the degree to which the intensity at one location in the image correlates with the intensity of the surrounding points at varying distances.⁴⁵ The more quickly g(r) decays, the smaller the structural features of the network.

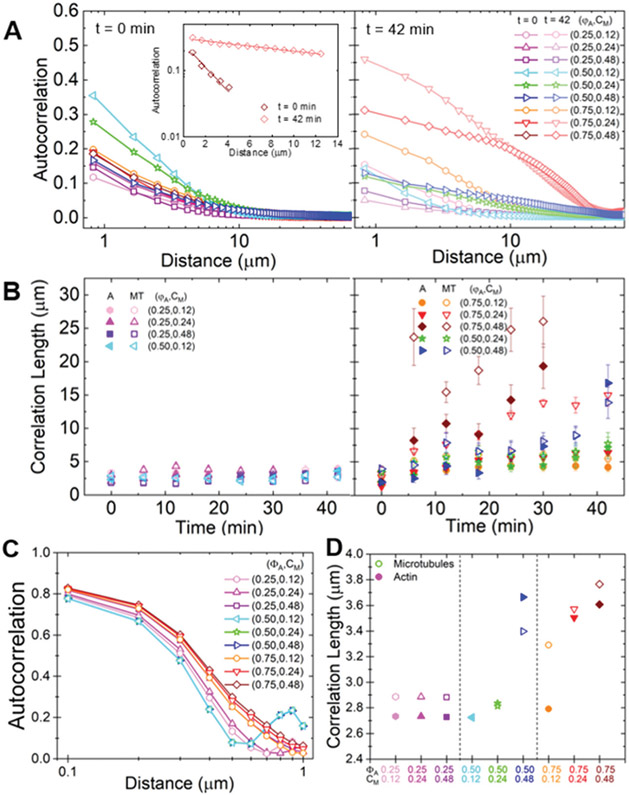
Fig. 3.

Spatial image autocorrelation analysis reveals that myosin activity increases correlation lengths in a tunable manner independent of measured velocities. (A) Average autocorrelation curves g(r) for the microtubule channel for all composite formulations at the beginning (left, t = 0 min, dark shades) and end (right, t = 42 min, light shades) of the experimental window. The inset shows example fits of g(r) curves to $g(r)=A{\mathrm{e}}^{-\frac{r}{\lambda }}$ at the initial and final times for the (Φ_A, c_M) = (0.75, 0.12) composite. (B) Average correlation lengths λ for actin (closed symbols) and microtubule (open symbols) channels for each composite formulation determined from exponential fits (see inset in A) to the corresponding autocorrelation curves. Data is divided into composites that exhibit minimal restructuring (left) versus substantial restructuring (right). Error bars in (A) and (B) represent the standard error of values across 3–5 replicates. (C) Autocorrelation curves g(r) for the microtubules in all simulated composites. (D) Correlation lengths λ for actin (filled symbols) and microtubules (open symbols) comprising each simulated composite, determined from exponential fits to the corresponding autocorrelation curves shown in (C). Simulations predict the state of the composite after contraction so should be compared to experimental data at the end of the experimental window.

As shown in Fig. 3A, g(r) curves generally broaden from initial to final time-points, indicating that structural feature sizes increase during activity. This broadening is particularly noticeable for (Φ_A, c_M) = (0.75, ≥0.24) composites, where we observe the formation of dense foci separated by large voids during activity (Fig. 1A). In general, the slower decay of g(r) suggests that myosin II motors rearrange the composites from homogenous meshes of individual filaments to networks of denser bundles or aggregates. In order to quantify the degree of restructuring and its dependence on composite formulation, we fit g(r) to an exponential $g(r)=A{\mathrm{e}}^{-\frac{r}{\lambda }}$, where λ is the characteristic decay length or correlation length (Fig. 3A inset).

Fig. 3B shows the average correlation lengths as a function of time, λ(t), for actin and microtubule channels for each composition. While the time-dependence of λ for both filament types displays a complex dependence on network composition, we can nonetheless crudely separate networks into those that appreciably restructure over time and those that do not. Specifically, we find that λ(t) stays roughly constant over time for all Φ_A = 0.25 conditions, as well as for the (Φ_A, c_M) = (0.50, 0.12) condition. This finding suggests that Φ_A = 0.25 networks are too rigid, and c_M = 0.12 μM networks contain insufficient motor density, to allow for noticeable rearrangement.

While the actin and microtubule networks in all compositions start with approximately the same λ values, networks containing the highest actin fraction or highest myosin concentration exhibit the greatest increase in λ over time, indicating the greatest degree of restructuring. Interestingly, unlike most other conditions, correlation lengths for actin filaments and microtubules markedly decouple from one another for the (Φ_A, c_M) = (0.75, 0.24) and (Φ_A, c_M) = (0.75, 0.48) formulations. While λ(t) for the microtubule channel reaches 15 ± 2 μm and 26 ± 4 μm, respectively, the corresponding actin correlation lengths only increase to 6.4 ± 0.9 μm and 17 ± 3 μm. This effect is also apparent, though subtler, in the Φ_A = 0.75 composite with lower motor concentration c_M = 0.12 μM. Given that myosin acts solely on the actin network, the more substantial restructuring of microtubules compared to actin in this composite is particularly noteworthy. Conversely, for the other formulation that exhibits the most extreme restructuring, (Φ_A, c_M) = (0.5, 0.48), the correlation lengths for actin and microtubule channels both increase ~5×.

To directly compare our experiments with simulations, we compute the spatial autocorrelation of the images of simulated composites, as well as the corresponding correlation lengths (Fig. 3C and D). Because the simulation images represent the state of the system after contraction, the results are best compared to the final time points in our experiments. As shown, both g(r) and λ have similar dependences on Φ_A and c_M for both experiment and simulations, and the corresponding values for the minimally restructured networks (all Φ_A = 0.25 formulations and (Φ_A, c_M) = (0.5, 0.12)) are comparable. Further, as with experiments, the most dramatic restructuring in simulations occurs for the Φ_A = 0.75 composites as well as the Φ_A = 0.5 composite with the highest myosin concentration. Moreover, the correlation length for the microtubules increases more than that of the actin in these actin-rich composites – just as in experiments – while for the Φ_A = 0.50 cases, microtubule λ values are comparable or lower than those for actin. The key difference between experiment and simulation results are the smaller distances over which the autocorrelations decay in simulations, which result in smaller correlation length values. This difference is due to the permanent filament crosslinking in simulated networks that hinders the large-scale restructuring that steric entanglements allow for.

To further shed light on these intriguing restructuring data, we generate spatially-resolved contour maps of the contractile and extensile strains experienced by our simulated composites (Fig. 4A). As in our experiments, the strain fields for actin and microtubule networks appear correlated for most conditions. While there are slightly more extensile regions in the microtubule network and more contractile regions for actin due to the larger stiffness of microtubules compared to actin, the degree and affinity of deformations are similar for both networks. The exception to this rule is Φ_A = 0.75. Similar to our SIA analysis (Fig. 3), we see significant changes in the structure of the microtubule networks that are distinct from the actin contractility. While the actin network undergoes homogeneous contractility that is stronger than the other network formulations (indicated by more red regions), the microtubule network separates into large distinct regions of deformation. The more homogeneous nature of the simulated composite strains compared to experiments arises from the crosslinking imposed in simulations.

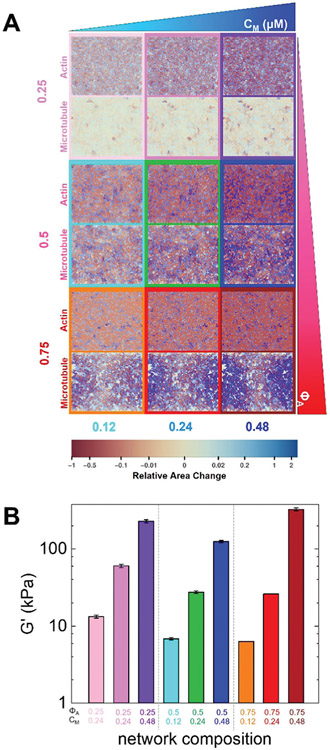
Fig. 4.

Active double-network modeling shows tunable restructuring and rigidity of myosin-driven actin–microtubule composites. (A) Heat maps for strains experienced by actin and microtubule networks in the active double-network model for myosin concentrations and molar actin fractions shown in Fig. 1. Contractile strains are shown in shades of red and extensile strains are shown in shades of blue, with darker colors representing larger strains, as described by the color scale which maps the color to the fractional change in area of each ~1 μm² region of the network. The strain maps for the actin network and microtubule network for each condition are shown in the top and bottom of each panel, respectively. Simulation box size is 88 × 72 μm for all images. (B) Elastic modulus G′ of a simulated active double-network for parameters shown in Fig. 1B. The values shown are the average and standard error over 5 simulation runs.

We also compute the elastic modulus G′ of our simulated double-network and show that for a given Φ_A, G′ is significantly larger for composites with higher myosin concentrations, due to the motors rigidifying the actin network via contraction (Fig. 4B). At the highest myosin concentration, the actin-rich composite (Φ_A = 0.75) has the largest G′ while for the lowest myosin concentration, the microtubule-rich composite (Φ_A = 0.25) has the largest G′ (Fig. 4). The rigidity in the actin–dense composites (at high c_M) arises from more pronounced contraction compared to the other networks, while in the microtubule–dense composites, the rigidity (at low c_M) comes from the steady-state rigidity of the microtubules themselves. The emergent low-rigidity regime at comparable actin and microtubule concentrations (Φ_A = 0.50) results from both networks being close to the rigidity percolation threshold, thereby allowing for restructuring via non-affine deformations. Similar to simulations, previous experiments⁴⁶ on similar composites showed that the elastic modulus G′ increased with increasing motor activity for all Φ_A values (0.25–0.75). However, the degree to which G′ increased depended on the actin fraction, just as it does in our simulations. Specifically, microtubule-rich (Φ_A = 0.25) composites exhibited the smallest increase in G′ (a factor of ~10), while Φ_A = 0.5 and Φ_A = 0.75 composites exhibited a ~100-fold increase. We note that while the trends in G′ are similar for simulations and experiments, simulation values are an order of magnitude higher (see ESI^† for conversion to experimental units), most likely due to the fact that in simulations all filament crossings are permanent (i.e., both actin and microtubule networks are completely crosslinked, see ESI^†) whereas in experiments, the only crosslinkers are the active, transient myosin motors.

To determine whether the varying degrees of composite restructuring and rigidity impact the dynamics over the course of activity, we perform time-resolved DDM over the same 6 min time intervals that we use for our SIA analysis (Fig. 5). Over these shorter time intervals, D(q, Δt) curves only reach plateaus for the composites with Φ_A ≥ 0.5 and c_M ≥ 0.24 μM. Fig. 5A shows time-resolved τ(q) curves for these formulations. For all cases and time-points, τ(q) curves for actin and microtubules are comparable, similar to our analysis over the entire activity window but at odds with our structural analysis for the Φ_A = 0.75 composites. Further, τ(q) curves for both Φ_A = 0.5 cases exhibit only modest time-dependence compared to the Φ_A = 0.75 cases which appear to appreciably decrease over the experimental window. By fitting each τ(q) curve to τ ~ (kq)⁻¹, we compute corresponding time-dependent contraction velocities (Fig. 5B). While the velocities for composites with equimolar actin and tubulin (Φ_A = 0.50) show minimal time-dependence, the high Φ_A cases accelerate during the activity time.

Fig. 5.

Time-resolved differential dynamic microscopy shows higher actin fractions result in accelerating contraction dynamics. (A) Characteristic decay time τ vs. wavenumber q for actin (filled symbols, left) and microtubule (open symbols, right) channels for consecutive 6 min intervals during the 45 min activation time of a representative time-series. Curves follow τ ~ q⁻¹ scaling, indicating ballistic motion. Varying colors and symbols correspond to different composite formulations and time intervals as depicted in the legend (lower right). τ(q) curves for the Φ_A = 0.75 composite (red, downward-pointing triangles) are lower in magnitude and show substantially more time-dependence compared to both Φ_A = 0.5 composites. Both Φ_A = 0.5 composites also have overlapping τ(q) curves, indicating negligible dependence of time-resolved dynamics on the myosin concentration c_M. (B) Contraction velocities for actin filaments (closed symbols) and microtubules (open symbols) for each 6 min interval of every analyzed time-series, extracted from fitting corresponding τ(q) curves. Error bars represent the standard error of values across 3–5 replicates. Symbol colors and shapes match Fig. 3 and correspond to (Φ_A, c_M) combinations shown in the legend.

Discussion

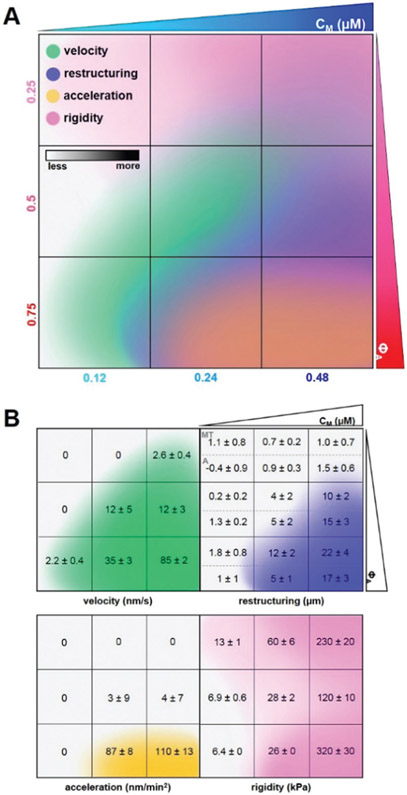
To bring together the results of our experimental and theoretical analyses, we construct a cartoon phase diagram that maps measured and simulated characteristics to composite formulation (Fig. 6A). The values provided in the lower panels (Fig. 6B) come directly from experiment or simulation, while the color gradients are qualitative representations of the measured values. The region of formulation space with comparable actin and microtubule concentrations (Φ_A = 0.5) and sufficient myosin concentrations (c_M ≥ 0.24 μM) exhibits measurable contractile dynamics and substantial restructuring without deleterious acceleration or decorrelation of actin and microtubule networks. Additionally, the degree of restructuring and rigidity in Φ_A = 0.5 composites can be tuned by increasing myosin concentration without appreciably altering the contraction rate. As such, sustained ballistic contraction and structural integrity over extended periods of time is achieved when composites reach a careful balance between increasing concentrations of motors (c_M) and microtubules (1 − Φ_A). We discuss this emergent behavior, and other intriguing results, below.

Fig. 6.

Cartoon phase diagram of active cytoskeleton composite dynamics mapped to the corresponding composite formulation (Φ_A, c_M) highlights tunability and desirable properties of active composites. (A) Comprehensive phase diagram showing how myosin-driven composite velocities (green, determined from DDM), restructuring (blue, determined via SIA), acceleration (yellow, determined from time-resolved DDM), and rigidity (pink, determined via double-network simulations) vary in formulation space (Φ_A, c_M). Darker shading of each color qualitatively indicates increasing metric values quantified within the separated figures in (B). Velocities are averaged over both actin and microtubule channels as we observed similar dynamics for both filaments in all cases. Degree of restructuring is calculated by taking the difference in final and initial correlation length (Δλ = λ_final − λ_initial), and is reported separately for microtubules (top, MT) and actin (bottom, A) because we observed instances of significant differences in Δλ for the two filaments. Acceleration is calculated by computing the average change in velocity over time. Rigidity is calculated by performing simulations under 0.005% shear to obtain the elastic modulus G′. Composites with Φ_A = 0.5 and sufficiently high c_M exhibit coordinated contractile dynamics and rearrangement without destructive network acceleration or decorrelation of actin and microtubule restructuring.

Our results suggest that higher ratios of semiflexible actin filaments to rigid microtubules offer less resistance to motor-generated forces and provide more pathways for force transmission. However, increasing flexibility past a certain threshold compromises material integrity, as evidenced by accelerating dynamics and decoupling of actin and microtubule networks in experiments, as well as larger simulated contraction and concomitantly higher modulus G′ following contraction. As such, while sufficient flexibility is necessary to ensure contraction, the rigid scaffold provided by microtubules is also necessary to sustain steady contraction and correlated restructuring of actin and microtubule networks over large spatiotemporal scales.

The significantly larger increase in λ(t) for microtubules compared to actin in Φ_A = 0.75 composites (Fig. 3B), also seen in the simulated contractile contour maps (Fig. 4A), suggests that microtubules are aligning and bundling more so than actin filaments, likely driven by entropic depletion interactions from the surrounding higher concentration actin network and facilitated by the active contraction of the actin network. This bundling increases the mesh size of the microtubule network and decreases its connectivity with the actin network, thereby providing less of a reinforcing scaffold to rigidity the actin network.^43,47 The microtubules are thus no longer able to provide sufficient extensile support against accelerating contraction. Notably, the average velocities and accelerations we measure are comparable for both actin and microtubule dynamics despite the ~2 − 3x differences in correlation length changes during activity. This separability of time-evolving structure and dynamics, not previously reported in single-substrate active systems, highlights the novel properties that can emerge in composite systems, which may prove useful in filtration and drug delivery applications where controlled structural changes are necessary to dynamically release or sequester payloads or toxins.

At equimolar concentrations of actin and microtubules (Φ_A = 0.5), we find another emergent regime in which restructuring can be tuned independently of dynamics by varying myosin concentration. While the contraction rate stays constant with increasing myosin concentration, in line with previous studies of disordered actomyosin networks,¹⁷ λ(t) increases dramatically. We can understand this interesting effect as due to increased actin bundling at higher c_M as the motors pull and crosslink actin filaments.

For a connected network with modest motor concentration, motors pull on individual filament pairs that collectively contract towards a central region. As c_M increases, more motors bind to a single filament, pulling on filament pairs and causing more local bundling and aggregation. Specifically, at c_M = 0.24 μM, the spacing between myosin minifilaments is ~6 μm, comparable to the ~7 μm length of actin filaments in the composite.³⁵ Thus, all filament pairs have ~1–2 bound motors. As c_M is doubled to 0.48 μM, the number of bound motors also doubles to ~2–4 so there are more motors than can act on a filament pair or cluster to contract a local region. As such, rather than contributing to increasing the contraction rate, the added energy input from the increased motor density goes to restructuring the network from a homogeneous mesh of individual filaments to that of bundles and aggregates with larger mesh sizes.

This effect is similar to the reported structural changes due to increasing actin crosslinker density in steady-state actin–microtubule composites.^23,24,48 As found in these previous studies,⁴³ the larger voids, in turn, promote microtubule mobility by providing less of a connected meshwork with which the microtubules can entangle to hinder their motion. This second order effect of actin bundling, namely increasing microtubule mobility, allows the microtubule network to restructure just as quickly as the actin network during contraction despite the more rigid nature of microtubules. We also note that increased actin bundling may increase the persistence length of the actin structures compared to that of individual filaments,^23,24,48 making the actin more rigid and thus more dynamically similar to microtubules.

Our collective results, which comprehensively map the dynamics, structure and mechanics of myosin-driven actin–microtubule composites to the concentrations of the constituent proteins, demonstrate the promise that cytoskeleton composites hold for creating tunable and resilient active materials. While crosslinked actomyosin systems have been extensively studied as a model for adaptive biomaterials,¹⁴ here we show that coupling microtubules to actomyosin systems greatly expands the phase space of possible dynamics and structure that cytoskeleton-inspired materials can access, and confers emergent and useful properties not attainable with single-substrate systems. Notably, the active dynamics and restructuring we report are obtained in the absence of crosslinkers and at lower protein concentrations than required for robust actomyosin contraction.

Our materials design goal is to identify the regions of phase space in which our materials exhibit sustained and steady ballistic contraction while maintaining network connectivity and resilience. However, our comprehensive phase map serves as a blueprint for the general design of active and adaptable flexible-stiff polymer materials that can be tuned for diverse applications including wound healing, micro-actuation, filtration, drug-delivery and soft robotics. Further, our results provide important insight into the different routes the cytoskeleton may use to alter its dynamics and structure. Specifically, studies have shown that interactions between actomyosin and microtubule networks are critical to diverse processes including cell migration, wound healing, cytokinesis, mechano-sensing, membrane ruffling, contractility and polarization.^9,26,49-51

While the protein concentrations we use are lower than the average concentrations found in cells,^40-42 these concentrations vary substantially in different regions of the cell, and further change during specific processes and phases in the life cycle.^40,41 Our studies highlight that varying the relative concentrations of actin, tubulin and myosin at specific regions in the cell may allow cells to access different dynamical and structural properties. Based on our extensive phase map, we expect that at higher protein concentrations than studied here, composites will display more contractility (from increased myosin and actin) and rigidity (from a higher degree of connectivity and more microtubules). At higher actin fractions (Φ_A > 0.75), we expect that the contractile acceleration and de-coupling of actin and microtubule structures may be enhanced. In future work, to more closely match the conditions of the cell, we will investigate composites with increased filament concentrations, variable microtubule lengths, crosslinking proteins and microtubule-associated kinesin motors.

Materials and methods

Protein preparation

The following cytoskeleton proteins are purchased: porcine brain tubulin (Cytoskeleton T240), HiLyte Fluor-488-labeled tubulin (Cytoskeleton TL488M-A), rabbit skeletal actin (Cytoskeleton AKL99), Alexa-568-labeled actin (ThermoFisher A12374), and rabbit skeletal myosin II (Cytoskeleton MY02). Both labeled and unlabeled tubulin are reconstituted to 5 mg ml⁻¹ with 80 mM PIPES (pH 6.9), 2 mM MgCl₂, 0.5 mM EGTA, and 1 mM GTP. Unlabeled actin is reconstituted to 2 mg ml⁻¹ in 5 mM Tris–HCl (pH 8.0), 0.2 mM CaCl₂, 0.2 mM ATP, 5% (w/v) sucrose, and 1% (w/v) dextran. Labeled actin is reconstituted to 1 mg ml⁻¹ in 5 mM Tris (pH 8.1), 0.2 mM CaCl₂, 0.2 mM dithiothreitol (DTT), 0.2 mM ATP, and 10% (w/v) sucrose. Myosin II is reconstituted to 10 mg ml⁻¹ in 25 mM PIPES (pH 7.0), 1.25 M KCl, 2.5% sucrose, 0.5% dextran, and 1 mM DTT. All cytoskeleton proteins are flash frozen in experimental-sized aliquots and stored at −80 °C. Immediately prior to use, enzymatically dead myosin is removed from myosin II aliquots using a spin-down protocol previously described.³⁷ The myosin II inhibitor, (−)-blebbistatin (Sigma B0560), is reconstituted in anhydrous DMSO and stored at −20 °C for up to 6 months.

Composite network assembly

To form actin–microtubule composite networks, actin monomers and tubulin dimers are polymerized for 30 min at 37 °C in PEM-100 (100 mM PIPES, 2 mM MgCl₂, and 2 mM EGTA) supplemented with 0.1% Tween, 1 mM ATP, and 1 mM GTP. Actin and tubulin are added in concentrations varying from 1.4–4.4 μM such that the total protein concentration is maintained at 5.8 μM. Actin filaments are stabilized with the addition of a 1 : 1 molar ratio of phalloidin to actin (1.4–4.4 μM), and microtubules are stabilized with the addition of a saturating concentration of Taxol (5 μM).^52,53 We see no signs of bundling of actin filaments due to the phalloidin stabilization. Specifically, prior to myosin activation, composites are visibly indistinguishable from those formed in the absence of phalloidin.³⁵ To facilitate fluorescent imaging, we include Alexa-568-labeled actin monomers and HiLyte-488 tubulin dimers at 18% and 7% of the total actin and tubulin concentrations, respectively. Immediately prior to imaging, an oxygen scavenging system (45 μg ml⁻¹ glucose, 0.005% β-mercaptoethanol, 43 μg ml⁻¹ glucose oxidase, and 7 μg ml⁻¹ catalase) is added to reduce photobleaching and 50 μM blebbistatin is added to inhibit myosin activity until blebbistatin is deactivated with 488 nm light. Spun-down myosin II is added at varying concentrations (c_M = 0.12–0.48 μM) to generate network activity.

Sample preparation

Sample chambers holding ~10 μL of solution are formed by adhering a glass coverslip to a glass slide using two strips of heated parafilm (~70 μm thick). Samples are loaded into chambers immediately after polymerization and chambers are sealed with epoxy. To create hydrophobic surfaces that myosin will not adhere to, coverslips and glass slides are passivated with 2% dichlorodimethylsilane as previously described.^37,54

Confocal microscopy

Networks are imaged using a Nikon A1R laser scanning confocal microscope with a 60× 1.4 NA objective (Nikon). Actin filaments are imaged using a 561 nm laser with 561 nm excitation and 595 nm emission filters. Microtubules are imaged using a 488 nm laser with 488 nm excitation and 525 nm emission filters. Myosin II motor activity is controlled by deactivating blebbistatin with the same 488 nm excitation used to image microtubules (continuous 360 ms pulses of 488 nm light over the duration of each experiment). While blebbistatin deactivation is typically achieved using 405 nm light,¹⁷ previous studies have shown successful photoinactivation of blebbistatin using 488 nm light.^37,55 256 × 256 pixel images (212 μm × 212 μm) are taken in the middle of the ~70 μm thick chamber for 45 min at 2.78 fps. Examples of time-series are shown in Movie S1 (ESI^†), and representative images are shown in Fig. 1. Experiments are performed on 3–5 different replicates.

Differential dynamic microscopy (DDM)

We perform differential dynamic microscopy (DDM) on each of the 3–5 time-series for each condition using custom Python scripts.⁵⁶ DDM analysis determines how quickly density fluctuations decay between images separated by a given lag time Δt.⁴⁴ We compute variances by taking a fast Fourier transform of differences in image intensity at different lag times, and the resulting power spectrum is radially averaged to generate an image structure function D(q, Δt). For systems that plateau at long lag times (see Fig. 2), we fit D(q, Δt) to the following model: D(q, Δt) = A(q) × (1 −f(q, Δt)) + B(q) where q is the wave vector, A(q) is the amplitude, B(q) is the background, and f(q, Δt) is the intermediate scattering function, which contains the dynamics of the system. To determine the type of motion and the corresponding rate, we model the intermediate scattering function as an exponential: $f(q,\Delta t)={\mathrm{e}}^{-{\left(\frac{\Delta t}{\tau (q)}\right)}^{\gamma }}$ where τ(q) is the decay time and γ is the scaling factor. If $\tau \sim \frac{1}{kq}$ then the system exhibits ballistic motion and k represents the corresponding velocity.

We analyze time-series over the entire 45 min or until the network disappears from the field of view. To determine whether dynamics changed over the course of activity, we also perform DDM analysis over consecutive smaller time intervals using the same Python script used for the 45 minute time-series analysis. Specifically, we divide the 7500 frames of each 45 minute series into successive 6 minute segments containing 1000 frames each. By comparing image structure functions for different time intervals in the time-series, we determine how the active dynamics vary over the course of the activity. We identify network acceleration during contraction by an upward trend in computed velocities over the 45 min activation time (Fig. 3).

Spatial image autocorrelation (SIA)

We perform spatial image autocorrelation (SIA) analysis on each of the 3–5 time-series for each condition using custom Python scripts.⁵⁷ SIA measures the correlation in intensity g of two pixels in an image as a function of separation distance r.⁴⁵ We generate autocorrelation curves by taking the fast Fourier transform of an image at a given time, multiplying by its complex conjugate, and then applying an inverse Fourier transform and normalizing by intensity:

$$g(r)=\frac{F^{-1}(\mid F(I(r)){\mid }^2)}{[I(r){]}^2}$$

The correlation length λ is determined by fitting the decaying section of each autocorrelation curve to an exponential: $g(r)=A{\mathrm{e}}^{\frac{-r}{\lambda }}$. To quantify how the composites rearrange over time, correlation lengths λ are computed at consecutive 6 minute intervals over the experimental time frame.

Modeling and simulations

We combine rigidity percolation theory^33,58-60 with an active double-network model made of a stiff microtubule network interacting with an active semiflexible actomyosin network. The construction of this active rigidly percolating double-network (RPDN)⁶¹ is described in the ESI.^† The bonds in the two networks are uniformly and randomly removed according to two different probabilities, 1 − p₁ for the stiff (microtubule) network, and 1 − p₂ for the semiflexible (actin) network, where 0 < p₁, p₂ < 1, and a continuous series of colinear bonds constitute a fiber. The values of p₁ and p₂ are obtained from experimental molar concentrations of tubulin and actin. The stretching moduli of the fibers in the microtubule and actin networks, α₁ and α₂, as well as their bending moduli, κ₁ and κ₂, are calculated from the known persistence lengths and cross-section diameters of microtubules and actin filaments (see ESI^†). The contraction of bonds in the actomyosin network is incorporated via a parameter δ which leads to increasingly reduced rest lengths as the myosin concentration is increased and is obtained from the ratio of experimental myosin and actin concentrations (described in ESI^†). The two networks interact via weak Hookean springs of spring constant α₃. The energy cost of deforming the RPDN is given by E = E₁(p₁, κ₁, α₁) + E₂(p₂, κ₂, α₂, δ) + E(p₁, p₂, α₃), where E₁ is the deformation energy of the microtubule network, E₂ is the deformation energy of the actomyosin network, and E₃ is the deformation energy of the bonds connecting the two networks (see ESI^† for details). The energy E is minimized using a multi-dimensional conjugate gradient (Polak–Ribiere) method as a function of the bond occupation probabilities, p₁ and p₂, and contraction parameter δ to obtain states of the active RPDN for different concentrations of actin, myosin, and microtubules.

Simulations performed under 0.005% shear are used to obtain the elastic modulus G′ obtained using the relationship G′ = 2ε/γ², where ε is the minimized energy per unit area of the simulation box and γ the applied strain (described in ESI^†). We convert G′ from simulation units to real units using the conversion factor $G_{\text{sim}}^{\prime }\approx 210\text{kPa}$, as described in ESI.^† Five simulations are run per condition to obtain the average quantities presented. Note that this model assumes permanent crosslinking of both networks, and does not incorporate time evolution, viscous dissipation, filament bundling, breaking, or buckling.