Skip to main content
PMC home page
JACS Au logoLink to JACS Au
. 2022 Jun 16;2(6):1383–1394. doi: 10.1021/jacsau.2c00085

Describing Chemical Reactivity with Frontier Molecular Orbitalets

Jincheng Yu †,‡, Neil Qiang Su †,§, Weitao Yang †,∥,*
PMCID: PMC9241161  PMID: 35783161

Abstract

graphic file with name au2c00085_0018.jpg

Locality in physical space is critical in understanding chemical reactivity in the analysis of various phenomena and processes in chemistry, biology, and materials science, as exemplified in the concepts of reactive functional groups and active sites. Frontier molecular orbitals (FMOs) pinpoint the locality of chemical bonds that are chemically reactive because of the associated orbital energies and thus have achieved great success in describing chemical reactivity, mainly for small systems. For large systems, however, the delocalization nature of canonical molecular orbitals makes it difficult for FMOs to highlight the locality of the chemical reactivity. To obtain localized molecular orbitals that also reflect the frontier nature of the chemical processes, we develop the concept of frontier molecular orbitalets (FMOLs) for describing the reactivity of large systems. The concept of orbitalets was developed recently in the localized orbital scaling correction method, which aims for eliminating the delocalization error in common density functional approximations. Orbitalets are localized in both physical and energy spaces and thus contain both orbital locality and energy information. The FMOLs are thus the orbitalets with energies highest among occupied orbitalets and lowest among unoccupied ones. The applications of FMOLs to hexadeca-1,3,5,7,9,11,13,15-octaene in its equilibrium geometry, inter- and intra-molecular charge-transfer systems, and two transition states of a bifurcating reaction demonstrate that FMOLs can connect quantum mechanical treatments of chemical systems and chemical reactivities by locating the reactive region of large chemical systems. Therefore, FMOLs extend the role of FMOs for small systems and describe the chemical reactivity of large systems with energy and locality insight, with potentially broad applications.

Keywords: orbitalets, frontier, locality, chemical reactivity, charge transfer

Introduction

Describing and predicting molecular properties, such as chemical reactivity, are fundamental tasks in chemistry and are essential for understanding various phenomena in biology and materials science. To this end, the concept of molecular orbital (MO) in the quantum mechanical treatment of chemical systems has achieved great success during the past many decades. The frontier molecular orbitals (FMOs), especially the highest occupied molecular orbitals (HOMOs) and the lowest unoccupied molecular orbitals (LUMOs), have been widely used by chemists to understand the reactivity and regioselectivity of various chemical systems.1−7 Despite their great success in small systems, FMOs suffer from the delocalization nature when applied to large systems. FMOs of large systems tend to span a large portion of the system, resulting in the loss of locality information that is important to identify the functional groups significantly involved in the reaction.

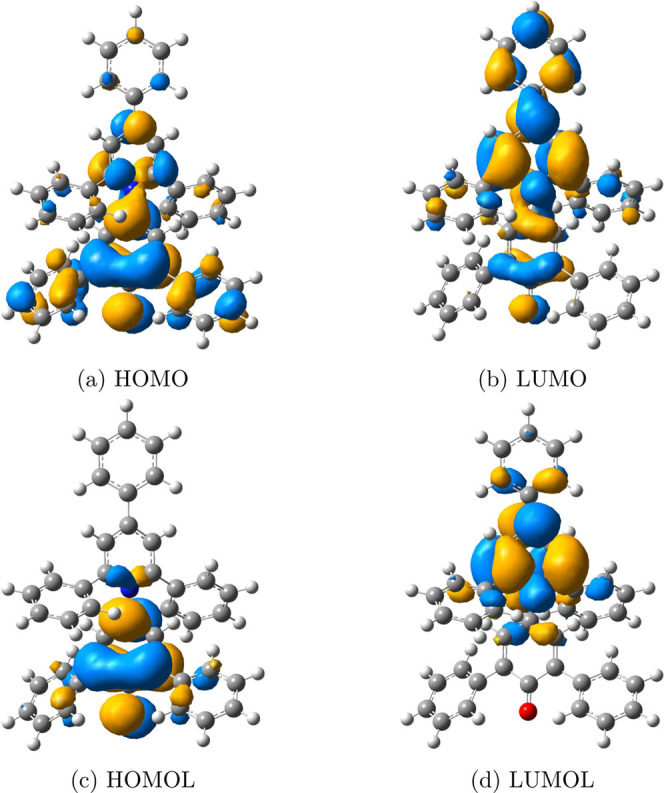
Consider the Diels–Alder (DA) reaction. It is one of the earliest reactions that can be described by FMOs,8 where the essence of a DA reaction can be successfully captured from the interaction between the FMOs of a diene molecule and a dienophile molecule. To be more specific, the HOMO of diene interacts with the LUMO of dienophile, while the LUMO of diene interacts with the HOMO of dienophile at the same time, as shown in Figure 1. The butadiene-like diene FMOs describe DA reactions in a clear and concise manner and have been used as a prototypical example in many textbooks. However, the clear picture can be blurred when the system is larger. Zhang et al.9 examined the effectiveness of FMOs on a hypothetical DA reaction between hexadeca-1,3,5,7,9,11,13,15-octaene and ethene. As shown in Figure 2a,b, the HOMO and LUMO of hexadecaoctaene spread out over the whole molecule, burying the butadiene-like model in massively delocalized FMOs. Hence, the delocalization character of FMOs significantly reduces the effectiveness of the ability to describe the reactivity of large chemical systems.

Figure 1.

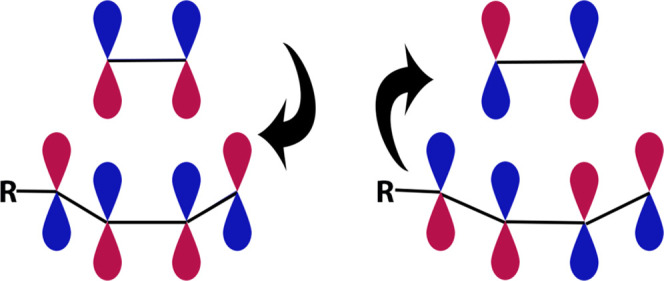
Figure 1

Open in a new tab

Illustration of DA reactions. According to Fukui’s theory, DA reactions should be described as the mutual delocalization of electrons between FMOs of the involved diene molecule and the dienophile molecule. Left: the LUMO of diene interacts with the HOMO of dienophile. Right: the HOMO of diene interacts with the LUMO of dienophile.

Figure 2.

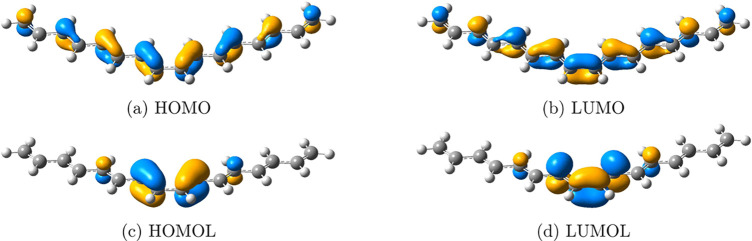
Figure 2

Open in a new tab

FMOs and frontier molecular orbitalets (FMOLs) of hexadecaoctaene. FMOs, (a) HOMO and (b) LUMO, spread out over the whole molecule, burying the butadiene-like model in massive delocalized orbitals. FMOLs, (c) highest occupied molecular orbitalet (HOMOL) and (d) lowest unoccupied molecular orbitalet (LUMOL), mostly locate on the central adjacent double bonds, highly resembling the butadiene-like orbitals in Figure 1. Iso = 0.05.

Unlike canonical molecular orbitals (CMOs) that are often delocalized over the entire molecule, localized molecular orbitals (LMOs) are limited to a small region of a system. In general, LMOs come from the linear combination of CMOs, with the way of combination decided by a chosen objective function. LMO models were designed to provide more chemical information in each local region. The earliest and still widely used LMOs are based on the Foster–Boys localization10 and Edmiston–Ruedenberg localization.11 Various other objective functions have been designed to localize CMOs for different purposes, and a large number of localization procedures have been designed to reduce the computational cost for both bulk and molecular systems.12−15 Although these approaches can provide LMOs that are effectively localized in physical space, the energy information cannot be preserved during the localization procedure. The orbital energies of these LMOs that are obtained from the expectation values of the one-electron Hamiltonian lose their physical meaning. Because of the loss of energy information, it is impossible to select the frontier orbitals from these LMOs. These LMOs cannot be used to describe chemical reactivity, which is dominated by the energetic frontier orbitals.

To connect the quantum mechanical treatments of chemical systems and chemists’ insight, many efforts have been devoted to finding a set of properly localized orbitals that keep part of the energy information. Weinhold et al. developed natural atomic orbitals (NAOs) and natural bonding orbitals (NBOs) using the density matrix.16−18 To date, these two orbital models have been widely used. NBOs are usually in accord with the Lewis structure description and thus have been called “a chemists’ basis set”.19 Despite the great success of the NBO model, Zhang et al.9 found that NBOs cannot provide the butadiene-like FMOs of the long-chain molecule. Instead of localizing the HOMO/LUMO in the butadiene-like region, NBOs can only identify several double bonds in the molecule. More recently, the resonance natural bonding orbitals (RNBOs)20 have been developed from the natural resonance theory. The RNBOs can adopt a multicenter character at the intermediate region of a reaction curve. Based on the NBO analysis, some other methods have been developed to describe complicated interactions. For example, by searching multicentered bonds, an adaptive natural density partitioning approach21 can provide a better description of cluster compounds.22−24 More recently, Zhang et al.9 developed the principal interacting orbital (PIO) analysis by applying principal component analysis twice on the off-diagonal elements of the NAO-based density matrix. PIOs can quantitatively describe interactions between various chemical fragments, which makes it easy to identify the pair of PIOs with the strongest interaction with each other.

In addition to the NBO analysis and the approaches developed from it, a number of other models aiming at describing chemical interactions have been developed. The Fukui function25−27 developed within density functional theory (DFT)28 is frequently utilized in predicting the reactivities of chemical systems. Based on the Fukui function, efforts have been devoted to improving the description of the chemical properties of various systems.29−31 Some other models have been developed for specific systems or specific properties. For example, charge decomposition analysis31 can describe donor–acceptor interactions quantitatively. The reactive hybrid orbital method32 was developed to measure the interactions in electrophilic aromatic substitution reactions. The frontier effective-for-reaction molecular orbitals33,34 were designed to identify the best frontier orbital for calculating pKa values of chemical systems. Fragment molecular orbitals35 and spatially constrained diabatic states36 have been applied to analyze donor–acceptor interactions of charge-transfer (CT) complexes. The orbitals from the Fermi–Löwdin orbital self-interaction correction approach37 that was developed to eliminate the self-interaction error have also been applied to describe the chemical properties of various systems.38−40 Natural orbitals for chemical valence (NOCV), which are defined as the eigenvectors of the chemical valence operator,41 can well describe the bond between the transition metals and the ligands by providing individual descriptions of the σ-donation and the π-back-donation contributions.42,43 More recently, the NOCV method has been combined with the extended transition-state (ETS) method,44 and the resulting ETS-NOCV methods can provide new understandings of the bond formation process by decomposing the different components of the chemical bond.45 Despite all of those efforts, a unified and computationally efficient method that can be applied to various systems is still lacking.

In this work, we develop a new LMO model, that is, the frontier molecular orbitalets (FMOLs), aiming at describing the reactivity of large chemical systems and extending the roles of FMOs for small systems. Orbitalets were first introduced to capture local fractional charges and spins for the newly developed density functionals, the localized orbital scaling correction (LOSC)46,47 and fractional-spin LOSC (FSLOSC),48 so as to systematically correct the delocalization error and static correlation error in commonly used density functional approximations.49−53 Here, we will further demonstrate that orbitalets not only properly capture the fractional charges and fractional spins but also localize FMOs in a way that best reflects the chemical reactivity of systems. Being localized in both physical space and energy space, orbitalets are able to combine the energy information from CMOs and the locality information from LMOs, making them a unique choice to clearly show the chemical properties of large systems.

The construction of orbitalets and the definition of FMOL will be introduced in the next section. The potential of FMOLs will be explored in the rest part of this paper. We will show that FMOLs are accurate indicators of chemical reactivity with locality information and thus can provide a better understanding of many complex problems in large systems.

Theory

Orbitalets are obtained by unitarily combining CMOs, ϕp =∑qUpqφq, the summation including both occupied and virtual CMOs in a manner determined by minimizing the following cost function46,47

graphic file with name au2c00085_m001.jpg 1
graphic file with name au2c00085_m002.jpg 2
graphic file with name au2c00085_m003.jpg 3

where r is the position operator and ĥ is the reference one-electron Hamiltonian of the system. The total cost function is composed of the physical space part Fr and the energy space part Fe. Taken from the Foster–Boys localization,54Fr shows how much the orbitalets spread out in the physical space. We note that a similar idea was proposed by Gygi et al.55−57 to include the Hamiltonian in the objective function to obtain orbitals that are localized in physical space while still being well confined in each local region of the eigenvalue spectrum. The key difference in our approach (eq 1) is that we always include both occupied and virtual CMOs in the localization and let the CMO energies and spatial delocalizations determine their mutual mixing. With this, the resulting fractional occupied LMOs are able to capture fractional charge information on each local region, which is needed for the LOSC correction. The larger the value of Fr, the wider the orbitalets spread. Fe is the cost function for energy delocalization. It shows the degree to which the orbitalets deviate from the eigenstates of the Hamiltonian (i.e., CMOs), which describe the energy structure of a real system. The smaller the value of Fe, the less the loss of energy information. In the above equations, C is a constant used to unify units and match magnitudes between the physical and energy spaces, and γ stands for the fraction of the energy cost part in the total cost function. The main function of C is to make sure that the value of γ is not too close to 1, which can make the optimization of γ easier. C is set to 1000 (in atomic unit) for tests in this work. By changing the value of γ, the weights of the two parts can be adjusted accordingly. If γ is equal to 1, Fr makes no contribution to the total cost function, so the orbitalets will be the same as CMOs. If γ is equal to 0, Fe has no contribution to the total spread function, and the orbitalets are just the generalized Foster–Boys LMOs, resulting in a very large deviation from the eigenfunctions of the Hamiltonian, which means that the orbitalets will completely lose the energy information and reach maximal localization in physical space. Taking hexadecaoctaene as an example, Fr and Fe, as functions of γ, can be found in Figure S1 in the Supporting Information (SI). γ is optimized to be 0.7959 by considering the reactions and CT systems studied in this paper and remains the same value for all of the studies in this work. Note, however, that this value can be adjusted if necessary when different systems are studied. For each system, there exists a range of γ that can be used to study the chemical reactivity.

The energy of an orbitalet is defined as the expectation value of the one-electron Hamiltonian with the corresponding orbitalet wave function, namely, ⟨ϕp|ĥ|ϕp⟩. It is the weighted average of the CMOs that have contributions to the orbitalet. The occupation number of an orbitalet is the expectation value of ρs, the reference one-electron density matrix of the system with the corresponding orbitalet wave function, namely, ⟨ϕp|ρs|ϕp⟩. The occupation numbers of orbitalets are fractionals ranging from 0 to 1. This divides the orbitalets into two sets: the occupied orbitalets with occupation numbers close to 1 and the unoccupied orbitalets with occupation numbers near 0. The highest occupied molecular orbitalet (HOMOL) is defined as the occupied orbitalet with the highest energy, and the lowest unoccupied molecular orbitalet (LUMOL) is defined as the unoccupied orbitalet with the lowest energy. HOMOL and LUMOL together are called FMOLs.

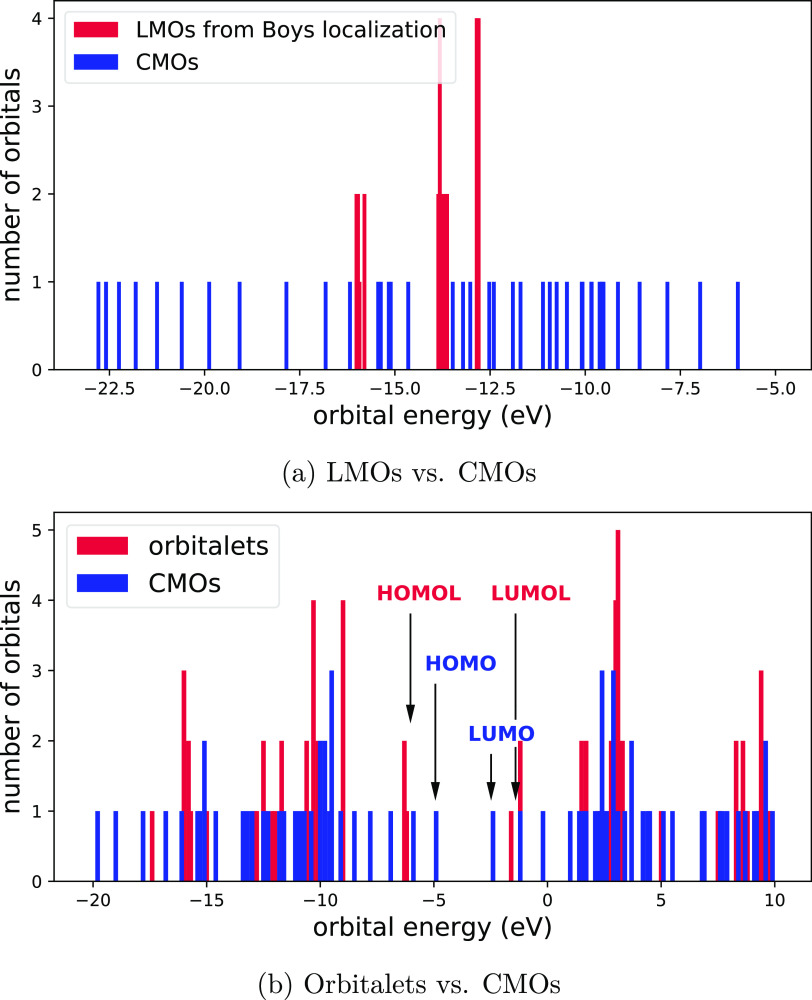
To understand orbitalets, here we take hexadecaoctaene as an example. Comparison between the energy structures of CMOs and LMOs from the Foster–Boys localization is shown in Figure 3a. Fine energy structures can be seen clearly from the bar graph of CMOs. When γ is set to 0, the overall energy distribution in Figure 3a indicates that the orbital energies completely lose their meaning and there is barely any structure. When γ is set to 0.7959, even though the fine structures of energy are blurred as compared to those of CMOs, the orbitalets can still retain the main energy information (see Figure 3b). The mix of CMOs that are close in energy makes the energies of the resulting orbitalets even closer; thus, a set of “frontier” orbitalets could be obtained, which are located in different local regions of the system. Therefore, orbitalets can maintain the overall energy structure of CMOs while trading some energy information for better localization in the physical space, which endows orbitalets with both energy and locality information. As will be shown below, the loss of energy information is small; thus, the orbitalets are very effective for the analysis of active sites, especially when the chemical system is large.

Figure 3.

Figure 3

Open in a new tab

Bar graphs showing orbital energy structures of hexadecaoctaene. (a) Comparison between energy structures of CMOs (γ = 1) and LMOs from the Foster–Boys localization (γ = 0). LMOs completely lose the energy information to reach the maximal localization in physical space. (a) Comparison between energy structures of CMOs (γ = 1) and orbitalets (γ = 0.7959). Orbitalets can maintain the overall energy structure of CMOs while sacrificing some energy information to achieve better localization in the physical space.

Computational Details

Structures of hexadecaoctaene, 1,3-dipole compounds, the donor-bridge–acceptor (DBA) system, and 2,6-diphenyl-4-(2,4,6-triphenyl-1-pyridinio)phenolate (betaine-30) were optimized with Gaussian 200958 using the B3LYP functional59−62 and 6-31G*63 basis sets. Structures of the transition states in the bifurcating reaction were offered by Lin’s group, and structures of intermolecular CT systems are from ref (64). SCF and post-SCF calculations were done with QM4D65 using the B3LYP functional. Basis sets used were cc-pVDZ66 for hexadecaoctaene and 6-31G* for all of the other systems. For the DBA system, to reduce the computational cost, the 2′,3′,5′-tri-O-(tert-butyldimethylsilyl)ribofuranosidyl group was approximated as a hydrogen atom.

Results and Discussion

Diels–Alder Reaction

The explanation of DA reactions is one of the most famous applications of the FMO theory. DA reactions are described as interactions between FMOs of the diene and the dienophile, as demonstrated in Figure 1. This figure suggests that chemists tend to concentrate on “reactive functional groups” when analyzing chemical reactions. However, the clear butadiene-like shape of the FMOs can be buried due to the delocalization nature of FMOs when the R group is large. For the hypothetical DA reaction between hexadeca-1,3,5,7,9,11,13,15-octaene and ethene,9 one may expect the frontier orbitals of hexadecaoctaene to be butadiene-like orbitals located at two adjacent double bonds in the middle. However, as shown in Figure 2a,b, the FMOs are undesirably delocalized over the whole molecule, presenting major challenges for applications to describe chemical reactivities.

Compared with CMOs, orbitalets contain both energy and locality information, allowing FMOLs to clearly reflect the most reactive site. For the hypothetical DA reaction studied in this work, Figure 2 shows the preference. As shown in Figure 2c,d, HOMOL and LUMOL of hexadecaoctaene are mainly localized on the central adjacent double bonds, with their shapes resembling FMOs of butadiene, which means that FMOLs are able to locate in the region where chemical reactions most likely occur. This picture is consistent with the chemists’ understanding of reactive functional groups with small perturbative effects from substitution.

Betaine-30 Intramolecular Charge-Transfer System

CT is one of the important phenomena in chemistry, physics, and materials science. Systems with a charge-transfer character have different dipole moments in their ground states and excited states. The observation that FMOLs can localize FMOs to a more specific fragment inspired the application of FMOLs to describe the charge-transfer character of chemical systems.

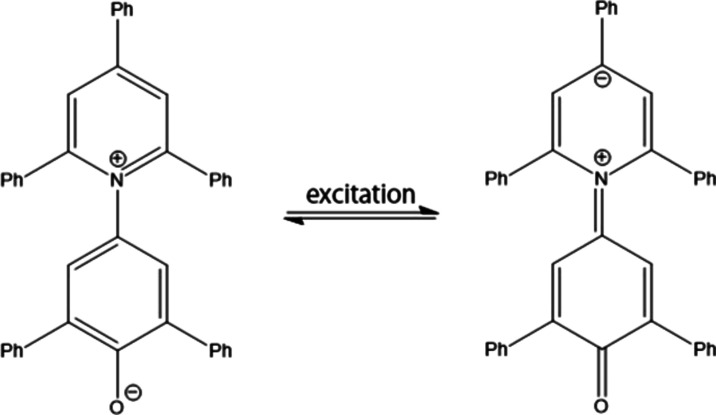
Reichardt’s dye, also known as betaine-30 (see Figure 4),67 shows negative solvatochromism because of the change in its dipole moment when the molecule is excited. In its ground state, the molecule remains in a charge-transferred state (D+–A–), while upon photoexcitation, the molecule turns into a D–A state. The dipole moment of this molecule is about 15 and 6.2 D in its ground and excited states, respectively.67

Figure 4.

Figure 4

Open in a new tab

Structure and CT process of betaine-30. The dipole moment of this molecule decreases upon excitation.

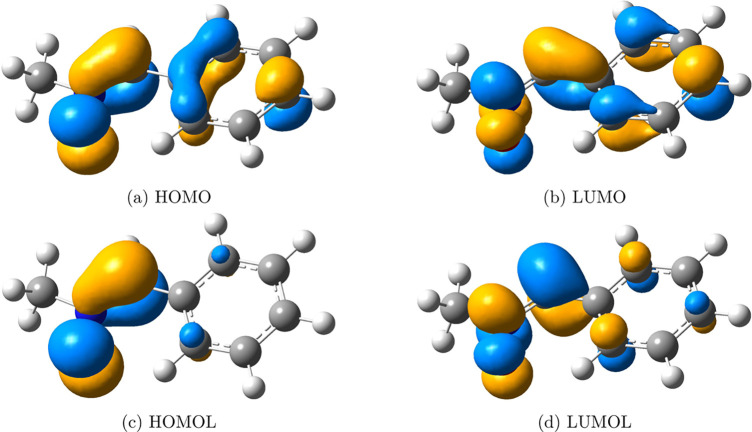
FMOs and FMOLs of betaine-30 are shown in Figure 5. FMOs show only a very blurred trend of the CT process from the lower part to the upper part of the molecule. However, it can be seen more clearly from the HOMOL/LUMOL pair. Figures 5c, d clearly show that the electron transfers from the lower aromatic ring to the upper aromatic ring when excited, which is consistent with the experimental result.67

Figure 5.

Figure 5

Open in a new tab

FMOs and FMOLs of betaine-30. FMOs, (a) HOMO and (b) LUMO, are too delocalized to show a clear trend of the CT process. FMOLs, (c) HOMOL and (d) LUMOL, clearly show that the electron transfers from the lower aromatic ring to the upper aromatic ring when the molecule is excited, which is consistent with the experimental result.67 Iso = 0.02.

Donor-Bridge–Acceptor Intermolecular Charge-Transfer System

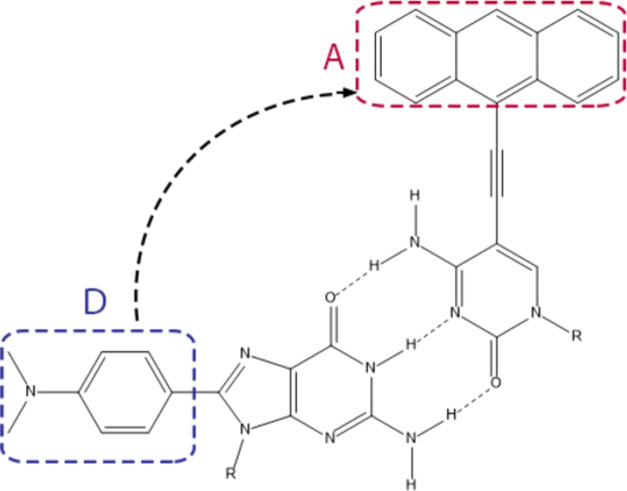
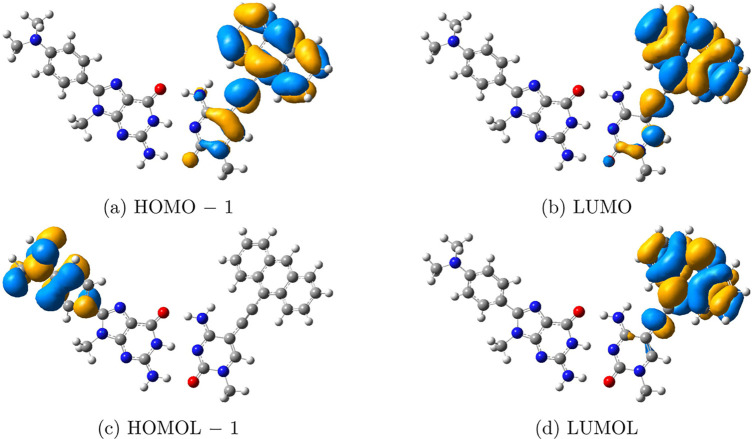
The success in the description of the single-molecular CT encouraged us to apply FMOL analysis to intermolecular CT systems. The DBA system, where an anthracene-derived acceptor and a dimethylaniline-containing donor are connected by guanosine–cytidine hydrogen bonds, is studied. As shown in Figure 6, an electron will transfer from the fragment in the blue box to the fragment in the red box when the system is excited.68 Orbitalets and CMOs near FMO(L)s were examined. As shown in Figure 7, although neither the HOMO-to-LUMO transition nor the HOMOL-to-LUMOL transition of the system can well explain the CT process, we do observe that the CT character can be largely captured by the (HOMOL – 1)-to-LUMOL transition. In the time-dependent DFT (TDDFT),69−71 the description of the excitation process contains contributions from a number of electron transitions between orbitals. It can be seen from the experimental result in Figure 6 that the main contribution should come from the HOMOL – 1-to-LUMOL transition. However, we did not observe any CMOs that have a similar shape as that of HOMOL – 1. (CMOs and orbitalets near HOMO(L) and LUMO(L) can be found in Figure S2 in the SI.) For this CT system, although the CT character is not captured by the HOMOL-to-LUMOL transition, the most important contribution can still be found using orbitalets.

Figure 6.

Figure 6

Open in a new tab

Structure of the donor-bridge–acceptor (DBA) CT system studied in this work. R = 2′,3′,5′-tri-O-(tert-butyldimethylsilyl)ribofuranosidyl.

Figure 7.

Figure 7

Open in a new tab

FMOs and FMOLs of the DBA system shown in Figure 6. (a) HOMO – 1 and (b) LUMO locate in the same area of the system, while the excitation from (c) HOMOL – 1 to (d) LUMOL agrees with the CT found in the experiment.68 Other CMOs and orbitalets near HOMO(L) and LUMO(L) can be found in Figure S2 in the SI. Iso = 0.02.

Tetracyanoethylene (TCNE)-Aromatic Molecule Intermolecular Charge-Transfer Systems

For intermolecular CT systems, three other systems with tetracyanoethylene (TCNE) being the acceptor have been tested. When the donor molecules are small (for example, benzene and naphthalene, as shown in Figure 8), the FMOs can predict directions of CT accurately enough. FMOLs are just a little more localized than FMOs. We tested the performance of FMOLs on the anthracene–TCNE system with the double bond in TCNE perpendicular to anthracene (V configuration) and parallel with anthracene (P configuration) (see Figure 9). For the V configuration, the situation is similar to that of small donor systems. FMOs are localized enough to show the CT character. However, for the P geometry, HOMO and LUMO spread over the whole system, making the boundary between the donor and acceptor unclear. FMOLs can improve the description by locating HOMOL on the donor molecule and LUMOL on the acceptor molecule. Results of configuration interaction single (CIS) calculations show the same CT character as FMOLs show, as shown in Figure S3 in the SI.

Figure 8.

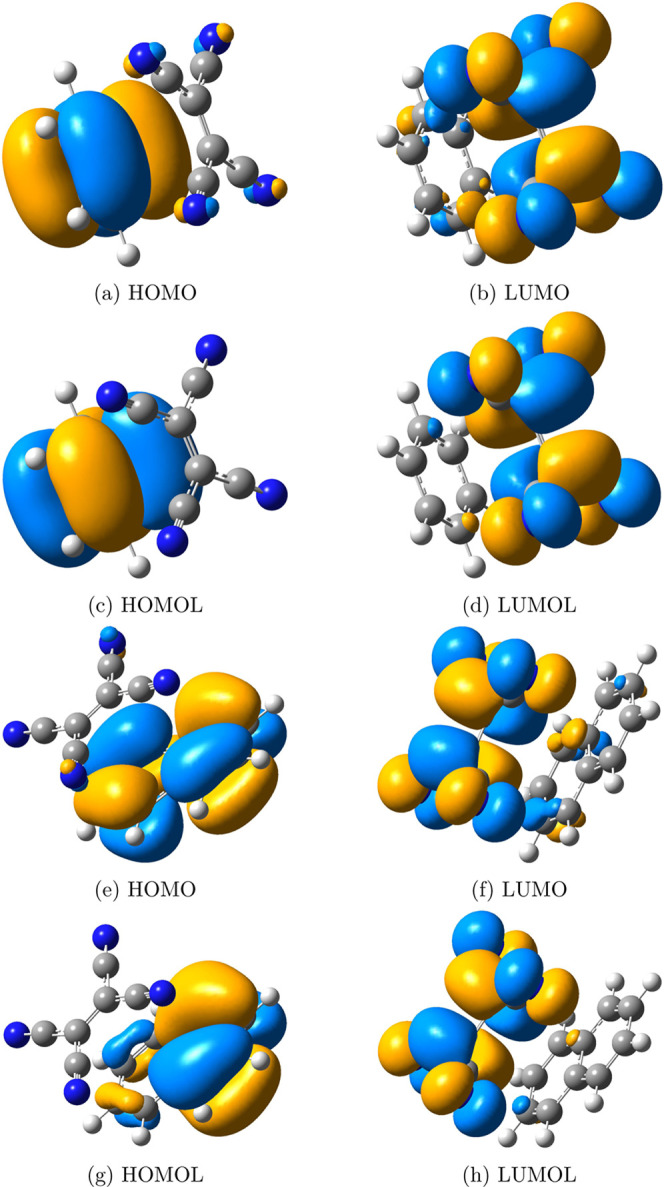
Figure 8

Open in a new tab

FMOs and FMOLs of the benzene–TCNE system and the naphthalene–TCNE system. (a) HOMO, (b) LUMO, (c) HOMOL, and (d) LUMOL of the benzene–TCNE system; (e) HOMO, (f) LUMO, (g) HOMOL, and (h) LUMOL of the naphthalene–TCNE system. As the systems are small, FMOs describe the CT character clearly, and only a small difference between FMOs and FMOLs can be observed. Iso = 0.02.

Figure 9.

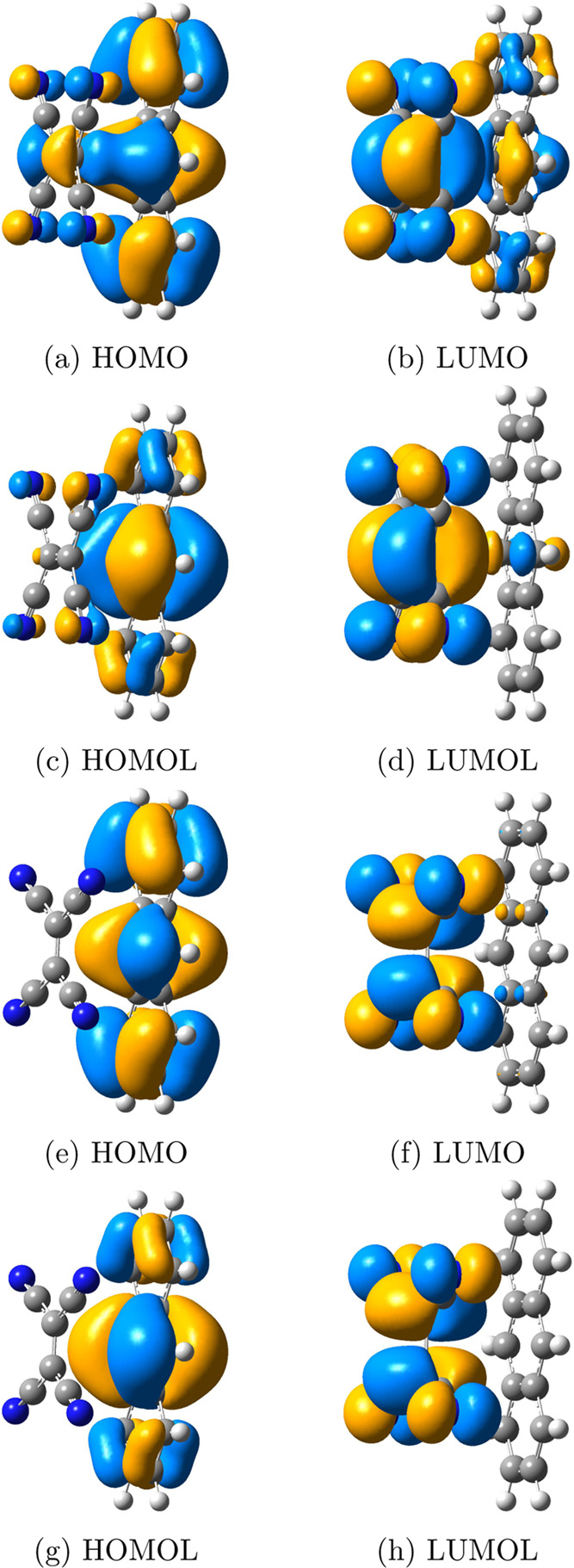
Figure 9

Open in a new tab

FMOs and FMOLs of the anthracene–TCNE systems with two different configurations: the double bond in TCNE is perpendicular to anthracene (V configuration) and parallel with anthracene (P configuration). (a) HOMO, (b) LUMO, (c) HOMOL, and (d) LUMOL of the P configuration; (e) HOMO, (f) LUMO, (g) HOMOL, and (h) LUMOL of the V configuration. FMOs perform better in the description of the CT character in the V configuration than in the P configuration. FMOLs further improve the description of the CT character in the P configuration by locating HOMOL on the donor molecule and LUMOL on the acceptor molecule. Iso = 0.02.

1,3-Dipolar Cycloaddition Reactions

1,3-Dipolar cycloaddition reactions are reactions between 1,3-dipole compounds and dipolarophiles. Common dipolarophiles include olefins, alkynes, and their derivatives. 1,3-Dipolar cycloaddition reactions are very similar to DA reactions in mechanism, with 1,3-dipole compounds in 1,3-dipolar cycloaddition reactions playing a similar role as diene molecules in DA reactions.

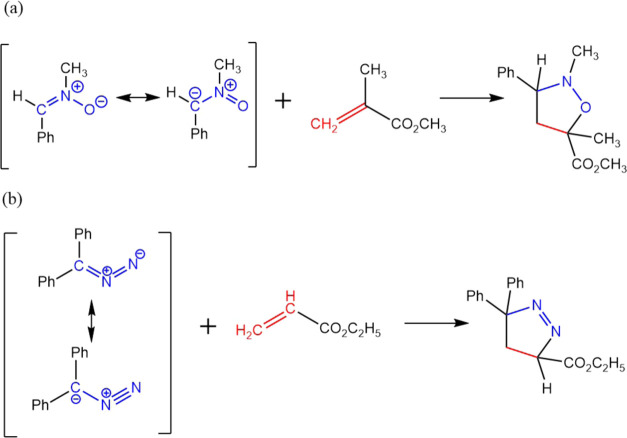
The addition of N-methyl-C-phenylnitrone to methyl methacrylate and the addition of diphenyldiazomethane to ethyl acrylate72 shown in Figure 10 are used to examine the effectiveness of FMOLs. As demonstrated in Figures 11 and 12, FMOLs of both the 1,3-dipole compounds are more localized on the atoms that are involved in the reactions than the corresponding FMOs, though the difference between FMOLs and FMOs is not as significant as that in the hexadecaoctaene molecule of the DA reaction. For these two 1,3-dipolar cycloaddition reactions, the FMOs are not so delocalized that they already provide a reasonable description of the reactive sites. In essence, FMOLs can improve the description of molecular reactivity when FMOs do not offer a clear description and stay consistent with FMOs when FMOs can accurately show the reactive region.

Figure 10.

Figure 10

Open in a new tab

Two 1,3-dipolar cycloaddition tested in this work. (a) Reaction between N-methyl-C-phenylnitrone and methyl methacrylate. (b) Reaction between diphenyldiazomethane and ethyl acrylate.

Figure 11.

Figure 11

Open in a new tab

FMOs and FMOLs of N-methyl-C-phenylnitrone. FMOs, (a) HOMO and (b) LUMO, are largely delocalized to the aromatic ring that is not the most reactive part of the molecule. In contrast, FMOLs, (c) HOMOL and (d) LUMOL, can clearly identify the reaction sites. Iso = 0.05.

Figure 12.

Figure 12

Open in a new tab

FMOs and FMOLs of diphenyldiazomethane. (a) HOMO, (b) LUMO, (c) HOMOL, and (d) LUMOL. FMOs of diphenyldiazomethane are localized properly to the reactive sites. Although FMOLs can make small improvements, FMOs and FMOLs are quite similar. Iso = 0.05.

Bifurcating Reactions

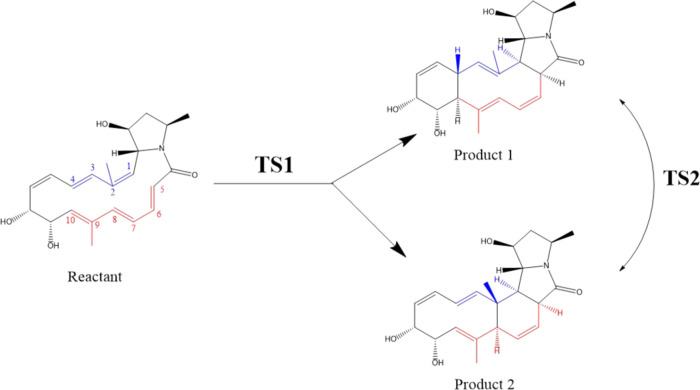
Here, we show the application of FMOLs to the analysis of more complex bifurcating reactions. In a bifurcating reaction, the reactants go through the same transition state into multiple product channels, forming different products from different channels. As shown in Figure 13, the same transition state (TS1) is formed by the reactants before they turn into product 1 or product 2. Once formed, product 1 and product 2 can transform into each other through the second transition state (TS2). Recently, Zhang et al. successfully applied the PIO analysis to the description of a bifurcating reaction (shown in Figure 14).9 However, the PIO analysis requires a priori segmentation of the system; a preliminary understanding of the reaction under study is necessary to perform the correct segmentation and PIO analysis. To test if FMOLs can provide a reasonable description of the same bifurcating reaction without dividing the system a priori, we plotted the FMOLs of the two transition states of the reaction. In the reaction, either a [6+4] or a [4+2] cycloaddition will take place through the same transition state, as shown in Figure 14.73 According to the Hükel–Möbius transition-state interaction model,74 HOMO is the most important orbital for analyzing the chemical interactions occurring during transition states. Therefore, we focus on the analysis of the HOMOLs of TS1 and TS2 in this section. The corresponding LUMOLs can be found in the SI.

Figure 13.

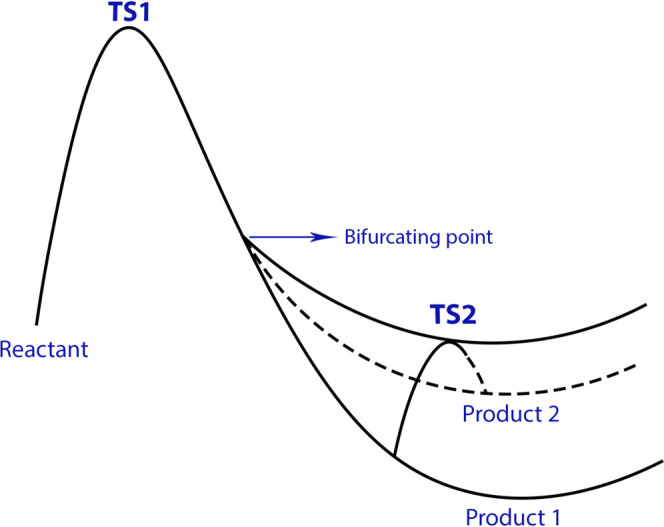
Figure 13

Open in a new tab

Schematic illustration of the potential energy surface of typical bifurcating reactions. Two different products can be formed through the same TS1. Once formed, the two products can transform from one to the other through TS2.

Figure 14.

Figure 14

Open in a new tab

Bifurcating reaction studied in this work. The blue part and the red part are where the reactions occur. Either a [6+4] or a [4+2] cycloaddition will take place.

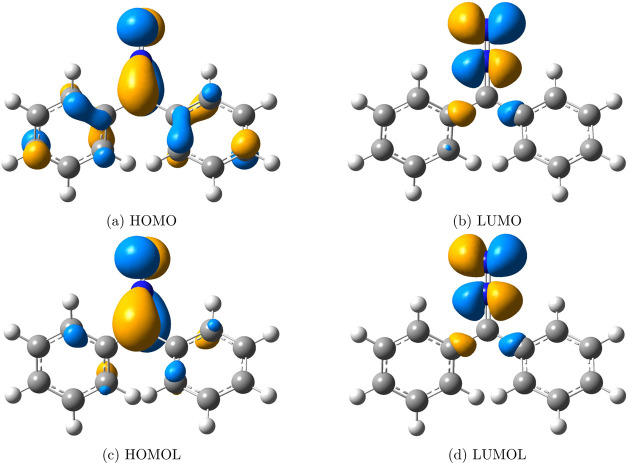
HOMOL of TS1 is shown in Figure 15. The interaction between HOMOL fragments of the same sign on carbon 1 (C1) and carbon 5 (C5) will result in the formation of the C1–C5 bond that exists in both products. This interaction can be achieved by rotating the bond linking C1 and C2 and the bond linking C5 and C6. Fragments of HOMOL on C4 and C10 indicate that they can interact with each other to form the C4–C10 bond for product 1, while fragments of HOMOL on C2 and C8 indicate that they can interact with each other to form the C2–C8 bond in product 2. HOMOL of TS2 can be found in Figure 16. As can be seen, HOMOL clearly shows the transition between the C4–C10 bond and the C2–C8 bond. Conversion between the two products is achieved by the transition.

Figure 15.

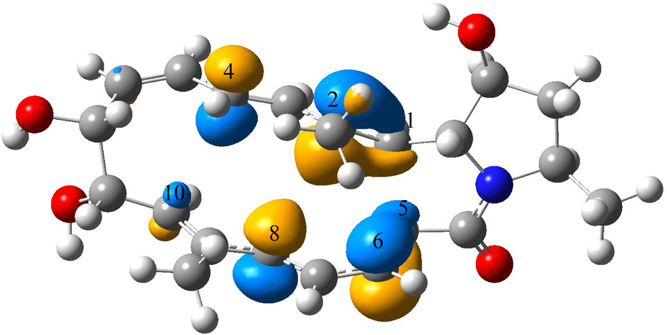
Figure 15

Open in a new tab

HOMOL for TS1 of the bifurcating reaction shown in Figure 14. Fragments on C4 and C10 indicate that they can interact with each other to form the C4–C10 bond in product 1; fragments on C2 and C8 indicate that they can interact with each other to form the C2–C8 bond in product 2; fragments on C1 and C5 indicate that they can interact with each other to form the C1–C5 bond that exists in both products. Iso = 0.05.

Figure 16.

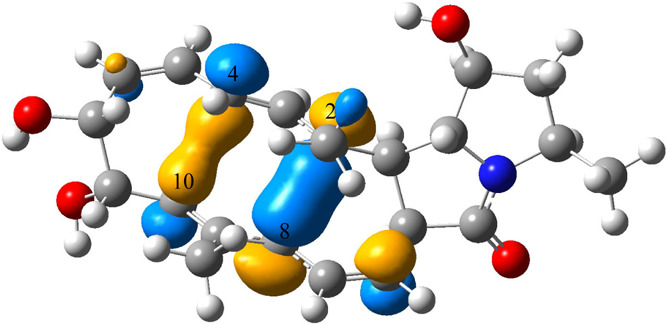
Figure 16

Open in a new tab

HOMOL for TS2 of the bifurcating reaction shown in Figure 14. HOMOL shows the formation of the C4–C10 bond in product 1 and the C2–C8 bond in product 2. Iso = 0.05.

Therefore, FMOLs can describe the bifurcating reaction by identifying the most important interactions based on the geometry of the transition states without fragmentation of the transition states. Interactions between fragments of FMOLs show clearly which parts of the molecule will be involved in the reaction and how will these chemical fragments interact with each other. Although these interacting fragments can also be found in FMOs (see the SI), the significance of these interactions is hidden with the delocalized orbitals.

Conclusions

To connect quantum mechanical description and chemists’ intuitions, we developed a new LMO model, the orbitalets that are localized in both physical and energy spaces. Containing both locality and energy information, FMOLs can be used to describe and predict the reactivity of a wide range of large systems. The successful application of FMOLs to several example systems shows that the FMOLs are effective in (i) finding the reactive functional groups of chemical systems in their equilibrium geometries, (ii) providing rapid chemical reaction analysis based on the geometries of the transition states, and (iii) capturing important electron transitions between orbitals in excitation CT processes that cannot be captured by CMOs. Therefore, FMOLs can be used as reactivity descriptors with the electron density mainly localized in the region where the chemical reaction really occurs. We believe that FMOLs can offer important insights into the study of many chemical phenomena in large and complex systems. In addition, the FMOLs should also be useful for bulk systems, in particular, for describing and predicting chemical reactivities on surfaces and in interfaces.75

Acknowledgments

J.Y. acknowledges the support from the National Institute of General Medical Sciences of the National Institutes of Health under award number R01-GM061870. W.Y. and N.Q.S. acknowledge the support from the National Science Foundation (grant no. CHE-1900338). N.Q.S. acknowledges the support from the National Natural Science Foundation of China (Grant No. 22073049). J.Y. was also supported by the Visiting International Student Scholarship from Duke University and International Travel Fellowship from Shandong University. Dr. Zhenyang Lin and Dr. Jing-Xuan Zhang kindly offered the coordinates of transition states of the bifurcating reaction, which the authors used for this study. Dr. Peng Zhang offered several CT models and helped with our understanding of CT.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.2c00085.

  • More calculation results; Fr and Fe of hexadecaoctaene (Figure S1); CMOs and orbitalets near FMO(L)s of the DBA CT system (Figure S2); CIS results of the TCNE–aromatic molecule CT systems (Figure S3); FMOs for TS1 and TS2 of the bifurcating reaction shown in Figure 14 (Figure S4); LUMOLs for TS1 and TS2 of the bifurcating reaction shown in Figure 14 (Figure S5); and HOMO and HOMOL of diphenyldiazomethane at Iso = 0.02 (Figure S6) (PDF)

Author Contributions

⊥ J.Y. and N.Q.S contributed equally to this work and share the first authorship.

The authors declare no competing financial interest.

Supplementary Material

au2c00085_si_001.pdf (4.7MB, pdf)

References

  1. Fukui K.; Yonezawa T.; Shingu H. A molecular orbital theory of reactivity in aromatic hydrocarbons. J. Chem. Phys. 1952, 20, 722–725. 10.1063/1.1700523. [DOI] [Google Scholar]
  2. Parr R. G.; Yang W. Density functional approach to the frontier-electron theory of chemical reactivity. J. Am. Chem. Soc. 1984, 106, 4049–4050. 10.1021/ja00326a036. [DOI] [Google Scholar]
  3. Fleming I.Frontier Orbitals and Organic Chemical Reactions; Wiley, 1977. [Google Scholar]
  4. Fujimoto H.; Fukui K.. Frontier Orbitals and Reaction Paths: Selected Papers of Kenichi Fukui; World Scientific, 1997; Vol. 7. [Google Scholar]
  5. Nguyen A. Q.; Anh N. T.; Nguyên T. A.. Frontier Orbitals: A Practical Manual; John Wiley & Sons, 2007. [Google Scholar]
  6. Fleming I.Molecular Orbitals and Organic Chemical Reactions; John Wiley & Sons, 2011. [Google Scholar]
  7. Woodward R. B.; Hoffmann R.. The Conservation of Orbital Symmetry; Elsevier, 2013. [Google Scholar]
  8. Fukui K.Theory of Orientation; Springer, 1975. [Google Scholar]
  9. Zhang J.-X.; Sheong F. K.; Lin Z. Unravelling Chemical Interactions with Principal Interacting Orbital Analysis. Chem. - Eur. J. 2018, 24, 9639–9650. 10.1002/chem.201801220. [DOI] [PubMed] [Google Scholar]
  10. Boys S. F. Construction of some molecular orbitals to be approximately invariant for changes from one molecule to another. Rev. Mod. Phys. 1960, 32, 296 10.1103/RevModPhys.32.296. [DOI] [Google Scholar]
  11. Edmiston C.; Ruedenberg K. Localized atomic and molecular orbitals. Rev. Mod. Phys. 1963, 35, 457 10.1103/RevModPhys.35.457. [DOI] [Google Scholar]
  12. Mauri F.; Galli G.; Car R. Orbital formulation for electronic-structure calculations with linear system-size scaling. Phys. Rev. B 1993, 47, 9973 10.1103/PhysRevB.47.9973. [DOI] [PubMed] [Google Scholar]
  13. Hierse W.; Stechel E. Order-N methods in self-consistent density-functional calculations. Phys. Rev. B 1994, 50, 17811 10.1103/PhysRevB.50.17811. [DOI] [PubMed] [Google Scholar]
  14. Yang W. Absolute-energy-minimum principles for linear-scaling electronic-structure calculations. Phys. Rev. B 1997, 56, 9294 10.1103/PhysRevB.56.9294. [DOI] [Google Scholar]
  15. Liu S.; Perez-Jorda J. M.; Yang W. Nonorthogonal localized molecular orbitals in electronic structure theory. J. Chem. Phys. 2000, 112, 1634–1644. 10.1063/1.480730. [DOI] [Google Scholar]
  16. Reed A. E.; Weinstock R. B.; Weinhold F. Natural population analysis. J. Chem. Phys. 1985, 83, 735–746. 10.1063/1.449486. [DOI] [Google Scholar]
  17. Reed A. E.; Weinhold F. Natural localized molecular orbitals. J. Chem. Phys. 1985, 83, 1736–1740. 10.1063/1.449360. [DOI] [Google Scholar]
  18. Glendening E. D.; Landis C. R.; Weinhold F. NBO 6.0: Natural bond orbital analysis program. J. Comput. Chem. 2013, 34, 1429–1437. 10.1002/jcc.23266. [DOI] [PubMed] [Google Scholar]
  19. Flener C.Quantum Mechanical Analysis of Donor-Acceptor Interactions in Organometallic Complexes and Comparative Analysis of Class Size and Teacher Experience on Student Experience Satisfaction and Learning; University of Illinois at Urbana-Champaign, 2009. [Google Scholar]
  20. Glendening E. D.; Weinhold F. Resonance Natural Bond Orbitals: Efficient Semilocalized Orbitals for Computing and Visualizing Reactive Chemical Processes. J. Chem. Theory Comput. 2019, 15, 916–921. 10.1021/acs.jctc.8b00948. [DOI] [PubMed] [Google Scholar]
  21. Zubarev D. Y.; Boldyrev A. I. Developing paradigms of chemical bonding: adaptive natural density partitioning. Phys. Chem. Chem. Phys. 2008, 10, 5207–5217. 10.1039/b804083d. [DOI] [PubMed] [Google Scholar]
  22. Zubarev D. Y.; Boldyrev A. I. Deciphering chemical bonding in golden cages. J. Phys. Chem. A 2009, 113, 866–868. 10.1021/jp808103t. [DOI] [PubMed] [Google Scholar]
  23. Sergeeva A. P.; Zubarev D. Y.; Zhai H.-J.; Boldyrev A. I.; Wang L.-S. A photoelectron spectroscopic and theoretical study of B16- and B162-: an all-boron naphthalene. J. Am. Chem. Soc. 2008, 130, 7244–7246. 10.1021/ja802494z. [DOI] [PubMed] [Google Scholar]
  24. Averkiev B. B.; Zubarev D. Y.; Wang L.-M.; Huang W.; Wang L.-S.; Boldyrev A. I. Carbon Avoids Hypercoordination in CB6-, CB62-, and C2B5- Planar Carbon- Boron Clusters. J. Am. Chem. Soc. 2008, 130, 9248–9250. 10.1021/ja801211p. [DOI] [PubMed] [Google Scholar]
  25. Yang W.; Parr R. G.; Pucci R. Electron density, Kohn-Sham frontier orbitals, and Fukui functions. J. Chem. Phys. 1984, 81, 2862–2863. 10.1063/1.447964. [DOI] [Google Scholar]
  26. Yang W.; Parr R. G. Hardness, softness, and the fukui function in the electronic theory of metals and catalysis. Proc. Natl. Acad. Sci. U.S.A. 1985, 82, 6723–6726. 10.1073/pnas.82.20.6723. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Ayers P. W.; Parr R. G. Variational principles for describing chemical reactions: the Fukui function and chemical hardness revisited. J. Am. Chem. Soc. 2000, 122, 2010–2018. 10.1021/ja9924039. [DOI] [PubMed] [Google Scholar]
  28. Kohn W.; Sham L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
  29. Morell C.; Grand A.; Toro-Labbe A. New dual descriptor for chemical reactivity. J. Phys. Chem. A 2005, 109, 205–212. 10.1021/jp046577a. [DOI] [PubMed] [Google Scholar]
  30. Cardenas C.; Muñoz M.; Contreras J.; Ayers P. W.; Gomez T.; Fuentealba P. Understanding chemical reactivity in extended systems: exploring models of chemical softness in carbon nanotubes. Acta Phys. Sin. 2018, 34, 631–638. 10.3866/PKU.WHXB201710201. [DOI] [Google Scholar]
  31. Fujimoto H.; Satoh S. Orbital interactions and chemical hardness. J. Phys. Chem. A 1994, 98, 1436–1441. 10.1021/j100056a011. [DOI] [Google Scholar]
  32. Hirao H.; Ohwada T. Theoretical study of reactivities in electrophilic aromatic substitution reactions: reactive hybrid orbital analysis. J. Phys. Chem. A 2003, 107, 2875–2881. 10.1021/jp027330l. [DOI] [Google Scholar]
  33. da Silva R. R.; Ramalho T. C.; Santos J. M.; Figueroa-Villar J. D. On the limits of highest-occupied molecular orbital driven reactions: the frontier effective-for-reaction molecular orbital concept. J. Phys. Chem. A 2006, 110, 1031–1040. 10.1021/jp054434y. [DOI] [PubMed] [Google Scholar]
  34. La Porta F. A.; Ramalho T. C.; Santiago R. T.; Rocha M. V.; da Cunha E. F. Orbital signatures as a descriptor of regioselectivity and chemical reactivity: the role of the frontier orbitals on 1, 3-dipolar cycloadditions. J. Phys. Chem. A 2011, 115, 824–833. 10.1021/jp108790w. [DOI] [PubMed] [Google Scholar]
  35. Dapprich S.; Frenking G. Investigation of donor-acceptor interactions: A charge decomposition analysis using fragment molecular orbitals. J. Phys. Chem. C 1995, 99, 9352–9362. 10.1021/j100023a009. [DOI] [Google Scholar]
  36. Sidis V. Diabatic potential energy surfaces for charge-transfer processes. Adv. Chem. Phys 1992, 82, 73–134. 10.1002/9780470141403.ch2. [DOI] [Google Scholar]
  37. Pederson M. R.; Ruzsinszky A.; Perdew J. P. Communication: Self-interaction correction with unitary invariance in density functional theory. J. Chem. Phys. 2014, 140, 121103 10.1063/1.4869581. [DOI] [PubMed] [Google Scholar]
  38. Li L.; Trepte K.; Jackson K. A.; Johnson J. K. Application of Self-Interaction Corrected Density Functional Theory to Early, Middle, and Late Transition States. J. Phys. Chem. A 2020, 124, 8223–8234. 10.1021/acs.jpca.0c06485. [DOI] [PubMed] [Google Scholar]
  39. Aquino F. W.; Shinde R.; Wong B. M. Fractional occupation numbers and self-interaction correction-scaling methods with the Fermi-Löwdin orbital self-interaction correction approach. J. Comput. Chem. 2020, 41, 1200–1208. 10.1002/jcc.26168. [DOI] [PubMed] [Google Scholar]
  40. Diaz C. M.; Baruah T.; Zope R. R. Fermi-Löwdin-orbital self-interaction correction using the optimized-effective-potential method within the Krieger-Li-Iafrate approximation. Phys. Rev. A 2021, 103, 042811 10.1103/PhysRevA.103.042811. [DOI] [Google Scholar]
  41. Nalewajski R. F.; Formosinho S. J.; Varandas A. J.; Mrozek J. Quantum mechanical valence study of a bond-breaking-bond-forming process in triatomic systems. Int. J. Quantum Chem. 1994, 52, 1153–1176. 10.1002/qua.560520504. [DOI] [Google Scholar]
  42. Mitoraj M.; Michalak A. Natural orbitals for chemical valence as descriptors of chemical bonding in transition metal complexes. J. Mol. Model. 2007, 13, 347–355. 10.1007/s00894-006-0149-4. [DOI] [PubMed] [Google Scholar]
  43. Michalak A.; Mitoraj M.; Ziegler T. Bond Orbitals from Chemical Valence Theory. J. Phys. Chem. A 2008, 112, 1933–1939. 10.1021/jp075460u. [DOI] [PubMed] [Google Scholar]
  44. Ziegler T.; Rauk A. On the calculation of bonding energies by the Hartree Fock Slater method. Theor. Chim. Acta 1977, 46, 1–10. 10.1007/BF02401406. [DOI] [Google Scholar]
  45. Mitoraj M. P.; Michalak A.; Ziegler T. A Combined Charge and Energy Decomposition Scheme for Bond Analysis. J. Chem. Theory Comput. 2009, 5, 962–975. 10.1021/ct800503d. [DOI] [PubMed] [Google Scholar]
  46. Li C.; Zheng X.; Su N. Q.; Yang W. Localized orbital scaling correction for systematic elimination of delocalization error in density functional approximations. Natl. Sci. Rev. 2018, 5, 203–215. 10.1093/nsr/nwx111. [DOI] [Google Scholar]
  47. Su N. Q.; Mahler A.; Yang W. Preserving Symmetry and Degeneracy in the Localized Orbital Scaling Correction Approach. J. Phys. Chem. Lett. 2020, 11, 1528–1535. 10.1021/acs.jpclett.9b03888. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Su N. Q.; Li C.; Yang W. Describing strong correlation with fractional-spin correction in density functional theory. Proc. Natl. Acad. Sci. U.S.A. 2018, 115, 9678–9683. 10.1073/pnas.1807095115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Cohen A. J.; Mori-Sánchez P.; Yang W. Insights into current limitations of density functional theory. Science 2008, 321, 792–794. 10.1126/science.1158722. [DOI] [PubMed] [Google Scholar]
  50. Mori-Sánchez P.; Cohen A. J.; Yang W. Localization and delocalization errors in density functional theory and implications for band-gap prediction. Phys. Rev. Lett. 2008, 100, 146401 10.1103/PhysRevLett.100.146401. [DOI] [PubMed] [Google Scholar]
  51. Cohen A. J.; Mori-Sánchez P.; Yang W. Fractional Spins and Static Correlation Error in Density Functional Theory. J. Chem. Phys. 2008, 129, 121104 10.1063/1.2987202. [DOI] [PubMed] [Google Scholar]
  52. Zheng X.; Cohen A. J.; Mori-Sánchez P.; Hu X.; Yang W. Improving band gap prediction in density functional theory from molecules to solids. Phys. Rev. Lett. 2011, 107, 026403 10.1103/PhysRevLett.107.026403. [DOI] [PubMed] [Google Scholar]
  53. Cohen A. J.; Mori-Sánchez P.; Yang W. Challenges for density functional theory. Chem. Rev. 2012, 112, 289–320. 10.1021/cr200107z. [DOI] [PubMed] [Google Scholar]
  54. Foster J. M.; Boys S. Canonical configurational interaction procedure. Rev. Mod. Phys. 1960, 32, 300 10.1103/RevModPhys.32.300. [DOI] [Google Scholar]
  55. Gygi F.; Fattebert J.-L.; Schwegler E. Computation of Maximally Localized Wannier Functions using a simultaneous diagonalization algorithm. Comput. Phys. Commun. 2003, 155, 1–6. 10.1016/S0010-4655(03)00315-1. [DOI] [Google Scholar]
  56. Giustino F.; Pasquarello A. Mixed Wannier-Bloch Functions for Electrons and Phonons in Periodic Systems. Phys. Rev. Lett. 2006, 96, 216403 10.1103/PhysRevLett.96.216403. [DOI] [PubMed] [Google Scholar]
  57. Dawes R.; Carrington T. Using simultaneous diagonalization and trace minimization to make an efficient and simple multidimensional basis for solving the vibrational Schrödinger equation. J. Chem. Phys. 2006, 124, 054102 10.1063/1.2162168. [DOI] [PubMed] [Google Scholar]
  58. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Zheng G.; Sonnenberg J. L.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Montgomery J. A. Jr; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Rega N.; Millam J. M.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farkas; Foresman J. B.; Ortiz J. V.; Cioslowski J.; Fox D. J.. et al. Gaussian 09, revision A.1; Gaussian Inc.: Wallingford, CT, 2009.
  59. Becke A. D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]
  60. Lee C.; Yang W.; Parr R. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  61. Becke A. D. Density-functional thermochemistry. I. The effect of the exchange-only gradient correction. J. Chem. Phys. 1992, 96, 2155–2160. 10.1063/1.462066. [DOI] [Google Scholar]
  62. Stephens P. J.; Devlin F.; Chabalowski C.; Frisch M. J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. B 1994, 98, 11623–11627. 10.1021/j100096a001. [DOI] [Google Scholar]
  63. Hehre W. J.; Ditchfield R.; Pople J. A. Self-consistent molecular orbital methods. XII. Further extensions of Gaussian-type basis sets for use in molecular orbital studies of organic molecules. J. Chem. Phys. 1972, 56, 2257–2261. 10.1063/1.1677527. [DOI] [Google Scholar]
  64. Aquino A. A. J.; Borges I.; Nieman R.; Köhn A.; Lischka H. Intermolecular interactions and charge transfer transitions in aromatic hydrocarbon-tetracyanoethylene complexes. Phys. Chem. Chem. Phys. 2014, 16, 20586–20597. 10.1039/C4CP02900C. [DOI] [PubMed] [Google Scholar]
  65. See http://www.qm4d.info for an in-house program for QM/MM simulations (accessed Mar 24, 2022).
  66. Dunning T. H. Jr Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. 10.1063/1.456153. [DOI] [Google Scholar]
  67. Kumpulainen T.; Lang B.; Rosspeintner A.; Vauthey E. Ultrafast elementary photochemical processes of organic molecules in liquid solution. Chem. Rev. 2017, 117, 10826–10939. 10.1021/acs.chemrev.6b00491. [DOI] [PubMed] [Google Scholar]
  68. Lin Z.; Lawrence C. M.; Xiao D.; Kireev V. V.; Skourtis S. S.; Sessler J. L.; Beratan D. N.; Rubtsov I. V. Modulating unimolecular charge transfer by exciting bridge vibrations. J. Am. Chem. Soc. 2009, 131, 18060–18062. 10.1021/ja907041t. [DOI] [PubMed] [Google Scholar]
  69. Casida M. E.Recent Advances in Density Functional Methods, Recent Advances in Computational Chemistry; World Scientific, 1995; Vol. 1, pp 155–192. [Google Scholar]
  70. Runge E.; Gross E. K. U. Density-Functional Theory for Time-Dependent Systems. Phys. Rev. Lett. 1984, 52, 997–1000. 10.1103/PhysRevLett.52.997. [DOI] [Google Scholar]
  71. Ullrich C. A.Time-Dependent Density-Functional Theory: Concepts and Applications; OUP Oxford, 2011. [Google Scholar]
  72. Huisgen R. Mechanism of 1, 3-dipolar cycloadditions. Reply. J. Org. Chem. 2002, 33, 2291–2297. 10.1021/jo01270a024. [DOI] [Google Scholar]
  73. Yu P.; Patel A.; Houk K. Transannular [6+ 4] and ambimodal cycloaddition in the biosynthesis of heronamide A. J. Am. Chem. Soc. 2015, 137, 13518–13523. 10.1021/jacs.5b06656. [DOI] [PubMed] [Google Scholar]
  74. Woodward R. B.; Hoffmann R. Stereochemistry of electrocyclic reactions. J. Am. Chem. Soc. 1965, 87, 395–397. 10.1021/ja01080a054. [DOI] [Google Scholar]
  75. Mahler A.; Williams J. Z.; Su N. Q.; Yang W.. Wannier Functions Dually Localized in Space and Energy. 2022, arXiv:2201.07751. arXiv.org e-Print archive. https://arxiv.org/abs/2201.07751.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

au2c00085_si_001.pdf (4.7MB, pdf)

Articles from JACS Au are provided here courtesy of American Chemical Society

RESOURCES