What is the Optimal Schedule for Multiparametric MRS? A Magnetic Resonance Fingerprinting Perspective

Summary

Clinical magnetic resonance spectroscopy (MRS) mainly concerns itself with the quantification of metabolite concentrations. Metabolite relaxation values, which reflect the microscopic state of specific cellular and sub-cellular environments, could potentially hold additional valuable information, but are rarely acquired within clinical scan times. By varying the flip angle, repetition time and echo time in a preset way (termed a schedule), and matching the resulting signals to a pre-generated dictionary – an approach dubbed magnetic resonance fingerprinting – it is possible to encode the spins’ relaxation times into the acquired signal, simultaneously quantifying multiple tissue parameters for each metabolite. Herein, we optimized the schedule to minimize the averaged root mean square error (RMSE) across all estimated parameters: concentrations, longitudinal and transverse relaxation time, and transmitter inhomogeneity. The optimal schedules were validated in phantoms and, subsequently, in a cohort of healthy volunteers, in a 4.5 mL parietal white matter single voxel and an acquisition time under 5 minutes. The average intra-subject, inter-scan coefficients of variation (CVs) for metabolite concentrations, T₁ and T₂ relaxation times were found to be 3.4%, 4.6% and 4.7% in-vivo, respectively, averaged over all major singlets. Coupled metabolites were quantified using the short echo time schedule entries and spectral fitting, and reliable estimates of glutamate+glutamine, glutathione and myo-inositol were obtained.

Introduction

Proton Magnetic Resonance Spectroscopy (MRS) quantifies the concentrations of several metabolites, including n-acetyl-asparate (NAA), choline (Cho) and creatine (Cr) containing compounds, myo-inositol (mI) and glutamine and glutamate (Glx); these metabolites act as markers for disease activity in multiple pathologies, ranging from cancer (1–3), Alzheimer’s disease (4,5) and dementia (5,6), to traumatic brain injury (7–10) and multiple sclerosis (11,12). Independent of their concentrations, which reflect the tissue’s biochemistry, metabolites’ relaxation times (T₁, T₂) provide information about their microscopic environment. For example, the relaxation times of NAA, which is primarily found in neurons (13), reflect the neuronal microenvironment and could act as independent markers of neurodegeneration or inflammation. A large body of evidence for altered metabolite relaxation times exists, in disorders such as multiple sclerosis (14–19), Alzheimer’s disease (20–22) and cancer (23–28), to name a few. However, conventional MRS protocols are not set up to measure metabolite T₁ and T₂ values within clinical scan times of approximately 5 minutes or less, and existing sequences for doing so – such as inversion recovery or multi-echo MRS – are not optimized for time efficiency and are rarely implemented in clinical settings.

A second need for multiparametric MRS data arises during signal quantification. The MRS signal is often weighted by various factors: pulsing too rapidly, at time scales of the order of T₁ or shorter, introduces T₁ saturation; non-zero echo times introduce T₂ weighting; and imperfectly calibrated transmitter voltages result in B₁₊ weighting. Correction of this weighting is crucial for accurate quantification of both absolute (in mM) and relative metabolite concentrations, and requires knowing each subject’s specific T₁, T₂ and B₁₊ values. Existing approaches often rely on tabulated population averaged values for T₁ and T₂, which could significantly bias the MRS signal (29). In many instances, exact information for a region of interest, pathology, gender, age group and tissue type is simply unavailable. A recent analysis has examined the cumulative effect of both of these benefits for a large number of neuropathologies and regions of interest, based on an extensive body of literature of metabolites’ concentration and relaxation values (30): Compared to conventional MRS, multiparametric MRS is predicted to improve the median area underneath the respective receiver operating characteristic curves of each method from 0.72 to 0.86; when confining the analysis to the ten cases showing the largest improvement, the predicted improvement becomes even more marked, increasing from 0.68 for conventional MRS to 0.92 for multiparametric MRS.

Previously, we have demonstrated the benefits of combining a variable schedule with single voxel spectroscopy (29) to simultaneously acquire metabolites’ concentrations, T₁ and T₂ relaxation times, alongside the radiofrequency transmitter’s inhomogeneity (B₁₊). This approach, coined Magnetic Resonance Spectroscopic Fingerprinting (MRSF), utilizes a schedule with variable sequence parameters such as the repetition time (TR), echo time (TE) and excitation flip angle (FA), as done in Magnetic Resonance Fingerprinting (31). The schedule encodes the spin parameters (T₁, T₂, B₁₊) into the time-varying signal, termed a fingerprint. The schedule has a substantial impact on the sequence’s ability to encode the spin parameters, and hence, its optimization is a major goal of fingerprinting. There have been several works which have addressed this problem in detail in the context of imaging (32,33). However, the unique sequence topologies of MRS, with their long minimum TRs and TEs, make the aforementioned imaging schedules unsuitable for spectroscopy. Furthermore, the low signal to noise ratio (SNR) associated with MRS plays an important factor in MRSF schedule design; the above works have not considered the effect of schedule length, which directly affects the SNR per schedule entry and, hence, has an important impact on the quality of the spectral MRS data.

In this work, we optimized the MRSF schedule to minimize the average root mean square error (RMSE) of T₁, T₂ and B₁₊. Several different schedule lengths were considered, while keeping the total acquisition time and SNR per unit time fixed, to determine whether there exists an optimal schedule length. Genetic algorithms with large starting population sizes were used to avoid local minima and accelerate convergence. Several previous works have used surrogate functions to estimate schedule performance, such as the dot product between dictionary elements (32). Here, we used Monte Carlo simulations to explicitly and precisely estimate the RMSE at each optimization step. The quantification of the concentrations and relaxation values using the optimal schedule were assessed in a brain phantom and in a cohort of 14 healthy volunteers.

Methods

MRSF Sequence

Each MRSF schedule consisted of N_ent consecutive, distinct entries, each with its own TR, TE and excitation flip angle (FA) in a PRESS sequence. All pulses were designed using an SLR algorithm with a peak radiofrequency amplitude of B₁=18.8 μT $\left(\sout{\gamma }{B}_1=800\hspace{0.17em}\text{Hz}\right)$; due to the variable flip angle, each excitation pulse had a different bandwidth and, consequently, slice selection gradient. Spins were initially driven into dynamic equilibrium by an initial playout of the schedule without water suppression, which was also used to measure reference water T₁, T₂ and B₁₊ values. The water-derived value of B₁₊ was used to constrain subsequent fittings of metabolite data. Once in dynamic equilibrium, the schedule was repeated N_avg times for signal averaging, keeping the total acquisition time $\left(N_{avg}+1\right)\cdot {\sum }_{i=1}^{N_{ent}}T{R}_i$ fixed at 5 minutes. We note that, much like for conventional MRS, a variable schedule also enters a dynamic equilibrium very quickly (within a time ≈5·T₁), in which the magnetization vector is identical at the beginning of each repetition of the schedule.

MRSF Schedule Optimization

A range of 9 schedule lengths were optimized (N_ent=5, 10, 15, 20, 25, 50, 60, 75 and 100). Optimization minimized the normalized Root Mean Square Error $\left(\overline{nRMSE}\right)$ of each schedule:

$$\overline{nRMSE}\equiv \frac{1}{\text{M}}{\sum }_{k=1}^M\left(nRMSE\left(T_{1,k}\right)+nRMSE\left(T_{2,k}\right)\right).$$ (1)

The summation is extended over a fixed set of five equispaced values of T_1,k∈[750, 1650] ms and T_2,k∈[125, 350] ms (k=1,…,5), for a total of M=25 terms. To speed up convergence, a fixed value of B₁₊=1 was assumed. The normalized RMSE for a quantity T is defined as: $nRMSE\left(T\right)=\frac{\sqrt{\text{bias}{\left(T\right)}^2+\text{var}\left(T\right)}}{T}$. The normalization by T ensures that relative – and not absolute – deviations are considered; This is similar to minimizing the coefficient of variation (CV), as opposed to the absolute value of the standard deviation. For a given schedule, $\overline{nRMSE}$ (Eq. (1)) was estimated using single-spin Monte-Carlo simulations as follows: given values of (T₁, T₂, B₁₊), the corresponding fingerprint was obtained by numerically solving the Bloch equations; noise was added; and fitting to a pre-generated dictionary was carried out. This was repeated 3,000 times, to generate a robust histogram, from which both the bias and variance of T₁ and T₂ could be calculated with a high degree of accuracy. The noise was normally distributed around zero. The noise’s standard deviation was calibrated to yield an SNR of 15 for a single, fully relaxed 90̊ excitation, and then scaled as $\sqrt{N_{avg}^{-1}}=\sqrt{\left({\sum }_{\text{j}=1}^{{\text{N}}_{\text{ent}}}T{R}_j\right)/\left(5\hspace{0.17em}\text{minutes}\right)}$, to keep the SNR per unit time fixed and ensure a fair comparison between the different schedule lengths.

Optimization was carried out using the built-in genetic algorithm toolbox of MATLAB 2017a (The Mathworks, Natick, MA). To reduce optimization complexity, discrete sets of values for FA=[0°, 5°, …, 150°], TR=[900, 910, …, 1600] ms and TE=[35, 40, …, 150] ms were used. Discretization is supported both by physical intuition, since small changes of a few milliseconds or degrees to sequence parameters are not expected to induce large changes to the acquired fingerprints; and by prior observations that the dictionary space is highly redundant (34–36). To avoid local minima, an initial population size of 500 was used, and the algorithm was repeated four times; all four solutions were evaluated using a higher resolution dictionary (see below), and the optimal solution was retained. The stopping criteria were set to a maximum of 200 generations, and a minimal change of 0.001 in the $\overline{nRMSE}$.

MRSF Schedule Evaluation

Following optimization, $\overline{nRMSE}$ was re-evaluated for each schedule using single-spin Monte-Carlo simulations employing a wider range of equispaced T₁, T₂ and B₁₊ values (T₁∈[750, …, 1650], T₂∈[125, …, 350], B₁₊∈[0.9, 1.0, 1.1] in Eq. (1)). A higher-resolution dictionary was used for fitting (T₁∈[600, …, 2500] ms, T₂∈[50, …, 600] ms and B₁₊∈[0.8, …, 1.2]).

To assess the impact of optimization, the performance of each schedule was compared to a randomly generated solution: for a given schedule length (N_ent), 20 random schedule were generated and the $\overline{nRMSE}$ was calculated for each. To assess the importance of “spin memory” – that is, the formation of inter-scan coherences between successive entries, which increase the amount of possible T₁ and T₂ weighting – each optimal schedule was randomly reshuffled 20 times; the $\overline{nRMSE}$ was calculated for each reshuffled schedule. Reshuffling was carried out using MATLAB’s randperm command, which returns a uniformly randomized reordering of a given vector.

To assess the contribution of each point in the schedule to T₁, T₂ and B₁₊ evaluation, an occlusion test was performed for the N_ent=10 case. A point $1\le M\le N_{ent}$ was selected, and the $\overline{nRMSE}$ was evaluated using Monte Carlo simulations as previously described, with the exception that the noise at point M was amplified ten-fold. This was done for all values of $M\in \left[1,N_{ent}\right]$.

Phantom Measurements

All measurements were carried out on a Siemens 3T Prisma MRI scanner using the body coil for transmission $\left(B_{1,max}=20\mu T\right)$ and a standard 20-channel receiver head coil (Siemens-Healthineers, Erlangen, Germany). A homogeneous spherical phantom containing 11 mM NAA (T₁/T₂=820/446 ms), 10 mM Cr (T₁/T₂=600/430 ms), 2 mM Cho (T₁/T₂=430/310 ms), 10 mM Glu, 5 mM Lac, 2 mM GABA and 8 mM mI was used. Sodium azide (NaN₃ 0.01%) and Gd-DTPA (0.5 mM) were added to prevent microbial growth and reduce T₁ and T₂, respectively. Tabulated values of T₁ and T₂ were recorded using prolonged inversion recovery and spin-echo single-voxel sequences.

A 1.5×1.5×1.5 cm³ voxel was placed at the phantom’s center and shimmed using the built-in shimming routines. The optimal N_ent=10 MRSF schedule was used, with a duration of ${\sum }_{i=1}^{N_{ent}}T{R}_i=14$ seconds per average, N_avg=20 averages and a total of 4:54 minutes. The dwell time was 0.5 ms, with 256 ms of acquisition. The acquisition was repeated N_rep=22 times, to produce multiple estimates of each peak’s parameters and assess the method’s bias and standard deviation. The total acquisition time for the entire protocol was 1:45 hours.

Spectra were summed over the averaging dimension, four-fold zero-filled and apodized with a 5 Hz Gaussian kernel along the spectral domain before being Fourier transformed. The peak intensities of NAA (2.01 ppm), Cr (3.0 ppm) and Cho (3.2 ppm) were obtained from the amplitudes of the phased real spectra for each of the N_ent=10 schedule entries, producing three separate fingerprints. Fitting to the MRSF dictionary was implemented using MATLAB’s fminsearch function, which maximized the dot product of the simulated and measured fingerprint (i.e. minimized its negative). Simulated fingerprints were generated using full 3D Bloch simulations. All three PRESS pulse profiles were taken into account, using a digital phantom with 100×10×10=10000 spins uniformly spread across a $3.5\times 3.5\times 3.5\hspace{0.17em}{\text{cm}}^3$ volume. The number of spins was selected based on convergence of the results to a stable value. To further increase stability and accelerate fitting, the fingerprint of the high-SNR, unsuppressed water reference scan was initially fit to the dictionary to extract the global B₁₊ value, which was then used to constrain fitting of the metabolites’ data. Note that the water data is acquired as the system attains dynamic equilibrium.

For each repetition, metabolite concentrations were assessed as follows: all scans with TE=35 ms were summed and fitted using LCModel v6.3c (37). Basis functions were generated for each of the metabolites in the phantom using in-house quantum mechanical simulations written in MATLAB. The first schedule entry of the water signal was used as the reference spectrum. The fitted results from LCModel were scaled to obtain relaxation-corrected, absolute-quantified concentrations as follows: let $\left(s_1,s_2,\dots ,s_{N_{ent}}\right)$ be the simulated fingerprint for the metabolite and $\left(w_1,w_2,\dots ,w_{N_{exc}}\right)$ the simulated fingerprint of the water signal. The metabolite and water signals for each of the schedule entries (after summation of all metabolite averages) are $S_j^{\left(met\right)}=\Lambda \cdot C_{met}\cdot s_j\cdot N_{avg}$ and $W_j^{\left(water\right)}=\Lambda \cdot C_{water}\cdot w_j$, respectively, where $C_{met}$, $C_{water}$ are their respective concentrations. The factor Λ accounts for factors which identically affect both acquisitions, such as coil sensitivity and electronics. The ratio ${\sum }_{j\in \left(TE=35\hspace{0.17em}ms\right)}^{⬚}{S}_j^{\left(met\right)}/W_1^{\left(water\right)}$ equals the output of LCModel when provided with the summed metabolite spectra of the TE=35 ms schedule entries, using the spectrum of the unsuppressed water’s first entry as a reference. This ratio also equals $\frac{C_{met}\cdot N_{avg}\cdot {\sum }_{j\in \left(TE=35\hspace{0.17em}ms\right)}^{⬚}{s}_j}{c_{water}\cdot w_1}$. Thus, LCModel’s output can be converted into absolute concentrations by scaling it by:

$$C_{water}\cdot \frac{1}{N_{avg}}\cdot \frac{w_1}{{\sum }_j{s}_j}$$ (2)

where the sum in the denominator is over the TE=35 ms schedule entries.

Using the TE=35 ms subset of spectra ensured that no destructive interference between different echo times took place, but also impaired the total SNR of the measurement. To quantitatively assess this loss, the total SNR of four cases was calculated using full 3D Bloch simulations: (i) A conventional PRESS, using the same SLR pulse as the FA=90° MRSF excitation pulse and a TR/TE=1500/35 ms, typical of in-vivo acquisitions which seek to optimize the SNR per unit time (38); (ii) The same as (i), but using TR=5000 ms to minimize T₁ weighting; (iii) Summing all MRSF schedule entries; (iv) Summing just the TE=35 ms subset of MRSF schedule entries. The simulations were carried out for each of the singlets in the phantom (NAA, Cho, Cr) using their measured T₁ and T₂ values, as estimated using MRSF. Results were averaged over all singlets. For each case, three quantities were compared: (i) The normalized voxel volume, equal to the simulated volume of the voxel, divided by its nominal volume. (ii) The weighted voxel volume, given by the normalized voxel volume but also including the effects of T₁ and T₂ relaxations. (iii) The SNR per unit time, normalized to the PRESS TR=5000 ms case. For MRSF, each of these quantities was calculated for each schedule entry, and averaged over all relevant entries (either all entries, or just the TE=35 ms entries).

In-Vivo Experiments

The inter-subject, inter-scan and intra-scan variability of MRSF were assessed in a cohort of 14 healthy volunteers. Participants were scanned after obtaining written informed consent, in accordance with the procedures approved by the Internal Review Board of Emek Medical Center (Afula, Israel). For each volunteer, a T₁-weighted MPRAGE scan (TR/TE/TI=2300/3.03/900 ms, FA=9°, FOV=256×256 mm² in plane, 1 mm isotropic resolution) was acquired for voxel placement and tissue segmentation. A single 1.5×1.5×2 cm³ voxel was positioned in parietal WM region, shimmed using the built-in scanner routines, and scanned using the optimal N_ent=10 schedule (TA=4:54 minutes). The MRSF scan was repeated three times, after which the subject was removed and repositioned inside the scanner, and all scans were repeated. In total, each volunteer was scanned a total of 3 × 2 = 6 times.

Metabolite concentrations were estimated using LCModel as described for the phantom. The simulated basis set consisted of Alanine, Aspartate, Creatine, GABA, Glucose, Glutamate, Glutamine, Glutathione, Choline, Lactate, myo-Inositol, NAA, NAAG and Taurine. The MPRAGE images were segmented into white matter (WM), gray matter (GM) and cerebrospinal fluid (CSF) maps using SPM12 (39), and the fraction of each map in the spectroscopic voxel was calculated $\left(f_{WM},f_{GM},f_{CSF}\right)$. These were used to normalize metabolite scans by CSF fraction (by dividing by $1-f_{CSF}$), to calculate the mean water concentration in the voxel ($C_{water}=f_{WM}{C}_{water}^{WM}+f_{GM}{C}_{water}^{GM}+f_{CSF}{C}_{water}^{CSF}$, and to assess reproducibility of voxel positioning.

There is no gold standard in-vivo and hence accuracy could not be assessed. Instead, we’ve estimated the inter-scan, intra-subject coefficient of variation for each subject $\left(k=1,\dots ,14\right)$ and each measured quantity $Q_{m,n}^{\left(k\right)}$ ($Q=T_1,T_2$, concentrations; m = 1,2 scan index; n = 1,2,3 repetition; $k=1,\dots ,14$ subject index): $C{V}_k=\frac{\sqrt{\left(\frac{1}{3}{\sum }_{n=1}^3\text{var}\left(Q_{1,n}^{\left(k\right)},Q_{2,n}^{\left(k\right)}\right)\right)}}{\text{mean}\left({\text{Q}}_{1,1}^{\left(\text{k}\right)},{\text{Q}}_{1,2}^{\left(\text{k}\right)},\dots ,{\text{Q}}_{2,3}^{\left(\text{k}\right)}\right)}$. The average CV per quantity was obtained by: $CV=\sqrt{{\sum }_{k=1}^{14}C{V}_k^2}$.

Result

MRSF Schedule Optimization

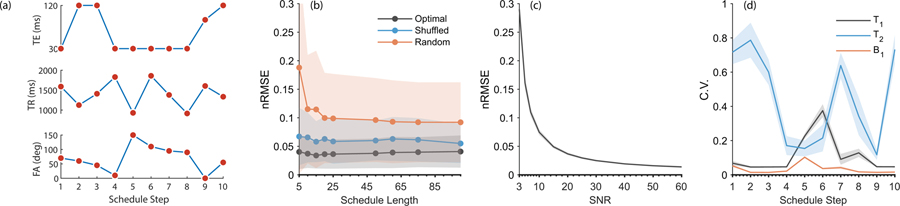
All optimization algorithm terminated by reaching the minimal tolerance for the target function, indicating a minimum has been reached. Optimization of a single schedule (N_ent=50) took about 2.5 hours on Intel i7–4790 desktop computer running in parallel on 4 cores. Total run time was 90 hours. Fig. 1a shows the N_ent=10 optimal schedule, and Supplementary Table S1 lists the full schedules for each N_ent. Supplementary Fig. S1 shows the time dynamics of M_z of a single spin with T₁=1000 ms, T₂=200 ms as it enters dynamic equilibrium following several iterations of the N_ent=10 schedule.

Figure 1.

Simulation results. (a.) The optimal schedule for N_ent=10, used for the phantom and in-vivo measurements. (b.) $\overline{nRMSE}$ as a function of schedule length (N_ent). Black: optimized schedule. The line corresponds to the mean, while the shaded regions correspond to one standard deviation, taken over four optimization results. Blue: $\overline{nRMSE}$ after reshuffling the order of the schedule entries. This indicates the order of excitations is meaningful, and supports the existence of “spin memory” between consecutive entries. Mean and standard deviation are taken over 20 random reshuffles. Red: $\overline{nRMSE}$ for 20 randomly generated schedules. Overall, optimization yields a three-fold improvement over a randomly generated schedule. (c.) $\overline{nRMSE}$ as a function of SNR, showing an approximate inverse relationship typical of many quantification algorithms. The black line corresponds to the mean over all optimized schedule lengths (N_ent), while the very narrow shaded patch corresponds to the standard deviation. (d.) Results of the occlusion test, showing how different points along the N_ent=10 schedule affect the estimation of various parameters (T₁, T₂ and B₁₊). For example, points 5 and 6 along the schedule are particularly important for T₁ quantification.

The optimal $\overline{nRMSE}$ varied between 3%−4%, indicating little to no dependence on N_ent. Fig. 1b shows the mean $\overline{nRMSE}$ for the optimal schedules (averaged over all four starting conditions) as a function of N_ent. The N_ent=10 schedule was chosen for phantom and in-vivo validations. Shuffling the order of schedule entries (Fig. 1b) approximately doubled the $\overline{nRMSE}$, indicating spin-memory plays an important role in schedule performance. Using completely random schedules triples and even quadruples the optimal $\overline{nRMSE}$, indicating schedule optimization is important for high quality estimates of relaxation parameters. The dependence of $\overline{nRMSE}$ on the SNR for all schedules is shown in Fig. 1c, where it approximately scales as SNR⁻¹, which is typical for many quantification algorithms (40). Fig. 1d shows the results of the occlusion test, which demonstrate T₁, T₂ and B₁₊ information is not encoded equally along the schedule. For example, T₂ estimation is most sensitive to perturbations in schedule entries 1, 2, 3, 7 and 10, while T₁ estimation is sensitive to entries 5, 6 and 8. This information is useful when examining the dictionary fitting residuals; for example, larger residuals for entries 5, 6 or 8 would indicate T₁ estimation could be compromised without impairing T₂ estimation.

Phantom Measurements

Table 1 lists estimated concentrations and relaxation times for the major singlets (NAA at 2.01 ppm, Cr at 3 ppm and Cho at 3.2 ppm) in the phantom. The CVs for T₁ quantification were 4%, 6.7% and 10.3%, respectively; the differences arise from the fact that NAA, Cr and Cho differ in their SNRs, which were 14.7, 14 and 9.7. The SNR was quantified from the first average of the first schedule entry using peak heights divided by the standard deviation of the noise, and was subsequently relaxation-corrected and scaled to correspond to a 90° homogeneous (B₁₊=1.0) excitation pulse; the scaling coefficient was obtained via full 3D Bloch simulations using each peak’s measured T₁, T₂ and B₁₊. The CVs for T₂ were 6.4%, 5.9% and 14.8%. B₁₊ was quantified using the water resonance, with a CV of less than 1%. The concentrations of each singlet were quantified from the results of the LCModel fits (to the summed TE=35 ms entries) and the relaxation correction factors (Eq. (2)), and yielded deviations of 0.1 mM or less from their true values, with CVs between 3.5%-5%. Overall, the phantom results exhibit minimal bias, with CVs that increase as SNR decreases (similarly to Fig. 1c). While LCModel produced reliable fits (CRLB<10%) for all metabolites in the phantom, they are omitted from the Table; the current MRSF framework uses the uncoupled Bloch equations which do not properly model the behavior of coupled resonances. Without true, reliable estimates of their T₁ and T₂ values, the concentrations of the coupled metabolites could not be accurately quantified.

Table 1.

Phantom quantification results. Results for concentrations, T₁ and T₂ are shown as deviations from their gold standard values. Mean±standard deviations are taken over all N_rep=22 repetitions. Concentrations were quantified using the summed TE=35 ms acquisitions, as fit by LCModel. CRLBs output by LCModel are averaged over all repetitions. Numbers in parentheses are CVs. T₁, T₂ and absolute concentrations are reported for all major singlets. B₁₊ was quantified using the reference water scan and used to constrain dictionary fitting for all other metabolites. The coupled metabolites in the phantom (mI, Glu, NAA multiplet, etc) were successfully fit (see Fig. 2h) but not quantified due to the lack of reliable T₁ and T₂ estimates for them.

Metabolite	ΔConc (mM)	CRLB	ΔT1 (ms)	ΔT2 (ms)	B1+
NAA (2.01 ppm)	−0.1±0.5 (4.2%)	3.4%	−8±32 (4%)	−5±32 (6.4%)	N/A
Cr (3 ppm)	0.0±0.5 (4.8%)	3.4%	5±41 (6.7%)	5±32 (5.9%)	N/A
Cho (3.2 ppm)	−0.1±0.1 (3.4%)	5%	−13±43 (10.3%)	−1±32 (14.8%)	N/A
Water	N/A	N/A	−12±3 (0.5%)	−11±3 (1.1%)	1.13±0.01 (0.8%)

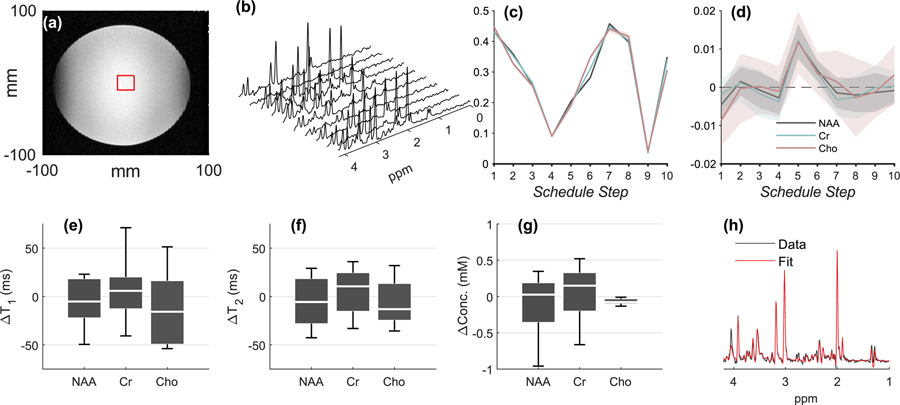
Fig. 2 showcases representative phantom results. Voxel positioning is shown in Fig. 2a. Spectra from the individual MRSF schedule entries are shown in Fig. 2b after averaging. The mean individual fingerprints of NAA, Cr and Cho are shown in Fig. 2c. The overall shapes of the fingerprints are very similar, but the differences between them are sufficiently large compared to their variability. Also note the fingerprints shown are divided by their L₂-norms; their un-normalized relative magnitudes can differ significantly due to concentration, T₁ and T₂ differences. Fig. 2d shows the mean±standard deviation of the dictionary fitting residual, i.e. the difference between the experimentally measured and simulated fingerprints, over all N_rep=22 repetitions. The means are within a standard deviation (shaded region) zero, indicating the high quality of the model used. This is a necessary – albeit not sufficient – condition for an accurate and precise estimation of T₁, T₂ and B₁₊. Taken together with the results of the occlusion test (Fig. 1d), this plot can be used to diagnose potential problems with the fitting procedure: large deviations at particular entries could affect the estimation of certain parameters more than others. In the current dataset, no such deviations are observed. Figs. 2e, 2f and 2g show boxplots of the differences between the tabulated phantom T₁, T₂ and concentrations, and those estimated from each of the 22 repetitions. The centers (medians) of the boxplots indicate the method’s accuracy (bias), while their width (inter-quartile range) indicates the method’s precision.

Figure 2.

Phantom results. (a.) Voxel placement. (b.) Spectra from all N_ent=10 schedule entries from a single MRSF acquisition, after summation of N_avg=20 averages. (c.) The normalized fingerprints of NAA, Cr and Cho from all N_rep=22 repetitions (mean±standard deviation). The similarity between different scans is so high that the outlines of the standard deviation can barely be seen. (d.) The mean±standard deviation of the residual for NAA, Cr, Cho, taken over N_rep=22 repetitions. All non-zero residuals are either within 1–2 standard deviations from zero, indicating the overall robustness of the dictionary fitting process. (e.) Box plots (median, inter-quartile range and whiskers) for $\Delta T_1$, the difference between the estimated and “true” T₁ in the phantom (as measured using a long inversion recovery experiment), from all N_rep=22 repetitions. The schedule’s precision (standard deviation) is reflected by the width of the boxplot, while its accuracy (bias) is reflected by its distance from the $\Delta T_1=0$ line. (f,g.) Boxplots for $\Delta T_2$ (as measured by a long multi-echo single voxel experiment) and ∆concentrations. (h.) Summed TE=35 ms schedule entries and corresponding LCModel fit from one of the 5-minute N_rep=22 repetitions. This fit was used to assess concentrations, as explained in the Methods section.

In-Vivo Experiments

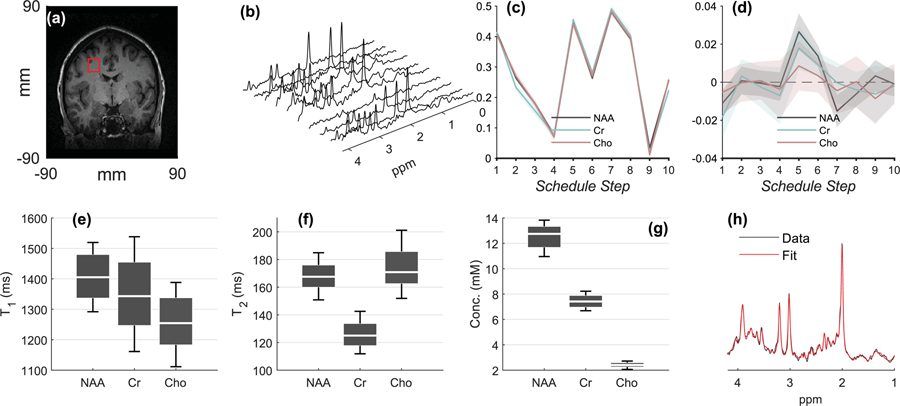
Fig. 3a shows voxel placement for a representative volunteer. Average tissue fractions were $f_{WM}=88.8\%\pm 4.5\%$, $f_{GM}=10.8\%\pm 4.2\%$ and $f_{CSF}=0.4\%\pm 0.3\%$, indicating reproducible voxel positioning and mostly WM content. The average SNR of the major singlets (NAA, Cr and Cho), calculated as for the phantom, was 11.3, 5.7 and 5.1, respectively. The linewidth of NAA was stable throughout: the mean full width at half maximum (FWHM) taken over all subjects was 7.7 Hz, and the mean deviation over the scan – quantified by dividing the standard deviation of the FWHM by its mean over 20 averages, and averaging the results over all scans and all subjects – was 11.2% (i.e. < 1 Hz). Such changes are consistent with normal physiological noise and indicate overall good measurement stability. The effect of any linewidth alterations during the measurement are already encapsulated in the reported CVs.

Figure 3.

In-vivo results. The plot follows a similar layout to Fig. 2. (a.) Voxel placement from a representative volunteer. (b.) Spectra from all N_ent=10 schedule entries from the same volunteer, after summation of N_avg=20 averages. (c.) The normalized fingerprints of NAA, Cr and Cho from the same volunteer (mean±standard deviation for all 3×2=6 scans). (d.) mean±standard deviation of the residual for NAA, Cr, Cho, taken over N_rep=22 repetitions. All non-zero residuals are either within 1–2 standard deviations from zero, indicating the overall robustness of the dictionary fitting process. (e-g.) Box plots for the CVs of T₁, T₂ and concentrations from all N_subj=14 volunteers. (h.) Summed TE=35 ms schedule entries and corresponding LCModel fit from a representative 5-minute scan from a single volunteer. This fit was used to assess concentrations, as explained in the Methods section.

Table 3 summarizes the results for all reliably quantified metabolites (CRLB≤20%), obtained by fitting the summed TE=35 ms spectrum of each volunteer using LCModel. It is impossible to assess accuracy (bias) in-vivo, since the true concentrations and relaxation values are unknown; thus, the Table lists the inter-subject mean±standard deviation, and also notes the inter-scan, intra-subject CV in parentheses; it is this quantity which describes MRSF’s precision. For the major singlets (NAA, Cr, Cho), T₁ and T₂ were quantified using the MRSF pipeline. For coupled metabolites, the relaxation values appearing in the Table are taken from the literature (41–46); we could not find references quantifying GSH’s transverse relaxation times at 3T, and a T₂=100 ms was assumed. These relaxation values were used to compute the relaxation-correction factor (Eq. (2)) necessary for absolute quantification. No attempts were made to remove any outliers while compiling Table 3. Note the in-vivo CVs on T₁ and T₂ (Table 3) are better in most cases than those recorded in the phantom (Table 1). This is because the relaxation times encountered in the phantom are quite different from those in-vivo (e.g. T₂s on the order of 400 ms), while our schedules were optimized for in-vivo values of T₁ and T₂.

Table 3.

In-vivo quantification results. Mean±standard deviations are taken over all 14 subjects, and represent inter-subject statistics. The inter-scan, intra-subject coefficient of variation for each quantity – corresponding to the precision of our method – is shown in parentheses. Concentrations were calculated by fitting the summed TE=35 ms acquisitions using LCModel. CRLBs output by LCModel are averaged over all subjects. Shown are only those metabolites for which CRLB<20%. As with the phantom, T1 and T2 were only quantified for the singlets; B1+ was quantified using the reference water scan and used to constrain dictionary fitting for all other metabolites. To perform absolute quantification for coupled metabolites, average literature values for T1 and T2 were used, indicated by daggers (†). The transverse relaxation time of GSH was not found in the literature and a T2=100 ms was assumed (indicated by a double dagger). Table 3 shows that coupled metabolites can be successfully fit using the proposed method.

Metabolite	Conc (mM)	CRLB	T1 (ms)	T2 (ms)	B1+
NAA (2.01 ppm)	12.5±1.1 (3.2%)	3.6%	1409±91 (4%)	168±13 (3%)	N/A
Cr (3 ppm)	7.4±0.7 (3.4%)	4.3%	1353±160 (5%)	126±12 (5%)	N/A
Cho (3.2 ppm)	2.4±0.3 (3.7%)	6.3%	1260±112 (5%)	174±20 (6%)	N/A
Glx	7.9±0.9 (5.4%)	8.7%	1200†	180†	N/A
GSH	1.8±0.5 (13%)	13.1%	397†	100††	N/A
mI	3.7±0.7 (6.4%)	8.6%	920†	196†	N/A
Water	N/A	N/A	1035±100 (2%)	70±4 (1%)	1.01±0.03 (0.4%)

Fig. 3b shows spectra from all N_ent=10 schedule entries from a representative volunteer. Fig. 3c shows the mean±standard deviation of the fingerprints of NAA, Cr and Cho, taken over all 14 volunteers, while Fig. 3d shows the residuals (compare to the phantom results in Figs. 2c and 2d). Figs. 3e, 3f and 3g present the distribution of measured T₁, T₂ values and concentrations for NAA, Cr and Cho from all volunteers, scans and repetitions. Finally, Fig. 3h presents a spectrum from a sample volunteer, obtained by summing just the TE=35 ms schedule entries, and its corresponding quality of the LCModel fit.

Discussion

In a previous publication we’ve outlined the general methodology of a variable-schedule multiparametric MRS framework (29). The current work extends the framework by optimizing the schedule and schedule length; by showing that LCModel fitting can also be used to fit the short echo time (TE=35 ms) schedule entries to obtain metabolite concentrations even for J-coupled metabolites, at an SNR that is comparable to a long-TR PRESS (Table 2); by shortening the total scan time to under 5 minutes; and by using a larger cohort of 14 volunteers to demonstrate the robustness of the proposed pipeline. Our in-vivo data, collected from a 4.5 mL voxel using standard hardware, shows this approach produces average inter-scan CVs of 3.4%, 4.6% and 4.7% for metabolite concentrations, T₁ and T₂ relaxation times, respectively, averaged over all major singlets.

Table 2.

SNR comparisons between PRESS and MRSF, in both the phantom and in-vivo, based on numerical 3D Bloch spin simulations. Simulations were run for each singlet (NAA, Cr, Cho), using its mean measured T₁ and T₂ values, and averaged over all singlets. Note that, on average, T₁ values in the phantom are shorter than in-vivo, while T₂ values are longer. The SNR per unit time of the TR=1500 ms PRESS was normalized to one. The table demonstrates that using just the short echo time (TE=35 ms) scans of MRSF for metabolite quantification yields approximately 60% of the optimal PRESS SNR. However, since T₁ is often unknown in-vivo, acquisitions with prolonged TRs are preferred, such as a PRESS with TR=5000 ms; relative to such an acquisition, the TE=35 MRSF scans yield approximately 0.61/0.78≈80% of the SNR.

	Normalized Voxel Volume	Weighted Voxel Volume	SNR per unit time
Phantom (average over all singlets)
PRESS (TR/TE=1500/35 ms)	0.87	0.48	1.00
PRESS (TR/TE=5000/35 ms)	0.87	0.54	0.59
MRSF (All TEs)	0.67	0.34	0.70
MRSF (TE=35 ms)	0.64	0.32	0.57
In-vivo (average over all singlets)
PRESS (TR/TE=1500/35 ms)	0.87	0.48	1.00
PRESS (TR/TE=5000/35 ms)	0.87	0.68	0.78
MRSF (All TEs)	0.67	0.31	0.67
MRSF (TE=35 ms)	0.64	0.32	0.61

Schedule optimization plays an important role in multiparametric MRS, as shown by Fig. 1b. Our results show that the $\overline{nRMSE}$ can be brought down to around 3–4% for an SNR of 15 for the different schedule lengths considered $\left(5\le N_{ent}\le 100\right)$. Schedules with as few as N_ent=5 entries also exhibit fairly low $\overline{nRMSE}$s. This is particularly attractive for incorporating fingerprinting schedules with other time-consuming acquisitions; for example, using echo planar spectroscopic imaging, a single 2D-MRSI slice can be sampled in under a minute. This leaves ample time to swap the conventional averaging dimension with a fingerprinting schedule to produce spatial multiparametric metabolite maps of the major singlets.

While we acquired our data using a PRESS with a variable excitation flip angle, the optimized schedules in Supplementary Table S1 were based on a single-spin pulse-acquire topology and could be applied to other popular single-voxel spin-echo based MRS localization modules, such as semiLASER (47). Not all modules are a-priori compatible, though: LASER (48) uses an adiabatic excitation; SPECIAL (49) uses a preparatory inversion pulse; and STEAM (50) and STRESS (51,52) both acquire stimulated echoes. These sequences’ spin evolution is somewhat different from a simple pulse-acquire sequence, and, while the schedules in Table S1 would likely perform well for them, they would likely require re-optimization for best results.

The Optimal Schedules do not Substantially Impair SNR

The variable schedule implies that MRSF acquisitions are sub-optimal from an SNR per unit time perspective. In this particular work, we only used the short echo time (TE=35 ms) spectra for quantifying metabolites’ concentrations. As shown by Table 2, when compared to an equivalent PRESS sequence with an optimal TR=1.2·T₁ and an FA=90° excitation pulse, the total SNR of the MRSF dataset is only 60% (when using the subset of TE=35 ms schedule entries) of that of the optimal PRESS sequence, averaged over all singlets using in-vivo values for T₁ and T₂ and assuming B₁₊=1.0. This reduction in SNR, however, is less severe than for an equivalent and optimal STEAM sequence. The reduction is even less severe – only 20% - when compared to long TR acquisitions, which are often favored as a method for minimizing T₁ weighting. Table 2 also reveals that a further increase in total SNR is possible by incorporating the long echo time schedule entries. Since such an approach would mix different echo times, a simple summation would confound quantification; a more correct approach would require a more advanced spectral fitting algorithms. Suitable approaches have been used in fitting 2D and multi-TE datasets, and could likely be extended to handle the full MRSF dataset (53).

Coupled Metabolites’ Concentrations Can Be Estimated Using Short Echo Times

The use of short echo time scans produces usable estimates of coupled metabolites, including myo-Inositol and Glx, even if their relaxation times are not quantified. This is reflected in the CRLBs estimated by LCModel (Table 3), which are in-line with other single-voxel MRS acquisitions in WM (42,45,46,54–56).

Dictionary Fitting for Coupled Metabolites Remains Challenging

The quantum nature of J-coupled metabolites excludes them from being fit to the simple Bloch-equation framework proposed in the current work. Further research into appropriate models which combine quantum mechanical evolution in Liouville space with relaxation is still required before dictionary-fitting approaches can be successfully applied to such coupled metabolites. Thus, the current work did not estimate the relaxation values of coupled metabolites. We note that, unlike NAA, Cr and Cho, where the per-subject values of T₁ and T₂ were used for relaxation correction in Table 3 (using Eq. (2)), the estimation of coupled metabolites’ concentrations was done using literature values for T₁ and T₂.

A related challenge concerns the use of spectral fitting to generate reproducible fingerprints. We have attempted to spectrally fit each of the individual N_ent=10 entries using LCModel, construct fingerprints for each metabolites – coupled and uncoupled alike – and fit those to the dictionary of 3D Bloch-simulated fingerprints using our described pipeline. Results have yielded either particularly large coefficients of variation or unrealistic estimates of T₁ and T₂, and, currently, the use of spectral fitting for generating individual fingerprints remains challenging. This holds true even for the singlets of NAA, Cr and Cho, for which spectral fitting produced up to two-fold larger coefficients of variation and biases.

Most metabolites have more than one spectral peak associated with them, often with differing relaxation values – e.g., Cr’s two singlets at 3.03 and 3.92 ppm (46). Hence, each peak or subgroup will have a different fingerprint associated with it. Using peak amplitudes (or integrated areas) to generate fingerprints, as done herein, effectively decouples the different peaks and avoids introducing any correlations between their estimated fingerprints. It remains to be seen whether spectral fitting will be able to generate reliable fingerprints in the future; if so, separate basis functions will have to be used for each chemical sub-group, to ensure their fingerprints remain unbiased.

Extending MRSF to Include Additional Spin Parameters

The schedule optimization only modeled T₁ and T₂ relaxation and transmitter inhomogeneity. The basic PRESS sequence has limited sensitivity to other metabolite parameters, such as diffusion or chemical exchange. Incorporating those would require investigating different sequence topologies; for example, adding diffusion weighting gradients in between the volume selective pulses of the PRESS sequence, as done for diffusion weighted MRS (57,58). One should however undertake such endeavors cautiously: the addition of model parameters often increases the estimation errors on those parameters. Additional parameters also increase the computational complexity of the simulations required for dictionary generation. Even though we decompose the 3D spin simulations into successive 1D simulations (59), simulating a single fingerprint requires on the order of ~ 1 second. This prohibits MRSF from generating a-priori even the simplest dictionaries, instead forcing dictionary matching to use real-time search algorithms, leading to a post-processing duration of approximately one minute to extract the relaxation parameters of all three singlets. This could be mitigated via the use of neural networks, which can search even high dimensional dictionary spaces within milliseconds (60).

Additional Caveats

The current study focused on a single region of interest and a particular voxel size. It should be noted that the CVs derived herein will depend on the quality and SNR of the spectral data. For example, the SNR of deep gray matter voxels might be lower due to reduced coil sensitivity and, consequently, their CVs will likely be higher. Similarly, smaller voxels, placed in smaller anatomical structures, might yield lower SNR and higher CVs. Thus, a careful re-evaluation of the method’s reproducibility must be carried out on a per-study basis, and until such additional experimental data is made available, any claims about wider applicability in the brain remain conjecture.

Conclusion

By optimizing the schedule, MRSF can be used to acquire the relaxation values of the major singlets, without significantly impairing the quantification of metabolite concentrations of both coupled and uncoupled resonances. Monitoring the unsuppressed water signal as the system is driven into dynamic equilibrium produces estimates of water’s T₁ and T₂ constants as well. The ability to acquire per-subject multiparametric spectroscopic data provides more accurate and robust absolute quantification of metabolite concentrations. Furthermore, ample evidence exists that metabolite relaxation times change in multiple neuropathologies, making them potential biomarkers. The multiparametric framework proposed herein thus also enhances the clinical relevance of single voxel MRS, all within a clinical timeframe of under five minutes.

Supplementary Material

Supplementary Figure S1

Figure S1. Approach to dynamic equilibrium for a single spin (T₁/T₂=1000/200 ms), in response to the optimal N_ent=10 schedule. Top: M_z as a function of time, obtained by solving the Bloch equations using simplified hard pulses. Each of the schedule entries is marked with a separate color (they are not equidistant since TR is not fixed). The longitudinal magnetization very quickly assumes a consistent pattern, confirming dynamic equilibrium is attained. Bottom: the residual, $\left|\Delta M_z\right|$, as a function of time, between M_z and the value of M_z following 100 consecutive applications of the schedule (i.e. M_z during dynamic equilibrium). The residual becomes negligible within just a few schedule entries, consistent with dynamic equilibrium.

List of Abbreviations

CRLB

Cramer Rao lower bound

CSF

Cerebrospinal fluid

CV

Coefficient of Variation

FA

Excitation flip angle

FWHM

Full width at half maximum

GM

Gray matter

MRF

Magnetic Resonance Fingerprinting

MRS

Magnetic Resonance Spectroscopy

MRSF

Magnetic Resonance Spectroscopic Fingerprinting

NAA

n-acetyl-aspartate

PRESS

Point resolved spectroscopy

RMSE

Root mean square error

SNR

Signal to noise ratio

SPM

Statistical Parametric Mapping

tCho

Total choline

tCr

Total creatine

TE

Echo time

TR

Repetition time

WM

White matter