Abstract
Hybrid organic–inorganic perovskites (HOIPs) have shown the encouraging development in solar cells that have achieved excellent device performance. One of the most important issues has been focused on finding Pb-free candidates with suitable bandgaps, which could accelerate the commercialization of environmentally friendly HOIP-based cells. Herein, we propose a new inverse design method, proactive searching progress (PSP), to efficiently discover potential HOIPs from universal chemical space by combining machine learning (ML) techniques. Compared to the pioneering work on this topic, we carried out our ML study based on 1201 collected HOIP samples with experimental bandgaps rather than theoretical properties. On the basis of 25 selected features, a weighted voting regressor ML model was constructed to predict bandgaps of HOIPs. The model comprehensively embedded four submodels and performed the coefficient determinations of 0.95 for leaving-one-out cross-validation and 0.91 for testing set. The feature analysis revealed that the tolerance factor (tf) below 0.971 and the new tolerance factor (τf) in 3.75–4.09 contributed to lower bandgaps and vice versa. By applying the PSP method, the Pb-free HOIPs with optimal bandgaps were successfully designed from a generated chemical space comprising over 8.20 × 1018 combinations, which included 733848 candidates (e.g., Cs0.334FA0.266MA0.400Sn0.769Ge0.003Pd0.228Br0.164I2.836) with an optimal bandgap of 1.34 eV for single junction solar cells, 1511073 large-bandgap candidates (e.g., Cs0.392FA0.016MA0.592Cr0.383Sr0.347Sn0.270Br1.171I1.829) for top parts in tandem solar cells (TSCs), and 20242 low-bandgap ones (e.g., MA0.815FA0.185Sn0.927Ge0.073I3) for bottom cells in TSCs. Finally, three new HOIPs were synthesized with an average bandgap error 0.07 eV between predictions and experiments. We are convinced that the proposed PSP method and ML progress could facilitate the discovery of new promising HOIPs for photovoltaic devices with the desired properties.
1. Introduction
Development of hyybrid organic–inorganic perovskites (HOIPs) has flourished in photovoltaic (PV) technology over the past decade, attributed to their exceptional merits including tunable bandgap, long carrier diffusion length, high light-absorption coefficient, low nonradiative loss, carrier mobility, simple solution processability, and low-cost experimental synthesis.1−4 HOIP materials have a universal formula, ABX3, in which the A site usually contains organic cations (such as MA+ → methylammonium, FA+ → formamidinium) or Cs+, the B site involves divalent metal cations (such as Pb2+, Sn2+, Ge2+, Ga2+), and the X site includes halogen anions (Cl–, Br–, I–). The typical HOIPs, e.g., MAPbI3, FAPbI3, and their derivatives, have been widely applied in single-junction devices, namely perovskite solar cells (PSCs), with the bandgap range of 1.40–1.70 eV whose power conversion efficiencies (PCEs) have elevated to 25.5%5 from the original 3.8%.6 In the meantime, ascribed to the fascinating property of their tunable bandgaps, HOIPs with low-bandgap (1.10–1.40 eV) are competent in serving as bottom cells for all-perovskite tandem solar cells, while the materials with a wide bandgap (1.70–2.30 eV) are suitable as top cells for all kinds of tandem solar cells7 in which their PCEs have reached 47.1%.5
However, HOIP photovoltaic materials still have unavoidable imperfections and more potential for further progress. One of the topic issues is the contaminant brought by the toxic element Pb that contributes to most solar cells with outstanding PCEs. In this context, more Pb-free HOIP materials are urgently needed to facilitate the commercial application in solar cells.3 Meanwhile, the bandgaps of HOIPs in efficient single junction cells are mostly lying at 1.45–1.55 eV, whose theoretical maximum PCEs are 31.02–32.07% according to the Shockley-Queisser (SQ) limit model.8−10 However, the optimum bandgap located in 1.20–1.40 eV renders the maximum PCEs of 32.7–33.7%, while the highest value 33.7% could be achieved at a bandgap of 1.34 eV. By adjusting the bandgap to the optimal value, the HOIP-based device may have a higher PCE. As for the case of tandem solar cells (TSCs), manipulating bandgaps of HOIPs is also essential to gain satisfactory PCEs. The ideal bandgap of the perovskite bottom cell is usually 1.20–1.30 eV, while the suitable bandgap for the perovskite top cell is close to 1.70 eV for Si or copper indium gallium selenide (CIGS) bottom cells (bandgap 1.10 eV) and 1.75–1.80 eV for perovskite bottom cells.11 Considering the demands of nontoxicity and suitable bandgap adjustment, it is still of paramount importance to discover Pb-free HOIPs with suitable bandgaps for both of PSCs and TSCs.
As experimental and quantum-based research has been suffering due to the large cost in human endeavor, time consumption, and trial-and-error attempts, machine learning (ML) has provided a more efficient strategy to assist materials design at lower expense, which has been continuously exerted in various fields such as electrocatalysis, batteries, polymers, alloys, and others.12−15 The ML technique has also been successfully applied in finding out promising HOIPs with desired properties. As a proof of concept, Lu et al.16 prepared 212 ABX3 HOIPs samples from high-throughput calculations along with their bandgaps calculated via the density functional theory (DFT) method in which 11 organic cations were considered in the A site, 32 divalent metal cations, and four halogen anions in the B and X sites. Fourteen features were selected by using last-place elimination for the gradient boosting regression (GBR) model, resulting the high model performance with a determination coefficient (R2) of 0.985 and mean squared error (MSE) of 0.085 eV. The sorted features indicated the importance of the tolerance factor (tf), octahedral factor (Of), and ionic charge in B site (ICB) that took the major contributions to the model performance. Then the bandgaps of 5158 virtually generated samples were predicted via the GBR model. By inspecting their proper predictions (0.9–1.6 eV), tf (0.8–1.2), Of (0.4–0.7), experimental accessibility, and nontoxicity, six HOIPs were finally selected with DFT-calculated bandgaps of 0.91–1.14 eV, namely C2H5OInBr3, C2H6NInBr3, NH3NH2InBr3, C2H5OSnBr3, NH4InBr3, and C2H6NSnBr3. Saidi et al.17 arranged 862 ABX3 HOIP structures along with their DFT-calculated bandgaps, in which 18 organic ions, Pb2+/Sn2+ cations, and Cl–/Br–/I– anions were included for A/B/X sites. A hierarchical convolutional neural network (HCNN) was trained based on atomic descriptors to predict the DFT bandgaps of HOIPs, exhibiting a low root mean squared error (RMSE) value of 0.02 eV. In our recent work,18 a robust extremely gradient boosting (XGBoost) model was fitted based on 102 DFT-optimized samples and atomic descriptors to identify the formability of DFT-optimized HOIP structures, which led the leaving-one-out cross-validation (LOOCV) accuracy of 95% and testing accuracy of 88%. By using the SHapley Additive exPlanations (SHAP) tool, we found that the radius and lattice constant of B site had the positive contribution to formability while the A site radius, tolerant factor, and first ionization of B site were the reverse case. Handy with the well-established XGBoost model, 198 nontoxic HOIPs were screened from 18560 generated structures with formability probabilities over 99%.
Although the bright prospect of the ML technique in discovering potential HOIP materials has been unveiled in these pioneering works, the majority of the relevant work paid large attention to DFT-based properties such as bandgap and formability instead of the experimental characteristics whose results tend to deviate from the experiments, e.g., the underestimated bandgaps calculated by generalized gradient approximation (GGA).3 Second, only limited organic cations in the A site (up to 18) have been reported in the current ML studies, while this work has collected 88 organic cations (both from experimental and theoretical publications) that are expected to extend the A site choices for experimentalists. Third, few researches have reported the virtual designs for the doped HOIPs, e.g., the formula as A′A″B′B″X′X″, though there already are cases of complex HOIP formulas in experiments such as Cs0.05FA0.79MA0.16Pb0.58Sn0.42I2.48Br0.52.19 Thus, it is meaningful to expand the chemical space to involve the doped structures, which may cause an enormous searching space, e.g., 4.6 × 1011 combinations in the case of A′A″A‴B′B″X′X″ (suppose 20 organic choices in the A site, 9 in the B site, 3 in the X site, and doping ratio step 0.01). In this situation, the traditional high-throughput ML prediction is no longer affordable using current computing power; thus, an innovative searching strategy is imperatively essential to avoid this dilemma. Last but not the least is the inadequate interpretations of the established models despite their qualified performances, which are basically important for a deep understanding of experimental principles. Theus, there is still a large capacity to be elevated in discovering new potential HOIPs with suitable bandgaps and nontoxicity.
Herein, we reviewed 9594 PSC publications from Web of Science in 2009–2021 and collected 1201 HOIP samples along with their experimental bandgaps. On the basis of the experimental sample set in 2009–2020, various robust models were built, resulting in four best models with the LOOCV R2 0.93–0.95 and testing R2 0.88–0.92. A weighted voting regressor (WVR) model was designed to embed the four well-fitted estimators, exhibiting a more comprehensive performance with LOOCV R2 0.95 and testing R2 0.91. The 42 samples in 2021 were set aside as the external set to validate the WVR model, indicating the R2 of 0.84. By combining the SHAP tool and WVR model, the relationships between the top 10 important features and HOIP formulas were successfully explored based on both the experimental data set and a virtually generated data set. Thereafter, we constructed a comprehensive chemical space for the doped HOIPs formulated as A′A″A‴B′B″B‴X′X″X‴, in which there were collected 88 organic fragments plus Cs/K/Rb in the A site, eight metal elements in the B site (excluding Pb), and Cl/Br/I in the X site, resulting in over 8.20 × 1018 combinations. In this regard, we proposed a new inverse design method, namely proactive searching progress (PSP), to efficiently discover Pb-free HOIPs with the desired bandgaps from such universal chemical space, which only took a few minutes to locate at least one candidate. As the explored result, we finally found 733848 HOIPs with a bandgap of 1.34 ± 0.05 eV for single junction solar cells, 20242 with 1.20 ± 0.05 eV for bottom cells in TSCs, and 764883 with 1.70 ± 0.05 eV as well as 746190 with 1.75 ± 0.05 eV for top cells in TSCs. The three new compositions of HOIPs were synthesized for model validation. Their bandgaps were characterized, resulting in an average error 0.07 eV from the predictions. We are convinced that such an inverse design method could help accelerate the development of HOIP materials beyond bandgaps. Since the developed inverse design methods are flexible and independent from the ML models, they could also be applied in discovering other materials with their desired properties.
2. Methods
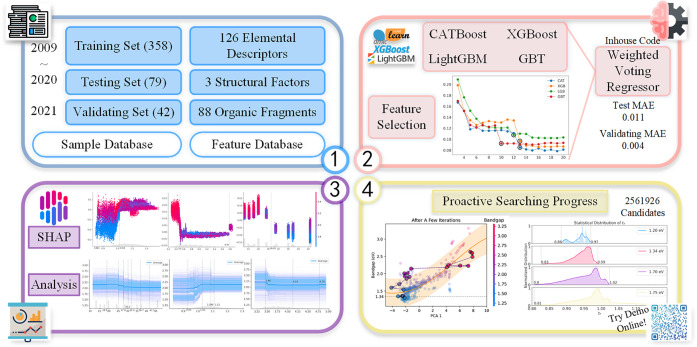
In this section, we illustrate the detailed processes of training ML models and the PSP method. In the training process, various ML packages were involved, including scikit-learn,20 XGBoost, CatBoost, LightGBM, and SHAP,21 which were used to fit robust models and analyze the relationships between features and HOIP structures. The self-developed reverse design method PSP was applied after the model building to find out the Pb-free candidate HOIPs with proper bandgaps. Most codes were packed into our Python package in https://pypi.org/project/fast-machine-learning/. Figure 1 illustrates the workflowchart concerning on the integrated package to construct ML models and search new candidate HOIPs via PSP. The applied codes are provided in GitHub: https://github.com/luktian/InverseDesignViaPSP. A demo of PSP method can be tried online at http://materials-data-mining.com/pspweb/.
Figure 1.
Workflowchart concerning on the integrated package to construct ML models and search new candidate HOIPs via PSP.
Data Collection and Feature Generation
In this study, we extracted 1201 HOIPs along with their experimental bandgap values from 9594 PSC publications from Web of Science (using the keyword “perovskite solar cells”) in 2009–2021. The sample number reduced to 479 from 1201 after cleansing the raw sample set in Code S1 of Supporting Information. The 437 samples collected in 2009–2020 were regarded as the history data for modeling and further divided into training and test sets. The 42 samples from 2021 were set aside as the external set to validate the generalization of ML model at last.
An integrated descriptor database was assembled from the Villars Database (https://mpds.io/) and Mendeleev Python package (https://github.com/lmmentel/mendeleev) to depict the structure information on the HOIP samples, which were furtherly divided into 34 base descriptors, eight string descriptors, and 66 other descriptors. The base descriptors refer to the basic chemical and physical properties for elements such as radius, volume, chemical potential, electronegativity, and others, while string descriptors involve categorical properties such as the block position in the periodic table, the lattice crystal structure of the simple substance, and the like. The string descriptors have been encoded into numeric data ahead of generating descriptors via the encoder method provided in scikit-learn.20 The 66 other descriptors contain relatively more sophisticated or pointless properties and hence would not be employed in our data set in pursuit of an as understandable model as possible. Regarding the lack of properties of the organic cations of the A site, e.g., MA+ in methylammonium lead iodide, some basic chemical and physical properties of the organic fragments were calculated and supplemented by using Gaussian22 and Multiwfn23 software, which involves molecular volume, electronegativity, chemical potential, molecular radius, ionic radius, vertical electron affinity, and others. The descriptor details are listed in Table S2, and quick instructions to generate the descriptor features for a HOIP sample are illustrated in Code S2 of the Supporting Information. Given an HOIP structure ABX3, the descriptors were generated for each site (A, B, X), and there were 42 descriptors calculated in each site and hence 126 descriptors for each sample. Three universal structural factors, namely Of,24tf,25 and tau factor (τf)26 were added, resulting in a total of 129 features.
Although the structural phases would have a large impact on bandgaps as well, it would not be considered in the model due to insufficient data. The phase information on the 479 samples is listed at https://github.com/luktian/InverseDesignViaPSP.
Feature Engineering and Model Training
The 129 features were preprocessed by pruning the variables with missing values or their standard deviations nearly to zero, bringing about 102 remnant features. To perform a reasonable division of the 437 samples, the size and distribution of samples in training and test sets were optimized in Code S3 of the Supporting Information, resulting the optimal parameters of training size 81.95% and test size 18.05% and random state 1959 (representing sample distributions).
The recursive feature addition (RFA)27 strategy was employed to search the optimal feature set, which determined the optimal feature set by iteratively adding one more top nth feature under a feature importance (FI) order. In this strategy, seven algorithms were considered in parallel, involving CatBoost (CAT), XGBoost (XGB), LightGBM (LGB), gradient boosting machine (GBM),28 support vector machine (SVM),29 decision tree regressor (DTR), and multiple linear regressor (MLR).20 The FI for tree-based algorithms was ranked by the feature contributions extracted from SHAP package,21 while FI for the other algorithms was calculated based on maximum relevance minimum redundancy (mRMR) method.30,31 The RMSE and R2 of LOOCV were regarded as indicators to determine the outstanding models. It was found that the CAT, XGB, LGB, and GBT models were the top 4 outstanding models based on 13, 13, 12, and 10 features screened in Code S4 of the Supporting Information. The contributions of selected features were calculated using SHAP package for each established model in Code S5 of Supporting Information.
The hyper-parameter optimizations for CAT, XGB, LGB, and LGB models were performed using the grid search (GS) approach in Code S6 of the Supporting Information. The tree number, learning rate, and tree depth were considered as the hyper-parameters for the models, and the LOOCV RMSE of the training set was used to indicate the model performance.
Weighted Voting Regressor and Model Analysis
Inspired from voting regressor (VR) implemented from scikit-learn20 that combines multiple regressors as submodels and returns the average predicted values, we developed a weighted voting regressor (WVR). Different from VR model, the submodel in WVR was trained based on individual feature sets, and the optimized weight coefficient was used to control the model contribution to the final prediction.
The SHAP values of the WVR model were then calculated in Code S8 of the Supporting Information that had overcome the incompatibility between the self-developed WVR model and SHAP package. In pursuit of a more comprehensive analysis of feature contributions to the model, in addition to the experimental data set, an extra virtual data set composed of mixed HOIPs formulated as A′A″B′B″X′X″ was generated as the input data for SHAP calculation. The organic fragments MA, FA, GA (diaminomethaniminium), EA (ethanaminium), and ED (ethane-1,2-diaminium) plus Cs were considered as the candidates for the A site with the elements Pb, Sn, Ge, Cd, and Pd for the B site and Cl, Br, and I for the X site. For the balance between calculating cost and precision, we set the doping range 0–1 for A/B site and 0–3 for X site along with the range step 0.25 for A/B site and 1.0 for X site, in which doping numbers for each site were all fixed at 2. As a result, the virtually generated data set comprised 45000 virtual HOIPs.
Proactive Searching Progress (PSP)
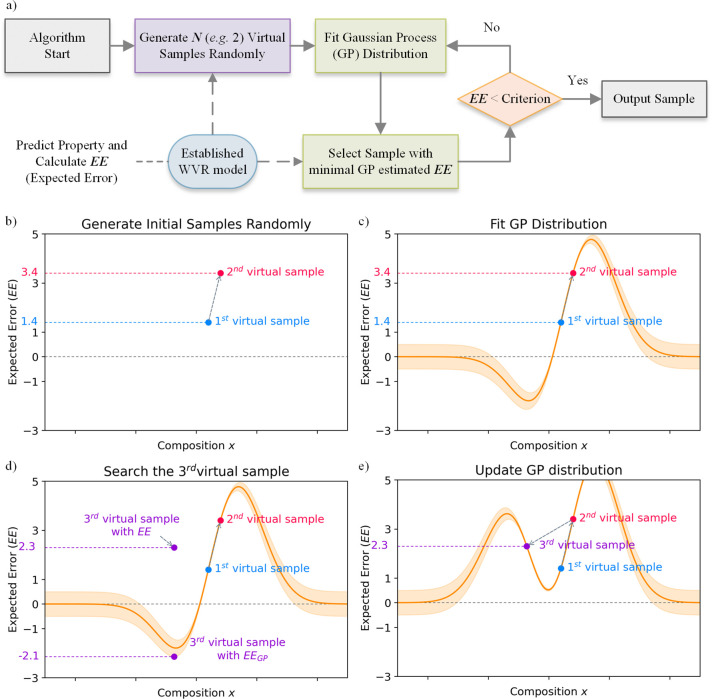
Given a set of material compositions {γi|γi = (γi1,γi2,...,γid)T, i ∈ R}, we could easily get their predicted outputs {oi|i ∈ R} from a well-fitted ML model and obtain a set of samples {(γi,oi)|i ∈ R}. The ML model plays the role of a function o = f(γ) that describes the distribution of the samples in the whole chemical space. In the case of searching the materials with desired property value o* from a universal chemical space, there would be large wastes of time and cost if all of the possibilities via the ML model o = f(γ) were traversed. Inspired from the sequential model-based optimization (SMBO) in the field of parameter optimization, we herein proposed PSP method, and introduced Gaussian process (GP) method to describe the local distribution g(γ) to approximate the ML model o′ = g(γ) ∼ o = f(γ) in partial chemical space. According to the simulated GP distribution, it could be easy to determine the compositions of next designed point by identifying the composition with the o′ closest to o* and predict the property value by using the ML model. By iteratively adding the newly explored points, the GP distribution would be updated by steps and behave more accurate for property estimation.
The core objective of PSP is to discover potential chemical compositions whose properties are close to the expected value o* predefined by the user. As the general workflow is concluded in Figure 2a, the initial virtual samples {γi|i ≥ 2} will be randomly generated from the whole chemical space at the initial step. The properties {oi|i ≥ 2} of the initial samples are predicted by using the established ML model to obtain the sample points {(γi,oi)|i ≥ 2}. Instead of the predicted property value oi, the expected error {EEi|EEi = |oi – o*|, i ∈ R,EEi → 0} between the prediction oi and expected property value o* is practically defined as the response of GP distribution to indicate the quality of each sample. The GP function approximates the distribution as
| 1 |
For illustrative purposes, Figure 2b–d considers the searching progress of a one-compositional material as a simple example in which the first and second samples with EE values of 1.4 and 3.4 are plotted in Figure 2b. The first generated samples are taken to describe the local distribution by GP method (or other likely methods), as shown in Figure 2(c). The plot data could be practically obtained from the GP distribution. Then the next designed point with the minimal EE estimated by GP method (EEGP) is determined in the fitted GP distribution, and the predicted property as well as EE are given via the ML model in Figure 2d. In the next step, a new designed point will be iteratively determined by the updated GP distribution in Figure 2e until the iteration reaches the maximum step predefined by the user. During the searching progress, once the EE is lower than the predefined criterion, the corresponding samples would be outputted. By only exploiting the local space directionally, PSP could accelerate the searching period and avoid the huge undesired compositions. Additionally, we established a demo of PSP method online to discover HOIP candidates for the illustrative purpose at http://materials-data-mining.com/pspweb/.
Figure 2.
General principle of the proactive searching progress (PSP) method. (a) Workflow details of PSP method. (b) First and second generated virtual samples. (c) Simulated GP distribution based on the first and second generated virtual samples. (d) Third virtual samples searched by GP distribution. (e) Updated GP distribution adjusted by the third virtual samples.
Results and Discussion
Model Construction
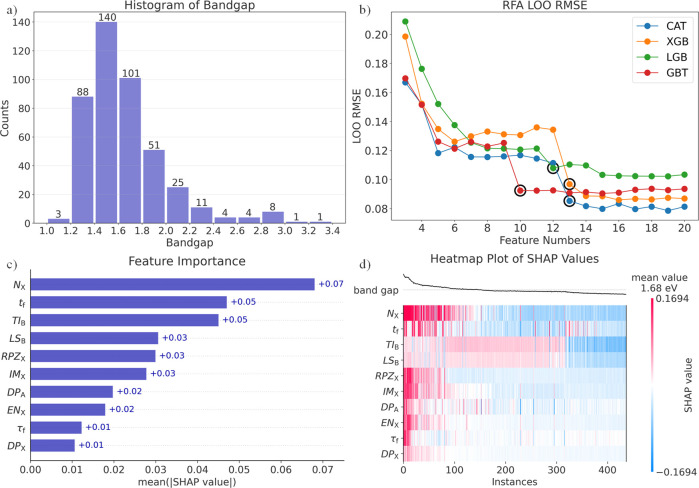
The 1159 samples from the publications in 2009–2020 were gathered, and 437 samples were retained after cleansing the duplicates in Code S1. As exhibited in Figure 3a, the bandgap ranges in 1.17–3.31 eV, and the most values were in the 1.20–2.00 eV range accounting for 86.96% of the whole set. Then 129 descriptors were generated for each sample, and 102 remained after preprocessing in Code S2. A reasonable training and test set were drawn in Code S3, rendering 358 training and 79 test samples.
Figure 3.
(a) Distribution of bandgaps for 437 HOIP samples. (b) Changing trends of LOOCV RMSEs for CAT, XGB, LGB, and GBM models extracted from RFA results. (c) Feature importance of top 10 features. (d) Distributions of SHAP values with feature values.
Given the preprocessed training set with 358 samples and 102 remnant features, an RFA strategy was employed to filter optimal features in Code S4. Figure 3b shows the decreasing trends of LOOCV RMSE values for CAT, XGB, LGB, and GBT models as the selected feature number increased in which RMSEs were fixed in 0.08–0.12 when the feature number was over 13. Figure S5b plots the same trend for SVM, DTR, and MLR but with higher RMSEs in 0.13–0.24, which signaled the much poorer model performance than the tree-based models. Figure S6 displayed the uprising trend of LOOCV R2 for the four tree-based models with R2 values over 0.89 based on the top 13 features and the other three models along with those lower than 0.85. The test metrics expressed in Figure S7–S8 indicated the same conclusions, and hence, the four tree-based models were retained for the further step.
By considering the balance between model performance and complexity, the inflection points circled in Figure 3b were selected for model construction in which the addition of the features triggered large promotions for the LOOCV RMSEs. As a result, the CAT, XGB, LGB, and GBT models were built up based on the top 13, 13, 12, and 10 features, respectively (Figure S10), whose LOOCV R2 were 0.94, 0.92, 0.90, and 0.93, respectively (Figure S6). The corresponding test R2 of the four models were 0.88, 0.89, 0.87, and 0.91, respectively (see in Figure S8), signifying the powerful predictivities and generalization abilities. After hyper-parameter optimization using the GS approach in Code S6, the LOOCV R2 of CAT, XGB, LGB, and GBT models increased to 0.95, 0.93, 0.93, and 0.93, respectively, while the corresponding test R2 were 0.91, 0.89, 0.88, and 0.92 respectively (Table S5). The relevant LOOCV and test RMSEs were 0.08–0.09 and 0.11–0.12. The 5-fold cross-validation (CV5) and 10-fold cross-validation (CV10) were additionally calculated in Table S5. The CV5 and CV10 R2 of the tree-based models were 0.90–0.95, and the RMSEs were 0.08–0.11, which might also indicate the good model performance.
To explicitly implement four well-fitted models, a meta-model could be introduced to integrate the fitted submodels and balance their individual weaknesses. For example, the voting regressor (VR) model from scikit-learn20 combines multiple different machine learning regressors (trained on the same feature set) and returns the average prediction. Inspired by the VR model, the weighted voting regressor (WVR) model was designed whose submodels were trained based on individual feature sets (e.g., XGB on 13 features while GBT on 10 features). The optimized weight coefficients were used to control the contributions of each submodel to the predicted values, and hence the weighted predictions were returned. In this context, a WVR model was fitted by combining CAT, XGB, LGB, and GBT models in Code S7. As shown in Table S7, the R2 and RMSE in LOOCV of WVR were 0.95 and 0.079 better than the values of XGB, LGB, and GBT, while the R2 and RMSE in WVR were 0.91 and 0.106 more favorable than the values of CAT, XGB, and LGB. Meanwhile, the CV5 and CV10 R2 were 0.94, and the corresponding RMSEs were 0.08. Hence, the WVR model complimented the weakness of each submodel and achieved a comprehensively superior performance than the submodels.
To further evaluate the generalization ability of the WVR model for the unknown samples, a separate validating set composed of 42 HOIP samples in 2021 was prepared. Listed in Table S7, the R2 of external validating set between experimental and predicted bandgaps was 0.84, higher than the external R2 in the submodels (0.74–0.80 in Table S5) and slightly lower than the testing R2 of 0.91 in the WVR model. The RMSE, MAE, and MSE of the external validating set in WVR model were 0.060, 0.041, and 0.004, respectively, exhibiting even better than the values of test set (0.106, 0.056, and 0.011), which indicated the powerful predicting power and low predicting errors (0.041–0.056 eV) of the WVR model.
Model Analysis
The SHAP values were calculated by utilizing the self-developed WVR model and SHAP method to analyze the feature contributions to model predictions in Code S8. Besides the experimental data set, a set of virtual data set composed of 45000 doped HOIP samples was employed for model interpretation via high-throughput computation.
Figure 3c exhibits the top 10 features ranked by their contributions extracted from SHAP values, whose vertical axis comprised feature ranking, and the horizontal axis shows the SHAP values for the features. Among the 10 features, five X-site descriptors accounted for 50%, and NX (representing element name in X site) took the most important position. In the remnants, structural and B-site descriptors counted 2, respectively, while the rest 1 was the one in A site. Figure 3d displays the distributions of SHAP values of features, where the horizontal axis comprises the sorted sample indexes according to model predictions. The red/blue color expresses the positive/negative SHAP values for each sample and feature, which further indicate the positive/negative contributions to predictions. The positive SHAP values for each feature (in red color) were mainly localized in the left part that corresponds to the higher bandgaps, while the negative values (in blue color) were located at the right part related to the lower predictions, thence indicating a well-separately isolated distribution of positive/negative SHAP values and the large contributions to the predictions of bandgaps. Similar plots for the virtual data set are drawn in Figure S18b,d.
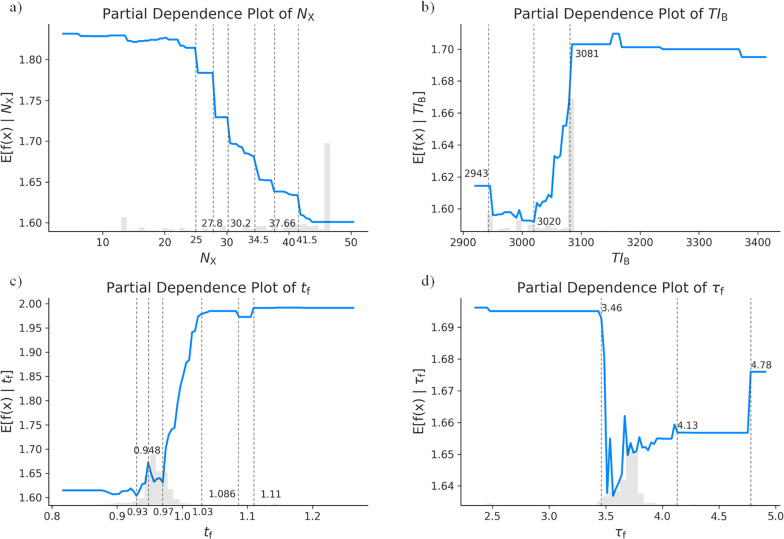
The scatter plots between the feature and SHAP values are drawn in Figures 4 and S19 with the color indicating the prediction value to acquire a further understanding of each feature. The partial dependence (PD)28 plots are drawn in Figures 5 and S21, which could signify the overall marginal effect that the feature had on the prediction.
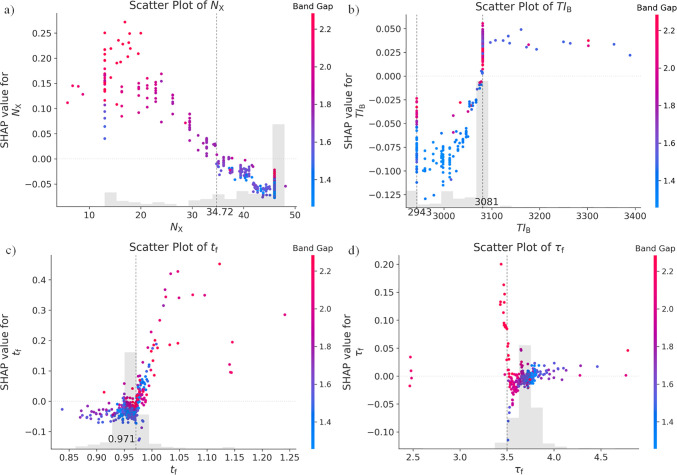
Figure 4.
Scatter plots of the features NX (a), TIB (b), tf (c), and τf (d) versus their SHAP values.
Figure 5.
Partial dependence (PD) plots of the features NX (a), TIB (b), tf (c), and τf (d) versus their predictions.
As shown in Figure 4a, NX was the element name in X site. The SHAP values for NX showed a decreasing trend as the NX values were increasing. The samples with lower NX values and hence corresponding higher SHAP values tended to express the larger bandgaps (in darker red color) and vice versa. By marking an inflection point (determining the SHAP values positive or negative) for NX of 34.72, the NX values over 34.72 would result in the negative SHAP values, and the ones lower than 34.72 led to the positive. The original values of NX have been converted to numbers in the procedure for generating descriptors in which Cl, Br, and I were signaled by 20, 13, and 46 respectively. Hence, in pursuit of a higher/lower bandgap, the ratio of I in the X site should be decreased/increased for a low/high NX value that would trigger a high/low SHAP value, which was consistent to the current domain knowledges.32−36 As indicated by the PD plot for NX in Figure 5, the same conclusion was extracted that the bandgap decreased as the NX value increased. The steep points that triggered sharp deceases in predictions were labeled on the plot. Specifically, the steep point 25.00 for NX might refer to the doped couple Br1.915I1.091 or Cl2.423I0.577, and 27.80 to Br1.655I1.345 or Cl2.100I0.900, 30.20 to Br1.455I1.545 or Cl1.846I1.154, 41.50 to Br0.409I2.591 or Cl0.519I2.481, respectively.
TIB signaled the third ionization energy of the element in the B site, in which the energies of Sn, Pb, Ge, Cd, and Pd were 2943, 3081, 3302, 3616, and 3177 kJ/mol, respectively. Indicated by the scatter plot in Figure 4b, the TIB value was proportional to its SHAP value and bandgap prediction. Hence, the higher bandgaps might require the B site elements with the higher third ionization energy, which would influence on the charge effect. Combining the relevant PD plots of TIB in Figure 5b, it could be noted that the steep points at 2943 and 3081 kJ/mol were the third ionizations of Sn and Pb, which revealed the overall increasing trending of the bandgap as the proportion of lead arose in the doped B site couple SnPb. When the TIB value was over 3081, the prediction was nearly unchanged and even slightly declined, indicating that the higher ratios of Ge/Cd/Pd might have little influence on bandgap.
As shown in Figure 4c, the SHAP values of tf had an overall increasing trend with the ascendent tf values, whose inflection point was around 0.971. The PD plot in Figure 5c displayed a sigmoid-like function trend in the experimental and virtual data sets, in which the tf range below/above 0.930/1.086 indicated steady prediction changes and the data in the range of 0.930–1.086 resulted in a steep increment for bandgap values. As for another structural factor τf, the inflection point of 3.50 could be noticed from the scatter plot in Figure 4d. The SHAP values were mostly positive as the τf value was lower than 3.50, while the values tended to be more negative as the τf value was over 3.50. The PD plot in Figure 5d showed that the τf ranges lower than 3.46, 4.13–4.78 and higher than 4.78 would render steady prediction trends, while the range 3.46–4.13 signaled an overall decreasing tendency. Since these two factors were both relevant to structural and geometric effects of HOIP samples, it might be comprehensive to take them into consideration together. If we seek HOIPs with lower bandgaps, the value of tf should not be over 0.971 and the value of τf is recommended to be 3.46–4.13, while HOIPs with tf > 1.014, τf < 3.46, and 4.13 < τf < 4.18 (4.18 determines the structure formability as indicated in reference26) tend to own the larger bandgaps.
The full discussion of six other important descriptors in the top 10 can be found in Code S8, which includes discussions on the virtual data set and the individual conditional expectation (ICE)37 plots.
Proactive Searching Progress
To exploit as much material space as possible, we collected 88 organic fragments (Table S4) and three inorganic elements Cs/K/Rb from experimental and theoretical publications for the A site, while eight metal elements Sn/Ge/Pd/Bi/Sr/Ca/Cr/La and three halogen elements Cl/Br/I were employed for the B and X sites. The doping range was set as 0–1 for A/B site and 0–3 for X site with the ratio step of 0.001 and the doping number 1–3. Thence the chemical space comprised over 8.20 × 1018 combinations for the formula A′A″A‴B′B″B‴X′X″X‴.
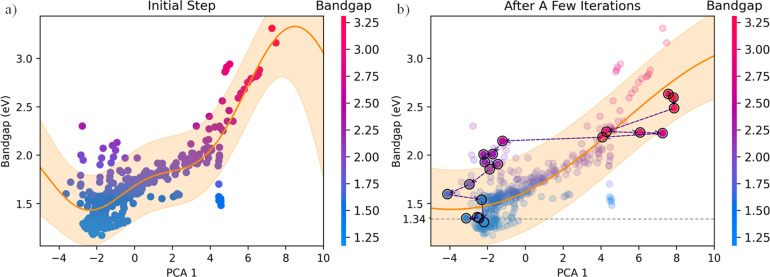
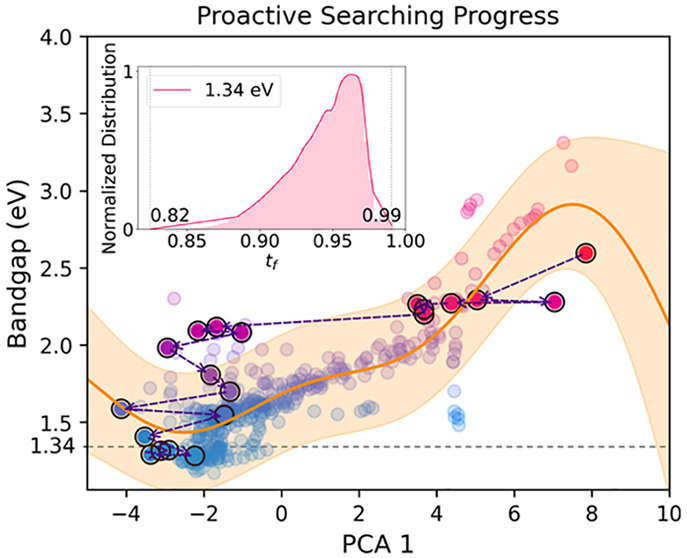
To efficiently search the material compositions with expected bandgap values from the universal chemical space, the PSP method was applied in this study. The material compositions were set as the combinations of the elements/fragments in each site and the relevant ratios. The material property was set as the bandgap of HOIPs, and the EE criterion was restrained less than 0.05 eV. The expected values were predefined as 1.34 eV for PSCs, 1.20 eV for bottom cells in TSCs, and 1.70 and 1.75 eV for top cells in TSCs. For illustrative purposes, the high-dimensional features for each HOIP samples were compressed into the first component via component analysis (PCA), and Figure 6a presents the distribution of bandgaps versus the first PCA component (PCA-1). After a few iterations in the progress of searching the samples with 1.34 eV bandgap, 20 virtual samples were drawn from the searched result in Figure 6b and linked by the dotted lines. The distribution of bandgaps was obviously changed from the original one, and the predictions had a decreasing trend as the searching progress proceeded, which exhibited an efficient way to design the samples with expected property values from a universal chemical space. An additional demo web could be accessed at http://materials-data-mining.com/pspweb/.
Figure 6.
Bandgap distribution in the initial step (a) and after a few iterations (b) versus the first component in principal component analysis.
Top Candidates
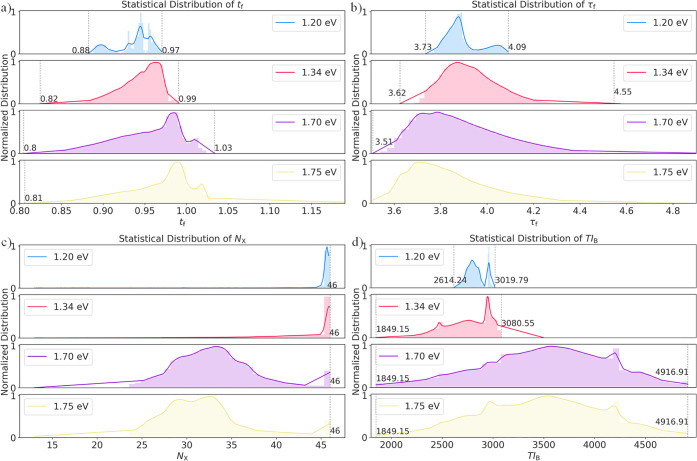
As a result of the PSP design, we obtained 820782 samples for the Pb-free HOIPs with bandgap 1.34 ± 0.05 eV, 22808 samples with 1.20 ± 0.05 eV, 984938 samples with 1.70 ± 0.05 eV, and 902401 samples with 1.75 ± 0.05 eV, respectively, in which the feature distributions for the four candidate sets are shown in Figure 7. As displayed in Figure 7a, the tf of low-bandgap HOIPs (1.20 and 1.34 eV) revealed a narrower range than the wide-bandgap ones (1.70 and 1.75 eV). The tf ranges of HOIPs with 1.20 and 1.34 eV were 0.88–0.97 and 0.83–0.99, while the cases of 1.70 and 1.75 eV were 0.80–1.02 and 0.81–1.20. Hence, the lower tf values (<0.97) could render a larger probability of low-bandgap samples and the higher tf values (>0.99) would lead to large-bandgap samples, which is consistent with the conclusion in model analysis. Simultaneously signaled by Figure 7b, the τf revealed an inverse trend that the peak of feature distribution was decreasing as the bandgap increased. The τf value of low-bandgap samples was concentrated at 3.75–4.09 and could be extended to 3.67–4.18 (considering the formability criterion), while the peaks of τf distribution of large-bandgap samples were around 3.60–3.90. Hence, the τf value fixed in 3.75–4.09 was essentially needed for seeking the low-bandgap samples, and the feature value should be controlled in 3.51–3.90 (or even lower) for the large-bandgap samples, which conducted the similar conclusion to the model analysis. In summary, the criterions tf < 0.97 and 3.75 < τf < 4.09 were recommanded for searching low-bandgap samples, while the criterions tf > 0.97, τf < 3.90 and 4.09 < τf < 4.18 were for the wide-bandgap ones. In the experimental sample set, we found that the most samples obeyed such criteria. For instance, the FAGeI3, MAGeI3, and FASnBr3 (bandgap 2.30, 2.00, 1.90 eV) had the tf of 1.12, 1.10, 1.00 and τf of 4.79, 4.77, 3.52. And Cs0.3FA0.7SnI3, MASnI3, FA0.25MA0.75SnI3 (bandgap 1.29, 1.30, 1.28 eV) owned the tf of 0.95, 0.96, 0.96 and τf of 3.81, 3.78, 3.76. After filtering by using the criterion τf < 4.18, 0.8 < tf < 1.2 and the existence of p-block elements in B site, there were 20242, 733848, 764883, and 746190 non-Pb samples left for the HOIPs with the bandgap of 1.20, 1.34, 1.70, and 1.75 eV, respectively.
Figure 7.
Statistical distributions of tf (a), τf (b), NX (c), and TIB (d) in explored candidate set.
Also exhibited in Figure 7c, NX of low-bandgap samples was centered at a value of 46, indicating the X site of most low-bandgap samples was composed of iodine. Meanwhile, the X site compositions of most large-bandgap samples was the mixture of bromine and iodine. As shown in Figure 7d, the TIB value of low-bandgap samples was concentrated in 1849–3080 kJ/mol, while the opposite value was spreading over 1800–5000 kJ/mol. The remnant feature distributions are accessible in Figure S23. The four candidate sets are accessible in our GitHub: https://github.com/luktian/InverseDesignViaPSP/tree/main/code9.
We also expanded our studies to several specific HOIP chemical systems to provide potential candidates for experimental researchers. For example, from our searching results, we found that the candidates Cs0.334FA0.266MA0.400Sn0.769Ge0.003Pd0.228Br0.164I2.836, Cs0.366FA0.338MA0.296Sn0.800Cr0.104-Pd0.096Br0.056I2.944, and Cs0.509FA0.412MA0.079Sn0.634Ge0.095Cr0.271Br0.109I2.891 had the optimal bandgap 1.34 eV, representing the Cs-FA-MA-Sn-Ge-Pd, Cs-FA-MA-Sn-Cr-Pd, and Cs-FA-MA-Sn-Ge-Cr mixed HOIPs, respectively, which might be potential non-Pb alternatives to the Cs0.05FA0.79MA0.16PbxSn1–xBr0.52I2.48 (x = 0, 0.084, 0.168, 0.252, 0.336, 0.420, with bandgap 1.35–1.61 eV) studied by Ji et al.19 In addition, the candidates Cs0.494MA0.217FA0.289Sn0.866Ge0.134Br0.377I2.623, Cs0.305FA0.273MA0.422Sn0.975Cr0.025Br0.264I2.736, and Cs0.300MA0.675FA0.025Sn0.817Pd0.183Br0.051I2.949 also had a bandgap of 1.34 eV and represented Cs-FA-MA-Sn-Ge, Cs-FA-MA-Sn-Cr, and Cs-FA-MA-Sn-Pd mixed HOIPs, respectively. One hundred thirty-five Cs-FA-MA-based candidates are provided in Table S9. The bandgaps of Cs-FA-MA based HOIPs could be adjusted to the ideal range 1.60–1.76 eV for the top part in tandem cells as well. For instance, the candidates Cs0.392FA0.016MA0.592Cr0.383Sr0.347Sn0.270Br1.171I1.829, and Cs0.445FA0.161MA0.394Pd0.508Cr0.228Sn0.263-Br1.094I1.906, were found with 1.67 eV bandgap, which were non-Pb substitutes of Cs0.15FA0.17MA0.68PbBr0.6I2.4 investigated by Sala et al.38 And 136 Cs-FA-MA based candidates are listed in Table S10. As for the HOIPs with bandgap 1.20 eV,39−41 the non-Pb candidates MA0.815FA0.185Sn0.927Ge0.073I3 (1.22 eV) and MA0.861FA0.139Sn0.914Ge0.086I3 (1.22 eV) were found, as compared to the experimental samples, e.g., FA0.55MA0.45Sn0.55Pb0.45I3 (1.24 eV),42 FA0.5MA0.5Sn0.5Pb0.5I3 (1.20 eV),43 and FA0.83Cs0.17Pb0.3Sn0.7I3 (1.23 eV).44 Twenty-seven MA-FA-Sn based candidates are supplied in Table S11. Moreover, from the explored samples, ASnI3 (A+ → ammonium), AGSnI3 (AG+ → hydrazinium), and XQSnI3 (XQ+ → sulfonium) were also found with low bandgaps of 1.29, 1.29, and 1.30 eV, whose formability probability were predicted over 99% in our recent study.45
Experimental Validation
A few studies on Sn–Ge mixed HOIPs have been reported in recent years due to their environmentally friendliness, high stability, and excellent optoelectronic properties.46−48 However, there is a lack of studies on the system MASnxGe1–xI3 according to our collected data, except for the end points MASnI3 and MAGeI3. To explore the bandgaps of Sn–Ge systems and validate the WVR model, a series of samples formulated as MASnxGe1–xI3 (x = 1, 0.85, 0.74, 0.66, 0) were synthesized, whose predicted bandgaps via the WVR model were 1.28, 1.41, 1.51, 1.59, 2.01 eV, respectively. The experimental details were provided in Section S3 of the Supporting Information. The optical absorbance spectrum of the material is shown in Figure S25. The optical bandgap was obtained by using the Tauc formula,49 which resulted in 1.23 and 2.02 eV for MASnI3 and MAGeI3 films, respectively. These two values are in good agreement with other reports.50,51 The initial incorporation of Ge (corresponding to x = 0.85) caused a sudden increase in the optical bandgap edge as compared to MASnI3. With increasing the Ge concentration (i.e., x changes from 0.85 to 0.66), the optical bandgap edge has a small shift to lower wavelength, resulting in bandgaps of 1.53, 1.55, 1.54 eV (corresponding to x = 0.85, 0.74, 0.66). The predictions of these three new compositions were consistent to the experimental bandgaps with the average error of 0.07 eV.
Conclusion
In summary, four tree-based ML models were built up, namely CAT, XGB, LGB, and GBM models, based on the filtered 13, 13, 12, and 10 features, respectively. After tuning the model parameters, the R2 values of LOOCV and testing set for four models were 0.90–0.94 and 0.88–0.91, respectively. By applying the self-developed WVR meta-model, the four submodels were embedded together, exhibiting the comprehensive performance of LOOCV R2 0.95 and testing R2 0.91. Then the top 10 features were analyzed by calculating the SHAP contributions based the experimental data set and a virtually generated data set, which revealed the mapping relationships between the formulas and bandgaps in detail. In particular, tf below 0.971 and τf in 3.75–4.09 were beneficial for a low bandgap (e.g., 1.20 and 1.34 eV), while tf over 0.971 and τf in 4.09–4.18 (or lower 3.90) contributed to a large bandgap (e.g., over 1.70 eV). To discover the new Pb-free HOIPs with suitable bandgaps, we generated a universal chemical space for the HOIP formula A′A″A‴B′B″B‴X′X″X‴, in which 91, 8, and 3 choices were considered for the A, B, and X sites, respectively, resulting in 8.20 × 1018 combinations. The inverse design method PSP was proposed to find out the candidate HOIPs with desired bandgaps, in which 733848, 764883, 746190, and 20242 candidates were found for the HOIPs whose bandgaps were 1.34 eV for PSCs, 1.70/1.75 eV for top cells in TSCs, and 1.20 eV for bottom cells in TSCs. From the searched results, Cs0.334FA0.266MA0.400Sn0.769Ge0.003Pd0.228Br0.164I2.836, Cs0.366FA0.338MA0.296Sn0.800Cr0.104Pd0.096-Br0.056I2.944, and Cs0.509FA0.412MA0.079-Sn0.634Ge0.095Cr0.271Br0.109I2.891 were found for Cs-FA-MA mixed HOIPs with optimal bandgap 1.34 eV for PSCs. Cs0.392FA0.016MA0.592Cr0.383Sr0.347-Sn0.27Br1.171I1.829 and Cs0.445FA0.161MA0.394Pd0.508Cr0.228Sn0.263Br1.094I1.906 were found for Cs-FA-MA mixed HOIPs with large bandgap for the top cells in TSCs, while MA0.815FA0.185Sn0.927Ge0.073I3 and MA0.86FA0.139Sn0.914Ge0.086I3 were found for the bottom cells in TSCs. We believed that the inverse design methods as well as the ML training processes could facilitate the development of both photovoltaic fields and other advanced materials.
Acknowledgments
This study was supported by the National Key Research and Development Program of China (No.2018YFB0704400), Shanghai Pujiang Program (21PJD024), the Key Research Project of Zhejiang Laboratory (No.2021PE0AC02), and Technology of Yunnan Province (No. 202002AB080001-1).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c01380.
Codes to train WVR model and conduct PSP method; SHAP plots for model analysis; sample distributions for explored virtual samples (PDF)
The authors declare no competing financial interest.
Notes
The full data set and codes are also available on at https://github.com/luktian/InverseDesignViaPSP. The codes are based on our Python package https://pypi.org/project/fast-machine-learning/.
Supplementary Material
References
- Luo D.; Su R.; Zhang W.; Gong Q.; Zhu R. Minimizing Non-Radiative Recombination Losses in Perovskite Solar Cells. Nat. Rev. Mater. 2020, 5, 44–60. 10.1038/s41578-019-0151-y. [DOI] [Google Scholar]
- Luo Q.; Wu R.; Ma L.; Wang C.; Liu H.; Lin H.; Wang N.; Chen Y.; Guo Z. Recent Advances in Carbon Nanotube Utilizations in Perovskite Solar Cells. Adv. Funct. Mater. 2020, 31, 2004765. 10.1002/adfm.202004765. [DOI] [Google Scholar]
- Wang M.; Wang W.; Ma B.; Shen W.; Liu L.; Cao K.; Chen S.; Huang W., Lead-Free Perovskite Materials for Solar Cells. Nano-Micro Lett. 2021, 13.62. 10.1007/s40820-020-00578-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu T.; Liu X.; Luo X.; Lin X.; Cui D.; Wang Y.; Segawa H.; Zhang Y.; Han L. Lead-Free Tin Perovskite Solar Cells. Joule 2021, 5, 863–886. 10.1016/j.joule.2021.03.001. [DOI] [Google Scholar]
- Green M. A.; Dunlop E. D.; Hohl-Ebinger J.; Yoshita M.; Kopidakis N.; Hao X. Solar Cell Efficiency Tables (Version 58). Prog. Photovoltaics 2021, 29, 657–667. 10.1002/pip.3444. [DOI] [Google Scholar]
- Kojima A.; Teshima K.; Shirai Y.; Miyasaka T. Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. 10.1021/ja809598r. [DOI] [PubMed] [Google Scholar]
- Zhang C.; Lu Y.-N.; Wu W.-Q.; Wang L. Recent Progress of Minimal Voltage Losses for High-Performance Perovskite Photovoltaics. Nano Energy 2021, 81, 105634. 10.1016/j.nanoen.2020.105634. [DOI] [Google Scholar]
- Rühle S. Tabulated Values of the Shockley–Queisser Limit for Single Junction Solar Cells. Sol. Energy 2016, 130, 139–147. 10.1016/j.solener.2016.02.015. [DOI] [Google Scholar]
- Shockley W.; Queisser H. J. Detailed Balance Limit of Efficiency of P-N Junction Solar Cells. J. Appl. Phys. 1961, 32, 510–519. 10.1063/1.1736034. [DOI] [Google Scholar]
- Polman A.; Knight M.; Garnett Erik C.; Ehrler B.; Sinke Wim C. Photovoltaic Materials: Present Efficiencies and Future Challenges. Science 2016, 352, aad4424. 10.1126/science.aad4424. [DOI] [PubMed] [Google Scholar]
- Tong J.; Jiang Q.; Zhang F.; Kang S. B.; Kim D. H.; Zhu K. Wide-Bandgap Metal Halide Perovskites for Tandem Solar Cells. ACS Energy Lett. 2021, 6, 232–248. 10.1021/acsenergylett.0c02105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen L.; Pilania G.; Batra R.; Huan T. D.; Kim C.; Kuenneth C.; Ramprasad R. Polymer Informatics: Current Status and Critical Next Steps. Mater. Sci. Eng., R 2021, 144, 100595. 10.1016/j.mser.2020.100595. [DOI] [Google Scholar]
- Haghighatlari M.; Vishwakarma G.; Altarawy D.; Subramanian R.; Kota B. U.; Sonpal A.; Setlur S.; Hachmann J. Chemml: A Machine Learning and Informatics Program Package for the Analysis, Mining, and Modeling of Chemical and Materials Data. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2020, 10, e1458. 10.1002/wcms.1458. [DOI] [Google Scholar]
- Masood H.; Toe C. Y.; Teoh W. Y.; Sethu V.; Amal R. Machine Learning for Accelerated Discovery of Solar Photocatalysts. ACS Catal. 2019, 9, 11774–11787. 10.1021/acscatal.9b02531. [DOI] [Google Scholar]
- Moosavi S. M.; Jablonka K. M.; Smit B. The Role of Machine Learning in the Understanding and Design of Materials. J. Am. Chem. Soc. 2020, 142, 20273. 10.1021/jacs.0c09105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu S.; Zhou Q.; Ouyang Y.; Guo Y.; Li Q.; Wang J. Accelerated Discovery of Stable Lead-Free Hybrid Organic-Inorganic Perovskites Via Machine Learning. Nat. Commun. 2018, 9, 3405. 10.1038/s41467-018-05761-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saidi W. A.; Shadid W.; Castelli I. E. Machine-Learning Structural and Electronic Properties of Metal Halide Perovskites Using a Hierarchical Convolutional Neural Network. npj Comput. Mater. 2020, 6, 36. 10.1038/s41524-020-0307-8. [DOI] [Google Scholar]
- Zhang S.; Lu T.; Xu P.; Tao Q.; Li M.; Lu W. Predicting the Formability of Hybrid Organic-Inorganic Perovskites Via an Interpretable Machine Learning Strategy. J. Phys. Chem. Lett. 2021, 12, 7423–7430. 10.1021/acs.jpclett.1c01939. [DOI] [PubMed] [Google Scholar]
- Ji L.; Zhang X.; Zhang T.; Wang Y.; Wang F.; Zhong Z.; Chen Z. D.; Xiao Z.; Chen L.; Li S. Band Alignment of Pb–Sn Mixed Triple Cation Perovskites for Inverted Solar Cells with Negligible Hysteresis. J. Mater. Chem. A 2019, 7, 9154–9162. 10.1039/C8TA11891D. [DOI] [Google Scholar]
- Pedregosa F.; Varoquaux G.; Gramfort A.; Michel V.; Thirion B.; Grisel O.; Blondel M.; Prettenhofer P.; Weiss R.; Dubourg V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Lundberg S. M.; Erion G.; Chen H.; DeGrave A.; Prutkin J. M.; Nair B.; Katz R.; Himmelfarb J.; Bansal N.; Lee S.-I. From Local Explanations to Global Understanding with Explainable Ai for Trees. Nat. Mach. Intell. 2020, 2, 56–67. 10.1038/s42256-019-0138-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.,,et al. Gaussian 16 Rev. C.01; Gaussian, Inc.: Wallingford, CT, 2016. [Google Scholar]
- Lu T.; Chen F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. 10.1002/jcc.22885. [DOI] [PubMed] [Google Scholar]
- Li C.; Soh K. C. K.; Wu P. Formability of Abo3 Perovskites. J. Alloys Compd. 2004, 372, 40–48. 10.1016/j.jallcom.2003.10.017. [DOI] [Google Scholar]
- Goldschmidt V. M. Die Gesetze Der Krystallochemie. Naturwissenschaften 1926, 14, 477–485. 10.1007/BF01507527. [DOI] [Google Scholar]
- Bartel C. J.; Sutton C.; Goldsmith B. R.; Ouyang R.; Musgrave C. B.; Ghiringhelli L. M.; Scheffler M. New Tolerance Factor to Predict the Stability of Perovskite Oxides and Halides. Sci. Adv. 2019, 5, eaav0693. 10.1126/sciadv.aav0693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guyon I.; Weston J.; Barnhill S.; Vapnik V. Gene Selection for Cancer Classification Using Support Vector Machines. Machine Learning 2002, 46, 389–422. 10.1023/A:1012487302797. [DOI] [Google Scholar]
- Jerome H. F. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat 2001, 29, 1189–1232. 10.1214/aos/1013203450. [DOI] [Google Scholar]
- Chang C.; Lin C. Libsvm: A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. 10.1145/1961189.1961199. [DOI] [Google Scholar]
- Ding C.; Peng H. Minimum Redundancy Feature Selection from Microarray Gene Expression Data. J. Bioinf. Comput. Biol. 2005, 03, 185–205. 10.1142/S0219720005001004. [DOI] [PubMed] [Google Scholar]
- Hanchuan P.; Fuhui L.; Ding C. Feature Selection Based on Mutual Information Criteria of Max-Dependency, Max-Relevance, and Min-Redundancy. IEEE TPAMI 2005, 27, 1226–1238. 10.1109/TPAMI.2005.159. [DOI] [PubMed] [Google Scholar]
- Kumawat N. K.; Dey A.; Kumar A.; Gopinathan S. P.; Narasimhan K. L.; Kabra D. Band Gap Tuning of Ch3nh3pb(Br1–Xclx)3 Hybrid Perovskite for Blue Electroluminescence. ACS Appl. Mater. Interfaces 2015, 7, 13119–13124. 10.1021/acsami.5b02159. [DOI] [PubMed] [Google Scholar]
- Kumawat N. K.; Tripathi M. N.; Waghmare U.; Kabra D. Structural, Optical, and Electronic Properties of Wide Bandgap Perovskites: Experimental and Theoretical Investigations. J. Phys. Chem. A 2016, 120, 3917–3923. 10.1021/acs.jpca.6b04138. [DOI] [PubMed] [Google Scholar]
- Aharon S.; Cohen B. E.; Etgar L. Hybrid Lead Halide Iodide and Lead Halide Bromide in Efficient Hole Conductor Free Perovskite Solar Cell. J. Phys. Chem. C 2014, 118, 17160–17165. 10.1021/jp5023407. [DOI] [Google Scholar]
- Tu Y.; Wu J.; Lan Z.; He X.; Dong J.; Jia J.; Guo P.; Lin J.; Huang M.; Huang Y. Modulated Ch3nh3pbi3–Xbrx Film for Efficient Perovskite Solar Cells Exceeding 18%. Sci. Rep. 2017, 7, 44603. 10.1038/srep44603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z. L.; Men B. Q.; Liu Y. F.; Gao H. P.; Mao Y. L. Effects of Precursor Solution Composition on the Performance and I-V Hysteresis of Perovskite Solar Cells Based on Ch3nh3pbi3-Xclx. Nanoscale Res. Lett. 2017, 12, 84. 10.1186/s11671-017-1872-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldstein A.; Kapelner A.; Bleich J.; Pitkin E. Peeking inside the Black Box: Visualizing Statistical Learning with Plots of Individual Conditional Expectation. arXiv 2013, 1309.6392. [Google Scholar]
- Sala J.; Heydarian M.; Lammar S.; Abdulraheem Y.; Aernouts T.; Hadipour A.; Poortmans J. Compositional Investigation for Bandgap Engineering of Wide Bandgap Triple Cation Perovskite. ACS Appl. Energy Mater. 2021, 4, 6377–6384. 10.1021/acsaem.1c00810. [DOI] [Google Scholar]
- Liao W.; Zhao D.; Yu Y.; Shrestha N.; Ghimire K.; Grice C. R.; Wang C.; Xiao Y.; Cimaroli A. J.; Ellingson R. J.; et al. Fabrication of Efficient Low-Bandgap Perovskite Solar Cells by Combining Formamidinium Tin Iodide with Methylammonium Lead Iodide. J. Am. Chem. Soc. 2016, 138, 12360–12363. 10.1021/jacs.6b08337. [DOI] [PubMed] [Google Scholar]
- Eperon G. E.; Leijtens T.; Bush K. A.; Prasanna R.; Green T.; Wang J. T.-W.; McMeekin D. P.; Volonakis G.; Milot R. L.; May R.; Palmstrom A.; Slotcavage D. J.; Belisle R. A.; Patel J. B.; Parrott E. S.; Sutton R. J.; Ma W.; Moghadam F.; Conings B.; Babayigit A.; Boyen H.-G.; Bent S.; Giustino F.; Herz L. M.; Johnston M. B.; McGehee M. D.; Snaith H. J.; et al. Perovskite-Perovskite Tandem Photovoltaics with Optimized Band Gaps. Science 2016, 354, 861–865. 10.1126/science.aaf9717. [DOI] [PubMed] [Google Scholar]
- Li Y.; Sun W.; Yan W.; Ye S.; Rao H.; Peng H.; Zhao Z.; Bian Z.; Liu Z.; Zhou H.; et al. 50% Sn-Based Planar Perovskite Solar Cell with Power Conversion Efficiency up to 13.6%. Adv. Energy Mater. 2016, 6, 1601353. 10.1002/aenm.201601353. [DOI] [Google Scholar]
- Gómez P.; Wang J.; Más-Montoya M.; Bautista D.; Weijtens C. H. L.; Curiel D.; Janssen R. A. J. Pyrene-Based Small-Molecular Hole Transport Layers for Efficient and Stable Narrow-Bandgap Perovskite Solar Cells. Sol. RRL 2021, 5, 2100454. 10.1002/solr.202100454. [DOI] [Google Scholar]
- Liu M.; Chen Z.; Yang Y.; Yip H.-L.; Cao Y. Reduced Open-Circuit Voltage Loss for Highly Efficient Low-Bandgap Perovskite Solar Cells Via Suppression of Silver Diffusion. J. Mater. Chem. A 2019, 7, 17324–17333. 10.1039/C9TA04366G. [DOI] [Google Scholar]
- Klug M. T.; Milot R. L.; Patel J. B.; Green T.; Sansom H. C.; Farrar M. D.; Ramadan A. J.; Martani S.; Wang Z.; Wenger B.; et al. Metal Composition Influences Optoelectronic Quality in Mixed-Metal Lead–Tin Triiodide Perovskite Solar Absorbers. Energy Environ. Sci. 2020, 13, 1776–1787. 10.1039/D0EE00132E. [DOI] [Google Scholar]
- Zhang S.; Lu T.; Xu P.; Tao Q.; Li M.; Lu W. Predicting the Formability of Hybrid Organic–Inorganic Perovskites Via an Interpretable Machine Learning Strategy. J. Phys. Chem. L 2021, 12, 7423–7430. 10.1021/acs.jpclett.1c01939. [DOI] [PubMed] [Google Scholar]
- Krishnamoorthy T.; Ding H.; Yan C.; Leong W. L.; Baikie T.; Zhang Z.; Sherburne M.; Li S.; Asta M.; Mathews N.; et al. Lead-Free Germanium Iodide Perovskite Materials for Photovoltaic Applications. J. Mater. Chem. A 2015, 3, 23829–23832. 10.1039/C5TA05741H. [DOI] [Google Scholar]
- Xiao Z.; Meng W.; Wang J.; Mitzi D. B.; Yan Y. Searching for Promising New Perovskite-Based Photovoltaic Absorbers: The Importance of Electronic Dimensionality. Mater. Horiz. 2017, 4, 206–216. 10.1039/C6MH00519E. [DOI] [Google Scholar]
- Ito N.; Kamarudin M. A.; Hirotani D.; Zhang Y.; Shen Q.; Ogomi Y.; Iikubo S.; Minemoto T.; Yoshino K.; Hayase S. Mixed Sn–Ge Perovskite for Enhanced Perovskite Solar Cell Performance in Air. J. Phys. Chem. L 2018, 9, 1682–1688. 10.1021/acs.jpclett.8b00275. [DOI] [PubMed] [Google Scholar]
- Tauc J.; Grigorovici R.; Vancu A. Optical Properties and Electronic Structure of Amorphous Germanium. Phys. Status Solidi B 1966, 15, 627–637. 10.1002/pssb.19660150224. [DOI] [Google Scholar]
- Handa T.; Yamada T.; Kubota H.; Ise S.; Miyamoto Y.; Kanemitsu Y. Photocarrier Recombination and Injection Dynamics in Long-Term Stable Lead-Free Ch3nh3sni3 Perovskite Thin Films and Solar Cells. J. Phys. Chem. C 2017, 121, 16158–16165. 10.1021/acs.jpcc.7b06199. [DOI] [Google Scholar]
- Kanoun A.-A.; Kanoun M. B.; Merad A. E.; Goumri-Said S. Toward Development of High-Performance Perovskite Solar Cells Based on Ch3nh3gei3 Using Computational Approach. Sol. Energy 2019, 182, 237–244. 10.1016/j.solener.2019.02.041. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.