Quantifying the environmental limits to fire spread in grassy ecosystems

Significance

Scientists and the public alike are gaining an increasing appreciation for the role of fire in the Earth system. Understanding and predicting fire behavior has become increasingly critical in the face of changing constraints on fire behavior. Here, we show that fires in grassy ecosystems are subject to threshold behaviors—widely hypothesized in theory, but rarely applied—which should be included in mechanistic models of fire behavior. We link these thresholds explicitly to fuel and weather conditions to facilitate their broad adoption in applied contexts, bridging the sizeable divide between theoretical and applied fire models.

Abstract

Modeling fire spread as an infection process is intuitive: An ignition lights a patch of fuel, which infects its neighbor, and so on. Infection models produce nonlinear thresholds, whereby fire spreads only when fuel connectivity and infection probability are sufficiently high. These thresholds are fundamental both to managing fire and to theoretical models of fire spread, whereas applied fire models more often apply quasi-empirical approaches. Here, we resolve this tension by quantifying thresholds in fire spread locally, using field data from individual fires (n = 1,131) in grassy ecosystems across a precipitation gradient (496 to 1,442 mm mean annual precipitation) and evaluating how these scaled regionally (across 533 sites) and across time (1989 to 2012 and 2016 to 2018) using data from Kruger National Park in South Africa. An infection model captured observed patterns in individual fire spread better than competing models. The proportion of the landscape that burned was well described by measurements of grass biomass, fuel moisture, and vapor pressure deficit. Regionally, averaging across variability resulted in quasi-linear patterns. Altogether, results suggest that models aiming to capture fire responses to global change should incorporate nonlinear fire spread thresholds but that linear approximations may sufficiently capture medium-term trends under a stationary climate.

Fire is a fundamental component of the Earth system, with widespread impacts on ecosystem structure and function, the global carbon cycle, and human society (1). The majority of global burned area and fire-related emissions originate in grassy savanna ecosystems (2, 3), making a process-based understanding of fire in these systems crucial for future fire predictions (4). Among fire managers in grassy systems, fire spread is often discussed in terms of thresholds: Fires spread only if grassy fuel is sufficiently abundant and dry. Fire managers exploit these thresholds by cutting firebreaks into continuous fuel layers or spraying water ahead of an advancing fire front to halt its progress. The existence of thresholds in fire spread is also frequently discussed in the fire science literature. Fire is discussed as spreading only if multiple “switches” are on, which could include fuel amount, fuel moisture, fire weather, and ignition (5). Additionally, thresholds in fire spread have been neatly demonstrated in controlled laboratory experiments with matchsticks (6) and in established theoretical physics models based on percolation theory (7, 8). However, despite the abundance of cross-disciplinary support for the existence of thresholds in fire spread, many applied local- and global-scale fire models include, at most, limited possibilities for thresholds [e.g., those using equations from ref. 9, inter alia CLM-Li (10), CTEM (11), ORCHIDEE-SPITFIRE (12), JSBACH-SPITFIRE (13), LPJ-GUESS-SPITFIRE (14), LPJ-LMfire (15), and MC-FIRE (16)]. The discrepancy between fire science and applied fire models prompts the question: Are thresholds in fire spread central to its landscape scale behavior, and should we be accounting for them when modeling fire’s ecological and Earth system impacts at large spatial scales?

Nonlinear thresholds may be intrinsic to the process of fire spread. Intuitively, fire spread can be described as an infection process (e.g., ref. 8) whereby an ignition ignites a flammable patch of fuel, which ignites, or “infects,” at least one neighboring patch of fuel, which infects other neighboring patches, and so on (17, 18). This approach can be formalized into a simple process-based model that predicts landscape burned area (proportion burned) based solely on the proportion of the landscape covered in fuel (fuel connectivity, ρ) and the probability that fire spreads from a burning patch of fuel to a neighboring patch of fuel (infection probability, λ). Within this framework, fire spread displays a strong threshold response to fuel connectivity and infection probability, spreading readily across landscapes with sufficient flammable fuel patches but dying out when fuel is too sparse or fuel flammability too low (e.g., if fuel moisture is too high).

Variants of the model described above have long been used in the theoretical literature to explore emergent behaviors in fire pattern (e.g., refs. 19–21) but have to date seen limited adoption in more applied contexts (e.g., ref. 17). The lack of uptake of fire thresholds in global fire models may be because the relationships between fire spread thresholds and fuel and weather conditions have not yet been quantified. Fuel condition is driven by seasonal to multiannual weather that regulates biomass accumulation and curing (22), while shorter-term variation in temperature, humidity, and wind speed further modify fuel flammability and thus fire behavior (9, 23). To integrate the theoretical and empirical perspectives on fire spread, we hypothesize that fuel biomass should capture the constraints of landscape-scale fuel connectivity on fire spread. Additionally, we hypothesize that the physical factors affecting ignition success and flame propagation, including fuel characteristics (moisture content) and weather conditions (temperature, humidity, and wind speed), should capture the constraints of infection probability on fire spread (17). We also expect infection probability to be correlated with the rate of spread of the fire front, an applied measure in grassy systems of how readily fire is spreading (17, 24).

Many regional and global coupled fire-vegetation or fire-vegetation-climate models use fire models that employ Rothermel’s equations (9) to predict the rate of spread of the fire front from fuel, moisture, topographic variables, and wind speed (although see refs. 25–27). Although mostly linear, Rothermel’s equations do include one important nonlinear threshold: the “moisture of extinction,” or the fuel moisture above which the rate of fire spread decreases to zero. Despite being widely applied, Rothermel’s “moisture of extinction” threshold may not be entirely correct (28). The threshold takes a maximum value of 40% of dry biomass and in grassy ecosystems is most commonly set to 15 to 20% of dry biomass (29), whereas empirical evidence suggests fire can burn when fuel is much wetter than this [as high as 100% of dry biomass (30)]. Moreover, theoretical models suggest that percolation processes may prevent fires from becoming large even when fire can spread locally with apparent success (i.e., when measured fire spread rate > 0, and infection probability > 0 but is not large), a phenomenon not captured in Rothermel’s approach. Third, Rothermel’s equations assume a linear relationship between fuel biomass and fire spread rate, and models using these equations assume a linear relationship between a landscape’s fuel connectivity and its proportion burned. This linear relationship is supported by empirical data collected over time at a regional scale in grassy systems (e.g., refs. 31–34) but is at odds with the predictions of percolation theory and with remotely sensed data, both of which show threshold-type declines in burned area when fuel connectivity is below ∼0.6 (22, 35). Together, these three limitations suggest that, while clearly useful, Rothermel’s equations do not offer the final picture for understanding how thresholds affect the process of fire spread at larger scales.

Given the need for reliable fire predictions, especially under climate change, it is imperative that we provide a timely direction for fire model development by bridging the sizeable gap between theoretical and applied fire models. Here, we begin to build this bridge by asking whether a simple fire infection model is useful for explaining emergent patterns in fire spread in grassy systems, how its parameters relate to widely recognized determinants of fire behavior, and whether this model explains patterns of burned area at larger scales and over time. To do this, we evaluated outcomes of model simulations against detailed field observations of 188 experimental fires in grassy savanna ecosystems in Kruger National Park (Kruger) and Hluhluwe-iMfolozi Park (HiP), South Africa, in Lopé National Park (Lopé), Gabon, and at the Cedar Creek Long Term Ecological Research site (Cedar Creek), East Bethel, MN, spanning a total mean annual precipitation (MAP) gradient of 496 mm to 1,442 mm. Then, using data from 1,004 fires in Kruger across a precipitation gradient of 496 to 737 mm MAP, we explicitly relate the model’s fuel connectivity and infection probability parameters to fuel moisture, fire weather (specifically, ambient temperature, relative humidity, and wind speed), and the rate of spread of the fire front. Finally, we used park-level observations of grassy biomass and burned area in Kruger to examine how landscape-scale observations scale to regional patterns over time. See Materials and Methods for more information about simulations, fire sampling, and regional monitoring datasets.

Results and Discussion

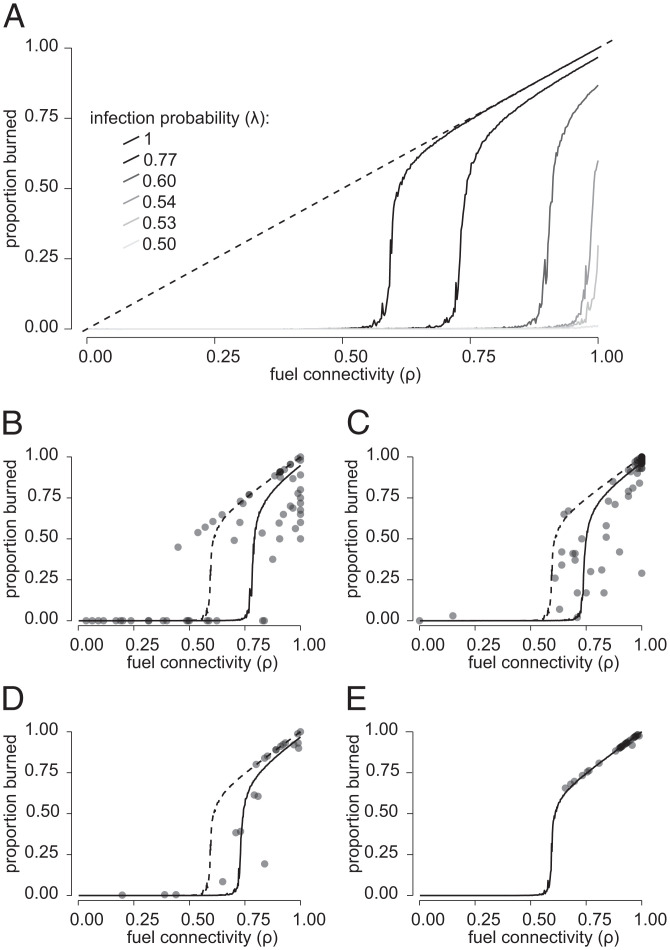
Using the infection model, we simulated a landscape’s proportion burned for 500 values of fuel connectivity and 100 values of infection probability (Materials and Methods). Consistent with past work (7, 8), model simulations suggested, first, that landscape burned area (proportion burned) should increase with fuel connectivity nonlinearly, such that below a threshold fuel connectivity proportion burned should be zero (or close to zero, since simulation landscapes are necessarily finite) but should rapidly approach the 1:1 line above this threshold (Fig. 1A). The actual value of the fuel connectivity threshold depends on the infection probability, and vice versa. For example, a minimum infection probability of 0.50 was needed for fire spread when fuels were continuous and fuel connectivity was at a maximum (ρ = 1). However, when fuel connectivity dropped to 0.55 and grass became patchy, fires would only spread if the infection probability was at a maximum (λ = 1). Both of these model characteristics are already well-established within percolation theory, although note that actual threshold values depend on details of landscape configuration (7).

Fig. 1.

Response of burned area (proportion burned) to fuel connectivity (ρ) in simulation (A; also depending on infection probability λ) and in empirical observations from Kruger National Park, South Africa (B; 496 to 737 mm MAP), Hluhluwe-iMfolozi, South Africa (C; 600 to 1,000 mm MAP), the Cedar Creek Ecosystem Science Reserve, East Bethel, MN (D; 775 mm MAP), and Lopé National Park, Gabon (E; 1,442 mm MAP). In B–E, dotted lines show the infection model simulation for λ = 1 and solid lines show the simulation with λ that minimized distance index (Materials and Methods) for the observed data (Kruger λ = 0.71, n = 61; HiP λ = 0.74, n = 30; Cedar Creek λ = 0.77, n = 66; Lopé λ = 1, n = 31). In all cases (B–E) the infection model was a better fit (lower distance index) to the data than linear, quadratic, two linear, exponential, logistic, van Bertalanffy, and Gompertz models.

The characteristic emergent properties of a fire infection model have not previously been demonstrated to exist in real fires. Here, by burning 108 fires, we showed that the modeled threshold-type relationships between fuel connectivity and proportion burned described patterns in real fires better than linear or other nonlinear models (Materials and Methods and Fig. 1 B–E). The only site to deviate from this pattern was the one with the highest rainfall (Lopé), where productivity is so high that fuel connectivity was always above the threshold value and thus proportion burned was always at its maximum potential. Our findings thus suggest that, at least at the scale of an individual fire, fire behavior is strongly nonlinear and that accounting for threshold behaviors in fire spread may improve predictions of fire size. Accurate prediction of fire size is essential for accurate prediction of fire-related emissions, and global fire model predictions currently diverge from each other and reality (36).

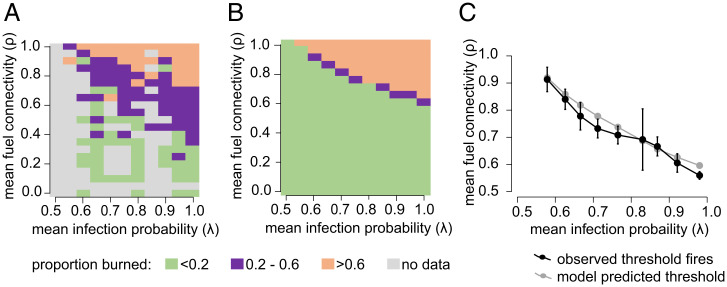
Moreover, as predicted by fire infection models, in the field data the fuel connectivity threshold value varied with changes in infection probability, and vice versa. We estimated the infection probability at the threshold for fire spread to evaluate whether the minimum possible infection probability increased as the fuel landscape became more disconnected (lower ρ) (17). Fires occurring at the threshold were those where proportion burned was above the minimum threshold for fire spread (where burned area approaches 0) but below the maximum possible (proportion burned >0.2 and <0.6) (Materials and Methods). We found that the behavior of “threshold” fires (Fig. 2B) closely approximated the predictions of the fire infection model (Fig. 2A) and that, as predicted, fire successfully spread at a lower infection probability when fuel connectivity was higher (Fig. 2C; expected vs. observed: R² = 0.96, P < 0.0001, with slope = 0.99 and intercept = −0.01). These results suggest that percolation processes and their associated thresholds may indeed govern fire spread at the landscape scale, at least in grassy systems.

Fig. 2.

Variation in burned area (proportion burned) with fuel connectivity (ρ) and infection probability (λ) in observed fires in Kruger (A) and according to model simulations (B). The response of the fire spread threshold to fuel connectivity (ρ) and infection probability (λ) is also explored in theory and in observed fires in Kruger through examination of “threshold fires” (those with burned area between 0.2 and 0.6, shown in purple in A and B). (C) The mean (± SE, minimum, maximum) values of fuel connectivity (ρ) and infection probability (λ) for all “threshold fires” was 0.72 (±0.04, 0.56, 0.91) and 0.77 (±0.05, 0.58, 0.98), respectively.

To maximize the real-world applicability of our results, we next examined whether estimates of fuel connectivity and infection probability could be parameterized using measurements of fuel biomass, fuel moisture, and instantaneous fire weather. As expected, fuel connectivity increased with grass biomass ($\text{ρ}=1.03*e^{-6.42*e^{-0.98*\mathit{mean} \mathit{grass} \mathit{biomass}}}$; adjusted R² = 0.98, P < 0.0001, n = 57; SI Appendix, Fig. S2). Consequently, the observed minimum fuel connectivity required for fire spread equated to a grass biomass of 2.4 tons⋅ha⁻¹, an estimate that is close to managers’ operational estimates of 2 tons⋅ha⁻¹ of grass biomass required to burn a successful fire (37). Moreover, this suggests that fires should occur more frequently in more productive systems, e.g., with higher rainfall (38), and that the fuel connectivity threshold can, in some grassy ecosystems, be parameterized using precipitation (39).

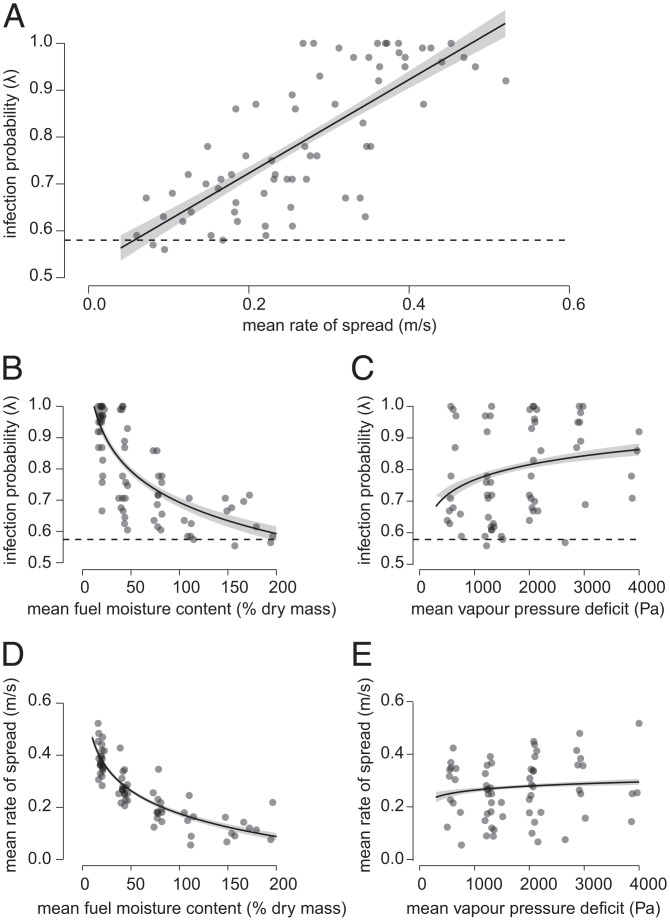
Also as expected, the infection probability increased linearly with the rate of spread of the fire front (adjusted R² = 0.53, P < 0.0001; Fig. 3A). Both infection probability and mean rate of spread of the fire front decreased with fuel moisture and increased with vapor pressure deficit, but to a lesser degree (R² = 0.64, P < 0.0001 and R² = 0.77, P < 0.0001, respectively; Fig. 3 B–E). Fuel moisture was the strongest predictor of infection probability, which suggests that, once a landscape has crossed the fuel connectivity threshold (i.e., has accumulated more than 2.4 tons⋅ha⁻¹ of grass biomass), fire spread is largely dictated by grass curing and by whether rain or dew recently fell. Currently, although global fire models do incorporate fuel moisture effects on fire spread, most set the fuel “moisture of extinction” at 15 to 20% of dry biomass in grassy ecosystems (sensu ref. 9). However, we found that 9% of fires in this study spread successfully with a fuel moisture of more than 100% of the dry biomass (SI Appendix, Fig. S3). This large discrepancy suggests that Rothermel’s laboratory-based controlled fuel-bed estimates may not be appropriate for use at larger scales, at least for predominantly fine, grassy fuels. A reevaluation of the “moisture of extinction” used in fire models may improve burned area predictions.

Fig. 3.

Response of the estimated fire infection probability (λ) to its mean rate of spread (ROS) (A) and response of fire infection probability (λ) and fire rate of spread to fuel moisture (FM) (B and D) and vapor pressure deficit (VPD) (C and E). Fitted curves show linear model results with SEs of fits shown in gray. A: $\lambda =0.92*\mathit{ROS}+0.55;$ adjusted R² = 0.53, P < 0.0001. B and C: $\lambda =-0.15*\text{ln}\left(FM\right)+0.07*\ln \left(\mathit{VPD}\right)+0.88$; adjusted R² = 0.65, P < 0.0001. D and E: $\mathit{ROS}=-0.13*\text{ln}\left(FM\right)+0.02*\text{ln}\left(\mathit{VPD}\right)+0.59$; adjusted R² = 0.77, P < 0.0001. In B and D, the curve shows predictions when VPD is held at a constant value of 2,004 Pa, and in C and E when FM is held at a constant value of 43% (the median value observed in the dataset). In A–C, dashed lines show the minimum infection probability (λ = 0.58) in observed “threshold fires” (those with burned area between 0.2 and 0.6) below which fire cannot successfully spread.

Surprisingly, we found that neither the estimated infection probability nor the rate of spread of a fire was associated with mean, maximum, or minimum wind speed during the burn. However, at shorter time intervals (<2 min), the instantaneous spread rate of fires increased with minimum wind speed (SI Appendix, Fig. S4), suggesting that wind does increase the speed of fire spread but that it varies so much on short time scales that extremely detailed measurements are required to capture its effects. Unfortunately, global wind speed products and predictions are not accurate (40), and thus fire models that depend on Rothermel’s equations to predict fire spread may not be robust. There are fire models that do not predict burned area using rate of spread [e.g., LPJ-GUESS-SIMFIRE (25), JULES-INFERNO (26, 27), GlobFIRM in LPJ-DGVM (41), and the fire model in refs. 42 and 43], but it is outside of the scope of this work to assess whether the approaches used in these models are more robust than those used in fire models using Rothermel’s equations. Until global wind speed products are more reliable, we should interpret Rothermel-based fire model predictions with caution and pay close attention to their associated sensitivity analyses. However, we also note that we did not capture fires under extreme wind conditions and so may have overestimated the severity of this problem.

Observations of individual fires clearly showed that fires grew large (higher proportion burned) nonlinearly in response to fuel connectivity and infection probability (Fig. 1). This contrasts with observations of regional burned area, where burned area increases linearly with rainfall (e.g., refs. 31–34). To resolve this apparent conflict, we evaluated how spatial and temporal variation in rainfall drives variation in thresholds that stop fires from spreading in Kruger, where wet-season rainfall variation largely determines grass productivity (38), fuel connectivity, and, therefore, fire extent. Across 533 long-term sites monitored from 1989 to 2018 (Materials and Methods), the probability that a site burned increased with fuel connectivity (estimated via grass biomass), with a shallow slope at ρ < 0.64 but a fivefold higher slope above ρ = 0.64 (SI Appendix, Fig. S5A). The 0.64 breakpoint is similar to the fuel connectivity threshold in infection model simulations (ρ = 0.53) and to the 0.6 grass cover (= 0.4 tree cover) threshold in remote sensing data below which burned area declines precipitously (22, 44, 45).

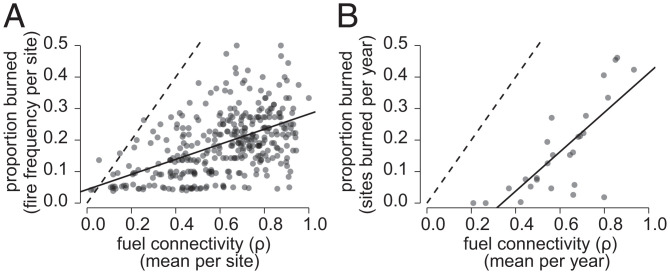
However, despite this nonlinearity, responses averaged in space or in time were more linear than the responses of individual fires to fuel connectivity. Across both models and data, spatial variation in fire frequency and temporal change in regional burned area increased linearly with fuel connectivity (Fig. 4 and SI Appendix, Fig. S5 B and C). These linearities, induced by averaging both in space and in time, suggest that widely observed linear responses of burned area and fire frequency to rainfall may also be the result of regional- to continental-scale averaging, rather than to linearity in the underlying relationship. This finding suggests that linear approximations of fire behavior may be appropriate in some contexts, for example under climate stablization scenarios or for medium-term forecasting, but that models that more completely capture nonlinear processes are likely to yield better projections of fire behavior, both on short time scales and, when climate is changing, on longer ones.

Fig. 4.

Response of site fire frequency (proportion burned) to average site fuel connectivity (ρ) across Kruger (A) and of park-wide burned area (proportion burned) to parkwide average fuel connectivity (ρ) across years (B). Fire frequency increases with average fuel connectivity of a site (slope = 0.24, intercept = 0.05, adjusted R² = 0.25, P < 0.0001) and annual park burned area increases with the fuel connectivity of the park in any given year (slope = 0.62, intercept = 0.20, adjusted R² = 0.59, P < 0.0001). All dotted lines show the relationship y = x, which represents the maximum possible burned area given the fuel connectivity of a landscape.

However, we also note that the definition of “short” vs. “long” time scales is likely to differ between grassy and nongrassy systems, since the times for fuel accumulation and drying differ. In grassy ecosystems, biomass accumulates quickly and burns frequently. As such, assuming a linear relationship between proportion burned and fuel connectivity may be sufficient to capture fire dynamics over just a few years of interest. Alternatively, in nongrassy ecosystems, like boreal forests or Mediterranean-type shrublands, where fuel accumulates more slowly and burns less frequently, far fewer burns are likely to occur over the same time period, such that averaging or linearizing the response of proportion burned to fuel connectivity is far less appropriate and may result in unreliable predictions (46). Consequently, we hypothesize that the nonlinearities in fire spread demonstrated in this study are as important, if not more important, to account for in nongrassy ecosystems as in grassy ecosystems. Direct observation of nongrassy systems is clearly required, especially to establish the correspondence between fuel connectivity and fuel biomass and between infection probability and fuel moisture and fire weather in these systems where the fuel bed may be more structurally complex. Long-distance infection (also known as ignition via “firebrands” or “spotting”) is also more prominent with woody fuels, which may change both theoretical predictions (20) and the relative importance of, e.g., wind speed (47).

Conclusion

In our study we demonstrate, using field data, that the nonlinear threshold dynamics of fire spread in grassy ecosystem are well captured by a process-based infection model (Figs. 1–3). Our parameterization of the fire-spread threshold using commonly measured and predictable fuel and weather variables now allows managers to plan their burns around conditions that allow intense daytime fires that safely extinguish themselves at night (see discussion of “open-ended firebreaks” in, e.g., ref. 48). This capacity is especially advantageous in areas where resources to construct firebreaks or supervise safe burns may be scarce but where regular burning is required to maintain ecosystem function and prevent excessive fuel accumulation. Additionally, given that our model is parameterized with commonly measured fuel and weather variables, we believe it can be widely applied by managers of grassy ecosystems to predict which parts of their managed landscapes are most vulnerable to climate change–induced extreme shifts in fire regimes. In doing so, we increase information flow to managers, and thus increase the feasibility of climate change adaptation, specifically in African systems (49).

In addition to the above, our findings imply that when an ecosystem crosses a threshold in either fuel connectivity or infection probability we would expect it to switch suddenly from a flammable to a nonflammable state, or vice versa. As climate change alters both the fuel connectivity and infection probability of fire-prone ecosystems, these types of transitions may become increasingly likely, and in some systems have already been observed (50, 51). As we step further into a no-analog future, fire models will play an increasingly important role in increasing resilience and facilitating adaptation to changing fire regimes. Although our analysis highlights important issues with running processed-based fire models at global scales, it also suggests some promising avenues of further research toward achieving an intermediate-complexity global fire model (44). First, the proportion of a landscape that burns during a fire is determined by the grass biomass available to burn, the fuel moisture content at the time of burning, and the vapor pressure deficit during the burn. Once enough grass biomass is available to support fire spread, fuel moisture is the strongest determinant of proportion burned. Our field data show that the fuel “moisture of extinction” threshold commonly used in fire models for grassy ecosystems is set at a value four to five times less than what the field data suggest is appropriate. This discrepancy may result in an underestimate of burned area in grassy ecosystems, a known problem in global fire models (52), but should be relatively easy to adjust. Second, wind speed did not affect the proportion burned, at least within the range of conditions examined in this study. Most global fire models rely on wind speed data that are far less precise than was available in our study, and this is a key parameter used by these models to predict rate of spread and thus burned area. Our findings highlight the urgent need to improve global-scale wind speed products and suggest caution in relying on fire models whose predictions are sensitive to changes in wind speed. Finally, although reconciling the infection model’s nonlinear predictions with observed linear patterns in burned area at regional and continental scales is possible, it is not always appropriate. The linear relationships currently used in many fire models may give reasonable predictions on long time scales spanning environmentally static conditions, but nonlinearities may substantially change predictions on shorter timescales or under changing environmental conditions. Thresholds in fire spread are central to its landscape-scale behavior, and we should be accounting for them when modeling fire’s ecological and Earth system impacts at large spatial scales.

Materials and Methods

Our infection model, based on ref. 17, was a simple cellular automaton with 500 × 500 cells with no interaction on the diagonals (Von Neumann neighborhood) and nonperiodic boundary conditions. Cells within the grid were arranged randomly and could be either flammable or nonflammable, with the proportion flammable representing the fuel connectivity parameter (ρ). Ignitions occurred randomly within the grid and an ignition falling on a flammable cell caused it to become a burning cell at T₁. At T₂, a burning cell either spread fire to a neighboring flammable cell with an infection probability of λ or the burning cell was extinguished with a probability of (1 − λ). The burning cell thus became a burned cell (nonflammable) at T₂, while the flammable neighboring cell became a burning cell (with a probability of λ). Once all burning cells had become burned cells (at T_x), the fire was extinguished and the proportion burned was recorded. The model was run for 500 values of ρ and 100 values of λ (equally space intervals between 0 and 1 in both cases), with each combination of parameters simulated for 100 ignitions and the mean proportion burned by these ignitions recorded. These simulations produced 100 infection curves of proportion burned as a function of ρ, or one curve for each value of λ.

To evaluate the model, we used data from 1,131 individual fires in grassy savanna ecosystems across a precipitation gradient (SI Appendix, Fig. S1). The wettest grassy system was Lopé (31 fires, 1,442 mm MAP), followed by HiP (30 fires, 600 to 1,000 mm MAP). Drier grassy sites all fell within Kruger (1,004 fires) and included Pretoriuskop (PKP, 212 fires, 737 mm MAP), Skukuza (SKZ, 240 fires, 550 mm MAP), Satara (SAT, 347 fires, 54 4mm MAP), and Mopani (MOP, 205 fires, 496 mm MAP). One non-African grassy system, Cedar Creek (66 fires, 775 mm MAP), was also included. See SI Appendix, Extended Methods for details on fire datasets. There were some unavoidable small differences in data collection across sites, and to avoid this confounding our results we have avoided doing any direct comparisons of parameters between sites.

For 188 fires (31 in Lopé, 30 in HiP, 61 Kruger, and 66 in Cedar Creek), ρ and proportion burned were measured directly by evaluating grass biomass and burn scarring (SI Appendix, Extended Methods). For the remaining fires, ρ was estimated from mean grass biomass using a Gompertz model [within the package easynls (53)] (adjusted R² = 0.98, P < 0.0001, n = 57) (54) (SI Appendix, Fig. S2), and proportion burned was estimated visually by consensus of two to five experts who drove or walked around the fire scar immediately after the burn. For all Kruger and Lopé fires, mean rate of spread of the fire front (meters per second), fuel moisture (percent of dry mass), vapor pressure deficit (a composite metric of air temperature and humidity, pascals), and wind speed (meters per second) during burning were measured (SI Appendix, Extended Methods).

To determine λ for a group of fires, we identified the simulated infection curve (described above) that best fitted the observed data by calculating a “distance index.” For each fire in the group, we calculated the minimum XY distance $[XY \mathit{distance}=\sqrt{{(\mathit{observed} X-\mathit{predicted} X)}^2+{(\mathit{observed} Y-\mathit{predicted} Y)}^2})]$ to each of the 100 simulated infection curves. We then determined the mean “distance index” for the group of fires, which was the mean of the minimum XY distances. We took the mean, and not the median, because we wanted our index to be sensitive to extreme deviations from the curve. The simulated infection curve that had the lowest distance index for the group of fires was considered to be the λ that best fit the data. The distance index of this fit was then compared to the same distance index of a linear and other nonlinear [quadratic, two linear, exponential, logistic, van Bertalanffy, and Gompertz; fitted with the package easynls (53)] fits. The model with the lowest overall distance index was considered the best fit to the observed data.

To estimate a λ for each of the 1,004 Kruger fires, we assumed that fires that burned under similar fuel moisture and fire weather conditions would have a similar λ. We thus binned fires according to their fuel moisture (0 to 32%, 32 to 64%, 64 to 96%, 96 to 128%, >128%), vapor pressure deficit (0 to 850 Pa, 850 to 1,700 Pa, 1,700 to 2,550 Pa, 2,550 to 3,400 Pa, >3,400 Pa), and wind speed (0 to 0.88 m/s, 0.88 to 1.76 m/s, 1.76 to 2.64 m/s, 2.64 to 3.52 m/s, >3.52 m/s). The size of the bins was the upper 98th percentile of the data divided into five equally sized bins. The resulting 125 groups of fires were all assigned a λ using the distance index fitting process described above, and groups with fewer than three fires were excluded. Each fitted λ was then associated with a mean rate of spread, fuel moisture, vapor pressure deficit, and wind speed, and each fire was associated with a fitted λ.

To evaluate fire spread occurring at the threshold values of ρ and λ we examined “threshold fires.” True threshold fires, occurring exactly at the threshold for fire spread, are, by definition, extremely rare. Therefore, we defined “threshold fires” to be those where proportion burned was above 0.2 (exceeding the minimum threshold for fire spread) and below 0.6 (not yet asymptoting at the maximum possible 1:1 line). The 0.2 cutoff was used because most of the experimental fires were burned in perimeter ignitions. A value of 0.2 ensured that fires that did not spread successfully but had some burning at the ignition locations were excluded from the threshold fires group. Using this group of threshold fires, we binned fitted λ into 0.05-wide bins and calculated the mean ρ and λ for each bin. These values were compared to model predicted estimates (Fig. 2).

To parameterize λ, we used data from the 1,004 Kruger fires. We modeled λ as a linear function of rate of spread. Then, we used generalized additive models (GAMs) [function gam in the package mgcv (55)] to model both λ and rate of spread as a function of mean fuel moisture, vapor pressure deficit, and wind speed during the burn. All smooths used “ts” thin plate splines (56), a smoothing parameter of 0.6, and the minimum number of knots that allowed the k-index to be nonsignificant (k′ < 1, P < 0.05) (57) (SI Appendix, Table S1). Although grass biomass may affect λ, since it had already been used to infer ρ for most fires it was not included as an independent variable. Similarly, fire intensity was also calculated using grass biomass and was not included as an independent variable. From the GAMs, we found 1) that wind speed was not a significant predictor of either λ or mean rate of spread of the fire front and 2) that the curves fitted by the GAM were not obviously nonlinear, but rather appeared log-linear (SI Appendix, Fig. S6). Therefore, we fitted linear models to the data, excluding wind speed as a predictor, and log-transforming fuel moisture and vapor pressure deficit. These linear models had lower Akaike information criterion values than the GAM models, and therefore these fits are presented in the main text.

To assess whether the predictions of our percolation model can be reconciled with observed linear trends between rainfall or grass biomass and burned area, we used long-term data on 533 sites in Kruger (SI Appendix, Extended Methods). Each site had grass biomass measured nearly every year since 1989. From this a ρ for each site for each year could be inferred. Whether or not a site burned in a year was inferred from park records of fire scars. The proportion of sites burned in a year and the fire frequency of sites across years were examined as a function of ρ, and these relationships were fitted using a linear model. The observed proportions of sites burned in a year and the fire frequencies of sites across years was also compared to model predictions using a linear model (assuming λ = 1 since Kruger fires mostly occur in the hot, dry season).

Data Availability

Ecological fire data have been deposited in Dryad (58).