Automated Eloquent Cortex Localization in Brain Tumor Patients Using Multi-task Graph Neural Networks

Abstract

Localizing the eloquent cortex is a crucial part of presurgical planning. While invasive mapping is the gold standard, there is increasing interest in using noninvasive fMRI to shorten and improve the process. However, many surgical patients cannot adequately perform task-based fMRI protocols. Resting-state fMRI has emerged as an alternative modality, but automated eloquent cortex localization remains an open challenge. In this paper, we develop a novel deep learning architecture to simultaneously identify language and primary motor cortex from rs-fMRI connectivity. Our approach uses the representational power of convolutional neural networks alongside the generalization power of multi-task learning to find a shared representation between the eloquent subnetworks. We validate our method on data from the publicly available Human Connectome Project and on a brain tumor dataset acquired at the Johns Hopkins Hospital. We compare our method against feature-based machine learning approaches and a fully-connected deep learning model that does not account for the shared network organization of the data. Our model achieves significantly better performance than competing baselines. We also assess the generalizability and robustness of our method. Our results clearly demonstrate the advantages of our graph convolution architecture combined with multi-task learning and highlight the promise of using rs-fMRI as a presurgical mapping tool.

1. Introduction

The eloquent cortex includes regions of the brain that are responsible for various cognitive and sensory processes, such as speech generation, language comprehension, and movement (Ojemann and Whitaker [1978], Tzourio-Mazoyer et al. [2004]). Identifying and subsequently avoiding these areas during a neurosurgey is crucial for recovery and postoperative quality of life. Namely, an incision in the eloquent cortex can cause permanent physical and cognitive damage (Berger et al. [1989], Fadul et al. [1988], Sawaya et al. [1998]).

Localizing the eloquent cortex can be challenging due to the variability of its anatomical boundaries across patients (Ojemann and Whitaker [1978], Tomasi and Volkow [2012]). More specifically, the language network has especially high interindividual variability (Tzourio-Mazoyer et al. [2004]). Mapping the eloquent cortex in brain tumor patients is even more difficult, as the functionality near the boundaries of slow growing tumors is often displaced, an effect known as neural plasticity (Duffau [2005], Thiel et al. [2001]). In higher grade tumors, there is a phenomenon of neurovascular uncoupling that can confound the identification of functionally intact tissue. It has also been shown that the tumor disrupts the local vascularture proximal and contralateral to the tumor site (Gabriel et al. [2014], Partovi et al. [2012], Zhang et al. [2016]), which also affects functional connectivity. Thus, eloquent cortex mapping remains an important and unsolved challenge in clinical practice (Berger et al. [1989], Duffau et al. [2003]).

The gold standard for mapping the eloquent cortex is invasive electrocortical stimulation (ECS) performed during surgery (Berger et al. [1989], Duffau et al. [2003], Gupta et al. [2007]). While ECS is highly specific, it imposes a significant burden on patients, who must remain awake and functioning during the procedure. Complications due to ECS arise for obese patients, patients with severe dysphasia, patients with severe respiratory complications, and patients with psychiatric history or emotional instability (Yang and Prashant [2019]). Furthermore, ECS is unavailable at the presurgical planning stage and is usually not available within the depth of the sulci, which puts more demands on the neurosurgeon and can increase surgical times (Kekhia et al. [2011], Rosazza et al. [2014]). As a result, noninvasive task-fMRI (t-fMRI) has been increasingly popular for preoperative brain mapping Bizzi et al. [2008], Giussani et al. [2010], Petrella et al. [2006], Sabsevitz et al. [2003], Tomczak et al. [2000]). Namely, high activations in response to a language or motor paradigm are considered biomarkers of the respective eloquent areas (Berger et al. [1989], Gabriel et al. [2014], Sair et al. [2016]). While task-fMRI is the most popular noninvasive mapping modality Binder et al. [1996], Suarez et al. [2009], the activations can be unreliable for certain populations, like children, the cognitively impaired, or aphasic patients, due to an inability to follow the task protocol, or excessive head motion (Kokkonen et al. [2009], Lee et al. [2016]).

Resting-state fMRI (rs-fMRI) captures spontaneous fluctuations in the brain at steady state (Biswal et al. [1995], Fox and Raichle [2007], Shimony et al. [2009]). While t-fMRI paradigms must be carefully designed to target a specific cognitive process, rs-fMRI provides a snapshot of the whole-brain, which can be used to isolate multiple functional systems (Lee et al. [2013], Smitha et al. [2017], Venkataraman et al. [2012]). Equally important, rs-fMRI is a passive modality and does not require the patient to perform a potentially challenging task for accurate localization. As a result, there is increasing interest in using rs-fMRI for presurgical mapping to circumvent the issues of t-fMRI (Ghinda et al. [2018], Lee et al. [2016], Leuthardt et al. [2018]).

Prior work includes a variety of statistical and machine learning approaches to localize the eloquent cortex using fMRI data. Starting with t-fMRI, the general linear model (GLM) is used to identify voxels with significant activation (Sair et al. [2016], Tomczak et al. [2000]). However, this method must be done on a per-patient basis and requires manual intervention to set the correct activation threshold. A more unified approach is presented in (Langs et al. [2010, 2014]). Here, the authors address the problem of varying anatomical boundaries through a functional embedding of the t-fMRI data based on diffusion maps and a subsequent Gaussian mixture model fit to the signal. This method was validated on a language t-fMRI paradigm in 7 tumor patients. While promising, this method has not yet been applied to rs-fMRI data.

Within the rs-fMRI domain, the simplest methods use seed-based correlation analysis to delineate subnetworks of the eloquent cortex. For example, the work of Wongsripuemtet et al. [2018] uses lateralized anatomical seeds to localize bilateral activations on the supplementary motor area in tumor patients. Going one step further, the methods proposed in Sair et al. [2016] and Tie et al. [2014] rely on group ICA to extract functional networks from the rs-fMRI data. However, these methods require an expert to either manually select the seed or choose the language components and threshold the ICA maps as a final post-processing step. Hence, they may not be practical in a prospective clinical setting.

Deep learning (DL) methods have been increasingly popular in the neuroimaging field, and consequently, have shown promise in automatically identifying the eloquent cortex from rs-fMRI in both healthy subjects and tumor patients. For example, the work of Hacker et al. [2013] uses a multi-layer perceptron to classify seed-based correlation maps into one of seven resting-state networks. This method first uses PCA for dimensionality reduction followed by a two hidden layer artifical neural network for classification. Trained with t-fMRI labels, the model is extended in Lee et al. [2016] to perform eloquent cortex localization in three separate tumor cases. While the results are promising, once again, the user must select an a priori seed for each network, which can affect performance. Additionally, it is trained on healthy subjects and may not accommodate changes in the brain organization due to the lesion. Finally, the large-scale study in Leuthardt et al. [2018] uses the same neural network architecture to identify eloquent subnetworks in 191 rs-fMRI and 83 t-fMRI scans of tumor patients. However, a success refers to whether the model identified any clinically relevant to-pographies within the scan. The study does not quantify the accuracy at the voxel or ROI level, which is the metric of interest during presurgical mapping.

1.1. Contributions

In contrast to prior work, we draw from the multitask learning (MTL) literature (Ruder [2017], Soltau et al. [2014], Xue et al. [2007], Zhang and Zhang [2014]) to simultaneously classify motor and language networks using a shared deep representation (Martino et al. [2011], Overvliet et al. [2011], Pool et al. [2015]). The goal of MTL is to improve the generalizability of a model by training it to perform multiple tasks at the same time (Caruana [1997]). Our architecture uses convolutional filters that act on rows and columns of the functional connectivity matrix (Kawahara et al. [2017]). The resulting graph neural network (GNN) mines the topological properties of the data in order to classify the eloquent brain regions. In addition, our training strategy can easily accommodate missing patient data in a way that optimizes the available information. This setup is highly advantageous, as the fMRI paradigms administered to each patient may vary depending on their case.

We validate our method using an in-house dataset collected at the Johns Hopkins Hospital (JHH) as well as publicly available data from the Human Connectome Project (HCP), in which we simulate tumors in the healthy brain and include performance on the healthy HCP data in the supplementary material. We demonstrate that our MTL-GNN achieves higher eloquent cortex detection than popular machine learning baselines. We further show that our model can recover clinically challenging bilateral language cases when trained on unilateral language cases. Using an ablation study, we assess the value of the multi-task portion of our network. Finally, we asssess robustness of our method by varying the functional parcellation used for analysis, jittering the tumor segmentations, quantifying the effects of data augmentation, and performing a hyperparameter sweep. Taken together, our results highlight the promise in using rs-fMRI as part of presurgical planning procedures.

2. Methods

2.1. Material

2.1.1. JHH tumor dataset

Our tumor cohort consists of 62 patients who underwent presurgical fMRI at the Johns Hopkins Hospital (JHH). The data was obtained using a 3.0 T Siemens Trio Tim system. Structural images were acquired via an MPRAGE sequence (TR = 2300 ms, TI = 900 ms, TE = 3.5 ms, flip angle = 9°, FOV = 24 cm, acquisition matrix = 256 × 256 × 176, slice thickness = 1 mm). Functional BOLD images were acquired using 2D gradient echo-planar imaging (TR = 2000 ms, TE = 30 ms, flip angle = 9°, FOV = 24 cm, acquisition matrix = 64 × 64 × 33, slice thickness = 4 mm, slice gap = 1 mm, interleaved acquisition). A more detailed description of the participants, the task paradigms, and acquisition protocol can be found in Sair et al. [2016].

The structural MRI was used for manual tumor segmentation via the MIPAV package (McAuliffe et al. [2001]). The segmentations were performed by a medical fellow and confirmed with an expert neuroradiologist. Fig. 1 illustrates structural the T1 MRI of four patients to motivate the heterogeniety in tumor size and location.

Figure 1:

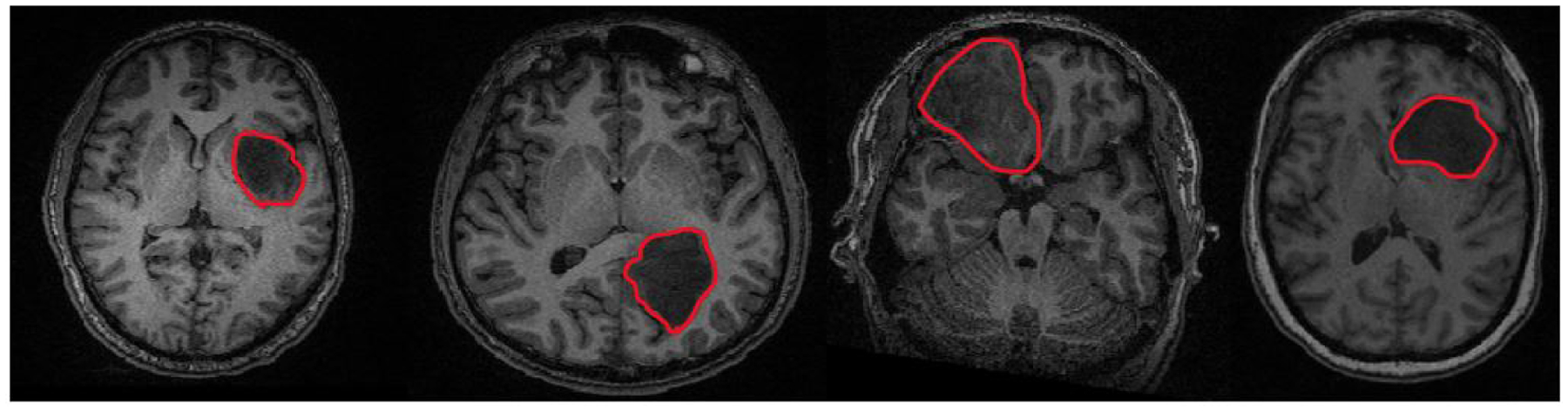
From (L-R), T1 scans of four separate brain tumor patients. Tumor size and location (outlined in red for clarity) vary throughout the JHH cohort.

T-fMRI data was acquired for all patients as part of the presurgical workup. In this work, t-fMRI is used to derive “pseudo-ground truth” eloquent class labels using the General Linear Model (GLM) implemented in SPM-8 (Penny et al. [2011]). The resulting activation maps were manually thresholded on a patient-specific basis and confirmed by an expert neuroradiologist. The t-fMRI is only used during the training phase of the model. Only resting-state fMRI information is included in the forward pass of the testing phase.

Three motor task paradigms (finger tapping, tongue moving, foot tapping) were used to target specific locations of the motor homonculus (Jack Jr et al. [1994]). Fig. 2 (L) shows the various sub-networks of interest for a single patient. Likewise, two language paradigms, sentence completion (SC) and silent word generation (SWG), were performed. These language tasks are designed to target both primary and secondary regions in the brain responsible for language generation (Benjamin et al. [2018], Pillai and Zaca [2011]). For each patient, instructions and practice sessions were provided. During acquisition, real-time fMRI maps for each task were monitored by the neuroradiologist to assess for global data quality; any task performance deemed suboptimal due to motion-related or other artifact was repeated. Since the t-fMRI was acquired as part of routine clinical care, not all patients performed each task. Finally, our cohort has 57 patients with left-hemisphere language networks and 5 patients with bilateral language networks. Fig. 2 (R) illustrates the high anatomical variabilitiy in language regions, especially due to tumor presence.

Figure 2:

L: The tongue, finger, and foot sub-networks for one patient. R: The language network for three separate patients. The language network boundaries are very variable from patient to patient.

Rs-fMRI was acquired while subjects were awake but passive in the scanner. The rs-fMRI data was preprocessed using SPM-8. The steps include slice timing correction, motion correction and registration to the MNI-152 template. The data was linearly detrended and physiological nuisance regression was performed using the CompCorr method (Behzadi et al. [2007]). The data was bandpass filtered from 0.01 to 0.1 Hz, and spatially smoothed with a 6 mm FWHM Gaussian kernel. Finally, images found to exceed the default noise threshold by the ArtRepair toolbox (Mazaika et al. [2009]) were removed (scrubbed) from the rs-fMRI volumes. As a common practice, we apply a functional parcellation (Craddock et al. [2012]) to the rs-fMRI data to increase the signal-to-noise (SNR) of our analysis and also reduce the input dimension to our model. In this work, we rely on the Craddocks atlas (Craddock et al. [2012]) with removed cerebellar regions (N = 384). The atlas was derived using spectral clustering on healthy rs-fMRI and is widely cited in the literature (Allen et al. [2014], Finn et al. [2015], Thirion et al. [2014]). We chose this parcellation because it provides an appropriate spatial resolution to map both the language network and the primary motor sub-networks (finger, foot, tongue). A region was determined belonging to the eloquent class if at least 80% of its voxel membership coincided with that of the thresholded GLM activation maps. Tumor regions were determined in a similar fashion based on the manual tumor segmentations. Due to varying tumor size and location, the distribution of our labels is variable, as 139 unique parcels are mapped to language by t-fMRI in at least one patient, 90 are mapped to finger, 84 are mapped to tongue, and 52 are mapped to foot. Confounders such as tumor size and handedness are intrinsically tied within the model, as handedness relates to laterality of language (e.g., we have 57 unilateral and 5 bilateral language subjects), and the tumor is explicitly modelled within our similarity graph. Table 1 presents information for the JHH cohort, where we report the number of patients that performed each task, the tumor grade and size, and demographics.

Table 1.

Patient, tumor and t-fMRI information for the JHH cohort.

Age			38±6.3
Sex (M,F)			37, 25
Tumor location (lobe)		Hemisphere
Frontal	21	Left	35
Parietal	18	Right	20
Temporal	17	Both	7
Occipital	6
Volume (×1000)mm3		WHO grade
<35	21	1	14
35–70	28	2	27
70–100	8	3	13
>100	5	4	8
Task protocol	Number of patients
Language	62
Finger	38
Tongue	41
Foot	18

2.1.2. Human Connectome Project Dataset

We conduct a proof-of-concept simulation study by applying our method to 100 subjects drawn from the Human Connectome Project (HCP1) dataset (Van Essen et al. [2013]), in which we simulate “fake tumors”. We limit the analysis to 100 subjects, so that the dataset is of comparable size to our JHH cohort. Details on the acquisition paramters, sequencing, and preprocessing for both rs-fMRI and t-fMRI can be found in (Van Essen et al. [2013]).

The language task for HCP was developed in (Binder et al. [2011]) to map the anterior temporal lobe for presurgical planning. The task consisted of alternating between story comprehension and performing basic arithmetic operations (addition, subtraction etc.). In both blocks, the participants received questions in the form of text-to-speech, to activate their language processing networks. For the motor task, participants were instructed to tap their left or right fingers, squeeze their left or right toes, or move their tongue to map motor areas (block design Buckner et al. [2011]). We used the FEAT software from FSL (Jenkinson et al. [2012]) to obtain GLM activation maps of the HCP t-fMRI.

The “fake tumors” overlayed onto the HCP1 connectomes are randomly created, and ensured to be spatially continuous, akin to a real tumor. We include this augmented dataset to simulate various issues the tumor introduces to our classification task and ultimately show robustness of our method. Our motivation for including the HCP simulation study is to evaluate our MT-GNN performance on real-world data with similar characteristics (i.e., resting-state functional connectivity inputs and labels derived from t-fMRI). Though we cannot model neural reorganization due to the tumor, our HCP simulation study provides a baseline of how removing functionality from these regions affects the overall performance. For the interested reader, we include the performance on the healthy HCP1 data without contamination in the supplementary material.

Finally, we have downloaded a second dataset of HCP subjects (HCP2) to use solely for hyperparameter tuning of our model and baseline approaches. Once tuned, these hyperparameters are fixed for all experiments. This second HCP dataset ensures that there is no bias from our hyperparameter selection that enters the training and testing procedures for the JHH and HCP1 datasets.

2.2. Multi-task GNN

Our chief modeling assumptions is that while the anatomical boundaries of the eloquent cortex may shift from patient to patient, the resting-state functional signatures of the language and motor network remain consistent (Langs et al. [2010, 2014], Nandakumar et al. [2019]). We construct a novel multi-task learning graph neural network (MT-GNN) to capture these patterns. A single-task version of our model appeared in Nandakumar et al. [2019]. In this paper we extend our preliminary work to simultaneously map different functional systems and handle missing training data, which is typical in clinical practice. Our MT-GNN is validated on multiple datasets compared with the single-task GNN. We also evaluate robustness and generalization.

Our MT-GNN architecture can simultaneously learn different areas of the eloquent cortex (language, finger, tongue, foot) by leveraging all available data and the shared representation for whole-brain rs-fMRI connectivity. Our architecture uses specialized convolutional filters, developed in (Kawahara et al. [2017]), that are designed to operate on similarity matrices. These filters aggregate information across a hub-like row-column intersection, rather than across the local spatial field of a standard convolution. As compared to (Kawahara et al. [2017]), our model includes three innovations. First, we treat the tumor as “missing data” to avoid biasing the eloquent cortex identification. Second, instead of collapsing the information into a single patient-wise prediction, we preserve the region-wise information. Finally, we use MT learning to simultaneously obtain eloquent cortex segmentations for multiple functional systems. Fig. 3 shows our pipeline from the unprocessed rs-fMRI scans to our input similarity matrix. Tumor regions are delineated and effectively ignored in our similarity matrix computation. Fig. 4 illustrates our MT-GNN pipeline. As seen, the input to our model is a rs-fMRI similarity matrix, and the output of each branch is a region-wise segmentation into eloquent, tumor, or background gray matter.

Figure 3:

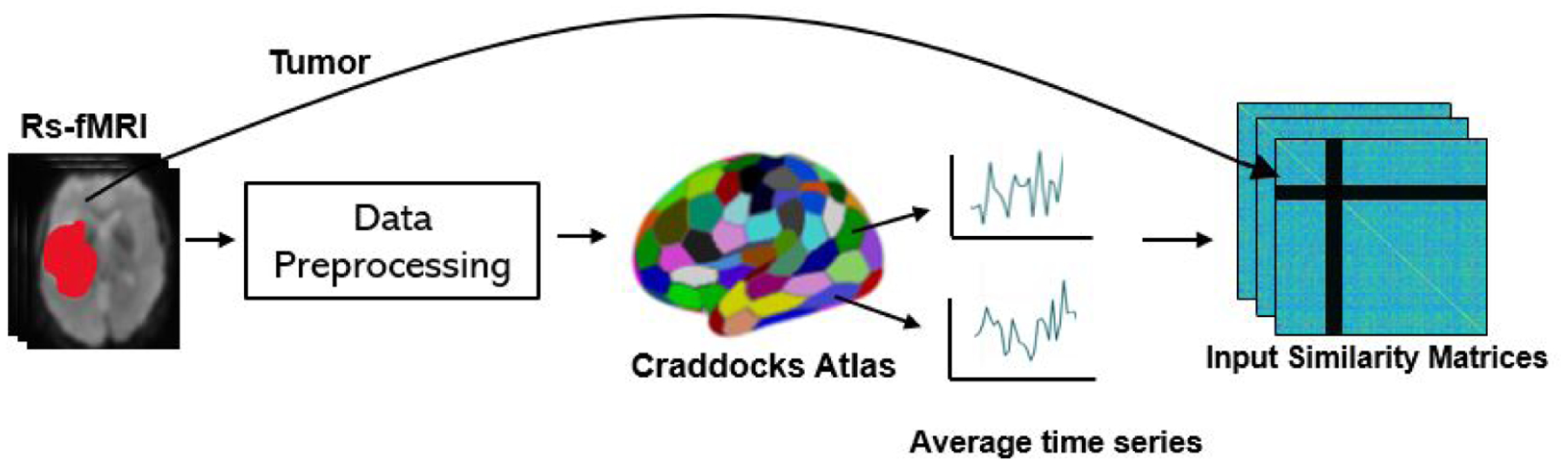
The data workflow of our model. The rs-fMRI data is preprocessed and then the Craddocks functional atlas is applied. The tumor boundaries are delineated and introduced as rows and columns of zeros in the input similarity matrix.

Figure 4:

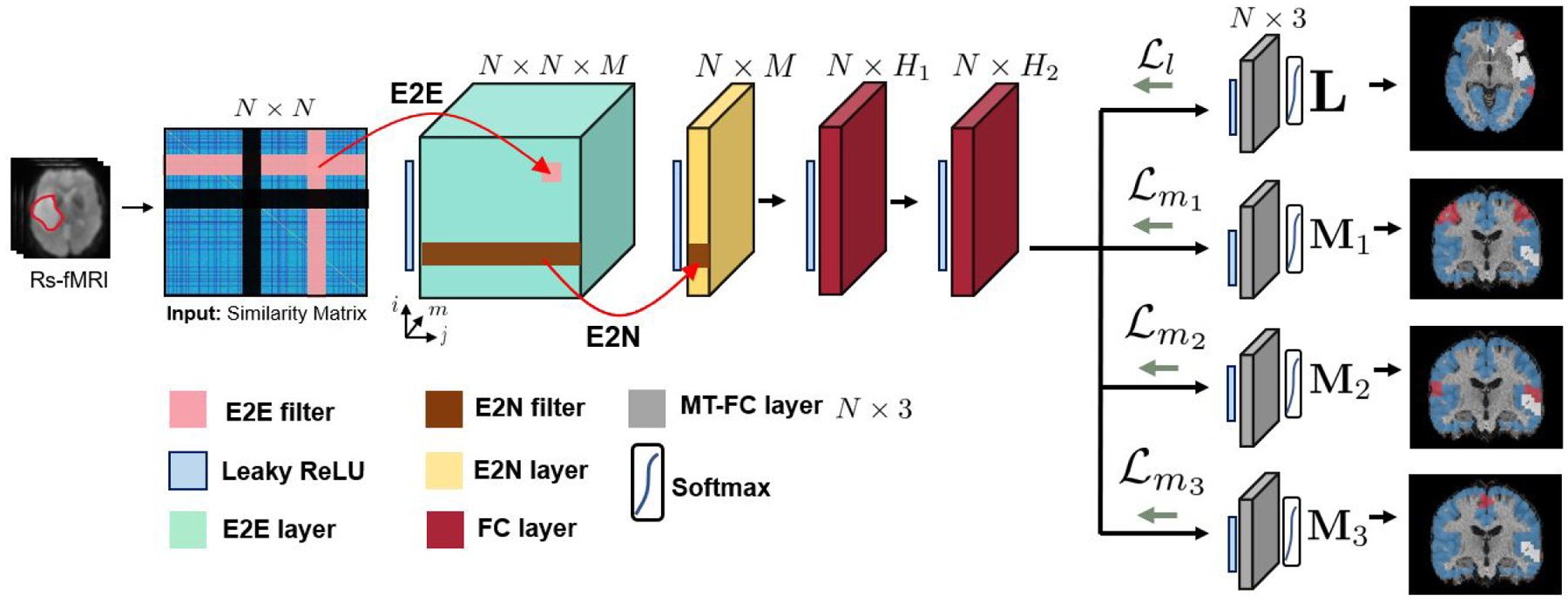
The overall workflow of our model. N is number of nodes, M is number of convolutional feature maps, H₁ is number of neurons in the first FC layer and H₂ is the number of neurons in the second FC layer. Our model uses specialized E2E and E2N filters as well as employs multi-task learning on a variety of available t-fMRI paradigms. Each grey module represents a separate 3-class segmentation task. The variables L, M₁, M₂ and M₃ represent the language, finger, tongue, and foot networks respectively, as shown by the segmentation maps where red, blue, and white refer to the eloquent, neither, and tumor classes respectively.

2.2.1. Graph construction

Our method treats the rs-fMRI connectivity as a weighted similarity graph, drawing inspiration from the graph theoretic literature (Langs et al. [2010, 2014]). Let N be the number of brain regions in our parcellation and T be the number of time points for a rs-fMRI scan. We define $x_i\in {ℝ}^{T\times 1}$ as the average time series extracted from region i. We normalize each time series to have zero mean unit variance. The input similarity matrix $W\in {ℝ}^{N\times N}$ is given by W = exp [X^TX − l]. The tumor regions disrupt connectivity, and therefore are treated differently in our model formulation (Duffau [2005], Gabriel et al. [2014], Nandakumar et al. [2018, 2019]). In this work, we opt to set all edges associated with tumor nodes to zero while maintaining the value of 1 on the diagonal. We also create a separate “tumor” class at the MT-GNN output, which allows the network to learn the patterns of zero values, so that it does not bias the eloquent cortex localization.

Our framework assumes that tumor boundaries have been predetermined (i.e. segmented) on the voxel level. While we rely on manual segmentations in this paper, our approach is agnostic to the segmentation method and can easily be applied to automated techniques (Havaei et al. [2017], Işın et al. [2016], Zhao et al. [2018]). Our similarity graph construction asserts that W_i,j > 0 for all non-tumor regions. Therefore, even two healthy regions with a strong negative correlation will still be more functionally similar than tumor regions in our model. Our network achieves near perfect (≈ 0.99) accuracy for the tumor class due to this setup, as expected due to the zeroing out of tumor regions.

2.2.2. Pre-MT network architecture

Our MT-GNN architecture employs both convolutional and fully-connected (FC) layers to extract features from the connectivity matrix. While a traditional convolutional assumes a grid-like field of view, our MT-GNN convolutions span full rows and columns of the graph, so they capture local neighborhood connectivity information associated with node pairs (edges). The two convolutional layers of our MT-GNN are from egde-to-edge (E2E) and egde-to-node (E2N) filters, which are taken from (Kawahara et al. [2017]). For completeness of describing our network architecture, we present the relevant equations from (Kawahara et al. [2017]) below.

Mathematically, an E2E filter is composed one row filter, one column filter, and a learned bias, which totals 2N + 1 parameters. Let m ∈ {1, ⋯, M} be the E2E filter index, $r^m\in {ℝ}^{1\times N}$ be the m-th row filter, $c^m\in {ℝ}^{N\times 1}$ be the m-th column filter and $b_m\in {ℝ}^{1\times 1}$ be the E2E bias for filter m. The feature map $A^m\in {ℝ}^{N\times N}$ output from E2E filter m is computed as

$$A_{i,j}^m=\varphi \left(\sum _{n=1}^N{r}_n^m{W}_{i,n}+c_n^m{W}_{n,j}+b_m\right),$$ (1)

where ϕ is the activation function. An E2E filter (pink in Fig. 4) for node pair (i, j) computes a weighted sum of connectivity strengths over all edges connected to either region i or j. We use these filters to learn the predictive connectivity patterns between brain regions. Even with symmetric input W, the derived E2E features are not guarenteed symmetric. This asymmetry is desirable for language localization, as these systems tend to be lateralized in the brain Tzourio-Mazoyer et al. [2004], Sair et al. [2016], Nandakumar et al. [2019]. At the E2E layer (green in Fig. 4), we have multiple different views along the M dimension of the edge-to-egde similarities within our connectome data. The E2N layer condenses our representation from size N × N × M after the E2E layer to N × M, yielding M features for each node. To obtain region-wise representations, our E2N filter performs a 1D convolution along the columns of each feature map, as the authors in Kawahara et al. [2017] did not see improvement in applying the convolution to either the columns or rows of each feature map. Furthermore, using a single orientation allows us to reduce the number of parameters in the network, which is critical given our small datasets (N < 100). Mathematically, let $g^m\in {ℝ}^{1\times N}$ be the m-th E2N filter and $d_m\in {ℝ}^{1\times 1}$ be the E2N bias for filter m. The E2N output $a^m\in {ℝ}^{N\times 1}$ from input A^m is computed as

$$a_i^m=\varphi \left(\sum _{n=1}^N{g}_n^m{A}_{i,n}^m+d_m\right).$$ (2)

The E2N filter computes a single value for each node i by taking a weighted combination of edges associated with it. The resulting E2N layer is shown in yellow.

Here, our modelling strategies depart from those in (Kawahara et al. [2017]), as our network operates on the node level, and does not condense the first dimension of the representation any further. We use two fully-connected layers with neurons H₁ and H₂ (shown in Fig. 4) to extract features before the multi-task (MT) portion. The network then branches off into the MT classifier, which effectively decouples the FC weights according to which functional system it is responsible for identifying. The grey blocks in Fig. 4 show the MT-FC layers, where we have four separate functional systems to identify. Each grey module performs a separate 3-class classification task, shown by the segmentation maps on the RHS of Fig.4. At a high level, the MT-FC layer leverages commonalities in the rs-fMRI connectivity patterns between the language and motor networks. This shared representation drastically reduces the number of parameters, relative to training the separate E2E and E2N layers in our preliminary work (Nandakumar et al. [2019]). Clinically, our model can be extended to an arbitrary number of tasks by adding more MT branches, thus providing a valuable tool for presurgical mapping. Our MT-GNN also constructs a shared representation for language and motor areas which may shed insight into brain organization.

2.2.3. Classification and loss functions

Each MT-FC layer has dimension N × 3 where N is the number of regions, and the three classes denote eloquent, tumor, and background gray matter, represented by the colors red, white, and blue respectively on the segmentation maps in Fig. 4. Recall that we treat the tumor as a separate learned class to remove any bias that zeroing out tumor edges might introduce into the model. We emphasize that the tumor detection accuracy is not the main goal or result of this work. Instead, our goal is to maximize the eloquent detection performance. We keep the tumor regions so the input connectivity matrix is of the same dimension for each patient. Removing the tumor regions would result in different size input matrices across patients, which our model is not designed to handle. Softmax is applied and each region is classified into one of the three classes with an argmax operator. One obstacle in our datasets is the limited number of eloquent class training samples, since the language and individual motor areas are small (see Fig. 2). For the JHH cohort, the average class membership is 4.7%, 10.1% and 85.2% for the eloquent, tumor, and background gray matter class respectively. Since the convolutional filters are designed to operate upon the whole-brain connectivity matrix, our class imbalance problem cannot be mitigated by traditional data augmentation techniques. Therefore, we train our model with a modified Risk-Sensitive Cross-Entropy (RSCE) loss function (Suresh et al. [2008]), which is designed to handle membership imbalance in multi-class setting. Let δ_i be the risk factor associated with class i. If δ_i is large, then we pay a larger penalty for misclassifying samples that belong to class i. Due to a training set imbalance, we select different penalty values for the language class ${\left\{{\delta }_i^l\right\}}_{i=1}^3$ and motor classes ${\left\{{\delta }_i^m\right\}}_{i=1}^3$ respectively.

Let L, M₁, M₂, and $M_3\in {ℝ}^{N\times 3}$ (Fig. 4) be the output of the language, finger, foot, and tongue MT-FC layers respectively. Each column of these matrices represents one of three classes: eloquent, tumor, and background. Let Y^l, $Y^{m_1}$, $Y^{m_1}$ and $Y^{m_3}\in {ℝ}^{N\times 3}$ be one-hot encoding matrices for the region-wise class labels of the language and motor subnetworks from t-fMRI. Our loss function is the sum of four terms:

$$\begin{gathered} {\mathcal{L}}_{\Theta }(W,Y)= \\ \underset{\text{Language Loss }{\mathcal{L}}_l}{\underbrace{-\sum _{i=1}^3{\delta }_i^l\text{log}{\left(L_i\right)}^T{Y}_i^l}}\underset{\text{Finger Loss }{\mathcal{L}}_{m_1}}{\underbrace{-\sum _{i=1}^3{\delta }_i^m\text{log}{\left(M_1^i\right)}^T{Y}_i^{m_1}}} \\ \underset{\text{Foot Loss }{\mathcal{L}}_{m_2}}{\underbrace{-\sum _{i=1}^3{\delta }_i^m\text{log}{\left(M_2^i\right)}^T{Y}_i^{m_2}}}\underset{\text{Tongue Loss }{\mathcal{L}}_{m_3}}{\underbrace{-\sum _{i=1}^3{\delta }_i^m\text{log}{\left(M_3^i\right)}^T{Y}_i^{m_3}}} \end{gathered}$$ (3)

The error from all four loss terms is backpropogated throughout the network during training, as illustrated by the green arrows in Fig. 4. Our framework allows for overlapping eloquent labels, as brain regions can be involved in multiple cognitive processes. To reiterate, our goal is to identify subnetworks of the eloquent cortex for presurgical planning. We take a supervised approach to this problem via multi-task classification. The model presented in this work focuses on localizing four eloquent subnetworks, as our in-house dataset contains task fMRI labels for three motor areas and one language area. We emphasize that our framework can be extended to any number of functional subsystems if the proper training labels exist. In this case, the user would simply add MT-FC layers and the corresponding cross-entropy term in the loss function. From a modeling standpoint, our edge-to-edge layer is designed to extract informative subnetworks from the rs-fMRI connectivity matrix to maximize downstream separation of the desire classes. Hence, the value of M (in this work between 8–16) is closely tied to the number of subnetworks extracted from the data.

2.2.4. Implementation details and hyperparameter selection

We used 10-fold cross validation (CV) on the HCP2 dataset to fix the hyperparameters for all experiments. In this manner, our evaluation on the HCP1 and JHH datasets do not include biased information from the hyperparameter selection. Fig. 5 shows the generalization gap between training and testing, which was used to determine epoch number. Overall, we observe stable training and validation curves, which gives us confidence in the optimization of our network. For the δ hyperparameters, we performed a coarse grid search from 0 – 10 in increments of of 10⁻¹ until we found a suitable range of performance. We then performed a finer grid search in increments of 10⁻² to obtain the final values shown in Table 2. We fixed the same δ values for the tumor and neither classes across branches.

Figure 5:

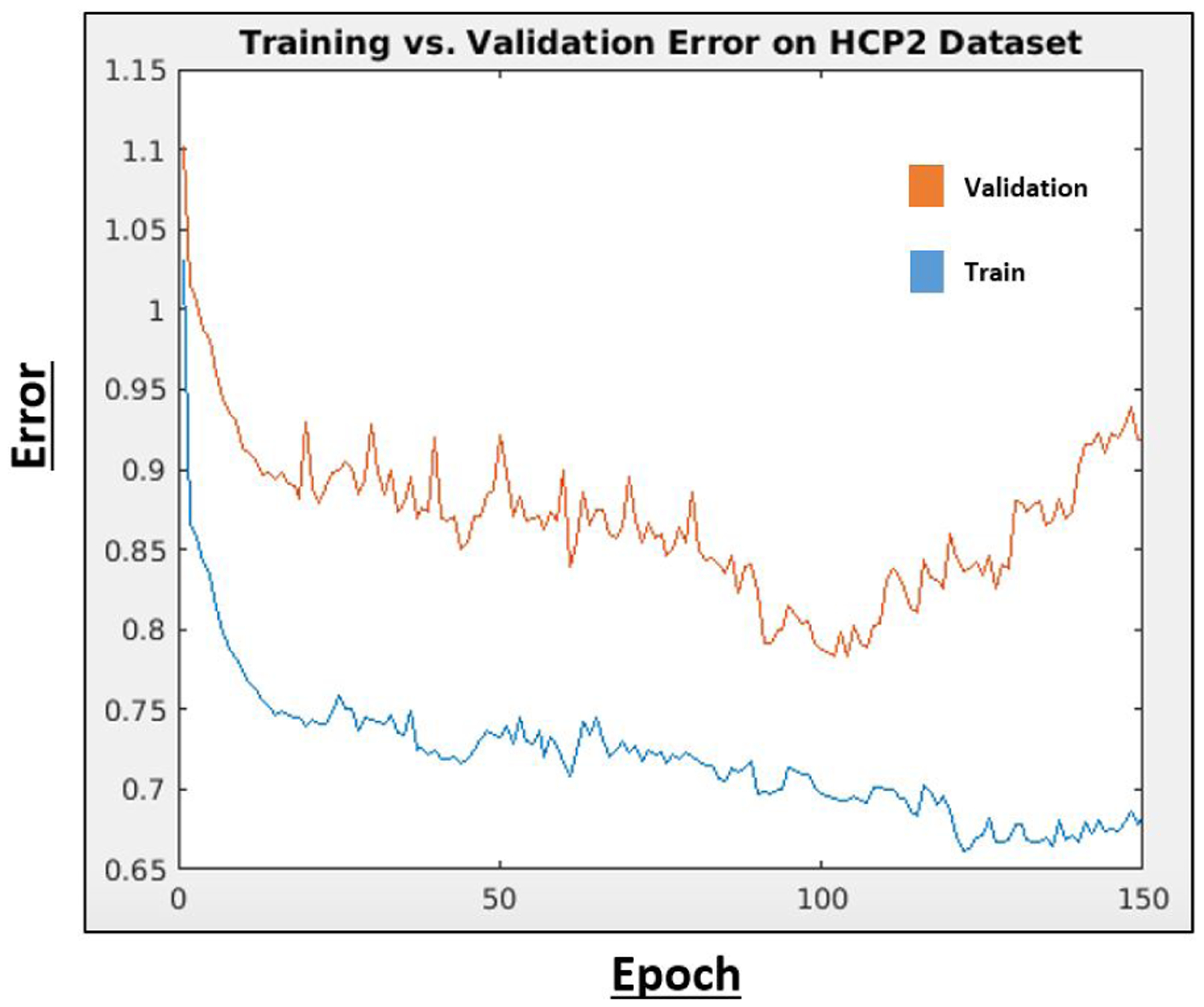
Training and validation error on HCP2 dtaset for early stopping.

Table 2.

Hyperparameters determined via CV on the separate HCP2 dataset. lr and wd refer to learning rate and weight decay

Parameter	value	Parameter	value
N	384	wd	5 × 10−5
M	8	Epochs	104
lr	0.005	δ m	(1.27, 0.46, 0.25)
H 1	64	δ l	(2.02, 0.46, 0.25
H 2	27

Due to the clinical protocol, most JHH patients have only undergone a subset of the three motor t-fMRI tasks. We handle this missing data during training by freezing the weights of the MT-FC layer in Fig. 4 that corresponds to the missing task when we backpropagate (García-Laencina et al. [2007], Zhang and Huan [2012]). Our strategy ensures that we mine the relevant information from the data present while preserving the fine-tuned layers of the branches that correspond to missing tasks. We train with batch size equal to one, to accommodate the missing tasks across patients. The number of subjects that performed each task is listed in Table 4. We implement our network in PyTorch (Paszke et al. [2017]) using the SGD optimizer. The LeakyReLU(x) = max(0, x)+0.33·min(0, x) activation function is applied at each hidden layer. A softmax activation is applied at the final layer for classification. With GPU available, the total training time of our model is 5 minutes.

Table 4.

Mean plus or minus standard deviation for eloquent class TPR, specificity, F1 and AUC for the JHH cohort, where the number of subjects who performed each task is shown in the first column. The final column shows the FDR corrected p-values for the associated t-scores where we compare AUC between our method against each baseline.

Task	Method	Eloquent TPR	Specificity	F1	AUC	t-score	p-value
Language	MTGNN	0.75 ± 0.011	0.72 ± 0.01	0.74 ± 0.013	0.76 ± 0.013
(N = 62)	FCNN	0.68 ± 0.014	0.63 ± 0.016	0.67 ± 0.013	0.70 ± 0.015	11.56	3.8 × 10−30
	RF	0.49 ± 0.034	0.65 ± 0.027	0.59 ± 0.029	0.61 ± 0.035	12.11	5.7 × 10−33
	SVM	0.46 ± 0.017	0.55 ± 0.019	0.45 ± 0.02	0.52 ± 0.012	50.76	≈ 0
Finger	MTGNN	0.85 ± 0.014	0.83 ± 0.016	0.82 ± 0.013	0.83 ± 0.015
(N = 38)	FCNN	0.77 ± 0.019	0.65 ± 0.016	0.73 ± 0.019	0.75 ± 0.017	8.36	2.7 × 10−16
	RF	0.48 ± 0.039	0.66 ± 0.028	0.57 ± 0.034	0.60 ± 0.029	24.22	1.7 × 10−128
	SVM	0.55 ± 0.02	0.54 ± 0.021	0.53 ± 0.015	0.54 ± 0.014	43.48	≈ 0
Foot	MTGNN	0.81 ± 0.023	0.81 ± 0.021	0.79 ± 0.019	0.78 ± 0.025
(N = 18)	FC-NN	0.71 ± 0.023	0.62 ± 0.025	0.68 ± 0.024	0.73 ± 0.025	9.32	5.5 × 10−20
	RF	0.45 ± 0.044	0.67 ± 0.038	0.51 ± 0.039	0.66 ± 0.047	10.58	2.0 × 10−25
	SVM	0.53 ± 0.028	0.57 ± 0.023	0.49 ± 0.025	0.54 ± 0.021	25.63	1.2 × 10−143
Tongue	MTGNN	0.82 ± 0.015	0.81 ± 0.012	0.82 ± 0.014	0.80 ± 0.014
(N = 41)	FC-NN	0.83 ± 0.019	0.80 ± 0.011	0.83 ± 0.018	0.80 ± 0.019	−0.91	0.82
	RF	0.38 ± 0.028	0.65 ± 0.029	0.52 ± 0.024	0.60 ± 0.031	18.96	3.5 × 10−79
	SVM	0.58 ± 0.021	0.51 ± 0.022	0.50 ± 0.025	0.53 ± 0.015	37.69	1.34 × 10− 309

2.3. Baseline methods

We evaluate the performance of our method against three baseline algorithms.

1. A Multi-class SVM on graph theoretic features

2. Separate Random Forest Classifiers on stacked similarity matrices

3. A Fully-connected neural network with a final MT-FC layer (FC-NN)

The first baseline is a multi-class linear SVM based on node degree, betweenness centrality, closeness centrality, and eigenvector centrality (Fortunato [2010], Opsahl et al. [2010]). We include this baseline as a traditional machine learning approach for network detection in graphs. We experimented with the RBF, Gaussian, and linear kernel classes and empirically determined that the linear kernel achieves the highest AUC metrics. We set the SVM hyperparameter c = 15.2 using CV on the HCP2 dataset. The second baseline is a Random Forest (RF) classifier on the row vectors of the rs-fMRI similarity matrices, thus taking the connectivity as its input feature vector. Here, we train and test one separate RF classifier for each of the four functional systems. We include this baseline to assess the predictive power of the raw rs-fMRI correlations. We have implemented the RF classifier in python using 250 decision trees. The tumor nodes and class are removed for the machine learning baselines, which operate on the node level.

Our deep learning baseline is an artifical neural network that contains only fully-connected layers (FC-NN). We include this baseline to observe the performance gains in adding the specialized E2E and E2N filters. The FC-NN has five hidden layers and then a final MT-FC layer. We include more hidden layers in the FC-NN than the MT-GNN because it achieved a beter trade-off between architecture depth and width. We optimized the hyperparameters for the FC-NN using the HCP2 dataset as well, resulting in δ_m = (1.34, 0.43, 0.31) and δ_l = (2.13, 0.43, 0.31). The tumor is handled in the same way for the MT-GNN (proposed) and FC-NN (baseline).

3. Experiments and results

Fig. 6 shows the evaluation workflow of our experiments. For each task, we report the eloquent class true positive rate (TPR) and eloquent class AUC. We note that all experiments in this work are performed on the parcel (ROI) and not voxel level. This dimensionality reduction is critical when working with a smaller clinical dataset. Eloquent class TPR is computed as the total number of correctly classified eloquent parcels divided by the total number of eloquent parcels. The AUC metric reported balances the tradeoff between the true and false positive rates of detecting the eloquent class. The reported statistics were determined using repeated 10-fold CV, where each run has a different fold membership. We report the mean and standard deviation of the metrics. To demonstrate statistically significant improvement, we perform a t-tost on the repeated 10-fold CV runs, which corrects for the independence assumption between samples (Bouckaert and Frank [2004]). Formally, let r be the number of times we repeat k-fold CV. We observe two learning algorithms A and B and measure their respective AUCs a_i,j and b_i,j for fold i and run j. Let x_i,j = a_i,j − b_i,j be the performance difference, n₂ be the number of testing samples, n₁ be the number of training samples, and ${\widehat{\sigma }}^2$ be the sample variance. The test statistic is is given by

$$t=\frac{\frac{1}{k\cdot r}{\sum }_{i=1}^k{\sum }_{j=1}^r{x}_{i,j}}{\sqrt{\left(\frac{1}{k\cdot r}+\frac{n_2}{n_1}\right){\widehat{\sigma }}^2}}.$$ (4)

The variable t in Eq. (4) follows a t-distribution with degrees of freedom df = kr − 1.

Figure 6:

We use repeated 10-fold CV for model training and testing. We repeat each CV 10 times, ensuring that fold membership changes for each run. We report the mean and standard deviation of eloquent class true positive rate (TPR), and eloquent class area under the curve (AUC). For each baseline, we report the FDR corrected p-value from the associated t-score between our MT-GNN and the baseline, as evaluated on the AUC metric. In addition, we report the specificity, F1 and t-scores for the main classification results shown in Tables 3 and 4.

The experimental results section is broken into 3 main subsections. In section 3.1, we show the results from the tumor simultation experiment in the HCP1 dataset. Section 3.2 contains the main JHH dataset and our bilateral language identification experiment. Section 3.3 includes an ablation study, where we evaluate the multi-task learning portion of our network. Finally, in section 3.4, we assess robustness of our method using varying functional atlases, corruption in tumor segmentations, and data augmentation techniques.

3.1. HCP simulation study

We validate our approach on a synthetic dataset which uses healthy connectomes with fake simulated tumors. This experiment provides a proof-of-concept for our methodology on data which has similar characteristics as our main JHH cohort. The “tumors” added to this dataset are randomly positioned but created to be spatially continuous with the same size as the real tumor segmentations we obtained from the JHH cohort.

The results for this experiment are summarized in Table 3, where we show that the MT-GNN has superior performance in all cases when compared to the baselines. Our performance gains are underscored by the t-test, where we observe very small p-values (p ≪ 0.001) for each competing baseline algorithm among each task present. Therefore, our method captures the complicated interactions between the eloquent cortex much better than the competing baseline algorithms. We also observe less performance variability across CV runs with our method compared to all of the baselines, which demonstrates robustness to the training data. We note that the RF classifier has low sensitivity and the mutli class SVM performs slightly better than chance. The performance of these machine learning baselines suggests that eloquent cortex mapping is a particularly challenging problem. Highlighted by the AUC column, the MT-GNN outperforms the FC-NN baseline in all cases. Using convolutional filters, the MT-GNN finds stereotypical connectivity patterns that identify the eloquent cortex. Compared to the motor network localization, all methods perform worse when identifying language networks, likely due to its higher anatomical variation. Fig. 7 shows boxplots of the AUC metric among all four methods and all four tasks. The colors red, blue, green and yellow refer to the MT-GNN, FC-NN, RF, and SVM algorithms respectively. Here we can see the performance gain and robustness of our method, which has larger median values and smaller deviations than the baselines. We repeat the performance of the algorithms on the healthy HCP dataset in the supplementary material as a way of guaging the effect that the additional tumor class has on this problem.

Table 3.

Mean plus or minus standard deviation for eloquent class true positive rate (TPR), specificity, F1 and AUC for the HCP cohort (100 subjects). The final column shows the FDR corrected p-values for the associated t-scores where we compare AUC between our method against each baseline.

Task	Method	Eloquent TPR	Specificity	F1	AUC	t-score	p-value
Language	MTGNN	0.67 ± 0.013	0.62 ± 0.012	0.63 ± 0.014	0.68 ± 0.01
	FCNN	0.59 ± 0.022	0.56 ± 0.021	0.58 ± 0.019	0.62 ± 0.018	14.08	3.5 × 10−44
	RF	0.32 ± 0.036	0.61 ± 0.026	0.45 ± 0.013	0.52 ± 0.034	17.02	1.8 × 10−64
	SVM	0.36 ± 0.026	0.49 ± 0.024	0.39 ± 0.018	0.51 ± 0.016	34.68	2.7 × 10−262
Finger	MTGNN	0.78 ± 0.011	0.75 ± 0.013	0.77 ± 0.014	0.82 ± 0.008
	FCNN	0.75 ± 0.014	0.69 ± 0.016	0.71 ± 0.015	0.73 ± 0.011	17.84	3.1 × 10−70
	RF	0.41 ± 0.026	0.71 ± 0.022	0.54 ± 0.023	0.58 ± 0.028	27.61	1.2 × 10−166
	SVM	0.41 ± 0.024	0.55 ± 0.028	0.42 ± 0.025	0.52 ± 0.015	52.66	≈ 0
Foot	MTGNN	0.83 ± 0.009	0.82 ± 0.008	0.8 ± 0.011	0.79 ± 0.009
	FC-NN	0.73 ± 0.016	0.65 ± 0.017	0.66 ± 0.013	0.71 ± 0.015	21.45	4.9 × 10−101
	RF	0.42 ± 0.025	0.74 ± 0.026	0.46 ± 0.021	0.58 ± 0.029	14.32	1.2 × 10−45
	SVM	0.50 ± 0.031	0.53 ± 0.028	0.48 ± 0.027	0.51 ± 0.013	65.72	≈ 0
Tongue	MTGNN	0.80 ± 0.01	0.78 ± 0.009	0.77 ± 0.011	0.78 ± 0.009
	FC-NN	0.76 ± 0.012	0.72 ± 0.014	0.73 ± 0.016	0.73 ± 0.015	7.63	9.1 × 10−14
	RF	0.44 ± 0.03	0.69 ± 0.032	0.50 ± 0.026	0.57 ± 0.032	23.73	2.1 × 10−123
	SVM	0.55 ± 0.023	0.52 ± 0.025	0.48 ± 0.024	0.53 ± 0.014	49.61	≈ 0

Figure 7:

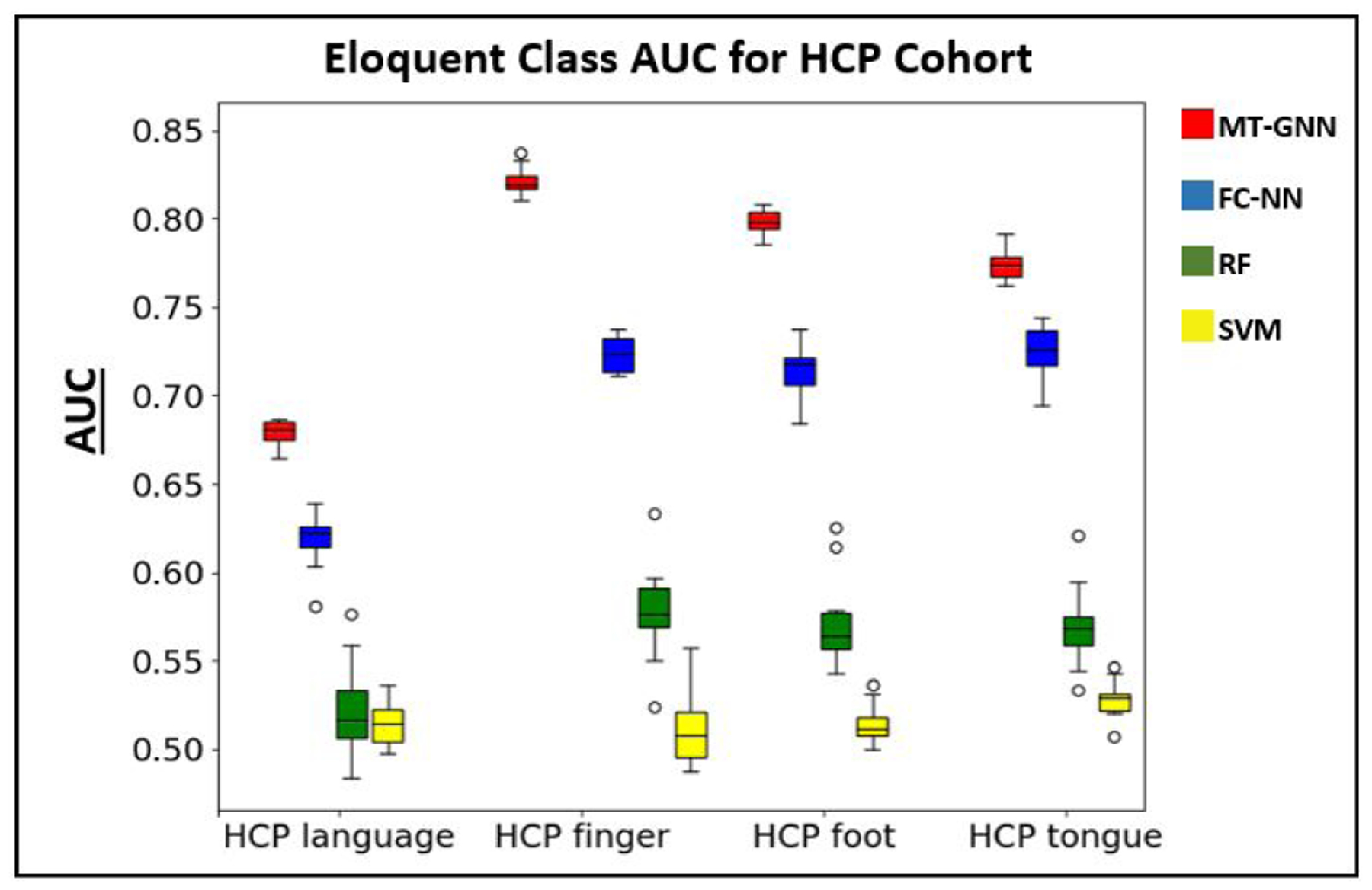
Boxplot for the AUC metric reported in Table 3 using 10 repeated 10-fold CVs. The colors red, blue, green and yellow refer to the MT-GNN, FC-NN, RF, and SVM methods respectively. We observe higher median performance and smaller deviations in our proposed method compared to the baseline algorithms.

3.2. JHH cohort and bilateral language experiment

Our primary localization task is on the JHH tumor cohort. Table 4 shows the eloquent class accuracy, AUC for detecting the eloquent class and t-scores for the JHH dataset. Once again, the MT-GNN has the best overall localization performance. Highlighted by the AUC and p-value column, the MT-GNN outperforms the baselines in nearly all cases, except for the tongue network. Similar to the HCP study, we observe smaller deviations with our method compared to all of the baselines, which shows robustness even when the method is trained and tested on different subsampled versions of the data. Among both the HCP simulation study and the JHH dataset, the HCP language task was the most challenging to localize, likely due to differences between the HCP and JHH language protocols. The HCP language task was designed to target language comprehension (Binder et al. [2011]) while the JHH sentence completion and silent word generation task were designed to target speech and language generation (Benjamin et al. [2018], Pillai and Zaca [2011], Sair et al. [2016]). Fig. 8 shows boxplots of the AUC metric among all four methods and tasks in the JHH cohort. Once again, we can see the robustness of our MT-GNN, which has larger median values for three out of the four tasks and smaller deviations for all four tasks compared to the baselines.

Figure 8:

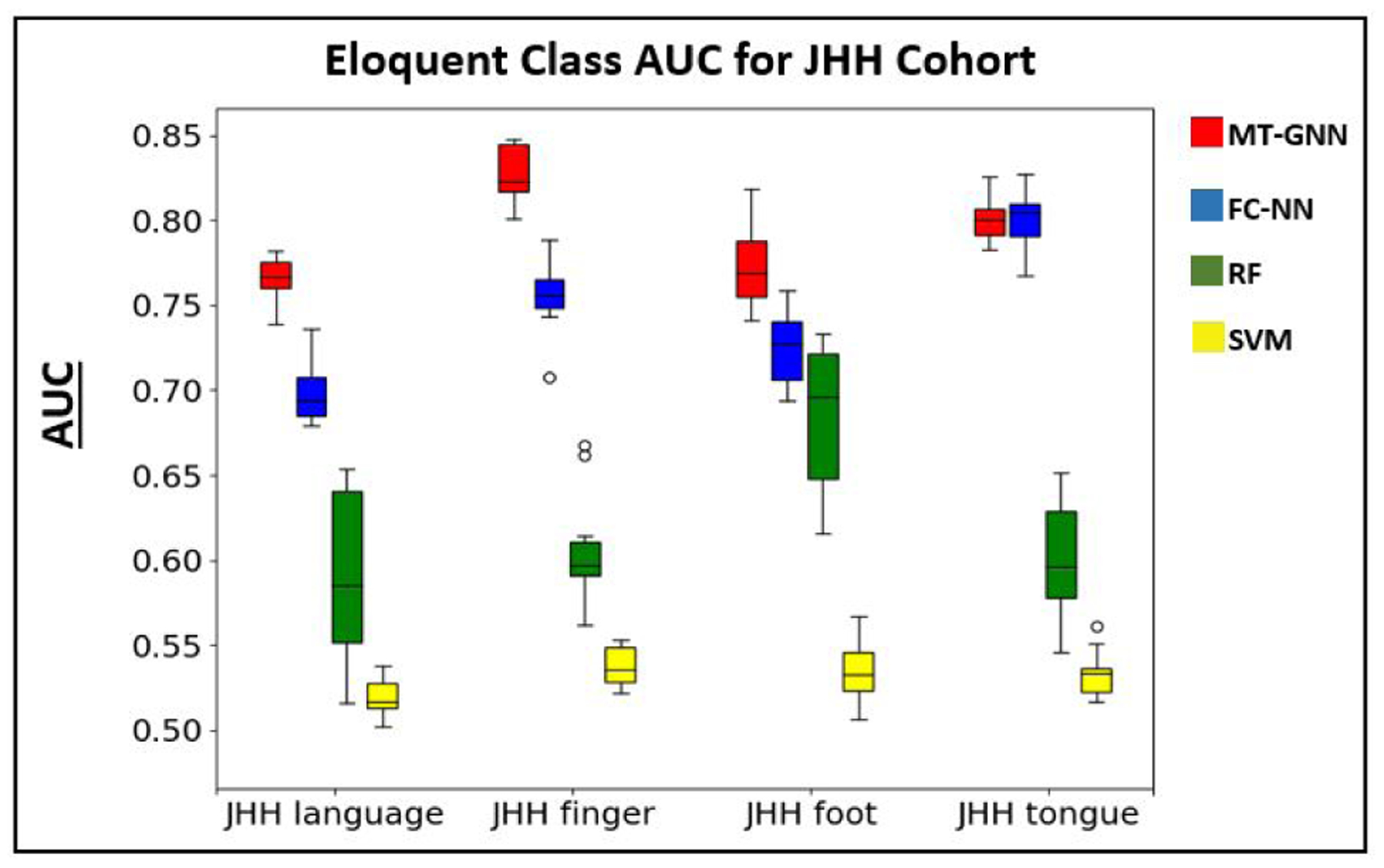
Boxplot for the AUC metric reported in Table 4. The colors red, blue, green and yellow refer to the MT-GNN, FC-NN, RF, and SVM methods respectively. We observe higher median performance in three out of four tasks and smaller deviations in all four tasks with the MT-GNN.

Our next experiment using the JHH cohort evaluates whether the proposed model and baselines can accurately identify bilateral language networks, even when this case is not present in the training set. This experiment assessess how well the models can identify unseen language regions based on intrinsic rs-fMRI connectivity patterns. We only perform this experiment on the JHH cohort because the JHH sentence completion and silent word generation tasks are designed to target lateralized systems, as compared to the HCP language processing and comprehension tasks. Here, we trained the model on 57 left-hemisphere language network patients and tested on the remaining 5 bilateral subjects. Table 5 shows the mean eloquent class and the overall accuracies for the 5 held out subjects. Our proposed model outperforms all baselines in both per-class and overall accuracy. Fig. 9 shows the ground truth (blue) and predicted (yellow) labels for one bilateral language network across methods. The MT-GNN shows the best trade-off between true positives and false positives compared to the baselines. We observe that the FC-NN overpredicts too many incorrect regions, the RF is unable to detect bilateral activation, and the SVM completely misses the correct activation pattern. We point out that due to a small sample size, the bilateral language identification experiment is not as conclusive as the main results, but rather provides a proof-of-concept and clinically valuable assessment on the JHH cohort. Specifically, this experiment provides evidence that our MT-GNN does not simply memorize nodes, but rather finds intrinsic connectivity patterns associated with language. In addition, language lateralization is a key problem in clinical neuroradiology, and the bilateral experiment is exciting preliminary evidence that our MT-GNN can be applied to other clinical problems in the future.

Table 5.

Mean class and overall accuracy for testing on 5 bilateral language subjets. As a comparison, the mean eloquent class TPR from table 4 is also shown in the final column.

Method	Bilateral TPR	overall	Eloquent TPR
MT-GNN	0.70	0.77	0.75
FC-NN	0.51	0.72	0.68
RF	0.33	0.76	0.49
SVM	0.41	0.63	0.46

Figure 9:

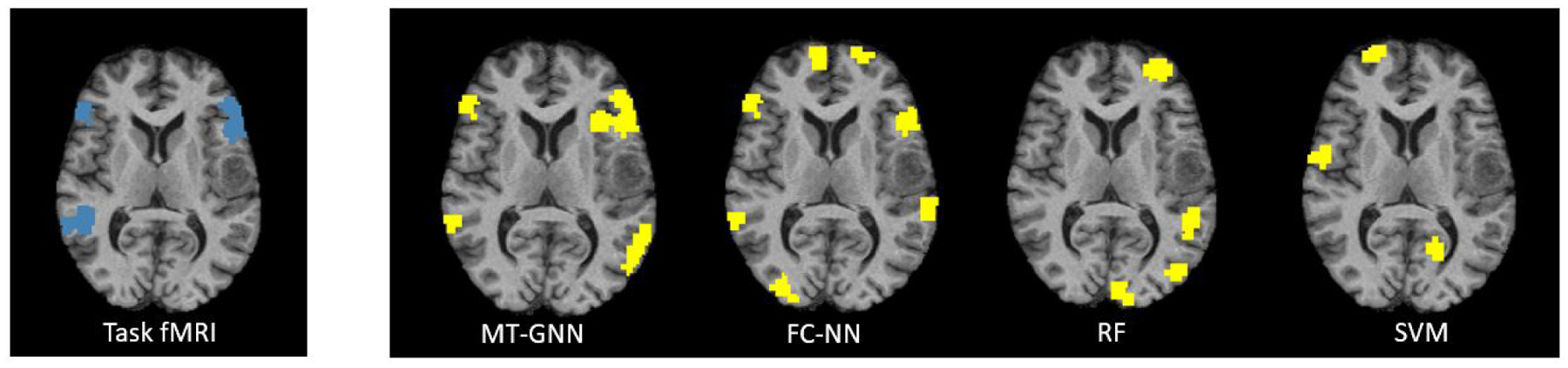
Task-fMRI “ground truth” activations (blue) and predicted (yellow) labels for one bilateral language network example across all algorithms. The MT-GNN has the highest localization accuracy.

3.3. Ablation study

In this section, we assess the value of adding the multi-task learning component to our network via an ablation study. Specifically, we evaluate performance on each of the four networks by removing the other three MT-FC layers from the model during training and testing. Therefore, each single GNN (SGNN) is trained separately for each task, and evaluated on that same task, without any information from the other three tasks present. Table 6 shows the mean eloquent TPR, AUC for eloquent class detection, and corrected p-value for AUC between the MT-GNN and SGNN for the JHH cohort. Highlighted by p < 0.01, our MT-GNN outperforms the SGNN in three out of four experiments. Fig. 10 shows the side-by-side boxplots for AUC between the MT-GNN and SGNN, where we can see a clear divide in performance between the two methods. The MT-GNN also has smaller variability, which shows robustness in our method.

Table 6.

Mean plus or minus standard deviation for eloquent TPR and AUC for the ablation study, where the cohort is shown in the first column. The final column shows the corrected p-values from the associated t-scores where we compare AUC between our method against the single GNN (SGNN)

Task	Method	TPR	AUC	p-value
Lang.	MT-GNN	0.75 ± 0.011	0.76 ± 0.013
	SGNN	0.73±0.019	0.72±0.026	1.5e-9
Finger	MT-GNN	0.85 ± 0.014	0.83 ± 0.015
	SGNN	0.82±0.021	0.81±0.027	0.28
Foot	MT-GNN	0.81 ± 0.023	0.78 ± 0.025
	SGNN	0.71±0.032	0.72±0.034	3.3e-3
Tongue	MT-GNN	0.82 ± 0.015	0.80 ± 0.014
	SGNN	0.79±0.019	0.77±0.023	2.2e-3

Figure 10:

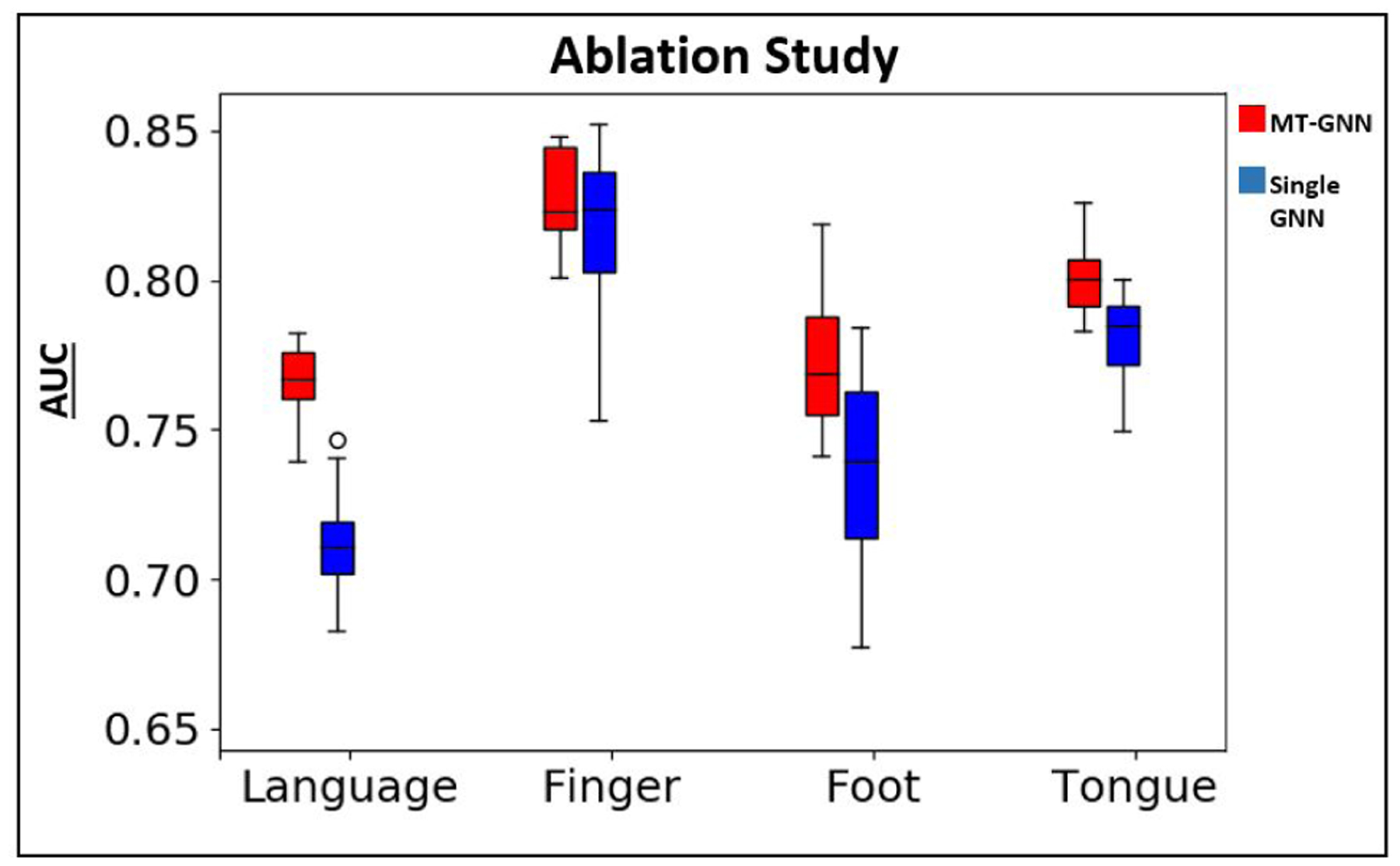
Ablation study boxplots for AUC between both cohorts. Red refers to MT-GNN and blue refers to single GNN.

3.4. Asessing model robustness

In this section, we assess the robustness of our model via the following experiments: (1) model evaluation on different scales of the Craddocks atlas (2) degrading the accuracy of tumor segmentations (3) boosting the training set via data augmentation and (4) sweeping the language class δ hyperparameter to observe the tradeoff between class accuracy and AUC.

3.4.1. Varying parcellation choice

It is understood that the choice of parcellation can affect the rs-fMRI connectivity due to varying spatial resolution (de Reus and Van den Heuvel [2013], Lord et al. [2016]). Therefore, we perform eloquent cortex localization using our MT-GNN on three additional scales of the Craddocks atlas (N = 262, N = 432, and N = 432 regions). We choose scales that are either coarser or finer than the original N = 384 atlas to observe the effect that varying parcel size has on performance.

Table 7 shows the evaluation metrics using the MT-GNN for the JHH cohort among all three atlases considered, where the p-values for are computed with respect to the original N = 384 atlas. Considering a p < 0.01 threshold, we observe only a significant difference in performance among one of four tasks present. We observe the N = 318 atlas outperforming the original in the foot functional subnetworks, denoted by a large p-value. Regarding the N = 262 atlas, however, three of the four tasks have a significant decrease in AUC. Our method is robust across the N = 384 and N = 318 scales but degrades in performance when the parcels become too coarse, as is the case with N = 262. This result implies that there is a certain spatial resolution in atlas choice that is necessary for our method to remain robust, likely due to the relatively small size of the networks we identify. However, we observe that the N = 432 atlas does not significantly outperform the N = 384 atlas, which suggests that there may be a limit of spatial resolution to which the chosen model architecture can achieve additional performance gains.

Table 7.

Mean plus or minus standard deviation for eloquent TPR and AUC when varying the parcellation atlas. The final column shows the corrected p-values for the associated t-scores where we compare AUC between N = 384 against N = 318 and N = 262.

Task	Atlas	TPR	AUC	p-value
Language	384	0.75±0.011	0.76±0.013
	432	0.77±0.014	0.77±0.012	0.11
	318	0.73±0.018	0.75±0.016	0.06
	262	0.71±0.014	0.74±0.017	1.3e-3
Finger	384	0.85±0.014	0.83±0.015
	432	0.88±0.013	0.84±0.013	0.73
	318	0.8 ± 0.016	0.80±0.017	2.7e-3
	262	0.76±0.019	0.79±0.014	7.0e-7
Foot	384	0.81±0.023	0.78±0.025
	432	0.82±0.012	0.78±0.023	0.52
	318	0.81±0.021	0.79±0.023	0.99
	262	0.78±0.027	0.77±0.024	0.49
Tongue	384	0.82±0.015	0.80±0.014
	432	0.83±0.011	0.82±0.015	0.96
	318	0.81±0.016	0.79±0.015	0.19
	262	0.78±0.019	0.76±0.017	4.9e-5

3.4.2. Degrading tumor segmentation

Next, we evaluate the performance of the MT-GNN on the JHH tumor cohort without perfect manual tumor segmentations. Here, we corrupt the tumor segmentations using a combination of translation, dilation, and/or shrinking operators on the original manual segmentations. We include this experiment to assess how robust our method is to the segmentation accuracy.

Fig. 11 shows boxplots for the AUC metric as the tumor segmentations become more corrupt, expressed by the dice coefficient between the corrupted and true segmentations on the x-axis. As expected, overall detection performance decreases as tumor corruption increases. This result is likely due to the network learning connectivity patterns from tumor regions, which are confounding features. Also, the corrupted tumor segmentations could encroach into the eloquent cortex regions, which would also derease performance. For relatively higher dice coefficients (> .85), we observe only a slight decrease in performance. Therefore, the model does not require perfect tumor segmentations to work, which is valuable in a clinical setting.

Figure 11:

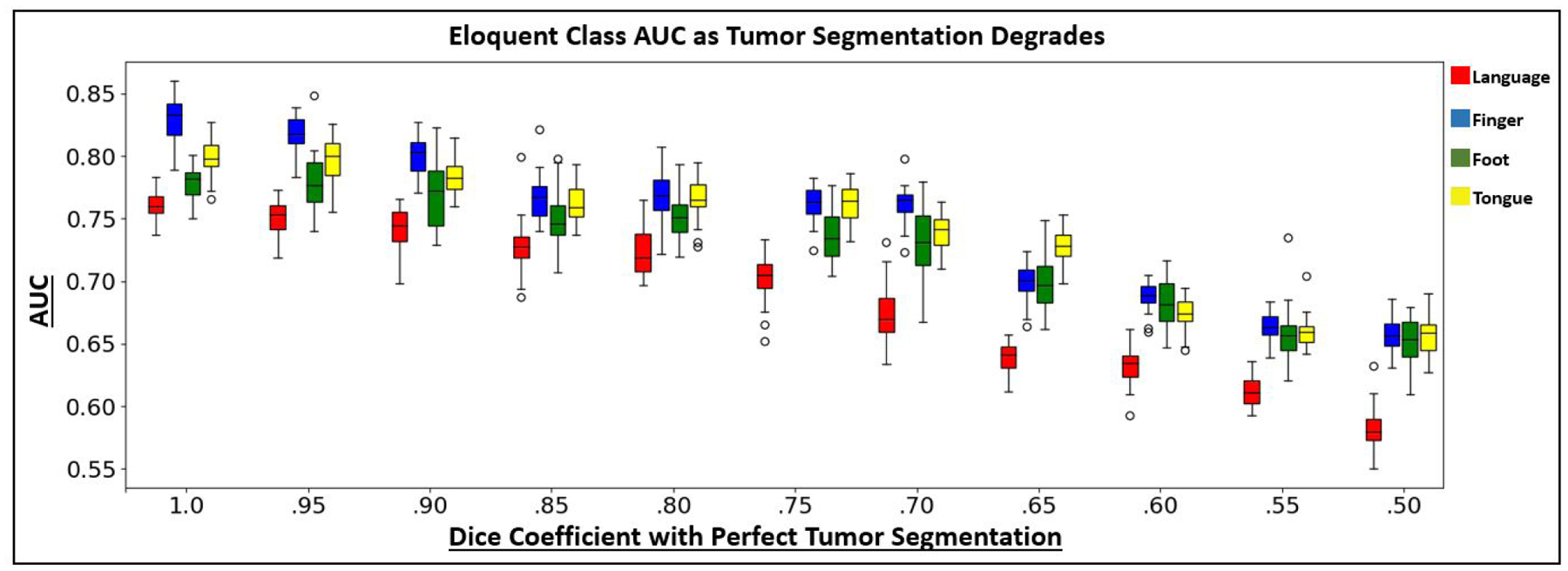
AUC boxplots using the MT-GNN on the JHH dataset as the tumor segmentations decrease in accuracy. The x-axis shows the dice coefficient of the corrupted tumor segmentation used for evaluation with the manual tumor segmentation. Corruption occurred via a combination of translating, dilating, or shrinking the manual segmentations. The colors red, blue, green and yellow refer to the JHH language, finger, foot and tongue tasks.

3.4.3. Boosting training set via data augmentation

Next, we use data augmentation to artificially increase the training set size. We include this experiment to probe the limitations of our small clinical dataset when training the highly parameterized deep network. Data augmentation has been shown to improve the performance of deep learning models due to obtaining a more comprehensive training set to help close the generalization gap (Perez and Wang [2017], Rashid and Louis [2019]). For the JHH cohort, we subsampled the time series data using a continuous sliding window to create 25 subject. Our evaluation strategy remained otherwise consistent and relies on the full connectivity matrix. Table 8 shows the localization performance, where the second row for each task corresponds to the augmented dataset. Overall, we observe similar performance with and without data augmentation, as highlighted by the lack of significant differences. However, we do observe smaller deviations with using augmentation, likely due to having more training samples. Ultimately, this experiment gives us confidence that the MT-GNN method effectively mines information from the original data and is probably not overfitting on a small dataset.

Table 8.

Mean plus or minus standard deviation for eloquent TPR and AUC with and without data augmentation. The final column shows the corrected p-values associated with the t-scores where we compare AUC between the original and augmented.

Task	Augment	TPR	AUC	p-value
Language	No	0.75 ± 0.011	0.76 ± 0.013
	Yes	0.76 ± 0.01	0.76 ± 0.011	0.21
Finger	No	0.85 ± 0.014	0.83 ± 0.015
	Yes	0.86 ± 0.011	0.84 ± 0.012	0.94
Foot	No	0.81 ± 0.023	0.78 ± 0.025
	Yes	0.80 ± 0.012	0.79 ± 0.015	0.85
Tongue	No	0.82 ± 0.015	0.80 ± 0.014
	Yes	0.80 ± 0.017	0.80 ± 0.013	0.39

3.4.4. Hyperparameter sweep for ${\delta }_1^l$

Finally, we sweep the language class hyperparameter ${\delta }_1^l$ while keeping the other hyperparameters constant and plot the AUC and class accuracy on the JHH dataset. For brevity, we only show the sweep for the language class, as the tradeoff between AUC and TPR for the motor class shows the same trend. Fig. 12 shows the results, where AUC is in red, eloquent class TPR is in blue, and ${\delta }_1^l$ is swept in increments of 0.1. As ${\delta }_1^l$ increases, we observe an increase in false-positives, for example, when ${\delta }_1^l$ exceeds 2.1, AUC drops as the true positive rate continues to rise. Clinically, it is more important to minimize false negatives (missing the eloquent cortex) than to minimize false positives, as there is a greater cost for damaging the eloquent cortex during surgery. Therefore, our weighted cross-entropy strategy proves useful, even if our model tends to overpredict the eloquent cortex class.

Figure 12:

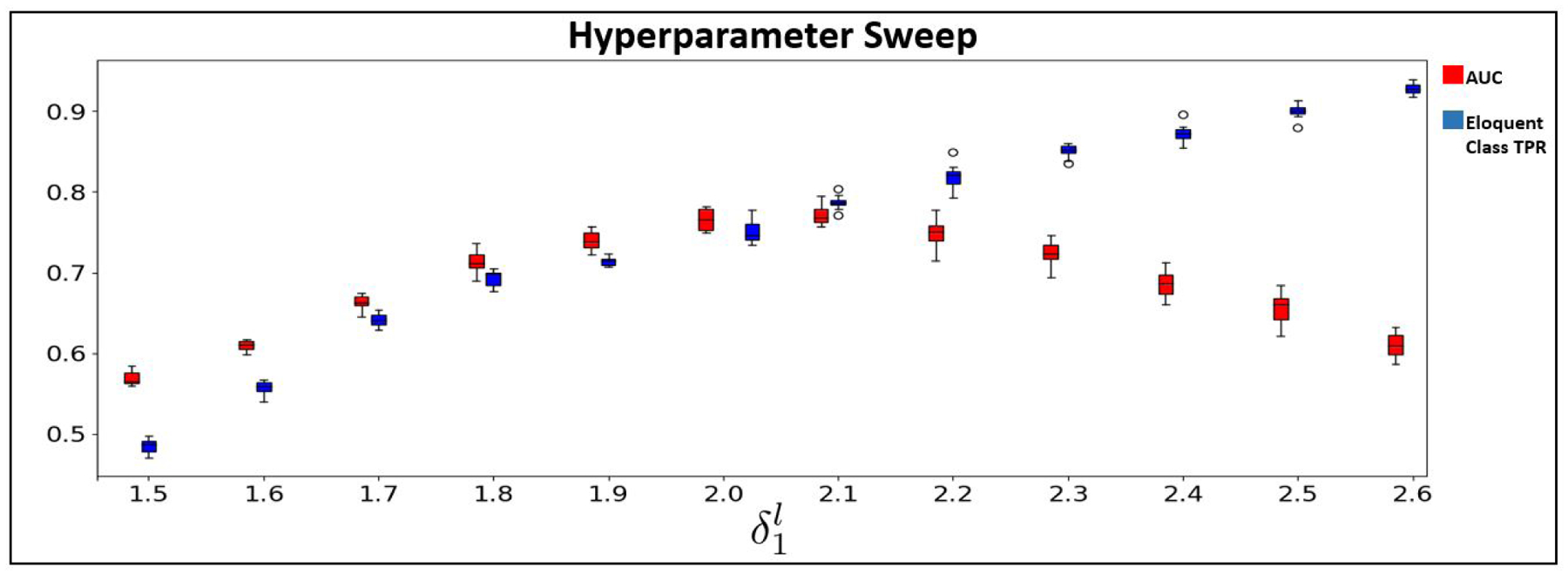
AUC (red) and class accuracy (blue) for the language class on the JHH cohort as δ_l,₁ is swept in increments of 0.1.

4. Discussion

We present a novel multi-task deep learning framework to identify language processing and motor sub-regions in brain tumor patients using rs-fMRI connectivity. In comparison to baseline methods, our model achieves higher and statistically significant region-based localization performance on both a synthetic and real world clinical dataset. We show that our model can recover clinically challenging bilateral language cases when trained on unilateral cases. Our ablation study further demonstrates the value of the multi-task portion of our network. Finally, we evaluate the robustness of our method, including varying the functional parcellation used, corrupting the tumor segmentations, performing data augmentation, and sweeping our weighted cross entropy loss hyperparameter for detecting the language class.

We observe that including the specialized convolutional layers aids in identifying patterns within the eloquent cortex distribution. To assess whether our network learns reproducible patterns, we visually inspected the weights with the highest E2E filter magnitudes. In this manner, we can assess which network features are considered the most important. Fig. 13 shows one example of a language connectivity hub that our model consistently identifies on the JHH dataset. We observe that this hub is lateralized on the left hemisphere, which is in line with the bulk of the JHH training data. Fig. 14 shows a symmetric language network hub that is consistently found during the HCP experiments. This network is bilateral because the HCP task is designed to target symmetrical areas of the anterior temporal lobe (ATL) while the JHH task is not. Though the network has many layers responsible for feature extraction, we conjecture that the MT-GNN performance gains relative to the FC-NN baseline are likely due to these reproducible connectivity hubs, which aid the downstream classification task. However, as deep learning models can lack interpretability, we emphasize that our speculation is heuristic and should be taken with a grain of salt.

Figure 13:

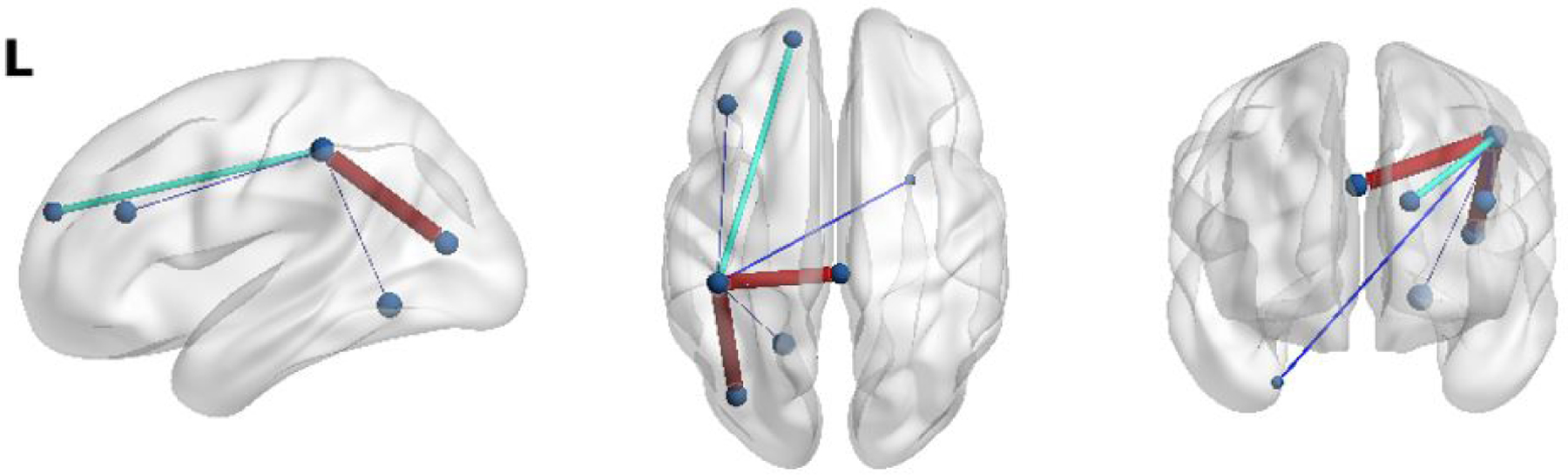
An example of a reproducible left-hemisphere only connectivity hub identified by our E2E filter when trained on the JHH dataset. We observe the nodes implicated resemble the activations in the language networks from Fig. 2.

Figure 14:

An example of a reproducible language network hub found in both hemispheres, when the MT-GNN is trained on the HCP dataset. The HCP story comprehension task is designed to target symmetric areas, which is captured in the identified language hub.

It is important to note that there exists potential confounding variables in our study, such as language laterality, tumor size, age, and gender. Here, language laterality refers to a quantitative measure between −1 and 1 that describes handedness of the subject. These confounders can affect the relationship between the input data and output variables of our study, thus causing unwanted bias in our algorithm. In the Supplementary Results, we address these potential confounders by plotting model performance against each confounder and assessing statistical significance on the correlation coefficients. All associated line of best fit plots are included in the Supplementary Results. For brevity, we have listed the p-values associated with the correlation coefficients between the confounders and the AUC metric for each classification task. Using a threshold of p < 0.05, we find no significant correlations between model performance against any of the four confounders. Figure 16 shows an example of the tumor size confounder analysis. As seen, there is no significant correlation between tumor size and model performance.

Figure 16:

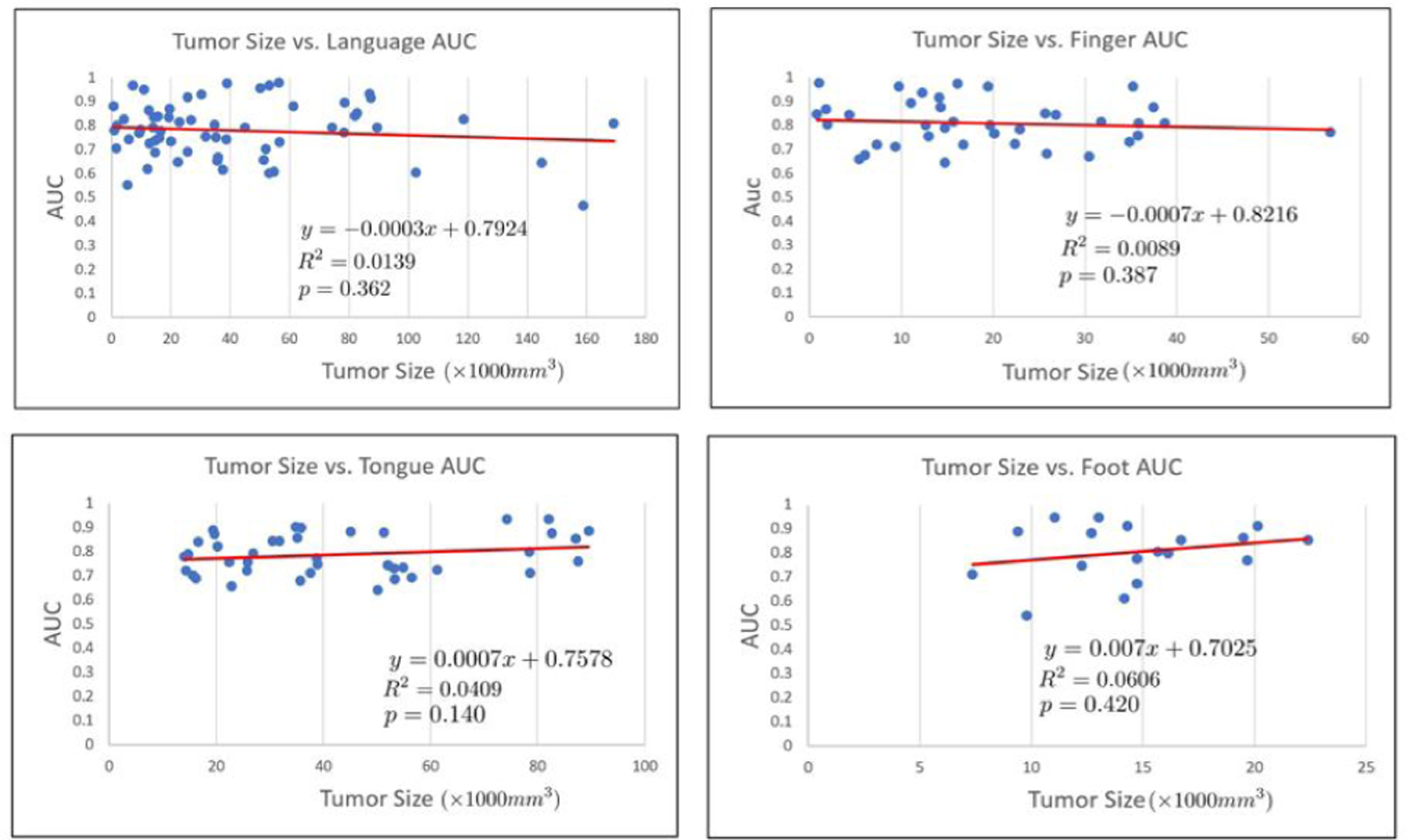
Tumor size vs. AUC for each of the classes of interest. The associated line of best fit equation, R² value, and p-value are shown. Tumor size is not significantly correlated with any of the four networks.

It is common in deep learning to first find an architecture that overfits to the training data and then apply it to the test data. In the Supplementary Results, we explore with different architectures to maximize overfitting to our training data. We then explore the effect of adding dropout to this overfit model and observe validation accuracy. We include this experiment to show the robustness and generalization capabilities of the main model presented in the manuscript.

Unlike our preliminary work (Nandakumar et al. [2019]), which constructs a separate GNN for each t-fMRI paradigm, this work shares the network parameters among all four tasks for both cohorts. Our method shows a substantial improvement in a threefold manner: (1) we save a large number of parameters, which is essential when working with smaller clinical datasets, (2) we find a shared latent representation of the eloquent cortex functional systems, and (3) we reduce training time by a factor of three. Highlighted by the ablation study, we observe that the single GNN (SGNN) cannot localize the eloquent regions as well as the MT-GNN. Due to our multi-branch loss function, our model has access to more training data compared to the SGNN case. Also, compared to the SGNN, our network finds a shared latent representation that models the complex interactions between the eloquent cortex that eventually helps with simultaneous classification. To highlight our localization performance, Fig. 15 illustrates the correct (blue) and false positive (red) detections by our MT-GNN in a patient with a large tumor in the inferior frontal gyrus. These results are aggregated across all four task branches of the model. We observe perfect sensitivity for the motor cortex localization (no false negative detections) and high accuracy for language despite the anatomical lesion.

Figure 15:

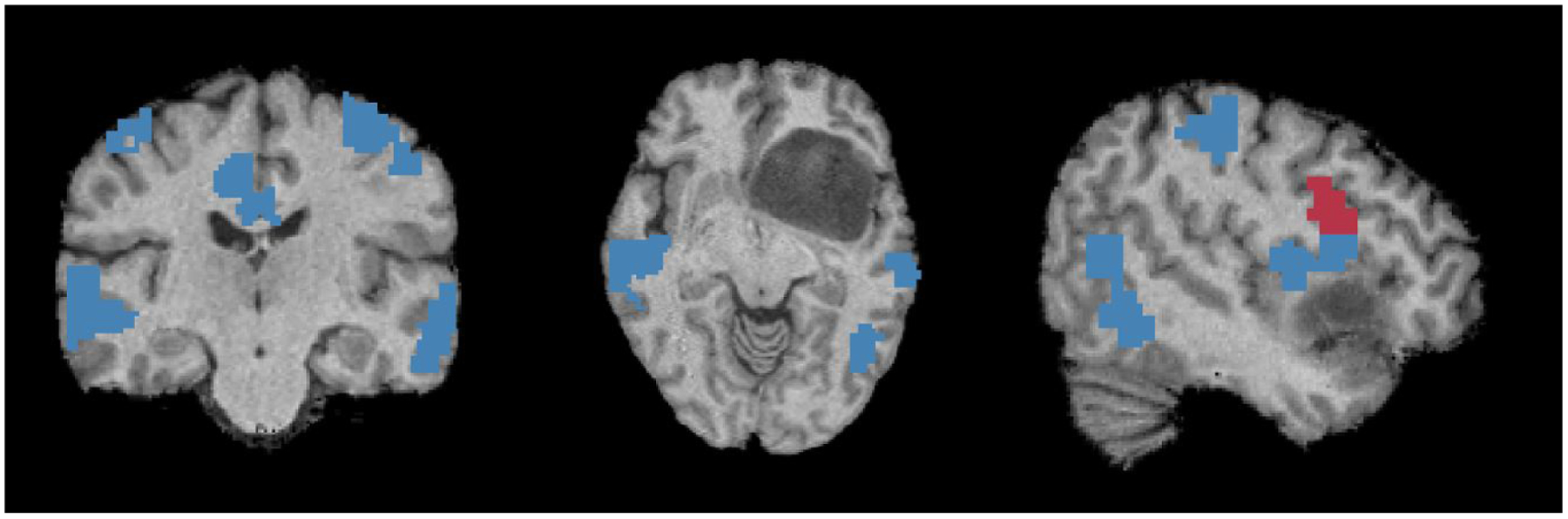
From (L-R) we show coronal, axial and saggital views of correct (blue) and incorrect (red) prediction by our model for the eloquent cortex in a challenging inferior frontal gyrus tumor case.

We acknowledge that a restriction of our model is to have tumor segmentations manually dilineated, which can be time consuming. However, we note that there exists a large body of work describing automated techniques for tumor segmentation (Havaei et al. [2017], Işın et al. [2016], Zhao et al. [2018]) where state-of-the-art performance is up to 0.85 dice overlap with the true segmentations. We observe that our method only slightly decreases in performance at this dice coefficient, shown by Fig. 11. Therefore, we believe our MT-GNN is a valuable tool for presurgical evaluation.

We note that the risk factor δ_c plays a role in the model performance Specifically, large values of δ_c encourage overprediction of the eloquent class, as illustrated in Fig. 12 in section 3.4.4. However, we emphasize that in this clinical application, false positive predictions are more desirable than false negative predictions, due to the severe outcomes of accidental damage to the eloquent cortex (Fadul et al. [1988], Sawaya et al. [1998]). Nonetheless, rectifying these overpredictions is a valuable direction for future work. In addition, we acknowledge that due to partial volume effects, our framework is conservative in handling the tumor, as the boundary parcels usually contain some number of healthy voxels. One future workaround is to use a spatially hierarchical learning scheme that increases resolution to the voxel level.

We note that there are different mathematical formulations available to construct the similarity graph. Our formulation is taken from (Langs et al. [2010]), where the full definition of $W_{ij}=\frac{<x_i,x_j>}{ϵ}$. Here, ϵ is the decay speed, which controls the apparent sparseness of the graph. In this work, we fixed ϵ = 1. Additionally, we zeroed out rows and columns corresponding to tumor regions. Experimenting with our similarity graph construction is an interesting line of future work.

Though we use the convolutional filters developed in Kawahara et al. [2017], our network and overall task are very distinct from that in Kawahara et al. [2017]. There are three key architectural differences to our MT-GNN, which allow it to perform the desired eloquent cortex localization. First, the original BrainNetCNN is designed to make a single patient-wise prediction from the input connectivity matrix. In contrast, our MT-GNN makes node-level predictions by preserving the node information through the fully-connected and multi-task (MT) layers. Second, our MT-GNN treats anatomical lesions as a separate learned class in order to remove any biases they introduce into the eloquent cortex detection. Finally, our MT portion uses the learned representation from the E2E and E2N layers to simultaneously identify multiple functional systems. Not only does this strategy reduce the total number of parameters (i.e., convolutional layers are shared), but our loss function can easily accommodate missing training data. Specifically, the weights of the missing task branches are frozen during backpropagation, while the shared representation is still updated based on the available tasks. Hence, our MT-GNN can mine information from the available training data. This feature is helpful in a clinical setting, as subjects are asked to perform different tasks based on their clinical condition.

Finally, our work has two notable advantages over existing methods. First, it operates on whole-brain resting-state fMRI connectivity in order to maximize the information used identify eloquent regions. Second, it explicitly models subject-specific tumor size and location information. For example, it is unclear how the Hacker et al. (Hacker et al. [2013]) method would perform when multiple seeds lie in the tumor region. Another highlight of our method is computational efficiency, as it considers just one N × N connectivity matrix per subject, as compared to the method in Lee et al. (Lee et al. [2016]) and Leuthardt et al. (Leuthardt et al. [2018]), which requires multiple correlation maps per subject (based on 169 seed locations). As discussed, these prior works also do not quantify accuracy on the voxel or ROI level. Our work reports both the eloquent detection accuracy and a statistically significant improvement in performance between our method and competing baselines.

5. Conclusion

We have introduced a novel deep learning method to simultaneously localize multiple areas of the eloquent cortex using rs-fMRI connectivity. Our MT-GNN captures a shared representation between nuanced functional sub-networks of interest for neurosurgery planning via a graph-based architecture. We validate our method on an in-house JHH cohort and on a subset of the HCP dataset with manually-created fake tumors. Quantitatively, our model achieves better performance than both conventional and deep learning baselines. We showed an example of a language connectivity hub in both cohorts that our network consistently recovers as well as an example of our localization. Finally, we demonstrate generalizability and robustness with our bilateral language, varying atlas, and tumor segmentation corruption experiments. Taken together, our results highlight the potential of using rs-fMRI to supplement the presurgical workup, with the ultimate goal of faster and more reliable tumor resections.

Table 9.

P-values of the correlation between confounder and AUC for each classification task. The analysis setup and scatter plots are provided in the Supplementary Results.

Task	Gender	Tumor size	Age	Laterality
Language	0.52	0.36	0.49	0.61
Finger	0.42	0.39	0.52
Foot	0.37	0.42	0.69
Tongue	0.33	0.14	0.63