Comparing trained and untrained probabilistic ensemble forecasts of COVID-19 cases and deaths in the United States

Abstract

The U.S. COVID-19 Forecast Hub aggregates forecasts of the short-term burden of COVID-19 in the United States from many contributing teams. We study methods for building an ensemble that combines forecasts from these teams. These experiments have informed the ensemble methods used by the Hub. To be most useful to policymakers, ensemble forecasts must have stable performance in the presence of two key characteristics of the component forecasts: (1) occasional misalignment with the reported data, and (2) instability in the relative performance of component forecasters over time. Our results indicate that in the presence of these challenges, an untrained and robust approach to ensembling using an equally weighted median of all component forecasts is a good choice to support public health decision-makers. In settings where some contributing forecasters have a stable record of good performance, trained ensembles that give those forecasters higher weight can also be helpful.

1. Introduction

Accurate short-term forecasts of infectious disease indicators (i.e., disease surveillance signals) can inform public health decision-making and outbreak response activities such as non-pharmaceutical interventions, site selection for clinical trials of pharmaceutical treatments, and the distribution of limited healthcare resources (Dean et al., 2020, Lipsitch et al., 2011, Wallinga et al., 2010). Epidemic forecasts have been incorporated into public health decision-making in a wide variety of situations, including outbreaks of dengue fever in Brazil, Vietnam, and Thailand (Colón-González et al., 2021, Lowe et al., 2016, Reich et al., 2016) and influenza in the U.S. McGowan et al. (2019).

These efforts frequently use ensemble forecasts that combine predictions from many models. In a wide array of fields, ensemble approaches have provided consistent improvements in accuracy and robustness relative to standalone forecasts (Gneiting and Raftery, 2005, Polikar, 2006). The usefulness of ensemble forecasts has also been demonstrated repeatedly in multiple infectious disease settings, including influenza, Ebola, dengue, respiratory syncytial virus, and others (Johansson et al., 2019, McGowan et al., 2019, Reich et al., 2019, Reis et al., 2019, Viboud et al., 2018, Yamana et al., 2016). In light of this record of strong performance, ensembles are natural candidates for forecasts used as an input to high-stakes public health decision-making processes.

This paper describes ensemble modeling efforts at the U.S. COVID-19 Forecast Hub (https://covid19forecasthub.org/, hereafter the “U.S. Hub”), from spring 2020 through spring 2022. Starting in April 2020, the U.S. Hub created ensemble forecasts of reported incident deaths one to four weeks ahead in the 50 states, Washington, D.C., and six territories, as well as at the national level by combining forecasts submitted by a large and variable number of contributing teams using different modeling techniques and data sources. In July 2020, forecasts of incident-reported COVID-19 cases were added. Of note, the U.S. Hub produces probabilistic forecasts in which uncertainty about future disease incidence is quantified through the specification of a predictive distribution that is represented by a collection of predictive quantiles. Since the inception of the U.S. Hub, these ensemble forecasts have been provided to the U.S. Centers for Disease Control and Prevention (CDC) and have been the basis of official CDC forecasting communications (US Centers for Disease Control and Prevention, 2021).

1.1. Related literature

A wide variety of standalone methodological approaches have been shown to be able to make forecasts of short-term outbreak activity that are more accurate than naive baseline forecasts in various epidemiological settings. Some approaches have used existing statistical frameworks to model associations between outcomes of interest and known or hypothesized drivers of outbreaks, such as recent trends in transmission or environmental factors. To cite just a few examples, methods used include multiscale probabilistic Bayesian random walk models (Osthus & Moran, 2021), Gaussian processes (Johnson et al., 2018), kernel conditional density estimation (Brooks et al., 2018, Ray et al., 2017), and generalized additive models (Lauer et al., 2018). Other models have an implicit or explicit representation of a disease transmission process, such as variations on the susceptible–infectious–recovered (SIR) compartmental model (Lega and Brown, 2016, Osthus et al., 2017, Pei et al., 2018, Shaman and Karspeck, 2012, Turtle et al., 2021). Aspects of these modeling frameworks can also be combined, for instance using time series methods to build models that have a compartmental structure or incorporate key epidemiological parameters such as the effective reproduction number $R_t$, or models that use a time series process to capture systematic deviations from a compartmental core (Agosto et al., 2021, Bartolucci et al., 2021, Osthus et al., 2019).

There is extensive literature on ensemble forecasting, but of particular relevance to the present work is the research on combining, calibrating, and evaluating distributional forecasts (Claeskens et al., 2016, Gneiting et al., 2007, Gneiting and Raftery, 2007, Ranjan and Gneiting, 2010). We note that prior work on forecast combination has mostly focused on combining forecasts represented as probability densities or probability mass functions rather than forecasts parameterized by a set of discrete quantile levels, which is the format of the forecasts in the present study. However, in psychological studies there is a long history of combining quantiles from multiple distributions as a mechanism for summarizing distributions of response times, error rates, and similar quantities across many subjects (Ratcliff, 1979, Vincent, 1912). More recently, this approach has also been used to combine probabilistic assessments from multiple subject matter experts or statistical models in fields such as security threat detection and economic forecasting (Busetti, 2017, Gaba et al., 2017, Hora et al., 2013, Lichtendahl Jr et al., 2013). In the context of infectious disease forecasting, Bracher et al. (2021) conducted a similar but less extensive analysis to the one presented here using data from a related forecast hub focusing on Germany and Poland. Taylor and Taylor (2021) recently explored several approaches to constructing quantile-based ensemble forecasts of cumulative deaths due to COVID-19 using the data from the U.S. Hub, although they did not generate ensemble forecasts in real time or appear to have used the specific versions of ground-truth data that were available for constructing ensembles in real time.

As mentioned above, ensemble forecasts have also been used in a variety of other applications in real-time forecasting of infectious diseases, often with seasonal transmission dynamics where many years of training data are available (Colón-González et al., 2021, Reich et al., 2019, Reis et al., 2019, Yamana et al., 2016). In such applications, simple combination approaches have generally been favored over complex ones, with equal-weighted approaches often performing similarly to trained approaches that assign weights to different models based on past performance (Bracher et al., 2021, Ray and Reich, 2018). These results align with theory suggesting that the uncertainty in weight estimation can pose a challenge in applications with a low signal-to-noise ratio (Claeskens et al., 2016).

1.2. Contributions of this article

This paper is focused on explaining the careful considerations that have gone into building a relatively simple “production” ensemble model for a difficult, high-stakes, real-time prediction problem: forecasting COVID-19 cases and deaths in the United States, to support public health decision-making. We do not empirically investigate the performance of complex forecast combination strategies from the online prediction literature, which generally require richer and larger training datasets.

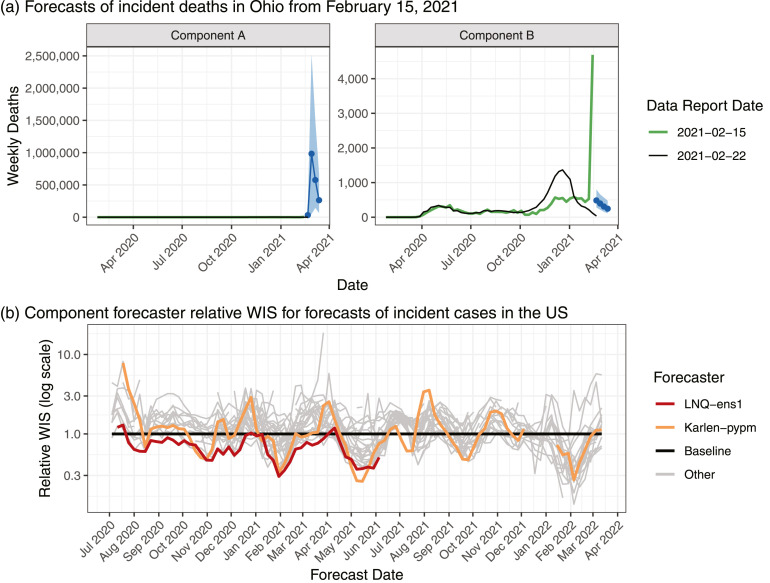
The goal of the U.S. Hub in developing an operational ensemble was to produce forecasts of the short-term trajectory of COVID-19 that had good performance on average and stable performance across time and different locations. Real-time forecasting for an emerging pathogen in an open, collaborative setting introduces important challenges that an ensemble combination method must be able to handle. First, teams occasionally submitted outlying component forecasts due to software errors, incorrect model assumptions, or a lack of robustness to input data anomalies (Fig. 1(a), Supplemental Figures 1 and 2). Second, some component models were generally better than others, but the relative performance of different models was somewhat unstable across time (Fig. 1(b), Supplemental Figures 3 and 4). In particular, some forecasters alternated between being among the best-performing models and among the worst-performing models within a span of a few weeks, which introduced a challenge for ensemble methods that attempted to weight component forecasters based on their past performance. In this manuscript, we explore and compare variations on ensemble methods designed to address these challenges and produce real-time forecasts that are as accurate as possible to support public health decision-makers.

Fig. 1.

(a) Predictive medians and 95% prediction intervals for incident deaths in Ohio generated on February 15, 2021 by two example component forecasters. The vertical axis scale is different in each facet, reflecting differences across several orders of magnitude in forecasts from different forecasters; the reference data are the same in each plot. The data that were available as of Monday, February 15, 2021 included a large spike in reported deaths that had been redistributed into the history of the time series in the version of the data available as of Monday, February 22, 2021. In this panel, forecaster names are anonymized to avoid calling undue attention to individual teams; similar behavior has been exhibited by many forecasters. (b) Illustration of the relative weighted interval score (WIS, defined in Section 2.5) of component forecasters over time; lower scores indicate better performance. Each point summarizes the skill of forecasts made on a given date for the one- to four-week-ahead forecasts of incident cases across all state-level locations.

We give detailed results from experiments that were run concurrently with the weekly releases of ensemble forecasts from the start of the U.S. Hub in 2020 through the spring of 2022, as documented in preliminary reports (Brooks et al., 2020, Ray et al., 2021). These experiments provided the evidence for decisions (a) to move to a median-based ensemble from one based on means in July 2020; (b) to switch to a trained ensemble for forecasts of deaths in November 2021; and (c) to implement a weight regularization strategy for that trained ensemble starting in January 2022. In a secondary analysis, we also consider the prospective performance of these methods in the closely related setting of forecasting cases and deaths in Europe, to examine the generalizability of the results from our experiments using data from the U.S.

The following sections document the format and general characteristics of COVID-19 forecasts under consideration, the ensemble approaches studied, and the results of comparing different approaches both during model development and during a prospective evaluation of selected methods.

2. Methods

We give an overview of the U.S. and European Forecast Hubs and the high-level structure of our experiments in Sections 2.1, 2.2, 2.3, 2.4, 2.5, and then describe the ensemble methods that we consider in Section 2.6.

2.1. Problem context: Forecasting short-term COVID-19 burden

Starting in April 2020, the U.S. Hub collected probabilistic forecasts of the short-term burden of COVID-19 in the U.S. at the national, state/territory, and county levels (Cramer et al., 2022); a similar effort began in February 2021 for forecasts of disease burden in 32 European countries (European COVID-19 Forecast Hub, 2021). In this manuscript, we focus on constructing probabilistic ensemble forecasts of weekly counts of reported cases and deaths due to COVID-19 at forecast horizons of one to four weeks for states and territories in the U.S. and for countries in Europe. A maximum horizon of four weeks was set by collaborators at the CDC as a horizon at which forecasts would be useful to public health practitioners while maintaining reasonable expectations of a minimum standard of forecast accuracy and reliability. Probabilistic forecasts were contributed to the Hubs in a quantile-based format by teams in academia, government, and industry. The Hubs produced ensemble forecasts each week on Monday using forecasts from teams contributing that week. In the U.S. Hub, seven quantile levels were used for forecasts of cases, and 23 quantile levels were used for forecasts of deaths; in the European Hub, 23 quantile levels were used for both target variables.

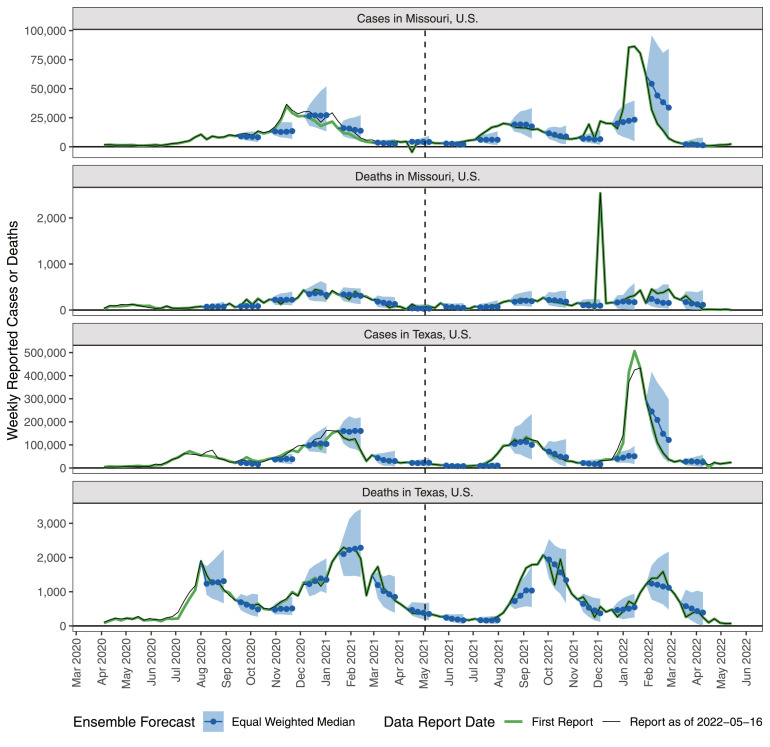
Weekly reported cases and deaths were calculated as the difference in cumulative counts on consecutive Saturdays, using data assembled by the Johns Hopkins University Center for Systems Science and Engineering as the ground truth (Dong et al., 2020). Due to changes in the definitions of reportable cases and deaths, as well as errors in reporting and backlogs in data collection, there were some instances in which the ground-truth data included outlying values, or were revised. Most outliers and revisions were inconsequential, but some were quite substantial in the U.S. as well as in Europe (Fig. 2). When fitting retrospective ensembles, we fit to the data that would have been available in real time. This is critical because the relative performance of different component forecasters may shift dramatically depending on whether originally reported or subsequently revised data were used to measure forecast skill. An ensemble trained using revised data can therefore have a substantial advantage over one trained using only data that were available in real time, and its performance is not a reliable gauge of how that ensemble method might have done in real time.

Fig. 2.

Weekly reported cases and deaths and example equally weighted median ensemble forecasts (predictive median and 95% interval) for selected U.S. states. Forecasts were produced each week, but for legibility, only forecasts originating from every sixth week are displayed. Data providers occasionally change initial reports (green lines) leading to revised values (black lines). Vertical dashed lines indicate the start of the prospective ensemble evaluation phase. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

The U.S. Hub conducted extensive ensemble model development in real time from late July 2020 through the end of April 2021, with smaller, focused experiments ongoing thereafter. We present results for the model-development phase as well as a prospective evaluation of a subset of ensemble methods in the U.S. starting with forecasts created on May 3, 2021 and continuing through March 14, 2022. We note that we continued examining a wider range of methods to inform weekly operational forecasting tasks, but the methods that we chose to evaluate prospectively were selected by May 3, 2021, the beginning of the prospective evaluation period, with no alterations thereafter. Real-time submissions of the relative WIS weighted median ensemble described below are on record in the U.S. Hub for the duration of the prospective evaluation period. In one section of the results below, we present a small post hoc exploration of the effects of regularizing the component forecaster weights; these results should be interpreted with caution, as they do not constitute a prospective evaluation. To examine how well our findings generalize, we also evaluated the performance of a subset of ensemble methods for prospective forecasts of cases and deaths at the national level for countries in Europe from May 3, 2021 to March 14, 2022.

2.2. Eligibility criteria

In the Forecast Hubs, not all forecasts from contributing models are available for all weeks. For example, forecasters may have started submitting forecasts in different weeks, and some forecasters submitted forecasts for only a subset of locations in one or more weeks.

The ensemble forecast for a particular location and forecast date included all component forecasts with a complete set of predictive quantiles (i.e., seven predictive quantiles for incident cases, 23 for deaths) for all four forecast horizons. Teams were not required to submit forecasts for all locations to be included in the ensemble. Some ensemble methods that we considered require historical forecasts to inform component model selection or weighting; for these methods, at least one prior submission was required. The Forecast Hubs enforced other validation criteria, including that predictions of incident cases and deaths were non-negative and predictive quantiles were properly ordered across quantile levels.

2.3. Notation

We denote the reported number of cases or deaths for location $l$ and week $t$ by $y_{l,t}$. A single predictive quantile from component forecaster $m$ is denoted by $q_{l,s,t,k}^m$, where $s$ indexes the week the forecast was created, $t$ indexes the target week of the forecast, and $k$ indexes the quantile level. The forecast horizon is the difference between the target date $t$ and the forecast date $s$. There are a total of $K=7$ quantile levels for forecasts of cases in the U.S., and $K=23$ quantile levels otherwise. The quantile levels are denoted by ${\tau }_k$ (e.g., if ${\tau }_k=0.5$ then $q_{l,s,t,k}^m$ is a predictive median). We collect the full set of predictive quantiles for a single model, location, forecast date, and target date in the vector $q_{l,s,t,1:K}^m$. We denote the total number of available forecasters by $M$; this changes for different locations and weeks, but we suppress that in the notation.

2.4. Baseline forecaster

In the results below, many comparisons are made with reference to an epidemiologically naive baseline forecaster that projects forward the most recent observed value with growing uncertainty at larger horizons. This baseline forecaster was a random walk model on weekly counts of cases or deaths, with $Y_{l,t}\mid Y_{l,t-1}=Y_{l,t-1}+{\varepsilon }_{l,t}$. The model used a non-parametric estimate of the distribution of the innovations ${\varepsilon }_{l,t}$ based on the observed differences in weekly counts $d_{l,s}=y_{l,s}-y_{l,s-1}$ over all past weeks $s$ for the specified location $l$. Predictive quantiles were based on the quantiles of the collection of these differences and their negations, using the default method for calculating quantiles in R. The inclusion of negative differences ensured that the predictive distributions were symmetric and the predictive median was equal to the most recent observed value. Forecasts at horizons greater than one were obtained by iterating one-step-ahead forecasts. Any resulting predictive quantiles that were less than zero were truncated to equal zero.

2.5. Evaluation metrics

To evaluate forecasts, we adopted the weighted interval score (WIS) (Bracher et al., 2021a). Let $q_{1:K}$ be predictive quantiles for the observed quantity $y$. The WIS is calculated as

$$\mathrm{WIS}(q_{1:K},y)=\frac{1}{K}\sum _{k=1}^{K}2\left\{{\mathbb{1}}_{(-\infty ,q_k]}\left(y\right)-{\tau }_k\right\}(q_k-y),$$

where ${\mathbb{1}}_{(-\infty ,q_k]}\left(y\right)$ is the indicator function that takes the value $1$ when $y\in (-\infty ,q_k]$ and $0$ otherwise. This is a negatively oriented proper score, meaning that negative scores are better and its expected value according to a given data generating process is minimized by reporting the predictive quantiles from that process. The WIS was designed as a discrete approximation to the continuous ranked probability score, and is equivalent to pinball loss, which is commonly used in quantile regression (Bracher et al., 2021a). We note that some other commonly used scores such as the logarithmic score and the continuous ranked probability score are not suitable for use with predictive distributions that are specified in terms of a set of predictive quantiles, since a full predictive density or distribution function is not directly available (see Supplemental Section 3 for further discussion).

To compare the skill of forecasters that submitted different subsets of forecasts, we used the relative WIS, as done in Cramer et al. (2022). The ensemble forecasters developed and evaluated in this manuscript provided all relevant forecasts; missingness pertains only to the component forecasters, and in the present work the relative WIS is primarily used to summarize component forecaster skill as an input to some of the trained ensemble methods described below. Let $\mathcal{I}$ denote a set of combinations of location $l$ and forecast creation date $s$ over which we desire to summarize model performance, and let ${\mathcal{I}}_{m,m^{\prime }}\subseteq \mathcal{I}$ be the subset of those locations and dates for which both models $m$ and $m^{\prime }$ provided forecasts through a forecast horizon of at least four weeks. The relative WIS of model $m$ over the set $\mathcal{I}$ is calculated as in Box I

Box I.

$${\mathrm{rWIS}}_{\mathcal{I}}^m=\frac{{\theta }^m}{{\theta }^{\text{baseline}}}\text{, where }$$

$${\theta }^m={\left(\prod _{m^{\prime }=1}^M\frac{{\left(4\cdot \left|{\mathcal{I}}_{m,m^{\prime }}\right|\right)}^{-1}\sum _{(l,s)\in {\mathcal{I}}_{m,m^{\prime }}}\sum _{t=s+1}^{s+4}\mathrm{WIS}(q_{l,s,t,1:K}^m,y_{l,t})}{{\left(4\cdot \left|{\mathcal{I}}_{m,m^{\prime }}\right|\right)}^{-1}\sum _{(l,s)\in {\mathcal{I}}_{m,m^{\prime }}}\sum _{t=s+1}^{s+4}\mathrm{WIS}(q_{l,s,t,1:K}^{m^{\prime }},y_{l,t})}\right)}^{\frac{1}{M}}$$

In words, we computed the ratio of the mean WISs for model $m$ and each other model $m^{\prime }$, averaging across the subset of forecasts shared by both models. ${\theta }^m$ was calculated as the geometric mean of these pairwise ratios of matched mean scores, and summarized how model $m$ did relative to all other models on the forecasts they had in common. These geometric means were then scaled such that the baseline forecaster had a relative WIS of 1; a relative WIS less than 1 indicated forecast skill that was better than the baseline model. We note that if no forecasts were missing, ${\mathcal{I}}_{m,m^{\prime }}$ would be the same for all model pairs, so that the denominators of each ${\theta }^m$ and of ${\theta }^{\text{baseline}}$ would cancel when normalizing relative to the baseline, and the relative WIS for model $m$ would reduce to the mean WIS for model $m$ divided by the mean WIS for the baseline model. We used the geometric mean to aggregate across model pairs to match the convention set in Cramer et al. (2022), but this detail is not critical: Supplemental Figure 5 illustrates that the relative WIS changes very little if an arithmetic mean is used instead.

We also assessed the probabilistic calibration of the models with the one-sided coverage rates of predictive quantiles, calculated as the proportion of observed values that were less than or equal to the predicted quantile value. For a well-calibrated model, the empirical one-sided coverage rate is equal to the nominal quantile level. A method that generates conservative two-sided intervals would have an empirical coverage rate that is less than the nominal rate for quantile levels less than 0.5 and empirical coverage greater than the nominal rate for quantile levels greater than 0.5.

2.6. Ensemble model formulations

All of the ensemble formulations that we considered obtain a predictive quantile at level $k$ by combining the component forecaster predictions at that quantile level:

$$q_{l,s,t,k}^{\mathrm{ens}}=f(q_{l,s,t,k}^1,\dots ,q_{l,s,t,k}^M).$$

We conceptually organize the ensemble methods considered according to two factors. First, trained ensemble methods use the past performance of the component forecasters to select a subset of components for inclusion in the ensemble and/or assign the components different weights, whereas untrained methods assign all component forecasters equal weight. Second, we varied the robustness of the combination function $f$ to outlying component forecasts. Specifically, we considered methods based on either a (weighted) mean, which can be sensitive to outlying forecasts, or a (weighted) median, which may be more robust to these outliers. The weighted mean calculates the ensemble quantiles as

$$q_{l,s,t,k}^{\mathrm{ens}}=\sum _{m=1}^M{w}_s^m{q}_{l,s,t,k}^m.$$

The weighted median is defined to be the smallest value $q$ for which the combined weight of all component forecasters with predictions less than or equal to $q$ is at least 0.5; the ensemble forecast quantiles are calculated as

$$q_{l,s,t,k}^{\mathrm{ens}}=inf\left\{q\in \mathbb{R}:\sum _{m=1}^M\underset{s}{\overset{m}{w}}{\mathbb{1}}_{(-\infty ,q]}\left(\underset{l,s,t,k}{\overset{m}{q}}\right)\ge 0.5\right\}.$$

In practice, we used the implementation of the weighted median in the matrixStats package for R, which linearly interpolates between the central weighted sample quantiles (Bengtsson, 2020). Graphically, these ensembles can be interpreted as computing a horizontal mean or median of the cumulative distribution functions of component forecasters (Supplemental Figure 7).

In trained ensemble methods that weight the component forecasters, the weights were calculated as a sigmoidal transformation of the forecasters’ relative WIS (see Section 2.5) over a rolling window of weeks leading up to the ensemble forecast date $s$, denoted by ${\mathrm{rWIS}}_s^m$:

$$w_s^m=\frac{exp(-{\theta }_s\cdot {\mathrm{rWIS}}_s^m)}{\sum _{m^{\prime }=1}^{M}exp(-{\theta }_s\cdot {\mathrm{rWIS}}_s^{m^{\prime }})}.$$

This formulation requires estimating the non-negative parameter ${\theta }_s$, which was updated each week. If ${\theta }_s=0$, the procedure reduces to an equal weighting scheme. However, if ${\theta }_s$ is large, better-performing component forecasters (with low relative WISs) are assigned higher weight. We selected ${\theta }_s$ by using a grid search to optimize the weighted interval score of the ensemble forecast over the training window, summing across all locations and relevant target weeks on or before time $s$:

$${\theta }_s=\underset{\theta }{arg\; min}\sum _l\sum _{r=s-1}^{s-a}\sum _{t=r+1}^{min(r+4,s)}\mathrm{WIS}(q_{l,r,t,1:K}^{\mathrm{ens},\theta },y_{l,t}).$$

The size of the training window, $a$, is a tuning parameter that must be selected; we considered several possible values during model development, as discussed below. In a post hoc analysis, we considered regularizing the weights by setting a limit on the weight that could be assigned to any one model. We implemented this regularization strategy by restricting the grid of values for ${\theta }_s$ to those values for which the largest component forecaster weight was less than the maximum weight limit.

In this parameterization, the component forecaster weights are, by construction, non-negative and sum to 1. When forecasts were missing for one or more component forecasters in a particular location and forecast date, we set the weights for those forecasters to 0 and renormalized the weights for the remaining forecasters so that they summed to 1.

Some trained ensembles that we considered used a preliminary component selection step, where the top few individual forecasters were selected for inclusion in the ensemble based on their relative WIS during the training window. The number of component forecasters selected is a tuning parameter that we explored during model development. This component-selection step may be used either in combination with the continuous weighting scheme described above, or with an equally weighted combination of selected forecasters. Throughout the text below, we use the term “trained” ensemble to refer generically to a method that uses component selection and/or weighting based on historical component forecaster performance.

Many other weighted ensembling schemes could be formulated. For example, separate weights could be estimated for different forecast horizons, for different quantile levels, or for subsets of locations. As another example, the weights could be estimated by directly minimizing the WIS associated with look-ahead ensemble forecasts (Taylor & Taylor, 2021). We explored these and other ideas during model development, but our analyses did not show them to lead to substantial gains, and thus we settled on the simpler weighting schemes presented above. Further discussion of alternative schemes is deferred to the supplement.

2.7. Data and code accessibility

All component model forecasts and code used for fitting ensemble models and conducting the analyses presented in this manuscript are available in public GitHub repositories (Cramer et al., 2021, Ray, 2020, Ray, 2021).

3. Results

We discuss the decisions that we made during model development in Section 3.1 before turning to a more focused discussion of the impact on ensemble forecast skill of using robust or non-robust combination mechanisms in Section 3.2, and trained or untrained methods in Section 3.3. Section 3.4 presents a post hoc evaluation of a variation on ensemble methods that regularizes the component forecaster weights. Results for the evaluation using forecasts in Europe are presented in Section 3.5.

Throughout this section, scores were calculated using the ground-truth data that were available as of May 16, 2022 unless otherwise noted. This allowed five weeks of revisions to accrue between the last target end date that was evaluated and the date of the data used for evaluation. When reporting measures of forecast skill, we dropped forecasts for which the corresponding reported value of weekly cases or deaths was negative. This could occur when an error in data collection was identified and corrected, or when the definition of a reportable case or death was changed. We included scores for all other outlying and revised data in the primary analysis because it was difficult to define objective standards for what should be omitted. However, a supplemental analysis indicated that the results about the relative performance of different ensemble methods were not sensitive to these reporting anomalies (Supplemental Section 5.4, Supplemental Figures 14 through 16).

3.1. Model development

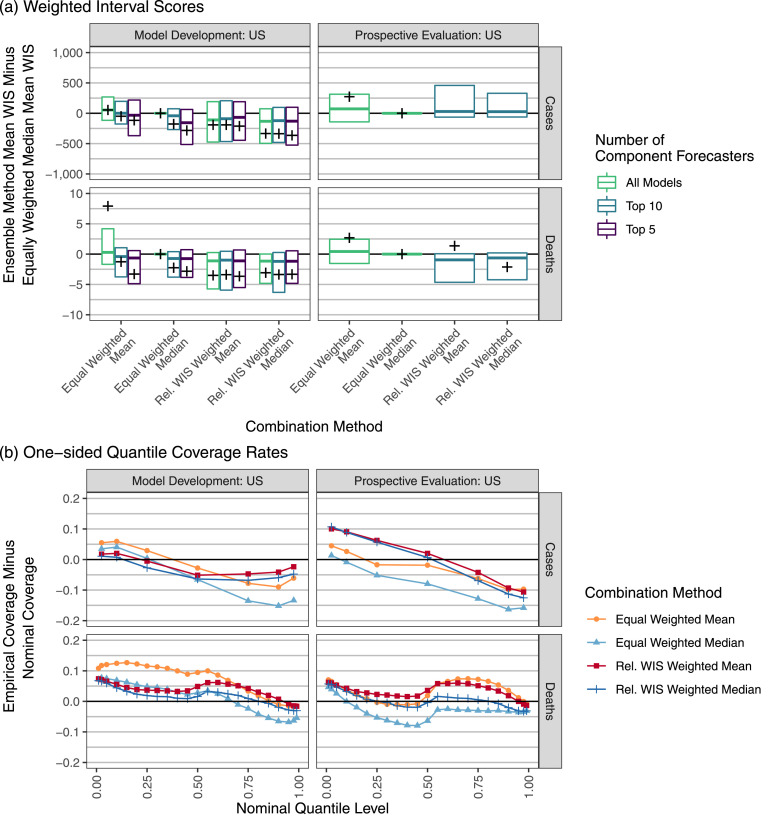
During model development, we evaluated many variations on trained ensemble methods. In these comparisons we take the equally weighted median ensemble as a reference approach because this is the method used for the production ensemble produced by the U.S. Hub during most of the time that we were running these experiments. As measured by the mean WIS over the model-development phase, the equally weighted median ensemble was better than the equally weighted mean ensemble, but both were outperformed by the trained ensemble variations using component forecaster selection and/or weighting (Fig. 3). The weighted approaches had stable performance no matter how many component forecasters were included. Approaches using an equally weighted combination of selected component forecasters were generally better only when top-performing component forecasters were included.

Fig. 3.

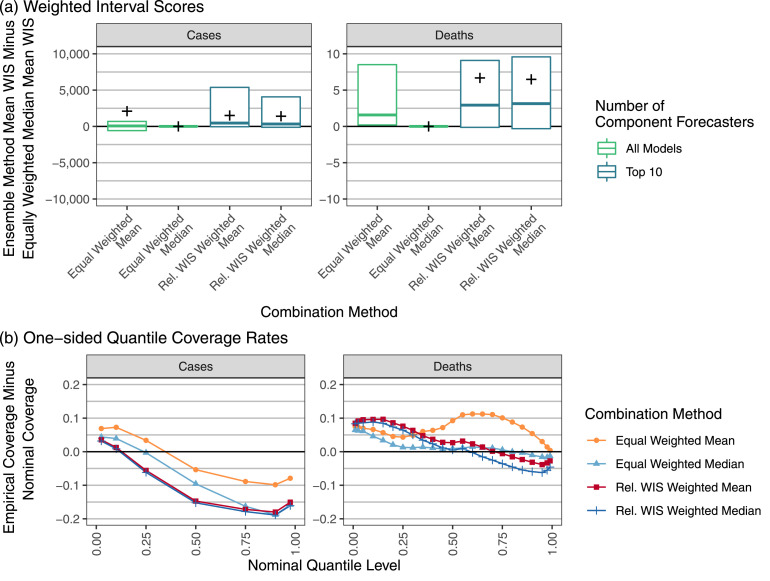
Performance measures for ensemble forecasts of weekly cases and deaths at the state level in the U.S. In panel (a) the vertical axis is the difference in mean WIS for the given ensemble method and the equally weighted median ensemble. Boxes show the 25th percentile, 50th percentile, and 75th percentile of these differences, averaging across all locations for each combination of forecast date and horizon. For legibility, outliers are suppressed here; Supplemental Figure 8 shows the full distribution. A cross is displayed at the difference in overall mean scores for the specified combination method and the equally weighted median averaging across all locations, forecast dates, and horizons. Large mean score differences of approximately 2005 and 2387 are suppressed for the Rel. WIS Weighted Mean and the Rel. WIS Weighted Median ensembles, respectively, in the prospective phase forecasts of cases. A negative value indicates that the given method outperformed the equally weighted median. The vertical axis of panel (b) shows the probabilistic calibration of the ensemble forecasts through the one-sided empirical coverage rates of the predictive quantiles. A well-calibrated forecaster has a difference of 0 between the empirical and nominal coverage rates, while a forecaster with conservative (wide) two-sided intervals has negative differences for nominal quantile levels less than 0.5 and positive differences for quantile levels greater than 0.5.

We also considered varying other tuning parameters, such as the length of the training window and whether component forecaster weights were shared across different quantile levels or across forecast horizons. However, we did not find strong and consistent gains in performance when varying these other factors (Supplemental Figures 17–22). Finally, we evaluated other possible formulations of weighted ensembles, with weights that were not directly dependent on the relative WIS of the component forecasters but were instead estimated by optimizing the look-ahead ensemble WIS over the training set. As measured by the mean WIS, the best versions of these other variations on weighted ensembles had similar performance to the best versions of the relative WIS weighted median considered in the primary analysis. However, they were more sensitive to settings like the number of component forecasters included and the training set window size (Supplemental Figures 17 and 18).

Based on these results, on May 3, 2021 we selected the relative WIS weighted ensemble variations for use in the prospective evaluation, as these methods had similar mean WISs to the best of the other variations considered, but were more consistent across different training set window sizes and numbers of component forecasters included. We used intermediate values for these tuning parameter settings, including 10 component forecasters with a training set window size of 12 weeks. We also included the equally weighted mean and median of all models in the prospective evaluation as reference methods. The following sections give a more detailed evaluation of these selected methods, describing how they performed during both the model-development phase and the prospective evaluation phase.

3.2. Comparing robust and non-robust ensemble methods

We found that for equally weighted ensemble approaches, robust combination methods were helpful for limiting the effects of outlying component forecasts. For most combinations of the evaluation phase (model development or prospective evaluation) and target variable (cases or deaths), the equally weighted median had better mean and worst-case WISs than the equally weighted mean, often by a large margin (Fig. 3, Supplemental Figure 8). Results broken down by forecast date show that the methods achieved similar scores most of the time, but the equally weighted mean ensemble occasionally had serious failures (Supplemental Figure 10). These failures were generally associated with instances where a component forecaster issued extreme, outlying forecasts, e.g., forecasts of deaths issued the week of February 15th in Ohio (Fig. 1).

There were fewer consistent differences between the trained mean and trained median ensemble approaches. This suggests that both trained approaches that we considered had similar robustness to outlying forecasts (if the outliers were produced by component forecasters that were downweighted or not selected for inclusion due to poor historical performance) or sensitivity to outlying forecasts (if they were produced by component forecasters that were selected and given high weight).

Panel (b) of Fig. 3 summarizes probabilistic calibration of the ensemble forecasts with one-sided quantile coverage rates. The median-based ensemble approaches generally had lower one-sided quantile coverage rates than the mean-based approaches, indicating a downward shift of the forecast distributions. This was associated with poorer probabilistic calibration for forecasts of cases, where the ensemble forecast distributions tended to be too low. For forecasts of deaths, which were better centered but tended to be too narrow, the calibration of the median-based methods was not consistently better or worse than the calibration of the corresponding mean-based methods.

3.3. Comparing trained and untrained ensemble methods

Averaging across all forecasts for incident cases and deaths in the model-development phase, the weighted median was better than the equally weighted median, and the weighted mean was better than the equally weighted mean (Fig. 3). However, in the prospective evaluation, the trained methods showed improved mean WIS relative to untrained methods when forecasting deaths, but were worse when forecasting cases. In general, the trained ensembles also came closer to matching the performance of a post hoc weighted mean ensemble for deaths than for cases (Fig. 4, Fig. 5). This post hoc weighted mean ensemble estimated the optimal weights for each week after the forecasted data were observed; it would not be possible to use this method in real time, but it gives a bound on the ensemble forecast skill that can be achieved using quantile averaging.

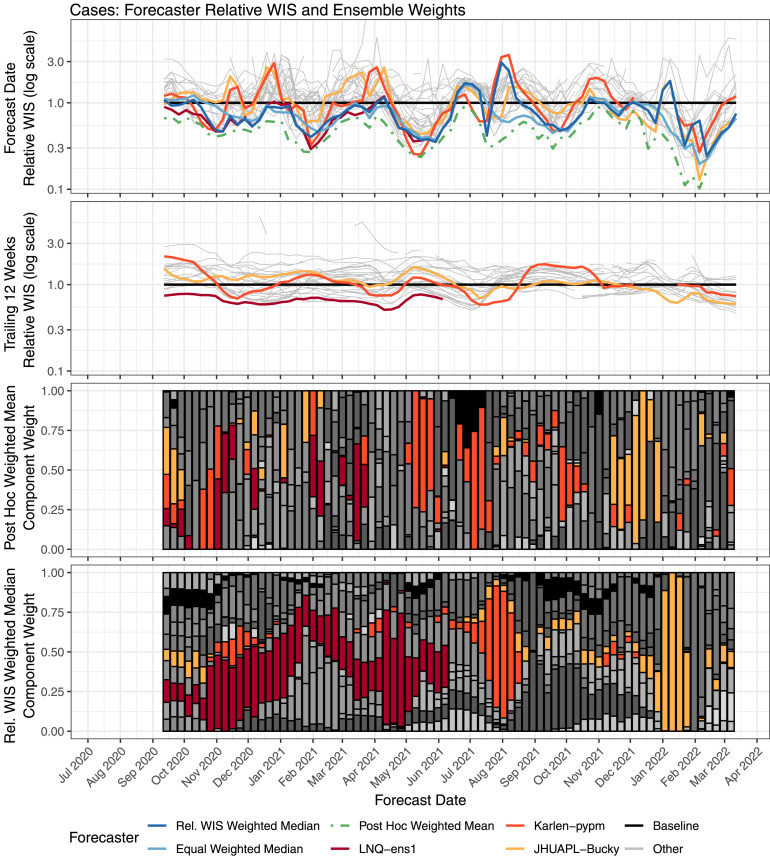
Fig. 4.

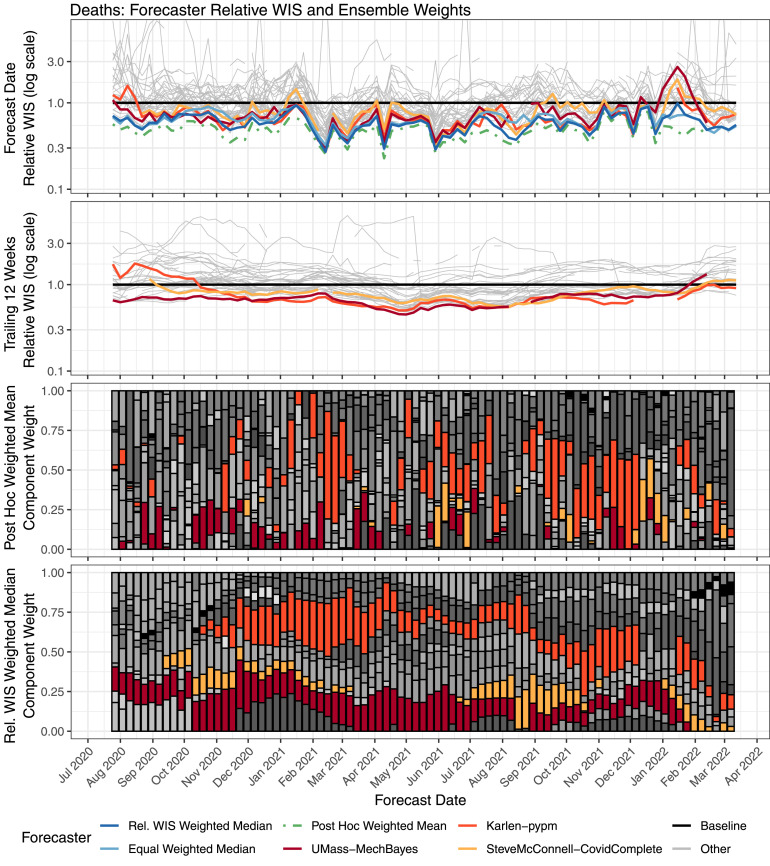
Performance of weekly case forecasts from component forecasters and selected ensembles, along with component forecaster weights. Component forecasters that were given high weight at key times are highlighted. The top row shows the relative WIS of forecasts made each week. The second row shows the relative WIS over the 12 weeks before the forecast date, for forecasts of quantities that were observed by the forecast date. These scores, which are used to compute the component weights in the relative WIS weighted median ensemble, are calculated using data available as of the forecast date. The third row shows component forecaster weights for the post hoc weighted mean ensemble, and the bottom row shows the component model weights for the relative WIS weighted median ensemble; each component forecaster is represented with a different color. Over the time frame considered, 31 distinct component forecasters were included in this top-10 ensemble.

Fig. 5.

Performance of weekly death forecasts from component forecasters and selected ensembles, along with component forecaster weights. Component forecasters that were given high weight at key times are highlighted. The top row shows the relative WIS of forecasts made each week. The second row shows the relative WIS over the 12 weeks before the forecast date, for forecasts of quantities that were observed by the forecast date. These scores, which are used to compute the component weights in the relative WIS weighted median ensemble, are calculated using data available as of the forecast date. The third row shows component forecaster weights for the post hoc weighted mean ensemble, and the bottom row shows the component model weights for the relative WIS weighted median ensemble; each component forecaster is represented with a different color. Over the time frame considered, 34 distinct component forecasters were included in this top-10 ensemble.

We believe that this difference in the relative performance of trained and untrained ensemble methods for cases and deaths is primarily due to differences in component model behavior for forecasting cases and deaths. A fundamental difference between these outcomes is that cases are a leading indicator relative to deaths, so that trends in cases in the recent past may be a helpful input for forecasting deaths—but there are not clear candidates for a similar leading indicator for cases (e.g., see McDonald et al. (2021) for an investigation of some possibilities that were found to yield only modest and inconsistent improvements in forecast skill). Indeed, the best models for forecasting mortality generally do use previously reported cases as an input to forecasting (Cramer et al., 2022), and it has previously been noted that deaths are an easier target to forecast than cases (Bracher et al., 2021, Reich et al., 2021). This is reflected in the performance of trained ensembles, which were often able to identify a future change in the direction of trends when forecasting deaths, but generally tended to predict a continuation of recent trends when forecasting cases (Supplemental Section 7, Supplemental Figures 25 and 26). An interpretation of this is that the component forecasters with the best record of performance for forecasting deaths during the training window were able to capture changes in trend, but the best component forecasters for forecasting cases were often simply extrapolating recent trends. While all ensemble methods tended to “overshoot” at local peaks in weekly incidence, this tendency was more pronounced for forecasts of cases than for forecasts of deaths—and training tended to exacerbate the tendency to overshoot when forecasting cases, but to mitigate this tendency when forecasting deaths (Supplemental Figure 25).

Another difference in component behavior when forecasting cases and deaths is illustrated in Fig. 4, Fig. 5, which explore the relationships between component forecaster performance and the relative performance of trained and untrained ensemble methods in more detail. For deaths, the trained ensemble was able to identify and upweight a few component forecasters that had consistently good performance (e.g., Karlen-pypm and UMass-MechBayes). This led to the consistently strong performance of the trained ensemble; it was always among the best models contributing to the U.S. Hub and was better than the equally weighted median ensemble in nearly every week.

For cases, the trained ensemble also had strong performance for many months when the LNQ-ens1 forecaster was contributing to the U.S. Hub. However, when LNQ-ens1 stopped contributing forecasts in June 2021, the trained ensemble shifted to weighting Karlen-pypm, which had less stable performance for forecasting cases. During July 2021, Karlen-pypm was the only forecaster in the U.S. Hub that predicted rapid growth at the start of the Delta wave, and it achieved the best relative WIS by a substantial margin at that time. However, that forecaster predicted continued growth as the Delta wave started to wane, and it had the worst relative WIS a few weeks later. A similar situation occurred during the Omicron wave in January 2022, when the JHUAPL-Bucky model was one of a small number of forecasters that captured the rise at the beginning of the wave, but it then overshot near the peak. In both of these instances, the post hoc weighting would have assigned a large amount of weight to the forecaster in question at the start of the wave, when it was uniquely successful at identifying rising trends in cases—but then shifted away from that forecaster as the peak neared. Trained ensembles that estimated weights based on past performance suffered, as they started to upweight those component forecasters just as their performance dropped. This recurring pattern highlights the challenge that nonstationary component forecaster performance presents for trained ensembles. Reinforcing this point, we note that in the post hoc weighted mean ensemble, the component forecaster weights are only weakly autocorrelated (Fig. 4, Fig. 5, Supplemental Figure 27), again suggesting that an optimal weighting may require frequently changing component weights to adapt to nonstationary performance.

During the model-development phase, the trained ensembles had better probabilistic calibration than their equally weighted counterparts (Fig. 3, panel (b)). During the prospective evaluation, the trained median ensemble had generally higher one-sided coverage rates, corresponding to better calibration in the upper tail but slightly worse calibration in the lower tail. The trained mean ensemble had slightly better calibration than the equally weighted mean when forecasting deaths in the prospective evaluation phase, but inconsistent gains across different quantile levels when forecasting cases. Supplemental Figures 12 and 13 show that the widths of 95% prediction intervals from both the equally weighted median ensemble and the relative WIS weighted median ensemble tended to rank near the middle of the widths of 95% prediction intervals from the component forecasters. This can be interpreted as an advantage if we are concerned about the possible influence of component forecasters with very narrow or very wide prediction intervals. However, it can also be viewed as a disadvantage, particularly if improved calibration could have been realized if the prediction intervals were wider. We return to this point in the discussion.

3.4. Post hoc evaluation of weight regularization

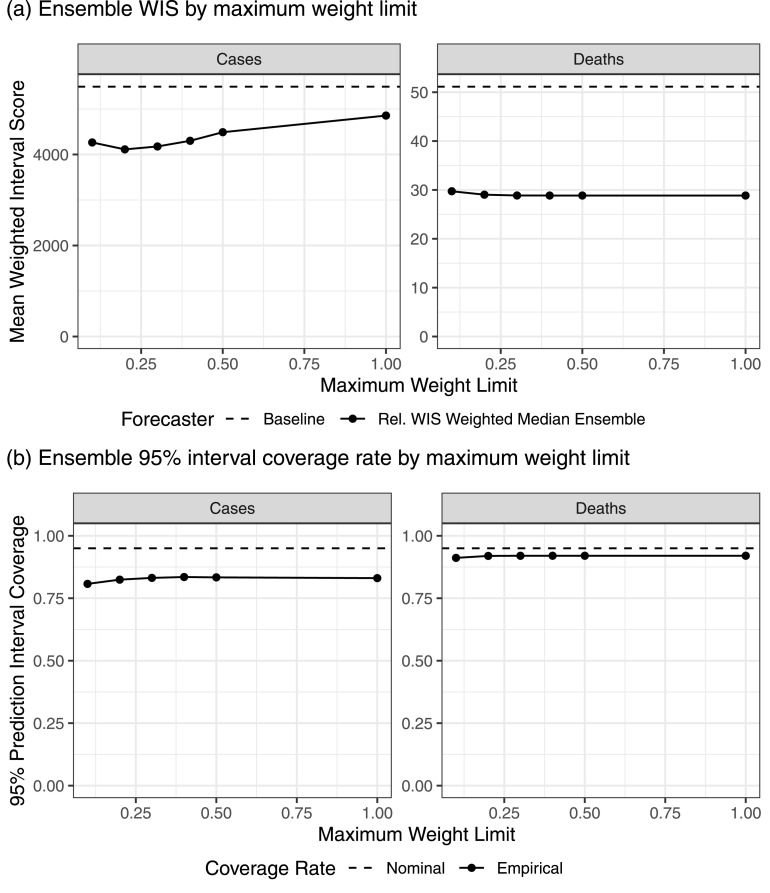
Motivated by the assignment of large weights to some component forecasters in the trained ensembles for cases (Fig. 4), in January 2022 we conducted a post hoc evaluation of trained ensembles that were regularized by imposing a limit on the weight that could be assigned to any one component forecaster (see Section 2.6). In this evaluation, we constructed relative WIS weighted median ensemble forecasts for all historical forecast dates up through the week of January 3, 2022. These ensemble fits included the top 10 component forecasters and were trained on a rolling window of the 12 most recent forecast dates, matching the settings that were selected for the prospective analysis. We considered six values for the maximum weight limit: 0.1, 0.2, 0.3, 0.4, 0.5, and 1.0. A weight limit of 1.0 corresponds to the unregularized method considered in the prospective evaluation, and a weight limit of 0.1 corresponds to an equally weighted median of the top 10 forecasters, which was previously considered during the model-development phase.

For both cases and deaths, the results of this analysis indicate that a weight limit as low as 0.1 was unhelpful (Fig. 6). When forecasting deaths, this regularization strategy had limited impact on the trained ensemble performance as long as the maximum weight limit was about 0.3 or higher, which is consistent with the fact that the trained ensembles for deaths rarely assigned a large weight to one model (Fig. 5). However, when forecasting cases, the regularization resulted in large improvements in mean WIS, with the best WIS at limits near 0.2 or 0.3. These improvements were concentrated in short periods near local peaks in the epidemic waves (Supplemental Figure 28). For both cases and deaths, smaller limits on the maximum weight were associated with a slight reduction in the empirical coverage rates of 95% prediction intervals. Based on these results, the U.S. Hub used a weight limit of 0.3 in trained ensemble forecasts starting in January 2022.

Fig. 6.

Mean WIS and 95% prediction interval coverage rates for relative WIS weighted median trained ensemble variations with varying sizes of a limit on the weight that could be assigned to any one model. In panel (a), the baseline forecaster is included as a reference. Results are for a post hoc analysis including forecast dates up to January 3, 2022.

3.5. Results in the european application

Fig. 7 summarizes weighted interval scores and calibration for the four selected ensemble methods when applied prospectively to forecast data collected in the European Forecast Hub. Consistent with what we observed for the U.S. above, the equally weighted median ensemble was generally better than the equally weighted mean. However, in the European evaluation, the trained methods had worse performance than the equally weighted median for forecasting both cases and deaths.

Fig. 7.

Performance measures for ensemble forecasts of weekly cases and deaths in Europe. In panel (a) the vertical axis is the difference in mean WIS for the given ensemble method and the equally weighted median ensemble. Boxes show the 25th percentile, 50th percentile, and 75th percentile of these differences, averaging across all locations for each combination of forecast date and horizon. For legibility, outliers are suppressed here; Supplemental Figure 9 shows the full distribution. A cross is displayed at the difference in overall mean scores for the specified combination method and the equally weighted median of all models, averaging across all locations, forecast dates, and horizons. A large mean score difference of approximately 666 is suppressed for the Equal Weighted Mean ensemble forecasts of deaths. A negative value indicates that the given method had better forecast skill than the equally weighted median. Panel (b) shows the probabilistic calibration of the forecasts through the one-sided empirical coverage rates of the predictive quantiles. A well-calibrated forecaster has a difference of 0 between the empirical and nominal coverage rates, while a forecaster with conservative (wide) two-sided intervals has negative differences for nominal quantile levels less than 0.5 and positive differences for quantile levels greater than 0.5.

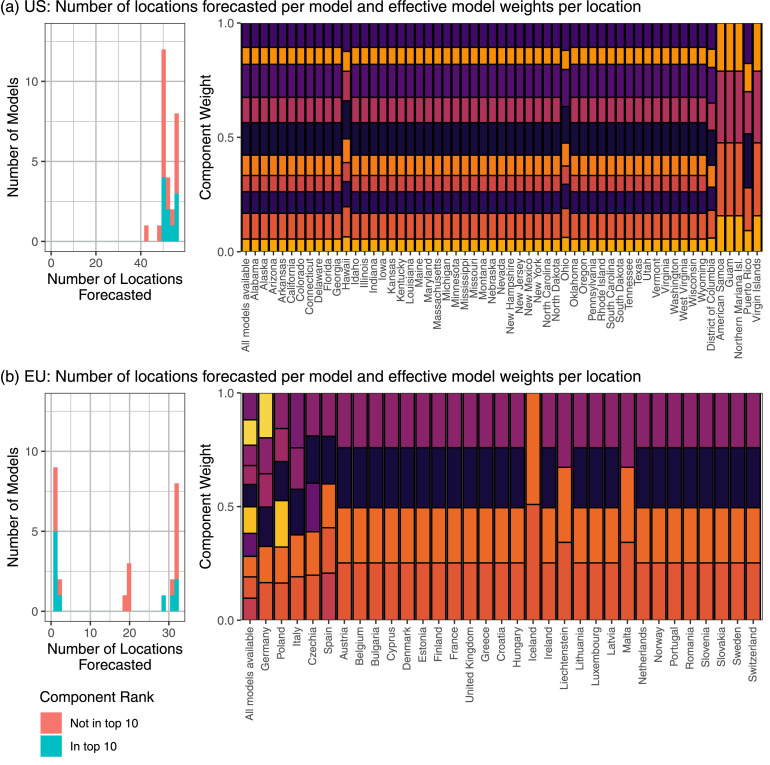
In a post hoc exploratory analysis, we noted that patterns of missingness in forecast submissions are quite different in the U.S. and in Europe (Fig. 8, Supplemental Figures 29 through 36). In the U.S. Hub, nearly all models submit forecasts for all of the 50 states, and many additionally submit forecasts for at least one of the District of Columbia and territories. However, in the European Hub, roughly half of contributing models submit forecasts for only a small number of locations. Because the trained ensembles selected for prospective evaluation select the top 10 individual forecasters by relative WIS, this means that in practice the trained ensembles only included a few component forecasters for many locations in Europe.

Fig. 8.

A comparison of the impacts of forecast missingness in the applications to the U.S. (panel (a)) and Europe (panel (b)). Within each panel, the histogram on the left shows the number of locations forecasted by each contributing forecaster in the week of October 11, 2021, colored by whether or not the forecaster was among the top 10 forecasters eligible for inclusion in the relative WIS weighted ensemble selected for prospective evaluation. The plot on the right shows the estimated weights that would be used if all of the top 10 models (each represented by a different color) were available for a given location (on the left side), and the effective weights used in each location after setting the weights for models that did not provide location-specific forecasts to 0 and rescaling the other weights proportionally to sum to 1. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

4. Discussion

In this work, we documented the analyses that have informed the selection of methods employed by the official U.S. Hub ensemble that is used by the CDC for communication with public health decision-makers and the public more generally. In this context, our preference is for methods that have stable performance across different locations and different points in time, and good performance on average.

Our most consistent finding is that robust ensemble methods (i.e., based on a median) are helpful because they are more stable in the presence of outlying forecasts than methods using a mean. Ensemble methods based on means have repeatedly produced extreme forecasts that are dramatically misaligned with the observed data, but median-based approaches have not suffered from this problem as much. This stability is of particular importance in the context of forecasts that will be used by public health decision-makers. These observations informed our decision to use an equally weighted median ensemble for the official U.S. Hub ensemble early on.

We have seen more mixed success for trained ensemble methods. Overall, trained ensemble methods did well when they were able to identify and upweight component forecasters with good and stable performance, but struggled when component forecaster skill varied over time. In the U.S., trained ensembles have a long record of good performance when forecasting deaths, and the U.S. Hub adopted the relative WIS weighted median ensemble as its official method for forecasting deaths in November 2021. However, trained methods have been less successful at forecasting cases in the U.S., both near peaks in weekly incidence (when they tend to overshoot) and at points where the performance of the component forecasters is inconsistent. Additionally, the trained methods we adopted did not translate well to a setting with a large number of missing component forecasts, as in the European Hub. To preserve the prospective nature of our analyses, we did not examine additional ensemble variations in the European application, but we hypothesize that these problems might be mitigated by including all component forecasters rather than the top 10, or by performing weight estimation separately in clusters of locations where the same component forecasters are contributing. Allowing for different weights in different locations may also be an effective strategy for addressing the impacts of differences in data availability and quality across different locations.

In this manuscript, we focused on relatively simple approaches to building ensemble forecasts. There are several opportunities for other directions that were not considered here, and the gap in performance between the ensemble methods we considered and an ensemble using post hoc optimal weights indicates that there may still be room for improvement in ensemble methods. In our view, the most central challenge for trained ensembles is the inconsistency of the relative performance of many component forecasters, which may in turn be responsible for the lack of strong short-term temporal correlation in the component forecaster weights that were estimated by the post hoc weighted mean ensemble. For models with a relatively long history of performance over multiple epidemic waves, we believe that the most promising approach to addressing this is by using weights that depend on covariates like recent trends in incidence. This might allow the ensemble to learn the conditions in which component forecasters have been more or less reliable, and upweight models locally during phases similar to those in which they have done well in the past. Similar approaches have been used for other infectious disease systems in the past, such as influenza (e.g., Ray & Reich, 2018), but they used a substantial amount of training data over multiple years.

There are several other possible directions for further exploration. We addressed the challenge posed by outlying component forecasts by using median-based combination mechanisms, but another approach would be to pre-screen the component forecasts and remove outlying forecasts. This is a difficult task because there are times when weekly cases and deaths grow exponentially, and occasionally only one or two models have captured this growth accurately (Supplemental Figures 1 and 2). A component screening method would have to be careful to avoid screening out methods that looked extreme relative to the data or other component forecasts but in fact accurately captured exponential growth (see Supplemental Section 1 for more discussion).

Another challenge is that the ensemble forecasts have not always been well calibrated. We are actively developing approaches to address this by post hoc recalibration of the ensemble forecasts. Another possible route forward would be to use a different method for ensemble construction. As we discussed above, the ensemble methods that we considered work by combining the predictions from component forecasters at each quantile level, and therefore tend to have a dispersion that ranks in the middle of the dispersions of the component forecasters. In contrast, an ensemble forecast obtained as a distributional mixture of component forecasts would exhibit greater uncertainty at times when the component forecasts disagreed with each other. However, such an approach would be impacted by extreme component forecasts and would likely require the development of strategies for screening outlying forecasts, as discussed above.

Additionally, our methods for constructing ensemble forecasts do not directly account for the fact that some component forecasters are quite similar to each other and may provide redundant information about the future of the pandemic. Ensembles generally benefit from combining diverse component forecasters, and it could be helpful to encourage this—for example, by clustering the forecasters and including a representative summary of the forecasts within each cluster as the ensemble components. There are also related questions about the importance of different component forecasters to ensemble skill; we plan to explore this direction in future work by using tools such as the Shapley value to describe the contribution of individual components to the full ensemble.

We used the WIS and probabilistic calibration to measure the extent to which forecasts are consistent with the data eventually observed. These summaries of performance are commonly used and provide useful insights into forecast performance, but it is worth noting that they do not necessarily reflect the utility of the forecasts for every particular decision-making context. Aggregated summaries of performance, such as overall quantile coverage rates, could obscure finer-scale details. For instance, a method with good coverage rates on average could have high coverage at times that are relatively unimportant and low coverage when it matters. Additionally, for some public health decision-making purposes, one or another aspect of a forecast may be more important. For example, some users may prioritize accurate assessments about when a new wave may begin, but other users may find accurate forecasts of peak intensity to be more important. Our evaluation metrics do not necessarily reflect the particular needs of those specific end users, and it is possible that different ensemble methods would be more or less appropriate to generate forecasts that serve different purposes.

Careful consideration and rigorous evaluation are required to support decisions about which ensemble methods should be used for infectious disease forecasting. As we discussed above, to obtain an accurate measure of a forecaster’s performance, it is critical that the versions of ground-truth data that would have been available in real time are used for parameter estimation. This applies as much to ensemble forecasters as it does to individual models. Additionally, it is important to be clear about what method development and evaluation were done retrospectively and what forecasts were generated prospectively in real time. We believe that to avoid disruptions to public health end users, a solid evidence base of stable performance in prospective forecasts should be assembled to support a change in ensemble methods. We followed these principles in this work, and we followed the EPIFORGE guidelines in describing our analysis ((Pollett et al., 2021); Supplemental Section 11).

The COVID-19 pandemic has presented a unique challenge for infectious disease forecasting. The U.S. and European Forecast Hubs have collected a wealth of forecasts from many contributing teams—far more than have been collected in previous collaborative forecasting efforts for infectious diseases such as influenza, dengue, and Ebola. These forecasts have been produced in real time to respond to an emerging pathogen that has been one of the most serious public health crises in the last century. This setting has introduced a myriad of modeling difficulties, from data anomalies due to new reporting systems being brought online and changing case definitions, to uncertainty about the fundamental epidemiological parameters of disease transmission, to rapidly changing social factors such as the implementation and uptake of non-pharmaceutical interventions. The behavior of individual models in the face of these difficulties has in turn affected the methods that were suitable for producing ensemble forecasts. We are hopeful that the lessons learned about infectious disease forecasting will help to inform effective responses from the forecasting community in future infectious disease crises.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following is the Supplementary material related to this article.

MMC S1

.