Meta-imputation: An efficient method to combine genotype data after imputation with multiple reference panels

Summary

Genotype imputation is an integral tool in genome-wide association studies, in which it facilitates meta-analysis, increases power, and enables fine-mapping. With the increasing availability of whole-genome-sequence datasets, investigators have access to a multitude of reference-panel choices for genotype imputation. In principle, combining all sequenced whole genomes into a single large panel would provide the best imputation performance, but this is often cumbersome or impossible due to privacy restrictions. Here, we describe meta-imputation, a method that allows imputation results generated using different reference panels to be combined into a consensus imputed dataset. Our meta-imputation method requires small changes to the output of existing imputation tools to produce necessary inputs, which are then combined using dynamically estimated weights that are tailored to each individual and genome segment. In the scenarios we examined, the method consistently outperforms imputation using a single reference panel and achieves accuracy comparable to imputation using a combined reference panel.

Introduction

Genotype imputation, which uses a reference panel of sequenced genomes to estimate unobserved genotypes for samples with sparse microarray data, has been widely used to infer genotypes in genome-wide association studies (GWASs).1, 2, 3 Genotype imputation helps improve power for detecting association signals, facilitates meta-analyses, and enables fine-mapping.^4,5

Over the last decade, large-scale whole-genome-sequencing projects such as 1000 Genomes (1000G),⁶ Haplotype Reference Consortium (HRC),⁷ and the Trans-Omics for Precision Medicine (TOPMed) Program⁸ have produced reference panels that include progressively larger numbers of samples. The successive increase in reference-sample size captures more rare variants and provides higher-resolution mapping in association studies. Although these widely used panels have been steadily increasing in resolution and accuracy, particularly in European-ancestry samples, the optimal choice of panel is often challenging for other ancestries (for example, the smaller 1000G reference panel sometimes outperforms the larger HRC panel in samples of South Asian ancestry^5,8). Furthermore, when imputing samples within a specific study population, smaller customized reference panels exist as alternatives to these widely used public panels and might yield even better imputation quality.^9,10 Examples in which using these customized reference panels can often provide higher accuracy include ongoing studies in Sardinia,¹¹ Finland,¹² Norway,¹³ and Iceland,¹⁴ among many others. Unfortunately, these customized reference panels may miss rare variants and haplotypes that could be covered by larger panels and may perform poorly for individuals with unique ancestry. Therefore, it is desirable to utilize genetic information from both customized panels and large-scale panels.¹⁵

An ideal solution is to construct a combined reference panel. However, different studies tend to use different variant-calling and filtering strategies, which can make it challenging to merge sequencing data.^8,16 It is desirable to consider the union set of variants across studies to use as much of the available information as possible. The gold-standard method to address such discrepancies between multiple datasets is to jointly call variants from all samples using their original sequence alignment files, which is a highly computationally intensive task. A relatively simple substitute for joint variant calling is cross-imputation, in which datasets are used as reference panels for each other and reciprocally imputed up to the union set of variants.¹⁷ Furthermore, another important concern is data-sharing restrictions. For example, individual-level genotype data in many reference panels are not publicly available; it may thus be impossible to directly merge them with other sequencing datasets.

In this paper, we introduce the idea of meta-imputation. Instead of combining the reference panels before imputation, we first impute using different reference panels separately and then combine the imputed results into a consensus dataset. By doing so, we can avoid accessing individual-level genotype data of the reference-panel samples and achieve the goal of improving imputation accuracy by incorporating genetic information from multiple sources.

Material and methods

Meta-imputation consists of two separate steps (Figure S1). First, we impute our target samples against two or more different reference panels. Then, we combine the imputation results using weights that are guided by the empirical performance of each of the panels in stretches of each individual genome. The meta-imputed result at each marker is then a weighted average of the estimated allele counts from imputation against each panel. The weights are individual and region specific and reflect that the optimal choice of reference panel varies along the genome. Weights for each region and individual are estimated through a hidden Markov model (HMM).

Leave-one-out imputation

To determine the optimal weights for each reference panel along the genome, we need to evaluate the performance of each panel along each imputed haplotype. Theoretically, if we knew the true genotype of the target haplotype at a marker, we could quantify the imputation accuracy at that marker by comparing the true genotype with the imputed haploid dosage. In practice, we mimic this approach by leave-one-out (LOO) imputation, in which each genotyped marker is masked and imputed in turn.

Our innovation is to use the genotyped markers in each genome to estimate these local weights for each individual. We do this by masking each observed genotype in turn and then trying to impute it based on information at flanking markers. We call the imputed results from this procedure LOO dosages. We evaluate local imputation performance for each reference panel by comparing the LOO dosages and the original genotypes at the masked sites, and we assign local weights accordingly.

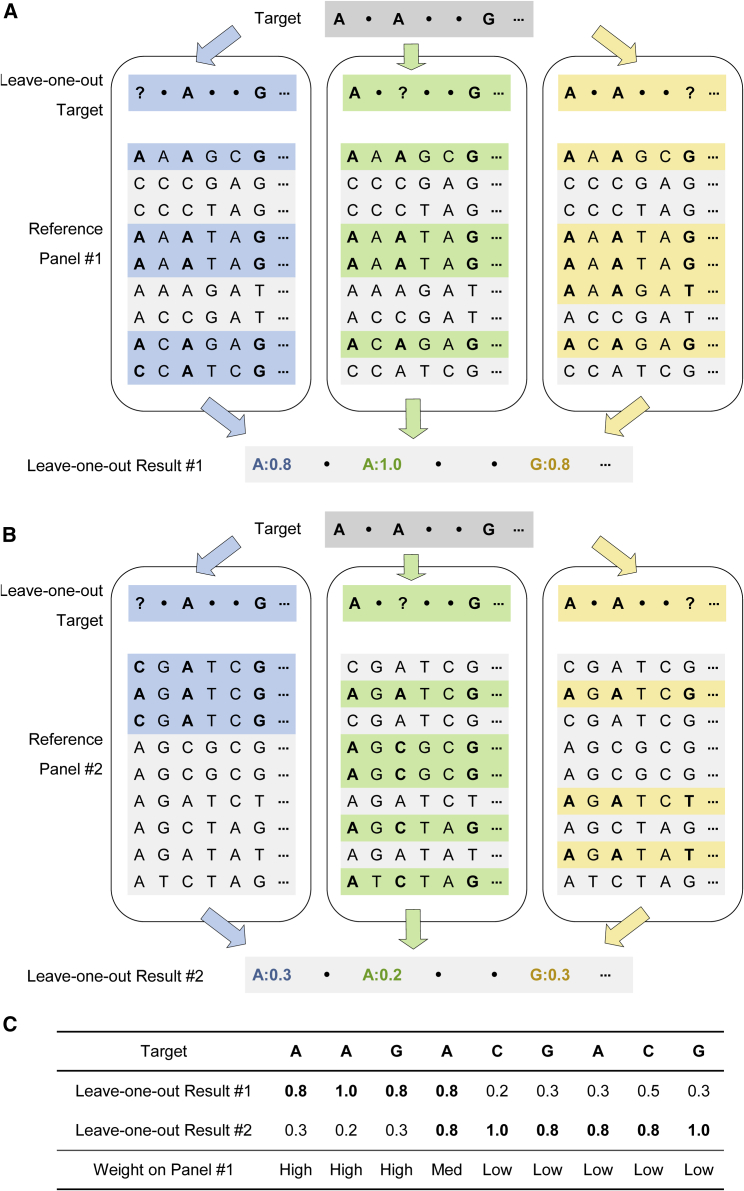
Figures 1A and 1B illustrate a simplified version of the LOO imputation algorithm using two reference panels. For easier understanding, we simplified HMM to estimation based on exact matching haplotypes. The target haplotype is genotyped at three markers (1, 3, and 6). First, we masked the observed allele at marker 1 and searched for matching haplotypes based on marker 3 and marker 6. According to the matching reference haplotypes (shaded in blue), the probability of observing “A” was 0.8 from panel #1 and 0.3 from panel #2. Similarly, we could obtain the LOO results at other genotyped markers. Figure 1C compares the LOO results from the two reference panels along the genome: panel #1 was more accurate at the beginning and panel #2 was more accurate at the end of the chunk, so in the weight-estimation process, we would assign panel #1 high weights at the beginning and low weights at the end of the chunk. Our expectation is that such weights will improve imputation at ungenotyped markers.

Figure 1.

An illustration of leave-one-out imputation

(A–C) LOO imputation on a small chunk of six genotype markers using reference panel #1 and reference panel #2 is illustrated in (A) and (B), respectively. The target haplotype is genotyped at three markers (1, 3, 6). During the LOO imputation procedure, one marker was masked at a time, denoted as “?” The figure simplifies the HMM procedure to estimating LOO results based on exact matching according to the unmasked markers (an HMM is used in the actual algorithm). For example, when performing LOO imputation using reference panel #1, we first masked the observed allele “A” at marker 1 and found five haplotype matches (shaded in blue) based on marker 3 and marker 6. The alleles from the five matches at marker 1 were AAAAC, which suggested a result of “A” with probability 0.8. Thus we determined that the probabilities of observing the true allele at markers 1, 3, and 6 were, respectively, 0.8, 1.0, and 0.8 from panel #1 and 0.3, 0.2, and 0.3 from panel #2. These were compared in (C) along with LOO results at other genotyped markers. Panel #1 was more accurate than panel #2 at the beginning but less accurate at the end, so ideally the weight on panel #1 should be high at the beginning and low at the end.

In practice, the LOO imputation utilizes the same Markov chain as the regular imputation, and the only difference in the model lies in the genotype-emission probability at the masked marker. Let $A_m$ denote the observed allele at marker $m$ in the target haplotype, $H_m$ denote the reference haplotype template at marker $m$, and $M$ denote the number of markers. In the HMM for the regular imputation, the probability of the underlying template at marker $m$ is given in Equation 1.

$$P\left(H_m|A_1,\dots ,A_M\right)\propto P\left(A_m|H_m\right)L_m\left(H_m\right)R_m\left(H_m\right)\text{,}$$ (Equation 1)

where $L_m(\cdot )$ and $R_m(\cdot )$ denote the left probability and right probability for the haplotype template at marker $m$, as defined in Equations 2 and 3, respectively.

$$L_m\left(H_m\right)=\{\begin{array}{l}1,m=1\hfill \\ {\sum }_{H_{m-1}}{L}_{m-1}\left(H_{m-1}\right)P\left(A_{m-1}\right|H_{m-1})P\left(H_{m-1}\right|H_m),1<m\le M\hfill \end{array}$$ (Equation 2)

$$R_m\left(H_m\right)=\{\begin{array}{l}{\sum }_{H_{m+1}}{R}_{m+1}\left(H_{m+1}\right)P\left(A_{m+1}\right|H_{m+1})P\left(H_{m+1}\right|H_m),1\le m<M\hfill \\ 1,m=M\hfill \end{array}$$ (Equation 3)

Assume that the genotype at marker m is observed. When calculating the LOO dosage for marker $m$, the observed genotype is masked and handled as if it were unknown. Hence, the corresponding genotype emission probability $P\left(A_m\right|H_m)$ is set to 1, whereas other components in Equation 1 remain the same as in the regular imputation, which yields the LOO posterior probability $\tilde{P}\left(H_m\right|A_1,\dots ,A_M)\propto L_m\left(H_m\right)R_m\left(H_m\right)$. Let $Y_1,\dots ,Y_N$ denote all the haplotypes in the reference panel and $Y_{n,m}$ denote the alternative allele count at marker $m$ of reference haplotype $Y_n$, then the LOO dosage at marker $m$ is represented as:

$$d_m={\sum }_{n=1}^N{Y}_{n,m}\times \tilde{P}(H_m=Y_n|A_1,\dots ,A_M)\text{.}$$ (Equation 4)

The LOO imputation is a built-in feature in the latest version of our Minimac4 imputation software,¹⁸ which runs at the same time of regular imputation with minimal additional computational cost. The time costs of imputation using Minimac4 with and without the LOO imputation feature are displayed in Table S1. The LOO imputation is computationally inexpensive because it does not require rerunning the forward and backward chains of the HMM that underlie genotype imputation and because it requires limited extra calculations at genotyped markers only.

Model description

We assume that the target genotypes are pre-phased prior to imputation, so that imputation is conducted on the same set of haplotypes using each reference panel in turn. The key meta-imputation problem is thus combining haploid allele dosages estimated using each of the available panels.

Assume that we have $K$ reference panels, containing a union set of $M$ markers, labeled in a chromosome order with indices $\mathrm{1,2},\mathrm{...},M$. For a target haplotype, we denote the imputed haploid dosages at marker $m$ from panel $k$ as $X_{k,m}$, and the meta-imputed haploid dosage at that marker is represented as their weighted average:

$$X_m={\sum }_{k=1}^K{w}_{k,m}{X}_{k,m}m=\mathrm{1,2},\dots ,M\text{,}$$ (Equation 5)

where $w_{k,m}$ represents the weight on panel $k$ at marker $m$, satisfying $0\le w_{k,m}\le 1$ and ${\sum }_{k=1}^K{w}_{k,m}=1$. For each target haplotype, weights are estimated through an HMM that we will describe next. The weights are tailored to each haplotype and vary along the genome. This integration step is implemented in the C++ package MetaMinimac2.

Weight estimation

As inspired by the Li and Stephens model,¹⁹ we use an HMM to estimate reference-panel weights using the LOO dosages and the observed alleles to guide our decisions about which panel is preferred along the genome. In this HMM, the hidden state $S_m$ represents the underlying choice of reference panel at marker $m$, and the emission state $A_m$ represents the observed allele (0, reference allele; 1, alternate allele).

The emission probability $P\left(A_m|S_m\right)$ is defined in Equation 6, where $d_{k,m}$ denotes the LOO dosage from panel $k$ at marker $m$. An ideal choice of reference panel will maximize the probability of the genotypes that are actually observed.

$$\begin{array}{l}P\left(A_m=1|S_m=k\right)=d_{k,m}\hfill \\ P\left(A_m=0|S_m=k\right)=1-d_{k,m}\hfill \end{array}$$ (Equation 6)

The transition probability $P\left(S_m\right|S_{m-1})$ is defined in Equation 7, where ${\lambda }_m$ represents the probability of a change in optimal reference panel between markers $m-1$ and $m$. We have found that our model is not very sensitive to reasonable choices of ${\lambda }_m$, and we typically set ${\lambda }_m=1-e^{-c\cdot dis{t}_m},$ where $dis{t}_m$ is the base-pair distance between the two markers and $c=2\times {10}^{-7}$.

$$P\left(S_m|S_{m-1}\right)=\{\begin{array}{l}\frac{{\lambda }_m}{K},S_m\ne S_{m-1}\hfill \\ 1-{\lambda }_m+\frac{{\lambda }_m}{K},S_m=S_{m-1}\hfill \end{array}$$ (Equation 7)

Finally, these quantities allow us to define the weight for panel $k$ at marker m as the posterior probability $w_{k,m}=P(S_m=k|A_1,\dots ,A_M)$ using the forward and backward algorithm.²⁰

After obtaining the weights at genotyped markers, weights at intervening markers are interpolated from flanking genotyped markers. When calculating the meta-imputed dosage at a specific marker (Equation 5), only reference panels including that marker are considered, and their weights are scaled so they sum to 1.0. An alternative strategy would be to assume a dosage of 0.0 where the marker is absent, avoiding rescaling. The optimal choice of strategy depends on whether markers are generally absent from a panel due to differences in allele frequency between populations and samples or, instead, due to differences in variant calling and filtering protocols.

Empirical assessment #1: African American samples from 1000G

To evaluate the ability of our method to accurately impute the genomes of admixed individuals, we selected a set of 1000G samples with admixed ancestry and created two panels for imputation—one with individuals with mostly European ancestry, and the other with individuals with mostly African ancestry. This setting is challenging because the optimal choice of panel will vary between individuals (depending on their degree of admixture) and also along the genome of each individual (depending on the ancestral origin of each chromosome segment).

Then we focused on 61 African American individuals in the Southwest United States (ASW) and extracted their genotypes for the Illumina Human1M-Duo BeadChip (19,883 out of 1,803,869 variants on chromosome 20) to mimic a typical GWAS dataset. Two reference panels were constructed, one of 503 European (from the 1000G CEU, FIN, GBR, IBS, and TSI samples) individuals and the other including 600 African (from the 1000G ACB, ESN, GWD, LWD, MSL, and YRI samples) individuals. The detailed distribution of reference populations is listed in Table S2. All genotype data and ancestry information are from the 1000G phase 3 release.⁶

We conducted meta-imputation on ASW samples using the European panel and African panel and evaluated the imputation accuracy by calculating aggregated $r^2$ between the imputed results and the masked genotype data. To obtain the aggregated $r^2$, we grouped the markers by the minor allele frequency (MAF) in the entire 1000G dataset. The aggregated $r^2$ for each group is calculated as the squared Pearson correlation between the imputed dosages and the true minor allele counts across the markers in the group.

Empirical assessment #2: Evaluation in South Asian samples from UK Biobank

To illustrate the capability of our method to improve imputation when used together with large reference panels, we tested it on individuals with South Asian ancestry in UK Biobank.²¹ Genomes for these individuals are hard to impute using reference panels such as HRC⁷ and TOPMed⁸ that include relatively few Asian-ancestry individuals despite their size. HRC⁷ and TOPMed⁸ are typically outstanding at imputing missing genotypes in the bulk of the UK Biobank samples, which are of European origin.

The UK Biobank released a whole-exome-sequencing dataset for approximately 50,000 individuals in March 2019.²¹ We imputed the UK Biobank array data across the autosomes and used the exome data as a truth set to evaluate the accuracy of imputed variants. We assigned ancestry to UK Biobank participants by running a supervised ADMIXTURE²² analysis with the Human Genome Diversity Project (HGDP) data²³ as a reference. Using a threshold of 70% genome content to classify an individual into a population, we identified 762 individuals as South Asian.

We meta-imputed genotypes for these 762 South Asian samples (pre-phased using Eagle v2.3.5²⁴ without a reference panel) across the autosomes using the TOPMed release 2 panel, which includes 97,256 individuals,⁸ and the 1000G phase 3 (GRCh38) panel, which includes 2,504 individuals.⁶ We evaluated the imputation accuracy by comparing the imputed results with the exome-sequencing data. For comparison, we repeated the experiment using several individuals with other ancestries and also after adding half of the exome variants to the array dataset, enabling us to evaluate whether the inclusion of rare and low-frequency variants in the scaffold used for imputation might improve results.

Finally, we constructed a combined panel for chromosome 20 by jointly calling the variants in 2,504 1000G samples and 86,594 TOPMed samples from their sequence alignment files, split it into two subpanels with singletons excluded, and compared the performance of meta-imputation and imputation using the combined panel.

Results

Meta-imputation in African American Samples

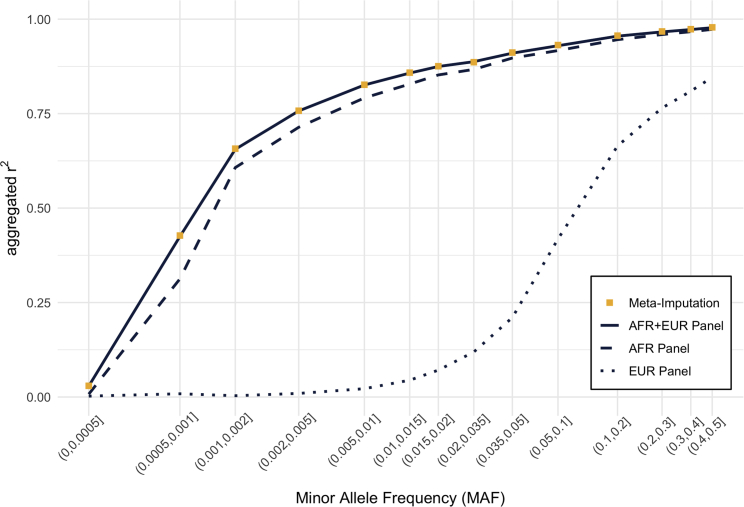
We first evaluated our method in the context of the 1000G ASW samples, using reference panels consisting of other 1000G samples of mainly African ancestry (the AFR panel), mainly European ancestry (the EUR panel), or the combination of all these individuals (the AFR + EUR panel). As shown in Figure 2, meta-imputation achieved the same accuracy as imputation using the combined AFR + EUR panel, which suggests that meta-imputation can serve as an efficient alternative when a combined reference panel is unavailable or impractical. Importantly, our results also show that the accuracy from meta-imputation was substantially greater than that from imputation using a single reference panel. For variants with MAF of 0.05%∼0.1%, meta-imputation achieved higher accuracy ($r^2=0.427$ between imputed dosages and actual genotypes) than imputation using the AFR panel alone ($r^2=0.313$) or using the EUR panel alone (r² = 0.009), and the accuracy of meta-imputation was comparable to that using the AFR + EUR panel ($r^2=0.425$). Overall, we observed the largest advantages of meta-imputation, compared to using one of the smaller panels, for rare variants.

Figure 2.

Comparison of imputation accuracy in African American samples

Imputation accuracy for the pseudo-GWAS ASW dataset was compared among (1) meta-imputation, (2) imputation using the combined AFR + EUR panel including both African and European ancestry genomes, (3) imputation using the homogeneous African (AFR) panel, and (4) imputation using the homogeneous European (EUR) panel. Variants were grouped according to minor allele frequency, which was estimated from the genotype data of 2,504 samples in the 1000 Genomes Project. Aggregated r² values were calculated for each variant group.

Meta-imputation in South Asian Samples

Next, we examined whether the benefits of meta-imputation would extend to settings where very large reference panels are available. Generally, these larger reference panels yield better imputation quality, but there are some exceptions. For example, it has been pointed out that the TOPMed panel sometimes underperforms compared with the much smaller 1000G panel, particularly for ancestries (such as South Asian) that are poorly represented in TOPMed.⁸ For this assessment, we used UK Biobank samples that have been exome sequenced and compared the results of imputation and meta-imputation with those of exome sequencing.

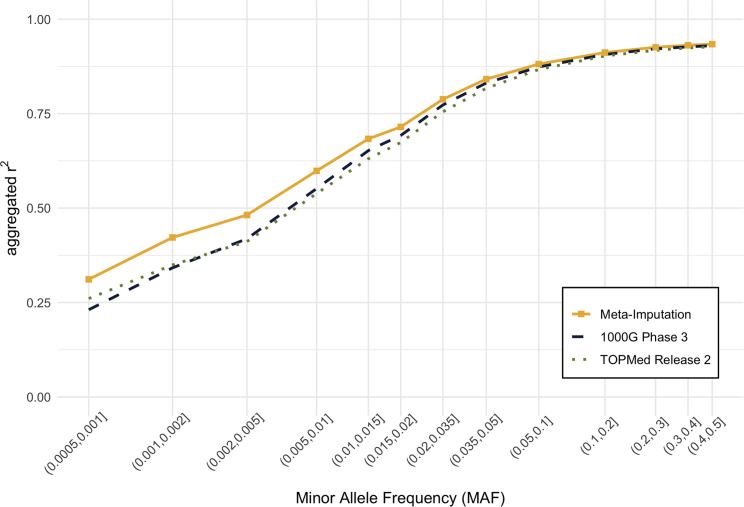
Figure 3 shows that the 1000G panel generally exhibited slightly better accuracy for imputing South Asian genomes than the TOPMed panel for variants with MAF > 0.2%. Our results also suggested that meta-imputation was able to improve the accuracy even further. For example, the imputation quality for variants with MAF of 0.05%∼0.1% increased from $r^2=0.231$ (using the 1000G panel alone) and $r^2=0.260$ (using the TOPMed panel alone) to $r^2=0.311$ (using meta-imputation with the 1000G and TOPMed panel imputation results as input). Also, the number of well-imputed (imputation $r^2>0.3$ reported by imputation software) variants on autosomes increased from 16,480,094 (imputation using 1000G panel) to 25,713,394 (meta-imputation), which suggests that 56% more variants would be available for downstream analyses.

Figure 3.

Comparison of imputation accuracy in South Asian samples

Imputation accuracy for 762 South Asian samples in UK Biobank data was compared among (1) meta-imputation, (2) imputation using 1000G phase 3 (GRCh38) panel, and (3) imputation using the TOPMed release 2 panel. Aggregated r² value was computed based on 918,144 variants shared by the 1000G panel, the TOPMed panel, and UK Biobank whole-exome-sequencing data. Variants were binned according to minor allele frequency, which was estimated from exome-sequencing data for the 762 samples.

We also evaluated a hypothetical combined panel including 1000G and TOPMed samples. For this analysis, we constructed a combined panel including the 1000G samples and most TOPMed samples and repeated the experiment on chromosome 20. The result (Figure S2) shows that meta-imputation achieves accuracy comparable to imputation using the combined panel even in this challenging setting where the reference panels differ greatly in size.

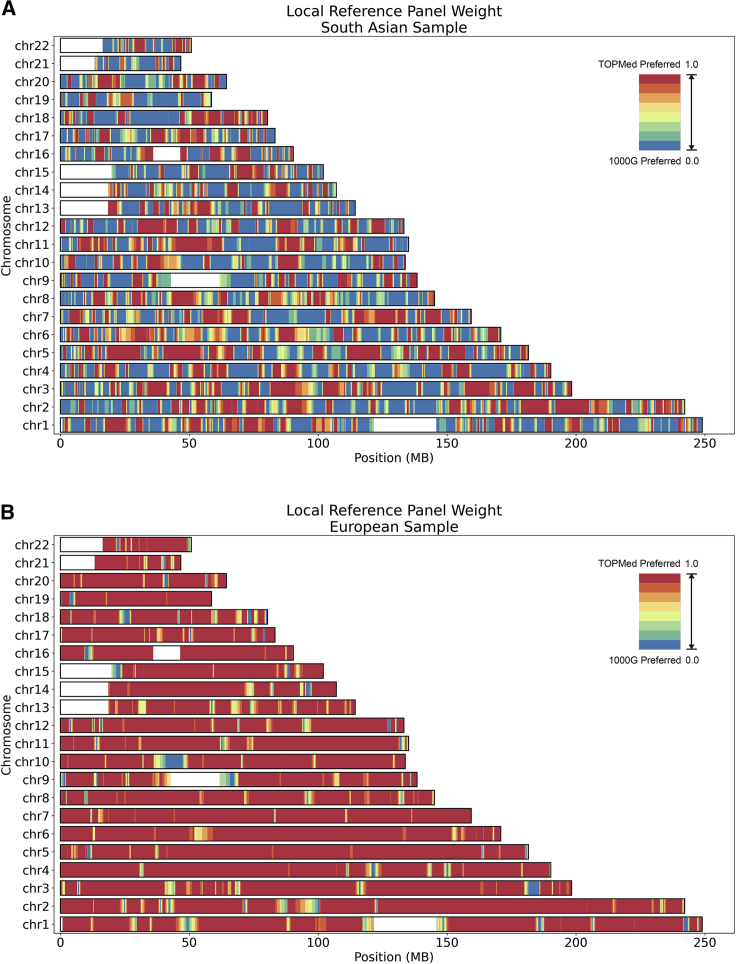
As part of meta-imputation, weights for each reference panel were estimated along each chromosome for each haplotype, reflecting the optimal choice of reference panel at each marker. Figure 4A illustrates the pattern of weights along the genome for a typical sample of South Asian ancestry, where red indicates a preference for TOPMed and blue indicates a preference for 1000G. In the example, both the 1000G panel and the TOPMed panel are favored in substantial portions of the genome. By contrast, meta-imputation generally places a much heavier weight on the TOPMed panel when tackling a European ancestry sample, as shown in Figure 4B.

Figure 4.

Genome-wide summary of weights used in meta-imputation

(A and B) UK Biobank samples were meta-imputed against the 1000G phase 3 panel and the TOPMed release 2 panel. The figures display the local weights on the TOPMed panel from the weight-estimation step, where red indicates a preference for TOPMed and blue indicates a preference for 1000G. (A) corresponds to the analysis of a sample haplotype with South Asian ancestry, where both the 1000G panel and the TOPMed panel were favored in substantial portions of the genome. (B) corresponds to the analysis of a sample haplotype with European ancestry, where the TOPMed panel was nearly always favored.

Computational time

In principle, meta-imputation is relatively inexpensive (computationally), but there are challenging details in implementation, particularly because input and output files can be extremely large. To achieve computational efficiency, in terms of both memory and CPU usage, we first calculate meta-imputation weights for each haplotype at genotyped markers only. The resulting weight matrices can then be used to scan through imputation results one marker at a time, reading panel-specific imputation results, interpolating weights, and outputting weighted meta-imputation dosages. Because meta-imputation combines imputed dosages, the cost of the meta-imputation step depends on the number of genotyped and imputed markers and on the number of individuals being processed, but not on the sizes of the reference-panel samples.

We tested meta-imputation performance on different numbers of individuals (Table 1). For this analysis, we used the 1000G phase 3 and TOPMed release 2 reference panels, which include 6,771,422 markers on chromosome 20 (1000G contains 1,052,215 markers; TOPMed contains 6,631,674 markers; 912,467 markers overlap). The single-core computational times of meta-imputation for 1,000, 2,000, 5,000, and 10,000 target samples are reported in Table 1. Generally, the computational requirements for our implementation of meta-imputation are linear with respect to the number of samples being imputed (earlier implementations were performed in quadratic time because of less-efficient memory and input/output usage). The per-sample time for the imputation step with the 1000G and TOPMed reference panels using Minimac4 was about 20 s and was about 2 s for the meta-imputation using MetaMinimac2. As chromosome 20 accounts for about 2% of the genome, these estimates translate to about 17 min per genome for imputation and 2 min for meta-imputation.

Table 1.

Computational time of meta-imputation for UK Biobank samples

Number of Samples	Time ([hh]:mm:ss)
	Step 1: Minimac4		Step 2: MetaMinimac2	Total
	1000G	TOPMed
1,000	21:57	5:42:37	38:45	6:43:19
2,000	43:34	11:06:08	1:16:57	13:06:39
5,000	1:45:44	26:40:53	3:12:12	31:38:49
10,000	3:34:10	53:15:35	6:14:16	63:04:01

The analysis was conducted on chromosome 20, which involved 17,388 genotyped markers in the target haplotypes and 6,771,422 markers in reference panels. 1000G phase 3 (GRCh38) panel contains 1,052,215 markers; TOPMed release 2 panel contains 6,631,674 markers; 912,467 markers overlap. All tests were conducted on Intel Xeon Platinum 8268 CPU @ 2.90 GHz using one core at a time.

Discussion

We have presented a convenient and efficient meta-imputation framework that enables researchers to merge imputed data generated using multiple reference panels. The meta-imputation procedure consists of two separate steps, imputation and integration, allowing investigators to incrementally consider new reference panels without repeating imputation steps using prior panels. As each panel is added, investigators need only impute the target samples against the new panel and can then combine the results with previously computed imputed result datasets. Our method does not require access to individual-level data from the reference panels and should perform gracefully even when the optimal choice of reference panel varies between individuals or along the genome of each individual. In principle, we expect our method to perform well even when reference panels have partial overlap.

We first illustrated the performance of our method for meta-imputation in samples of African American ancestry using reference panels consisting mainly of European haplotypes, mainly of African haplotypes, or their combination—a challenging situation for meta-imputation. As the proportion of African ancestry will vary between individuals and along the genome of each individual, achieving accurate meta-imputation requires weights that are highly customizable—varying between individuals and along the genome of each individual. We also evaluated our methods in samples of South Asian ancestry using reference panels with a large disparity in size. In these scenarios, meta-imputation not only outperformed imputation using either panel alone but also compared well with imputation against the merged panel in terms of accuracy. Therefore, we propose that it will be safe to use our method even when the reference panels used for the initial imputation step are both sub-optimal, as our MetaMinimac2 algorithm is able to incorporate the best information from the different imputation results to yield much-improved genotype dosages.

Improved imputation accuracy brings greater statistical power in GWASs. In the scenarios we examined (see supplemental information and Figure S4), the power of GWASs using meta-imputed dosages is comparable to the power of a hypothetical GWAS using imputed dosages from a merged panel. A previous recommendation for conducting GWASs when multiple reference panels are available was to conduct multiple GWASs (one for each set of imputation results) and to use the smallest p value at each marker after imputation, carrying out simulations to estimate an appropriate multiple-testing correction.¹⁵ This approach also approximates the power of analysis with a combined panel. One of the reasons is that it may capture some of the features of multiple imputation,²⁵ and we speculate that the power of GWASs using our approach might be further improved in the multiple-imputation framework. Although the best p value also performs well, our approach provides important advantages. First, because it produces a single consensus set of imputed dosages, the computational effort required to analyze additional phenotypes is more modest. Additionally, this consensus set of imputed dosages can serve as input to a variety of additional analyses—including trait co-localization^26,27 and fine-mapping.28, 29, 30

In the scenarios we examined, meta-imputation consistently produced better accuracy than imputation using only one of the available reference panels. However, it is not necessarily the case that every variant would gain in imputation quality. A challenging question concerns handling of variants that are present in only a subset of the reference panels. If a variant is present in one reference panel only, we opted to preserve the original imputed results for that variant. This is appropriate if we expect the presence or absence of a variant to be due to technical reasons, such as arbitrary differences in filtering criteria or accessibility of different parts of the genome using different sequencing technologies. An alternative would be to score variants that are absent from one panel as if they always match the reference genome in haplotypes from that panel, assigning them a dosage of zero. The optimal choice between these two alternatives will depend on the details of how panels were generated and whether panel-specific variants reflect patterns of natural variation or technical artifacts due to variant calling and filtering.

Because meta-imputation works on a per-haplotype basis, its performance relies on the quality of pre-phasing. Switch errors in phasing may result in decreased imputation accuracy and misleading weights, so meta-imputation should directly benefit from evolving phasing algorithms.^24,31,32 The accuracy of meta-imputation could also be affected by factors including the density of genotype array and choice of variants. We would expect that a denser genotype array may bring improved accuracy as it could provide more information and better reflect the local performance of each reference panel. In our experiment (see supplemental information and Figure S3), supplementing the common variant array genotypes with the exome variants did not make a substantial difference in the imputation accuracy. This is because the weights estimated using common variants are also close to the ideal weights for imputation of rare variants.

In the current era, where imputation reference panels are often shared through convenient imputation servers,^7,8,18 which increase user convenience and protect genetic information in the panel, our approach allows results from different servers to be combined and also allows researchers who create their own panels to combine results generated using these panels with results generated from one or more imputation servers. We hope that these meta-imputation strategies will continue to extend the reach of imputation toward rarer and rarer variants and facilitate studies in diverse populations, where supplementing publicly available reference panels with complementary targeted panels is likely to be especially useful.

Published: May 3, 2022

Web resources

• 1000 Genomes Project, https://www.internationalgenome.org/

• ADMIXTURE software, https://dalexander.github.io/admixture/

• Eagle 2 software, https://alkesgroup.broadinstitute.org/Eagle/

• Human Genome Diversity Project, https://www.hagsc.org/hgdp/

• Michigan Imputation Server, https://imputationserver.sph.umich.edu

• Minimac4 software, https://github.com/statgen/Minimac4

• TOPMed Imputation Server, https://imputation.biodatacatalyst.nhlbi.nih.gov

• Trans-Omics for Precision Medicine Program, https://topmed.nhlbi.nih.gov

• UK Biobank, https://www.ukbiobank.ac.uk

Data and code availability

The MetaMinimac2 software is written in C++ and can be downloaded from https://github.com/yukt/MetaMinimac2. The tool for calculating aggregated $r^2$ between imputed results and true genotypes is available at https://github.com/yukt/aggRSquare. Michigan Imputation Server and TOPMed Imputation Server provide free genotype imputation services using Minimac4 with the option to generate necessary input files for MetaMinimac2.