Abstract
This article describes dynamical simulations of the assembly of an icosahedral protein shell around a bicomponent fluid cargo. Our simulations are motivated by bacterial microcompartments, which are protein shells found in bacteria that assemble around a complex of enzymes and other components involved in certain metabolic processes. The simulations demonstrate that the relative interaction strengths among the different cargo species play a key role in determining the amount of each species that is encapsulated, their spatial organization, and the nature of the shell assembly pathways. However, the shell protein–shell protein and shell protein–cargo component interactions that help drive assembly and encapsulation also influence cargo composition within certain parameter regimes. These behaviors are governed by a combination of thermodynamic and kinetic effects. In addition to elucidating how natural microcompartments encapsulate multiple components involved within reaction cascades, these results have implications for efforts in synthetic biology to colocalize alternative sets of molecules within microcompartments to accelerate specific reactions. More broadly, the results suggest that coupling between self-assembly and multicomponent liquid–liquid phase separation may play a role in the organization of the cellular cytoplasm.
I. INTRODUCTION
Compartmentalization is essential for many biological functions, including metabolism, cellular signaling, and genetic storage. While membrane-enveloped organelles are a prominent mode of compartmentalization in eukaryotic cells, it has become apparent that liquid–liquid phase separation1–14 and proteinaceous organelles15–17 play an important role in organizing the cytoplasm for all kingdoms of life. For example, in bacteria, certain metabolic pathways are enabled by bacterial microcompartments, which are organelles consisting of a large protein shell assembled around a dense complex of enzymes and reactants.18–25 Other protein-shelled compartments include encapsulins26,27 and gas vesicles26,28 in bacteria and archaea and vault particles in eukaryotes.29 From a practical perspective, there is great interest in exploiting principles and materials from biology to achieve similar nanoscale compositional control for synthetic biology and drug delivery applications. In particular, researchers have demonstrated the ability to target new molecules to microcompartment interiors and to transfect the systems into non-native organisms, including bacterial and plant cells, suggesting a basis for designing microcompartments as customizable nanoreactors (e.g., Refs. 22 and 30–43).
Many of these cellular functions and biotechnology applications require compartments that assemble around multiple cargo species. For example, metabolism relies on achieving high local concentrations of the enzymes and reactants involved in a reaction cascade, while the formation of cellular signaling complexes requires colocalizing signaling proteins and their regulatory ligands.11,21,44 Similarly, applications in synthetic biology require targeting multiple species to microcompartment interiors (e.g., Refs. 22, 24–26, 30, 31, 34–43, and 45–52). In particular, microcompartments could be exploited to increase the efficiency of arbitrary multienzyme cascades if the species are encapsulated with controlled stoichiometry. Thus, understanding the factors that control the amount and composition of packaged cargo is essential for understanding both natural and reengineered functions of microcompartments.
Previous experimental and modeling studies of microcompartments and other shells provide an important starting point for understanding multicomponent encapsulation. The outer shells of microcompartments are roughly icosahedral, with diameters ranging from 40 to 400 nm, and assemble from pentameric, hexameric, and pseudo-hexameric (trimer-of-dimer) protein oligomers.18,19,26,53–59 Recent atomic-resolution structures of small, empty microcompartment shells, as well as computational modeling,60–67 have elucidated mechanisms that control the structure and size of microcompartment shells. More broadly, previous modeling studies have shown the assembly of empty icosahedral shells68–94 and templating effects of a cargo consisting of a nanoparticle or RNA molecule on shell assembly.75,81–83,95–119 However, alternative models are needed for microcompartment encapsulation of multicomponent cargo complexes that do not have a specific size, structure, or composition.
Although previous experiments successfully targeted particular cargo species to microcompartment interiors,22,30–43 the factors that control cargo coalescence and encapsulation remain incompletely understood. In some microcompartments, shell–cargo attractions are mediated by “scaffold proteins” such as the CcmN protein in β-carboxysomes,120 while in other systems core enzymes have a short “encapsulation peptide” sequence that binds to the shell inner surface.26,31,35–37,39,121 Similarly, cargo–cargo attractions may be mediated by scaffolds, such as CcmM in β-carboxysomes120 or potentially through direct pair interactions between cargo molecules.36,37
Previous experimental and modeling studies suggest that the packaged cargo of microcompartments undergoes phase separation, either prior to or during assembly of the outer protein shell.60–62,65,120,122–126 Furthermore, some microcompartments fulfill similar functions as liquid–liquid phase separated domains in cells—for example, the composition, structure, and function of the RuBisCO complex within carboxysomes have strong similarities to those of the pyrenoid, which is a liquid domain consisting of RuBisCO and other components that enables carbon fixation within plant cells.127–130 It is, therefore, likely that some factors that control the composition of liquid–liquid phase separated domains in cells (e.g., Refs. 2, 6, 8, 10, 12–14, and 131–145) also affect the composition of microcompartment cargoes. However, in the case of microcompartment assembly, thermodynamic and kinetic factors resulting from coupling between liquid–liquid phase separation and assembly of the crystalline shell could have significant effects. Previous computational modeling of microcompartment assembly has focused on encapsulation of a single cargo species, either driven by direct cargo–cargo pair attractions60,61,65 or mediated by scaffolds.62
In this work, we build on these previous studies, by studying a minimal computational model for a microcompartment shell that assembles around a cargo containing two species. We investigate the amount and composition of the encapsulated cargo as a function of the affinities among these cargo species, and of the shell–cargo and shell–shell affinities. The simulation results suggest that the relative cargo–cargo affinities are the most important factor in determining the amount and composition of packaged cargo. However, within certain parameter ranges, varying the shell–cargo and shell–shell affinities provides an alternative means to sensitively control the packaged cargo. These effects are governed by a combination of thermodynamic and kinetic factors arising due to coupling between cargo coalescence and shell assembly.
II. RESULTS AND DISCUSSION
A. Model overview
We simulate the dynamics of microcompartment assembly in the presence of two cargo species, which we denote as “R” and “G.” There are numerous control parameters in the microcompartment system, many of which have been explored in previous studies.60–67 Here, our objective is to focus on the effect of interaction parameters on cargo encapsulation. To avoid complexities associated with assembly into different shell geometries,61,62,65,66 we use a minimal model for the shell developed in Perlmutter et al.,60 for which the energy minimum corresponds to a T = 3 icosahedral shell in the Caspar–Klug nomenclature,146 comprising 12 pentamers and 20 hexamers (Sec. IV A and Fig. 1). Although our model is motivated by bacterial microcompartments, it is sufficiently general to describe other proteinaceous shells, including viruses and microcompartments that are reengineered to encapsulate designer cargoes (e.g., Refs. 22, 30–39, 41, 46–48, 50–52, and 147–156).
FIG. 1.
Description of the model. (a) Each shell subunit contains “Attractors” (green circles) on the perimeter, which define the shape of the subunit. (b) Attractive interactions between Attractors drive subunit dimerization. Complementary pairs of Attractors are indicated by green arrows in (a) for the pentamer–hexamer interface and in (b) for the hexamer–hexamer interface. A combination of Top–Top (T) and Bottom–Bottom (b) repulsions controls the subunit–subunit angle in a complete shell. (c) Bottom pseudoatoms “B” bind cargo molecules (shown as R and G). (d) The cargo molecules have attractive interactions between each other that depend on pair type.
1. Interaction parameters
Efficient assembly and cargo loading generically require three classes of interactions: interactions between shell subunits that drive shell assembly, interactions between shell subunits and one or more cargo species, and interactions between cargo particles that drive cargo coalescence.60 While in some systems, one or more of these interactions can be mediated by auxiliary proteins (e.g., the CCmM and CCmN proteins in β-carboxysomes), for simplicity we model all interactions as direct pair interactions in this work.
We have explored assembly dynamics over a range of the simulation control parameters that most strongly affect the amount and composition of encapsulated cargo—these are the interaction potential well-depths that control the binding free energy (affinity) between each type of cargo pair, ɛGG, ɛRR, and ɛRG, as well as between shell–cargo and shell–shell pairs, ɛSC and ɛSS (see Appendix B). To minimize the number of parameters, we assume that both cargo species have the same binding affinity to shell subunits; i.e., ɛSC is equal for R and G particles. For convenience, throughout this article, we refer to the well-depths as “affinities.” We approximately relate ɛSC and ɛSS to the actual affinities in Appendix A and Table I. Throughout this article, all energy values are given in units of the thermal energy, kBT, and all lengths are given in units of the cargo diameter, r∗, which translates to r∗ ≈ 13 nm for carboxysomes (see Sec. IV B).
TABLE I.
The shell–shell binding affinity for the default affinity parameter values. The binding free energy and dissociation constant for hexamer dimerization [ghh, from Eq. (A1)] and from the shell–shell and shell–cargo interactions in a complete shell complex with ɛSC = 6 kBT [from Eq. (A3)]. The standard state concentration is 1M. *Does not include cargo–cargo contributions, which will increase (decrease) the effective shell dissociation constant below (above) the threshold for cargo vapor–liquid coexistence (see Perlmutter et al.60).
| Shell–shell affinity parameter | ɛSS/kBT | 2.0 | 3.5 |
| Hex–hex affinity | ghh/kBT | 4 | −0.5 |
| Hex–hex dissociation constant | M | 7 × 107 | 6 × 105 |
| Free energy per subunit in shell* | Δgshell/kBT | −15 | −27 |
| Dissociation constant from shell* | M | 0.4 | 1 × 10−6 |
We consider ranges of affinity parameters relevant to biological microcompartments (see Sec. IV B for details). Except where mentioned otherwise, we consider two shell–shell affinities (ɛSS/kBT = 2, 3.5), which are, respectively, below and above the transition between one-step and two-step assembly pathways (discussed in Sec. II C). Both cases are below the threshold for assembly of empty shells (containing no cargo). Importantly, dimerization is very unfavorable, but the assembled shells are stable (see Table I). The unfavorable dimerization affinities reflect the essential role that cargo plays in assembly at these shell–shell affinities, the cooperative nature of assembly, and the fact that a significant nucleation barrier is essential to avoid kinetic traps.60,80,89,157 We primarily focus on a representative shell–cargo affinity ɛSC = 6 kBT, which corresponds to a free energy per shell subunit of gSC ≈ −14 kBT. Our simulations span the range of cargo–cargo affinities in the vicinity of vapor–liquid coexistence (ɛvl ≈ 1.3 kBT at our simulated cargo concentration), but they remain below the threshold for cargo crystallization at ɛfs ≈ 3 kBT. With ɛvl as a reference point, we denote cargo–cargo affinities as “weak” for ɛRR ≲ 1.1 kBT, “moderate” for 1.2 ≲ ɛRR ≲ 1.4, and “strong” for ɛRR ≳ 1.5 kBT (with analogous definitions for ɛGG and ɛRG).
Our shell subunit and cargo concentrations map to ∼1 and 10 μM, respectively, which are reasonable based on quantities found within bacterial cells.
2. Simulated systems
There are multiple thermodynamic and kinetic factors that could influence the amount and composition of encapsulated cargo. Thermodynamic effects include the interplay between cargo–cargo and shell–cargo affinities, and the finite size of the encapsulated cargo globule. Kinetic effects arise from the fact that once a shell closes, even with relatively weak shell–shell affinities typical of productive assembly, exchange of shell subunits or cargo particles does not occur on experimentally relevant timescales. Thus, an assembling shell may trap its contents far out of equilibrium. To distinguish these effects, we begin by describing large simulations of cargo in the absence of shell subunits to approximate a bulk system (Sec. II B). We then describe the dynamical assembly of shells and cargo particles (Secs. II C and II D). We compare the results of these finite-time dynamical simulations against simulations with assembled but permeable shells, which allow the encapsulated cargo to equilibrate with the bulk.
B. Cargo phase behavior without shell subunits
We begin by briefly summarizing the bulk phase behavior of the cargo in the absence of shell subunits, as a reference point from which to understand how shell assembly can change cargo coalescence. We focus on parameter regimes relevant to our shell assembly simulations; more comprehensive descriptions of the phase behavior of a binary Lennard-Jones (LJ) system can be found in, e.g., Refs. 158–160. In particular, we consider equal stoichiometry between R and G molecules and cargo–cargo affinities (ɛij < 1.8 for ij = RR, GG, RG) that maintain the system in vapor and/or liquid phases but are below the crystallization threshold (the vapor–fluid and crystallization transitions for a single species occur at ɛvl = 1.3 and ɛfs ≈ 3). Within these limits, the phase behavior can be classified as follows: homogeneous demixed (no phase coexistence), phase separation of one cargo species (a dense phase rich in one cargo species in coexistence with a dilute phase containing an excess of the other), phase separation and mixing of both cargo species (coexistence between dilute and dense phases, with both species homogeneously mixed within both phases), and phase separation with demixing (coexistence between three phases—a dilute phase, a dense phase rich in R, and a dense phase rich in G). We consider weak, moderate, and strong R–G affinities: ɛRG = 1.0, 1.3, 1.6. For each of these, Fig. 2 summarizes the bulk phase behaviors as a function of the R–R and G–G affinities ɛRR and ɛGG. Specifically, Figs. 2(a)–2(c) compare the driving force for phase separation for each of the two species by showing the fraction of R particles fR in the high-density phase (hereafter referred to as “globule”). Figures 2(d)–2(f) quantify the extent of nonrandom compositional mixing within the high-density phase, fUL. Here, we define the mean fraction of unlike neighbors in the first solvation shell around each particle as , with nij the number of cargo neighbor pairs of species i and j with a neighbor pair defined as two particles with separations of r < 1.2. For random mixing, we expect frand = 2fR(1 − fR), so the plots indicate the difference between randomness and the results: .
FIG. 2.

The bulk phase behavior of cargo particles (in the absence of shell subunits) as a function of their binding affinities. (a)–(c) The fraction of R particles in the high-density phase, fR, as a function of the R–R and G–G affinities for different R–G affinities: (a) weak ɛRG = 1.0, (b) moderate ɛRG = 1.3, and (c) strong ɛRG = 1.6. All energies are given in units of the thermal energy, kBT. The symbols on the plot identify corresponding snapshots below each plot that illustrate the phase behavior at the indicated value of ɛRG. (d)–(f) For the same parameters, the fraction of unlike cargo particles in the first solvation shell relative to random mixing, fUL, defined in the text. Each simulation contains 46 938 total cargo particles, with equal composition of R and G.
For weak R–G affinities [ɛRG = 1.0, Fig. 2(a)], the system exhibits no phase separation, coexistence between a phase rich in one species and a dilute phase, or coexistence among a dilute phase and separate phases for each species. In the latter case, the R-rich and G-rich phases are attracted to each other by the weak but nonzero R–G affinities, leading to formation of one globule with an interface separating the two phases. The interface between these two phases becomes more diffuse with decreasing ɛRR and ɛGG and/or increasing ɛRG because the surface tension between the two domains decreases. For moderate R–G affinities, i.e., ɛRG = 1.3, Fig. 2(b), we observe no phase separation, coexistence between a phase rich in one species and a dilute phase, or coexistence between a dilute phase and a dense phase containing both species.
For strong R–G affinities [ɛRG = 1.6, Fig. 2(c)], we always observe mixing of both species within the dense phase, with the fraction of R or G particles depending on the relative magnitudes of ɛRR and ɛGG. Since the primary driving force for phase separation is ɛRG in this case, fluctuations in fR and fUL are smaller than for the other systems.
C. Assembly pathways
We now consider how cargo and shell affinities affect the dynamics of assembly and cargo encapsulation. In a previous work, simulations with a single cargo species showed that assembly pathways are strongly affected by the net strength of cargo–cargo affinities.60 In particular, at our simulated volume fraction of 0.003, weak cargo–cargo affinities (ɛRR < 1.7) and/or the higher shell–shell affinities (ɛSS > 2.5) lead to one-step pathways in which shell assembly is concomitant with cargo coalescence, while strong cargo–cargo and lower shell–shell affinities (ɛRR > 1.7 and ɛSS < 2.5) allow two-step pathways in which a cargo globule coalesces, followed by disordered adsorption of shell subunits onto the globule surface and then cooperative rearrangement into an assembled shell. Other interaction combinations, such as high cargo–cargo and shell–shell affinities, lead to pathways in between these two extremes.
The case of two cargo species exhibits qualitatively similar classes of assembly pathways. Figures 3(a) and 3(b) show snapshots from typical simulations at shell–shell affinity ɛSS = 3.5, leading to one-step assembly pathways. In Fig. 3(a), the cargo–cargo affinities are uniform and relatively strong ɛRR = ɛGG = ɛRG = 1.7, leading to rapid and simultaneous coalescence of cargo and shell assembly, resulting in a uniform mixture of both cargo types within the complete shell (Multimedia view). In Fig. 3(b), the R–R affinities (ɛRR = 1.7) are stronger than the G–G and R–G affinities (ɛGG = ɛRG = 1.3), leading to simultaneous assembly and coalescence of a nearly pure R domain (Multimedia view).
FIG. 3.

Figures 3(c)–3(e) show trajectories with a weaker shell–shell interaction of ɛSS = 2.0, for which shell nucleation is slow and we observe two-step assembly pathways. In Fig. 3(c), the cargo–cargo affinities are strongest for R–R, and the assembly pathway closely resembles that for a single species—a domain of nearly pure R particles condenses, with subsequent assembly and encapsulation by the shell (Multimedia view).
We observe a more interesting coupling between cargo composition and shell assembly for strong R–R and G–G affinities (ɛRR = ɛGG = 1.7) and moderate R–G affinities ɛRG = 1.3 [Fig. 3(d)]. The cargo initially coalesces into a globule that is mixed, albeit with significant compositional fluctuations, consistent with the bulk cargo phase behavior under these parameters [the purple filled hexagon in Fig. 2(b)]. At these parameters, the domain is large enough to form two shells and shell closure couples to compositional fluctuations and occurs preferentially in the vicinity of an interface between R-rich and G-rich domains. In particular, we observe closure at the interface and consequently purified cargo encapsulation, meaning that the encapsulated cargo within an individual shell is nearly pure R or G (Multimedia view).
The origins of coupling between shell closure and compositional fluctuations can be understood from the competing forces that govern shell closure. For the shell to close, curvature of the assembling shell must first generate the formation of a “neck” of cargo, i.e., a narrow region of cargo particles that connects a shell assembly to the remainder of the globule or to other assemblies [e.g., see Fig. 3(d) at t = 43 and Fig. 3(e) at t = 34]. Then, additional shell subunits must assemble to close the shell, causing the neck to break and the completed shell to separate from the remainder of the globule [Fig. 3(d) at t = 224 and Fig. 3(e) at t = 143]. The processes of forming and then breaking the neck increase the total cargo interfacial area and correspondingly reduce the number of cargo–cargo interactions. Thus, they are accompanied by a free energy barrier with a height that increases with cargo surface tension and correspondingly increases with cargo–cargo affinity. In Fig. 3(e), the R–R affinities are stronger (ɛRR = 2.0), resulting in a larger barrier for closure within the R-rich portion of the globule, and thus a complete shell forms only around G particles (Multimedia view).
1. Shell closure locks the encapsulated cargo composition out of equilibrium
After a shell closes, fluctuations of subunits large enough to allow cargo particles to escape are extremely rare because all subunits have their maximum number of interactions. Thus, the cargo composition is essentially fixed once the shell completes. However, as noted in Sec. II D, the cargo remains fluid in the range of cargo–cargo affinities that we focus on, and, thus, the cargo can spatially reorganize inside of the shell even after its completion.
D. Factors that control the composition of encapsulated cargo
1. Cargo–cargo affinity
Under most conditions, the cargo–cargo affinities have the strongest effect on the amount and composition of encapsulated cargo. We begin by considering one-step assembly pathways obtained with moderate shell–cargo affinities ɛSC = 6.0 and the higher shell–shell affinities ɛSS = 3.5. These conditions allow assembly over a broad range of cargo–cargo affinities.
Figures 4–7 show observables that characterize cargo properties, as well as the assembly yield, quantified as the fraction of subunits within complete shells [fs, Fig. 4(d)]. Because the most interesting variations occur at moderate R–G affinities, we present most results in this figure with varying R–R and G–G affinities at fixed ɛRG = 1.3. First, Fig. 4(c) shows that the amount of packaged cargo increases monotonically with the net encapsulation driving force; i.e., increasing either or both of ɛRR and ɛGG raises the number of encapsulated cargo particles NC, which asymptotically approaches the value corresponding to crystalline density (NC ≈ 150).60 This demonstrates that cargo–cargo cohesive interactions are essential to obtain full shells.60 Importantly though, NC does not reach crystalline density until cargo–cargo affinities nearly reach the bulk crystallization threshold ɛfs ≈ 3 kBT. Reference 60 found that well-formed shells cannot assemble when the cargo crystallizes, because the solid cargo cannot be deformed by assembly subunits, thus preventing shell closure. They also measured radial distribution functions for a single cargo species system, which showed that confinement by the shell imposes layering on the encapsulated cargo due to steric effects, but that the cargo remains fluid. The same effect is present for the bicomponent system studied in the present work, since the two cargo species differ only in their cargo–cargo affinities.
FIG. 4.
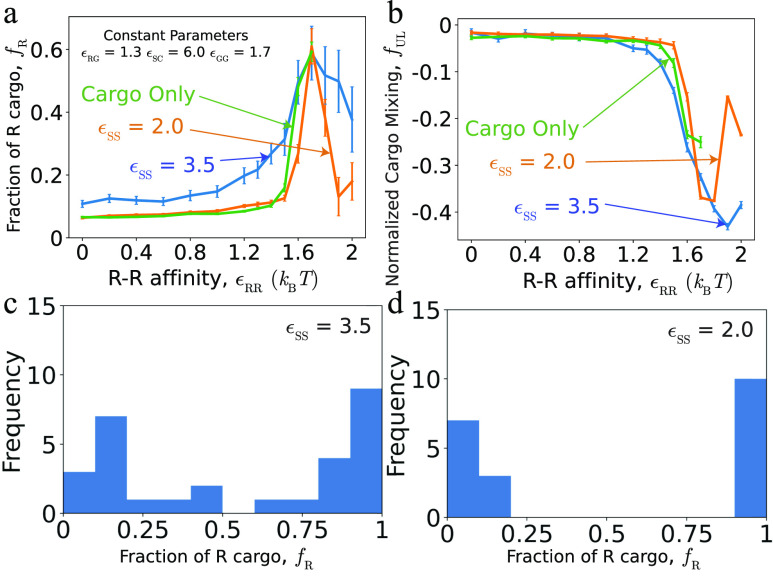
Effect of cargo–cargo affinities on encapsulation for one-step assembly pathways. (a)–(c) Characterization of the encapsulated cargo as a function of the G–G and R–R affinities, for fixed R–G affinity ɛRG = 1.3. (a) The fraction of R particles averaged over all shells fR to characterize the average composition of encapsulated cargo. Snapshots show cutaway views of assembled shells, to illustrate the cargo morphology at corresponding symbols on the plot. (b) The fraction of unlike cargo particles in first solvation shells, fUL, averaged over all shells. (c) The mean number of encapsulated cargo particles per shell, to indicate cargo loading efficiency. (d) The fraction of subunits in complete shells, revealing the effect of cargo–cargo affinities on shell assembly. (e) The shell-to-shell variability of cargo composition, σR,shell, defined as the standard deviation of fR over shells, is shown as a function of the R–R and G–G affinities for three indicated values of ɛRG. High values of σR,shell ≳ 0.4 indicate that different shells have encapsulated pure domains of, respectively, R or G cargo species. To simplify the presentation, we only consider equal R–R and G–G affinities, ɛRR = ɛGG. For (a)–(e), other parameter values are ɛRG = 1.3, shell–cargo affinity ɛSC = 6.0, and shell–shell affinity ɛSS = 3.5.
FIG. 7.
Effects of shell–cargo and shell–shell affinity on cargo composition reveal thermodynamic and kinetic influences on encapsulation. (a) The fraction of encapsulated R particles fR as a function of shell–cargo affinity ɛSC, for shell–shell affinities ɛSS = 2.0, and ɛSS = 3.5. To assess the importance of dynamics on these results, fR is also shown for the “equilibrium” simulations in which cargo can exchange between shell interiors and the bulk. Other parameters are ɛGG = 1.7 and ɛRR = ɛRG = 1.3. (b) Cargo composition fR as a function of shell–shell affinity ɛSS, at a constant shell–cargo affinity of ɛSC = 6.0. Other parameters are ɛRR = 1.3, with ɛGG = 1.7 and ɛRG = 1.3. The “equilibrium” results are also shown, as a straight line since they do not depend on ɛSS.
Next, to determine the relative loading of the two cargo species, Fig. 4(a) shows the fraction of R species averaged over all shells, fR, as a function of ɛGG and ɛRR. Further, to characterize the arrangement of cargo particles within shells, Fig. 4(b) shows the fraction of unlike particles in the first solvation shell (fUL). The snapshots surrounding Fig. 4(a) illustrate typical arrangements of the encapsulated cargo in each regime. Comparing Figs. 4(a) and 4(b) with results from the bulk cargo system in the absence of microcompartment shells [Figs. 2(b) and 2(e)] shows that the composition and mixing of the two cargo species within shells is similar to the case of bulk cargo coalescence for this parameter regime. However, we will see below that shell assembly has a more significant effect on cargo properties in other parameter regimes.
Figure 5 compares these results to two-step assembly pathways that occur for lower shell–shell affinities, ɛSS = 2.0. Since we observe significant assembly only for a narrow range of strong cargo–cargo affinities (Fig. 6, discussed next), we present these results as a function of ɛRR for fixed ɛGG = 1.7. We see that average cargo loading and composition are qualitatively similar between the two cases, although there are quantitative differences revealing deviations from equilibrium, which we consider in more detail in Sec. II D 2.
FIG. 5.
Comparison of cargo encapsulation for one-step and two-step pathways. The fraction of R cargo in completed shells fR (a) and the fraction of unlike cargo particles in first solvation shells fUL (b) are shown as a function of ɛRR for the lower and higher shell–shell affinities ɛSS = 2.0 and ɛSS = 3.5. Other parameters are ɛGG = 1.7, ɛRG = 1.3, and ɛSC = 6.0. Histograms of cargo composition within individual shells to illustrate shell-to-shell variability, for the peak in panel (a) at ɛRR = ɛGG = 1.7 and ɛRG = 1.7, for (c) one-step and (d) two-step pathways.
FIG. 6.
Fraction of shell subunits in complete shells in the two-step assembly pathway regime, ɛSS = 2.0 and ɛRG = 1.3.
However, the composition of cargo within individual shells can differ significantly from the mean. Figure 4(e) shows the shell-to-shell variability of cargo composition, σR,shell, defined as the standard deviation of the fraction of R particles within each shell: . Because compositional fluctuations depend strongly on the ratio of ɛRR and ɛGG to ɛRG, we present the results as a function of equal R–R and G–G interactions (ɛRR = ɛGG), for weak, moderate, and strong ɛRG. In each case, as the R–R and G–G affinities exceed ɛRG, there is a transition from shells containing uniformly mixed cargo to nearly pure domains of R or G particles respectively, within different shells, corresponding to large σR,shell.
Interestingly, this variability arises in different ways depending on the class of assembly pathways. To illustrate this difference, Figs. 5(c) and 5(d) show histograms of cargo compositions measured within individual shells for one-step and two-step pathways, respectively. These parameters correspond to the maximum in Fig. 5(a), where fR and fUL are approximately equal for the two pathways, but the mechanisms underlying the cargo separation differ. In one-step pathways, as shown in Fig. 3(b), a compositional fluctuation in the initial cargo globule nucleus leads to preferential coalescence of the same cargo type as shell assembly proceeds, with the shell eventually closing around a nearly pure domain. However, for these parameters, we do occasionally observe shells that encapsulate two domains separated by an interface [see Fig. 5(c)]. In contrast, two-step assembly pathways form purified shells via the compositional fluctuation mechanism discussed in Sec. II C and shown in Fig. 3(d). This leads to highly purified cargo globules within individual shells [see Fig. 5(d)].
a. Cargo–cargo affinities also affect shell assembly.
While our focus in this article is on factors that control cargo encapsulation, it is important to note that the driving force for cargo cohesion in turn affects the extent and robustness of shell assembly. Figures 4(d) and 6 show the fraction of subunits in complete shells fs as a function of cargo–cargo affinities for ɛSS = 2.0 and ɛSS = 3.5, respectively. We observe that assembly occurs over a broad range of cargo–cargo affinity values for the higher shell–shell affinity [ɛSS = 3.5, Fig. 4(d)], but for the lower shell–shell affinity (ɛSS = 2.0, Fig. 6), significant assembly requires at least one strong cargo–cargo affinity; i.e., ɛij ≥ 1.7 for at least one of ij ∈ {RR, GG, RG}. This result indicates that nucleation of shell assembly for ɛSS ≲ 2.5 requires adsorption onto a cargo globule and thus requires that cargo–cargo affinities are sufficient to drive cargo phase separation. This observation is consistent with results from simulations with a single cargo species.60
2. Shell–shell and shell–cargo affinities affect cargo packaging through equilibrium and nonequilibrium mechanisms
Although the cargo–cargo affinities most strongly affect the amount and properties of encapsulated cargo, the shell protein affinities (ɛSC and ɛSS) can also modulate cargo encapsulation. These effects depend on an interplay between thermodynamic and kinetic effects. The assembly trajectories in our simulations begin from an initial condition of dispersed subunits and cargo that are significantly out of equilibrium. Moreover, once a shell closes, the timescale for reconfiguration to another shell morphology or exchange of the encapsulated cargo is much longer than assembly timescales since all subunits have their maximum number of interactions. Therefore, even though the dynamics satisfy microscopic reversibility, trajectories are not guaranteed to approach equilibrium on the finite timescales of simulations and experiments.157
To distinguish between equilibrium and kinetic effects, we compare the results of our assembly simulations to the alternative “equilibrium” or permeable-shell system described above, in which shells are completely assembled but are made permeable to cargo particles, thus allowing the encapsulated cargo to fully equilibrate with cargo particles in solution (see Sec. IV). The amount and composition of encapsulated cargo in these simulations is, thus, independent of assembly kinetics (and shell–shell affinities). Figure 8 compares the results of assembly trajectories at parameters leading to one-step assembly (corresponding to Fig. 4) with the equilibrium simulations. Over much of parameter space, the amount and compositions of encapsulated cargo are similar between the two systems, indicating that trajectories are near equilibrium during assembly. This can be understood since the diffusional exchange of cargo particles between the partially encapsulated cargo globule and bulk is rapid compared to shell growth under those conditions.
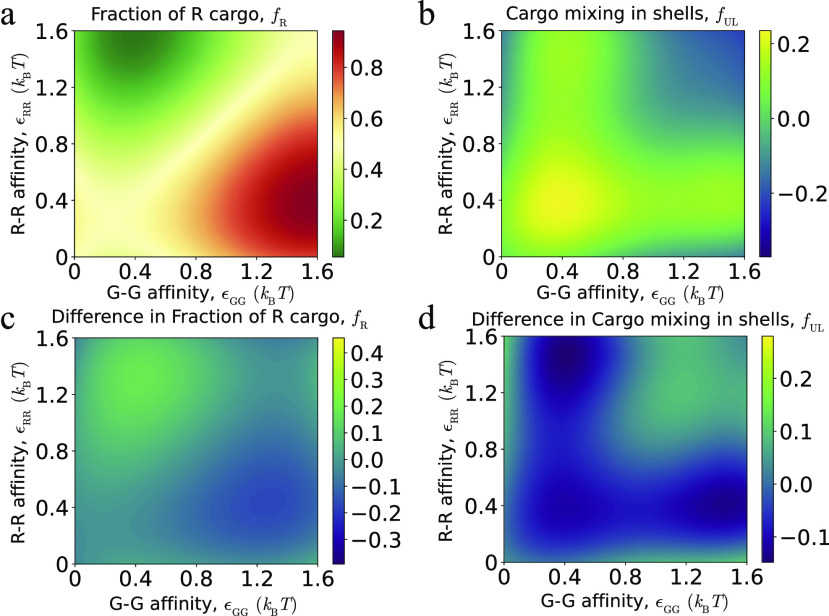
FIG. 8.
Comparison of encapsulated cargo between equilibrium and dynamical simulations. (a) and (b) The fraction of R particles (a) and mixing (b) are shown as a function of R–R and G–G affinities. Other parameters are ɛRG = 1.3 and ɛSC = 6.0, as in Fig. 4. (c) and (d) Difference between cargo encapsulation in dynamical assembly simulations and equilibrium. The plots show the differences between the quantities fR and fUL for the dynamical simulations in Fig. 4 (with ɛSS = 3.5) and equilibrium simulations [panels (a) and (b) of this figure].
However, we do observe significant deviations from equilibrium cargo encapsulation under certain parameter ranges. These effects are strongly dependent on the shell–shell and shell–cargo affinities, since they are key determinants affecting the extent to which assembly is out of equilibrium.
For example, Fig. 5(a) shows the dependence of fR on ɛRR for one-step (ɛSS = 3.5) and two-step (ɛSS = 2.0) assembly pathways. For moderate cargo–cargo affinities ɛRR ≲ 1.5, the two-step assembly and equilibrium results closely agree, while the one-step simulations result in higher fR. This difference arises because the initial globule is enriched in R particles (since the globule nucleation is driven in part by shell–cargo attractive interactions that are agnostic to particle type), and the rapid one-step assembly pathways do not allow the cargo globule time to fully equilibrate with the bulk. In contrast, the slow onset of nucleation and assembly in the two-step pathways allows globule equilibration. Interestingly, the situation reverses at high ɛRR ≳ 1.6, where there is an abrupt drop in fR for the two-step case. This arises because the strong R–R affinities favor segregation of the two cargo species and a high surface tension that inhibits closure of a shell around R particles. A comparable trajectory is shown in Fig. 3(e). Notice that a shell successfully assembles around the cargo particles with weaker affinities (G), but only a malformed structure forms around the R globule because the shell subunits are unable to close around a commensurate-sized piece of the globule. Note that we do not show the permeable-shell results for such high ɛRR because the strong cargo–cargo affinities result in a cargo globule that extends outside of the shell, which is an artifact of the permeable-shell condition imposed in those simulations.
We also observe that the extent of cargo mixing within shells [Fig. 5(b)] decreases with increasing ɛRR. This is partially an equilibrium effect due to the increasing drive for cargo segregation, especially as the R–R and G–G affinities exceed the R–G affinity (ɛRG = 1.3). However, while the two-step results are close to equilibrium, mixing is further reduced for the one-step assembly trajectory. This effect can be attributed to the coupling between composition fluctuations and interfacial effects within the globule during the initial stage of the two-step pathway described in Sec. II C and Fig. 3(d). Due to interfacial tension, the boundary between the two domains provides a “weak point” for insertion of shell subunits, and, thus, shell closure tends to occur in the vicinity of the interface. The closing shell becomes enriched in the cargo species that dominates the domain on the same side of the interface as the assembling shell; this composition is then effectively locked in by shell closure.
Having compared the differences in cargo encapsulation between the two classes of assembly pathways, we now consider parameter values between these two extremes. Figs. 7(a) and 7(b), respectively, show the effects of shell–cargo and shell–shell affinities on the composition of encapsulated cargo. Here, we have focused on the case for which cohesive interactions between pairs of G particles are stronger than for R–R and R–G, ɛGG = 1.7 and ɛRR = ɛRG = 1.3, for which the equilibrium and bulk composition of R particles is about 20%. Fig. 7(a) shows that for weak shell–cargo affinities, the encapsulated fraction of the R particles is significantly smaller than the equilibrium value, but that it monotonically increases with ɛSC. The trend is the same for both shell–shell affinities, except that higher shell–cargo affinities are required to observe assembly for lower shell–shell affinities. Similarly, Fig. 7(b) shows that fR increases monotonically with shell–shell affinity. These trends can be understood as follows. At low ɛSC, the cargo–cargo affinities are the primary driving force for encapsulation, which at these parameters favors encapsulation of the G cargo and, thus, small fR. The fact that fR in the dynamical assembly simulations is smaller than that observed in the bulk cargo and equilibrium simulations suggests that the initial globule that nucleates is enriched in G, and that the shell closes before there is sufficient time for the globule composition to equilibrate with the bulk. However, as ɛSC or ɛSS increases, the strong shell–cargo affinities enhance nucleation, allowing a cargo globule to form with a composition closer to the bulk composition, fR = 0.5.
III. CONCLUSIONS
We have performed equilibrium and dynamical simulations to investigate the encapsulation of multicomponent fluid cargoes by self-assembling microcompartments. To elucidate mechanisms that control the amount and composition of cargo encapsulation, we compared these results against simulations of cargo coalescence in the absence of microcompartment assembly.
Our simulation results show that the binding affinities among the different cargo species are the strongest determinant of the assembly pathway as well as the amount, composition, and spatial organization of cargo within assembled shells. Analogous to the case of encapsulation of a single component cargo,57,60,61,120,122,123,161 the simulations exhibit two broad classes of assembly pathways. Relatively strong cargo–cargo affinities and low shell–shell affinities lead to two-step assembly in which the cargo first forms a globule, followed by adsorption and assembly of the shell around the globule. Weaker cargo–cargo affinities and higher shell–shell affinities drive one-step assembly in which cargo coalescence and shell assembly occur simultaneously. However, the bicomponent cargo allows for more diverse assembly pathways and morphologies, depending on when and if the two components mix within the encapsulated globule. In particular, we observe assembly pathways ranging from coalescence and encapsulation of a nearly pure globule of a single cargo species, to coalescence of a phase-separated globule with each phase becoming encapsulated in different shells, to encapsulation of a globule consisting of a uniform mixture of both species. Correspondingly, the assembled shells can contain a variety of cargo compositions and morphologies, ranging from highly enriched in a single species to nearly uniform mixing of the two species. In regimes where both cargo species are encapsulated, the two species may be uniformly mixed within each shell, or separated, with each individual shell containing an encapsulated cargo that is nearly pure in one or the other species.
While the relative strengths of the different cargo–cargo binding affinities (ɛRR, ɛGG, and ɛRG) determine cargo composition and mixing, the net cargo–cargo affinity most strongly influences the amount of cargo that is encapsulated. In particular, for low cargo–cargo affinities, we observe poor cargo loading (e.g., shells that are nearly empty except for a layer of cargo at the surface). Further, depending on the strength of the subunit–subunit affinities, there is a threshold value of cargo–cargo affinities below which assembled microcompartments are either unstable or fail to nucleate on relevant timescales [Figs. 4(d) and 6].
While cargo composition and mixing within assembled shells is qualitatively similar to the behavior of cargo coalescence in bulk (in the absence of microcompartments) in many parameter regimes, our simulations also identify parameter regimes in which the shell–cargo and shell–shell binding affinities can be manipulated to control cargo encapsulation (e.g., Figs. 5 and 7). A combination of thermodynamic and kinetic mechanisms underlie these effects. In particular, we see a marked difference between the properties of the encapsulated cargo in shells that assemble by one-step or two-step pathways. When cargo–cargo affinities are asymmetric, leading to preferential encapsulation of one species, weaker shell–cargo and shell–shell affinities and two-step assembly pathways tend to enhance the degree of preferential encapsulation, leading to more purified cargo. This behavior reflects the fact that the cargo globule that nucleates in the first step tends to be enriched in the species with higher affinities, and, if assembly occurs more rapidly than the process of cargo exchange with bulk, shell closure locks in this out-of-equilibrium composition. Similarly, when the set of cargo–cargo affinities places the system close to ternary phase coexistence (a dilute phase and two dense phases, respectively, rich in either cargo species), two-step assembly pathways can enhance separation of the cargo species. This result can be explained at least in part by the tendency of assembling shells to close in the vicinity of transient interfaces between domains of the two cargo species (Fig. 2).
The latter predictions can be tested in microcompartment systems by performing mutagenesis of shell protein–protein binding interfaces (to alter shell–shell affinities) or “encapsulation peptides” that mediate shell–cargo interactions.162–165 Similarly, cargo–cargo affinities may be tuned through mutagenesis, but they are less well understood at present. Depending on the system, cargo–cargo affinities may arise from direct pair interactions, scaffold-mediated interactions, or a combination of the two.31,36,39,121,122,126,166,167
A. Outlook
It will be interesting to extend our model to explicitly incorporate scaffold-mediated cargo–cargo and shell–cargo interactions, for example as Mohajerani et al.62 did for a single-component cargo. More broadly, the predictions from our models can be extended beyond microcompartments, for example to reengineered viral capsids46–48,51,147–155 or synthetic capsids constructed via protein engineering (e.g., Refs. 168–170) or DNA origami171 to assemble around specific cargoes. In some of these cases, the shell–cargo interactions are driven by “scaffolds” attached to the inner surface of the capsid. For example, many virus capsid proteins have flexible peptide tails that drive RNA encapsulation,172–174 while Sigl et al.171 designed DNA origami capsid subunits with single-stranded DNA oligomers that bound to complementary strands on cargo particles. Previous simulations of microcompartments62 and virus assembly106,175–178 suggest that the properties of such scaffolds can be designed to manipulate the spatial organization of the cargo. Finally, it will be important to allow for shell assembly into different geometries to study coupling between shell size and cargo composition.
IV. METHODS
A. Computational model
We consider a minimal model for microcompartment assembly and encapsulation of two species of cargo particles, denoted as “R” and “G.” Microcompartment shells assemble from pentameric, hexameric, and pseudo-hexameric (trimeric) protein oligomers [e.g., Fig. 3(a) in Ref. 58 and Refs. 18, 19, and 179]. Experiments suggest that these oligomers are the basic assembly units, meaning that smaller protein complexes do not contribute significantly to the assembly process.19,180 To focus on factors that control the composition of encapsulated cargo, we consider a minimal shell model developed in Perlmutter et al.,60 with only pentamer and hexamer subunits that have interactions designed to drive assembly into a T = 3 shells (containing 12 pentamers and 20 hexamers in a truncated icosahedron geometry). Our model builds on previous simulations of microcompartment assembly with no cargo66 or one cargo species,60,61,65 as well as previous models for virus assembly.76,79,80,83,102,175–177,181–183
1. Shell–shell interactions
In our model, shell subunits interact through both repulsive and attractive forces. The repulsions consist of “Top” (T) pseudoatoms that exist above the plane of the hexamer and “Bottom” (B) pseudoatoms that exist below the plane. More specifically, we denote the top pseudoatoms as “TH” and “TP,” respectively, for hexamer and pentamer subunits, and similarly the bottom pseudoatoms as “BH” and “BP.” All pairs of Top and Bottom pseudoatoms (excepting those on the same subunit) interact via a repulsive Lennard-Jones potential [Eq. (B3)]. The Top–Top diameters and repulsion strengths set the shell spontaneous curvature and bending modulus (Appendix B).
Microcompartment protein shell assembly is primarily driven by interactions along the edges of the hexameric and pentameric subunits.58 We represent these interactions by “Attractors” on the perimeter of each shell subunit. Complementary Attractors on nearby subunits have short-range interactions modeled by a Morse potential [Eq. (B4) in Appendix B]. Attractors that are not complementary do not interact. The arrangement of Attractors on subunit edges is shown in Fig. 1, with pairs of complementary Attractors indicated by cyan double-headed arrows. The shell–shell binding affinity is proportional to the well-depth of the Morse potential between complementary Attractors, ɛSS.
To focus on the role of interaction strengths in determining cargo encapsulation, we consider shell subunits that preferentially form only T = 3 shells. To enforce this restriction, only three of the six edges of a hexamer have attractive interactions with pentamers, and there are no pentamer–pentamer attractive interactions (see Fig. 1).
2. Shell–cargo interactions
We model attractive interactions between hexamer subunits and the cargo particles by a Morse potential between cargo particles and subunit “B” pseudoatoms, with well-depth ɛSC. These interactions represent the effect of “encapsulation peptides” that target cargo to microcompartment interiors by mediating cargo–hexamer interactions.31,39,121,122,166 To minimize the number of parameters, we keep ɛSC the same for both cargo species. We also add a layer of “Excluders” in the plane of the “Top” pseudoatoms, which represent shell–cargo excluded volume interactions. Since the shell–shell interaction geometries are already controlled by the Attractor, Top, and Bottom pseudoatoms, we do not consider Excluder–Excluder interactions.
3. Cargo–cargo interactions
In natural microcompartment systems, the interior cargo undergoes phase separation prior to or during shell assembly. The attractions between cargo particles that drive phase separation may be mediated by microcompartment scaffolding proteins (e.g., Refs. 120, 122, and 126) and/or direct pair interactions between cargo particles.36 Similarly, in synthetic systems, it is possible to engineer direct pair or scaffold-mediated attractions cargo molecules. In our model, we represent these scenarios in a minimal manner. We model both species of cargo particles with spherically symmetric excluded volume and direct pair attractions, implemented via an attractive Lennard-Jones (LJ) potential, with well-depth values ɛGG, ɛRR, and ɛRG for pairs of G–G, R–R, and R–G particles.
B. Mapping simulation parameters to biological microcompartments
1. Relevant ranges of affinities
Although affinities among microcompartment components have not been measured, we estimate relevant ranges of our control parameters based on experimental observations of carboxysomes as follows:
a. Shell–shell affinities.
Because empty carboxysome shells are not typically observed in cells (for wild-type carboxysomes), we have focused on shell–shell affinities that are below the threshold for empty shell assembly (ɛSS ≈ 4 kBT). Furthermore, experimental observations suggest that α-carboxysomes assemble by one-step assembly pathways,57,120,161 whereas β-carboxysomes122,123 and many other microcompartments23,179 assemble by two-step pathways. Therefore, except where mentioned otherwise, we consider two cases (ɛSS/kBT = 2, 3.5), which are, respectively, below and above the transition between one-step and two-step assembly pathways (discussed in Sec. II C).
b. Shell–cargo affinities.
Since the shell subunits robustly assemble around RuBisCO in both α and β carboxysomes, we have focused on shell–cargo affinities that are strong enough to observe this (ɛSC = 6 kBT, free energy gSC ≈ −14 kBT) except where mentioned otherwise.
c. Cargo–cargo affinities.
For the case of α-carboxysomes, the RuBisCO does not undergo phase separation in the absence of shell proteins at physiological conditions,57,120,161 but it can phase separate without shell proteins under nonphysiological conditions.126,128 Thus, we infer that the effective cargo–cargo affinity for α-carboxysomes is near but below the threshold for phase separation, which corresponds to a cargo–cargo affinity of ɛvl ≈ 1.3 kBT at our simulated cargo concentration. In contrast, for β-carboxysomes, the RuBisCO undergoes phase separation before shell assembly, suggesting a cargo–cargo affinity above ɛvl but below crystallization (ɛfs). Our simulations span this range.
2. Length scales
Although the model is designed to be generic, we can approximately map it to carboxysomes by setting the cargo diameter (the unit length scale in the model) to that of the RuBisCO holoenzyme, implying r∗ ≈ 13 nm. However, to enable tractable simulation of long assembly timescales, we have set the subunit/cargo size ratio to be larger than in carboxysomes—model subunits have a side length of r∗ and are thus about three times larger than carboxysome hexamers (side length nm). See Ref. 62 for further discussion.
C. Simulations and systems
We performed simulations using the Langevin dynamics algorithm in HOOMD [which uses graphical processing units (GPUs) to accelerate molecular dynamics simulations184], and periodic boundary conditions in a cubic box to represent a bulk system. The subunits were modeled as rigid bodies.185 Each simulation was performed in the NVT ensemble, using the HOOMD fundamental units,186 with the unit length scale r∗ defined as the circumradius of the pentagonal subunit (the cargo diameter is also set to r∗), and energies given in units of the thermal energy, kBT. The simulation timestep was 0.005 in dimensionless time units for all systems.
1. Systems
We simulated several systems as follows:
a. Shell assembly and cargo encapsulation.
For dynamical simulations of shell assembly in the presence of cargo, each simulation contained enough subunits to form four complete microcompartments (48 pentamers and 80 hexamers), in a cubic simulation box with side length 40r∗. Each simulation also contained 854 cargo particles, with composition 50% “R” and “G,” respectively. With r∗ = 13 nm, this corresponds to concentrations of cp = 0.6, ch = 1, and cc = 10 μM for pentamers, hexamers, and cargo.
We performed most simulations for 2 × 106 timesteps; simulations in the two-step assembly regime were performed for longer, 2 × 107 timesteps, as they assemble more slowly.
b. Bulk simulations without shell subunits.
We also performed large simulations of cargo without shell subunits, to determine the phase behavior of the cargo as a function of the cargo–cargo affinities. Each of these simulations contained 46 938 cargo particles (50% “R” and “G,” respectively) in a box with side length 160, to maintain the same cargo concentration as in the shell assembly simulations. We performed each simulation for 2 × 107 timesteps.
c. Equilibrium cargo encapsulation.
To identify effects of out-of-equilibrium dynamics of shell assembly on the properties of the encapsulated cargo, we performed additional simulations in which we simulated cargo dynamics in the presence of an assembled shell that was made permeable to cargo. In particular, these simulations consisted of a fully assembled immobile shell placed in the center of the box, with one missing pentamer to allow permeability to occur with the surrounding cargo. While the shell could not move, the ɛSC was still active. Each simulation contained 854 cargo particles with box side length 40r∗ to maintain the same cargo concentration and composition as in the other systems. We performed each simulation for 2 × 106 timesteps, which we determined was sufficient to achieve equilibration of cargo inside of the shell by monitoring the amount, composition, and mixing of the encapsulated cargo.
2. Initial conditions
Except for the equilibrium cargo encapsulation systems, all simulations were initialized with random positions for cargo particles and shell subunits (except that significant overlaps between pseudoatoms were forbidden). The equilibrium cargo encapsulation simulations were initialized with an assembled microcompartment shell whose subunits were fixed throughout the simulation, and the cargo particles were initialized with random locations with overlaps forbidden.
3. Statistical significance
For most systems, we performed ten independent trials at each parameter set. For most parameter sets at which we report statistical errors, we performed 20 independent trials. For parameter sets that resulted in low probability events , we performed 60 trials to ensure low statistical error.
ACKNOWLEDGMENTS
This work was supported by Award No. R01GM108021 from the National Institute of General Medical Sciences and the Brandeis Center for Bioinspired Soft Materials, an NSF MRSEC, Grant No. DMR-2011846. Computational resources were provided by NSF XSEDE computing resources (Maverick, Bridges, and Comet) and the Brandeis HPCC, which is partially supported by Grant No. DMR-2011846.
APPENDIX A: SHELL–SHELL AND SHELL–CARGO BINDING FREE ENERGY VALUES
We estimated the subunit–subunit binding free energy values as functions of the well-depth parameter ɛSS by measuring the dimerization equilibrium constant in simulations of subunits only capable of forming dimers. For both pentamer–hexamer and hexamer–hexamer dimers, we obtain binding free energies that are linear functions of the well-depth ɛSS.60 We interpret the y-intercept as the binding entropy. Setting r∗ = 13 nm and using the conventional standard state concentration of 1M (rather than as in Ref. 60) gives
| (A1) |
where gph and ghh are the binding affinities for pentamer–hexamer and hexamer–hexamer pairs. The dissociation constants are then given by and . Table I shows the results for hexamer–hexamer dimerization; the values for pentamer–hexamer association are approximately the same. Similarly, we estimated the shell subunit adsorption free energy by performing simulations of subunits that cannot assemble (ɛSS = 0) in the presence of a cargo globule as60
| (A2) |
For the free energy of shell assembly, we consider a shell comprised of npent = 12 pentamers and nhex hexamers, which have nph pentamer–hexamer contacts with binding energy ɛph and nhh hexamer–hexamer contacts with energy ɛhh. For our T = 3 model, nhex = 20, nph = 60, and nhh = 30. The assembly free energy is then given by
| (A3) |
where sconfig accounts for the configurational entropy associated with subunit and shell symmetries: , and γ and AC are the surface tension and area of the cargo globule. Finally, we define an effective dissociation constant for the complex as with Δgshell = ΔGshell/(npent + nhex) the free energy per subunit averaged over pentamers and hexamers (see Table I). However, this calculation is only approximate since it neglects changes in binding entropy between dimerization and the full complex. Furthermore, to simplify the calculation and focus on the shell subunits, we have neglected cargo–cargo contributions to the complex stability. This provides a reasonable estimate for cargo–cargo affinities near liquid–vapor coexistence, but it over/underestimates the shell stability for weaker/stronger cargo–cargo affinities. For a full analysis including cargo–cargo contributions, see Perlmutter et al.60
APPENDIX B: MODEL DETAILS
In our model, all potentials can be decomposed into pairwise interactions. Potentials involving shell subunits further decompose into pairwise interactions between their constituent building blocks—the Excluders, Attractors, “Top,” and “Bottom” pseudoatoms. It is convenient to express the total energy of the system as the sum of three terms, involving shell–shell (USS), cargo–cargo (UCC), and shell–cargo (USC) interactions, each summed over all pairs of the appropriate type,
| (B1) |
where ∑shell i ∑shell j<i is the sum over all distinct pairs of shell subunits in the system, ∑shell i ∑cargo j is the sum over all shell–cargo particle pairs, etc.
1. Shell–shell interaction potentials
The shell–shell potential USS is the sum of the attractive interactions between complementary Attractors, and geometry guiding repulsive interactions between “Top”–“Top,” “Bottom”–“Bottom,” and “Top”–“Bottom” pairs. There are no interactions between members of the same rigid body. Thus, for notational clarity, we index rigid bodies and nonrigid pseudoatoms in Roman, while the pseudoatoms comprising a particular rigid body are indexed in Greek. For subunit i, we denote its Attractor positions as {aiα} with the set comprising all Attractors α, its “Top” position ti, and its “Bottom” position bi.
The shell–shell interaction potential between two subunits i and j is then defined as
| (B2) |
The function Ł is defined as the repulsive component of the Lennard-Jones potential shifted to zero at the interaction diameter,
| (B3) |
with θ(x) being the Heaviside function. The function is a Morse potential,
| (B4) |
with Vshift(rcut) being the value of the (unshifted) potential at rcut.
The parameter ɛSS sets the strength of the shell–shell attraction at each Attractor site, Nai is the number of Attractor pseudoatoms in subunit i, and ɛangle scales the repulsive interactions that enforce the geometry.
2. Shell–shell interaction parameter values
a. Attractors
The strength of attractive interactions is parameterized by the well-depth ɛSS for a pair of Attractors on hexamers as follows. Hexamer–hexamer edge Attractor pairs (A2-A6, A3-A5, and A5-A6) have a well-depth of ɛSS. Because vertex Attractors (A1, A4) have multiple partners in an assembled structure, whereas edge Attractors have only one, the well-depth for the vertex pairs (A1-A4 and A4-A4) is set to 0.5ɛSS. Similarly, for pentamer–hexamer interactions, the well-depth for edge Attractor pairs (A2-A5, A3-A6) is ɛSS, while the vertex interaction pairs (A1-A4 and A4-A4) have 0.5ɛSS.
b. Repulsive interactions
The “Top” and “Bottom” heights, or distance out of the Attractor plane, are set to h = 1/2rb, with rb = 1 the distance between a vertex Attractor and the center of the pentagon. For all simulations, shells have T = 3 preferred curvature and σtb = 1.8rb is the diameter of the “Top”–“Bottom” interaction (this prevents subunits from binding in inverted configurations76) while σb = 1.5rb is the diameter of the “Bottom”–“Bottom” interaction. In contrast to the latter parameters, σt,ij, the effective diameter of the “Top”–“Top” interaction, depends on the species of subunits i and j; denoting a pentagonal or hexagonal subunit as “p” or “h,” respectively, σt, pp = 2.1rb, σt, hh = 2.4rb, and σt, ph = 2.2rb. The parameter r0 is the minimum energy Attractor distance, set to 0.2rb, ρ = 4rb determines the width of the attractive interaction, and is the cutoff distance for the Attractor potential. Since the interactions just described are sufficient to describe assembly of the shell subunits, we included no Excluder–Excluder interactions.
3. Cargo–cargo interactions
The interaction between cargo particles is given by a sum over all interacting pairs,
| (B5) |
with being the full Lennard-Jones interaction,
| (B6) |
and NRR, NGG, and NRG as the number of R–R, G–G, and R–G pairs in the system, and the cargo diameter σC = rb and cutoff are the same for all cargo species.
4. Shell–cargo interactions
The shell–cargo interaction is modeled by a short-range repulsion between cargo–Excluder and cargo–“Top” pairs representing the excluded volume, plus an attractive interaction between pairs of cargo particles and shell subunit “Bottom” pseudoatoms. For subunit i with Excluder positions {xiα} and “Bottom” psuedoatom bi, and cargo particle j with position Rj, the potential is given by
| (B7) |
| (B8) |
| (B9) |
where ɛSC parameterizes the shell–cargo interaction strength, Nx, Nt, and Nb are the numbers of Excluders and “Top” and “Bottom” pseudoatoms on a shell subunit, σex = 0.5rb and σt = 0.5rb are the effective diameters of the Excluder–cargo and “Top”–cargo repulsions, is the minimum energy Attractor distance, the width parameter is ρSC = 2.5rb, and the cutoff is set to .
AUTHOR DECLARATIONS
Conflict of Interest
The authors have no conflicts to disclose.
DATA AVAILABILITY
The data that support the findings of this study are openly available in Open Science Framework at http://doi.org/10.17605/OSF.IO/SKZ7F.
REFERENCES
- 1.Brangwynne C. P., Eckmann C. R., Courson D. S., Rybarska A., Hoege C., Gharakhani J., Jülicher F., and Hyman A. A., “Germline P granules are liquid droplets that localize by controlled dissolution/condensation,” Science 324, 1729–1732 (2009). 10.1126/science.1172046 [DOI] [PubMed] [Google Scholar]
- 2.Brangwynne C. P., Tompa P., and Pappu R. V., “Polymer physics of intracellular phase transitions,” Nat. Phys. 11, 899–904 (2015). 10.1038/nphys3532 [DOI] [Google Scholar]
- 3.Lee C. F., Brangwynne C. P., Gharakhani J., Hyman A. A., and Jülicher F., “Spatial organization of the cell cytoplasm by position-dependent phase separation,” Phys. Rev. Lett. 111, 088101 (2013). 10.1103/PhysRevLett.111.088101 [DOI] [PubMed] [Google Scholar]
- 4.Brangwynne C. P., “Phase transitions and size scaling of membrane-less organelles,” J. Cell Biol. 203, 875–881 (2013). 10.1083/jcb.201308087 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Weber S. C. and Brangwynne C. P., “Getting RNA and protein in phase,” Cell 149, 1188–1191 (2012). 10.1016/j.cell.2012.05.022 [DOI] [PubMed] [Google Scholar]
- 6.Hyman A. A. and Brangwynne C. P., “Beyond stereospecificity: Liquids and mesoscale organization of cytoplasm,” Dev. Cell 21, 14–16 (2011). 10.1016/j.devcel.2011.06.013 [DOI] [PubMed] [Google Scholar]
- 7.Hyman A. A. and Simons K., “Beyond oil and water—Phase transitions in cells,” Science 337, 1047–1049 (2012). 10.1126/science.1223728 [DOI] [PubMed] [Google Scholar]
- 8.Bergeron-Sandoval L.-P., Safaee N., and Michnick S. W., “Mechanisms and consequences of macromolecular phase separation,” Cell 165, 1067–1079 (2016). 10.1016/j.cell.2016.05.026 [DOI] [PubMed] [Google Scholar]
- 9.Feric M., Vaidya N., Harmon T. S., Mitrea D. M., Zhu L., Richardson T. M., Kriwacki R. W., Pappu R. V., and Brangwynne C. P., “Coexisting liquid phases underlie nucleolar subcompartments,” Cell 165, 1686–1697 (2016). 10.1016/j.cell.2016.04.047 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hnisz D., Shrinivas K., Young R. A., Chakraborty A. K., and Sharp P. A., “A phase separation model for transcriptional control,” Cell 169, 13–23 (2017). 10.1016/j.cell.2017.02.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Stone M. B., Shelby S. A., Núñez M. F., Wisser K., and Veatch S. L., “Protein sorting by lipid phase-like domains supports emergent signaling function in B lymphocyte plasma membranes,” Elife 6, e19891 (2017). 10.7554/eLife.19891 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zhu L. and Brangwynne C. P., “Nuclear bodies: The emerging biophysics of nucleoplasmic phases,” Curr. Opin. Cell Biol. 34, 23–30 (2015). 10.1016/j.ceb.2015.04.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Banani S. F., Lee H. O., Hyman A. A., and Rosen M. K., “Biomolecular condensates: Organizers of cellular biochemistry,” Nat. Rev. Mol. Cell Biol. 18, 285–298 (2017). 10.1038/nrm.2017.7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Joseph J. A., Espinosa J. R., Sanchez-Burgos I., Garaizar A., Frenkel D., and Collepardo-Guevara R., “Thermodynamics and kinetics of phase separation of protein-RNA mixtures by a minimal model,” Biophys. J. 120, 1219–1230 (2021). 10.1016/j.bpj.2021.01.031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Yeates T. O., Kerfeld C. A., Heinhorst S., Cannon G. C., and Shively J. M., “Protein-based organelles in bacteria: Carboxysomes and related microcompartments,” Nat. Rev. Microbiol. 6, 681–691 (2008). 10.1038/nrmicro1913 [DOI] [PubMed] [Google Scholar]
- 16.Nott T. J., Petsalaki E., Farber P., Jervis D., Fussner E., Plochowietz A., Craggs T. D., Bazett-Jones D. P., Pawson T., Forman-Kay J. D., and Baldwin A. J., “Phase transition of a disordered nuage protein generates environmentally responsive membraneless organelles,” Mol. Cell 57, 936–947 (2015). 10.1016/j.molcel.2015.01.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zaslavsky B. Y., Ferreira L. A., Darling A. L., and Uversky V. N., “The solvent side of proteinaceous membrane-less organelles in light of aqueous two-phase systems,” Int. J. Biol. Macromol. 117, 1224–1251 (2018). 10.1016/j.ijbiomac.2018.06.030 [DOI] [PubMed] [Google Scholar]
- 18.Kerfeld C. A., Heinhorst S., and Cannon G. C., “Bacterial microcompartments,” Annu. Rev. Microbiol. 64, 391 (2010). 10.1146/annurev.micro.112408.134211 [DOI] [PubMed] [Google Scholar]
- 19.Tanaka S., Kerfeld C. A., Sawaya M. R., Cai F., Heinhorst S., Cannon G. C., and Yeates T. O., “Atomic-level models of the bacterial carboxysome shell,” Science 319, 1083–1086 (2008). 10.1126/science.1151458 [DOI] [PubMed] [Google Scholar]
- 20.Rae B. D., Long B. M., Badger M. R., and Price G. D., “Functions, compositions, and evolution of the two types of carboxysomes: Polyhedral microcompartments that facilitate CO2 fixation in cyanobacteria and some proteobacteria,” Microbiol. Mol. Biol. Rev. 77, 357–379 (2013). 10.1128/mmbr.00061-12 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bobik T. A., Lehman B. P., and Yeates T. O., “Bacterial microcompartments: Widespread prokaryotic organelles for isolation and optimization of metabolic pathways,” Mol. Microbiol. 98, 193–207 (2015). 10.1111/mmi.13117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chowdhury C., Sinha S., Chun S., Yeates T. O., and Bobik T. A., “Diverse bacterial microcompartment organelles,” Microbiol. Mol. Biol. Rev. 78, 438–468 (2014). 10.1128/MMBR.00009-14 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kerfeld C. A. and Melnicki M. R., “Assembly, function and evolution of cyanobacterial carboxysomes,” Curr. Opin. Plant Biol. 31, 66–75 (2016). 10.1016/j.pbi.2016.03.009 [DOI] [PubMed] [Google Scholar]
- 24.Polka J. K., Hays S. G., and Silver P. A., “Building spatial synthetic biology with compartments, scaffolds, and communities,” Cold Spring Harbor Perspect. Biol. 8, a024018 (2016). 10.1101/cshperspect.a024018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kerfeld C. A., Aussignargues C., Zarzycki J., Cai F., and Sutter M., “Bacterial microcompartments,” Nat. Rev. Microbiol. 16, 277 (2018). 10.1038/nrmicro.2018.10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sutter M., Boehringer D., Gutmann S., Günther S., Prangishvili D., Loessner M. J., Stetter K. O., Weber-Ban E., and Ban N., “Structural basis of enzyme encapsulation into a bacterial nanocompartment,” Nat. Struct. Mol. Biol. 15, 939–947 (2008). 10.1038/nsmb.1473 [DOI] [PubMed] [Google Scholar]
- 27.Nichols R. J., LaFrance B., Phillips N. R., Oltrogge L. M., Valentin-Alvarado L. E., Bischoff A. J., Nogales E., and Savage D., “Discovery and characterization of a novel family of prokaryotic nanocompartments involved in sulfur metabolism,” Elife 10, e59288 (2020). 10.7554/eLife.59288 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Pfeifer F., “Distribution, formation and regulation of gas vesicles,” Nat. Rev. Microbiol. 10, 705–715 (2012). 10.1038/nrmicro2834 [DOI] [PubMed] [Google Scholar]
- 29.Kickhoefer V. A., Rajavel K. S., Scheffer G. L., Dalton W. S., Scheper R. J., and Rome L. H., “Vaults are up-regulated in multidrug-resistant cancer cell lines,” J. Biol. Chem. 273, 8971–8974 (1998). 10.1074/jbc.273.15.8971 [DOI] [PubMed] [Google Scholar]
- 30.Chessher A., Breitling R., and Takano E., “Bacterial microcompartments: Biomaterials for synthetic biology-based compartmentalization strategies,” ACS Biomater. Sci. Eng. 1, 345–351 (2015). 10.1021/acsbiomaterials.5b00059 [DOI] [PubMed] [Google Scholar]
- 31.Lehman B. P., Chowdhury C., and Bobik T. A., “The N terminus of the PduB protein binds the protein shell of the Pdu microcompartment to its enzymatic core,” J. Bacteriol. 199, e00785 (2017). 10.1128/jb.00785-16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Long B. M., Badger M. R., Whitney S. M., and Price G. D., “Analysis of carboxysomes from Synechococcus PCC7942 reveals multiple Rubisco complexes with carboxysomal proteins CcmM and CcaA,” J. Biol. Chem. 282, 29323–29335 (2007). 10.1074/jbc.m703896200 [DOI] [PubMed] [Google Scholar]
- 33.Long B. M., Tucker L., Badger M. R., and Price G. D., “Functional cyanobacterial β-carboxysomes have an absolute requirement for both long and short forms of the CcmM protein,” Plant Physiol. 153, 285–293 (2010). 10.1104/pp.110.154948 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Mayer M. J., Juodeikis R., Brown I. R., Frank S., Palmer D. J., Deery E., Beal D. M., Xue W.-F., and Warren M. J., “Effect of bio-engineering on size, shape, composition and rigidity of bacterial microcompartments,” Sci. Rep. 6, 36899 (2016). 10.1038/srep36899 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Quin M. B., Perdue S. A., Hsu S.-Y., and Schmidt-Dannert C., “Encapsulation of multiple cargo proteins within recombinant Eut nanocompartments,” Appl. Microbiol. Biotechnol. 100, 9187–9200 (2016). 10.1007/s00253-016-7737-8 [DOI] [PubMed] [Google Scholar]
- 36.Slininger Lee M. and Tullman-Ercek D., “Practical considerations for the encapsulation of multi-enzyme cargos within the bacterial microcompartment for metabolic engineering,” Curr. Opin. Syst. Biol. 5, 16 (2017). 10.1016/j.coisb.2017.05.017 [DOI] [Google Scholar]
- 37.Slininger Lee M. F., Jakobson C. M., and Tullman-Ercek D., “Evidence for improved encapsulated pathway behavior in a bacterial microcompartment through shell protein engineering,” ACS Synth. Biol. 6, 1880 (2017). 10.1021/acssynbio.7b00042 [DOI] [PubMed] [Google Scholar]
- 38.Hagen A., Sutter M., Sloan N., and Kerfeld C. A., “Programmed loading and rapid purification of engineered bacterial microcompartment shells,” Nat. Commun. 9, 2881 (2018). 10.1038/s41467-018-05162-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kinney J. N., Salmeen A., Cai F., and Kerfeld C. a., “Elucidating essential role of conserved carboxysomal protein CcmN reveals common feature of bacterial microcompartment assembly,” J. Biol. Chem. 287, 17729–17736 (2012). 10.1074/jbc.m112.355305 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ferlez B., Sutter M., and Kerfeld C. A., “A designed bacterial microcompartment shell with tunable composition and precision cargo loading,” Metab. Eng. 54, 286–291 (2019). 10.1016/j.ymben.2019.04.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kalnins G., Cesle E.-E., Jansons J., Liepins J., Filimonenko A., and Tars K., “Encapsulation mechanisms and structural studies of GRM2 bacterial microcompartment particles,” Nat. Commun. 11, 388–413 (2020). 10.1038/s41467-019-14205-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Juodeikis R., Lee M. J., Mayer M., Mantell J., Brown I. R., Verkade P., Woolfson D. N., Prentice M. B., Frank S., and Warren M. J., “Effect of metabolosome encapsulation peptides on enzyme activity, coaggregation, incorporation, and bacterial microcompartment formation,” MicrobiologyOpen 9, e1010 (2020). 10.1002/mbo3.1010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Künzle M., Mangler J., Lach M., and Beck T., “Peptide-directed encapsulation of inorganic nanoparticles into protein containers,” Nanoscale 10, 22917–22926 (2018). 10.1039/c8nr06236f [DOI] [PubMed] [Google Scholar]
- 44.Alberts B., Essential Cell Biology (Garland Science, New York; London, 2010). [Google Scholar]
- 45.Huttanus H. M. and Feng X., “Compartmentalized metabolic engineering for biochemical and biofuel production,” Biotechnol. J. 12, 1700052 (2017). 10.1002/biot.201700052 [DOI] [PubMed] [Google Scholar]
- 46.Patterson D. P., Prevelige P. E., and Douglas T., “Nanoreactors by programmed enzyme encapsulation inside the capsid of the bacteriophage P22,” ACS Nano 6, 5000–5009 (2012). 10.1021/nn300545z [DOI] [PubMed] [Google Scholar]
- 47.Patterson D. P., Schwarz B., Waters R. S., Gedeon T., and Douglas T., “Encapsulation of an enzyme cascade within the bacteriophage P22 virus-like particle,” ACS Chem. Biol. 9, 359–365 (2014). 10.1021/cb4006529 [DOI] [PubMed] [Google Scholar]
- 48.Wörsdörfer B., Pianowski Z., and Hilvert D., “Efficient in vitro encapsulation of protein cargo by an engineered protein container,” J. Am. Chem. Soc. 134, 909–911 (2012). 10.1021/ja211011k [DOI] [PubMed] [Google Scholar]
- 49.Cai F., Bernstein S. L., Wilson S. C., and Kerfeld C. A., “Production and characterization of synthetic carboxysome shells with incorporated luminal proteins,” Plant Physiol. 170, 1868–1877 (2016). 10.1104/pp.15.01822 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Lee S. M., Bond N., Callaway C., Clark B., Farmer E., Mallard M., and Jang S. S., “Dissipative particle dynamics simulation of multicompartment micelle nanoreactor with channel for reactants,” RSC Adv. 8, 37866–37871 (2018). 10.1039/c8ra07023g [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Chakraborti S., Korpi A., Kumar M., Stępień P., Kostiainen M. A., and Heddle J. G., “Three-dimensional protein cage array capable of active enzyme capture and artificial chaperone activity,” Nano Lett. 19, 3918–3924 (2019). 10.1021/acs.nanolett.9b01148 [DOI] [PubMed] [Google Scholar]
- 52.Edwardson T. G. W. and Hilvert D., “Virus-inspired function in engineered protein cages,” J. Am. Chem. Soc. 141, 9432–9443 (2019). 10.1021/jacs.9b03705 [DOI] [PubMed] [Google Scholar]
- 53.Price G. D. and Badger M. R., “Evidence for the role of carboxysomes in the cyanobacterial CO2-concentrating mechanism,” Can. J. Bot. 69, 963–973 (1991). 10.1139/b91-124 [DOI] [Google Scholar]
- 54.Shively J. M., Ball F., Brown D. H., and Saunders R. E., “Functional organelles in prokaryotes: Polyhedral inclusions (carboxysomes) of Thiobacillus neapolitanus,” Science 182, 584–586 (1973). 10.1126/science.182.4112.584 [DOI] [PubMed] [Google Scholar]
- 55.Shively J. M., Ball F. L., and Kline B. W., “Electron microscopy of the carboxysomes (polyhedral bodies) of Thiobacillus neapolitanus,” J. Bacteriol. 116, 1405–1411 (1973). 10.1128/jb.116.3.1405-1411.1973 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Iancu C. V., Ding H. J., Morris D. M., Dias D. P., Gonzales A. D., Martino A., and Jensen G. J., “The structure of isolated Synechococcus strain WH8102 carboxysomes as revealed by electron cryotomography,” J. Mol. Biol. 372, 764–773 (2007). 10.1016/j.jmb.2007.06.059 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Iancu C. V., Morris D. M., Dou Z., Heinhorst S., Cannon G. C., and Jensen G. J., “Organization, structure, and assembly of α-carboxysomes determined by electron cryotomography of intact cells,” J. Mol. Biol. 396, 105–117 (2010). 10.1016/j.jmb.2009.11.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Sutter M., Greber B., Aussignargues C., and Kerfeld C. A., “Assembly principles and structure of a 6.5-MDa bacterial microcompartment shell,” Science 356, 1293 (2017). 10.1126/science.aan3289 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Sutter M., Laughlin T. G., Sloan N. B., Serwas D., Davies K. M., and Kerfeld C. A., “Structure of a synthetic β-carboxysome shell,” Plant Physiol. 181, 1050–1058 (2019). 10.1104/pp.19.00885 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Perlmutter J. D., Mohajerani F., and Hagan M. F., “Many-molecule encapsulation by an icosahedral shell,” eLife 5, e14078 (2016). 10.7554/eLife.14078 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Mohajerani F. and Hagan M. F., “The role of the encapsulated cargo in microcompartment assembly,” PLoS Comput. Biol. 14, e1006351 (2018). 10.1371/journal.pcbi.1006351 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Mohajerani F., Sayer E., Neil C., Inlow K., and Hagan M. F., “Mechanisms of scaffold-mediated microcompartment assembly and size control,” ACS Nano 15, 4197–4212 (2021). 10.1021/acsnano.0c05715 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Mahalik J. P., Brown K. A., Cheng X., and Fuentes-Cabrera M., “Theoretical study of the initial stages of self-assembly of a carboxysome’s facet,” ACS Nano 10, 5751–5758 (2016). 10.1021/acsnano.5b07805 [DOI] [PubMed] [Google Scholar]
- 64.Young E. J., Burton R., Mahalik J. P., Sumpter B. G., Fuentes-Cabrera M., Kerfeld C. A., and Ducat D. C., “Engineering the bacterial microcompartment domain for molecular scaffolding applications,” Front. Microbiol. 8, 1441 (2017). 10.3389/fmicb.2017.01441 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Rotskoff G. M. and Geissler P. L., “Robust nonequilibrium pathways to microcompartment assembly,” Proc. Natl. Acad. Sci. U. S. A. 115, 6341–6346 (2018). 10.1073/pnas.1802499115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Li Y., Kennedy N. W., Li S., Mills C. E., Tullman-Ercek D., and Olvera de la Cruz M., “Computational and experimental approaches to controlling bacterial microcompartment assembly,” ACS Cent. Sci. 7, 658–670 (2021). 10.1021/acscentsci.0c01699 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Garcia-Alles L., Lesniewska E., Root K., Aubry N., Pocholle N., Mendoza C., Bourillot E., Barylyuk K., Pompon D., Zenobi R., Reguera D., and Truan G., “Spontaneous non-canonical assembly of CcmK hexameric components from β-carboxysome shells of cyanobacteria,” PLoS One 12, e0185109 (2017). 10.1371/journal.pone.0185109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Chen T. and Glotzer S. C., “Simulation studies of a phenomenological model for elongated virus capsid formation,” Phys. Rev. E 75, 051504 (2007). 10.1103/PhysRevE.75.051504 [DOI] [PubMed] [Google Scholar]
- 69.Bruinsma R. F., Gelbart W. M., Reguera D., Rudnick J., and Zandi R., “Viral self-assembly as a thermodynamic process,” Phys. Rev. Lett. 90, 248101 (2003). 10.1103/physrevlett.90.248101 [DOI] [PubMed] [Google Scholar]
- 70.Zandi R., Reguera D., Bruinsma R. F., Gelbart W. M., and Rudnick J., “Origin of icosahedral symmetry in viruses,” Proc. Natl. Acad. Sci. U. S. A. 101, 15556–15560 (2004). 10.1073/pnas.0405844101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Berger B., Shor P. W., Tucker-Kellogg L., and King J., “Local rule-based theory of virus shell assembly,” Proc. Natl. Acad. Sci. U. S. A. 91, 7732–7736 (1994). 10.1073/pnas.91.16.7732 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Schwartz R., Garcea R. L., and Berger B., “‘Local rules’ theory applied to polyomavirus polymorphic capsid assemblies,” Virology 268, 461–470 (2000). 10.1006/viro.1999.0180 [DOI] [PubMed] [Google Scholar]
- 73.Rapaport D. C., “Self-assembly of polyhedral shells: A molecular dynamics study,” Phys. Rev. E 70, 051905 (2004). 10.1103/PhysRevE.70.051905 [DOI] [PubMed] [Google Scholar]
- 74.Nguyen H. D., Reddy V. S., and Brooks C. L. III, “Invariant polymorphism in virus capsid assembly,” J. Am. Chem. Soc. 131, 2606–2614 (2009). 10.1021/ja807730x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Elrad O. M. and Hagan M. F., “Mechanisms of size control and polymorphism in viral capsid assembly,” Nano Lett. 8, 3850–3857 (2008). 10.1021/nl802269a [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Johnston I. G., Louis A. A., and Doye J. P. K., “Modelling the self-assembly of virus capsids,” J. Phys.: Condens. Matter 22, 104101 (2010). 10.1088/0953-8984/22/10/104101 [DOI] [PubMed] [Google Scholar]
- 77.Rapaport D. C., “Studies of reversible capsid shell growth,” J. Phys.: Condens. Matter 22, 104115 (2010). 10.1088/0953-8984/22/10/104115 [DOI] [PubMed] [Google Scholar]
- 78.Nguyen H. D. and Brooks C. L., “Generalized structural polymorphism in self-assembled viral particles,” Nano Lett. 8, 4574 (2008). 10.1021/nl802828v [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Mateu M. G., “Assembly, stability and dynamics of virus capsids,” Arch. Biochem. Biophys. 531, 65–79 (2013). 10.1016/j.abb.2012.10.015 [DOI] [PubMed] [Google Scholar]
- 80.Hagan M. F., “Modeling viral capsid assembly,” Adv. Chem. Phys. 155, 1–68 (2014). 10.1002/9781118755815.ch01 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Perlmutter J. D. and Hagan M. F., “Mechanisms of virus assembly,” Annu. Rev. Phys. Chem. 66, 217–239 (2015). 10.1146/annurev-physchem-040214-121637 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Bruinsma R. F. and Klug W. S., “Physics of viral shells,” Annu. Rev. Condens. Matter Phys. 6, 245–268 (2015). 10.1146/annurev-conmatphys-031214-014325 [DOI] [Google Scholar]
- 83.Hagan M. F. and Zandi R., “Recent advances in coarse-grained modeling of virus assembly,” Curr. Opin. Virol. 18, 36 (2016). 10.1016/j.coviro.2016.02.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Rapaport D. C., “Molecular dynamics simulation of reversibly self-assembling shells in solution using trapezoidal particles,” Phys. Rev. E 86, 051917 (2012). 10.1103/PhysRevE.86.051917 [DOI] [PubMed] [Google Scholar]
- 85.Rapaport D. C., Johnson J. E., and Skolnick J., “Supramolecular self-assembly: Molecular dynamics modeling of polyhedral shell formation,” Comput. Phys. Commun. 121–122, 231–235 (1999). 10.1016/s0010-4655(99)00319-7 [DOI] [Google Scholar]
- 86.Mendoza C. I. and Reguera D., “Shape selection and mis-assembly in viral capsid formation by elastic frustration,” eLife 9, e52525 (2020). 10.7554/eLife.52525 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Wagner J. and Zandi R., “The robust assembly of small symmetric nanoshells,” Biophys. J. 109, 956 (2015). 10.1016/j.bpj.2015.07.041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Schwartz R., Shor P. W., Prevelige P. E., and Berger B., “Local rules simulation of the kinetics of virus capsid self-assembly,” Biophys. J. 75, 2626–2636 (1998). 10.1016/s0006-3495(98)77708-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Hagan M. F. and Chandler D., “Dynamic pathways for viral capsid assembly,” Biophys. J. 91, 42–54 (2006). 10.1529/biophysj.105.076851 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Wilber A. W., Doye J. P. K., Louis A. A., Noya E. G., Miller M. A., and Wong P., “Reversible self-assembly of patchy particles into monodisperse icosahedral clusters,” J. Chem. Phys. 127, 085106 (2007). 10.1063/1.2759922 [DOI] [PubMed] [Google Scholar]
- 91.Baschek J. E., Klein H. C. R., and Schwarz U. S., “Stochastic dynamics of virus capsid formation: Direct versus hierarchical self-assembly,” BMC Biophys. 5, 22 (2012). 10.1186/2046-1682-5-22 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Castelnovo M., Verdier T., and Foret L., “Comparing open and closed molecular self-assembly,” Europhys. Lett. 105, 28006 (2014). 10.1209/0295-5075/105/28006 [DOI] [Google Scholar]
- 93.Castelnovo M., Muriaux D., and Faivre-Moskalenko C., “Entropic control of particle sizes during viral self-assembly,” New J. Phys. 15, 035028 (2013). 10.1088/1367-2630/15/3/035028 [DOI] [Google Scholar]
- 94.Boettcher M. A., Klein H. C. R., and Schwarz U. S., “Role of dynamic capsomere supply for viral capsid self-assembly,” Phys. Biol. 12, 016014 (2015). 10.1088/1478-3975/12/1/016014 [DOI] [PubMed] [Google Scholar]
- 95.Fejer S. N., Chakrabarti D., and Wales D. J., “Emergent complexity from simple anisotropic building blocks: Shells, tubes, and spirals,” ACS Nano 4, 219–228 (2010). 10.1021/nn9013565 [DOI] [PubMed] [Google Scholar]
- 96.Kusters R., Lin H.-K., Zandi R., Tsvetkova I., Dragnea B., and van der Schoot P., “Role of charge regulation and size polydispersity in nanoparticle encapsulation by viral coat proteins,” J. Phys. Chem. B 119, 1869–1880 (2015). 10.1021/jp5108125 [DOI] [PubMed] [Google Scholar]
- 97.Zandi R. and van der Schoot P., “Size regulation of ss-RNA viruses,” Biophys. J. 96, 9–20 (2009). 10.1529/biophysj.108.137489 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Hagan M. F., “Controlling viral capsid assembly with templating,” Phys. Rev. E 77, 051904 (2008). 10.1103/physreve.77.051904 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Hagan M. F., “A theory for viral capsid assembly around electrostatic cores,” J. Chem. Phys. 130, 114902 (2009). 10.1063/1.3086041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Belyi V. A. and Muthukumar M., “Electrostatic origin of the genome packing in viruses,” Proc. Natl. Acad. Sci. U. S. A. 103, 17174–17178 (2006). 10.1073/pnas.0608311103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Twarock R., Bingham R. J., Dykeman E. C., and Stockley P. G., “A modelling paradigm for RNA virus assembly,” Curr. Opin. Virol. 31, 74–81 (2018). 10.1016/j.coviro.2018.07.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Zandi R., Dragnea B., Travesset A., and Podgornik R., “On virus growth and form,” Phys. Rep. 847, 1 (2020). 10.1016/j.physrep.2019.12.005 [DOI] [Google Scholar]
- 103.Li S., Roy P., Travesset A., and Zandi R., “Why large icosahedral viruses need scaffolding proteins,” Proc. Natl. Acad. Sci. U. S. A. 115, 10971–10976 (2018). 10.1073/pnas.1807706115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Li S., Zandi R., Travesset A., and Grason G. M., “Ground states of crystalline caps: Generalized jellium on curved space,” Phys. Rev. Lett. 123, 145501 (2019); arXiv:1906.03301. 10.1103/physrevlett.123.145501 [DOI] [PubMed] [Google Scholar]
- 105.van der Schoot P. and Zandi R., “Impact of the topology of viral RNAs on their encapsulation by virus coat proteins,” J. Biol. Phys. 39, 289–299 (2013). 10.1007/s10867-013-9307-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Erdemci-Tandogan G., Wagner J., van der Schoot P., Podgornik R., and Zandi R., “RNA topology remolds electrostatic stabilization of viruses,” Phys. Rev. E 89, 032707 (2014). 10.1103/PhysRevE.89.032707 [DOI] [PubMed] [Google Scholar]
- 107.Siber A., Zandi R., and Podgornik R., “Thermodynamics of nanospheres encapsulated in virus capsids,” Phys. Rev. E 81, 051919 (2010). 10.1103/PhysRevE.81.051919 [DOI] [PubMed] [Google Scholar]
- 108.Dykeman E. C., Stockley P. G., and Twarock R., “Packaging signals in two single-stranded RNA viruses imply a conserved assembly mechanism and geometry of the packaged genome,” J. Mol. Biol. 425, 3235–3249 (2013). 10.1016/j.jmb.2013.06.005 [DOI] [PubMed] [Google Scholar]
- 109.Patel N., Dykeman E. C., Coutts R. H. A., Lomonossoff G. P., Rowlands D. J., Phillips S. E. V., Ranson N., Twarock R., Tuma R., and Stockley P. G., “Revealing the density of encoded functions in a viral RNA.” Proc. Natl. Acad. Sci. U. S. A. 112, 2227 (2015). 10.1073/pnas.1420812112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Dykeman E. C., Stockley P. G., and Twarock R., “Solving a Levinthal’s paradox for virus assembly identifies a unique antiviral strategy,” Proc. Natl. Acad. Sci. U. S. A. 111, 5361–5366 (2014). 10.1073/pnas.1319479111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Dykeman E. C., Stockley P. G., and Twarock R., “Building a viral capsid in the presence of genomic RNA,” Phys. Rev. E 87, 022717 (2013). 10.1103/PhysRevE.87.022717 [DOI] [PubMed] [Google Scholar]
- 112.Morton V. L., Dykeman E. C., Stonehouse N. J., Ashcroft A. E., Twarock R., and Stockley P. G., “The impact of viral RNA on assembly pathway selection,” J. Mol. Biol. 401, 298–308 (2010). 10.1016/j.jmb.2010.05.059 [DOI] [PubMed] [Google Scholar]
- 113.Zhang R., Wernersson E., and Linse P., “Icosahedral capsid formation by capsomer subunits and a semiflexible polyion,” RSC Adv. 3, 25258–25267 (2013). 10.1039/c3ra44533j [DOI] [Google Scholar]
- 114.Zhang R. and Linse P., “Topological effects on capsomer-polyion co-assembly,” J. Chem. Phys. 140, 244903 (2014). 10.1063/1.4883056 [DOI] [PubMed] [Google Scholar]
- 115.Zhang R. and Linse P., “Icosahedral capsid formation by capsomers and short polyions,” J. Chem. Phys. 138, 154901 (2013). 10.1063/1.4799243 [DOI] [PubMed] [Google Scholar]
- 116.Angelescu D. G., Stenhammar J., and Linse P., “Packaging of a flexible polyelectrolyte inside a viral capsid: Effect of salt concentration and salt valence,” J. Phys. Chem. B 111, 8477–8485 (2007). 10.1021/jp068384o [DOI] [PubMed] [Google Scholar]
- 117.Angelescu D. G. and Linse P., “Monte Carlo simulations of flexible polyelectrolytes inside viral capsids with dodecahedral charge distribution,” Phys. Rev. E 75, 051905 (2007). 10.1103/PhysRevE.75.051905 [DOI] [PubMed] [Google Scholar]
- 118.Panahandeh S., Li S., and Zandi R., “The equilibrium structure of self-assembled protein nano-cages,” Nanoscale 10, 22802–22809 (2018). 10.1039/c8nr07202g [DOI] [PubMed] [Google Scholar]
- 119.Panahandeh S., Li S., Marichal L., Leite Rubim R., Tresset G., and Zandi R., “How a virus circumvents energy barriers to form symmetric shells,” ACS Nano 14, 3170–3180 (2020). 10.1021/acsnano.9b08354 [DOI] [PubMed] [Google Scholar]
- 120.Cai F., Dou Z., Bernstein S. L., Leverenz R., Williams E. B., Heinhorst S., Shively J., Cannon G. C., and Kerfeld C. A., “Advances in understanding carboxysome assembly in prochlorococcus and synechococcus implicate CsoS2 as a critical component,” Life 5, 1141 (2015). 10.3390/life5021141 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Fan C., Cheng S., Liu Y., Escobar C. M., Crowley C. S., Jefferson R. E., Yeates T. O., and Bobik T. A., “Short N-terminal sequences package proteins into bacterial microcompartments,” Proc. Natl. Acad. Sci. U. S. A. 107, 7509–7514 (2010). 10.1073/pnas.0913199107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Cameron J. C., Wilson S. C., Bernstein S. L., and Kerfeld C. A., “Biogenesis of a bacterial organelle: The carboxysome assembly pathway.” Cell 155, 1131–1140 (2013). 10.1016/j.cell.2013.10.044 [DOI] [PubMed] [Google Scholar]
- 123.Chen A. H., Robinson-Mosher A., Savage D. F., Silver P. A., and Polka J. K., “The bacterial carbon-fixing organelle is formed by shell envelopment of preassembled cargo,” PLoS One 8, e76127 (2013). 10.1371/journal.pone.0076127 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Wunder T., Cheng S. L. H., Lai S.-K., Li H.-Y., and Mueller-Cajar O., “The phase separation underlying the pyrenoid-based microalgal Rubisco supercharger,” Nat. Commun. 9, 5076–5110 (2018). 10.1038/s41467-018-07624-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Chaijarasphong T., Nichols R. J., Kortright K. E., Nixon C. F., Teng P. K., Oltrogge L. M., and Savage D. F., “Programmed ribosomal frameshifting mediates expression of the α-carboxysome,” J. Mol. Biol. 428, 153–164 (2016). 10.1016/j.jmb.2015.11.017 [DOI] [PubMed] [Google Scholar]
- 126.Oltrogge L. M., Chaijarasphong T., Chen A. W., Bolin E. R., Marqusee S., and Savage D. F., “Multivalent interactions between CsoS2 and Rubisco mediate α-carboxysome formation,” Nat. Struct. Mol. Biol. 27, 281 (2020). 10.1038/s41594-020-0387-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Rochaix J.-D., “The pyrenoid: An overlooked organelle comes out of age,” Cell 171, 28–29 (2017). 10.1016/j.cell.2017.09.012 [DOI] [PubMed] [Google Scholar]
- 128.Wang H., Yan X., Aigner H., Bracher A., Nguyen N. D., Hee W. Y., Long B. M., Price G. D., Hartl F. U., and Hayer-Hartl M., “Rubisco condensate formation by CcmM in β-carboxysome biogenesis,” Nature 566, 131–135 (2019). 10.1038/s41586-019-0880-5 [DOI] [PubMed] [Google Scholar]
- 129.He S., Chou H.-T., Matthies D., Wunder T., Meyer M. T., Atkinson N., Martinez-Sanchez A., Jeffrey P. D., Port S. A., Patena W., He G., Chen V. K., Hughson F. M., McCormick A. J., Mueller-Cajar O., Engel B. D., Yu Z., and Jonikas M. C., “The structural basis of Rubisco phase separation in the pyrenoid,” Nat. Plants 6, 1480 (2020). 10.1038/s41477-020-00811-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Meyer M. T., Itakura A. K., Patena W., Wang L., He S., Emrich-Mills T., Lau C. S., Yates G., Mackinder L. C. M., and Jonikas M. C., “Assembly of the algal CO2-fixing organelle, the pyrenoid, is guided by a Rubisco-binding motif,” Sci. Adv. 6, eabd2408 (2020). 10.1126/sciadv.abd2408 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Brangwynne C. P., “Soft active aggregates: Mechanics, dynamics and self-assembly of liquid-like intracellular protein bodies,” Soft Matter 7, 3052 (2011). 10.1039/c0sm00981d [DOI] [Google Scholar]
- 132.Style R. W., Sai T., Fanelli N., Ijavi M., Smith-Mannschott K., Xu Q., Wilen L. A., and Dufresne E. R., “Liquid-liquid phase separation in an elastic network,” Phys. Rev. X 8, 011028 (2018). 10.1103/physrevx.8.011028 [DOI] [Google Scholar]
- 133.Jacobs W. M. and Frenkel D., “Phase transitions in biological systems with many components,” Biophys. J. 112, 683–691 (2017). 10.1016/j.bpj.2016.10.043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134.Jacobs W. M., “Self-assembly of biomolecular condensates with shared components,” Phys. Rev. Lett. 126, 258101 (2021). 10.1103/physrevlett.126.258101 [DOI] [PubMed] [Google Scholar]
- 135.Perry S. L., “Phase separation: Bridging polymer physics and biology,” Curr. Opin. Colloid Interface Sci. 39, 86–97 (2019). 10.1016/j.cocis.2019.01.007 [DOI] [Google Scholar]
- 136.Sanchez-Burgos I., Espinosa J. R., Joseph J. A., and Collepardo-Guevara R., “Valency and binding affinity variations can regulate the multilayered organization of protein condensates with many components,” Biomolecules 11, 278 (2021). 10.3390/biom11020278 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Zhou J., Kondylis P., Haywood D. G., Harms Z. D., Lee L. S., Zlotnick A., and Jacobson S. C., “Characterization of virus capsids and their assembly intermediates by multicycle resistive-pulse sensing with four pores in series,” Anal. Chem. 90, 7267–7274 (2018). 10.1021/acs.analchem.8b00452 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 138.Best R. B., “Computational and theoretical advances in studies of intrinsically disordered proteins,” Curr. Opin. Struct. Biol. 42, 147–154 (2017). 10.1016/j.sbi.2017.01.006 [DOI] [PubMed] [Google Scholar]
- 139.Dignon G. L., Zheng W., Best R. B., Kim Y. C., and Mittal J., “Relation between single-molecule properties and phase behavior of intrinsically disordered proteins,” Proc. Natl. Acad. Sci. U. S. A. 115, 9929–9934 (2018). 10.1073/pnas.1804177115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140.Dignon G. L., Zheng W., Kim Y. C., Best R. B., and Mittal J., “Sequence determinants of protein phase behavior from a coarse-grained model,” PLoS Comput. Biol. 14, e1005941 (2018). 10.1371/journal.pcbi.1005941 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 141.Dignon G. L., Zheng W., and Mittal J., “Simulation methods for liquid–liquid phase separation of disordered proteins,” Curr. Opin. Chem. Eng. 23, 92–98 (2019). 10.1016/j.coche.2019.03.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142.Ianiro A., Wu H., van Rijt M. M. J., Vena M. P., Keizer A. D. A., Esteves A. C. C., Tuinier R., Friedrich H., Sommerdijk N. A. J. M., and Patterson J. P., “Liquid–liquid phase separation during amphiphilic self-assembly,” Nat. Chem. 11, 320–328 (2019). 10.1038/s41557-019-0210-4 [DOI] [PubMed] [Google Scholar]
- 143.Posey A. E., Holehouse A. S., and Pappu R. V., “Phase separation of intrinsically disordered proteins,” Methods Enzymol. 611, 1–30 (2018). 10.1016/bs.mie.2018.09.035 [DOI] [PubMed] [Google Scholar]
- 144.Ruff K. M., Pappu R. V., and Holehouse A. S., “Conformational preferences and phase behavior of intrinsically disordered low complexity sequences: Insights from multiscale simulations,” Curr. Opin. Struct. Biol. 56, 1–10 (2018). 10.1016/j.sbi.2018.10.003 [DOI] [PubMed] [Google Scholar]
- 145.Alberti S., Gladfelter A., and Mittag T., “Considerations and challenges in studying liquid-liquid phase separation and biomolecular condensates,” Cell 176, 419–434 (2019). 10.1016/j.cell.2018.12.035 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146.Caspar D. L. D. and Klug A., “Physical principles in construction of regular viruses,” Cold Spring Harbor Symp. Quant. Biol. 27, 1–24 (1962). 10.1101/sqb.1962.027.001.005 [DOI] [PubMed] [Google Scholar]
- 147.Douglas T. and Young M., “Host–guest encapsulation of materials by assembled virus protein cages,” Nature 393, 152–155 (1998). 10.1038/30211 [DOI] [Google Scholar]
- 148.Douglas T. and Young M., “Viruses: Making friends with old foes,” Science 312(3), 873 (2006). 10.1126/science.1123223 [DOI] [PubMed] [Google Scholar]
- 149.Goodall C. P., Schwarz B., Selivanovitch E., Avera J., Wang J., Miettinen H., and Douglas T., “Controlled modular multivalent presentation of the CD40 ligand on P22 virus-like particles leads to tunable amplification of CD40 signaling,” ACS Appl. Bio Mater. 4, 8205–8214 (2021). 10.1021/acsabm.1c00718 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 150.Robinson S. A., Hartman E. C., Ikwuagwu B. C., Francis M. B., and Tullman-Ercek D., “Engineering a virus-like particle to display peptide insertions using an apparent fitness landscape,” Biomacromolecules 21, 4194–4204 (2020). 10.1021/acs.biomac.0c00987 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 151.Minten I. J., Hendriks L. J. A., Nolte R. J. M., and Cornelissen J. J. L. M., “Controlled encapsulation of multiple proteins in virus capsids,” J. Am. Chem. Soc. 131, 17771–17773 (2009). 10.1021/ja907843s [DOI] [PubMed] [Google Scholar]
- 152.Rhee J.-K., Hovlid M., Fiedler J. D., Brown S. D., Manzenrieder F., Kitagishi H., Nycholat C., Paulson J. C., and Finn M. G., “Colorful virus-like particles: Fluorescent protein packaging by the Qβ capsid,” Biomacromolecules 12, 3977–3981 (2011). 10.1021/bm200983k [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Rurup W. F., Snijder J., Koay M. S. T., Heck A. J. R., and Cornelissen J. J. L. M., “Self-sorting of foreign proteins in a bacterial nanocompartment,” J. Am. Chem. Soc. 136, 3828–3832 (2014). 10.1021/ja410891c [DOI] [PubMed] [Google Scholar]
- 154.Rurup W. F., Verbij F., Koay M. S. T., Blum C., Subramaniam V., and Cornelissen J. J. L. M., “Predicting the loading of virus-like particles with fluorescent proteins,” Biomacromolecules 15, 558–563 (2014). 10.1021/bm4015792 [DOI] [PubMed] [Google Scholar]
- 155.Dashti N. H., Abidin R. S., and Sainsbury F., “Programmable in vitro coencapsidation of guest proteins for intracellular delivery by virus-like particles,” ACS Nano 12, 4615–4623 (2018). 10.1021/acsnano.8b01059 [DOI] [PubMed] [Google Scholar]
- 156.Faulkner M., Zhao L.-S., Barrett S., and Liu L.-N., “Self-assembly stability and variability of bacterial microcompartment shell proteins in response to the environmental change,” Nanoscale Res. Lett. 14, 54 (2019). 10.1186/s11671-019-2884-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 157.Whitelam S. and Jack R. L., “The statistical mechanics of dynamic pathways to self-assembly,” Annu. Rev. Phys. Chem. 66, 143–163 (2015). 10.1146/annurev-physchem-040214-121215 [DOI] [PubMed] [Google Scholar]
- 158.Smit B., “Phase diagrams of Lennard-Jones fluids,” J. Chem. Phys. 96, 8639–8640 (1992). 10.1063/1.462271 [DOI] [Google Scholar]
- 159.Lopes J. N. C., “Phase equilibra in binary Lennard-Jones mixtures: Phase diagram simulation,” Mol. Phys. 96, 1649–1658 (1999). 10.1080/00268979909483108 [DOI] [Google Scholar]
- 160.Shen V. and Errington J., “Determination of fluid-phase behavior using transition-matrix Monte Carlo: Binary Lennard-Jones mixtures,” J. Chem. Phys. 122, 064508 (2005). 10.1063/1.1844372 [DOI] [PubMed] [Google Scholar]
- 161.Dai W., Chen M., Myers C., Ludtke S. J., Pettitt B. M., King J. A., Schmid M. F., and Chiu W., “Visualizing individual RuBisCO and its assembly into carboxysomes in marine cyanobacteria by cryo-electron tomography,” J. Mol. Biol. 430, 4156–4167 (2018). 10.1016/j.jmb.2018.08.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 162.Parsons J. B., Frank S., Bhella D., Liang M., Prentice M. B., Mulvihill D. P., and Warren M. J., “Synthesis of empty bacterial microcompartments, directed organelle protein incorporation, and evidence of filament-associated organelle movement,” Mol. Cell 38, 305–315 (2010). 10.1016/j.molcel.2010.04.008 [DOI] [PubMed] [Google Scholar]
- 163.Choudhary S., Quin M. B., Sanders M. A., Johnson E. T., and Schmidt-Dannert C., “Engineered protein nano-compartments for targeted enzyme localization,” PLoS One 7, e33342 (2012). 10.1371/journal.pone.0033342 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 164.Lassila J. K., Bernstein S. L., Kinney J. N., Axen S. D., and Kerfeld C. A., “Assembly of robust bacterial microcompartment shells using building blocks from an organelle of unknown function,” J. Mol. Biol. 426, 2217–2228 (2014). 10.1016/j.jmb.2014.02.025 [DOI] [PubMed] [Google Scholar]
- 165.Condezo G. N. and San Martín C., “Localization of adenovirus morphogenesis players, together with visualization of assembly intermediates and failed products, favor a model where assembly and packaging occur concurrently at the periphery of the replication center,” PLoS Pathog. 13, e1006320 (2017). 10.1371/journal.ppat.1006320 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 166.Aussignargues C., Paasch B. C., Gonzalez-Esquer R., Erbilgin O., and Kerfeld C. A., “Bacterial microcompartment assembly: The key role of encapsulation peptides,” Commun. Integr. Biol. 8, e1039755 (2015). 10.1080/19420889.2015.1039755 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 167.Ryan P., Forrester T. J. B., Wroblewski C., Kenney T. M. G., Kitova E. N., Klassen J. S., and Kimber M. S., “The small RBcS-like domains of the β-carboxysome structural protein CcmM bind RubisCO at a site distinct from that binding the RbcS subunit,” J. Biol. Chem. 294, 2593–2603 (2019). 10.1074/jbc.ra118.006330 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 168.Bale J. B., Gonen S., Liu Y., Sheffler W., Ellis D., Thomas C., Cascio D., Yeates T. O., Gonen T., King N. P., and Baker D., “Accurate design of megadalton-scale two-component icosahedral protein complexes,” Science 353, 389–394 (2016). 10.1126/science.aaf8818 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 169.Butterfield G. L., Lajoie M. J., Gustafson H. H., Sellers D. L., Nattermann U., Ellis D., Bale J. B., Ke S., Lenz G. H., Yehdego A., Ravichandran R., Pun S. H., King N. P., and Baker D., “Evolution of a designed protein assembly encapsulating its own RNA genome,” Nature 552, 415–420 (2017). 10.1038/nature25157 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 170.Golub E., Subramanian R. H., Esselborn J., Alberstein R. G., Bailey J. B., Chiong J. A., Yan X., Booth T., Baker T. S., and Tezcan F. A., “Constructing protein polyhedra via orthogonal chemical interactions,” Nature 578, 172–176 (2020). 10.1038/s41586-019-1928-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 171.Sigl C., Willner E. M., Engelen W., Kretzmann J. A., Sachenbacher K., Liedl A., Kolbe F., Wilsch F., Aghvami S. A., Protzer U. et al. , “Programmable icosahedral shell system for virus trapping,” Nat. Mater. 20, 1281 (2021). 10.1038/s41563-021-01020-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 172.Fox J. M., Wang G., Speir J. A., Olson N. H., Johnson J. E., Baker T. S., and Young M. J., “Comparison of the native CCMV virion with in vitro assembled CCMW virions by cryoelectron microscopy and image reconstruction,” Virology 244, 212–218 (1998). 10.1006/viro.1998.9107 [DOI] [PubMed] [Google Scholar]
- 173.Schneemann A., “The structural and functional role of RNA in icosahedral virus assembly,” Annu. Rev. Microbiol. 60, 51–67 (2006). 10.1146/annurev.micro.60.080805.142304 [DOI] [PubMed] [Google Scholar]
- 174.Speir J. A., Munshi S., Wang G., Baker T. S., and Johnson J. E., “Structures of the native and swollen forms of cowpea chlorotic mottle virus determined by X-ray crystallography and cryo-electron microscopy,” Structure 3, 63–78 (1995). 10.1016/s0969-2126(01)00135-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 175.Perlmutter J. D., Qiao C., and Hagan M. F., “Viral genome structures are optimal for capsid assembly,” eLife 2, e00632 (2013). 10.7554/eLife.00632 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 176.Perlmutter J. D., Perkett M. R., and Hagan M. F., “Pathways for virus assembly around nucleic acids,” J. Mol. Biol. 426, 3148 (2014). 10.1016/j.jmb.2014.07.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 177.Perlmutter J. D. and Hagan M. F., “The role of packaging sites in efficient and specific virus assembly,” J. Mol. Biol. 427, 2451 (2015). 10.1016/j.jmb.2015.05.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 178.Li S., Erdemci-Tandogan G., Wagner J., van der Schoot P., and Zandi R., “Impact of a nonuniform charge distribution on virus assembly,” Phys. Rev. E 96, 022401 (2017). 10.1103/PhysRevE.96.022401 [DOI] [PubMed] [Google Scholar]
- 179.Kerfeld C. A. and Erbilgin O., “Bacterial microcompartments and the modular construction of microbial metabolism,” Trends Microbiol. 23, 22–34 (2015). 10.1016/j.tim.2014.10.003 [DOI] [PubMed] [Google Scholar]
- 180.Sutter M., Faulkner M., Aussignargues C., Paasch B. C., Barrett S., Kerfeld C. A., and Liu L.-N., “Visualization of bacterial microcompartment facet assembly using high-speed atomic force microscopy,” Nano Lett. 16, 1590–1595 (2016). 10.1021/acs.nanolett.5b04259 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 181.Wales D. J., “The energy landscape as a unifying theme in molecular science,” Philos. Trans. R. Soc. London 363, 357–375 (2005). 10.1098/rsta.2004.1497 [DOI] [PubMed] [Google Scholar]
- 182.Fejer S. N., James T. R., Hernández-Rojas J., and Wales D. J., “Energy landscapes for shells assembled from pentagonal and hexagonal pyramids,” Phys. Chem. Chem. Phys. 11, 2098–2104 (2009). 10.1039/b818062h [DOI] [PubMed] [Google Scholar]
- 183.Ruiz-Herrero T. and Hagan M. F., “Simulations show that virus assembly and budding is facilitated by membrane microdomains,” Biophys. J. 108, 585 (2015). 10.1016/j.bpj.2014.12.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 184.Anderson J. A., Lorenz C. D., and Travesset A., “General purpose molecular dynamics simulations fully implemented on graphics processing units,” J. Comput. Phys. 227, 5342–5359 (2008). 10.1016/j.jcp.2008.01.047 [DOI] [Google Scholar]
- 185.Nguyen T. D., Phillips C. L., Anderson J. A., and Glotzer S. C., “Rigid body constraints realized in massively-parallel molecular dynamics on graphics processing units,” Comput. Phys. Commun. 182, 2307–2313 (2011). 10.1016/j.cpc.2011.06.005 [DOI] [Google Scholar]
- 186.Anderson J., http://codeblue.umich.edu/hoomd-blue/doc/page_units.html.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are openly available in Open Science Framework at http://doi.org/10.17605/OSF.IO/SKZ7F.