A model of actin-driven endocytosis explains differences of endocytic motility in budding and fission yeast

Abstract

A comparative study (Sun et al., 2019) showed that the abundance of proteins at sites of endocytosis in fission and budding yeast is more similar in the two species than previously thought, yet membrane invaginations in fission yeast elongate twofold faster and are nearly twice as long as in budding yeast. Here we use a three-dimensional model of a motile endocytic invagination (Nickaeen et al., 2019) to investigate factors affecting elongation of the invaginations. We found that differences in turgor pressure in the two yeast species can largely explain the paradoxical differences observed experimentally in endocytic motility.

INTRODUCTION

As in plant cells, endocytosis in yeast cells occurs under high turgor pressure estimated to be ∼10 atm in fission yeast (Basu et al., 2014; Lacy et al., 2018) and about a fifth to half of that in budding yeast (de Maranon et al., 1996; Schaber et al., 2010). Transient assembly of small, dense networks of actin filaments at endocytic sites (termed “actin patches”) is necessary for robust endocytosis in yeast (Aghamohammadzadeh and Ayscough, 2009; Basu et al., 2014), suggesting that assembly of an actin patch around a nascent invagination of the plasma membrane may generate a pulling force sufficient to elongate the invagination under such pressures. Many studies have investigated the mechanisms of force generation at endocytic sites in yeast (Carlsson and Bayly, 2014; Scher-Zagier and Carlsson, 2016; Carlsson, 2018; Kaksonen and Roux, 2018; Lacy et al., 2018; Mund et al., 2018; Nickaeen et al., 2019).

A comparative study of endocytosis in fission and budding yeast (Sun et al., 2019) found that with the exception of twofold more polymerized actin in fission yeast the abundances of proteins participating in patch assembly are more similar than previously thought. Nevertheless, elongation of an endocytic invagination is twofold faster (∼52 nm/s) in fission yeast than in budding yeast (∼24 nm/s). The fast elongation rates in both yeasts indicate that driving forces generated at endocytic sites substantially overpower resistance from turgor pressure, not just withstand it.

For the turgor pressure of 10 atm, a rough estimation of a resisting force acting on a cylindrical tubule with a typical radius of ∼30 nm yields ∼3000 pN (Carlsson, 2018; Lacy et al., 2018). Simulations based on a spatial model of a motile invagination proposed by Nickaeen et al. (2019) showed that an actin patch assembling around such a tubule can generate tangential pulling forces of ∼2500 pN that can withstand a turgor pressure of ∼9 atm. For lower turgor pressures, the tubule would elongate, albeit slowly, for example, at only ∼2 nm/s against a turgor pressure of ∼7 atm.

Yet the simulations of the model made another prediction that the assembling patch would also generate normal forces, which squeeze the tubule at its base and stretch it at its middle, thus transforming the invagination shape from cylindrical to flasklike (or “head–neck”) as observed in electron micrographs of budding yeast (Kukulski et al., 2012; Buser and Drubin, 2013). Previous modeling studies also predicted endocytic invaginations with head–neck shapes (Dmitrieff and Nédélec, 2015; Ma and Berro, 2021). Since the resisting force is the product of turgor pressure and the cross-sectional area at the base of the invagination, the transition to the head–neck shape may dramatically reduce resistance due to turgor pressure, leading to faster elongation rates even for turgor pressures of ∼10 atm.

Our previous study, as well as works of others (Carlsson and Bayly, 2014; Mund et al., 2018), modeled the invaginations as spherocylinders. In those simulations, we approximated the reduction in resistance due to the putative shape change by replacing fixed resistance with a resistance decreasing over time. The elongation rate increased fourfold, to ∼8 nm/s, which is still significantly lower than the 25–50 nm/s range reported by Sun et al., (2019).

In this study, we solved our model in geometries mimicking flasklike invaginations. The solutions yielded higher driving forces, because, in contrast with cylindrical shapes for which pulling forces are viscous in nature, active stresses also contribute to the forces driving flasklike invaginations. Consistent with the experimental data (Sun et al., 2019), invagination is faster and deeper at high turgor pressures, because at higher initial resistance, more actin filaments accumulate by the time the driving force overcomes the resistance, producing higher driving forces during elongation.

RESULTS

Model

Our model, described in detail in Nickaeen et al. (2019), couples kinetics of actin nucleation, polymerization, and turnover constrained by counts of each participating protein over time (Berro et al., 2010), with the mechanics of the assembling filamentous meshwork approximated as that of a visco-active gel (Kruse et al. 2005; Prost et al., 2015). Mathematically, the model consists of advection-reaction equations governing densities of proteins involved in patch assembly (see Eq (S1) in the Supplemental Material), and a force-balance equation yielding actin velocities [Eq (S2) of the Supplemental Material]. In the advection-reaction equations, reaction rates and rate constants from the experimental literature (Berro et al., 2010; see also Supplemental Table S1 in the Supplemental Material) were modified to reflect effects of forces and filament densities on polymerization kinetics. The equation, which governs actin flow, balances active forces, originating from impingement of polymerized subunits on existing filaments, with viscous forces that arise due to entanglement and cross-linking of branched filaments. The active and viscous forces derive, respectively, from repulsive and viscous stresses in the meshwork of overlapping actin filaments, which are both proportional to the square of local density of poly­merized subunits; the viscous stresses are also proportional to the local average of filament lengths [Gardel et al., 2003; Nickaeen et al., 2019; see also Eq (S3) in the Supplemental Material]. The coefficients determining scales of the stresses were inferred from rheological properties of actin filament networks (Mullins et al., 1998; Gardel et al., 2003; Tseng and Wirtz, 2004).

Through interactions with the membrane, the flow of polymerized actin exerts on the invagination driving forces parallel to its axis. The resultant driving force (f_drive) and resistance due to turgor pressure (f_resist) are the factors determining elongation rate in our model. We ignore small resistive forces due to membrane surface tension. We also assume sufficient supply of lipids by way of exocytosis and lateral diffusion and impose no constraint on total area of the invaginated membrane.

To determine the time-dependent driving force f_drive (t), we integrate over the surface of the invagination, for each t, the active and viscous forces exerted on the invagination by actin flow and then project the resultant force on the invagination axis [see Supplemental Material, Eq (S4)].

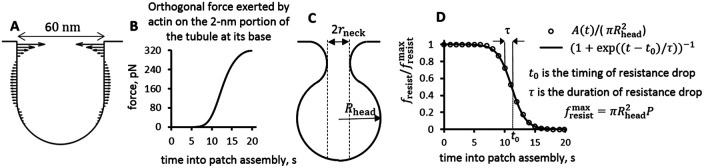
As mentioned in the Introduction, the resistive force can also depend on time, even at a fixed turgor pressure. Indeed, our previous study revealed that an assembling actin patch produces not only a pulling force but also generates orthogonal forces that squeeze the base of the invagination and stretch its middle (Figure 1A). As actin filaments accumulate around a nascent spherocylindrical invagination, squeezing forces at the base of the invagination can reach the magnitude amounting to additional pressure of ∼8.5 atm (Figure 1B). It is therefore likely that at some point during patch assembly, the nascent invaginations, such as the one shown in Figure 1A, acquire head–neck shapes (Figure 1C). Such shapes were observed in electron micrographs of invaginations in budding yeast (Kukulski et al., 2012; Buser and Drubin, 2013) and predicted theoretically for a membrane elongated under high turgor pressure by a point force exerted at its tip (Dmitrieff and Nédélec, 2015; Ma and Berro, 2021). Because turgor pressure is isotropic and thus pushes on the upper surface of the head of the invagination as well, the transition from cylindrical shape to flasklike shape, such as in Figure 1C, results in f_resist(t) decreasing with time (Figure 1D). We specify this function later in this subsection (see also Figure 1D, Eq (2) below, and Nickaeen et al. (2019)].

FIGURE 1:

An assembling endocytic actin patch exerts strong squeezing forces at its base of an initial invagination. (A) Example of distribution of orthogonal forces in an (r, z)-section of a nascent invagination adapted from simulation results in Figure 5A of Nickaeen et al. (2019). (B) Time dependence of squeezing force acting on the 2 nm wide portion at the base of the nascent tubule in (A), from a simulation described in Figure 5A of Nickaeen et al. (2019). The force of 320 pN applied to a 2 nm-wide band with the radius of 30 nm amounts to additional pressure of ≈ 8.5 atm. (C) Cartoon of a head–neck (flasklike) shape with radii r_neck and R_head; since turgor pressure P is isotropic, f_resist for this shape diminishes to 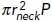. (D) Graph of f_resist (t) normalized to 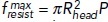[dots, A(t) is the cross-action area at the base, see the text] is well approximated by function {1 + exp[(t – t₀)/τ]}^–1 (solid curve) with the fitted timing (t₀) and duration (τ) of the resistance decrease caused by shape change.

Solving for dynamics of the invagination shape would involve mechanics of a moving membrane (Powers, 2010) and require reliable experimental data describing rheological characteristics of both the membrane and its protein coat. Lacking this information, we initialize invaginations as already having head–neck shapes with specified head and neck radii R_head and r_neck, which do not change as the neck elongates. As in Nickaeen et al. (2019), we assume that all points of the membrane move with the same speed u(t) described by a linear force-velocity relation,

1

where μ is the invagination mobility coefficient. The inverse of the mobility, representing “resistivity” of the invagination with respect to a net driving force, is likely determined by viscosity of the membrane and its protein coat, including links to actin filaments. Our model is only modestly sensitive to μ (see The head–neck invaginations elongate faster and to greater depths under higher turgor pressures), so this parameter is not critical for explaining the twofold differences in elongation rates and depths reported in Sun et al. (2019). Note that for the invagination to elongate, the driving force must exceed the resistance of turgor pressure; therefore, Eq. (1) holds only for 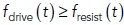, whereas for .

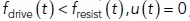Because the resistance of turgor pressure is proportional to the invagination cross-section area near its base (Nickaeen et al., 2019), we can gain insight into general behavior of f_resist (t) by estimating the time dependence of this area, A (t), for the example illustrated by Figure 1A. To compute the resistive force normalized to its maximum, 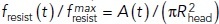, where 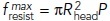and P is the turgor pressure, we assumed Hookean elasticity of the protein coat for this case (i.e., that the diameter of the opening decreases in proportion to the squeezing force shown in Figure 1B) with such stiffness that the opening would close when the squeezing force reached its maximum. Notably, the results (dotted curve in Figure 1D) are accurately fitted by the function 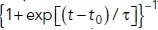with suitable timing t₀ and duration τ of the resistance descent (solid curve in Figure 1D with t₀ ≈ 11.1 s and τ ≈ 1.2 s). While the assumptions made above may be simplistic (e.g., the coat elasticity may not be Hookean), the formulation of f_resist (t) in terms of the timing and duration of the resistance drop is fairly general. We therefore approximate the resistive force in this study by the following function of time,

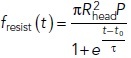2

and treat t₀ and τ as model parameters [see also Eq (2*) in The head–neck invaginations elongate faster and to greater depths under higher turgor pressures]. Note that because the reduction of resistance occurs due to the shape change, t₀ in our model also represents the time around which the transition to a head–neck shape takes place.

Nucleation-promoting factors (NPFs)—the proteins that stimulate Arp2/3 complex to nucleate branched actin filaments—reside on the invaginating membrane where they concentrate in narrow rings around the membrane. Fission yeast has two rings of NPFs, one that remains in the initial position at the base of the invagination at the plasma membrane and the other that moves with the tip of the tubule (Arasada and Pollard, 2011; Arasada et al., 2018), whereas budding yeast has one ring of NPFs that remains near the base of the invagination (Mund et al., 2018). As with cylindrical shapes (Nickaeen et al., 2019), simulations of both arrangements of NPFs on head–neck surfaces yielded similar elongation rates and tip displacements. To avoid duplication, we employ the two-zone arrangement of NPFs characteristic of fission yeast to illustrate our findings throughout this paper.

In summary, we assume that a nascent endocytic invagination begins to elongate when the driving force exerted on it by the assembling actin patch overcomes resistance of turgor pressure, and that the elongation rate is proportional to the difference of the two forces [(Eq (1)]. Dynamics of the driving force depend on mechanical stresses developing in the patch. Thus the driving force is ultimately determined by the nucleation and polymerization kinetics of actin and by the flow of actin filaments. The latter is governed by local force balance in the patch subjected to a no-slip condition at the interface with the invaginated membrane. Given that the invagination shape likely transforms in the process from cylindrical to flasklike, we further assume that the turgor resistance decreases with time [Eq (2)]. A mathematical description of the model and its numerical solution are detailed in the Supplemental Material [Eqs (S1)–(S4)] and in Nickaeen et al. (2019). Because the invaginations in our model are axially symmetric, we compute and present actin densities in (r, z) coordinates (see Methods).

Changing the shape of the invagination from cylindrical to flasklike amplifies driving forces, yielding faster elongation and longer displacements

If only the reduction of resistance, described by Eq (2), is taken into account, cylindrical invaginations did not elongate as fast as observed experimentally (see Introduction). Seeking faster elongations, we noted that the shape change should also affect the driving force. Indeed, driving forces originate from stresses in the actin filament meshwork surrounding the invagination, and while the forces pulling cylindrical invaginations derive from viscous stresses, the driving forces exerted on curved invaginations would have additional contributions from active stresses due to the actin flow pushing on the upper surface of the invagination head. This would not only increase the driving force during elongation but might also make elongation rates more sensitive to the invagination mobility coefficient μ [Eq (1)].

The elongation rates of cylindrical invaginations are essentially insensitive to μ because the viscous driving forces depend on shear rates of actin flow at the invagination that are lower for invaginations with higher mobility (see the black and gray dashed curves in Figure 3, A and B discussed later in this section). As a result, the increase of μ is counterbalanced by the drop in the viscous pulling force, leaving the elongation rate u(t) virtually unchanged (Nickaeen et al., 2019). In contrast, the forces driving a flasklike invagination might be less sensitive to reductions in shear rates. The reason is that active stresses are by definition independent of shear rates and so are their contributions to the driving force.

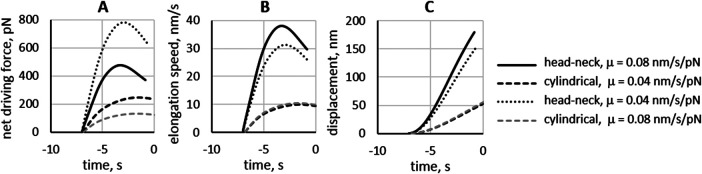
FIGURE 3:

Invaginations with “head–neck” shape have higher driving forces than cylindrical invaginations, yielding faster elongation and longer displacements. Dependence of (A) net driving force, f_net = f_drive – f_resist, (B) elongation rates, and (C) displacements on the invagination geometry and μ. The model was solved with the same parameters (with the exception of invagination mobility) for the invagination with head–neck shape (r_neck/R_head = 0.1) and mobility coefficients μ = 0.08 μm/s/pN (solid curves) and 0.04 μm/s/pN (dotted curves) and for the cylindrical invagination with μ = 0.08 μm/s/pN (gray dashed curves) and 0.04 μm/s/pN (black dashed curves). The head–neck invaginations began to move at t_begin = –7 s, and the cylindrical invaginations started to elongate at t_begin = –6.8 s. Vesicle scission, terminating elongation, is thought to occur when polymerized actin reaches its maximum. For the head–neck invaginations, t_scission = –0.8 s for μ = 0.08 μm/s/pN and –0.6 s for μ = 0.04 μm/s/pN, and for the cylindrical invaginations, t_scission = 0 s for μ = 0.04 μm/s/pN and 0.9 s for μ = 0.08 μm/s/pN. The displacements at t_scission were 179 nm (solid curve), 153 nm (dotted curve), 64 nm (gray dashed curve), and 52 nm (black dashed curve).

We tested these hypotheses by solving the model in geometries mimicking invaginations with head–neck shapes. To maximize elongation rates, we explored shapes with small ratios r_neck/R_head (the head radius was fixed at 30 nm). Given the reported similarity of protein abundances in fission and budding yeast, we ran all simulations with the same set of reaction rate constants and abundances of soluble proteins taken from Berro et al. (2010) and Nickaeen et al. (2019). Similarly, we uniformly applied coefficients setting the scales for active and viscous stresses as they were derived in our previous study. Results were consistent with our expectations, as exemplified by a solution obtained for an invagination with r_neck/R_head = 0.1 (Figure 2) using the same parameters as for the cylindrical invagination in our previous study (Figure 7 in Nickaeen et al., 2019), with the exception of the mobility coefficient value μ = 0.08 nm/(s∙pN), which is twice the one used for the cylindrical invagination¹.

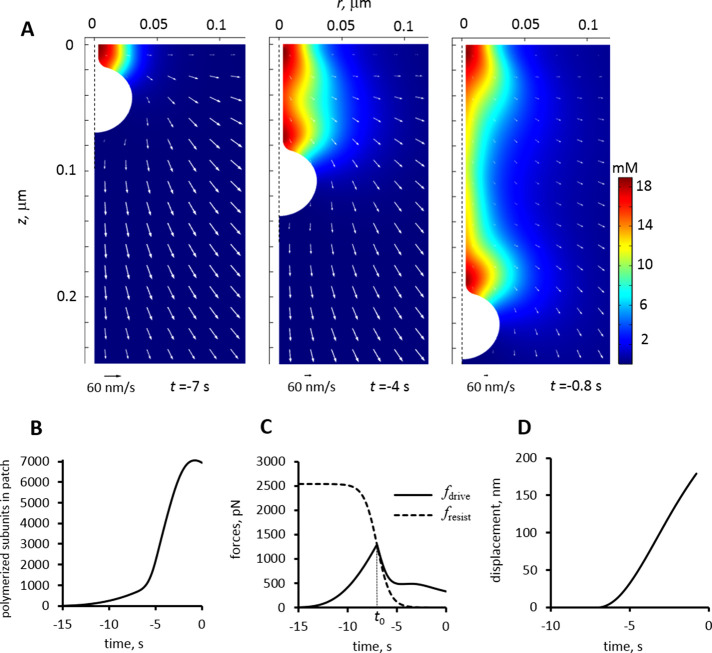
FIGURE 2:

Modeling an elongating invagination with head–neck shape. We simulated elongation of the head–neck invagination described by r_neck/R_head = 0.1 using the following parameters: P = 9 atm, t₀ = –7 s (13 s into patch assembly), τ = 0.66 s, and μ = 0.08 nm/s/pN. Similar to experimental studies, the time here and below is offset by –20 s so that the times of actin peaks would be around time zero. (A) The (r, z) sections of 3D distributions of actin densities (pseudocolors) and velocities (white arrows) are shown for three times: (left) beginning of elongation, (middle) actin half maximum, and (right) actin peak. Extracellular space is white; vertical dashed lines represent the axis of symmetry of model geometry. Velocity scale bars correspond to 60 nm/s. (B) Polymerized actin as a function of time. The numbers of subunits were counted inside a growing cylinder embedding the moving invagination: r_cyl = 0.06 μm, 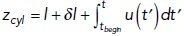, where t_begin denotes the beginning of elongation and lengths are in μm: the initial invagination length l = 0.07 μm and short extra length δl = 0.003 μm. (C) Time dependence of driving force (solid curve) and resistance due to turgor pressure described by Eq (2) (dashed curve); the invagination mobility used is μ = 0.08 μm/s/pN. (D) Displacement is ∼180 nm at the time actin peaks, which is thought to coincide with scission, yielding average elongation rate ∼30 nm/s over the duration of elongation, t_scission – t_begin.

The snapshots of the (r, z) sections in Figure 2A correspond to the beginning of elongation (left), actin half-maximum (middle), and actin peak (right). The times in this figure and below are offset by –20 s so that on the transformed scale, actin peaks, which are thought to coincide with the scission of the endocytic vesicle (Sun et al., 2019), occur around time zero (Figure 2B). Thus the offset readings are close to times before scission.

A nascent invagination begins to elongate (Figure 2D) at the time t_begin when the solid curve in Figure 2C, depicting the driving force, intersects with the dashed graph of the resistance of turgor pressure. In this particular example, t_begin coincides with t₀, but generally may deviate from it, as discussed in the next section. The driving force, rising at t < t_begin, starts “shadowing” the descending f_resist (t) immediately after t_begin (Figure 2C). This transition is largely a result of an abrupt drop of the viscous component of f_drive caused by the decrease in the shear rate, as the moving invagination catches up with the surrounding actin flow.

Assuming the vesicle scission coincides with the time of maximum actin, the simulated duration of elongation is 6.2 s. Notably, the maximum displacement 179 nm (Figure 2D) yielded by the model is within the range of displacements measured in yeast: ∼125 nm in budding yeast and ∼200 nm in fission yeast (Sun et al., 2019). The average elongation rate is then 179 nm/6.2 s = 28.9 nm/s. The maximum elongation rate, achieved at t = –3.3 s, is 38 nm/s. Both the average and the maximum values are in the range of speeds reported by Sun et al. (2019). Thus, solving the model in geometries mimicking curved flasklike invaginations and with the amplified invagination mobility produced elongation rates and displacements comparable with experimental data.

The factors contributing to the greater speeds and displacements can be elucidated further by comparing simulations that differ only by invagination shape and mobility. For this, we reran the simulation described above with μ = 0.04 nm/(s∙pN) and compared results of both simulations with the solutions of the same model for the cylindrical invagination with μ = 0.04 nm/(s∙pN) from our previous study and for the cylindrical invagination with μ = 0.08 nm/(s∙pN) (Figure 3).

Changing the shape from cylindrical to flasklike produced a threefold higher maximum of the net driving force, f_net (t) = f_drive (t) –f_resist (t) (dotted and black dashed curves in Figure 3A).

Because all four solutions were obtained with the same f_resist (t), the higher f_net reflects the anticipated increase of f_drive. Note that both head-neck and cylindrical invaginations with higher mobility experience lower f_net (dotted vs. solid and black vs. gray dashed curves in Figure 3A) because the contributions of viscous stresses to f_drive depend on shear rates, which are lower for higher μ, as discussed above. Yet overall, the elongation rates u(t) = μ f_net(t) are noticeably faster for the head–neck invagination with the higher μ (solid and dotted curves in Figure 3B), which validates the prediction that the elongation of curved invaginations is more sensitive to μ than that of the cylindrical invaginations (dashed curves in Figure 3, B and C). The maximum elongation rates in Figure 3B were as follows: (solid curve) 38.0 nm/s, (dotted curve) 31.2 nm/s, (black dashed curve) 9.9 nm/s, and (gray dashed curve) 10.5 nm/s. Higher elongation rates translate into larger maximal dispacements 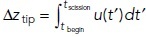, where t_scission is intepreted as the time of the peak of actin (Figure 3C). The Figure 3 legend gives the values of t_begin and t_scission for each of the solutions. Based on these data, the average elongation rates are (solid curve) 28.9 nm/s, (dotted curve) 23.9 nm/s, (black dashed curve) 7.7 nm/s, and (gray dashed curve) 8.3 nm/s.

In this study, we do not explicitly model the transition of a nascent cylindrical invagination into a flask shape. Instead, initial invaginations in our simulations are already of a head–neck shape, with R_head and r_neck that the invagination would assume as a result of shape change. Obviously, this contradicts the premise of Eq (2) that the transformation of shape occurs around time t₀. However, the errors caused by this inconsistency are likely small for two reasons. First, both the time dependence of the driving force before elongation and t_begin are essentially independent of initial shape. Indeed, according to Figure 3, the cylindrical and head–neck invaginations, simulated with the same f_resist (t), begin to elongate at approximately the same time, suggesting that during the time before the elongation, f_drive (t) is similar for all shapes. Simulations of invaginations with different r_neck/R_head and f_resist (t), described in the next section, also show that the pre-elongation f_drive (t) are virtually independent of shape (see Figure 4A). This gives us leeway in defining shapes during the time before the elongation. Second, by using at t < t_begin a fixed head–neck shape with the head and neck radii that would arise from shape transformation, we capture a makeup of the driving force in terms of active and viscous components at t = t_begin. Unlike the total driving force, the pre-elongation active and viscous components significantly depend on shape, and the composition of f_drive (t) at = t_begin in terms of these components defines the behavior of the driving force during elongation and, ultimately, the characteristics of motility of the invagination.

FIGURE 4:

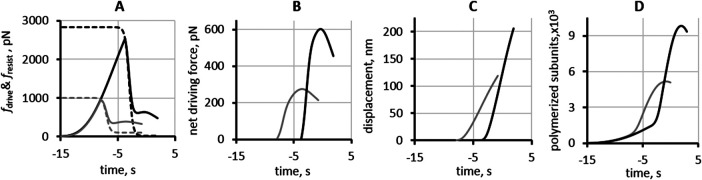
Output of simulations of models using optimized parameters for budding yeast (gray curves) and fission yeast (black curves). (A) Solid curves are f_drive (t); dashed curves are graphs of f_resist (t), see Eq (2*); (B) net forces f_net (t) = f_drive (t) – f_resist (t), with f_drive (t) and f_resist (t) from (A); (C) displacements; (D) polymerized actin, with the maxima of 9826 subunits in fission yeast and 5165 subunits in budding yeast. The budding yeast results are from the simulation with r_neck/R_head = 1/3. Values of t₀ used in the simulations (Table 3) are “near-saturation” as evident from graphs in A. Simulated displacements (C) and elongations rates (Table 4) are in reasonable quantitative agreement with the experimental data in Sun et al. (2019). Results for polymerized actin in (D) predict that at scission, actin patches in budding yeast have fewer polymerized actin subunits than in fission yeast (see discussion in The model predicts that the peak numbers of actin are lower in budding yeast than fission yeast).

The head–neck invaginations elongate faster and to greater depths under higher turgor pressures

One might assume that elongation would be fastest if the resistive force were fixed at a low value. However, simulations of a head–neck invagination moving against a constant resistive force of 28.3 pN yielded average elongation rates of only ∼15 nm/s (Table 1) in spite of resistance two orders of magnitude lower than experienced by a cylindrical invagination under a turgor pressure of 10 atm.

TABLE 1:

Average rates of elongation of a head–neck invagination (r_neck/R_head = 0.1; R_head = 30 nm) against resistive force of 28.3 pN with three invagination mobility coefficients and different arrangements of NPFs.

Mobility coefficient, nm/s/pN	Average elongation rate, nm/s
	Two rings of NPFs: one fixed at the base, the other moving with invagination	One ring of NPFs fixed on invagination at the base	One ring of NPFs on flat cell membrane surrounding the invagination opening (as in Mund et al., 2018)
0.01	8.1	7.3	—
0.04	12.6	13.6	—
0.08	14.3	16.6	13.2

This counterintuitive behavior arises because the driving force overcomes the resistance early during patch formation. At this point, the actin flow is slow and the viscous component dominates the driving force, resulting in slow elongation. When the active component subsequently grows stronger, the viscous component decreases and even becomes resistive.These factors keep the overall driving force down, yielding relatively slow rates during the entire elongation. Conversely, a stronger and longer lasting initial resistance gives the driving force a chance to build up and may produce faster elongation rates and deeper invaginations once the driving force overcomes the resistance.

To test this prediction, we compared simulations with lower turgor pressure representative of budding yeast and the other with high turgor pressures characteristic of fission yeast. We also varied the invagination mobility coefficient μ and the parameter t₀ approximating the timing of shape change; as above, t₀ was offset by –20 s. In all simulations, the neck–head ratio was r_neck/R_head = 0.1 and the duration of shape change was τ = 0.33 s. Table 2 summarizes the simulation parameters and results including: the duration of elongation computed as t_scission – t_begin with t_scission intepreted as the time of the peak of actin, the maximum displacement defined as the displacements at 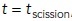, the average elongation rate (the ratio of the maximum displacement and the corresponding duration of elongation), and the peak amount of polymerized actin computed as described in the Figure 2 legend.

TABLE 2:

Parameters and results of simulations with varying P, t₀, and μ.

	Simulations	Simulation parameters			Simulation results
		Turgor pressure (P), atm	Timing of resistance descent (t0 ), s	Mobility coefficient (μ), nm/(s∙pN)	Duration of elongation, s	Maximum displacement, nm	Average elongation rate, nm/s	Maximum elongation rate, nm/s	Maximum number of patch actin subunits, ×103
Lower turgor pressure	1	5	–6	0.08	5.8	185	32.0	39.3	7.3
	2	3.5	–7	0.08	6.2	176	28.4	34.8	6.2
	3	3.5	–8.5	0.08	7.5	185	24.6	29.7	5.2
	4	3.5	–8.5	0.16	7.1	197	27.8	33.4	5.4
	5	3.5	–8.5	0.32	6.7	200	29.8	35.8	5.5
Higher turgor pressure	6	9	–4	0.08	5.2	202	38.8	46.8	9.4
	7	9	–4	0.16	5.1	222	43.5	52.9	10.2
	8	9	–4	0.32	5.1	236	46.8	56.7	10.6
	9	10	–3	0.32	5.0	237	47.7	59.0	11.2

As predicted, the simulated elongation rates were faster and the displacements longer at higher turgor pressures. Also, the timing of the resistance reduction t₀ correlated positively with elongation rates (see simulations 2 and 3) and the simulation outcomes were only modestly sensitive to μ, consistent with results in Figure 3, B and C. While both P and t₀ influence the motility of invaginations (Table 2), the impact of P is overarching because turgor pressure limits the effect of t₀ on both t_begin and f_drive (t) at t > t_begin. Indeed, both f_drive(t_begin) and t_begin saturate with increasing t₀ at the values controlled by turgor pressure, 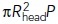and 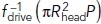, respectively [ stands for the inverse function of f_drive (t)]. This is because the time t_begin is the solution of f_drive (t) = f_resist(t) and f_resist (t) ≤ 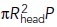[Eq (2)]; note also that f_drive(t_begin) is the absolute maximum of f_drive (t) (Figures 1, C and D, and 3, A and C). The saturation begins at 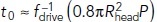+ 1.3τ, for which 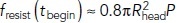(see the Supplemental Material). Interestingly, the “near-saturation” values of t₀ used in simulations 1, 2, and 6–9 (Table 2) resulted in longer elongations at lower turgor pressures, which is consistent with results in Figure 3 of Sun et al. (2019).

The simulation results in Table 2 agree qualitatively with the observations that invaginations in budding yeast move slower and are shorter than in fission yeast (Sun et al., 2019), which is consistent with the different turgor pressures explaining these differences in the two species. Quantitatively, though, our simulations significantly overestimated the displacements in budding yeast. Note also that the elongation rates in simulations 3 and 9 are similar to those in budding and fission yeast, but they were obtained with the fourfold difference of the invagination mobility in the two yeasts, which may not be realistic.

We ran additional simulations with varying model parameters to find better agreement with reported data. Simulations with parameter sets termed “optimized” (Table 3) yielded results more consistent with the measurements by Sun et al. (2019) (Table 4). In these sets, mobility coefficients μ and durations of resistance reduction τ are similar for both yeasts. Parameters that differ include turgor pressure P, pressure-dependent “near-saturation” values of t₀, and neck–head ratios r_neck/R_head (recall that all simulations in Table 2 were run with the same r_neck/R_head = 0.1). The shapes of the invaginations may differ in the two species because of different normal forces or rigidities of the protein coat, or both. The coat rigidities are unknown, but the compressing force might be weaker in budding yeast because of lower turgor pressure, which contributes to squeezing the invagination neck, so the invaginations in budding yeast would likely have larger ratios r_neck/R_head. We solved the model for budding yeast with two values of r_neck/R_head. Simulations with r_neck/R_head = ¹/₅ (r_neck = 6 nm) yielded elongation rates closer to the observations, whereas simulations with r_neck/R_head = ¹/₃ (r_neck = 10 nm) better approximated the observed displacements (Table 4).

TABLE 3:

Optimized parameter sets for simulating invagination motility in fission and budding yeast.

Parameters	Fission yeast	Budding yeast
μ, nm/(s∙pN)	0.08
τ, s	0.33
P, atm	10	3.5
t0, s	–3.0	–7.0
rneck/Rhead	1/10	1/5	1/3

TABLE 4:

Comparison of simulation outcomes of models with optimized parameter sets with experimental data of Sun et al. (2019).

Simulation outputs	Fission yeast		Budding yeast
	Theory, P = 10 atm rneck/Rhead = 0.1	Experiment	Theory, P = 3.5 atm rneck/Rhead = 0.2	Theory, P = 3.5 atm rneck/Rhead = 1/3	Experiment
Duration of elongation, s	4.7	4.0–5.0	5.7	6.0	4.0–5.0
Maximum displacement, nm	205	∼200	141	119	125
Average elongation rate, nm/s	43.7	51.8	24.8	19.8	23.8
Maximum elongation rate, nm/s	48.1		27.6	21.9

We introduced additional minor changes to simulations run with optimized parameters, aimed at improving the overall consistency of the model and the agreement of the simulation results with experimental observations. We replaced Eq (2) with a more accurate version of f_resist (t) that after the invagination changes shape does not drop to zero but rather approaches ,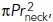

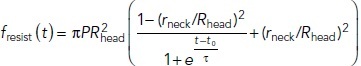2*

In determining durations of elongation and average elongation rates, we took into account that immediately after t_begin, the invaginations elongate much slower than during the ensuing near-linear increase in displacement (see Figures 1D and 2C). Similar to the experimental study (Sun et al., 2019), we evaluated the elongation durations and rates for the fast near-linear increase of displacements, starting at the inflection point and ending when polymerized actin reaches its maximum. The inflection points of the displacement time dependencies for the budding yeast invaginations were –6.9 s with r_neck/R_head = ¹/₅ and –6.8 s with r_neck/R_head = ¹/₃ and –2.8 s for fission yeast with r_neck/R_head = 0.1. The corresponding end times were –1.2 s, –0.8 s, and 1.9 s.

Figure 4 compares results for budding and fission yeast obtained with the optimized parameter sets. Graphs in panels A and B illustrate how turgor pressure affects f_drive (t) and f_net(t) = f_drive(t) – f_resist(t). In panel A the dashed curves are f_resist(t) described by Eq (2*) with the maximum resistance controlled by turgor pressure and thus is lower in budding yeast.

Consequently, in budding yeast elongation begins earlier during patch assembly and requires a weaker driving force, yielding lower f_net (panel B), slower elongation, and shorter displacements (panel C).

Simulation results obtained with optimized parameter sets agree reasonably well with the experimental data of Sun et al. (2019) (Table 4). The comparison reinforces the conclusion that different turgor pressures in the two yeast species are a major determinant in the observed differences of elongation rates and depths of their endocytic invaginations.

The model predicts that the peak numbers of actin are lower in budding yeast than fission yeast

Feedback between kinematics of the invagination and the accumulation of actin around the invagination explains why simulations of the model produce more polymerized actin in patches assembling under higher turgor pressures (Table 2; Figure 4D) in spite of using a fixed set of kinetic parameters for actin nucleation, polymerization, and severing (Berro et al., 2010; Nickaeen et al., 2019). Indeed, the amounts of actin polymerizing in patches under different turgor pressures are similar until the invaginations begin to move (Figure 4D) when the rate of polymerization and elongation increases abruptly (Figure 2, B and D).

The velocities of actin filaments (and of active Arp2/3) in the immediate vicinity of a stationary initial invagination are close to zero (due to the no-slip condition reflecting the binding of actin filaments to the coat proteins), so actin dendritic nucleation is confined to a limited space around the invagination neck (Figure 2A, left), and as the density of actin filaments increases over time, polymerization slows due to excluded volume effects. Once the invagination starts to move, its elongation speed and consequently the velocities of the filament network in the vicinity of the invagination increase sharply, as evident from the time dependences of net driving force (Figure 4B) [recall that according to Eq (1), u(t) ∝ f_net(t)]. As a result, the space where new filaments can nucleate and grow expands as well. Therefore, the rate with which the invagination elongates influences the rate of actin accumulation in the patch, which is cumulatively reflected in the peak amounts of polymerized actin (Table 2).

The peak amounts of actin in endocytic patches estimated with traces of GFP-actin are ∼4100–7500 subunits for fission yeast (Sirotkin et al., 2010; Arasada and Pollard, 2011) and ∼3600 subunits for budding yeast (Manenschijn et al., 2019). The maximum numbers of actin in patches are higher in the simulations than the experimental values for both yeasts, but the ratios are roughly similar: the optimized fission yeast parameters yielded the maximum of 9829 polymerized subunits, whereas simulations of budding yeast produced maxima of 5637 subunits with r_neck/R_head = ¹/₅ and 5165 subunits with r_neck/R_head = ¹/₃. We obtained these numbers from simulation results by integrating actin densities inside an elongating cylindrical surface that encompasses the high-density filament meshwork of the patch. The white rectangular box in Figure 5 represents a cross-section of this surface.

FIGURE 5:

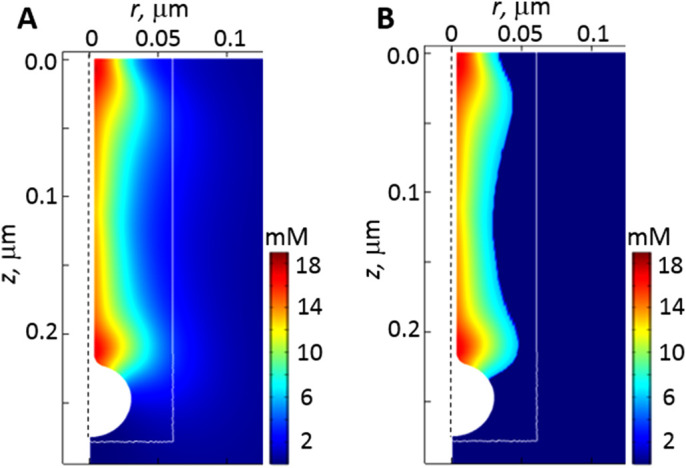
Deriving the number of actin subunits in patches from simulated actin densities. We determined the number of actin subunits in a patch by integrating actin densities within a cylinder outlined in white, which elongates with the invagination (see Figure 2 legend). (A) Snapshot of actin densities (pseudocolors) at the time of peak actin (t = 1.9 s), obtained with optimized parameters for fission yeast (Table 3). (B) Actin densities from A exceeding 6 mM: thresholding eliminates contributions from light-blue subspaces inside the box that may not be detected experimentally. (Vertical dashed lines represent the axis of symmetry of model geometry.)

Figure 5A is a snapshot of the actin density distribution at the time of maximum patch actin in fission yeast (t = 1.9 s) obtained with optimized parameters (Table 3). Note that the white box includes light-blue spaces with relatively low densities of actin filaments, which may not be detected experimentally. Contributions from such spaces can be eliminated by imposing a density threshold. Figure 5B shows a patch of filament meshwork with densities exceeding 6 mM. Such thresholding lowers the number of subunits from 9829 to 5469 subunits, in the range of the experimental estimates for fission yeast. Importantly, applying the same threshold to simulation results obtained with the budding yeast parameters (Table 3) yielded a near proportionate decrease of the patch subunit count from 5637 to 2591 subunits for r_neck/R_head = ¹/₅ and from 5165 to 2489 subunits for r_neck/R_head = ¹/₃, thus maintaining the approximately twofold ratio of the numbers of subunits in the patches of the two yeasts.

The differences between the experimental estimates and simulated numbers of polymerized subunits may also reflect a modest bias against the incorporation of GFP-actin into filaments.

DISCUSSION

Sun et al. (2019) recorded endocytic events in budding and fission yeast in the same microscope field. The side-by-side comparison revealed remarkable similarities of the abundance of proteins at sites of endocytosis in the two yeasts, yet endocytic invaginations elongated twice as fast to twofold greater depths in fission yeast than budding yeast (Sun et al., 2019). In this study, we show that a molecularly explicit model of forces exerted by actin filaments on endocytic invaginations (Nickaeen et al., 2019) explains these differences. Counterintuitively, higher turgor pressures favor faster, deeper membrane invaginations using the same parameters of actin nucleation and polymerization.

At the core of our theory is an observation that polymerization of a dense network of actin filaments around an endocytic invagination not only produces a driving force parallel to the axis of invagination but also exerts orthogonal forces that compress the base of the invagination and stretch its middle. If sufficiently strong, these forces deform the nascent, cylindrical invagination into a flasklike shape as observed in electron micrographs of invaginations in budding yeast (Kukulski et al., 2012; Buser and Drubin, 2013). The estimates of orthogonal forces exerted by actin at the invagination base (Nickaeen et al., 2019) amount to an extra squeezing pressure with the maximum of ∼8.5 atm, transforming the invagination shape from cylindrical to flasklike. Interestingly, the flask shapes, also predicted by the models of a membrane pulled under high turgor pressure by a point force at its tip (Dmitrieff and Nédélec, 2015; Ma and Berro, 2021), had wider necks than in electron micrographs. The orthogonal forces exerted by actin at the base of invagination could help narrow the neck.

The shape change, in turn, affects the driving and resistive forces. Since turgor pressure is isotropic, its resistance declines during the transition to a head–neck shape (Nickaeen et al., 2019). We find that this transition also changes composition of the driving force in terms of viscous and active components due to active stresses that the polymerization of the actin filament network produces on the upper side of the invagination head. Once the driving force overcomes the declining resistive force and the invagination begins to elongate, the active component of the driving force becomes dominant and produces faster elongations and deeper invaginations (Figure 3).

Further, we find that higher turgor pressure favors faster elongations and longer displacements. For higher turgor pressure, the driving force has a chance to grow before it matches higher initial resistance. This results in higher net driving force during elongation as the resistive force drops. Thus the difference of turgor pressure in the two yeasts is a plausible explanation for the observed differences in motility characteristics of their endocytic invaginations.

The model also predicts, in qualitative agreement with experimental data on actin accumulation in endocytic patches (Sirotkin et al., 2010; Arasada and Pollard, 2011; Manenschijn et al., 2019), that the peak amounts of actin in the patches must be lower in budding yeast than in fission yeast because of feedback between the elongation rate and the rate of actin accumulation. Another prediction is that the ratio r_neck/R_head of the invaginations is lower in budding yeast than in fission yeast.

The modeling in this study employs certain simplifications. We describe actin filament meshwork continuously in terms of concentrations of proteins participating in actin assembly without resolving individual filaments. Given the large numbers of polymerized subunits in the patch, this approach yields reasonably accurate results while avoiding logistical burdens of discrete stochastic simulations. In this approximation, the concentration of barbed ends serves as an estimate for the local filament density, and the ratio of the density of polymerized subunits to barbed ends estimates the local average number of subunits per filament.

Our model does not include membrane mechanics and, therefore we do not solve for shape dynamics. We model elongation of a head–neck invagination by increasing the length of its neck at a rate governed by Eq (1) without changing the predefined radii of the head or neck. Parameters associated with the shape of the invagination, such as the ratio of radii r_neck/R_head and the time t₀ around which shape change takes place, are constrained by available experimental data. A more rigorous approach, based on mechanics of moving membranes (Powers, 2010), would yield the dynamic geometry of the invagination along with the distributions of velocities and densities of polymerized actin. Of note, solving a free boundary model of invaginations elongating in a visco-active environment is significantly more involved than the determination of shapes of static invaginations, which was carried out in Dmitrieff and Nédélec (2015), Zhang et al. (2015), and Ma and Berro (2021). Notwithstanding the challenges, formulating and solving such a model will be possible once detailed knowledge is available on the composition and rheological properties of the endocytic membrane and its protein coat.

Even with its simplifications, our model reproduced experimentally observed elongation rates and displacements of endocytic invaginations in fission and budding yeast and uncovered the connection between turgor pressure and motility of endocytic invaginations in yeast.

METHODS

Request a protocol through Bio-protocol.

The coupled system of the reaction-transport equations [Eqs (S1), (S1*), and (S1**)], force-balance equation [Eq (S2)], and Eq (1) was solved using a moving-mesh solver of COMSOL Multiphysics, a software package for solving spatial multiphysics problems on finite element meshes (COMSOL Multiphysics, 2015). Because the invaginations were modeled as axially symmetric, computations were simplified by reducing the original three-dimensional (3D) problem to an equivalent 2D model formulated in (r, z) coordinates. Mathematical details of the model and its numerical solution are discussed in the Supplemental Material [Eqs (S1)–(S4)]. More details about the model and its numerical solution can be found in the supplemental material of (Nickaeen et al., 2019).

The supplemental COMSOL simulation file, Figure2.mph, includes all details of the model implementation with parameters yielding the results of Figure 2. Using this file, one can reproduce other results reported in this study by running it in the COMSOL Multiphysics environment with accordingly modified parameters.

Abbreviation used:

NPFs

nucleation promoting factors.