Bayesian hierarchical models for high-dimensional mediation analysis with coordinated selection of correlated mediators

Abstract

We consider Bayesian high-dimensional mediation analysis to identify among a large set of correlated potential mediators the active ones that mediate the effect from an exposure variable to an outcome of interest. Correlations among mediators are commonly observed in modern data analysis; examples include the activated voxels within connected regions in brain image data, regulatory signals driven by gene networks in genome data, and correlated exposure data from the same source. When correlations are present among active mediators, mediation analysis that fails to account for such correlation can be suboptimal and may lead to a loss of power in identifying active mediators. Building upon a recent high-dimensional mediation analysis framework, we propose two Bayesian hierarchical models, one with a Gaussian mixture prior that enables correlated mediator selection and the other with a Potts mixture prior that accounts for the correlation among active mediators in mediation analysis. We develop efficient sampling algorithms for both methods. Various simulations demonstrate that our methods enable effective identification of correlated active mediators, which could be missed by using existing methods that assume prior independence among active mediators. The proposed methods are applied to the LIFECODES birth cohort and the Multi-Ethnic Study of Atherosclerosis (MESA) and identified new active mediators with important biological implications.

1 |. INTRODUCTION

Mediation analysis attempts to explain the intermediate mechanism through which an exposure affects an outcome, and quantify the indirect effect transmitted by the mediator variable between the exposure and the outcome.¹

To formally define the direct and indirect effects, a causal approach to mediation analysis based on the counterfactual framework has been proposed, with the key assumptions for identification and causal interpretation being specified.^2,3 This framework further gave rise to other extensions in mediation analysis, such as exposure-mediator interaction,⁴ survival data,⁵ and so on.

The fast development in high-throughput biological technology has provided tremendous opportunities for mediation analysis with large-scale omics data. Modern omics studies often collect a large number of mediators with the goal for identifying active mediators that mediate the effect from an exposure variable to an outcome variable. In many of these modern data applications, there often exists a substantial correlation among mediators. For example, in functional MRI (fMRI) studies, the brain images are composed of a large number of voxels/regions and true signals usually represent connected regions. Our study is particularly motivated by two large-scale data, one in environmental science and one in genomics. The first is the LIFECODES birth cohort, one of the nation’s largest pregnancy cohorts aimed at advancing care and improving outcomes in high-risk pregnancies.⁶ This study collected data on a large group of endogenous biomarkers of lipid metabolism, inflammation, and oxidative stress. These biomarkers are hypothesized to mediate the effects of prenatal exposure to environmental contamination on adverse pregnancy outcomes.⁷ Moderate to strong correlations across those biomarkers are observed, and such correlations occur not only for biomarkers within the same biological pathways but also for biomarkers between different pathways. The second is the Multi-Ethnic Study of Atherosclerosis (MESA) data.⁸ In this study, high-dimensional DNA methylation (DNAm) are hypothesized to mediate the effect of neighborhood factors on blood glucose level, which is a critical variable linked to diabetes and heart diseases. Like the first study, these DNAm data are also correlated with each other. Performing mediation analysis with a high-dimensional set of mediators that may be correlated with each other is an important first step toward understanding the molecular basis of complex diseases and subsequent development of prevention and treatment strategies.

Several mediation analysis methods have been recently developed to accommodate high-dimensional mediators obtained from large-scale genomic data. For example, Zhang et al⁹ propose sure independent screening and minimax concave penalty techniques to study how the high-dimensional DNAm mediate the effect of smoking on lung function; Zhao and Luo¹⁰ develop a new convex, Lasso-type penalty on the indirect effects to identify brain pathways from the language stimuli to the outcome region activity. In addition to the frequentist methods, Song et al¹¹ propose a Bayesian variable selection method with separate shrinkage priors on the exposure-mediator effects and mediator-outcome effects, respectively. Song et al¹² further replace the two separate priors with relevant joint priors for a direct target on the nonzero indirect effect in mediator selection. Those methods enable a joint analysis of high-dimensional mediators and a valid procedure for the identification of active mediators. However, to the best of our knowledge, none of the existing methods for high-dimensional mediation analysis has accounted for the possible correlation structure among active mediators. As explained in the above paragraph, such correlation is highly prevalent. When the truly active mediators are correlated with one another, then the existing methods that fail to account for such correlation may lead to a loss of power. A more effective mediation analysis will require methods that can incorporate the useful correlation information of high-dimensional mediators into the model building process. We attempt to fill this gap in the literature.

Our proposed methods are based on a recently developed high-dimensional mediation analysis framework,¹² which introduced a Gaussian mixture model (GMM) as a joint prior on the exposure-mediator and mediator-outcome effect to allow for a targeted penalization on the indirect effect. This method has been shown to enjoy excellent and robust performance for mediator selection and effect estimation. GMM assumes that each mediator can be independently categorized into one of the four components based on association pattern, and its group indicator follows the same multinomial distribution as the other mediators. With the goal of utilizing the correlation structure among mediators in the modeling process, we aim to replace the independent priors on the mediators’ group indicators with two priors that introduce coordinated selection on active mediators that may be correlated with each other. One prior is based on the Potts distribution,¹³ a generalization from the Ising distribution, which allows for more than two groups and complex dependency between correlated neighboring variables. The other prior is based on a jointly modeling of the mediator-specific mixing probabilities via a logistic normal distribution,¹⁴ with the group probabilities reflecting the underlying correlation structure. Both methods allow for high-dimensional mediation analysis with the possible coordinated selection of active mediators via another layer in the Bayesian hierarchy. Both methods are built off the GMM proposed in Song et al,¹² and thus inherit the merits of the GMM method for high-dimensional mediation analysis. Furthermore, the proposed methods incorporate the structural information into a prior that favors selection of correlated mediators, and are expected to allow the identification of correlated active mediators that could be missed otherwise. Our methods rely on exact posterior sampling to provide estimates of quantities of interest and characterize uncertainty in estimation. The proposed methods will also facilitate the interpretation of the results, particularly for the selected mediators with high correlations.

We note that our methods are built upon a long history of similar methods in other related statistics areas. Indeed, Bayesian variable selection with covariate structural information has received much interest over the years. Bayesian group Lasso¹⁵ and Bayesian sparse group selection method¹⁶ allow for the inclusion of grouping effects and lead to more parsimonious models with reduced estimation error compared with standard Lasso. Yuan and Lin¹⁷ also develop a correlation prior on the binary selection indicators to distinguish models with the same size. Bayesian graphical models represent another stream of work on structural variable selection. Cai et al¹⁸ utilize the graph Laplacian matrix to encode the network information into the regression coefficients. Stingo et al¹⁹ propose the simultaneous selection of pathways and genes, using the pathway summaries of the group behavior and structure dependency within pathways to inform the selection. Along with the above methods, emerging literature considers the extension of the “spike-and-slab” type of mixture prior²⁰ in combination with Markov random field (MRF) prior to incorporate graph information. Ising prior, a binary spatial MRF, and its variations have been effectively applied to induce sparsity and accommodate selection dependency. Li and Zhang²¹ and Chekouo et al²² show that the structural information through Ising priors can greatly improve selection and prediction accuracy over the independent priors. In addition to smoothing over the latent selection indicators, recent studies deploy different types of “slab distribution,” such as the Dirichlet Process,²³ the group fused Lasso prior,²⁴ and so on, to include the grouping and smoothing effect in the nonzero regression coefficients due to local dependence or high correlation. Those methodologies have illustrated how the structural or correlated information can be incorporated into Bayesian framework to deliver better variable selection. However, these existing approaches are not designed specifically for mediation models with multivariate mediators and thus not directly applied to high-dimensional mediation analysis.

The rest of the article is organized as follows. In Section 2, we first define the causal effects of interest for the multivariate mediation analysis with the counterfactual framework. Then we review the mediation estimands under the linear regression models with multiple mediators and one continuous outcome. In Section 3, we propose two novel methods to explicitly incorporate correlation structure among mediators while jointly analyzing them. Simulation studies are carried out and discussed in Section 4. We illustrate our methods by applying them to LIFECODES and MESA cohort in Section 5, and conclude the article with a discussion in Section 6.

2 |. NOTATIONS, DEFINITIONS, AND MODELS

We adopt the counterfactual framework for causal mediation analysis in a high-dimensional setting. Consider a study of n subjects and for subject i, i = 1, …, n, we collect data on one exposure A_i, p potential mediators ${\mathit{\text{M}}}_i={\left(M_i^{(1)},M_i^{(2)},\dots ,M_i^{(p)}\right)}^{\top }$, one outcome Y_i, and q covariates ${\mathit{\text{C}}}_i={\left(C_i^{(1)},\dots ,C_i^{(q)}\right)}^{\top }$. In particular, we focus on the case where Y_i and M_i are all continuous variables. We define ${\mathit{\text{M}}}_i(a)=\left(M_i^{(1)}(a),M_i^{(2)}(a),\dots ,M_i^{(p)}(a)\right)$ as the ith subject’s counterfactual value of the p mediators if he/she received exposure a, and define Y_i(a, m) as the ith subject’s counter factual outcome if the subject’s exposure were set to a and mediators were set to m. The effect of an exposure can be decomposed into its direct effect and effect mediated through mediators, that is, indirect effect. The natural direct effect (NDE) of the given subject is defined as Y_i(a, M_i(a^⋆)) − Y_i(a^⋆, M_i(a^⋆)), where the exposure changes from a^⋆ (the reference level) to a and mediators are hypothetically controlled at the level that would have naturally been with exposure a^⋆. The natural indirect effect (NIE) of the given subject is defined by Y_i(a, M_i(a)) − Y_i(a, M_i(a^⋆)), the change in counterfactual outcomes when mediators change from M_i(a^⋆) to M_i(a) while fixing exposure at a. The total effect (TE), Y_i(a, M_i(a)) − Y_i(a^⋆, M_i(a^⋆)), can then be expressed as the summation of the NDE and the NIE: Y_i(a, M_i(a)) − Y_i(a^⋆, M_i(a^⋆)) = Y_i(a, M_i(a)) − Y_i(a, M_i(a^⋆)) + Y_i(a, M_i(a^⋆)) − Y_i(a^⋆, M_i(a^⋆)) = NIE + NDE.

The counterfactual variables are useful concepts to formally define causal effects, but they are not necessarily observed. In order to estimate the average NDE and NIE from observed data, further assumptions are required, including the consistency assumption and four nonunmeasured confounding assumptions.²⁵ We elaborate those assumptions in Section 1 of the supporting information (SI). It has been shown that under those assumptions, the average NDE and NIE can be identified by modeling Y_i|A_i, M_i, C_i and M_i|A_i, C_i using observed data.¹¹ Therefore, we can work with the two conditional models for Y_i|A_i, M_i, C_i and M_i|A_i, C_i, and subsequently propose two linear models for these two conditional relationships. For the outcome model, we assume

$$Y_i={\mathit{\text{M}}}_i^{\top }{\mathit{\beta }}_{\mathit{\text{m}}}+A_i{\beta }_a+{\mathit{\text{C}}}_i^{\top }{\mathit{\beta }}_{\mathit{\text{c}}}+{ϵ}_{Yi},$$ (1)

where β_m = (β_m1, …, β_mp)^⊤, β_c = (β_c1, …, β_cq)^⊤, and ${ϵ}_{Yi}~\text{N}\left(0,{\sigma }_e^2\right)$. For the mediator model, we consider a multivariate regression model that jointly analyzes all p potential mediators together as dependent variables:

$${\mathit{\text{M}}}_i=A_i{\mathit{\alpha }}_{\mathit{\text{a}}}+{\mathit{\alpha }}_{\mathit{\text{c}}}{\mathit{\text{C}}}_i+{\mathit{ϵ}}_{Mi},$$ (2)

where α_a = (α_a1, …, α_ap)^⊤; ${\mathit{\alpha }}_{\mathit{\text{c}}}={\left({\mathit{\alpha }}_{\mathit{\text{c}}\mathbf{1}}^{\top },\dots ,{\mathit{\alpha }}_{\mathit{\text{cp}}}^{\top }\right)}^{\top }$ , α_c1, …, α_cp are q-by-1 vectors; ϵ_Mi ~ MVN(0, Σ), with Σ capturing the residual error covariance. ϵ_Yi and ϵ_Mi are assumed to be independent of each other and independent of A_i and C_i. Under the identifiability assumptions discussed in SI and the modeling assumptions (linearity, no exposure-mediator interaction in the outcome and mediator model) in (1)–(2), we can express causal effects with the model coefficients as below.¹¹ In the rest of the article, we refer to NDE as direct effect and NIE as indirect/mediation effect.

$$\text{NDE}=E\left[Y_i\left(a,{\mathit{\text{M}}}_i\left(a^{\star }\right)\right)-Y_i\left(a^{\star },{\mathit{\text{M}}}_i\left(a^{\star }\right)\right)\mid {\mathit{\text{C}}}_i\right]={\beta }_a\left(a-a^{\star }\right).$$

$$\text{NIE}=E\left[Y_i\left(a,{\mathit{\text{M}}}_i(a)\right)-Y_i\left(a,{\mathit{\text{M}}}_i\left(a^{\star }\right)\right)\mid {\mathit{\text{C}}}_i\right]=\left(a-a^{\star }\right){\mathit{\alpha }}_{\mathit{\text{a}}}^{\top }{\mathit{\beta }}_{\mathit{\text{m}}}=\left(a-a^{\star }\right)\sum _{j=1}^p{\alpha }_{\mathit{\text{aj}}}{\beta }_{\mathit{\text{mj}}}.$$

$$\text{TE}=E\left[Y_i\left(a,{\mathit{\text{M}}}_i(a)\right)-Y_i\left(a^{\star },{\mathit{\text{M}}}_i\left(a^{\star }\right)\right)\mid {\mathit{\text{C}}}_i\right]=\left({\beta }_a+{\mathit{\alpha }}_{\mathit{\text{a}}}^{\top }{\mathit{\beta }}_{\mathit{\text{m}}}\right)\left(a-a^{\star }\right).$$

3 |. METHOD

Recent application of univariate mediation analysis methods at genome-wide scale^26,27 recognizes the need for decomposing the null hypothesis of zero indirect effect into three null components: zero exposure on mediator effect, zero mediator on outcome effect, and both. Such composite structure of the null hypothesis in the univaraite mediation analysis can be naturally captured by the four-component Gaussian mixture model developed in the presence of high-dimensional mediators.¹² Following Song et al,¹² we also consider a four-component Gaussian mixture for the effects of the jth mediator,

$${\left[{\beta }_{\mathit{\text{mj}}},{\alpha }_{\mathit{\text{aj}}}\right]}^{\top }~{\pi }_{1j}{\text{MVN}}_2\left(0,{\mathit{\text{V}}}_1\right)+{\pi }_{2j}{\text{MVN}}_2\left(0,{\mathit{\text{V}}}_2\right)+{\pi }_{3j}{\text{MVN}}_2\left(0,{\mathit{\text{V}}}_3\right)+{\pi }_{4j}{\mathit{\delta }}_0$$

with a prior probabilities π_kj (k ∈ Ω, Ω = {1, 2, 3, 4}) summing to one and MVN₂ denoting a bivariate Gaussian distribution. The first component represents active mediators, where both the exposure-mediator effect α_aj and mediator-outcome effect β_mj are nonzero and V₁ models their covariance. The inactive mediator will fall into one of the remaining three components. The second component corresponds to mediators with nonzero β_mj but zero α_aj, and the third component corresponds to mediators with nonzero α_aj but zero β_mj. Both V₂ and V₃ are low-rank matrices restricting that only β_mj or α_aj is nonzero, that is, ${\mathit{\text{V}}}_2=\left[\begin{array}{cc}{\sigma }_2^2& 0\\ 0& 0\end{array}\right]$ and ${\mathit{\text{V}}}_3=\left[\begin{array}{cc}0& 0\\ 0& {\sigma }_3^2\end{array}\right]$. Mediators with both exposure-mediator effect and mediator-outcome effect being zero belong to the fourth component, and δ₀ is a point mass at zero. We specify a conjugate inverse-Wishart prior on V₁, V₁ ~ Inv-Wishart(Ψ₀, ν), where Ψ₀ = diag{ψ₀₁, ψ₀₂} is a diagonal matrix, and ν is the degree of freedom. We also assign inverse-gamma priors to ${\sigma }_2^2$ and ${\sigma }_3^2$, that is, ${\sigma }_2^2~\text{Inv-Gamma}\left(v/2,{\psi }_{01}/2\right)$, ${\sigma }_3^2~\text{Inv-Gamma}\left(v/2,{\psi }_{02}/2\right)$, where ν, ψ₀₁, and ψ₀₂ are the same parameters used in the inverse-Wishart distribution. In both simulation studies and real data examples, we set ψ₀₁ and ψ₀₂ as the sample variances of the nonzero β_m and α_a fitted through Bi-Lasso. The degree of freedom ν in the inverse-Wishart distribution is set to be two, which makes the distribution reasonably noninformative while still well-defined.

We introduce a membership indicator variable γ_j for the jth mediator, where γ_j = k if [β_mj, α_aj]^⊤ is from Gaussian component k, k ∈ {1, 2, 3, 4}. If we assume independence among π_k1, π_k2, …, π_kp (and subsequently γ₁, γ₂, …, γ_p), then each mediator is independent a priori and the prior distribution on [β_m, α_a]^⊤ after integrating out {π_kj} (or {γ_j}) is essentially a separable product of distributions of [β_mj, α_aj]^⊤. This is akin to the concept of “separable prior” in Ročková and George.²⁸ In contrast, the previously developed GMM method¹² assumes a common set of π₁, π₂, π₃, π₄ for all the mediators a priori. This specification ties mediators together through the mixing probabilities and enables information sharing across mediators, making the priors “nonseparable.” However, since this previous GMM approach assumes the same mixing probabilities for all the mediators a priori, it does not differentiate highly correlated mediators from uncorrelated ones to inform coordinated mediator selection. Specifically, when the jth and (j + 1)th mediators are highly correlated with each other, because such correlation often implies common biological mechanism underlying both mediators, then one mediator being active becomes informative on the other being active in the sense that γ_j and γ_j+1 are more likely to be same. To enable coordinated selection of correlated active mediators, we consider embedding the correlation information to {π_kj}’s or γ_j’s. In the following sections, we describe the proposed methods with more details.

3.1 |. Hierarchical Potts mixture model: GMM-Potts

The Potts model¹³ was initially developed as a generalization of the Ising model in statistical physics. However, it has enjoyed great success as a prior model for the spatial modeling in image analysis,^29,30 disease mapping,³¹ genetics studies,³² and so on. In those applications, Potts models incorporate spatial Markovian dependency by assigning homogeneous relationships for the “neighboring” regions. In the context of mediation analysis, we allocate the high-dimensional mediators into four Gaussian components based on their exposure-mediator and mediator-outcome effects. We think of the highly correlated mediators as neighbors and we attempt to assign them to different mediation components through a Potts model.

To specifically formulate our Potts mixture model, we assume that γ = (γ₁, γ₂, …, γ_p) follows a Potts distribution,

$$p\left(\mathit{\gamma }\mid {\mathit{\theta }}_0,{\mathit{\theta }}_1\right)=c{\left({\mathit{\theta }}_0,{\mathit{\theta }}_1\right)}^{-1}\text{exp}\left\{\sum _{i=1}^p{\theta }_{0k}I\left[{\gamma }_i=k\right]\right\}\times \text{exp}\left\{\sum _{i=1}^p\sum _{i~j}\sum _{k=1}^4{\theta }_{1k}I\left[{\gamma }_i={\gamma }_j=k\right]\right\},$$ (3)

where i ~ j indicates neighboring pairs and I(·) is the indicator function. The neighboring relationship can be defined in terms of domain knowledge, or, in our case, the mediator correlation information. θ₀ = (θ₀₁, θ₀₂, θ₀₃, θ₀₄) effectively determines the four group proportions a priori in the absence of mediator correlation. θ₁ = (θ₁₁, θ₁₂, θ₁₃, θ₁₄) represents how mediator correlation determines the extent to which one mediator being selected into one group affects the probability of its neighboring mediators being selected into the same group. For θ_1k > 0, the Potts distribution encourages configurations where “neighboring mediators” belong to the same group; and the larger θ_1k, the tighter this coupling. When θ₁ = 0, group membership of one mediator is independent of that of its neighbors. Based on the full probability distribution in Equation (3), the probability for the jth mediator belonging to component k conditional on its neighbors is,

$$p\left({\gamma }_j=k\mid {\left\{{\gamma }_i\right\}}_{i\ne j},{\mathit{\theta }}_0,{\mathit{\theta }}_1\right)=\frac{\text{exp}\left\{{\theta }_{0k}\right\}\times \text{exp}\left\{{\sum }_{i~j}{\theta }_{1k}I\left[{\gamma }_i={\gamma }_j=k\right]\right\}}{{\sum }_{k=1}^4\text{exp}\left\{{\theta }_{0k}\right\}\times \text{exp}\left\{{\sum }_{i~j}{\theta }_{1k}I\left[{\gamma }_i={\gamma }_j=k\right]\right\}}.$$ (4)

This conditional probability depends on the neighbors of the jth mediator and demonstrates the Markov property of the Potts distribution.

We develop a Markov chain Monte Carlo (MCMC) sampling strategy for the proposed model. A key challenge for inference is the exact calculation of the normalizing constant c(θ₀, θ₁) in Potts distribution, as it requires the summation over the entire space of γ which consists of 4^p states. Even for a moderate number of mediators, c(θ₀, θ₁) is computationally intractable, and this complicates the Bayesian inference. Due to the intractable normalizing constant in Potts distribution, the update of θ₀, θ₁ cannot be handled by the standard Metropolis Hastings (MH) algorithm. To address this issue, we employ the double MH sampler³³ to generate auxiliary variables via the MH transition kernels and eliminate the normalizing constants. For θ₀, θ₁, we consider normal priors, and the prior means of {θ_0k} are set to have the desired inclusion probability while the prior means of {θ_1k} are set to be the same positive number. This prior information favors the grouping of correlated mediators. According to Equation (4), the updating of γ can be realized through single site Gibbs sampling. Since the sampling space of γ is huge and discrete, the efficiency of the standard Gibbs updates can be improved by the Swendsen-Wang (SW) algorithm.³⁴ The SW algorithm partitions the whole set of mediators into blocks within which the mediators belong to the same normal component, and then updates each block independently. Following the strategy in Higdon,³⁴ we alternate between the single site Gibbs updates of γ and SW updates to ensure movement in large patches and fast mixing of the algorithm. The detailed algorithm is given in the SI.

In our Potts mixture model, the “neighboring” mediators are predefined to capture the correlation structure among mediators. Based on our experience, including too many neighbors into the model will cause irrelevant noises to the group probabilities and blur the cluster boundary, while including too few neighbors will certainly lose some of the important structural information. In this article, we apply the common clustering method on the p(p − 1)/2 pairwise correlations across the p mediators to divide them into two groups: high correlation and background noise. This procedure essentially sets a correlation threshold for neighbors and nonneighbors in a data dependent way. In the procedure, we define the ith mediator and jth mediator as neighbors if their pairwise correlation is above this threshold. The threshold may be determined in other ways to reflect the prior knowledge on the neighborhood structure and relationships across mediators.

We refer to our Potts mixture model as GMM-Potts. GMM-Potts translates the correlation structure into a neighboring graph and incorporates the local dependency among mediators through mediators’ predefined neighbors. For each mediator, its four-component group probabilities will be dependent on its neighboring correlated mediators but not the nonneighboring ones. This local dependency feature of GMM-Potts is unique compared with the previous GMM and does not incur much additional computational burden.

3.2 |. Hierarchical GMM with correlated selection: GMM-CorrS

GMM-Potts requires a hard thresholding rule to determine the neighboring graph among mediators. If the neighbors and nonneighbors of mediators are not correctly specified or difficult to specify as in the case of a weak correlation structure, then GMM-Potts may incur a loss of performance. To avoid the need of neighborhood prespecification and allow for a more direct incorporation of correlation structure, we consider an alternative approach for coordinated selection of correlated mediators here. This alternative approach is again built upon the GMM framework. Specifically, for each mediator, we assume that the selection/group indicator γ_j follows a multinomial distribution with parameters π_1j, π_2j, π_3j, π_4j, and ${\sum }_{k=1}^4{\pi }_{\mathit{\text{kj}}}=1$. We propose to jointly model all the mediators’ mixing probabilities and their continuous dependence structure via latent logistic normal distributions. The logistic normal¹⁴ has been studied in the context of analyzing compositional data, such as bacterial composition in human microbiome data³⁵ and topics proportions associated with document collections in correlated topics model.³⁶ In mediation analysis, it would allow for a flexible covariance structure among mediators and give a more realistic model where correlated mediators will have similar group probabilities a priori.

In particular, we employ a Pólya-Gamma (PG) latent variable representation of the multinomial distribution to enable coordinated mediator selection. Our approach is motivated in part by computational considerations. Specifically, a naive incorporation of the Gaussian correlation structure among multinomial parameters as described in the previous paragraph imposes substantial computational challenge, as it would break the Dirichlet-multinomial conjugacy commonly used in mixture models. Approximation techniques such as variational inference are feasible, but they do not always come with the theoretical guarantees as MCMC.³⁷ Our approach extends a similar approach in Bayesian logistic regression inference. Specifically, Bayesian logistic regression has long been explored given its inconvenient analytic form of the likelihood and the nonexistence of a conjugate prior for parameters of interest. Recently, Polson et al³⁸ construct a new data-augmentation strategy based on the novel class of Pólya-Gamma (PG) distributions, and the method is notably simpler and more efficient than the previous schemes for Bayesian hierarchical models with binomial likelihoods.³⁹ To extend that approach to multinomial logit models and facilitate MCMC computation, we leverage a logistic stick-breaking representation in the PG latent variable augmentation⁴⁰ to formulate the multinomial distribution in terms of latent variables with the jointly Gaussian likelihoods. First, we rewrite four-dimensional multinomial in terms of three binomial densities ${\tilde{\pi }}_{j1}$, ${\tilde{\pi }}_{j2}$, and ${\tilde{\pi }}_{j3}$,

$$p\left({\gamma }_j=1\right)={\tilde{\pi }}_{j1}={\pi }_{j1},$$

$$p\left({\gamma }_j=2\mid {\gamma }_j\ne 1\right)={\tilde{\pi }}_{j2}={\pi }_{j2}/\left(1-{\pi }_{j1}\right),$$

$$p\left({\gamma }_j=3\mid {\gamma }_j\ne 1\text{ or }2\right)={\tilde{\pi }}_{j3}={\pi }_{j3}/\left(1-{\pi }_{j1}-{\pi }_{j2}\right),$$

$$p\left({\gamma }_j=4\mid {\gamma }_j\ne 1\text{ or }2\text{ or }3\right)={\tilde{\pi }}_{j4}={\pi }_{j4}/\left(1-{\pi }_{j1}-{\pi }_{j2}-{\pi }_{j3}\right)=1,$$

$$\text{Multinomial}\left({\gamma }_j\mid 1,\left\{{\pi }_{j1},{\pi }_{j2},{\pi }_{j3},{\pi }_{j4}\right\}\right)=\prod _{k=1}^3\text{Binomial}\left(I\left({\gamma }_j=k\right)\mid n_{\mathit{\text{jk}}},{\tilde{\pi }}_{\mathit{\text{jk}}}\right)\text{,}$$

where n_jk = 1 −∑_k′<k I(γ_j = k′), n_j1 = 1. The multinomial distribution is now expressed with three binomial distributions and each ${\tilde{\pi }}_{\mathit{\text{jk}}}$ describes the faction of the remaining probability for the kth group (details in the SI). To better aid the interpretation of the above stick-breaking representation, we may consider a testing strategy for the indirect effect β_mjα_aj implemented on each mediator. By doing that, we will get the subset of active mediators with β_mjα_aj ≠ 0, that is, γ_j = 1. For the remaining mediators with β_mjα_aj = 0, we further consider the following three cases: p(γ_j = 2|γ_j ≠ 1) is the conditional probability of having nonzero β_mj effect but zero α_aj given that β_mjα_aj = 0; p(γ_j = 3|γ_j ≠ 1 or |2) is the conditional probability of having nonzero α_aj effect given that β_mj = 0; and the rest of the mediators will surely have β_mj = α_aj = 0, that is, γ_j = 4. We note that under the sparsity assumption, for most of the mediators, ${\tilde{\pi }}_{j2}\approx {\pi }_{j2}$, ${\tilde{\pi }}_{j3}\approx {\pi }_{j3}$ due to the small values of π_j1 and π_j2.

Then, we define $b_{\mathit{\text{jk}}}=\text{logit}\left({\tilde{\pi }}_{\mathit{\text{jk}}}\right)$ for k = 1, 2, 3 and j = 1, 2, …, p. We stack the 3 × p b_jk’s as one random vector, and assume a multivariate normal prior on it, that is,

$$\begin{gathered} \mathit{\text{b}}≔{\left\{b_{\mathit{\text{jk}}}\right\}}_{j=1,\dots ,p;k=1,2,3}, \\ \mathit{\text{b}}~\text{MVN}\left(\mathit{\text{a}},\text{diag}\left\{{\sigma }_{d1}^2,{\sigma }_{d2}^2,{\sigma }_{d3}^2\right\}\otimes \mathit{\text{D}}\right), \end{gathered}$$ (5)

where ⊗ denotes the Kronecker product. The logistic transformation maps the transformed multinomial parameters to the 3p-dimensional open real space. The prior mean a = {a_jk}_{j=1,…, p;k=1,2,3}, and it is chosen such that a_jk = a_j′_k for k = 1, 2, 3 and 1 ≤ j < j′ ≤ p. It reflects our prior belief on the overall group proportions and induces sparsity for the first three groups. The D is a p-by-p covariance matrix and will incorporate the mediator wise correlation/structure dependency to the transformed mixing probabilities. In our setting, we estimate the correlation matrix among mediators from data and replace the negative correlations with their absolute values. For technical reasons, we then find the nearest positive definite matrix to the absolute correlation matrix, and use that as the D matrix in model fitting. Based on our practical experience, this approximation does not alter the absolute values of the correlation in D much. In this way, both the positive and negative correlation among mediators will encourage similar values on π_1j’s, therefore favoring the selection of correlated mediators. Since the variation level may be different for $\text{logit}\left({\tilde{\pi }}_{j1}\right)$, $\text{logit}\left({\tilde{\pi }}_{j2}\right)$, and $\text{logit}\left({\tilde{\pi }}_{j3}\right)$, we introduce the groupwise ${\sigma }_{\mathit{\text{dk}}}^2$, k = 1, 2, 3 for a more general covariance pattern. This correlation embedded GMM exploits the whole correlation information from all the mediators and does not require the predefined neighbors as in the GMM-Potts model.

We refer to the above model as GMM-CorrS. We develop an MCMC algorithm to infer parameters through data augmentation with Pólya-Gamma variables.³⁸ The augmented posterior leads to conditional distributions from which we can easily draw samples and the entire vector b can be sampled as a block in a single Gibbs update. The detailed derivation and algorithm can be found in the SI. The software for implementing both GMM-Potts and GMM-CorrS can be found at https://github.com/yanys7/Correlated_GMM_Mediation.

4 |. SIMULATIONS

We evaluate the performance of the proposed models compared with existing methods under different scenarios through simulations.

4.1 |. Small sample scenarios: n = 100, p = 200

4.1.1 |. Simulation design

Following settings in Song et al,¹² we adopt the four-component structure to generate the exposure-mediator and mediator-outcome effects, that is, simulate [β_mj, α_aj]^⊤ from

$${\left[{\beta }_{\mathit{\text{mj}}},{\alpha }_{\mathit{\text{aj}}}\right]}^{\top }~{\pi }_1\text{MVN}\left(\mathbf{0},\left[\begin{array}{ll}0.5\hfill & 0.2\hfill \\ 0.2\hfill & 0.5\hfill \end{array}\right]\right)+{\pi }_2\text{MVN}\left(\mathbf{0},\left[\begin{array}{cc}0.5& 0\\ 0& 0\end{array}\right]\right)+{\pi }_3\text{MVN}\left(\mathbf{0},\left[\begin{array}{cc}0& 0\\ 0& 0.5\end{array}\right]\right)+{\pi }_4{\mathit{\delta }}_0.$$

To introduce sparsity, we assume the proportion of active mediators π₁ = 0.05, and the other three null components π₂ = 0.05, π₃ = 0.10, π₄ = 0.80. We generate a p-vector of correlated mediators for the ith individual from ${\mathit{\text{M}}}_i=A_i{\mathit{\alpha }}_a+{\mathit{ϵ}}_{M_i}$, where the continuous exposure {A_i, i = 1, …, n} is independently sampled from a standard normal distribution. The residual errors ${\mathit{ϵ}}_{M_i}\sim \text{MVM}\left(\mathbf{0},\mathbf{\Sigma }\right)$ and Σ models the correlation structure across mediators. For the outcome, we simulate it from the linear model: $Y_i={\mathit{\text{M}}}_i^{\top }{\mathit{\beta }}_{\mathit{\text{m}}}+A_i{\beta }_a+{ϵ}_{Y_i}$, with β_a = 0.5, and the residual error ${ϵ}_{Y_i}\sim \text{N}\left(0,1\right)$.

For the correlation structure, we assume 10 highly correlated blocks of size 10 × 10, within which the pairwise correlation of mediators is ρ₁, for example, ρ₁ = 0.5 − 0.03 |i − j| or 0.9 − 0.05 |i − j|, and the correlation between blocks (ρ₂) is relatively weak (eg, ρ₂ = 0 or 0.1). Such correlation structure mimics the local dependency due to physical adjacency or biologically functional pathway of biomarkers, which is commonly seen in the high-dimensional mediators. There are 10 active mediators, and they are assumed to cluster within one block or scatter over a few blocks, while the other blocks contain no active mediators. We also consider settings where there is no correlation or such structural information underlying active mediators, that is, setting Σ to be identical matrix or estimated covariance based on a random subset of DNAm from MESA. For the Bayesian methods, we check the MCMC convergence by running ten chains and computing the potential scaled reduction factors (PSRF).⁴¹ The estimated 95% confidential interval of the PSRFs for all the PIPs is [1.0, 1.2], indicating good mixing and convergence of the algorithms.

The GMM-Potts model needs the input of a reliable neighborhood matrix. In practice, we may not be able to specify a completely precise neighborhood structure, but instead a deviated version of that. To examine how sensitive our GMM-Potts model is to the incorrect neighborhood relationship, we randomly convert a proportion of r neighboring mediator pairs to be nonneighboring, and randomly convert the same amount of nonneighboring pairs to be neighbors. The other configurations are the same as in the previous simulations. We vary the perturbation rate r from 0.05 to 0.5 to mimic different degrees of bias. In addition, for the GMM-CorrS, since it directly takes the correlation matrix as an input, we examine its sensitivity to the observed correlation matrix by adding mild changes from N(0, σ²) to the estimated matrix. We vary σ from 0.1 to 0.3 for different levels of noise.

4.1.2 |. Evaluation metrics

To examine the mediator selection accuracy, for the proposed GMM-Potts and GMM-CorrS methods as well as GMM, we use PIP to rank and select mediators. We calculate the true positive rate (TPR) for active mediators based on the fixed 10% false discovery rate (FDR). For the estimation accuracy, we calculate the mean square error (MSE) of the indirect effects for both nonnull and null mediators, denoted as MSE_nonnull and MSE_null. We perform 200 replicates for each scenario and report the means of those metrics in the result tables.

4.1.3 |. Competing methods

In addition to the proposed methods, we consider the following existing methods: GMM with no correlated information included, Bi-Lasso (apply two separate Lasso regressions⁴² to the outcome and mediator model, respectively), Bi-Ridge (apply two separate ridge regressions⁴³ to the outcome and mediator model, respectively), and Pathway Lasso.¹⁰ In Bi-Lasso and Bi-Ridge, we adopt 10-fold cross validation to choose the tuning parameter in each regression separately. The three frequentist methods provide optimized solutions of β_m, α_a to the three different penalized likelihoods, and the marginal indirect contribution from each mediator, that is, β_mjα_aj, is used to rank mediators for the TPR calculation.

4.1.4 |. Simulation results

Table 1 shows the results under the small sample scenarios with n = 100, p = 200. Overall, by leveraging mediators’ correlation structure, the two proposed approaches, GMM-Potts and GMM-CorrS, substantially improve the selection accuracy over the other methods. When the active mediators are concentrated within one block, the GMM-Potts achieves the highest TPR (>0.90) at a fixed 10% FDR for identifying this whole block, followed by GMM-CorrS (~0.80 TPR). The advantage of the proposed methods grows with stronger correlations. Without such “group selection” ability, the GMM under independent priors tends to lose half of the power for detecting correlated mediators. On the other hand, if the active ones are evenly distributed into two blocks, then highly correlated mediators within the same block may not be concurrently active. This could happen if their correlation does not mainly link with mediation as we assume, and therefore may disturb mediator selection. Under those settings, we do observe power decrease for the proposed methods. Particularly, the GMM-Potts model becomes less preferable as it smoothes over nonmediating neighbors to infer active mediators, while GMM-CorrS uses a more flexible Gaussian distribution for dependent group probabilities and thus has the best TPR. In the settings where there is no systematic correlation structure underlying mediators, we find that GMM-CorrS behaves quite similarly to the GMM, and outperforms the others. GMM-Potts is less robust presumably due to the inclusion of irrelevant neighbors, but still better than the frequentist methods. The three frequentist methods have relatively poor selection performance with highly correlated mediators, and Bi-Lasso is most competitive under zero or weak correlation. In terms of the effects estimation, the proposed methods mostly achieve the smallest MSE_nonnull and a reasonable level of MSE_null. Among the three frequentist methods, since in general Lasso tends to select less correlated variables than the elastic net type penalty, Bi-Lasso has a relatively larger MSE_nonnull but noticeably smaller MSE_null than the pathway Lasso. Given the sparse setup in the above simulations, Bi-Ridge does not exhibit much advantage over the other methods.

TABLE 1.

Simulation results of n = 100, p = 200 under different correlation structures

ρ1 = 0.5 − 0.03|i − j|, ρ2 = 0
	(A) Signals in one block			(B) Signals in two blocks
Method	TPR	MSEnonnull	MSEnull ×10−4	TPR	MSEnonnull	MSEnull ×10−4
GMM-CorrS	0.78	0.029	1.360	0.62	0.039	1.919
GMM-Potts	0.93	0.035	2.251	0.49	0.040	2.112
GMM	0.45	0.042	1.211	0.46	0.047	1.203
Bi-Lasso	0.26	0.238	0.520	0.23	0.238	0.584
Bi-Ridge	0.22	0.283	2.639	0.21	0.286	2.642
Pathway Lasso	0.24	0.233	2.598	0.23	0.180	6.405
ρ1 = 0.9 − 0.05|i − j|, ρ2 = 0.1
	(A) Signals in one block			(B) Signals in two blocks
Method	TPR	MSEnonnull	MSEnull ×10−4	TPR	MSEnonnull	MSEnull ×10−4
GMM-CorrS	0.81	0.208	1.146	0.49	0.182	4.080
GMM-Potts	0.92	0.171	3.515	0.41	0.233	1.651
GMM	0.33	0.206	2.158	0.22	0.201	3.112
Bi-Lasso	0.11	0.342	0.173	0.13	0.343	0.179
Bi-Ridge	0.15	0.322	2.170	0.16	0.326	1.690
Pathway Lasso	0.21	0.237	5.495	0.19	0.264	3.457
No systematic correlation structure (signals in two blocks)
	(A) ρ1 = 0			(B) Weak correlation from MESA
Method	TPR	MSEnonnull	MSEnull ×10−4	TPR	MSEnonnull	MSEnull ×10−4
GMM-CorrS	0.52	0.020	1.042	0.44	0.023	1.780
GMM-Potts	0.46	0.043	1.970	0.40	0.030	3.041
GMM	0.52	0.021	0.805	0.45	0.023	1.642
Bi-Lasso	0.45	0.081	0.542	0.35	0.139	0.740
Bi-Ridge	0.35	0.238	3.645	0.28	0.247	4.003
Pathway Lasso	0.35	0.164	0.314	0.32	0.177	0.400

Note: TPR: true positive rate at false discovery rate (FDR) = 0.10. MSE_nonnull: mean squared error for the indirect effects of active mediators. MSE_null: mean squared error for the indirect effects of inactive mediators. The results are based on 200 replicates for each setting. Bolded TPRs indicate the top two performers.

Tables 2 and 3 summarize the sensitivity analysis for GMM-Potts and GMM-CorrS, respectively, regarding the input correlation structure. As expected, with increasing noise added to the correlation structure, the overall accuracy of GMM-Potts and GMM-CorrS gets reduced. However, the power of our methods remains 75% of the original level for reasonable r and σ (r < 0.3, σ < 0.3). Even with large r = 0.5 and σ = 0.3, GMM-CorrS still has better performance (TPR, MSE_nonnull) over methods with no structural information in all the settings, and GMM-Potts does for most of the settings. Generally speaking, the proposed methods are not sensitive to small alteration of the input correlation structure. In addition, we also perform sensitivity analysis on the ψ parameters (ψ₀₁ and ψ₀₂) in the covariances of both mixture models. We find that the posterior inference is robust to mild changes in ψ′s, especially as we increase the values of ψ′s. The results also show that model fitting criteria, such as the deviance information criterion (DIC), can be used to select the optimal ψ′s. More details can be found in Section 7 of the supporting file.

TABLE 2.

Sensitivity analysis for Potts mixture model (GMM-Potts) for n = 100, p = 200

ρ1 = 0.5 − 0.03|i − j|, ρ2 = 0
	(A) Signals in one block			(B) Signals in two blocks
Perturbation rate	TPR	MSEnonnull	MSEnull ×10−4	TPR	MSEnonnull	MSEnull ×10−4
0	0.93	0.035	2.251	0.49	0.040	2.112
0.05	0.78	0.076	1.496	0.44	0.091	1.733
0.1	0.72	0.077	1.578	0.43	0.091	1.827
0.2	0.69	0.087	1.568	0.42	0.086	1.822
0.3	0.61	0.097	1.736	0.41	0.088	2.019
0.4	0.53	0.102	1.525	0.40	0.085	1.952
0.5	0.49	0.094	2.082	0.41	0.081	1.847
ρ1 = 0.9 − 0.05|i − j|, ρ2 = 0.1
	(A) Signals in one block			(B) Signals in two blocks
Perturbation rate	TPR	MSEnonnull	MSEnull ×10−4	TPR	MSEnonnull	MSEnull ×10−4
0	0.92	0.171	3.515	0.41	0.233	1.651
0.05	0.91	0.180	0.819	0.33	0.191	1.876
0.1	0.91	0.181	1.203	0.35	0.183	2.156
0.2	0.91	0.175	1.393	0.32	0.201	1.815
0.3	0.89	0.174	1.129	0.32	0.177	2.081
0.4	0.88	0.173	1.395	0.32	0.200	1.492
0.5	0.83	0.166	2.046	0.30	0.188	1.884

TABLE 3.

Sensitivity analysis for the Gaussian mixture model with correlated selection (GMM-CorrS) for n = 100, p = 200

ρ1 = 0.5 − 0.03|i − j|, ρ2 = 0
	(A) Signals in one block			(B) Signals in two blocks
Noise level	TPR	MSEnonnull	MSEnull ×10−4	TPR	MSEnonnull	MSEnull
0	0.78	0.029	1.360	0.62	0.039	1.919
0.1	0.71	0.029	2.481	0.56	0.036	2.246
0.2	0.60	0.031	2.575	0.50	0.037	2.043
0.3	0.53	0.033	2.235	0.47	0.037	1.910
ρ1 = 0.9 − 0.05|i − j|, ρ2 = 0.1
	(A) Signals in one block			(B) Signals in two blocks
Noise level	TPR	MSEnonnull	MSEnull ×10−4	TPR	MSEnonnull	MSEnull ×10−4
0	0.81	0.208	1.146	0.49	0.182	4.080
0.1	0.72	0.168	4.017	0.40	0.127	3.288
0.2	0.63	0.170	3.442	0.37	0.130	3.370
0.3	0.54	0.176	3.413	0.34	0.133	3.283

4.2 |. Large sample scenarios: n = 1000, p = 2000

4.2.1 |. Simulation design

Next, we examine the settings for n = 1000, p = 2000. We simulate the exposure, exposure-mediator and mediator-outcome effects using the same distribution as above. For the correlation structure, we now consider 50 blocks of size 20 × 20, with relatively high within-block mediator correlation ρ₁ and zero between-block correlation. We first set the four group proportions same as in the small sample scenarios, and the resultant 100 active mediators are assumed to evenly distribute over five blocks. The other blocks contain no active mediators. In one of the settings, we use the covariance matrix estimated from a random subset of DNAm in MESA as Σ to simulate mediators with no underlying systematic correlation structure.

Then we study a much sparser setting with only 10 active mediators to better reflect the situation we observe in the MESA application. The 10 active mediators exist in two blocks, each of which contains five active ones and 15 inactive ones. Furthermore, we consider another worse-case scenario for GMM-Potts model by reducing ρ₁ to 0.25 and remaining the high sparsity. The weak correlation makes it hard for GMM-Potts model to identify the true neighboring relationship via the clustering method, and the performance of the Potts model is quite dependent on the smoothing effects from the predefined neighbors.

4.2.2 |. Simulation results

Table 4 shows the results under the large sample scenarios with n = 1000, p = 2000. Our methods enjoy up to 30% power gain on mediator selection utilizing the correlation structure compared with the other methods. In the first setting, both methods identify almost all the active blocks, and GMM-Potts has a slightly higher TPR (0.97) at 10% FDR than GMM-CorrS (TPR = 0.92). When the mediator correlation has no implication for mediation effects in the second setting, the overall performance of GMM-CorrS is similar to that of GMM, and better than GMM-Potts. Those patterns are consistent with what we have observed in the small sample scenarios. Under the much sparser settings with only 10 active mediators and varied correlation ρ₁, the GMM-CorrS maintains good and stable performance with TPR around 0.80. By contrast, the performance of GMM-Potts is dependent on how obvious the correlation patterns are and subsequently how well the clustering method does in defining neighbors and nonneighbors. For example, with ρ₁ = 0.5 − 0.02 i − j, the GMM-Potts models can accurately identify the underlying correlation structure and achieve the highest TPR (0.85), smallest MSE (MSE| | nonnull = 0.002, MSE_null = 7.607 ×10⁻⁷). However, as the within-block correlation ρ₁ reduces to 0.25, it becomes challenging for the clustering method to separate true correlation vs noise, and we do observe many noisy pairs in the neighborhood matrix. As a consequence, the results of GMM-Potts model get compromised by the inclusion of those irrelevant neighbors. This setting is actually in agreement with our observation of the ambiguous correlation structure and sparse signals in the MESA application, which may not fare well for GMM-Potts model. Among the other three frequentist methods, Bi-Lasso performs best regarding to the selection and estimation accuracy.

TABLE 4.

Simulation results of n = 1000, p = 2000 under different correlation structures, p₁₁ is the number of true active mediators

p11 = 100, signals in five blocks
	(A) ρ1 = 0.5 − 0.02|i − j|			(B) Weak correlation from MESA
Method	TPR	MSEnonnull	MSEnull ×10−4	TPR	MSEnonnull	MSEnull ×10−4
GMM-CorrS	0.92	0.031	0.440	0.83	0.002	0.240
GMM-Potts	0.97	0.030	0.018	0.76	0.004	1.013
GMM	0.76	0.077	0.630	0.84	0.002	0.176
Bi-Lasso	0.73	0.031	0.199	0.65	0.042	0.446
Bi-Ridge	0.32	0.244	2.680	0.36	0.202	3.795
Pathway Lasso	0.44	0.112	1.162	0.42	0.107	1.427
p11 = 10, signals in two blocks
	(A) ρ1 = 0.5 − 0.02|i − j|			(B) ρ1 = 0.25
Method	TPR	MSEnonnull	MSEnull ×10−4	TPR	MSEnonnull	MSEnull ×10−4
GMM-CorrS	0.83	0.003	0.015	0.82	0.002	0.017
GMM-Potts	0.85	0.002	0.008	0.61	0.018	0.228
GMM	0.80	0.003	0.013	0.81	0.002	0.016
Bi-Lasso	0.73	0.013	0.036	0.76	0.010	0.035
Bi-Ridge	0.41	0.061	1.508	0.39	0.063	1.517
Pathway Lasso	0.55	0.046	0.133	0.56	0.047	0.141

Note: TPR: true positive rate at false discovery rate (FDR) = 0.10. MSE_nonnull: mean squared error for the indirect effects of active mediators. MSE_null: mean squared error for the indirect effects of inactive mediators. The results are based on 200 replicates for each setting. Bolded TPRs indicate the top two performers.

We note that the TPR results shown in the above tables represent the best selection performances one can achieve with the proposed methods, as we know the underlying true signals and can perfectly specify the 10% FDR thresholds. But that is not the case with real data applications. Therefore, we examine the empirical FDR estimates using (a) the local FDR approach⁴⁴ for a targeted 10% FDR (specifically, we sort the p local FDRs from all the mediators and find the cutoff value on the local FDRs to declare significance), (b) median PIP cutoff, and (c) 0.90 PIP cutoff, along with the corresponding TPR estimates. Detailed procedure and the empirical estimates, including the empirical FDRs for simulations in this section, are provided in the SI. Under the small sample scenarios (Table S1), the local FDR approach provides decent and well-controlled empirical FDR for both of the proposed methods, while the estimates by median PIP cutoff and 0.90 PIP cutoff tend to be either slightly overestimated or very conservative. Under the large sample scenarios (Table S2), the local FDR approach and median PIP cutoff still produces reasonable FDR estimates for GMM-CorrS across different settings and for GMM-Potts when neighbors reflect connected signals. However, including irrelevant neighbors in GMM-Potts could lead to increased false discoveries, and instead a more stringent 0.90 PIP cutoff may be used if one seeks a lower limit on the false discovery. Therefore in practice, we would recommend the local FDR and 0.90 PIP cutoff for reasonable FDR estimates and control, and we recognize the potential caveat concerning inflated FDR for GMM-Potts.

In addition to the above simulation scenarios, we also perform simulations where there is a single active mediator in each block. The simulation results are presented in Table S3. We find that the three GMM-based methods behave quite similarly to each other, and outperform the frequentist methods. Such pattern still holds when we use a different n/p ratio, for example, n = 100, p = 500 (see Table S4). Along with the selection and estimation performance, we report the computational cost for these two proposed methods in Table 5. For both the small sample scenario with n = 100, and the large sample scenario with n = 1000, the proposed algorithms can be finished in a reasonable amount of time. We do acknowledge that future development of new algorithms and/or new methods will likely be required to scale our methods to handle thousands of subjects and millions of mediators.

TABLE 5.

The average runtime of the proposed methods with (n, p) = (100, 200), (100, 500), and (1000, 2000)

Method	n = 100, p = 200	n = 100, p = 500	n = 1000, p = 2000
GMM-CorrS	3.5 min	0.97 h	9.8 h
GMM-Potts	2.2 min	0.44 h	4.0 h

Note: Comparison was carried out on a single core of Intel(R) Xeon(R) Platinum 8176 CPU @ 2.10GHz. For both proposed methods, we in total ran 150 000 iterations.

To summarize our findings from the simulations, GMM-CorrS takes the overall correlation structure among mediators directly into the modeling process, and shows excellent performance and robustness under different correlation structures. On the other hand, the performance of GMM-Potts is related to how well the prespecified neighborhood matrix reflects the underlying connection of active mediators. When the correlation-based neighboring relationship has good implication on similar mediation effects, GMM-Potts usually achieves the best selection and estimation accuracy. Its performance will likely get compromised by the inclusion of irrelevant neighbors.

5 |. DATA APPLICATION

In this section, we study two real data applications of the proposed methods: the LIFECODES birth cohort and the MESA cohort. These two data sets have different correlation strength among mediators and thus can serve to demonstrate the advantages of each of the proposed methods. Specifically, in the LIFECODES birth cohort, the biomarkers present a relatively clear correlation/neighborhood structure. We thus expect GMM-Potts model to work well based on our observation from simulations. On the other hand, the correlation structure in the MESA cohort is relatively weak. We thus expect a better performance from GMM-CorrS compared with GMM-Potts there.

5.1 |. The LIFECODES birth cohort

In this application, we consider a set of n = 161 pregnant women registered at the Brigham and Women’s Hospital in Boston, MA between 2006 and 2008. We are interested in the mediation mechanism linking environmental contaminant exposure during pregnancy to preterm birth through endogenous signaling molecules. Those endogenous biomarkers are derived from lipids, peptides, and DNA, and the lipids and peptide derived biomarkers were measured from subjects’ plasma samples, while the oxidative stress markers of DNA damage were measured from subjects’ urine samples. Both the urine and plasma specimens were collected at one study visit between 23.1 and 28.9 weeks gestation. We focus on p = 61 available endogenous biomarkers as potential mediators, including 51 eicosanoids, five oxidative stress biomarkers and five immunological biomarkers. The correlation structure across mediators are shown in Figure 1, and clear pattern with moderate to strong correlations can be observed. For the prenatal exposure to environmental toxicants, we focus the attention of this present study on one class of environmental contaminants, polycyclic aromatic hydrocarbons (PAHs). PAHs are a group of organic contaminants that form due to the incomplete combustion of hydrocarbons, and commonly present in tobacco smoke, smoked and grilled food products, polluted water and soil, and vehicle exhaust gas.⁴⁵ Previous studies have suggested association between PAH exposure and adverse birth outcomes.⁴⁶ Since the PAH class contains multiple chemical analytes in our study, we follow Aung et al⁷ to construct an environmental risk score for the PAH class and use that risk score as the exposure variable. The continuous birth outcome, gestational age, was recorded at delivery for each participant, and preterm is defined as delivery prior to 37 weeks gestation. Since the cohort is oversampled for preterm cases, we multiply the data by the case-control sampling weights to adjust for that. We log-transform all measurements of the exposure metabolites and endogenous biomarkers. We apply the proposed methods with the aforementioned exposure, mediator and outcome variables, controlling for age and maternal BMI from the initial visit, race, and urinary specific gravity levels in both regressions of the mediation analysis.

FIGURE 1.

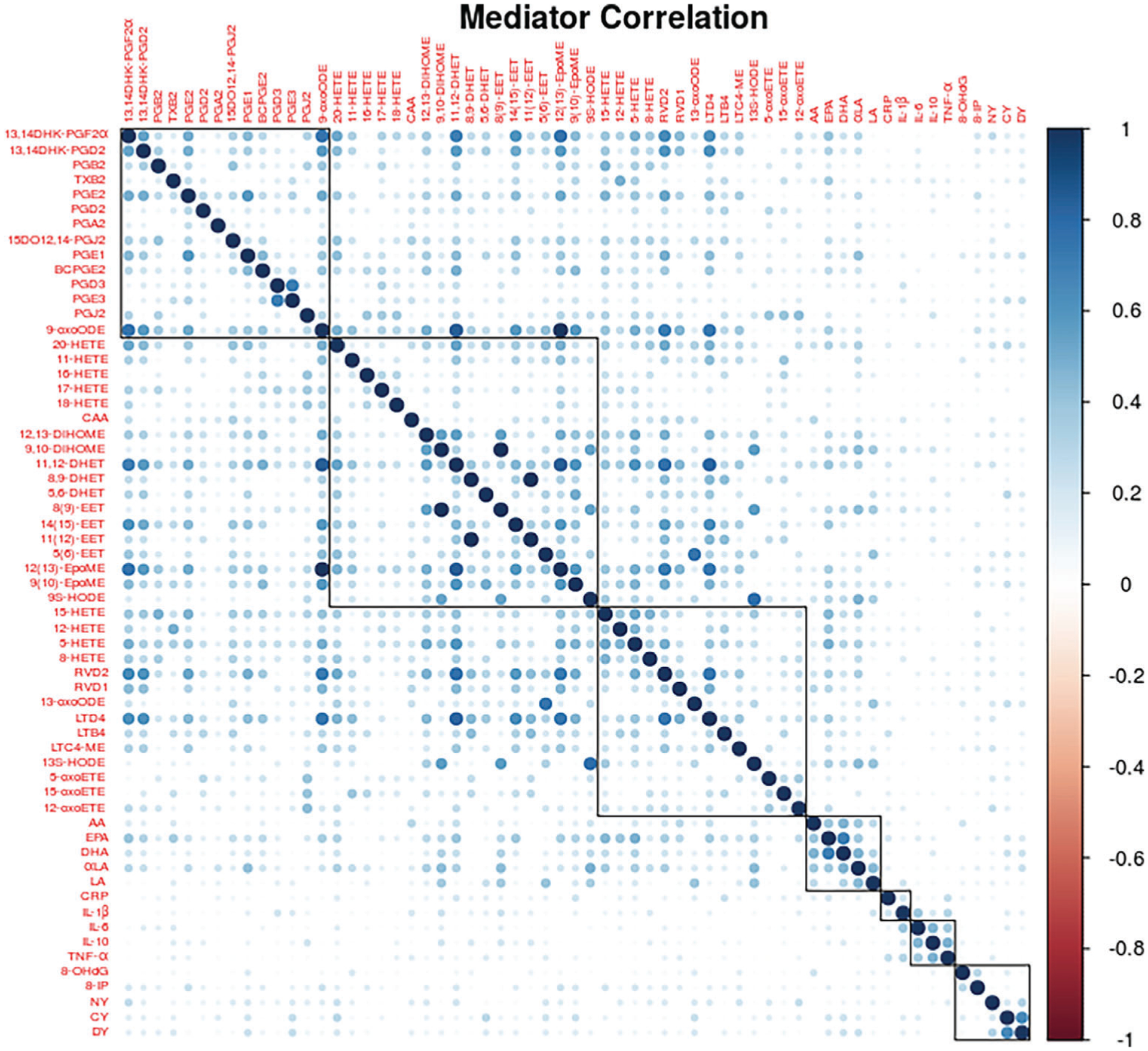
Correlations among biomarkers in LIFECODES birth cohort. The negative correlations (~37% of all the pairwise correlations) were replaced with their absolute values. The 61 biomarkers were grouped by literature derived biological pathways or processes (black lines)

The results are summarized in Table 6. Based on 10% FDR using the local FDR approach, GMM-Potts identifies four biomarkers for actively mediating the impact of PAH exposure on gestational age at delivery, 8,9-epoxy-eicosatrienoic acid (8(9)-EET), 9,10-dihydroxy-octadecenoic acid (9,10-DiHOME), 12,13-epoxy-octadecenoic acid (12(13)-EpoME), 9-oxooctadeca-dienoic acid (9-oxoODE), while both GMM-CorrS and GMM only identifies two of them, 8(9)-EET and 9,10-DiHOME. We also report the indirect effect estimates and their 95% credible intervals for selected mediators, and the direction of effects are consistent among different methods. Among the four biomarkers, 8(9)-EET, 9,10-DiHOME, and 12(13)-EpoME belong to the same Cytochrome p450 (CYP450) pathway, while 9-oxoODE is within cyclooxygenase (COX) pathway. CYP450 is a family of enzymes that function to metabolize environmental toxicants, drugs, and endogenous compounds,⁴⁷ and thus the PAH exposure may cause perturbations in the functions of these enzymes. It has also been suggested that the group of CYP450 metabolites as well as the related genes may play a role in the etiology of preterm delivery,⁴⁸ and the underlying mechanisms involve increased maternal oxidative stress and inflammation.⁴⁹ This evidence helps explain the potential mediating mechanism of CYP450 metabolites from PAH exposure to preterm delivery. Additionally, single biomarker analysis also demonstrated the protective effect of 12(13)-EpoME on preterm.⁵⁰ We also performed the posterior predictive checks on the outcome model for the three methods, in which the data generated from the posterior predictive distribution are compared with the observed outcome. We find the Bayesian predictive P-values⁵¹ of the GMM-Potts model are 0.72 and 0.48 for sample first and second moments, respectively, which are closest to 0.5 among the three methods and indicate the most adequate fit of the outcome model.

TABLE 6.

Summary of the identified active mediators from the data application on LIFECODES study based on 10% FDR with the local FDR approach

Method	Selected mediators	PIP	${\widehat{\beta }}_{\mathit{\text{mj}}}{\widehat{\alpha }}_{\mathit{\text{aj}}}$ (95% CI)
Polycyclic aromatic hydrocarbons → biomarkers → gestational age
GMM-Potts	12(13)-EpoME	0.99	0.419 (0.295, 0.579)
	8(9)-EET	0.98	0.368 (0.179, 0.567)
	9-oxoODE	0.97	−0.296 (−0.441, 0.000)
	9,10-DiHOME	0.87	−0.185 (−0.383, 0.000)

Note: Compared with GMM-CorrS and GMM, the GMM-Potts model achieves the most adequate fit of the outcome model based on posterior predictive check. The two additional findings from GMM-Potts are marked in blue. Besides the PIP, we also report the posterior estimates ${\widehat{\beta }}_{\mathit{\text{mj}}}{\widehat{\alpha }}_{\mathit{\text{aj}}}$ (ie, the marginal indirect contribution of the jth mediator to the joint NIE) and its 95% credible interval (CI).

Besides the estimated correlation structure, we also consider the input of biological pathway based structural information. That is, only mediators within the same literature derived biological pathway or process are treated as neighbors in GMM-Potts and have nonzero pairwise correlations in GMM-CorrS. The findings are shown in Table S7 of the SI. GMM-Potts identifies a subset of the above four biomarkers: 8(9)-EET, 9,10-DiHOME, and GMM-CorrS declares the other two biomarkers as active mediators: 12(13)-EpoME, 9-oxoODE. The overlapping lists of active mediators add confidence to our findings, and also reveal the fact that only adjusting for biological pathways may lose the correlated information between different pathways.

5.2 |. The MESA cohort

In this application, we study the mediation mechanism of DNAm in the pathway from neighborhood socioeconomic disadvantage to blood glucose. We focus on n = 1226 participants with no missing data, and a subset of p = 2000 CpG sites that have the strongest marginal associations with neighborhood disadvantage for computational reasons. As the exposure, neighborhood socioeconomic disadvantage evaluates the neighborhood social conditions from dimensions of education, occupation, income and wealth, poverty, employment, and housing. Previous literature has demonstrated the relationship between DNA methylation patterns and socially patterned stressors including low adult socioeconomic status (SES)⁵² and unfavorable neighborhood conditions.⁵³ It has also been long known that disadvantaged neighborhood conditions can lead to a variety of health problems, such as chronic psychological distress⁵⁴ and increased risk of cardiovascular disease.⁵⁵ The outcome, glucose, is one of the most important blood parameters and should be kept within a safe range in order to support vital body functions and reduce the risk of diabetes and heart disease.⁵⁶ Multiple evidence has supported the association between differential DNAm patterns and glucose metabolism.⁵⁷ However, the underlying molecular mechanisms that link neighborhood conditions to physical health profiles are not fully elucidated. To take a step forward, we apply the proposed methods for high-dimensional mediation analysis on DNAm. In the outcome model, we adjust for age, gender, race/ethnicity, childhood SES and adult SES (more details on the SES variables can be found at Smith et al⁵³). In the mediator model, we control for age, gender, race/ethnicity, childhood SES, adult SES, and enrichment scores for four major blood cell types (neutrophils, B cells, T cells, and natural killer cells) to account for potential contamination by nonmonocyte cell types. All the continuous variables are standardized to have zero mean and unit variance. In general, the correlation among DNAm in our study is relatively weak, and only 3% of DNAm pairs have correlation larger than 0.2.

The results can be found in Table 7. Because of the relatively ambiguous correlation structure observed across mediators in MESA, we do not expect big improvement from our methods. Indeed, the GMM-CorrS identifies one more CpG site as active mediators compared with GMM, and three other CpG sites are detected by both GMM-CorrS and GMM. The rank correlation for the mediator rank lists obtained from the two methods is 0.74, indicating the high consistency between them. The indirect effect estimates from the GMM-CorrS are also close to those from the GMM. The one additional finding of CpG site by GMM-CorrS, cg27090988, is close to the gene OGG1. This gene, which is involved in the repair of oxidative DNA damage, has been shown up-regulated in type 2 diabetic islet cell mitochondria, and studies have suggested a crucial role of oxidative DNA damage in the pathogenesis of type 2 diabetes (T2D).^58,59 We also examine the nearby genes to the other three jointly selected CpG sites. Among them, MYBPC3 is a known cardiomyopathy gene,⁶⁰ and the increased risk of cardiac hypertrophy and heart failure is likely to alter the glucose metabolism;⁶¹ the expression level of CD101, a protein involved in innate immunity, was found associated with T2D in a Mendelian randomization analysis.⁶² As shown in the simulations, GMM-Potts is not quite suitable for a weak correlation structure as in the MESA data, and the method does not identify any active mediators based on 10% FDR.

TABLE 7.

Summary of the identified active mediators from the data application on MESA study based on 10% FDR using the local FDR approach

Method	Selected mediators	Nearby genes	PIP	${\widehat{\beta }}_{\mathit{\text{mj}}}{\widehat{\alpha }}_{\mathit{\text{aj}}}$ (95% CI)
Neighborhood SES → biomarkers → glucose
GMM-CorrS	cg19515398	EIF2C2	0.97	−0.013 (−0.026, 0.000)
	cg04000940	MYBPC3	0.96	0.016 (0.000, 0.029)
	cg17907003	CD101	0.88	0.016 (0.000, 0.034)
	cg27090988	OGG1	0.84	−0.011 (−0.024, 0.000)

Note: We include the nearby gene, PIP, the posterior estimates ${\widehat{\beta }}_{\mathit{\text{mj}}}{\widehat{\alpha }}_{\mathit{\text{aj}}}$ (ie, the marginal indirect contribution of the jth mediator to the joint NIE) and its 95% credible interval (CI) for each selected CpG site. The one additional finding from GMM-CorrS is marked in blue. The GMM-Potts does not identify any active mediators based on 10% FDR.

6 |. DISCUSSION

In this article, we present two hierarchical Bayesian approaches to incorporating the correlation structure across mediators in high-dimensional mediation analysis: (1) through a logistic normal for mixing probabilities (GMM-CorrS), or (2) through a Potts distribution on the group indicators (GMM-Potts). The consequent “nonseparable” priors of both methods inform the grouping and selection of correlated mediators under the composite structure of mediation. The simulation studies show that utilizing the correlation pattern in active mediators, the proposed methods greatly enhance the selection and estimation accuracy over the methods that do not account for such correlation, and maintain decent and comparable performance under no obvious or misspecified correlation structure. In addition, the analysis on the LIFECODES birth cohort and MESA cohort indicates that our methods can promote the detection of new active mediators, which may have important implications on future research in targeted interventions for preterm birth and diabetes.

Between the two proposed methods, GMM-CorrS shows excellent performance and robustness under different correlation structures, while the performance of GMM-Potts is relatively heavily dependent on how well the prespecified neighborhood matrix reflects the underlying connection among active mediators. In particular, when the correlation-based neighborhood matrix captures the main correlation structure and has good predictive power on the correlated mediation effects, GMM-Potts usually achieves the best selection and estimation accuracy. Therefore, in data analysis, we would recommend using the GMM-Potts when one is confident that the prespecified neighborhood matrix well captures the clustering pattern of active mediators, or when there are relatively strong domain knowledge on such mediator grouping structure. If that is not the case, then it would be safer to start from GMM-CorrS. There are several limitations of the proposed methods. First, for GMM-CorrS, it requires the inversion of a p × p matrix in each iteration of the sampling algorithm, and as p increases to the scale of hundreds of thousands, that step could become the computational bottleneck of the method. Techniques on matrix approximation or fast parallel matrix inversion will be required to speed up the computing time and reduce the memory footprint. Second, for GMM-Potts, smoothing over arbitrary or inaccurately specified neighbors may have a negative effect on its performance, and this can be further improved by imposing adaptive weight for each neighbor to reflect their relative importance. Moreover, the method can be extended to allow for simultaneous inference of both the active mediators and the neighborhood/network structure linking them. In that way, the neighborhood/network structure among mediators does not need to be known a priori. It can also be easily extended to more than two groups by introducing group-specific parameters θ_0k and θ_1k in the Potts distribution. This will facilitate the needs for multiple mediator groups.

As promising directions for future work, we note that there may be other ways to incorporate mediators’ correlation into the modeling process. Recently, testing the multivariate mediation effects from groups of potential mediators has received growing attention,⁶³ and the variance component tests developed by Huang²⁷ can naturally take into account the correlation within groups. Other frequentist extensions involving a sparse group Lasso type method by treating β_mj and α_aj as a group is also worth developing in the future. Also, Bobb et al⁶⁴ develop a Bayesian kernel machine regression to incorporate the structure of the multipollutant mixtures into the hierarchical model. Those methodologies may provide insightful perspective to applying correlation kernels under the global testing setup in the context of high-dimensional mediation analysis.

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available upon request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.