A Bottom-up Approach to Testing Hypotheses That Have a Branching Tree Dependence Structure, with Error Rate Control

Abstract

Modern statistical analyses often involve testing large numbers of hypotheses. In many situations, these hypotheses may have an underlying tree structure that both helps determine the order that tests should be conducted but also imposes a dependency between tests that must be accounted for. Our motivating example comes from testing the association between a trait of interest and groups of microbes that have been organized into operational taxonomic units (OTUs) or amplicon sequence variants (ASVs). Given p-values from association tests for each individual OTU or ASV, we would like to know if we can declare a certain species, genus, or higher taxonomic group to be associated with the trait. For this problem, a bottom-up testing algorithm that starts at the lowest level of the tree (OTUs or ASVs) and proceeds upward through successively higher taxonomic groupings (species, genus, family etc.) is required. We develop such a bottom-up testing algorithm that controls a novel error rate that we call the false selection rate. By simulation, we also show that our approach is better at finding driver taxa, the highest level taxa below which there are dense association signals. We illustrate our approach using data from a study of the microbiome among patients with ulcerative colitis and healthy controls.

1. Introduction

Many large-scale hypothesis testing problems in biology have a branching tree structure. For example, Yekutieli (2008) considered tests of genetic linkage in which a genome-wide test was first applied; if this test was significant, tests for linkage on each chromosome were considered. If any chromosome showed evidence of linkage, the p and q arms were tested, and so on. In this example, the genome-wide test is at the “top” of a tree with a branching structure. The next level is comprised of chromosome-level tests, and moving down the tree corresponds to increasing localization of the linkage signal. For this example, the “top-down” strategy that Yekutieli (2008) used is a natural choice. The null hypothesis being tested at each node in the tree is the “global” null hypothesis that none of the tests below this node are significant.

Some problems are not well suited to the top-down approach. Our motivating example is the 16S rRNA microbiome study, where bacterial sequences are typically grouped into operational taxonomic units (OTUs) or assigned to amplicon sequence variants (ASVs). Then, the association between each OTU or ASV and a trait of interest is calculated (for simplicity, we use the term OTU to refer generically to either ASVs, OTUs, or any other bacterial feature that is used to classify bacteria hierarchically). Typically, many OTUs will belong to the same species. After testing association between each OTU and a trait, we may wish to determine if any species of microbes are associated with the trait; this is a reasonable strategy as bacteria in the same species typically have similar properties (i.e., thrive in the same environment or produce similar lipids). Depending on our findings, we may then wish to test larger groups corresponding to successively higher taxonomic ranks (i.e., genus, family, order, class, phylum, and kingdom). The natural ordering of hypotheses in this example starts at the bottom of the tree and proceeds upward. Further, it may be desirable to continue to test hypotheses at higher levels of the tree even if no findings have been made at a lower level, since an accumulation of weak signals from lower levels may coalesce into a detectable signal at a higher level. The scientific questions of interest thus motivate development of a bottom-up approach to testing tree-structured hypotheses.

A second example of a situation where bottom-up testing may be appropriate arises in studies of the association between genes and a trait or disease outcome. We may be interested in testing whether groupings of genes that are mapped to gene ontology (GO) terms in a common pathway are significantly associated with the trait or disease outcome under study. In particular, we may use data from the GO project to construct a tree of ontology terms, in which each node comprises a list of genes and the child nodes of a parent node are a mutually-exclusive partition of the genes in the parent node. The root node of such a tree might be a single GO term such as “immune response”. Using the p-values from tests of association between the trait of interest and the genes included in this tree, we can first test for significant association at the gene level, then move up through the tree testing whether gene groupings dictated by the GO hierarchy show evidence of association, while controlling a single error rate. This approach is particularly attractive for secondary analyses of publicly-available data, as we may only have available p-values at a set of SNPs or polymorphic loci. We note this application is distinct from the usual enrichment test for GO terms.

The false discovery rate (FDR) has largely replaced the family-wise error rate to control the error made when testing many hypotheses. Benjamini and Hochberg (1995) proposed a simple way to to control the FDR when testing independent hypotheses, which extends easily to hypotheses having positive regression dependence (Benjamini and Yekutieli, 2001). However, an adjustment to the Benjamini and Hochberg procedure to allow arbitrary dependence between tests (Benjamini and Yekutieli, 2001) is very conservative in most settings. For this reason, testing procedures that control FDR for specific patterns of dependence have been investigated (Storey et al., 2004; Qiu et al., 2005; Efron, 2007; Sun and Cai, 2009; Fan et al., 2012).

A number of testing procedures have been proposed for tree-structured hypotheses. In addition to the top-down approach of Yekutieli (2008), Meinshausen (2008) and Rosenbaum (2008) developed a similar top-down approach but aimed at controlling the family-wise error rate. Benjamini and Heller (2007),Heller et al. (2018), and Benjamini and Bogomolov (2014) also developed top-down approaches but limited to two-level tree structures. Motivated by the microbiome example, our goal is to develop a procedure for testing tree-structured hypotheses that controls an appropriate error rate like the FDR, but that proceeds in a bottom-up fashion.

For a bottom-up testing strategy, the “global” null hypothesis may not be appropriate. We return to the microbiome example. When considering if we should declare a certain node (say, a genus) to be associated with the trait we are studying, we adopt the following approach: if a large proportion of species from that genus influence the trait, we should conclude the genus influences the trait. Conversely if only a few of the species from a genus are non-null, then a better description of the microbes that influence occurrence of the trait is a list of associated species. Finding taxa that can be said to influence a trait in this sense is the first goal of our approach. The second goal is to locate the highest taxa in the tree for which we can conclude many taxa below, but not any ancestors above, influence risk; we refer to such taxa as driver taxa. In the genetic association example, a driver node would correspond to the set of genes in the highest-level GO term that shows evidence of association. Note that these goals are incommensurate with the “global” null hypothesis, which stipulate that a node is associated if any node below it is associated.

The rest of this paper is organized as follows. In Section 2, we propose a modified null hypothesis for bottom-up testing that adjusts for selection decisions at lower levels of tree. We further develop an error criterion we call the false selection rate (FSR) that corresponds to this modified null hypothesis, and propose an algorithm for assessing the significance of association between taxonomic units (or, more generally, nodes in the tree) and a trait under study that controls the FSR. In Section 3, we compare our proposed methods with existing methods using simulated data. In Section 4, we apply our new methods to data on the human gut microbiome from a study of inflammatory bowel disease (IBD), and detect driver taxa that are associated with ulcerative colitis (UC). Section 5 contains a discussion of our results and some possible future directions implied by our work.

2. Methods

2.1. Preliminaries

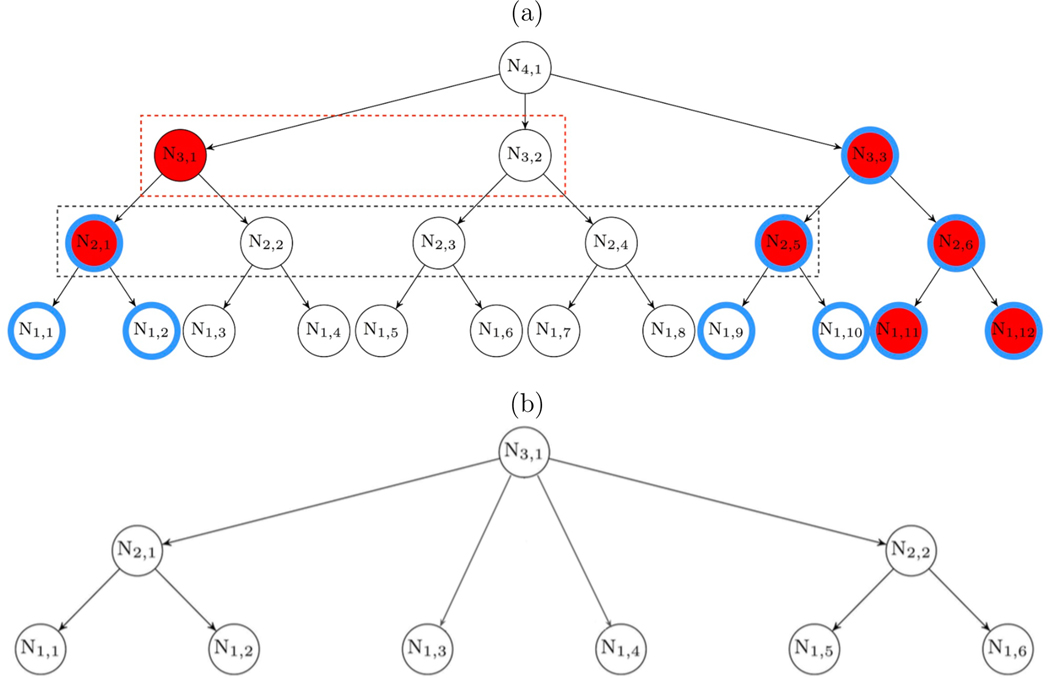
The hypotheses we test form the nodes of a branching tree; here, we review the terminology we use. The root node is the “top” of the tree; while we focus on trees with one root node, our method can be readily extended to handle trees with multiple root nodes as discussed in the Discussion section. For any two nodes that are directly connected, the node closest to (furthest from) the root is the parent (child ) node. The set of child nodes of a parent are its offspring. A node is an inner node if it has at least one child node; otherwise it is a leaf node. The ancestors of a node are all the nodes traversed in a path from that node to the root. The descendants of a node are all nodes having that node as an ancestor. A subtree is a tree rooted at an inner node of the full tree, comprised of the subtree root and all its descendants. For example, in Figure 1(a), the tree rooted at N_3,1 that includes inner nodes N_3,1, N_2,1, N_2,2, and leaf nodes N_1,1, N_1,2, N_1,3, N_1,4 is a subtree of the full tree. Because each node corresponds to a hypothesis, we will sometimes refer to testing a node as shorthand for testing the hypothesis at that node. We will refer to a node at which we have rejected the null hypothesis as a detected node, and a detected node is a driver node if none of its ancestors are detected.

Figure 1:

(a) A hypothetical example of a set of hypotheses having a dependence structure corresponding to a complete tree. Nodes are labeled by level (first subscript) and then numbered within level (second subscript). Nodes highlighted with blue circles are truly associated. A node colored red indicates it is detected (declared to be associated with the trait of interest by a testing method). With the bottom-up methods, all nodes at the bottom level are tested at level 1, nodes inside the black box are tested at level 2, and nodes inside the red box are tested at level 3. (b) A hypothetical example illustrating an incomplete tree. In this example, it makes scientific sense to assign nodes N_1,3 and N_1,4 to level 1 even though they have a different depth than the other leaf nodes. For example, these two nodes could correspond to OTUs that are missing a species assignment but share a genus with the other leaf nodes.

The depth of a node is the number of edges between that node and the root node. We use the term level to describe sets of nodes that will be tested together. In the simplest case such as in Figure 1 (a), nodes that have the same depth are assigned to the same level; we call such a tree complete. For incomplete trees such as that shown in Figure 1 (b), level is assigned by the investigator and does not necessarily correspond to depth. For example, in a phylogenetic (taxonomic) tree, level typically corresponds to the taxonomic rank (species, genus, etc.); a phylogenetic tree is then incomplete when the leaf nodes (OTUs) have missing taxonomic assignment below a certain level.

2.2. A Bottom-Up Procedure for Complete Trees

Our first inferential goal is to detect all nodes in the tree (e.g., taxa for the microbiome example) that are associated with a trait of interest. Our second goal is to locate any driver nodes. We assume that p-values for the association tests at all leaf nodes are available, and propose a method to calculate p-values for inner nodes in Section 2.2.5. We wish to avoid declaring a node to be associated solely because a few offspring nodes are strongly associated; thus we restrict claims of association to nodes in which most offspring are associated. For this goal, the global null hypothesis, which specifies a node is associated if even one offspring node is associated, is not appropriate. The conjunction null hypothesis (Price and Friston, 1997) that a node is only associated if all offspring nodes are associated is worth considering; however, tests of the conjunction null hypothesis are known to be conservative in many situations, as the p-value is determined by selecting the largest p-value from the p-values at each offspring, and then comparing the selected p-value to the uniform distribution on [0, 1] (Friston et al., 2005). However, it does easily lead to a bottom-up procedure; after propagating the largest p-value from offspring nodes to their parent nodes, nodes are then detected using the standard BH (Benjamini and Hochberg, 1995) procedure. We report results from this procedure even though we do not recommend it, due to its low power.

2.1.1. Modified null hypothesis

We aim to develop a bottom-up procedure that avoids the low power of testing the conjunction null hypothesis, but still finds taxa for which most offspring are associated. We notice that a parent node may be detected as significantly associated using an omnibus test of offspring association if even a single offspring has a strong-enough association. To avoid such cases, we propose to test a modified null hypothesis that among the offspring that have not been previously detected at a lower level, none are associated, against the alternative that some previously-undetected offspring are associated. The modified null hypothesis is intermediate between the global and conjunction null hypotheses: a node will only be found to be associated if the association signal from many offspring together imply association for the parent (like the conjunction null) but the way the association signal from previously-undetected nodes is combined is like a test of the global null hypothesis.

To illustrate the modified null, consider the hypothetical example in Figure 1 (a). Nodes highlighted with blue circles are truly associated; N_2,1 and N_3,3 are driver taxa. Although N_3,1 is associated under the global null hypothesis because N_1,1 and N_1,2 are its descendants, we would prefer to conclude that N_2,1 rather than N_3,1 explains the association signal among the descendants of N_3,1 because half of the descendants of N_3,1 are not truly associated. This is achieved by using the modified null hypothesis; N_3,1 is not associated under the modified null hypothesis, because N_2,1 has been detected and N_2,2 is not associated.

2.2.2. Weights to account for multiplicity

The modified null hypothesis has another important implication: the testing at one level may decide hypotheses at one or more higher levels. This occurs when all offspring of a parent node are detected, in which case the parent node is not tested but automatically detected. For example, since both offspring of N_2,6 in Figure 1(a) are detected, we should immediately conclude that N_2,6 is associated. Similarly, having already detected N_2,6, if we determine that N_2,5 is associated, then N_3,3 would have no undetected offspring and should be determined to be associated as well.

The difficulty with including both such offspring and their parent in the detection list is that an incorrect decision on a single node can result in multiple false decisions. To resolve this, we introduce weights ω_l,j that count the number of detections that could arise when testing node N_l,j. Consider the example shown in Figure 1 (a). Assume at level 1, nodes N_1,11 and N_1,12 have been detected. Then, at level 2, the remaining nodes to be tested are N_2,1–N_2,5 (inside the black box). Suppose p-values for these nodes are calculated as described in Section 2.2.5. We consider testing nodes at each level in ascending order of p-values and for now assume p_2,1 < p_2,2 < p_2,3 < p_2,4 < p_2,5. Rejecting the modified null hypothesis at N_2,1 only detects N_2,1; rejecting the null at N_2,2 will detect N_2,2 and N_3,1 (2 nodes); rejecting the null at N_2,3 will detect N_2,3; rejecting the null at N_2,4 will detect N_2,4 and N_3,2 (2 nodes); rejecting the null at N_2,5 will detect N_2,5, N_3,3, and N_4,1 (3 nodes). Thus, for this ordering, we define the weights (ω_2,1, ω_2,2, ω_2,3, ω_2,4, ω_2,5) = (1, 2, 1, 2, 3). Now, suppose instead that the p-values were ordered as p_2,5 < p_2,1 < p_2,2 < p_2,3 < p_2,4; then the weights would be (ω_2,5, ω_2,1, ω_2,2, ω_2,3, ω_2,4) = (2, 1, 2, 1, 3). Although these weights are different, the sorted weights (ω_2,(1), ω_2,(2), ω_2,(3), ω_2,(4), ω_2,(5)) = (1, 1, 2, 2, 3) are the same. Thus, the (unsorted) weights (ω_l,1, ω_l,2,..., ${\omega }_{l,n_l^{*}}$) depend on the p-values at level l and are thus random (even conditional on the detection events below level l). However, we show in Appendix A.1 that, for complete trees, the sorted weights ω_l,(1) ≤ ω_l,(2) ≤ ... ≤ ${\omega }_{l,(n_l^{*})}$ are unique regardless of the ordering of p-values.

2.2.3. FSR

When we use the modified null to determine the true association status, we must introduce a novel error rate, which we call the false selection rate (FSR). We use the term FSR rather than modified FDR because the “selection” of nodes as being associated or not is influenced by decisions made at lower levels, so that our procedure has the same spirit as “forward selection” in the field of variable selection. We reserve the term “discovery” as in the FDR for situations where decisions are based on a test statistic that is calculated for each node without regard to decisions at other nodes. In fact, the term FSR has been used by Wu et al. (2007) in variable selection to describe the proportion of uninformative variables included in a selected model. Wu et al. (2007) tune the selection procedure to control the FSR, although the problems they consider do not have a tree structure and they require the introduction of pseudovariables to achieve FSR control. To formally define the FSR, let R_l,j indicate the jth node at level l (i.e., node N_l,j) is detected, i.e.

$$R_{l,j}=\mathbb{I}\left(\text{node}{N}_{l,j}isdetected\right),$$

where $\mathbb{I}$(.) is the indicator function. Let ${\mathcal{U}}_{l,j}$ denote the set of undetected offspring of the jth node on level l = 2,..., L; note that at the bottom level ${\mathcal{U}}_{1,j}=\varnothing$. For those nodes where ${\mathcal{U}}_{l,j}\ne \varnothing$ (for which we actually conduct a test of the modified null hypothesis), we define $V_{l,j}^m$ to indicate a false selection:

$$V_{l,j}^m=\mathbb{I}\left(R_{l,j}=1\text{but the}modified\text{null hypothesis at node}{N}_{l,j}\text{is true given}{\mathcal{U}}_{l,j}\right).$$

Assuming a tree with L levels that has n_l (l = 1, 2,...,L) nodes at level l, among which we order the nodes such that the first $n_l^{*}$ nodes have undetected offspring, the FSR under the modified null hypothesis is given by

$$\text{FSR}=\mathbb{E}\left[\frac{{\sum }_{l=1}^L{\sum }_{j=1}^{n_l^{*}}{\omega }_{l,j}{V}_{l,j}^m}{\left({\sum }_{l=1}^L{\sum }_{j=1}^{n_l^{*}}{\omega }_{l,j}{R}_{l,j}\right)\vee 1}\right],$$ (1)

where the weights ω_l,j are as defined in section 2.2.2. Note that in (1) the value of $V_{l,j}^m$ is only required at nodes that are actually tested $\left({\mathcal{U}}_{l,j}\ne \varnothing \right)$, not nodes that are detected because all their offspring are detected $\left({\mathcal{U}}_{l,j}=\varnothing \right)$. For the latter nodes, if we let $V_{l,j}^m$ be equal to the value of $V_{l^{*},j^{*}}^m$ where (l^*, j^*) is the node whose detection resulted in detection of node (l, j), then we can rewrite the FSR in (1) as

$$\text{FSR}=\mathbb{E}\left[\frac{{\sum }_{l=1}^L{\sum }_{j=1}^{n_l}{V}_{l,j}^m}{\left({\sum }_{l=1}^L{\sum }_{j=1}^{n_l}{R}_{l,j}\right)\vee 1}\right].$$ (2)

We distinguish the FSR from the FDR, for which we use the global null hypothesis to determine true association status, and the FDRc, for which we use the conjunction null. We define $V_{l,j}^g\text{and}{V}_{l,j}^c$ to indicate a false discovery was made under the global null and conjunction null, respectively so that $V_{l,j}^g=\mathbb{I}(R_{l,j}=1$ but the global null hypothesis at node N_l,j is true). and $V_{l,j}^c=\mathbb{I}(R_{l,j}=1$ but the conjunction null hypothesis at node N_l,j is true). The FDR and FDRc each take the form of (2) but with $V_{l,j}^m$ replaced by $V_{l,j}^g$ or $V_{l,j}^c$, respectively. Note that if the global null hypothesis at N_l,j is true, then the modified null hypothesis at N_l,j is true, which in turn implies the conjunction null hypothesis at N_l,j is true. Thus, $V_{l,j}^g\le V_{l,j}^m\le V_{l,j}^c$ holds at every node, which in turn implies that the three error rates FSR, FDR and FDRc are related by

$$\text{FDR}\le \text{FSR}\le \text{FDRc}.$$

This implies that controlling FSR is a more stringent criterion than controlling FDR, and so a testing procedure that controls the FSR will automatically control the FDR. However, controlling FSR does not guarantee control of FDRc. We return to this issue in section 2.2.5 when we select a test statistic to test the modified null hypothesis so as to make the FSR similar to the FDRc.

2.2.4. Testing procedure

We now construct a testing procedure that tests the nodes in the tree level by level, starting at level l = 1. For each level l = 1,...,L, our testing procedures consist of two elements: a set of thresholds to determine which nodes are detected at level l, and a way of aggregating the p-values from the undetected nodes at level l to give p-values for nodes that have undetected offspring; discussion of the actual statistic used for aggregating the p-values is deferred to Section 2.2.5. Our goal is to control the error rate so that the FSR ≤ q. In analogy with the concept of alpha spending in interim analysis (Demets and Lan, 1994), we allocate to each level l a target level q_l (l = 1, 2,..., L) chosen so that ${\sum }_{l=1}^L{q}_l=q$. We note here that we do not guarantee the FSR at each level is controlled at level q_l, just that the overall FSR is controlled at level q. Without prior knowledge on which level the driver nodes might be located, we recommend q_l = qn_l/n, which assumes that all nodes in the tree have equal importance. We show later that this partitioning scheme achieved the most robust performance in detecting driver nodes via a sensitivity analysis over simulated data.

We now describe how to assign p-value thresholds to control FSR. Without loss of generality, assume the p-values for nodes that have undetected offspring at level l, p_l,1, p_l,2,..., $p_{l,n_l^{*}}$, have been sorted in ascending order, and let the sorted values be denoted by $p_{l,(1)}\le p_{l,(2)}\le \cdots \le p_{l,\left(n_l^{*}\right)}$. Let $d_l^{*}$ denote the (as yet unknown) number of nodes detected at level l. We seek a set of ascending thresholds ${\alpha }_{l,1}\le {\alpha }_{l,2}\le \cdots \le {\alpha }_{l,n_l^{*}}$ by which we reject the modified null hypothesis at $d_l^{*}>0$ nodes (corresponding to $p_{l,(1)}\le {\alpha }_{l,1},p_{l,(2)}\le {\alpha }_{l,2},\dots ,p_{l,\left(d_l^{*}\right)}\le {\alpha }_{l,d_l^{*}}$ but $p_{l,\left(d_l^{*}+1\right)}>{\alpha }_{l,d_l^{*}+1}$; we accept the modified null hypothesis at all nodes in level $l\text{if}{p}_{l,(1)}>{\alpha }_{l,1}$ in which case we take $d_l^{*}=0$, or reject the modified null hypotheses at all nodes in level l if $p_{l,(1)}\le {\alpha }_{l,1},p_{l,(2)}\le {\alpha }_{l,2},\dots ,p_{l,\left(n_l^{*}\right)}\le {\alpha }_{l,n_l^{*}}$ in which case we take $d_l^{*}=n_l^{*}$. We adopt the thresholds {α_l,j} given by

$$\frac{{\alpha }_{l,j}}{1-{\alpha }_{l,j}}=\left(\frac{D_{l-1}+{\sum }_{k=1}^j{\omega }_{l,(k)}}{{\sum }_{k=j}^{n_l^{*}}{\omega }_{l,(k)}}\times q_l\right)\mathrm{\Lambda }\frac{{\tau }_0}{1-{\tau }_0}.$$ (3)

where $D_{l-1}={\sum }_{l^{\prime }=1}^{l-1}{\sum }_{j=1}^{n_{l^{\prime }}^{*}}{\omega }_{l^{\prime },j}{R}_{l^{\prime },j}$ for l ≥ 2 is the cumulative number of detections made up to and including the (l − 1)th level as well as their ancestors that are automatically detected, D₀ = 0, and τ₀ is a pre-specified constant to prevent nodes with large p-values from being detected (if a large number, say m, of null hypotheses can be easily rejected because of very low p-values, then q × m nodes with large p-values can be said to be detected, while still controlling the overall error rate at level q); we set τ₀ = 0.5, so we do not detect nodes with p-values ≥ 0.5, which are treated as null hypotheses as in Storey (2002). At each level, the thresholds (3) are a variant of the thresholds in the step-down test proposed by Gavrilov et al. (2009), which have been used to control FDR in some applications as they have been shown to be more powerful than the standard BH procedure. Theorem 1 asserts that our bottom-up procedure with thresholds (3) control the FSR at q.

Theorem 1.

Assume the three conditions hold: (C1) nodes on the same level have the same depth; (C2) p-values for null nodes follow the uniform distribution U[0, 1]; (C3) at each level, the p-value for a null node is independent of the p-values at all other nodes. Then the bottom-up procedure with thresholds (3) ensures that the FSR ≤ q.

The proof of this theorem is provided in Appendix A.2. Condition (C1) assumes a complete tree, and will be relaxed in Section 2.3. Conditions (C2) and (C3) at inner (parent) nodes can be satisfied by our proposal below for obtaining p-values for inner nodes, which is based on Conditions (C2) and (C3) at leaf nodes.

2.2.5. Calculating p-values for inner nodes

There are two ways to imagine calculating p-values for inner nodes in a bottom-up testing algorithm for tree-structured hypotheses. In the first approach, p-values for inner nodes are determined entirely from the p-values of their offspring (and hence, are determined by the p-values at leaf nodes). In the second approach, p-values for inner nodes are calculated by applying a test statistic to pooled data (e.g., aggregating read count data from OTUs to higher-level taxa as in Tang et al. (2016)). The second approach may lose statistical power as pooling data may result in effects being cancelled out if some offspring nodes are protective while others increase risk. More importantly, it is hard to know how to condition the distribution of a test statistic of a parent node that uses pooled data from offspring nodes on the results of tests of data from the constituent offspring nodes. For these reasons, we seek an algorithm that operates entirely on the p-values of the leaf nodes.

We consider how to aggregate the p-values from level l that correspond to the undetected offspring of a parent node at level l + 1. Recall that ${\mathcal{U}}_{l+1,j}$ denotes the set of undetected offspring nodes for the parent node N_l+1,j and ${\mathcal{U}}_{l+1,j}\ne \varnothing \text{for}j=1,\dots ,n_{l+1}^{*}$. Note that the p-values of the undetected nodes at level l necessarily exceed the threshold ${\alpha }_{l,d_l^{*}+1}$, and are hence not uniformly distributed on the interval [0, 1]. However, since this is the only restriction on these p-values, it follows that, under either the global or modified null hypothesis, the p-values for nodes that were not detected at level l are uniformly distributed on the interval $\left[{\alpha }_{l,d_l^{*}+1},1\right]$; equivalently, adjusted p-values $p_{l,k}^{\prime }=\left(p_{l,k}-{\alpha }_{l,d_l^{*}+1}\right)/\left(1-{\alpha }_{l,d_l^{*}+1}\right)$ are uniformly distributed on the interval [0, 1]. To combine the adjusted p-values, we use Stouffer’s Z score:

$$Z_{l+1,j}=\frac{1}{\sqrt{\left|{\mathcal{U}}_{l+1,j}\right|}}\sum _{k\in {\mathcal{U}}_{l+1,j}}{\mathrm{\Phi }}^{-1}\left(1-p_{l,k}^{\prime }\right),$$ (4)

where Φ is the standard normal cumulative distribution function and $\left|{\mathcal{U}}_{l+1,j}\right|$ represents the cardinality of ${\mathcal{U}}_{l+1,j}$. The $Z_{l+1,j}$ calculated using the undetected null nodes in ${\mathcal{U}}_{l+1,j}$ follows a standard normal distribution N (0, 1) under the modified null hypothesis conditional on the pattern of detection at level l and Conditions (C2) and (C3) at level l. Thus, $p_{l+1,j}=1-\mathrm{\Phi }\left(Z_{l+1,j}\right)$; in addition, p_l+1,j and p_l+1,j′ are independent since, on any tree, ${\mathcal{U}}_{l+1,j}\cap {\mathcal{U}}_{l+1,j^{\prime }}=\varnothing$ as each undetected node at level l is a member of exactly one of the sets ${\mathcal{U}}_{l+1,j}$. We use Stouffer’s Z-score as it is known to be powerful when small or moderate non-null effects appear in the majority of individual tests as opposed to Fisher’s method, which is powerful when only a few large non-null effects are present (Loughin, 2004). Our simulation also indicated that using Stouffer’s Z-score gives a better control of FDRc than using Fisher’s method (the results based on Fisher’s method not shown).

2.2.6. The algorithm

We summarize the proposed procedure in the following algorithm.

• (Input) p-values at the leaf nodes (level l = 1)

• (Step 1) At level l, determine which nodes are detected using thresholds α_l,j (3).

• (Step 2) At level l + 1, for nodes that have undetected offspring, aggregate these offspring p-values into a Z score using (4) and convert it into a p-value

• (Ascend) Iterate between steps 1 and 2 until we reach the root node of the tree

• (Output) A list of detected nodes and a list of driver nodes

2.3. Incomplete Trees

In Section 2.2, we only considered complete trees where nodes on the same level all have the same depth. Here we consider more general trees where depth and level do not coincide. For example, in the tree from Figure 1 (b), nodes N_1,3 and N_1,4 have different depth from the other leaf nodes, although they are all on the same level. In the microbiome example, this would occur whenever some of the lower taxonomic ranks (e.g., species and genus) of an OTU are not known. We describe here how our approach can be extended to incomplete trees.

For an incomplete tree, the sorted weights (ω_l,(1), ω_l,(2),..., ${\omega }_{l,\left(n_l^{*}\right)}$) depend on the ordering of p-values. In Figure 1 (b), when N_1,6 has the largest p-value among all leaf nodes, for example, p_1,1 < p_1,2 < p_1,3 < p_1,4 < p_1,5 < p_1,6, the weights are (ω_1,1, ω_1,2, ω_1,3, ω_1,4, ω_1,5, ω_1,6) = (1, 2, 1, 1, 1, 3) and the sorted weights are (1, 1, 1, 1, 2, 3); if N_1,4 has the largest p-value, for example, p_1,1 < p_1,2 < p_1,5 < p_1,6 < p_1,3 < p_1,4, the weights are (ω_1,1, ω_1,2, ω_1,5, ω_1,6, ω_1,3, ω_1,4) = (1, 2, 1, 2, 1, 2) and the sorted weights are (1, 1, 1, 2, 2, 2). To account for this ambiguity, we seek a single set of sorted weights that will control FSR for any possible ordering of p-values.

For the two sets of weights just considered, note that the cumulative sums of sorted weights ${\sum }_{k=1}^j{\omega }_{l,(k)}$ for the first set, given by (1, 2, 3, 4, 6, 9) are element-wise less than or equal to the cumulative sums of the sorted weights of the second set, given by (1, 2, 3, 5, 7, 9). Thus, if we were to use the first set of ordered weights in (4), the thresholds α_l,j would be smaller (i.e., more stringent) than the thresholds calculated using the second set of sorted weights. As a result, using the first set of ordered weights would allow us to control the FSR for either of the two orderings of p-values. Using the recursive algorithm we describe in Appendix A.3, we can show that the first set of weights in this example do in fact guarantee FSR control for any ordering of p-values. In general, this algorithm finds the set of sorted weights ${\tilde{\omega }}_{l,(1)}\le \cdots \le {\tilde{\omega }}_{l,\left(n_l^{*}\right)}$ for level l that correspond to weights obtained by some “least favorable” ordering of p-values and satisfy the inequalities

$$\sum _{k=1}^j{\tilde{\omega }}_{l,(k)}\le \sum _{k=1}^j{\omega }_{l,(k)},j=1,\dots ,n_l^{*},$$

for all possible sets of sorted weights $\left({\omega }_{l,(1)},\dots ,{\omega }_{l,\left(n_l^{*}\right)}\right)$ induced by different orderings of p-values. Because the weights corresponding to the “least favorable” ordering of p-values result in the most stringent thresholds among all possible weights {ω_l,(k)}, we call them the “least favorable weights”. Note that these weights are needed to ensure the control of FSR for any ordering of p-values and no other weights can provide such a guarantee, as we can never completely rule out that the “least favorable” ordering corresponds to the true ordering. We then adopt thresholds calculated using $\left\{{\tilde{\omega }}_{l,(k)}\right\}$, given by

$$\frac{{\alpha }_{l,j}}{1-{\alpha }_{l,j}}=\left(\frac{D_{l-1}+{\sum }_{k=1}^j{\tilde{\omega }}_{l,(k)}}{{\sum }_{k=j}^{n_l^{*}}{\tilde{\omega }}_{l,(k)}}\times q_l\right)\mathrm{\Lambda }\frac{{\tau }_0}{1-{\tau }_0}.$$ (5)

Theorem 2 ensures control of the FSR using the least favorable weights.

Theorem 2.

Under Conditions (C2) and (C3) in Theorem 1, the bottom-up procedure with thresholds (5) ensures the FSR defined in (1) is ≤ q.

The proof of Theorem 2 can be found in Appendix A.4. When a tree is complete, the least favorable weights reduce to the unique sorted weights regardless of the ordering of p-values. Thus the testing procedure presented here encompasses the one presented in Section 2.2 as a special case. To implement this procedure, we simply modify the algorithm in Section 2.2.6 by replacing the thresholds given in (3) by the thresholds given in (5).

Finally, we dismiss two alternative approaches for handling incomplete trees. One approach would be to fill in the missing levels with unique ancestors for each node. For example, each OTU having class as the lowest known taxonomic classification would be assigned its own (unknown) species and (unknown) genus. This is unsatisfactory both scientifically, as we then assert that the “correct” species and genus for this OTU is different from any other OTU, and statistically, as the p-value for the species and genus level tests are necessarily identical to the p-value for the OTU. Another possible solution is to place each leaf node at the level just below the nearest inner nodes. However, this strategy can still be unsatisfactory for applications such as the microbiome, as it is scientifically questionable to treat some OTUs at the same level as higher taxa such as families.

2.4. Separate FSR Control

The testing procedures we have described so far assume that we wish to detect nodes at all levels of the tree while controlling the overall FSR at some rate q. In some situations we may want to have separate FSR control at lower-level nodes and higher-level nodes. For example, we may wish to first determine which OTUs are detected while controlling FSR at some rate q₁; then we may wish to conduct a second, separate analysis of taxa starting at the species level and continuing up the phylogenetic tree, while controlling the FSR of the second analysis at some rate q₋₁.

The procedures presented in Sections 2.2 and 2.3 do not guarantee that the FSR at each level l is controlled at q_l (except for level 1 which always has FSR controlled at q₁) because of the cumulative effect of D_l−1 in (3) and (5), which creates a dependence between the nodes detected at each level. If we break this dependence by re-starting the counter D_l−1 at some level, it is then possible to separately control FSR below and above the level. We describe such an algorithm in Appendix A.5 and illustrate its use in Section 4 where we show an analysis that controls both FSR at the OTU level and FSR among taxonomic groups from species to phylum. In principle, the approach could be used to divide the nodes into more than two groups, simply by re-zeroing the counter in D_l−1 at the appropriate levels.

3. Simulation Studies

We conducted simulation studies to assess the performance of our bottom-up tests, and to compare with three competing approaches: (1) the naïve approach that calculates the p-value for an inner node by using Stouffer’s Z-score to aggregate the p-values from all leaf nodes that are its descendants, then applies the BH procedure on the collection of p-values from all nodes; (2) the top-down approach of Yekutieli (2008) as implemented in the R package structSSI (Sankaran and Holmes, 2014), with p-values for inner nodes calculated in the same way as in the naïve approach; and (3) the conjunction-null test that assigns a p-value to an inner node by the largest p-value from all offspring nodes (equivalently, the largest p-value from all corresponding leaf nodes) and applies the BH procedure as in the naïve approach. All methods take p-values at leaf nodes as input. The nominal level for all error rates was set to 10%.

To simulate p-values at leaf nodes, we first selected a number of inner or leaf nodes to be driver nodes and assumed that all offspring of driver nodes (including all its leaf nodes) were associated with the trait of interest. We independently sampled p-values for associated leaf nodes from distributions that have enriched probability at values close to zero. We used the Beta distribution Beta(1/β, 1) where β > 1, which has a relatively heavy right tail (Figure S1) and mimics the empirical distributions of p-values observed in the IBD data (Figure S2). To assess the robustness of our results, we also considered sampling p-values from a Gaussian-tailed model (i.e., first drawing a value X ∼ N (β, 1) and then obtaining the p-value p = 1 − Φ(X), where Φ is the standard normal cumulative distribution function), which has frequently been used to study the performance of FDR procedures (Storey, 2002; Barber and Ramdas, 2017; Javanmard et al., 2018) and which has a smaller right tail (Figure S1). In both models, β characterizes the overall association strength (e.g., effect size of the trait on the microbiome). For all simulations we assumed that all leaf nodes that were not descendants of driver nodes were null with p-values sampled independently from the U[0, 1] distribution.

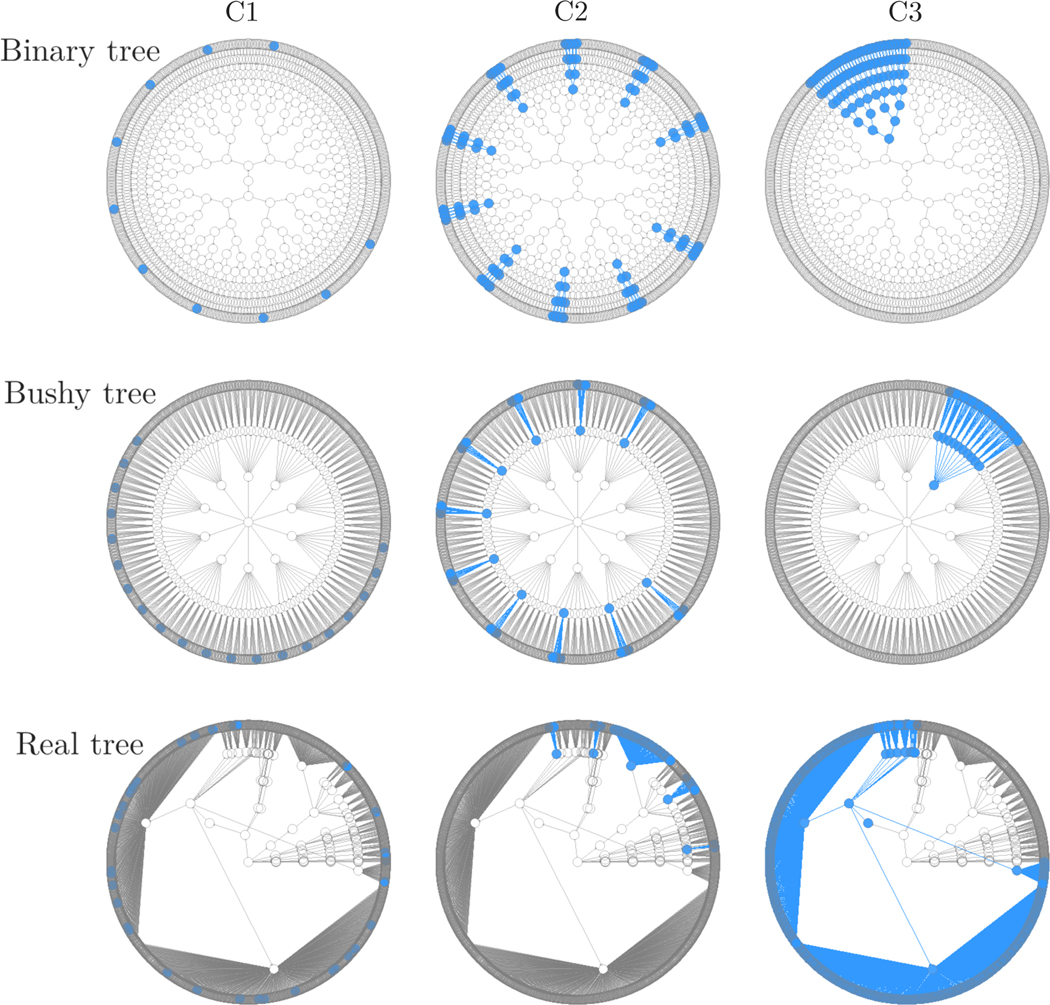
We considered three tree structures, shown in Figure 2. The first is a complete binary tree with 2 children for each inner node and 10 levels, which has 1023 nodes of which 512 are leaves. The second is a complete “bushy” tree with 10 children for each inner node and 4 levels, which has 1111 nodes of which 1000 are leaves. The third is a real phylogenetic tree for the inflammatory bowel syndrome data (Halfvarson et al., 2017) that we analyze in Section 4. This tree has 8 levels, 249 inner nodes, and 2360 leaf nodes, with large variation in the number of child nodes at different inner nodes. It is incomplete, having extensive (> 50%) missing assignments at the genus and species levels, and a few at the family level.

Figure 2:

The three tree structures (binary, bushy, and real) and three causal patterns (C1, C2, and C3) for simulation studies. The real phylogenetic tree structure was obtained from the IBD data and, for simplicity of exposition, skipped the genus and species levels which have extensive missing assignments. The root node is always located at the center of each tree and the leaf nodes are represented by the outermost ring. The top of each blue subtree is a designated driver node, which can be an inner or leaf node.

For each tree structure, we then considered three causal patterns, differentiated by the level of the selected driver nodes (Figure 2). The first pattern (C1) is characterized by sparse driver nodes located at the leaf nodes; the second (C2) by several driver nodes located at an intermediate level, chosen so that ∼10% of leaf nodes were associated; and the third (C3) by a single driver node at a higher level, inducing association with a large subtree. In particular, for C1 we randomly selected 10/20/36 leaf nodes for the binary/bushy/real trees. For C2, we randomly chosen 10 out of 64 nodes at level 4 for the binary tree, 10 out of 100 nodes at level 2 for the bushy tree, and 5 out of 48 nodes at the family level (level 4) for the real tree. For C3, we randomly picked one node at level 7 for the binary tree, one node at level 3 for the bushy tree and, for the real tree, the class Clostridia from level 6 (covering ∼80% of all leaf nodes). Each of the 3 × 3 = 9 scenarios was replicated 1000 times.

3.1. Error Rates

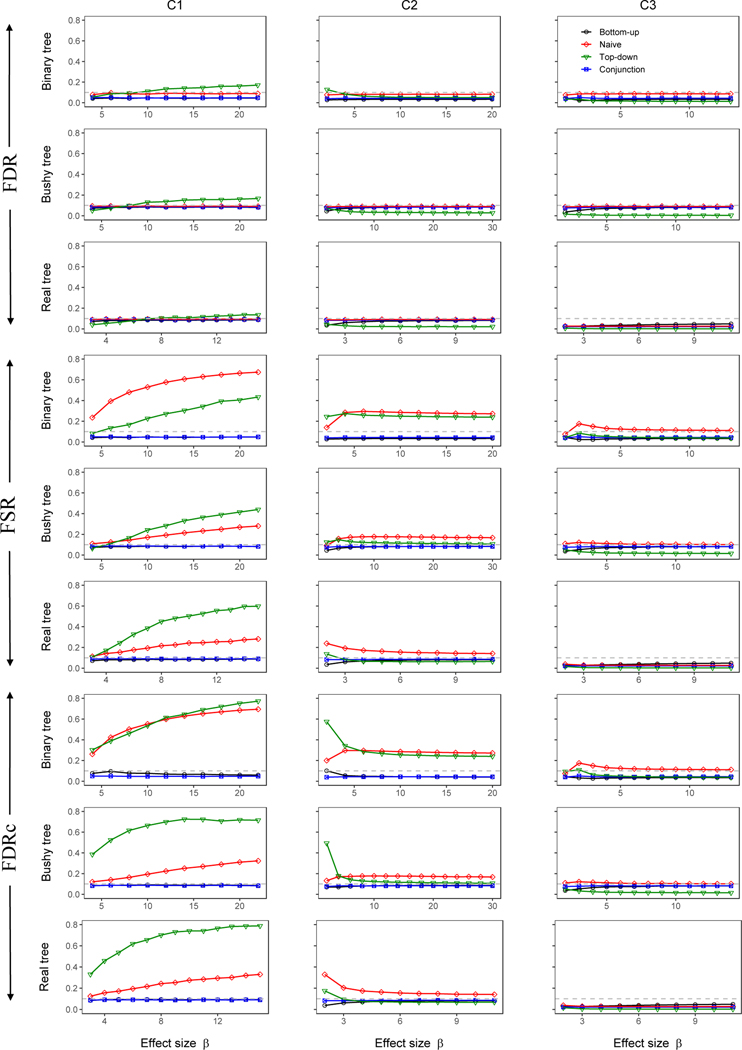
Direct comparison of the methods we consider is complicated by the fact that each method was designed to control a different error rate. In particular, the bottom-up test was designed to control FSR (under the modified null), the naive and top-down approaches control FDR (under the global null), and the conjunction-null test control FDRc (under the conjunction null). For this reason, we evaluated each approach by the error rate they were designed to control, but also examined their performance in controlling other types of error rates. The FSR of the top-down and naïve approaches were calculated by using the list of detected nodes (as determined by Benjamini and Hochberg (1995) for the naïve method and Yekutieli (2008) for the top-down method), then proceeding level by level as if these detections were the result of tests of the modified null hypothesis. The FSR was then calculated using the definition (1).

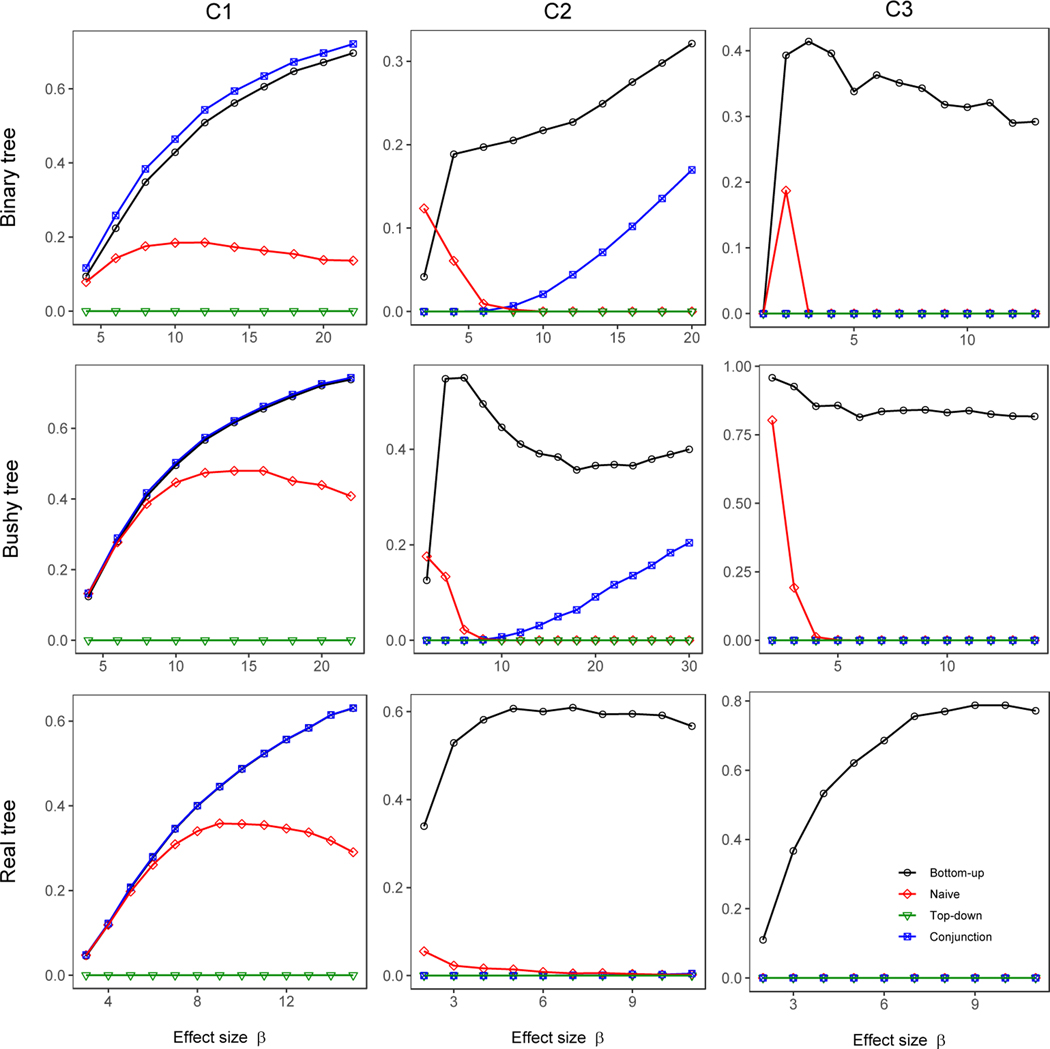
Figure 3 displays these results for the nine (= 3 × 3) scenarios we considered, for the simulations that used the Beta distribution for non-null leaves. In all 9 scenarios our bottom-up method always controlled FSR. In contrast, the naïve and top-down methods typically had inflated FSR, with the most severe inflation occurring in C1, where the driver nodes were simulated exclusively at leaf nodes, causing many higher-level nodes to be falsely detected by these methods. As expected, our method also controlled FDR; in fact, the FDR is only less than the FSR for at most 5% across all simulation scenarios, indicating that our control of the FSR is not very conservative compared to the FDR control. The top-down method, although designed to control FDR, still yielded slightly inflated FDR occasionally; this is likely due to violation of the independence assumption between the p-value at a node and the p-values of all its ancestors, which is required by the top-down method (Yekutieli, 2008). The naïve method always controlled FDR because the BH procedure is known to be robust to such positive correlations. Despite a lack of theoretical results, we found that our bottom-up method controlled FDRc well in all scenarios we considered. The naïve and top-down methods typically had inflated FDRc, and FDRc for these methods resembled their FSR, consistent with the notion that FSR approximates FDRc. The conjunction-null test controlled all error rates, as expected. Figure S3 shows the same patterns of FSR, FDR, and FDRc for simulations based on the Gaussian-tailed model.

Figure 3:

Error rates for testing all nodes in the tree. The non-null p-values at leaf nodes were simulated from a Beta(1/β, 1) distribution.

3.2. Accuracy and Pinpointing Driver Nodes

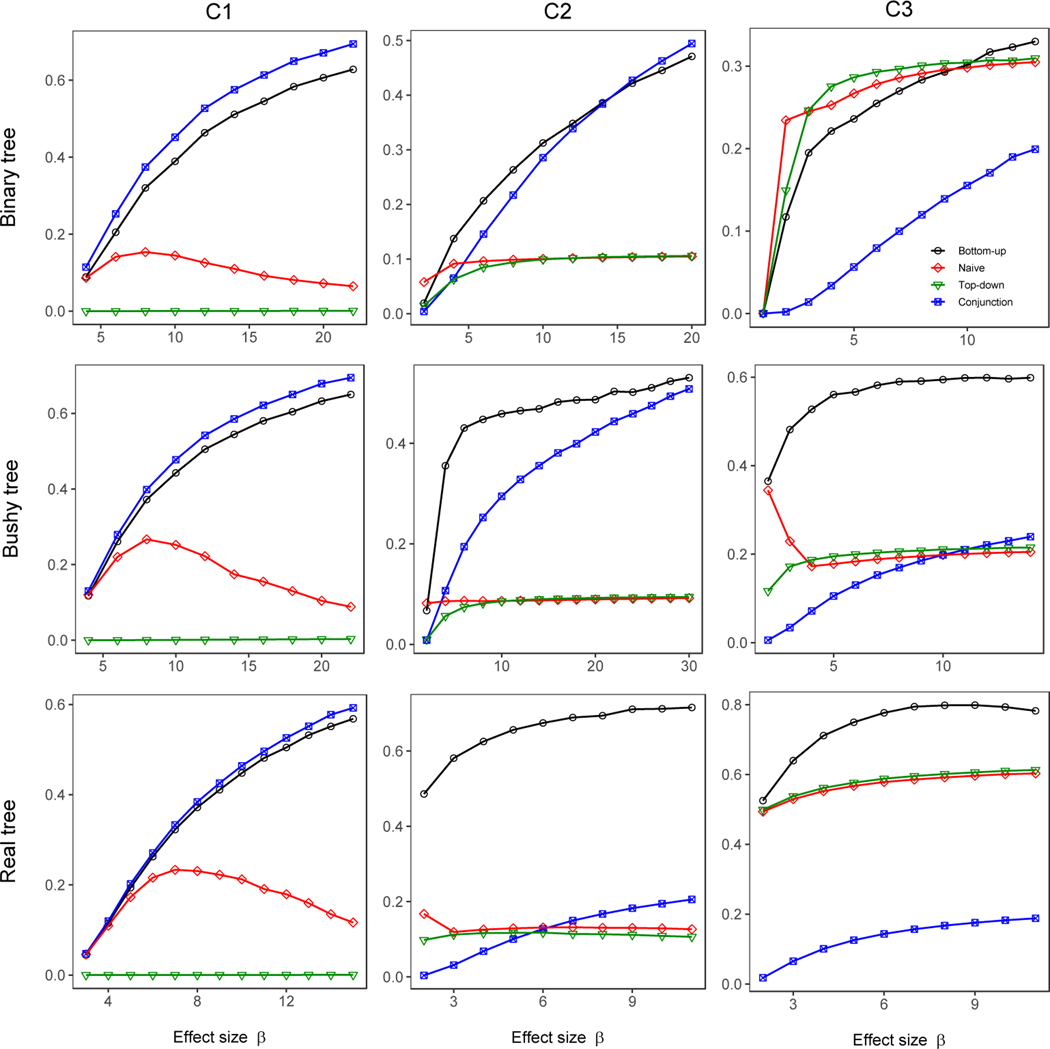
As our simulations were conducted under the conjunction null hypothesis, the driver nodes and all of its descendants are the truly associated nodes. We measured the accuracy of detected nodes against truly associated nodes by calculating a Jaccard similarity between the two sets. We used a weighted Jaccard similarity to account for the branching-tree topology of the hypotheses we test, because detecting a node with offspring implies the offspring are detected in some sense, even if they were not individually detected. For example, identifying a genus as being associated with the trait of interest implies the species and OTUs that belong to this genus are associated, even if we did not detect them (and hence are not included in the list of detected nodes). For this reason, we calculated the Jaccard similarity by weighting each node by the number of leaf nodes that are its descendants. The weighted Jaccard similarity is then the sum of the weights of correctly-detected nodes, divided by the total weight assigned to either detected or truly associated nodes.

Examining Figure 4 we see that the bottom-up approach has the best or second-best accuracy in all cases we examined, making it the best overall choice. The test of the conjunction hypothesis slightly outperforms our bottom-up test when only leaf nodes are truly associated (causal pattern C1). As soon as inner nodes are truly associated, as in C2 and C3, the conjunction-null test becomes very conservative. The bottom-up approach performed best for C2 and C3 except for the binary tree in C3, where the naïve and top-down approaches performed better at low parameter values. When considering these results, it should also be noted the naïve method (but not the top-down method) had elevated FSR and FDRc for this simulation.

Figure 4:

Accuracy (weighted Jaccard similarity) of detected nodes against truly associated nodes (including the driver nodes and all of their descendants at all levels). The non-null p-values at leaf nodes were simulated from a Beta(1/β, 1) distribution.

Our method is most different from existing methods in their ability to pinpoint driver nodes. We say a driver node is “pinpointed” if it is detected to be associated and none of its ancestors are detected. We evaluated the percentage of driver nodes that were pinpointed and showed the results in Figures 5 and S5. Our bottom-up method detected many more driver nodes than the naïve, top-down, and conjunction-null methods. The naïve method pinpointed some driver nodes when the association signals were weak, but inevitably detected their ancestors as the signals became stronger. By design, the top-down method always fails to pinpoint any driver nodes since it only tests nodes below the root node if the root node is detected. Note that the percentage of driver nodes pinpointed by our method sometimes decreased as the effect size increased, because more (but not all) descendants were detected and removed from the statistic for the driver nodes, which thus aggregated less information. For the Beta-based simulations, undetected driver nodes remained a possibility regardless of the effect size, as the Beta distribution always generates a non-negligible portion of p-values that were close to one even when the effect size was extremely large. For the Gaussian-tailed simulation, all driver nodes were eventually detected, as large p-values became more infrequent as the effect size increased. We note that the conjunction-null test can easily fail to detect higher-level nodes (including driver nodes) when some offspring of these nodes have large p-values, as in our Beta-based simulations.

Figure 5:

Percentage of driver nodes that were pinpointed. The non-null p-values at leaf nodes were simulated from a Beta(1/β, 1) distribution.

We partitioned the total error rate q into q₁,..., q_L in proportion to the number of nodes at each level. Because this choice is somewhat arbitrary, we have also done a sensitivity analysis comparing the ability to pinpoint driver nodes (Figure S6) of the “default” option just described with a number of alternatives. In the limited simulations we performed, we found that the optimal partition was likely determined by the true causal pattern. In particular, increasing q_l at the bottom level would identify more driver nodes in C1; and increasing q_l at high levels would identify more driver nodes in C2. However, in C3 using either the bushy tree or the real tree, our default option outperformed the alternatives that assign more weight at high levels. Overall, our default partition achieved the most robust performance in detecting driver nodes over all scenarios that we have considered here.

4. Inflammatory Bowel Disease (IBD) Data

IBD is a chronic disease accompanied by inflammation in the human gut. The two most common subtypes are ulcerative colitis (UC) and Crohn’s disease. Halfvarson et al. (2017) investigated the longitudinal dynamics of the microbial community in an IBD cohort of 60 subjects with UC and 9 healthy controls. The microbial community was profiled by sequencing the V4 region of the 16S rRNA gene. Sequence data were processed into an OTU table through the QIIME pipeline. Our goal was to identify taxa that have differential abundance between the UC and control groups at baseline.

We removed OTUs that were present in fewer than 10 samples and dropped 4 OTUs that failed to be assigned any taxonomy. The assigned taxonomy grouped the 2360 OTUs into 249 taxonomic categories (i.e., inner nodes) corresponding to kingdom, phylum, class, order, family, genus, and species levels. Note that 15.2%, 56.9%, and 91.3% OTUs have missing assignment at the family, genus, and species level, respectively. As there were no obvious confounders provided with these data, we used the Wilcoxon rank-sum test to compare the OTU relative abundances between case and control groups to obtain p-values for each OTU.

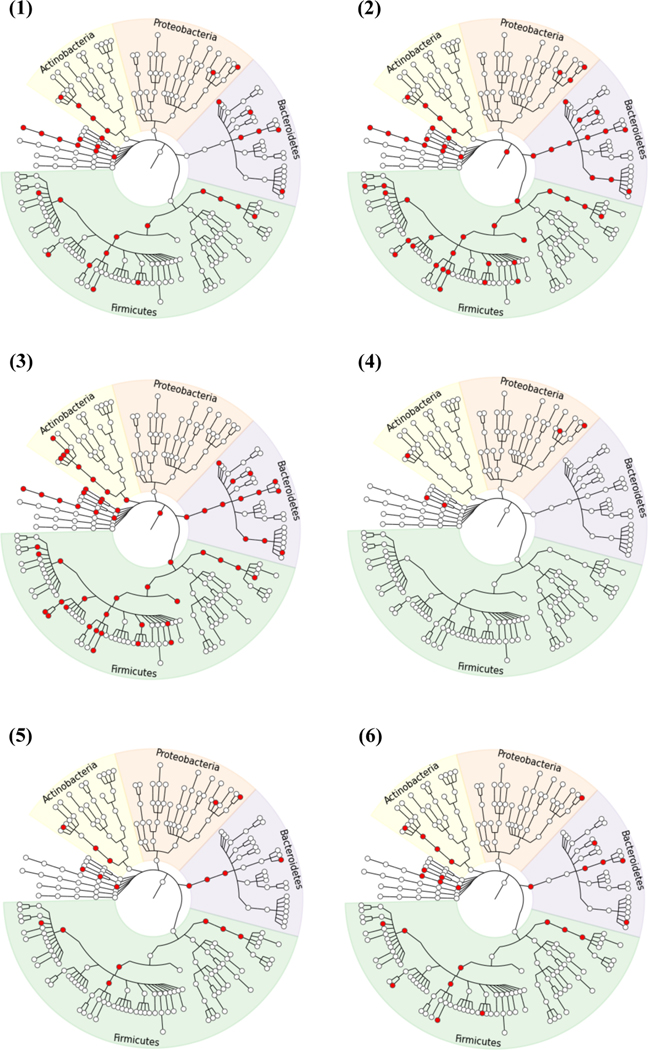
We applied the (one-stage) bottom-up test with nominal FSR of 10% as well as the naïve and top-down methods with nominal FDR of 10%. The detected taxa can be visualized in Figure 6. The bottom-up test identified 127 OTUs, 6 species, 9 genera, 7 families, 5 orders, 6 classes, and 1 phylum. We inferred that the driver taxa were: phylum Verrucomicrobia; classes Chloroplast, Clostridia, Coriobacteriia, Erysipelotrichi and RF3; families Prevotellaceae and S24–7; genera Morganella and [Prevotella]; and species ovatus and radicincitans; see Table S1 for more details. In contrast, both the naïve and top-down methods identified the root node and many taxa at high levels, suggesting their inability to pinpoint the real driver taxa. In addition, the top-down method did not detect some lower-level taxa in phylum Proteobacteria that were detected by all other methods. The conjunction-null test detected 142 OTUs but only 5 taxa, each of which contained a single OTU. All these results are consistent with the findings of our simulation studies.

Figure 6:

Taxa (marked in red) detected to be differentially abundant between the UC and control groups in the IBD data by (1) the one-stage bottom-up test, (2) the naive method, (3) the top-down method, (4) the conjunction-null test, (5) the two-stage bottom-up test with nominal FSRs 9.046% and 0.954% for OTUs and taxa, and (6) the two-stage bottom-up test with nominal FSRs 5% and 5% for OTUs and taxa. The levels from the center outward are kingdom, phylum, class, order, family, genus and species. The OTU level is supposed to be located at the outermost layer and has been omitted to simplify the figure. The plots were generated using GraPhlAn (http://huttenhower.sph.harvard.edu/graphlan).

The bottom-up results in the previous paragraph controls the FSR of all discoveries at 10%, as well as the FSR of the discoveries made at the lowest (OTU) level, which is always controlled at level q₁ in our approach. For the IBD data, our default choice for q₁ is 10% × (2360/2609) = 9.046% for the discoveries at the OTU level, which also include 1 species, 2 genera, 1 order, and 1 class, each of which has a single descendent OTU that was detected. Since the one-stage procedure was used, we cannot conclude that the remaining taxon discoveries are controlled with FSR of 10% − 9.046% = 0.954%. However, if we apply the two-stage approach we can separately control these FSRs at 9.046% and 0.954%; the results at the OTU level are unchanged, but at stage 2 we now detect 1 species, 1 genus, 3 families, 4 orders, 3 classes and 2 phyla; note the cost of separate control of the stage-2 FSR resulted in detection of 15 fewer taxa. Nevertheless, the detected driver taxa (phyla Bacteroidetes and Verrucomicrobia, classes Chloroplast, Coriobacteriia and Erysipelotrichi, order Clostridiales, genus Morganella, and species radicincitans) largely overlapped with those by the one-stage procedure.

The assignment of over 90% of FSR to the OTU level may be questionable if we want to use the two-stage approach to control FSR for OTUs and higher taxa. Thus, we also applied the two-stage bottom-up test that splits the overall FSR 10% into 5% and 5% for OTU and taxon analyses. At stage 1, we detected 79 OTUs, as well as 1 species, 1 genus, 1 order, and 1 class because they each have only one OTU which was detected; among these OTUs and taxa we can declare we control FSR at 5%. At stage 2, we detected 4 species, 4 genera, 5 families, 4 orders, 3 classes, and 2 phyla, among which we can declare we control FSR at 5%. Interestingly, the list of driver taxa was identical to that obtained by the previous two-stage approach except for the absence of genus Morganella.

5. Discussion

In this work, we presented a bottom-up approach to testing hypotheses that have a branching tree dependence structure. Our procedure tests hypotheses in a tree level by level, starting from the bottom and moving up, rather than starting from the top and moving down. Our analysis is novel in several respects. First, we developed a novel modified null hypothesis, which is more suitable for our goal of detecting nodes in which a dense set of child nodes are associated with the trait of interest, and have developed a stepwise procedure that ensures rigorous control of an error rate for all hypotheses that are tested. Second, we have recognized that the bottom-up testing approach for tree-structured hypotheses is intrinsically more like a model selection problem than a simultaneous testing problem; this has motivated us to propose control of the FSR rather than the more standard FDR. It is interesting to see that techniques like FSR control, developed for model selection, are required for a problem that involves only structured hypothesis testing. Our simulation studies confirmed the control of FSR and demonstrated good performance of our method compared to existing methods using a measure of accuracy based on a weighted Jaccard similarity. Further, our bottom-up method is more successful at pinpointing driver nodes, offering highly interpretable results, while the existing methods frequently fail at this task. Finally, although our method was not designed to control FDRc, our simulations showed that use of Stouffer’s Z score to combine information leads to approximate control of FDRc as well.

Our method can easily be extended to very general tree structures. We can easily handle trees in which the leaf nodes are not all at level 1. With some modifications, our method can also be applied to trees with multiple (correlated) root nodes such as trees generated by pathways, by using our bottom-up testing procedure up to the level right below the root level and applying to the root level the standard BH procedure, which is robust to positive correlations. We expect this modified procedure to control FSR (and hence FDR and, approximately, FDRc).

Although our approach is very general, it does have some limitations that could benefit from further development. First, we treated p-values at leaf nodes with equal weight. In some applications, different leaf nodes may have varying importance and may be weighted differently. Second, it may be of interest to consider alternative partitioning of the total FSR that can improve performance at pre-specified levels of particular importance if, for example, finding genera that were associated with a trait was of particular interest. Further, we assumed independence between null leaf nodes because it is required by both Stouffer’s method for combining p-values and the step-down procedure for controlling the error rate of decisions. To ensure this condition, pruning can be used to restrict analysis to a subset of leaf nodes that are nearly independent. We have also explored through simulation studies that our method may still control FSR when there are weak dependencies among null leaf nodes (Figure S7). However, we found that strong dependencies tend to lead to inflated FSR. In such cases, it is possible to extend our method to account for arbitrary dependencies using the Cauchy combination test for combining p-values (Liu and Xie, 2019; Liu et al., 2019).

Our methods have been implemented in the R package. Our program is extremely computationally efficient. For example, for the one-stage bottom-up procedure on the IBD data, it took 1.3 seconds on a laptop with a 2.5 GHz Intel Core i7 processor and 8 GB RAM.